1

1

U

U

og

og

ó

ó

lnione wsp

lnione wsp

ó

ó

ł

ł

rz

rz

ę

ę

dne dla uk

dne dla uk

ł

ł

ad

ad

ó

ó

w

w

elektromechanicznych

elektromechanicznych

L.p.

Wielkość

Współrz.

Układ mechaniczny

Układ elektryczny

Uogólniona Ruch

postępowy

Ruch
obrotowy

Pojemność Indukcyjn.

1

Współrzędna

q

k

x

k

ϕ

k

Q

k

Ψ

k

2

Prędkość

3

Pęd

p

k

m

k

v

k

J

k

Ω

k

Ψ

k

=

ΣL

ki

i

ki

Q

k

=Cu

k

4

Siła
wewnętrzna

f

k

-k

k

x

k

-k

k

ϕ

k

-u

Ck

-i

Ck

5

Wymuszenie

G

k

F

k

(t)

M

k

(t)

U

k

(t)

i

k

(t)

dt

dq

v

k

k

=

dt

dx

v

k

k

=

dt

dQ

i

k

k

=

dt

d

u

k

k

Ψ

=

dt

d

k

k

ϕ

=

Ω

2

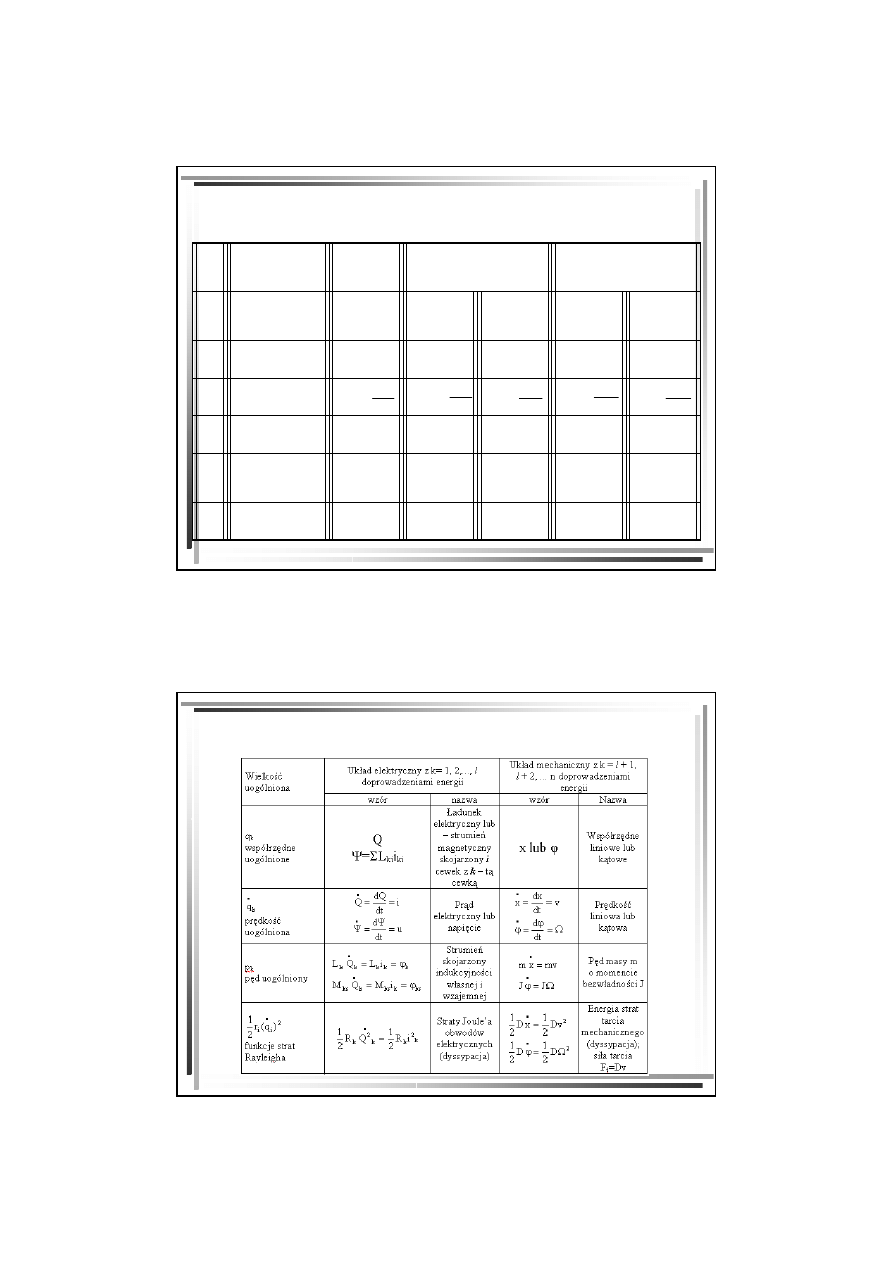
Wielkości układów elektrycznych i mechanicznych

2

3

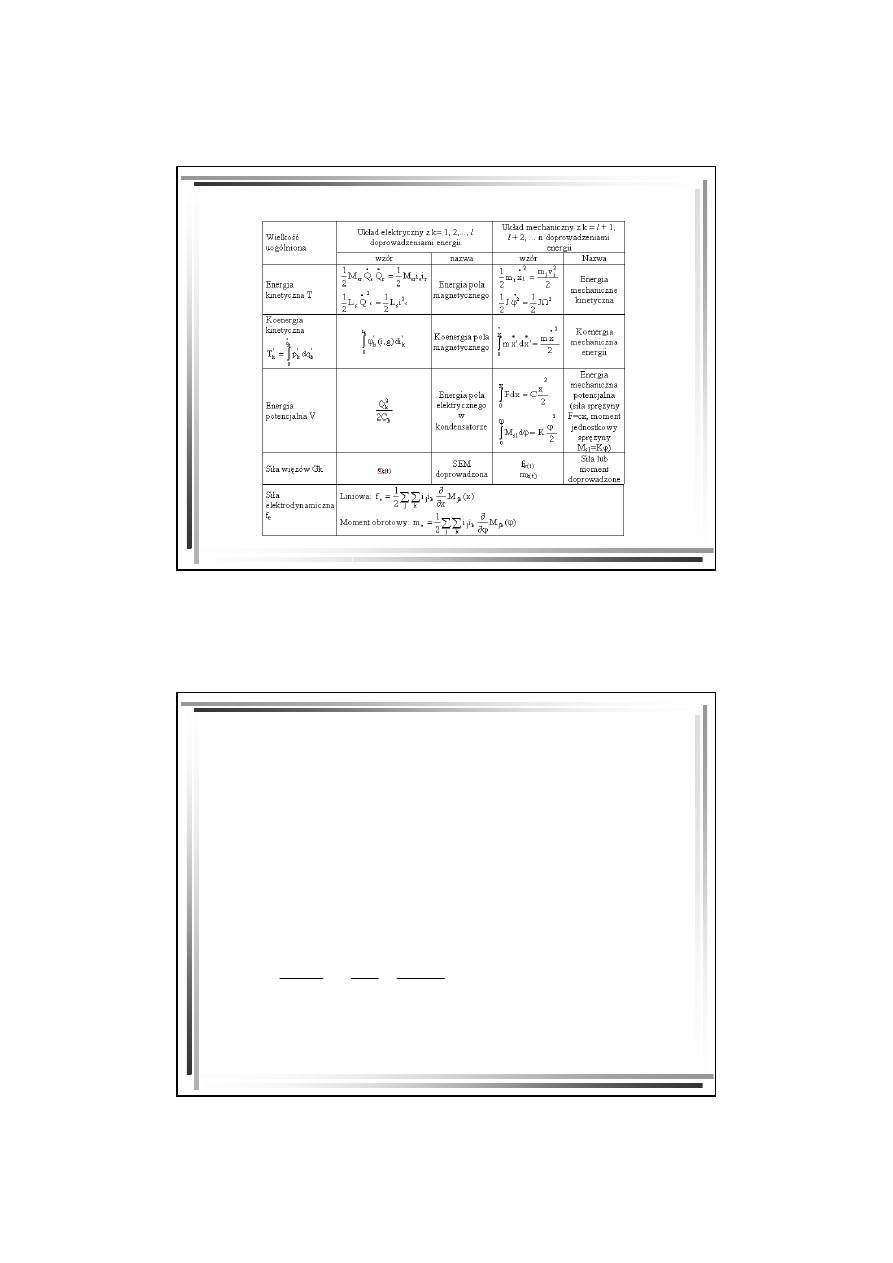
Wielkości układów elektrycznych i mechanicznych
(cd)

4

Równania Eulera-Langrange’a

•

Dla

układów konserwatywnych liniowych

funkcja

Lagrange’a przyjmie postać:

L = T – V

•

W tym przypadku równanie Eulera – Lagrange’a
ma postać:

•

gdzie (i=1,2,3,...,n).

0

q

L

dt

d

q

L

i

i

=

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

∂

∂

−

∂

∂

•

3

5

Równania Eulera-Langrange’a

•

Dla

układów dysypatywnych liniowych

należy uwzglednić

energię kinetyczna strat oraz energię potencjalną sił
więzów narzuconych przez zewnętrzne źródła energii.

•

W tym przypadku funkcja Lagrange’a przyjmie postać:

L

FQ

= (T + T

F

) – (V + V

Q

)

•

W przypadku

układów dysypatywnych nieliniowych

funkcja Lagrange’a przyjmuje postać:

L

FQ

= (T

’

+ T

F

’

) – (V + V

Q

)

gdzie T

’

– koenergia kinetyczna zmagazynowana w

układzie, przy czym dla układów liniowych T

’

= T.

∫

∫

−

=

=

k

q

0

'
k

k

G

t

0

F

dq

)

t

(

G

V

oraz

Fdt

T

6

Po podstawieniu L

FG

do równania *, po prostych

przekształceniach (pamiętając, że T

F

nie zależy od q

k

i

V

G

– od

) otrzymamy równanie Eulera-Lagrange’a

dla układu elekromechanicznego dysypatywnego (łac.
dissipare = rozpraszać), tzn. -dla układu zawierającego
straty mocy i źródła energii:

k

q

•

n

...,

,2,

1

k

G

q

F

q

L

dt

d

q

L

k

i

i

k

=

−

=

∂

∂

−

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

∂

∂

−

∂

∂

•

•

4

7

Funkcję stanu Lagrange 'a L dla układów liniowych
określamy jako różnicę energii kinetycznej T i
potencjalnej V

W przypadku układów nieliniowych, należy używać
bardziej ogólnej definicji funkcji Lagrange a:

L=T’-V

przy czym:

∫

∑

•

•

=

•

•

•

=

n

1

q

,...,

q

0

,...,

0

n

1

k

k

n

1

n

1

'
k

'

q

d

)

t

;

q

,...,

q

;

q

,...,

q

(

p

'

T

8

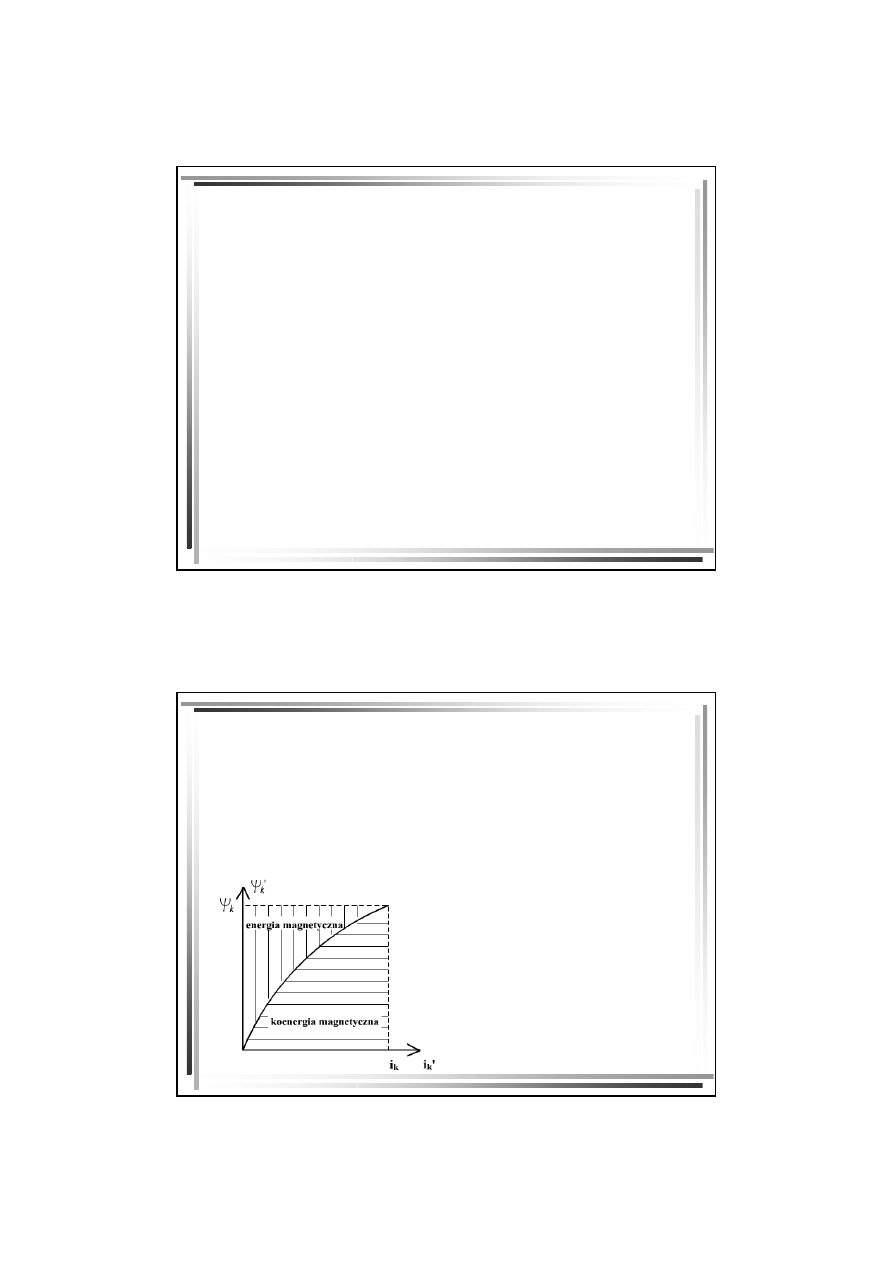
Koenergia kinetyczna, której całkowanie przeprowadza się
według

najdogodniejszej drogi jest charakterystyką

magnesowania i-tego magazynu energii.

Znakiem "prim" pod całką oznaczono zmienne całkowania,
a wielkości bez "prim" są granicami (p’

k

-oznacza pęd

uogólniony):

Koenergia k-tego

obwodu nieliniowego

5

9

Energia układu elektromechanicznego

Energię układu elektromechanicznego możemy
wyznaczyć z zależności:

- energia kinetyczna elektryczna układu

∑

∑

∫

=

=

Ψ

Ψ

=

=

Ψ

Ψ

=

n

1

j

j

kj

k

k

n

1

k

k

....

0

....

0

n

,.....,

k

,....,

1

j

i

)

i

,

x

(

M

d

)

t

(

i

T

n

1

(

3-22)

- koenergia kinetyczna elektryczna układu

∑

∑

∫

=

=

=

=

Ψ

Ψ

=

n

1

j

j

kj

k

k

n

1

k

k

i

....

i

0

....

0

'

n

,.....,

k

,....,

1

j

i

)

i

,

x

(

M

di

)

t

(

T

n

1

10

k

k

k

k

n

1

k

k

p

....

p

0

....

0

v

m

p

dp

)

t

(

v

T

n

1

=

=

∑

∫

=

- energia kinetyczna mechaniczna układu dla ruchu
postępowego:

- energia kinetyczna mechaniczna układu dla ruchu
obrotowego

k

k

k

k

n

1

k

k

p

....

p

0

....

0

J

p

dp

)

t

(

T

n

1

ω

=

ω

=

∑

∫

=

6

11

- koenergia kinetyczna mechaniczna układu dla ruchu
postępowego:

- kinetyczna mechaniczna układu dla ruchu obrotowego:

- energia potencjalna elektryczna (zmagazynowana w
kondensatorach)

k

n

1

k

k

k

v

....

v

0

....

0

'

dv

)

t

(

v

m

T

n

1

∑

∫

=

=

k

n

1

k

k

k

....

0

....

0

'

d

)

t

(

J

T

n

1

ω

ω

=

∑

∫

=

ω

ω

∫ ∑

=

=

−

−

=

n

1

Q

....

Q

0

....

0

n

1

k

k

k

Ck

k

Ck

C

)

t

(

Q

u

;

dQ

)

u

(

V

12

∫

∑

=

−

−

=

n

1

x

....

x

0

....

0

n

1

k

k

k

k

dx

)

x

k

(

V

∫

∑

ϕ

ϕ

=

ϕ

ϕ

−

−

=

n

1

....

0

....

0

n

1

k

k

k

k

d

)

k

(

V

∫

∑

=

=

=

=

t

0

.

n

1

k

2

k

k

'

F

F

)

i

(

R

2

1

F

dt

F

T

T

- energia potencjalna mechaniczna (zmagazynowana
w sprężynach) ruchu postępowego

- energia potencjalna mechaniczna (zmagazynowana
w sprężynach) ruchu obrotowego

- energia i koenergia kinetyczna strat (dysypatywna)
elektryczna

7

13

∫

∑

=

=

=

=

t

0

.

n

1

k

2

k

k

'

F

F

)

v

(

D

2

1

F

dt

F

T

T

∫

∑

=

ω

=

=

=

t

0

.

n

1

k

2

k

k

'

F

F

)

(

D

2

1

F

dt

F

T

T

∫

∑

=

−

=

−

=

k

Q

0

.

n

1

k

k

k

Q

k

k

Q

Q

)

t

(

U

V

dQ

)

t

(

U

V

- energia i koenergia kinetyczna strat (dysypatywna)
mechaniczna ruchu postepowego

- energia i koenergia kinetyczna strat (dysypatywna)
mechaniczna ruchu obrotowego

- energia potencjalna elektryczna sił więzów
narzuconych przez zewnętrzne źródła

14

∫

∑

=

−

=

−

=

k

x

0

.

n

1

k

k

k

Q

k

k

Q

x

)

t

(

F

V

dx

)

t

(

F

V

∫

∑

ϕ

=

ϕ

−

=

ϕ

−

=

k

0

.

n

1

k

k

k

Q

k

k

Q

)

t

(

M

V

d

)

t

(

M

V

- energia potencjalna mechaniczna sił zewnętrznych
przy ruchu postępowym

- energia potencjalna mechaniczna sił zewnętrznych
przy ruchu obrotowym