
1
Podstawowe człony dynamiczne
•modele matematyczne
•charakterystyki czasowe
•charakterystyki częstotliwościowe
•przykłady realizacji

2
Podstawowe człony dynamiczne
Człony:
proporcjonalny
inercyjny pierwszego rzędu
całkujący idealny
całkujący rzeczywisty
różniczkujący idealny
różniczkujący rzeczywisty
oscylacyjny
opóźniający
3
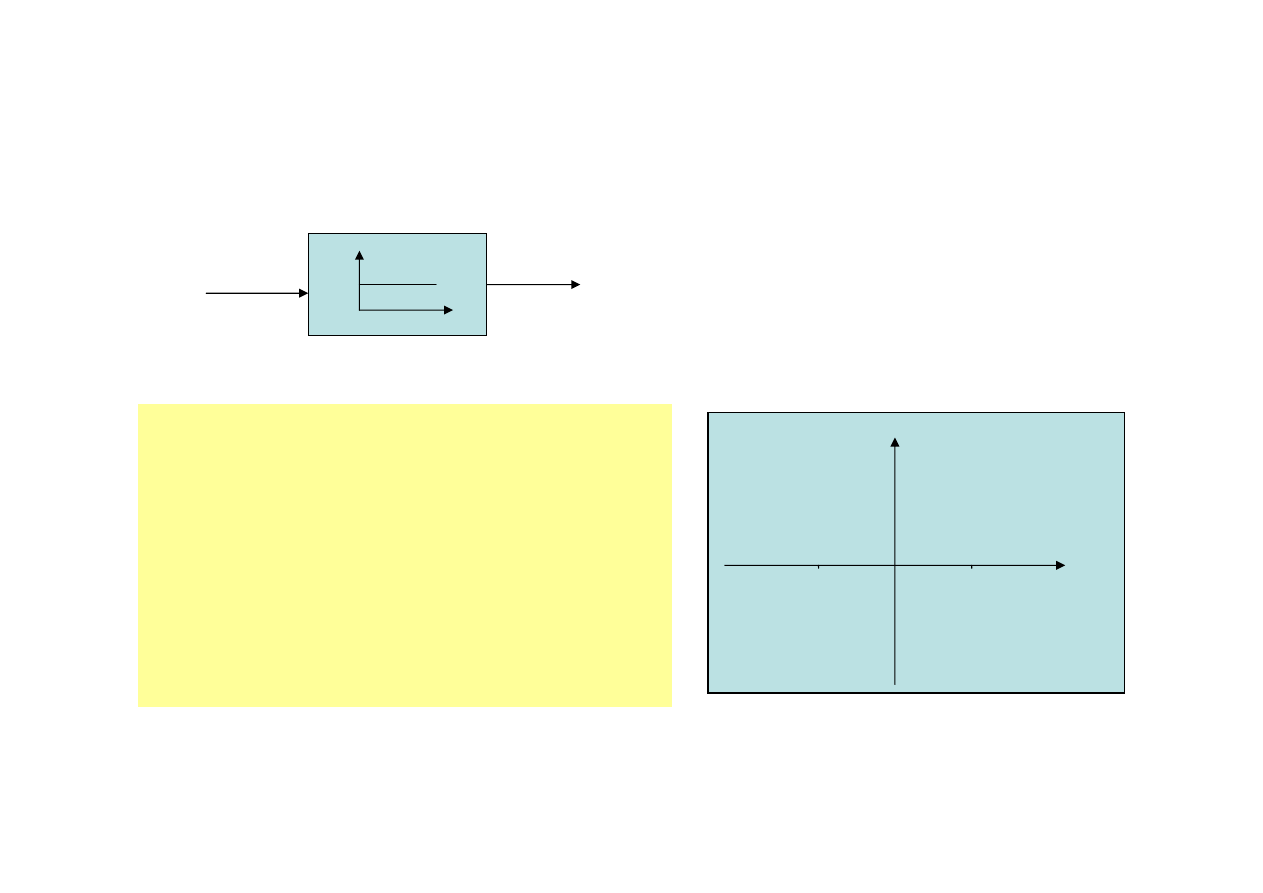
Człon proporcjonalny
u(t)
y(t)
y(t) = k u(t)
k współczynnik wzmocnienia
K(s) = k
K(j
ω) = k
h(t) = k 1(t)
charakterystyka skokowa
k(t) = k
δ(t)
charakterystyka impulsowa
k>0
(k<0)
P(
ω)
Q(
ω)
4
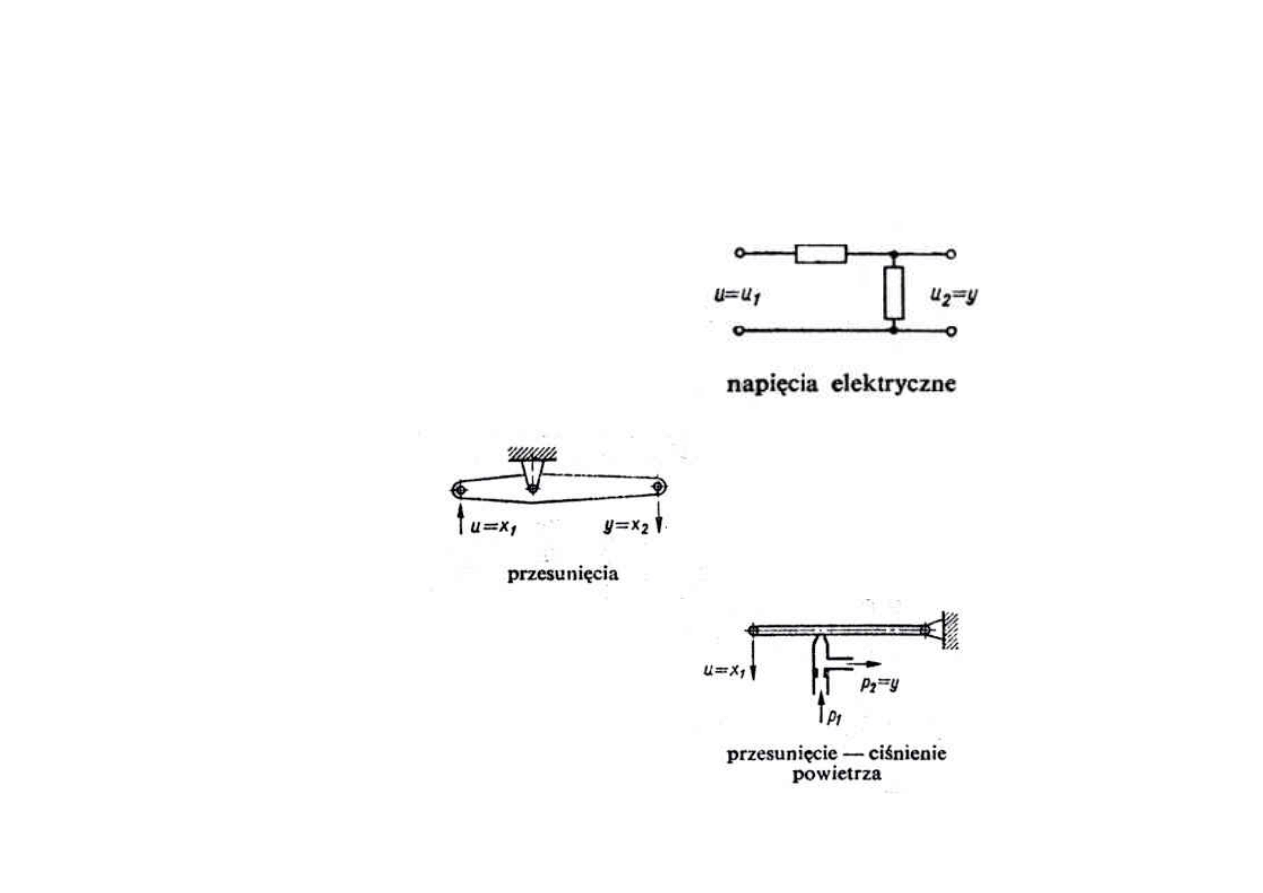
Przykłady realizacji
dzielnik napięcia
dźwignia
układ pneumatyczny
5
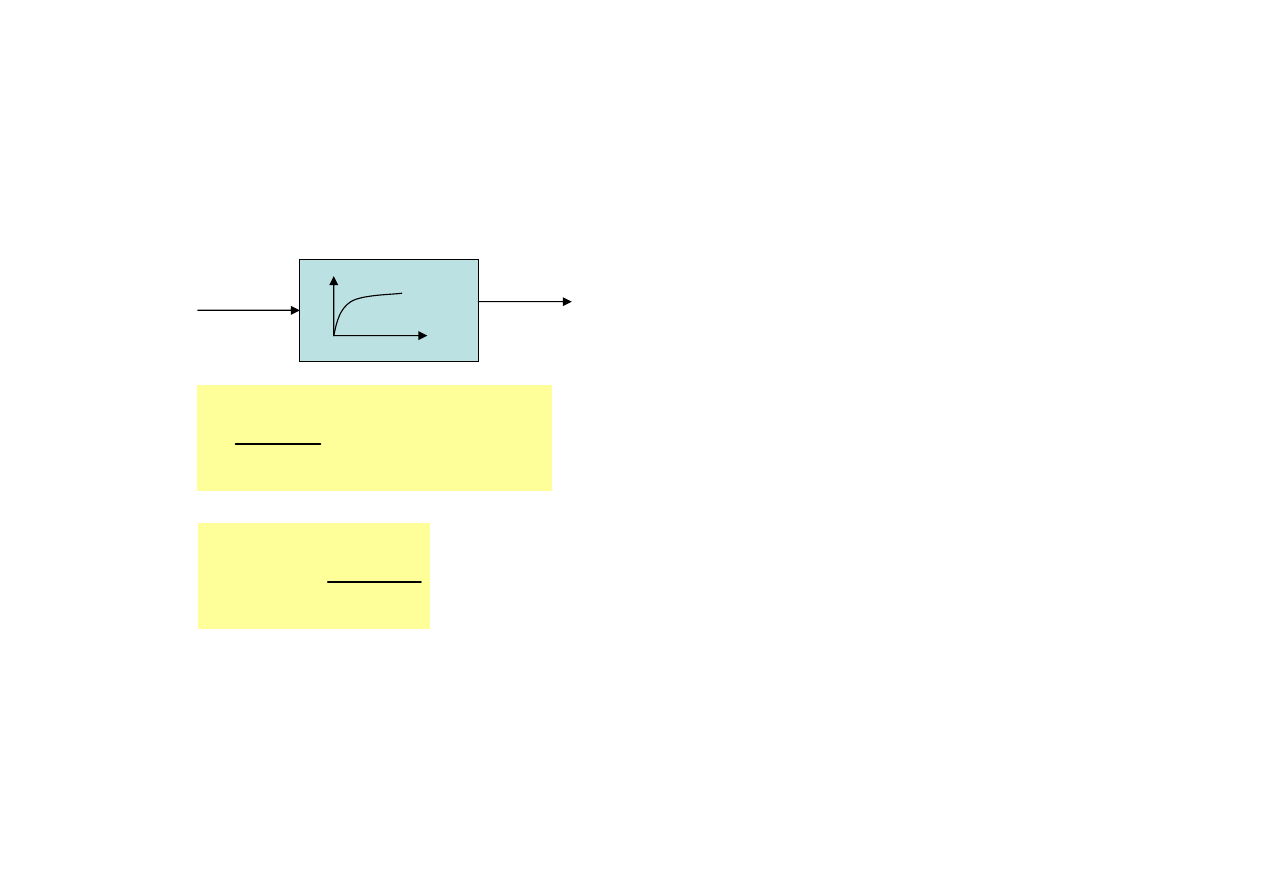
Człon inercyjny I rzędu
u(t)
y(t)
k współczynnik wzmocnienia
T stała czasowa
)
(
)
(
)
(
t
ku
t
y
dt
t
dy
T
=
+
1
)
(
+
=
Ts
k
s
K

6
)
(
)
(
)
(
t
u
t
y
dt
t
dy
T
=
+
{
}
{ }
{ }
{ }
{ }
)
(
)
(
)
(
)
(
)
(
)
(
s
ku
s
y
s
Tsy
t
u
kL
y
L
dt
dy
TL
t
u
kL
y
L
dt
dy
T
L
t
ku
L
y
dt
dy
T
L
=
+
=
+
⎭
⎬
⎫
⎩
⎨
⎧
=
+
⎭
⎬
⎫
⎩
⎨
⎧
=
⎭
⎬
⎫
⎩
⎨
⎧
+
1
)
(
+
=
Ts
k
s
K
czyli
L
7
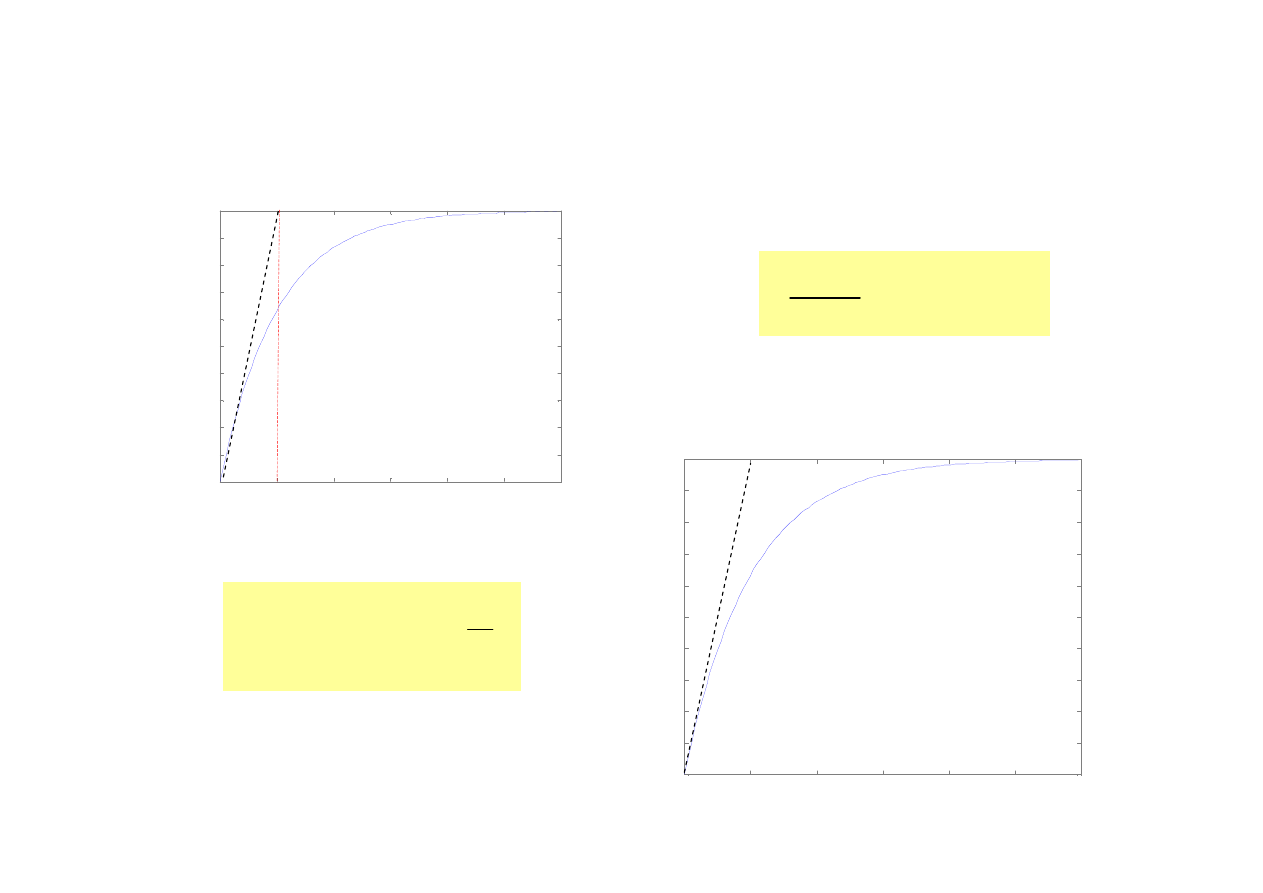
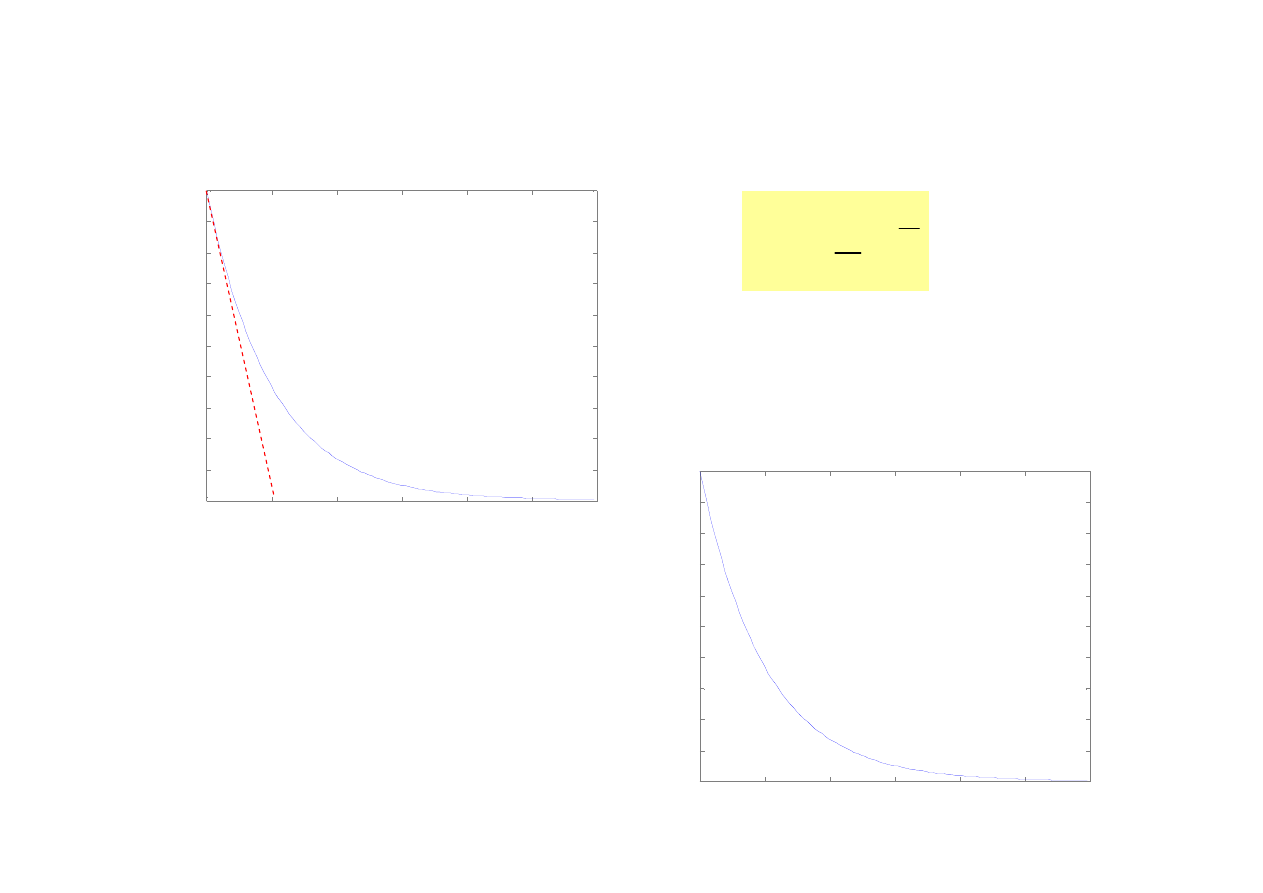
Człon inercyjny I rzędu –
charakterystyka skokowa
1
)
(
+
=
Ts
k
s
K
Time (sec.)
Am
pl
itu
de
Step Response
0
1
2
3
4
5
6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
From: U(1)
To
: Y
(1
)
)
(
)
(
)
(
t
ku
t
y
dt
t
dy
T
=
+
k=1 T=1
Time (sec.)
A
m
pli
tud
e
Step Response
0
5
10
15
20
25
30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
From: U(1)
To
: Y
(1
)
k=1 T=5
)
1
(
)
(
T
t
e
k
t
h
−
−
=
8
Time (sec.)
Amp
lit
ud
e
Impulse Response
0
1
2
3
4
5
6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
From: U(1)
To
: Y
(1
)
Time (sec.)
Amp
lit
ud
e
Impulse Response
0
5
10
15
20
25
30
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
From: U(1)
To
: Y
(1
)
k=1
T=5
k=1
T=1
charakterystyka impulsowa
T
t
e
T
k
t
k
−
=
)
(
Człon inercyjny I rzędu

9
Człon inercyjny I rzędu
Transmitancja widmowa K(j
ω)
2
2
2
2
1
)
(
1
)
(
)
(
)
(
)
(
)
(
)
(
1
)
(
T
T
k
Q
T
k
P
jQ
P
j
K
j
K
s
K
sT
k
s
K
j
s
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
=
+
=
+
=
=
+
=
=
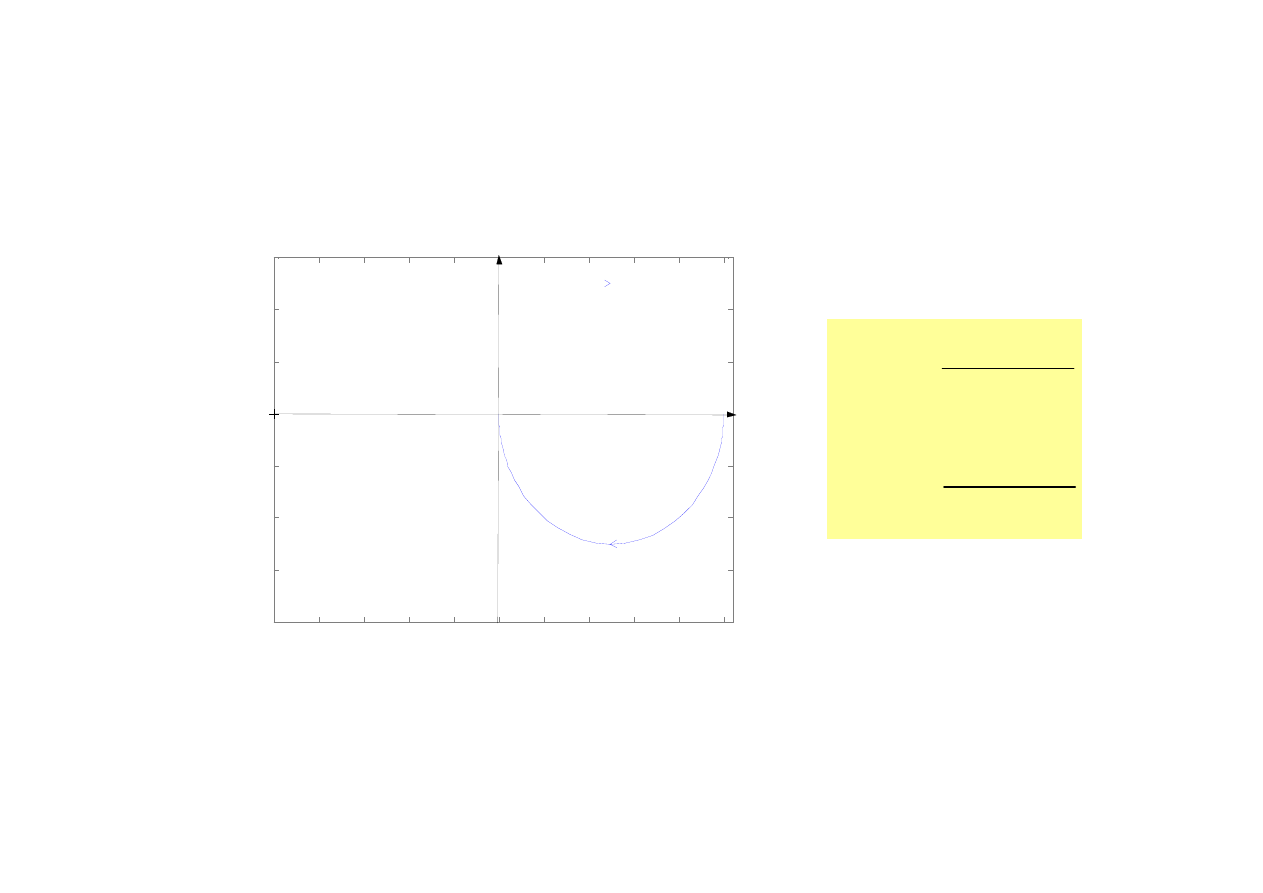
10
Człon inercyjny I rzędu
Real Axis
Im
ag
in
ar
y A
xi
s
Charakterystyka amplitudowo-fazowa
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
From: U(1)
To
: Y
(1
)
2
2
2
2
1
)
(
1
)
(
T
T
k
Q
T
k
P
ω
ω
ω
ω
ω
+
−
=
+
=
k=1
T=2
k
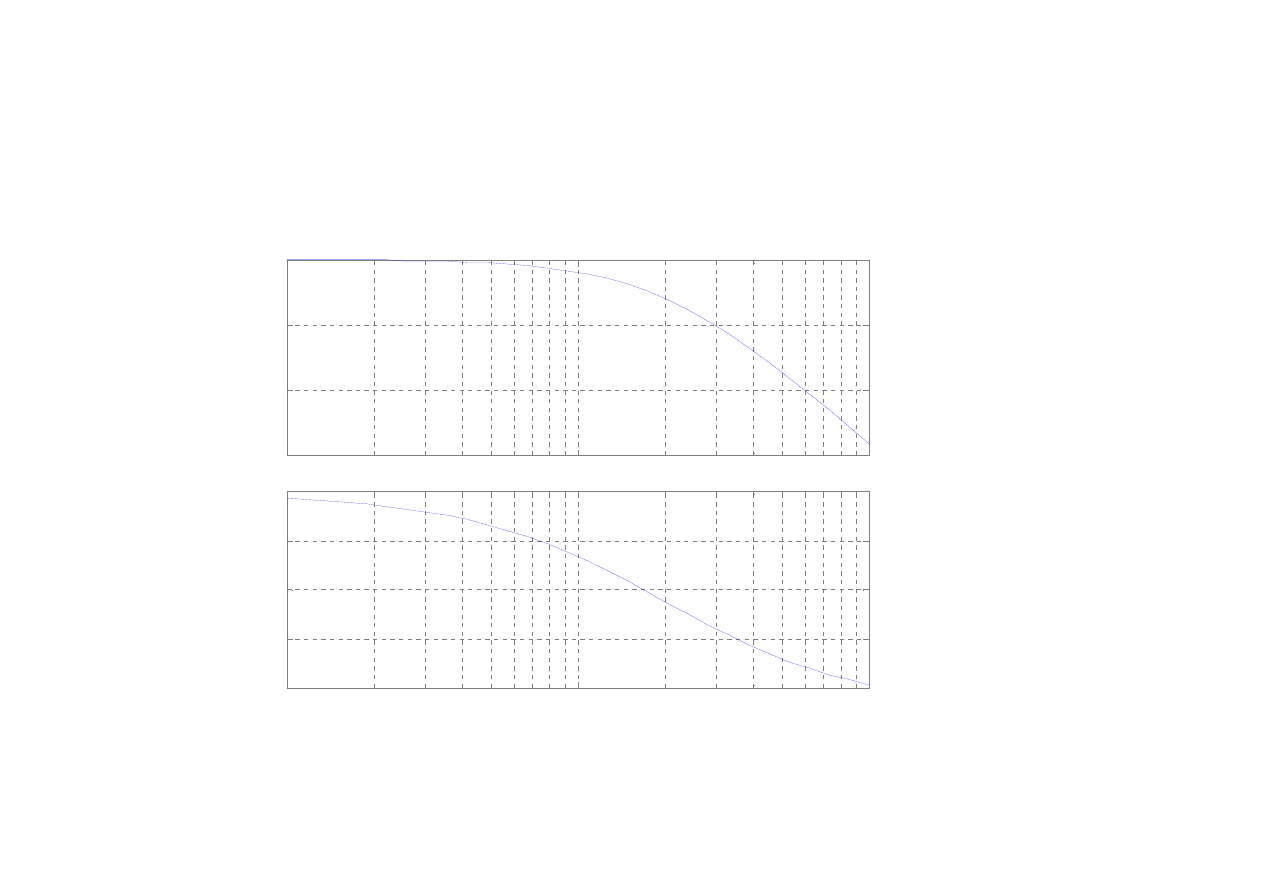
11
Człon inercyjny I rzędu
Frequency (rad/sec)
P
has
e
(deg)
; M
agnit
ude (
dB
)
-15
-10
-5
0
From: U(1)
10
-2
10
-1
10
0
-80
-60
-40
-20
0
To
: Y
(1
)
Charakterystyka logarytmiczna amplitudowa
Charakterystyka logarytmiczna fazowa
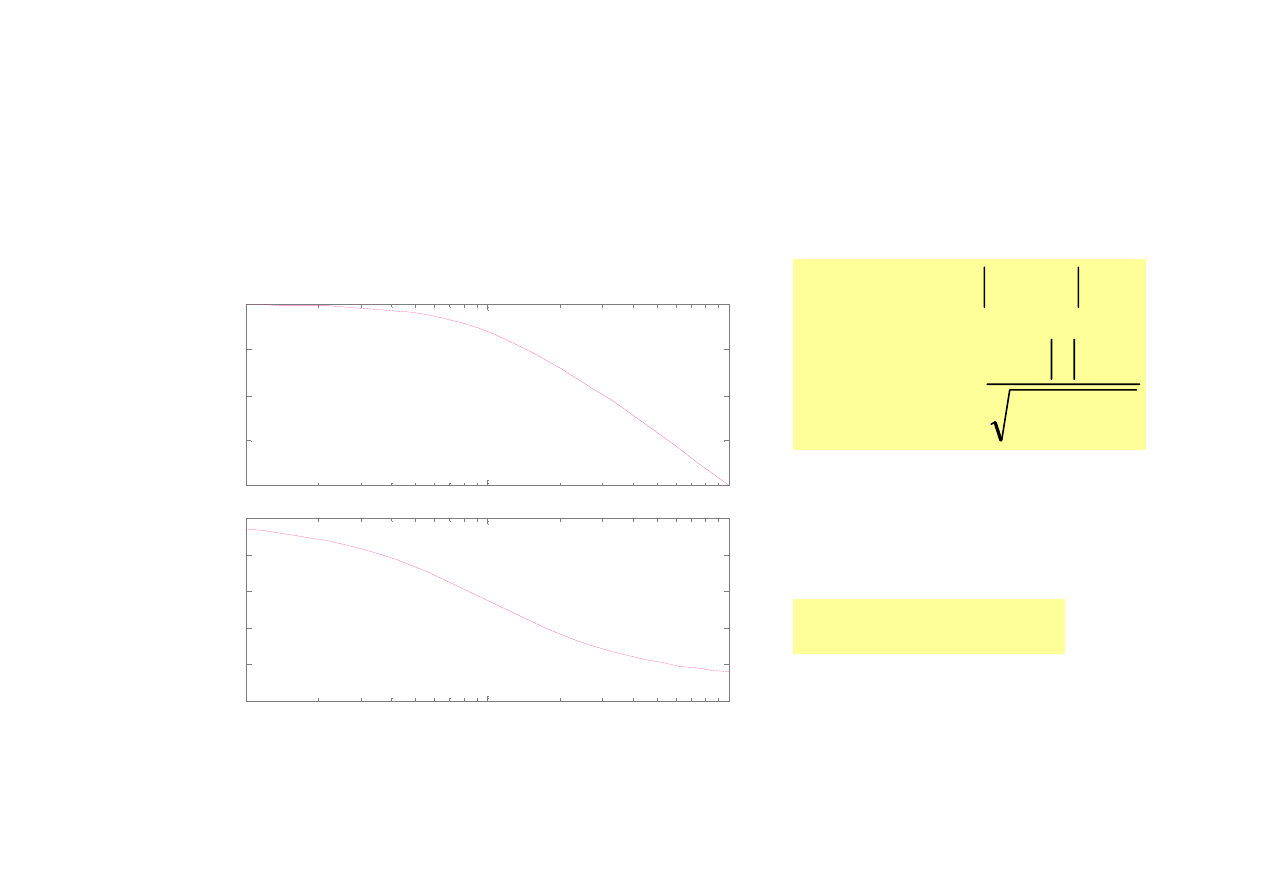
12
Frequency (rad/sec)
P
has
e (
deg
);
M
agn
itude
(
dB
)
20
25
30
35
40
From: U(1)
10
2
10
3
10
4
-100
-80
-60
-40
-20
0
To
: Y
(1
)
Charakterystyka dla T=0.001 k=100
2
)
(
1
lg
20
)
(
)
(
lg
20
)
(
T
k
Lm
j
K
Lm
ω
ω
ω
ω
+
=
=
Człon inercyjny I rzędu
T
arctg
ω
ω
ϕ
−
=
)
(
13
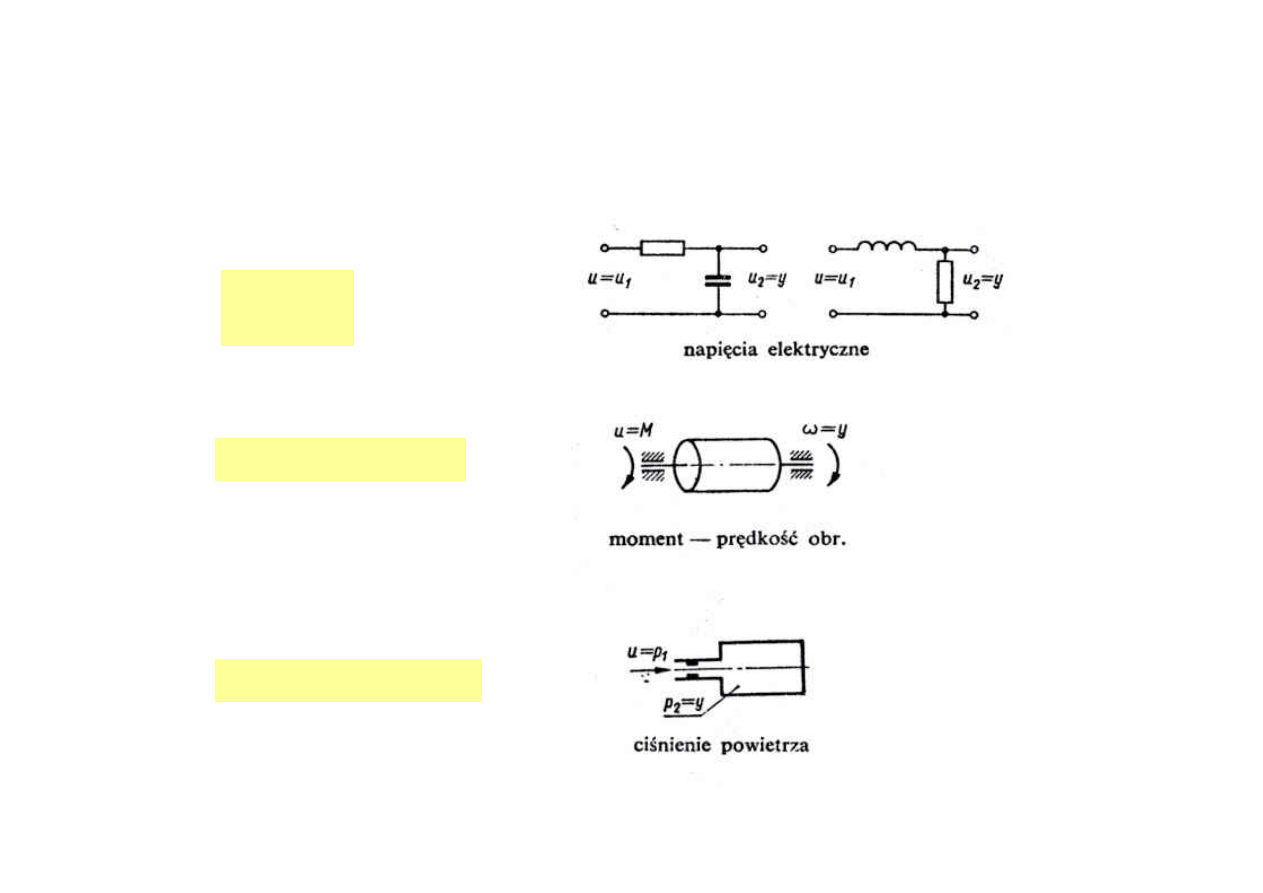
Przykłady realizacji
układ RC
układ LR
układ mechaniczny
układ pneumatyczny
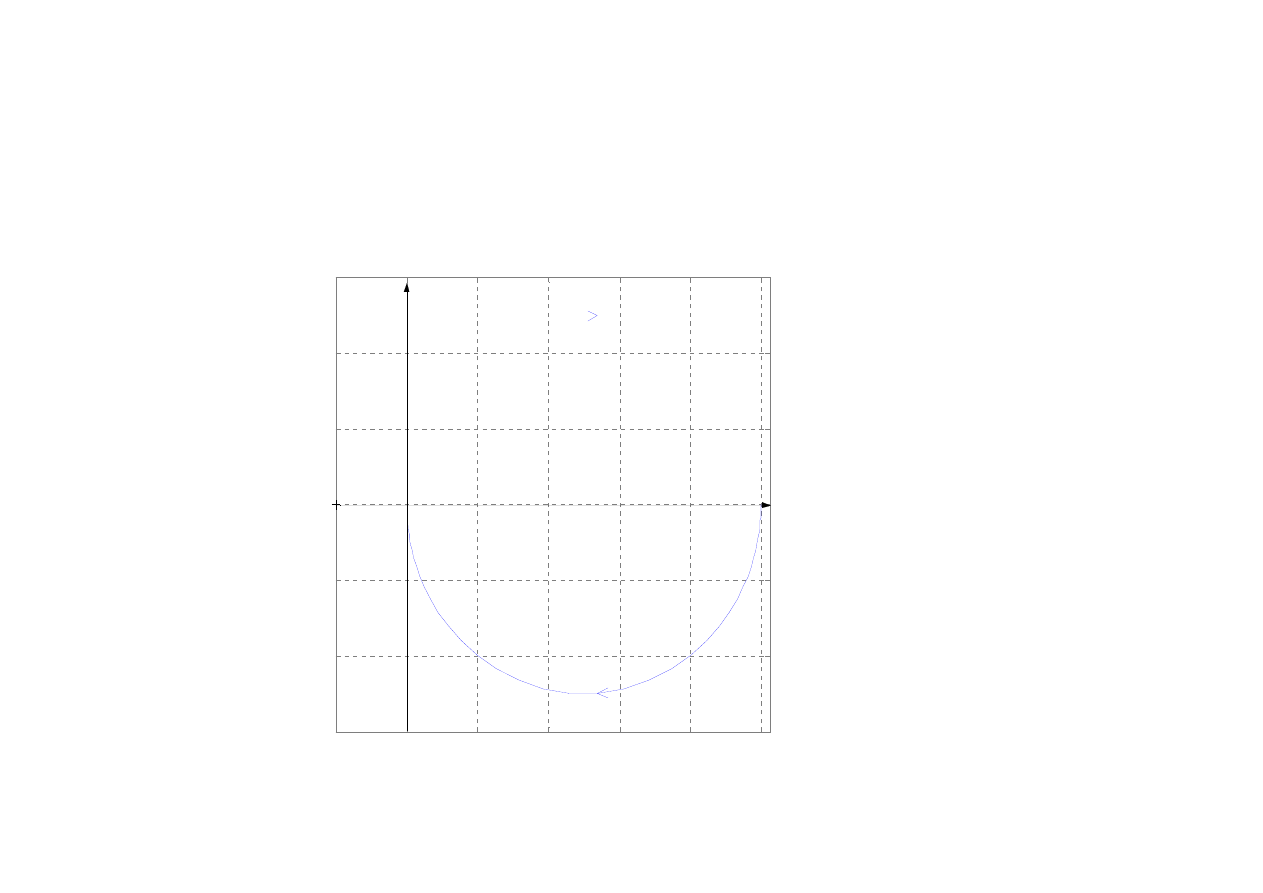
14
Człon inercyjny I rzędu
Real Axis
Im
ag
in
ar
y A
xi
s
Nyquist Diagrams
-1
0
1
2
3
4
5
-3
-2
-1
0
1
2
3
From: U(1)
To
: Y
(1
)
k=5
T=1
k
15
Człon inercyjny n-tego rzędu
u(t)
y(t)
…
k
1
, T
1
k
n
, T
n
∏
=
=
+
=
+
+
=
n
i
i
i
i
n
n
sT
k
s
K
sT
k
sT
k
s
K
1
1
1
1
)
(
1
1
)
(
K

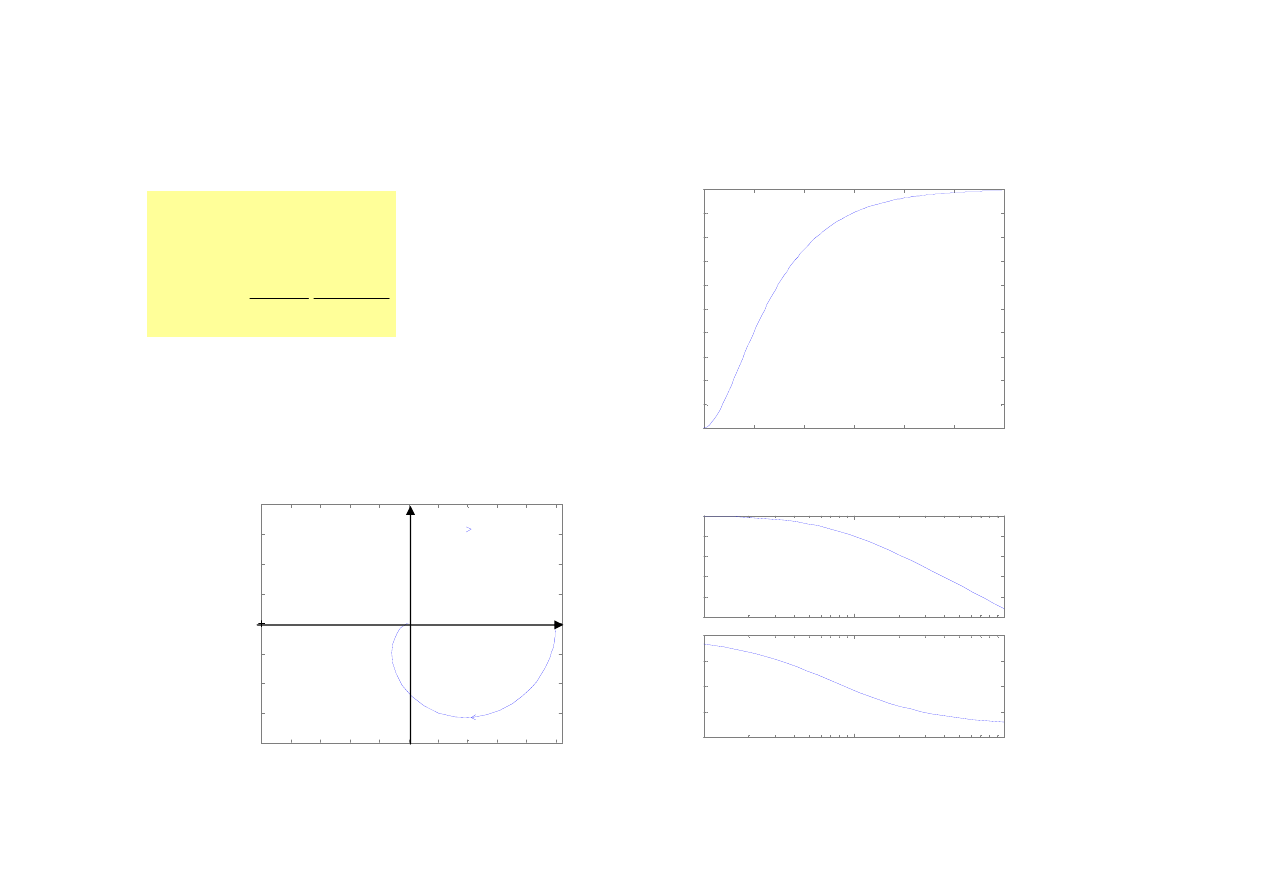
16
Człon inercyjny n-tego rzędu
n=1
n=2
n=4
h(t)
∏
=
=
+
=
+
+
=
n
i
i
i
i
n
n
sT
k
s
K
sT
k
sT
k
s
K
1
1
1
1
)
(
1
1
)
(
K
17
Człon inercyjny n-tego rzędu
1
2
1
1
1
)
(
2
+
+
=
=
s
s
s
K
n
Time (sec.)
A
m
pl
itud
e
Step Response
0
2
4
6
8
10
12
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
From: U(1)
To
: Y
(1
)
Real Axis
Im
ag
inar
y A
xis
Nyquist Diagrams
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
From: U(1)
To
: Y
(1
)
Frequency (rad/sec)
P
ha
se (
deg)
; M
agn
itude
(
dB
)
Bode Diagrams
-50
-40
-30
-20
-10
0
From: U(1)
10
-1
10
0
10
1
-200
-150
-100
-50
0
To
: Y
(1
)
18
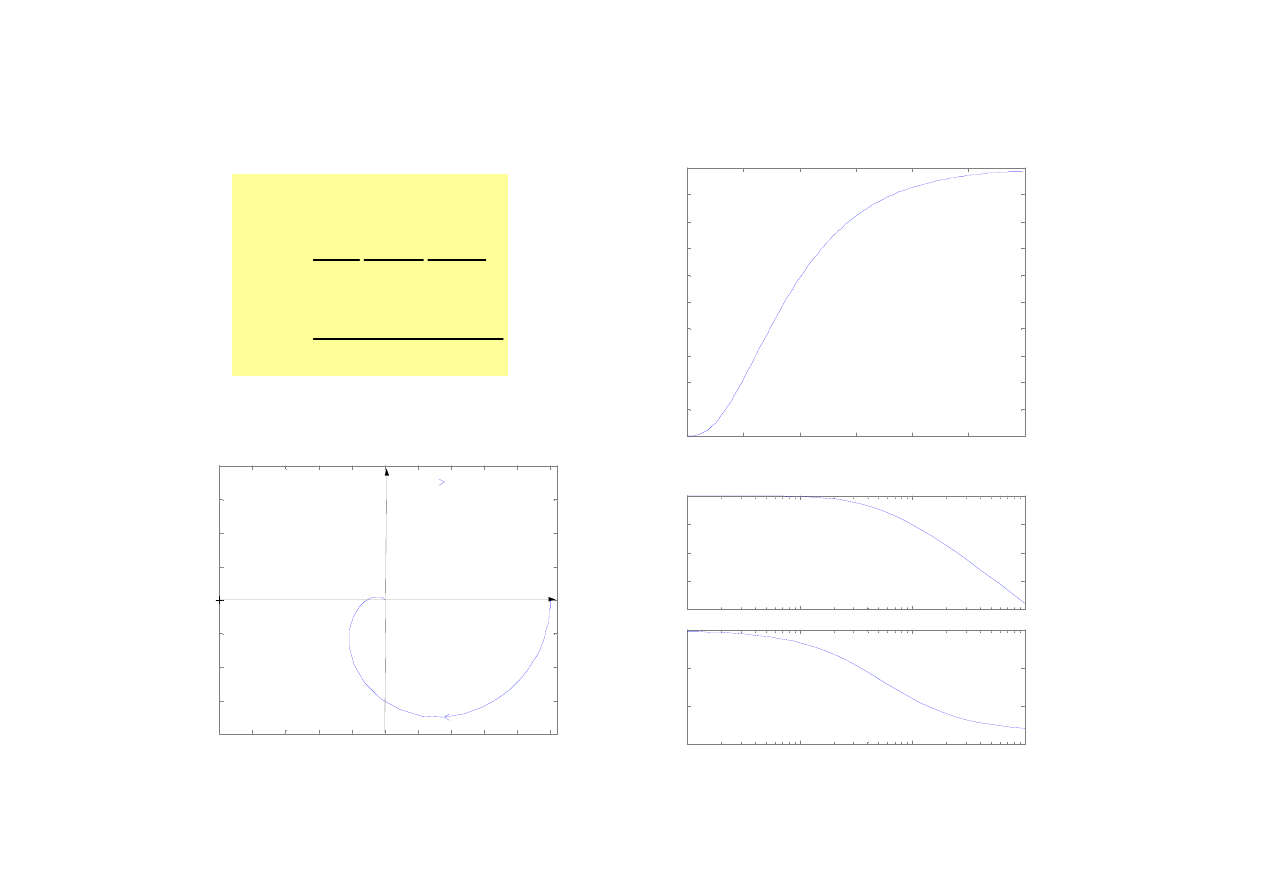
Człon inercyjny n-tego rzędu
1
6
11
6
1
)
(
1
3
1
1
2
1
1
1
)
(
3
2
3
+
+
+
=
+
+
+
=
=
s
s
s
s
K
s
s
s
s
K
n
Frequency (rad/sec)
P
has
e (
deg)
; M
agn
itu
de (
dB
)
Bode Diagrams
-80
-60
-40
-20
0
From: U(1)
10
-2
10
-1
10
0
10
1
-300
-200
-100
0
To
: Y
(1
)
Real Axis
Im
ag
inar
y A
xi
s
Nyquist Diagrams
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
From: U(1)
To
: Y
(1
)
Time (sec.)
Am
pl
itu
de
Step Response
0
3
6
9
12
15
18
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
From: U(1)
To
: Y
(1
)
19
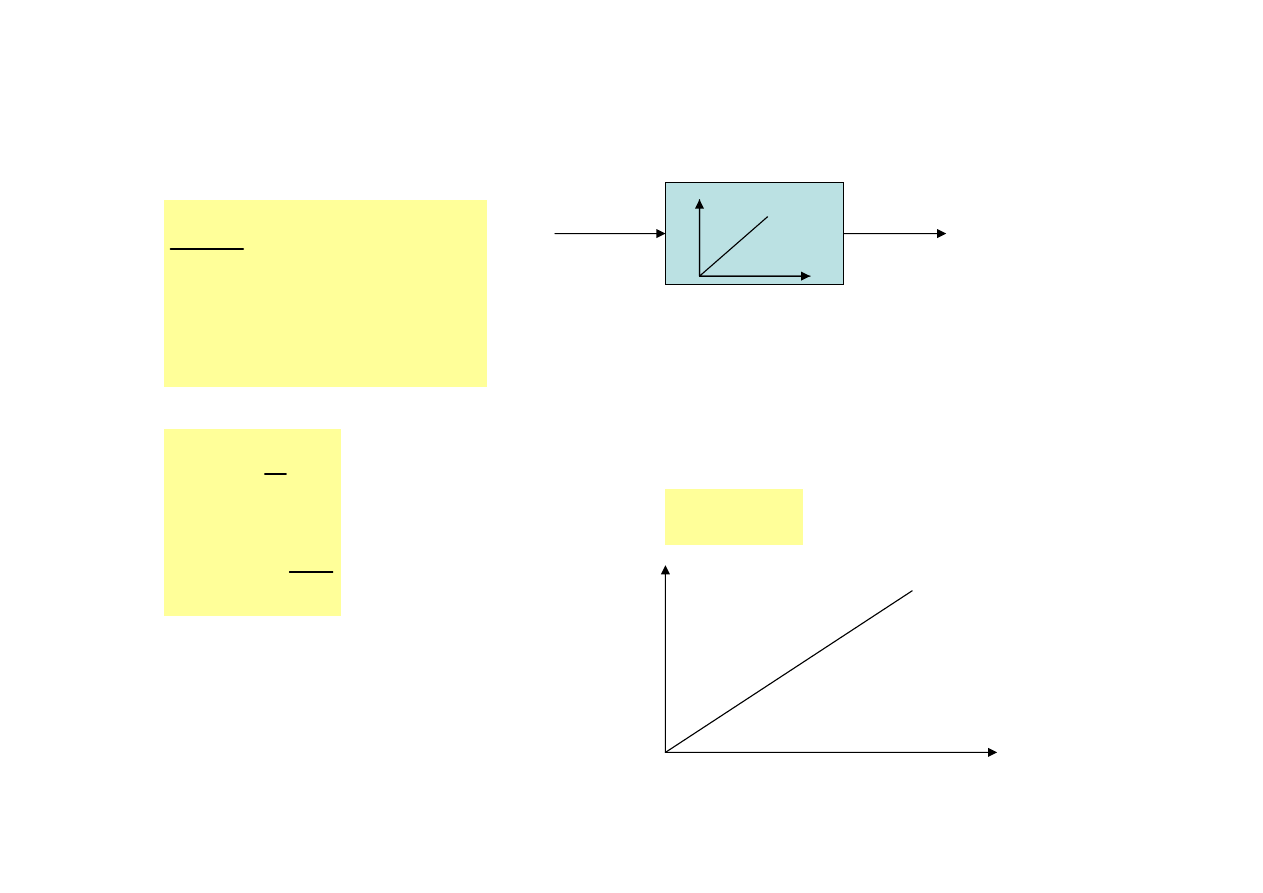
Człon całkujący idealny
∫
=
=
t
dt
t
ku
t
y
albo
t
ku
dt
t
dy
0
)
(
)
(
)
(
)
(
ω
ω
j
k
j
K
s
k
s
K
=
=
)
(
)
(
u(t)
y(t)
kt
t
h
=
)
(
charakterystyka skokowa
t
20
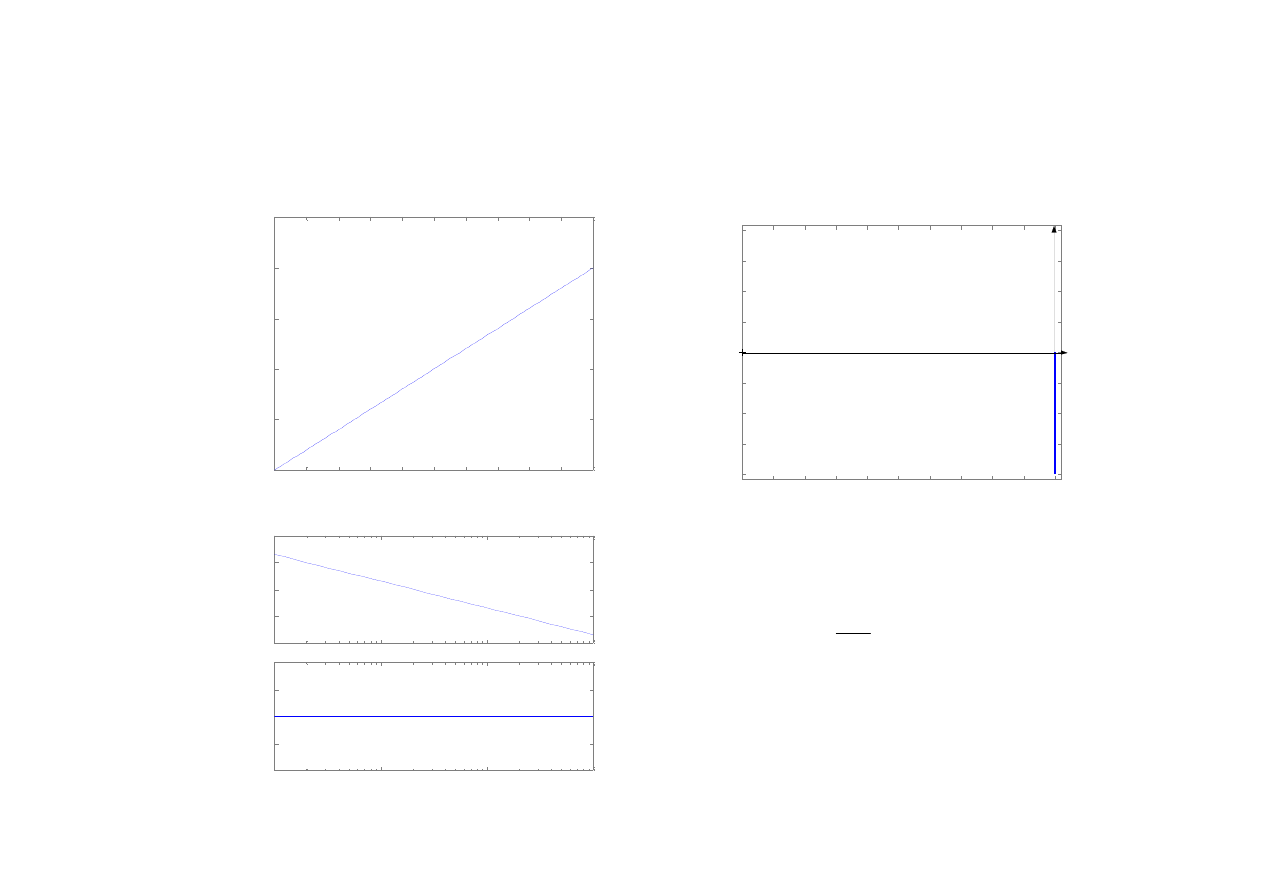
Człon całkujący idealny
Time (sec.)
A
m
plit
ude
Step Response
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
5
10
15
20
25
From: U(1)
To
: Y
(1
)
Frequency (rad/sec)
P
ha
se (
deg)
; M
ag
nit
ude
(
dB
)
Bode Diagrams
-20
0
20
40
60
From: U(1)
10
-1
10
0
10
1
10
2
-91
-90.5
-90
-89.5
-89
To
: Y
(1
)
Real Axis
Im
aginar
y A
xis
Nyquist Diagrams
-1
-0.9
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
-2000
-1500
-1000
-500
0
500
1000
1500
2000
From: U(1)
To
: Y
(1
)
h(t)
s
s
K
20
)
(
=
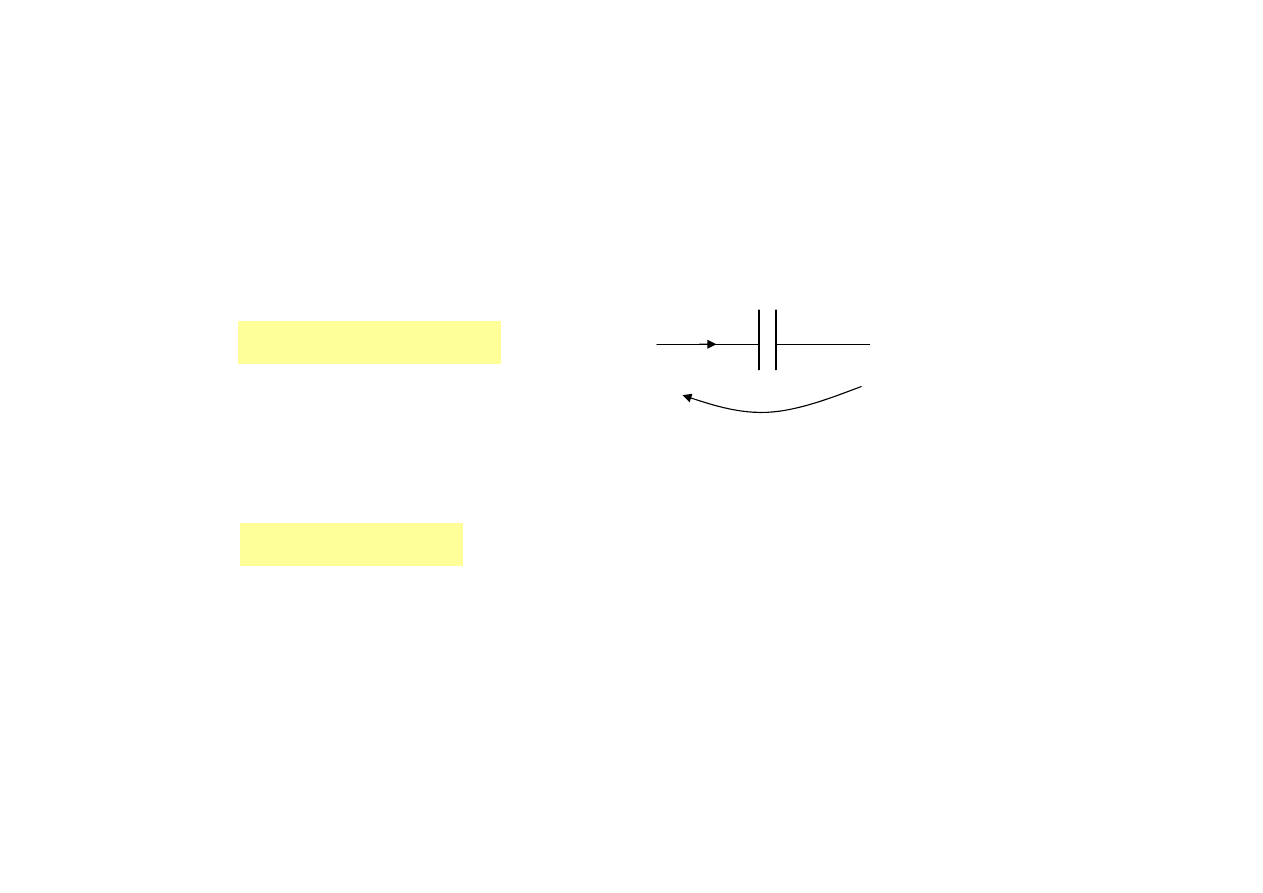
21
Człon całkujący idealny
przykłady
idealny kondensator
u(t)=i
y(t)=U
licznik odległości
u(t) prędkość kątowa koła
y(t) przebyta droga
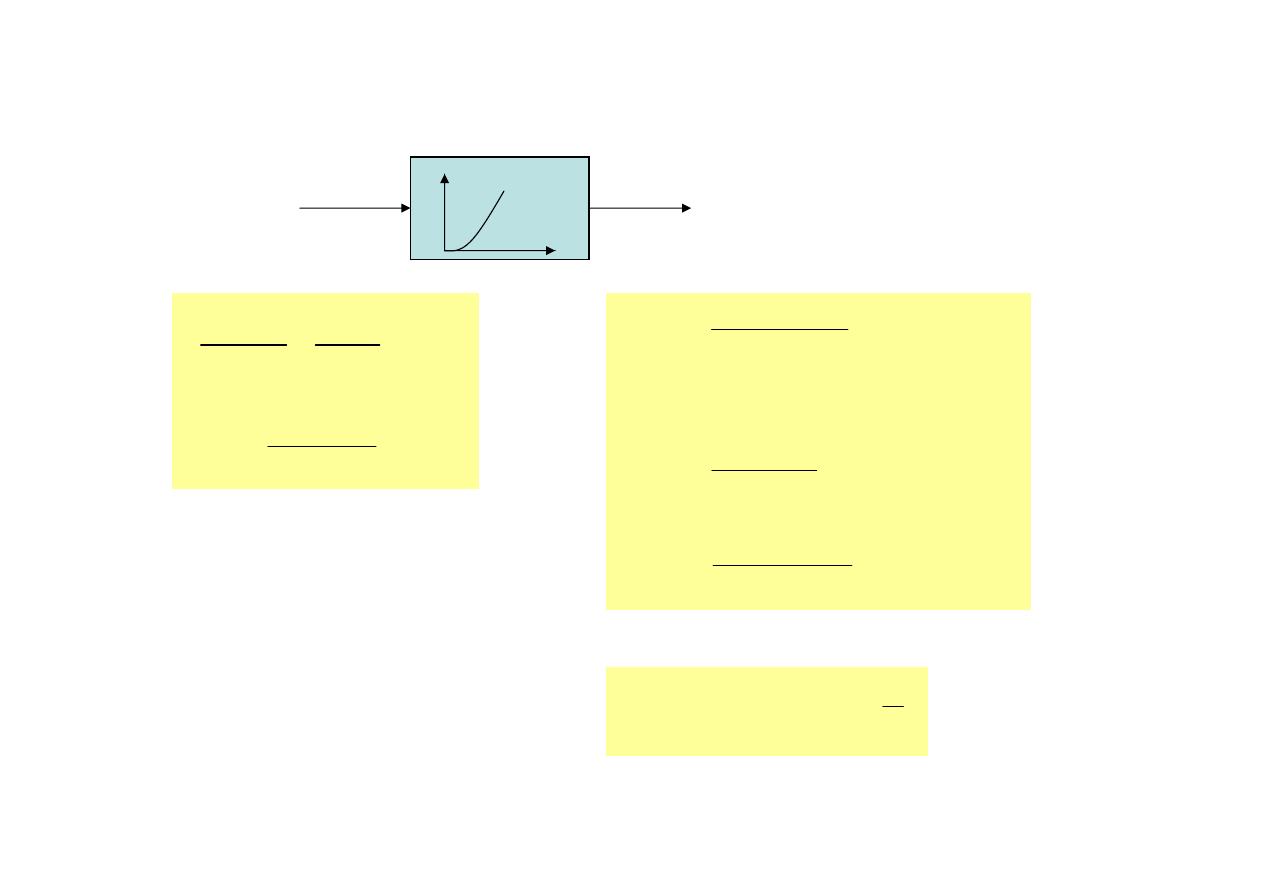
22
Człon całkujący rzeczywisty
)
1
(
)
(
)
(
)
(
)
(
2
2
sT
s
k
s
K
t
ku
dt
t
dy
dt
t
y
d
T
+
=
=
+
]
)
(
1
[
)
(
)
(
1
)
(
)
(
)
(
)
1
(
)
(
2
2
T
k
Q
T
kT
P
jQ
P
T
j
j
k
j
K
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
=
+
−
=
+
=
+
=
u(t)
y(t)
)
1
(
)
(
T
t
e
kT
kt
t
h
−
−
−
=
charakterystyka skokowa
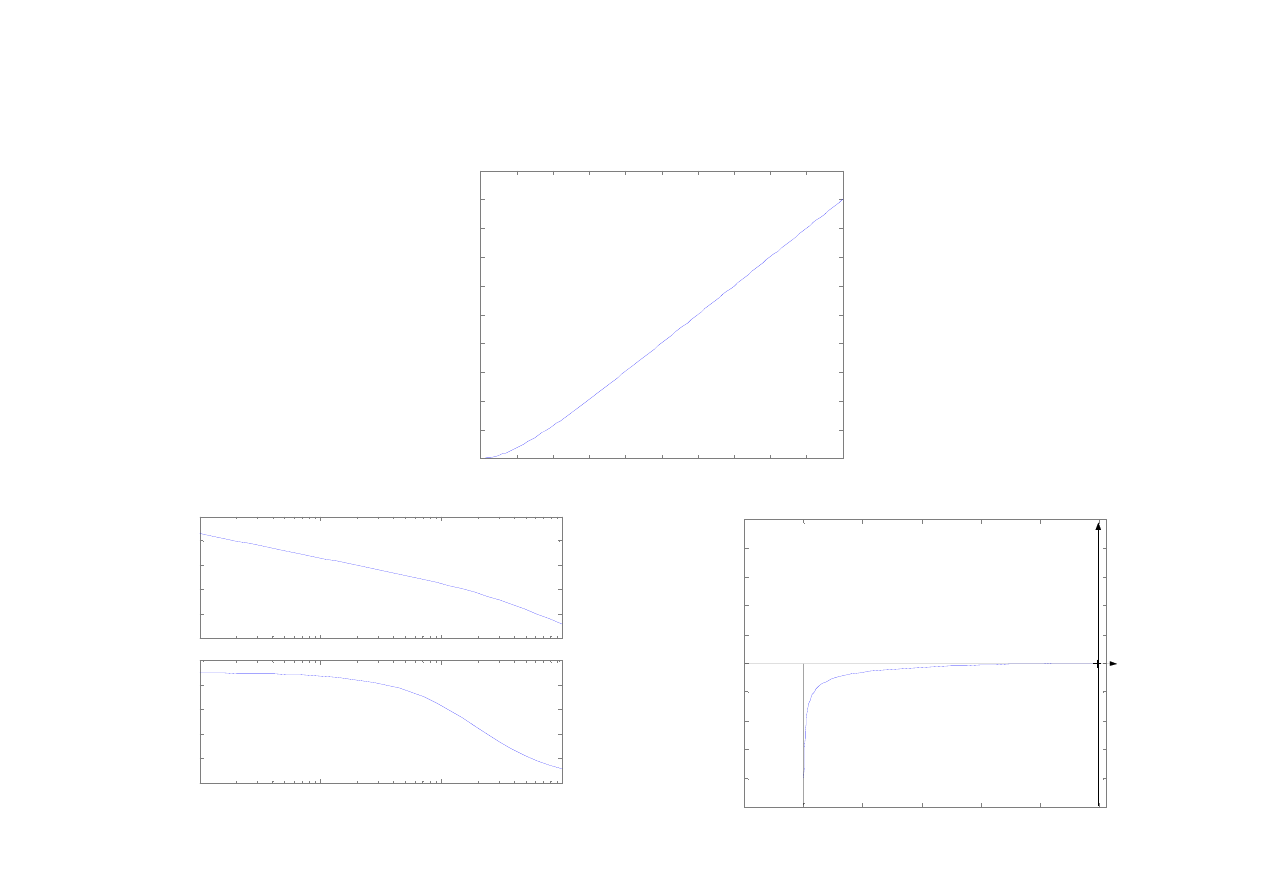
23
Człon całkujący rzeczywisty
Time (sec.)
A
m
pl
itude
Step Response
0
5
10
15
20
25
30
35
40
45
50
0
100
200
300
400
500
600
700
800
900
1000
From: U(1)
To
: Y
(1
)
Frequency (rad/sec)
P
ha
se (
deg)
; M
agni
tude
(d
B
)
Bode Diagrams
0
20
40
60
80
100
From: U(1)
10
-3
10
-2
10
-1
10
0
-180
-160
-140
-120
-100
-80
To
: Y
(1
)
Real Axis
Im
ag
inar
y A
xi
s
Nyquist Diagrams
-120
-100
-80
-60
-40
-20
0
-2500
-2000
-1500
-1000
-500
0
500
1000
1500
2000
2500
From: U(1)
To
: Y
(1
)
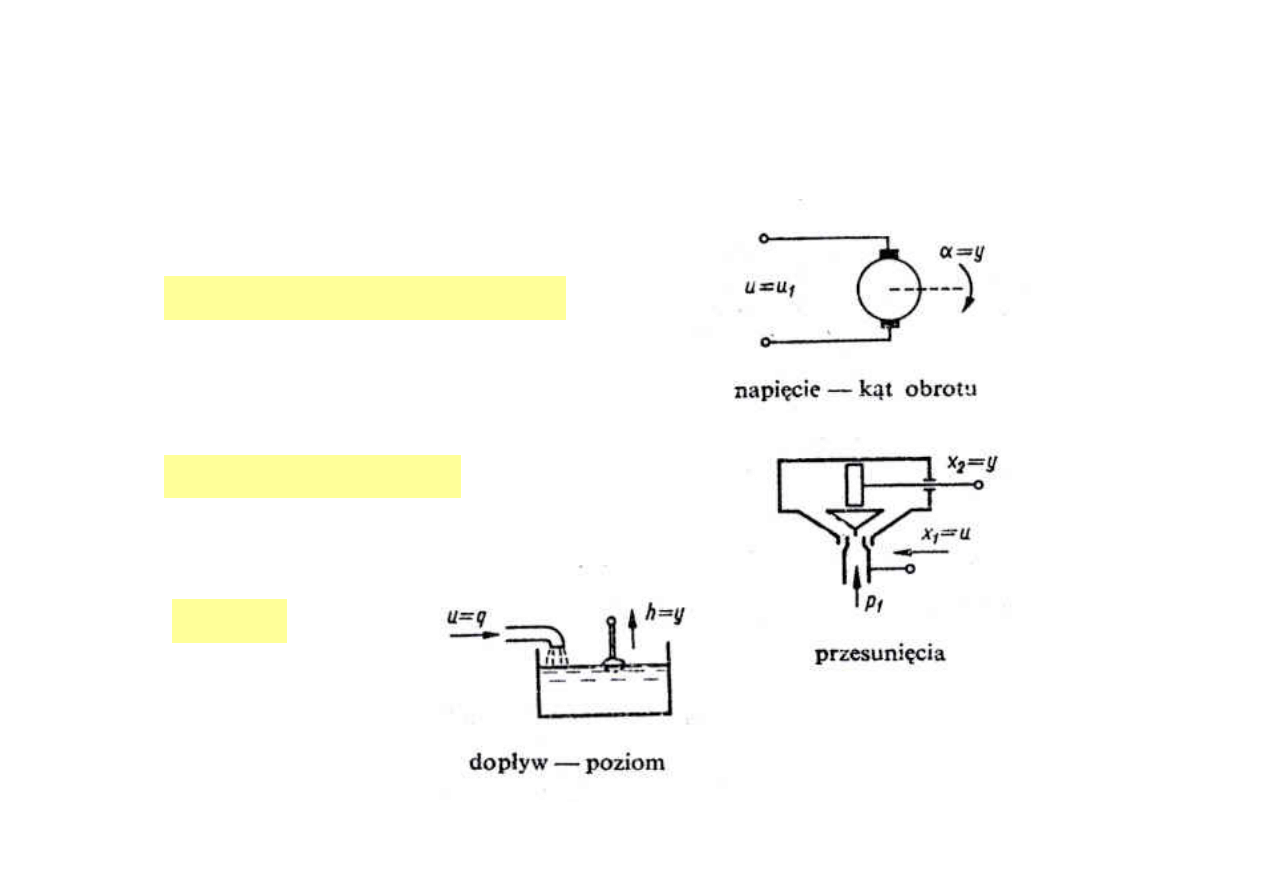
24
Człon całkujący rzeczywisty
przykłady
silnik elektryczny prądu stałego
siłownik pneumatyczny
zbiornik
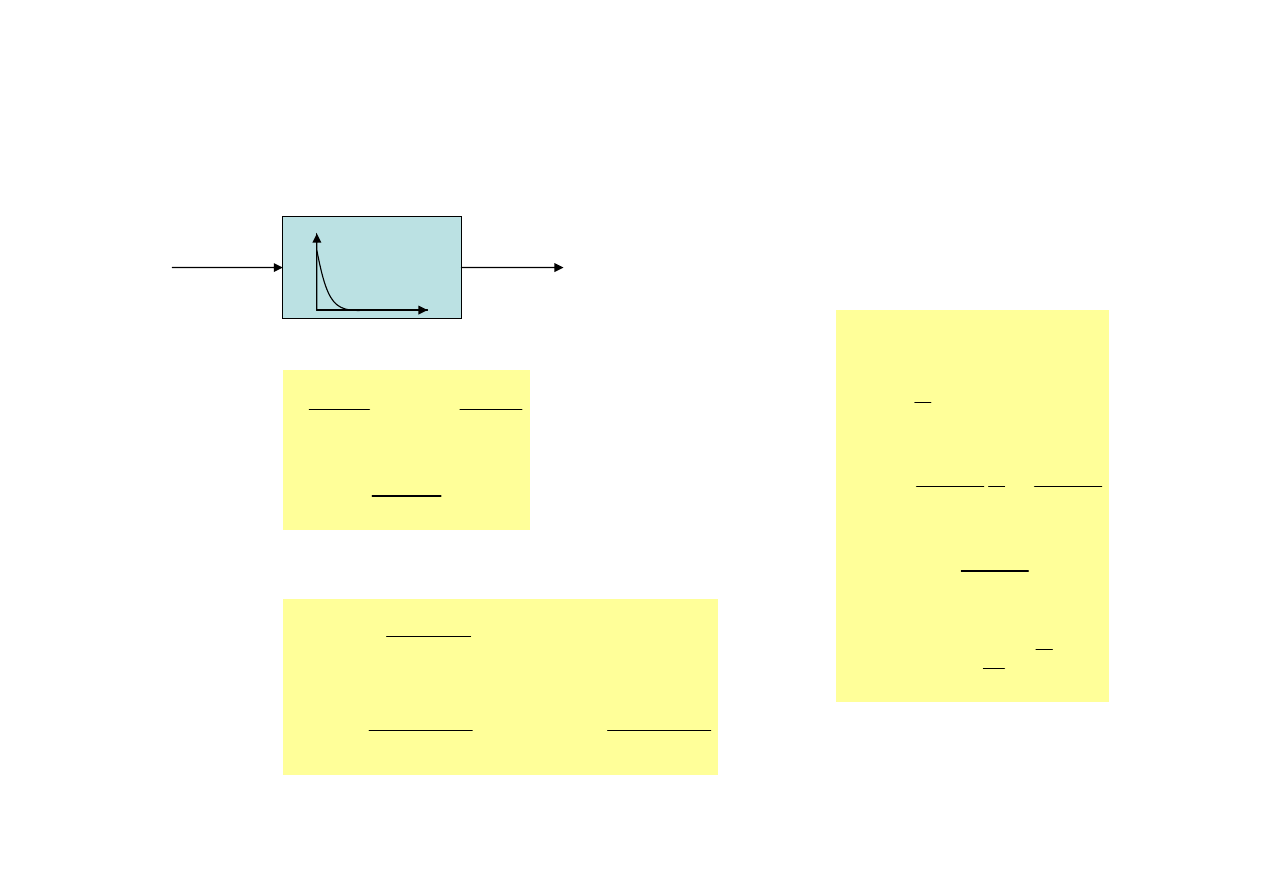
25
Człon różniczkujący rzeczywisty
sT
ks
s
K
dt
t
du
k
y
dt
t
dy
T
+
=
=
+
1
)
(
)
(
)
(
T
t
e
T
k
t
h
t
y
sT
k
L
t
y
sT
k
s
sT
ks
s
y
s
s
u
s
u
s
K
s
y
−
−
=
=
+
=
+
=
+
=
=
=
)
(
)
(
}
1
{
)
(
1
1
1
)
(
1
)
(
)
(
)
(
)
(
1
u(t)
y(t)
2
2
2
)
(
1
)
(
)
(
1
)
(
)
(
)
(
1
)
(
T
k
Q
T
kT
P
jQ
P
T
j
jk
j
K
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
=
+
=
+
=
+
=
26
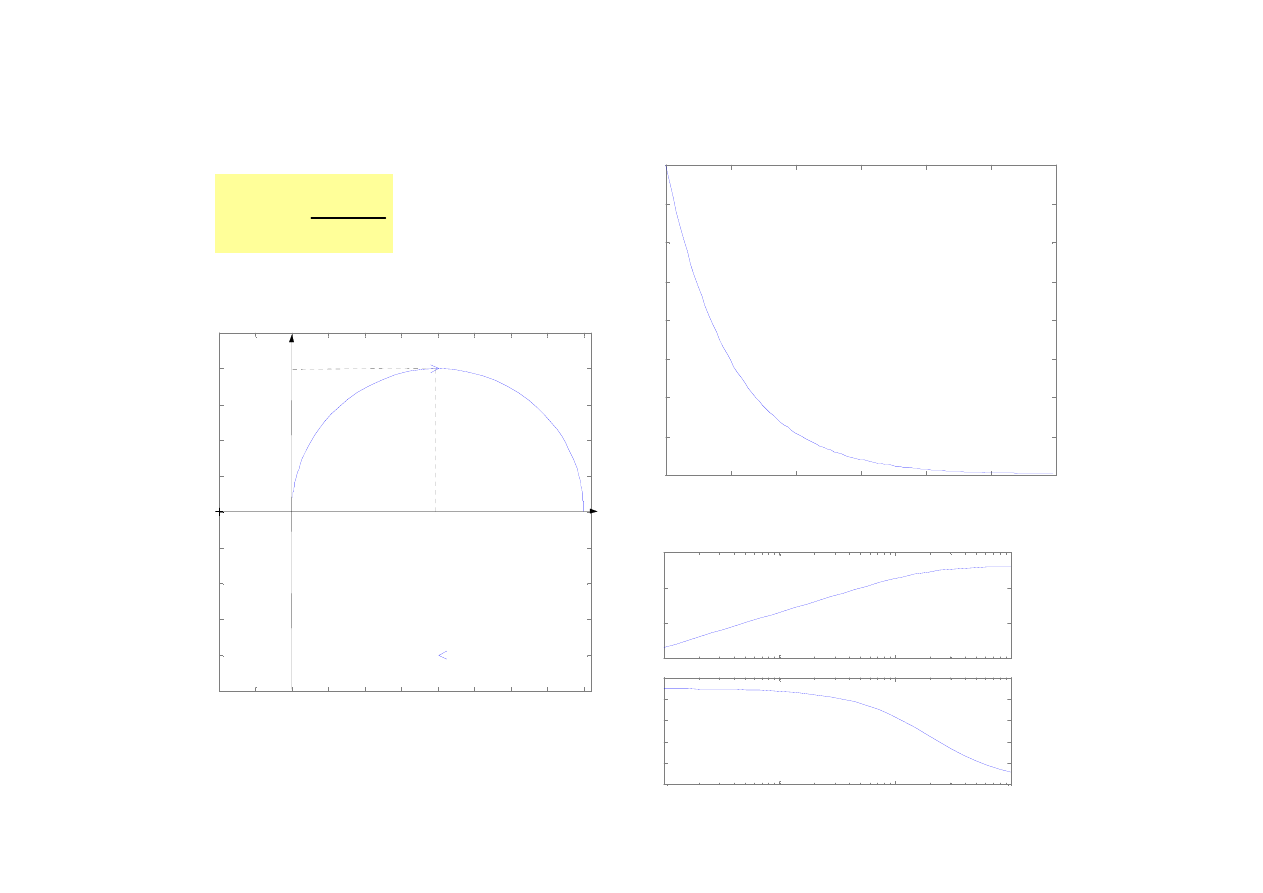
Człon różniczkujący rzeczywisty
sT
ks
s
K
+
=
1
)
(
Frequency (rad/sec)
P
has
e (
deg)
;
M
agni
tu
de
(
dB
)
Bode Diagrams
-40
-20
0
20
From: U(1)
10
-3
10
-2
10
-1
10
0
0
20
40
60
80
100
To
: Y
(1
)
Time (sec.)
Amp
lit
ud
e
Step Response
0
5
10
15
20
25
30
0
0.5
1
1.5
2
2.5
3
3.5
4
From: U(1)
To
: Y
(1
)
Real Axis
Im
aginar
y A
xis
Nyquist Diagrams
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
From: U(1)
To
: Y
(1
)
k/2T
k/2T
k/T
ω=0
27
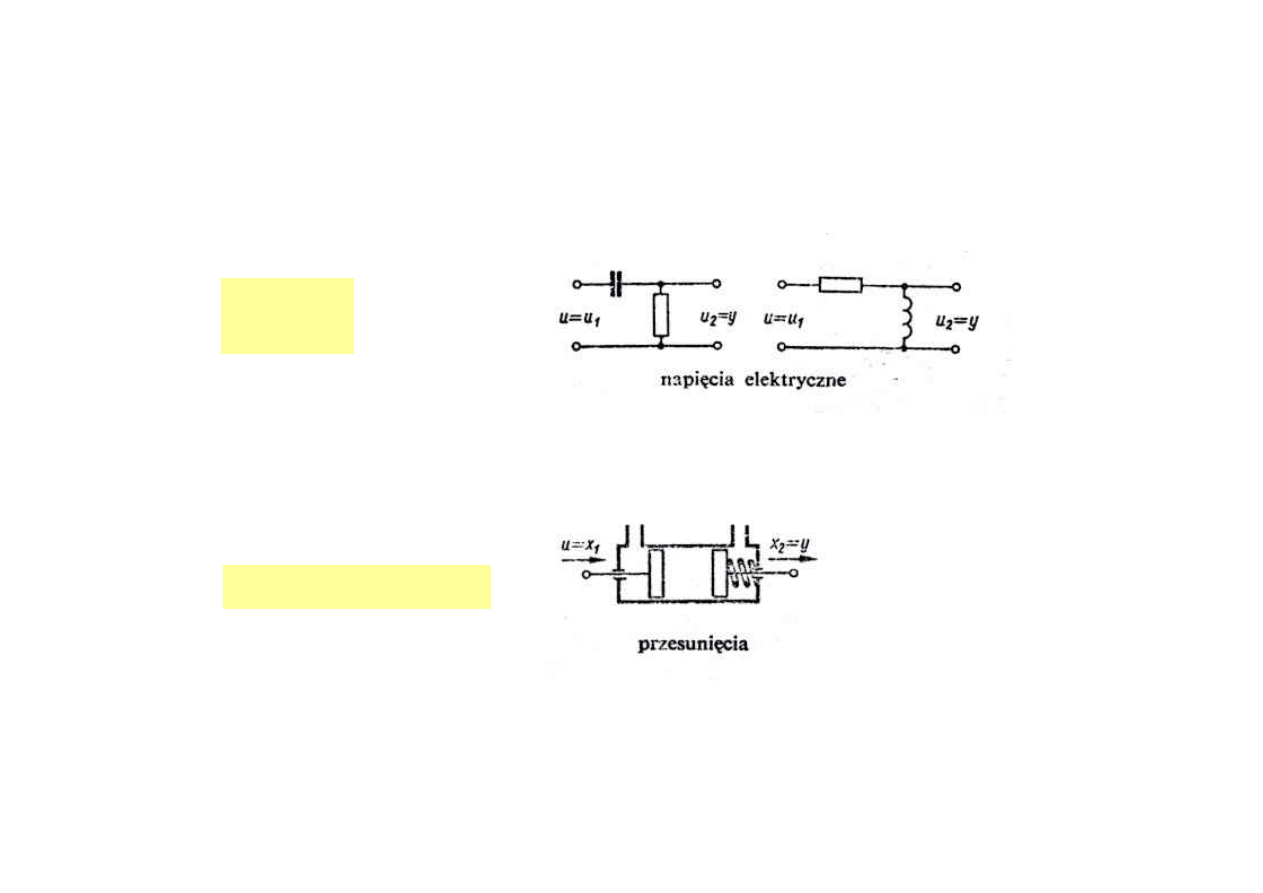
Człon różniczkujący rzeczywisty
układ CR
układ RL
układ pneumatyczny
28
Człon różniczkujący idealny
k
j
j
K
ks
s
K
dt
t
du
k
t
y
ω
ω
=
=
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1
)
(
t
k
t
h
to
t
t
u
gdy
δ
=
=
u(t)
y(t)
t
h(t) = k
δ
(t)

29
przykład
idealny kondensator
y(t)=i
u(t)=U
Człon różniczkujący idealny
30
Człon oscylacyjny
u(t)
y(t)
u
k
y
dt
dy
dt
y
d
ku
y
dt
dy
T
dt
y
d
T
n
n
n
n
n
2
2
2
2
2
2
2
2
lub
2
ω
ω
ςω
ς
=
+
+
=
+
+
2
2
2
2
2
2
)
(
1
2
)
(
n
n
n
n
n
s
s
k
s
K
s
T
s
T
k
s
K
ω
ςω
ω
ς
+
+
=
+
+
=
ω
n
pulsacja drgań własnych nietłumionych
T
n
okres drgań własnych nietłumionych
ζ
współczynnik tłumienia względnego
k współczynnik wzmocnienia
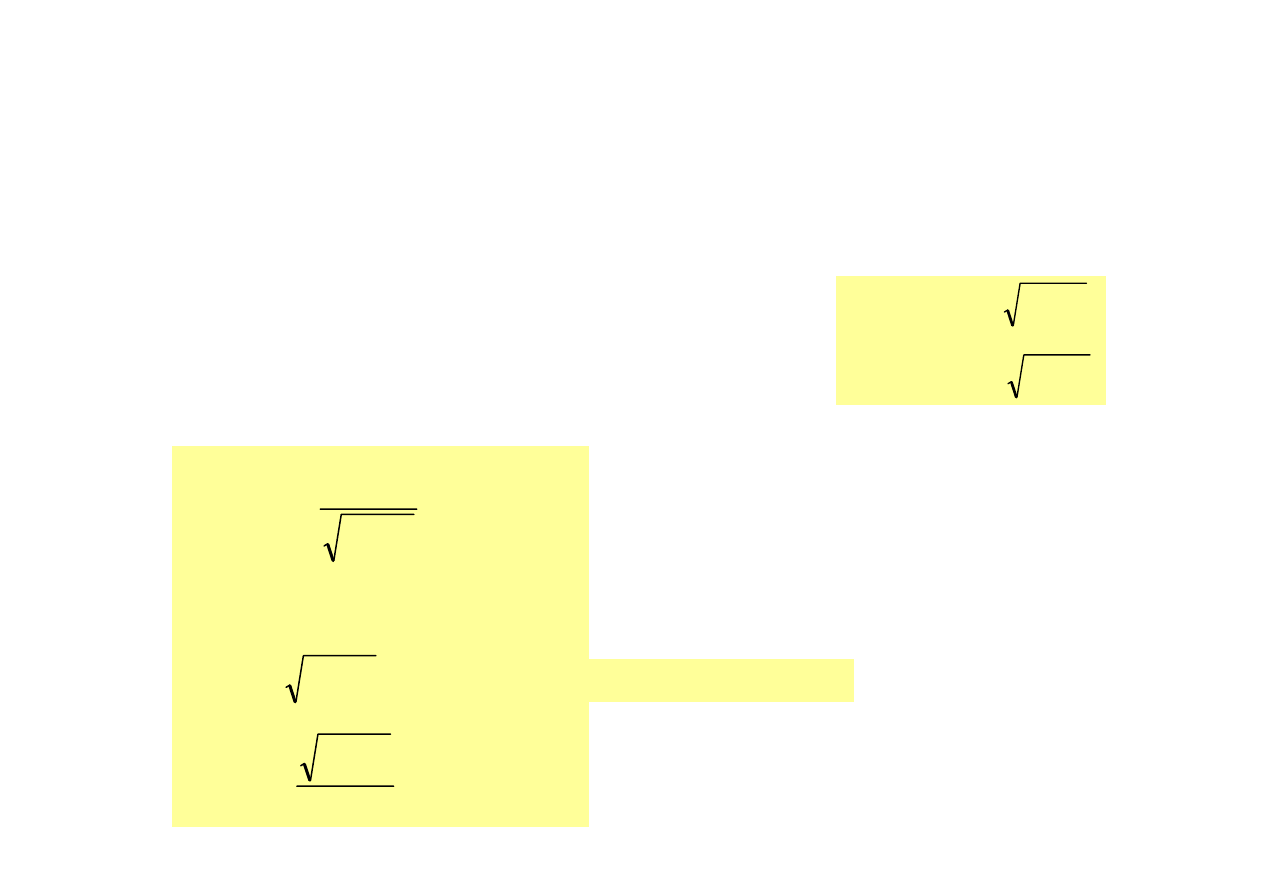
31
Człon oscylacyjny
Bieguny transmitancji, dla 0 <
ζ < 1
czyli rozwiązania równania M(s) = s
2
+2s
ζω
n
+
ω
n
2
= 0
są zespolone sprzężone o ujemnej części rzeczywistej:
)
1
(
)
1
(
2
2
2
1
ς
ς
ω
ς
ς
ω
−
−
−
=
−
+
−
=
j
s
j
s
n
n
Charakterystyka skokowa dana jest wzorem:
ς
ς
ϕ
ς
ω
ω
ϕ
ω
ς
ς
ω
2
2
2
1
1
)
sin(
1
1
)
(
−
=
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
−
=
−
arctg
gdzie
t
e
k
t
h
n
w
w
t
n
pulsacja drgań własnych tłumionych
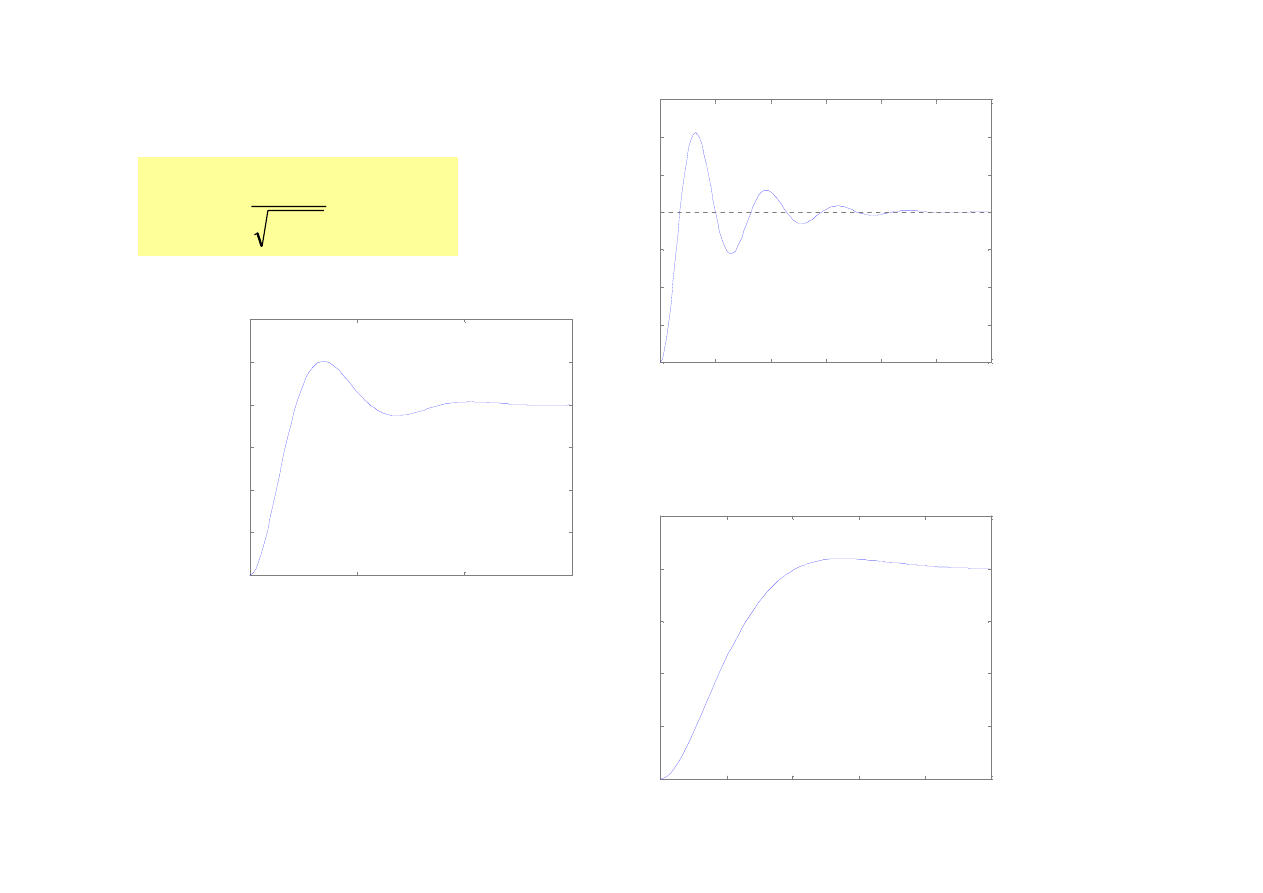
32
Time (sec.)
A
m
pl
itud
e
Step Response
0
5
10
15
0
5
10
15
20
25
30
From: U(1)
To
: Y
(1
)
Człon oscylacyjny
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
−
=
−
)
sin(
1
1
)
(
2
ϕ
ω
ς
ς
ω
t
e
k
t
h
w
t
n
Time (sec.)
A
m
plit
ud
e
Step Response
0
1.6
3.2
4.8
6.4
8
0
5
10
15
20
25
From: U(1)
To
: Y
(1
)
Time (sec.)
A
m
plit
ud
e
Step Response
0
5
10
15
20
25
30
0
5
10
15
20
25
30
35
From: U(1)
To
: Y
(1
)
k=20
ω
n
= 1
ζ = 0,2
k=20
ω
n
= 1
ζ = 0,7
k=20
ω
n
= 1
ζ = 0,4
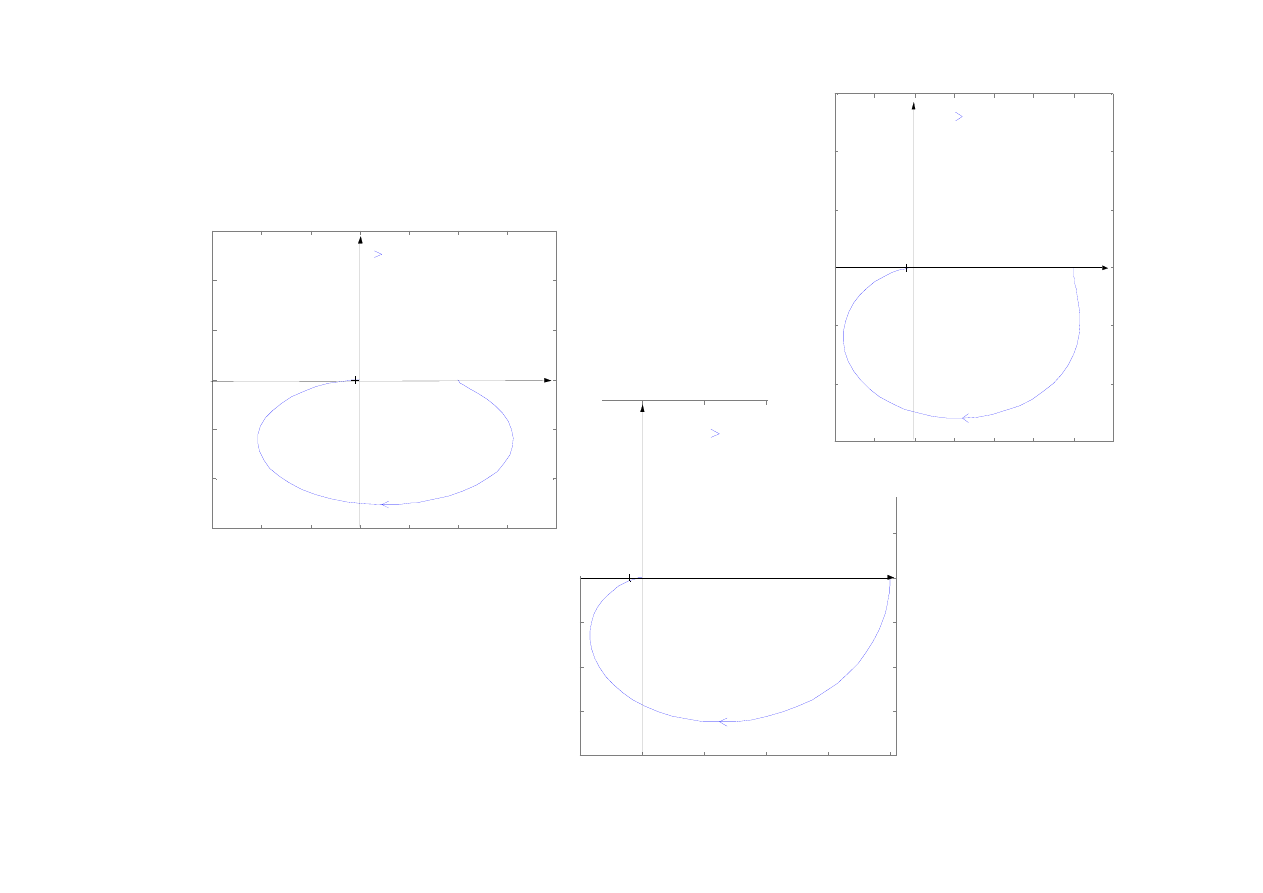
33
Real Axis
Im
agi
nar
y A
xi
s
Nyquist Diagrams
-5
0
5
10
15
20
-20
-15
-10
-5
0
5
10
15
20
From: U(1)
To
: Y
(1
)
k=20
ω
n
= 1
ζ = 0,7
Człon oscylacyjny
Real Axis
Im
agi
nar
y A
xi
s
Nyquist Diagrams
-10
-5
0
5
10
15
20
25
-30
-20
-10
0
10
20
30
From: U(1)
To
: Y
(1
)
Real Axis
Im
ag
ina
ry
A
xis
Nyquist Diagrams
-30
-20
-10
0
10
20
30
40
-60
-40
-20
0
20
40
60
From: U(1)
To
: Y
(1
)
k=20
ω
n
= 1
ζ = 0,2
k=20
ω
n
= 1
ζ = 0,4
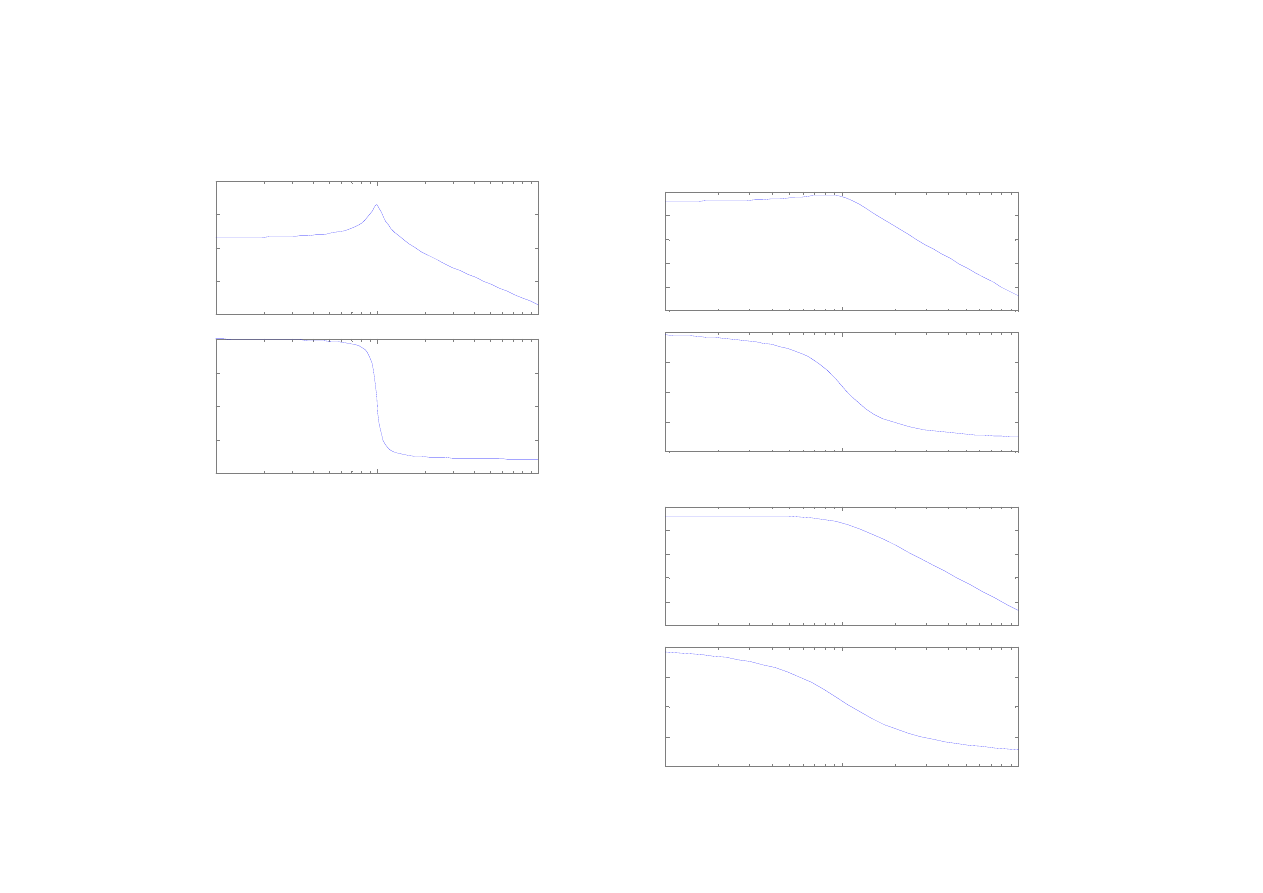
34
Człon oscylacyjny
Frequency (rad/sec)
P
has
e (
deg
);
M
ag
ni
tud
e
(d
B
)
Bode Diagrams
-20
-10
0
10
20
30
From: U(1)
10
-1
10
0
10
1
-200
-150
-100
-50
0
To
: Y
(1
)
Frequency (rad/sec)
P
has
e (
deg
);
M
ag
ni
tud
e
(d
B
)
Bode Diagrams
-20
-10
0
10
20
30
From: U(1)
10
-1
10
0
10
1
-200
-150
-100
-50
0
To
: Y
(1
)
Frequency (rad/sec)
P
has
e (
de
g)
;
M
agn
itud
e (
dB
)
Bode Diagrams
-20
0
20
40
60
From: U(1)
10
-1
10
0
10
1
-200
-150
-100
-50
0
To
: Y
(1
)
k=20
ω
n
= 1
ζ = 0,1
k=20
ω
n
= 1
ζ = 0,2
k=20
ω
n
= 1
ζ = 0,4
35
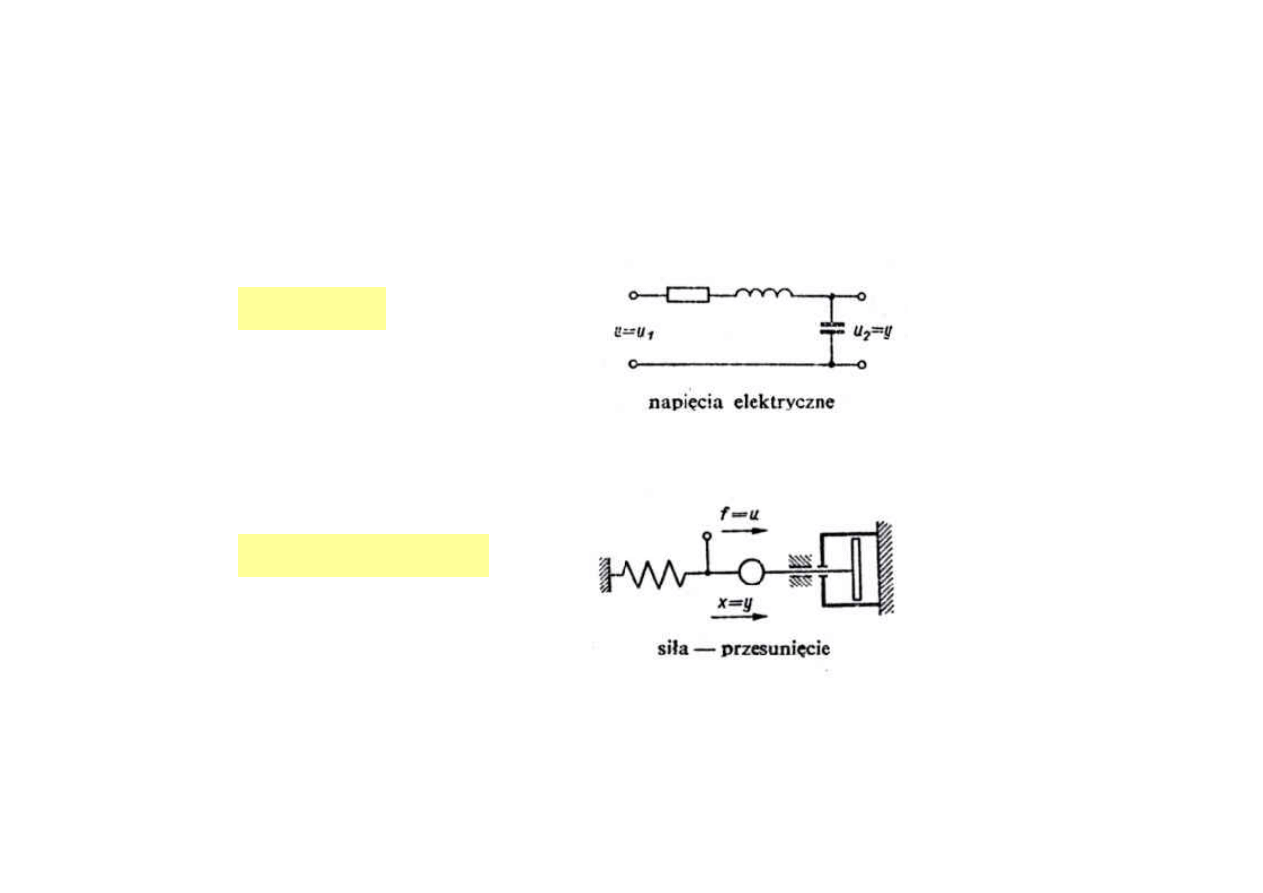
Człon oscylacyjny
Przykłady
układ RLC
układ mechaniczny
36
Człon opóźniający
0
)
(
sT
ke
s
K
−
=
)
(
)
(
0
T
t
ku
t
y
−
=
)
(
1
)
(
0
T
t
k
t
h
−
=
0
)
(
T
j
ke
j
K
ω
ω
−
=
t
h(t)
Q(
ω)
P(
ω)
u(t)
y(t)
37
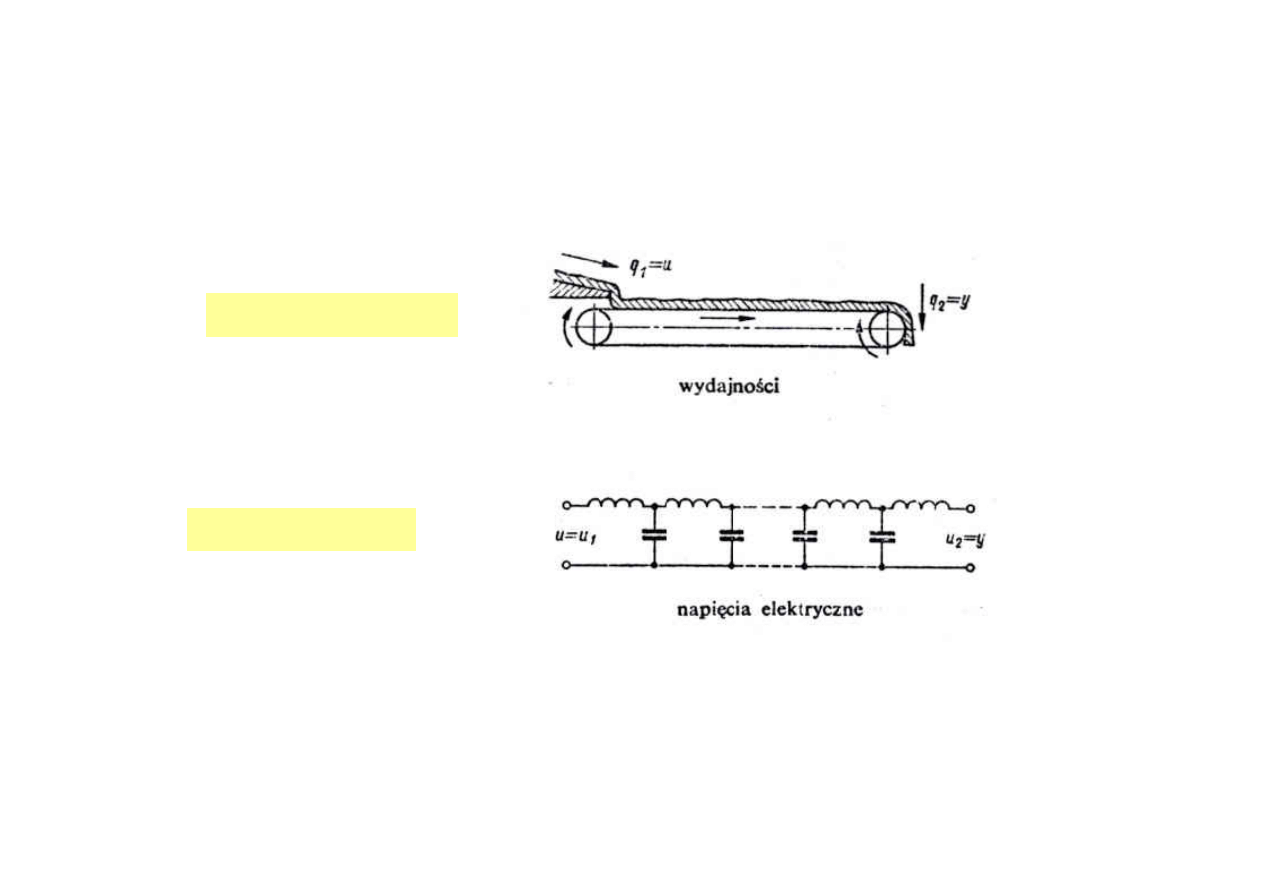
Człon opóźniający
układ elektryczny
układ mechaniczny
Wyszukiwarka
Podobne podstrony:
Podstawowe czlony dynamiczne id Nieznany
Lab5 Modelowanie dynamiki id 25 Nieznany
Dynamika id 145246 Nieznany
Modele dynamiczne id 305054 Nieznany
Dynamika a id 145299 Nieznany
Dynamika I id 145322 Nieznany
Analiza dynamiki id 59972 Nieznany
dynamika 4 id 145261 Nieznany
LAB2 pret krata dynamika id 259 Nieznany
4 dynamika id 38203 Nieznany (2)
programowanie dynamiczne id 396 Nieznany
Lab5 Modelowanie dynamiki id 25 Nieznany
Dynamika id 145246 Nieznany
4 Dynamika bryly sztywnej id 37 Nieznany (2)
zestaw 6 dynamika cd id 588136 Nieznany
Bania dynamiczne pali id 79279 Nieznany
dynamika kolo1 id 145330 Nieznany
Dynamika Atmosfery id 145300 Nieznany
więcej podobnych podstron