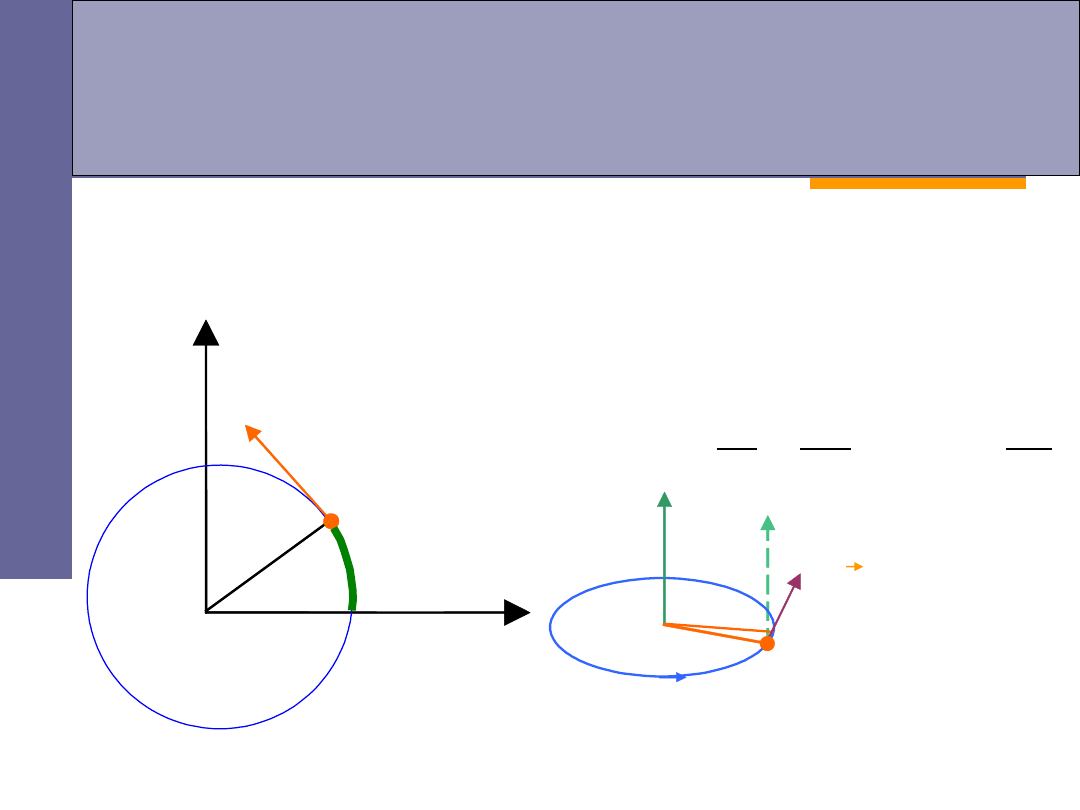
Ruch obrotowy punktu materialnego



ruch obrotowy po okręgu -

szczególny przypadek płaskiego

ruchu krzywoliniowego





r

s

x

y

v



A



droga kątowa –

położenie punktu A określamy za

pomocą kąta



r

s











droga liniowa

–

wyrażamy za pomocą drogi

kątowej



w sposób następujący:



prędkość kątowa:

r

dt

d

dt

ds







dt

d





















r

v





A









prędkość liniowa punktu A:

r

v













kierunek wektora



dany jest przez

regułę śruby
prawoskrętnej

dt

d











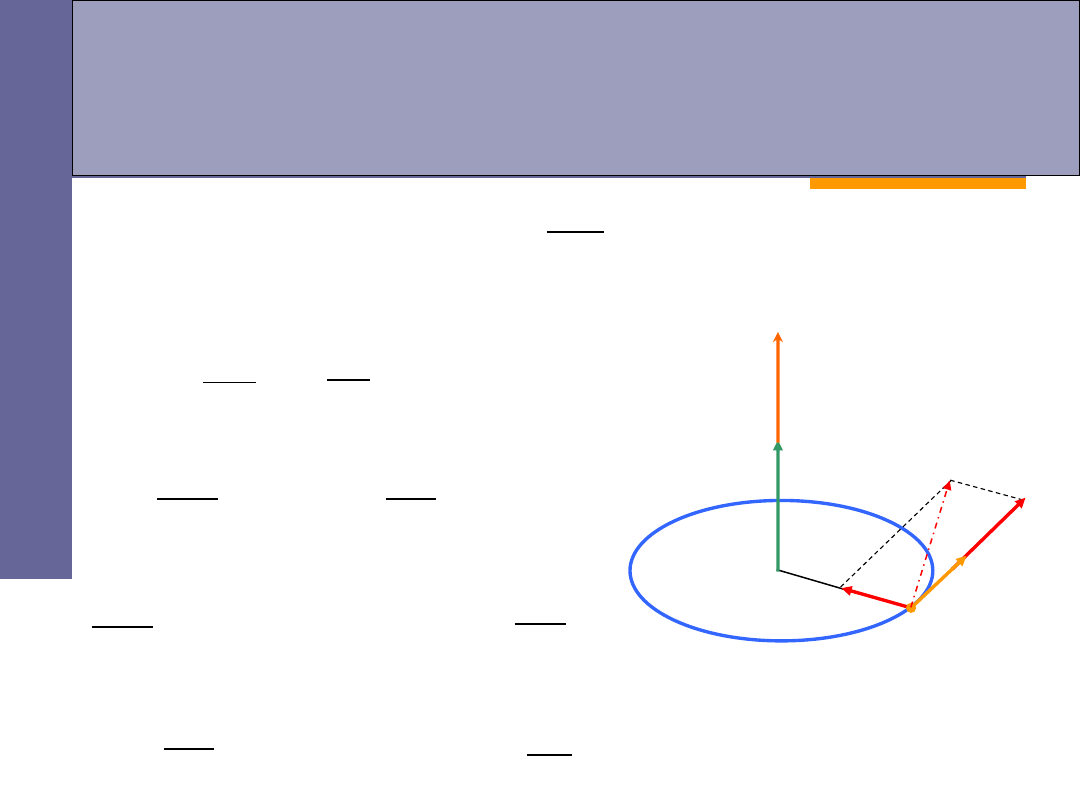
ruch przyspieszony

ruch opóźniony













r

















r





dt

v

d

a









przyspieszenie kątowe:



przyspieszenie styczne i dośrodkowe:

)

(

r

dt

d











dt

r

d

r

dt

d





















r

dt

d

a

s













r











dt

r

d

a

n













v











dt

v

d

a

s









|

|

r

v

a

n

2

|

|







s

a



v







n

a







a



Ruch obrotowy punktu materialnego

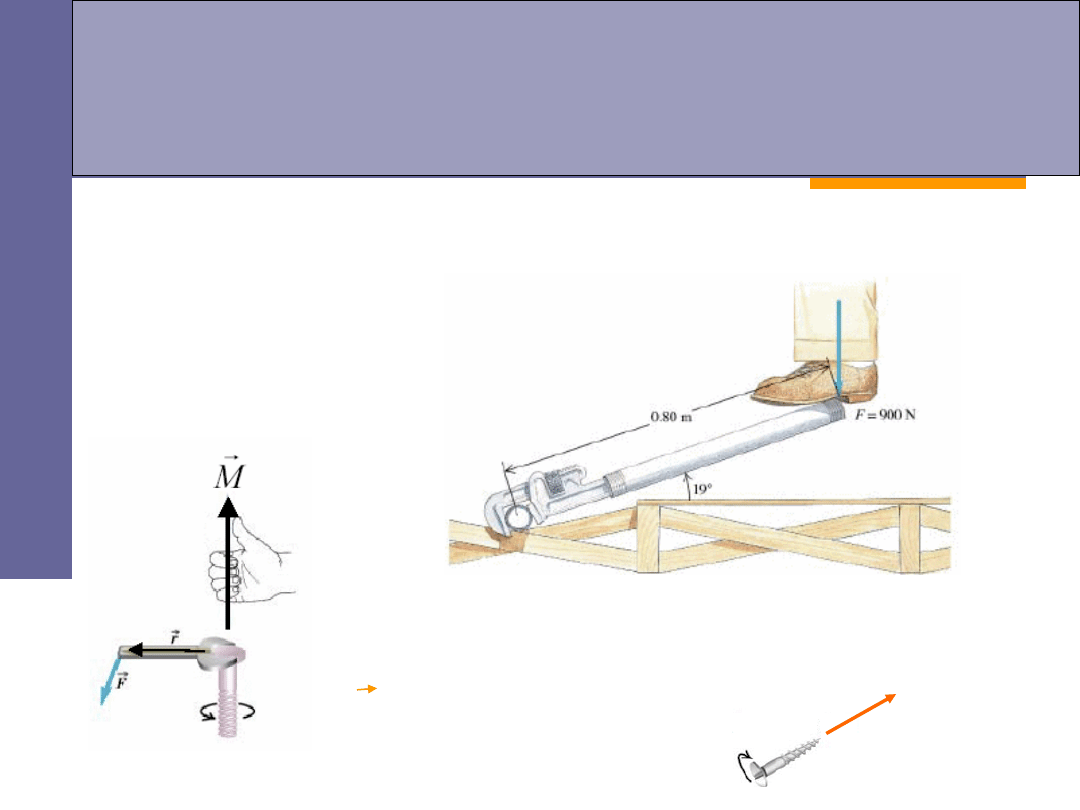
Moment siły

F

r

M













kierunek momentu sił wyznaczamy z reguły śruby

prawoskrętnej,

Wielkością fizyczną wywołującą obrót bryły sztywnej jest

moment

siły

(tzw.

moment obrotowy

):

Aby

spowodować ruch obrotowy bryły sztywnej niezbędna jest siła.



r

nazywamy ramieniem siły,

M





gdy:

0

||





M

F

r







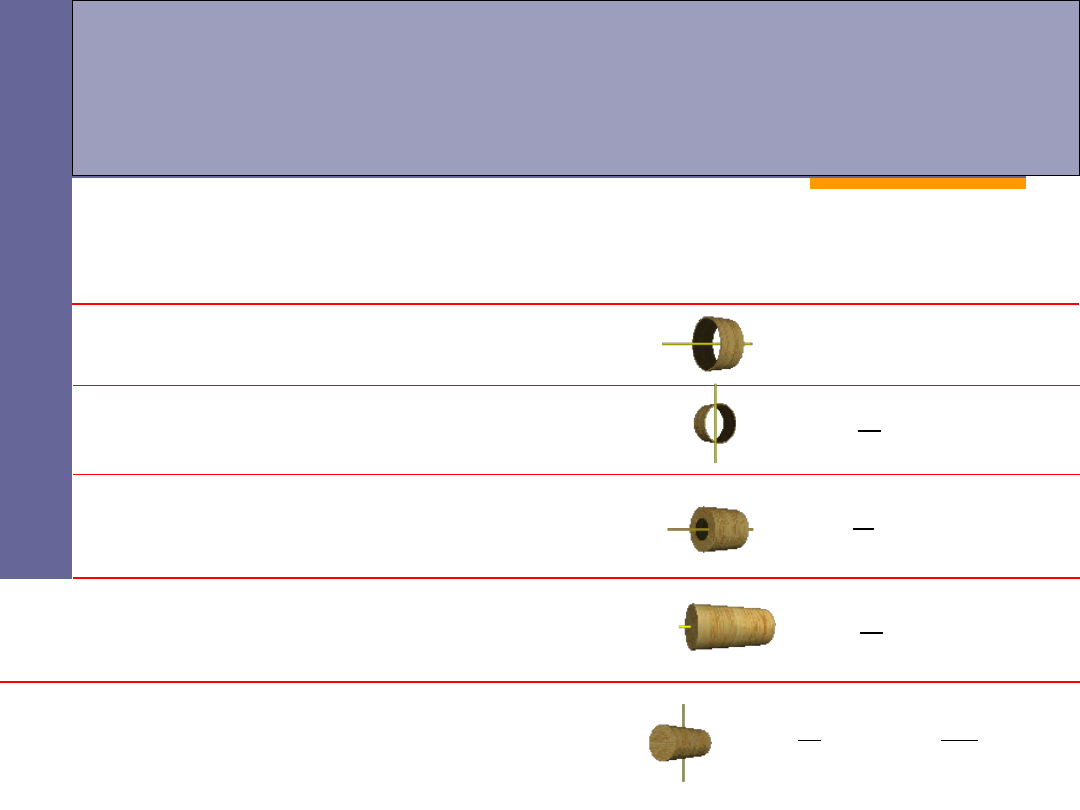
Moment bezwładności

-

przykłady





2

2

2

1

2

1

r

r

m

I









2

r

m

I







moment bezwładności

I

jest analogiczną wielkością do masy

m

w ruchu

postępowym. Chociaż masa ciała nie zależy od jego położenia to moment
bezwładności zależy od osi, wokół której obraca się ciało:



cienki pierścień o masie

m

i promieniu

r

obracający się wokół własnej osi:



pierścień o masie

m

i promieniach

r

1

i

r

2

obracający się wokół własnej osi:



walec o masie

m

, długości

L

i promieniu

r

obracający się wokół własnej osi:

2

2

1

r

m

I







cienki pierścień o masie

m

i promieniu

r

obracający się wokół osi prostopadłej:

2

2

1

r

m

I







walec o masie

m

, długości

L

i promieniu

r

obracający się wokół osi prostopadłej do

niego i przechodzącej przez środek:

2

2

12

1

4

1

L

m

r

m

I









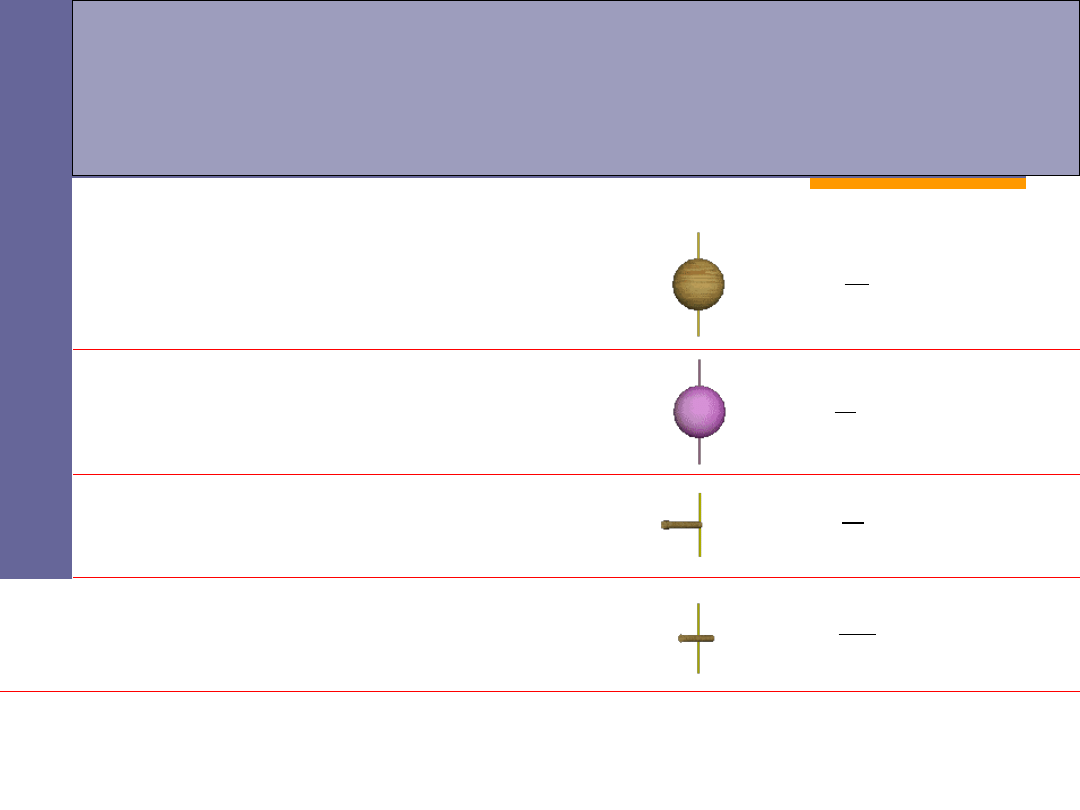
Moment bezwładności

-

przykłady

2

3

2

r

m

I





2

12

1

L

m

I





2

5

2

r

m

I







kula o masie

m

i promieniu

r

obracająca się wokół własnej osi:



sfera o masie

m

i promieniu

r

obracająca się wokół własnej osi:



pręt o masie

m

i długości

L

obracający się wokół osi prostopadłej
do niego i przechodzącej przez jego koniec:

2

3

1

L

m

I







pręt o masie

m

i długości

L

obracający się wokół osi prostopadłej
do niego i przechodzącej przez jego środek:



jednostką momentu bezwładności jest

2

m

kg



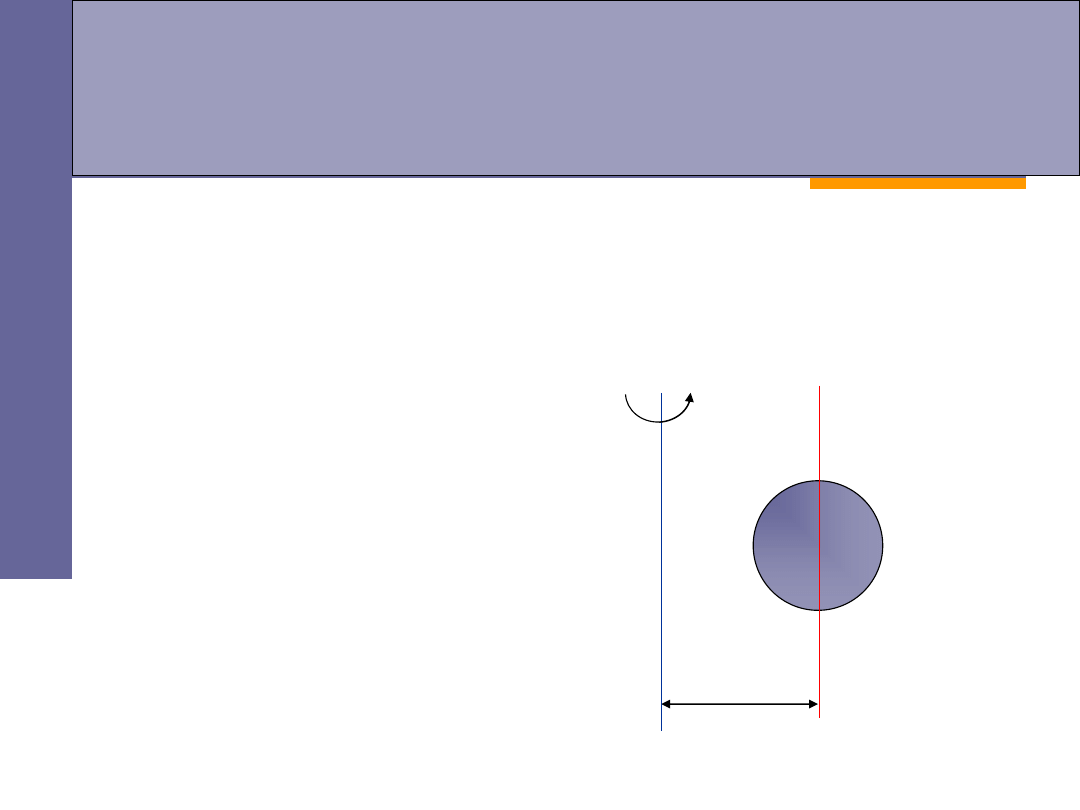
Twierdzenie Steinera

0

I

m





2

a

m

I

I

o







Moment

bezwładności

I

bryły sztywnej względem dowolnej osi jest

równy sumie momentu bezwładności

I

o

względem osi równoległej

przechodzącej przez środek masy bryły oraz iloczynu masy tej bryły
i kwadratu

odległości

a

obu osi:

a

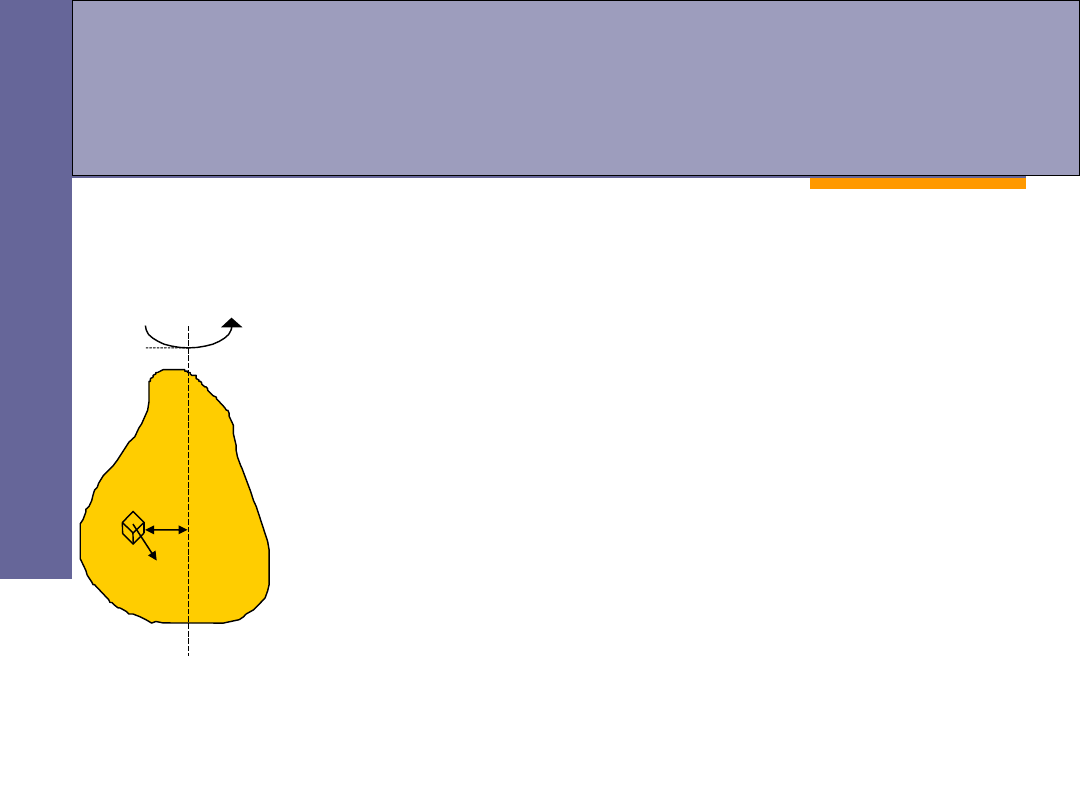
II zasada dynamiki dla ruchu
obrotowego

Moment sił działających na bryłę sztywną jest
równy iloczynowi momentu bezwładności tej bryły
i jej przyspieszenia kątowego





i

m



i

F



i

r

















n

i

i

i

i

r

m

r

M

1





i ostatecznie:



otrzymamy:













n

i

i

i

r

m

1

2









I

M











I

M

II zasada dynamiki dla ruchu
obrotowego

– moment pędu (kręt)

Pochodna momentu pędu bryły względem czasu jest
równa momentowi siły działającej na bryłę sztywną



II zasadę dynamiki możemy zapisać:











I

M

dt

d

I









dt

I

d

)

(









dt

L

d

M







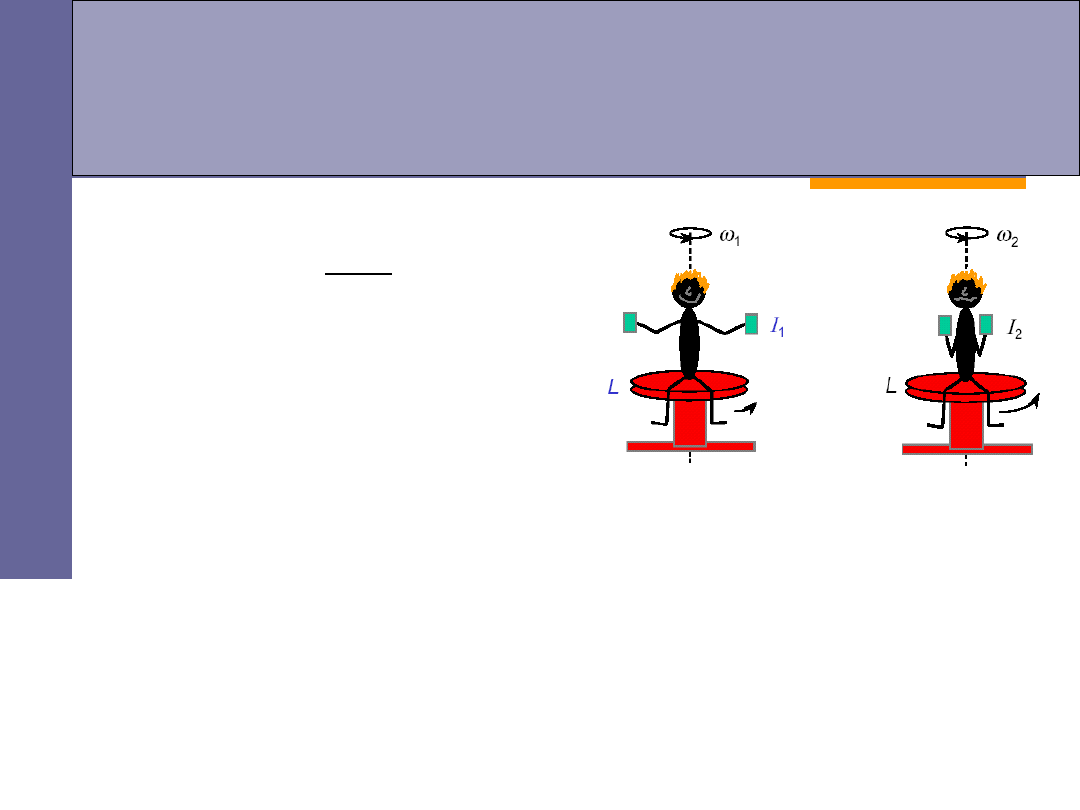
Zasada zachowania momentu
pędu (krętu)

0



M



const

L







Jeżeli moment wypadkowy sił
zewnętrznych działających
na bryłę równa się zeru,

to całkowity moment pędu

(kręt) pozostaje stały.

dt

L

d

M









moment sił zewnętrznych wynosi zero,



moment pędu jest zachowany,

2

2

1

1











I

I



ponieważ:

2

1

I

I





zatem:

1

2









zmniejszenie momentu bezwładności

przyspiesza

obrót

Energia kinetyczna ruchu
obrotowego

2

2

2

2

1

2

1













i

i

i

i

ki

r

m

v

m

E













n

i

i

i

r

m

1

2

2

2

1





Energię kinetyczną –

obliczamy sumując energię kinetyczną

poszczególnych punktów bryły:



dla całej bryły mamy zatem:











n

i

i

i

k

r

m

E

1

2

2

2

1



2

2

1







I

E

k

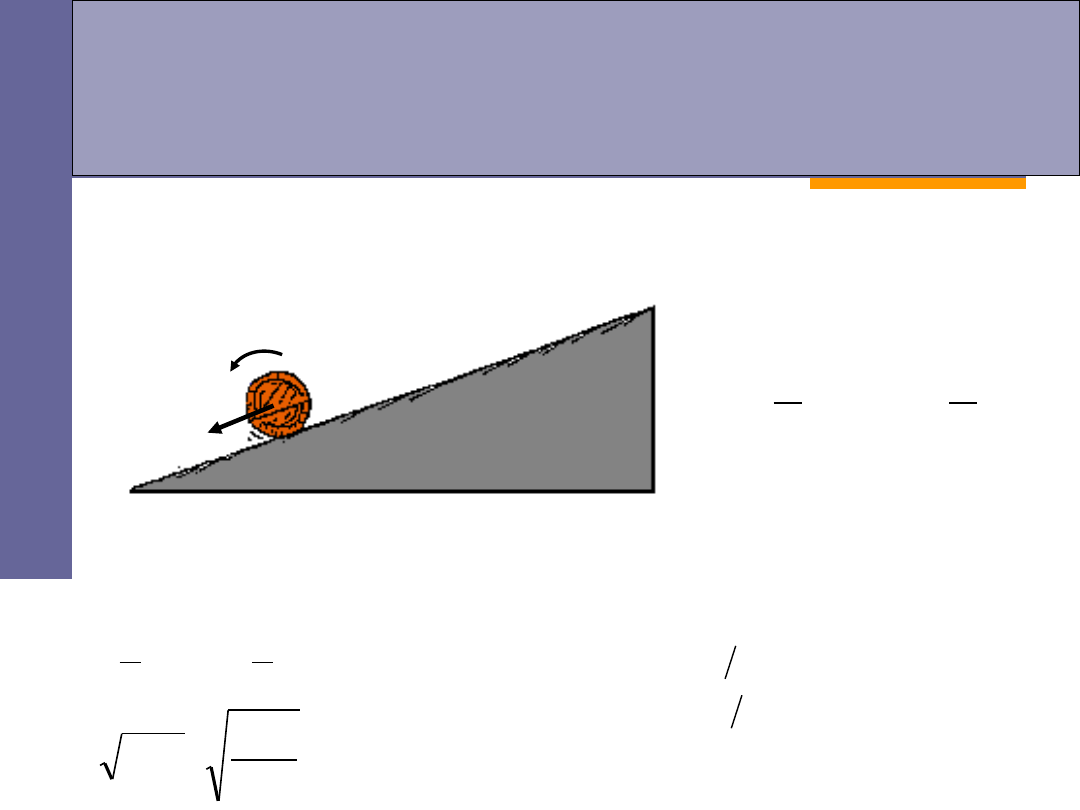
Energia kinetyczna ruchu
postępowo – obrotowego

1

1

2







c

gh

v

k

v



m





2

2

2

1

2

1











I

v

m

E

k

2

2

2

1

2

1

k

k

I

v

m

mgh











2

r

m

c

I

r

v

































kula

5

2

,

walec

2

1

ściance

cienkiej

o

rura

1

c





Energia kinetyczna

obracającej się bryły jest sumą energii kinetycznej

ruchu obrotowego i energii kinetycznej środka masy:



jeżeli wysokość równi wynosi

h

, a promień ciała

r

, to obliczmy prędkość ciała

u podstawy równi:

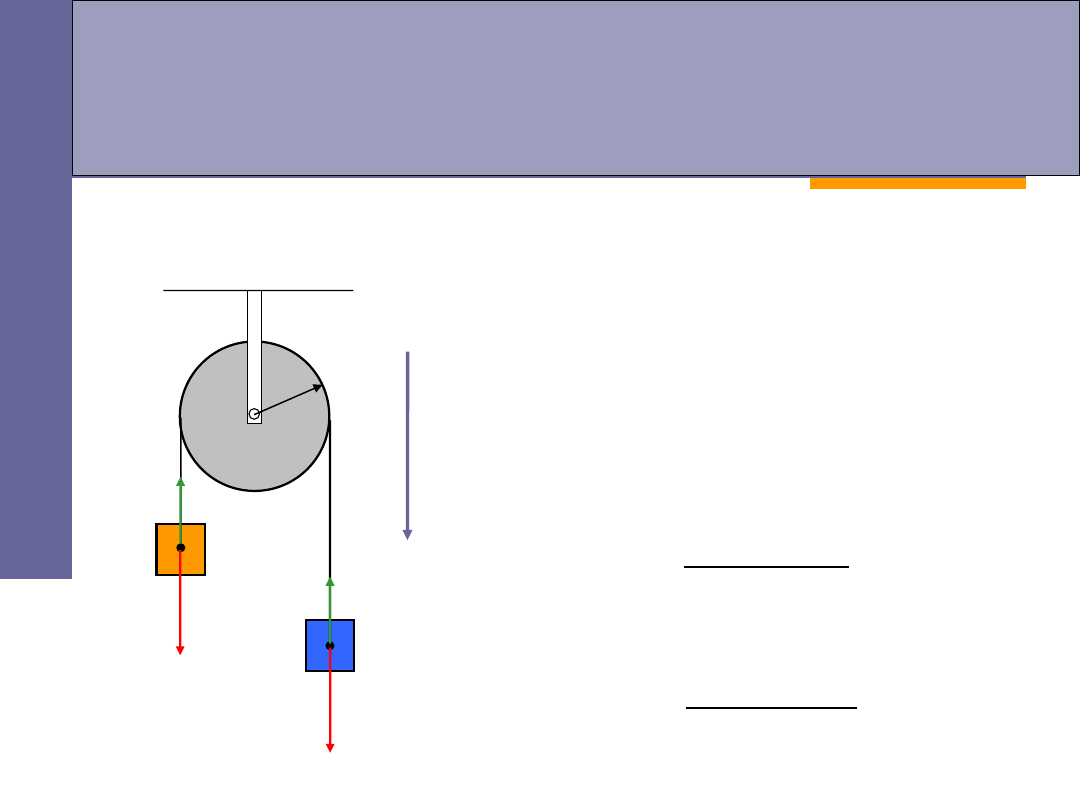
Przykłady – maszyna Atwooda

g

m



1

g

m



2

N





obliczmy przyspieszenie, z jakim poruszają się masy oraz naciąg nici:

bloczek nieruchomy:

g

m

N

a

m















1

1

m

1

m

2

m

r

N



a



N

g

m

a

m















2

2

g

m

m

a

m

m















)

(

)

(

1

2

2

1

g

m

m

m

m

a













2

1

1

2

g

m

m

m

m

N













2

1

2

1

2

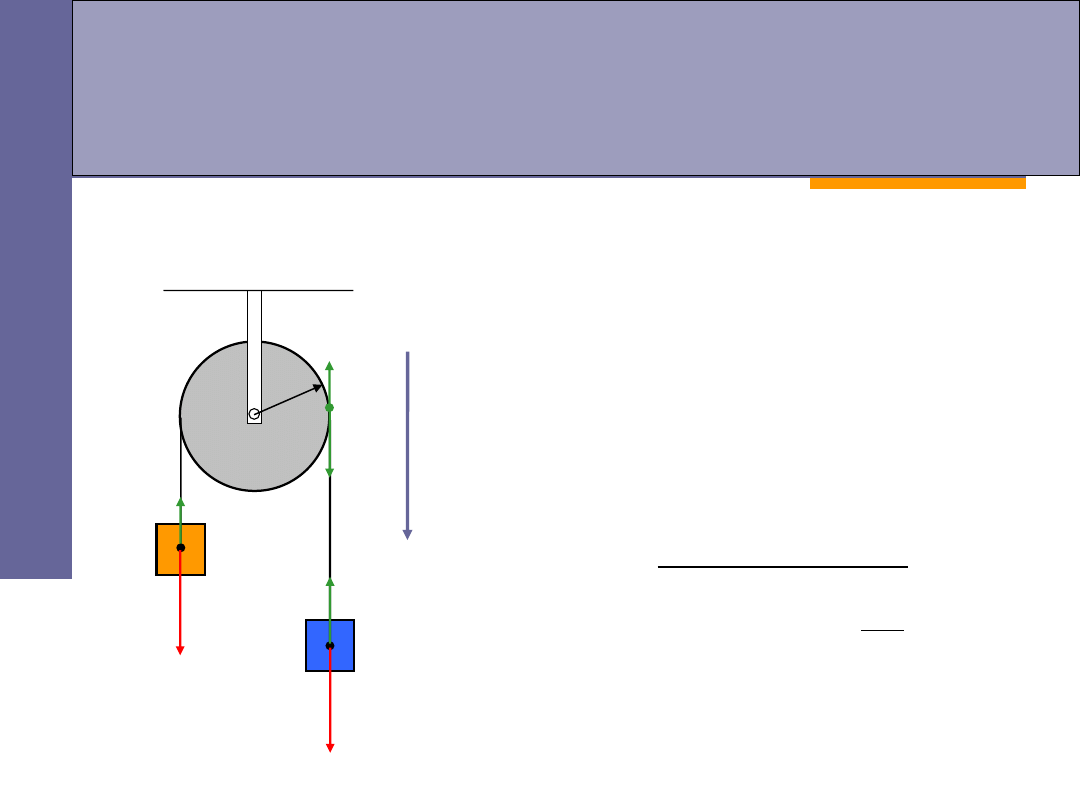
Przykłady – maszyna Atwooda

g

m



1

g

m



2

2

N





obliczmy przyspieszenie, z jakim poruszają się masy oraz naciąg nici:

bloczek ruchomy:

g

m

N

a

m















1

1

1

m

1

m

2

m

r

1

N



a



2

2

2

N

g

m

a

m















g

m

m

m

m

m

a















2

2

1

1

2

......

1



N



2

N



1

N

























I

N

N

r

M

)

(

1

2

......

2



N



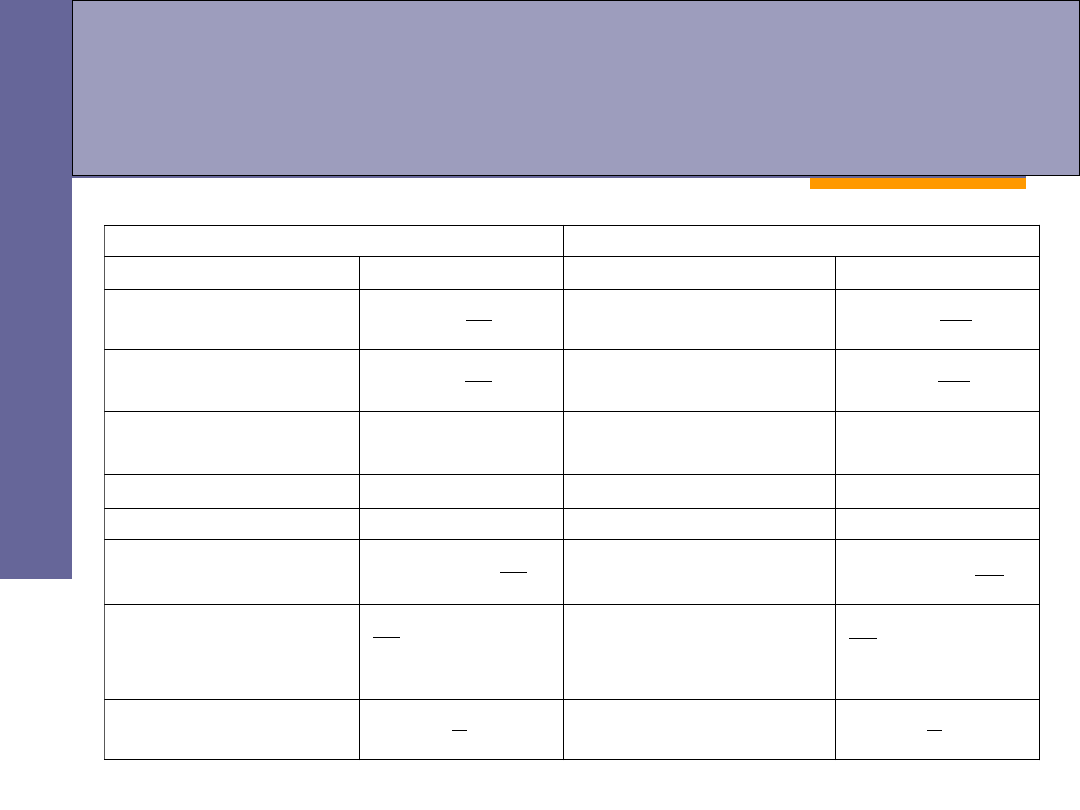
Analogia między ruchem
postępowym i obrotowym

Ruch prostoliniowy

Ruch obrotowy

Droga liniowa

s



Droga kątowa





Prędkość liniowa

dt

s

d

v







Prędkość kątowa

dt

d











Przyspieszenie
liniowe

dt

v

d

a







Przyspieszenie
kątowe

dt

d











Masa

m

Moment
bezwładności

I

Pęd

v

m

p









Moment pędu











I

L

Siła

F



Moment siły

M



II zasada dynamiki

dt

p

d

a

m

F













II zasada dynamiki

dt

L

d

I

M















Zasada
zachowania pędu

const

p

dt

p

d











0

Zasada zachowania
momentu pędu

const

L

dt

L

d











0

Energia kinetyczna

2

2

1

v

m

E

k





Energia kinetyczna

2

2

1







I

E

k