BRYŁA SZTYWNA

Zad. 1.
Człowiek o masie m stoi na brzegu płyty o promieniu R i momencie bezwładności I, mogącej
obracać się bez tarcia wokół osi prostopadłej do płaszczyzny płyty i przechodzącej przez jej
środek. Człowiek zaczyna poruszać się po obwodzie płyty. Jaką drogę względem płyty pokona
człowiek do momentu kiedy zatoczy on pełen okrąg w nieruchomym układzie odniesienia?

Zad. 2.

Ile wynosi praca, jaką należy wykonać, aby koło zamachowe o momencie bezwładności I
rozpędzić tak, by wykonywało n obrotów w ciągu jednostki czasu?

Zad. 3.

Wirówka obracająca się z częstotliwością 3000 obr./min została wyłączona i zatrzymała się
po czasie 30 s. Oblicz średnie przyspieszenie kątowe i całkowitą liczbę obrotów od chwili
wyłączenia wirówki do jej zatrzymania.

Zad. 4.

Nieruchomy walec o momencie bezwładności 25 kg∙m

2

został wprawiony w ruch obrotowy

wokół osi równoległej do tworzącej i przechodzącej przez jego środek. Moment siły względem
osi obrotu wynosił 50 Nm. Po jakim czasie od chwili rozpoczęcia obracania się walec wykona 400
obrotów? Wiadomo, że jego prędkość kątowa rośnie liniowo, poczynając od wartości 0.

Zad. 5.

Metalowe koło o momencie bezwładności 120 kg∙m

2

wiruje z prędkością kątową 25 1/s wokół

osi przechodzącej przez środek koła. Oblicz moment siły hamującej, która spowoduje
zatrzymanie się koła po czasie 20 s.

Zad. 6.

Koło zamachowe pod wpływem siły napędzającej obracało się z częstotliwością 16 Hz. Kiedy
wyłączono silnik napędzający koło, zatrzymało się ono po 50 s. Jaki był moment siły hamującej?
Moment bezwładności koła wynosił 50 kg∙m

2

.

Zad. 7.

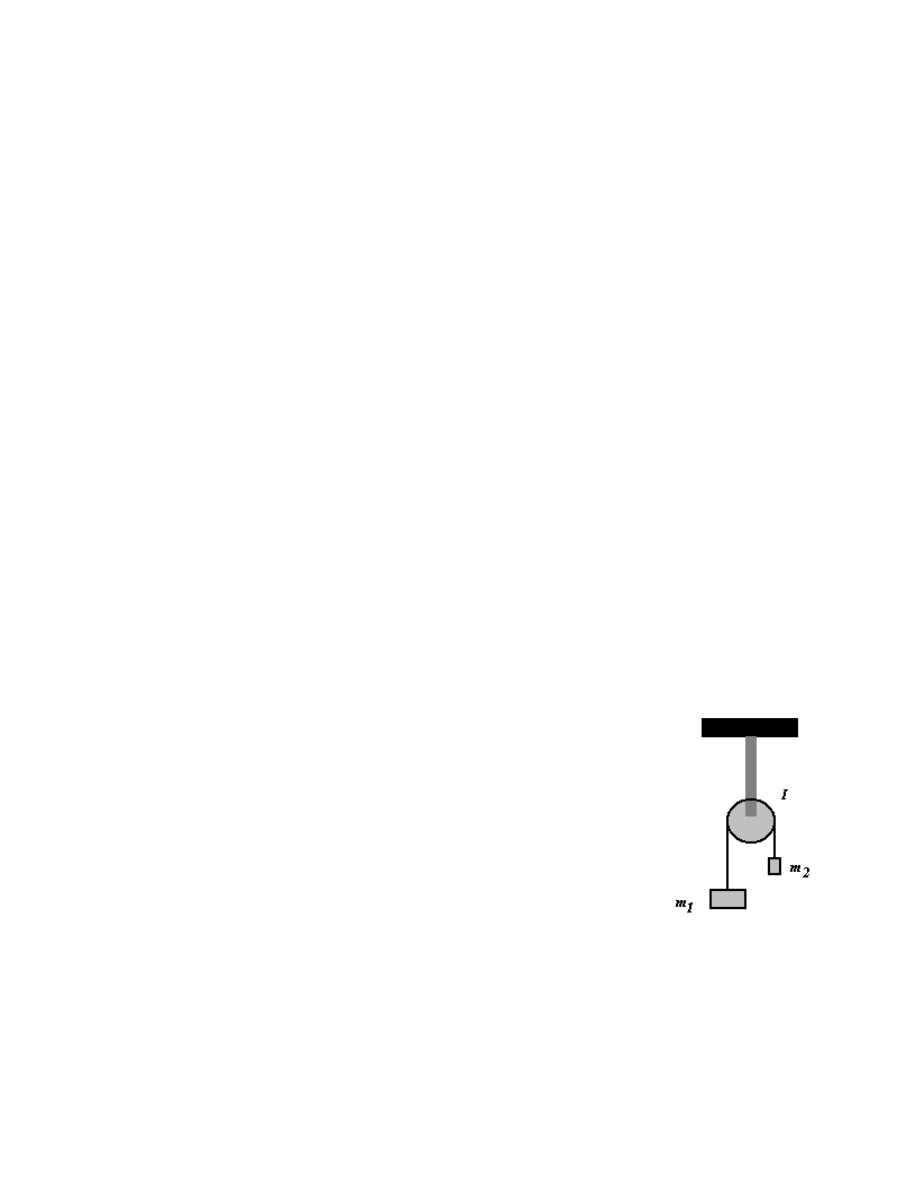
Przez blok nieruchomy o momencie bezwładności I i promieniu R,
przerzucono nić i na jego końcach umieszczono dwa ciężarki o masach m

1

i m

2

. Jakie będą siły napinające nici po obu stronach bloku, jeżeli układ

ciężarków zacznie poruszać się pod wpływem siły ciężkości?

Zad. 8.
Na jednorodny walec o masie 4 kg nawinięta jest linka, na której końcu umocowany jest ciężarek
o masie 1 kg. Z jakim przyspieszeniem będzie opadał ciężarek? Walec może swobodnie i bez
tarcia obracać się względem osi przechodzącej przez jego środek.

Zad. 9.

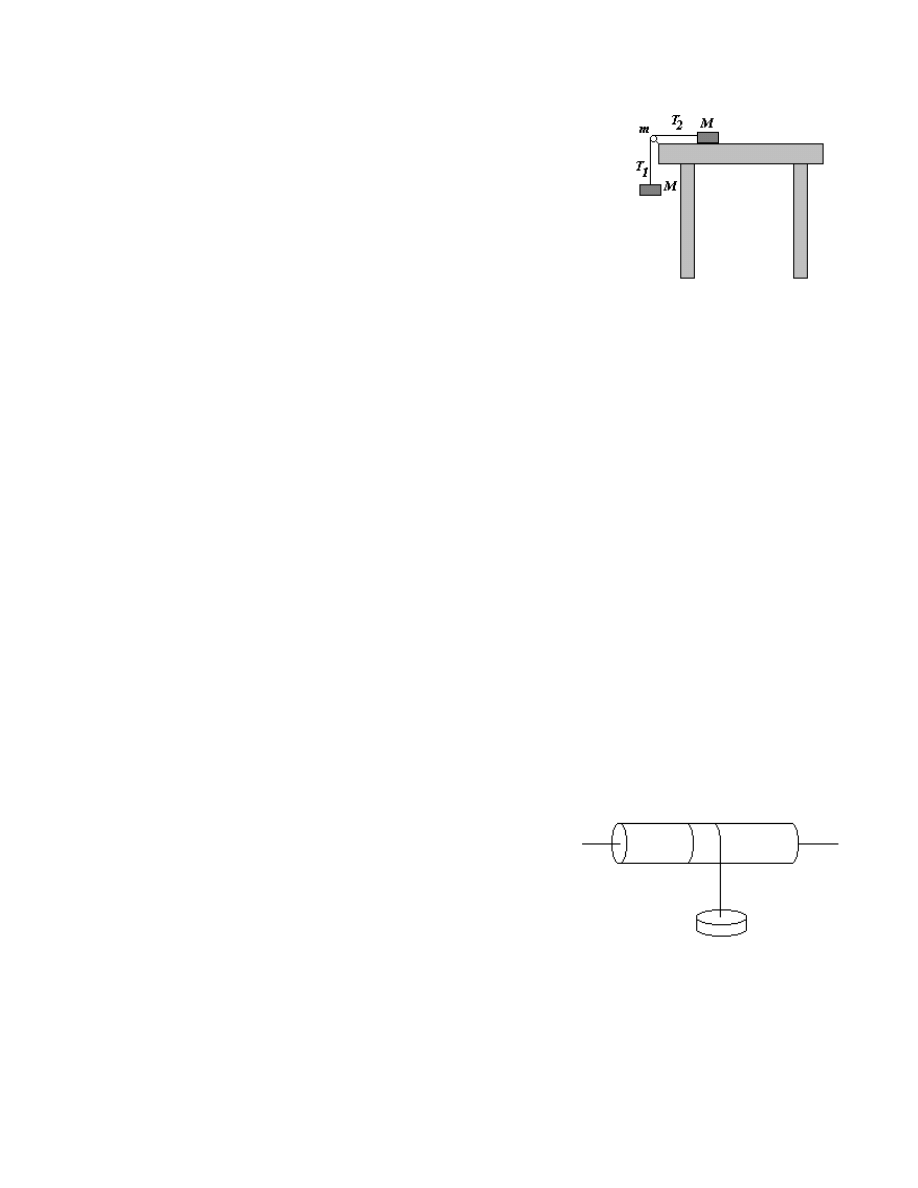
Blok nieruchomy o masie 0,5 kg umieszczony jest na krawędzi
stołu. Przez blok przełożono linkę, do której końców
przymocowano dwa jednakowe ciężarki o masach 0,5 kg. Z jakim
przyspieszeniem będzie przesuwał się ciężarek po stole?
Współczynnik tarcia o stół wynosi 0,2.

Zad. 10.

Po stole toczy się bez poślizgu moneta o masie 50 g z szybkością 4 m/s.
Jaka jest jej energia całkowita?

Zad. 11.

Jednorodna kula toczy się bez poślizgu po poziomej powierzchni. Jaki jest stosunek energii
kinetycznej ruchu postępowego kuli do jej całkowitej energii kinetycznej?

Zad. 12.

Obręcz i krążek o jednakowych masach toczą się bez poślizgu po poziomej powierzchni
z jednakowymi prędkościami v. Oblicz całkowitą energię kinetyczną krążka. Całkowita energia
kinetyczna obręczy wynosi 16 J.

Zad. 13.

Energia kinetyczna wału obracającego się z częstotliwością 10 obr/s wynosi 120 J. Jaki jest
moment pędu wału?

Zad. 14.

Z jaką liniową szybkością v będzie się poruszać środek masy obręczy staczającej się bez poślizgu
z równi pochyłej w jej najniższym punkcie? Wysokość równi wynosi 1 m, a obręcz zaczęła staczać
się ze szczytu równi z zerową prędkością początkową.

Zad. 15.

Wentylator obracał się z częstotliwością 15 obr/s. Po wyłączeniu zasilania wentylatora jego
łopatki wykonały jeszcze 75 obrotów, a siły oporów ruchu wykonały pracę 43,3 J. Jakie wartości
mają moment bezwładności obracającej się części wentylatora i moment sił oporów ruchu?
Zakładamy, że prędkość obrotowa wentylatora od chwili wyłączenia go malała liniowo.

Zad. 16.

Na walec o promieniu 10 cm i momencie bezwładności 0,49
kg∙m

2

nawinięta jest linka, do której końca przywiązany jest

ciężarek o masie 2 kg. Walec może swobodnie obracać się
wokół osi przechodzącej przez jego środek. Jaką różnicę
wysokości powinien pokonać ciężarek, aby swobodnie
opadając pod wpływem siły ciężkości spowodować obracanie
się walca z częstotliwością 3 obr/min?

Zad. 17.

Jednorodny pręt o długości 15 cm stoi pionowo na stole. Jaką prędkość będzie miał górny koniec
pręta w chwili dotknięcia stołu, jeżeli pręt wywróci się bez poślizgu?

Zad. 18.

Platforma obrotowa o masie 341 kg wiruje w płaszczyźnie poziomej z częstotliwością 12 obr/min
wokół osi przechodzącej przez jej środek. Na brzegu platformy stoi człowiek o masie 75 kg.
Z jaką częstotliwością będzie obracać się platforma, jeżeli człowiek przejdzie do jej środka?
Platforma ma kształt dużego krążka, człowieka można uznać za masę skupioną w jednym punkcie.

Zad. 19.

Łyżwiarz wiruje na lodzie z częstotliwością 1Hz, mając rozłożone szeroko ręce. Jeśli przyciągnie
ręce do tułowia jego moment bezwładności zmaleje z 2,94 do 0,98 kg∙m

2

. Z jaką częstotliwością

będzie obracać się łyżwiarz po przyciągnięciu rąk?

Zad. 20.

Oblicz moment bezwładności „hantli” składającej się z cienkiego pręta o masie m

1

= 0,1 kg

i długości l = 0,2 m oraz dwóch kul o masach m

2

= 0,5 kg i o promieniach R = 5 cm względem osi

prostopadłej do pręta i przechodzącej przez jego środek ciężkości.

Zad. 21.

Kulka o bardzo małym promieniu, której masa wynosi m = 1 g porusza się po okręgu
o promieniu R = 12 cm. Oblicz moment pędu tej kulki względem środka okręgu, jeżeli okres
ruchu tej kulki wynosi T = 0,2 s.

Zad. 22.

Jednorodny walec o masie m = 3 kg i promieniu R = 20 cm obraca się wokół osi symetrii
z częstotliwością f = 100 1/s. Oblicz moment pędu walca.

Zad. 23.

Przy uruchomieniu silnika elektrycznego na jego wirnik o momencie bezwładności I = 3 kg∙m

2

działa moment siły M = 30 N∙m. Po jakim czasie wirnik osiągnie częstotliwość f = 1200 obr/min?

Zad. 24.

Cienka obręcz o promieniu R = 5 cm toczy się bez poślizgu z równi pochyłej o kącie nachylenia α
= 30

o

. Jaką prędkość kątową będzie miała obręcz po czasie t = 5 s od początku ruchu?

Zad. 25.

Jednorodny walec o masie m = 0,4 kg obraca się jednostajnie wokół osi tak, że jego energia
kinetyczna wynosi E = 10 J. Oblicz prędkość liniową punktów na obwodzie walca.

Zad. 26.

Jaką pracę należy wykonać, aby słup telegraficzny o masie M = 200 kg, do którego wierzchołka
przymocowano poprzeczkę o masie m = 30 kg, podnieść z położenia poziomego do pozycji
pionowej, jeżeli długość słupa jest równa l = 10 m? Przyspieszenie ziemskie przyjąć g = 10 m/s

2

.

Zad. 27.

Znaleźć hamujący moment siły, który może zatrzymać w ciągu czasu t = 20 s koło zamachowe
o masie m = 50 kg i promieniu R = 0,3 m obracające się z częstotliwością f = 30 s

-1

. Założyć,

że masa koła zamachowego rozmieszczona jest na jego obwodzie. Jaka praca będzie potrzebna
do zatrzymania tego koła zamachowego?

Zad. 28.

Dwie poziome tarcze wirują wokół pionowej osi przechodzącej przez ich środek. Momenty
bezwładności tarcz wynoszą I

1

oraz I

2

, a ich prędkości kątowe α

1

i α

2

. Po upadku tarczy górnej na

dolną obie tarcze (w wyniku działania sił tarcia) obracają się razem jak jedno ciało. Wyznaczyć:

a) prędkość kątową tarcz po złączeniu;

b) pracę wykonaną przez siły tarcia.

Zad. 29.

Na brzegu poziomo ustawionej tarczy o momencie bezwładności I (względem osi pionowej
przechodzącej przez środek tarczy) i promieniu R znajduje się człowiek o masie m. Obliczyć
prędkość kątową tarczy, gdy człowiek zacznie poruszać się wzdłuż jej brzegu z prędkością v
względem niej.

Zad. 30.

Człowiek siedzi na krześle obrotowym trzymając oburącz za oś pionowo obracające wokół tej osi
(pionowej) z prędkością kątową ω

o

koło rowerowe o momencie bezwładności I

o

. Wyznaczyć

prędkość kątową ω

1

ruchu obrotowego krzesła po:

a) obróceniu przez człowieka koła o kąt 180

o

;

b) zahamowaniu koła przez człowieka.

Moment bezwładności stolika z człowiekiem wynosi I.

Zad. 31.

Listwa drewniana o długości l i masie m może się obracać dookoła osi prostopadłej do listwy,
przechodzącej przez jej środek. W koniec listwy trafia pocisk o masie m

1

, lecący z prędkością v

1

w kierunku prostopadłym do osi i do listwy. Znaleźć prędkość kątową, z jaka listwa zacznie się
obracać, gdy utkwi w niej pocisk.