Dynamika bryły sztywnej



ruch obrotowy punktu materialnego



definicja bryły sztywnej



dynamika bryły sztywnej



ruch obrotowy



ruch obrotowo

– postępowy



moment bezwładności



II zasada dynamiki dla ruchu obrotowego

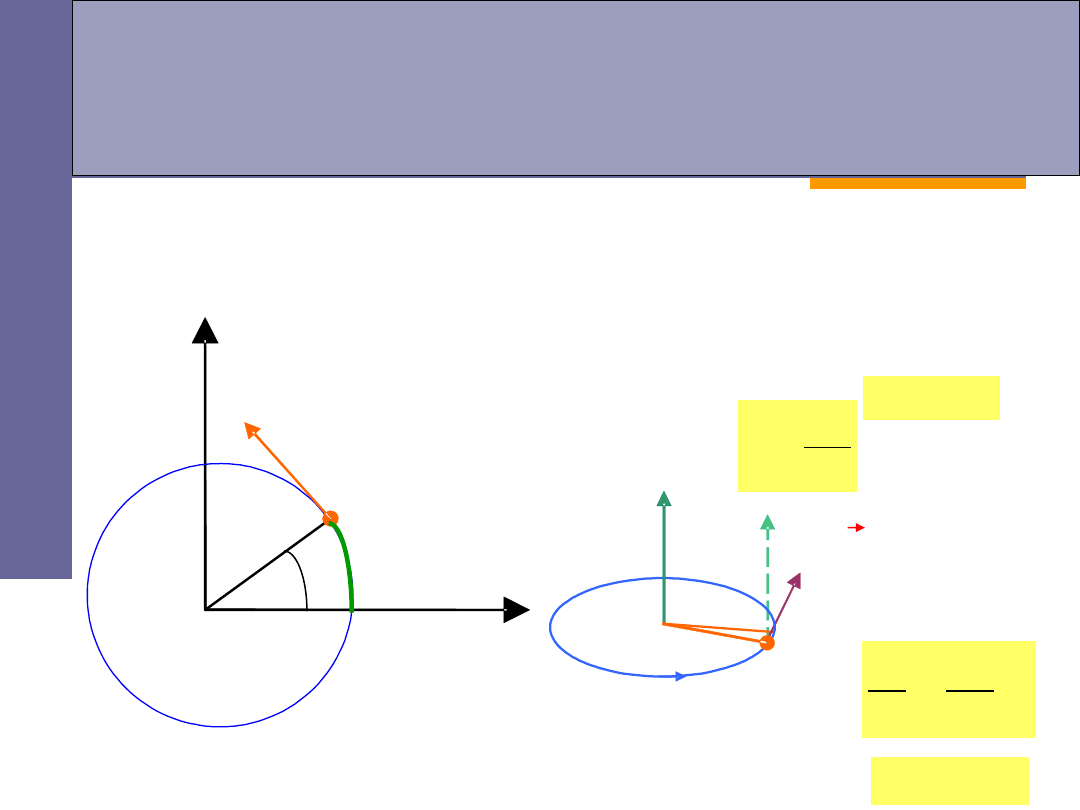
Ruch obrotowy punktu materialnego



ruch obrotowy po okręgu -

szczególny przypadek płaskiego

ruchu krzywoliniowego



droga kątowa

–

położenie punktu A określone za

pomocą kąta

j

r

s





j



droga liniowa

s

–

za pomocą drogi kątowej

j

:



prędkość kątowa:

r

dt

d

dt

ds





j

dt

d

j











prędkość liniowa punktu A:

r













v

kierunek wektora



dany jest przez

regułę śruby
prawoskrętnej

j

s

x

y

A

r



v



j





A





r



v



dt

d











dt

d

a

v









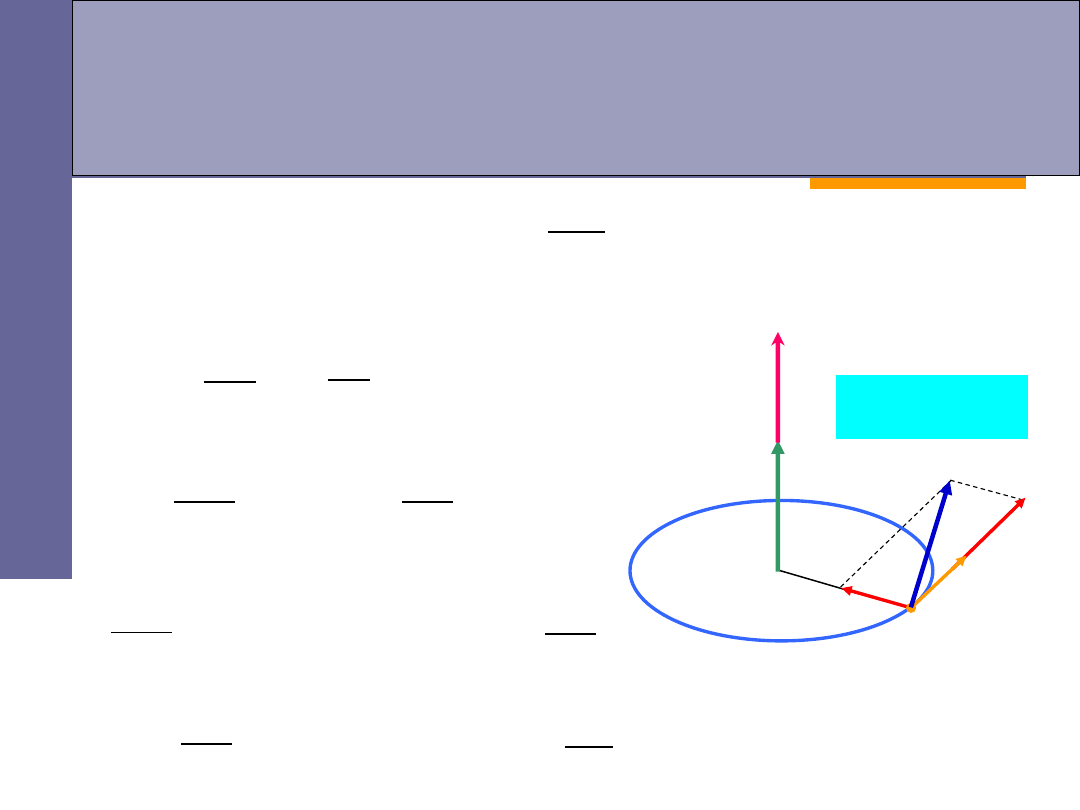
przyspieszenie kątowe:



przyspieszenie liniowe



styczne i dośrodkowe

:

)

(

r

dt

d











dt

r

d

r

dt

d





















r

dt

d

a

s













r











dt

r

d

a

n













v











dt

d

a

s

v

|

|





r

a

n

2

v

|

|







Ruch obrotowy punktu materialnego

s

a



v







n

a







a



r



n

s

a

a

a











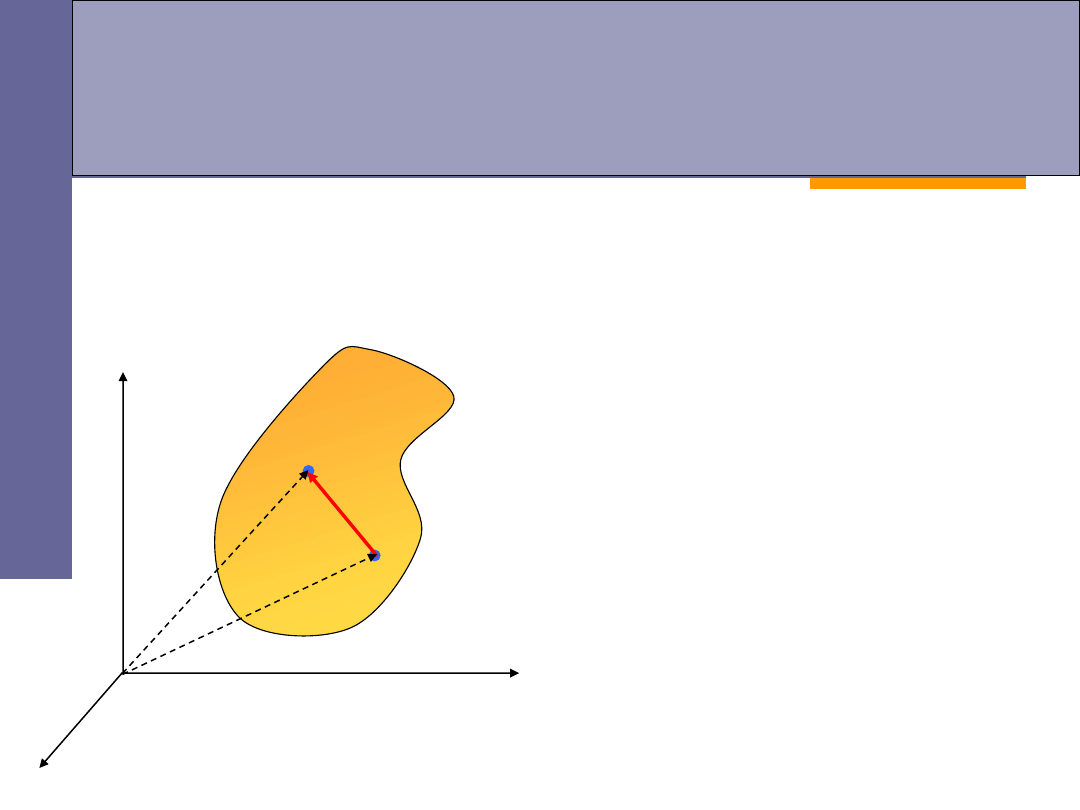
Dynamika bryły sztywnej



Bryłą sztywną

nazywamy ciało stałe, w którym odległość dwu

dowolnie wybranych punktów nie ulega zmianie, mimo działających
na to ciało sił.

x

z

y

m

1

m

2

i

r



ij

r



j

r



const

r

r

r

j

i

ij







|

|

|

|







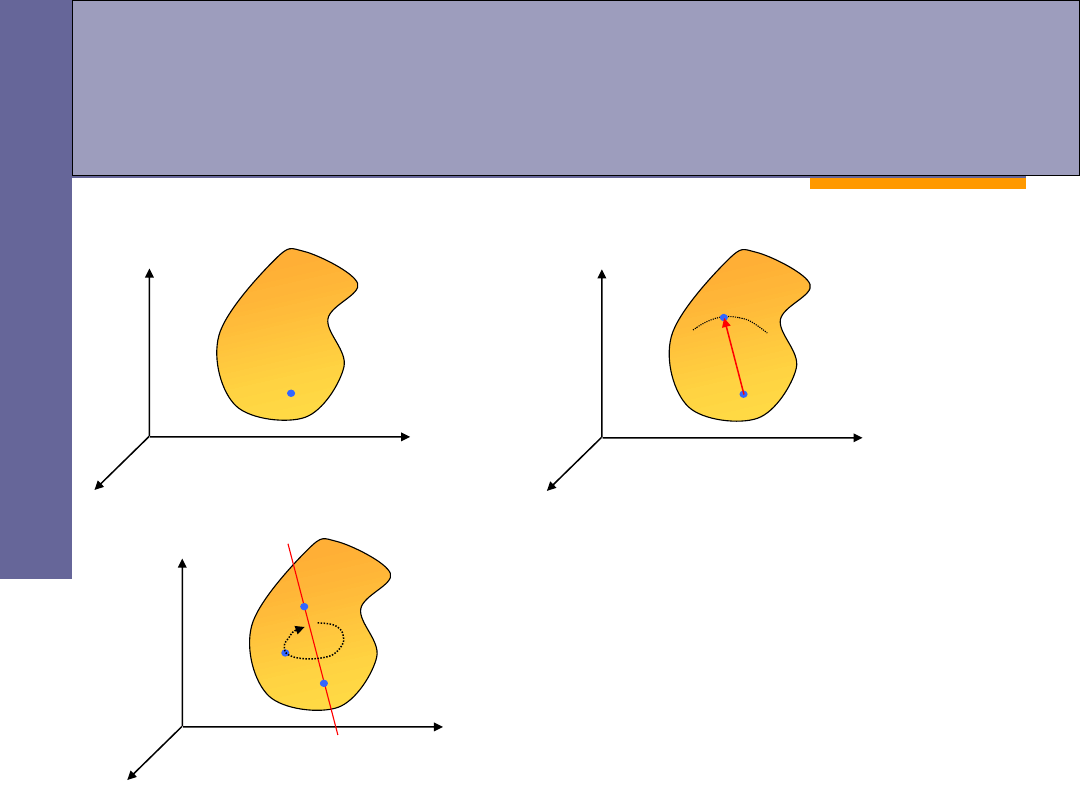
Rodzaje ruchów bryły sztywnej



stopnie swobody:



f = 3

x

z

y

m

1

x

z

y

m

1

m

2

r





f = 2

jeden punkt unieruchomiony

dwa punkty unieruchomione

x

z

y

m

1

m

2

m

3



f = 1

Bryła sztywna ma

sześć

stopni swobody!

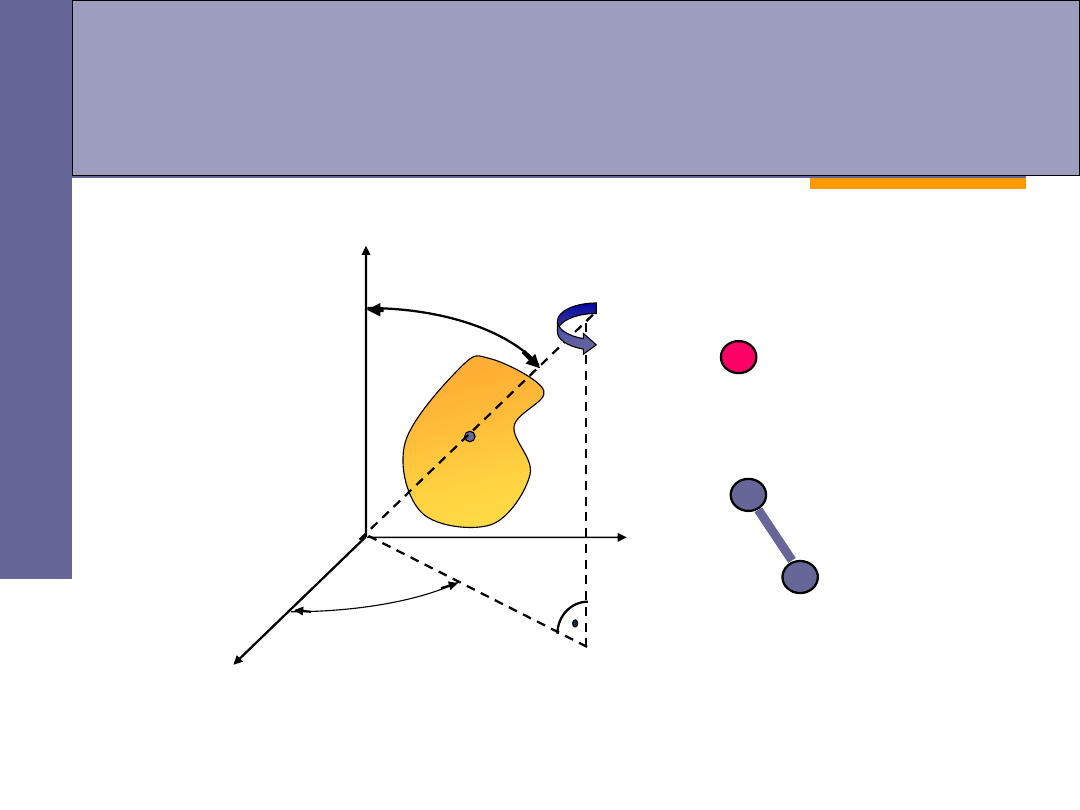
f = 6

f = 3

f = 5

0

– środek

masy

x

z

y

0







Rodzaje ruchów bryły sztywnej

Stopnie swobody

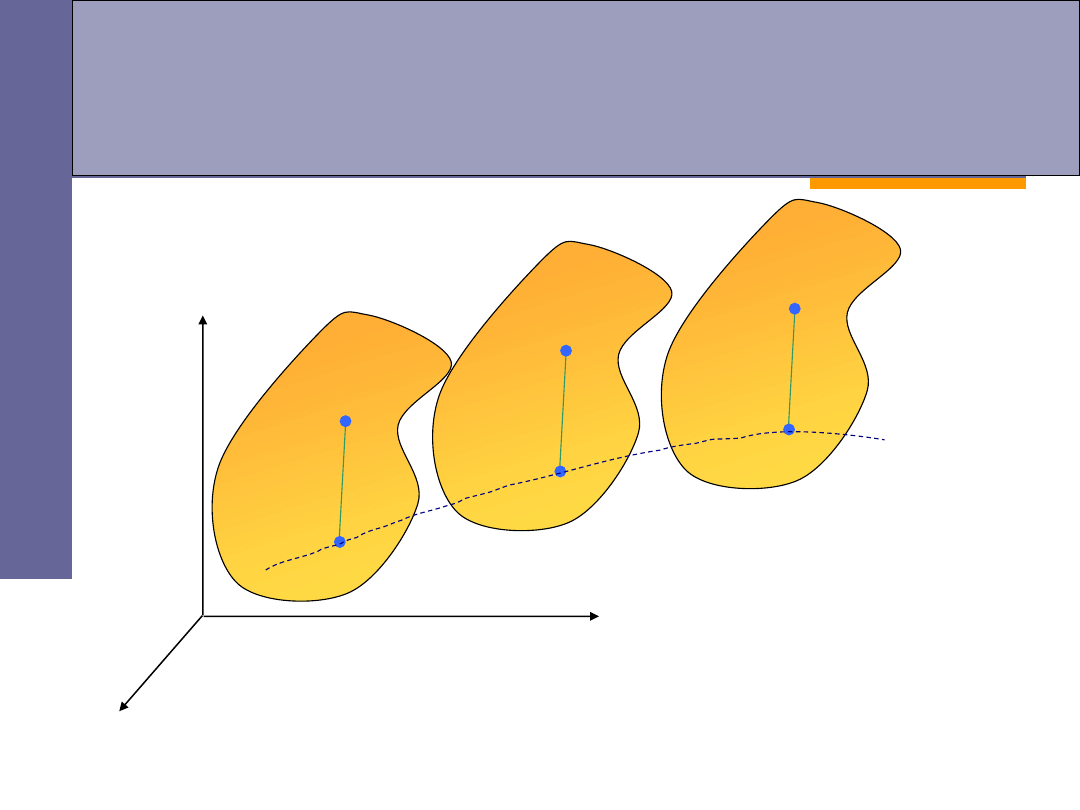
Rodzaje ruchów bryły sztywnej



ruch postępowy:



wektory prędkości i przyspieszenia są takie same dla

wszystkich punktów,

x

y

z



dowolny odcinek łączący dwa punkty zachowuje stałe

położenie do siebie równoległe

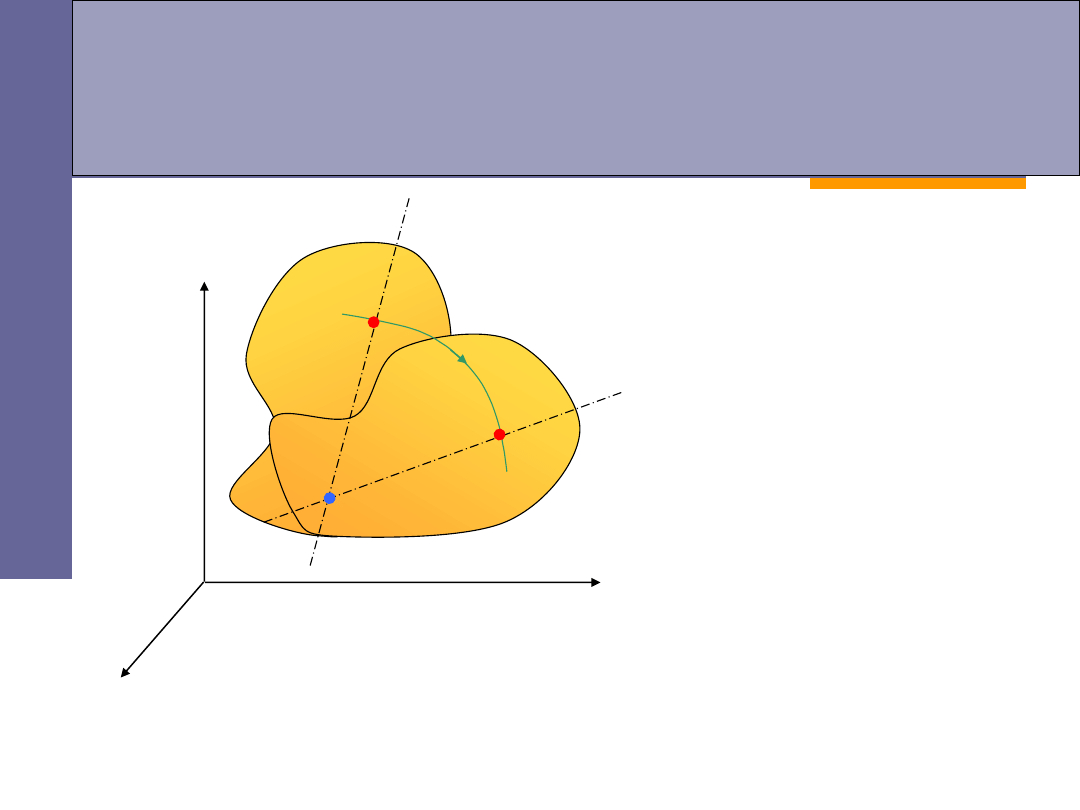
Rodzaje ruchów bryły sztywnej



ruch obrotowy:



wszystkie punkty poruszają się po okręgach, których

środki leżą na jednej prostej zwaną

osią obrotu

,

x

y

z

oś



poszczególne punkty bryły mają

tę samą prędkość kątową,



poszczególne punkty bryły mają

różne prędkości liniowe

,

zależne od odległości od osi obrotu.

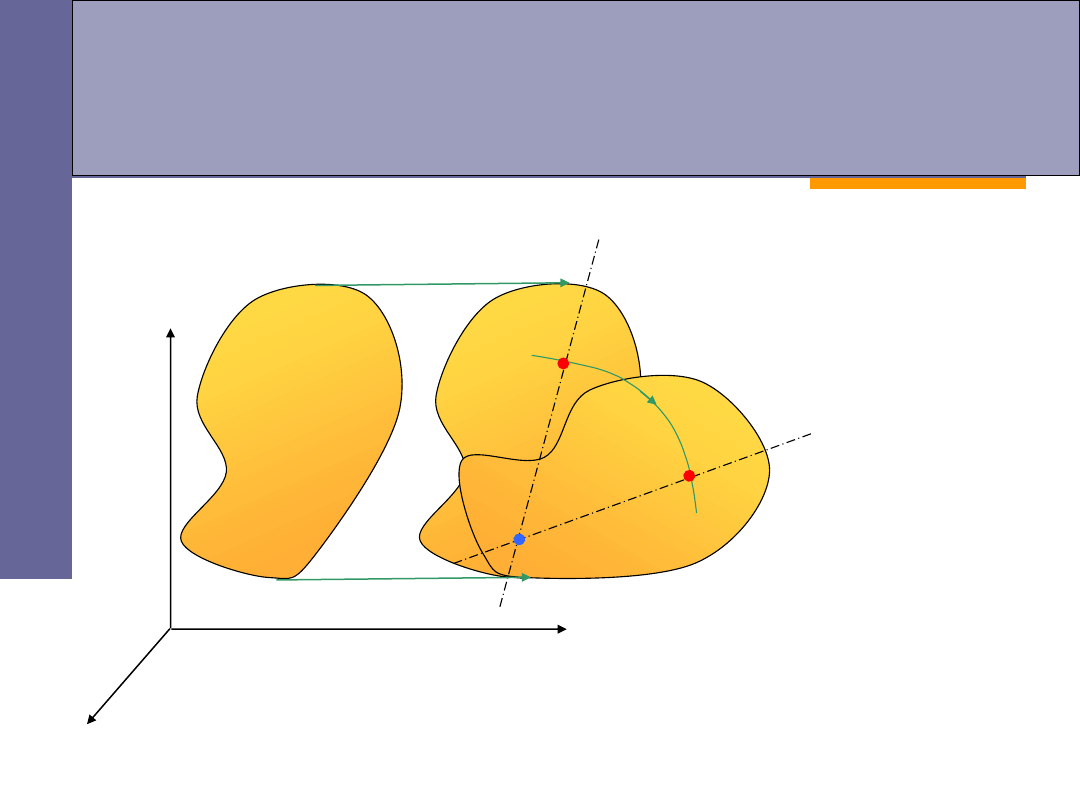
Rodzaje ruchów bryły sztywnej



ruch postępowo – obrotowy:



dowolny ruch ciała sztywnego można

złożyć

z ruchu

postępowego

i

obrotowego

x

y

z

oś

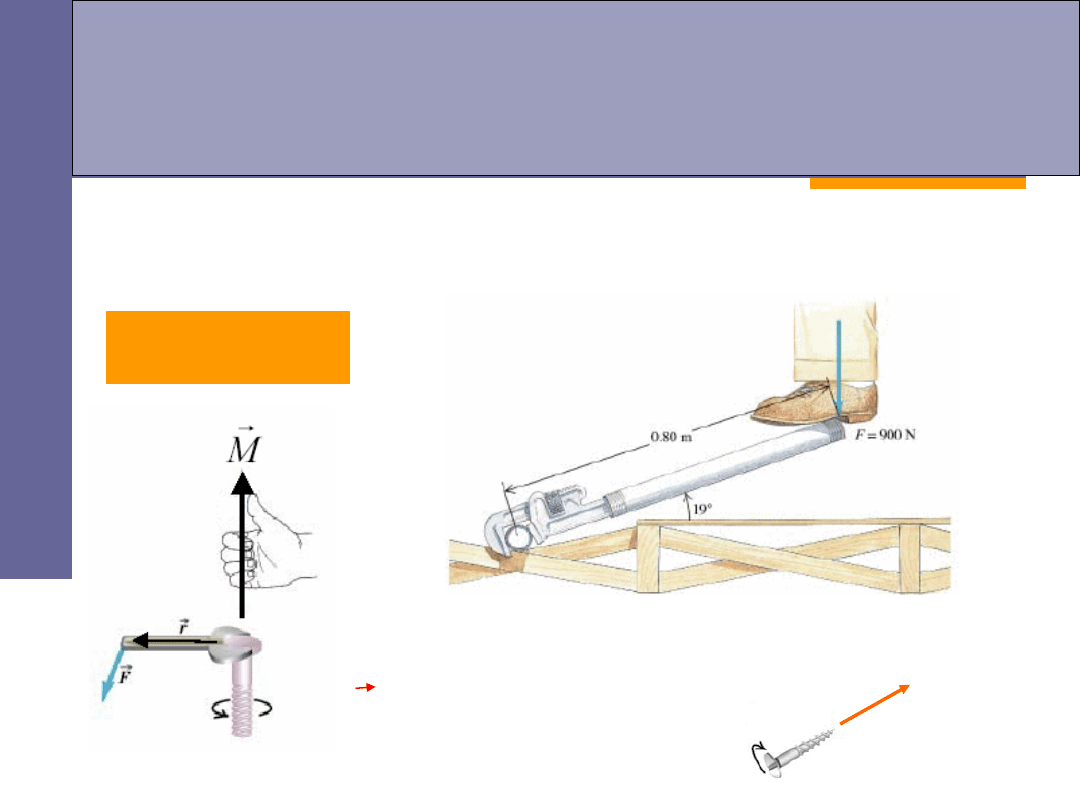
Moment siły

F

r

M











Wielkością fizyczną wywołującą obrót bryły sztywnej jest

moment

siły

(tzw.

moment obrotowy

):

Aby

spowodować ruch obrotowy bryły sztywnej niezbędna jest siła.



r

nazywamy ramieniem siły,



kierunek

momentu siły wyznaczamy z reguły śruby

prawoskrętnej,

M





gdy:

0

||





M

F

r







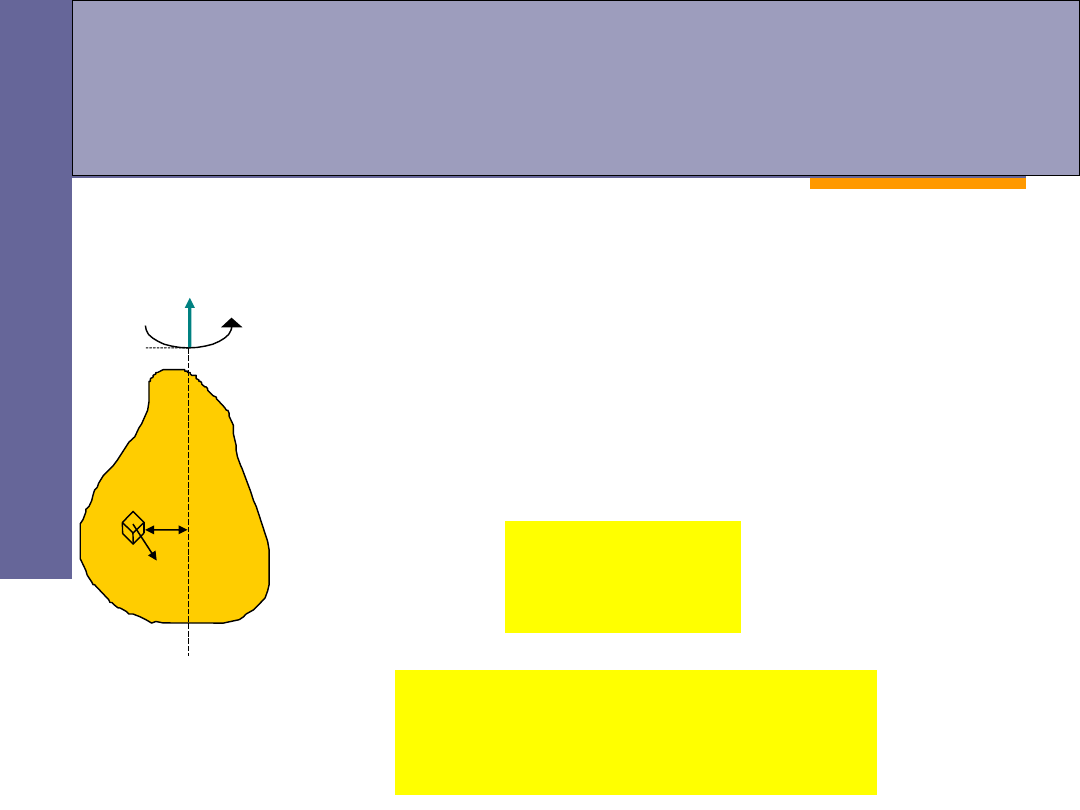
Moment bezwładności



podzielmy bryłę sztywną na zbiór

n

punktów materialnych

o masach

D

m

1

,

D

m

2

,….,

D

m

n

Przeanalizujmy

ruch obrotowy

bryły sztywnej wokół stałej osi ze stałą

prędkością kątową



odległości poszczególnych mas od osi obrotu wynoszą

r

1

, r

2

,…., r

n



momentem bezwładności

I

bryły sztywnej względem danej osi

nazywamy sumę iloczynów mas poszczególnych punktów bryły

sztywnej i kwadratów odległości od danej osi:







D



n

i

i

i

r

m

I

1

2



w przypadku bryły o ciągłym rozkładzie masy:

dm

r

r

m

I

n

i

M

i

i

n















D



1

2

2

lim





i

m

D

i

v



i

r



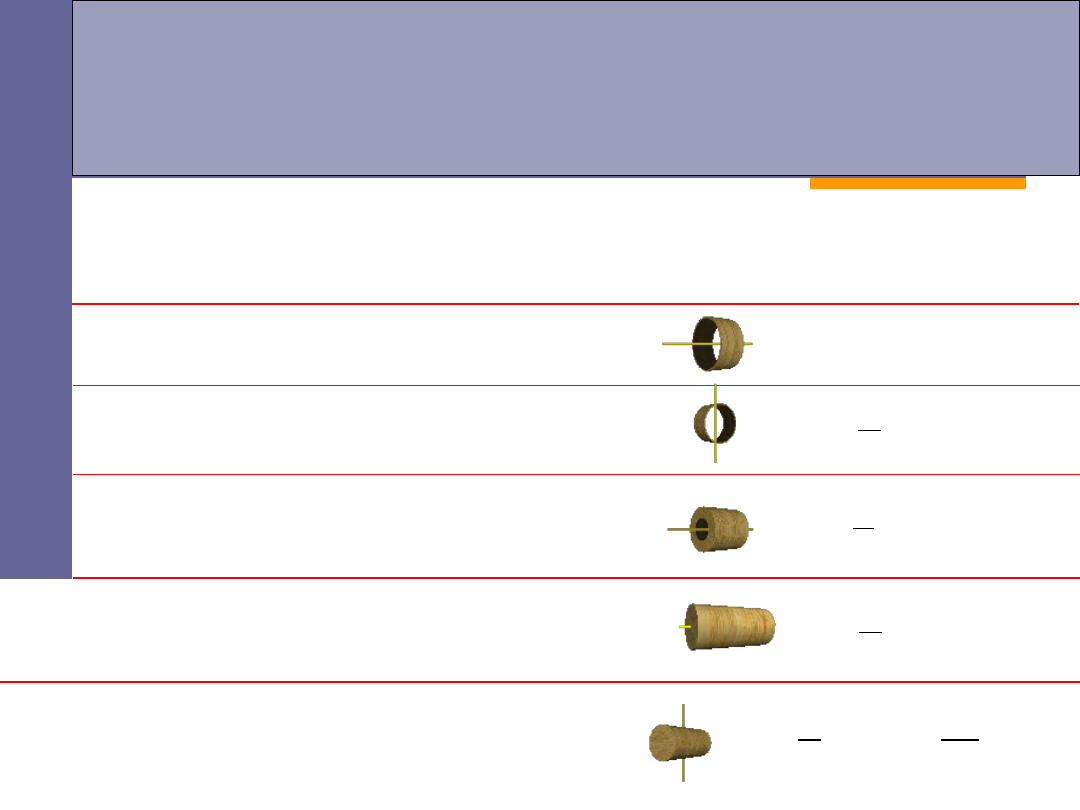
Moment bezwładności

-

przykłady





2

2

2

1

2

1

r

r

m

I









2

r

m

I







moment bezwładności

I

jest analogiczną wielkością do masy

m

w ruchu

postępowym. Chociaż masa ciała nie zależy od jego położenia to moment
bezwładności zależy od osi, wokół której obraca się ciało:



cienki pierścień o masie

m

i promieniu

r

obracający się wokół własnej osi:



pierścień o masie

m

i promieniach

r

1

i

r

2

obracający się wokół własnej osi:



walec o masie

m

, długości

L

i promieniu

r

obracający się wokół własnej osi:

2

2

1

r

m

I







cienki pierścień o masie

m

i promieniu

r

obracający się wokół osi prostopadłej:

2

2

1

r

m

I







walec o masie

m

, długości

L

i promieniu

r

obracający się wokół osi prostopadłej do

niego i przechodzącej przez środek:

2

2

12

1

4

1

L

m

r

m

I









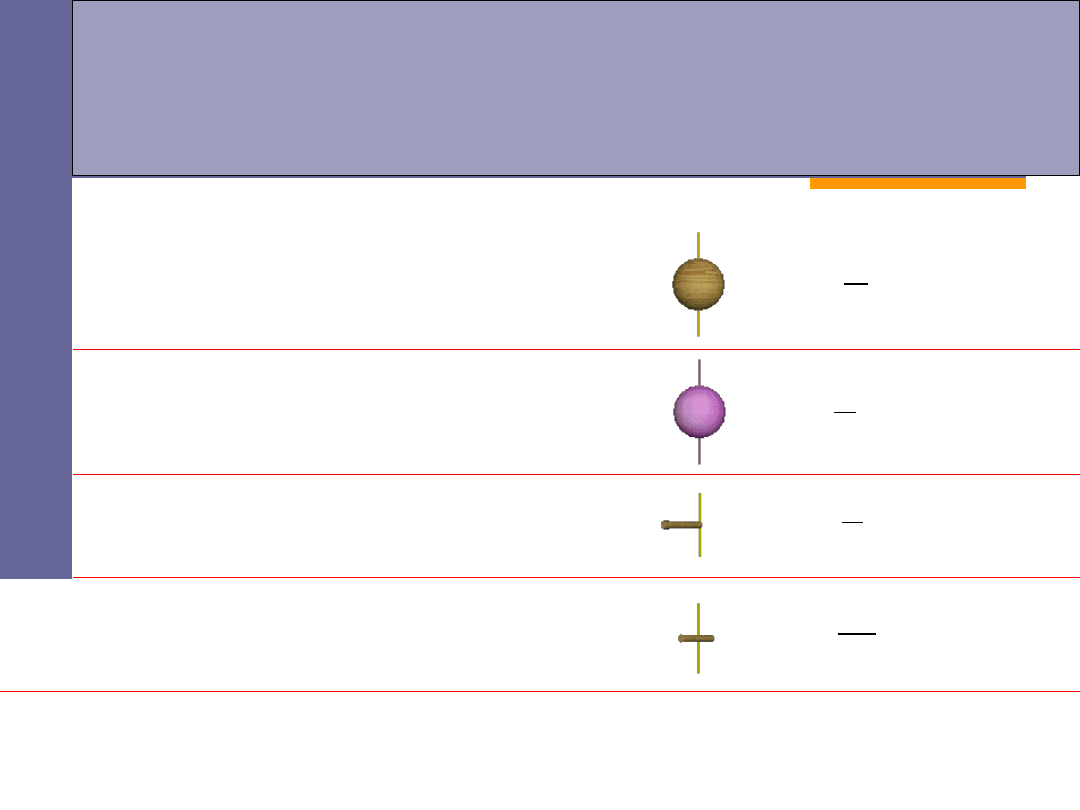
Moment bezwładności

-

przykłady

2

3

2

r

m

I





2

12

1

L

m

I





2

5

2

r

m

I







kula o masie

m

i promieniu

r

obracająca się wokół własnej osi:



sfera o masie

m

i promieniu

r

obracająca się wokół własnej osi:



pręt o masie

m

i długości

L

obracający się wokół osi prostopadłej

do niego i przechodzącej przez jego koniec:

2

3

1

L

m

I







pręt o masie

m

i długości

L

obracający się wokół osi prostopadłej

do niego i przechodzącej przez jego środek:



jednostką momentu pędu jest

2

1

m

kg



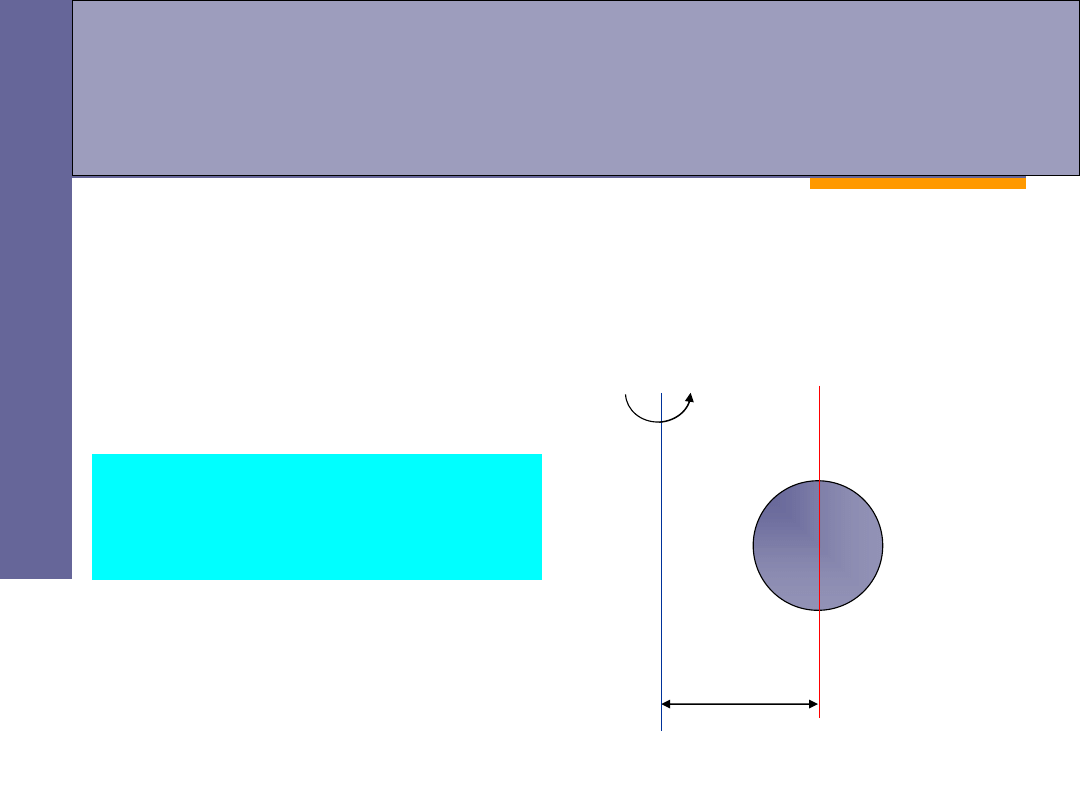
Twierdzenie Steinera

0

I

m





2

a

m

I

I

o







Moment

bezwładności

I

bryły sztywnej względem dowolnej osi jest

równy sumie momentu bezwładności

I

o

względem osi równoległej

przechodzącej przez środek masy bryły oraz iloczynu masy tej bryły

i kwadratu

odległości

a

obu osi:

a

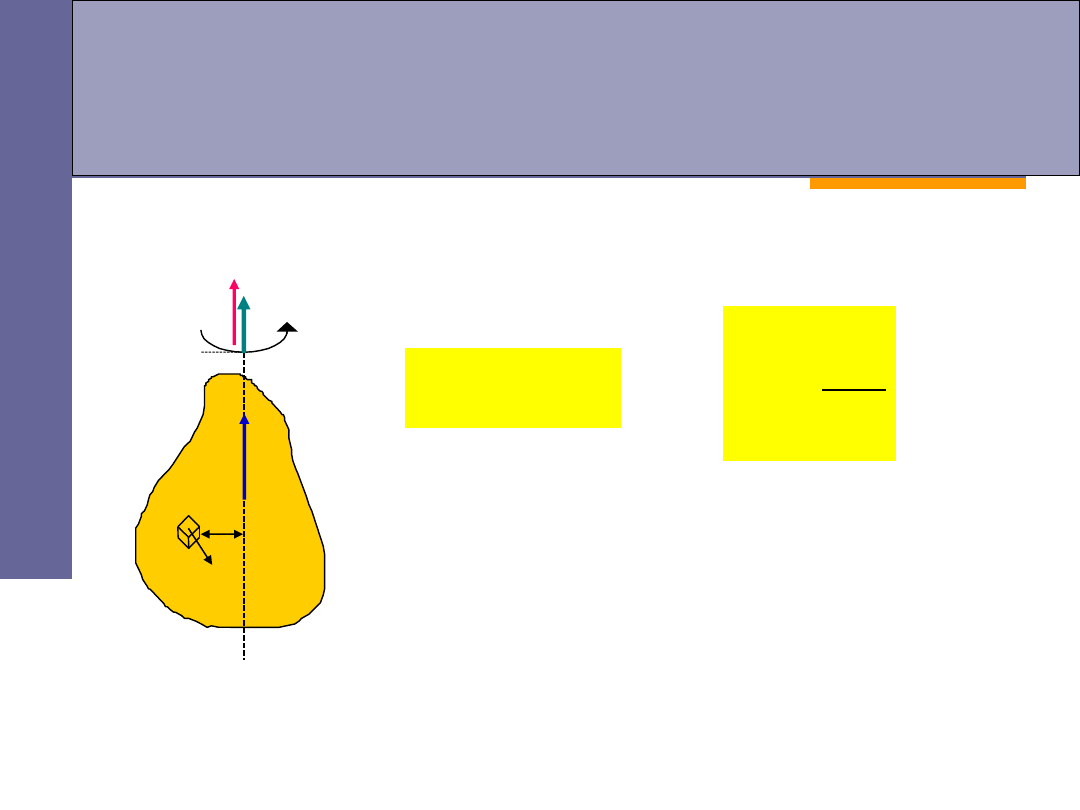
II zasada dynamiki ruchu obrotowego

P

rzyspieszenie kątowe bryły sztywnej jest

proporcjonalne do m

omenty siły wypadkowej

działającej na bryłę; współczynnikiem
proporcjonalności jest odwrotność momentu
bezwładności.











I

M

Ruch obrotowy

bryły sztywnej wokół

stałej osi





i

m

D

i

F



i

r







M



I

M









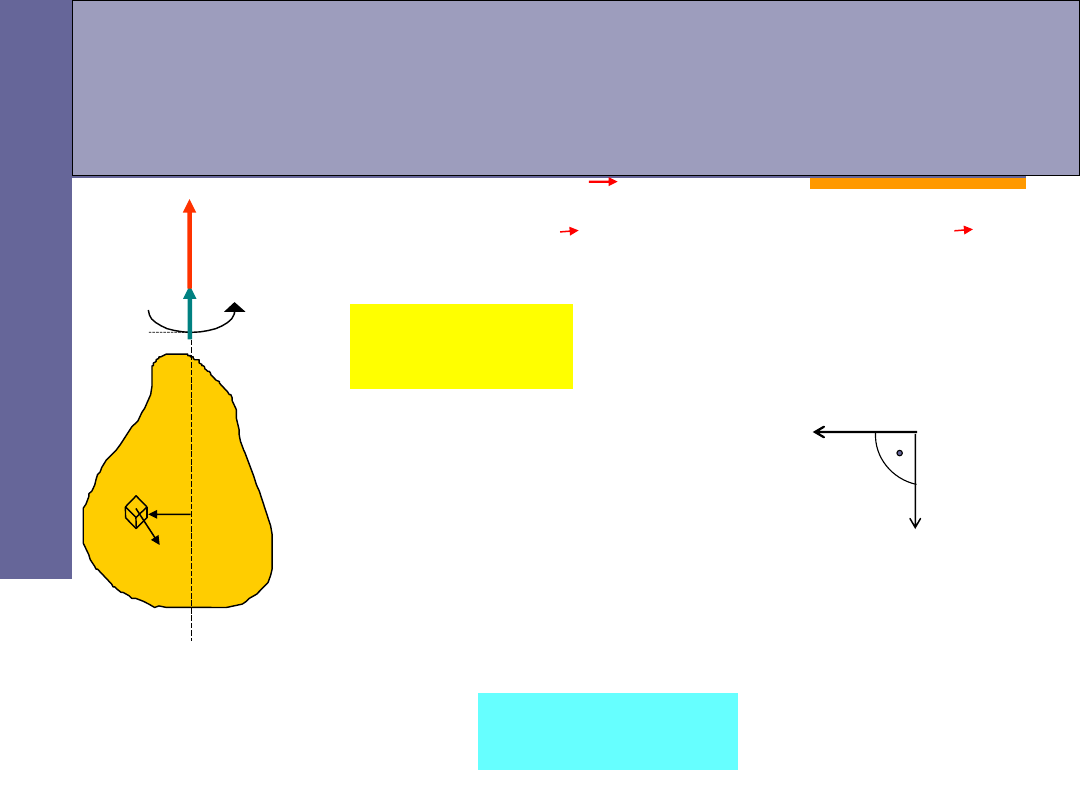
II zasada dynamiki ruchu obrotowego
–

moment pędu (kręt)

i

i

i

p

r

L













dla całej bryły :







D





n

i

i

i

m

r

L

1

i

v



podstawiając:

r







v









D





n

i

i

i

i

r

m

r

L

1







D







n

i

i

i

m

r

1

2









I













I

L

)

v

(

i

i

i

i

m

r

L









D









i

m

D

i

v



i

r



L





Moment pędu (kręt)

L

punktu

materialnego o masie

D

m

i

i wektorze wodzącym

r

i

, poruszającego się z prędkością

v

i

względem osi obrotu, definiujemy wzorem:

i

r



i

v



II zasada dynamiki ruchu obrotowego

– moment pędu (kręt)

Wypadkowy m

oment siły działający na bryłę sztywną

powoduje zmianę momentu pędu bryły. Pochodna momentu
pędu względem czasu jest równa momentowi siły.



II zasadę dynamiki możemy zapisać w postaci:











I

M

dt

d

I









dt

I

d

)

(









dt

L

d

M







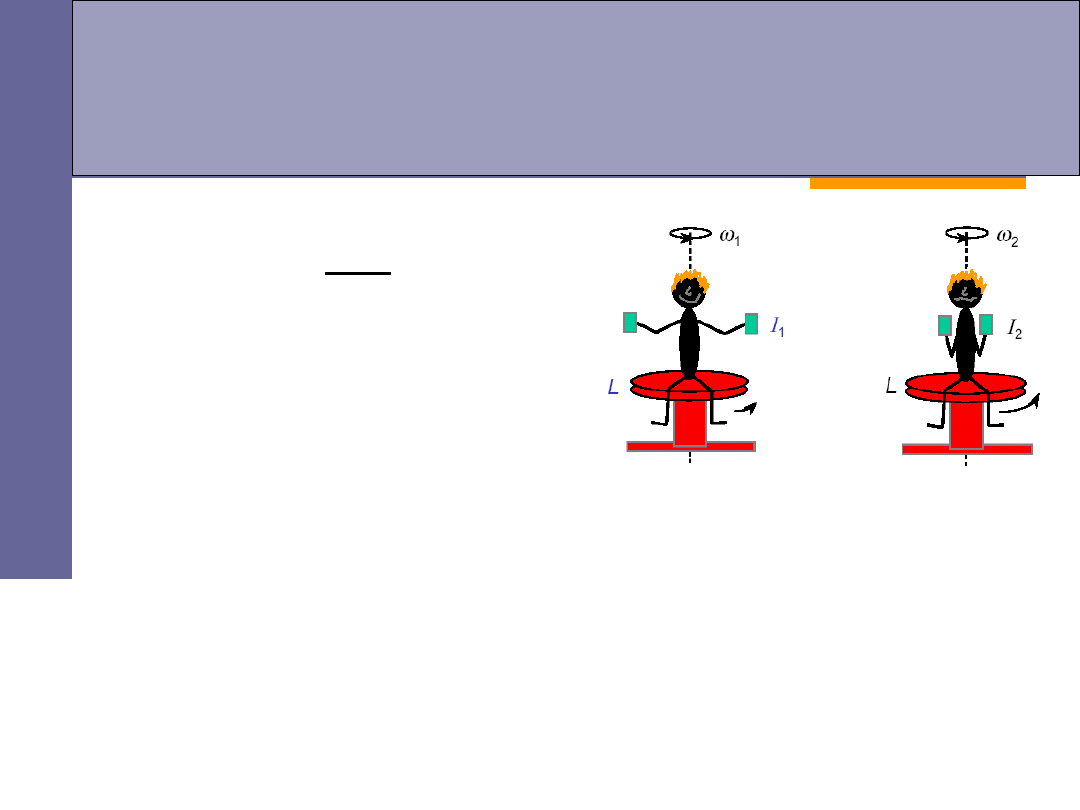
Zasada zachowania momentu
pędu (krętu)

0



M



const

L







Jeżeli moment wypadkowy sił
zewnętrznych działających
na bryłę równa się zeru,

to całkowity moment pędu

(kręt) pozostaje stały.

dt

L

d

M









moment sił zewnętrznych wynosi zero,



moment pędu jest zachowany,

2

2

1

1











I

I



ponieważ:

2

1

I

I





zatem:

1

2









zmniejszenie momentu bezwładności

przyspiesza obrót:

Energia kinetyczna ruchu
obrotowego

2

2

2

2

1

v

2

1













i

i

i

i

ki

r

m

m

E













n

i

i

i

r

m

1

2

2

2

1





Energię kinetyczną –

obliczamy sumując energie kinetyczne

poszczególnych punktów bryły:



dla całej bryły mamy zatem:











n

i

i

i

k

r

m

E

1

2

2

2

1



2

2

1







I

E

k

Energia kinetyczna ruchu
postępowo – obrotowego

v



m





1

1

2

v







c

gh

k



Energia kinetyczna

obracającej się bryły jest sumą energii kinetycznej

ruchu obrotowego i energii kinetycznej środka masy:



jeżeli wysokość równi wynosi

h

,

a promień ciała

r

, to obliczmy prędkość liniową

ciała u podstawy równi

v

k

:

2

2

2

1

v

2

1











I

m

E

k

2

2

2

1

v

2

1

k

k

I

m

mgh











2

v

r

m

c

I

r

































kula

5

2

,

walec

2

1

ściance

cienkiej

o

rura

1

c

23:54

1

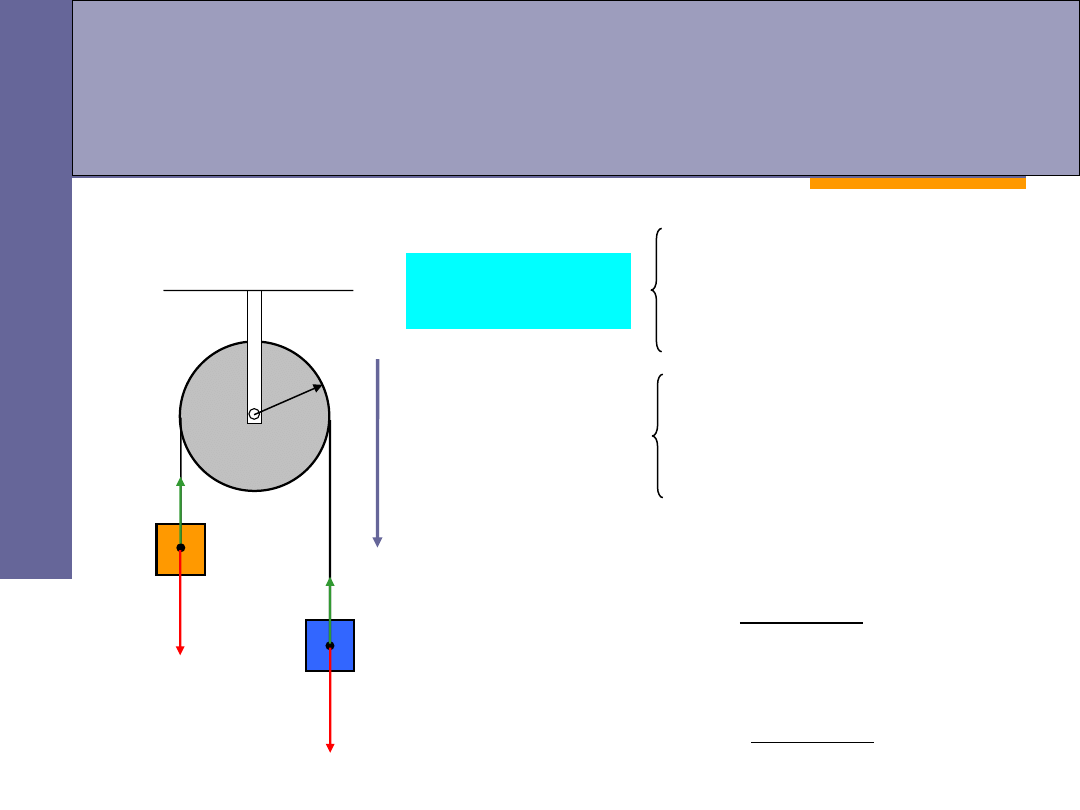
Przykłady – maszyna Atwooda



obliczmy przyspieszenie, z jakim poruszają się masy oraz naciąg nici:

g

m

Q





1

1



g

m

Q





2

2



2

N



bloczek nieruchomy:

m

1

m

2

m

r

1

N



a



g

m

m

a

m

m











)

(

)

(

1

2

2

1

g

m

m

m

m

a









2

1

1

2

g

m

m

m

m

N









2

1

2

1

2

g

m

N

a

m















1

1

1

2

2

2

N

g

m

a

m















N

g

m

a

m









2

2

g

m

N

a

m









1

1

Siły naciągu nici:
N

1

=N

2

=N

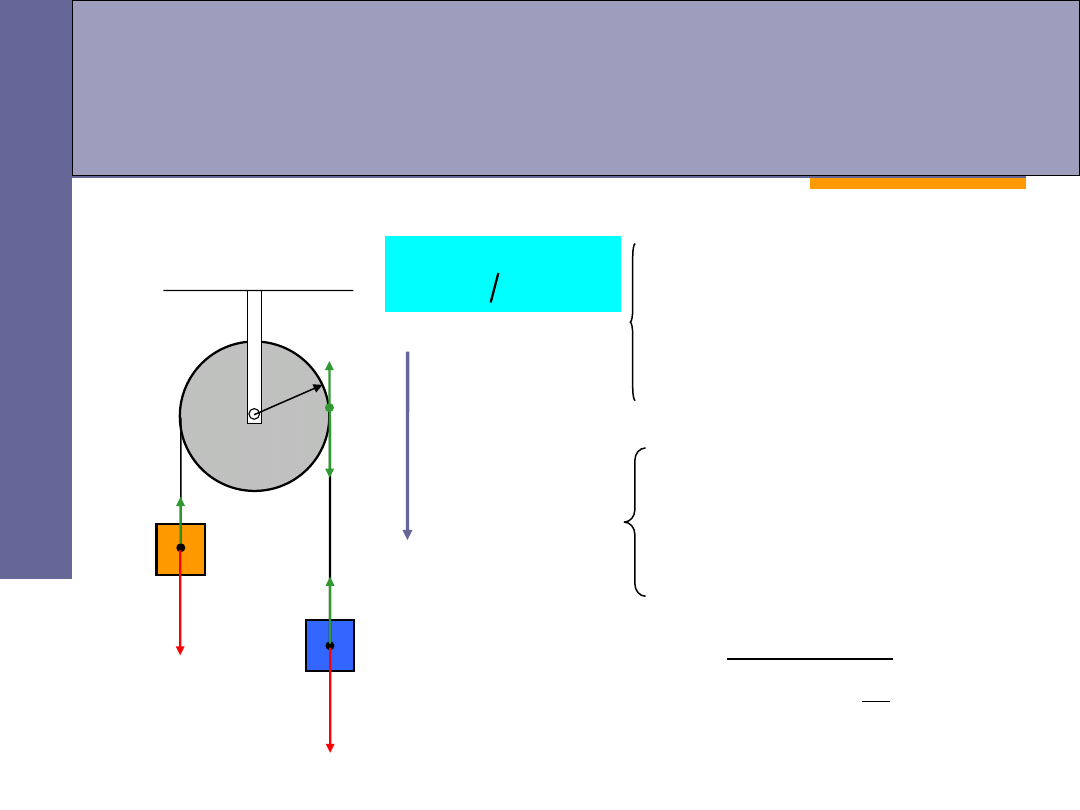
Przykłady – maszyna Atwooda



obliczmy przyspieszenie, z jakim poruszają się masy oraz naciąg nici:

g

m



1

g

m



2

2

N



bloczek ruchomy:

m

1

m

2

m

r

1

N



a



2

N



1

N



g

m

m

m

m

m

a











2

2

1

1

2

......

1



N

......

2



N

r

a

I

N

N

r

M

/

)

(

1

2









2

2

2

N

g

m

a

m









g

m

N

a

m









1

1

1

g

m

N

a

m















1

1

1

2

2

2

N

g

m

a

m





































I

N

N

r

M

)

(

1

2

Siły naciągu nici:
N

1

=N

2

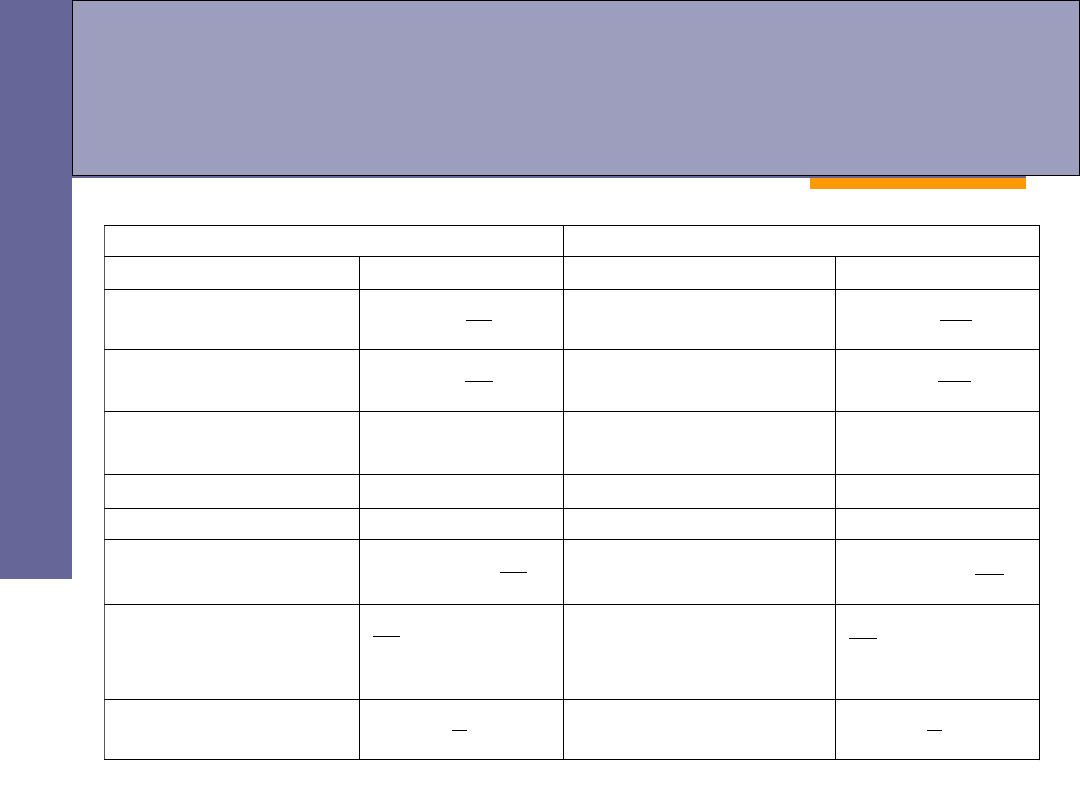
Analogia między ruchem
postępowym i obrotowym

Ruch prostoliniowy

Ruch obrotowy

Droga liniowa

s



Droga kątowa

j



Prędkość liniowa

dt

s

d

v







Prędkość kątowa

dt

d

j









Przyspieszenie
liniowe

dt

v

d

a







Przyspieszenie
kątowe

dt

d











Masa

m

Moment
bezwładności

I

Pęd

v

m

p









Moment pędu











I

L

Siła

F



Moment siły

M



II zasada dynamiki

dt

p

d

a

m

F













II zasada dynamiki

dt

L

d

I

M















Zasada
zachowania pędu

const

p

dt

p

d











0

Zasada zachowania
momentu pędu

const

L

dt

L

d











0

Energia kinetyczna

2

2

1

v

m

E

k





Energia kinetyczna

2

2

1







I

E

k