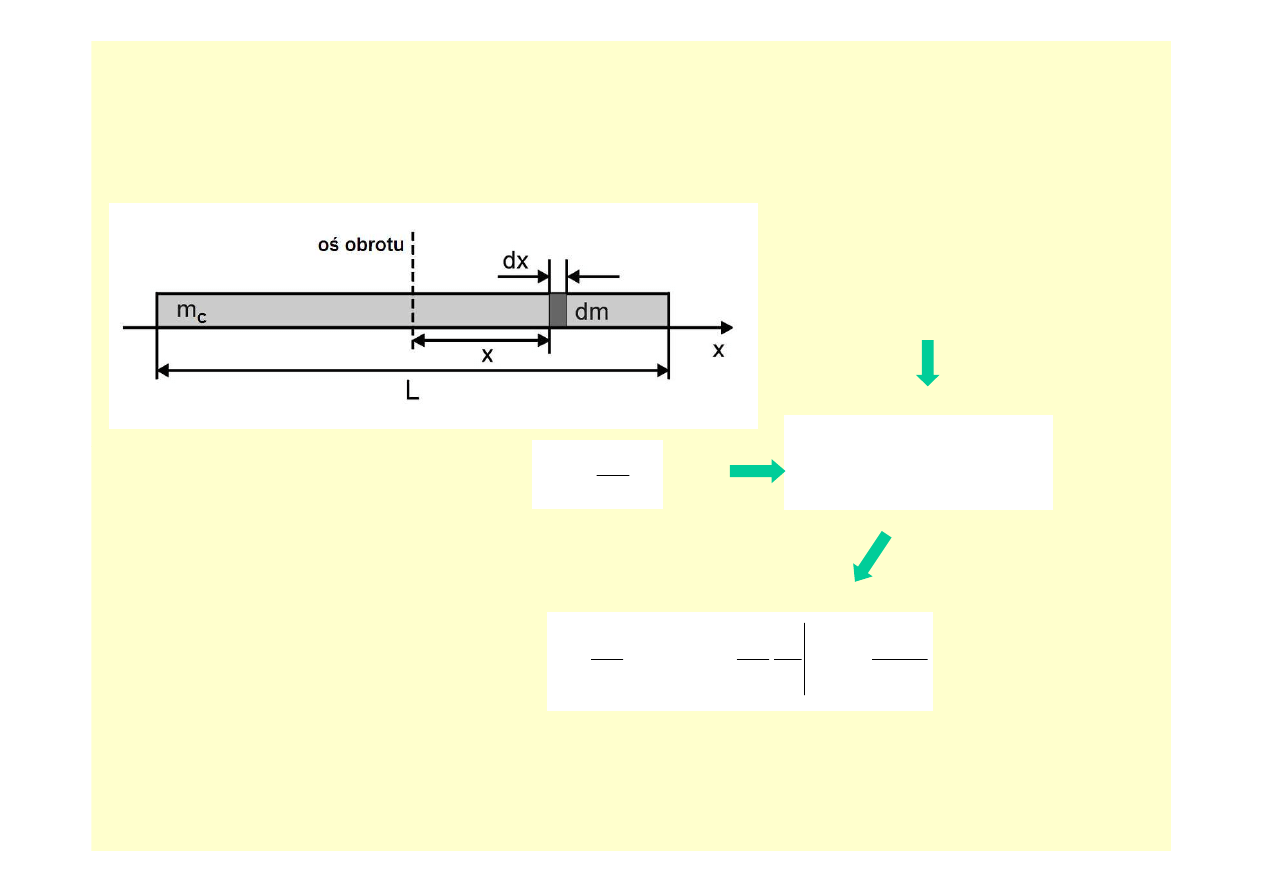
Przykład:

liczenie momentu bezwładno

ś

ci pr

ę

ta o masie M i długo

ś

ci L.

Moment bezwładno

ś

ci elementu

o masie dm wynosi x

2

dm

∫

∑

=

=

2

/

2

2

d

d

L

m

x

m

x

I

m

∫

∑

−

=

=

2

/

2

2

d

d

L

i

i

i

m

x

m

x

I

x

L

m

m

c

d

d

=

je

ż

eli pr

ę

t ma stał

ą

g

ę

sto

ść

:

12

3

d

2

2

/

2

/

3

2

/

2

/

2

L

m

x

L

m

x

x

L

m

I

c

L

L

c

L

L

c

=

=

=

−

−

∫

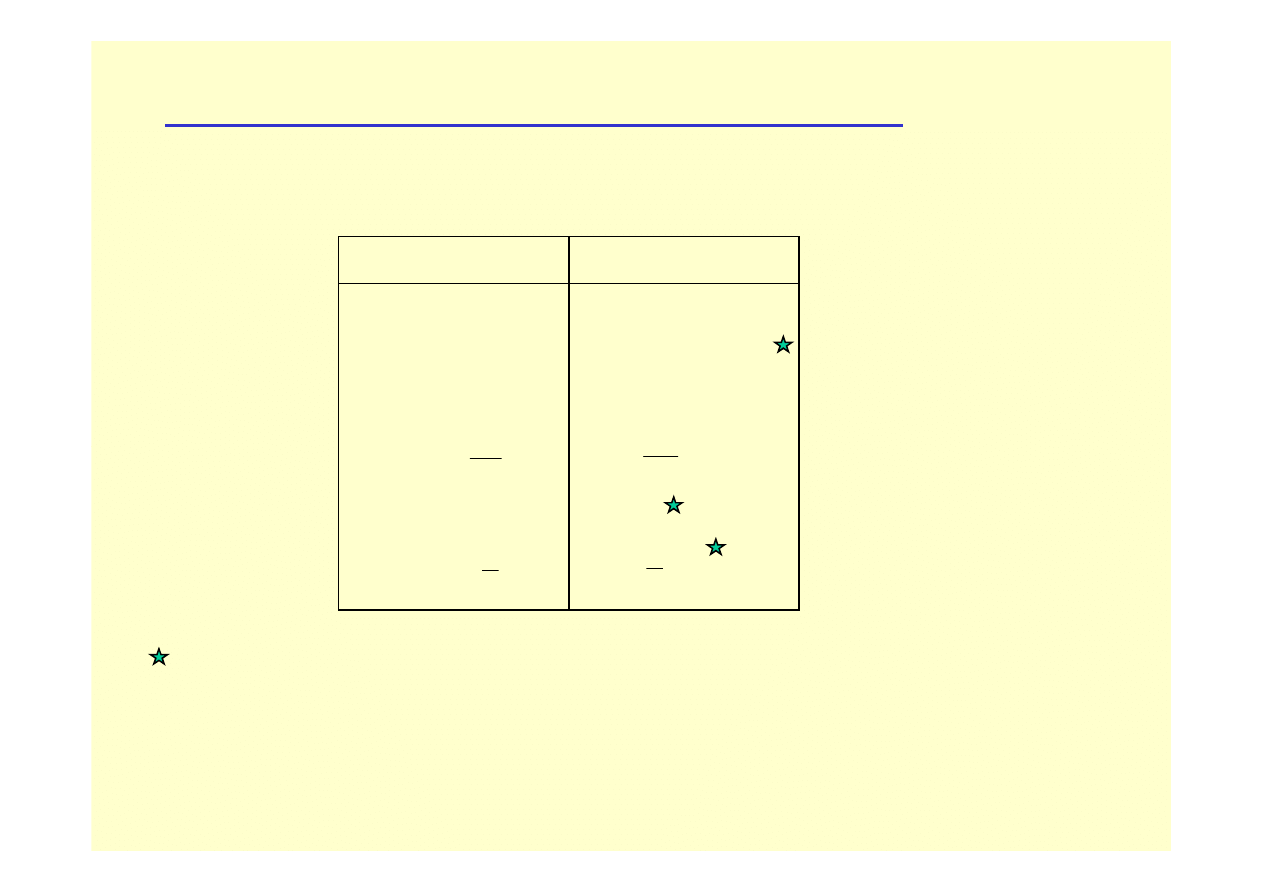
Ruch post

ę

powy

Ruch obrotowy

d

m

m

=

=

p

F

F

v

p

a,

v,

r,

d

,

Ι

I

=

×

=

=

×

=

L

M

F

r

M

ω

L

p

r

L

ε,

ω,

,

ϕϕϕϕ

Analogie ruchu obrotowego do ruchu post

ę

powego

2

2

1

d

d

v

m

E

m

t

k

=

=

=

a

F

p

F

2

2

1

d

d

Iω

E

I

t

k

=

=

=

ε

M

L

M

przypadek szczególny,

L

||

ω

ω

ω

ω

oraz

M

||

εεεε

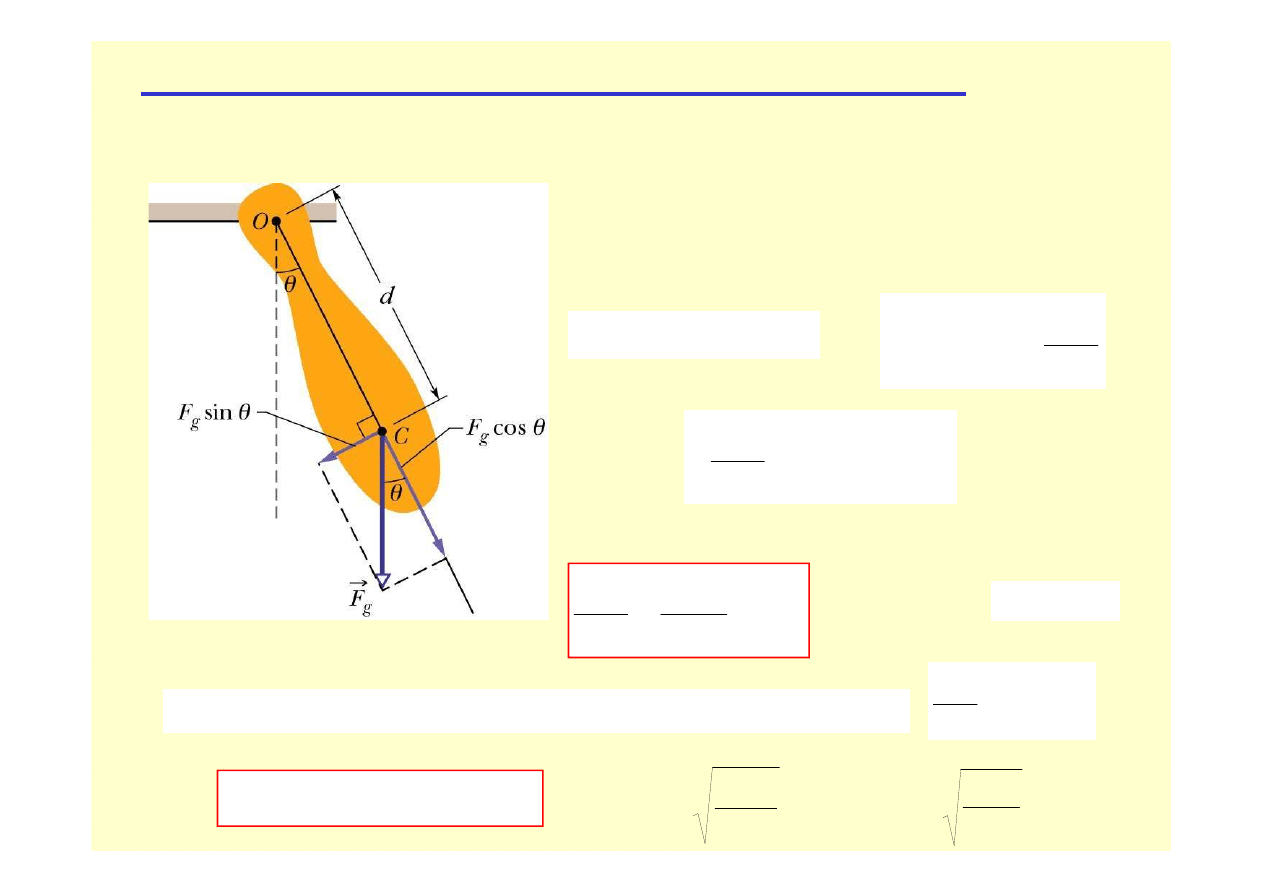
Przykład ruchu (1): Wahadło fizyczne

moment siły
powoduj

ą

cy

ruch:

2

2

d

d

t

I

I

M

θ

ε

=

=

θ

θ

sin

d

2

mgd

I

−

=

θ

sin

d

mg

M

−

=

II zasada dynamiki
Newtona dla bryły
sztywnej:

czyli:

PRZYKŁADY RUCHU BRYŁY SZTYWNEJ

θ

θ

sin

d

d

2

mgd

t

I

−

=

dla małych wychyle

ń

θ

:

0

d

d

2

2

=

+

θ

θ

I

mgd

t

poniewa

ż

:

θ

θ

≈

sin

rozwi

ą

zanie równania oscylatora drga

ń

harmonicznych:

)

cos(

)

(

0

0

ϕ

ω

θ

θ

+

=

t

t

I

mgd

=

0

ω

mgd

I

T

π

2

=

0

d

d

2

0

2

2

=

+

θ

ω

θ

t

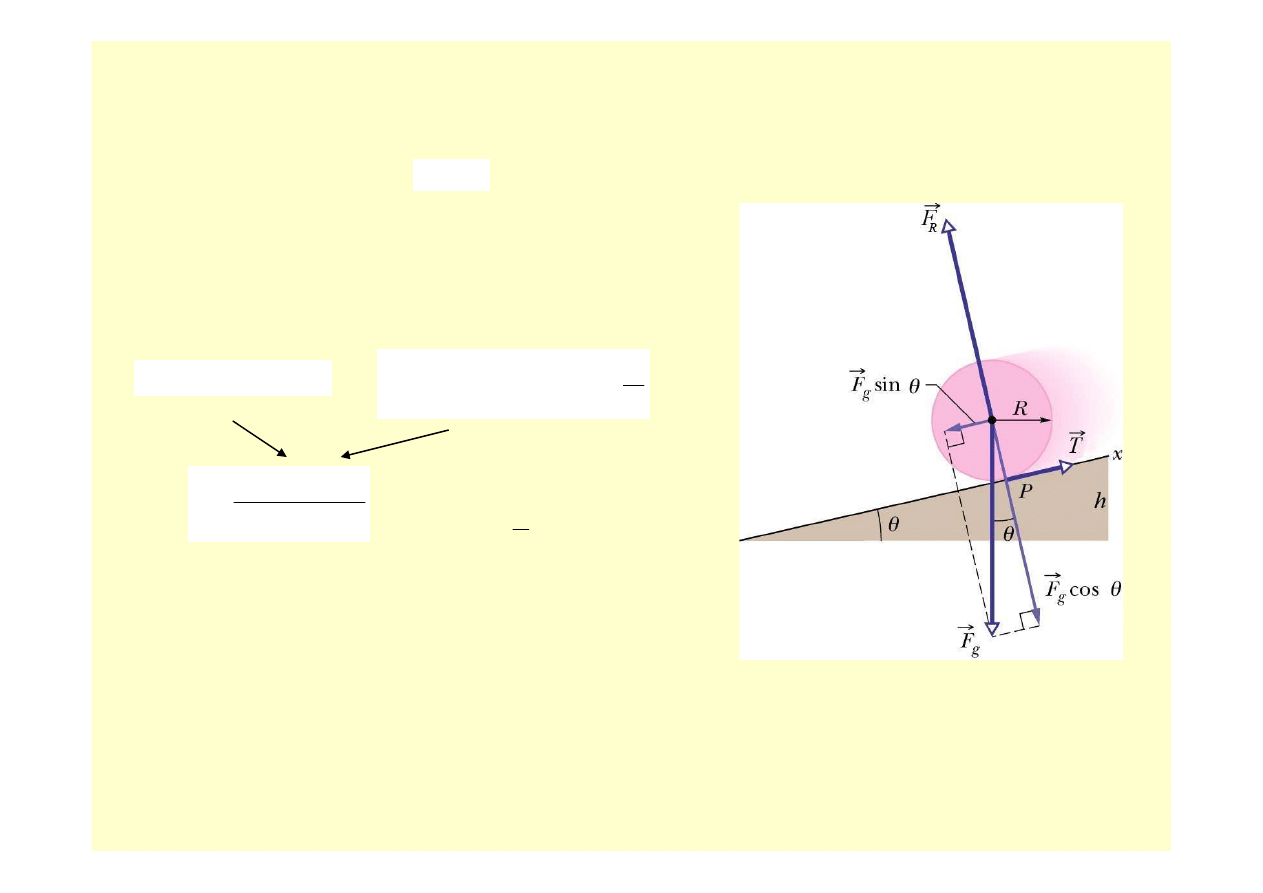
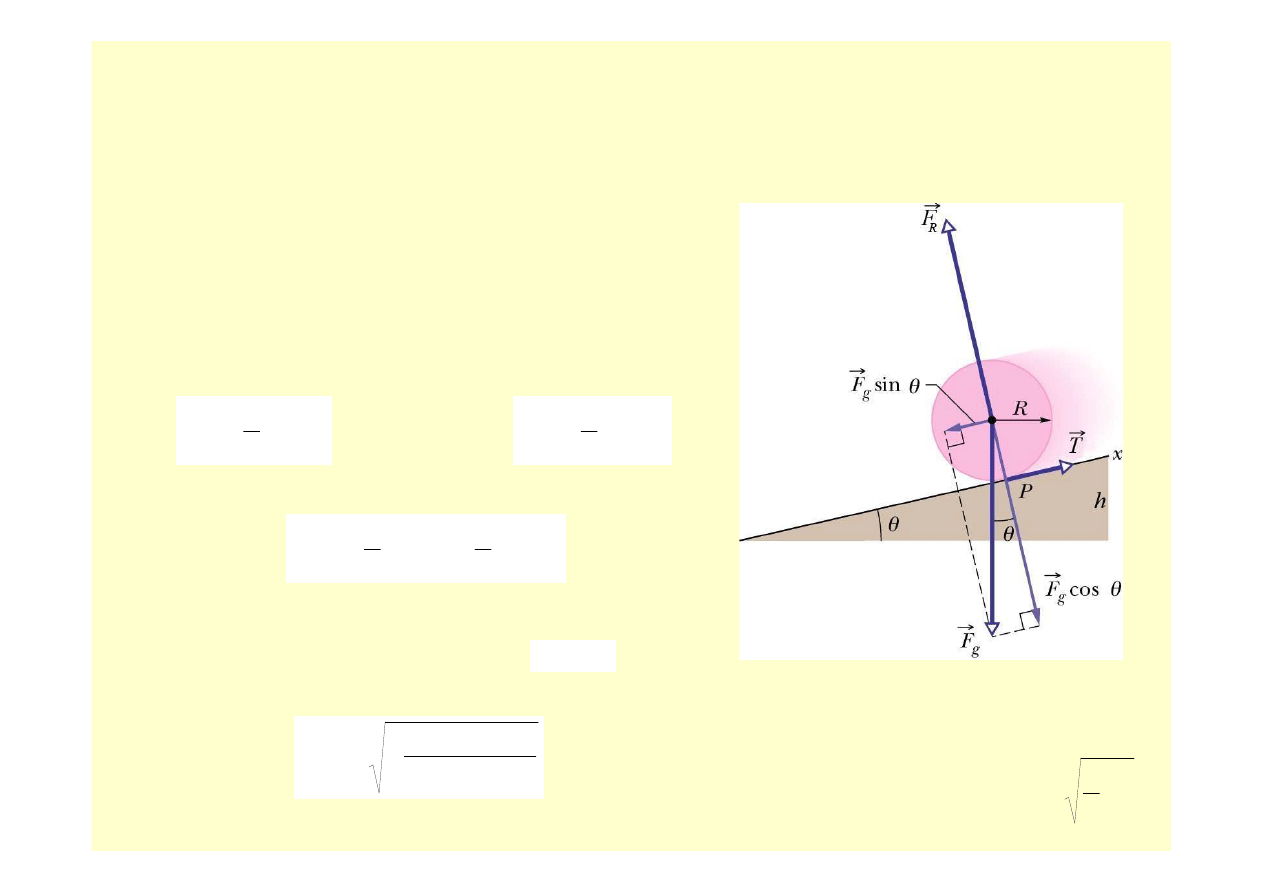
Przykład ruchu (2): Toczenie si

ę

(bez po

ś

lizgu) po równi pochyłej

– równania ruchu

Toczenie bez po

ś

lizgu:

R

a

ε

=

ma

T

mg

=

−

θ

sin

ruch post

ę

powy

ruch obrotowy

R

a

I

I

RT

M

SM

SM

=

=

=

ε

.

θ

sin

3

2

g

a

=

np. dla walca:

2

/

sin

R

I

m

mg

a

SM

+

=

θ

Przykład ruchu (3): Toczenie si

ę

(bez po

ś

lizgu) po równi pochyłej

– równania ruchu

ruch post

ę

powy

ruch obrotowy

2

2

1

SM

kp

m

E

v

=

2

2

1

ω

I

E

SM

ko

=

Z zasady zachowania energii

2

SM

kp

R

ω

=

v

2

SM

ko

2

2

2

1

2

1

ω

SM

SM

I

m

mgh

+

=

v

Toczenie bez po

ś

lizgu

np. dla walca

gh

SM

3

4

=

v

2

/

2

R

I

m

mgh

SM

SM

+

=

v

const.

0

d

d

=

⇒

=

=

L

L

M

t

KONSEKWENCJE ZASADY ZACHOWANIA
MOMENTU PĘDU I DRUGIEJ ZASADY DYNAMIKI
DLA RUCHU OBROTOWEGO

const.

=

=

ω

ωω

ω

Ι

L