Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 przykłady do wykładu 2
Problem 1
Zmierzono poziom Morza Północnego w pewnym punkcie:
t
[h]
0 2 4 6 8 10
h
[m] 1,0 1,6 1,4 0,6 0,2 0,8
Pływ ma okres 12h.
Proszę aproksymować dane funkcją:
12
2
cos
12
2
sin
)
(
2
1
0
*
t
a
t
a
h
t
h
π
π
+
+
=
rozwiązując liniowe zadanie aproksymacji średniokwadratowej. (Nie jest
możliwe rozwiązanie tego zdania dla funkcji
12
2
0
0
)
t
t
(
sin
A
h
)
t
(
h
−
+
=
π
,
do której nie wszystkie parametry wchodzą liniowo.
t
0 2 4 6 8 10
( )
1
0
=
t
ϕ
1 1 1 1 1 1
0
sin
3
π
sin
3
2
π
sin
π
sin
3
4
π
sin
3
5
π
sin
( )
12
2
1
t
sin
t
π
ϕ
=
0
2
3
2
3
0
2
3
−
2
3
−
0
cos
3
π
cos
3
2
π
cos
π
cos
3
4
π
cos
3
5
π
cos
( )
12
2
2
t
cos
t
π
ϕ
=
1
2
1
2
1
−
-1
2
1
−
2
1
( )
t
h
1,0 1,6 1,4 0,6 0,2 0,8
,
0
,
,
0
,
,
0
,
2
1
2
0
1
0
=
=
=
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
[
]
6
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
,
0
0
=
+
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
ϕ
ϕ
PW2 1

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 przykłady do wykładu 2
3
4
3
4
3
0
4
3
4
3
0
2
3
2
3
0
2
3
2
3
0
2
3
2
3
0
2
3
2
3
0
,
1
1
=
+
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
ϕ
ϕ
3
4
1
4
1
1
4
1
4
1
1
2
1
2
1
1
2
1
2
1
1
2
1
2
1
1
2
1
2
1
1
,
2
2
=
+
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
⎥⎦
⎤
⎢⎣
⎡
−
−
−
=
ϕ
ϕ
[
]
6
,
5
8
,
0
2
,
0
6
,
0
4
,
1
6
,
1
0
,
1
8
,
0
2
,
0
6
,
0
4
,
1
6
,
1
0
,
1
1
1
1
1
1
1
,
0
=
+
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
h
ϕ
3
2
3
8
,
0
2
3
2
,
0
0
2
3
4
,
1
2
3
6
,
1
0
8
,
0
2
,
0
6
,
0
4
,
1
6
,
1
0
,
1
2
3
2
3
0
2
3
2
3
0
,
1
=
⋅
−
⋅
−
+
⋅
+
⋅
+
=
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
h
ϕ
8
,
0
4
,
0
1
,
0
6
,
0
7
,
0
8
,
0
0
,
1
8
,
0
2
,
0
6
,
0
4
,
1
6
,
1
0
,
1
2
1
2
1
1
2
1
2
1
1
,
2
=
+
−
−
−
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥⎦
⎤
⎢⎣
⎡
−
−
−
=
h
ϕ
Układ równań normalnych redukuje się do:
PW2 2
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 przykłady do wykładu 2
⎪
⎪
⎩
⎪⎪
⎨
⎧
=
=
=
h
a
h
a
h
h
,
,
,
,
,
,
2
2
2
2
1
1
1
1
0
0
0
0
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
8
0
3
6
5
3
3
6
2
1
0
,
,
a
a
h
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
267
0
577
0
933
0
2
1
0
,
,
,
a
a
h
12
2
cos
267
,
0
12
2
sin
577
,
0
933
,
0
)
(
*
t
t
t
h
π
π
+
+
=
Problem 2
Rozwiaż liniowe zadanie aproksymacji średniokwadratowej danych z tabeli
funkcją
:
x
c
c
)
x
(
f
*
1
0
+
=
x
1 3 4 6 7
f(x)
-2,1 -0,9 -0,6 0,6 0,9
Funkcje bazowe:
( )
( )
x
x
x
=
=
1
0
1
ϕ
ϕ
. Współczynniki wag =1.
Układ równań normalnych
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
f
,
f
,
c
c
,
,
,
,
1
0
1
0
1
1
0
1
1
0
0
0
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
[
]
5
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
=
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
ϕ
ϕ
,
[
]
21
7
6
4
3
1
7
6
4
3
1
1
1
1
1
1
1
0
=
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
ϕ
ϕ
,
PW2 3
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 przykłady do wykładu 2
[
]
111
49
36
16
9
1
7
6
4
3
1
7
6
4
3
1
1
1
=
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
ϕ
ϕ
,
[
]
1
2
9
0
6
0
6
0
9
0
1
2
9
0
6
0
6
0
9
0
1
2
1
1
1
1
1
0
,
,
,
,
,
,
,
,
,
,
,
f
,
−
=
+
+
−
−
−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
ϕ
[
]
7
2
3
6
6
3
4
2
7
2
1
2
9
0
6
0
6
0
9
0
1
2
7
6
4
3
1
1
,
,
,
,
,
,
,
,
,
,
,
f
,
=
+
+
−
−
−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
ϕ
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
7
2
1
2
111
21
21
5
1
0
,
,
c
c
⎥
⎦
⎤
⎢
⎣
⎡−
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
7
2
1
2
5
21
21
111
441
555
1
1
0
,
,
c
c
(
) (
)
(
) (
)
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
+
−
⋅
−
⋅
−
+
−
⋅
=
⎥
⎦
⎤
⎢
⎣
⎡
5053
0
5421
2
6
57
8
289
114
1
7
2
5
1
2
21
7
2
21
1
2
111
114
1
1
0
,
,
,
,
,
,
,
,
c
c
x
,
,
)
x
(
f
*
5053
0
5421
2
+
−
=
Problem 3
Znajdź wielomian interpolacyjny stosując
• Wzór Lagrange’a
• Metodę rodziny trójkatnej
i
0 1 2 3
x
i
-2 1 2 4
y
i
3 1 -3 8
PW2 4

Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 przykłady do wykładu 2
Ze wzoru Lagrangea dla n = 3:
( )
(
)(
)
(
)
(
)(
) (
)
(
)(
)
(
)
(
)(
)
(
)
(
)(
)
(
)
(
)(
)
(
)
(
)(
)(
)
(
)(
)(
)
(
)(
)(
)
(
)(
)(
)
(
)(
)(
)
( )( )( )
(
)(
)(
)
(
)( )(
)
(
)( )(
)
(
)( )(
)
(
) (
) (
) (
)
6
6
25
2
3
3
2
4
4
9
2
8
6
3
8
3
16
4
4
9
1
8
14
7
24
1
2
4
1
4
2
4
2
1
2
8
4
2
1
2
2
2
4
1
2
3
4
1
2
1
2
1
4
2
2
1
4
2
2
2
1
2
4
2
1
3
2
3
2
3
2
3
2
3
2
3
2
2
1
2
0
2
2
1
0
3
3
2
1
2
0
2
3
1
0
2
3
1
2
1
0
1
3
2
0
1
3
0
2
0
1
0
3
2
1
0
+
−
−
=
=
+
−
−
+
+
−
−
+
+
−
−
+
−
+
−
−
=
=
−
−
+
−
−
+
+
−
−
+
−
−
+
−
−
−
+
−
−
+
+
−
−
−
−
−
−
−
−
−
=
=
−
−
−
−
−
−
+
+
−
−
−
−
−
−
+
−
−
−
−
−
−
+
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
x
x
x
x
x
x
x
x
x
x
x
x
y
x
x
x
x
x
x
x
x
x
x
x
x
y
x
x
x
x
x
x
x
x
x
x
x
x
y
x
W
n
Metodą rodziny trójkątnej:
( )
( )
(
)
( )
(
)
(
)(
)
(
)
(
)(
)
( )
(
)
(
)(
)
(
)(
)(
)
(
)
(
)(
)
(
)(
)(
)
3
2
2
4
1
4
2
4
1
4
2
4
6
5
2
4
3
2
3
8
6
5
1
2
2
2
2
2
3
2
3
3
3
2
2
1
3
1
3
2
3
1
3
0
3
1
3
0
3
0
3
1
0
3
3
1
2
0
2
0
2
1
0
2
2
0
1
0
1
1
0
0
2
=
−
−
+
−
+
+
+
+
−
=
=
−
−
−
−
−
−
−
−
−
=
−
=
−
+
+
+
−
−
=
−
−
−
−
−
=
−
=
+
−
=
−
−
=
=
=
x
x
x
x
x
x
x
x
x
x
c
x
x
c
c
x
p
c
x
x
x
x
x
x
c
c
x
p
c
x
x
c
x
p
c
x
p
c
Po podstawieniu współczynników c do p(x) dostajemy:
( )
(
) (
)(
) (
)(
)(
)
(
) (
)( ) (
)( )(
)
(
) (
)
6
6
25
2
3
3
2
4
4
3
2
2
6
5
3
4
3
2
3
2
1
2
3
2
1
2
6
5
2
3
2
3
2
3
2
3
2
2
1
0
3
1
0
2
0
1
0
+
−
−
=
=
+
−
−
+
−
+
−
−
−
=
=
−
−
+
+
−
+
−
+
−
=
=
−
−
−
+
−
−
+
−
+
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
c
x
x
x
x
c
x
x
c
c
x
p
Problem 4
Oblicz metodą Hornera wartość
( )
6
6
25
2
3
3
2
2
3
+
−
−
=
x
x
x
x
p
dla x=1 .:
(
)
(
)
3
2
1
0
3
2
2
1
3
0
)
(
a
x
a
x
a
x
a
a
x
a
x
a
x
a
x
P
+
+
+
=
=
+
+
+
=
b
0
=a
0
a
1
a
2
a
3
PW2 5
+x
b
0
+x b
1
+x b
2
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 przykłady do wykładu 2
PW2 6
=
x)
=b
1
= b
2
b
3
=P(
+
+
+
+
=
−
−
1
1
1
0
)
(
L
2/3 -3/2 -25/6 6
n
n
n
n
a
x
a
x
a
x
a
x
P
n
i
i
i
b
x
P
n
i
xb
a
b
a
b
=
=
+
=
=
−
)
(
,
,
1
,
1
0
0
L
+1 2/3
-1 5
-1 5/6
=-5/6
=
-5 1
roblem 5
omian interpolacyjny dla sin(x) stosując węzły –1, -1/3, 1/3, 1. Oszacuj błąd
x -1
-1/3
1/3 1
P
Znajdź wiel
interpolacji.
y=sin(x) -0.8415
-0.3272 0.3272 0.8415
( )
( )
(
)
( )
(
)
(
)(
)
( )
(
)
(
)(
)
(
)(
)(
)
........
......
3
1
3
1
1
3
1
1
3
1
7714
.
0
8415
.
0
3272
.
0
7714
.
0
1
3
1
8415
.
0
3272
.
0
8415
.
0
2
3
1
3
0
3
1
3
0
3
0
3
1
0
3
3
1
2
0
2
0
2
1
0
2
2
0
1
0
1
1
0
0
2
=
−
−
−
−
−
−
−
−
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛ +
⎟
⎠
⎞
⎜
⎝
⎛ +
⎟
⎠
⎞
⎜
⎝
⎛ +
−
+
−
=
−
−
−
−
−
=
=
+
−
+
−
=
−
−
=
−
=
=
x
x
x
x
x
x
x
x
x
x
c
x
x
c
c
x
p
c
x
x
x
x
x
x
c
c
x
p
c
x
x
c
x
p
c
x
p
c
…………………………..
(x)=-0.1576x
3
+0.9991x
P
)
(
)
(
)!
1
(
1
)
(
)
(
0
)
1
(
∏
=
+
−
+
=
−
n
i
i
n
x
x
f
n
x
P
x
f
ξ
)
(
)
(
sin
!
4
1
)
(
)
sin(
3
0
)
4
(
∏
=
−
=
−
i
i
x
x
x
P
x
ξ
)
sin(
)'
cos
(
'
))'
sin(
(
)
(
cos
)
(
sin
)
3
(
)
4
(
x
x
x
=
−
=
−
=
=
ξ
ξ
[
]
⎥
⎦
⎤
⎢
⎣
⎡
−
≤
−
∏
=
≤
≤
−
≤
≤
−
)
(
max
)
sin(
max
!
4
1
)
(
)
sin(
3
0
1
1
1
1
i
i
x
x
x
x
x
x
P
x
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne ET3 przykłady do wykładu 2
1975
.
0
8415
.
0
!
4
1
)
(
)
sin(
≤
−
x
P
x
=0.0069
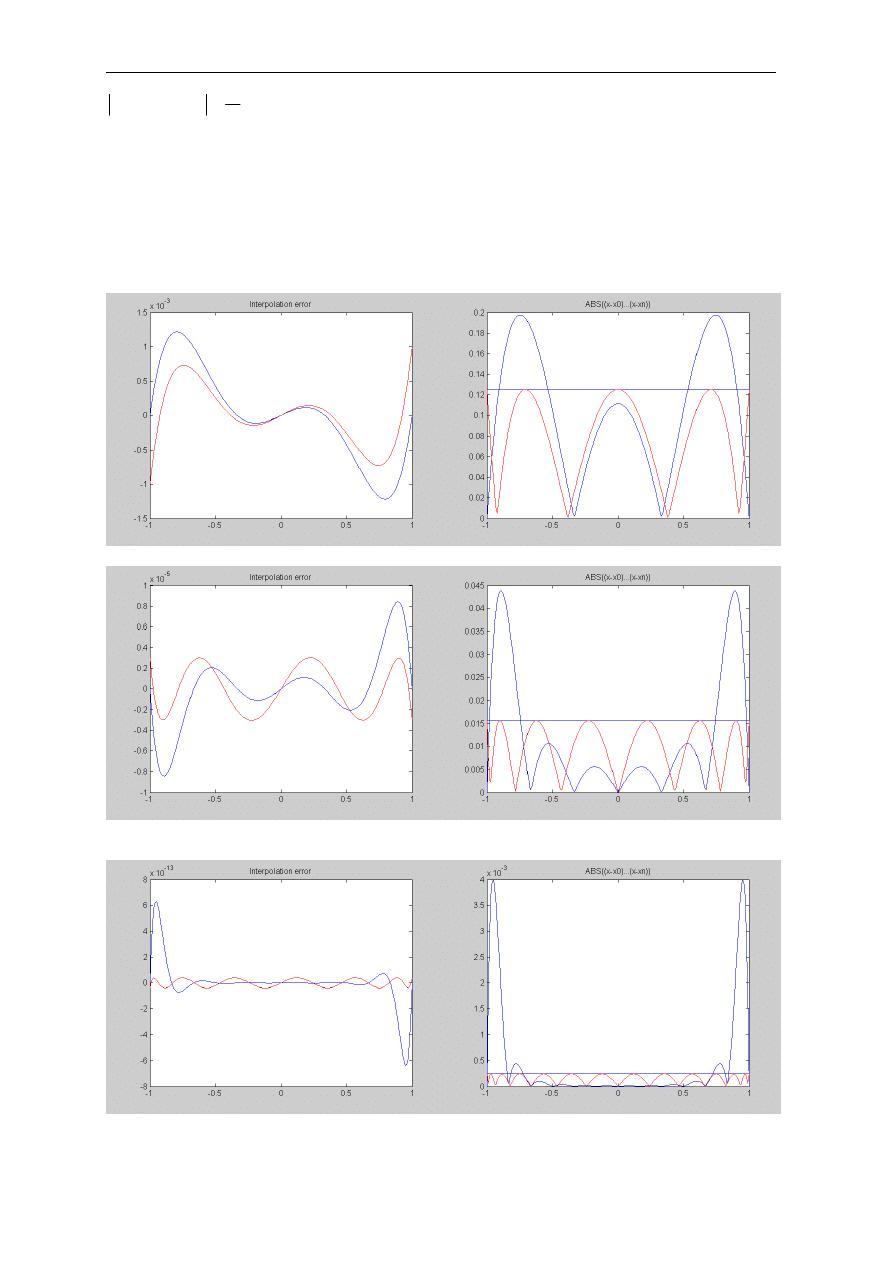
tosując węzły Czebyszewa dostajemy:
(x)= -0.1585x +0.9990x
orównanie wyników:
blue – węzły równoodległe
,
red węzły Czebyszewa
S
3
P
P
(linia pozioma = 2
-n
)
:
n=3
n=6
=12
n
PW2 7
Document Outline
Wyszukiwarka
Podobne podstrony:
Nowy folder Przykłady do w3
Nowy folder Przykłady do w4
Nowy folder, Przykłady do w3
Nowy folder, Przykłady do w4
cw 16 odpowiedzi do pytan id 1 Nieznany
IMIR przyklady praca energia id Nieznany
Oswietlenie LED do akwarium id Nieznany
Noktowizyjny obraz do kamery id Nieznany
3 Przykladowy opis obrazu 2 id Nieznany (2)
Nowy folder, przykładW5Gauss
Antropologia Slowa do druku id Nieznany (2)
Podstawy programowania 1 W2 id Nieznany
POZYCJE WYJSCIOWE DO CWICZEN id Nieznany
materialy do wykladow 1 i 2 id Nieznany
Materialy dla studentow W2 id 2 Nieznany
91 Nw 10 Zgrzewarka do folii id Nieznany (2)
Nowy folder (3) wkr 2012 cw4 I1 Nieznany
Mechanika Techniczna I Skrypt przyklady do rozwiazania id 291
więcej podobnych podstron