1

Praca wykonana przez sił

ę

zmienn

ą

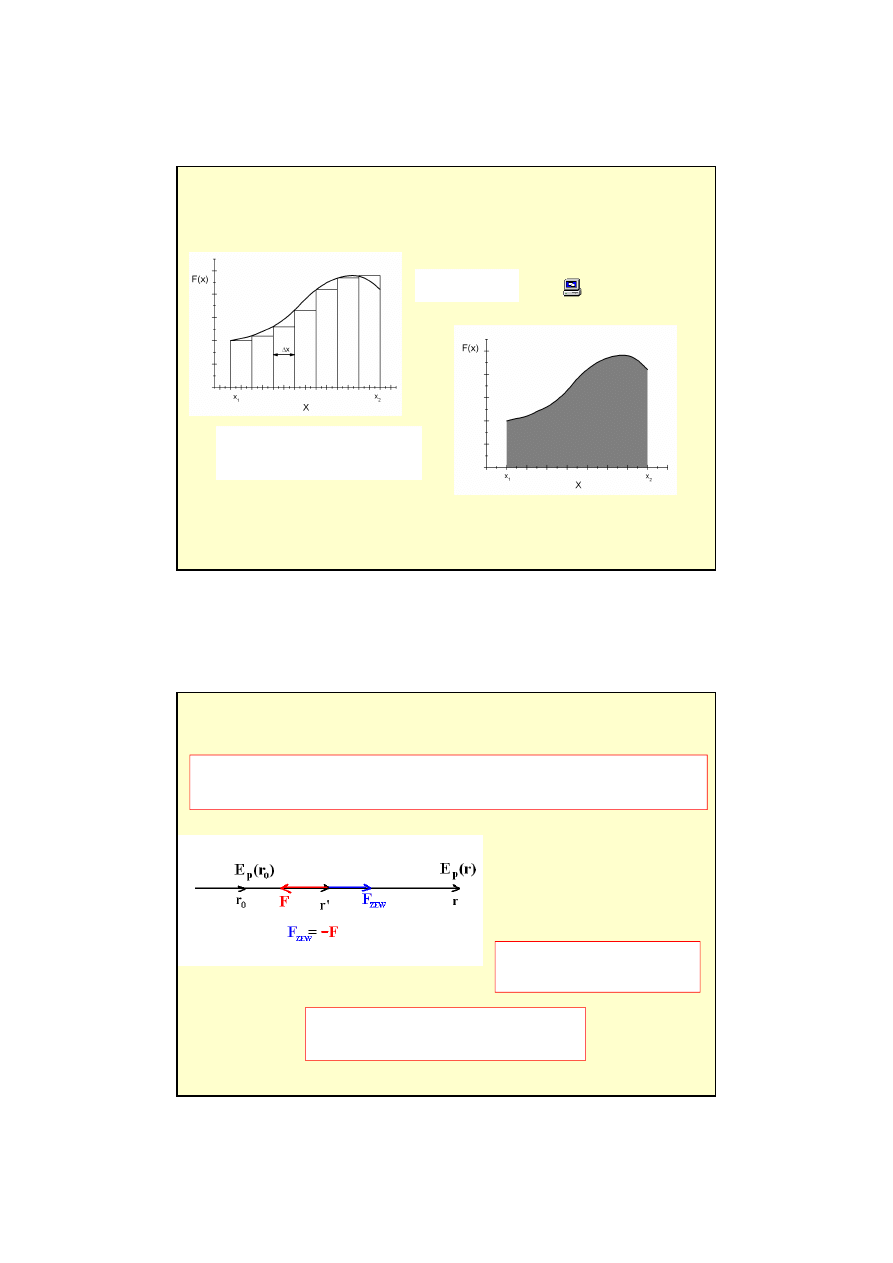
Przykład:

Zmienna siła F(x) (równoległa do przemieszczenia)

i

i

i

W

F x

δ

= ∆

∑

∫

∞

=

→

∆

=

∆

=

1

0

2

1

d

)

(

lim

i

x

x

i

i

x

x

x

F

x

F

W

Całkowanie funkcji F(x) w zadanych granicach odpowiada liczeniu pola
powierzchni pod krzyw

ą

F(x) w zadanym przedziale

Gdy działaj

ą

siły zachowawcze

, mo

ż

na wprowadzi

ć

poj

ę

cie

energii potencjalnej E

p

.

Energi

ę

potencjaln

ą

mo

ż

na traktowa

ć

jako zgromadzon

ą

w polu sił zachowawczych

prac

ę

, która mo

ż

e by

ć

w przyszło

ś

ci całkowicie odzyskana lub zamieniona na inn

ą

u

ż

yteczn

ą

form

ę

energii.

Energi

ę

potencjaln

ą

nazywa si

ę

energi

ą

(funkcj

ą

) stanu.

Dla siły

zachowawczej F

z

równowa

ż

onej

przez sił

ę

zewn

ę

trzn

ą

F

zew

:

z

zew

p

W

W

E

F

F

−

=

=

∆

0

0

( ) d

( ) d

r

r

p

zew

r

r

E

F

r

r

F r

r

∆

=

= −

∫

∫

0

0

0

( )

( )

( )

( ) d

r

p

p

p

p

r

E r

E r

E

E r

F r

r

=

+ ∆

=

−

∫

Punkt r

0

nazywamy punktem odniesienia i zazwyczaj wybieramy go tak,

ż

eby energia potencjalna w tym punkcie odniesienia E

p

(r

0

) była równa zeru.

Energia potencjalna

2

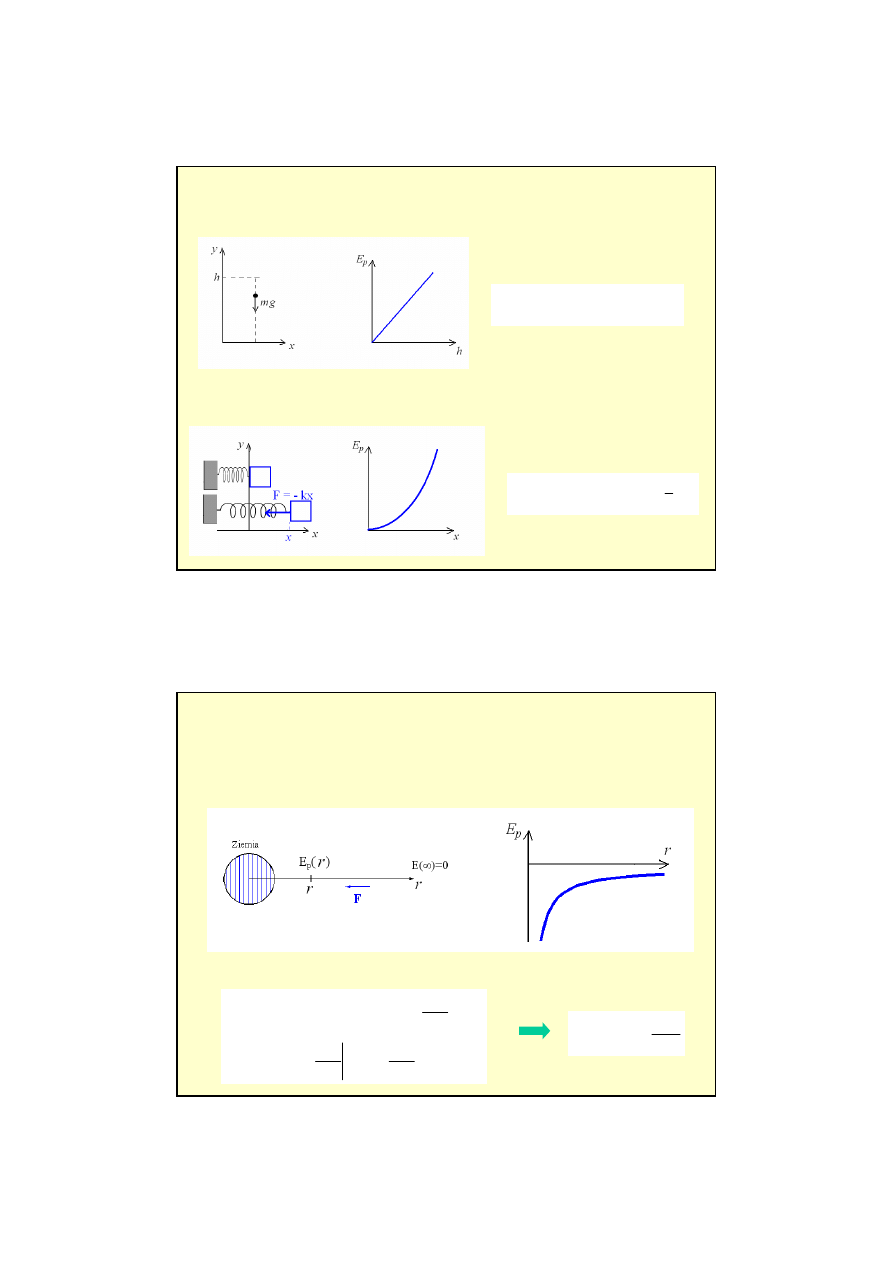
Przykłady

Energia potencjalna w pobliżu powierzchni Ziemi (punkt odniesienia na powierzchni Ziemi y

0

= 0)

mgh

y

mg

E

y

E

h

p

p

=

−

−

=

∫

0

d

)

(

)

0

(

)

(

0

)

0

(

=

p

E

dla:

Energia potencjalna idealnej nieważkiej sprężyny (punkt odniesienia x

0

= 0)

2

0

1

( )

(0)

(

) d

2

x

p

p

E

x

E

kx

x

kx

=

− −

=

∫

0

)

0

(

=

p

E

dla:

Energia potencjalna w dowolnym punkcie nad powierzchnią Ziemi, odległym o r od środka Ziemi
(zerową energię potencjalną przypisujemy punktowi odniesienia w nieskończoności r → ∞).

2

( )

( )

d

d

r

r

p

p

r

Mm

E r

E

F r

G

r

r

Mm

Mm

G

G

r

r

∞

∞

∞





=

∞ −

= − −

=









−

= −

∫

∫

r

Mm

G

r

E

p

−

=

)

(

0

)

(

=

∞

p

E

dla:

3

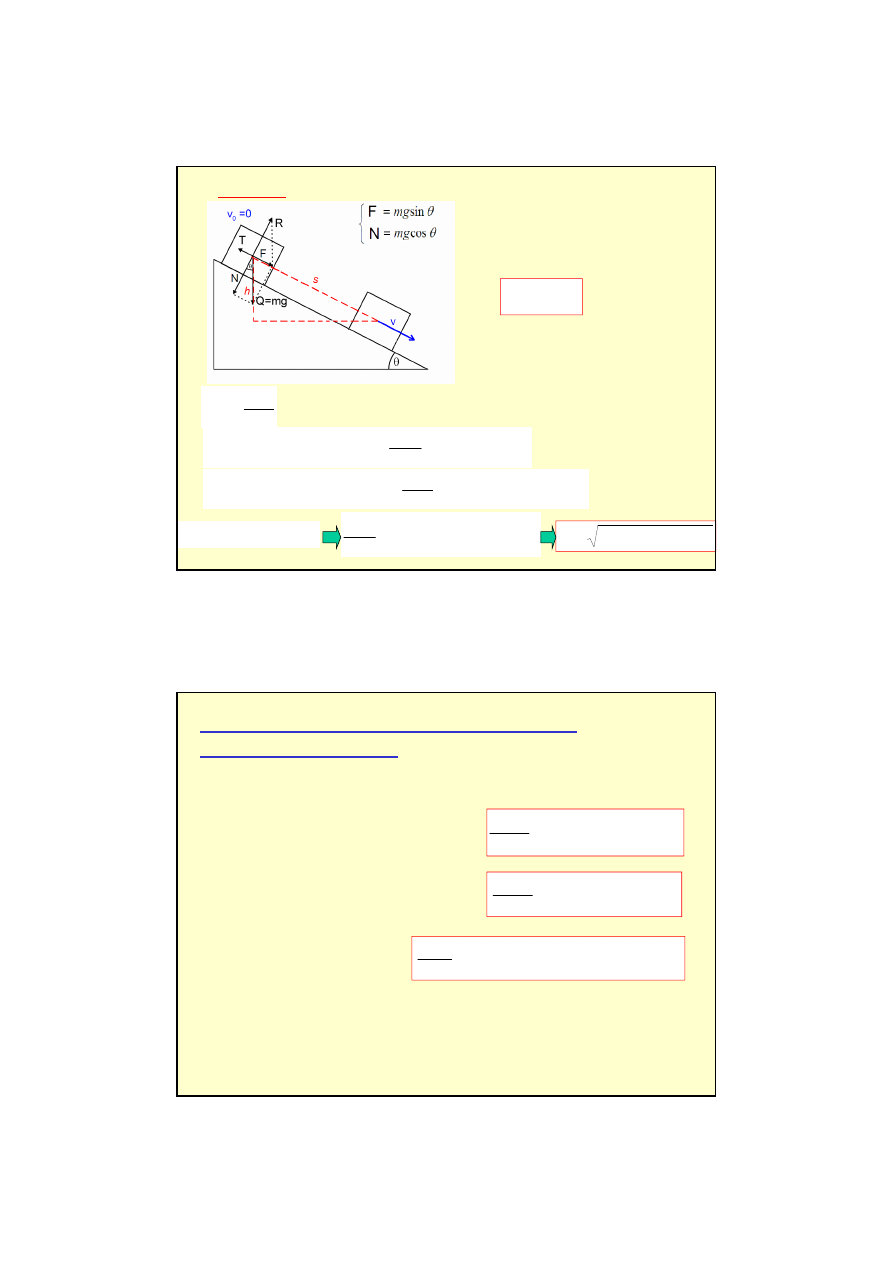
Przykład

s

f

>

θ

tg

θ

mg

f

θ

mg

θ

mg

f

N

f

T

T

F

s

s

s

cos

sin

cos

max

max

>

=

=

>

2

2

v

m

E

k

=

∆

mgh

mg

h

smg

W

E

F

p

−

=

−

=

−

=

−

=

∆

θ

θ

θ

sin

sin

sin

θ

θ

θ

θ

ctg

cos

sin

)

cos

(

k

k

k

T

f

mgh

mg

f

h

mg

f

s

W

U

=

=

−

−

=

−

=

∆

0

=

∆

+

∆

+

∆

U

E

E

p

k

0

ctg

2

2

=

−

+

mgh

f

mgh

m

k

θ

v

)

ctg

1

(

2

θ

k

f

gh

−

=

v

ZASADY ZACHOWANIA DLA UKŁADU
ODOSOBNIONEGO (nie działaj

ą

siły zewn

ę

trzne)

const.

t

=

⇒

=

cał

cał

p

p

0

d

d

Zasada zachowania pędu :

const.

t

=

⇒

=

cał

cał

L

L

0

d

d

Zasada zachowania momentu pędu :

Zasada zachowania energii :

const.

U

E

0

p

=

+

+

=

⇒

=

k

E

E

t

d

E

d

cał

cał

4

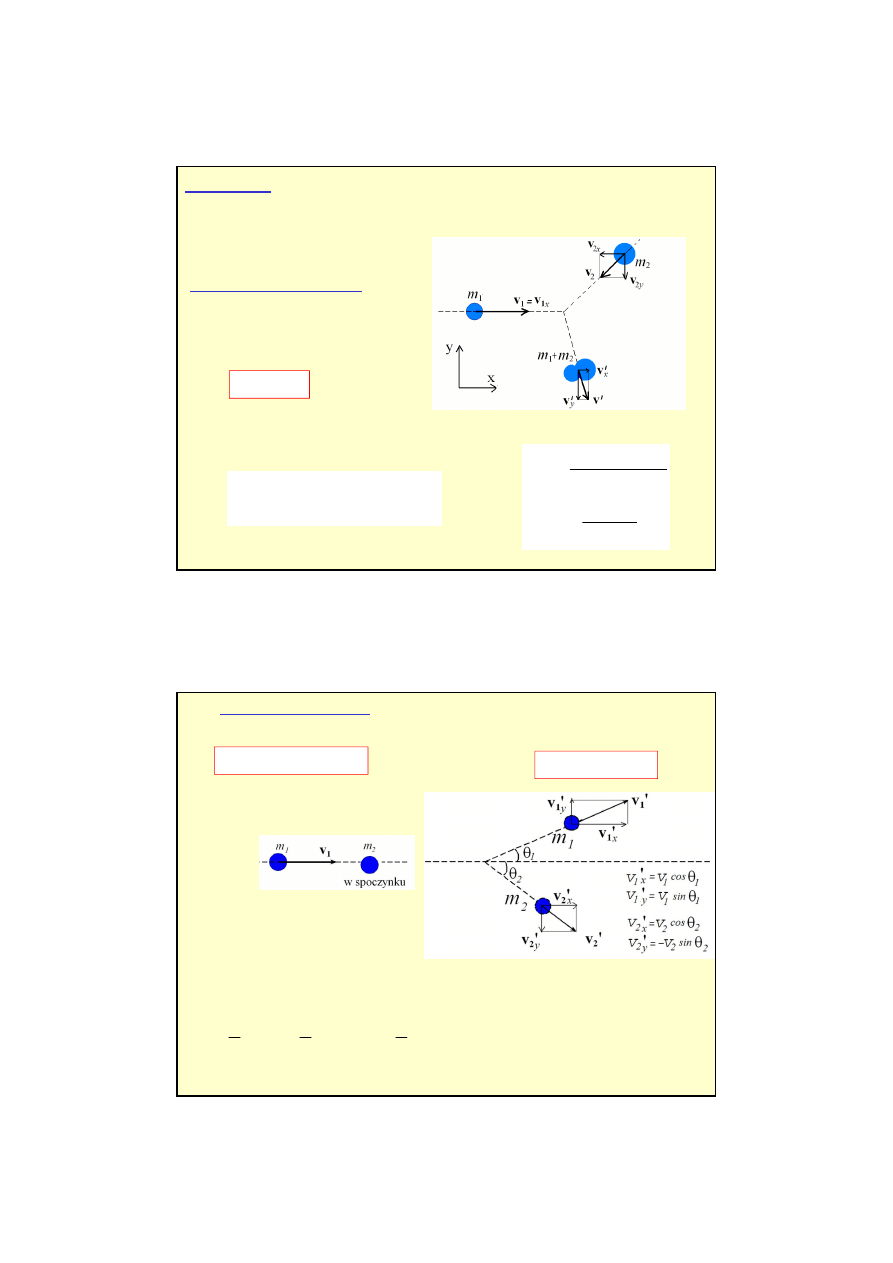
Zderzenia:

-doskonale niesprężyste
-doskonale sprężyste
-inne

p

1

+p

2

=p’

doskonale niesprężyste:

-zas. zach. energii mechanicznej –

-niespełniona

- zas. zach. pędu -

spełniona













+

−

=

+

−

=

2

1

2

2

2

1

2

2

1

1

'

'

m

m

m

m

m

m

m

y

y

x

x

x

v

v

v

v

v







+

=

−

+

=

−

'

(

'

(

2

1

2

2

2

1

2

2

1

1

y

y

x

x

x

m

m

m

m

m

m

m

)v

v

)v

v

v

Uwaga: w równaniach uwzględniono znaki „+” i „-”

dla przykładu pokazanego na rysunku

przykład zderzenia niecentralnego:







−

=

+

=

2

2

2

1

1

1

2

2

2

1

1

1

1

1

sin

'

sin

'

0

cos

'

cos

'

θ

θ

θ

θ

v

v

v

v

v

m

m

m

m

m

2

2

2

1

)

'

(

)

'

(

v

v

v

m

2

1

+

m

2

1

=

m

2

1

2

1

2
1

1

zas. zach. energii

zas. zach. pędu

p

1

+p

2

=p

1

’+ p

2

’

doskonale sprężyste:

- zas. zach. energii mechanicznej -

spełniona

- zas. zach. pędu -

spełniona

E

k1

+E

k2

=E

k1

’+ E

k2

’

Uwaga: w równaniach uwzględniono znaki „+” i „-” przed i po zderzeniu dla przykładu pokazanego na

rysunku

5

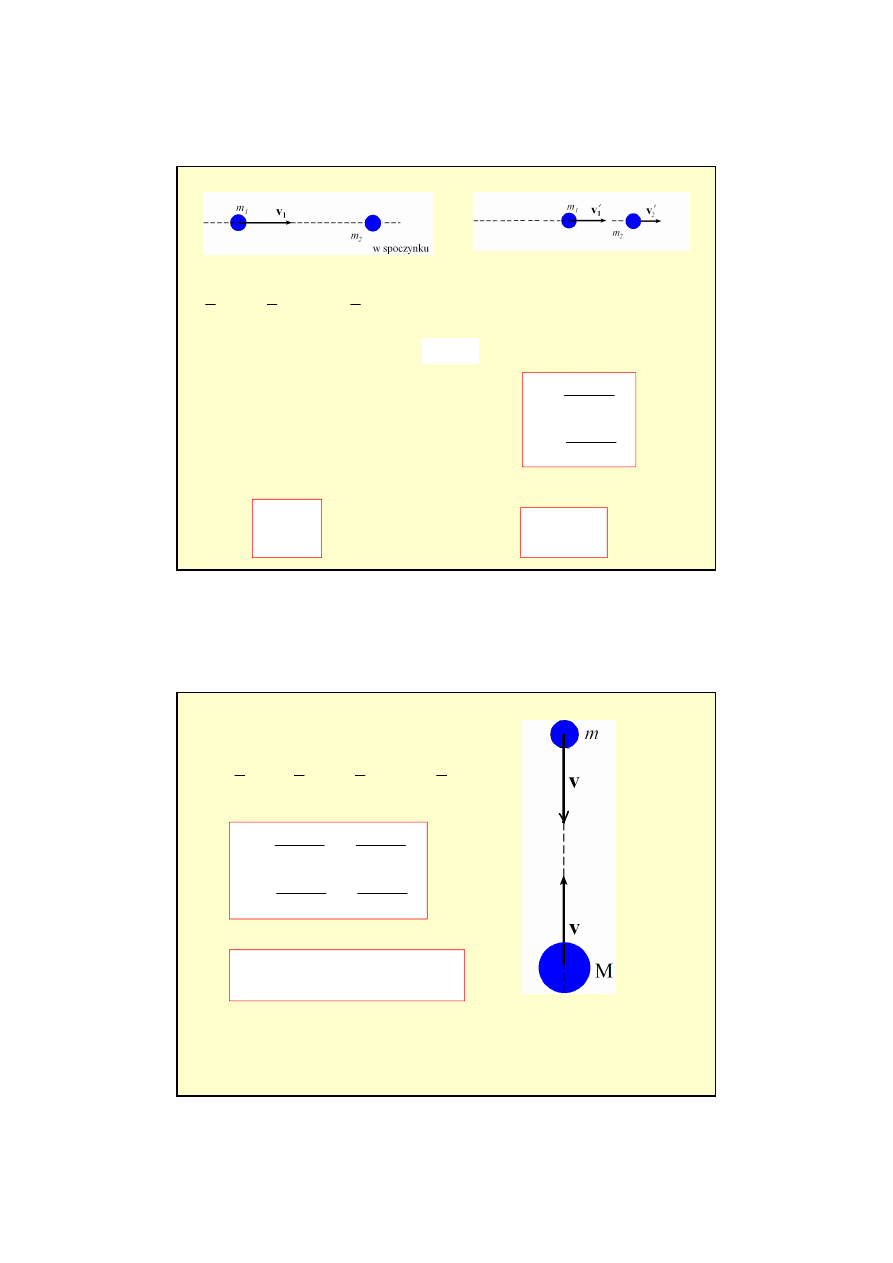
przykład zderzenia centralnego (

θ

1

= θ

2

=0

)









+

=

2

2

2

1

2

2

1

1

1

1

)

'

(

)

'

(

'

'

v

v

v

v

v

v

m

2

1

+

m

2

1

=

m

2

1

m

m

m

2

1

2

1

1

zas. zach. energii

zas. zach. pędu







+

−

=

−

2

2

1

1

2

2

1

1

1

)

'

(

)

'

)(

'

(

'

)

'

(

v

v

v

v

v

v

v

v

m

=

m

m

m

2

1

1

1







+

=

−

'

)

'

(

'

)

'

(

2

1

2

2

1

1

1

v

v

v

v

v

v

=

m

m

1







+

+

=

−

'

)

'

(

)

'

(

)

'

(

2

1

1

2

1

1

1

v

v

v

v

v

v

v

=

m

m

1

1













+

=

+

−

=

v

v

v

v

1

1

m

m

m

m

m

m

m

1

2

1

2

1

2

2

1

1

2

'

'

przypadek szczególny gdy m

1

=m

2

=m:







=

=

1

2

1

'

0

'

v

v

v

1

1

'

v

v

≠

1

1

2

'

'

0

≈ −





→



v

v

v

przypadek szczególny gdy m

1

<<m

2:

mniejsza piłeczka (m) odbije się na wysokość prawie dziewięciokrotnie
wyższą niż wieksza (M).

1

2

2

2

1

2

'

'

(

')

(

')

2

2

M

m

m

M

1

1

1

1

M

=

+ M

m

m

2

2

2

2

−

=

+







+



v

v

v

v

v

v

v

v

1

2

2

2

1

2

'

2

'

M

m

M

M

m

M

m

M

m

M

M

m

m

m

−



=

+



+

+





−



=

−



+

+



v

v

v

v

v

v

1

2

'

2

3

'

dla M

m

≈ +

=



>>



≈



v

v

v

v

v

v