4. Dynamika bryły sztywnej

W poprzednim rozdziale omówiono ruch postępowy ciała oraz niektóre aspekty dynamiki punktu materialnego. Poniżej przedstawione zostaną niektóre własności ruchu obrotowego bryły sztywnej. Bryłą sztywną nazywamy ciało, w którym nie zmieniają się wzajemne odległości punktów bryły w trakcie jej ruchu. Dynamika bryły sztywnej zajmuje się ruchem ciała z uwzględnieniem jego masy, działających na niego sił i jego zmianą orientacji w przestrzeni.

• ruch obrotowy

Przypomnijmy, że ruch obrotowy to taki ruch, w którym potrafimy wskazać przynajmniej chwilową oś obrotu (prosta na której leżą punkty nieruchome). W ruchu obrotowym ciała oprócz mas poszczególnych jego elementów ważne są również ich odległości od osi obrotu. Z faktem tym wiążą się podstawowe pojęcia: środek masy i środek ciężkości. Pierwszy z nich określa punkt, wokół którego jest równomiernie rozmieszczona masa bryły.

Rys. 15 Wyznaczanie środka masy i środka ciężkości dla bryły sztywnej

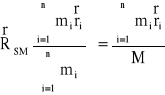
Środek ciężkości określa wzór:

.

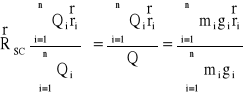
Z ostatniego wzoru wynika, że jeśli g_i = g = const (pole grawitacyjne jest jednorodne) to po podzieleniu licznika i mianownika przez g otrzymujemy wzór na położenie środka masy. Tak więc w jednorodnym polu grawitacyjnym środek ciężkości pokrywa się ze środkiem masy.

Rys. 16 Środek masy dwóch punktów materialnych.

Rozpatrzmy teraz przykład dwóch punktów materialnych o masach M i m.

Obliczmy teraz współrzędną środka masy układu a oraz wartość b.

Dzieląc stronami powyższe równania otrzymujemy:

.

Wynika stąd, że odległości środka masy od poszczególnych mas układu są w odwrotnej proporcji do mas tych elementów.

W ruchu obrotowym definiujemy prędkość kątową i przyspieszenie kątowe jako pochodne kąta skierowanego. Kąt skierowany to wektor o wartości równej wartości kąta obrotu, jego kierunek jest prostopadły do płaszczyzny kąta płaskiego a zwrot określa reguła śruby prawoskrętnej.

Rys. 17 Kąt skierowany

Moment pędu i moment siły definiujemy jako iloczyn wektorowy promienia i odpowiedniej wielkości (pędu lub siły).

• momenty bezwładności, twierdzenie Steinera

Obliczmy teraz energię kinetyczną bryły w ruchu obrotowym. Załóżmy, że bryła składa się z „n” punktów materialnych o masach m_i odległych o r_i od osi obrotu. Pamiętajmy też, że dla bryły sztywnej prędkości kątowe wszystkich elementów muszą być jednakowe i że prędkość liniowa w ruchu po okręgu równa jest iloczynowi prędkości kątowej i promienia.

Wielkość oznaczoną symbolem I nazywamy momentem bezwładności względem osi obrotu a jego wartość obliczamy sumując iloczyny mas i kwadratów ich odległości od osi obrotu. Dla bryły ciągłej napiszemy:

.

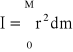
Wykorzystując moment bezwładności i zakładając symetryczny rozkład gęstości masy względem osi obrotu możemy zapisać wzór na moment pędu:

.

Powyżej mówiliśmy o osiowym momencie bezwładności. W fizyce spotykamy też momenty bezwładności względem płaszczyzny, punktu i tzw. momenty dewiacyjne odpowiadające za reakcje w łożyskach mocujących oś obrotu (np. „bicie” nie wyważonego koła samochodowego). Rodzaje i sposoby liczenia tych momentów bezwładności przedstawia tabelka.

moment bezwładności	odległość	Wzór I=
względem osi np. x
względem np. płaszczyzny xy	r = z
względem pn. 0
dewiacyjny np. xy	-

Tabela 2 Rodzaje i wzory do obliczenia momentów bezwładności

Dla osiowo symetrycznych brył otrzymujemy momenty bezwładności w postaci iloczynu stałej k, masy bryły m i kwadratu promienia (lub długości). Przykładowo dla krążka płaskiego lub walca
dla pręta
i dla kuli
(dla osi obrotu przechodzących przez środek masy).

Obliczając energię kinetyczną toczącego się ciała musimy wybrać układ odniesienia. Jeśli wybierzemy układ związany ze środkiem masy to energia kinetyczna będzie się składała z energii kinetycznej ruchu postępowego i energii kinetycznej ruchu obrotowego wokół osi obrotu O. Jeśli natomiast wybierzemy układ związany z chwilową osią obrotu O' to będziemy mieć tylko jeden składnik związany z energią kinetyczną ruchu obrotowego (ponieważ prędkość chwilowej osi obrotu = 0).

O:
, O':
.

Porównując wzory oraz uwzględniając związek miedzy prędkością liniową i kątową oraz mnożąc przez 2 otrzymujemy:

.

Stąd otrzymujemy twierdzenie Steinera:

.

Twierdzenie to mówi, że moment bezwładności bryły względem osi 0' jest równy sumie jej momentu bezwładności względem osi 0, równoległej i przechodzącej przez środek masy w odległości r od osi 0' oraz iloczynu masy bryły i kwadratu tej odległości.

Poniżej zostanie przedstawiony prosty przykład obliczania wzoru na moment bezwładności bez konieczności całkowania dla wybranych brył. Policzymy moment bezwładności pręta. Powinniśmy otrzymać wzór w postaci I=kml². Podzielimy pręt o masie m i długości l na dwie części o masach m/2 i długościach l/2 (rysunek 18).

Rys. 18. Obliczanie momentu bezwładności pręta

Moment bezwładności całego pręta i jego połówek będzie miał podobną postać. Całkowity moment bezwładności będzie sumą momentów dwóch połówek liczonych dla środkowej osi (tu zastosujemy twierdzenie Steinera).

,

Porównując oba wzory wyznaczamy:

.

• zasady dynamiki dla ruchu postępowego i obrotowego

Bardzo ważnymi są równania dynamiki definiujące siłę i moment siły:

,

.

Pierwsze z nich umożliwia podanie zasad dynamiki dla ruchu postępowego.

Pierwsza zasada dynamiki dla ruchu postępowego mówi, że jeśli na ciało (układ ciał) nie działają żadne siły lub działające siły się równoważą (wypadkowa siła równa jest 0) to pęd ciała (układu ciał) jest stały. Jeśli założymy stałość masy to można powiedzieć, że ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym (prędkość jest stała).

Druga zasada dynamiki dla ruchu postępowego mówi, że jeśli na ciało (układ ciał) działa niezrównoważona siła zewnętrzna (wypadkowa sił jest różna od zera) to ciało zmienia swój pęd wprost proporcjonalnie do działającej siły. Mówimy też, że zmiana pędu ciała jest równa popędowi działającej siły.

Jeśli założymy stałość masy otrzymamy:

.

Można więc sformułować tą zasadę w postaci: jeśli na ciało działa niezrównoważona siła zewnętrzna to porusza się ono z przyspieszeniem wprost proporcjonalnym do działającej siły a współczynnikiem proporcjonalności jest odwrotność masy.

Trzecia zasada dynamiki dla ruchu postępowego mówi, że jeśli na ciało (układ ciał) nie działają żadne siły lub wypadkowa sił zewnętrznych jest równa 0 to suma sił wewnętrznych jest równa 0. W przypadku dwóch ciał powiemy, że w układzie izolowanym jeśli ciało A działa na ciało B siłą
to ciało B działa na ciało A siłą
o tej samej wartości i tym samym kierunku lecz przeciwnym zwrocie (siły te różnią się oczywiście również punktami zaczepienia).

Ruch obrotowy opisujemy podobnie jak postępowy zastępując wielkości kinematyczne

ruch postępowy	Ruch obrotowy
masa - m	moment bezwładności - I
wektor położenia -	kąt skierowany -
prędkość liniowa -	Prędkość kątowa -
przyspieszenie liniowe -	Przyspieszenie kątowe -
pęd -	moment pędu -
siła -	moment siły -

Tabela 3 Odpowiedniki kinematyczne i dynamiczne ruchu postępowego i obrotowego

(dynamiczne) jednego odpowiednikami drugiego ruchu (tabela). Proponuję czytelnikowi sformułowanie zasad dynamiki dla ruchu obrotowego.

• warunki statyki

W mechanice ważnymi z punktu widzenia warunków konstrukcji maszyn lub budowli są warunki statyki wynikające z warunków równowagi (dla prędkości = 0). Podajemy je z punktu widzenia braku ruchu postępowego jak i obrotowego.

Najprostszym przykładem zastosowania obu tych warunków jest dźwignia jednostronna.

Rys.19 Dźwignia jednostronna

Z warunków równowagi otrzymujemy równania:

Ponieważ ostatni moment siły jest równy zero (r=0) a pierwsze dwa są przeciwne stąd:

a-lF=0,

czyli działająca siła

.

Wynika stąd wniosek, że dla odchylenia takiej belki wystarczy siła tyle razy mniejsza ile razy większe ma ona ramię od ramienia siły
.

Drugi przykład przedstawia bloczek nieruchomy o masie m i promieniu r z zawieszonymi ciężarkami o masach M₁ i M₂ (rysunek20).

Rys. 20 Bloczek nieruchomy

Przy rozwiązywaniu tego typu problemów postępujemy zgodnie z algorytmem:

1. zaznaczamy wszystkie siły działające na poszczególne ciała nie zapominając o naciągach, które zaznaczamy parami w punktach styczności linki z najbliższymi ciałami (zawsze w kierunku linki),

2. zaznaczamy obieg dodatni (znak + na rysunku),

3. zapisujemy równania ruchu postępowego wstawiając siły ze znakiem + jeśli są zgodne z wybranym obiegiem i - gdy są przeciwne,

4. zapisujemy równania ruchu obrotowego wstawiając momenty sił ze znakiem + jeśli są zgodne z wybranym obiegiem i - gdy są przeciwne,

5. uzupełniamy układ równań o równanie wiążące przyspieszenia w ruchu postępowym i obrotowym oraz równania na moment bezwładności krążka i ciężary ciał,

6. sprawdzamy liczbę niewiadomych i liczbę niezależnych równań i rozwiązujemy układ równań.

ruch postępowy - M₁ : N₁ - Q₁ = M₁ a

M₂ : Q₂ - N₂ = M₂ a

Ruch obrotowy - rN₂ - rN₁ = Iε

Moment bezwładności - I =
mr²

Związek między przyspieszeniami - ε =

Ciężary - Q₁ = M₁ g

Q₂ = M₂ g

Otrzymaliśmy układ 7 równań na 7 niewiadomych (N₁, N₂, Q₁, Q₂, a, I, ε), z którego możemy obliczyć np. przyspieszenie liniowe układu.

---