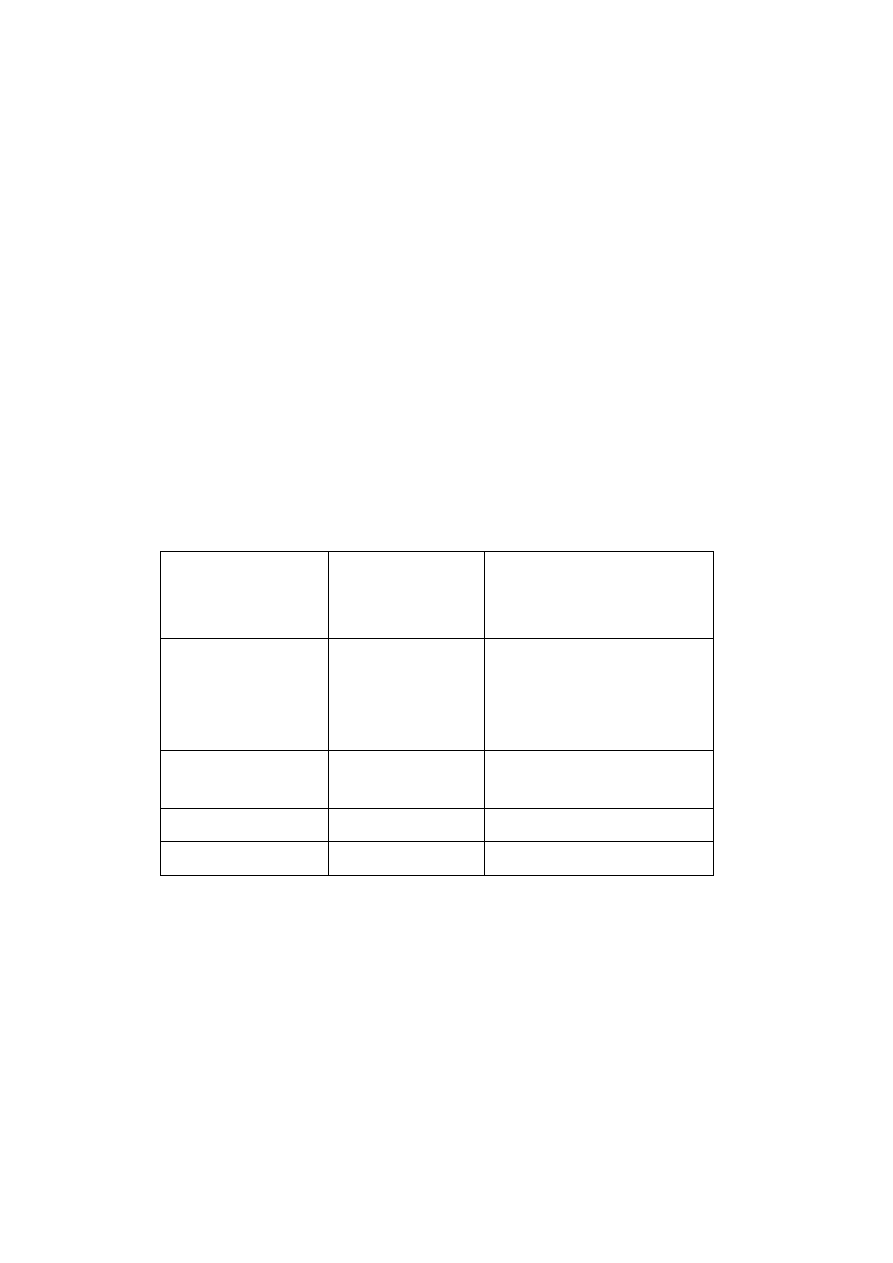
WYBRANE PROBLEMY DYNAMIKI ATMOSFERY

Na cząstkę powietrza w atmosferze działają siły: ciężkości, gradientu

ciśnienia, Coriolisa, siła odśrodkowa i siła tarcia.

Skale ruchów powietrza są bardzo rozległe zarówno pod względem czasu

jak i przestrzeni. Zakres ten obejmuje zarówno bezładne mikro ruchy

poszczególnych cząsteczek jak i globalną cyrkulację całej atmosfery.

Skale ruchów atmosferycznych (wg Iribarne’a, 1988)

Skala

przestrzenna

Typowe

wymiary

[km]

Przykłady

Planetarna

10 000

komórka Hadleya –
cyrkulacja
atmosferyczna,
równik-bieguny

Synoptyczna

1 000

cyklony strefy
umiarkowanej

Mezoskalowa 100

burze

Skala drobna

<10

małe chmury Cumulus

Ruchy poszczególnych cząstek, z wyjątkiem górnych krańców atmosfery,

nie mają znaczenia w dynamice atmosfery. Atmosferę traktuje się jako ośrodek

ciągły, płyn.

Opis ruchu powietrza

Metody opisu ruchu powietrza

Do opisu ruchu powietrza stosuje się dwa sposoby: metodę Eulera i

metodę Lagrange’a.

Metoda Eulera – określa się właściwości powietrza jako funkcję położenia w

przestrzeni

)

(rr

i czasu (t). Ruch powietrza charakteryzuje prędkość, która jest

zależna od czasu i przestrzeni:

( )

t

r

v

v

,

r

=

Opis ten jest obrazem przestrzennego rozkładu prędkości powietrza w każdej

chwili.

Metoda Lagrange’a – powietrze traktowane jest jako zbiór małych

cząstek, których prędkość jest funkcją czasu. Metoda ta opisuje historię ruchu

każdej cząstki w powietrzu, zmiany w wędrującej cząsteczce. Opis ten

nazywany jest analizą wędrowną.

Rodzaje rozkładów prędkości

Dowolne pole prędkości małej cząstki powietrza można traktować jako

wynik nałożenia się na siebie kilku prostych rodzajów pola ruchu. Główne

rodzaje podstawowych rozkładów prędkości, to:

1) ruch postępowy zwany także translacją liniową, w którym prędkość

cząsteczki powietrza jest stała. Cząstka porusza się po prostej ze stałą

prędkością oraz bez zmiany kształtu;

2) obrót cząsteczki – na podobieństwo obrotu ciała sztywnego;

3) ekspansja izotropowa – rozszerzanie się lub kurczenie się cząsteczki bez

zmiany kształtu;

4) deformacja – zmiana kształtu bez zmiany objętości cząstki;

Dowolne pole prędkości można rozłożyć na te cztery rodzaje ruchu.

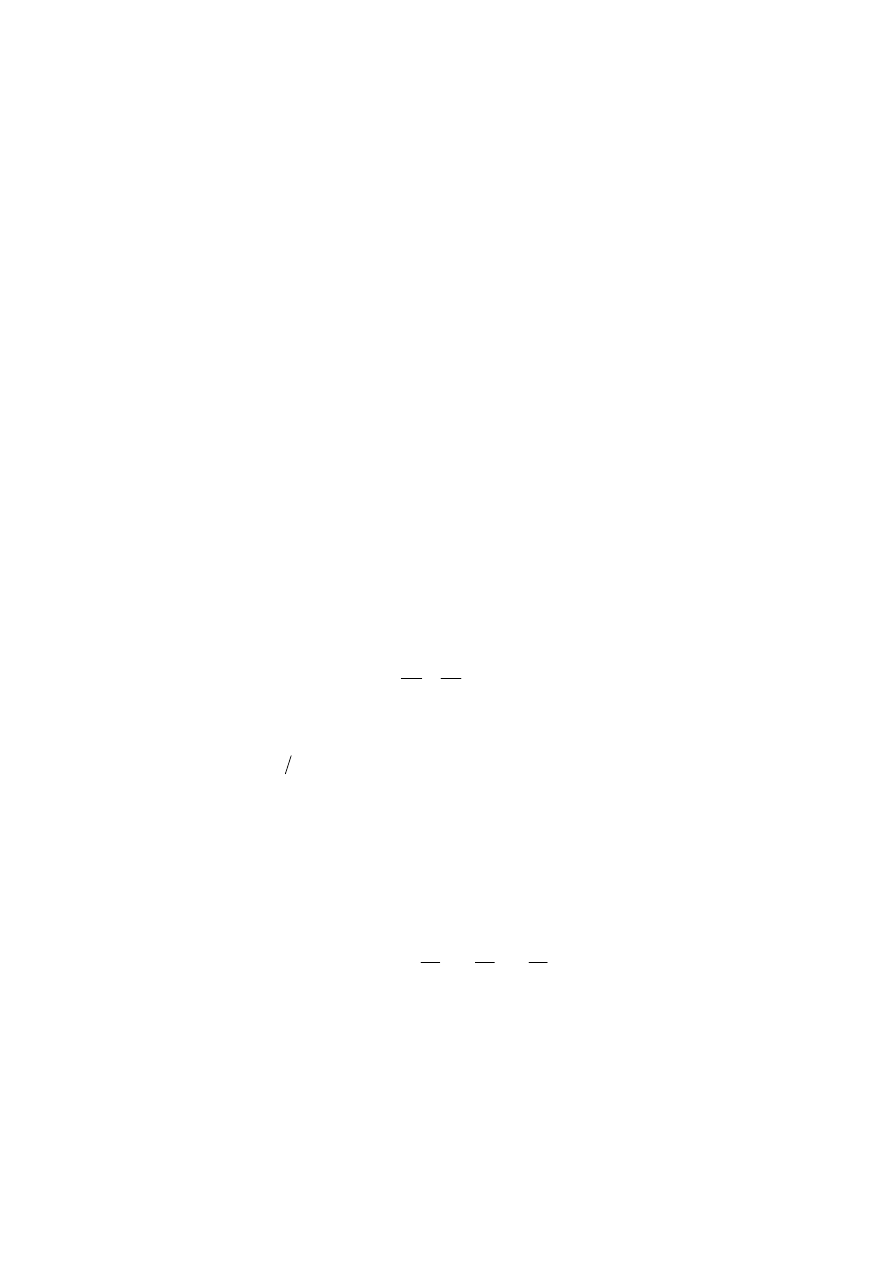
Przyspieszenie cząstki powietrza

Zgodnie

z

drugą zasadą dynamiki Newtona, przyspieszenie cząstki równe

jest sile wypadkowej działającej na cząstkę, podzielonej przez jej masę.

Przyspieszenie to można także określić z opisu metodą Eulera pola prędkości w

atmosferze.

Pole prędkości

)

,

( t

r

v

r

określa się jako funkcję położenia

r

r

i czasu t.

z

k

y

j

x

i

r

v

r

r

r

+

+

=

z

y

x

v

k

v

j

v

i

v

r

v

v

r

+

+

=

gdzie:

k

j

i

r

r

r

,

,

są trzema wersorami w kartezjańskim układzie współrzędnych.

Przyspieszenie cząstki

a

r

, pochodna zupełna po czasie, zwana także

substancjalną, składa się z dwóch członów:

( )

v

v

t

v

dt

v

d

a

r

r

v

r

r

r

∇

+

∂

∂

=

=

Pierwszy składnik

t

v

∂

∂r

, pochodna lokalna określa zmianę prędkości w punkcie

r

r

.

Drugi człon wynika z ruchu samej cząstki. Jest to tzw. pochodna

konwekcyjna (zwana czasem adwekcyjną). Symbol

)

(

∇

r

r

v

oznacza operator:

( )

z

v

y

v

x

v

v

z

y

x

∂

∂

+

∂

∂

+

∂

∂

=

∇

⋅

r

r

gdzie:

∇

r

=

∇ − operator Hamiltona (nabla), wektor symboliczny

k

z

j

y

i

x

r

r

r

∂

∂

+

∂

∂

+

∂

∂

=

∇

Przykładowo, składowa przyspieszenia wzdłuż osi x przyjmuje postać:

z

v

v

y

v

v

x

v

v

t

v

a

x

z

x

y

x

x

x

x

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

=

Równanie ruchu

Równanie ruchu wyraża równość iloczynu gęstości i przyspieszenia z

wektorową sumą sił działających na cząstkę powietrza o jednostkowej objętości.

R

v

p

g

dt

v

d

r

r

r

r

r

r

+

×

+

∇

−

=

ω

ρ

ρ

ρ

2

lub

R

v

p

g

dt

v

d

r

r

r

r

r

r

+

+

∇

−

=

ϕ

ω

ρ

ρ

ρ

sin

2

gdzie:

ρ

− gęstość powietrza,

g

− przyspieszenie ziemskie,

p

− ciśnienie,

ω

r

− prędkość kątowa Ziemi,

R

r

− siła tarcia,

ϕ − szerokość geograficzna

v

− prędkość cząstki powietrza.

Równanie ciągłości

Równanie

ciągłości zamyka równanie ruchu, opisując rozkład ciśnienia i

gęstości. Wyprowadzić je można z zasady zachowania masy. W postaci

różniczkowej przyjmuje formę stanowiącą lokalną postać zasady zachowania

masy.

0

=

∇

+

∂

∂

v

t

r

r

ρ

ρ

Dla warunków małych zmian gęstości

ρ równanie ciągłości przyjmuje postać:

(

)

0

div

0

=

=

∇

v

v

r

r

r

Główne siły działające na cząstkę powietrza w atmosferze

1. Siła ciężkości

Duża masa Ziemi wywołuje siłę ciężkości, działającą na cząstkę

powietrza. Jest ona jedną z największych sił działających i jest skierowana do

środka Ziemi. Na cząstkę o objętości ΔV działa siła:

g

V

F

g

ρ

Δ

=

gdzie: ΔV – objętość cząstki,

ρ

− gęstość powietrza,

g

− przyspieszenie ziemskie.

Cząstka powietrza jest nieruchoma względem powierzchni Ziemi. Obrót

Ziemi dookoła swojej osi powoduje wystąpienie siły odśrodkowej, która działa

również na cząstkę powietrza. Siła odśrodkowa jest jednak bardzo mała w

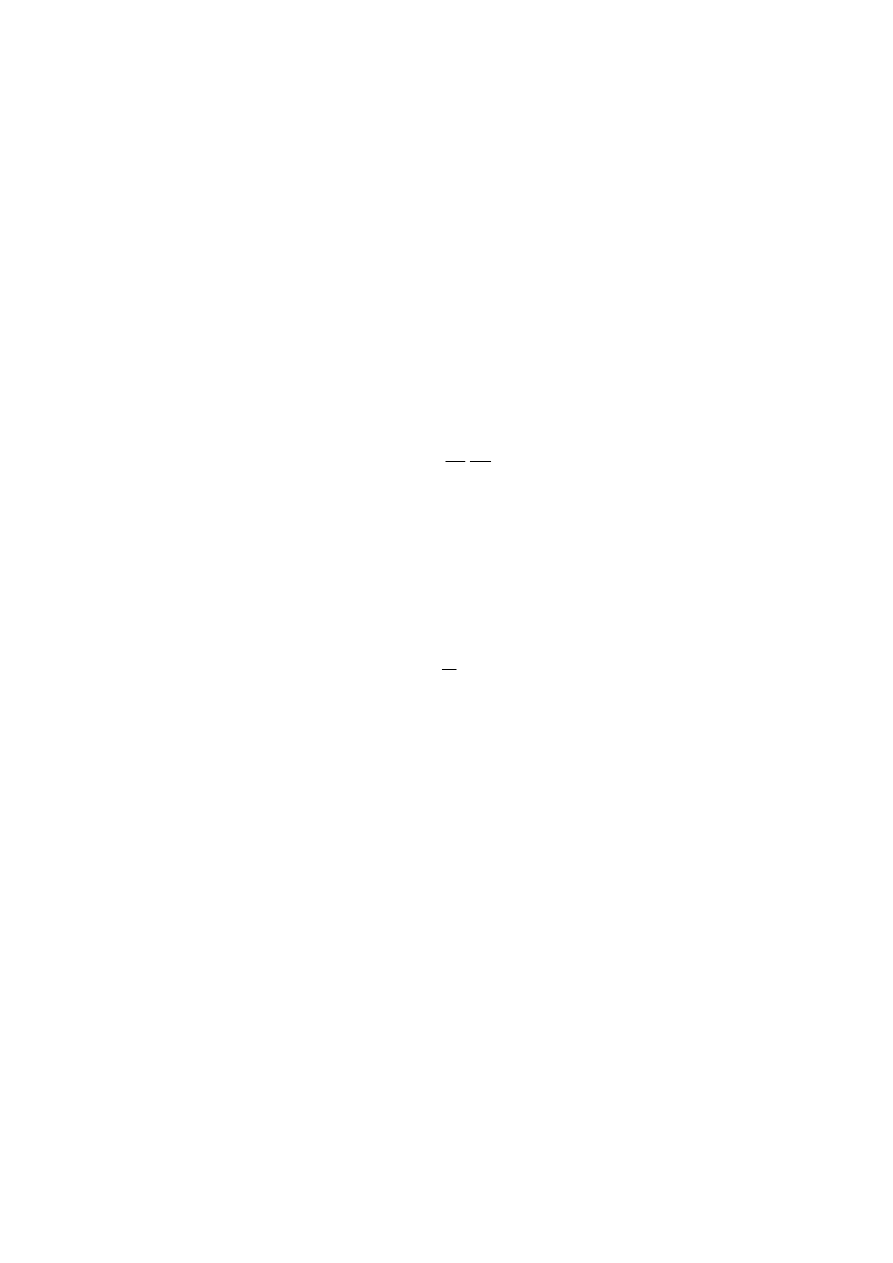
porównaniu z siłą ciężkości. Zwykle się ją pomija lub dodaje do siły ciężkości,

otrzymując tzw. skuteczną siłę ciężkości.

2. Siła gradientu ciśnienia

Gdy

ciśnienie na przeciwległych powierzchniach cząstki jest różne, na

cząstkę działa siła wypadkowa, skierowana do wnętrza cząstki. Nazywamy ją

siłą gradientu ciśnienia. Siła działająca na jednostkę masy wyraża się wzorem:

dn

dp

G

ρ

1

−

=

gdzie dp/dn oznacza zmianę ciśnienia dp na drodze dn.

Postać tę można uogólnić dla pola ciśnienia p w atmosferze:

p

G

∇

=

ρ

1

W atmosferze wektor gradientu ciśnienia można rozłożyć na składową

pionową i poziomą. Składowa pionowa jest prawie całkowicie równoważona

przez skierowaną przeciwnie siłę ciężkości.

W ruchu poziomym powietrza atmosferycznego rozważa się zatem tylko

składową poziomą gradientu, która jest główną przyczyną ruchu poziomego

(wiatru) w atmosferze.

3. Siła Coriolisa

Siła Coriolisa uwzględnia obrót Ziemi wokół swojej osi, co powoduje, że

układy odniesienia związane sztywno z powierzchnią Ziemi nie są układami

inercjalnymi.

F

c

= 2 m · v · ω · sin

ϕ

oraz przyspieszenie

C = 2 v · ω · sin

ϕ

gdzie: F

c

– siła Coriolisa,

C

–

przyspieszenie

Coriolisa,

v

–

prędkość cząsteczki (ciała),

ω – prędkość ruchu obrotowego Ziemi (ω = 7,29

× 10

−5

1/s),

ϕ − szerokość geograficzna.

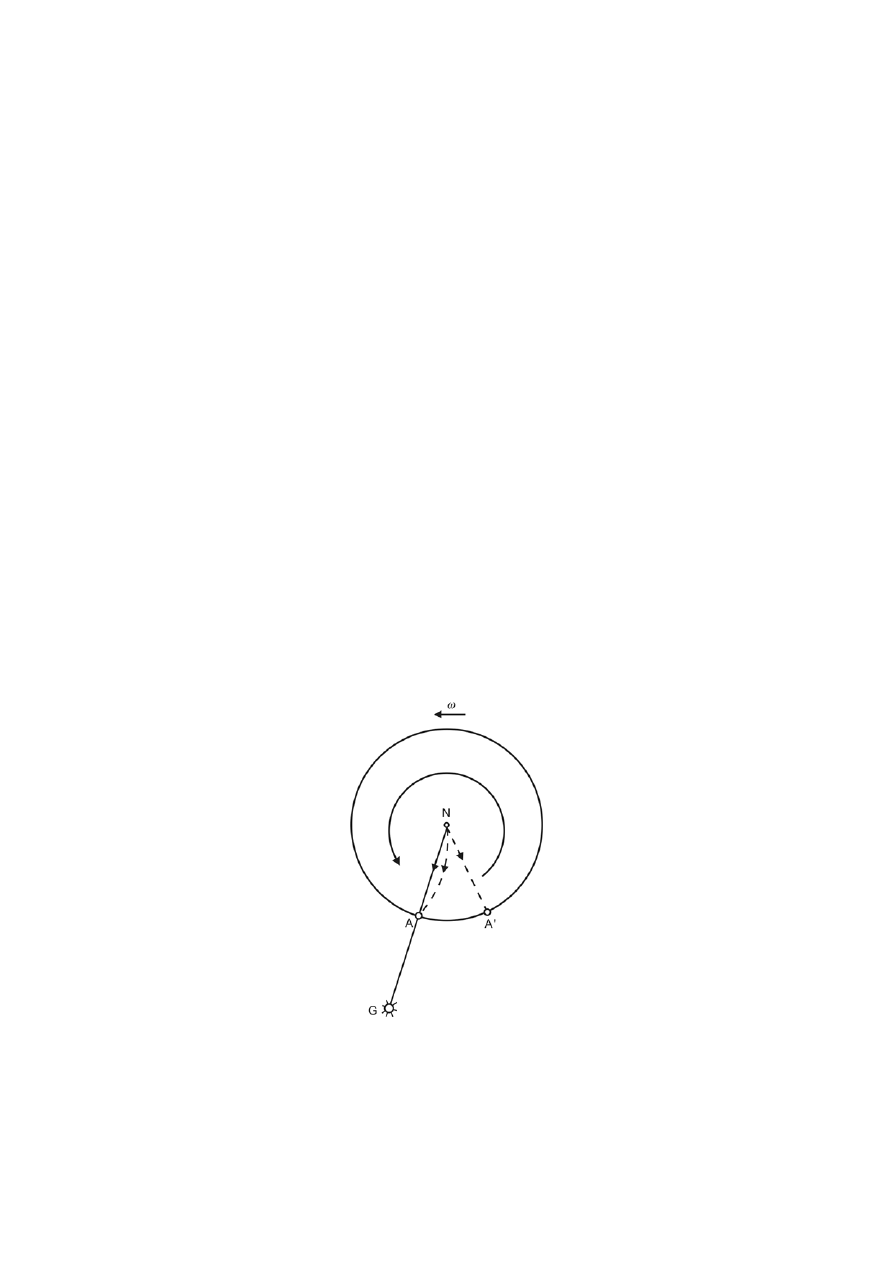
Wyjaśnienie działania siły Coriolisa

Siła Coriolisa jest siłą pozorną, powodującą odchylenie wszelkich ciał

będących w ruchu względem powierzchni Ziemi. Odchylenie to jest związane z

obrotem płaszczyzny horyzontu wokół pionowej składowej wektora prędkości

kątowej obrotu Ziemi.

Wektor siły Coriolisa jest skierowany prostopadle do wektora

prędkości ciała i w prawo względem kierunku prędkości – na półkuli

północnej, a w lewo – na półkuli południowej.

Przyspieszenia spowodowane działaniem siły Coriolisa są tego samego

rzędu, co przyspieszenia wywołane siłą gradientu ciśnienia. Przyspieszenia te

mogą się zatem nawzajem równoważyć.

4. Siła odśrodkowa

Siła odśrodkowa występuje przy krzywoliniowym ruchu cząsteczki

powietrza. Dla jednostkowej masy wyraża się wzorem:

r

v

F

o

2

=

gdzie: F

o

– siła odśrodkowa,

v

–

prędkość liniowa ruchu cząsteczki,

r

–

promień krzywizny toru cząsteczki.

Siła odśrodkowa skierowana jest wzdłuż promienia krzywizny w stronę

wypukłości toru (na zewnątrz).

Wpływ siły odśrodkowej jest odczuwalny dopiero dla większych prędkości

ruchu (wiatru), praktycznie uwzględnia się go dla v > 15 m/s (54 km/godz).

5. Siła tarcia

Siła tarcia ma wpływ przede wszystkim na ruch powietrza w dolnej,

przyziemnej warstwie troposfery. Powoduje zmniejszenie prędkości wiatru

(ruchu) w tej warstwie i zmienia także kierunek poruszającego się

powietrza.

Wyróżnia się:

⎯ tarcie wewnętrzne (lepkość) powstaje wtedy, gdy dwie warstwy gazu

przemieszczają się równolegle względem siebie;

⎯

⎯ tarcie zewnętrzne polega na oddziaływaniu ciał w miejscu ich styku,

przeciwstawiające wzajemnemu przesuwaniu się tych ciał (poślizgowe).

Bezpośrednio przy powierzchni Ziemi, w warstwie o milimetrowej grubości,

prędkość ruchu powietrza jest równa zeru. W wyniku ruchów cieplnych,

turbulencji dynamicznej i termicznej, chwiejnej równowagi atmosfery następuje

jednak pionowa wymiana cząsteczek między warstwami nieruchomej i

przemieszczającej się. W rezultacie elementy masy powietrza o małej prędkości

(małym pędzie) zostają przenoszone na większą wysokość, a elementy o

większej prędkości (większym pędzie) z góry na dół. W wyniku tego w pewnej

warstwie, licząc od podłoża, prędkość wiatru wzrasta. Jest to warstwa tarcia,

której wysokość górnej granicy wynosi ok. 500 do 1000 m i zależy zarówno od

rodzaju podłoża, jak i stateczności atmosfery (większa jest nad lądem, mniejsza

nad morzami i oceanami).

Wiatry geostroficzny i gradientowy

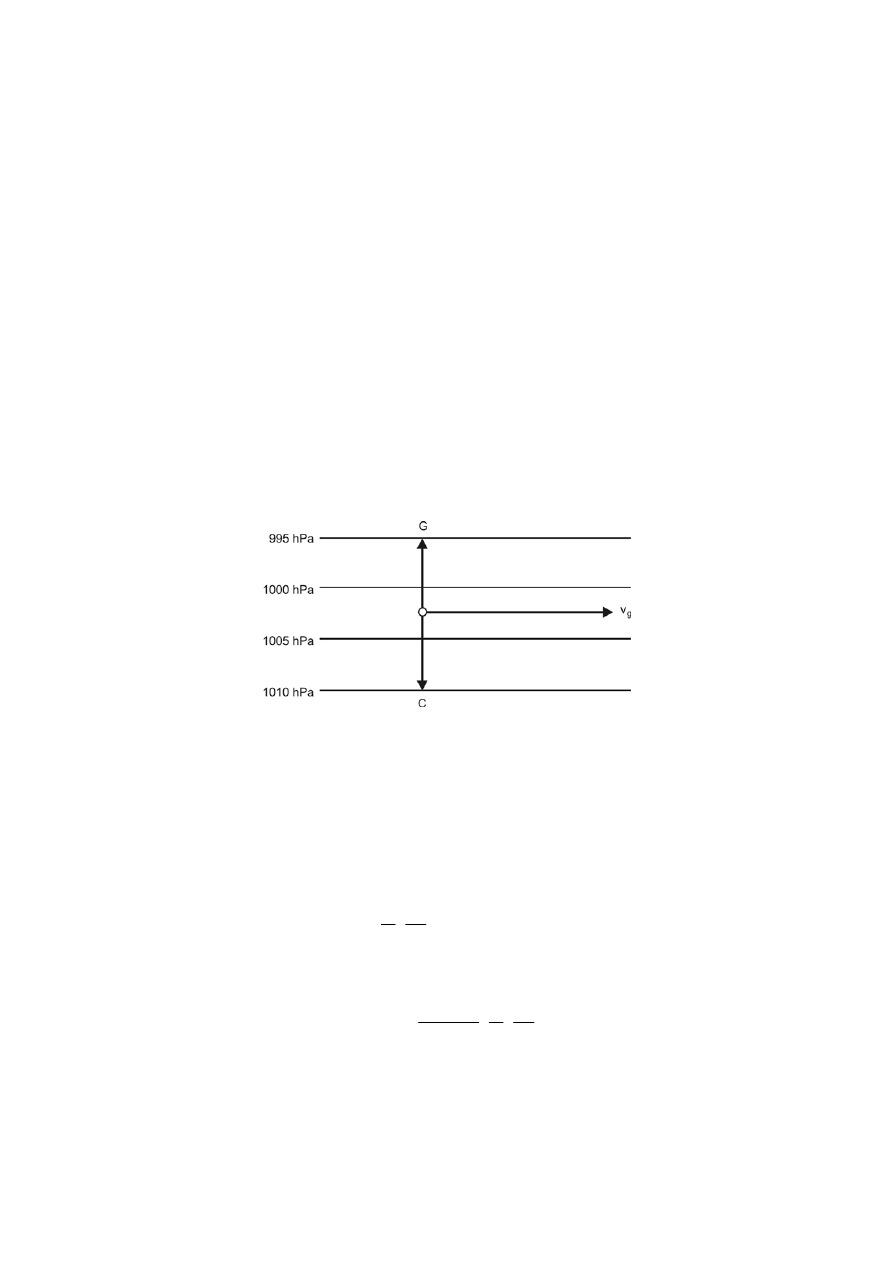
1. Wiatr geostroficzny

Wiatr geostroficzny jest to model jednostajnego ruchu powietrza w

układzie izobar prostoliniowych i równoległych do siebie, przy założeniu braku

tarcia.

Na cząstkę powietrza będą więc działać tylko dwie siły: siła poziomego

gradientu ciśnienia i siła Coriolisa.

Wiatr geostroficzny wieje prostopadle do siły Coriolisa, równolegle do

izobar.

Powstawanie wiatru geostroficznego na półkuli północnej

Prędkość wiatru geostroficznego można obliczyć z warunku równowagi sił

gradientu i Coriolisa:

ϕ

ω

ρ

sin

2

1

v

dn

dp =

⋅

stąd:

dn

dp

v

v

g

⋅

⋅

=

=

ρ

ϕ

ω

1

sin

2

1

gdzie: v

g

– prędkość wiatru geostroficznego.

Kierunek wiatru geostroficznego pokrywa się z kierunkiem izobar.

Na półkuli północnej jego zwrot jest taki, że po lewej stronie znajduje się

obszar niskiego ciśnienia, a po prawej wysokiego. Prawo to nosi nazwę reguły

Buysa-Ballota.

W pobliżu równika, gdzie sin

ϕ → 0, pojęcie wiatru geostroficznego traci

sens.

2. Wiatr gradientowy

Wiatr gradientowy jest to rozszerzenie modelu wiatru geostroficznego na

izobary kołowe. Cząsteczki powietrza poruszają się poziomo ruchem

jednostajnym po koncentrycznych torach kołowych.

Krzywizna toru powoduje, że oprócz sił gradientu ciśnienia i Coriolisa

wystąpi jeszcze siła odśrodkowa, skierowana na zewnątrz krzywizny.

Ponieważ ruch jest jednostajny, wypadkowa tych sił musi być równa zeru.

Rozważa się dwa przypadki wiatru gradientowego na półkuli północnej –

na obszarze niżu i na obszarze wyżu dla izobar kołowych.

W niżu N siła poziomego gradientu ciśnienia jest skierowana wzdłuż

promienia do środka niżu, natomiast siła odśrodkowa na zewnątrz. Jest

jednak zbyt mała, by zrównoważyć siłę gradientu ciśnienia G. Siła Coriolisa

C musi więc być skierowana również na zewnątrz jak siła odśrodkowa, by

równoważyć siłę gradientu ciśnienia.

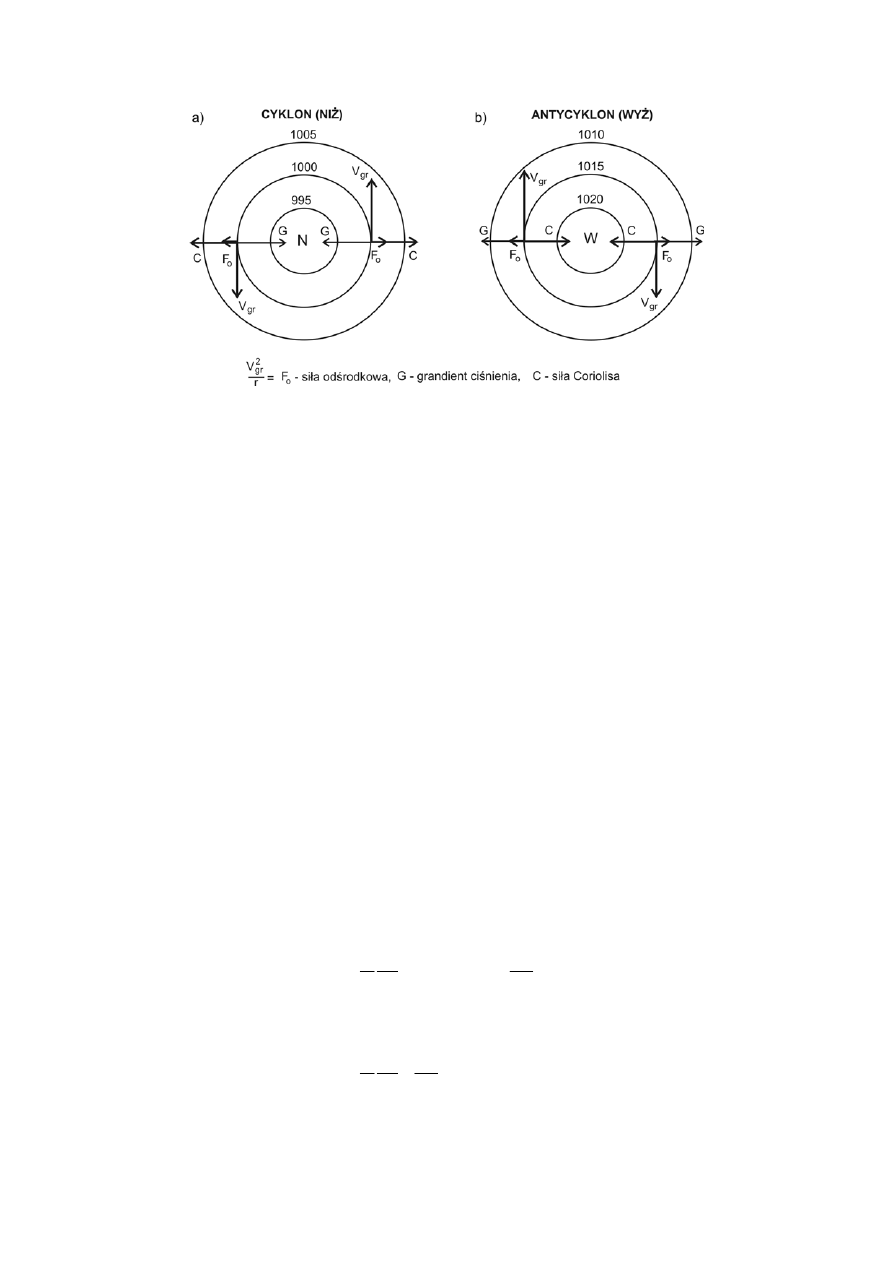
Powstawanie wiatru gradientowego na półkuli północnej: a) niż, b) wyż

Ponieważ siła Coriolisa jest skierowana prostopadle do wektora prędkości

i odchylona w prawo, wiatr gradientowy w niżu krąży w kierunku

przeciwnym do ruchu wskazówek zegara.

W wyżu W, układ sił jest inny.

Gradient ciśnienia skierowany jest na zewnątrz, tak jak siła odśrodkowa.

Siła Coriolisa równoważy zatem obie te siły. Z warunku prostopadłości wektora

prędkości do siły Coriolisa i odchylenia siły w prawo, wiatr gradientowy w

wyżu krąży zgodnie z ruchem wskazówek zegara.

Prędkość wiatru gradientowego można obliczyć z warunku równowagi sił.

Dla niżu:

r

v

v

dr

dp

gr

gr

2

sin

2

1

+

=

ϕ

ω

ρ

i dla wyżu

ϕ

ω

ρ

sin

2

1

2

gr

gr

v

r

v

dr

dp

=

+

lub

r

v

v

dr

dp

gr

gr

2

sin

2

1

−

=

ϕ

ω

ρ

gdzie: v

gr

– prędkość wiatru gradientowego.

Równania te można przekształcić dalej do postaci dla niżu:

dr

dp

r

r

r

v

gr

⋅

+

+

=

ρ

ϕ

ω

ϕ

ω

2

2

2

sin

sin

i dla wyżu

dr

dp

r

r

r

v

gr

⋅

−

−

=

ρ

ϕ

ω

ϕ

ω

2

2

2

sin

sin

W ostatnim równaniu, wartość pod pierwiastkiem musi być dodatnia (lub zero),

stąd ograniczenie:

ϕ

ρω

2

2

sin

r

dr

dp ≤

Wynika stąd graniczna maksymalna prędkości wiatru w wyżu:

ϕ

ω

sin

max

r

v

gr

=

Dla niżu nie ma takiego ograniczenia, stąd prędkości wiatru w niżach

(cyklonach) osiągają ogromne wartości.

W niskich szerokościach geograficznych wyraz 2 vω sin

ϕ jest bardzo

mały i może być pominięty. Jest to model tzw. wiatru cyklostroficznego,

wiejącego równolegle do izobar kołowych z niskim ciśnieniem w centrum, w

którym prędkość może osiągać duże wartości:

dr

dp

r

v

v

gr

c

⋅

±

=

=

ρ

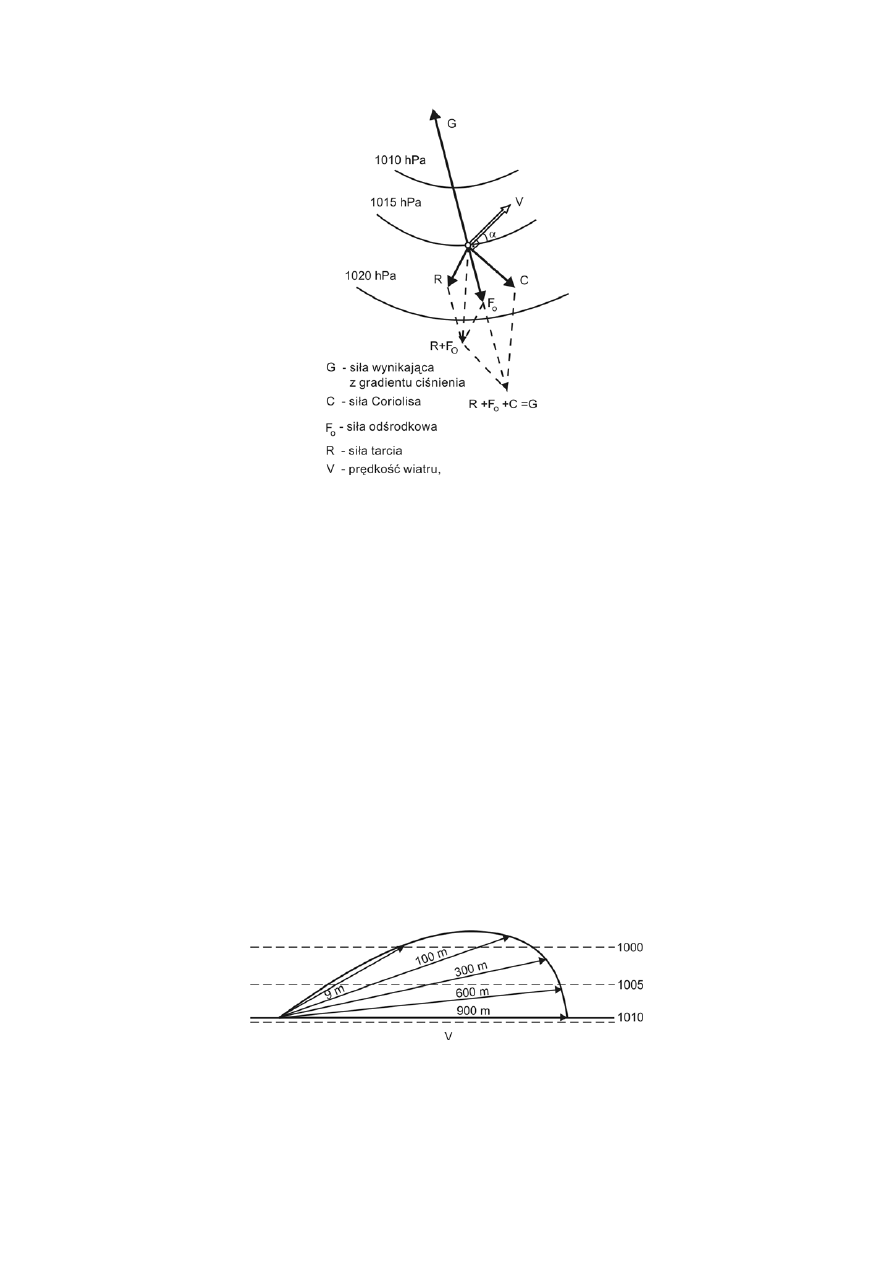
Wpływ tarcia w przyziemnej warstwie powietrza

Wiatry gradientowy i geostroficzny są przybliżeniami wiatru

rzeczywistego. W swobodnej atmosferze, powyżej warstwy tarcia (powyżej 500

do 1500 m) różnice są niewielkie, tak więc zależności teoretyczne mogą być

wykorzystane do obliczeń praktycznych.

W warstwie tarcia w pobliżu powierzchni Ziemi siła tarcia jest znaczna i

powoduje odchylenie wiatru od kierunku równoległego do izobar oraz

zmniejszenie jego prędkości względem prędkości teoretycznej.

Siła poziomego gradientu ciśnienia jest równoważona przez

wypadkową sił Coriolisa i tarcia. Wynika stąd, że w tym przypadku siła

gradientu nie leży na jednej prostej z siłą Coriolisa, a siła tarcia nie tworzy

kąta 180

° z wektorem prędkości. Wektor prędkości „

v

r

” będzie odchylony

od izobar w stronę niższego ciśnienia

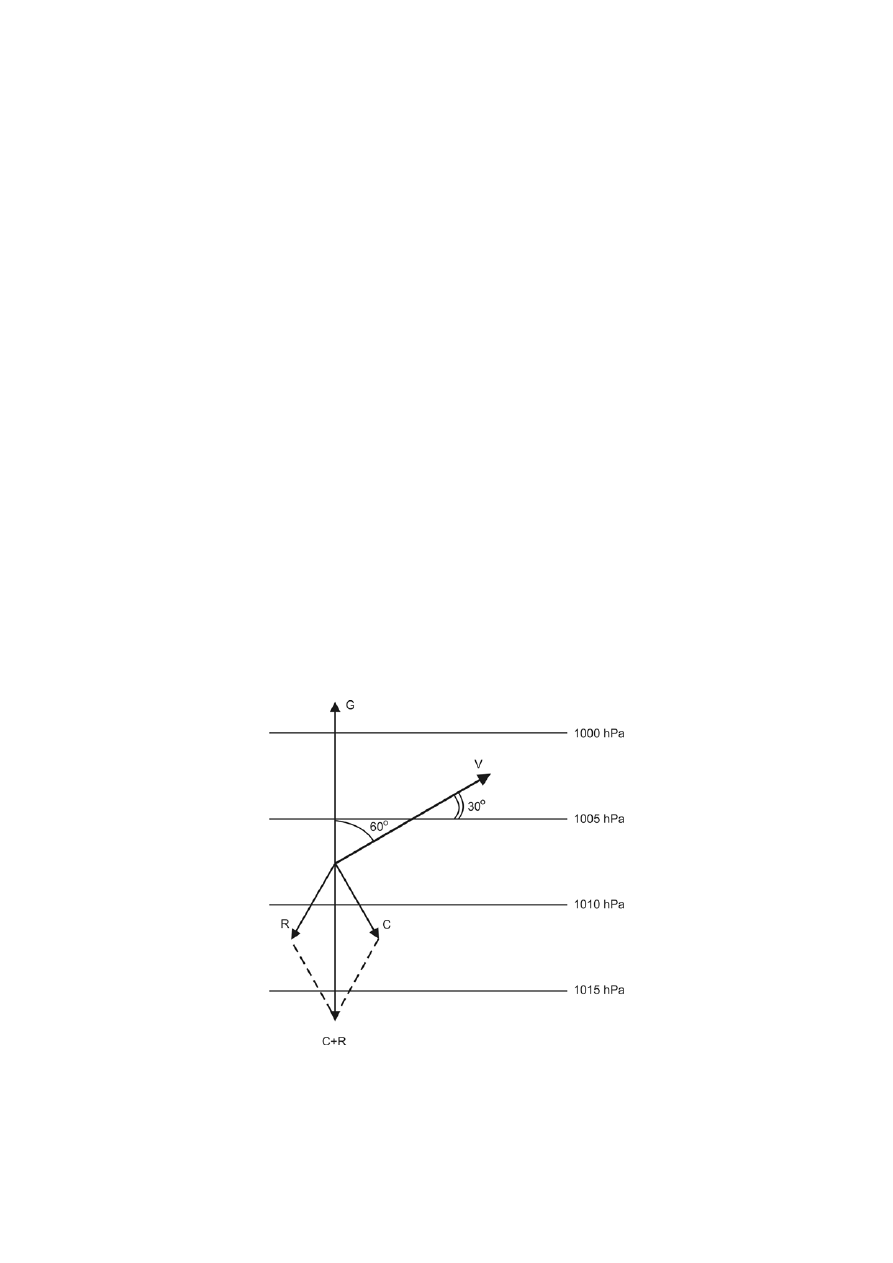
Wpływ siły tarcia na kierunek wiatru – izobary prostoliniowe

Wpływ siły tarcia na kierunek wiatru – izobary kołowe

Wiatr odchyla się od izobar nad morzem średnio o kąt ok. 20

°, a nad

lądem o ok. 30

° – 45° w stronę niższego ciśnienia, natomiast wektor siły

tarcia

R

r

tworzy z prędkością kąt ok. 130

° − 150°.

Zmiany wiatru w warstwie tarcia można przedstawić graficznie

wykreślając ze wspólnego punktu wektory prędkości wiatru na różnych

wysokościach. Krzywa łącząca końce wektorów nazywa się spiralą Ekmana.

Spirala Ekmana. Prędkości i kierunki wiatru na różnych wysokościach od

powierzchni Ziemi do granicy warstwy tarcia

Wpływ tarcia zanika z wysokością. Dla wysokości 600

− 900 m wiatr

wieje już niemal równolegle do izobar.

Pionowy

rozkład prędkości wiatru (tachoida wiatru) w warstwie w

pobliżu powierzchni Ziemi opisywany jest za pomocą formuł empirycznych

opracowanych przez różnych autorów. Najbardziej rozpowszechnione są

formuły przyjmujące logarytmiczny profil wiatru, np. formuła Rohwera:

516

,

1

log

516

,

1

log

+

+

=

a

a

z

z

v

v

gdzie: v, v

a

– odpowiednio prędkości wiatru na wysokościach z i z

a

[m/s],

z,

z

a

– wysokości, na których określamy prędkość wiatru [m].

Wiatry dolne. Linie prądu

Wiatry dolne są ściśle związane z ogólnym rozkładem ciśnienia na

poziomie morza. Ich prędkość wynika przede wszystkim z gradientu ciśnienia, a

kierunek jest zgodny z regułą Buysa-Ballota.

Na półkuli północnej, w niżu wiatry wieją przeciwnie do ruchu

wskazówek zegara, przecinając izobary w kierunku niskiego ciśnienia, w wyżu

natomiast wieją zgodnie z ruchem wskazówek zegara.

Obraz ruchu powietrza w danej chwili można przedstawić za pomocą

linii prądu, krzywych, do których w każdym punkcie wektory prędkości

wiatru są styczne.

Im

prędkość wiatru jest większa, tym wektory prędkości przedstawione w

postaci strzałek są dłuższe i tym gęściej przebiegają linie prądów

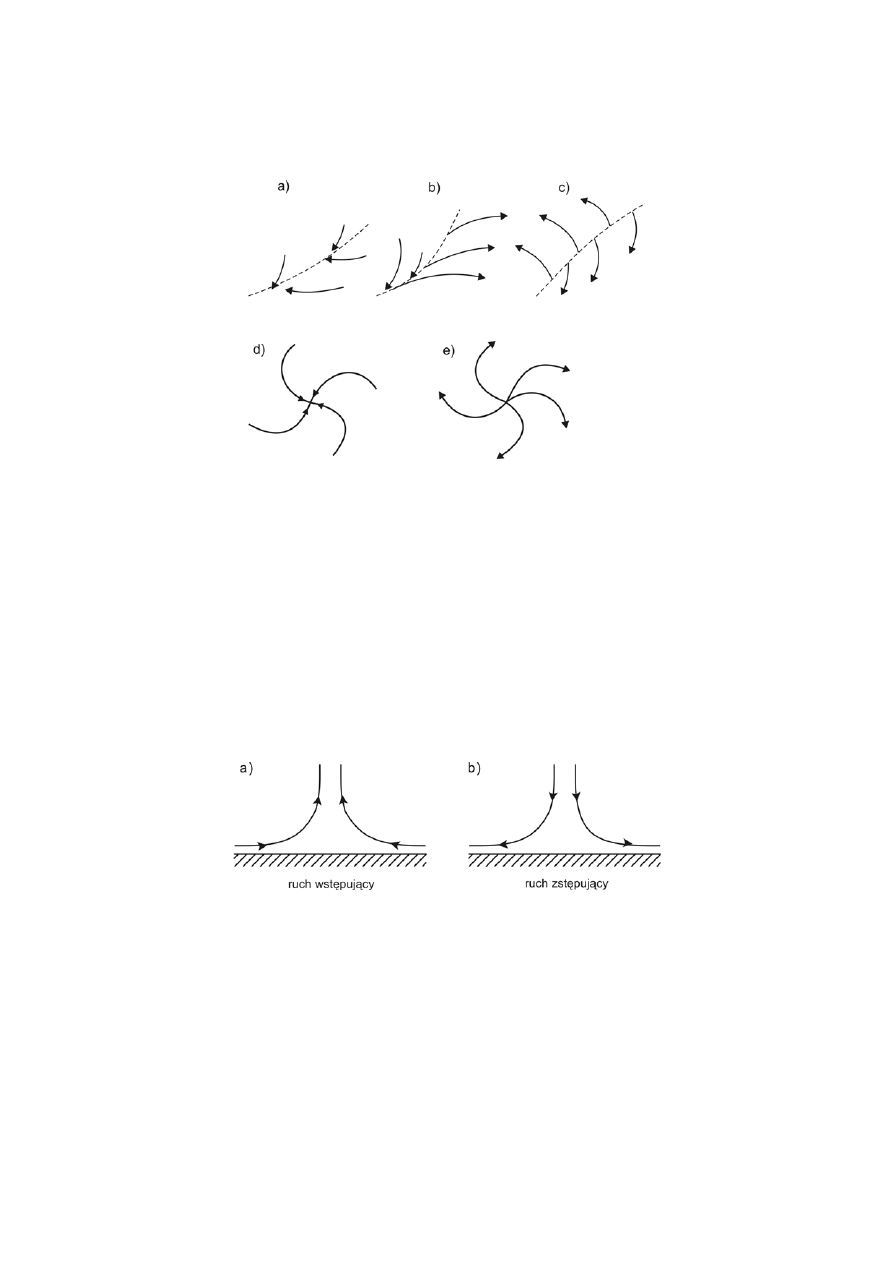
Linie oraz punkty zbieżności i rozbieżności: a) linia zbieżności,

b) linia jednostronnej zbieżności, c) linia rozbieżności, d) punkt zbieżności

(konwergencji), e) punkt rozbieżności (dywergencji)

Efekt zbieżności i rozbieżności linii prądów poziomych w przekroju pionowym

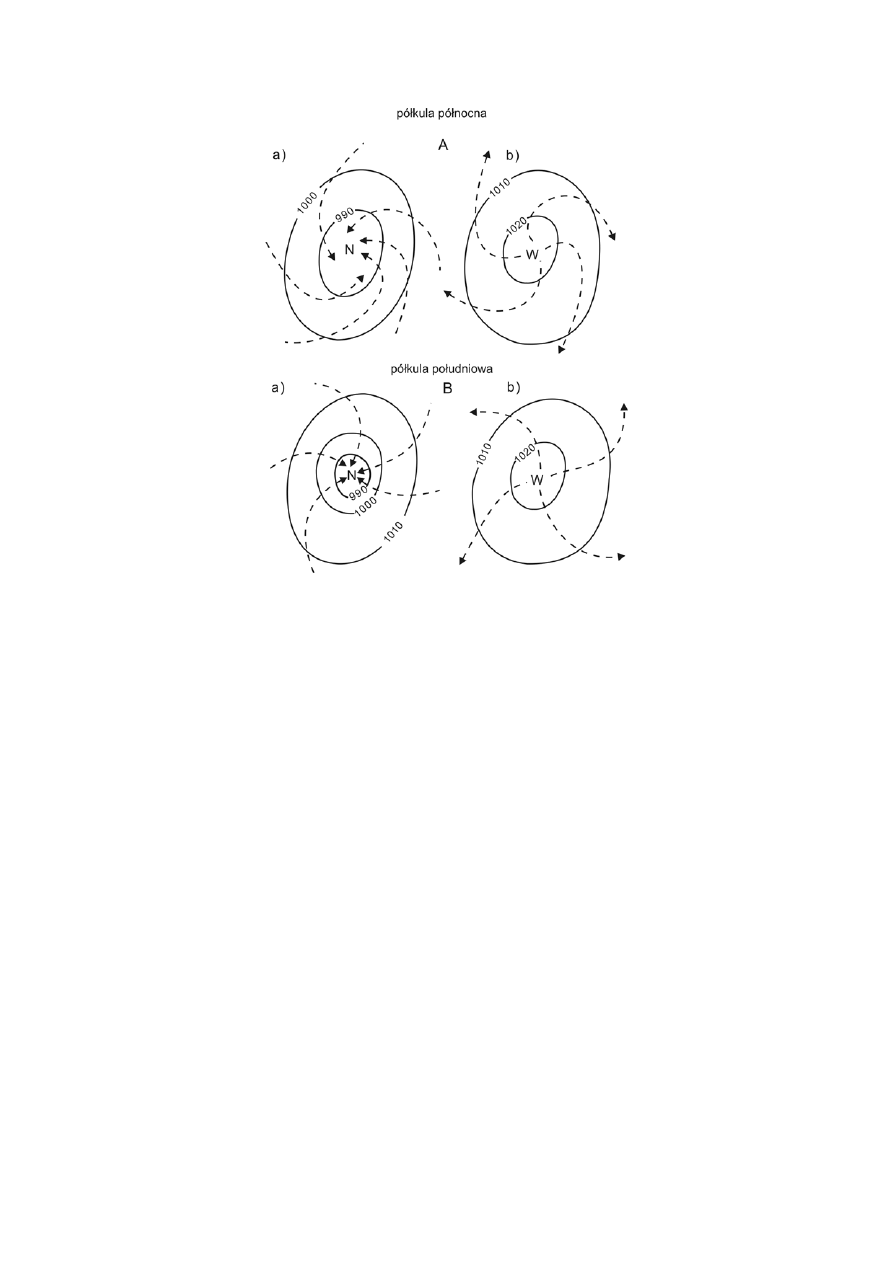
Linie prądów w niżu i wyżu: A – półkula północna, B – półkula południowa;

a) niż, b) wyż

Na

półkuli północnej linie prądów powietrznych w ośrodkach niżowych

– cyklonalnych, przyjmują kształt spiral, skierowanych ku środkowi i

zakrzywionych przeciwnie do ruchu wskazówek zegara

W ośrodkach wyżowych – antycyklonalnych jest sytuacja przeciwna –

linie prądów przybierają kształt spiral rozbiegających się z jednego punktu i

zakrzywionych zgodnie z ruchem wskazówek zegara

Na

półkuli południowej, skręt linii prądów jest przeciwny w niżu,

zgodnie z ruchem wskazówek zegara, natomiast w wyżu przeciwnie do tego

ruchu.

Ruchy

wstępujące, charakterystyczne dla niżów, związane są ze

zmniejszeniem równowagi atmosfery i sprzyjają kondensacji pary wodnej a

więc powstawaniu zachmurzenia i opadów.

W wyżach ruchy zstępujące przyczyniają się do zwiększenia

równowagi atmosfery, zaniku zachmurzenia i braku opadów.

Charakterystyczne dla wyżu są również słabe na ogół wiatry.

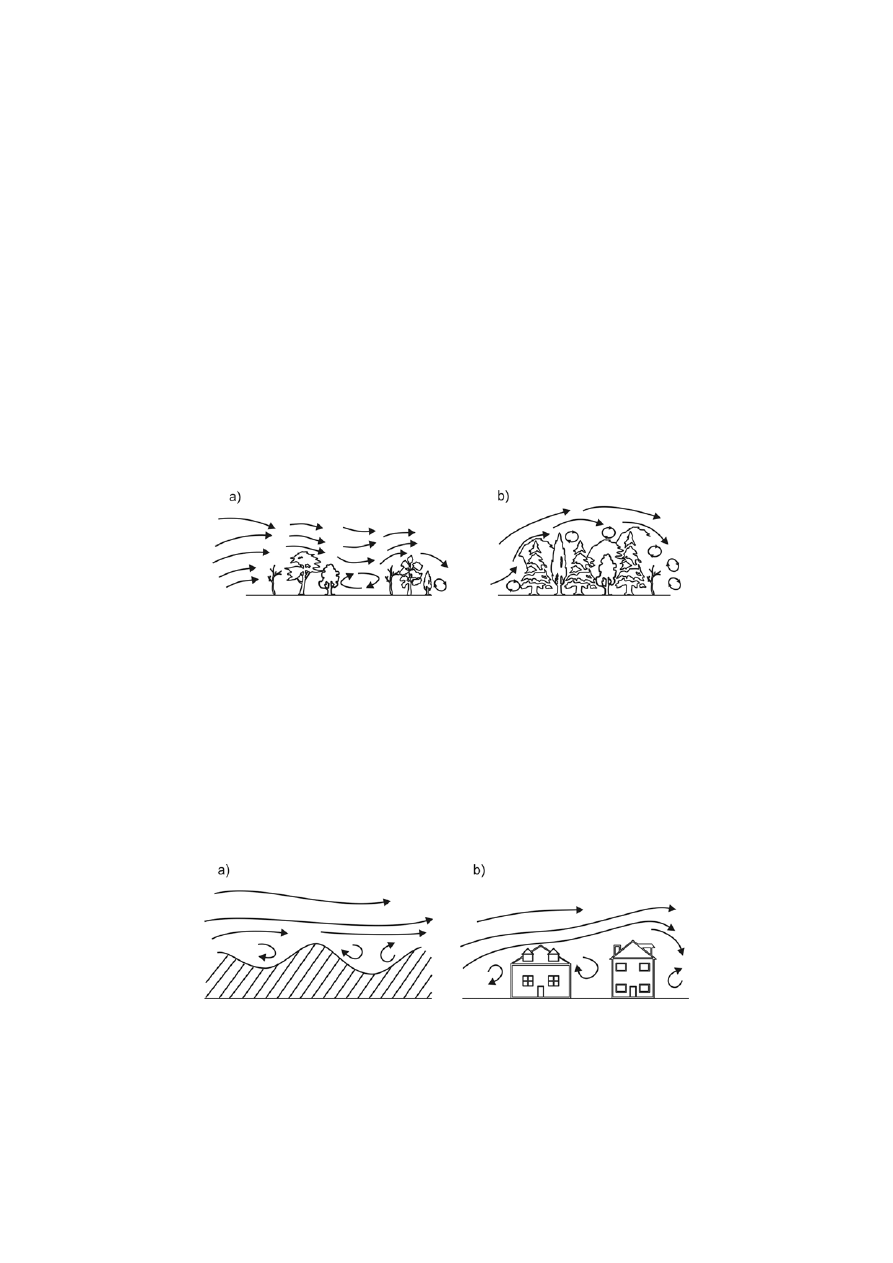
Typowe przykłady wpływu powierzchni Ziemi na ruch

powietrza

Wpływ ukształtowania powierzchni Ziemi (rzeźby terenu) i przeszkód

znajdujących się na niej na poziomy ruch powietrza w jej pobliżu jest

oczywisty. Oprócz dynamicznego wpływu wywołanego przeszkodami

naturalnymi, takimi jak ukształtowanie terenu, kompleksy leśne, czy też

sztucznymi, zbudowanymi przez człowieka (budowle), występuje też wpływ

termiczny, wynikający z różnych własności termicznych powierzchni terenu.

Wpływ podłoża na wiatr – zawirowania powietrza przepływającego:

a) nad odosobnionymi skupiskami drzew, b) nad większym obszarem leśnym

o różnym zagęszczeniu i wysokości

Wpływ różnego rodzaju przeszkód terenowych na pole wiatru

Wpływ podłoża na wiatr: a) prędkość powietrza < 8 m/s,

b) prędkość powietrza > 8 m/s

Termiczny wpływ powierzchni ziemi na ruch powietrza

Termiczno-dynamiczny wpływ powierzchni ziemi na poziomy ruch powietrza

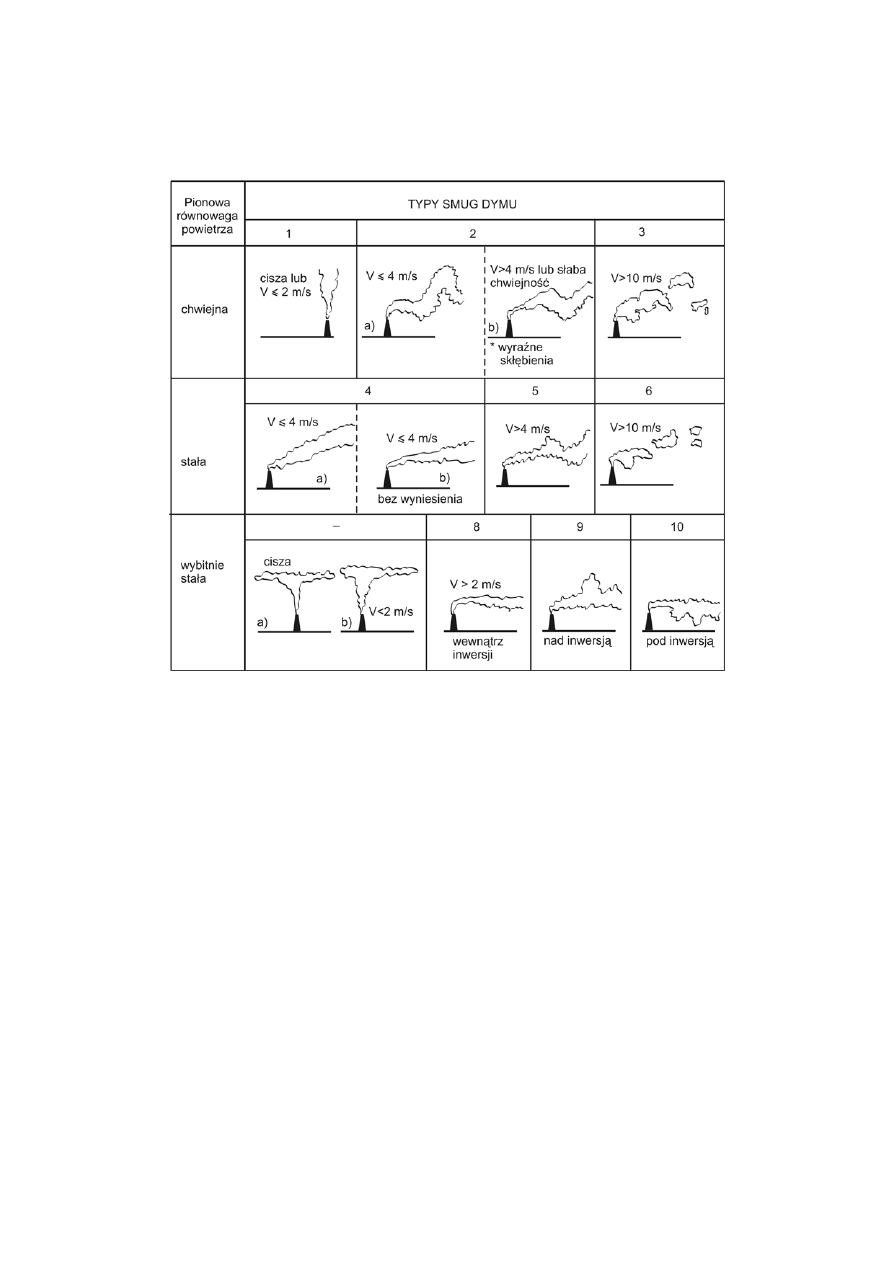
Rodzaje smug dymów przemysłowych (Parczewski, 1977)