I EA Podstawy robotyki – laboratorium

II SERIA

5. Modelowanie dynamiki ramienia robota

metodą Lagrange'a

Celem ćwiczenia jest zapoznanie się z oddziaływaniami dynamicznymi,

jakie występują w parach kinematycznych robotów wieloprzegubowych.
Analiza dynamiki powinna być przeprowadzona na podstawie uproszczonego
modelu matematycznego pojedynczego ramienia napędzanego w przegubie.
Model ten powinien być wyprowadzony metodą równań Lagrange'a II
rodzaju na podstawie podanych danych i założeń upraszczających. Proces
modelowania dynamiki może być wspomagany za pomocą pakietu
SYMBOLIC TOOLBOX Matlaba. Po wyznaczeniu równań dynamiki przegubu
należy wykonać badania symulacyjne modelu w środowisku Matlab lub
Matlab-SIMULINK.

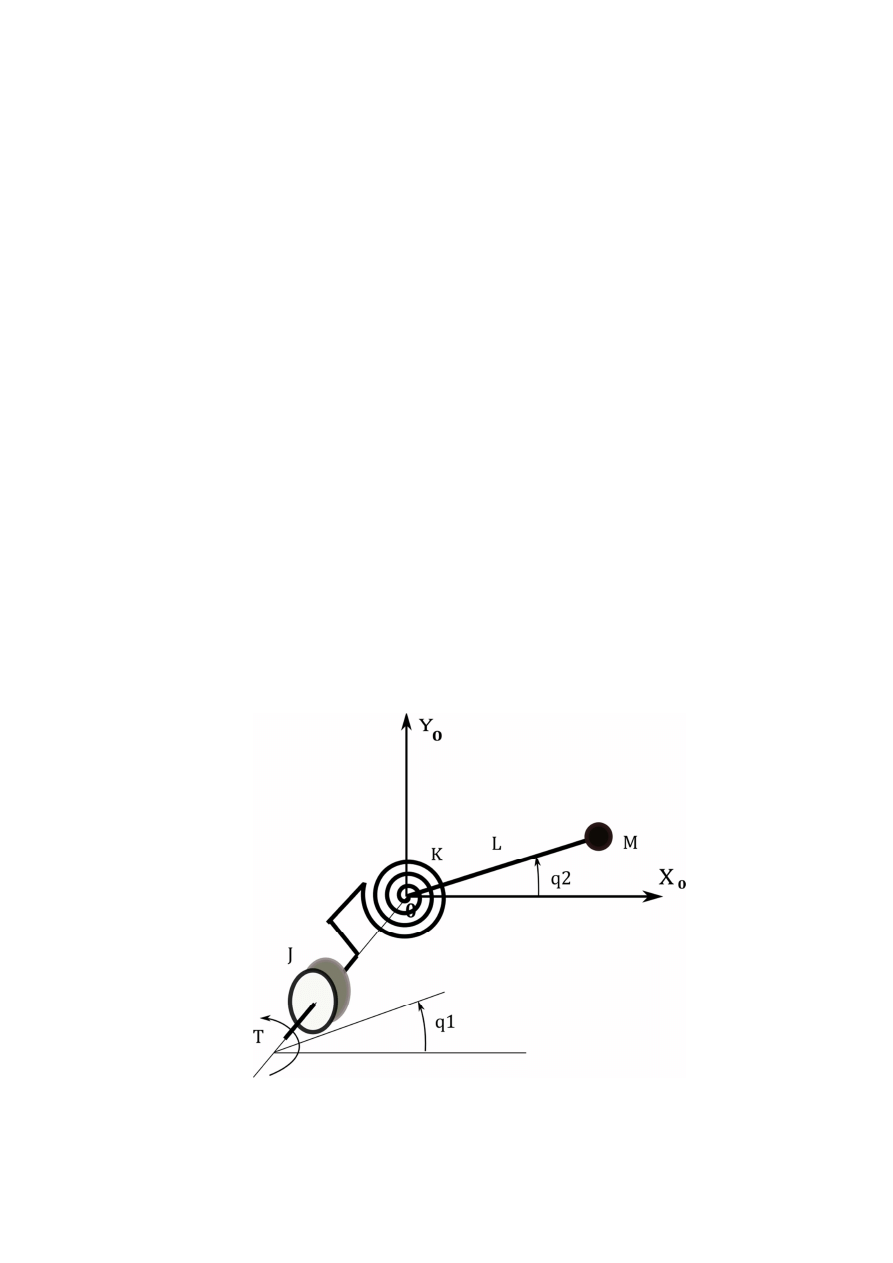
1. Dane jest ramię robota z przegubem uwzględniającym jego sztywność i

bezwładność (rys. 1). Model fizyczny ramienia stanowi masa skupiona M na
jego końcu. Długość ramienia liczona od osi obrotu wynosi L.

Rys. 1. Analizowany ramię robota

Rys. 1. Model fizyczny ramienia i przegubu robota: M – masa ramienia, L – długość

ramienia, K - sprężystość przegubu, J – moment bezwładności silnika i prze-

kładni, q1 – położenie przegubu, q2 – położenie ramienia, T – moment napędowy

2. Wiedząc, że energia kinetyczna jest równa

K =

1
2

J ˙

q

1

2

+

1
2

J

r

˙

q

2

2

,

J

r

=

ML

2

,

a energia potencjalna wynosi

P=

1
2

K

(

q

1

−

q

2

)

2

+

M g Lsin (q

2

)

wyznaczyć funkcję Lagrange'a L=K-U układu.

3. Wyprowadzić dynamiczne równania ruchu układu wyznaczając wymagane

pochodne i podstawiając je do równań Lagrange'a II rodzaju

d

d t

∂

L

∂ ˙q

i

−

∂

L

∂

q

i

=

T

i

, i=1,2 .

4. Przedstawić wyprowadzone równania w notacji macierzowej

D(q) ¨q+C (q , ˙q)+G(q)=T

gdzie: D – macierz bezwładności układu, C – macierz sił odśrodkowych i
Coriolisa, G – wektor grawitacji, T – wektor momentów zewnętrznych.

5. Rozwiązać powyższy układ ze względu na przyspieszenia

¨q= D(q)

−

1

[

T −C (q , ˙q)−G (q)

]

a następnie poprzez podstawienie

˙

q

1

=ω

1,

˙

q

2

=ω

2

sprowadzić do układu

czterech równań różniczkowych I rzędu. Układ taki stanowi podstawę do
zastosowania procedur całkowania numerycznego w Matlabie.

6. Zakodować powyższy model w postaci m-funkcji Matlaba

dq=nazwa_

układu(t,q)

, gdzie:

q=[q

1

q

2

ω

1

ω

2

]

T

- wektor współrzędnych,

dq=[ ˙

q

1

˙

q

2

˙

ω

1

˙

ω

2

]

T

- wektor pochodnych po czasie wektora współrzędnych.

7. Stosując procedurę całkowania numerycznego

ode45

lub złożony w postaci

bloków w Simulinku schemat wykonać symulację zachowania się układu dla:

a) różnych przebiegów czasowych wymuszeń: moment stały, sinusoidalny,

ramp, chirp;

b) dla różnych wartości współczynnika sprężystości: 0, 100, 1000, 10000.

c) dla dołączonego do modelu tarcia wiskotycznego (proporcjonalnego do

prędkości,

T

t i

=

k

v i

˙q

i

=

k

v i

ω

i

, i=1,2

).

L [m]

*)

M [kg]

J [kgm^2]

K

[Nm/rad^2]

0,5

1,0

0,0025

100

*)

Wartości parametrów mogą być zmienione przez prowadzącego.

8. Opracować wnioski z ćwiczenia; zamieścić otrzymane przebiegi symulacyjne.