Strona 1 z 6
Opracował: mgr inż. Jerzy Wołoszyn (
Instrukcja do Laboratorium 1
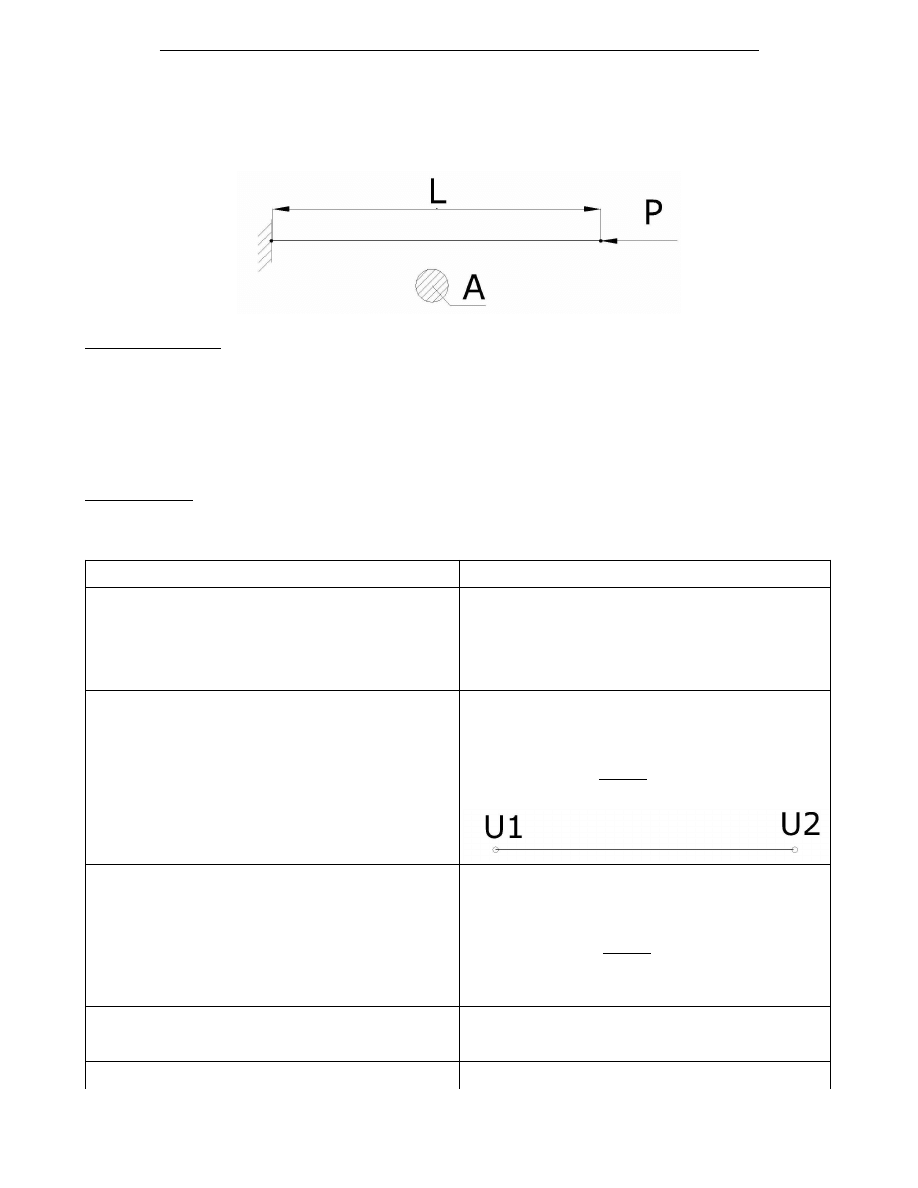
W zadaniu 1 (rys. 1) należy wyznaczyć przemieszczenie pręta.
Rys. 1
Dane do zadania:
p =1000 [N] – siła ,
E =2*10e11 [Pa] – moduł Younga,
L =2 [m] - długość pręta,
ro =7850 [kg/m3] – gęstość materiału,
A =0.003 [m2] – przekrój poprzeczny elementu.
Rozwiązanie:
Zadanie zostanie rozwiązane przy wykorzystaniu elementu skończonego typu pręt o liniowej
funkcji kształtu.
Kod Programu (Matlab)
Interpretacja Graficzna
p = -1000; % minus bo skierowana w lewo
E = 2e11; % czyli 2 * 10^11
L = 2; % długość pręta
ro= 7850; % gęstość – do macierzy mas
A = 0.003; % pole przekroju
1. Wprowadzenie danych materiałowych oraz
wymiarów.
PORADA:
1.komentarze w Matlabie – po znaku %.
2. Wyłączenie linii kodu %{
%}
k = [1 -1; -1 1] ;
k12 = ((E*A)/L)*k;
% macierz sztywności
2. Budowa macierzy sztywności dla elementu
prętowego w lokalnym układzie współrzędnych
[ ]
2
U
1
U
L
A
E
=
k
1
1
1
1
2
U
1
U
12
−
−
⋅
k12(1,1)=1; k12(1,2)=0;
k12(2,1)=0;
albo:
k12 = [ 1 0 ;
0 k12(2,2) ]; % wizualnie
% atrakcyjne
3. Odebranie stopni swobody (brak
przemieszczeni na kierunku U w węźle 1)
[ ]
2
U
1
U
L
A
E
=
k
1
0
0
1
2
U
1
U
12
⋅
umes = inv(k12) * [0;p]
3. Wyznaczenie przemieszczeń węzłowych
[ ] [ ]
{ }
P
k
=
u
⋅
−
1
12
u = (L/(A*E))*p
4. Rozwiązanie analityczne
Strona 2 z 6
Opracował: mgr inż. Jerzy Wołoszyn (
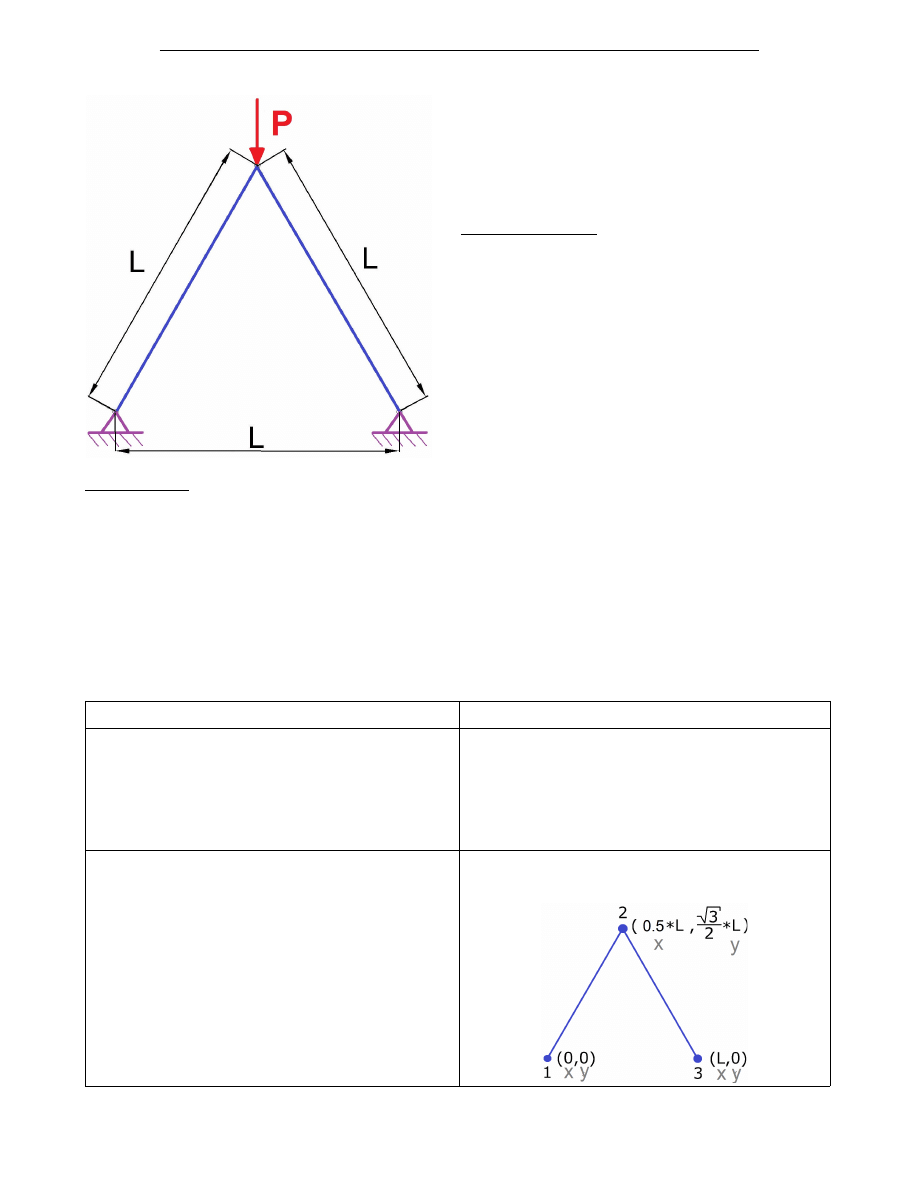
W zadaniu 2 (rys. 2) należy wyznaczyć przemieszczenia w węzłach.
Dane do zadania:
p=1000 [N] – siła ,
E=2e11 [Pa] – moduł Younga,
L=2 [m] - długość pręta,
ro=7850 [kg/m3] – gęstość materiału,
A=0.003 [m2] – przekrój poprzeczny elementu.
Rys.2. Przykład 2.
Rozwiązanie:
Zadanie zostanie rozwiązane przy wykorzystaniu elementu skończonego typu pręt o liniowej
funkcji kształtu.
Programy pomocnicze do obliczenia sin – ów i cos – ów :
1.
policz_cosinusa.m
function cosinus = policz_cosinusa(x1,x2,y1,y2)
cosinus = (x2-x1) / sqrt( (x2 - x1)^2 + (y2 – y1)^2 );
2.
policz_sinusa.m
function sinus = policz_sinusa(x1,x2,y1,y2)
sinus = (y2-y1)/ sqrt( (x2 - x1)^2 + (y2 - y1)^2 );
Kod Programu (Matlab)
Interpretacja Graficzna
p = -1e3;
% czyli p w dół, wartość 1000 [N]
E = 2e11;
% moduł Younga
L = 2;
% długość pręta
ro = 7850;
% gęstość – do macierzy mas
A = 0.003;
% pole przekroju
1. Wprowadzenie danych materiałowych oraz
wymiarów.
% współrzędne punktów
% 1 2 3
x = [ 0, 0.5*L , L ];
y = [ 0, (sqrt(3)/2)*L , 0 ];
2. Budowa geometrii kratownicy (wprowadzenie
współrzędnych)
Strona 3 z 6
Opracował: mgr inż. Jerzy Wołoszyn (
K=[ 1 0 -1 0;
% „forma podstawowa”
0 0 0 0;
-1 0 1 0;
0 0 0 0 ];
%4x4 bo ruch na u i v
k12=((E*A)/L)*k;
% element 1-2
k23=((E*A)/L)*k;
% element 2-3
3. Zdefiniowanie macierzy sztywności dla
elementu prętowego w jego lokalnym układzie
współrzędnych
[ ]
−
−
⋅
=
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
1
L
A
E
k
c12 = policz_cosinusa(x(1),x(2),y(1),y(2))
s12 = policz_sinusa(x(1),x(2),y(1),y(2))
c23 = policz_cosinusa(x(2),x(3),y(2),y(3))
s23 = policz_sinusa(x(2),x(3),y(2),y(3))
DC12=[ c12 s12 0 0 ;
-s12 c12 0 0 ;
0 0 c12 s12 ;
0 0 -s12 c12 ];
% kopiuj -> [ctrl]+[h] = zamień 12 na 23
DC23=[ c23 s23 0 0 ;
-s23 c23 0 0 ;
0 0 c23 s23 ;
0 0 -s23 c23 ];
ko12 = DC12' * k12 * DC12; % ukł.globalny
ko23 = DC23' * k23 * DC23; % ukł.globalny
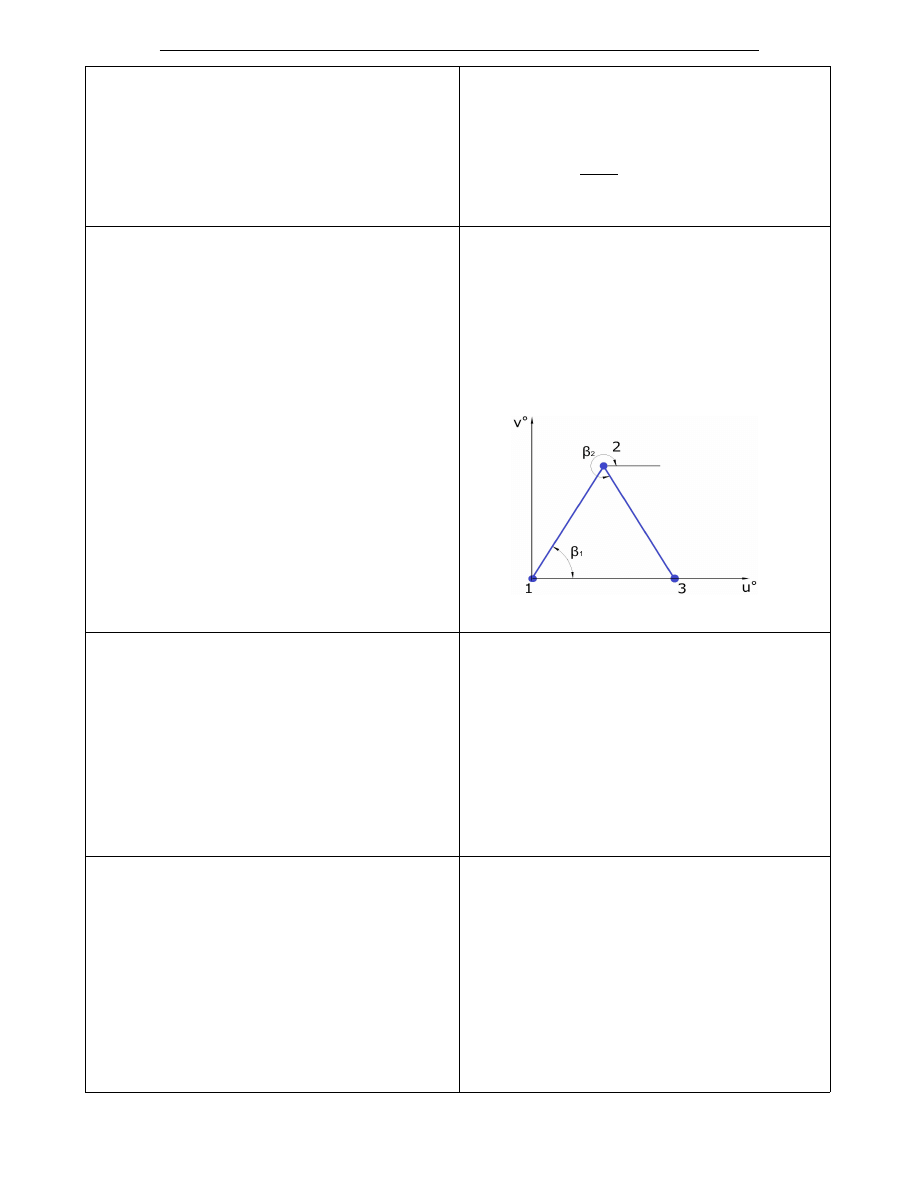
4. Transformacja z lokalnego układu
współrzędnych do układu globalnego
2
23
2
23
1
12
1
12
sin
cos
sin
cos
β
β
β
β
=
=
=
=
s
c
s
c
[DC]=
−
−
c
s
0
0
s
c
0
0
0
0
c
s
0
0
s
c
[ ]
[ ] [ ] [ ]
DC
k
DC
=
k
o
⋅
⋅
T
K = zeros(6);
gdzie = [1 2 3 4];
% gdzie się odwołać?
K(gdzie,gdzie) = K(gdzie,gdzie) + ko12;
gdzie = [3 4 5 6];
% gdzie się odwołać?
K(gdzie,gdzie) = K(gdzie,gdzie) + ko12;
5. Budowa globalnej macierzy sztywności
(agregacja macierzy)
[ ]
[ ]
3
3
2
2
1
1
0
0
0
0
0
0
0
0
0
23
0
23
0
23
0
23
0
23
0
23
0
23
0
23
0
23
0
23
0
23
0
12
0
23
0
12
0
12
0
12
0
23
0
23
0
23
0
12
0
23
0
12
0
12
0
12
0
12
0
12
0
12
0
12
3
3
2
0
12
2
0
12
1
0
12
1
0
12
V
U
V
U
V
U
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
=
k
=
K
V
U
V
U
V
U
o
g
+
+
+
+
K(:,[1 2 5 6]) = 0; % dowolny wiersz, […] kolumny
K([1 2 5 6],:) = 0; % wiersze [...] , dowolne kol.
K(1,1) = 1;
K(2,2) = 1;
K(5,5) = 1;
K(6,6) = 1;
K
% wyświetl i sprawdź
6. Odebranie stopni swobody
[ ]
[ ]
3
V
3
U
2
V
2
U
1
V
1
U
1
0
0
0
0
0
0
1
0
0
0
0
0
0
k
k
k
k
0
0
0
0
k
k
k
k
0
0
0
0
0
0
1
0
0
0
0
0
0
1
=
k
=
K
0
23
0
12
0
23
0
12
0
23
0
12
0
23
0
12
3
V
3
U
2
V
2
U
1
V
1
U
o
g
+
+
+
+
=
Strona 4 z 6
Opracował: mgr inż. Jerzy Wołoszyn (
% to samo tylko w pętli:
%
odebranie_stopni_swobody = [1 2 5 6];
for i=1:1:length(odebranie_stopni_swobody)
gdzie = odebranie_stopni_swobody(i);
K(:,gdzie) = 0;
K(gdzie,:) = 0;
K(gdzie,gdzie) = 1;
end
umes=inv(K)*[0;0;0;p;0;0]
% przemieszczenia
7. Wyznaczenie przemieszczeń węzłowych
[ ] [ ]
}
{
1
P
k
u
⋅
=
−
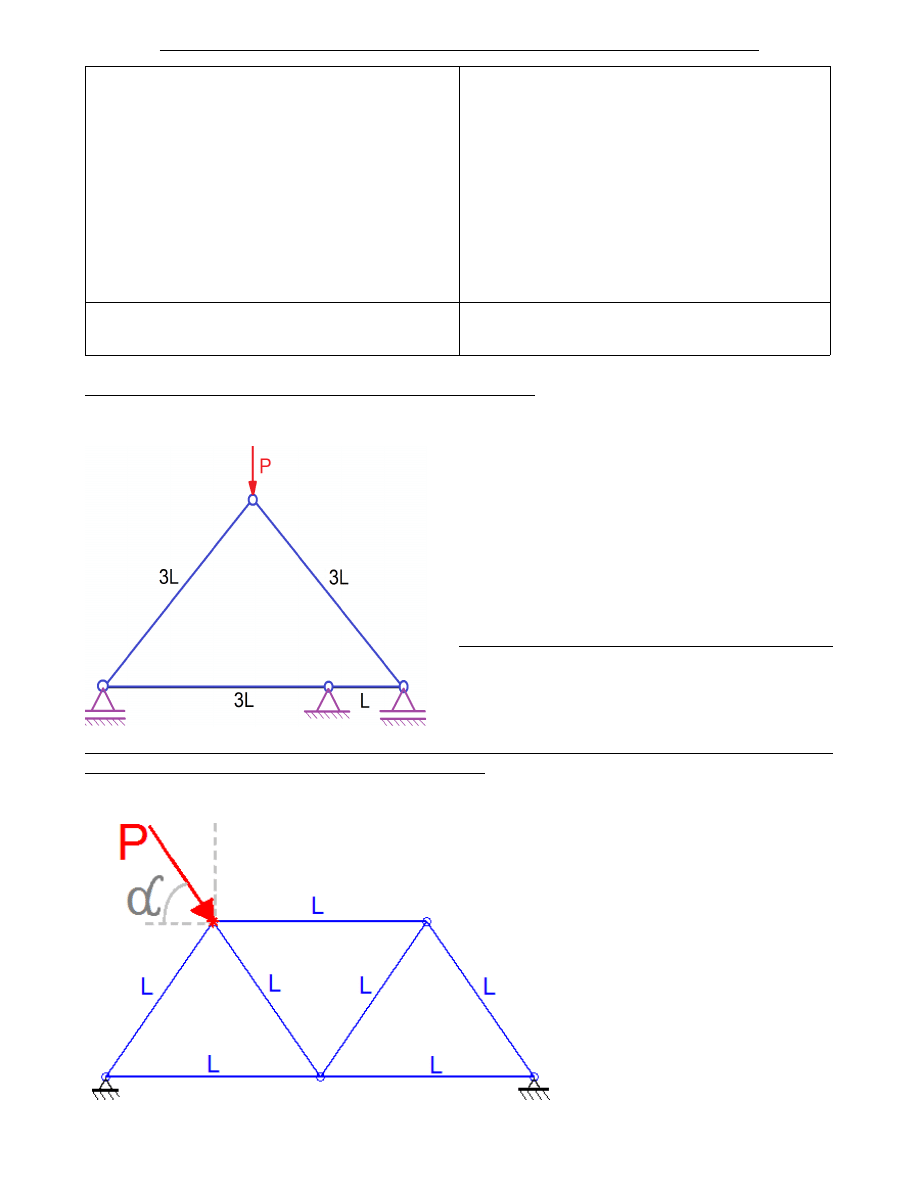
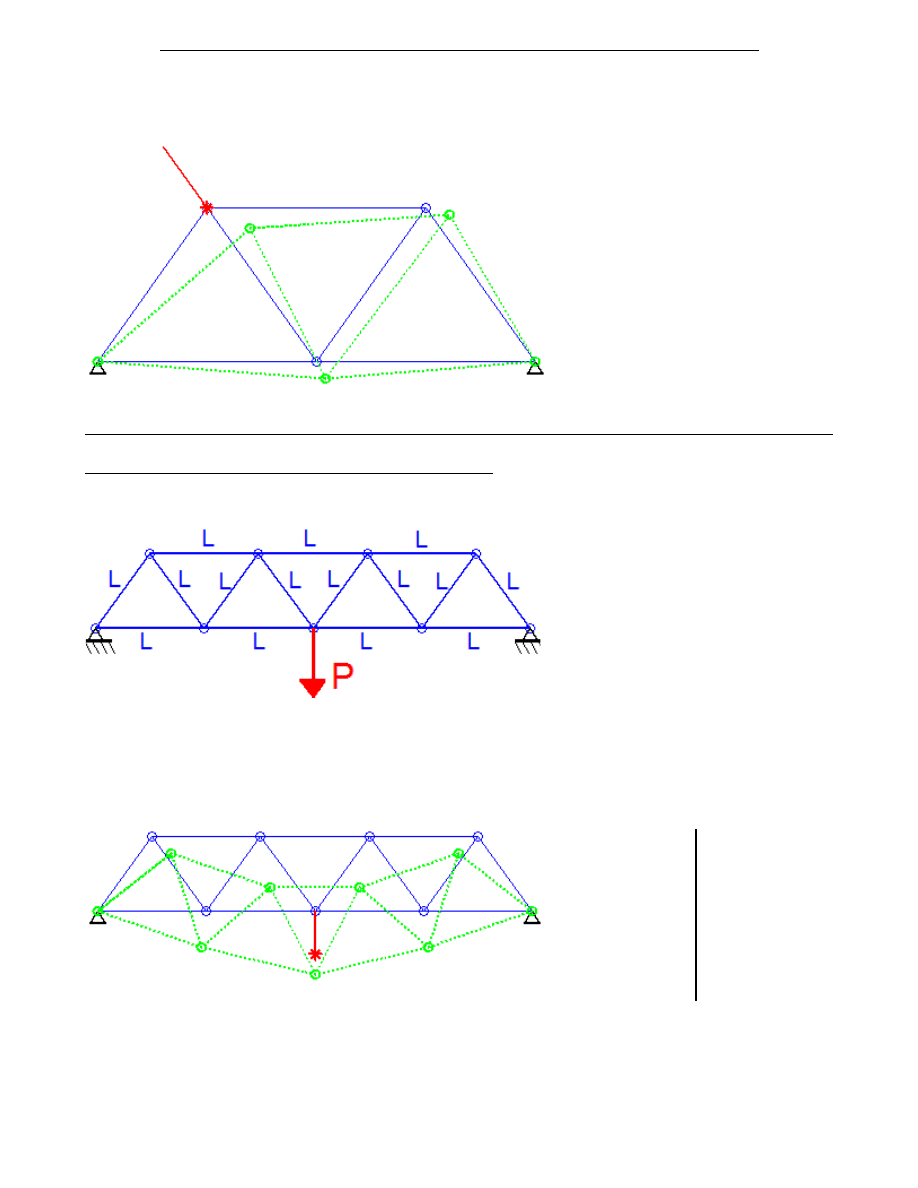
Zadanie 3 (rys.3) do samodzielnego rozwiązania.
Wyznacz przemieszczenia poszczególnych węzłów przyjmując element skończony jako element
prętowy.
Dane do zadania:
p=3 [kN] – siła ,
E=2e11 [Pa] – moduł Younga,
L=2 [m] - długość pręta,
ro=7850 [kg/m3] – gęstość materiału,
A=0.003 [m2] – przekrój poprzeczny elementu.
Zadanie 3* - do samodzielnego rozwiązania
Wyznacz przemieszczenia poszczególnych węzłów przyjmując element skończony jako element
prętowy.
Dane do zadania:
P=3 [kN] – siła ,
α = π/6,
E=2e11 [Pa] – moduł Younga,
L=2 [m] - długość pręta,
ro=7850 [kg/m
3
] – gęstość,
A=0.003 [m
2
] – pole przekroju
poprzecznego
elementu.
Strona 5 z 6
Opracował: mgr inż. Jerzy Wołoszyn (
3* - rozwiązanie:
Przemieszczenia na x:
1.0e-004 *
0
0.0289
0
0.0722
0.1299
Przemieszczenia na y:
1.0e-005 *
0
-0.6667
0
-0.2500
-0.7500
Zadanie 3*
* - do samodzielnego rozwiązania
Wyznacz przemieszczenia poszczególnych węzłów przyjmując element skończony jako element
prętowy.
Dane do zadania:
P=3 [kN] – siła ,
E=2e11 [Pa] – moduł Younga,
L=2 [m] - długość pręta,
ro=7850 [kg/m
3
] – gęstość,
A=0.003 [m
2
] – pole przekroju
poprzecznego
elementu.
3** - rozwiązanie:
Przemieszczenia na x:
1.0e-004 *
0
-0.0289
0.0000
0.0289
0
-0.1155
-0.0577
0.0577
0.1155
Przemieszczenia na y:
1.0e-004 *
0
-0.2833
-0.5000
-0.2833
0
-0.1333
-0.4000
-0.4000
-0.1333
u1
v1
u2
v2
u3
v3
Strona 6 z 6
Opracował: mgr inż. Jerzy Wołoszyn (
1
2
3
1
2
3
4
1
2
3
4
5
6
1
2
3
4
5
6
7
8
u1 v1
u2
v2
u3
v3
u1
v1
u2
v2
u3
v3
u4
v4
1
2
3
4
5
6
7
8
9
u1
v1
u2
v2
u3
v3
u4
v4
1
u1
2
v1
3
u2
4
v2
5
u3
6
v3
7
u4
8
v4
9
u5
10
v5
11
u6
12
v6
13
u7
14
v7
15
u8
16
v8
17
u9
18
v9
u1
v1
u2
v2
u3
v3
u4
v4
u5
v5
u6
v6
u7
v7
u8
v8
u9
v9
Wyszukiwarka
Podobne podstrony:
Lab5 Modelowanie dynamiki id 25 Nieznany
Matlab intro id 287680 Nieznany
MATLAB cw 2 id 287670 Nieznany
KRYTYKA LITERACKAwpigulce id 25 Nieznany
kurs ZERO OSN wiczenie 03 id 25 Nieznany
konspekt Matlab 2012 id 245613 Nieznany
lab11 RapidPrototyping EN id 25 Nieznany
MATLAB rozdzial5 id 768819 Nieznany
matlab Komendy id 287424 Nieznany
pinf13 matlab cz3 id 358238 Nieznany
ksiegowosc ngo,24 06 2010 id 25 Nieznany
Lab5 Modelowanie dynamiki id 25 Nieznany
lab1 12 id 258878 Nieznany
FCKU1 lab1(6na6) id 169034 Nieznany
dsp lab1 id 144058 Nieznany
mnozenie do 25 2[1] id 304290 Nieznany
więcej podobnych podstron