40

5. Wykresy w Matlabie

Wykresy w Matlabie tworzy się z pomocą funkcji graficznych. Funkcje graficzne

realizują:

•

prezentację danych w postaci wykresów 2- i 3-wymiarowych,

•

usuwanie rysunku, zmianę skali, dodawanie napisów,

•

wykonanie rysunków figur geometrycznych: linie, wielokąty,

•

dowolne kształtowanie wyglądu tworzonego rysunku i operowanie na jego

najmniejszych składowych.

Funkcja

plot

Wykres funkcji o ogólnej postaci y= f(x) tworzy się za pomocą polecenia plot.
Typowe wywołania funkcji plot są następujące:

plot(x) - wykres zależności wektora x od numeru współrzędnych tego wektora;

plot(x1,y1,x2,y2,...) - wykres wielu funkcji y1=f1(x1), y2=f2(x2), ...

przedstawionych jednocześnie na tym samym rysunku;

plot(x1,y1,'typ linii',x2,y2,'typ lini', ... ) - wykres wielu funkcji y1=f1(x1),

y2=f2(x2), ... przedstawionych jednocześnie na tym samym rysunku; przy czym każda
funkcja rysowana jest linią określoną przez typ linii ujęty w apostrofy;

plot(x1,y1,'kolor',x2,y2,'kolor', ... ) - wykres wielu funkcji y1=f1(x1), y2=f2(x2),

... przedstawionych jednocześnie na tym samym rysunku; przy czym każda funkcja
rysowana jest kolorem określonym przez zmienną kolor ujętą w apostrofy.

Przy korzystaniu z funkcji plot, należy pamiętać, że wszystkie pary macierzy
x1,y1,x2,y2, ... muszą mieć takie same wymiary.

Dopuszczalnymi liniami na wykresach są następujące typy linii:

linia

ciągła

(-)

linia

kreskowana

(--)

linia

kreska-kropka

(-.)

linia

kropkowana

(:)

Zamiast wykresów w postaci ciągłych linii można tworzyć wykresy w postaci
punktów, np.

kółeczka w punktach

(o)

41

iksy w punktach

(x)

krzyżyki w punktach

(+)

gwiazdki w punktach

(*)

Dopuszczalnymi kolorami linii są następujące typy kolorów:

czerwony

(r)

zielony

(g)

niebieski

(b)

biały

(w)

niewidzialny (i)

żółty

(y)

czarny

(k)

siny

(c)

karmazynowy

(m)

Do opisu wykresów można wykorzystać następujące polecenia:

xlabel('Tekst opisu osi x') - opis osi x

ylabel('Tekst opisu osi y') - opis osi y

title('Tekst tytułu')

- opis tytułu

text(x, y, 'Tekst')

- dowolny tekst z podaniem pozycji (x, y) na rysunku,

gtext('Tekst')

- dowolny tekst ustawiony myszą,

grid

-

linie

siatki

pokrywające rysunek w obu osiach,

grid on

- włączone linie siatki,

grid off

- wyłączone linie siatki.

legend

- legenda do wykresu.

Przykłady tworzenia wykresów za pomocą funkcji plot

% Skrypt ryssin.m - wykres funkcji sin(x)
x = -pi:0.1:pi; y=sin(x); plot(x,y);
return

% Skrypt opisrys.m - opisywanie wykresow
% xlabel(tekst, nazwa1,wartosc1,nazwa2,wartosc2,...)
% ylabel(tekst, nazwa1,wartosc1,...)
% text(x,y,tekst)
% grid on - pomocnicza siatka
xlabel('opis osi x'); ylabel('opis osi y');
text(0.2,0.7,'opis rysunku'); grid on;
return

42

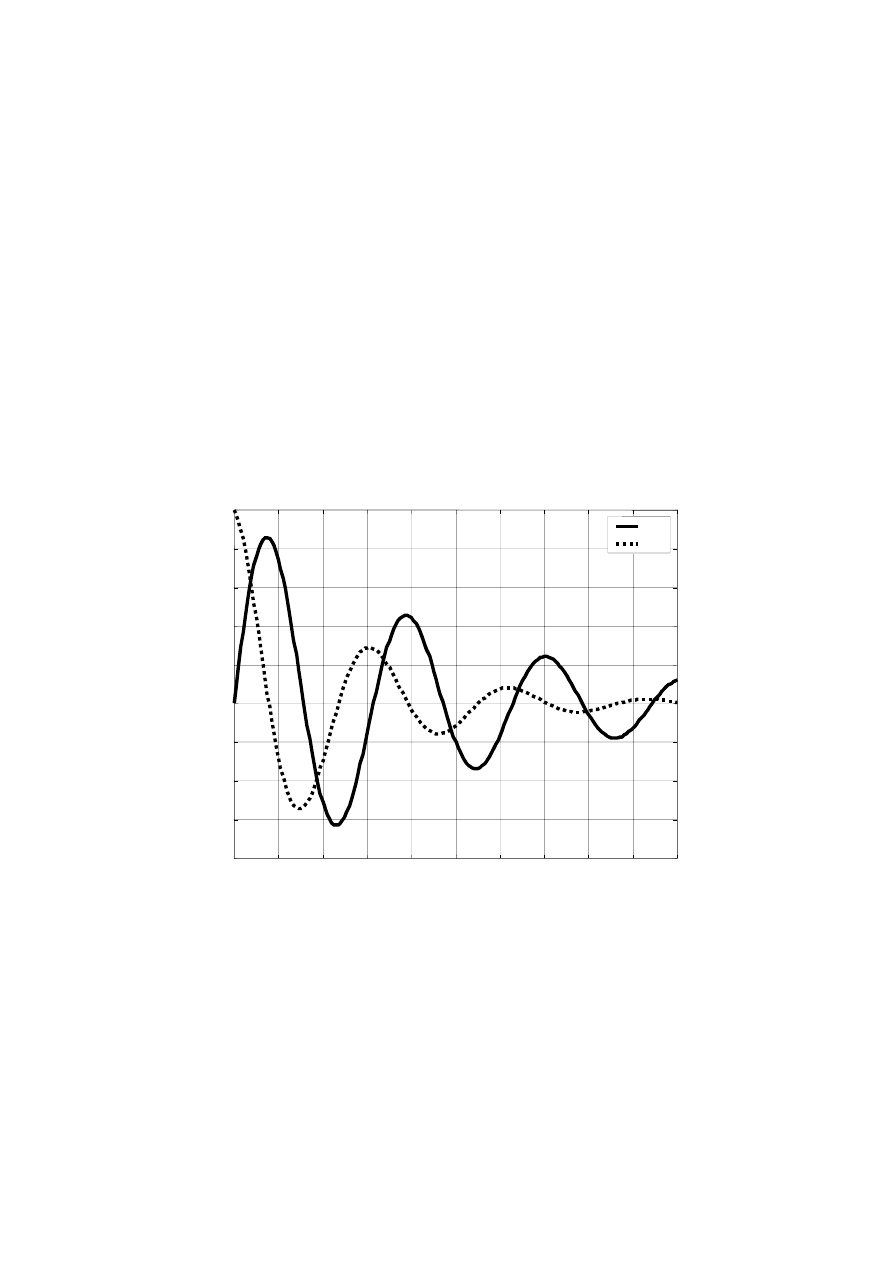
% Skrypt sincosex.m - wykres tlumionych funkcji sin oraz cos
t=0:0.1:20; % przedzial czasu
y1=sin(t).*exp(-0.1*t); % tlumiona sinusoida
y2=cos(t).*exp(-0.2*t); % tlumiona cosinusoida
plot(t,y1,'k-',t,y2,'k:'); grid on;
xlabel('czas t'); ylabel('y1, y2');
title('Wykres tlumionych funkcji okresowych');
text(2,0.9,'y1 - sinusoida tlumiona');
text(1,0.1,'y2 - cosinusoida tlumiona');
legend('y1','y2'); return

Wykres funkcji otrzymany w wyniku działania skryptu sincosex.m pokazano na
rys. 5.1.

0

2

4

6

8

10

12

14

16

18

20

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

czas t

y1,
y2

Wykres tlumionych funkcji okresowych

y1 - sinusoida tlumiona

y2 - cosinusoida tlumiona

y1

y2

Rys. 5.1. Wykres tłumionej sinusoidy i cosinusoidy

Uruchomienie

skryptu

sincosex w wersji 4.2 Matlaba daje w wyniku wykres

niewidoczny ze względu na czarne tło okna. W tym przypadku należy zmienić kolor
wykresu z czarnego ‘k’ , np. na niebieski ‘b’.

43

Ręczne skalowanie rysunku

Należy w tym przypadku wydać polecenie

axis(wektor)

gdzie

wektor = [xmin xmax ymin ymax] - określa wartości minimalne i maksymalne w

obu osiach.

Powrót do automatycznego skalowania osi odbywa się po wydaniu polecenia

axis('normal')

Nakładanie rysunków na siebie

Rysunki nakłada się na siebie poleceniem hold, i tak:

hold on

- zatrzymuje istniejący na ekranie rysunek, umożliwiając nałożenie na

istniejący rysunek następnego rysunku,

hold off -

wyłącza opcję hold on, powoduje zatarcie poprzedniego wykresu w

momencie tworzenia następnego

shg

- przywołuje na ekran ostatnio wygenerowany wykres,

clg

-

czyści ekran graficzny.

Podział ekranu graficznego na okna

Matlab

umożliwia podział ekranu graficznego na kilka okien za pomocą polecenia

subplot(hva)

gdzie

h, v - liczby naturalne z przedziału (1

÷

9),

h - liczba podziałów okna w osi poziomej (horizontal),

v

- liczba podziałów okna w osi pionowej (vertical),

a

- numer aktywnego okna.

Przykładowo, przy wyborze:
h=v=2

istnieją 4 okna,

h=1, v=2 lub h=2, v=1 istnieją 2 okna.

Do wykresów okienkowych odnoszą się wszystkie reguły tworzenia i opisu
wykresów.


Wykreślanie funkcji za pomocą fplot

Wykres funkcji zdefiniowanej jako m-plik może być wykonany za pomocą funkcji

fplot. Funkcja fplot wykreśla funkcję o podanej nazwie w podanym przedziale
określonym przez argument

fplot(Nazwa_funkcji, przedział)

gdzie

44

przedział = [xmin xmax ymin ymax]

Parametr Nazwa_funkcji powinien być nazwą m-pliku funkcyjnego.

Możliwe są także wywołania funkcji fplot z większą liczbą argumentów, np.

fplot(Nazwa_funkcji, przedział, 'rodzaj_linii') - kreśli wykres funkcji za

pomocą wyspecyfikowanego rodzaju linii,

[x, y] = fplot(Nazwa_funkcji, przedział, ...) - zwraca x oraz y takie, że spełniają

zależność y = Nazwa_funkcji(x).

Wykresy tworzone za pomocą funkcji fplot są na ogół dokładniejsze od
tworzonych za pomocą funkcji plot. Ilustruje to przykład wykresu uwikłanych funkcji
trygonometrycznych.

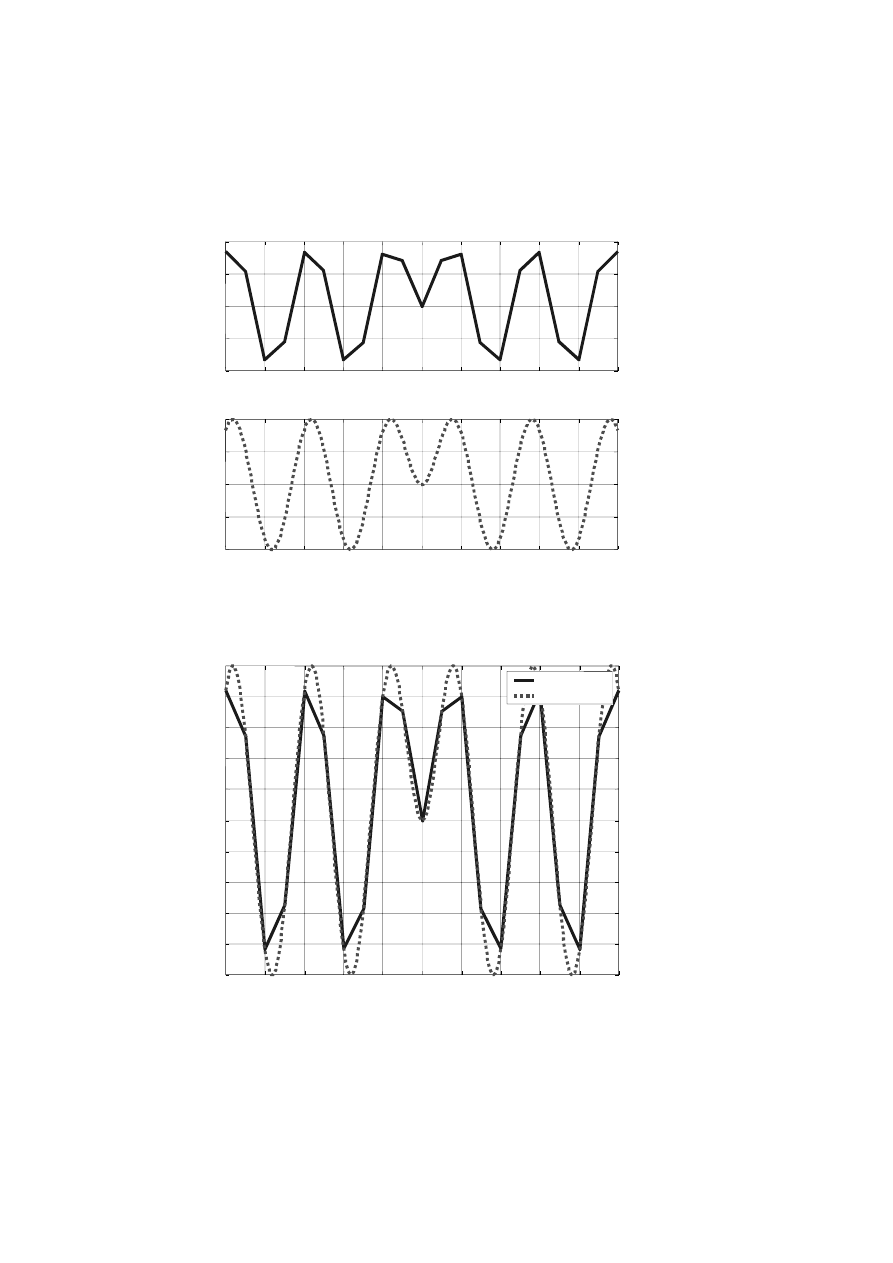
Przykład wykresu funkcji nieliniowej za pomocą plot oraz fplot

function y=sinatan(x)
% funkcja sinatan() jest zdefiniowana w pliku sinatan.m
y=sin(x.*atan(x));
return

function rysfplot
%wykres funkcji za pomoca funkcji fplot
% fplot(f,granice,dokladnosc,N,'rodzajlinii',P1,P2,...)
% parametry P1,P2,... sa parametrami funkcji f
% y = f(x,P1,P2,...(
% f - lancuch zawierajacy nazwe pliku rysowanej funkcji
% granice=[xa xb] - 2 elementowy wektor przedzialu dla x
% N - minimalna liczba punktów przy sporzadzaniu wykresu
xa=-10; xb=10; dx=1; % przedzial i przyrost x
x = xa:dx:xb; y = sinatan(x);
% uzycie plot
subplot(2,1,1); plot(x,y,'b-'); grid on;
title('Wykres funkcji sinatan() za pomoca plot')
% uzycie fplot
subplot(2,1,2); fplot('sinatan',[xa xb],'r:'); grid on;
title('Wykres funkcji sinatan() za pomoca fplot');
disp('Dalej? Nacisnij dowolny klawisz!'); pause;
% zapamietanie punktow generowanych przez fplot
[xx,yy] = fplot('sinatan',[xa xb]);
% uzycie plot dla punktow x,y oraz xx,yy
clf; % usuwa wszystkie aktywne rysunki z okna
plot(x,y,'b-',xx,yy,'r:'); grid on;
legend('wykres plot','wykres fplot');
title('Wykres sinatan() za pomoca plot i fplot ');
return

45

-10

-8

-6

-4

-2

0

2

4

6

8

10

-1

-0.5

0

0.5

1

Wykres funkcji sinatan() za pomoca plot

-10

-8

-6

-4

-2

0

2

4

6

8

10

-1

-0.5

0

0.5

1

Wykres funkcji sinatan() za pomoca fplot

Rys. 5.2a. Wykres uwikłanych funkcji trygonometrycznych wykonanych za pomocą plot oraz fplot w

oknie podzielonym na dwa okienka

-10

-8

-6

-4

-2

0

2

4

6

8

10

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

Wykres sinatan() za pomoca plot i fplot w jednym oknie

wykres plot

wykres fplot

Rys. 5.2b. Wykres uwikłanych funkcji trygonometrycznych za pomocą plot oraz fplot w jednym oknie

46

Różnice między tworzeniem wykresu za pomocą plot oraz fplot pokazano na rys.
5.2 a, b.

Wykresy w układzie współrzędnych biegunowych

W układzie biegunowym współrzędne punktów to promień od początku układu i

kąt między promieniem a dodatnią półosią x. Wykres tworzy funkcja polar

polar(alfa,r,’typ linii’)

gdzie

alfa – wektor określający przedział zmienności kąta w radianach,

r – wektor określający przedział zmienności promienia,

‘typ linii’ – typ linii jak w funkcji plot.

Wymiary macierzy alfa oraz r muszą być identyczne.

Wykres koła o zadanym promienu R

function kolo(R)
% wykres kola o promieniu R
if nargin < 1
R=1; % domyslny promien kola
end
alfa = 0:0.1:2*pi; % przedzial zmiennosci kata
nalfa=length(alfa);% liczba wartosci kata w zadanym przedziale
r = ones(1,nalfa)*R; % staly promien R w przedziale kata
polar(alfa,r,'bx'); % wykres
title('Kolo o zadanym promieniu R');
return

Wykresy zmiennych zespolonych

Jeżeli jedynym argumentem funkcji plot będzie macierz zespolona z

plot(z)

to działanie funkcji będzie równoważne wywołaniu

plot( real(z), imag(z) )

Jeżeli funkcja plot zostanie wywołana z wieloma argumentami o wartościach
zespolonych, np. dwoma

plot(z1,z2)

to części urojone zostaną pominięte.

Zmienne zespolone można przedstawiać na rysunku w postaci wektorów o
wspólnym początku. Służy do tego funkcja compass

compass(z,’typ linii’)

47

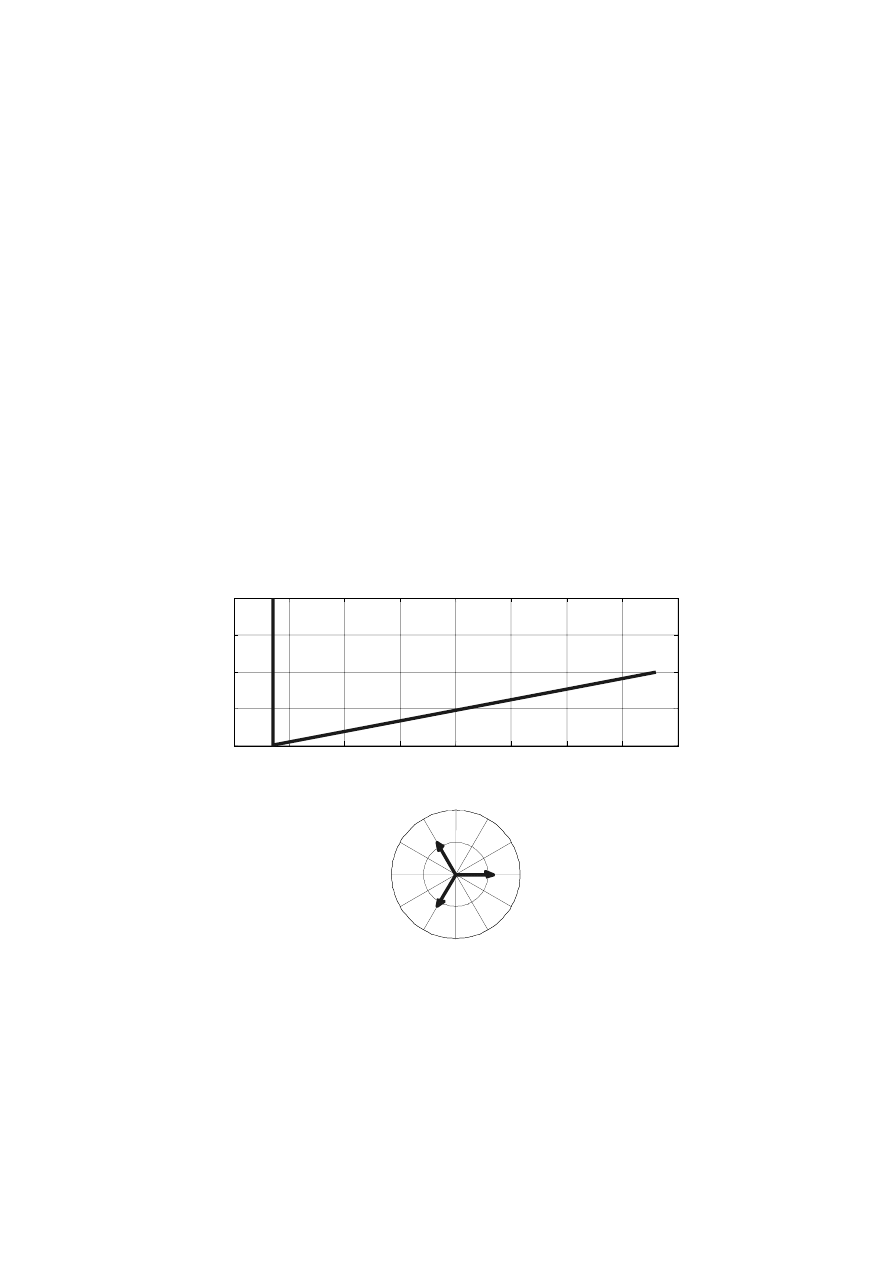
Działanie funkcji compass ilustruje skrypt rys_sem.m wykreślający 3-fazowe
zespolone siły elektromotoryczne za pomocą funkcji plot oraz compass.

Wykres 3-fazowych zespolonych sił elektromotorycznych

% skrypt rys_sem.m - wykres zespolonych sem
j=sqrt(-1); E=400/sqrt(3);
Ea = E;
Eb = E*exp(j*( -2*pi/3) );
Ec = E*exp(j*( 2*pi/3) );
E3f=[Ea Eb Ec]; % sem 3-fazowe
% wykres zespolnych sem za pomoca plot
subplot(2,1,1); plot(E3f,'b-'); grid on;
title('Wykres sem E3f=[Ea Eb Ec] za pomoca plot');
% wykres zespolnych sem za pomoca compass
subplot(2,1,2); compass(E3f,'b-');
title('Wykres sem E3f=[Ea Eb Ec] za pomoca compass');
return

Wynik działania skryptu rys_sem pokazuje rys. 5.3.

-150

-100

-50

0

50

100

150

200

250

-200

-100

0

100

200

Wykres sem E3f=[Ea Eb Ec] za pomoca plot

200

400

30

210

60

240

90

270

120

300

150

330

180

0

Wykres sem E3f=[Ea Eb Ec] za pomoca compass

Rys. 5.3. Wykresy 3-fazowych zespolonych sił elektromotorycznych za pomocą funkcji plot oraz

compass

48

Wykresy

3-wymiarowe

Współrzędne pojedynczego punktu uzyskuje się poprzez odwołanie
xij=X(i,j)
yij=Y(i,j)
zij=Z(i,j)

Najczęściej najpierw ustala się prostokątną siatkę XY za pomocą funkcji meshgrid, a
następnie wylicza się punkty Z

[X,Y]=meshgrid(x,y)

Wiersze macierzy X są kopiami wektora x, a kolumny macierzy Y są kopiami
wektora y. Wymiary macierzy X,Y to n=length(y) – wierszy oraz m=lemgth(x) –
wierszy.

Wykres powierzchni tworzy funkcja mesh

mesh(x,y,z,c)

gdzie c – macierz zawierająca indeksy kolorów. Jeżeli macierz c zostanie pominięta,
to c = z.

Do tworzenia wykresów można stosować również inne funkcje

meshc – działa jak mesh i umieszcza wykres poziomicowy

meshz – działa jak mesh plus krawędzie wykresu

surf – rysuje kolorową powierzchnię

surfc – działa jak surf plus wykres poziomicowy

waterfall – rysowane linie odpowiadające tylko wierszom macierzy

Do wykresów 3-wymiarowych stosują się te same polecenia opisu osi i rysunku co

i w plot. Działanie funkcji tworzących wykresy 3-wymiarowe ilustruje przykładowa
funkcja ryskosztg() wykreślająca charakterystyki kosztów wytwarzania mocy przez 2
współpracujące ze sobą turbozespoły.

Koszty wytwarzania mocy czynnej przez dwa turbozespoły

function ryskoszt(a1,b1,P1min,P1max,a2,b2,P2min,P2max)
% Funkcja ryskoszt() wykresla koszty wytwarzania mocy
% przez 2 turbozespoly o zadanych charakterystykach
% i mocach zawartych w przdziale od Pmin do Pmax
% K = a1*P1^2 + b1*P + a2*P2^2 + b2*P2
if nargin < 8 a1=0.5; end
if nargin < 7 b1=1.5; end
if nargin < 6 P1min=0.2; end

49

if nargin < 5 P1max=2; end
if nargin < 4 a2=0.2; end
if nargin < 3 b2=2.5; end
if nargin < 2 P2min=0.4; end
if nargin < 1 P2max=4; end
disp('Charakterystyka kosztow turbozespolu 1:');
disp('a1='),disp(a1); disp('b1='),disp(b1);
disp('P1min='),disp(P1min); disp('P1max='),disp(P1max);
disp('Charakterystyka kosztow turbozespolu 2:');
disp('a2='),disp(a2); disp('b2='),disp(b2);
disp('P2min='),disp(P2min); disp('P2max='),disp(P2max);
dP1=(P1max-P1min)/100;
dP2=(P2max-P2min)/100;
P1=P1min:dP1:P1max;
P2=P2min:dP2:P2max;
[x,y]=meshgrid(P1,P2);
z=a1*x.^2+b1*x + a2*y.^2+b2*y;
%
mesh(x,y,z);
title('3-wymiarowy wykres calkowitych kosztow wytwarzania');
xlabel(' Generator 1 - MW');
ylabel(' Generator 2 - MW');
zlabel('Calkowity koszt wytwarzania ');
grid on; hold on;
disp('Dalej? Wcisnij ENTER'); pause;
meshz(x,y,z); disp('Dalej? Wcisnij ENTER'); pause;
meshc(x,y,z); disp('Dalej? Wcisnij ENTER'); pause;
surf(x,y,z); disp('Dalej? Wcisnij ENTER'); pause;
surfl(x,y,z); disp('Dalej? Wcisnij ENTER'); pause;
surfc(x,y,z); disp('Dalej? Wcisnij ENTER'); pause;
return

Tworzenie wykresów jest szczególnie korzystne przy analizowaniu przebiegów
czasowych wielkości elektrycznych takich jak napięcia, prądy, czy moce. Ilustruje to
funkcja analizująca przebieg prądu zwarcia 3-fazowego w rozdzielczej sieci
elektroenergetycznej.

Przebieg czasowy prądu zwarcia 3-fazowego

Ze

względu na symetrię napięć i prądów rozdzielcza sieć elektroenergetyczna

może być zamodelowana w postaci jednofazowego obwodu liniowego, rys. 5.4.
Załóżmy, że do obwodu doprowadzone jest napięcie sinusoidalne

u = U

m

sin(

u

+

t

ψ

ω

) (5.1)

gdzie:

U

m

=

2

U - wartość maksymalna napięcia,

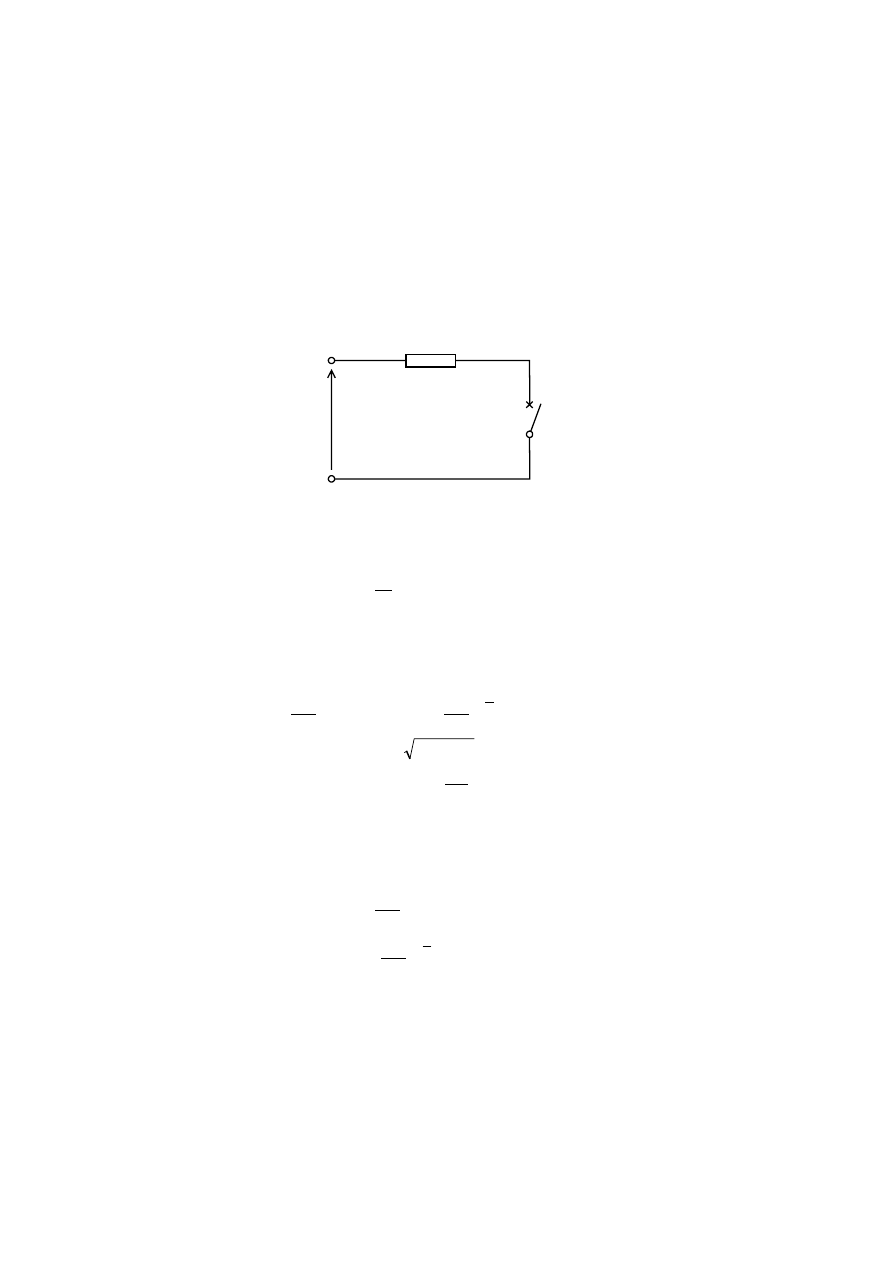
50

U - wartość skuteczna napięcia,

f

2

π

ω

=

- pulsacja,

f - częstotliwość,

u

ψ

- faza napięcia w chwili t = 0.

R + jX

u

W

Rys. 5.4. Obwód elektryczny nieobciążony zwierany przez wyłącznik

Stan nieustalony po załączeniu wyłącznika opisany jest równaniem różniczkowym

)

t

sin(

U

dt

di

L

Ri

u

m

ψ

ω

+

=

+

(5.2)

gdzie i oznacza wartość chwilową prądu.

Po

rozwiązaniu równania różniczkowego przy warunku początkowym i(t=0) = 0

otrzymuje się następujący wzór na prąd zwarciowy

)

sin(

e

Z

U

)

t

sin(

Z

U

i

u

t

L

R

m

u

m

ϕ

ψ

ϕ

ψ

ω

−

−

−

+

=

−

(5.3)

2

2

X

R

Z

+

=

(5.4)

)

R

L

(

arctg

ω

ϕ

=

(5.5)

gdzie Z - impedancja obwodu,

ϕ

- przesunięcie fazowe.

Ze wzoru wynika, że prąd zwarciowy jest sumą dwóch prądów składowych

DC

AC

i

i

i

+

=

(5.6)

)

t

sin(

Z

U

i

u

m

AC

ϕ

ψ

ω

−

+

=

(5.7)

)

sin(

e

Z

U

i

u

t

L

R

m

DC

ϕ

ψ

−

−

=

−

(5.8)

gdzie:

i

AC

- składowa okresowa o stałej amplitudzie,

51

i

DC

- składowa nieokresowa.

Składowa nieokresowa ma charakter prądu stałego zanikającego w czasie
stosownie do stałej czasowej

R

L

a

=

τ

(5.9)

Funkcja

kreśląca przebieg prądu czasowego została zapamiętana w pliku rysz3f.m.

Tworzone są przebiegi prądu zwarciowego w obwodzie o domyślnych parametrach
R=0.1, X=0.8, U = 1, psiU=30

o

lub o parametrach wczytanych z klawiatury.

function [T,iAC,iDC,iz3f] = rysz3f(R,X,U,psi)
% funkcja [T,iAC,iDC,iz3f] = rysz3f(R,X,U,psi)
% rysuje przebieg pradu zwarcia 3-fazowego
% w obwodzie wynikajacym z tw. Thevenina
% parametry w jedn. wzgl. /pu/ w odniesieniu do mocy 100 MVA
% i napiecia znamionowego w miejscu zwarcia
% sa podawane jako argumenty wywolania
% albo sa czytane z klawiatury w kolejnosci
% R - rezystancja, X – reaktancja
% U - wart. skut. napiecia, psi - kat nap. w st.
%
% Napiecie zasilajace
% Um = sqrt(2)*U
% u = Um*sin(w*t + psi)
%
% Rownanie rozniczkowe opisujace stan nieustalony po zwarciu
% R*i + L*di/dt = Um*sin(w*t+psi)
% X = w*L =2*pi*50*L
% Z = sqrt(R^2+X^2)
% fi = atan(X/R)
%
% iAC = Um/Z * sin(w*t +psi - fi)
% tau = L/R
% iDC = - Um/Z*exp(-t/tau)*sin(pis-fi)
% izw = iAC + iDC
%

% CZYTANIE DANYCH
%

if

nargin < 4

psi=30;

if

nargin < 3

U=1;

if

nargin < 2

X=0.8;

52

if

nargin < 1

R=0.1;

end

end
end
end

Um = sqrt(2)*U; % amplituda nap. zasilajacego
Z = sqrt(R^2+X^2); % impedancja pozorna
fi = atan(X/R); % kat impedancji
psi=psi/180*pi; % przeliczenie kata na radiany
w = 2*pi*50; % czestosc napiecia
L = X/w; % indukcyjnosc obwodu
tau = L/R; %stala zanikania
disp('Parametry obwodu:');
disp(' R= '),disp(R); disp(' X= '),disp(X);
disp(' L= '),disp(L);
disp(' tau=L/R= '),disp(tau);
disp(' U= '),disp(U);
disp(' psi= '),disp(psi);
disp(' fi = '),disp(fi);
% WYZNACZANIE PRZEBIEGOW PRADU
Tmax = 0.2 ; % max czas analizy
T = 0:0.002:Tmax; % przedzial czasu analizy od 0 do 1 sekundy
nT=length(T); % liczba punktow czasowych
p0 = zeros(1,nT); % os zerowa
Im = Um/Z; % amplituda pradu
iAC = Um/Z * sin(w.*T + psi - fi); % skladowa okresowa
iDC = - Um/Z*exp(-T./tau)*sin(psi-fi); %skladowa nieokresowa
izw3f = iAC + iDC; % prad zwarcia 3-fazowego
% PRZEBIEGI CZASOWE PRADU ZWARCIOWEGO
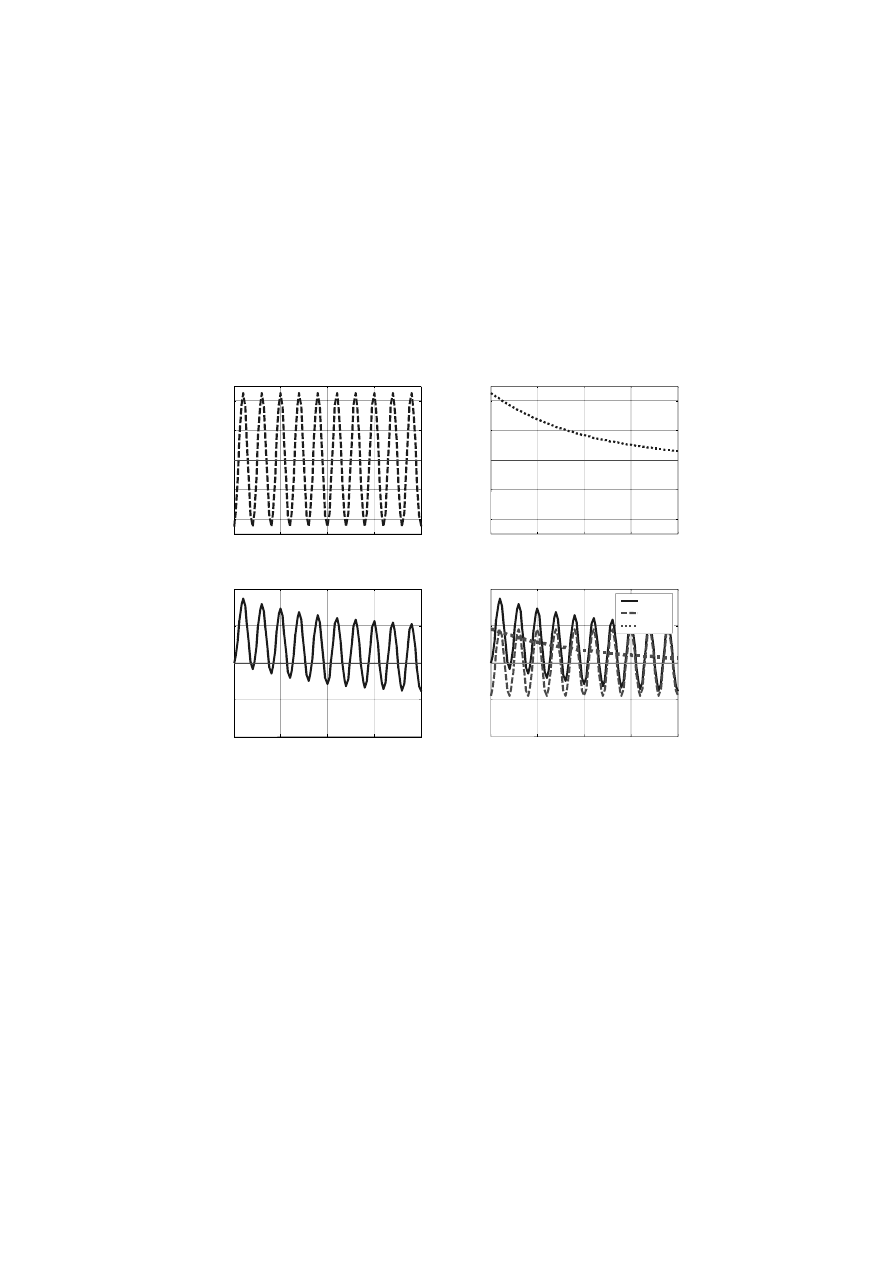
subplot(221),plot(T,iAC,'--', T,p0);
title(' iAC - skladowa okresowa');
xlabel('t,s');
% skalowanie wykresu przy pomocy axis ([xmin xmax ymin ymax]);
Imax = 1.1*Im; % skala osi rzednych dla iAC, iDC
Imax2=2*Imax; % skala osi rzednych dla pradu zwarciowego
axis([0 Tmax -Imax Imax]); grid on;
subplot(222),plot(T,iDC,':', T, p0);
title(' iDC - skladowa nieokresowa ');
axis([0 Tmax -Imax Imax]);
xlabel( 't, s'); grid on;
subplot(223),plot(T,izw3f,'-', T, p0);
title(' i = iAC + iDC - prad zwarciowy');
axis([0 Tmax -Imax2 Imax2]); xlabel('t,s'); grid on;
subplot(224),plot(T,izw3f,'-',T,iAC,'--',T,iDC,':', T,p0);
legend('izw3f', 'iAC', 'iDC');
title(' Prad zwarciowy z zaznaczeniem iAC oraz iDC');

53

axis([0 Tmax -Imax2 Imax2]); xlabel('t,s'); grid on;
disp('Zakonczono wykreslanie przebiegu pradow zwarciowych');
return

Po wywołaniu funkcji z parametrami wejściowymi rysz3f(0.1,0.4,1,45) otrzymuje

się przebiegi prądów zwarciowych pokazane na rys. 5.5.

0

0.05

0.1

0.15

0.2

-4

-2

0

2

4

iAC - skladowa okresowa

t,s

0

0.05

0.1

0.15

0.2

-4

-2

0

2

4

iDC - skladowa nieokresowa

t, s

0

0.05

0.1

0.15

0.2

-5

0

5

i = iAC + iDC - prad zwarciowy

t,s

0

0.05

0.1

0.15

0.2

-5

0

5

Prad zwarciowy z zaznaczeniem iAC oraz iDC

t,s

izw3f

iAC

iDC

Rys. 5.5. Przebiegi czasowe prądu zwarciowego uzyskane za pomocą funkcji rysz3f().

Zadanie do samodzielnego rozwiązania

Zadanie 1
Prąd zwarcia 3 –fazowego fazy L1 nieobciążonego generatora opisać następującym
wzorem

54































+















−

−















+

−

+

=

−

)

t

2

cos(

x

1

x

1

cos

x

1

x

1

e

5

.

0

)

t

cos(

)

t

(

c

x

U

i

''
q

''
d

''
q

''
d

/

t

''
d

m

1

L

ψ

ω

ψ

ψ

ω

τ

(5.10)
gdzie

















+















−

−

+













−

−

=

d

d

'
d

'

d

'
d

''
d

''

d

''
d

x

1

x

1

x

1

)

T

/

t

exp(

x

1

x

1

)

T

/

t

exp(

x

)

t

(

c

(5.11)

W przebiegu prądu zwarciowego można wyróżnić następujące składowe:

-

składowa okresowa o częstotliwości 50 Hz ,

-

składowa okresowa o częstotliwości 100 Hz,

- składowa

nieokresowa.

Przykładowe parametry generatora i hydrogeneratora podano w Tab. 5.1.

Tabela 5.1. Wartości średnie parametrów generatorów synchronicznych

Parametr generatora synchronicznego

Turbogenerator
600 MVA

Hydrogenerator
150 MVA

Reaktancja synchroniczna podłużna x

d

2

0.93

Reaktancja synchroniczna poprzeczna x

q

1.85 0.69

Reaktancja przejściowa podłużna

'
d

x

0.39 0.3

Reaktancja przejściowa poprzeczna

'
q

x

0.52 -

Reaktancja podprzejściowa podłużna

''

d

x

0.28 0.25

Reaktancja podprzejściowa poprzeczna

''

q

x

0.32 0.27

Stała czasowa przejściowa podłużna

'

d

T

, s

0.85 3.3

Stała czasowa podprzejściowa podłużna

''

d

T

, s

0.028 0.02

Stała czasowa zanikania nieokresowych prądów zwarcia wynika ze stosunku

indukcyjności podprzejściowej

''
d

L

do rezystancji uzwojeń generatora R

R

x

R

L

''

d

''
d

ω

τ

=

=

(5.11)

W przypadku dużych generatorów stała czasowa zanikania

τ

ma wartość mniejszą od

stałej przejściowej, np. 0.025 s.

Poniżej podano przykładową postać funkcji rysz3fgs(), która wykreśla przebieg
prądu zwarciowego nieobciążonego generatora synchronicznego.

55

function [t,ia,zanikanie]=...
rysz3fgs(tau,taubisd,tauprimd,xq,xd,xprimd,xbisq,xbisd,Ug,psi);
%function [t,ia,zanikanie]=...
%rysz3fgs(tau,taubisd,tauprimd,xq,xd,xprimd,xbisq,xbisd,Ug,psi)
% w przypadku braku parametrow ejsciowych
% przyjmowane sa wartosci domyslne
tau =0.025; % - stala czasowa zanikania
% nieokresowych pradow zwarcia
taubisd =0.028; % - stala czasowa podprzejscowa podluzna
tauprimd =0.85; % - stala czasowa przejsciowa podluzna
xq=1.85; % - reaktancja sychroniczna poprzeczna
xd=2; % - reaktancja synchroniczna podluzna
xprimd=0.39; % - raktancja przejsciowa podluzna
xbisq=0.32; % - reaktancja podprzejsciowa poprzeczna
xbisd=0.28; % - reaktancja podprzejsciowa podluzna
Ug=1.05; % - napiecie generatora przed zwarciem
psi=0; % - poczatkowy kat napiecia
Um=sqrt(2)*Ug; % amplituda napiecia
t0=0; tmax=0.5; dt=0.001;
t=t0:dt:tmax;
omega=2*pi*50;
%
ct=xbisd.*(1/xbisd-1/xprimd).*exp(-t./taubisd)...
+(1/xprimd-1/xd).*exp(-t/tauprimd)+1/xd;
%
%skladowe prady pradu zwarcia ia
%skladowa 50 Hz
i50Hz = Um/xbisd*( ct.*cos(omega.*t + psi ) );
% skladowa nieokresowa
inok = Um/xbisd*( -0.5*exp(-t./tau).* ...
( (1/xbisd+1/xbisq )*cos(psi) ) );
% skladowa 100 Hz
i100Hz = Um/xbisd*( -0.5*exp(-t./tau).*...
( -(1/xbisd-1/xbisq).*cos(2*omega.*t+psi) ) );
% prad zawrciowy w fazie A
iA = i50Hz + i100Hz + inok;
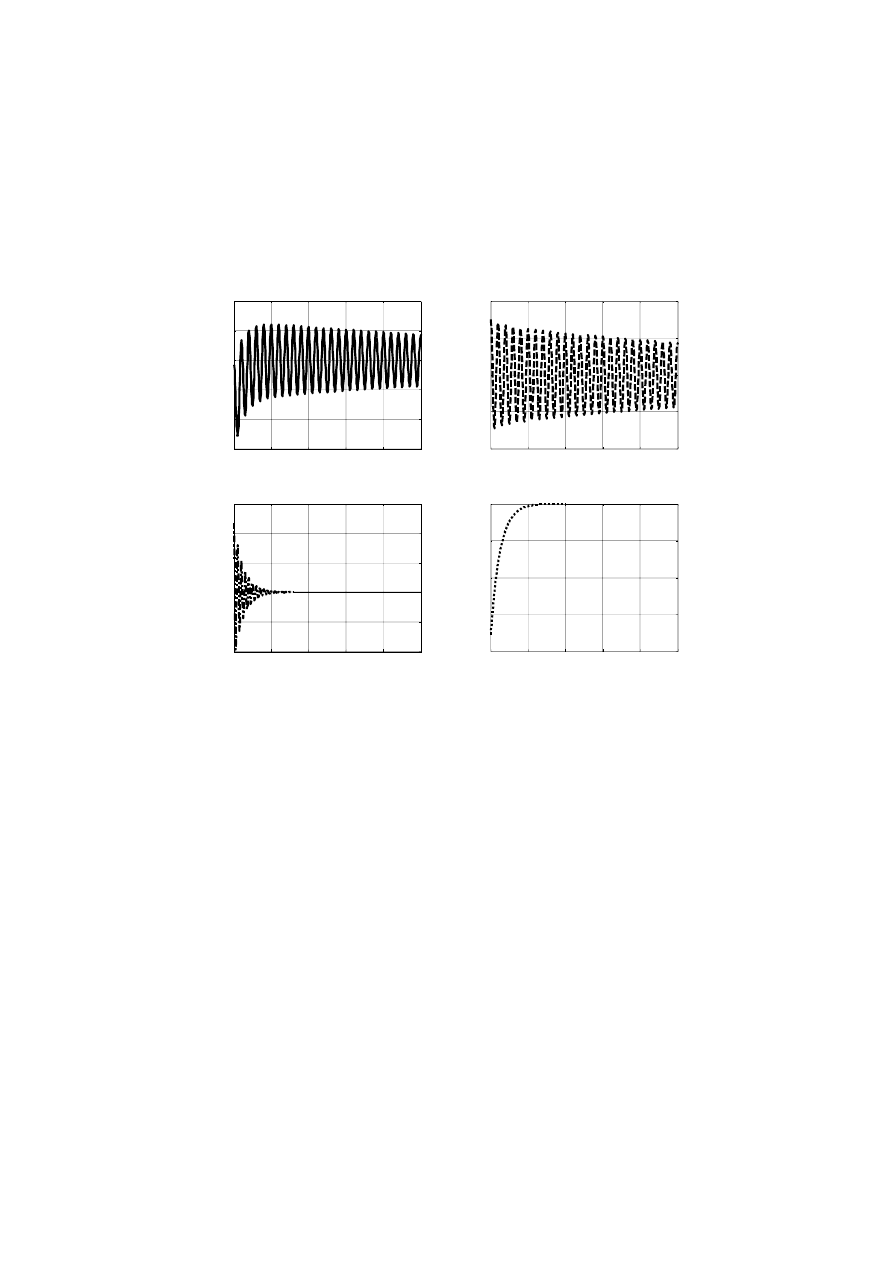
%poszczegolne wykresy
subplot(2,2,1),plot(t,iA,'k-');
title('prad zwarciowy'),grid on;
subplot(2,2,2),plot(t,i50Hz,'k--');
title('skladowa okresowa 50Hz'),grid on;
subplot(2,2,3),plot(t,i100Hz,'k-.');
title('skladowa okresowa 100Hz'),grid on;
subplot(2,2,4),plot(t,inok,'k:');
title('skladowa nieokresowa'),grid on;
return

56

Wynik działania funkcji rysz3fgs() pokazano na rys. 5.6.

0

0.1

0.2

0.3

0.4

0.5

-30

-20

-10

0

10

20

prad zwarciowy

0

0.1

0.2

0.3

0.4

0.5

-20

-10

0

10

20

skladowa okresowa 50Hz

0

0.1

0.2

0.3

0.4

0.5

-1

-0.5

0

0.5

1

1.5

skladowa okresowa 100Hz

0

0.1

0.2

0.3

0.4

0.5

-20

-15

-10

-5

0

skladowa nieokresowa

Rys. 5.6. Przebiegi czasowe prądu zwarciowego uzyskane za pomocą funkcji rysz3fgs().

Należy zmodyfikować funkcję rysz3fgs() w taki sposób, aby realizowała
następujące dodatkowe działania:

-

wywołanie z parametrami lub czytanie parametrów z klawiatury,

-

tworzenie wykresów za pomocą funkcji fplot zamiast plot.