1

SYSTEMY ELEKTROENERGETYCZNE

Rozdział

3

OBLICZANIE ROZPŁYWÓW MOCY

Łódź, 2011 rok

Andrzej Kanicki

2

OBLICZANIE PRZEPŁYWÓW MOCY. 

Rozpływ mocy w zamkniętej sieci elektroenergetycznej

Typy węzłów w obliczeniach rozpływów mocy i wielkości znane:

1)

Odbiorcze

2)

Generatorowe

3)

Bilansujący

Węzły odbiorcze nazywamy węzłami typu PQ

a generatorowe typu PU.

Równanie mocy w i‐tym węźle odbiorczym jest postaci:

Wielkości znane to admitancje własna i wzajemna węzła, wielkości nieznane
to napięcia w węzłach. 
Napięcia można zapisać

w układzie współrzędnych biegunowych lub 

prostokątnych, czyli:

const.

=

o

P

const.

=

o

Q

const.

=

G

P

const.

=

G

U

const.

=

U

const.

0

=

=

δ

∑

≠

=

∗

∗

∗

∗

⋅

⋅

+

⋅

=

⋅

=

N

i

j

j

ij

j

i

ii

i

i

i

i

Y

U

U

Y

U

I

U

S

1

2

1

,

2

,

1

2

1

−

=

+

=

=

N

i

jU

U

e

U

U

i

i

j

i

i

i

K

δ

[

]

[

]

T

T

T

T

T

T

2

1

lub

U

U

X

U

X

=

=

δ

3

OBLICZANIE PRZEPŁYWÓW MOCY. 

Rozpływ mocy w zamkniętej sieci elektroenergetycznej  

( )

( )

0

=

=

−

X

F

S

X

S

z

0

2

1

2

2

2

=

−

+

i

i

i

U

U

U

(

)

(

)

[

]

0

sin

cos

1

2

=

−

−

⋅

+

−

⋅

⋅

⋅

+

⋅

∑

≠

=

i

N

i

j

j

j

i

ij

j

i

ij

j

i

ii

i

P

B

G

U

U

G

U

δ

δ

δ

δ

(

)

(

)

[

]

0

cos

sin

1

2

=

−

−

⋅

−

−

⋅

⋅

⋅

+

⋅

−

∑

≠

=

i

N

i

j

j

j

i

ij

j

i

ij

j

i

ii

i

Q

B

G

U

U

B

U

δ

δ

δ

δ

Dla węzłów odbiorczych do rozwiązania w obliczeniach rozpływów mocy 
jest równanie:

gdzie:       to moce zadane w węźle.            
Dla węzła generatorowego mamy dodatkowo równanie dla napięcia zadanego:

Równanie mocy w układzie biegunowym jest postaci:

z

S

4

OBLICZANIE PRZEPŁYWÓW MOCY. 

Rozpływ mocy w zamkniętej sieci elektroenergetycznej

(

)

(

)

0

1

2

2

2

1

1

1

1

2

=

−

⋅

+

⋅

⋅

+

⋅

−

⋅

⋅

+

⋅

∑

∑

≠

=

≠

=

i

N

i

j

j

N

i

j

j

j

ij

j

ij

i

j

ij

j

ij

i

ii

i

P

U

B

U

G

U

U

B

U

G

U

G

U

(

)

(

)

0

2

1

2

1

2

1

1

1

2

=

−

⋅

−

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

−

∑

∑

≠

=

≠

=

i

N

i

j

j

N

i

j

j

j

ij

j

ij

i

j

ij

j

ij

i

ii

i

Q

U

B

U

G

U

U

B

U

G

U

G

U

( )

k

k

X

X

ϕ

=

+1

( )

0

0

X

X

ϕ

=

Warunki zbieżności procesu iteracyjnego są

następujące: 

1) Jeśli funkcja          

jest różniczkowalne i wypukła w pewnym otoczeniu punktu

( )

X

ϕ

to 

warunkiem zbieżności jest:

0

X

{ }

( )

1

max

<

=

∈

j

W

j

λ

ρ

( )

[

]

0

det

0

=

−

j

λ

X

J

( )

{ }

W

j

i

dla

x

x

x

j

i

∈

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

=

,

0

0

∂

ϕ

∂

X

J

Równanie mocy w układzie prostokątnym jest postaci:

Równania mocy rozwiązywane są

metodami iteracyjnymi, czyli:

Szukanym rozwiązaniem jest wektor      , który:

0

X

5

OBLICZANIE PRZEPŁYWÓW MOCY. 

Rozpływ mocy w zamkniętej sieci elektroenergetycznej

2) Jeśli istnieje liczba naturalna     większa lub równa jedności oraz rzeczywista 

taka, że: 

p

c

c

p

k

k

k

=

−

−

+

∞

⇒

0

0

1

lim

X

X

X

X

W praktycznych obliczeniach rozpływów mocy zbieżności procesu 

iteracyjnego kontroluje się

następująco: 

N

i

dla

U

U

U

k

i

k

i

k

i

K

,

2

,

1

1

1

=

<

−

=

+

+

ε

Δ

N

i

dla

U

U

U

U

k

i

k

i

k

i

k

i

K

,

2

,

1

1

1

=

−

<

−

−

+

Iteracje te powtarza się

tak długo, dopóki poprawki napięciowe we 

wszystkich węzłach sieci będą

miały wartość

mniejszą

od założonej 

dokładności obliczania modułów napięć

węzłowych    : 

ε

Warunek powyższy może być

również

sformułowany dla mocy czynnych i 

biernych.

6

OBLICZANIE PRZEPŁYWÓW MOCY. 

Rozpływ mocy w zamkniętej sieci elektroenergetycznej

W obliczeniach rozpływów mocy musimy pamiętać

o wielu różnych

ograniczeniach, które musza być

spełnione. 

1) Niezależnie od typu węzła mamy:

2) Dla węzła typu PU 

W przypadku osiągnięcia jednego z tych ograniczeń

należy zmienić

typ

tego węzła na PQ. 

3) W transformatorach mamy: 

a zmiany przekładnia napięciowej i kątowej transformatora mogą
odbywać

się

skokowo: 

∞

=

=

≤

≤

K

K

,

2

,

1

,

2

,

1

dla

max

min

k

N

i

U

U

U

i

k

i

i

∞

=

=

≤

≤

K

K

,

2

,

1

,

2

,

1

dla

max

min

k

G

i

Q

Q

Q

i

k

i

i

∞

=

=

≤

≤

K

K

,

2

,

1

,

2

,

1

dla

max

min

k

M

i

i

k

i

i

ϑ

ϑ

ϑ

∞

=

=

≤

≤

K

K

,

2

,

1

,

2

,

1

dla

max

min

k

M

i

i

k

i

i

α

α

α

M

j

j

stare

j

nowe

j

K

,

2

,

1

dla

=

+

=

ϑ

Δ

ϑ

ϑ

M

j

j

stare

j

nowe

j

K

,

2

,

1

dla

=

+

=

α

Δ

α

α

7

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda Gaussa

⎟

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎜

⎝

⎛

⋅

−

−

⋅

=

∑

≠

=

+

N

i

j

j

k

j

ij

k

i

i

i

ii

k

i

U

Y

U

jQ

P

Y

U

1

*

1

1

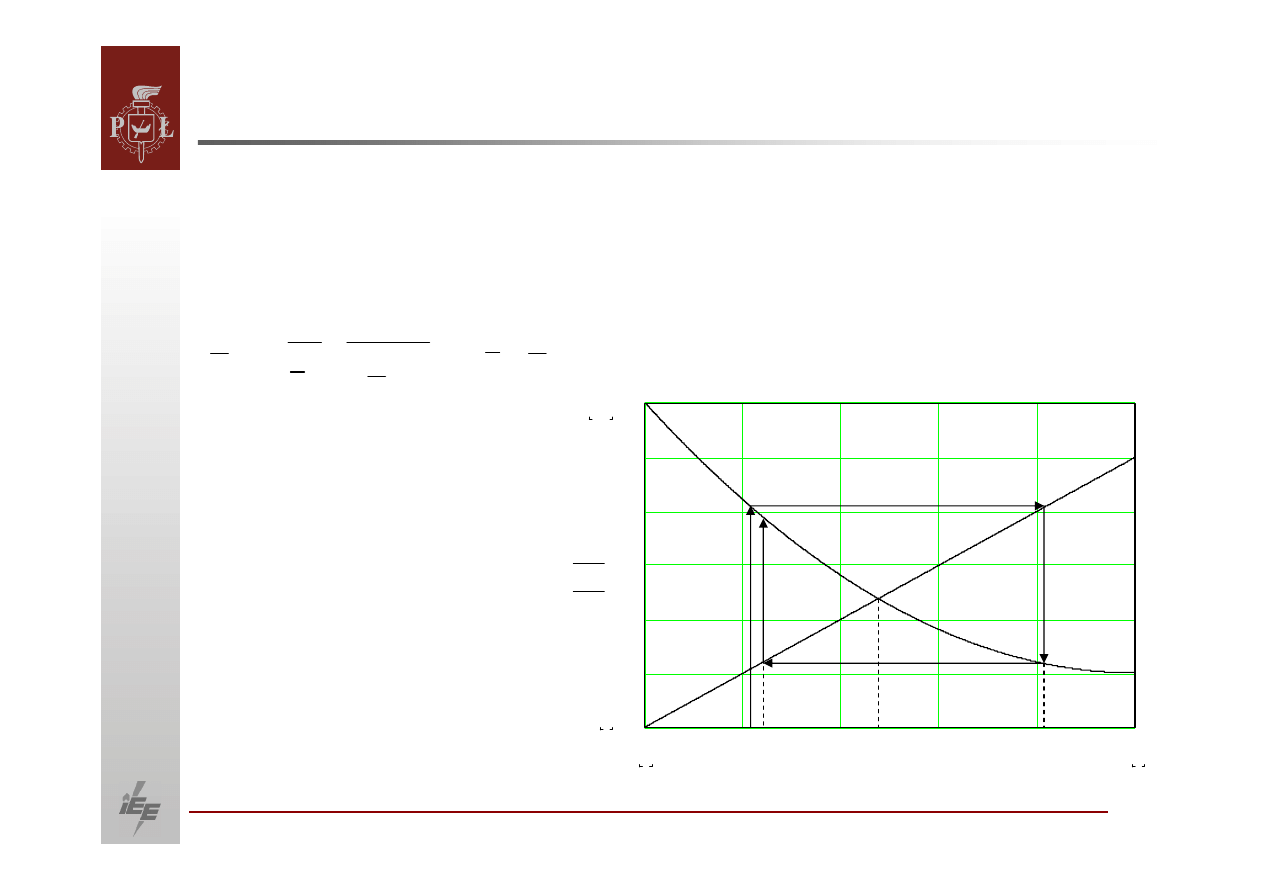
W metodzie Gaussa funkcję

iteracyjną

uzyskuje się

z odpowiednio 

przekształconego równania na moc co zapewnia optymalną

zbieżność

procesu iteracyjnego: 

0

0.2

0.4

0.6

0.8

1

0

0.2

0.4

0.6

0.8

1

1.2

1.2

0

y x

( )

y1 x

( )

1

0

x

( )

x

y

ϕ

=

x

y

=

0

x

1

x

2

x

0

x

Ilustracja procesu 

iteracyjnego w metodzie 

Gaussa 

8

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda Gaussa

( )

( )

∑

∑

≠

=

≠

=

+

⋅

−

⋅

−

⋅

+

⋅

=

N

i

j

j

k

j

ij

N

i

j

j

k

j

ij

k

i

k

i

ii

k

i

k

i

ii

k

i

U

b

U

a

U

U

b

U

U

a

U

1

1

2

2

1

2

1

2

1

1

( )

( )

∑

∑

≠

=

≠

=

+

⋅

−

⋅

+

⋅

+

⋅

−

=

N

i

j

j

k

j

ij

N

i

j

j

k

j

ij

k

i

k

i

ii

k

i

k

i

ii

k

i

U

a

U

b

U

U

a

U

U

b

U

1

1

2

2

1

2

1

2

1

2

2

ii

ii

i

ii

i

ii

Y

B

Q

G

P

a

⋅

−

⋅

=

2

ii

ii

i

ii

i

ii

Y

G

Q

B

P

b

⋅

+

⋅

=

2

ii

ii

ij

ii

ij

ij

Y

B

B

G

G

a

⋅

+

⋅

=

2

ii

ii

ij

ii

ij

ij

Y

G

B

B

G

b

⋅

−

⋅

=

We współrzędnych prostokątnych mamy:

Metoda Gaussa ‐

Seidla 

[

]

T

k

N

k

i

k

i

k

i

k

k

U

U

U

U

U

K

K

,

,

,

,

1

1

1

1

1

1

+

+

−

+

+

=

U

9

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda klasyczna Newtona‐Raphsona

( )

( )

0

X

J

X

F

X

F

=

⋅

+

≈

k

k

k

Δ

( ) ( )

k

k

k

X

F

J

X

⋅

−

=

−1

Δ

k

X

X

j

i

k

X

F

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

∂

∂

J

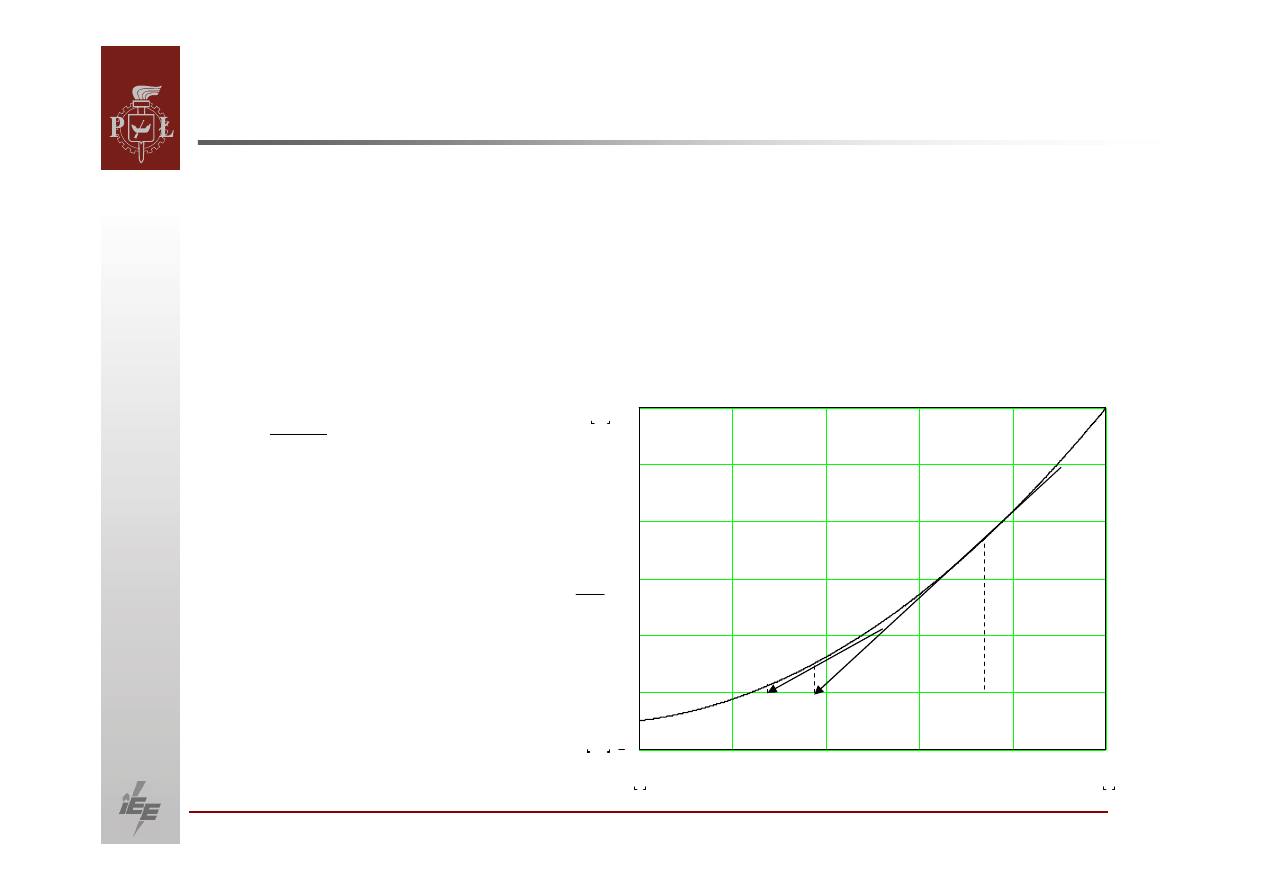
W metodzie klasycznej Newtona‐Raphsona

funkcję

iteracyjną

tworzy się, 

wykorzystując liniowe przybliżenia przyrostów funkcji czyli przez rozkład 
funkcji nieliniowej na szereg Taylora: 

0

0.2

0.4

0.6

0.8

1

2

0

2

4

6

8

10

10

1

−

y x

( )

1

0

x

0

x

1

x

( )

x

F

y

=

0

x

2

x

10

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda klasyczna Newtona‐Raphsona

( )

( )

k

k

k

k

k

k

X

F

J

X

X

X

X

⋅

−

=

+

=

−

+

1

1

Δ

( )

k

k

k

k

X

J

S

X

F

Δ

Δ

⋅

−

=

=

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

U

L

M

N

H

Q

P

Δ

δ

Δ

Δ

Δ

obl

i

zad

i

i

P

P

P

−

=

Δ

obl

i

zad

i

i

Q

Q

Q

−

=

Δ

Z równania na rozkład funkcjo noeliniowej

wynika zależność

iteracyjna: 

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

−

−

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

−

=

j

obl

i

j

obl

i

j

zad

i

j

i

P

P

P

P

δ

Δ

∂

∂

δ

Δ

∂

∂

δ

Δ

∂

∂

δ

Δ

∂

Δ

∂

H

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

j

obl

i

U

P

Δ

∂

∂

N

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

j

obl

i

Q

δ

Δ

∂

∂

M

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

j

obl

i

U

Q

Δ

∂

∂

L

11

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda klasyczna Newtona‐Raphsona

i

k

≠

(

)

ki

ki

ki

ki

i

k

i

obl

k

ki

B

G

U

U

P

H

δ

δ

δ

∂

∂

cos

sin

⋅

−

⋅

⋅

⋅

=

=

(

)

ki

ki

ki

ki

k

i

obl

k

ki

B

G

U

U

P

N

δ

δ

∂

∂

sin

cos

⋅

+

⋅

⋅

=

=

(

)

ki

ki

ki

ki

i

k

i

obl

k

ki

B

G

U

U

Q

M

δ

δ

δ

∂

∂

sin

cos

⋅

+

⋅

⋅

⋅

−

=

=

(

)

ki

ki

ki

ki

k

i

obl

k

ki

B

G

U

U

Q

L

δ

δ

∂

∂

cos

sin

⋅

−

⋅

⋅

=

=

i

k

=

(

)

[

]

∑

≠

=

⋅

−

⋅

⋅

⋅

−

=

=

N

k

j

j

kj

kj

kj

kj

j

k

k

obl

k

kk

B

G

U

U

P

H

1

cos

sin

δ

δ

δ

∂

∂

2

k

kk

k

kk

U

B

Q

H

⋅

−

−

=

Podmacierze                    są

postaci:

L

M

N

H

i

,

,

(

)

[

]

∑

≠

=

⋅

+

⋅

⋅

+

⋅

⋅

=

=

N

k

j

j

kj

kj

kj

kj

j

kk

k

k

obl

k

kk

B

G

U

G

U

U

P

N

1

sin

cos

2

δ

δ

∂

∂

k

kk

k

k

kk

U

G

U

P

N

⋅

+

=

12

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda klasyczna Newtona‐Raphsona

(

)

[

]

∑

≠

=

⋅

+

⋅

⋅

⋅

=

=

N

k

j

j

kj

kj

kj

kj

j

k

k

obl

k

kk

B

G

U

U

Q

M

1

sin

cos

δ

δ

δ

∂

∂

2

k

kk

k

kk

U

G

P

M

⋅

−

=

(

)

[

]

∑

≠

=

⋅

−

⋅

⋅

+

⋅

⋅

−

=

=

N

k

j

j

kj

kj

kj

kj

j

kk

k

k

obl

k

kk

B

G

U

B

U

U

Q

L

1

cos

sin

2

δ

δ

∂

∂

k

kk

k

k

kk

U

B

U

Q

L

⋅

−

=

Podobne wyprowadzenie można wykonać

w przypadku przedstawienia 

wektora szukanych napięć

węzłowych w układzie współrzędnych 

prostokątnych: 

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

2

1

U

U

L

M

N

H

Q

P

Δ

Δ

Δ

Δ

i

k

≠

k

i

k

i

i

obl

k

ki

U

I

U

I

P

H

1

2

2

1

⋅

−

⋅

=

=

δ

∂

∂

i

k

i

k

i

i

obl

k

ki

U

U

I

U

I

U

P

N

2

2

1

1

⋅

+

⋅

=

=

∂

∂

k

i

k

i

i

obl

k

ki

U

I

U

I

Q

M

2

2

1

1

⋅

−

⋅

−

=

=

δ

∂

∂

i

k

i

k

i

i

obl

k

ki

U

U

I

U

I

U

Q

L

1

2

2

1

⋅

−

⋅

=

=

∂

∂

∑

=

⋅

=

+

=

N

j

ij

j

i

i

i

Y

U

jI

I

I

1

2

1

Tylko dla

13

OBLICZANIE PRZEPŁYWÓW MOCY. 

Zmodyfikowana i rozłączna metoda Newtona 

W zmodyfikowanej metodzie Newtona funkcja iteracyjna ma tu postać: 

( )

( )

k

k

k

X

F

J

X

X

⋅

−

=

−

+

1

1

1

W rozłącznej metodzie Newtona równanie:  

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⋅

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

k

k

k

k

k

k

k

k

U

L

M

N

H

Q

P

Δ

δ

Δ

Δ

Δ

zapisuje się

w postaci:

wykorzystując fakt, że podmacierze poza główną

przekątną

mają

elementy 

o wartościach

bliskich zeru. Otrzymujemy do rozwiązania 2 równania:

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⋅

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

k

k

k

k

k

k

U

L

H

Q

P

Δ

δ

Δ

Δ

Δ

0

0

( )

( )

k

k

P

k

k

k

k

k

P

J

P

H

Δ

δ

Δ

δ

δ

δ

⋅

−

=

⋅

−

=

−

−

+

1

1

1

( )

( )

k

k

QU

k

k

k

k

k

Q

J

U

Q

L

U

U

Δ

Δ

⋅

−

=

⋅

−

=

−

−

+

1

1

1

14

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda Stotta, metoda van Nessa

Metoda Stotta

to połączenie metody rozłącznej i zmodyfikowanej. 

( )

k

k

k

P

H

Δ

δ

δ

⋅

−

=

−

+

1

1

1

( )

k

k

k

Q

L

U

U

Δ

⋅

−

=

−

+

1

1

1

Metoda van

Nessa

jest modyfikacją

metody Newtona‐Rapsona, polegającą

na

pominięciu w

macierzy

Jacobiego

elementów wzajemnych, tzn.: 

i

j

dla

M

N

L

H

ij

ij

ij

ij

≠

=

=

=

=

0

Różne od zera są

elementy własne macierzy : 

0

≠

ii

H

0

≠

ii

N

0

≠

ii

M

0

≠

ii

L

Współczynniki podmacierzy Jacobiego

różne od zera mają

postać: 

2

j

jj

j

j

j

jj

U

B

Q

P

H

⋅

−

−

=

=

δ

∂

∂

j

jj

j

j

j

j

jj

U

G

U

P

U

P

N

⋅

+

=

=

∂

∂

2

j

jj

j

j

j

jj

U

G

P

Q

M

⋅

−

=

=

δ

∂

∂

j

jj

j

j

j

j

jj

U

B

U

Q

U

Q

L

⋅

−

=

=

∂

∂

15

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda van Nessa

Uzyskuje się

macierz Jacobiego

w

postaci

macierzy quazidiagonalnej

o podmacierzach na diagonali stopnia 2x2. 

⎥

⎦

⎤

⎢

⎣

⎡

=

jj

jj

jj

jj

j

L

M

N

H

J

j

jj

j

jj

j

U

N

H

P

Δ

δ

Δ

Δ

⋅

+

⋅

=

j

jj

j

jj

j

U

L

M

Q

Δ

δ

Δ

Δ

⋅

+

⋅

=

Po rozwiązaniu mamy gotowe wzory na moduł

i argument napięcia: 

jj

jj

jj

jj

j

jj

j

jj

j

L

H

M

N

Q

H

P

M

U

−

⋅

−

⋅

=

Δ

Δ

Δ

jj

jj

j

j

j

H

N

U

P

⋅

−

=

Δ

Δ

δ

Δ

16

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda stałoprądowa 

W metodzie stałoprądowej przyjmuje się

następujące założenia upraszczające: 

1) Pomija się

rezystancje gałęzi                                  .

2) Nie uwzględnia się

parametrów poprzecznych elementów. 

3) Gdy rozpatrywane są

tylko stany o dużym zapasie stabilności, czyli o bardzo

małych rozchyłach kątowych w poszczególnych gałęziach, co można zapisać: 

4) Napięcia w węzłach są

równe wartościom znamionowym: 

0

=

ij

r

(

)

j

i

j

i

δ

δ

δ

δ

−

≈

−

sin

(

)

1

cos

≈

−

j

i

δ

δ

in

i

U

U

≈

Uwzględnienie wyżej przedstawionych uproszczeń

pozwala na napisanie 

wzoru na moc w gałęzi jako: 

(

)

j

i

ij

ij

δ

δ

b

U

P

−

⋅

⋅

−

=

2

n

0

=

ij

Q

(

)

j

i

ij

ij

δ

δ

b

P

−

⋅

−

=

pu

pu

ij

ij

x

b

1

−

=

17

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda stałoprądowa

Moc węzłowa w węźle i‐tym wynosi: 

(

)

⎟

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎜

⎝

⎛

⋅

−

−

=

−

⋅

−

=

=

∑

∑

∑

∑

≠

=

≠

=

≠

=

≠

=

w

i

j

j

j

ij

w

i

j

j

ij

i

w

i

j

j

j

i

ij

w

i

j

j

ij

i

δ

b

b

δ

δ

δ

b

P

P

1

pu

1

pu

1

pu

1

pu

pu

)

(

(

)

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

⋅

+

⋅

−

=

∑

≠

=

w

i

j

j

j

ij

i

ii

i

δ

B

δ

B

P

1

Stosując zapis macierzowy, można przedstawić

stałoprądowy model sieci: 

⎥

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎢

⎣

⎡

⋅

⎥

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎢

⎣

⎡

−

=

⎥

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎢

⎣

⎡

w

n

1

ww

wn

w

nw

nn

n

w

n

w

n

δ

δ

δ

B

B

B

B

B

B

B

B

B

P

P

P

M

M

K

K

M

O

M

O

M

K

K

M

O

M

O

M

K

K

M

M

1

1

1

1

11

1

δ

B

P

⋅

−

=

18

OBLICZANIE PRZEPŁYWÓW MOCY. 

Metoda stałoprądowa. Uwzględnienie współczynników relaksacji 

Macierz susceptancji węzłowych

jest macierzą

osobliwą.

Z

macierzy

susceptancji węzłowych wykreśla się

wiersz i kolumnę

odpowiadające numerowi węzła bilansującego otrzymując nową, nieosobliwą
macierz susceptancji węzłowych            . Mamy więc:

B

new

B

(

)

new

new

new

new

new

P

B

P

X

δ

⋅

−

=

⋅

=

−1

Uwzględnienie współczynników relaksacji polega na zmianie obliczonej 
poprawki napięciowej o pewną

wartość: 

(

)

k

i

k

i

k

i

k

i

k

i

k

i

U

U

k

U

U

k

U

U

1

1

1

1

1

1

1

1

1

−

⋅

+

=

⋅

+

=

+

+

+

Δ

(

)

k

i

k

i

k

i

k

i

k

i

k

i

U

U

k

U

U

k

U

U

2

2

2

2

2

2

1

1

1

−

⋅

+

=

⋅

+

=

+

+

+

Δ

lub

(

)

k

i

k

i

k

i

k

i

k

i

k

i

U

U

k

U

U

k

U

U

−

⋅

+

=

⋅

+

=

+

+

+

1

1

1

Δ

(

)

k

i

k

i

k

i

k

i

k

i

k

i

k

k

δ

δ

δ

δ

Δ

δ

δ

−

⋅

+

=

⋅

+

=

+

+

+

1

1

1

1

>

k

metoda nadrelaksacji, 

1

<

k

metoda podrelaksacji. 

new

new

new

δ

B

P

⋅

−

=

19

OBLICZANIE PRZEPŁYWÓW MOCY. 

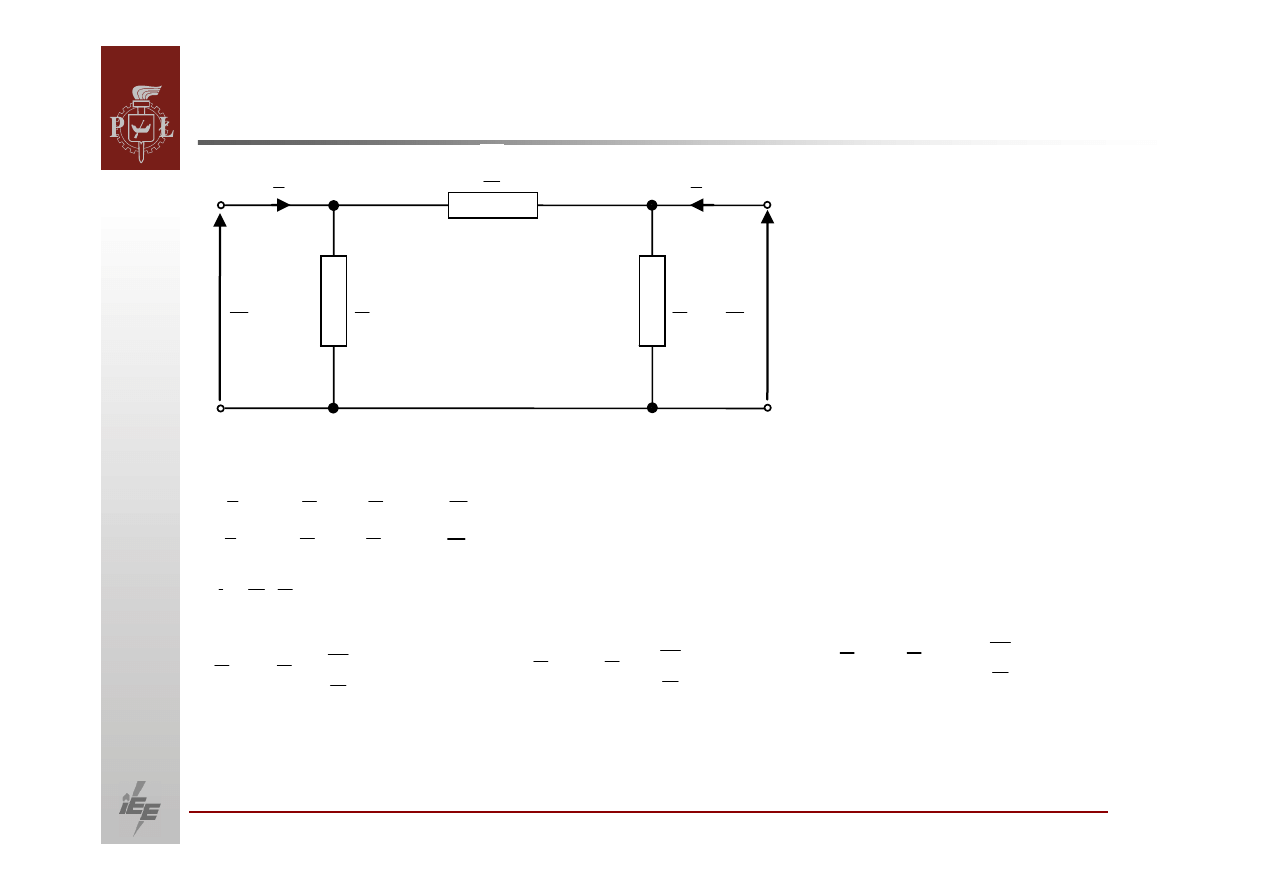
Obliczenia w sieci wielonapięciowej

Z

n

I

m

I

n

Y

m

Y

n

m

n

U

m

U

Równanie potencjałów węzłowych tego elementu jest postaci: 

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

m

n

mm

mn

nm

nn

m

n

U

U

Y

Y

Y

Y

I

I

U

Y

I

⋅

=

Z

Y

Y

n

nn

1

+

=

Z

Y

Y

m

mm

1

+

=

Z

Y

Y

mn

nm

1

−

=

=

20

OBLICZANIE PRZEPŁYWÓW MOCY. 

Obliczenia w sieci wielonapięciowej

Załóżmy, że węzły n oraz m chcemy mieć

na innym poziomie napięcia: 

n

n

n

U

U

ϑ

⋅

=

′

m

m

m

U

U

ϑ

⋅

=

′

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

′

′

m

n

m

n

m

n

U

U

U

U

ϑ

ϑ

0

0

U

T

U

⋅

=

'

⎥

⎦

⎤

⎢

⎣

⎡

=

m

n

ϑ

ϑ

0

0

T

Zależność

między prądami węzłowymi na starym i nowym poziomie napięcia 

będą

postaci: 

( )

( )

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

−

∗

−

∗

m

n

m

n

m

n

I

I

I

I

1

1

'

'

0

0

ϑ

ϑ

( )

I

T

I

⋅

=

−

∗ 1

'

21

OBLICZANIE PRZEPŁYWÓW MOCY. 

Obliczenia w sieci wielonapięciowej

Wyjściowe równanie potencjałów węzłowych przeliczamy na nowe poziomy 
napięć

następująco: 

( )

( )

( )

U

T

T

Y

T

I

T

⋅

⋅

⋅

⋅

=

⋅

−

−

∗

−

∗

1

1

1

otrzymując: 

'

'

'

U

Y

I

⋅

=

( )

( )

1

1

'

−

−

∗

⋅

⋅

=

T

Y

T

Y

∗

⋅

⋅

=

T

Z

T

Z

'

lub po odwróceniu macierzy        : 

'

Y

Podstawiając elementy macierzy admitancyjnej otrzymamy macierz 
admitancyjną

sieci sprowadzoną: 

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

⋅

⋅

⋅

⋅

⋅

⋅

=

∗

∗

2

2

'

1

1

1

1

m

m

m

m

n

n

m

m

n

m

n

n

n

n

Y

Y

Y

Y

ϑ

ϑ

ϑ

ϑ

ϑ

ϑ

Y

22

OBLICZANIE PRZEPŁYWÓW MOCY. 

Obliczenia w sieci wielonapięciowej

Powyższa macierz jest niesymetryczna, nie posiada, więc swego odpowiednika
w postaci obwodu elektrycznego pasywnego jak wyjściowa macierz 
admitancyjna. 

Gdy przekładnie sprowadzenia są

liczbami rzeczywistymi to: 

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

⋅

⋅

⋅

⋅

⋅

⋅

=

2

2

'

1

1

1

1

m

m

m

m

n

n

m

m

n

m

n

n

n

n

Y

Y

Y

Y

ϑ

ϑ

ϑ

ϑ

ϑ

ϑ

Y

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎣

⎡

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

⋅

−

⋅

⋅

−

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

2

2

'

1

1

1

1

1

1

1

1

m

m

m

n

m

n

n

n

Z

Y

Z

Z

Z

Y

ϑ

ϑ

ϑ

ϑ

ϑ

ϑ

Y

Macierz admitancyjna

sieci sprowadzana jest teraz symetryczna. 

Gdy: 

ϑ

ϑ

ϑ

=

=

m

n

23

OBLICZANIE PRZEPŁYWÓW MOCY. 

Obliczenia w sieci wielonapięciowej

Macierz admitancyjna

sieci sprowadzona jest postaci: 

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

−

⋅

−

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

2

2

2

2

'

1

1

1

1

1

1

1

1

ϑ

ϑ

ϑ

ϑ

Z

Y

Z

Z

Z

Y

m

n

Y

Typowym wariantem przekształcenia sprowadzenia, jest jego zastosowanie 
dla gałęzi z transformatorem. Założono, że impedancje gałęzi obliczono na 
poziomie napięcia węzła n a przekładnia

transformatora zdefiniowano, jako: 

m

n

T

U

U

=

ϑ

Wtedy mamy: 

1

=

n

ϑ

T

m

ϑ

ϑ

1

=

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

−

⋅

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

∗

2

'

1

1

1

1

T

m

T

T

n

Z

Y

Z

Z

Z

Y

ϑ

ϑ

ϑ

Y

24

OBLICZANIE PRZEPŁYWÓW MOCY. 

Obliczenia w sieci wielonapięciowej

W przypadku, gdy zainstalowany transformator posiada tylko regulację
podłużną, tzn.: 

T

T

ϑ

ϑ

=

Macierz admitancyjna

tej gałęzi wyraża się

wzorem: 

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

−

⋅

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

2

'

1

1

1

1

T

m

T

T

n

Z

Y

Z

Z

Z

Y

ϑ

ϑ

ϑ

Y

Moc w gałęzi łączącej węzły m oraz n wynosi:

∗

∗

∗

∗

∗

⋅

+

⋅

⋅

−

=

n

n

T

m

n

n

n

Y

U

Z

U

U

Z

U

S

2

2

ϑ

2

2

2

2

T

m

m

T

n

m

T

m

m

Y

U

Z

U

U

Z

U

S

ϑ

ϑ

ϑ

⋅

⋅

+

⋅

⋅

−

⋅

=

∗

∗

∗

∗