1

SYSTEMY ELEKTROENERGETYCZNE 

Rozdział

4

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO

Łódź, 2011 rok

Andrzej Kanicki

2

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Pojęcia stabilności

Stabilność

lokalna systemu elektroenergetycznego (SE) to stabilność

jego pracy

podczas małych zakłóceń. 
Do tych zakłóceń

można zaliczyć: 

1.

załączanie, wyłączanie małych odbiorów, 

2.

załączanie, wyłączanie pojedynczych generatorów, 

3.

załączanie, wyłączanie pojedynczych linii,

4.

działanie układów regulacji napięcia i częstotliwości. 

Definicja stabilności
Rozwiązanie          równania różniczkowego lub układu równań

różniczkowych

nazywamy stabilnym (stabilnym

w sensie Lapunowa), jeżeli dla dowolnego 

i

dowolnego

czasu      można dobrać

taką

liczbę

, że dla wszystkich 

punktów startowych spełniających ograniczenie: 

zachodzi: 

dla każdego         .

( )

t

x

1

0

>

ε

0

t

η

η

<

−

)

(

)

(

0

1

0

2

t

x

t

x

ε

<

−

)

(

)

(

1

2

t

x

t

x

0

t

t

>

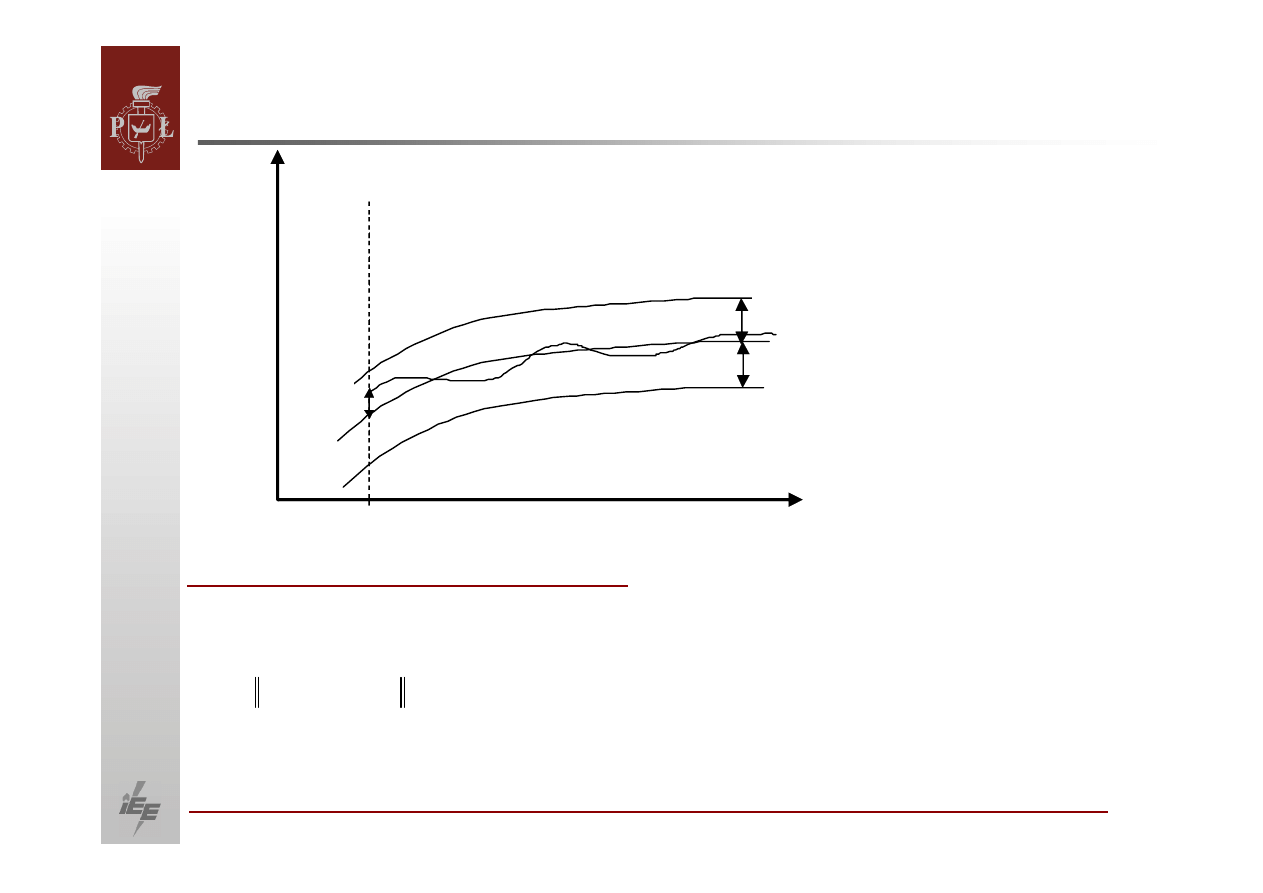
3

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Pojęcia stabilności

t

0

t

ε

ε

η

( )

t

x

Definicja stabilności asymptotycznej
Rozwiązanie          równania różniczkowego lub układu równań

różniczkowych 

nazywamy stabilnym asymptotycznie, jeżeli jest stabilne a ponadto: 

( )

t

x

1

0

)

(

)

(

lim

0

1

0

2

=

−

∞

→

t

x

t

x

t

4

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Pojęcia stabilności

Załóżmy, że system elektroenergetyczny opisano za pomocą

układu równań

różniczkowych nieliniowych postaci: 

Niech       będzie punktem, dla którego mamy: 

Funkcję

nieliniową

możemy zlinearyzować

w pewnym otoczeniu punktu 

. W tym celu funkcję

rozwiniemy w szereg Taylora do postaci: 

W wyniku pominięcia reszty z rozwinięcia w szeregu Taylora otrzymaliśmy 
opis naszego obiektu za pomocą

układu równań

różniczkowych liniowych 

postaci: 

)

(X

F

X =

dt

d

r

X

0

)

(

=

r

X

F

)

(X

F

r

X

)

(X

F

)

(

)

(

X

R

X

A

X

F

+

⋅

=

X

A

X

⋅

=

dt

d

5

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Pojęcia stabilności

gdzie: 

Powyższe równanie jest przybliżeniem liniowym układu równań

różniczkowych 

nieliniowych a cała operacja operacją

linearyzacji. 

Do równania nieliniowego i jego przybliżenia liniowego słuszne są

następujące 

twierdzenia tzw. pierwszej metody Lapunowa. 
Twierdzenie 1
Układ równań

różniczkowych nieliniowych jest stabilny asymptotycznie 

lokalnie tzn. w otoczeniu punktu linearyzacji, jeśli jego przybliżenie liniowe jest 

stabilne asymptotycznie. 
Twierdzenie 2
Układ równań

różniczkowych nieliniowych jest niestabilny jeśli jego 

przybliżenie liniowe jest niestabilne. 

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎣

⎡

=

=

n

n

n

n

x

f

x

f

x

f

x

f

d

d

∂

∂

∂

∂

∂

∂

∂

∂

L

M

O

M

L

1

1

1

1

X

F

A

6

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Pojęcia stabilności

Twierdzenie 3
O stabilności układu równań

różniczkowych nieliniowych nie można nic 

wnioskować

jeśli jego przybliżenie liniowe jest stabilne ale nie asymptotycznie. 

Musimy rozważyć

problem czy układ równań

różniczkowych liniowych 

jest stabilny. 
W tym celu musimy obliczyć

wartości własne      macierzy    .  

Znając wartości własne możemy rozwiązanie układu równań

różniczkowych 

liniowych zapisać

jako: 

O stabilności rozważanego układu równań

różniczkowych liniowych możemy 

wnioskować

w oparciu o poniższe twierdzenie. 

i

λ

A

0

)

(

det

=

⋅

−

1

A

i

λ

( )

∑

=

⋅

=

n

j

t

ij

i

i

e

a

t

x

1

λ

7

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Pojęcia stabilności

Twierdzenie 4
Układ równań

różniczkowych liniowych jest stabilny wtedy i tylko wtedy, kiedy 

wszystkie wartości własne macierzy     mają

niedodatnie części rzeczywiste. 

Twierdzenie 5
Układ równań

różniczkowych liniowych jest stabilny asymptotycznie wtedy i 

tylko wtedy, kiedy wszystkie wartości własne macierzy     mają

ujemne części 

rzeczywiste. 

A

A

8

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Model matematyczny systemu elektroenergetycznego 

Należy określić

układ równań

różniczkowych opisujących system

elektroenergetyczny w

stanach

przejściowych. 

Podstawą

określenia przybliżonego modelu matematycznego systemu 

elektroenergetycznego będzie analiza stałych czasowych przebiegów 

powstających w stanach przejściowych. Najprostszy model musi 

uwzględniać

zjawiska o najdłuższej stałej czasowej pomijając zjawiska 

o

krótkich

stałych czasowych czyli zakładamy, że zjawiska te są

bezinercyjne. 

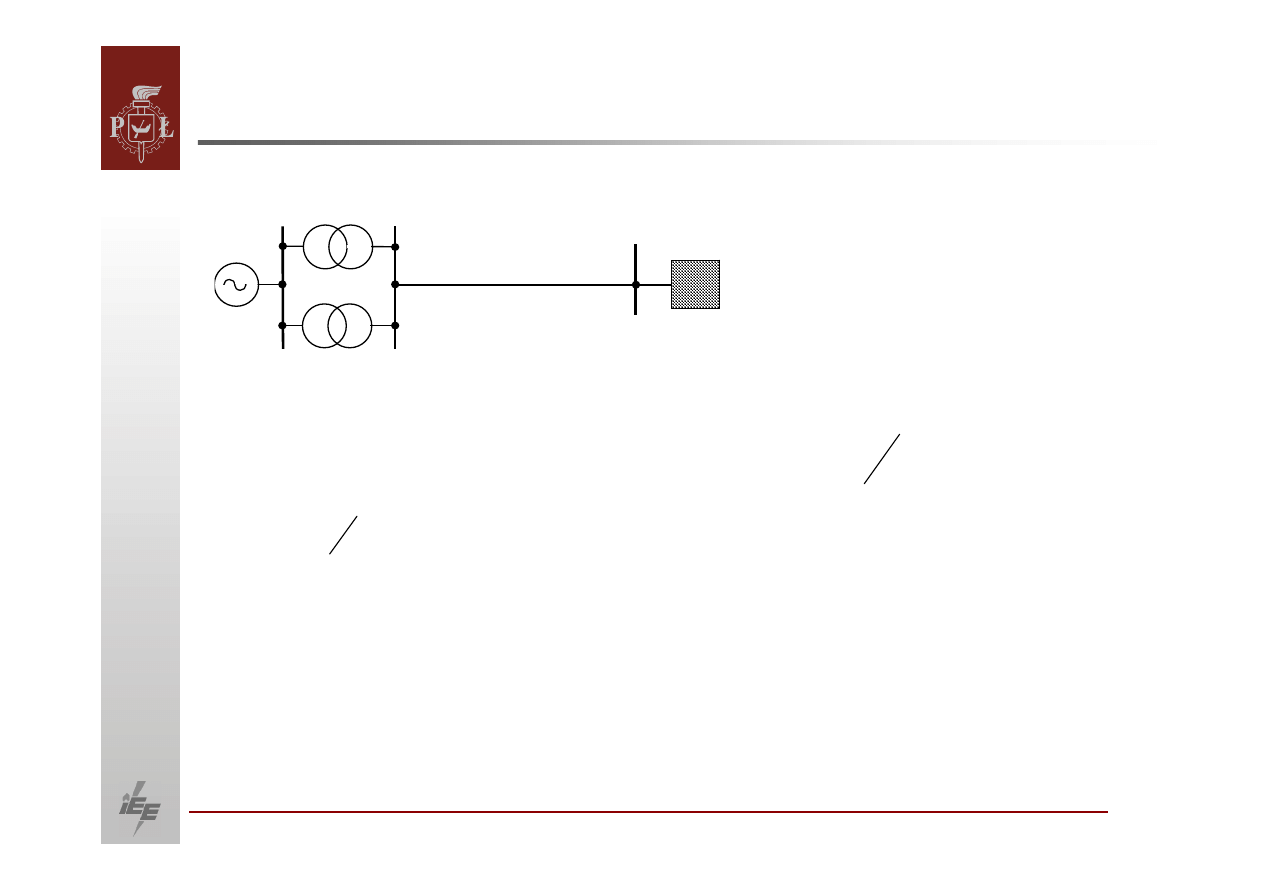
W wysokonapięciowym

systemie elektroenergetycznym mamy do czynienia 

z

dwoma

rodzajami elementów: 

1.

urządzenia przesyłowo‐rozdzielcze, stała czasowa składowej aperiodycznej     

nie większa niż

0,2 s, i nie wywołuje znaczących momentów działających na 

wał

generatora, 

2.

generatory, w których można wyróżnić

następujące elementy wraz z ich 

stałymi czasowymi: 

•

uzwojenia stojana, których stała czasowa składowej aperiodycznej jest 

nie większa niż

0,2s, 

•

uzwojenia tłumiące, stała czasowa      nie większa niż

0,2 s, 

"

d

T

9

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Model matematyczny systemu elektroenergetycznego

•

uzwojenia wzbudzenia, stała czasowa                         ,

•

wirująca masa wirnika, stała czasowa                        . 

s

T

d

)

6

,

0

6

(

÷

=

′

s

T

m

)

12

4

(

÷

=

W pierwszym przybliżeniu, będziemy modelować

generator jako układu równań

różniczkowych opisujących dynamikę

mas wirujących wirnika. 

Energia kinetyczna mas wirujących       jest zdefiniowana wzorem: 

Zgodnie z zasadą

zachowania energii mamy, że w każdej chwili zamianie mocy

działających na wirnik a więc mocy mechanicznej        i elektrycznej  
towarzyszy zmiana energii kinetycznej, czyli: 

k

E

2

2

ω

⋅

=

J

E

k

m

P

e

P

e

m

k

P

P

t

d

E

d

−

=

ei

mi

i

i

i

P

P

t

d

d

J

−

=

⋅

⋅

ω

ω

10

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Model matematyczny systemu elektroenergetycznego

Mamy także: 

t

d

d

i

i

δ

ω

=

mi

i

mi

M

P

⋅

=

ω

ei

i

ei

M

P

⋅

=

ω

oraz fakt występowania momentu (mocy) tłumiącego           to otrzymamy: 

Di

M

Di

ei

mi

i

i

M

M

M

dt

d

J

−

−

=

⋅

2

2

δ

Równanie ruchu obrotowego wirnika i‐tego generatora zapiszemy też

jako

układ równań: 

i

i

dt

d

ω

δ

=

Di

ei

mi

i

i

M

M

M

dt

d

J

−

−

=

⋅

ω

lub 

dt

d

D

P

P

dt

d

J

i

i

ei

mi

i

i

i

δ

ω

ω

⋅

−

−

=

⋅

⋅

11

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Model matematyczny systemu elektroenergetycznego

Moment bezwładności wirnika generatora można wyrazić

w funkcji 

mechanicznej stałej czasowej      :

m

T

2

S

N

m

S

T

J

ω

⋅

=

Mechaniczna stała czasowa ma interpretację

fizyczną. Jeśli pominiemy 

tłumienie i do nieruchomego wirnika nieobciążonego generatora przyłożymy 

znamionowy moment turbiny to przyspieszenie wirnika jest następujące: 

W skutek działania takiego przyspieszenia prędkość

rośnie liniowo i po czasie 

wirnik generatora uzyskuje prędkość

synchroniczną. 

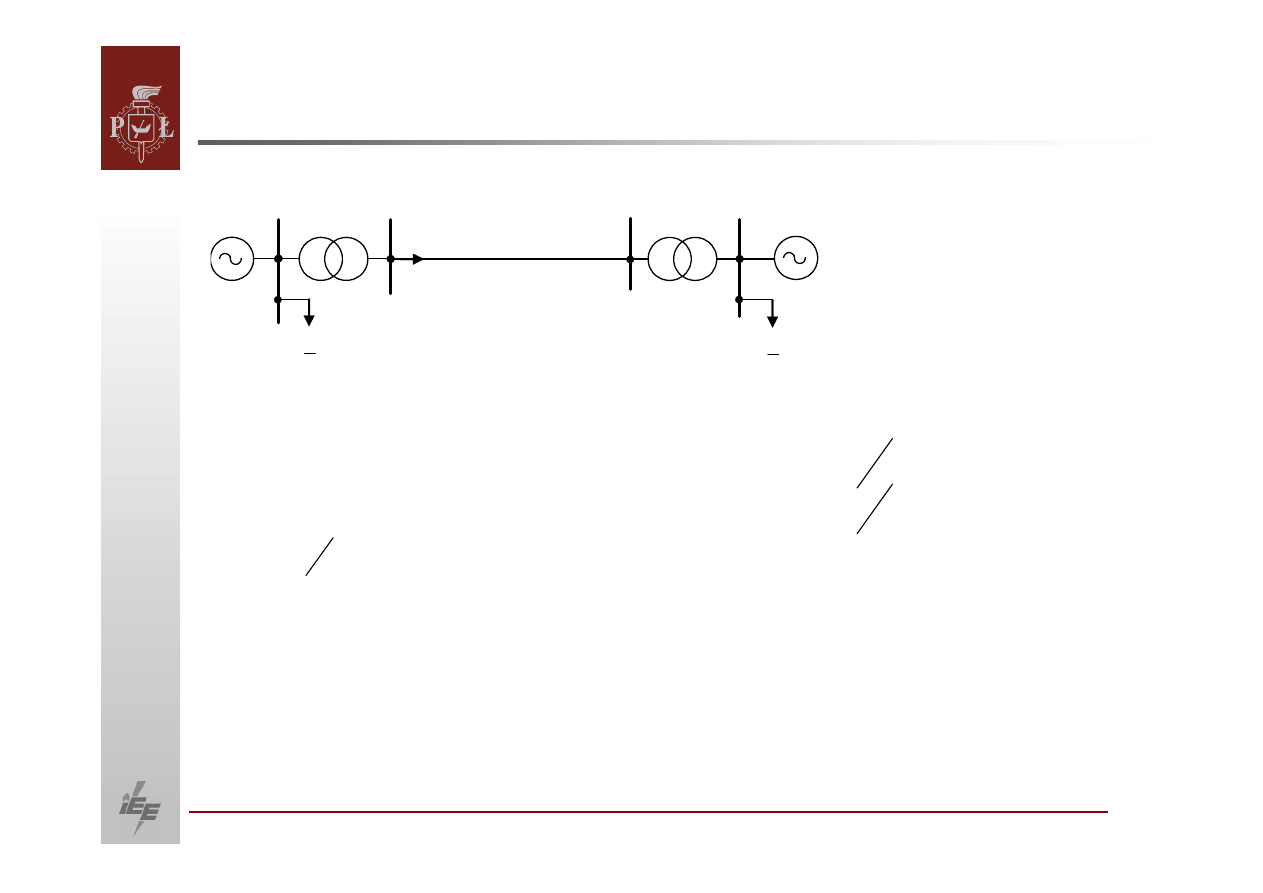
W przypadku rozważania najprostszego układu pracy generatora, układu 

generator‐sieć

sztywna równanie ruchu wirnika generatora są

postaci:

m

S

mN

mN

S

m

S

S

mN

N

m

S

S

T

M

M

T

M

S

T

dt

d

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

δ

ε

=

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

=

=

2

2

m

T

t

=

dt

d

D

)

sin(

Z

U

E

sin

Z

E

P

dt

d

J

i

i

ii

i

s

di

ii

di

mi

i

i

i

δ

α

δ

α

δ

ω

⋅

−

−

⋅

⋅

−

⋅

−

=

⋅

⋅

2

2

2

12

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Model matematyczny systemu elektroenergetycznego

Przy pominięciu rezystancji w obwodzie mamy:

Kołysania wirnika generatora przy chwilowym zaburzeniu bilansu mocy

czynnej

Wprowadzimy pojęcie współczynnika bezwładności:

Wtedy równanie ruchu wirnika generatora ma postać: 

Pierwszy składnik powyższego równania możemy zapisać: 

dt

d

D

X

U

E

P

dt

d

J

i

i

i

s

di

mi

i

i

i

δ

δ

δ

ω

⋅

−

⋅

⋅

−

=

⋅

⋅

sin

2

2

i

i

i

J

M

ω

⋅

=

dt

d

M

D

M

P

P

dt

d

i

i

i

i

ei

mi

i

δ

δ

⋅

−

−

=

2

2

i

i

i

i

ei

i

mi

ei

H

d

dP

P

P

P

δ

Δ

δ

Δ

δ

Δ

⋅

=

⋅

=

=

−

13

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania wirnika generatora

Równanie ruchu wirnika generatora linearyzujemy wokół

rozważanego 

pewnego kąta początkowego                       . Uwzględniając to mamy:

lub w postaci:

gdzie:

Ogólne rozwiązanie równania ruchu wirnika generatora i jego pochodne są

postaci:

0

)

0

(

δ

δ

Δ

=

=

t

0

2

2

=

⋅

+

⋅

+

i

i

i

i

i

i

i

M

H

dt

d

M

D

dt

d

δ

Δ

δ

Δ

δ

Δ

0

2

2

=

⋅

+

⋅

+

i

i

i

i

i

h

dt

d

d

dt

d

δ

Δ

δ

Δ

δ

Δ

i

i

i

M

D

d

=

i

i

i

M

H

h

=

t

e

A

λ

δ

Δ

⋅

=

t

e

A

dt

d

λ

λ

δ

Δ

⋅

⋅

=

t

e

A

dt

d

λ

λ

δ

Δ

⋅

⋅

=

2

2

2

14

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania wirnika generatora

Po podstawieniu tych funkcji do równania ruch wirnika generatora 

otrzymujemy: 

Równanie to nazywane jest równaniem charakterystycznym równania ruch 

wirnika generatora. 
Rozwiązania tego równania są

następujące: 

Powyższe wielkości to wartości własne układu. 
W zależności od wartości wyrażenia pod pierwiastkiem, wartości własne      

oraz        mogą

być

rzeczywiste lub zespolone. 

Rozwiązanie równania różniczkowego jest postaci: 

0

2

=

+

⋅

+

h

d

λ

λ

2

4

2

4

2

2

2

1

h

d

d

h

d

d

⋅

−

+

−

=

⋅

−

−

−

=

λ

λ

1

λ

2

λ

t

t

e

A

e

A

2

1

2

1

λ

λ

δ

Δ

⋅

+

⋅

=

15

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania wirnika generatora

Musimy teraz wyznaczyć

stałe      i       .

W wyniku rozwiązania powyższego układu równań

mamy: 

Ogólna postać

rozwiązania: 

Zakładając, że:

Wartości własne są

zmiennymi zespolonymi o postaci: 

1

A

2

A

0

2

2

1

1

0

2

1

=

⋅

+

⋅

=

+

A

A

A

A

λ

λ

δ

1

2

1

0

2

1

2

2

0

1

λ

λ

λ

δ

λ

λ

λ

δ

−

⋅

−

=

−

⋅

=

A

A

(

)

t

t

e

e

2

1

2

1

2

0

1

λ

λ

λ

λ

λ

λ

δ

δ

Δ

⋅

−

⋅

⋅

−

=

0

>

d

h

d

⋅

< 4

2

w

w

j

j

ω

α

λ

ω

α

λ

+

−

=

−

−

=

2

1

2

4

2

2

d

h

d

w

−

⋅

=

=

ω

α

16

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Model matematyczny systemu elektroenergetycznego

Rozważymy wszystkie możliwe przypadki tego rozwiązania: 

1.

gdy 

9 gdy 

9 gdy

Wartości własne  oraz  są

teraz zmiennymi rzeczywistymi. 

2.

gdy

Wartości własne są

teraz zmiennymi rzeczywistymi a rozwiązanie

ma 

postać: 

Kąt     rośnie aperiodycznie a więc taki punkt jest punktem niestabilnym. 

0

>

h

0

>

h

h

d

⋅

< 4

2

(

)

(

)

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⋅

+

⋅

⋅

⋅

=

−

t

t

e

w

w

w

t

ω

ω

α

ω

δ

δ

Δ

α

sin

cos

0

h

d

⋅

> 4

2

0

0

2

1

<

<

λ

λ

0

<

h

0

0

2

1

>

<

λ

λ

δ

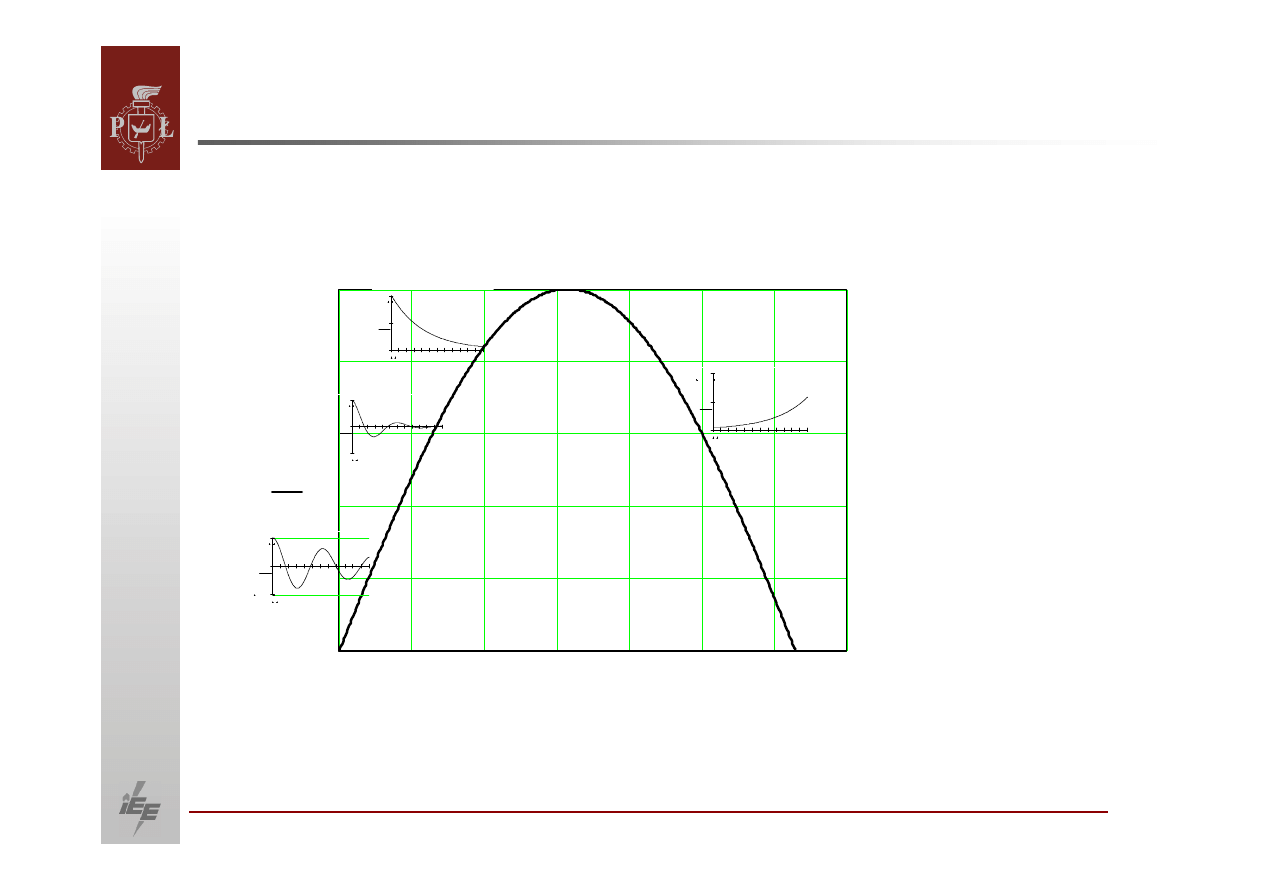
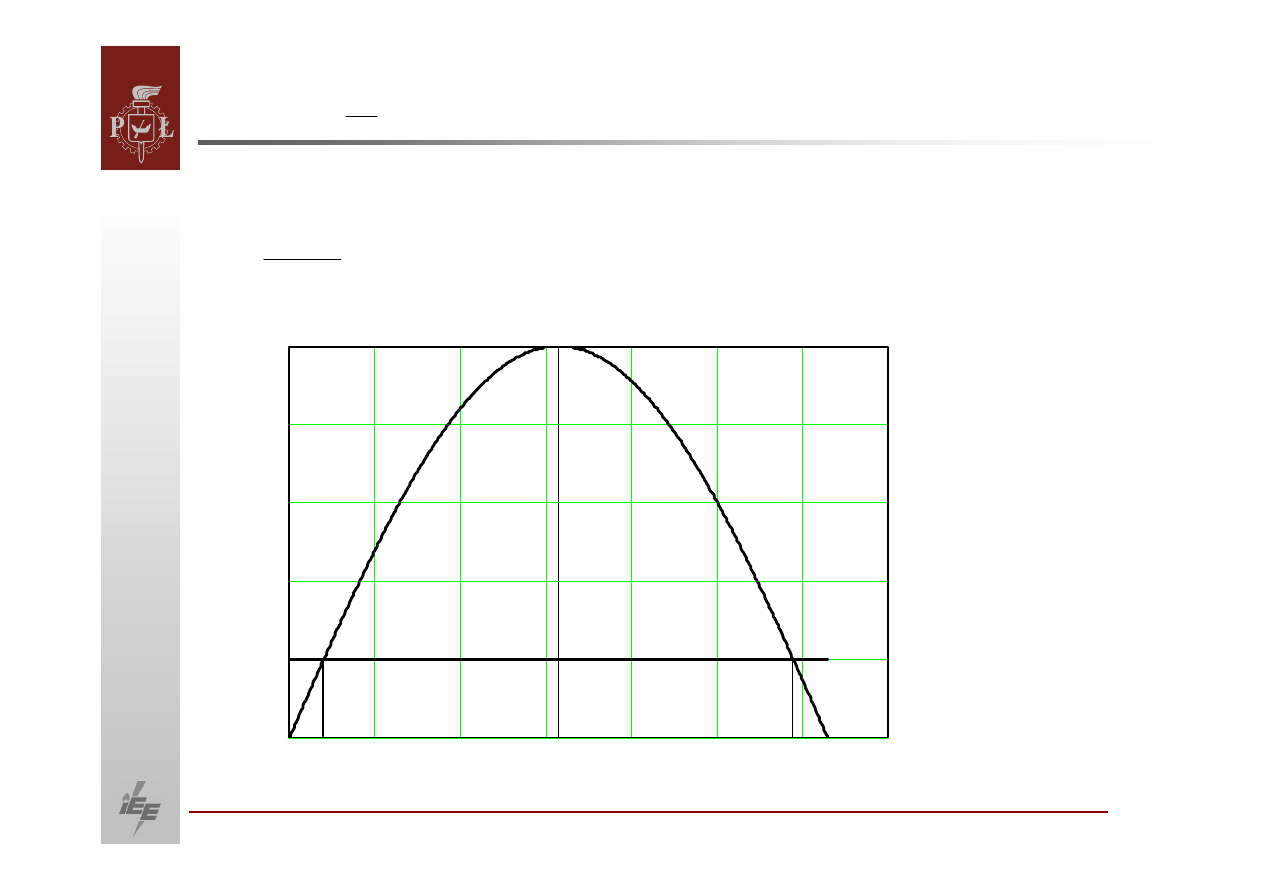
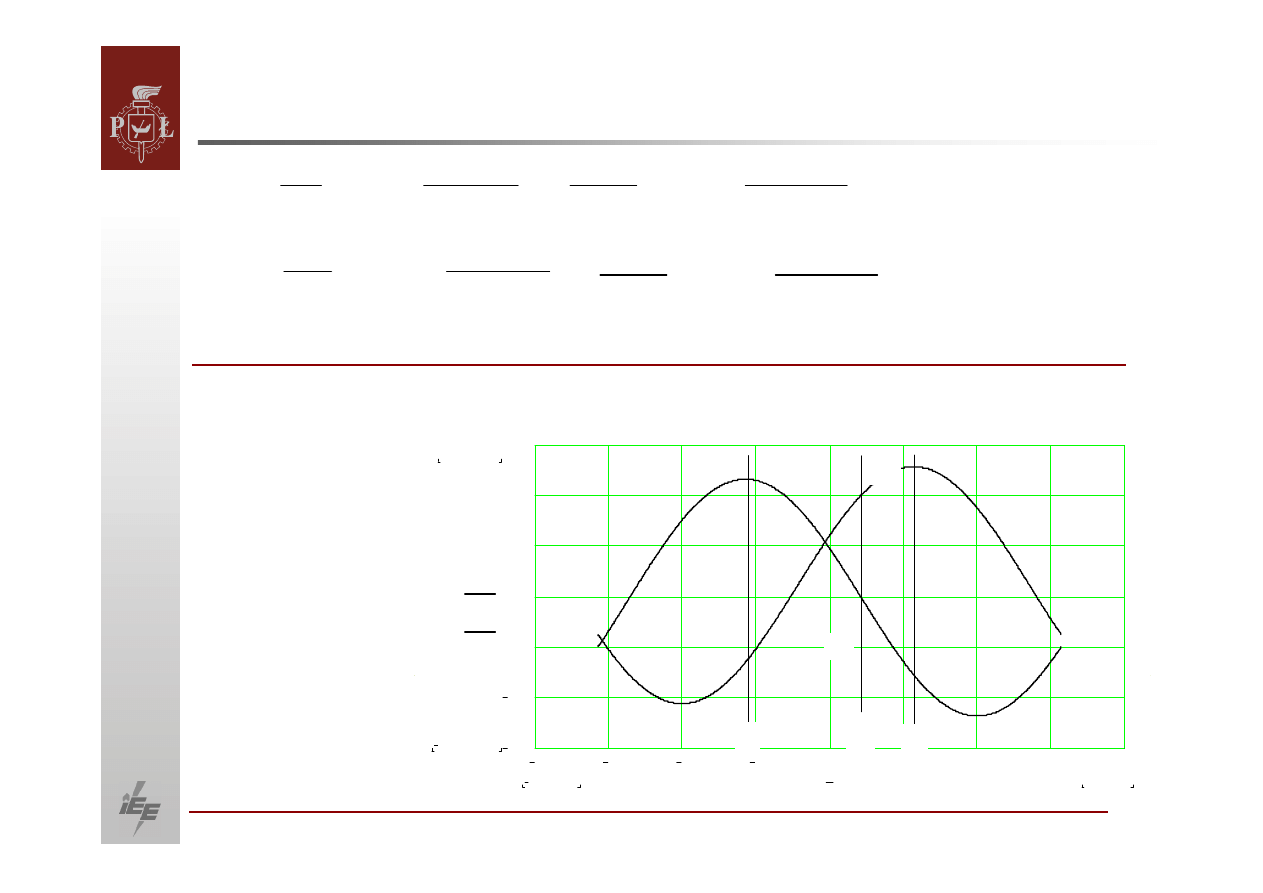
17

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Model matematyczny systemu elektroenergetycznego

Przykładowe przebiegi kąta po małym zakłóceniu w różnych punktach pracy 

generatora. 

0

0.5

1

1.5

2

2.5

3

3.5

0

1

2

3

4

5

P1

i

δ i⋅

1

0.781

−

δ

i

1

0

α i⋅

1

0

δ

i

12

0

α i

⋅

20.086

0

δ

i

12

0

α i

⋅

1

1

−

δ

i

12

0

α i

⋅

18

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

δ

d

P

d

W przypadku rozważenia układu generator – sieć

sztywna pominiemy w 

pierwszym etapie rezystancje układu. Wtedy:

δ

sin

⋅

⋅

=

E

s

g

e

X

U

E

P

A

B

0

δ

m

P

0

δ

Π

−

e

P

δ

gr

δ

0

0.5

1

1.5

2

2.5

3

3.5

0

1

2

3

4

5

P1

i

P2

i

δ i

P

19

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

δ

d

P

d

W przypadku, gdy momenty mechaniczny jest równy mocy 

elektromagnetycznej tzn. 

wirnik obraca się

ze stałą

prędkością

obrotową. 

Gdy 

to wirnik zmniejsza lub zwiększa swoją

prędkość. 

W pewnej chwili został

dołączony do rozpatrywanej sieci nowy odbiór o mocy , 

przy czym odbiór ten jest załączony na pewien krótki czas – załączenie to ma 

charakter zakłócenia. Wtedy 

i

wirnik będzie hamowany czyli zacznie maleć

jego prędkość

obrotowa. 

0

=

+

e

m

M

M

0

=

+

e

m

P

P

0

≠

+

E

m

P

P

e

e

e

P

P

P

Δ

+

=

1

m

e

P

P

>

1

m

e

M

M

>

1

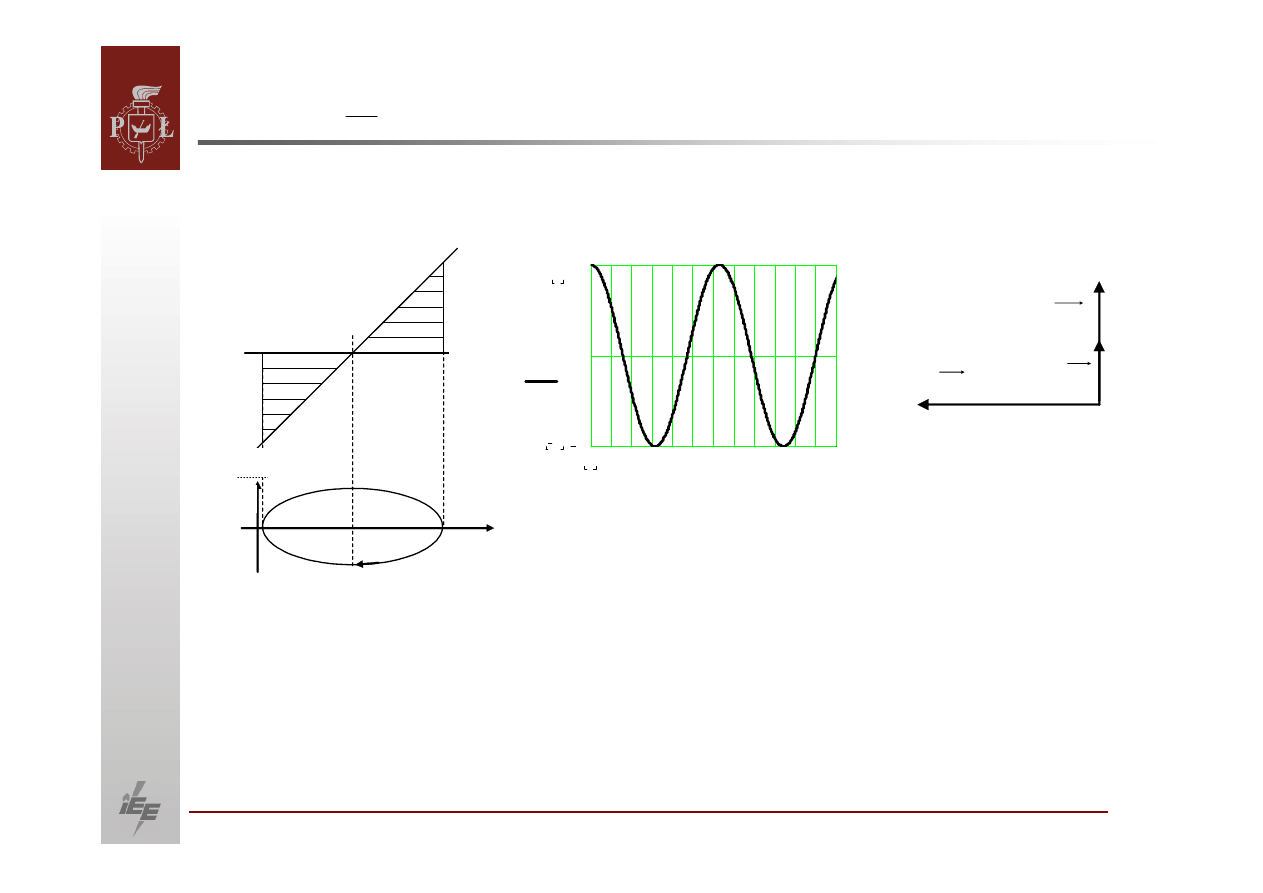
20

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

δ

d

P

d

Mamy teraz dwie różne sytuacje: 

1.

Praca w punkcie A 

Dołączenie dodatkowej mocy powoduje, że generator znajduje się

w

punkcie

2. 

Wirnik będzie hamowany, czyli zacznie maleć

jego prędkość

obrotowa 

wywołując zmniejszenie kąta i

w

konsekwencji

zmniejszenie mocy 

przesyłanej z generatora do sieci sztywnej zgodnie z charakterystyką. 

A

2

3

4

5

m

P

e

P

ω

δ

a)

b)

1

1

P1

i

12

0

δ i.

1

0

1

ω

Δ

e

P

Δ

δ

Δ

21

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

Wtedy moc niezbilansowana maleje. W punkcie

A moc elektryczna 

i

mechaniczna

są

sobie równe, lecz ruch wirnika nie zostanie zatrzymany. 

W trakcie swojej drogi od punktu 2 do A w wirniku została zgromadzona 

pewna ilość

energii kinetycznej hamującej a prędkość

obrotowa jest 

mniejsza od synchronicznej. 
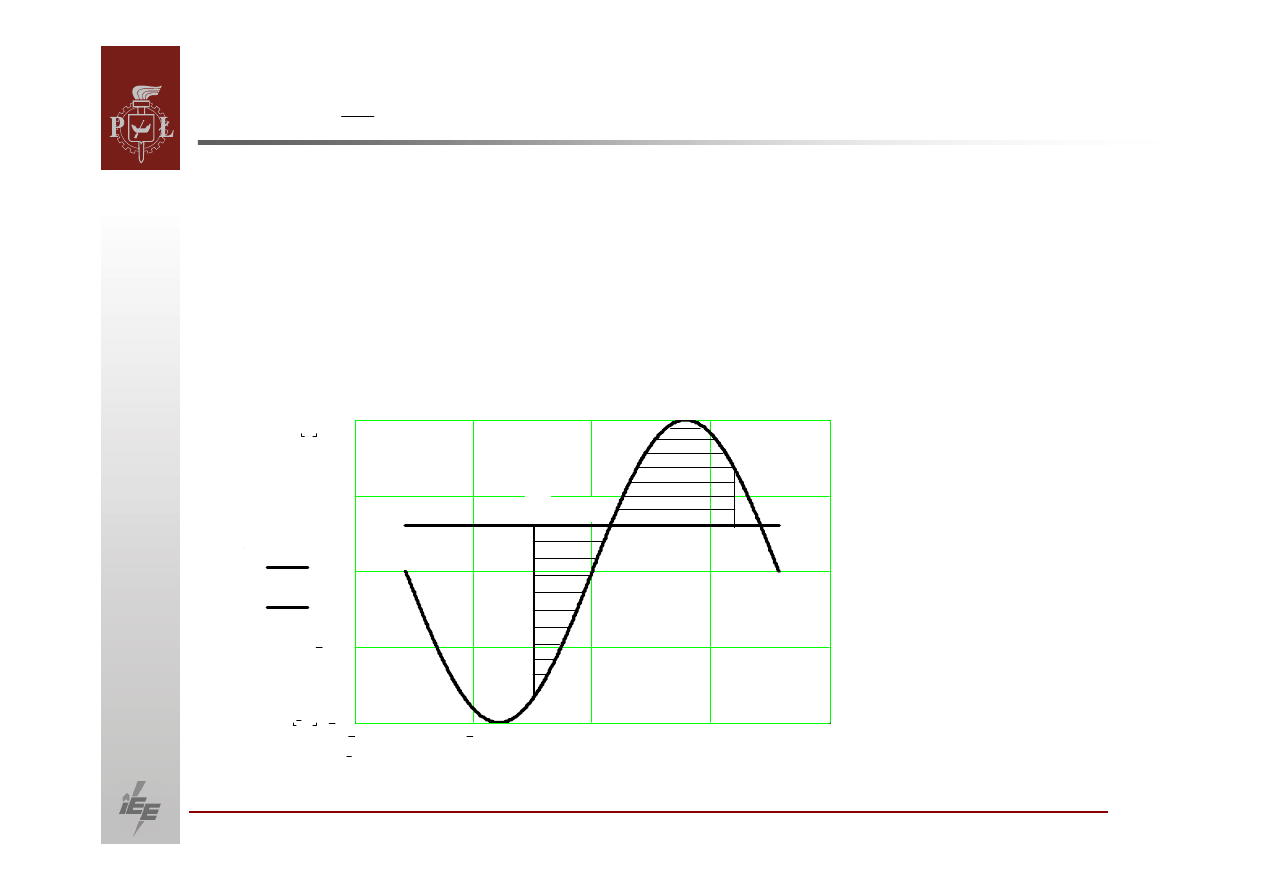
Energia kinetyczna hamująca wynosi: 

Zakładają, że zmiany prędkości obrotowej są

niewiele różne od 

synchronicznej to energia kinetyczna hamując jest proporcjonalna do 

pola powierzchni A, 2, 3. 
Po minięciu punktu A prędkość

zacznie rosnąć. Teraz wirnik wychyli się

do 

punktu 5 gromadząc po drodze energię

kinetyczną

przyspieszającą. 

Położenie punktu 5 wynika z równości

energii kinetycznej hamującej 

i przyspieszającej. Można, więc stwierdzić, że pole powierzchni A, 5, 4 

musi być

równe polu A, 2, 3. 

(

)

∫

⋅

−

=

t

d

P

P

E

e

m

kh

Δ

(

)

(

)

∫

∫

⋅

−

⋅

=

⋅

−

=

δ

ω

δ

ω

Δ

d

P

P

d

P

P

E

e

m

e

m

kh

1

δ

d

P

d

22

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

Ten wywód nosi nazwę

metody równych powierzchni. 

W punkcie 5 zrównały się

energie kinetyczne hamująca i przyspieszająca, 

lecz mamy różnicę

mocy. Moc napędowa jest większa od hamującej i wirnik

będzie przyspieszał

dalej. 

2.

Praca w punkcie B 

1

1

P1

i

Pm

i

4

4

δ j

i

.

4

2

0

2

4

1

0.5

0

0.5

1

A

B

2

3

4

5

δ

d

P

d

23

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

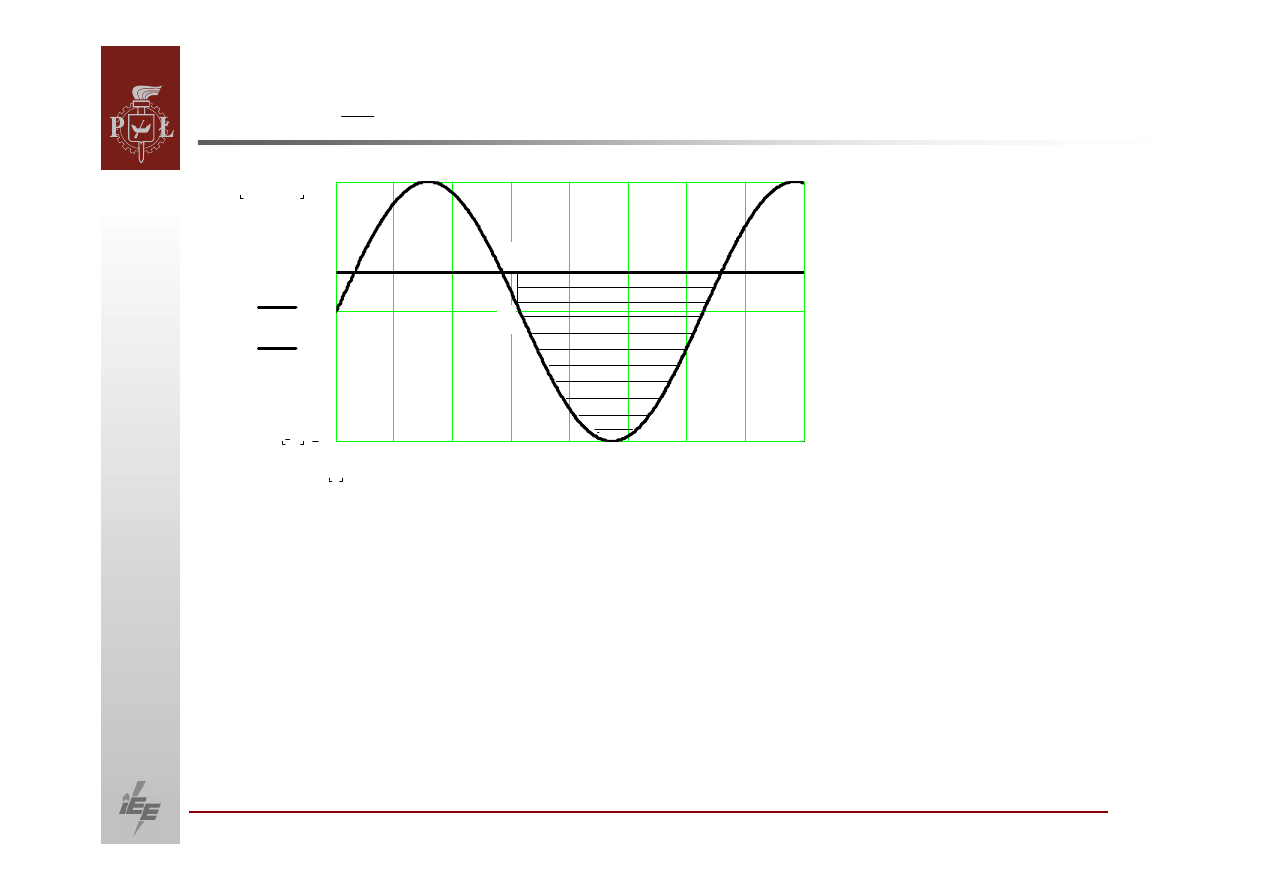
Dołączenie dodatkowej mocy powoduje, że generator znajduje się

w

punkcie

2.

Wirnik będzie hamowany, czyli zacznie maleć

jego prędkość

obrotowa 

wywołując zmniejszenie kąta  i

w

konsekwencji

powiększenie mocy 

przesyłanej z generatora do sieci sztywnej zgodnie z charakterystyką. 
Wtedy moc niezbilansowana 

wzrośnie. W punkcie

A moc elektryczna i

mechaniczna

są

sobie równe, lecz 

ruch wirnika nie zostanie zatrzymany. W trakcie swojej drogi od punktu 2 

do A w wirniku została zgromadzona pewna ilość

energii kinetycznej 

hamującej (pole 3, 2, A) a prędkość

obrotowa jest mniejsza od 

synchronicznej. W tym wypadku ustali jednak się

nowy stabilny punkt 

pracy, punkt A, lecz nie będzie to wyjściowy punkt B. 

Następny przypadek to odłączenie od rozpatrywanej sieci odbioru o mocy 

( )

e

z

e

m

P

P

P

Δ

δ

−

−

e

P

Δ

δ

d

P

d

24

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

0.999995

1

P1

i

Pm

i

8

0

δ i.

0

1

2

3

4

5

6

7

8

1

0

1

A

B

2

3

C

Moc elektryczna jest mniejsza od mocy mechanicznej wirnik będzie 

przyspieszany, czyli zacznie rosnąć

prędkość

obrotowa. 

Powiększenie kąta  powoduje powiększenie mocy przesyłanej z generatora 

do sieci sztywnej. Wtedy moc niezbilansowana wzrośnie co prowadzi do 

destabilizacji pracy maszyny. W tym wypadku nie ustali jednak się

nowy 

stabilny punkt pracy a prędkość

wirnika będzie rosła w nieskończoność. 

δ

d

P

d

25

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

Reasumując powyższe rozważania o zmianach mocy elektrycznej można 

stwierdzić, że:
9Punkt A jest punktem pracy stabilnej.
9Punkt B jest punktem pracy niestabilnej.
9Stabilna praca jest tylko na odcinku, gdzie             . 

9Gdy wartość

praca generatora jest niestabilna. 

9Warunek         jest kryterium określania granicy równowagi statycznej. 

9Granica równowagi statycznej występuje, gdy            . 

Pochodną

mocy po kącie: 

nazywamy mocą

synchronizującą

generatora. Moc synchronizująca jest miarą

zapasu stabilności generatora. 

0

≥

δ

d

dP

0

<

δ

d

dP

δ

d

dP

0

=

δ

d

dP

δ

δ

cos

⋅

⋅

=

E

S

g

X

U

E

d

dP

δ

d

P

d

26

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

Dotychczas analizowano generator, gdy brak jest działania jego regulatorów 

wzbudzenia. Wtedy granicę

równowagi statycznej nazywamy naturalną

granicą

równowagi statycznej. Rozważmy teraz układ, w którym generator jest jednak 

wyposażony w regulator wzbudzenia. Regulator wzbudzenia stara się

utrzymać

stałe napięcie generatora poprzez zmianę

napięcia wzbudzenia 

z

ograniczeniami

wynikającymi z

dopuszczalnego

jego zakresu pracy. 

Rozważany regulator wzbudzenia może być: powolny lub Szybki. 

Jako regulator szybki będziemy uważali taki regulator, który utrzymuje stałą

wartość

napięcia na zaciskach generatora bezpośrednio po zmianie obciążenia. 

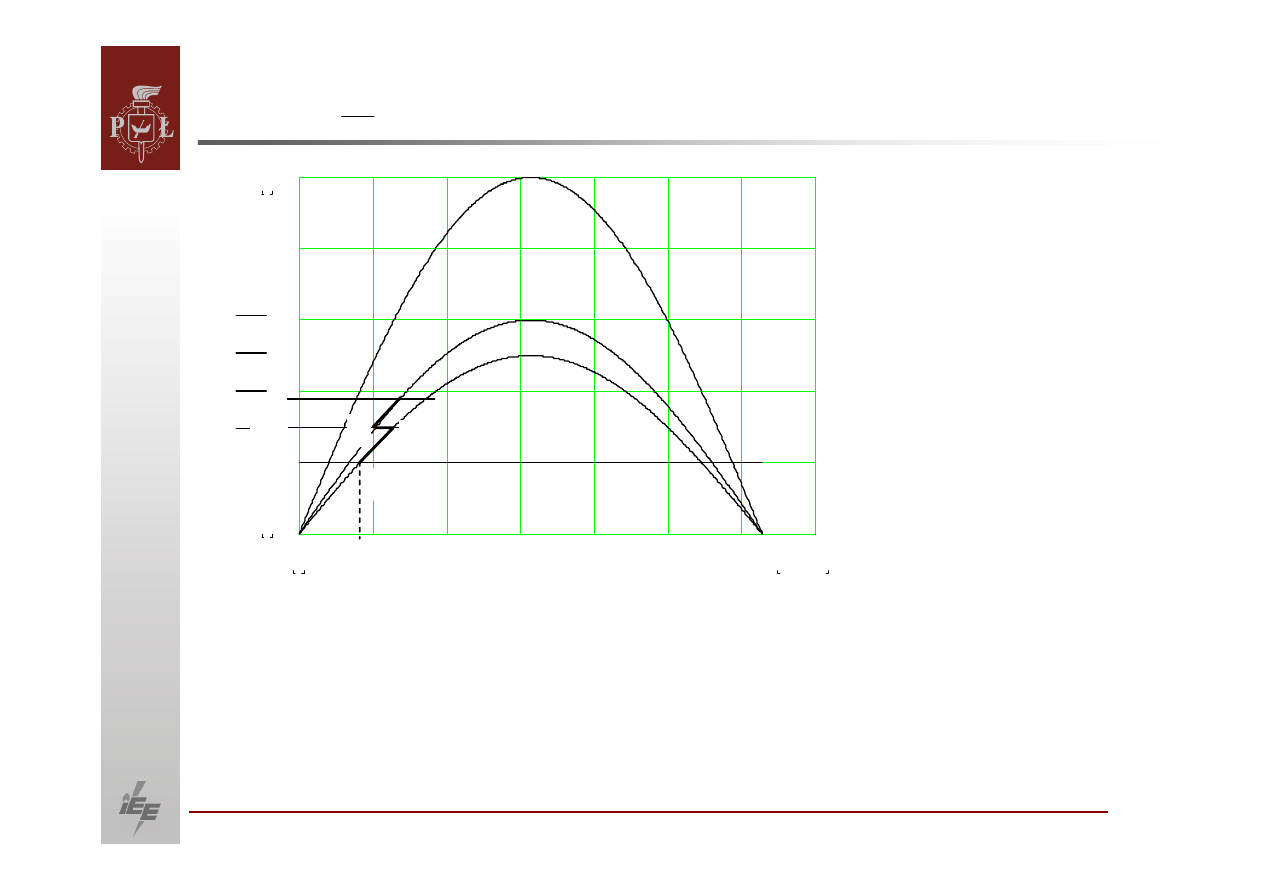
W regulatorze powolnym po zmianie obciążenia z wartości

(punkt A) do 

następuje zmiana kąta zgodnie z wyjściową

charakterystyką

(punkt B) 

a dopiero później regulator zwiększa napięcie wzbudzenia tak, aby napięcie na 

zaciskach generatora było stałe. Zmiana napięcia wzbudzenia powoduje 

powiększenie siły elektromotoryczne generatora w efekcie charakterystyki       .
Generatora znajdzie się

w

punkcie

C. Kolejne etapy pracy są

więc następujące: 

zwiększenie obciążenia przy stałym wzbudzeniu i zwiększenie napięcia 

wzbudzenia. 

0

P

1

P

( )

δ

P

δ

d

P

d

27

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

5

0

P1

i

P3

i

P4

i

P2

i

3.141593

0

δ i.

0

0.5

1

1.5

2

2.5

3

3.5

0

1

2

3

4

5

B

C

A

0

P

1

P

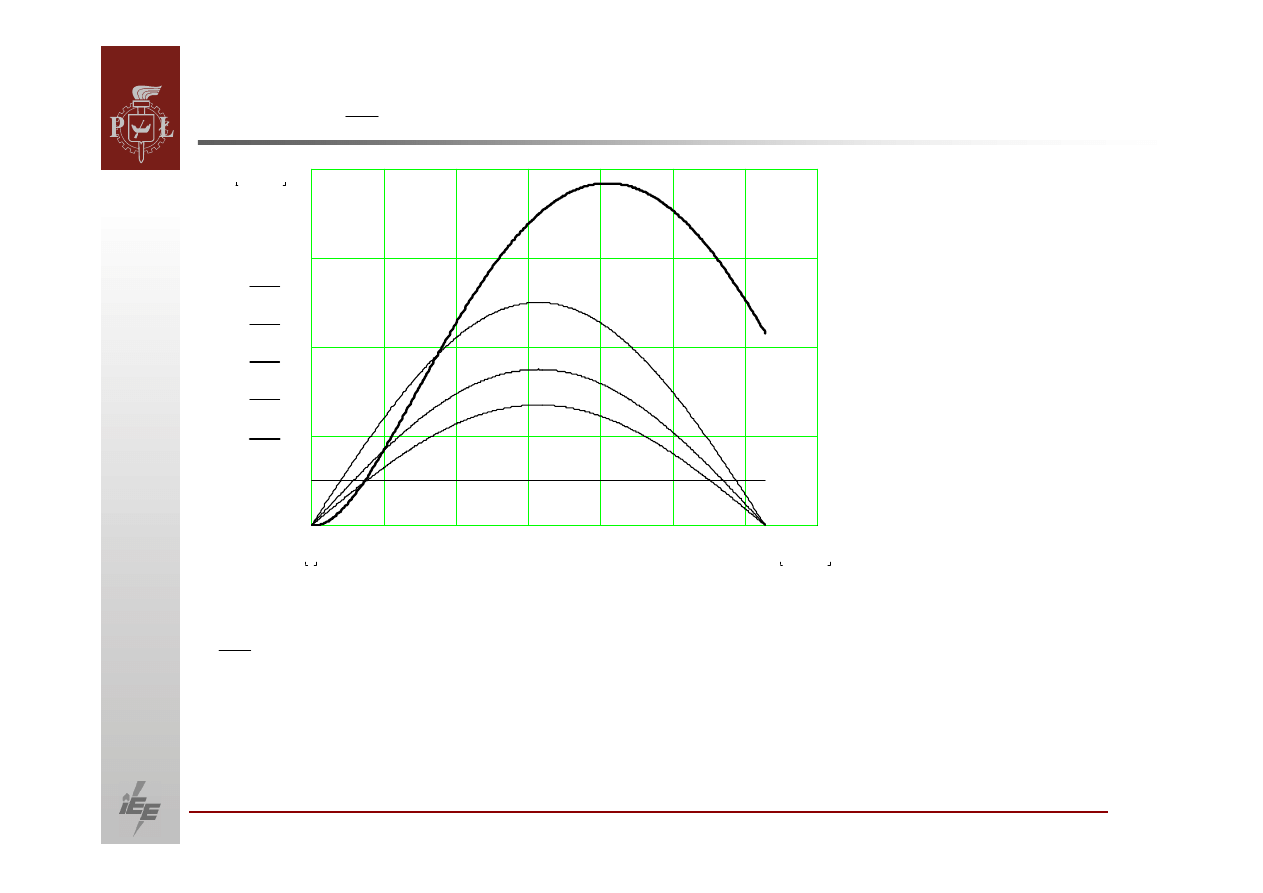
W regulatorze szybkim po zmianie obciążenia następuje natychmiastowa 

zmiana napięcia wzbudzenia tak, że napięcie na zaciskach generatora pozostaje 

stałe. W wyniku zamiast klasycznej zależności mocy czynnej od kąta 

otrzymujemy przebieg jak na rysunku poniżej.

δ

d

P

d

28

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

7.680401

0

P1

i

P3

i

P4

i

P2

i

P6

i

3.141593

0

δ i.

0

0.5

1

1.5

2

2.5

3

3.5

0

2

4

6

8

Warunek 

jest dla niej spełniony przy kącie            . W aktualnie stosowanych 

regulatorach osiąga się

. 

0

=

δ

d

dP

°

> 90

δ

°

≈ 120

δ

δ

d

P

d

29

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

Jest to tzw. sztuczna (dynamiczna) granica równowagi statycznej. Moc 

graniczna jest wtedy większa od mocy granicznej równowagi naturalnej. 
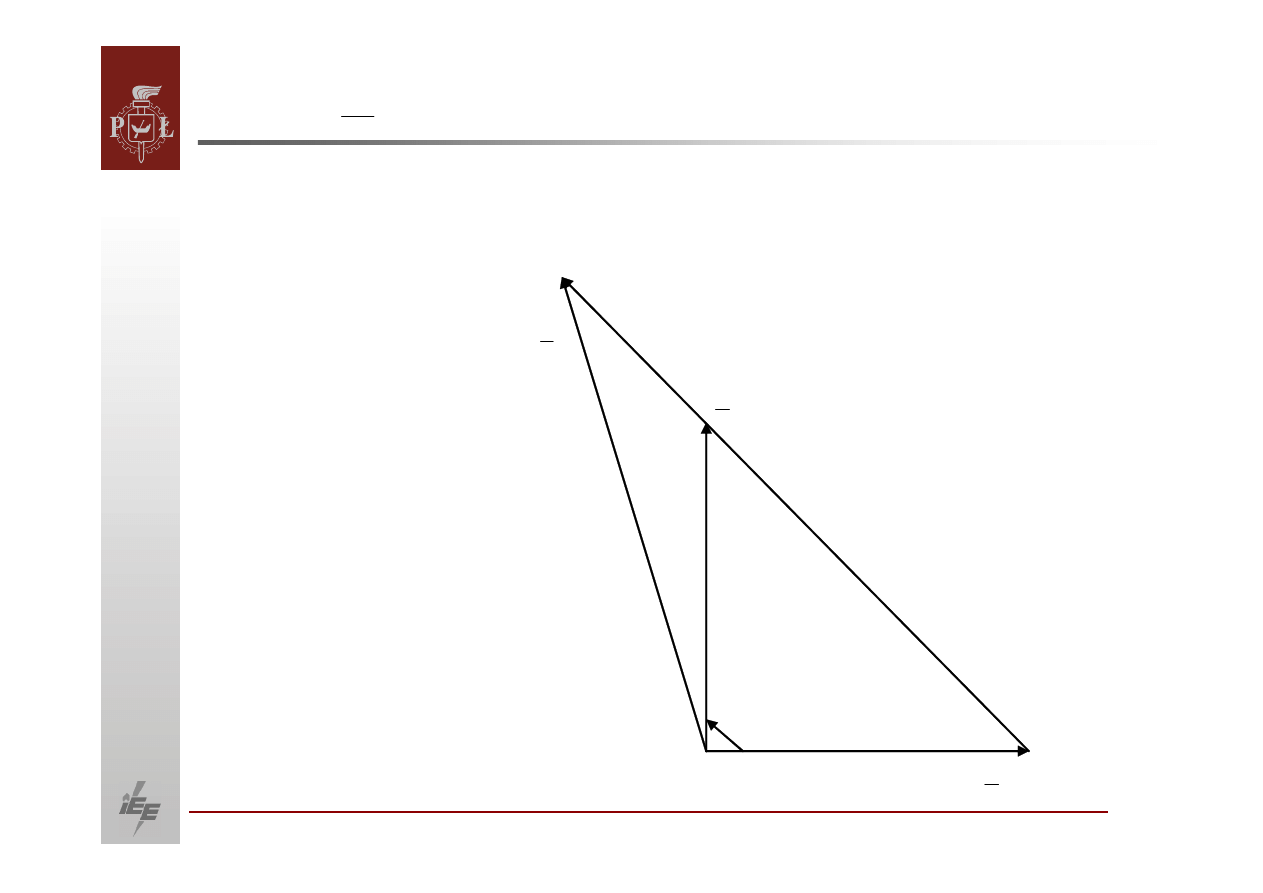
Wykres wskazowy generatora w przypadku występowania sztucznej granicy 

równowagi statycznej. 

g

U

d

E

o

90

S

U

δ

d

P

d

30

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryterium

Z powyższego wykresu wskazowego wynika, że kąt 90 stopni jest tu również

utrzymywany jednak nie pomiędzy siłą

elektromotoryczną

generatora 

i napięciem

sieci sztywnej a pomiędzy napięciem na zaciskach generatora 

i napięciem

sieci sztywnej. 

Określenie punktu pracy względem granicy równowagi definiuje się

przez trzy 

współczynniki zapasu stabilności statycznej: 

o

o

gr

p

P

P

P

k

−

=

o

o

gr

k

δ

δ

δ

δ

−

=

o

gr

o

u

U

U

U

k

−

=

δ

d

P

d

31

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kryteria        w układzie wielomaszynowym  

W przestrzeni o współrzędnych                                  zbiór punktów stabilnych 

nazywamy obszarem stabilności lokalnej. Wewnątrz tego obszaru mamy stany 

stabilne. Na zewnątrz niestabilne. Brzeg obszaru stabilności nazywamy 

powierzchnią

stanów granicznych. 

(

)

,

,

,

,

1

,

2

,

1

n

n

n

n

−

δ

δ

δ

K

δ

d

P

d

32

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia 

Rozważymy teraz wpływ tłumienia pochodzącego od uzwojeń

tłumiących na 

przebiegi kołysań

wirnika generatora. W tym celu przeanalizujemy przypadek 

pracy generatora w

punkcie

stabilnym A po

pojawieniu

się

dodatkowego 

obciążenia mocą

czynną. Dołączenie dodatkowej mocy powoduje, że generator 

znajduje się

w

punkcie

2. 

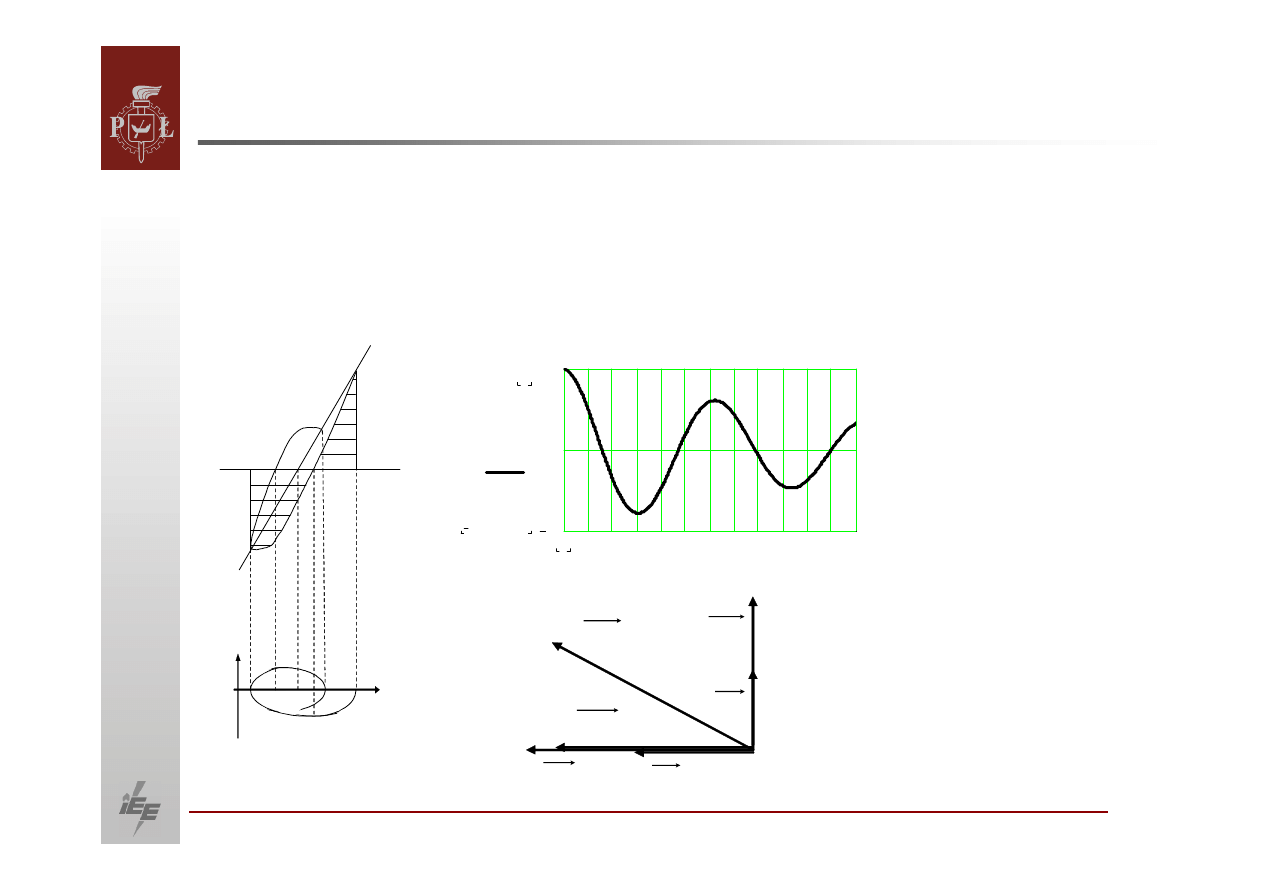
A

2

3

4

5

6 7

ω

δ

a)

b)

m

P

e

P

8

1

0.781262

P1

i

12

0

δ i.

1

0

1

ω

Δ

e

P

Δ

δ

Δ

D

e

Δ

D

i

Δ

D

P

33

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

Wirnik będzie hamowany, czyli zacznie maleć

jego prędkość

obrotowa 

wywołując zmniejszenie kąta i

w

konsekwencji

zmniejszenie mocy przesyłanej 

z

generatora

do sieci sztywnej. Prędkość

obrotowa jest różna od 

synchronicznej a więc pojawia się

poślizg i

tym

samym składnik mocy 

tłumiącym w równaniu różniczkowym ruchu wirnika staje się

różny od zera. 

Moc elektryczna jest zmniejszana o składnik

proporcjonalny do mocy 

tłumiącej.
Ruch wirnika nie odbywa się

po charakterystyce          , lecz poniżej. W wyniku 

pole hamowania jest określone punktami 2, 3, 4 a nie jak poprzednio 2, 3, A. 
W punkcie 4 mamy najmniejszą

prędkość

obrotową

wirnika. W tej sytuacji 

wirnik również

w ruchu przyspieszającym nie osiągnie takiego kąta jak 

uprzednio lecz punkt 6. Moc także nie osiągnie wartości takiej jak w

chwili

początkowej, lecz mniejszą. 
Wychylenie do punktu 5 będzie takie aby zakreskowane pole górne 2, 3, 4 

(energia kinetyczna hamująca) było równe zakreskowanemu polu dolnemu 
4, 5, 6 (energia kinetyczna przyspieszająca). 

( )

δ

P

34

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

W punkcie 5 wirnik zaczyna mieć

dodatni poślizg (rys.

b) i

dlatego

moc tłumiąca 

zmienia znak i dodaje się

do mocy elektrycznej. Krzywa zmian mocy w

funkcji

kąta leży powyżej charakterystyki mocy elektrycznej generowanej. Ruch 

przebiega do punktu 5 przez 7 do 8. W punkcie 7 znów mamy równość

mocy, 

lecz nie energii kinetycznych i prędkości, 

dlatego drgania trwają

dalej. 

Punktem końcowym tych drgań

będzie punkt A. Na rysunku b naszkicowano 

początkowy przebieg prędkości obrotowej wirnika w

funkcji

kąta.

Jest to tzw. portret fazowy, czyli najlepszy widok zmiennych stanu. Rys. c 

obrazuje przebieg zmian mocy czynnej w funkcji czasu. Widać

z niego

oscylacyjne tłumiony charakter tych zmian. 

Rys.

d

obrazuje nam zmienne uczestniczące w procesie zaprezentowane jako 

wektory. Tak jak poprzednio tak i

tu

zmiana prędkości obrotowej jako 

pochodna zmiany kąta wyprzedza go w

fazie

o

90

stopni. 

Wektor reprezentujący zmiany mocy jest w fazie z wektorem kąta. Uzwojenie 

tłumiące generatora zachowuje się

jak klatka silnika asynchronicznego, jeśli 

tylko pojawi się

zmiana prędkości obrotowej wirnika. 

35

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

W uzwojeni tłumiącym indukuje się

siła elektromotoryczna proporcjonalna do 

poślizgu i leżąca

w

fazie

z

nim. Znaczna rezystancja uzwojenia tłumiącego 

powoduje, że prąd w uzwojeniu tłumiącym jest opóźniony w fazie względem 

siły elektromotorycznej. Moc tłumiąca jest równa iloczynowi siły 

elektromotorycznej i rzutowi prądu tłumienia na oś

siły elektromotorycznej. 

Z tego rozważania widać, że rezystancja uzwojenia tłumiącego powinna być

duża w porównaniu do jego reaktancji. 
Rozważymy wpływ układu regulacji napięcia na przebieg procesu kołysań

wirnika wywołanych zakłóceniem w

poborze

mocy czynnej. W tym celu 

wyprowadzimy zależność

na napięcie na zaciskach generatora w

funkcji

kąta 

pomiędzy jego siła elektromotoryczną

i napięciem

sieci sztywnej. 

G

L

UE

36

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

Prąd płynący w układzie

wynosi: 

Stąd napięcie generatora: 

Moduł

napięcie generatora: 

(

)

X

X

j

U

e

E

I

d

S

j

d

G

+

′

−

′

=

δ

=

+

′

−

′

+

′

+

=

+

=

S

d

j

d

d

S

G

S

G

U

X

X

X

e

E

X

X

X

U

I

X

j

U

U

δ

⎥

⎦

⎤

⎢

⎣

⎡

′

+

⎟

⎠

⎞

⎜

⎝

⎛

′

+

′

+

′

=

δ

δ

sin

cos

d

d

S

d

d

E

j

E

U

X

X

X

X

X

( )

2

2

cos

2

d

d

S

d

S

d

d

G

E

E

U

X

X

U

X

X

X

X

X

U

′

+

⋅

′

⋅

⋅

′

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛ ′

+

′

=

δ

37

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

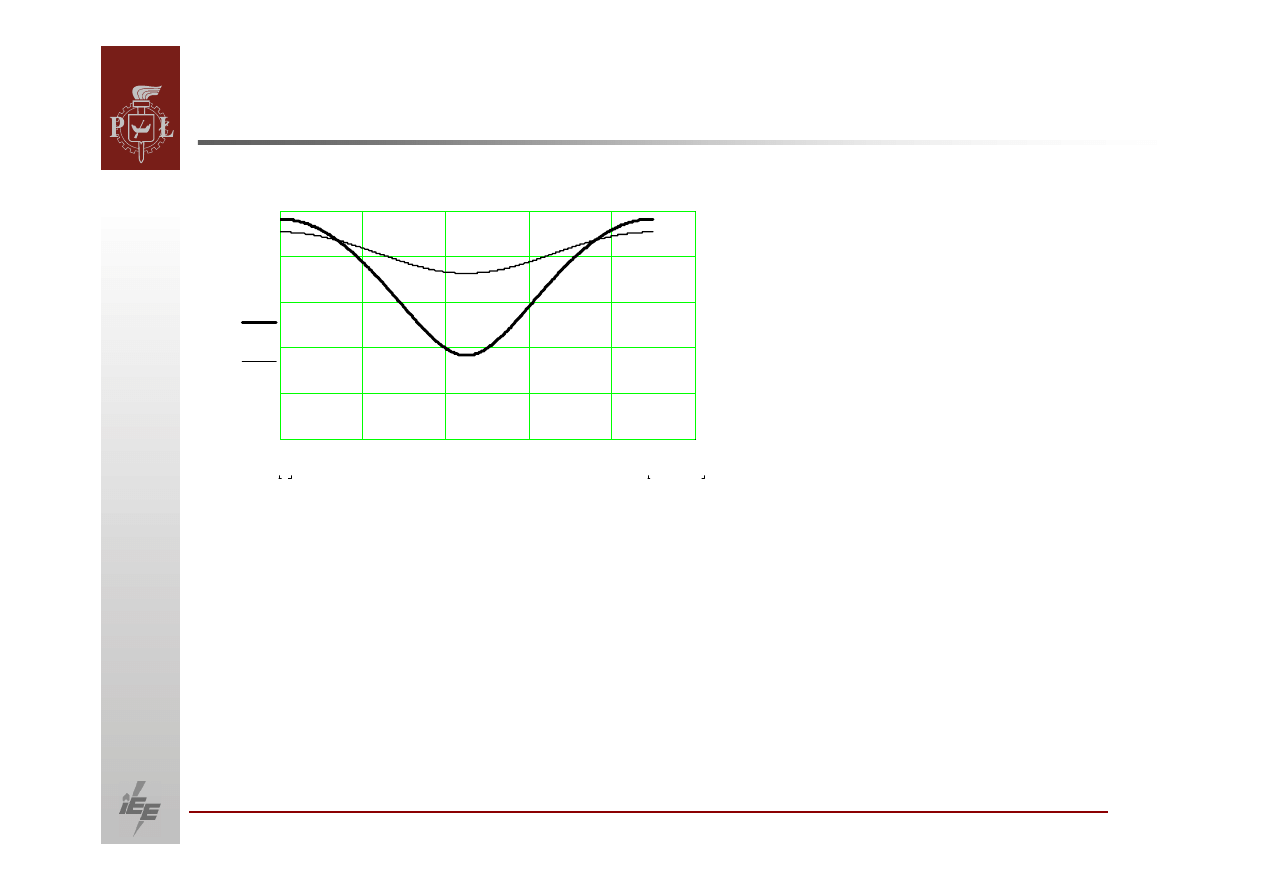
Przebieg napięcia na zaciskach generatora w

funkcji

kąta. 

1

0

U

i

U1

i

6.283185

0

δ i.

0

1.4

2.8

4.2

5.6

7

Z wykresu tego wynika, że podczas kołysań

wirnika wywołanych zakłóceniem 

w poborze mocy czynnej powstają

znaczne zmiany napięcia generatora. Zmiany 

te będą

zauważone przez regulator napięcia generatora, który obserwując 

obniżenie napięcia generatorowego zareaguje i

podniesie

napięcie wzbudzenie 

a

w

konsekwencji

napięcie na zaciskach generatora. Zwiększenie się

napięcia 

generatorowego powyżej wartości zadanej regulatora spowoduje obniżenie 

napięcia wzbudzenia, czyli napięcie na zaciskach generatora. 

38

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

Uzwojenie tłumiące leży w

osi

synchronicznej podłużnej maszyny. W tej

samej 

osi leży uzwojenie wzbudzające generatora. W tej sytuacji zmiany prądu 

wzbudzenie są

transformowane nie tylko do uzwojeń

statora, ale także do 

uzwojenia tłumiącego. 
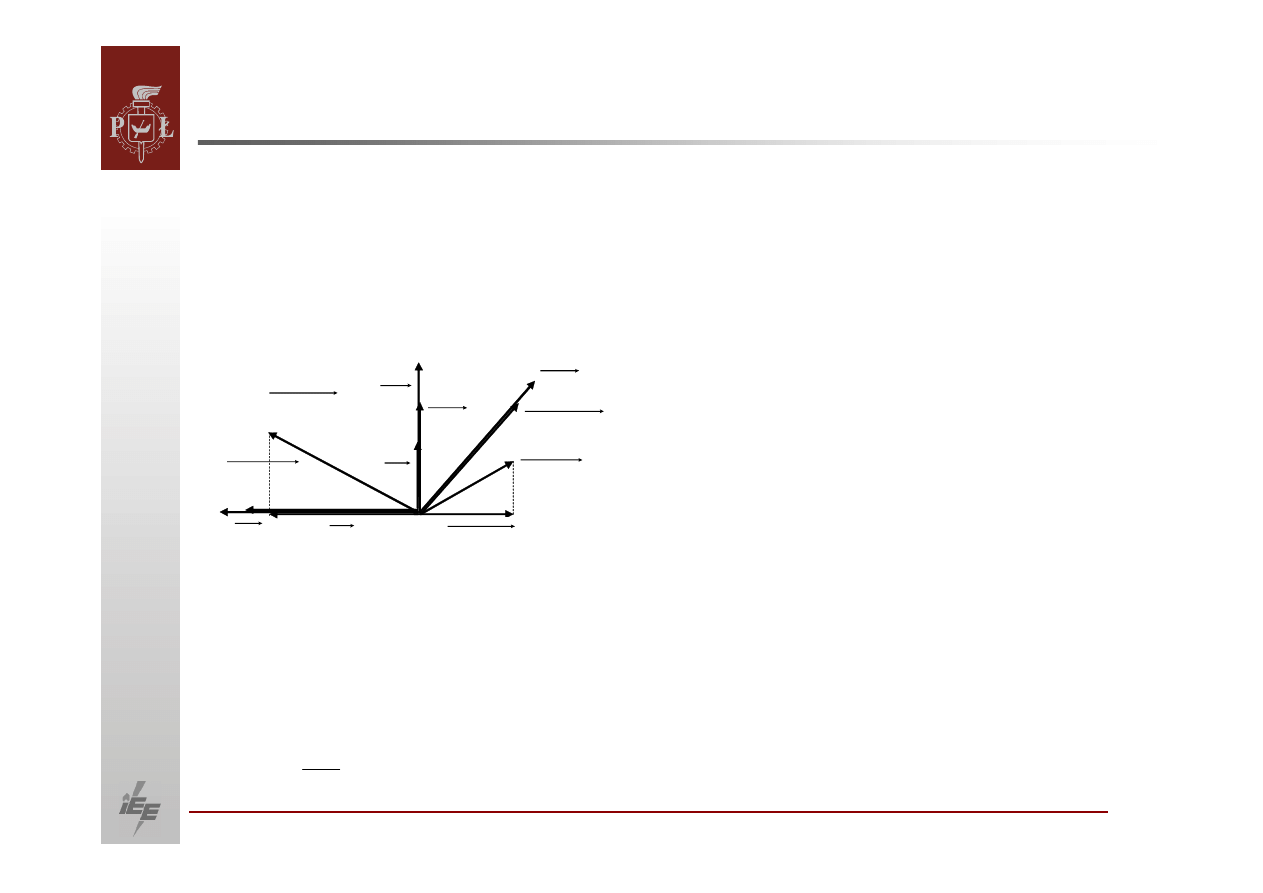
Wykres wskazowy dla układu tłumienia z regulacją

wzbudzenia. 

W automatycznym

regulatorze napięcia (wzbudzenia) wielkość

mierzona, czyli 

napięcie i

wielkość

zadana tworzą

uchyb regulacji:

a pochodna napięcia po kącie jest ujemna w stabilnym obszarze pracy, czyli:  

ω

Δ

e

P

Δ

δ

Δ

( )

ω

Δ

Δ

D

e

( )

ω

Δ

Δ

D

i

D

P

r

U

Δ

f

E

Δ

( )

f

E

D

e

Δ

Δ

( )

f

E

D

i

Δ

( )

f

E

D

P

Δ

U

U

U

zad

r

−

=

Δ

δ

δ

δ

Δ

∂

=

∂

∂

∂

−

=

r

r

K

U

U

39

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

Uchyb regulacji           jest wielkością

proporcjonalną

do zmian kąta i na

wykresie wskazowym jego wektor będzie w fazie z wektorem

.

Automatyczny regulator napięcia wzmacnia uchyb regulacyjny wymuszając we 

wzbudnicy generatora zmianę

napięcia wzbudzenia o wartość

.

Automatyczny regulator napięcia i

wzbudnica

mają

pewną

bezwładność

to na 

wykresie wskazowym wektor          będzie się

opóźniał

o pewien kąt w stosunku

do wektora uchybu regulacyjnego          .
To opóźnienie wynika ze stałych czasowych regulatora i

wzbudnicy. Zmiana 

napięcia wzbudzenia spowoduje powstanie w uzwojeniu tłumiącym siły 

elektromotorycznej              . Wektor tej siły                leży w fazie z wektorem

wymuszającym. Pod wpływem siły elektromotorycznej               w uzwojeniu

tłumiącym popłynie prąd             , którego wskaz              będzie opóźniony w 

stosunku do siły elektromotorycznej o pewien kąt wynikający ze stosunku 

rezystancji do reaktancji obwodu tłumiącego. 
Prąd płynący w uzwojeniu tłumiącym a wywołany

zmianami napięcia 

wzbudzenia odejmuje się

od prądu płynącego w uzwojeniu tłumiącym 

a wywołanym

zmianami prędkości obrotowej wirnika. 

r

U

Δ

δ

Δ

f

E

Δ

f

E

Δ

r

U

Δ

( )

f

E

D

e

Δ

( )

f

E

D

e

Δ

( )

f

E

D

e

Δ

( )

f

E

D

i

Δ

( )

f

E

D

i

Δ

40

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Kołysania z uwzględnieniem tłumienia i

regulacji

wzbudzenia

Oznacza to, że prąd płynący w uzwojeniu tłumiącym w wyniku działania 

regulatora napięcia osłabia prąd płynący w uzwojeniu tłumiącym a wywołanym

zmianami prędkości obrotowej wirnika a

w

konsekwencji

zmniejsza moc 

tłumiącą. 
Zostaną

teraz przeanalizowane czynniki prowadzące do pojawienia się

ujemnej 

mocy tłumiącej. Wielkością

wyjściową

tej analizy był

uchyb regulacyjny 

regulatora napięcia. Duży uchyb regulacyjny to w efekcie duży prąd płynący 

w uzwojeniu tłumiącym w wyniku działania regulatora napięcia. Duży efekt 

regulacyjny może być

spowodowany przez:

9Dużą reaktancję pomiędzy generatorem (elektrownią) a węzłem sieci 
sztywnej. 
9Duże obciążenie sieci. 
9Duże wzmocnienie regulatora napięcia bardzo korzystne dla regulacji 
napięcia (napięcie szybciej wraca do wartości zadanej), ale niekorzystne dla 
tłumienia. 
9Duże opóźnienie wprowadzane przez układ regulacji napięcia a więc
niekorzystna jest wzbudnica elektromaszynowa w odróżnieniu od wzbudnicy 
tyrystorowej. 

41

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 1 

kV

5

,

10

=

G

U

Obliczyć

moc graniczną

równowagi statycznej układu. 

G

T

T

L

UE

A

B

C

10 kV

220 kV

220 kV

MVA

150

=

NG

S

%

150

=

d

X

kV

5

,

10

=

NG

U

MVA

100

=

NT

S

%

12

=

Z

U

Δ

kV

10,5

kV

220

=

ϑ

km

Ω

4

,

0

=

kL

X

km

150

=

l

∞

=

Z

S

kV

215

=

S

U

Zadanie rozwiązać

dla trzech przypadków gdy generator: 

9nie jest wyposażony w regulator wzbudzenia a obciążony jest mocą

9jest wyposażony w szybki regulator wzbudzenia utrzymujący 
9jest wyposażony w wolny regulator wzbudzenia utrzymujący 

MW

150

=

N

P

kV

5

,

10

=

G

U

1

cos

=

ϕ

kV

5

,

10

=

G

U

42

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 1

Impedancje elementów na poziomie

kV

5

,

10

Ω

10

,

1

150

5

,

10

100

150

100

2

2

=

⋅

=

⋅

=

NG

NG

d

G

S

U

X

X

Ω

0662

,

0

100

2

5

,

10

100

12

2

100

2

2

=

⋅

⋅

=

⋅

⋅

=

NT

NT

z

T

S

U

U

X

Δ

Ω

137

0

220

5

10

150

4

0

1

2

2

,

,

,

l

X

X

T

k

L

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

=

⋅

⋅

=

ϑ

Ω

31

,

1

137

,

0

0662

,

0

10

,

1

=

+

+

=

+

+

=

∑

L

T

G

X

X

X

X

Przypadek 1: generator nie jest wyposażony w regulator wzbudzenia 

kV

3

,

10

220

5

,

10

215

1

5

,

10

=

⋅

=

⋅

=

T

S

S

U

U

ϑ

=

⋅

+

=

⋅

+

=

5

,

10

10

,

1

150

5

,

10

5

,

10

5

,

10

j

U

X

P

j

U

E

G

G

G

G

G

kV

9

,

18

8

,

15

5

,

10

3

,

56

°

=

+

=

j

e

j

MW

149

31

,

1

3

,

10

9

,

18

5

.

10

=

⋅

=

⋅

=

∑

X

U

E

P

S

G

gr

43

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 1

Przypadek 2: generator jest wyposażony w szybki regulator wzbudzenia 

MW

531

137

,

0

0662

,

0

3

,

10

5

,

10

5

,

10

=

+

⋅

=

+

⋅

=

L

T

S

G

gr

X

X

U

U

P

Przypadek 3: generator jest wyposażony w wolny regulator wzbudzenia

Wykres wskazowy napięcia sieci sztywnej, napięcia i siły

elektromotorycznej 

generatora wyposażonego w wolny regulator wzbudzenia. 

S

U

G

U

d

E

U

Δ

α

44

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 1

W celu wyznaczenia siły elektromotorycznej zastosujemy metodę

iteracyjną. 

Założymy, że 

°

= 20

α

kV

5

,

10

20

°

=

j

G

e

U

(

)

=

−

°

+

°

⋅

=

−

=

3

,

10

20

sin

20

cos

5

,

10

j

U

U

U

S

G

GS

Δ

(

)

kV

59

,

3

433

,

0

j

+

−

=

(

)

=

⋅

+

−

=

+

+

+

⋅

=

203

,

0

31

,

1

59

,

3

433

,

0

j

X

X

X

X

X

U

U

L

T

L

T

G

GS

Δ

Δ

(

)

kV

1

,

23

79

,

2

j

+

−

=

Część

rzeczywista straty napięcia powinna być

równa napięciu sieci sztywnej ze 

znakiem minus, wniosek przyjęto zbyt mały kąt. Założymy, że 

°

= 30

α

(

)

=

−

°

+

°

⋅

=

−

=

3

,

10

30

sin

30

cos

5

,

10

j

U

U

U

S

G

GS

Δ

(

)

kV

25

,

5

21

,

1

j

+

−

=

(

)

=

⋅

+

−

=

+

+

+

⋅

=

203

,

0

31

,

1

25

,

5

21

,

1

j

X

X

X

X

X

U

U

L

T

L

T

G

GS

Δ

Δ

(

)

kV

8

,

33

80

,

7

j

+

−

=

45

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 1

Założymy, że 

°

= 34

α

(

)

=

−

°

+

°

⋅

=

−

=

3

,

10

34

sin

34

cos

5

,

10

j

U

U

U

S

G

GS

Δ

(

)

kV

87

,

5

60

,

1

j

+

−

=

(

)

=

⋅

+

−

=

+

+

+

⋅

=

203

,

0

31

,

1

87

,

5

60

,

1

j

X

X

X

X

X

U

U

L

T

L

T

G

GS

Δ

Δ

(

)

kV

9

,

37

3

,

10

j

+

−

=

Część

rzeczywista straty napięcia jest równa napięciu sieci sztywnej ze znakiem 

minus, kąt jest właściwy.
Siła elektromotoryczna generatora jest równa części urojonej straty napięcia, 

czyli: 

kV

9

,

37

=

d

E

MW

298

31

,

1

3

,

10

9

,

37

5

.

10

=

⋅

=

⋅

=

∑

X

U

E

P

S

d

gr

46

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

Obliczyć

moc graniczną

równowagi statycznej układu jak na rysunku. 

G1

T1

1

S

L

T2

A

B

C

15 kV

110 kV

110 kV

15 kV

2

S

D

G2

LBC

P

MVA

600

1

=

NG

S

%

150

=

d

X

kV

75

,

15

1

=

NG

U

MVA

600

2

=

NG

S

%

150

=

d

X

kV

75

,

15

2

=

NG

U

MVA

315

1

=

NT

S

%

12

=

Z

U

Δ

kV

15

kV

110

=

ϑ

MVA

315

2

=

NT

S

%

12

=

Z

U

Δ

kV

15

kV

110

=

ϑ

km

Ω

4

,

0

=

kL

X

km

10

=

l

MW

200

1

=

P

ind.

8

,

0

cos

1

=

ϕ

kV

75

,

15

=

A

U

MW

200

2

=

P

ind.

8

,

0

cos

2

=

ϕ

kV

75

,

15

=

D

U

MW

100

=

LBC

P

Generator nie jest wyposażony w regulator wzbudzenia. 

47

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

Impedancje elementów na poziomie 

kV

15

Ω

620

,

0

600

75

,

15

100

150

100

2

2

2

1

=

⋅

=

⋅

=

=

N

N

d

G

G

S

U

X

X

X

Ω

0945

,

0

315

75

,

15

100

12

100

2

2

2

1

=

⋅

=

⋅

=

=

N

N

z

T

T

S

U

U

X

X

Δ

Ω

0744

0

110

15

10

4

0

1

2

2

,

,

l

X

X

T

k

L

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

=

⋅

⋅

=

ϑ

Obliczenia mocy w węzłach A i D

(

)

MVA

150

200

6

,

0

8

,

0

200

200

sin

cos

1

1

1

1

1

j

j

P

j

P

S

+

=

⋅

+

=

⋅

+

=

ϕ

ϕ

(

)

MVA

150

200

6

,

0

8

,

0

200

200

sin

cos

2

2

2

2

2

j

j

P

j

P

S

+

=

⋅

+

=

⋅

+

=

ϕ

ϕ

Zastąpienie odbiorów impedancjami

(

)

Ω

5953

,

0

7938

,

0

150

200

75

,

15

2

*

1

2

1

j

j

S

U

Z

A

o

+

=

−

=

=

(

)

Ω

5953

,

0

7938

,

0

150

200

75

,

15

2

*

2

2

2

j

j

S

U

Z

D

o

+

=

−

=

=

48

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

Schemat zastępczy

1

o

Z

2

o

Z

1

d

E

2

d

E

1

G

jX

2

G

jX

(

)

2

1

T

L

T

X

X

X

j

+

+

Obliczenia impedancji własnej generatora 1

(

)

=

+

+

+

⋅

=

+

⋅

=

5953

,

0

7938

,

0

620

,

0

5953

,

0

7938

,

0

620

,

0

2

2

2

2

j

j

j

j

Z

X

j

Z

X

j

Z

o

G

o

G

a

(

)

Ω

3983

,

0

1448

,

0

j

+

=

(

)

=

+

+

+

=

2

1

T

L

T

a

b

X

X

X

j

Z

Z

=

+

⋅

+

+

=

0744

,

0

2

0945

,

0

3983

,

0

1448

,

0

j

j

j

(

)

Ω

6617

,

0

1448

,

0

j

+

=

(

) (

)

=

+

+

+

+

⋅

+

=

+

=

5953

,

0

7938

,

0

6617

,

0

1448

,

0

5953

,

0

7938

,

0

6617

,

0

1448

,

0

1

1

j

j

j

j

Z

Z

Z

Z

Z

o

b

o

b

c

(

)

Ω

3757

,

0

2059

,

0

j

+

=

49

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

=

+

+

=

+

=

620

,

0

3757

,

0

2059

,

0

1

11

j

j

X

j

Z

Z

G

c

(

)

Ω

0168

,

1

9957

,

0

2059

,

0

3

,

78

°

=

+

=

j

e

j

Obliczenia impedancji własnej generatora 2

Ω

0168

,

1

3

,

78

22

o

j

e

Z

=

Obliczenia impedancji wzajemnej generator 1 ‐

generator 2

W celu obliczenia impedancji wzajemnej generator 1 ‐

generator 2 musimy 

przekształcić

dwie gwiazdy występujące w schemacie zastępczym na trójkąty. 

Zaczniemy od gwiazdy złożonej z impedancji: 

1

G

X

j

1

o

Z

(

)

2

1

T

L

T

X

X

X

j

+

+

(

)

(

)

=

+

+

⋅

+

+

+

+

=

1

2

1

1

2

1

1

1

o

T

L

T

G

T

L

T

G

D

G

Z

X

X

X

j

X

j

X

X

X

j

X

j

Z

=

+

⋅

+

+

=

5953

,

0

7938

,

0

5906

,

0

620

,

0

2634

,

0

620

,

0

j

j

j

j

j

(

)

Ω

9822

,

0

1317

,

0

j

+

−

=

50

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

(

)

(

)

=

+

+

⋅

+

+

+

+

=

1

2

1

1

2

1

1

0

G

T

L

T

o

T

L

T

o

D

X

j

X

X

X

j

Z

X

X

X

j

Z

Z

(

)

=

⋅

+

+

+

+

=

620

,

0

2634

,

0

5953

,

0

7938

,

0

2634

,

0

5953

,

0

7938

,

0

j

j

j

j

j

(

)

Ω

1117

,

1

1310

,

1

j

+

=

Łączymy równolegle gałęzie: 

0

D

Z

2

o

Z

(

) (

)

=

+

+

+

+

⋅

+

=

+

⋅

=

5953

,

0

7938

,

0

1117

,

1

131

,

1

5953

,

0

7938

,

0

1117

,

1

131

,

1

2

0

2

0

j

j

j

j

Z

Z

Z

Z

Z

o

D

o

D

DD

(

)

Ω

3916

,

0

4699

,

0

j

+

=

Przekształcamy gwiazdę

na trójkąt dla impedancji: 

DD

Z

D

G

Z

1

2

G

X

j

=

⋅

+

+

=

DD

G

D

G

G

D

G

Z

X

j

Z

X

j

Z

Z

2

1

2

1

12

(

)

=

+

⋅

+

−

+

+

+

−

=

3916

,

0

4699

,

0

62

,

0

9822

,

0

1317

,

0

62

,

0

9822

,

0

1317

,

0

j

j

j

j

j

(

)

Ω

3518

,

2

1370

,

2

9819

,

0

7

,

114

°

=

+

−

=

j

e

j

51

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

Obliczenie mocy płynących z generatorów

ϑ

sin

2

1

2

1

1

⋅

+

+

⋅

=

T

L

T

G

G

A

T

X

X

X

U

U

P

(

)

1062

,

0

75

,

15

75

,

15

2634

,

0

100

sin

2

1

2

1

1

=

⋅

⋅

=

⋅

+

+

⋅

=

G

G

T

L

T

A

T

U

U

X

X

X

P

ϑ

=

⋅

⋅

−

=

ϑ

cos

2

1

2

1

2

1

2

1

1

LT

T

G

G

LT

T

G

A

T

X

U

U

X

U

Q

Mvar

3

,

5

1062

,

0

1

2634

,

0

75

,

15

2634

,

0

75

,

15

2

2

2

=

−

⋅

−

=

=

+

+

+

=

+

=

3

,

5

100

150

200

1

1

1

j

j

S

S

S

A

T

o

G

(

)

MVA

3

,

155

300

j

+

=

(

)

=

−

−

+

=

−

=

3

,

5

100

150

200

2

2

2

j

j

S

S

S

D

T

o

G

(

)

MVA

3

,

155

100

j

+

=

52

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

Obliczenia modułów sił

elektromotorycznych generatorów

=

⋅

+

⋅

+

=

1

1

1

1

1

1

1

1

G

G

G

G

G

G

G

d

U

X

P

j

U

X

Q

U

E

(

)

kV

8

,

24

8

,

11

9

,

21

75

,

15

62

,

0

300

75

,

15

62

,

0

3

,

155

75

,

15

3

,

28

°

=

+

=

⋅

+

⋅

+

=

j

e

j

j

=

⋅

+

⋅

+

=

2

2

2

2

2

2

2

2

G

G

G

G

G

G

G

d

U

X

P

j

U

X

Q

U

E

(

)

kV

2

,

22

9

,

3

9

,

21

75

,

15

62

,

0

100

75

,

15

62

,

0

3

,

155

75

,

15

2

,

10

°

=

+

=

⋅

+

⋅

+

=

j

e

j

j

Wyznaczenie mocy granicznej równowagi statycznej układu 

Ω

0168

,

1

11

=

Z

°

=

7

,

11

11

α

Ω

0168

,

1

22

=

Z

Ω

3518

,

2

12

=

Z

°

=

7

,

11

22

α

°

−

=

7

,

24

12

α

kV

8

,

24

1

=

d

E

kV

2

,

22

2

=

d

E

°

=

−

=

+

=

3

,

65

7

,

24

90

90

12

α

δ

gr

53

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 2

=

⋅

+

⋅

=

12

2

1

11

11

2

1

1

sin

Z

E

E

Z

E

P

d

d

d

gr

α

MW

358

3518

,

2

2

,

22

8

,

24

7

,

11

sin

0168

,

1

8

,

24

2

=

⋅

+

⋅

=

=

⋅

−

⋅

=

12

2

1

22

22

2

2

2

sin

Z

E

E

Z

E

P

d

d

d

gr

α

MW

136

3518

,

2

8

,

24

2

,

22

7

,

11

sin

0168

,

1

2

,

22

2

−

=

⋅

−

⋅

=

357.736439

136.438108

P1

i

P2

i

3.141593

3.141593

δ i. π

4

3

2

1

0

1

2

3

4

200

100

0

100

200

300

400

P

1

P

2

1

2

3

Przebiegi mocy w funkcji kąta rozchylenia wektorów sił

elektromotorycznych

54

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

Obliczyć

czy dla układu jak na rysunku można przesłać

nadwyżkę

mocy 

z

generatora

do systemu. Dla tej sytuacji obliczyć

maksymalną

długość

linii, aby 

zachować

stabilną

pracę. 

G

T

1

S

L

A

B

220 kV

220 kV

UE

MVA

250

=

NG

S

%

220

=

d

X

kV

75

,

15

=

NG

U

ind.

8

,

0

cos

=

NG

ϕ

MVA

250

=

NT

S

%

11

=

Z

U

Δ

kV

15

kV

31

2

=

ϑ

km

Ω

4

,

0

=

kL

X

km

50

=

l

MW

100

1

=

P

ind.

8

,

0

cos

1

=

ϕ

kV

2315

=

A

U

kV

231

=

B

U

Generator jest wyposażony w wolny regulator wzbudzenia utrzymujący stałe 

napięcie na szynach A wynoszące 

kV

231

55

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

Impedancje elementów na poziomie

kV

220

( )

Ω

7

,

517

15

231

250

75

,

15

100

220

100

2

2

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

=

⋅

⋅

=

T

N

N

d

G

S

U

X

X

ϑ

Ω

48

,

23

250

231

100

11

100

2

2

=

⋅

=

⋅

=

N

N

z

T

S

U

U

X

Δ

Ω

20

50

4

,

0

=

⋅

=

⋅

=

l

X

X

k

L

Obliczenia mocy odbioru 1

(

)

MVA

0

,

75

100

6

,

0

8

,

0

100

100

sin

cos

1

1

1

1

1

j

j

P

j

P

S

+

=

⋅

+

=

⋅

+

=

ϕ

ϕ

Zastąpienie odbioru impedancją

(

)

Ω

1

,

256

5

,

341

75

100

231

2

*

1

2

1

j

j

S

U

Z

A

o

+

=

−

=

=

Obliczenia siły elektromotorycznej generatora

Ω

2

,

541

48

,

23

7

,

517

=

+

=

+

=

T

G

GT

X

X

X

56

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

=

⋅

+

⋅

+

=

A

GT

G

A

GT

G

A

d

U

X

P

j

U

X

Q

U

E

(

)

kV

3

,

469

3

,

234

7

,

406

231

2

,

541

100

231

2

,

541

75

231

9

,

29

°

=

+

=

⋅

+

⋅

+

=

j

e

j

j

Obliczenie impedancji wzajemnej generator 1 – sieć

sztywna

Przekształcamy gwiazdę

na trójkąt dla impedancji: 

GT

X

j

1

o

Z

L

X

j

=

⋅

+

+

=

1

1

12

o

L

G

L

GT

Z

X

j

X

j

X

j

X

j

Z

=

+

⋅

+

+

=

1

,

256

5

,

341

20

2

,

541

20

2

,

541

j

j

j

j

j

(

)

Ω

8

,

576

4

,

576

28

,

20

0

,

92

°

=

+

−

=

j

e

j

Obliczenie czy można przesłać

nadwyżkę

mocy z generatora do systemu

°

−

=

−

=

−

=

0

,

2

92

90

90

12

12

θ

α

°

=

−

=

+

=

0

,

88

0

,

2

90

90

12

α

δ

gr

°

=

9

,

29

S

d

U

E

δ

°

=

<

°

=

0

,

88

9

,

29

gr

U

E

S

d

δ

δ

Linią

można przesłać

nadwyżkę

mocy z

generatora

do systemu. 

57

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

Moc czynna płynąca linią

MW

100

100

8

,

0

250

cos

1

=

−

⋅

=

−

⋅

=

P

S

P

N

NG

L

ϕ

Moc bierna płynąca linią

0375

,

0

231

231

20

100

sin

=

⋅

⋅

=

⋅

⋅

=

S

A

L

L

U

U

X

P

ϑ

°

=

=

15

,

2

sin

ϑ

ϑ

arc

=

⋅

⋅

−

=

ϑ

cos

2

L

S

A

L

A

L

X

U

U

X

U

Q

Mvar

87

,

1

0375

,

0

1

20

231

20

231

2

2

2

=

−

⋅

−

=

Obliczenie mocy generatora

(

)

MVA

9

,

76

200

87

,

1

100

75

100

1

1

j

j

j

S

S

S

L

o

G

+

=

+

+

+

=

+

=

Obliczenie siły elektromotorycznej generatora

=

⋅

+

⋅

+

=

A

GT

G

A

GT

G

A

d

U

X

P

j

U

X

Q

U

E

1

1

(

)

kV

3

,

623

6

,

468

1

,

411

231

2

,

541

200

231

2

,

541

9

,

76

231

7

,

48

°

=

+

=

⋅

+

⋅

+

=

j

e

j

j

58

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

Obliczenie czy układ po przesłaniu nadwyżki mocy z

generatora

do systemu jest 

stabilny 

°

=

<

°

=

°

+

°

=

+

=

0

,

88

85

,

50

15

,

2

7

,

48

gr

U

E

U

E

A

d

S

d

δ

ϑ

δ

δ

Zwiększenie długości linii do 250 km

Ω

100

250

4

,

0

=

⋅

=

⋅

=

l

X

X

k

L

Obliczenie impedancji wzajemnej generator 1 – sieć

sztywna

=

⋅

+

+

=

1

1

12

o

L

G

L

GT

Z

jX

jX

jX

jX

Z

=

+

⋅

+

+

=

1

,

256

5

,

341

100

2

,

541

100

2

,

541

j

j

j

j

j

(

)

Ω

4

,

724

2

,

717

4

,

101

0

,

98

°

=

+

−

=

j

e

j

Moc bierna płynąca linią

1874

,

0

231

231

100

100

sin

=

⋅

⋅

=

⋅

⋅

=

S

A

L

L

U

U

X

P

ϑ

°

=

=

8

,

10

sin

ϑ

ϑ

arc

59

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

=

⋅

⋅

−

=

ϑ

cos

2

L

S

A

L

A

L

X

U

U

X

U

Q

Mvar

45

,

9

1874

,

0

1

100

231

100

231

2

2

2

=

−

⋅

−

=

Obliczenie mocy generatora

(

)

MVA

5

,

84

200

45

,

9

100

75

100

1

1

j

j

j

S

S

S

L

o

G

+

=

+

+

+

=

+

=

Obliczenie siły elektromotorycznej generatora

=

⋅

+

⋅

+

=

A

GT

G

A

GT

G

A

d

U

X

P

j

U

X

Q

U

E

1

1

(

)

=

+

=

⋅

+

⋅

+

=

6

,

468

9

,

428

231

2

,

541

200

231

2

,

541

5

,

84

231

j

j

kV

2

,

635

5

,

47

°

=

j

e

Obliczenie czy układ po przesłaniu nadwyżki mocy z

generatora

do systemu jest 

stabilny 

°

=

−

=

−

=

−

+

=

+

=

0

,

82

0

,

98

180

180

90

90

90

12

12

12

θ

θ

α

δ

gr

°

=

<

°

=

°

+

°

=

+

=

0

,

82

3

,

58

8

,

10

5

,

47

gr

U

E

U

E

A

d

S

d

δ

ϑ

δ

δ

60

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

Zwiększenie długości linii do 600 km

Ω

240

600

4

,

0

=

⋅

=

⋅

=

l

X

X

k

L

Obliczenie impedancji wzajemnej generator 1 – sieć

sztywna

=

⋅

+

+

=

1

1

12

o

L

G

L

GT

Z

jX

jX

jX

jX

Z

=

+

⋅

+

+

=

1

,

256

5

,

341

240

2

,

541

240

2

,

541

j

j

j

j

j

(

)

Ω

0

,

994

7

,

963

4

,

243

2

,

104

°

=

+

−

=

j

e

j

Moc bierna płynąca linią

4498

,

0

231

231

240

100

sin

=

⋅

⋅

=

⋅

⋅

=

S

A

L

L

U

U

X

P

ϑ

°

=

=

7

,

26

sin

ϑ

ϑ

arc

=

⋅

⋅

−

=

ϑ

cos

2

L

S

A

L

A

L

X

U

U

X

U

Q

Mvar

8

,

23

4498

,

0

1

240

231

240

231

2

2

2

=

−

⋅

−

=

61

STABILNOŚĆ

LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. 

Zadanie 3

Obliczenie mocy generatora

(

)

MVA

8

,

98

200

8

,

23

100

75

100

1

1

j

j

j

S

S

S

L

o

G

+

=

+

+

+

=

+

=

Obliczenie siły elektromotorycznej generatora

=

⋅

+

⋅

+

=

A

GT

G

A

GT

G

A

d

U

X

P

j

U

X

Q

U

E

1

1

(

)

=

+

=

⋅

+

⋅

+

=

6

,

468

4

,

462

231

2

,

541

200

231

2

,

541

8

,

98

231

j

j

kV

3

,

658

4

,

45

°

=

j

e

Obliczenie czy układ po przesłaniu nadwyżki mocy z

generatora

do systemu jest 

stabilny 

°

=

−

=

−

=

8

,

75

2

,

104

180

180

12

θ

δ

gr

°

=

<

°

=

°

+

°

=

+

=

8

75

1

72

7

26

4

45

,

,

,

,

gr

U

E

U

E

A

d

S

d

δ

ϑ

δ

δ