
1
SYSTEMY
ELEKTROENERGETYCZNE
Rozdzia
ł
4
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO
Łód
ź,
2009
rok
Andrzej Kanick
i

2
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Poj
ę
cia
stabilno
ści
Stabilno
ść
loka
lna
systemu
el
ektroenergetyczneg
o
(SE)
to
st
abilno
ść
jego
pracy
podczas
ma
łych
zak
łóce
ń
.
Do
tych
zak
łóce
ń
mo
żna
zaliczy
ć:
1.
za
łą
czanie,
wy
łą
czanie
ma
łych
odbiorów,
2.
za
łą
czanie,
wy
łą
czanie
pojedynczych
generatorów,
3.
za
łą
czanie,
wy
łą
czanie
pojedynczych
linii,
4.
dzia
łanie
uk
ładów
regulacji
napi
ę
cia
i
cz
ę
stotliwo
ści.
Definicja
stabilno
ści
Rozwi
ązanie
równania
ró
żniczkowego
lub
uk
ładu
równa
ń
ró
żniczkowych
nazywamy
st
abilnym
(stabilnym
w
sensie
Lapunowa),
je
żeli
dla
dowolnego
i
dowolnego
czasu
mo
żna
dobra
ć
tak
ą
liczb
ę
, ż
e
dla
wszystkich
punktów
st
art
o
wych
spe
łniaj
ących
ogranic
zenie:
zachodzi:
dla
ka
żdego
.
()
t
x
1
0
>
ε
0
t
η
η
<
−
)
(
)
(
0
1
0
2
t
x
t
x
ε
<
−
)
(
)
(
1
2
t
x
t
x
0
t
t
>
3
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Poj
ę
cia
stabilno
ści
t
0
t
ε
ε
η
()
t
x
Definicja
stabilno
ści
asymptotycznej
Rozwi
ązanie
równania
ró
żniczkowego
lub
uk
ładu
równa
ń
ró
żniczkowych
nazywamy
st
abilnym
asymptotycznie,
je
żeli
jest
st
abilne
a
ponadto:
()
t
x
1
0
)
(
)
(
lim
0
1
0
2
=
−
∞
→
t
x
t
x
t

4
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Poj
ę
cia
stabilno
ści
Za
łó
żmy,
ż
e
system
elektroenergetyczn
y
opisano
za
pomoc
ą
uk
ładu
równa
ń
ró
żniczkowych
nie
liniowych
postaci:
Niech
b
ędzie
punktem,
dla
którego
mamy:
Funkcj
ę
nieliniow
ą
mo
żemy
zlinearyzowa
ć
w
pewnym
otoczeniu
punktu
. W
tym
celu
funkcj
ę
rozwiniemy
w
szereg
Taylora
do
posta
ci:
W
wyniku
pomini
ę
cia
reszty
z
rozwini
ęcia
w
szeregu
Taylora
otrzymali
śmy
opis
naszego
obie
ktu
za
pomoc
ą
uk
ładu
równa
ń
ró
żniczkowych
liniowych
postaci:
)
(X
F
X
=
dt
d
r
X
0
)
(
=
r
X
F
)
(X
F
r
X
)
(X
F
)
(
)
(
X
R
X
A
X
F
+
⋅
=
X
A
X
⋅
=
dt
d

5
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Poj
ę
cia
stabilno
ści
gdzie:
Powy
ższe
równanie
jest
przybli
żeniem
liniowym
uk
ładu
równa
ń
ró
żniczkowych
nie
liniowych
a
ca
ła
operacja
operacj
ą
linearyzacji.
Do
równania
nie
liniowego
i
jego
przybli
żenia
liniowego
s
łuszne
s
ą
nast
ępuj
ące
twierdzenia
tzw.
pierwszej
metody
Lapunowa.
Twierdzenie
1
Uk
ład
równa
ń
ró
żniczkowych
nie
liniowych
jest
st
abilny
asymptotycznie
loka
lnie
tzn.
w
otoczeniu
punktu
linearyzacji,
je
śli
jego
przybli
żenie
liniowe
je
st
stabilne
asymptotycznie.
Twierdzenie
2
Uk
ład
równa
ń
ró
żniczkowych
nie
liniowych
jest
niestabilny
je
śli
jego
przybli
żenie
liniowe
je
st
niestabilne.
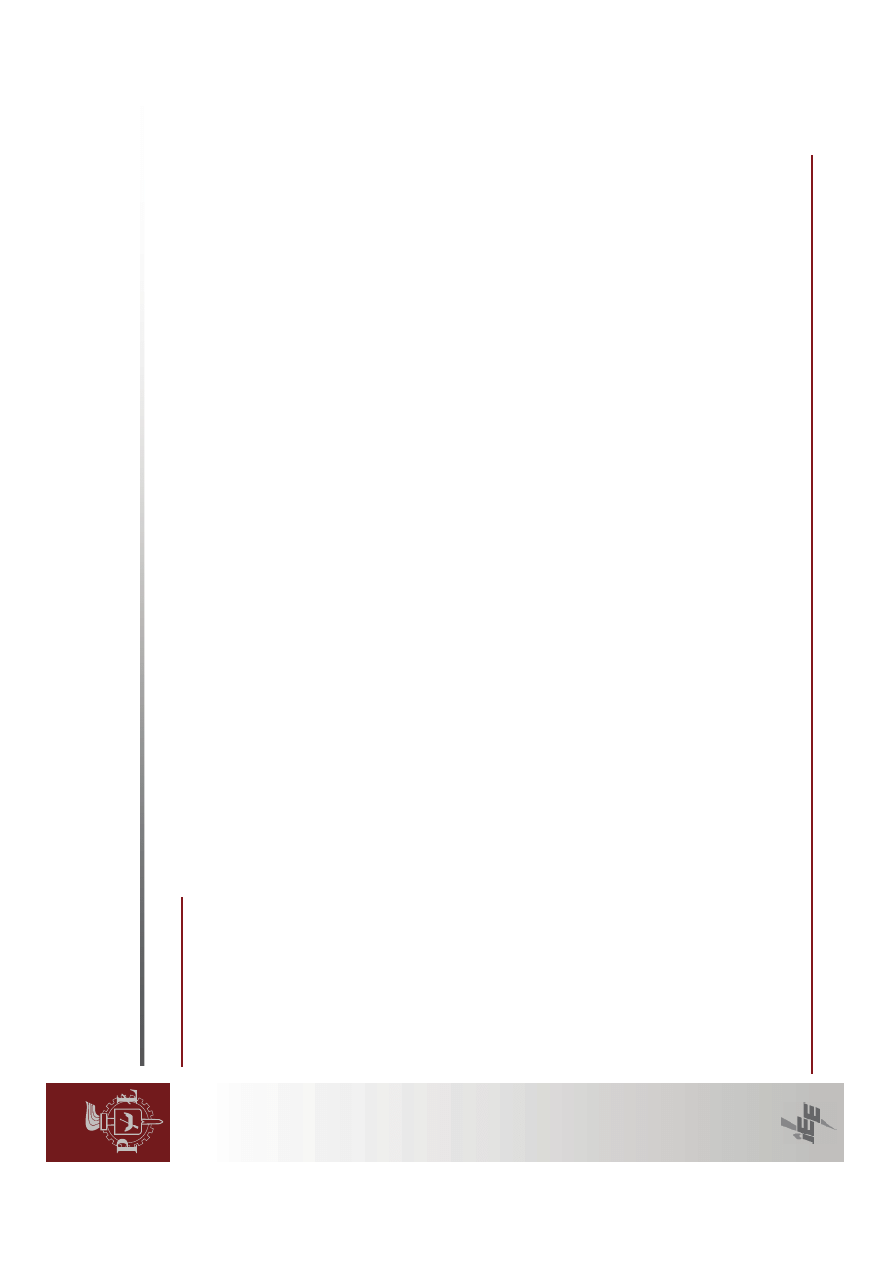
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
=
n
n
n
n
x
f
x
f
x
f
x
f
d
d
∂
∂
∂
∂
∂
∂
∂
∂
L
M
O
M
L
1
1
1
1
X
F
A
6
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Poj
ę
cia
stabilno
ści
Twierdzenie
3
O
stabilno
ści
uk
ładu
równa
ń
ró
żniczkowych
nieliniowyc
h
nie
mo
żna
nic
wnioskowa
ć
je
śli
jego
przybli
żenie
liniowe
jest
st
ab
ilne
ale
nie
asymptotycznie.
Musimy
rozwa
ży
ć
problem
czy
uk
ład
równa
ń
ró
żniczkowych
liniowych
jest
st
abilny.
W
tym
celu
musimy
obliczy
ć
warto
ści
w
łas
ne
macierzy
.
Znaj
ąc
warto
ści
w
łasne
mo
żemy
rozwi
ązanie
uk
ładu
równa
ń
ró
żniczkowych
liniowych
zapisa
ć
jako:
O
stabilno
ści
rozwa
żanego
uk
ładu
równa
ń
ró
żniczkowych
liniowych
mo
żemy
wnioskowa
ć
w
oparciu
o
poni
ższe
twierdzenie.
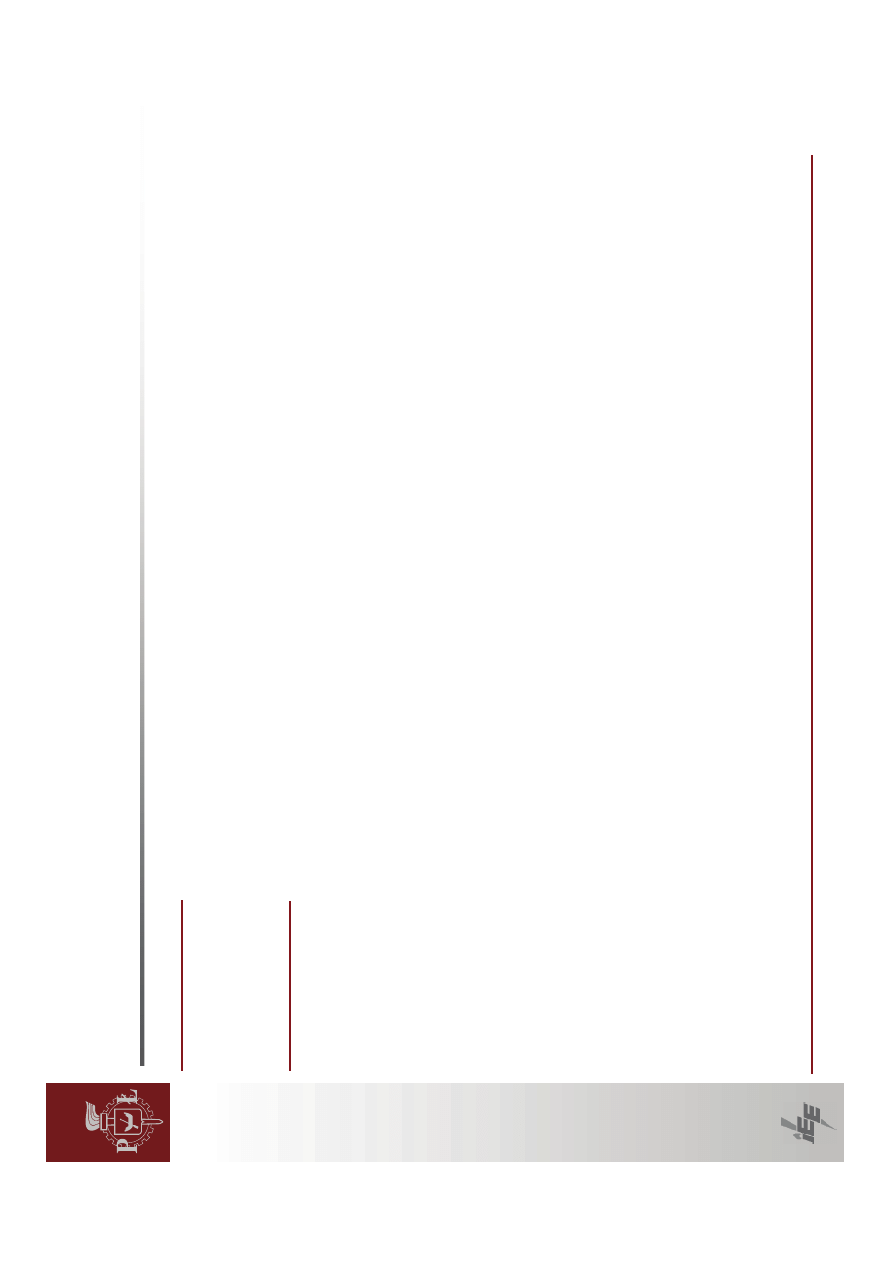
i
λ
A
0
)
(
det
=
⋅
−
1
A
i
λ
()
∑
=
⋅
=
n
j
t
ij
i
i
e
a
t
x
1
λ
7
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Poj
ę
cia
stabilno
ści
Twie
rdzenie
4
Uk
ład
równa
ń
ró
żniczkowych
liniowych
je
st
stabilny
wtedy
i
tyl
ko
wtedy,
kiedy
wszystkie
warto
ści
w
łas
ne
macierzy
maj
ą
niedodatnie
cz
ęś
ci
rzeczywiste.
Twierdzenie
5
Uk
ład
równa
ń
ró
żniczkowych
liniowych
je
st
stabilny
asymptotycznie
wtedy
i
tylko
wtedy,
kiedy
wszystkie
warto
ści
w
łasne
macierzy
maj
ą
ujemne
cz
ęś
ci
rzeczywiste.
A
A

8
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Model
matematyczn
y
systemu
elektroenergetycznego
Nale
ży
okre
śli
ć
uk
ład
równa
ń
ró
żniczkowych
opisuj
ących
syst
em
el
ektroenergetyczn
y
w
stanach
przej
ściow
ych.
Podstaw
ą
okre
ślenia
przybli
żonego
modelu
matematycznego
systemu
el
ektroenergetyczneg
o
b
ędzie
analiza
sta
łych
czasowych
przebiegów
powstaj
ących
w
stanach
przej
ściow
ych.
Najprostszy
model
musi
uwzgl
ę
dnia
ć
zjawiska
o
najd
łu
ższej
sta
łej
czasowej
pomijaj
ąc
zjawiska
o
krótkich
sta
łych
czasowych
czyli
zak
ładamy,
ż
e
zjawiska
te
s
ą
bezinercyjne.
W
w
ysokonapi
ęciowym
systemie
elektroenergetyczn
ym
mamy
do
czynienia
z
dwoma
rodzajami
el
ementów:
1.
urz
ądzenia
przesy
łowo
‐rozdzie
lcze,
sta
ła
czasowa
sk
ładowe
j aperiodycznej
nie
wi
ę
ksza
ni
ż
0,2
s,
i
nie
wywo
łuje
znacz
ących
momentów
dzia
łaj
ących
na
wa
ł
generatora,
2.
generatory,
w
których
mo
żna
wyró
żni
ć
nast
ępuj
ące
elementy
wraz
z
ich
sta
łymi
czasowymi:
•
uzwojenia
stojana,
których
sta
ła
czasowa
sk
ładowej
aperiodycznej
jest
nie
wi
ę
ksza
ni
ż
0,2s,
•
uzwojenia
t
łumi
ące,
st
ał
a
czasowa
nie
wi
ę
ksza
ni
ż
0,2
s,
" d
T

9
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Model
matematyczn
y
systemu
elektroenergetycznego
•
uzwojenia
wzbudzenia,
sta
ła
czasowa
,
•
wiruj
ąca
masa
wirnika,
sta
ła
czasowa
.
s
T
d
)6,
0
6(
÷
=
′
s
T
m
)
12
4(
÷
=
W
pierwszym
przybli
żeniu,
b
ędziemy
modelowa
ć
generator
jako
uk
ładu
równa
ń
ró
żniczkowych
opisuj
ących
dynamik
ę
mas
wiruj
ących
wirnika.
Energia
kinetyczna
mas
wiruj
ących
jest
zdefiniowana
wzorem:
Zgodnie
z
zasad
ą
zachowania
energii
mamy,
ż
e
w
ka
żdej
chwili
zamianie
mocy
dzia
łaj
ących
na
wirnik
a
wi
ę
c
mocy
mechanicznej
i elektrycznej
towarzyszy
zmiana
energii
kinetycznej,
czyli:
k
E
2
2
ω
⋅
=
J
E
k
m
P
e
P
e
m
k
P
P
t
d
E
d
−
=
ei
mi
i
i
i
P
P
t
d
d
J
−
=
⋅
⋅
ω
ω

10
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Model
matematyczn
y
systemu
elektroenergetycznego
Mamy
tak
że:
t
d
d
i
i
δ
ω
=
mi
i
mi
M
P
⋅
=
ω
ei
i
ei
M
P
⋅
=
ω
oraz
fakt
wyst
ępowania
momentu
(mocy)
t
łumi
ącego
to
otrzymamy:
Di
M
Di
ei
mi
i
i
M
M
M
dt
d
J
−
−
=
⋅
2
2
δ
Równanie
ruchu
obrotowego
wirnika
i‐
tego
generatora
zapiszemy
te
ż
jako
uk
ład
równa
ń
:
i
i
dt
d
ω
δ
=
Di
ei
mi
i
i
M
M
M
dt
d
J
−
−
=
⋅
ω
lub
dt
d
D
P
P
dt
d
J
i
i
ei
mi
i
i
i
δ
ω
ω
⋅
−
−
=
⋅
⋅

11
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Model
matematyczn
y
systemu
elektroenergetycznego
Moment
bezw
ładno
ści
wirnika
generatora
mo
żna
wyrazi
ć
w
funkcji
mechanicznej
sta
łej
czasowej
:
m
T
2
S
N
m
S
T
J
ω
⋅
=
Mechaniczna
sta
ła
czasowa
ma
in
terpretacj
ę
fi
zy
czn
ą.
Je
śli
pominiemy
tł
umienie
i
do
nieruchomego
wirnika
nieobci
ąż
onego
generatora
przy
ło
żymy
znamionowy
moment
turbiny
to
przyspieszenie
wirnika
jest
nast
ępuj
ące:
W
skutek
dzia
łania
takiego
przyspieszenia
pr
ędko
ść
ro
śnie
liniowo
i
po
czasie
wirnik
generatora
uzyskuje
pr
ędko
ść
synchroniczn
ą.
W
przypadku
rozwa
żania
najprostszego
uk
ładu
pracy
generatora,
uk
ładu
generator
‐sie
ć
sztywna
równanie
ruchu
wirnika
generatora
s
ą
postaci:
m
S
mN
mN
S
m
S
S
mN
N
m
S
S
T
M
M
T
M
S
T
dt
d
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
δ
ε
=
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
=
2
2
m
T
t
=
dt
d
D
)
sin(
Z
U
E
sin
Z
E
P
dt
d
J
i
i
ii
i
s
di
ii
di
mi
i
i
i
δ
α
δ
α
δ
ω
⋅
−
−
⋅
⋅
−
⋅
−
=
⋅
⋅
2
2
2

12
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Model
matematyczn
y
systemu
elektroenergetycznego
Przy
pom
in
ię
ciu
rezystancji
w
obwodzie
mamy:
Ko
łysania
wirnika
ge
ne
ratora
przy
chwilowym
zaburzeniu
bilansu
mocy
czynnej
Wprowadzimy
poj
ęcie
wspó
łczynnika
bezw
ładno
ści:
Wtedy
równanie
ruchu
wirnika
generatora
ma
posta
ć:
Pierwszy
sk
ładnik
powy
ższego
równania
mo
żemy
zapisa
ć:
dt
d
D
X
U
E
P
dt
d
J
i
i
i
s
di
mi
i
i
i
δ
δ
δ
ω
⋅
−
⋅
⋅
−
=
⋅
⋅
sin
2
2
i
i
i
J
M
ω
⋅
=
dt
d
M
D
M
P
P
dt
d
i
i
i
i
ei
mi
i
δ
δ
⋅
−
−
=
2
2
i
i
i
i
ei
i
mi
ei
H
d
dP
P
P
P
δΔ
δΔ
δ
Δ
⋅
=
⋅
=
=
−
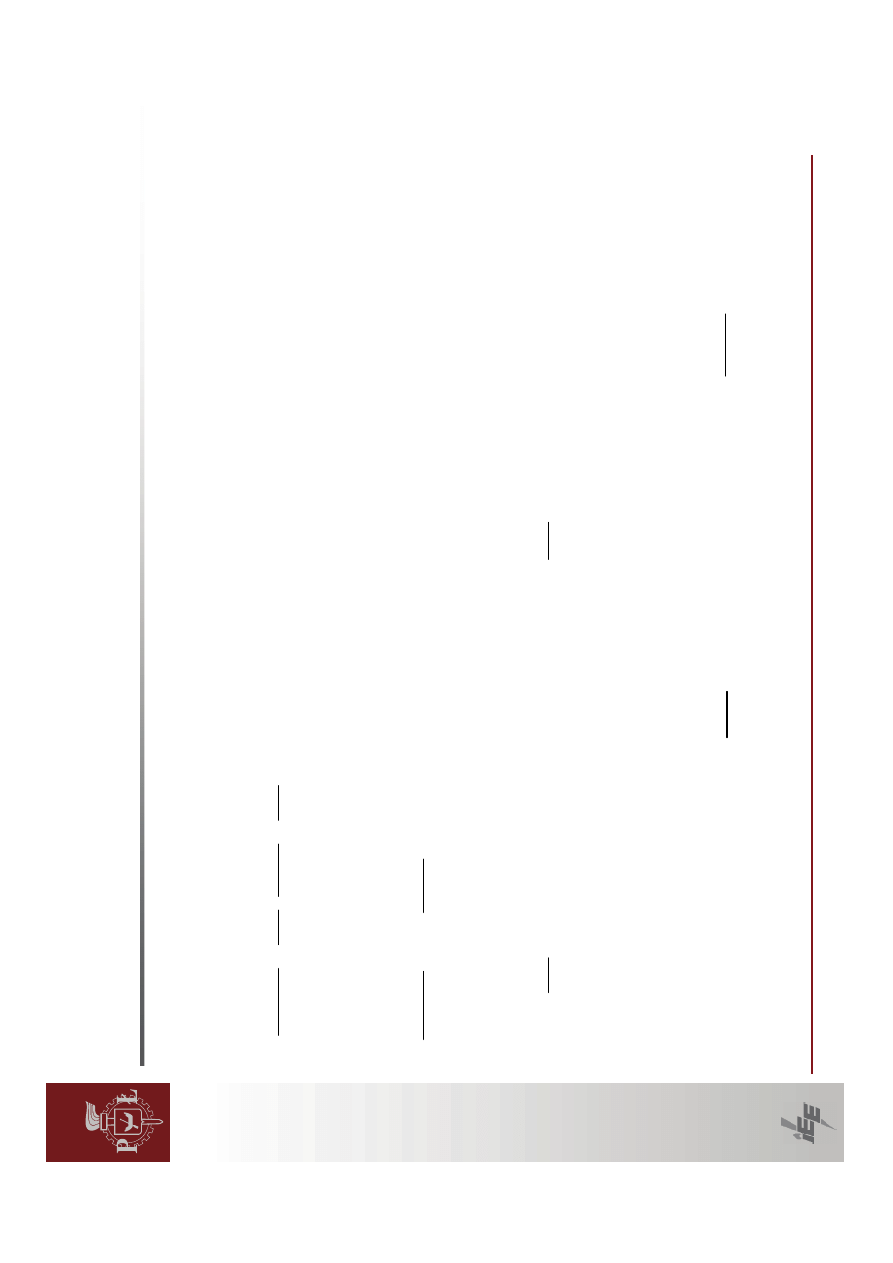
13
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
wirnika
ge
ne
ratora
Równanie
ruchu
wirnika
generatora
linearyzujemy
wokó
ł
rozwa
żanego
pewnego
k
ąta
pocz
ątkowego
. Uwzgl
ędniaj
ąc
to
mamy:
lub
w
postaci:
gdzie:
Ogólne
rozwi
ązanie
równania
ruchu
wirnika
generatora
i
jego
pochodne
s
ą
postaci:
0
)0
(
δ
δΔ
=
=
t
0
2
2
=
⋅
+
⋅
+
i
i
i
i
i
i
i
M
H
dt
d
M
D
dt
d
δΔ
δΔ
δΔ
0
2
2
=
⋅
+
⋅
+
i
i
i
i
i
h
dt
d
d
dt
d
δΔ
δΔ
δΔ
i
i
i
M
D
d
=
i
i
i
M
H
h
=
t
e
A
λ
δΔ
⋅
=
t
e
A
dt
d
λ
λ
δΔ
⋅
⋅
=
t
e
A
dt
d
λ
λ
δΔ
⋅
⋅
=
2
2
2

14
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
wirnika
ge
ne
ratora
Po
podstawieniu
tych
funkcji
do
równania
ruch
wirnika
generatora
otrzymujemy:
Równanie
to
nazywane
jest
równaniem
charakterystycznym
równania
ruch
wirnika
generatora.
Rozwi
ązania
tego
równania
s
ą
nast
ępuj
ące:
Powy
ższe
wielko
ści
to
warto
ści
w
łas
ne
uk
ładu.
W
zale
żno
ści
od
warto
ści
wyra
żenia
pod
pierw
ia
st
kie
m,
warto
ści
w
łasne
oraz
mog
ą
by
ć
rzeczywiste
lub
zespolone.
Rozwi
ązanie
równania
ró
żniczkowego
jest
postaci:
0
2
=
+
⋅
+
h
d
λ
λ
2
4
2
4
2
2
2
1
h
d
d
h
d
d
⋅
−
+
−
=
⋅
−
−
−
=
λ
λ
1
λ
2
λ
t
t
e
A
e
A
2
1
2
1
λ
λ
δΔ
⋅
+
⋅
=

15
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
wirnika
ge
ne
ratora
Musimy
teraz
wyznaczy
ć
sta
łe
i
.
W
wyniku
rozwi
ązania
powy
ższego
uk
ładu
równa
ń
mamy:
Ogólna
posta
ć
rozwi
ązania:
Zak
ładaj
ąc,
ż
e:
Warto
ści
w
łasne
s
ą
zmiennymi
zespolonymi
o
postaci:
1
A
2
A
0
2
2
1
1
0
2
1
=
⋅
+
⋅
=
+
A
A
A
A
λ
λ
δ
1
2
1
0
2
1
2
2
0
1
λ
λ
λ
δ
λ
λ
λ
δ
−
⋅
−
=
−
⋅
=
A
A
(
)
t
t
e
e
2
1
2
1
2
0
1
λ
λ
λ
λ
λ
λ
δ
δΔ
⋅
−
⋅
⋅
−
=
0
>
d
h
d
⋅
<
4
2
w
w
j
j
ω
α
λ
ω
α
λ
+
−
=
−
−
=
2
1
2
4
2
2
d
h
d
w
−
⋅
=
=
ω
α

16
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Model
matematyczn
y
systemu
elektroenergetycznego
Rozwa
żymy
wszystkie
mo
żliwe
przypadki
teg
o
rozwi
ązania:
1.
gdy
9
gdy
9
gdy
Warto
ści
w
łas
ne
oraz
s
ą
teraz
zmiennymi
rzeczywistymi.
2.
gdy
Warto
ści
w
łasne
s
ą
teraz
zmiennymi
rzeczywistymi
ar
o
zw
ią
zanie
m
a
posta
ć:
K
ąt
ro
śnie
ap
er
io
dycznie
a
wi
ęc
taki
punkt
jest
punktem
niestabilnym.
0
>
h
0
>
h
h
d
⋅
<
4
2
()
()
⎥ ⎦
⎤
⎢ ⎣
⎡
⋅
⋅
+
⋅
⋅
⋅
=
−
t
t
e
w
w
w
t
ω
ω
α
ω
δ
δΔ
α
sin
cos
0
h
d
⋅
>
4
2
0
0
2
1
<
<
λ
λ
0
<
h
0
0
2
1
>
<
λ
λ
δ
17
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Model
matematyczn
y
systemu
elektroenergetycznego
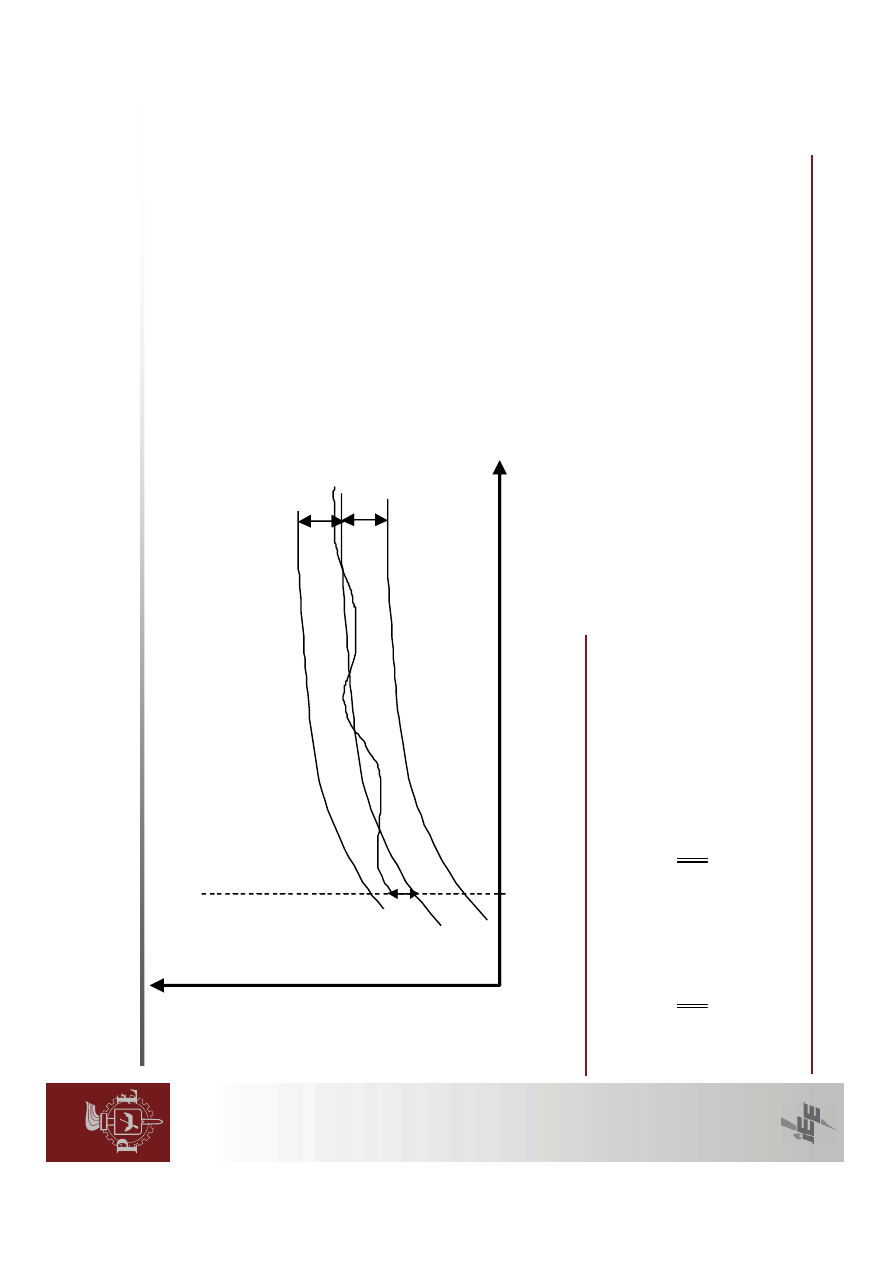
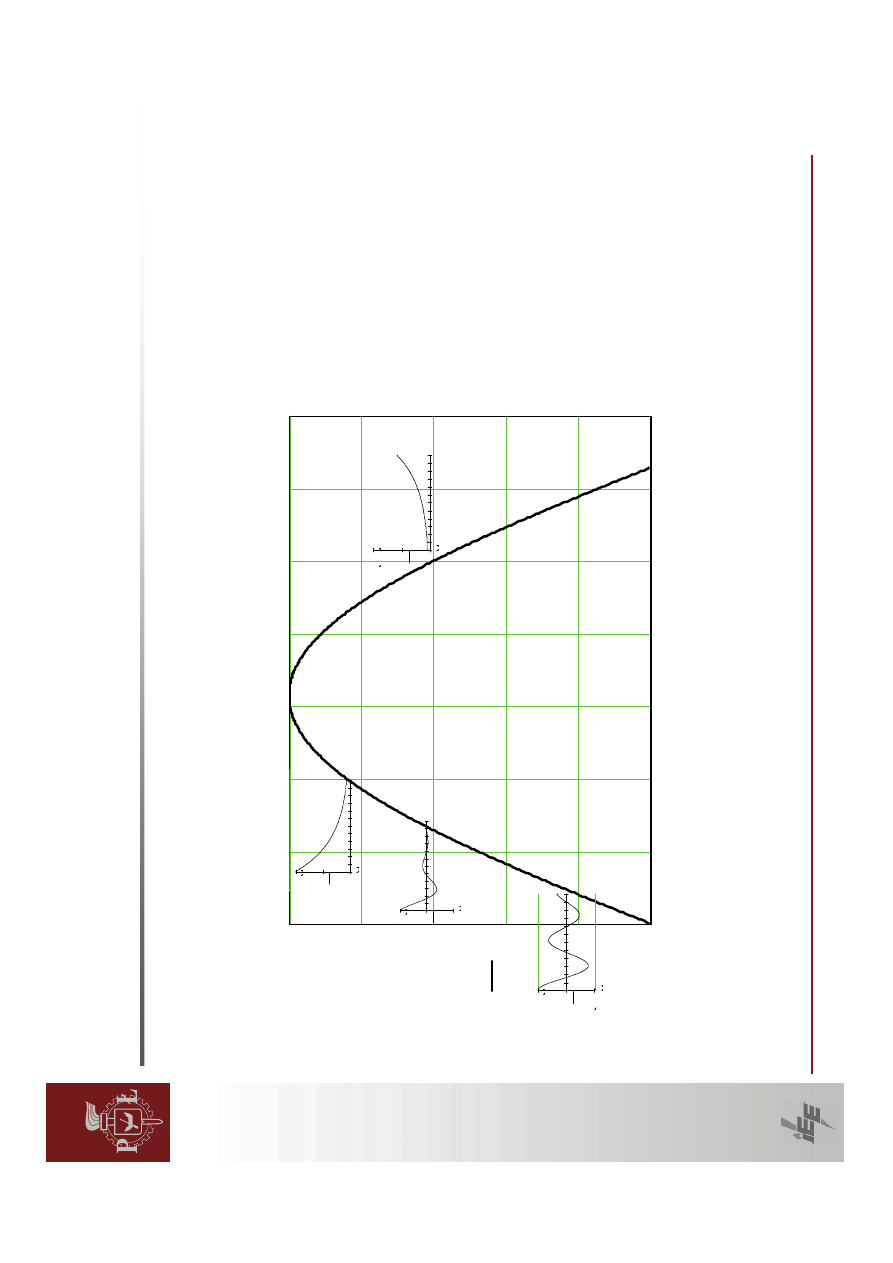
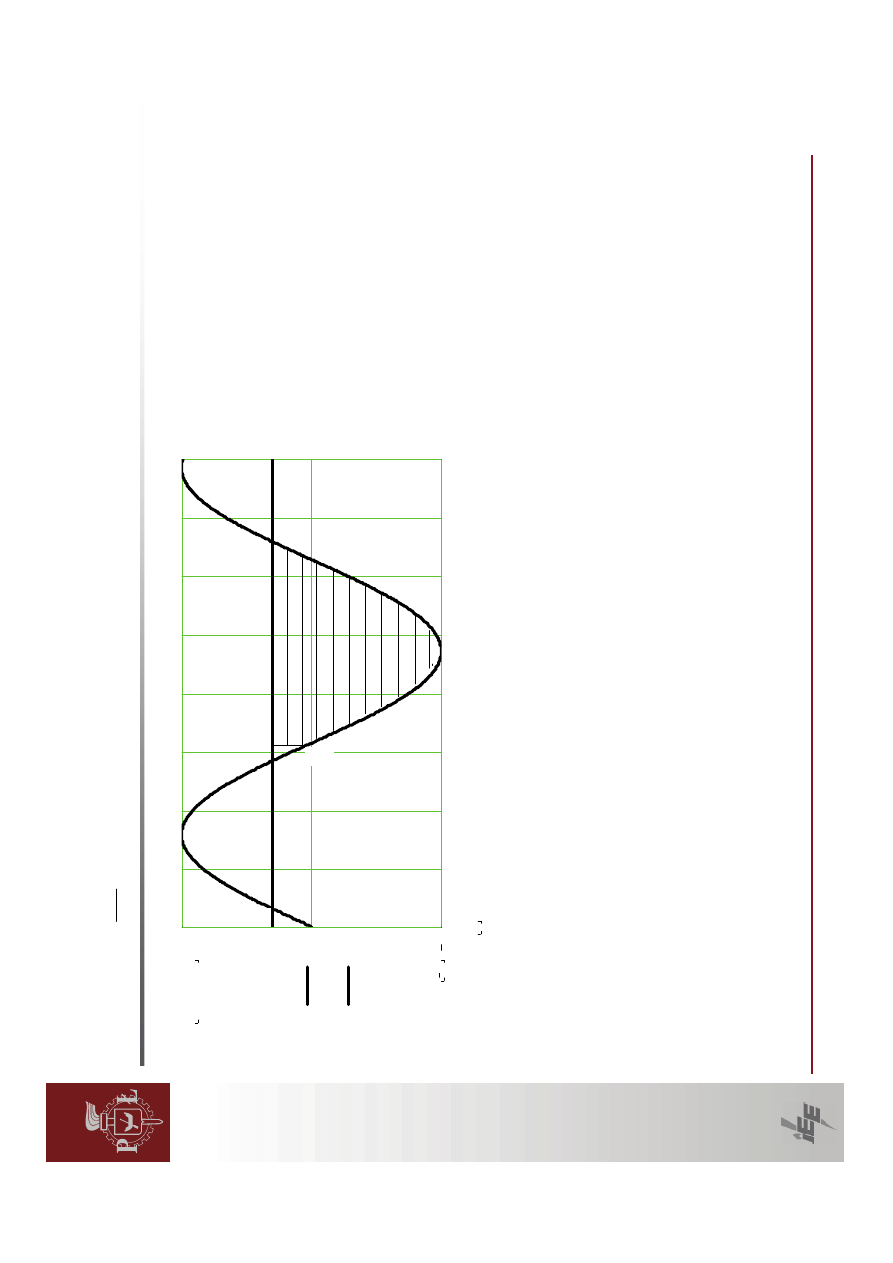
Przyk
ładowe
przeb
ieg
i k
ąta
po
ma
łym
zak
łóceniu
w
ró
żnych
punktach
pracy
generatora.
0
0.5
1
1.5
2
2.5
3
3.
5
0
1
2
3
4
5
P1
i
δ
i⋅
1
0.781
−
δ
i
1
0
α
i⋅
1
0
δ
i
12
0
α
i⋅
20.086
0
δ
i
12
0
α
i⋅
1
1
−
δ
i
12
0
α
i⋅
18
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
δ
d
P
d
W
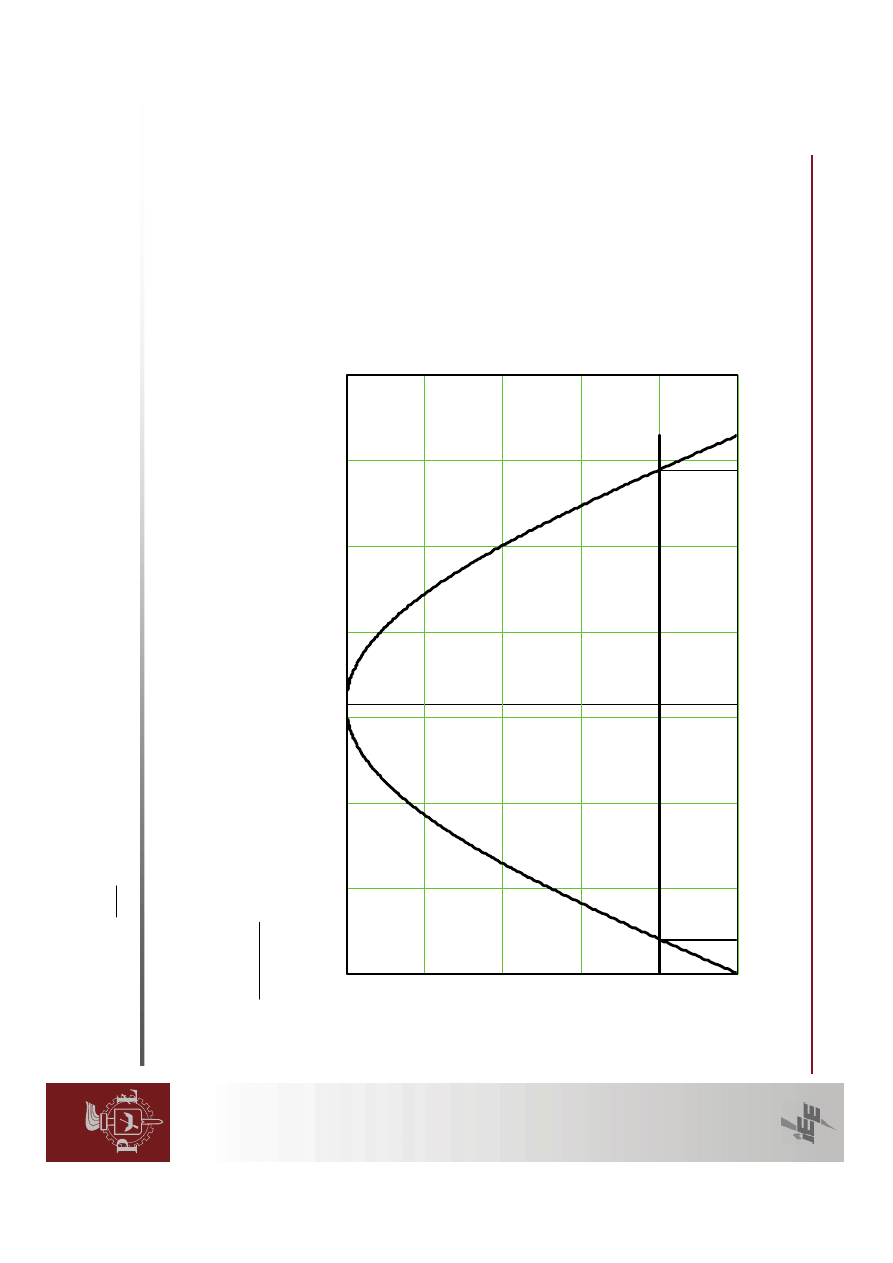
przypadku
rozwa
żenia
uk
ładu
generator
–s
ie
ć
sztywna
pominiemy
w
pierwszym
etapie
rezystancje
uk
ładu.
Wtedy:
δ
sin⋅
⋅
=
E
s
g
e
X
U
E
P
A
B
0
δ
m
P
0
δ
Π
−
e
P
δ
gr
δ
0
0.
5
1
1.5
2
2.5
3
3.5
0
1
2
3
4
5
P1
i
P2
i
δ
i
P

19
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
δ
d
P
d
Wp
rz
yp
ad
ku
, gdy
momenty
mechaniczny
je
st
równy
mocy
el
ektromagnetycznej
tzn.
wirnik
obraca
si
ę
ze
sta
łą
pr
ędko
ści
ą
obrotow
ą.
Gdy
to
wirnik
zmniejsza
lub
zwi
ę
ksza
swoj
ą
pr
ę
dko
ść
.
W
pewnej
chwili
zosta
ł
do
łą
czony
do
rozpatrywanej
sieci
nowy
odbiór
o
mocy
,
przy
czym
odbiór
ten
jest
za
łą
czony
na
pewien
krótki
czas
–z
ałą
czenie
to
ma
charakter
zak
łócenia.
Wtedy
i
wirnik
b
ędzie
hamowany
czyli
zacznie
male
ć
jego
pr
ędko
ść
obrotowa.
0
=
+
e
m
M
M
0
=
+
e
m
P
P
0
≠
+
E
m
P
P
e
e
e
P
P
P
Δ
+
=
1
m
e
P
P
>
1
m
e
M
M
>
1
20
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
δ
d
P
d
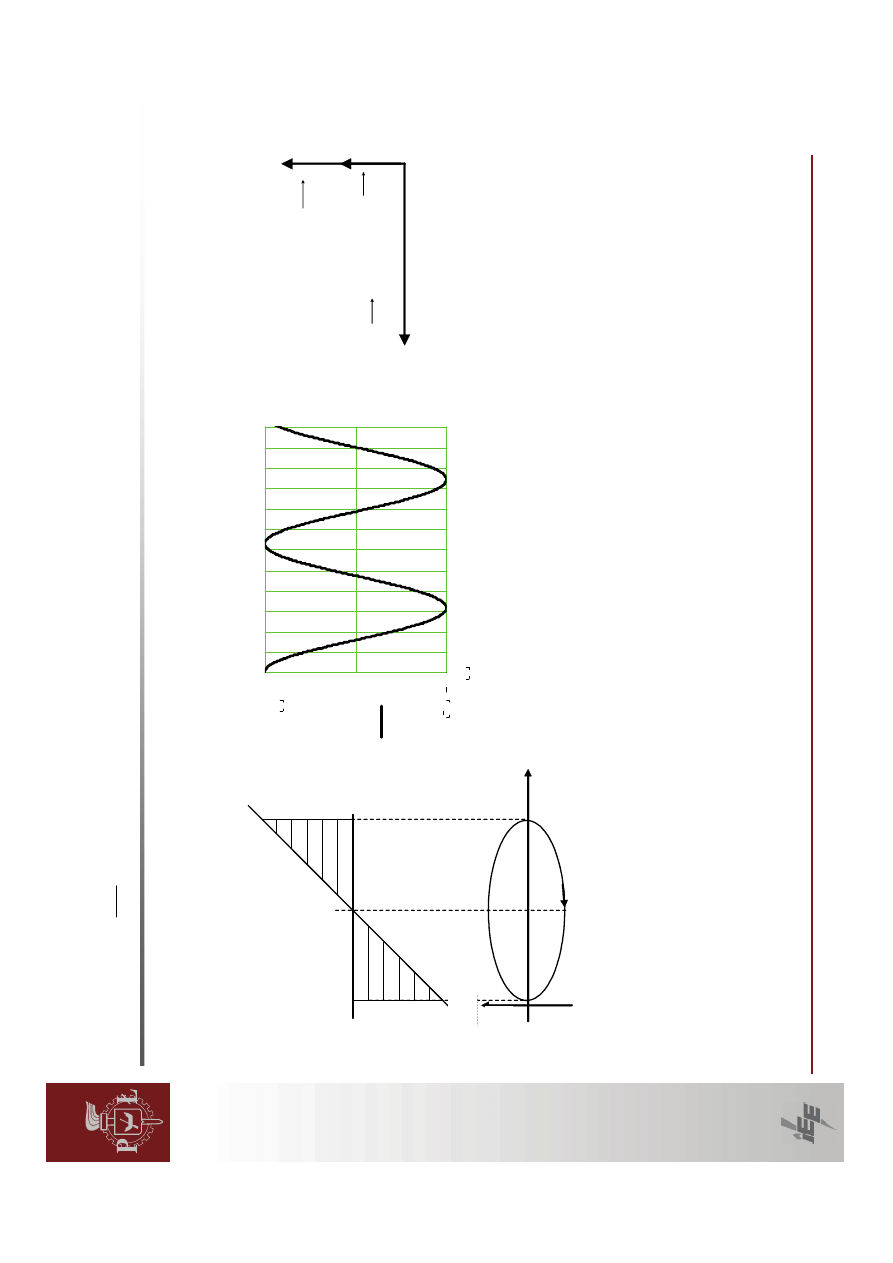
Mamy
teraz
dwie
ró
żne
sytuacje:
1.
Praca
w
punkcie
A
Do
łą
czenie
dodatkowej
mocy
powoduje,
ż
e
generator
znajduje
si
ę
w
punkcie
2.
Wirnik
b
ędzie
hamowany,
czyli
zacznie
male
ć
jego
pr
ędko
ść
obrotowa
wywo
łuj
ąc
zmniejszenie
k
ąta
i
w
konsekwencji
zmniejszenie
mocy
przesy
łanej
zg
en
e
ra
to
rad
o
sieci
sztywnej
zgodnie
zc
h
ar
ak
te
ry
st
yk
ą.
A
2
3
4
5
m
P
e
P
ω
δ
a)
b)
1
1
P1
i
12
0
δ
i.
1
0
1
ωΔ
e
P
Δ
δΔ

21
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
Wtedy
moc
niezbilansowana
maleje.
W
punkcie
A
moc
el
ektryczna
i
m
echaniczna
są
sobie
równe,
lecz
ruch
wirnika
nie
zostanie
zatrzymany.
Wt
ra
kc
ie
sw
o
je
j drogi
od
punktu
2
do
A
ww
ir
n
ik
u
zo
st
ał
a
zgromadzona
pewna
ilo
ść
energii
kinetycznej
hamuj
ącej
ap
rę
dko
ść
obrotowa
jest
mniejsza
od
synchronicznej.
Energia
kinetyczna
hamuj
ąca
wynosi:
Zak
ładaj
ą,
ż
e
zmiany
pr
ędko
ści
obrotowej
s
ą
niewiele
ró
żne
od
synchronicznej
to
energia
kinetyczna
hamuj
ąc
jest
proporcjonalna
do
pola
powierzchni
A,
2,
3.
Po
mini
ęciu
punktu
A
pr
ędko
ść
zacznie
rosn
ąć
. Teraz
wirnik
wychyli
si
ę
do
punktu
5
gromadz
ąc
po
drodze
energi
ę
kinetyczn
ą
przyspiesz
aj
ąc
ą.
Po
ło
żenie
punktu
5
wynika
zr
ó
w
n
o
ści
energii
kinetycznej
hamuj
ącej
ip
rz
ys
p
ie
sz
aj
ącej.
Mo
żna,
wi
ę
c
stwierdzi
ć,
ż
e
pole
powierzchni
A,
5,
4
musi
by
ć
równe
polu
A,
2,
3.
()
∫
⋅
−
=
t
d
P
P
E
e
m
kh
Δ
()
()
∫
∫
⋅
−
⋅
=
⋅
−
=
δ
ω
δ
ω
Δ
d
P
P
d
P
P
E
e
m
e
m
kh
1
δ
d
P
d
22
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
Ten
wywód
nos
i nazw
ę
metody
równych
powierzchni.
W
punkcie
5
zrówna
ły
si
ę
energie
kinetyczne
hamuj
ąca
i
przyspieszaj
ąca,
lecz
mamy
ró
żnic
ę
mocy
. Moc
nap
ędowa
jest
wi
ę
ksza
od
hamuj
ącej
iw
ir
n
ik
b
ędzie
przyspiesza
ł
dalej.
2.
Praca
w
punkcie
B
1
1
P1
i
Pm
i
4
4
δ
j i
.
4
2
0
2
4
1
0.
5
0
0.
5
1
A
B
2
3
4
5
δ
d
P
d

23
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
Do
łą
czenie
dodatkowej
mocy
powoduje,
ż
e
generator
znajduje
si
ę
w
punkcie
2.
Wirnik
b
ędzie
hamowany,
czyli
zacznie
male
ć
jego
pr
ędko
ść
obrotowa
wywo
łuj
ąc
zmniejszenie
k
ąta
i
w
konsekwencji
powi
ę
kszenie
mocy
przesy
łanej
zg
en
e
ra
to
rad
o
sieci
sztywnej
zgodnie
zc
h
ar
ak
te
ry
st
yk
ą.
Wtedy
moc
niezbilansowana
wzro
śnie.
W
punkcie
A
moc
el
ektryczna
i
m
echaniczna
są
sobie
równe,
lecz
ruch
wirnika
nie
zostanie
zatrzymany.
Wt
ra
kc
ie
sw
o
je
j drogi
od
punktu
2
do
A
ww
ir
n
ik
u
zo
st
ał
a
zgromadzona
pewna
ilo
ść
energii
kinetycznej
hamuj
ącej
(pole
3,
2,
A)
ap
rę
dko
ść
obrotowa
jest
mniejsza
od
synchronicznej.
W
tym
wypad
ku
ustali
jednak
si
ę
nowy
sta
bilny
punkt
pracy,
punkt
A,
lecz
nie
b
ędzie
to
wyj
ściowy
punkt
B.
Nast
ępny
przypadek
to
od
łą
czenie
od
rozpatrywanej
sieci
odbioru
o
mocy
()
e
z
e
m
P
P
P
Δ
δ
−
−
e
P
Δ
δ
d
P
d
24
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
0.
99
99
95
1
P1
i
Pm
i
8
0
δ
i.
0
1
2
3
4
5
6
7
8
1
0
1
A
B
2
3
C
Moc
elektryczna
jest
mniejsza
od
mocy
mechanicznej
wirnik
b
ędzie
przyspieszany,
czyli
zacznie
rosn
ąć
pr
ędko
ść
obrotowa.
Powi
ę
kszenie
k
ąta
pow
odu
je
powi
ę
kszenie
mocy
przesy
łanej
z
generatora
do
sieci
sztywnej.
Wtedy
moc
niezbilansowana
wzro
śnie
co
prowadzi
do
destabilizacji
pracy
maszyny.
W
tym
wypadku
nie
ustali
jednak
si
ę
nowy
stabilny
punkt
pracy
a
pr
ędko
ść
wirnika
b
ę
dzie
ros
ła
w
niesko
ń
cz
on
o
ść
.
δ
d
P
d

25
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
Reasumuj
ąc
powy
ższe
rozwa
żania
o
zmianach
mocy
elektrycznej
mo
żna
stwierdzi
ć,
ż
e:
9
Punkt
A
jest
punktem
pracy
stabilnej.
9
Punkt
B
jest
punktem
pracy
niestabilnej.
9
Stabilna
praca
jest
tylko
na
odcinku,
gdzie
.
9
Gdy
warto
ść
praca
generatora
jest
niestabilna.
9
Warunek
jest
kryterium
okre
ślania
granicy
równowagi
st
atycznej.
9
Granica
równowagi
statycznej
wyst
ępuje,
gdy
.
Pochodn
ą
mocy
po
k
ącie:
nazywamy
moc
ą
synchronizuj
ąc
ą
generatora.
Moc
synchronizuj
ąca
jest
miar
ą
zapasu
stabilno
ści
generatora.
0
≥
δ
d
dP
0
<
δ
d
dP
δ
d
dP
0
=
δ
d
dP
δ
δ
cos⋅
⋅
=
E
S
g
X
U
E
d
dP
δ
d
P
d

26
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
Dotychczas
analizowano
generator,
gdy
brak
jest
dzia
łania
jego
regula
torów
wzbudzenia.
Wtedy
granic
ę
równowagi
st
atycznej
nazywamy
naturaln
ą
granic
ą
równowagi
st
atycznej.
Rozwa
żmy
teraz
uk
ład,
w
którym
generator
jest
jednak
wyposa
żony
w
regulator
wzbudzenia.
Regulator
wzbudzenia
star
a
si
ę
utrzyma
ć
sta
łe
napi
ę
cie
generatora
poprzez
zmian
ę
napi
ę
cia
wzbudzenia
z
ograniczeniami
w
ynikaj
ącymi
z
dopuszczalnego
jego
zakresu
pracy.
Rozwa
żany
regulator
wzbudzenia
mo
że
by
ć:
powolny
lub
Szybki.
Jako
regulator
szybki
b
ędziemy
uwa
żali
taki
regulator,
który
utrzymuje
sta
łą
warto
ść
napi
ę
cia
na
zaciskach
generatora
bezpo
średnio
po
zmianie
obci
ąż
enia.
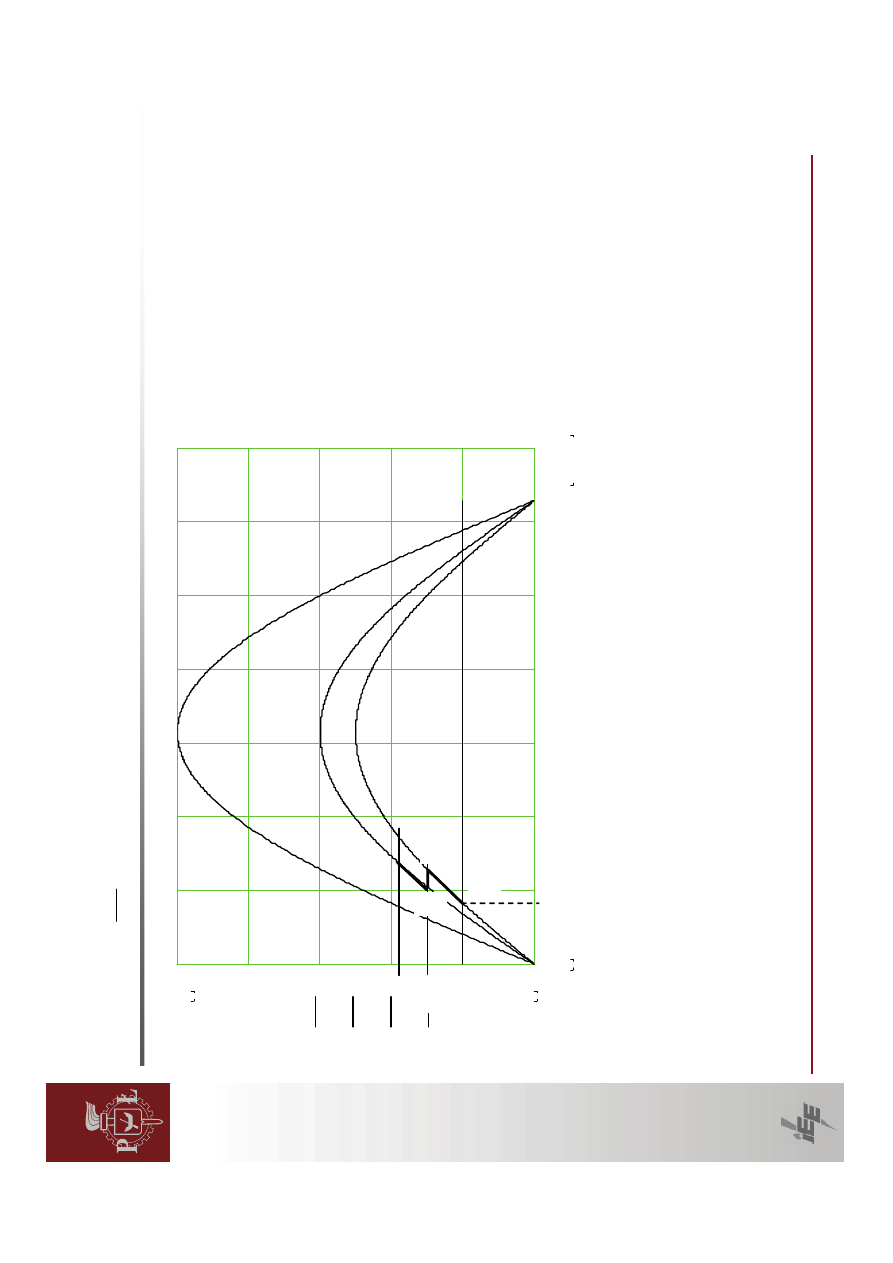
W
regulatorze
powolnym
po
zmianie
obci
ąż
enia
zw
ar
to
ści
(punkt
A)
do
nast
ępuje
zmiana
k
ąta
zgodnie
zw
yj
ściow
ą
charakterystyk
ą
(punkt
B)
ad
o
p
ie
rop
ó
źniej
regulator
zwi
ę
ksza
napi
ę
cie
wzbudzenia
tak,
aby
napi
ęcie
na
zaciskach
generatora
by
ło
st
ał
e.
Zmiana
napi
ęcia
wzbudzenia
pow
odu
je
powi
ększenie
si
ły
elektromotoryczne
generatora
w
efekcie
charakterystyki
.
Generatora
znajdzie
si
ę
w
punkcie
C.
Kolejne
etapy
pracy
s
ą
wi
ę
c
nast
ępuj
ące:
zwi
ę
kszenie
obci
ąż
enia
przy
sta
łym
wzbudzeniu
i
zwi
ę
kszenie
napi
ę
cia
wzbudzenia.
0
P
1
P
()
δ
P
δ
d
P
d
27
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
5
0
P1
i
P3
i
P4
i
P2
i
3.1
415
93
0
δ
i.
0
0.5
1
1.5
2
2.5
3
3.5
0
1
2
3
4
5
B
C
A
0
P
1
P
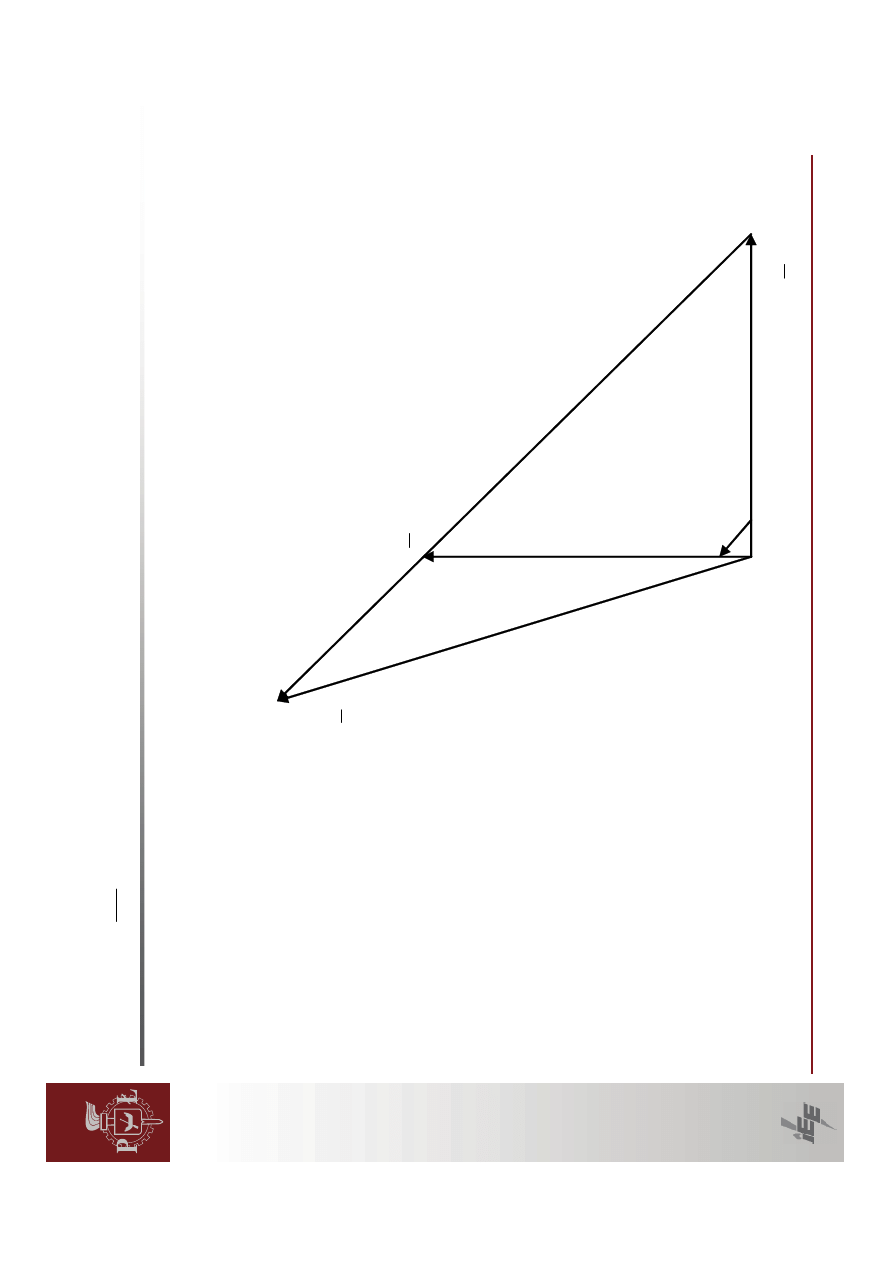
W
regulatorze
szybkim
po
zmianie
obci
ąż
enia
nast
ępuje
natychmiastowa
zmiana
napi
ę
cia
wzbudzenia
tak,
ż
e
napi
ę
cie
na
zaciskach
generatora
pozostaje
sta
łe.
W
wyniku
zamiast
klasycznej
zale
żno
ści
mocy
czynnej
od
k
ąta
otrzymujemy
przebieg
jak
na
rysunku
poni
żej.
δ
d
P
d

28
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
7.
68
0401
0
P1
i
P3
i
P4
i
P2
i
P6
i
3.
14
1593
0
δ
i.
0
0.5
1
1.
5
2
2.
5
3
3.
5
0
2
4
6
8
Warunek
jest
dla
niej
spe
łniony
przy
k
ącie
. W
ak
tualnie
stosowanych
regulatorach
osi
ąga
si
ę
.
0
=
δ
d
dP
°
>
90
δ
°
≈
120
δ
δ
d
P
d
29
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
Jest
to
tzw.
sztuczna
(dynamiczna)
granica
równ
ow
agi
statycznej.
Moc
graniczna
jest
wtedy
wi
ę
ksza
od
mocy
granicznej
równowagi
naturalnej.
Wykres
wskazowy
generatora
wp
rz
yp
ad
ku
w
ys
tę
powania
sztucznej
granicy
równowagi
st
atycznej.
g
U
d
E
o
90
S
U
δ
d
P
d

30
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryterium
Z
powy
ższego
wykresu
wskazowego
wynika,
ż
e
ką
t
90
stopni
jest
tu
równie
ż
utrzymywany
jednak
nie
pomi
ędzy
si
łą
elektromotoryczn
ą
generatora
in
ap
ię
ciem
sieci
sztywnej
a
pomi
ę
dzy
napi
ęciem
na
zaciskach
generatora
in
ap
ię
ciem
sieci
sztywnej.
Okre
śleni
e
punktu
pracy
wzgl
ędem
granicy
równowagi
definiuje
si
ę
przez
trzy
wspó
łczynniki
zapasu
stabilno
ści
statycznej:
o
o
gr
p
P
P
P
k
−
=
o
o
gr
k
δ
δ
δ
δ
−
=
o
gr
o
u
U
U
U
k
−
δ
d
P
d

31
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Kryteria
w
uk
ład
zie
wielomaszynowym
W
przestrzeni
o
wspó
łrz
ędnych
zbiór
punktów
st
abilnych
nazywamy
obszarem
stabilno
ści
loka
lnej.
Wewn
ątrz
tego
obszaru
mamy
st
an
y
stabilne.
Na
zewn
ątrz
niestabilne.
Brzeg
obsza
ru
stabilno
ści
nazywamy
powierzchni
ą
stanów
granicznych.
(
)
,
,
,
,1
,2
,1
n
n
n
n
−
δ
δ
δ
K
δ
d
P
d
32
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
Rozwa
żymy
teraz
wp
ływ
t
łumienia
pochodz
ącego
od
uzwoje
ń
tł
umi
ących
na
przebiegi
ko
łysa
ń
wirnika
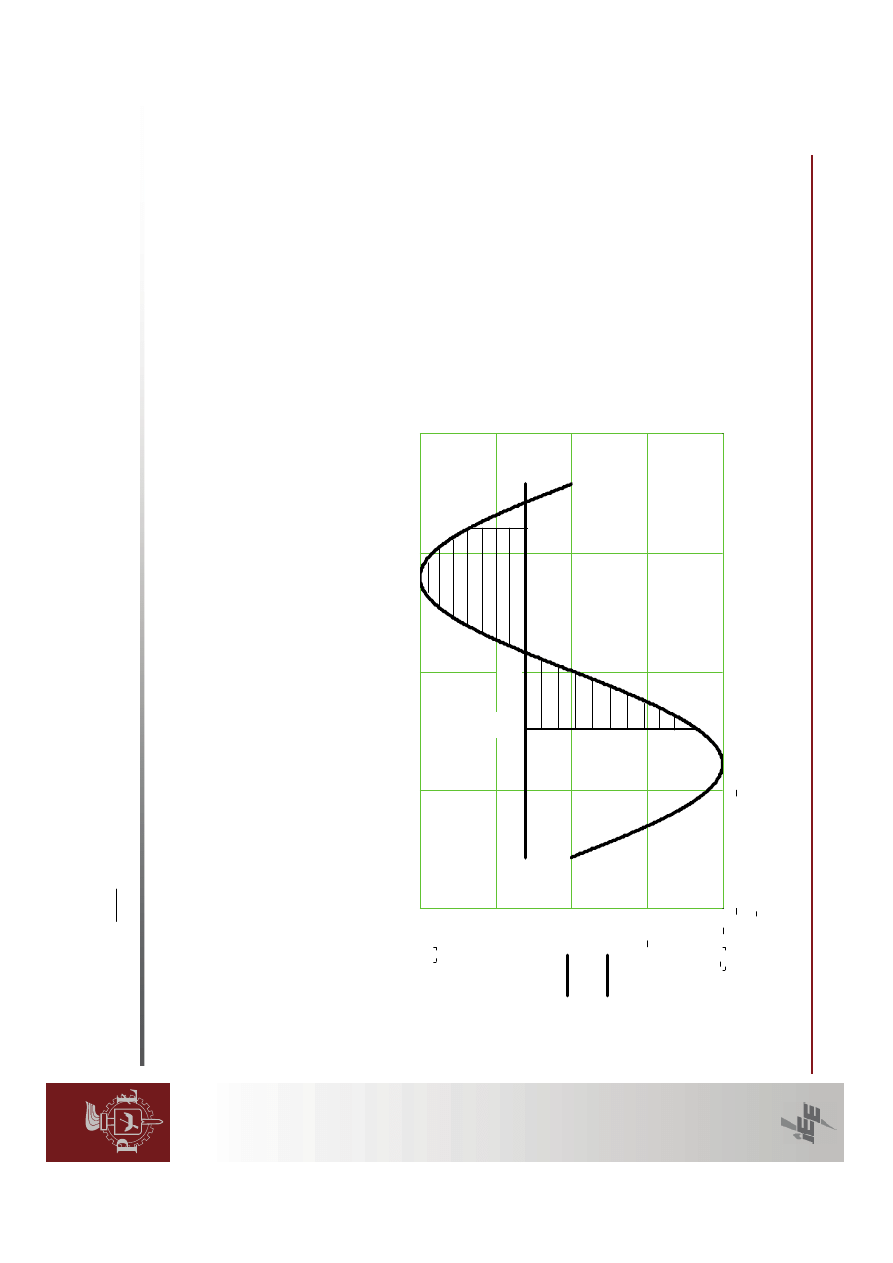
generatora.
W
tym
celu
przeanalizujemy
przypadek
pracy
generatora
w
punkcie
stabilnym
A
po
pojawieniu
si
ę
dodatkowego
obci
ąż
enia
moc
ą
czynn
ą.
Do
łą
czenie
dodatkowej
mocy
powoduje,
ż
e
generator
znajduje
si
ę
w
punkcie
2
.
A
2
3
4
5
6
7
ω
δ
a)
b)
m
P
e
P
8
1
0.
78
12
62
P1
i
12
0
δ
i.
1
0
1
ωΔ
e
P
Δ
δΔ
D
e
Δ
D
i
Δ
D
P

33
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
Wirnik
b
ędzie
hamowany,
czyli
zacznie
male
ć
jego
pr
ędko
ść
obrotowa
wywo
łuj
ąc
zmniejszenie
k
ąta
i
w
konsekwencji
zmniejszenie
mocy
prze
sy
łanej
z
generatora
d
o
sieci
sztywnej.
Pr
ę
dko
ść
obrotowa
jest
ró
żna
od
synchronicznej
aw
ię
cp
o
ja
w
ia
si
ę
po
ślizg
i
tym
samym
sk
ładnik
mocy
tł
umi
ącym
w
równaniu
ró
żniczkowym
ruchu
wirnika
st
aje
si
ę
ró
żny
od
zera.
Moc
elektryczna
jest
zmniejszana
os
kł
adnik
p
roporcjonalny
do
mocy
tł
umi
ącej.
Ruch
wirnika
nie
odbywa
si
ę
po
charakterystyce
, lecz
poni
żej.
W
wyniku
pole
hamowania
jest
okre
ślo
ne
punktami
2,
3,
4
an
ie
ja
k
poprzednio
2,
3,
A.
W
punkcie
4
mamy
najmniejsz
ą
pr
ędko
ść
obrotow
ą
wirnika.
W
tej
sytuacji
wirnik
równie
ż
w
ruchu
przyspiesza
ją
cym
nie
osi
ągnie
taki
ego
k
ąta
jak
uprzednio
lecz
punkt
6.
Moc
tak
że
nie
osi
ągnie
warto
ści
takiej
jak
w
chwili
pocz
ątkowej,
lecz
mniejsz
ą.
Wychylenie
do
punktu
5
b
ędzie
takie
aby
za
kre
skowane
pole
górne
2,
3,
4
(energia
kinetyczna
hamuj
ąca)
by
ło
równe
zakreskowanemu
polu
dolnemu
4,
5,
6
(energia
kinetyczna
przyspies
zaj
ąca).
(
)
δ
P

34
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
W
punkcie
5
wirnik
zaczyna
mie
ć
dodatni
po
ślizg
(rys.
b)
i
d
latego
moc
t
łumi
ąca
zmienia
znak
id
o
d
aj
es
ię
do
mocy
elektrycznej.
Krzywa
zmian
mocy
w
funkcji
ką
ta
le
ży
powy
żej
charakterystyki
mocy
elektrycznej
generowanej.
Ruch
przebiega
do
punktu
5
przez
7
do
8.
W
punkcie
7
znów
mamy
równo
ść
mocy,
lecz
nie
energii
kinetycznych
i
pr
ędko
ści,
dlatego
drgania
trwaj
ą
dalej.
Punktem
ko
ń
cowym
tych
drga
ń
b
ędzie
punkt
A.
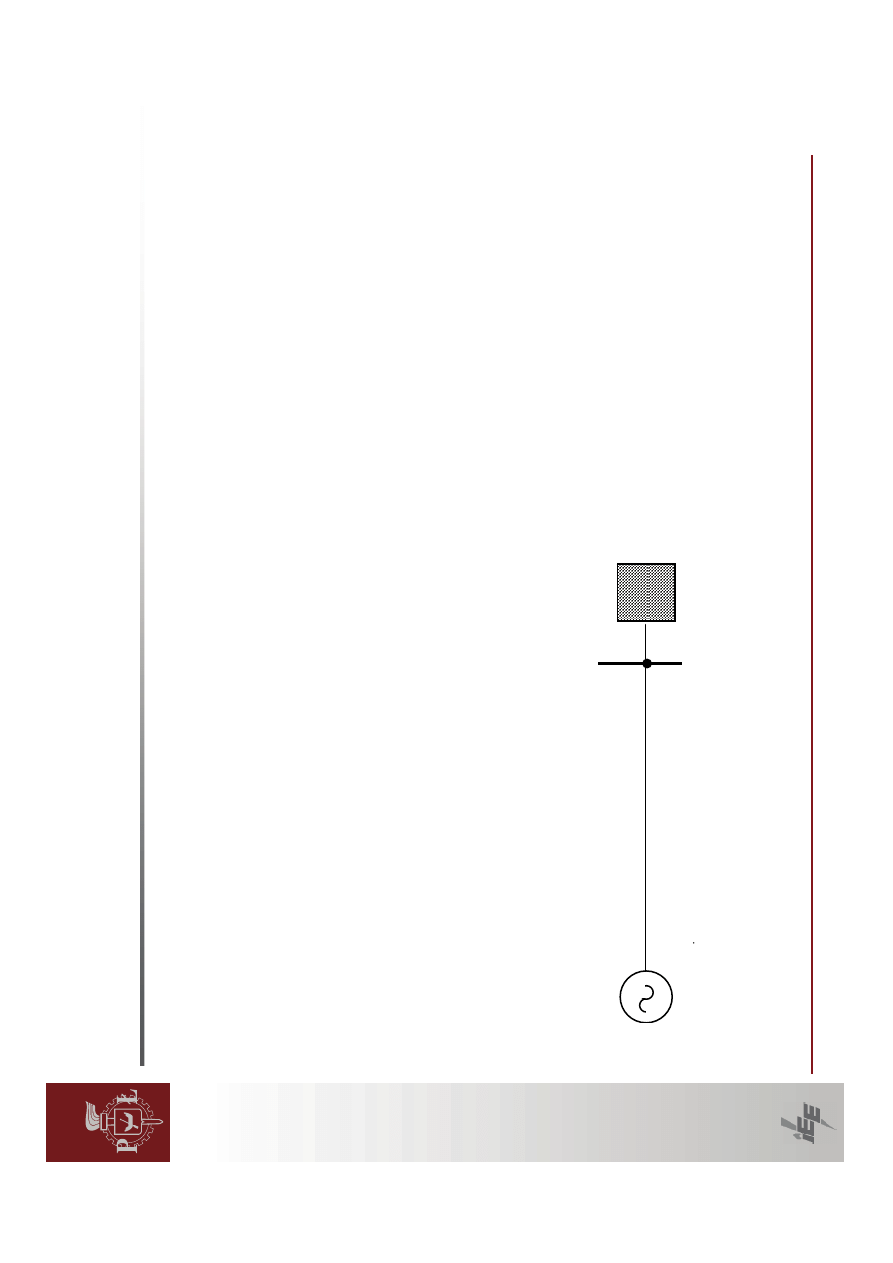
Na
rysunku
b
naszkicowano
pocz
ątkowy
przeb
ieg
pr
ędko
ści
obrotowej
wirnika
w
funkcji
ką
ta.
Jest
to
tzw.
port
re
t
faz
o
w
y,
czyli
najlepszy
widok
zmiennych
st
anu.
Rys.
c
obrazuje
przebieg
zmian
mocy
czynnej
w
funkcji
czasu.
Wida
ć
zn
ie
go
oscylacyjne
t
łumiony
charakter
tych
zmian.
Rys.
d
o
brazuje
nam
zmienne
uczes
tnicz
ące
wp
ro
ce
si
ez
ap
re
ze
n
to
w
an
e
jako
wektory.
Tak
jak
poprzednio
tak
i
tu
zmiana
pr
ędko
ści
obrotowej
jako
pochodna
zmiany
k
ąta
wyprzedza
go
w
fazie
o
90
stopni.
Wektor
reprezentuj
ący
zmiany
mocy
jest
wf
az
ie
zw
ek
to
re
mk
ąta.
Uzwojenie
tł
umi
ące
generatora
zachowuje
si
ę
jak
klatka
silnika
asynchronicznego,
je
śli
tylko
pojawi
si
ę
zmiana
pr
ę
dko
ści
obrotowej
wirnika.
35
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
W
uzwojeni
t
łumi
ącym
indukuje
si
ę
si
ła
elektromotoryczna
proporcjonalna
do
po
ślizgu
il
eżą
ca
w
fazie
z
n
im.
Znaczna
rezystancja
uzwojenia
t
łumi
ącego
powoduje,
ż
e
pr
ąd
wu
zw
o
je
n
iu
tł
umi
ącym
jest
opó
źniony
w
fazie
wzgl
ędem
si
ły
elektromotorycznej.
Moc
t
łumi
ąca
jest
równa
iloczynowi
si
ły
elektromotorycznej
i
rzutowi
pr
ądu
t
łumienia
na
o
ś
si
ły
elektromotorycznej.
Z
tego
rozwa
żania
wida
ć,
ż
e
rezystancja
uzwojenia
t
łumi
ącego
powinna
by
ć
du
ża
wp
o
ró
w
n
an
iud
o
jego
reaktancji.
Rozwa
żymy
wp
ływ
uk
ładu
regulacji
napi
ę
cia
na
przebieg
procesu
ko
łysa
ń
wirnika
wywo
łanych
za
kł
óceniem
w
poborze
mocy
czynnej.
W
tym
celu
wyprowadzimy
zale
żno
ść
na
napi
ęcie
na
zaciskach
generatora
w
funkcji
ką
ta
pomi
ę
dzy
jego
si
ła
elektromotoryczn
ą
in
ap
ię
ciem
sieci
sztywnej.
G
L
UE

36
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
Pr
ąd
p
łyn
ący
wu
kł
adzi
e
w
ynos
i:
St
ąd
napi
ęcie
generatora:
Modu
ł
napi
ę
cie
generatora:
()
X
X
j
U
e
E
I
d
S
j
d
G
+
′
−
′
=
δ
=
+
′
−
′
+
′
+
=
+
=
S
d
j
d
d
S
G
S
G
U
X
X
X
e
E
X
X
X
U
I
X
j
U
U
δ
⎥ ⎦
⎤
⎢ ⎣
⎡
′
+⎟ ⎠
⎞
⎜ ⎝
⎛
′
+
′
+
′
=
δ
δ
sin
cos
d
d
S
d
d
E
j
E
U
X
X
X
X
X
()
2
2
cos
2
d
d
S
d
S
d
d
G
E
E
U
X
X
U
X
X
X
X
X
U
′
+
⋅
′
⋅
⋅
′
⋅
+
⎟ ⎠
⎞
⎜ ⎝
⎛
′
+
′
=
δ

37
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
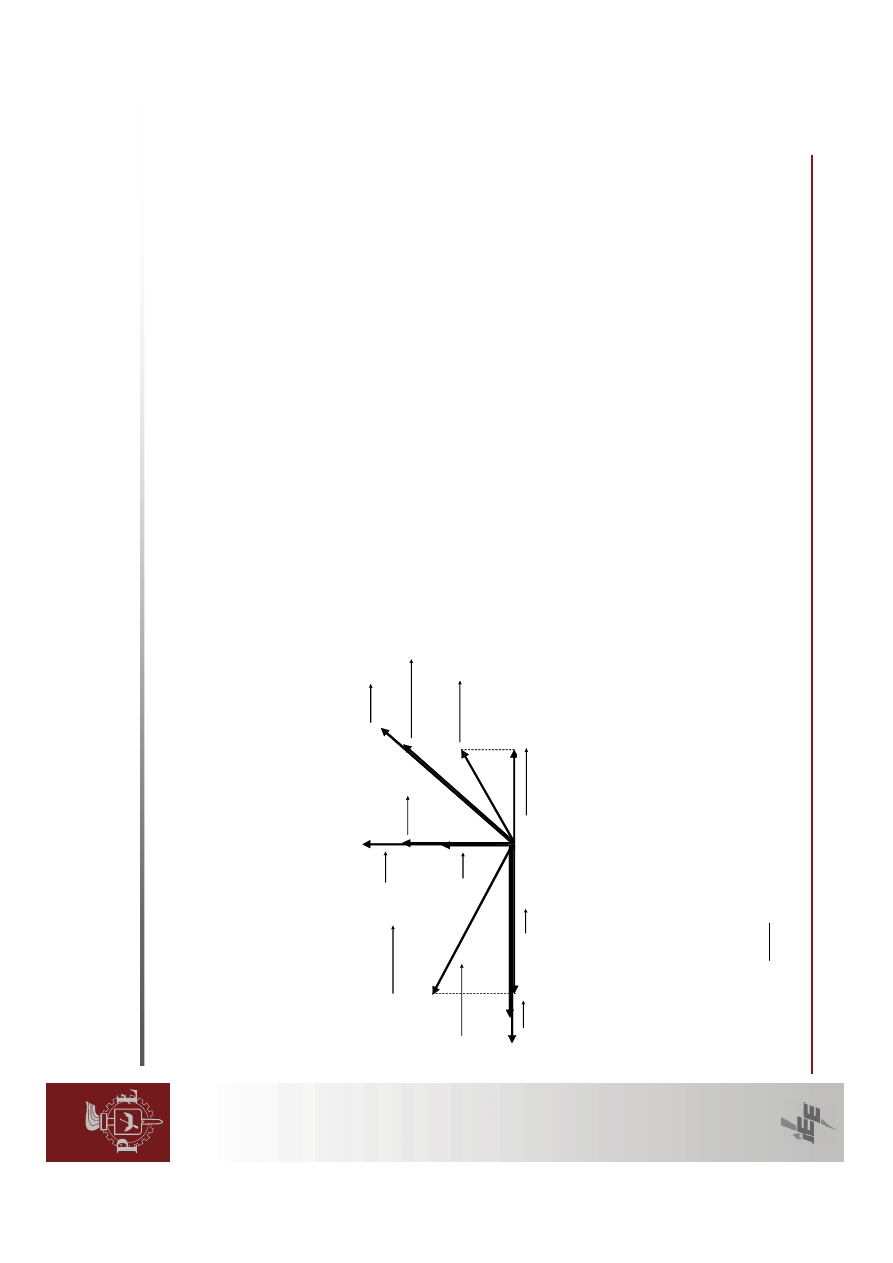
Przebieg
napi
ę
cia
na
zaciskach
generatora
w
funkcji
ką
ta.
1
0
U
i
U1
i
6.
28
31
85
0
δ
i.
0
1.
4
2.
8
4.
2
5.
6
7
Z
wykresu
tego
wynika,
ż
e
podczas
ko
łysa
ń
wirnika
wywo
łanych
zak
łóceniem
wp
o
b
o
rz
e
m
o
cy
czynnej
powstaj
ą
znaczne
zmiany
napi
ęcia
generatora.
Zmiany
te
b
ęd
ą
zauwa
żone
przez
regulator
napi
ę
cia
generatora,
który
obserwuj
ąc
obni
żenie
napi
ęcia
generatorowego
zareaguje
i
p
odniesie
napi
ę
cie
wzbudzenie
a
w
konsekwencji
napi
ę
cie
na
zaciskach
generatora.
Zwi
ę
kszenie
si
ę
napi
ę
cia
generatorowego
powy
żej
warto
ści
zadanej
regulatora
spowoduje
obni
żenie
napi
ę
cia
wzbudzenia,
czyli
napi
ę
cie
na
zaciskach
generatora.
38
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
Uzwojenie
t
łumi
ące
le
ży
w
o
si
synchronicznej
pod
łu
żnej
maszyny.
W
tej
samej
osi
le
ży
uzwojenie
wzbudzaj
ące
generatora.
W
tej
sytuacji
zmiany
pr
ądu
wzbudzenie
s
ą
transformo
wane
nie
tylko
do
uzwoje
ń
statora,
ale
tak
że
do
uzwojenia
t
łumi
ącego
.
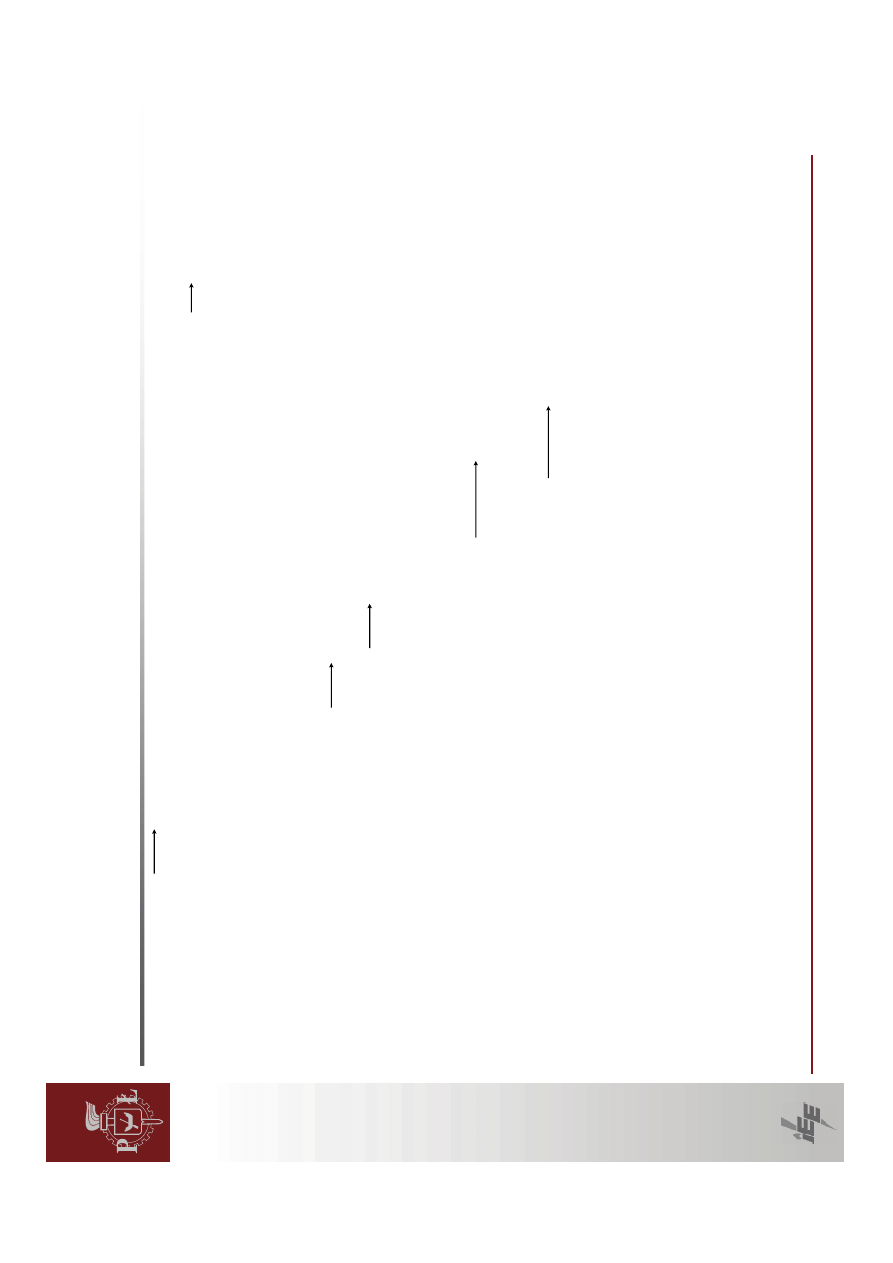
Wykres
wskazowy
dla
uk
ładu
t
łumienia
zr
eg
u
la
cj
ą
wzbudzenia.
W
automatycznym
regulatorze
napi
ęcia
(wzbudzenia)
wielko
ść
mierzona,
czyli
napi
ę
cie
i
w
ielko
ść
zadana
twor
zą
uchyb
regulacji:
a
pochodna
nap
ię
cia
po
k
ącie
jest
ujemna
ws
ta
b
iln
ymo
b
sz
ar
ze
pracy,
czyli:
ωΔ
e
P
Δ
δΔ
()
ωΔ
Δ
D
e
()
ωΔ
Δ
D
i
D
P
r
U
Δ
f
E
Δ
()
f
E
D
e
Δ
Δ
()
f
E
D
i
Δ
()
f
E
D
P
Δ
U
U
U
zad
r
−
=
Δ
δ
δ
δ
Δ
∂
=
∂
∂
∂
−
=
r
r
K
U
U
39
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
Uchyb
regulacji
jest
wielko
ści
ą
proporcjonaln
ą
do
zmian
k
ąta
in
a
wykresie
wskazow
ym
jego
we
ktor
b
ędzie
wf
az
ie
zw
ek
to
re
m
.
Automatyczny
regulator
napi
ęcia
wzmacnia
uchyb
regulacyjny
wymuszaj
ąc
we
wzbudnicy
generatora
zmian
ę
napi
ęcia
wzbudzenia
o
warto
ść
.
Automatyczny
regulator
napi
ęcia
i
w
zbudnica
maj
ą
pewn
ą
bezw
ładno
ść
to
na
wykresie
wskazow
ym
wektor
b
ędzie
si
ę
opó
źnia
ł
o
pewien
k
ąt
ws
to
su
n
ku
do
wektora
uchybu
regulacyjnego
.
To
opó
źnienie
wynika
ze
st
ał
ych
czasowych
regulatora
i
wzbudnicy.
Zm
ian
a
napi
ę
cia
wzbudzenia
spowoduje
powstanie
wu
zw
o
je
n
iu
tł
umi
ącym
si
ły
elektromotorycznej
. Wektor
tej
si
ły
le
ży
wf
az
ie
zw
ek
to
re
m
wymuszaj
ącym.
Pod
wp
ływem
si
ły
elektromotorycznej
wu
zw
o
je
n
iu
tł
umi
ącym
pop
łynie
pr
ąd
, którego
wskaz
b
ę
dzie
opó
źniony
w
stosunku
do
si
ły
elektromotorycznej
op
ew
ie
nk
ąt
wynikaj
ący
ze
stosunku
rezystancji
do
reaktancji
obwodu
t
łumi
ącego
.
Pr
ąd
p
łyn
ący
wu
zw
o
je
n
iu
tł
umi
ącym
aw
yw
o
łany
zmianami
napi
ę
cia
wzbudzenia
odejmuje
si
ę
od
pr
ądu
p
łyn
ącego
wu
zw
o
je
n
iu
tł
umi
ącym
aw
yw
o
łanym
zmianami
pr
ędko
ści
obrotowej
wirnika.
r
U
Δ
δΔ
f
E
Δ
f
E
Δ
r
U
Δ
(
)
f
E
D
e
Δ
()
f
E
D
e
Δ
(
)
f
E
D
e
Δ
(
)
f
E
D
i
Δ
()
f
E
D
i
Δ

40
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Ko
łysania
z
uwzgl
ę
dnieniem
t
łumienia
i
regulacji
wzbudzenia
Oznacza
to,
ż
e
pr
ąd
p
łyn
ący
wu
zw
o
je
n
iu
tł
umi
ącym
ww
yn
ik
u
d
zi
ał
ania
regulatora
napi
ęcia
os
łabia
pr
ąd
p
łyn
ący
wu
zw
o
je
n
iu
tł
umi
ącym
aw
yw
o
łanym
zmianami
pr
ę
dko
ści
obrotowej
wirnika
a
w
konsekwencji
zmniejsza
moc
tł
umi
ąc
ą.
Zostan
ą
teraz
przeanalizowane
czynniki
prowadz
ące
do
pojawienia
si
ę
ujemnej
mocy
t
łumi
ącej.
Wielko
ści
ą
wy
jś
ciow
ą
tej
analizy
by
ł
uchyb
regulacyjny
regulatora
napi
ęcia.
Du
ży
uchyb
regulacyjny
to
we
fe
kc
ie
d
u
ży
pr
ąd
p
łyn
ący
wu
zw
o
je
n
iu
tł
umi
ącym
ww
yn
ik
u
d
zi
ał
ania
regulatora
napi
ę
cia.
Du
ży
efekt
regulacyjny
mo
że
by
ć
spowodowany
przez:
9
Du
żą
reaktancj
ę
pomi
ędzy
generatorem
(elektrowni
ą)
aw
ęz
łem
sieci
sztywnej.
9
Du
że
obc
iąż
enie
sieci.
9
Du
że
wzmocnienie
regulatora
napi
ę
cia
bardzo
korzystne
dla
regulacji
napi
ę
cia
(napi
ęcie
sz
ybciej
wraca
do
warto
ści
zadanej),
al
e
niekorzystne
dla
tł
umienia.
9
Du
że
opó
źnienie
wprowadzane
przez
uk
ład
regulacji
napi
ęcia
aw
ię
c
niekorzystna
jest
wzbudnica
elektromaszyn
owa
wo
d
ró
żnieniu
od
wzbudnicy
tyrystorowej.
41
STABILNO
ŚĆ
LOKALNA
SYSTEMU
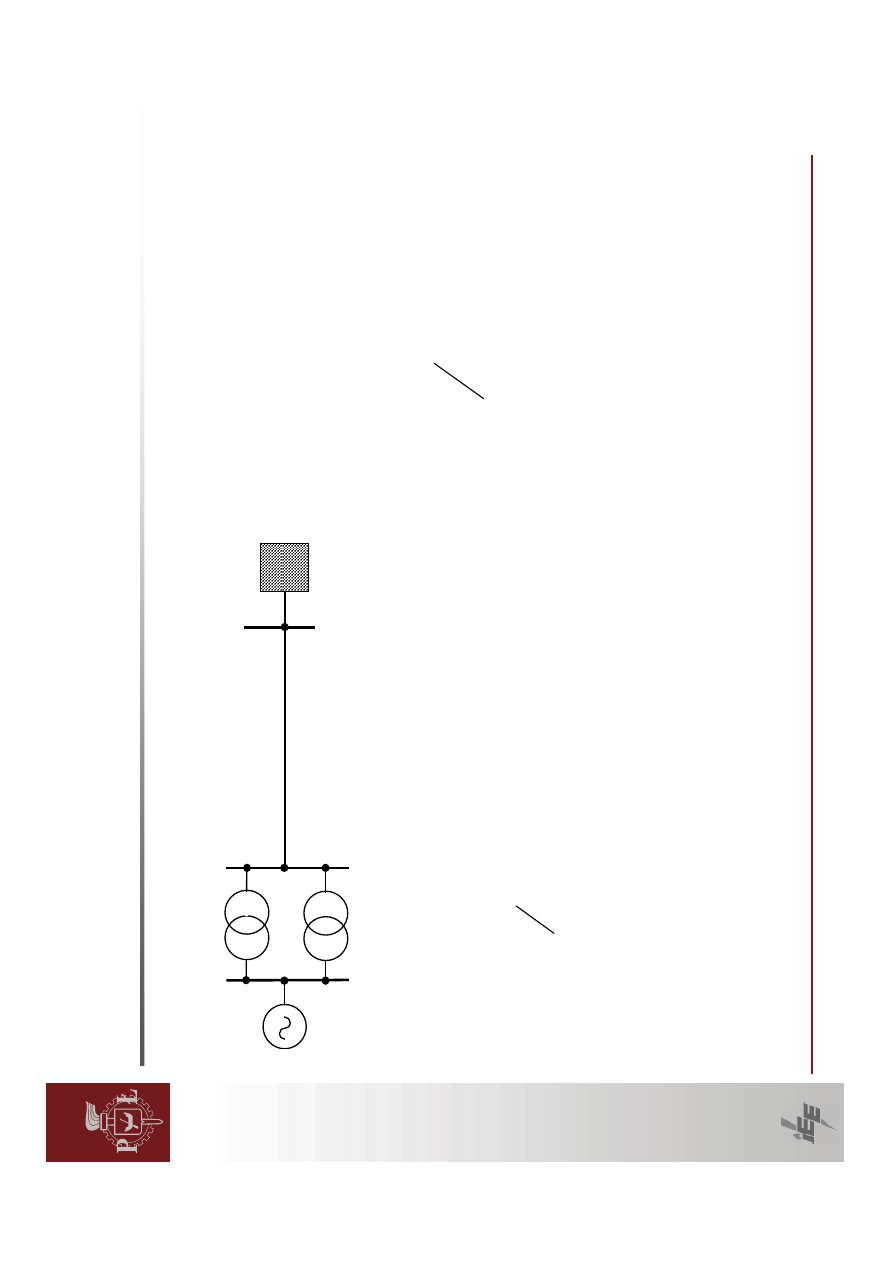
ELEKTROENERGETYCZNEGO.
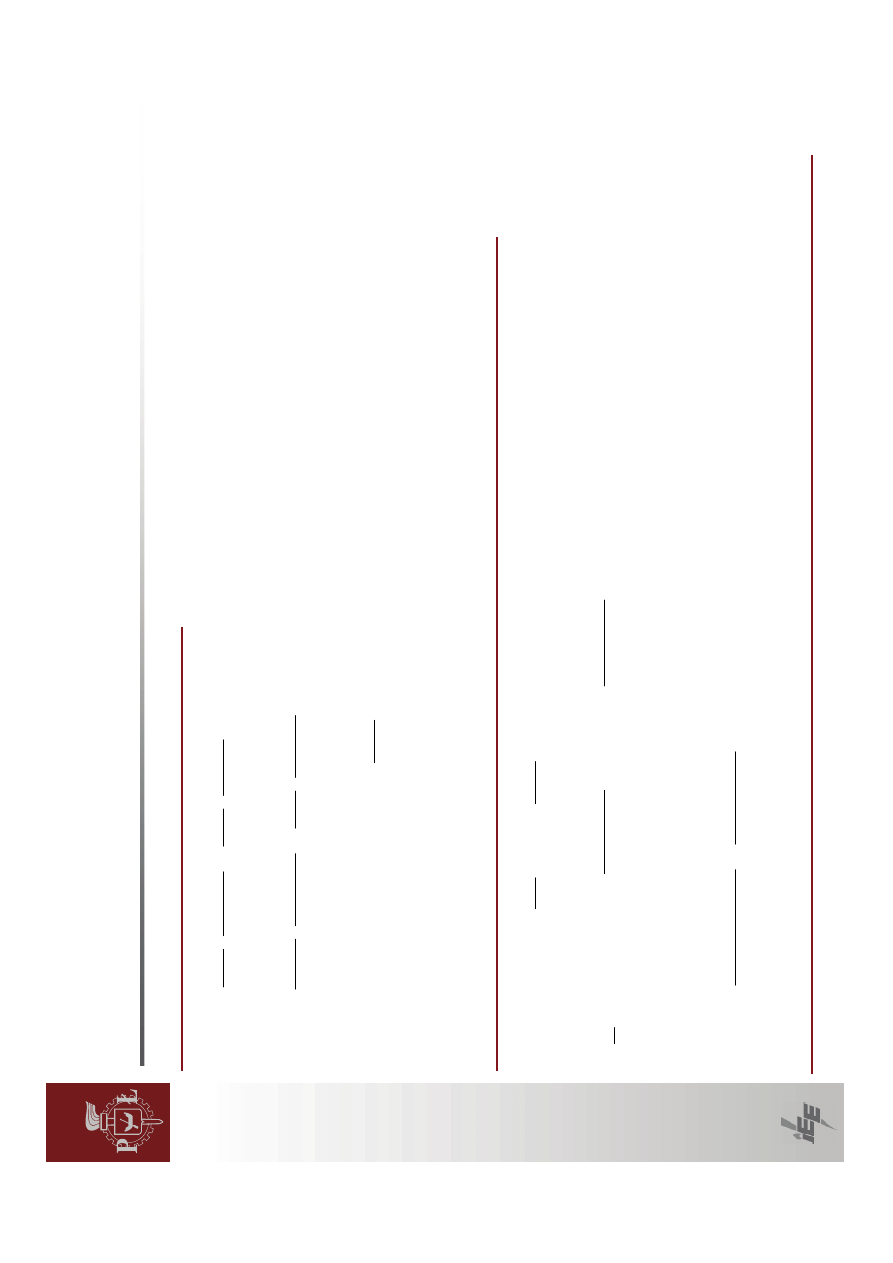
Zadanie
1
Obliczy
ć
moc
graniczn
ą
równowagi
statycznej
uk
ładu.
G
T
T
L
UE
A
B
C
10 kV
220 kV
220 kV
MVA
150
=
NG
S
%
150
=
d
X
kV
5,
10
=
NG
U
MVA
100
=
NT
S
%
12
=
Z
U
Δ
kV
10,5
kV
220
=
ϑ
km
Ω
4,
0
=
kL
X
km
150
=
l
∞
=
Z
S
kV
215
=
S
U
Zadanie
rozwi
ąza
ć
dla
trzech
przypadków
gdy
generator:
9
nie
jest
wyposa
żony
w
regulator
wzbudzenia
a
obci
ąż
ony
jest
moc
ą
9
jest
wyposa
żony
w
szybki
regulator
wzbudzenia
utrzymuj
ący
9
jest
wyposa
żony
w
wolny
regulator
wzbudzenia
utrzymuj
ący
MW
150
=
N
P
kV
5,
10
=
G
U
kV
5,
10
=
G
U
1
cos
=
ϕ
42
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
1
Impedancje
elementów
na
poziomie
kV
5,
10
Ω
10,1
150
5,
10
100
150
100
2
2
=
⋅
=
⋅
=
NG
NG
d
G
S
U
X
X
Ω
0662,
0
100
2
5,
10
100
12
2
100
2
2
=
⋅
⋅
=
⋅
⋅
=
NT
NT
z
T
S
U
U
X
Δ
Ω
137,
0
220
5,
10
150
4,
0
2
2
=
⎟ ⎠
⎞
⎜ ⎝
⎛ ⋅
⋅
=
⋅
⋅
=
T
k
L
l
X
X
ϑ
Ω
31,1
137,0
0662,
0
10,1
=
+
+
=
+
+
=
∑
L
T
G
X
X
X
X
Przypadek
1:
generator
nie
jest
wyposa
żony
w
regulator
wzbudzenia
kV
3,
10
220
5,
10
215
1
5,
10
=
⋅
=
⋅
=
T
S
S
U
U
ϑ
=
⋅
+
=
⋅
+
=
5,
10
10,1
150
5,
10
5,
10
5,
10
j
U
X
P
j
U
E
G
G
G
G
G
kV
9,
18
8,
15
5,
10
3,
56
°
=
+
=
j
e
j
MW
149
31,1
3,
10
9,
18
5.
10
=
⋅
=
⋅
=
∑
X
U
E
P
S
G
gr
43
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
1
Przypadek
2:
generator
jest
wyposa
żony
w
szybki
regulator
wzbudzenia
MW
531
137,
0
0662,
0
3,
10
5,
10
5,
10
=
+
⋅
=
+
⋅
=
L
T
S
G
gr
X
X
U
U
P
Przypadek
3:
generator
jest
wyposa
żony
w
wolny
regulator
wzbudzenia
Wykres
wskazowy
napi
ęcia
sieci
szt
ywnej,
napi
ę
cia
is
iły
e
lektromotorycznej
generatora
wyposa
żonego
w
wolny
regulator
wzbudzenia.
S
U
G
U
d
E
U
Δ
α

44
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
1
W
celu
wyznaczenia
si
ły
elektromoto
rycznej
zastosujemy
metod
ę
it
e
ra
cyjn
ą.
Za
ło
żymy,
ż
e
°
=
20
α
kV
5,
10
20
°
=
j
G
e
U
(
)
=
−
°
+°
⋅
=
−
=
3,
10
20
sin
20
cos
5,
10
j
U
U
U
S
G
GS
Δ
()
kV
59,
3
433,
0
j
+
−
=
()
=
⋅
+
−
=
+
+
+
⋅
=
203,
0
31,1
59,
3
433,
0
j
X
X
X
X
X
U
U
L
T
L
T
G
GS
Δ
Δ
()
kV
1,
23
79,
2
j
+
−
=
Cz
ęść
rzeczyw
ista
straty
napi
ęcia
powinna
by
ć
równa
napi
ęciu
sieci
szt
ywnej
ze
znakiem
minus,
wniosek
przy
ję
to
zbyt
ma
ły
k
ąt.
Za
ło
żymy,
ż
e
°
=
30
α
(
)
=
−
°
+°
⋅
=
−
=
3,
10
30
sin
30
cos
5,
10
j
U
U
U
S
G
GS
Δ
()
kV
25,
5
21,1
j
+
−
=
()
=
⋅
+
−
=
+
+
+
⋅
=
203,
0
31,1
25,
5
21,1
j
X
X
X
X
X
U
U
L
T
L
T
G
GS
Δ
Δ
()
kV
8,
33
80,
7
j
+
−
=

45
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
1
Za
ło
żymy,
ż
e
°
=
34
α
(
)
=
−
°
+°
⋅
=
−
=
3,
10
34
sin
34
cos
5,
10
j
U
U
U
S
G
GS
Δ
()
kV
87,
5
60,1
j
+
−
=
()
=
⋅
+
−
=
+
+
+
⋅
=
203,
0
31,1
87,
5
60,1
j
X
X
X
X
X
U
U
L
T
L
T
G
GS
Δ
Δ
()
kV
9,
37
3,
10
j
+
−
=
Cz
ęść
rzeczyw
ista
straty
napi
ęcia
jest
równa
napi
ę
ciu
sieci
sztywnej
ze
zna
kie
m
minus,
k
ąt
jest
w
ła
ściwy
.
Si
ła
elektromotoryczna
generatora
jest
równa
cz
ęś
ci
urojonej
straty
napi
ęcia,
czyli:
kV
9,
37
=
d
E
MW
298
31,1
3,
10
9,
37
5.
10
=
⋅
=
⋅
=
∑
X
U
E
P
S
d
gr

46
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
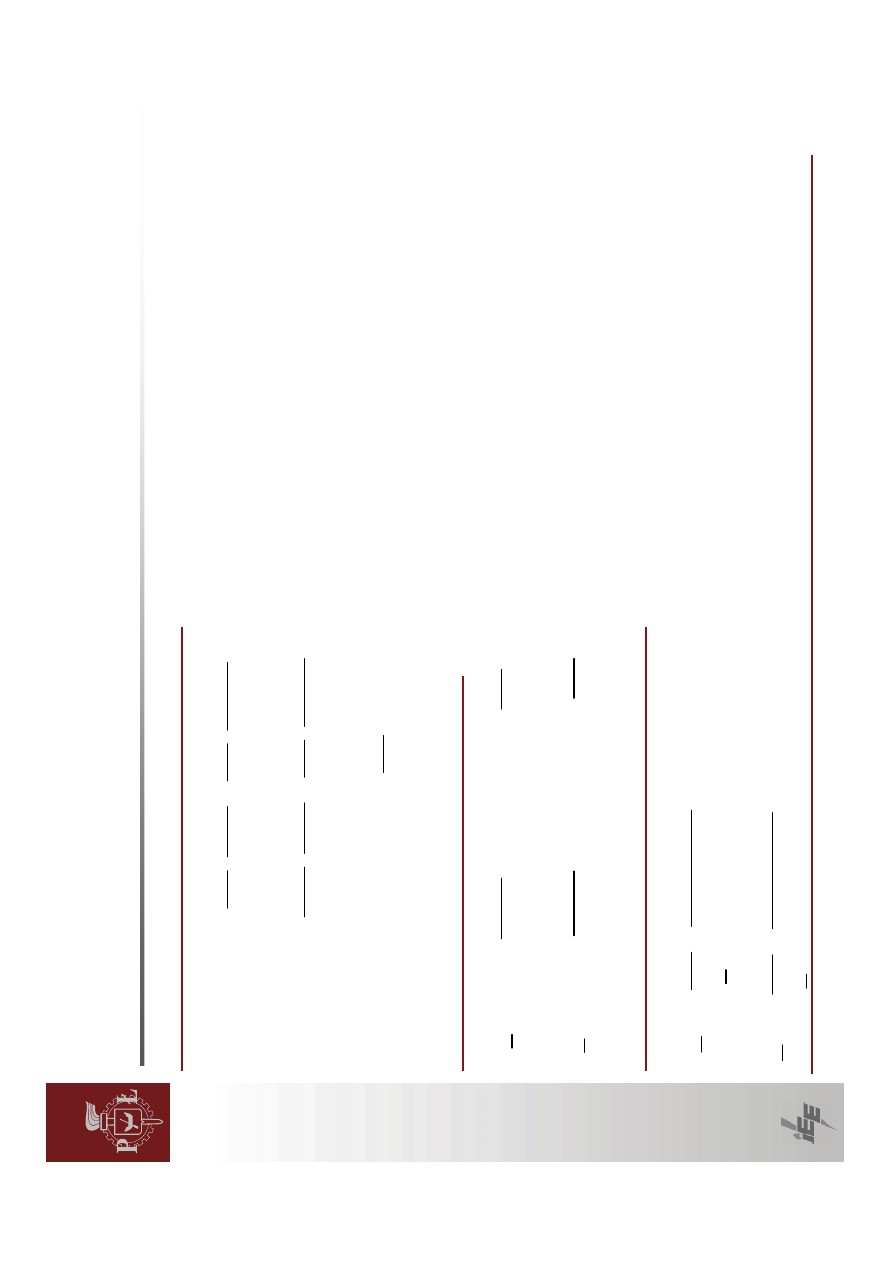
Zadanie
2
Obliczy
ć
moc
graniczn
ą
równowagi
statycznej
uk
ładu
jak
na
rysunku.
G1
T1
1
S
L
T2
A
B
C
15 kV
110 kV
110 kV
15 kV
2
S
D
G2
LBC
P
MVA
600
1
=
NG
S
%
150
=
d
X
kV
75,
15
1
=
NG
U
MVA
600
2
=
NG
S
%
150
=
d
X
kV
75,
15
2
=
NG
U
MVA
315
1
=
NT
S
%
12
=
Z
U
Δ
kV
15
kV
110 =
ϑ
MVA
315
2
=
NT
S
%
12
=
Z
U
Δ
kV
15
kV
110 =
ϑ
km
Ω
4,
0
=
kL
X
km
10
=
l
MW
200
1
=
P
ind.
8,
0
cos
1
=
ϕ
kV
75,
15
=
A
U
MW
200
2
=
P
ind.
8,
0
cos
2
=
ϕ
kV
75,
15
=
D
U
MW
100
=
LBC
P
Generator
nie
jest
wyposa
żony
w
regulator
wzbudzenia.
47
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
2
Impedancje
elementów
na
poziomie
kV
15
Ω
620,
0
600
75,
15
100
150
100
2
2
2
1
=
⋅
=
⋅
=
=
N
N
d
G
G
S
U
X
X
X
Ω
0945,
0
315
75,
15
100
12
100
2
2
2
1
=
⋅
=
⋅
=
=
N
N
z
T
T
S
U
U
X
X
Δ
Ω
0744,
0
110
15
10
4,
0
2
2
=
⎟ ⎠
⎞
⎜ ⎝
⎛ ⋅
⋅
=
⋅
⋅
=
T
k
L
l
X
X
ϑ
Obliczenia
mocy
w
w
ęz
łach
A
i
D
()
MVA
150
200
6,
0
8,
0
200
200
sin
cos
1
1
1
1
1
j
j
P
j
P
S
+
=
⋅
+
=
⋅
+
=
ϕ
ϕ
()
MVA
150
200
6,
0
8,
0
200
200
sin
cos
2
2
2
2
2
j
j
P
j
P
S
+
=
⋅
+
=
⋅
+
=
ϕ
ϕ
Zast
ąpienie
odbiorów
impedancjami
()
Ω
5953,
0
7938,
0
150
200
75,
15
2
* 1
2
1
j
j
S
U
Z
A
o
+
=
−
=
=
()
Ω
5953,
0
7938,
0
150
200
75,
15
2
* 2
2
2
j
j
S
U
Z
D
o
+
=
−
=
=
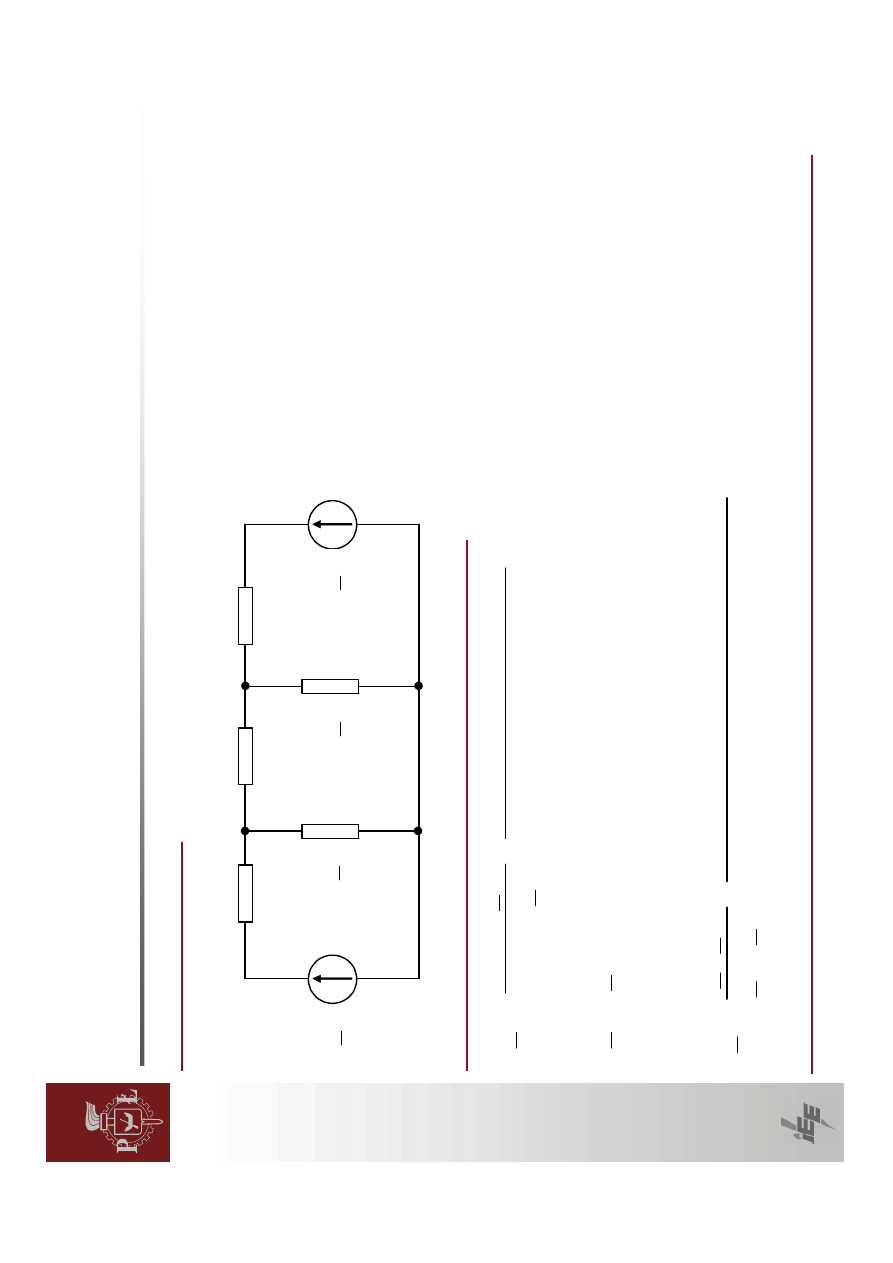
48
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
2
Schemat
zast
ępczy
1o
Z
2o
Z
1d
E
2
d
E
1
G
jX
2
G
jX
(
)
2
1
T
L
T
X
X
X
j
+
+
Obliczenia
impedancji
w
łasnej
generatora
1
(
)
=
+
+
+
⋅
=
+
⋅
=
5953,
0
7938,
0
620,
0
5953,
0
7938,
0
620,
0
2
2
2
2
j
j
j
j
Z
Xj
Z
Xj
Z
o
G
o
G
a
()
Ω
3983,
0
1448,
0
j
+
=
()
=
+
+
+
=
2
1
T
L
T
a
b
X
X
X
j
Z
Z
=
+
⋅
+
+
=
0744,
0
2
0945,
0
3983,
0
1448,
0
j
j
j
()
Ω
6617,
0
1448,
0
j
+
=
(
)(
)
=
+
+
+
+
⋅
+
=
+
=
5953,
0
7938,
0
6617,
0
1448,
0
5953,
0
7938,
0
6617,
0
1448,
0
1
1
j
j
j
j
Z
Z
Z
Z
Z
o
b
o
b
c
()
Ω
3757,
0
2059,
0
j
+
=

49
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
2
=
+
+
=
+
=
620,
0
3757,
0
2059,
0
1
11
j
j
Xj
Z
Z
G
c
()
Ω
0168,1
9957,
0
2059,
0
3,
78
°
=
+
=
j
e
j
Obliczenia
impedancji
w
łasnej
generatora
2
Ω
0168,1
3,
78
22
o
j
e
Z
=
Obliczenia
impedancji
wzajemnej
generator
1
‐
gene
ra
to
r
2
W
celu
obliczenia
impedancji
wzajemnej
generator
1
‐
gene
ra
to
r
2
musimy
przekszta
łci
ć
dwie
gwiazdy
wyst
ępuj
ące
w
schemacie
zast
ępczym
na
trójk
ąty.
Zaczniemy
od
gwiazdy
z
ło
żonej
zi
m
p
ed
an
cj
i:
1
G
X
j
1o
Z
(
)
2
1
T
L
T
X
X
X
j
+
+
()
(
)
=
+
+
⋅
+
+
+
+
=
1
2
1
1
2
1
1
1
o
T
L
T
G
T
L
T
G
D
G
Z
X
X
X
j
Xj
X
X
X
j
Xj
Z
=
+
⋅
+
+
=
5953,
0
7938,
0
5906,
0
620,
0
2634,
0
620,
0
j
j
j
j
j
()
Ω
9822,
0
1317,
0
j
+
−
=
50
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
2
()
(
)
=
+
+
⋅
+
+
+
+
=
1
2
1
1
2
1
1
0
G
T
L
T
o
T
L
T
o
D
Xj
X
X
X
j
Z
X
X
X
j
Z
Z
(
)
=
⋅
+
+
+
+
=
620,
0
2634,
0
5953,
0
7938,
0
2634,
0
5953,
0
7938,
0
j
j
j
j
j
()
Ω
1117,1
1310,1
j
+
=
Łą
czymy
równolegle
ga
łę
zie:
0
D
Z
2o
Z
(
)(
)
=
+
+
+
+
⋅
+
=
+
⋅
=
5953,
0
7938,
0
1117,1
131,1
5953,
0
7938,
0
1117,1
131,1
2
0
2
0
j
j
j
j
Z
Z
Z
Z
Z
o
D
o
D
DD
()
Ω
3916,
0
4699,
0
j
+
=
Przekszta
łcamy
gwiazd
ę
na
trójk
ąt
dla
impedancji:
DD
Z
D
G
Z
1
2
G
Xj
=
⋅
+
+
=
DD
G
D
G
G
D
G
Z
X
j
Z
X
j
Z
Z
2
1
2
1
12
(
)
=
+
⋅
+
−
+
+
+
−
=
3916,
0
4699,
0
62,
0
9822,
0
1317,
0
62,
0
9822,
0
1317,
0
j
j
j
j
j
()
Ω
3518,
2
1370,
2
9819,
0
7,
114
°
=
+
−
=
j
e
j
51
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
2
Obliczenie
mocy
p
łyn
ących
z
generatorów
ϑ
sin
2
1
2
1
1
⋅
+
+
⋅
=
T
L
T
G
G
A
T
X
X
X
U
U
P
()
1062,
0
75,
15
75,
15
2634,
0
100
sin
2
1
2
1
1
=
⋅
⋅
=
⋅
+
+
⋅
=
G
G
T
L
T
A
T
U
U
X
X
X
P
ϑ
=
⋅
⋅
−
=
ϑ
cos
2
1
2
1
2
1
2 1
1
LT
T
G
G
LT
T
G
A
T
X
U
U
X
U
Q
Mvar
3,
5
1062,
0
1
2634,
0
75,
15
2634,
0
75,
15
2
2
2
=
−
⋅
−
=
=
+
+
+
=
+
=
3,
5
100
150
200
1
1
1
j
j
S
S
S
A
T
o
G
()
MVA
3,
155
300
j
+
=
(
)
=
−
−
+
=
−
=
3,
5
100
150
200
2
2
2
j
j
S
S
S
D
T
o
G
()
MVA
3,
155
100
j
+
=
52
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
2
Obliczenia
modu
łów
si
ł
elektromotorycznych
generatorów
=
⋅
+
⋅
+
=
1
1
1
1
1
1
1
1
G
G
G
G
G
G
G
d
U
X
P
j
U
X
Q
U
E
()
kV
8,
24
8,
11
9,
21
75,
15
62,
0
300
75,
15
62,
0
3,
155
75,
15
3,
28
°
=
+
=
⋅
+
⋅
+
=
j
e
j
j
=
⋅
+
⋅
+
=
2
2
2
2
2
2
2
2
G
G
G
G
G
G
G
d
U
X
P
j
U
X
Q
U
E
()
kV
2,
22
9,
3
9,
21
75,
15
62,
0
100
75,
15
62,
0
3,
155
75,
15
2,
10
°
=
+
=
⋅
+
⋅
+
=
j
e
j
j
Wyznaczenie
mocy
gran
icznej
równowagi
statycznej
uk
ładu
Ω
0168,1
11
=
Z
°
=
7,
11
11
α
Ω
0168,1
22
=
Z
Ω
3518,
2
12
=
Z
°
=
7,
11
22
α
°
−
=
7,
24
12
α
kV
8,
24
1
=
d
E
kV
2,
22
2
=
d
E
°
=
−
=
+
=
3,
65
7,
24
90
90
12
α
δ
gr
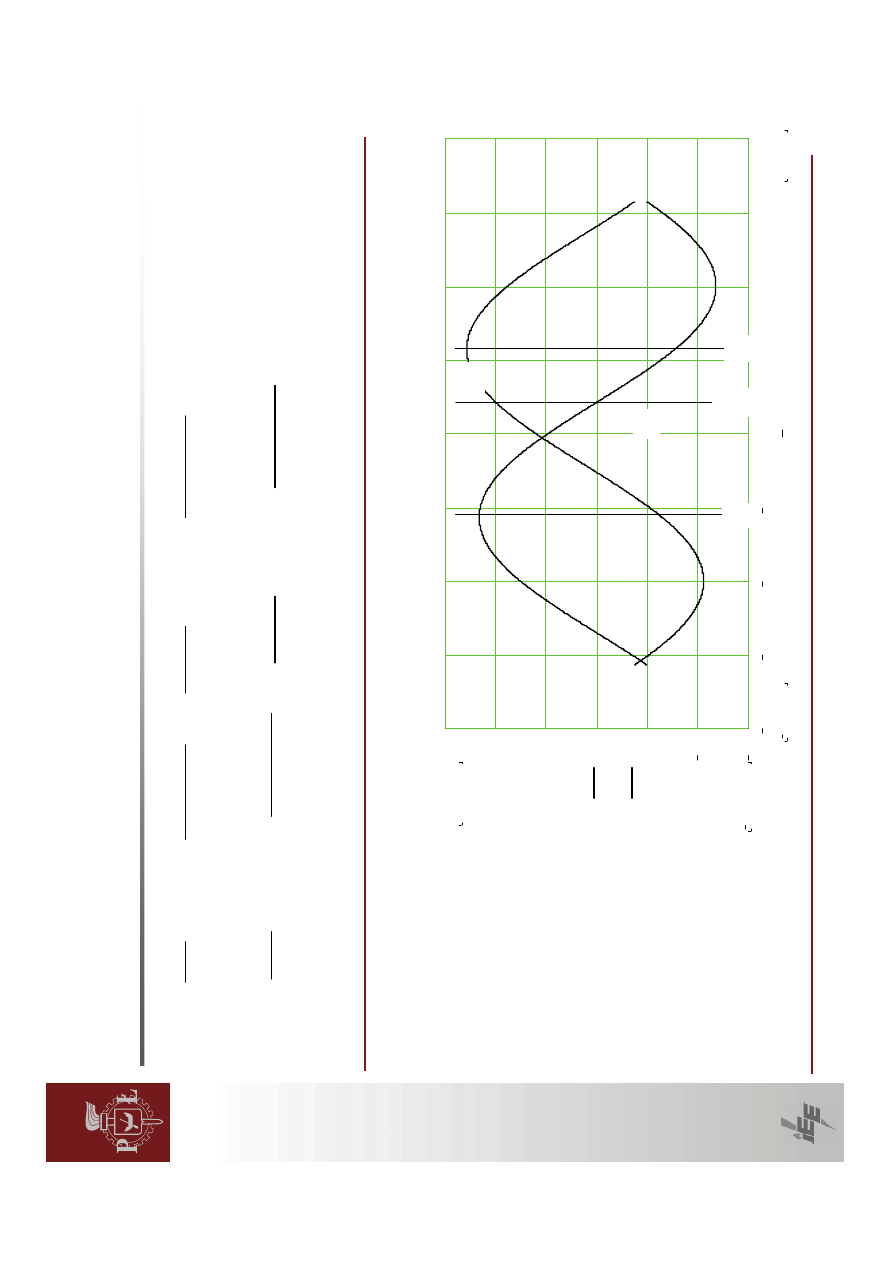
53
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
2
=
⋅
+
⋅
=
12
2
1
11
11
2 1
1
sin
Z
E
E
Z
E
P
d
d
d
gr
α
MW
358
3518,
2
2,
22
8,
24
7,
11
sin
0168,1
8,
24
2
=
⋅
+
⋅
=
=
⋅
−
⋅
=
12
2
1
22
22
2 2
2
sin
Z
E
E
Z
E
P
d
d
d
gr
α
MW
136
3518,
2
8,
24
2,
22
7,
11
sin
0168,1
2,
22
2
−
=
⋅
−
⋅
=
35
7.
73
64
39
13
6.
43
81
08
P1
i
P2
i
3.
14
159
3
3.
14
159
3
δ
i.
π
4
3
2
1
0
1
2
3
4
20
0
10
0
0
10
0
20
0
30
0
40
0
P
1
P
2
1
2
3
Przebiegi
mocy
w
funkcji
k
ąta
rozchylenia
wektorów
si
ł
elektromotorycznych
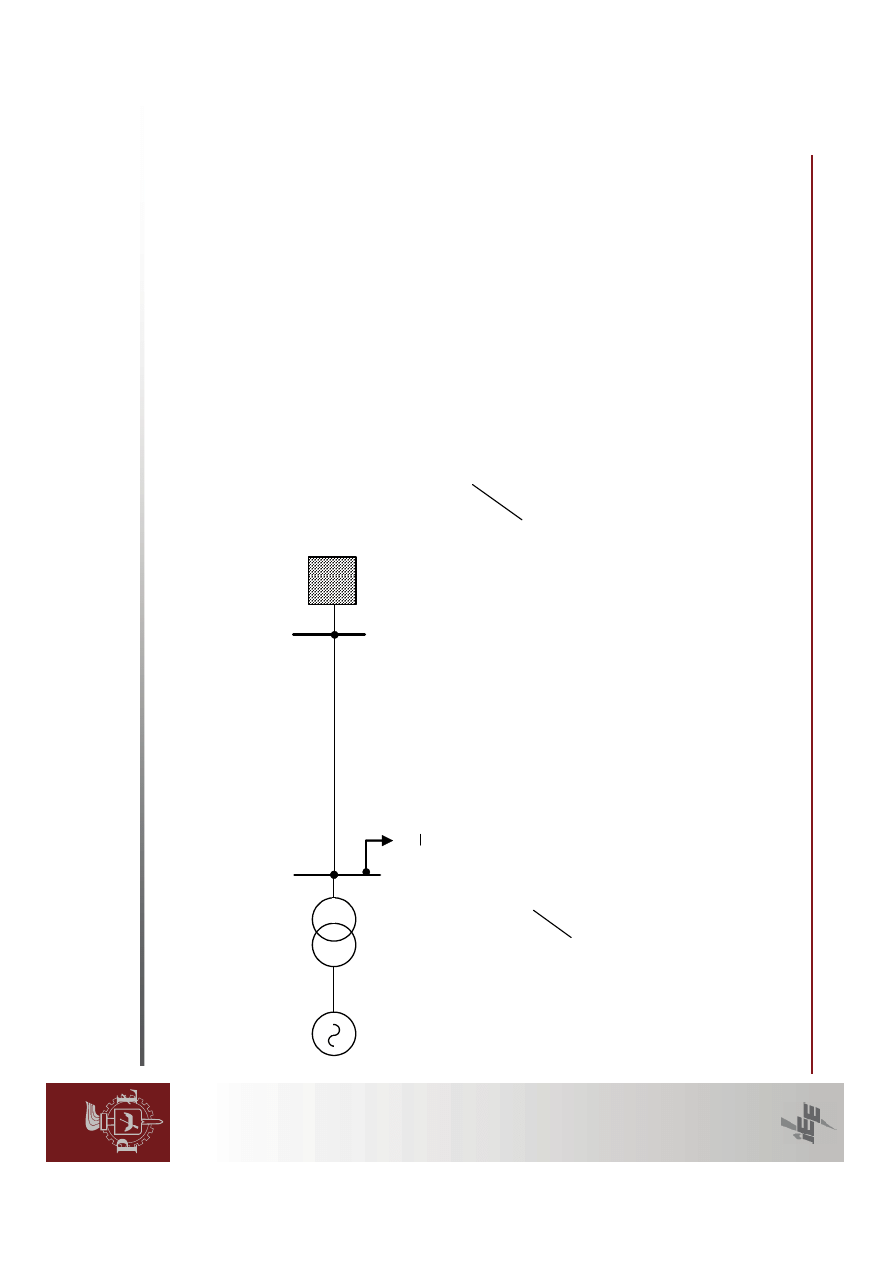
54
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
Obliczy
ć
czy
dla
uk
ładu
jak
na
rysunku
mo
żna
przes
ła
ć
nadwy
żk
ę
mocy
z
generatora
d
o
syst
emu.
Dla
tej
sytua
cji
obliczy
ć
maksymaln
ą
d
ługo
ść
linii,
aby
zachowa
ć
stabiln
ą
prac
ę.
G
T
1
S
L
A
B
220 kV
220
kV
UE
MVA
250
=
NG
S
%
220
=
d
X
kV
75,
15
=
NG
U
ind.
8,
0
cos
=
NG
ϕ
MVA
250
=
NT
S
%
11
=
Z
U
Δ
kV
15
kV
312
=
ϑ
km
Ω
4,
0
=
kL
X
km
50
=
l
MW
100
1
=
P
ind.
8,
0
cos
1
=
ϕ
kV
2315
=
A
U
kV
231
=
B
U
Generator
jest
wyposa
żony
ww
o
ln
y
re
gu
la
to
r
wzbudzenia
utrzymuj
ący
sta
łe
napi
ę
cie
na
sz
ynach
A
wynosz
ące
kV
231
55
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
Impedancje
elementów
na
poziomie
kV
220
()
Ω
7,
517
15
231
250
75,
15
100
220
100
2
2
2
2
=
⎟ ⎠
⎞
⎜ ⎝
⎛ ⋅
⋅
=
⋅
⋅
=
T
N
N
d
G
S
U
X
X
ϑ
Ω
48,
23
250
231
100
11
100
2
2
=
⋅
=
⋅
=
N
N
z
T
S
U
U
X
Δ
Ω
20
50
4,
0
=
⋅
=
⋅
=
l
X
X
k
L
Obliczenia
mocy
odbioru
1
()
MVA
0,
75
100
6,
0
8,
0
100
100
sin
cos
1
1
1
1
1
j
j
P
j
P
S
+
=
⋅
+
=
⋅
+
=
ϕ
ϕ
Zast
ąpienie
odbioru
impedancj
ą
()
Ω
1,
256
5,
341
75
100
231
2
* 1
2
1
j
j
S
U
Z
A
o
+
=
−
=
=
Obliczenia
si
ły
elektromotorycznej
generatora
Ω
2,
541
48,
23
7,
517
=
+
=
+
=
T
G
GT
X
X
X

56
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
=
⋅
+
⋅
+
=
A
GT
G
A
GT
G
A
d
U
X
P
j
U
X
Q
U
E
()
kV
3,
469
3,
234
7,
406
231
2,
541
100
231
2,
541
75
231
9,
29
°
=
+
=
⋅
+
⋅
+
=
j
e
j
j
Obliczenie
impedancji
wzajemnej
generator
1
–s
ie
ć
sztywna
Przekszta
łcamy
gwiazd
ę
na
trójk
ąt
dla
impedancji:
GT
Xj
1o
Z
L
Xj
=
⋅
+
+
=
1
1
12
o
L
G
L
GT
Z
Xj
Xj
Xj
Xj
Z
=
+
⋅
+
+
=
1,
256
5,
341
20
2,
541
20
2,
541
j
j
j
j
j
()
Ω
8,
576
4,
576
28,
20
0,
92
°
=
+
−
=
j
e
j
Obliczenie
czy
mo
żna
przes
ła
ć
nadwy
żk
ę
mocy
zg
en
e
ra
to
rad
o
syst
emu
°
−
=
−
=
−
=
0,
2
92
90
90
12
12
θ
α
°
=
−
=
+
=
0,
88
0,
2
90
90
12
α
δ
gr
°
=
9,
29
S
d
U
E
δ
°
=
<°
=
0,
88
9,
29
gr
U
E
S
d
δ
δ
Lini
ą
mo
żna
przes
ła
ć
nadwy
żk
ę
mocy
z
generatora
d
o
systemu.
57
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
Moc
czynna
p
łyn
ąca
lini
ą
MW
100
100
8,
0
250
cos
1
=
−
⋅
=
−
⋅
=
P
S
P
N
NG
L
ϕ
Moc
bierna
p
łyn
ąca
lini
ą
0375,
0
231
231
20
100
sin
=
⋅
⋅
=
⋅
⋅
=
S
A
L
L
U
U
X
P
ϑ
°
=
=
15,
2
sin
ϑ
ϑ
arc
=
⋅
⋅
−
=
ϑ
cos
2
L
S
A
L
A
L
X
U
U
X
U
Q
Mvar
87,1
0375,
0
1
20
231
20
231
2
2
2
=
−
⋅
−
=
Obliczenie
mocy
generatora
(
)
MVA
9,
76
200
87,1
100
75
100
1
1
j
j
j
S
S
S
L
o
G
+
=
+
+
+
=
+
=
Obliczenie
si
ły
elektromotorycznej
generatora
=
⋅
+
⋅
+
=
A
GT
G
A
GT
G
A
d
U
X
P
j
U
X
Q
U
E
1
1
()
kV
3,
623
6,
468
1,
411
231
2,
541
200
231
2,
541
9,
76
231
7,
48
°
=
+
=
⋅
+
⋅
+
=
j
e
j
j

58
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
Obliczenie
czy
uk
ład
po
przes
łaniu
nadwy
żki
mocy
z
generatora
d
o
syst
emu
jest
stabilny
°
=
<°
=°
+°
=
+
=
0,
88
85,
50
15,
2
7,
48
gr
U
E
U
E
A
d
S
d
δ
ϑ
δ
δ
Zwi
ę
kszenie
d
ługo
ści
linii
do
250
km
Ω
100
250
4,
0
=
⋅
=
⋅
=
l
X
X
k
L
Obliczenie
impedancji
wzajemnej
generator
1
–s
ie
ć
sztywna
=
⋅
+
+
=
1
1
12
o
L
G
L
GT
Z
jX
jX
jX
jX
Z
=
+
⋅
+
+
=
1,
256
5,
341
100
2,
541
100
2,
541
j
j
j
j
j
()
Ω
4,
724
2,
717
4,
101
0,
98
°
=
+
−
=
j
e
j
Moc
bierna
p
łyn
ąca
lini
ą
1874,
0
231
231
100
100
sin
=
⋅
⋅
=
⋅
⋅
=
S
A
L
L
U
U
X
P
ϑ
°
=
=
8,
10
sin
ϑ
ϑ
arc
59
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
=
⋅
⋅
−
=
ϑ
cos
2
L
S
A
L
A
L
X
U
U
X
U
Q
Mvar
45,
9
1874,
0
1
100
231
100
231
2
2
2
=
−
⋅
−
=
Obliczenie
mocy
generatora
(
)
MVA
5,
84
200
45,
9
100
75
100
1
1
j
j
j
S
S
S
L
o
G
+
=
+
+
+
=
+
=
Obliczenie
si
ły
elektromotorycznej
generatora
=
⋅
+
⋅
+
=
A
GT
G
A
GT
G
A
d
U
X
P
j
U
X
Q
U
E
1
1
()
=
+
=
⋅
+
⋅
+
=
6,
468
9,
428
231
2,
541
200
231
2,
541
5,
84
231
j
j
kV
2,
635
5,
47
°
=
j
e
Obliczenie
czy
uk
ład
po
przes
łaniu
nadwy
żki
mocy
z
generatora
d
o
syst
emu
jest
stabilny
°
=
−
=
−
=
−
+
=
+
=
0,
82
0,
98
180
180
90
90
90
12
12
12
θ
θ
α
δ
gr
°
=
<°
=°
+°
=
+
=
0,
82
3,
58
8,
10
5,
47
gr
U
E
U
E
A
d
S
d
δ
ϑ
δ
δ
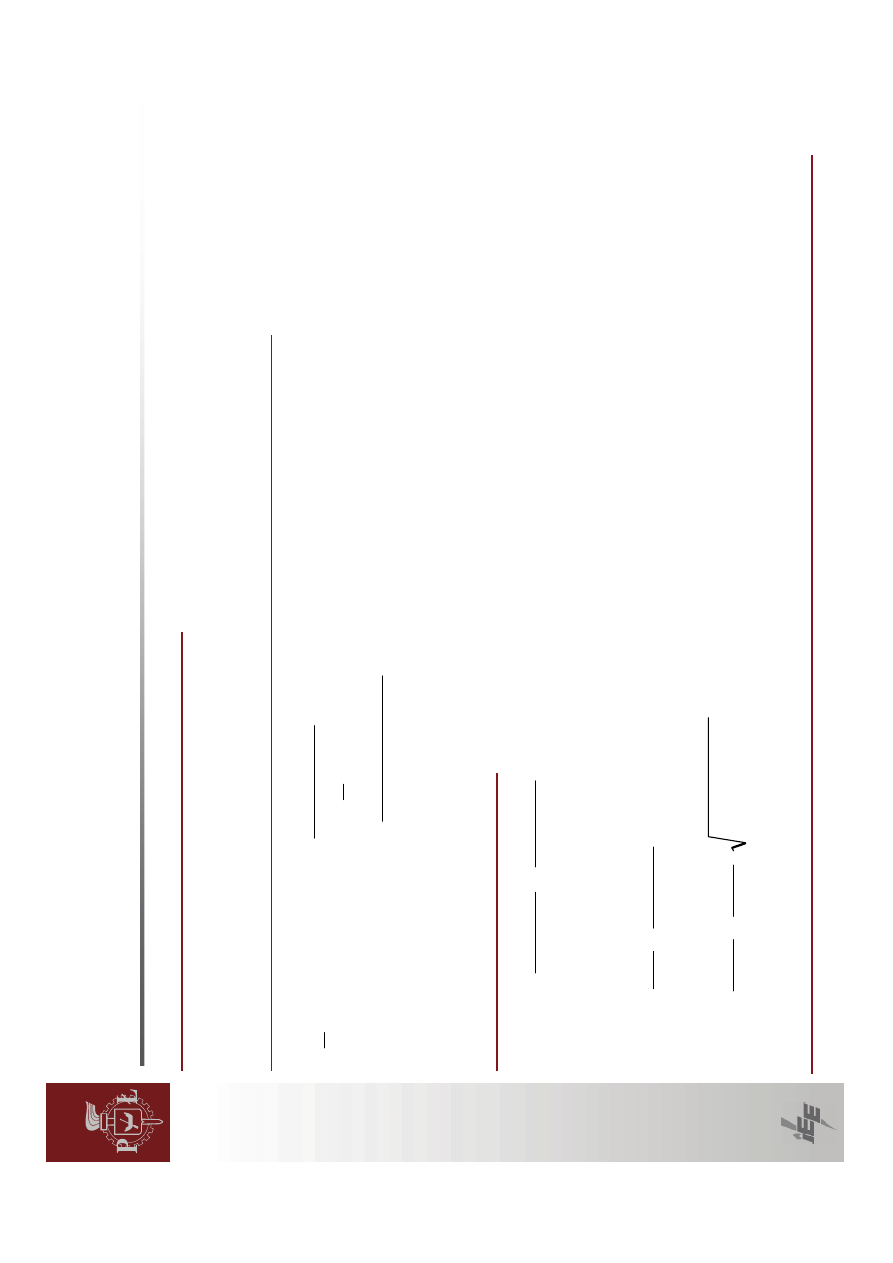
60
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
Zwi
ę
kszenie
d
ługo
ści
linii
do
600
km
Ω
240
600
4,
0
=
⋅
=
⋅
=
l
X
X
k
L
Obliczenie
impedancji
wzajemnej
generator
1
–s
ie
ć
sztywna
=
⋅
+
+
=
1
1
12
o
L
G
L
GT
Z
jX
jX
jX
jX
Z
=
+
⋅
+
+
=
1,
256
5,
341
240
2,
541
240
2,
541
j
j
j
j
j
()
Ω
0,
994
7,
963
4,
243
2,
104
°
=
+
−
=
j
e
j
Moc
bierna
p
łyn
ąca
lini
ą
4498,
0
231
231
240
100
sin
=
⋅
⋅
=
⋅
⋅
=
S
A
L
L
U
U
X
P
ϑ
°
=
=
7,
26
sin
ϑ
ϑ
arc
=
⋅
⋅
−
=
ϑ
cos
2
L
S
A
L
A
L
X
U
U
X
U
Q
Mvar
8,
23
4498,
0
1
240
231
240
231
2
2
2
=
−
⋅
−
=
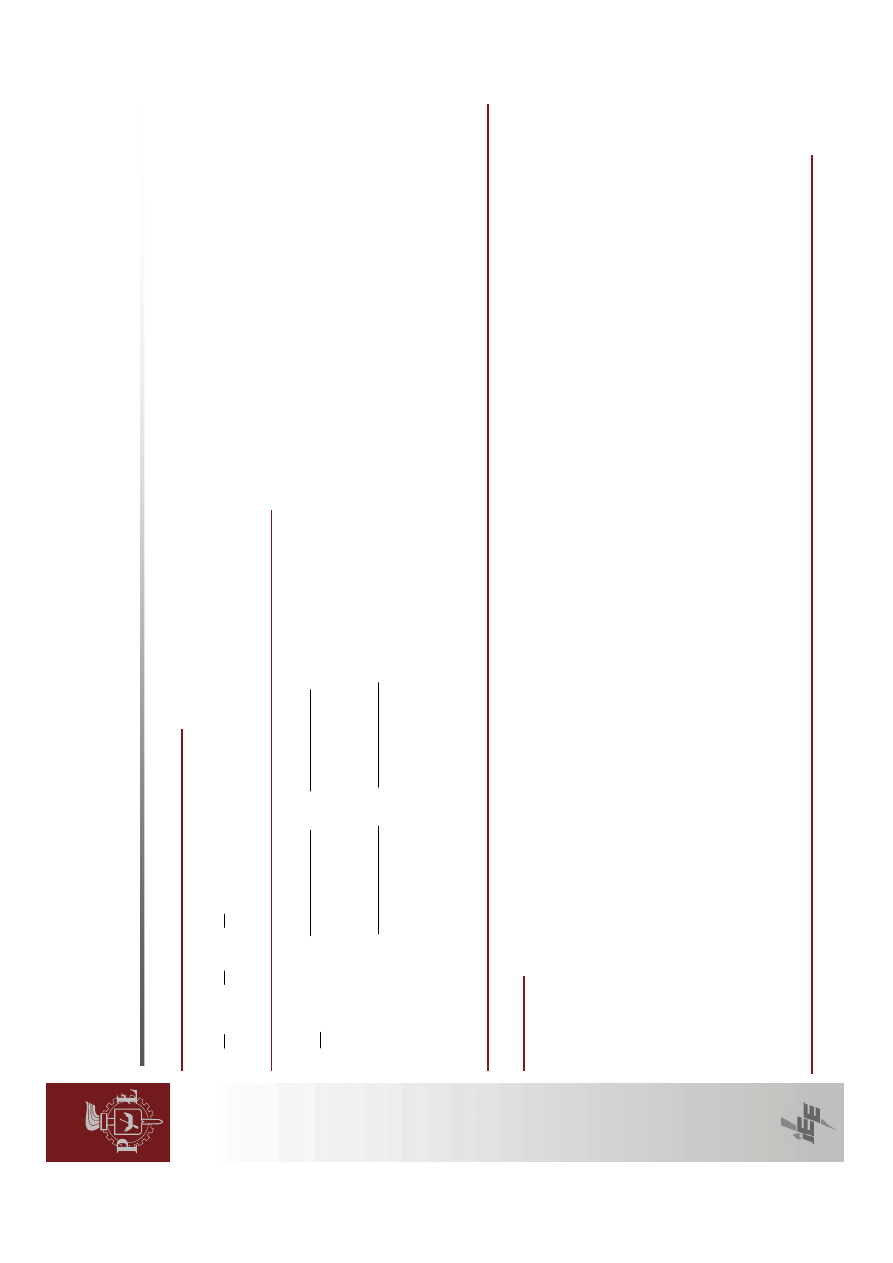
61
STABILNO
ŚĆ
LOKALNA
SYSTEMU
ELEKTROENERGETYCZNEGO.
Zadanie
3
Obliczenie
mocy
generatora
(
)
MVA
8,
98
200
8,
23
100
75
100
1
1
j
j
j
S
S
S
L
o
G
+
=
+
+
+
=
+
=
Obliczenie
si
ły
elektromotorycznej
generatora
=
⋅
+
⋅
+
=
A
GT
G
A
GT
G
A
d
U
X
P
j
U
X
Q
U
E
1
1
()
=
+
=
⋅
+
⋅
+
=
6,
468
4,
462
231
2,
541
200
231
2,
541
8,
98
231
j
j
kV
3,
658
4,
45
°
=
j
e
Obliczenie
czy
uk
ład
po
przes
łaniu
nadwy
żki
mocy
z
generatora
d
o
syst
emu
jest
stabilny
°
=
−
=
−
=
8,
75
2,
104
180
180
12
θ
δ
gr
°
=
<°
=°
+°
=
+
=
8,
75
1,
72
8,
23
4,
45
gr
U
E
U
E
A
d
S
d
δ
ϑ
δ
δ
Document Outline
- SYSTEMY ELEKTROENERGETYCZNE Rozdział 4STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Pojęcia stabilności
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Pojęcia stabilności
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Pojęcia stabilności
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Pojęcia stabilności
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Pojęcia stabilności
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Pojęcia stabilności
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Model matematyczny systemu elektroenergetycznego
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Model matematyczny systemu elektroenergetycznego
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Model matematyczny systemu elektroenergetycznego
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Model matematyczny systemu elektroenergetycznego
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Model matematyczny systemu elektroenergetycznego
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania wirnika generatora
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania wirnika generatora
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania wirnika generatora
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Model matematyczny systemu elektroenergetycznego
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Model matematyczny systemu elektroenergetycznego
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryterium
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kryteria w układzie wielomaszynowym
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Kołysania z uwzględnieniem tłumienia i regulacji wzbudzenia
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 1
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 1
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 1
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 1
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 1
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 2
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
- STABILNOŚĆ LOKALNA SYSTEMU ELEKTROENERGETYCZNEGO. Zadanie 3
Wyszukiwarka
Podobne podstrony:
Kanicki Systemy Rozdział 6
Kanicki Systemy Rozdzial 10 id Nieznany
Kanicki Systemy Rozdzial 5 id 2 Nieznany
Kanicki Systemy Rozdzial 3 id 2 Nieznany
Kanicki Systemy Rozdział 2
Kanicki Systemy Rozdział 7
Kanicki Systemy Rozdział 4
Kanicki Systemy Rozdział 6
Kanicki Systemy Rozdzial 10 id Nieznany
Kanicki Systemy Rozdział 3
Kanicki Systemy Rozdział 5
Obowiązki i uprawnienia operatora systemu rozdzielczego w świetle obowiązujących postanowień Prawa e
rozdzial 1 system?nkowy i?nki ok
rozdział v funkcja systemu szkolnego w procesach reprodukcji społecznej wg szcepańskiego OTRVY22YB
więcej podobnych podstron