1

SYSTEMY ELEKTROENERGETYCZNE 

Rozdział

7

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO

Łódź, 2011 rok

Andrzej Kanicki

2

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Wprowadzenie 

Stabilność

globalna systemu elektroenergetycznego to stabilność

jego pracy 

podczas dużych zakłóceń. Do zakłóceń

tych można zaliczyć:

9załączanie, wyłączanie wielkich odbiorów,
9załączanie, wyłączanie grup generatorów, całych elektrowni,
9załączanie, wyłączanie linii w sieci elektroenergetycznej,
9powstanie zwarcia.
Najgroźniejszym zakłóceniem jest oczywiście zwarcie, podczas którego 

następuje gwałtowna redukcja pobieranej mocy czynnej z generatorów, gdy 

tymczasem moc mechaniczna turbin pozostaje stała. Ta nierównowago 

momentów napędowego i hamującego prowadzi do szybkiego wzrostu kątów 

między wirnikami generatorów oraz ich prędkości obrotowych. 
W praktyce inżynierskiej badanie równowagi dynamicznej ogranicza się

bardzo 

często tylko do sprawdzenia czy równowaga jest zachowana dla pierwszego 

wahnięcia wirnika. 
W układach elektroenergetycznych przy pominięciu wpływu działania 

regulatorów na zjawisko stabilności takie założenie jest dopuszczalne. 

3

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

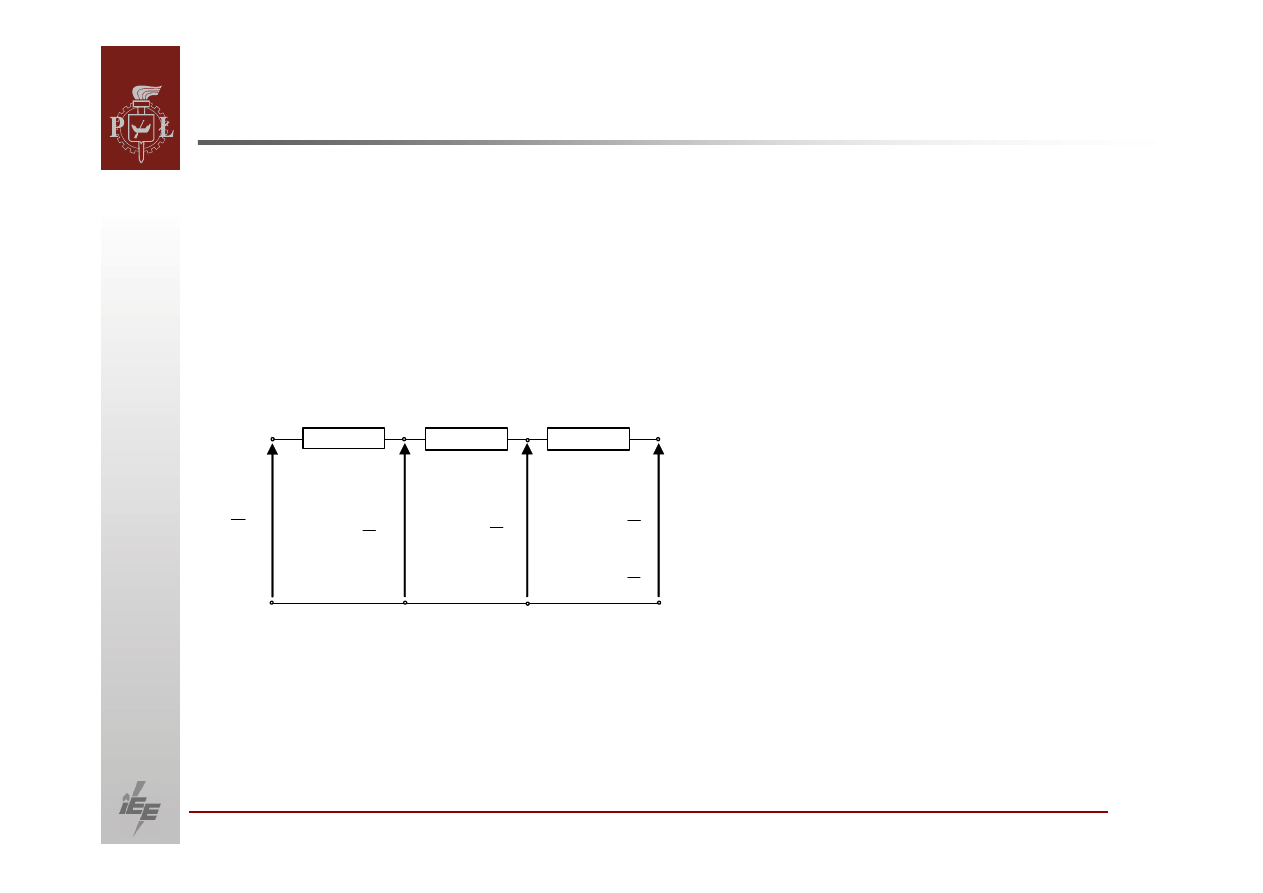
Model matematyczny generatora 

W badaniach stanów ustalonych generatory są

modelowane za pomocą

reaktancji synchronicznej podłużnej, za którą

występuje siła elektromotoryczna 

synchroniczna generatora. 
Do badania równowagi dynamicznej przyjmuje się, że generator jest 

reprezentowany przez siłę

elektromotoryczną

przejściową

za reaktancją

przejściową. 

d

E

d

E

G

U

d

E′

d

E″

d

X ′′

d

d

X

X

′′

−

′

d

d

X

X

′

−

4

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

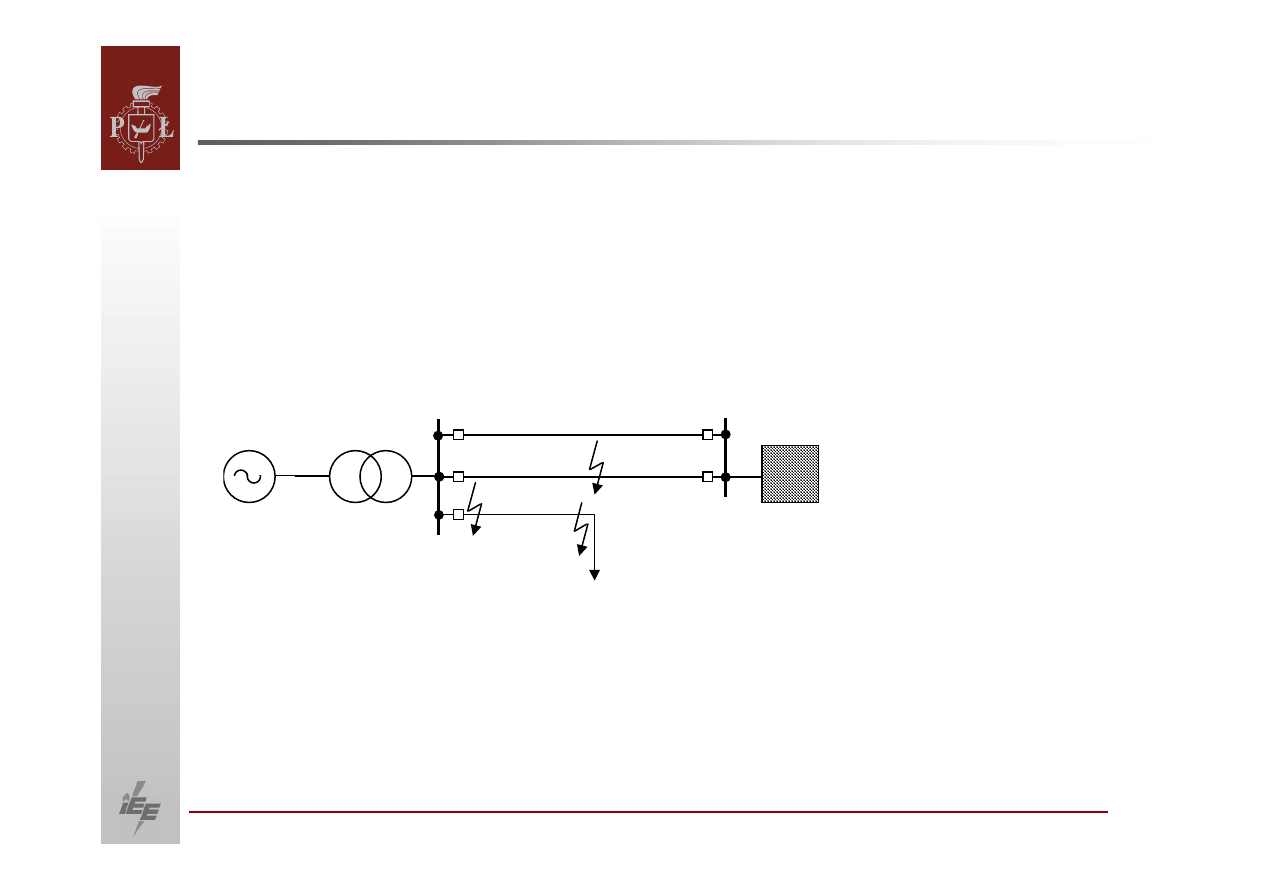
Zastosowanie metody równych powierzchni 

Została już

opisana metoda równych powierzchni. Metoda ta polega określeniu 

powierzchni pola odpowiadającym energii kinetycznej przyspieszającej 

i hamującej

na wykresie mocy w funkcji kąta pomiędzy siłą

elektromotoryczną

przejściową

a napięciem sieci sztywnej. Równowaga zostanie zachowana, jeśli 

te pola mogą

być

równe sobie i

nie

zostanie zachowana, jeśli pole 

przyspieszające i hamujące

nie są

sobie równe. 

G

T

L1

A

B

220 kV

220 kV

UE

L3

L2

1

3

2

5

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

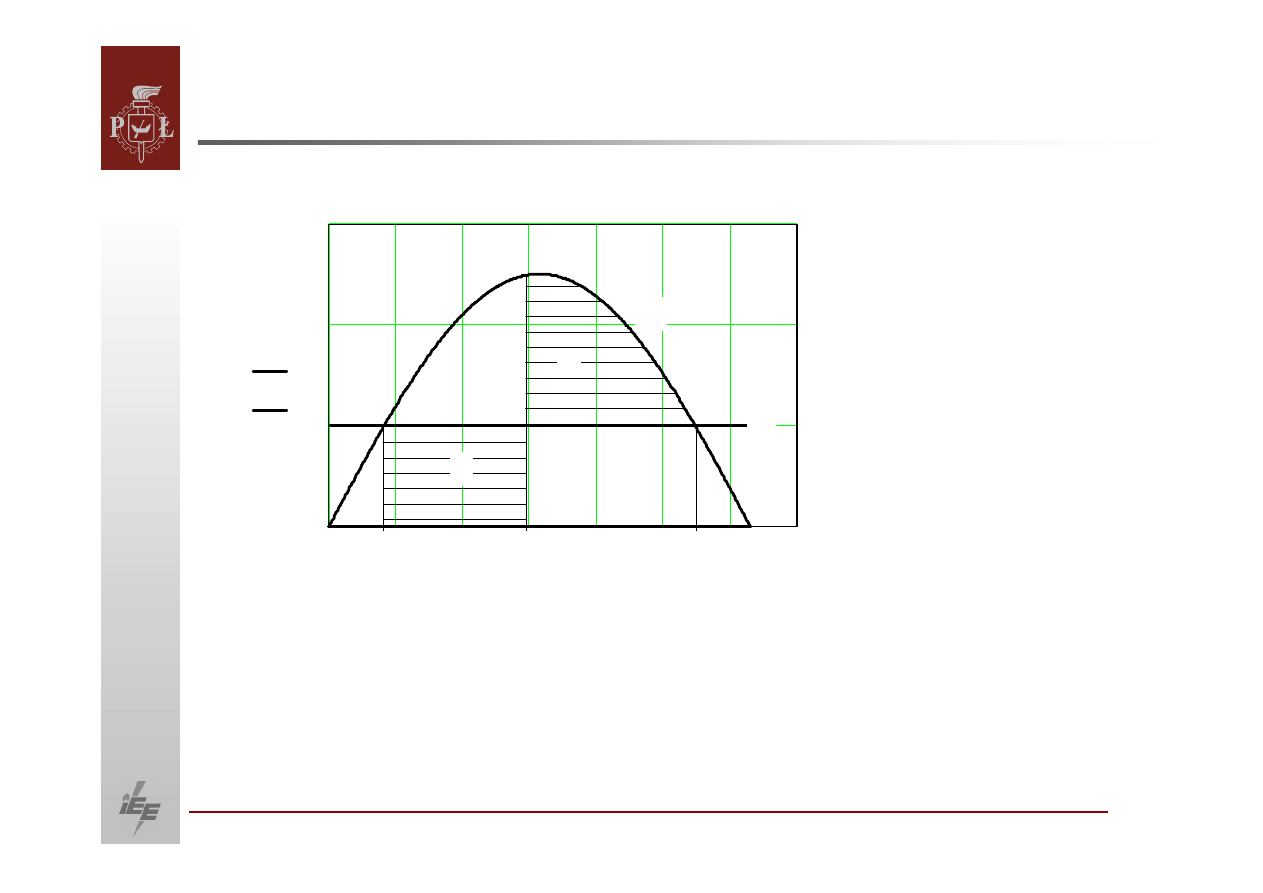
Zastosowanie metody równych powierzchni 

Pola reprezentujące energie kinetyczne dla zwarcia trójfazowego w

punkcie

1 

0

0.5

1

1.5

2

2.5

3

3.5

0

1

2

3

P1

i

P2

i

δ i

1

S

2

S

0

e

P

eZ

P

m

P

0

δ

′

mx

δ

′

0

δ

Π

′

−

P

A

B

δ

′

6

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Badanie stabilności dynamicznej podczas zwarć

niesymetrycznych

W miejscu zwarcia niesymetrycznego trzeba włączyć

dodatkową

sztuczną

gałąź

o impedancji zależnej od rodzaju zwarcia, i

tak

impedancja ta wynosi: 

•

trójfazowe ………………….

•

dwufazowe ………………..

•

jednofazowe ………………

•

dwufazowe z ziemią

…..

0

Z

=

Δ

( )

2

Z

Z

=

Δ

( )

( )

0

2

Z

Z

Z

+

=

Δ

( )

( )

( )

( )

0

2

0

2

Z

Z

Z

Z

Z

+

=

Δ

7

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

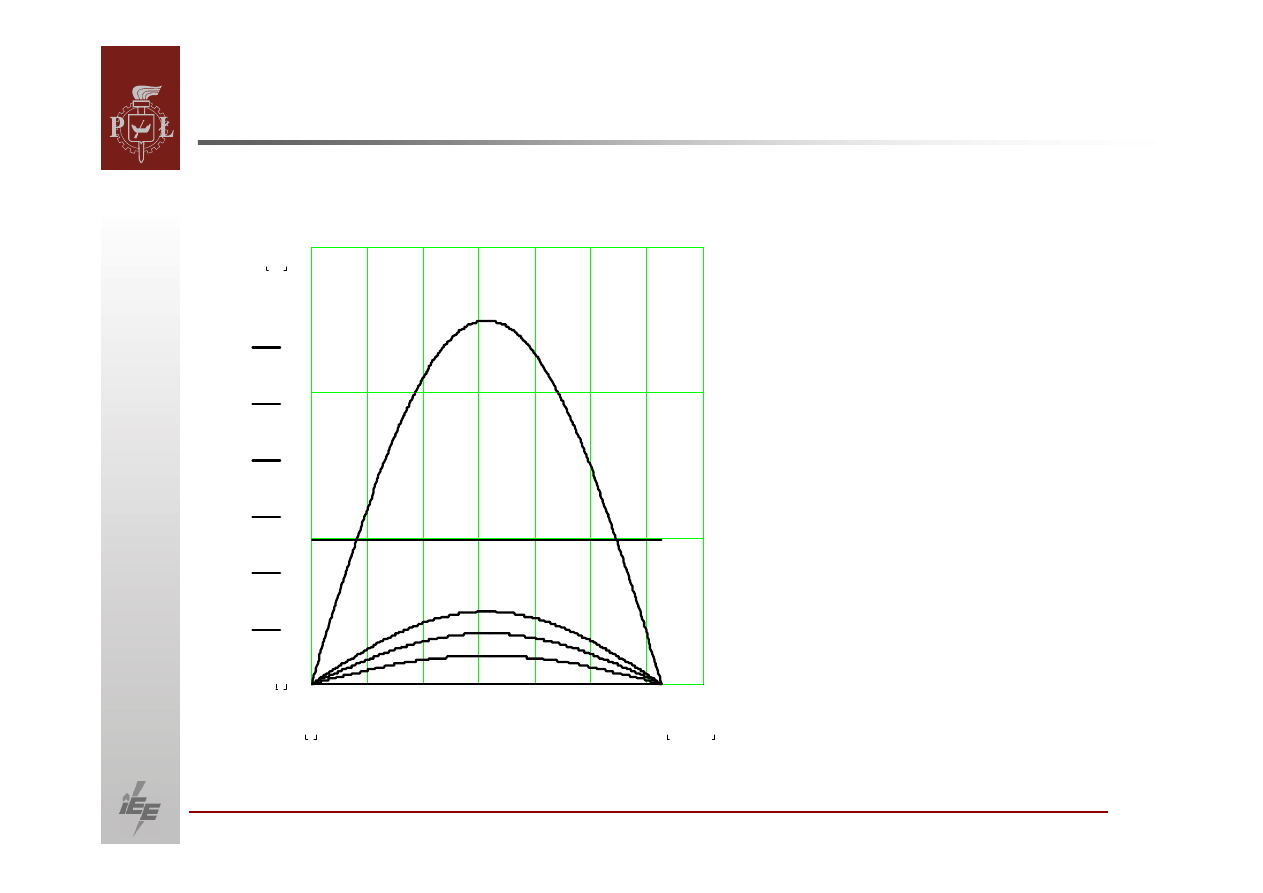
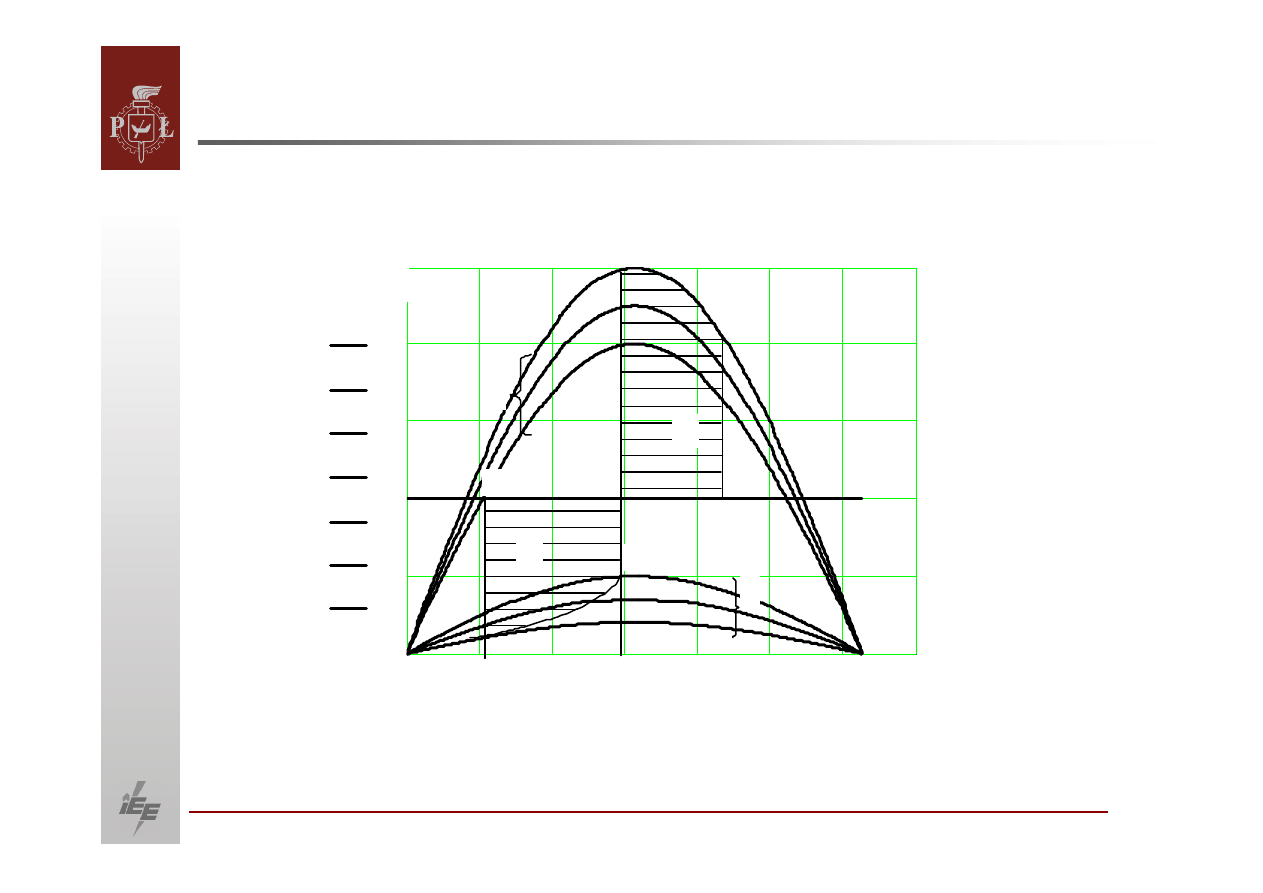
Badanie stabilności dynamicznej podczas zwarć

niesymetrycznych

Charakterystyki mocy dla różnych rodzajów zwarć

2.5

0

P1

i

P2

i

P3

i

P4

i

P5

i

P6

i

3.14159

0

δ i.

0

0.5

1

1.5

2

2.5

3

3.5

0

1

2

3

8

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

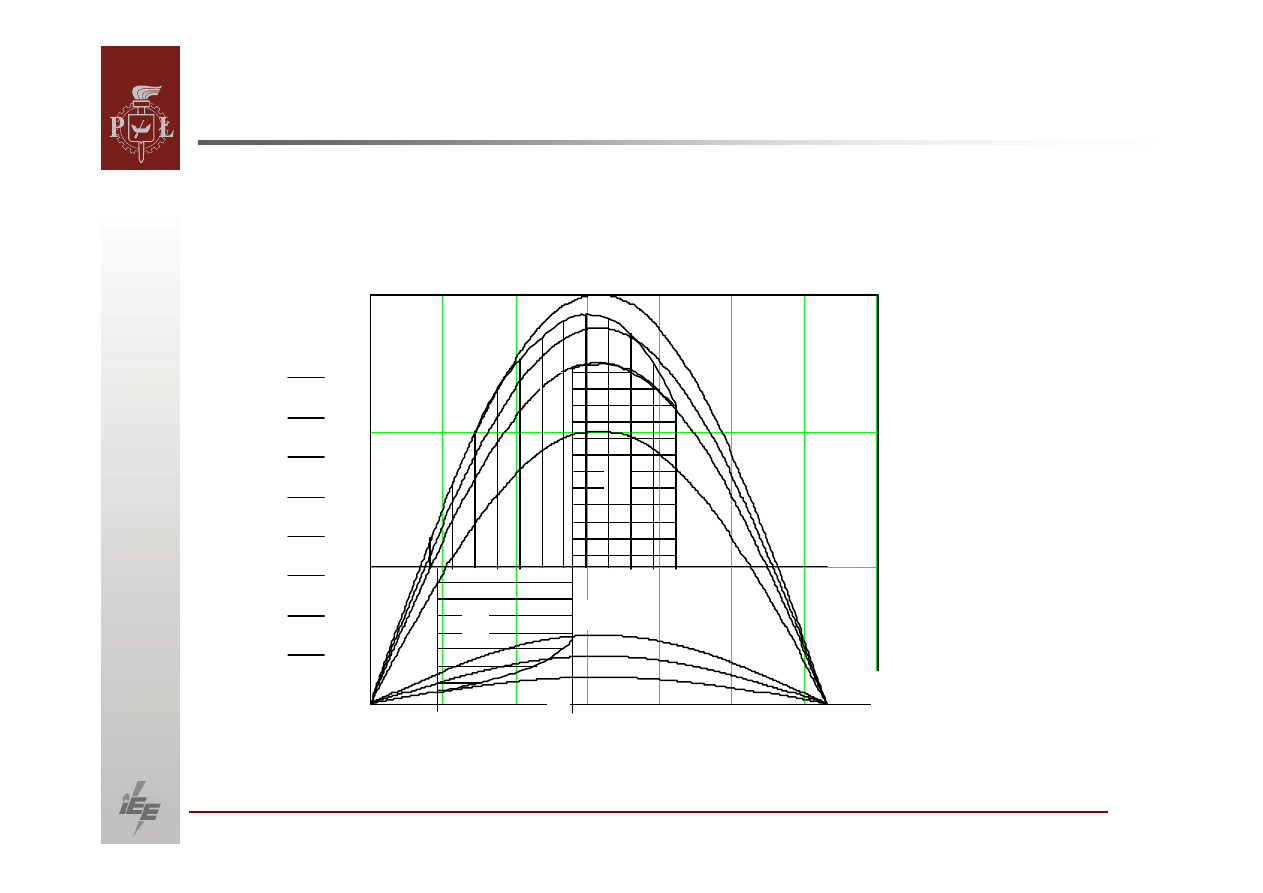
Wpływ regulacji wzbudzenia 

Charakterystyki mocy z uwzględnieniem

regulacji wzbudzenie generatora 

P1

i

P2

i

P3

i

P4

i

P5

i

P6

i

P7

i

δ i.

0

0.5

1

1.5

2

2.5

3

3.5

0

0.5

1

1.5

2

2.5

1

P

δ’

2

S

1

5

1

2

3

4

3’

S

2

6

7

9

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Wpływ regulacji wzbudzenia

Wahania wirnika generatora dla zwarcia w sieci o dużej

impedancji 

łączącej generator z siecią

sztywną

0

0.5

1

1.5

2

2.5

3

3.5

0

1

2

3

P1

i

P2

i

P3

i

P4

i

P5

i

P6

i

P7

i

P8

i

δ i

S

3

P

δ’

1

S

1

2

3

4

5

6

7

3’

8

9

S

2

10

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania 

Zadanie 1

Elektrownia oddaje moc czynną

przy napięciu na zaciskach 

generatora                                  . Na początku linii L2 wystąpiło zwarcie 

trójfazowe. Obliczyć

największy czas dopuszczalny czas trwania zwarcia 

dopuszczalny ze względu na równowagę

dynamiczną. Pominąć

rezystancje 

elementów sieci. 

MW

100

=

G

P

kV

10,5

=

=

NG

G

U

U

G

T

L1

A

B

220 kV

220 kV

UE

L2

11

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Dane:
G: 

T:

L:

UE:

MVA

120

=

N

S

%

20

=

′

d

X

kV

5

,

10

=

N

U

ind.

8

,

0

cos

=

N

ϕ

s

5

,

12

=

m

T

MVA

150

=

N

S

%

5

,

10

=

z

U

Δ

5

,

10

220

=

T

ϑ

km

Ω

4

,

0

=

k

X

km

200

=

l

kV

220

=

B

U

12

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Impedancje elementów na poziomie napięcia 10,5 kV 

Ω

184

,

0

120

5

,

10

100

20

100

2

2

=

⋅

=

⋅

′

=

N

N

d

G

S

U

X

X

Ω

077

,

0

150

5

,

10

100

5

,

10

100

2

2

=

⋅

=

⋅

=

N

N

z

T

S

U

U

X

Δ

Ω

182

,

0

220

5

,

10

200

4

,

0

1

2

2

2

=

⋅

⋅

=

⋅

⋅

=

T

k

L

l

X

X

ϑ

13

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Obliczenie kąta pomiędzy napięciem na zaciskach generatora i napięciem

sieci 

sztywnej oraz mocy biernej generatora 

ϑ

sin

⋅

+

⋅

=

L

T

S

G

G

X

X

U

U

P

(

)

235

,

0

5

,

10

5

,

10

259

,

0

100

sin

=

⋅

⋅

=

⋅

+

⋅

=

S

G

L

T

G

U

U

X

X

P

ϑ

(

)

o

6

,

13

235

,

0

sin

arc

=

=

ϑ

=

+

⋅

−

+

=

ϑ

cos

2

L

T

S

G

L

T

G

G

X

X

U

U

X

X

U

Q

Mvar

9

,

11

235

,

0

1

259

,

0

5

,

10

259

,

0

5

,

10

2

2

2

=

−

⋅

−

=

14

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Obliczenia modułu siły elektromotorycznej generatora 

Wyznaczenie mocy granicznej równowagi układu 

Obliczenie kąta początkowego 

=

⋅

+

⋅

+

=

′

G

G

G

G

G

G

G

d

U

X

P

j

U

X

Q

U

E

(

)

kV

85

,

10

75

,

1

7

,

10

5

,

10

184

,

0

100

5

,

10

184

,

0

9

,

11

5

,

10

3

,

9

o

j

e

j

j

=

+

=

⋅

+

⋅

+

=

=

+

+

⋅

′

=

L

T

G

S

d

gr

X

X

X

U

E

P

MW

257

182

,

0

077

,

0

184

,

0

5

,

10

85

,

10

=

+

+

⋅

=

rad.

4

,

0

9

,

22

6

,

13

3

,

9

'

0

=

=

+

=

+

′

=

′

o

U

E

G

d

ϑ

δ

δ

15

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Wyznaczenie kąta granicznego zwarcia. Energia kinetyczna przyspieszająca  

Energia kinetyczna hamująca 

(

)

(

)

0

0

1

δ

δ

δ

δ

′

−

′

⋅

=

′

−

′

⋅

=

x

G

x

m

P

P

S

(

)

[

]

=

′

−

′

−

⋅

−

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

′

⋅

=

∫

′

−

′

x

m

e

P

d

P

S

x

δ

δ

Π

δ

δ

Π

δ

0

1

2

0

(

)

=

′

−

′

−

⋅

−

′

⋅

′

=

∫

′

−

′

x

G

gr

P

d

P

x

δ

δ

Π

δ

δ

δ

Π

δ

0

0

sin

(

)

(

)

x

G

x

gr

gr

P

P

P

δ

δ

Π

δ

δ

Π

′

−

′

−

⋅

−

′

⋅

+

′

−

⋅

−

=

0

0

cos

cos

16

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Wyznaczenie kąta granicznego zwarcia. Porównanie pól i obliczenie kąta 

granicznego dla zwarcia.

(

)

(

)

x

G

x

gr

gr

x

G

P

P

P

P

δ

δ

Π

δ

δ

δ

δ

′

−

′

−

⋅

−

′

⋅

+

′

⋅

=

′

−

′

⋅

0

0

0

cos

cos

(

)

(

)

x

gr

gr

x

G

x

G

P

P

P

P

δ

δ

δ

δ

Π

δ

δ

′

⋅

+

′

⋅

=

′

−

′

−

⋅

+

′

−

′

⋅

cos

cos

0

0

0

(

)

x

gr

gr

G

P

P

P

δ

δ

δ

Π

′

⋅

+

′

⋅

=

′

⋅

−

⋅

cos

cos

2

0

0

(

)

(

)

010

0

9

22

257

4

0

2

100

2

0

,

,

cos

,

cos

P

P

cos

o

o

gr

G

x

−

=

−

⋅

−

⋅

=

′

−

′

⋅

−

⋅

=

′

Π

δ

δ

Π

δ

o

x

6

,

90

=

′

δ

17

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Wyznaczenie dopuszczalnego czasu trwania zwarcia. Ruch wirnika podczas 

zwarcia jest opisany równaniem różniczkowym o postaci:  

Równanie to można rozwiązać

analitycznie poprzez dwukrotne scałkowanie w 

przedziale 

( )

S

m

S

NG

m

P

t

d

d

S

T

ω

δ

ω

=

⋅

⋅

2

2

2

x

δ

δ

′

−

′

0

NG

m

S

m

x

S

T

t

P

⋅

⋅

⋅

⋅

=

′

−

′

2

2

0

ω

δ

δ

18

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 1

Z powyższego równania wyznaczamy dopuszczalny czas trwania zwarcia: 

(

)

S

m

x

NG

m

P

S

T

t

ω

δ

δ

⋅

′

−

′

⋅

⋅

⋅

=

0

2

rad.

182

,

1

7

,

67

9

,

22

6

,

90

0

0

=

=

−

=

′

−

′

δ

δ

x

s

336

,

0

50

2

100

182

,

1

120

5

,

12

2

==

⋅

⋅

⋅

⋅

⋅

⋅

=

Π

t

19

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

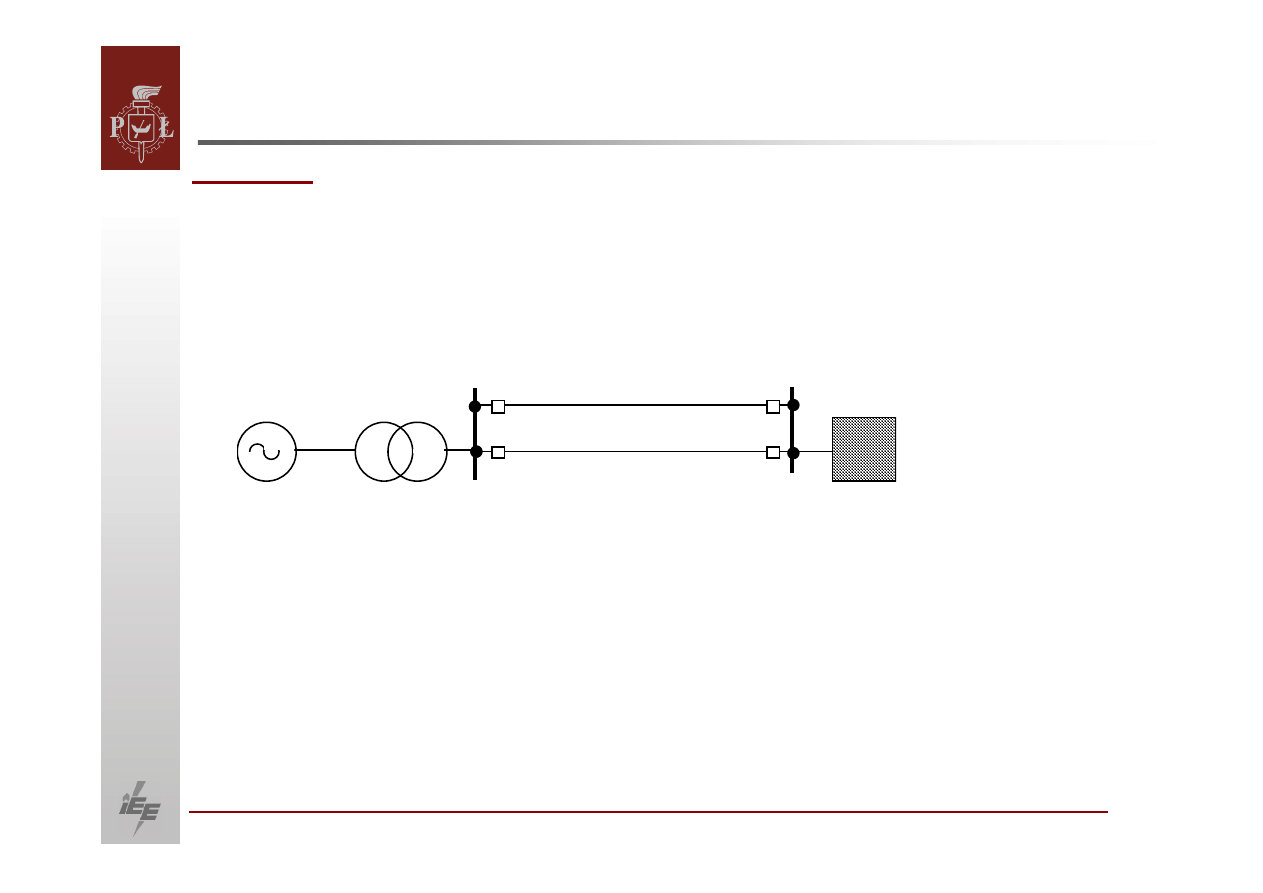
Elektrownia w układzie jak na rysunku oddaje moc czynną

przy 

napięciu na zaciskach generatora                                   . 
Zbadać

równowagę

po wyłączeniu linii L1. 

MW

200

=

G

P

kV

10,0

=

=

NG

G

U

U

G

T

L1

A

B

220 kV

220 kV

UE

L2

20

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

Dane:
G:

T:

L1, L2:

UE:

MVA

300

=

N

S

%

20

=

′

d

X

kV

0

,

10

=

N

U

ind.

8

,

0

cos

=

N

ϕ

s

0

,

12

=

m

T

MVA

400

=

N

S

%

0

,

11

=

z

U

Δ

0

,

10

220

=

T

ϑ

km

Ω

4

,

0

=

k

X

km

200

=

l

kV

220

=

B

U

21

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

Rozwiązanie
Impedancje elementów na poziomie napięcia 10 kV 

Napięcie sieci sztywnej na poziomie 10 kV 

Ω

0667

,

0

300

10

100

20

100

2

2

=

⋅

=

⋅

′

=

N

N

d

G

S

U

X

X

Ω

0275

,

0

400

10

100

11

100

2

2

=

⋅

=

⋅

=

N

N

z

T

S

U

U

X

Δ

Ω

166

,

0

220

10

200

4

,

0

1

2

2

2

1

=

⋅

⋅

=

⋅

⋅

=

T

k

L

l

X

X

ϑ

kV

10

220

10

220

1

10

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

T

S

S

U

U

ϑ

22

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

Obliczenie kąta pomiędzy napięciem na zaciskach generatora i napięciem

sieci 

sztywnej oraz mocy biernej generatora w stanie normalnym 

ϑ

sin

10

⋅

+

⋅

=

L

T

S

G

G

X

X

U

U

P

(

)

223

,

0

10

10

166

,

0

2

1

0275

,

0

200

sin

10

=

⋅

⎟

⎠

⎞

⎜

⎝

⎛

+

⋅

=

⋅

+

⋅

=

S

G

L

T

G

U

U

X

X

P

ϑ

(

)

o

9

,

12

223

,

0

sin

arc

=

=

ϑ

=

⋅

+

⋅

−

+

=

ϑ

cos

10

2

L

T

S

G

L

T

G

G

X

X

U

U

X

X

U

Q

Mvar

6

,

22

223

,

0

1

1115

,

0

10

1115

,

0

10

2

2

2

=

−

−

=

23

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

Obliczenia modułu siły elektromotorycznej generatora 

Wyznaczenie mocy granicznej równowagi układu przed wyłączeniem 

=

⋅

+

⋅

+

=

′

G

G

G

G

G

G

G

d

U

X

P

j

U

X

Q

U

E

(

)

kV

3

,

10

33

,

1

2

,

10

10

0667

,

0

200

10

0667

,

0

6

,

22

10

4

,

7

o

j

e

j

j

=

+

=

⋅

+

⋅

+

=

=

⋅

+

+

⋅

′

=

′

L

T

G

S

d

gr

X

X

X

U

E

P

2

1

10

MW

578

166

,

0

2

1

0275

,

0

0667

,

0

10

3

,

10

=

⋅

+

+

⋅

=

24

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

Wyznaczenie mocy granicznej równowagi układu po wyłączeniu 

Obliczenie kąta początkowego 

=

+

+

⋅

′

=

′′

L

T

G

S

d

gr

X

X

X

U

E

P

10

MW

396

166

,

0

0275

,

0

0667

,

0

10

3

,

10

=

+

+

⋅

=

rad.

354

,

0

3

,

20

9

,

12

4

,

7

'

0

=

=

+

=

+

′

=

′

o

U

E

G

d

ϑ

δ

δ

25

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

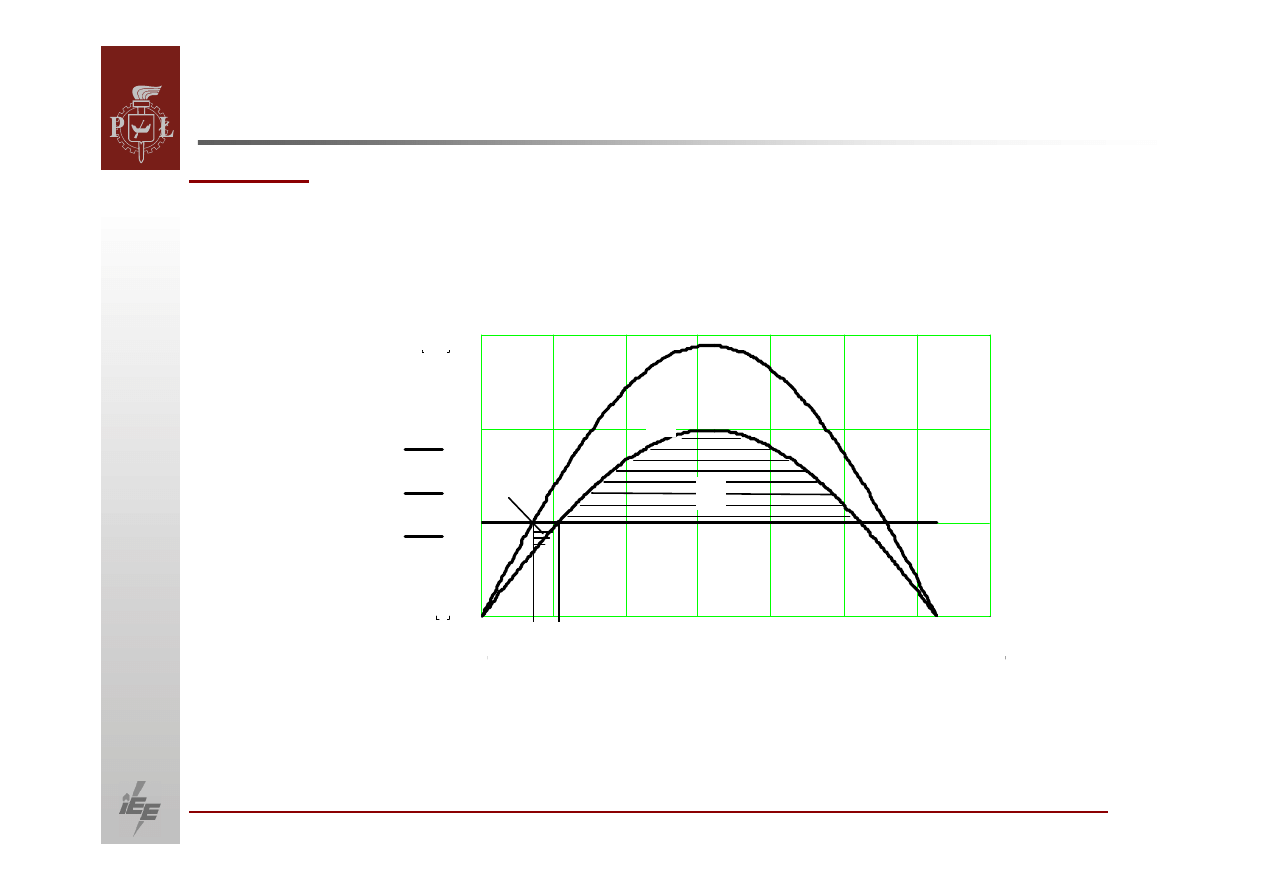
Charakterystyki mocy 

578

0

P 1

i

P 2

i

P 3

i

3.141593

0

δ i.

0

0.5

1

1.5

2

2.5

3

3.5

0

200

400

600

P′

P ′′

0

δ

′

k

δ

′

1

S

δ

′

P

2

S

26

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

Obliczenie kąta końcowego 

Obliczenie pola 

505

,

0

396

200

sin

=

=

′′

=

′

gr

m

k

P

P

δ

(

)

rad.

529

0

3

30

505

0

sin

arc

,

,

,

o

k

=

=

=

′

δ

1

S

(

)

∫

′

′

=

′

⋅

′

⋅

′′

−

′

−

′

⋅

=

k

d

P

P

S

gr

k

m

δ

δ

δ

δ

δ

δ

0

sin

0

1

(

)

(

)

=

′

−

′

⋅

′′

−

′

−

′

⋅

=

k

gr

k

m

P

P

δ

δ

δ

δ

cos

cos

0

0

(

)

(

)

rad.

MW

30

,

5

863

,

0

938

,

0

396

354

,

0

529

,

0

200

=

−

⋅

−

−

⋅

=

27

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 2

Obliczenie pola 

Ponieważ

– równowaga będzie zachowana. 

2

S

(

)

(

)

∫

′

−

′

=

′

−

′

−

⋅

−

′

⋅

′

⋅

′′

=

k

k

k

k

m

gr

P

d

P

S

δ

Π

δ

δ

δ

Π

δ

δ

sin

2

(

)

(

)

(

)

=

′

−

′

−

⋅

−

′

−

−

′

⋅

′′

=

k

k

m

k

k

gr

P

P

δ

δ

Π

δ

Π

δ

cos

cos

(

)

(

)

rad.

MW

8

.

266

529

,

0

529

,

0

200

836

,

0

863

,

0

396

=

−

−

⋅

−

+

⋅

=

Π

2

1

S

S

<

28

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

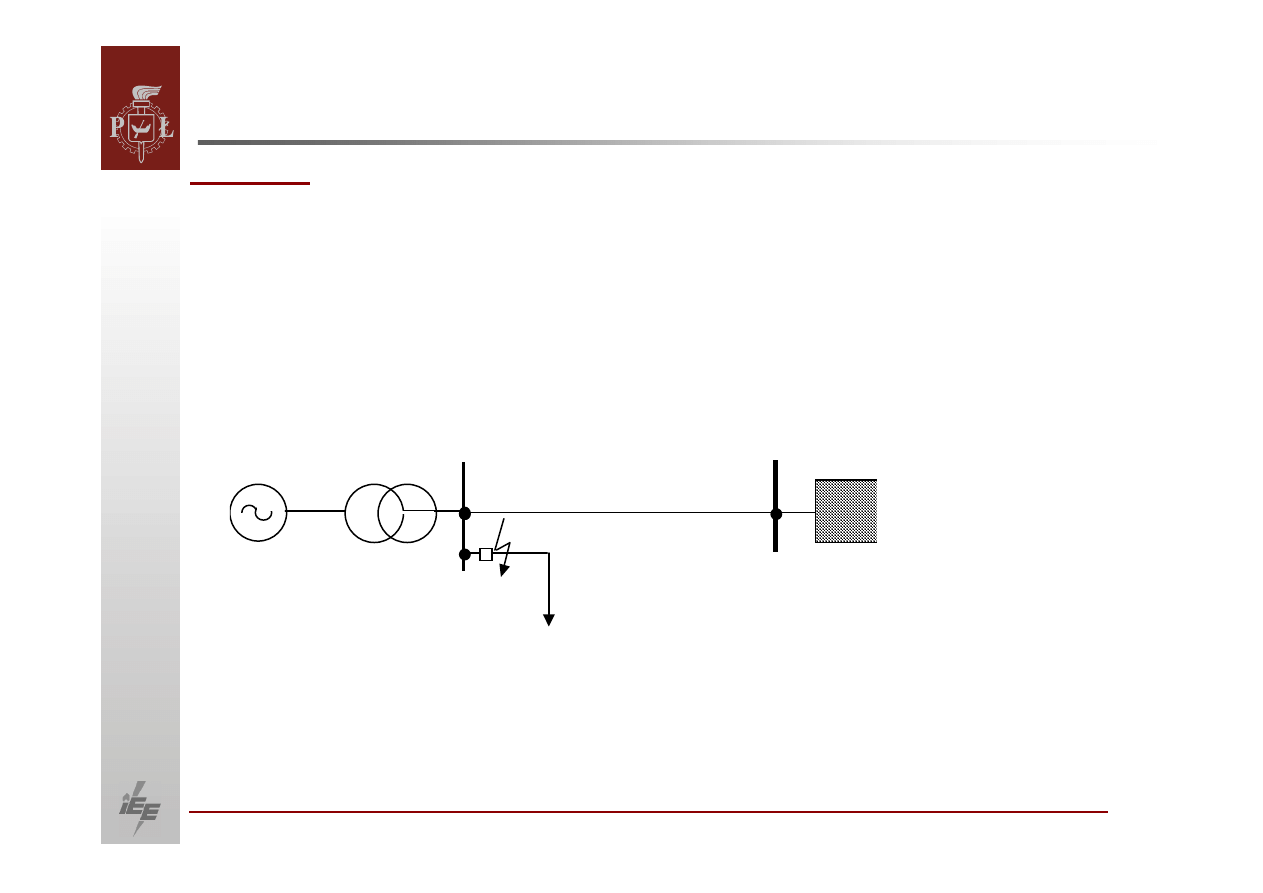
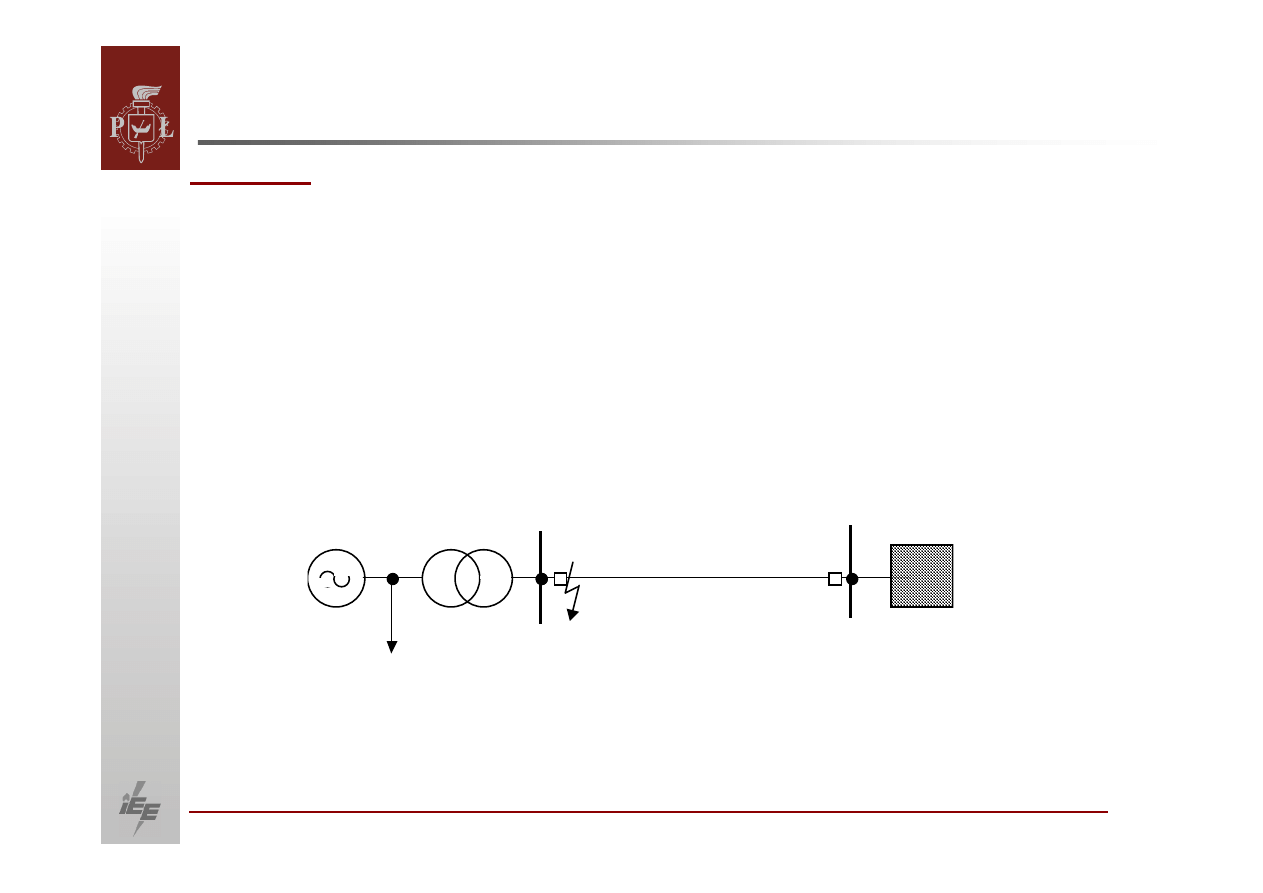
Elektrownia w układzie jak na rysunku oddaje moc czynną

przy 

napięciu na zaciskach generatora                                   , przy czym odbiór pobiera 

50 MW przy                        . Na początku linii powstaje zwarcie trójfazowe 

wyłączone po czasie 0,2

s. Linia jest wyposażona w automatykę

SPZ

z

czasem

przerwy beznapięciowej równym 0,25

s. Zbadać

równowagę

układu przy 

założeniu udanej operacji SPZ. Odbiór zamodelować

stałą

impedancją. 

MW

200

=

G

P

kV

10,0

=

=

NG

G

U

U

ind.

8

,

0

cos

=

ϕ

G

T

L1

A

B

220 kV

220 kV

UE

odbiór

29

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Dane:

G:

T:

L1:

UE:

MVA

300

=

N

S

%

20

=

′

d

X

kV

0

,

10

=

N

U

ind.

8

,

0

cos

=

N

ϕ

s

0

,

12

=

m

T

MVA

300

=

N

S

%

0

,

11

=

z

U

Δ

0

,

10

220

=

T

ϑ

km

Ω

4

,

0

=

k

X

km

150

=

l

kV

220

=

B

U

30

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Rozwiązanie 
Impedancje elementów na poziomie napięcia 10 kV 

Napięcie sieci sztywnej na poziomie 10 kV 

Ω

0667

,

0

300

10

100

20

100

2

2

=

⋅

=

⋅

′

=

N

N

d

G

S

U

X

X

Ω

0367

,

0

300

10

100

11

100

2

2

=

⋅

=

⋅

=

N

N

z

T

S

U

U

X

Δ

Ω

124

,

0

220

10

150

4

,

0

1

2

2

2

1

=

⋅

⋅

=

⋅

⋅

=

T

k

L

l

X

X

ϑ

kV

10

220

10

220

1

10

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

T

S

S

U

U

ϑ

31

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Obliczenie kąta pomiędzy napięciem na zaciskach generatora i napięciem

sieci 

sztywnej oraz mocy biernej generatora w stanie normalnym 

MW

150

50

200

=

−

=

−

=

o

G

L

P

P

P

ϑ

sin

10

⋅

+

⋅

=

L

T

S

G

L

X

X

U

U

P

(

)

(

)

241

,

0

10

10

124

,

0

0367

,

0

150

sin

10

=

⋅

+

⋅

=

⋅

+

⋅

=

S

G

L

T

L

U

U

X

X

P

ϑ

(

)

o

9

,

13

241

,

0

sin

arc

=

=

ϑ

=

⋅

+

⋅

−

+

=

ϑ

cos

10

2

L

T

S

G

L

T

G

L

X

X

U

U

X

X

U

Q

Mvar

3

,

18

241

,

0

1

161

,

0

10

161

,

0

10

2

2

2

=

−

−

=

32

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Obliczenia modułu siły elektromotorycznej generatora 

Obliczenie kąta początkowego 

Mvar

5

37

8

0

6

0

50

,

,

,

cos

sin

P

Q

o

o

o

o

=

⋅

=

⋅

=

ϕ

ϕ

Mvar

8

,

55

5

,

37

3

,

18

=

+

=

+

=

o

L

G

Q

Q

Q

=

⋅

+

⋅

+

=

′

G

G

G

G

G

G

G

d

U

X

P

j

U

X

Q

U

E

(

)

kV

5

10

33

1

4

10

10

0667

0

200

10

0667

0

8

55

10

3

7

o

,

j

e

,

,

j

,

,

j

,

,

=

+

=

⋅

+

⋅

+

=

rad.

370

,

0

2

,

21

9

,

13

3

,

7

'

0

=

=

+

=

+

′

=

′

o

U

E

G

d

ϑ

δ

δ

33

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Zastąpienie odbioru impedancją

Obliczenie impedancji wzajemnej generator – sieć

sztywna dla układu przed 

zwarciem 
W celu obliczenia impedancji wzajemnej generator 1 – sieć

sztywna musimy 

przekształcić

gwiazdę

złożoną

z impedancji:          ,         oraz                 

występującą

w schemacie zastępczym na trójkąt. 

(

)

Ω

96

,

0

28

,

1

5

,

37

50

10

2

*

1

2

1

j

j

S

U

Z

G

o

+

=

−

=

=

G

X

j

1

o

Z

(

)

L

T

X

X

j

+

(

)

(

)

=

+

⋅

+

+

+

=

1

12

o

L

T

G

L

T

G

Z

X

X

j

X

j

X

X

j

X

j

Z

(

)

(

)

=

+

+

⋅

+

+

+

=

96

,

0

28

,

1

124

,

0

0367

,

0

0667

,

0

124

,

0

0367

,

0

0667

,

0

j

j

j

j

j

(

)

Ω

2315

,

0

231

,

0

0054

,

0

3

,

91

o

j

e

j

=

+

−

=

34

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Obliczenie impedancji własnej generatora dla układu przed zwarciem 

Obliczenie impedancji wzajemnej generator – sieć

sztywna dla układu podczas 

zwarcia 
Zwarcie występuje na drodze generator – sieć

sztywna to                 . 

(

)

(

)

=

+

+

⋅

+

+

=

1

1

11

o

L

T

o

L

T

G

Z

X

X

j

Z

X

X

j

X

j

Z

(

) (

)

(

) (

)

=

+

+

+

+

⋅

+

+

=

96

,

0

28

,

1

124

,

0

0367

,

0

96

,

0

28

,

1

124

,

0

0367

,

0

0667

,

0

j

j

j

j

j

(

)

Ω

2177

,

0

2174

,

0

00114

,

0

0

,

87

o

j

e

j

=

+

=

∞

=

z

Z

12

35

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Obliczenie impedancji własnej generatora dla układu podczas zwarcia 

Obliczenie impedancji wzajemnej generator – sieć

sztywna dla układu 

z wyłączoną

linią

Przerwa występuje na drodze generator – sieć

sztywna to                  . 

=

+

⋅

+

=

1

1

11

o

T

o

T

G

z

Z

X

j

Z

X

j

X

j

Z

(

)

(

)

=

+

+

+

⋅

+

=

96

,

0

28

,

1

0367

,

0

96

,

0

28

,

1

0367

,

0

0667

,

0

j

j

j

j

j

(

)

Ω

1029

,

0

1029

,

0

00066

,

0

6

,

89

o

j

e

j

=

+

=

∞

=

o

Z

12

36

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Obliczenie impedancji własnej generatora dla układu z wyłączoną

linią

Wyznaczenie charakterystyki mocy układu przed zwarciem 

Ponieważ

to pomijamy tę

wielkość. Wtedy mamy: 

=

+

+

=

+

=

96

,

0

28

,

1

0667

,

0

1

11

j

j

Z

X

j

Z

o

G

o

(

)

Ω

641

,

1

027

,

1

28

,

1

7

,

38

o

j

e

j

=

+

=

( )

(

)

12

12

12

10

11

11

2

sin

sin

α

δ

α

−

′

⋅

⋅

′

+

⋅

′

=

′

Z

U

E

Z

E

P

S

d

d

o

3

,

1

12

=

α

( )

=

′

⋅

⋅

′

+

⋅

′

=

′

12

12

10

11

11

2

sin

sin

δ

α

Z

U

E

Z

E

P

S

d

d

MW

sin

454

5

,

26

sin

2315

,

0

10

5

,

10

3

sin

2177

,

0

5

,

10

12

12

2

δ

δ

′

⋅

+

=

′

⋅

⋅

+

⋅

=

o

37

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Wyznaczenie charakterystyki mocy układu podczas zwarcia 

Wyznaczenie charakterystyki mocy układu z wyłączoną

linią

( )

MW

48

,

7

4

,

0

sin

1029

,

0

5

,

10

sin

2

11

11

2

=

⋅

=

⋅

′

=

′′

o

z

z

d

Z

E

P

α

( )

MW

4

,

52

7

,

38

sin

641

,

1

5

,

10

sin

2

11

11

2

=

⋅

=

⋅

′

=

′′′

o

o

o

d

Z

E

P

α

38

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

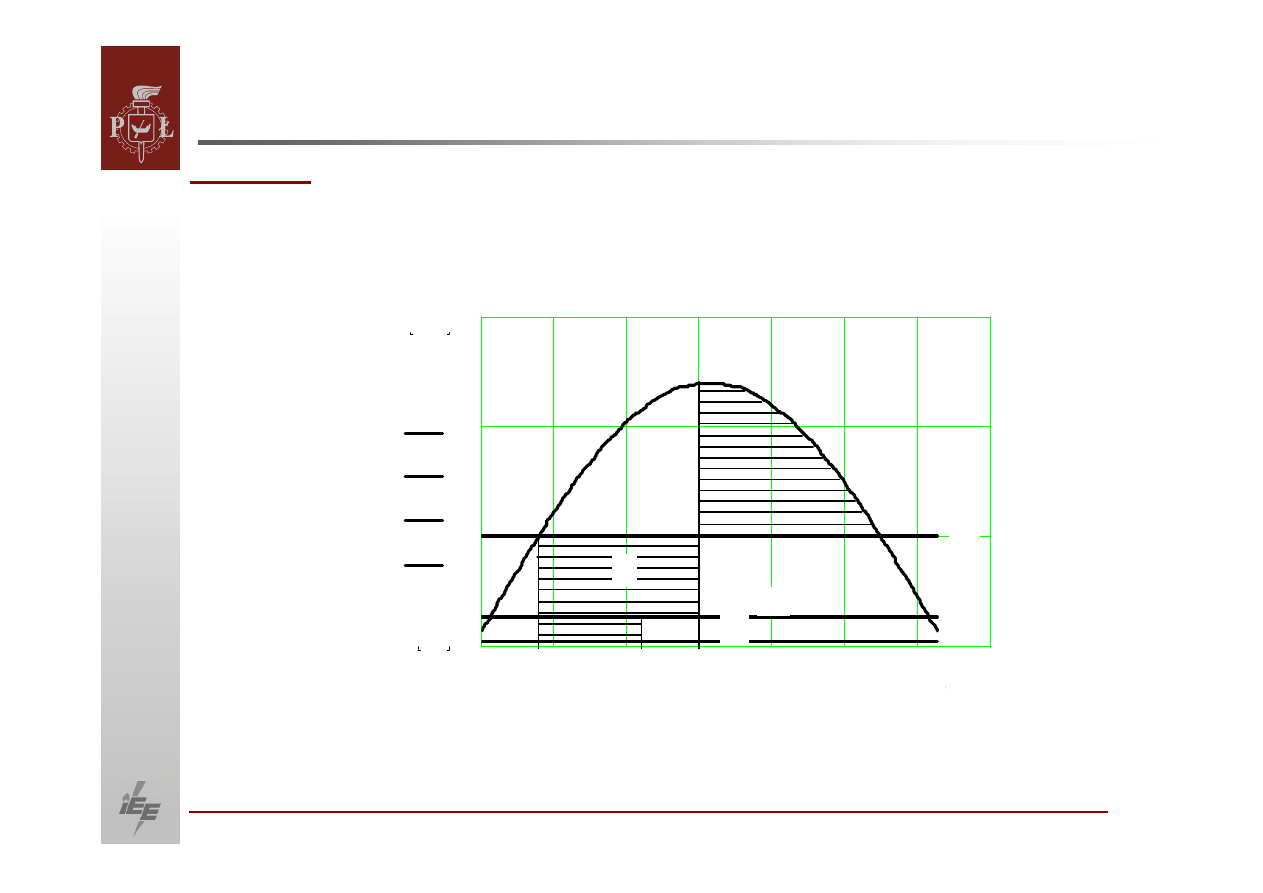
Charakterystyki mocy 

480.5

7.48

P 1

i

P 2

i

P 3

i

P 4i

3.141593

0

δ i.

0

0.5

1

1.5

2

2.5

3

3.5

0

200

400

600

P′

P ′′

P ′′′

m

P

P

δ

′

0

δ

′

1

δ

′

x

δ

′

1

S

2

S

39

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Wyznaczenie kąta 

Wyznaczenie kąta 
W celu wyznaczenia tego kąta  założymy, że wyznaczymy maksymalną

jego 

wartość

korzystając z metody równych pól. 

1

δ

′

NG

m

S

G

S

T

t

P

⋅

⋅

⋅

⋅

=

′

−

′

2

2

0

1

ω

δ

δ

(

)

(

)

=

⋅

⋅

⋅

⋅

⋅

⋅

−

+

=

⋅

⋅

⋅

⋅

′′

−

+

′

=

′

300

12

2

2

,

0

50

2

48

,

7

200

37

,

0

2

2

2

0

1

Π

ω

δ

δ

NG

m

S

G

S

T

t

P

P

o

5

.

40

rad.

706

,

0

=

=

x

δ

′

(

) (

) (

) (

)

=

′

−

′

⋅

′′′

−

+

′

−

′

⋅

′′

−

=

1

0

1

1

δ

δ

δ

δ

x

G

G

P

P

P

P

S

(

) (

) (

) (

)

=

−

′

⋅

−

+

−

⋅

−

=

706

,

0

4

,

52

200

37

,

0

706

,

0

48

,

7

200

x

δ

x

δ

′

⋅

+

−

=

6

,

147

51

,

39

40

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Przyjmując, że               mamy: 

Równanie powyższe można rozwiązać

metodą

iteracyjną. W wyniku jej 

zastosowania mamy, że: 

(

)

(

)

=

′

−

′

−

⋅

−

′

⋅

′

⋅

+

=

∫

′

−

′

x

G

P

d

S

x

δ

δ

Π

δ

δ

δ

Π

δ

0

2

0

sin

454

5

,

26

(

)

(

)

−

−

⋅

−

′

⋅

+

′

⋅

−

−

⋅

=

37

.

0

cos

454

cos

454

5

,

26

37

,

0

5

,

26

Π

δ

δ

Π

x

x

(

)

=

′

⋅

+

−

⋅

−

x

δ

Π

200

37

,

0

200

57

,

57

5

,

173

cos

454

−

′

⋅

+

′

⋅

=

x

x

δ

δ

2

1

S

S

=

57

,

57

5

,

173

cos

454

6

,

147

51

,

39

−

′

⋅

+

′

⋅

=

′

⋅

+

−

x

x

x

δ

δ

δ

0

06

,

18

9

,

25

cos

454

=

−

′

⋅

+

′

⋅

x

x

δ

δ

.

rad

623

,

1

93

=

=

′

o

x

δ

41

STABILNOŚĆ

GLOBALNA SYSTEMU ELEKTROENERGETYCZNEGO 

Zadania

Zadanie 3

Obliczenie maksymalnego czasu przerwy beznapięciowej 

Równowaga układu jest zachowana, ponieważ

(

)

(

)

=

⋅

′′′

−

′

−

′

⋅

⋅

⋅

=

S

G

x

NG

m

mx

P

P

S

T

t

ω

δ

δ

1

2

(

)

(

)

s

377

,

0

50

2

4

,

52

200

706

,

0

623

,

1

300

12

2

=

⋅

⋅

⋅

−

−

⋅

⋅

⋅

=

Π

s

25

,

0

s

377

,

0

=

>

=

p

mx

t

t