
1
SYSTEMY ELEKTROENERGETYCZNE
Rozdział
2
OBLICZANIE PRZEPŁYWÓW MOCY
Łódź, 2011 rok
Andrzej Kanicki
2
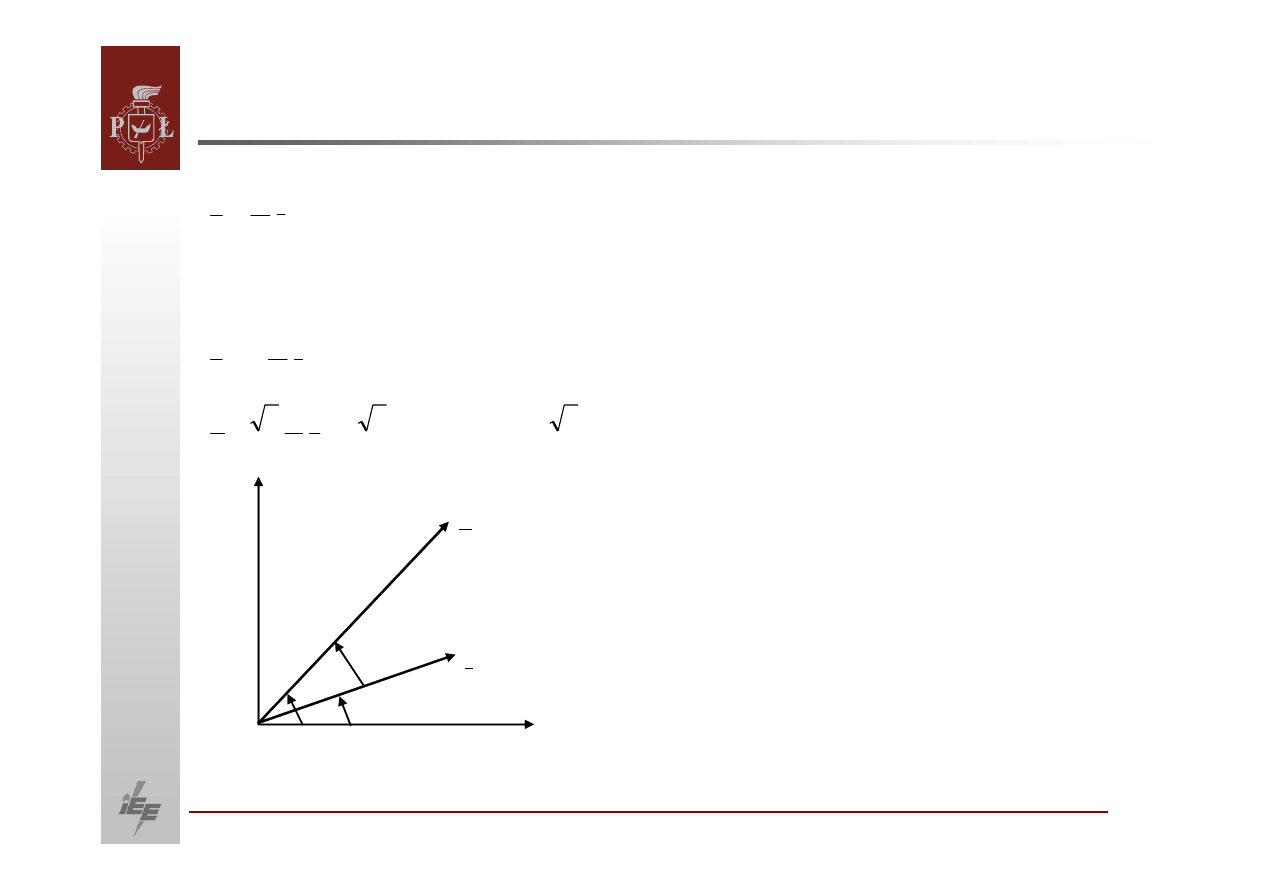
OBLICZANIE PRZEPŁYWÓW MOCY
Przepływ mocy w układzie promieniowym
(
)
ϕ
ϕ
−
ϕ
∗
=
=
=
j
j
e
I
U
e
I
U
I
U
S
i
u
i
u
ϕ
−
ϕ
=
ϕ
(
)
ϕ
ϕ
−
ϕ
∗
=
=
=
j
j
e
I
U
3
e
I
U
3
I
U
3
S
i
u
(
)
(
)
Q
j
P
j
S
e
I
U
e
I
U
I
U
S
j
j
i
u
+
=
+
⋅
=
=
=
=
−
∗
ϕ
ϕ
ϕ
ϕ
ϕ
sin
cos
3
3
3
Im
Re
U
I
U
ϕ
I
ϕ
ϕ

3
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
Przyjmujemy, że kierunek dodatni to prąd odbierany z węzła. Z tego założenia
wynika, że:
9Moc czynna pobierana z węzła jest dodatnia a moc dostarczana do węzła
ujemna,
9Moc bierna indukcyjna pobierana z węzła jest dodatnia tzn. moc bierna
pojemnościowa pobierana do węzła ujemna,
9Moc bierna indukcyjna dostarczana do węzła jest ujemna tzn. moc bierna
pojemnościowa dostarczana do węzła dodatnia.
Rozpatrując odcinek linii pomiędzy węzłami A i B a zawierający jedynie
elementy wzdłużne mamy:
B
L
B
AB
B
A
I
Z
U
U
U
U
⋅
⋅
+
=
+
=
3
Δ
*
*
3
B
B
B
U
S
I
⋅
=
(
) (
)
=
−
⋅
+
=
*
B
B
B
L
L
AB
U
jQ
P
jX
R
U
Δ

4
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
=
⋅
−
⋅
+
⋅
+
⋅
=
*
*
B
L
B
L
B
B
L
B
L
B
U
R
Q
X
P
j
U
X
Q
R
P
B
B
L
B
L
B
B
L
B
L
B
U
U
R
Q
X
P
j
U
X
Q
R
P
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
−
⋅
+
⋅
+
⋅
=
2
2
B
B
U
U
=
B
L
B
L
B
B
L
B
L
B
B
A
U
R
Q
X
P
j
U
X
Q
R
P
U
U
⋅
−
⋅
+
⋅
+
⋅
+
=
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
−
⋅
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
+
⋅
+
=
B
L
B
L
B
B
L
B
L
B
B
A
U
R
Q
X
P
U
X
Q
R
P
U
U
W przypadku, gdy można założyć, że to:
Moduł
napięcia w węźle początkowym wynosi:

5
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
(
)
2
2
2
2
2
2
3
B
L
B
B
B
L
B
L
B
L
U
R
Q
P
U
R
S
R
I
P
⋅
+
=
⋅
=
⋅
⋅
=
Δ
*
2
*
3
L
B
Y
B
Y
Y
U
I
U
S
⋅
=
⋅
⋅
=
Δ
L
B
Y
Y
U
I
⋅
=
3
L
B
Y
G
U
P
⋅
=
2
Δ
L
B
Y
B
U
Q
⋅
−
=
2
Δ
0
>
L
B
0
<
Y
Q
Δ
Wzdłużne straty mocy w rozpatrywanej linii będą
wynosić:
Gdyby w linii należało uwzględnić
elementy poprzeczne to straty mocy w
elementach poprzecznych można wyliczyć
z zależności:
Gdy elementem poprzecznym jest jedynie pojemność
linii to a straty są
ujemne

6
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
Zadanie 1
Dana jest sieć
elektroenergetyczna
G
G
T1
T1
A
B
C
D
E
T2
UE
15 kV
110 kV
110 kV
220 kV
L
B
S
MVA
150
=
rG
S
kV
75
,
15
=
rG
U
%
180
=
d
X
MVA
150
1
=
rT
S
kV
15,75
kV
121
1
=
T
υ
%
11
1
=
krT
u
MVA
500
2
=
rT
S
kV
10
1
kV
220
2
=
T
υ
%
9
2
=
krT
u
km
Ω
4
,
0
=
kL
X
km
40
=
L
l
∞
=
′′
UE
k
S
3
Dane elementów sieci:
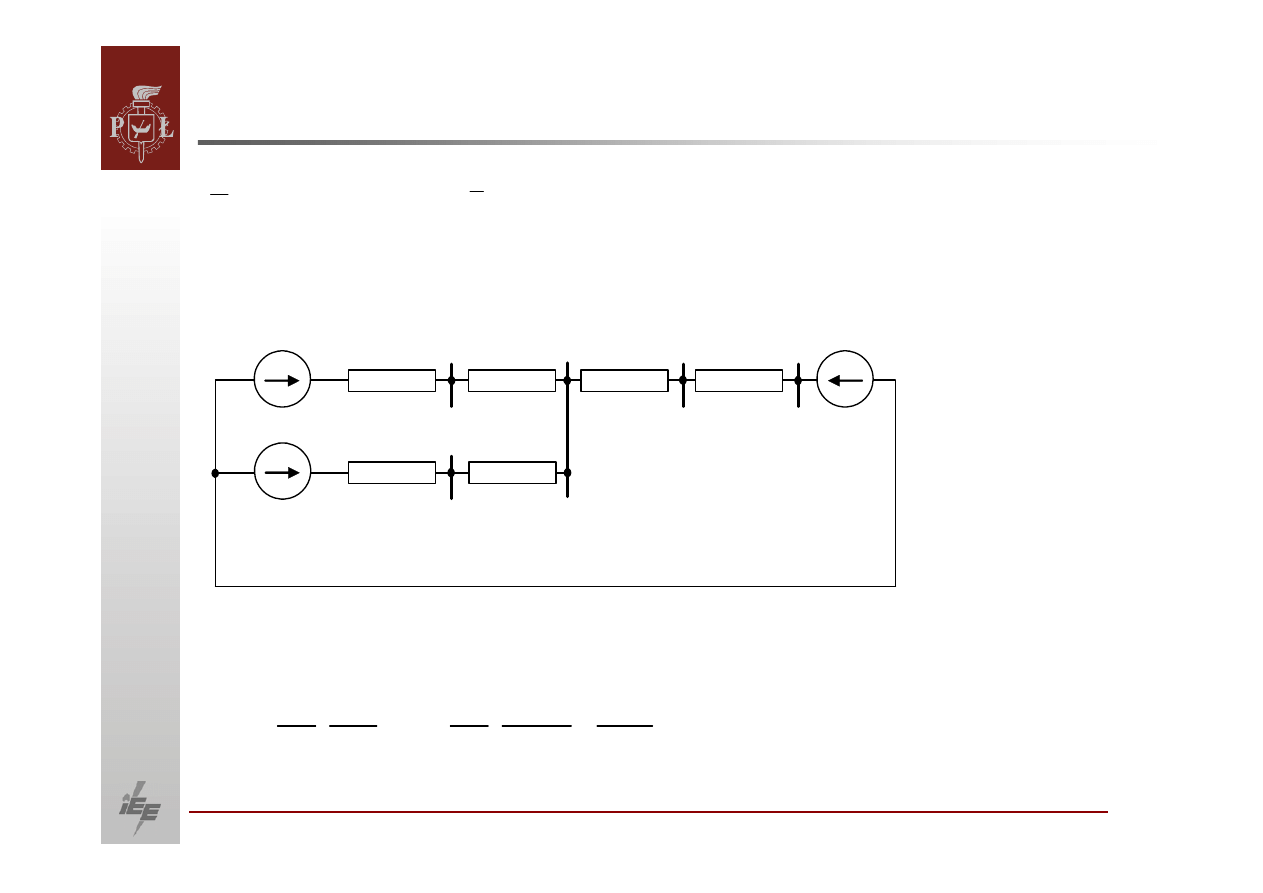
7
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
kV
110
=
B
U
(
)
MVA
0
200
j
S
B
+
=
Obliczyć
rozpływ mocy, napięcia w węzłach i narysować
wykres wskazowy.
D
X
G
X
T1
E
X
G
X
T1
A
X
L
X
T2
B
C
E
d
E
d
E
UE
Ω
7
,
176
75
,
15
121
150
75
,
15
100
180
100
2
2
2
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
=
⋅
⋅
=
T
rG
rG
d
G
S
U
X
X
υ
Schemat zastępczy
Obliczanie impedancji elememtów
na poziomie 110 kV

8
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
Ω
74
,
10
150
121
100
11
2
1
=
⋅
=
T
X
Ω
00
,
16
40
4
,
0
=
⋅
=
L
X
Ω
178
,
2
500
110
100
9
2
2
=
⋅
=
T
X
=
⋅
−
⋅
+
⋅
+
⋅
=
*
*
B
AB
B
AB
B
B
AB
B
AB
B
AB
U
R
Q
X
P
j
U
X
Q
R
P
U
Δ
kV
09
,
29
110
0
0
16
200
110
16
0
0
200
j
j
=
⋅
−
⋅
+
⋅
+
⋅
=
kV
8
,
113
09
,
29
0
,
110
81
,
14
o
j
AB
B
A
e
j
U
U
U
=
+
=
+
=
Δ
kV
8
,
113
09
,
29
0
,
110
2
2
=
+
=
A
U
o
81
,
14
110
09
,
29
=
=
tg
arc
A
U
ϕ
Napięcie na szynach A:

9
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
0
2
2
2
=
⋅
+
=
L
B
B
B
R
U
Q
P
P
Δ
Mvar
89
,
52
00
,
16
110
200
2
2
2
2
2
=
⋅
=
⋅
+
=
L
B
B
B
X
U
Q
P
Q
Δ
(
)
MVA
89
,
52
0
,
200
j
S
S
S
B
A
+
=
+
=
Δ
Zakładamy, że
A
A
U
U
=
(
) (
)
MVA
45
,
26
100
89
,
52
200
2
1
2
1
1
j
j
S
S
A
T
+
=
+
⋅
=
⋅
=
=
⋅
−
⋅
+
⋅
+
⋅
+
=
′
A
T
T
T
T
A
T
T
T
T
A
G
U
R
Q
X
P
j
U
X
Q
R
P
U
U
1
1
1
1
1
1
1
1
(
)
=
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⋅
+
=
438
,
9
496
,
2
8
,
113
8
,
113
74
,
10
100
8
,
113
74
,
10
45
,
26
8
,
113
j
j
kV
7
,
116
438
,
9
3
,
116
640
,
4
o
j
e
j
=
+
=
kV
7
,
116
7
,
116
45
,
19
81
,
14
640
,
4
"
o
o
o
j
j
j
G
e
e
e
U
=
⋅
=
kV
19
,
15
75
,
15
121
1
7
,
116
1
45
,
19
45
,
19
1
"
o
o
j
j
T
G
G
e
e
U
U
=
⋅
=
⋅
=
υ

10
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
Mvar
873
,
8
74
,
10
8
,
113
45
,
26
100
2
2
2
1
2
2
1
2
1
1
=
⋅
+
=
⋅
+
=
T
A
T
T
T
X
U
Q
P
Q
Δ
(
)
MVA
32
,
35
0
,
100
873
,
8
45
,
26
0
,
100
1
1
j
j
j
S
S
S
T
T
G
+
=
+
+
=
+
=
Δ
MVA
1
,
106
32
,
35
100
2
2
=
+
=
G
S
=
⋅
−
⋅
+
⋅
+
⋅
+
=
*
*
G
G
G
G
G
G
G
G
G
G
G
d
U
R
Q
X
P
j
U
X
Q
R
P
U
E
=
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
+
⋅
+
=
4
,
151
48
.
53
7
,
116
7
,
116
7
,
176
0
,
100
7
,
116
7
,
176
32
,
35
7
,
116
j
j
(
)
kV
8
,
227
4
,
151
2
,
170
62
,
41
o
j
e
kV
j
=
+
=
(
)
kV
7
,
198
4
,
111
kV
8
,
227
8
,
227
71
,
60
45
,
19
26
,
41
j
e
e
e
E
j
j
j
d
+
=
=
⋅
=
°
o
o
kV
65
,
29
121
75
,
15
8
,
227
71
,
60
71
,
60
o
j
j
d
e
e
E
=
⋅
=
°
jw
883
,
1
75
,
15
65
,
29
71
,
60
71
,
60
o
o
j
j
d
e
e
E
=
=

11
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
=
⋅
−
⋅
+
⋅
+
⋅
+
=
*
2
2
*
2
2
B
T
B
T
B
B
T
B
T
B
B
C
U
R
Q
X
P
j
U
X
Q
R
P
U
U
(
)
kV
960
,
3
0
,
110
0
,
110
178
,
2
0
,
200
0
,
110
*
2
j
j
U
X
P
j
U
B
T
B
B
−
=
⋅
−
=
⋅
−
=
kV
1
,
110
960
,
3
0
,
110
062
,
2
o
j
C
e
j
U
−
=
−
=
o
77
,
62
062
,
2
71
,
60
=
+
=
−
=
C
G
δ
δ
δ
12
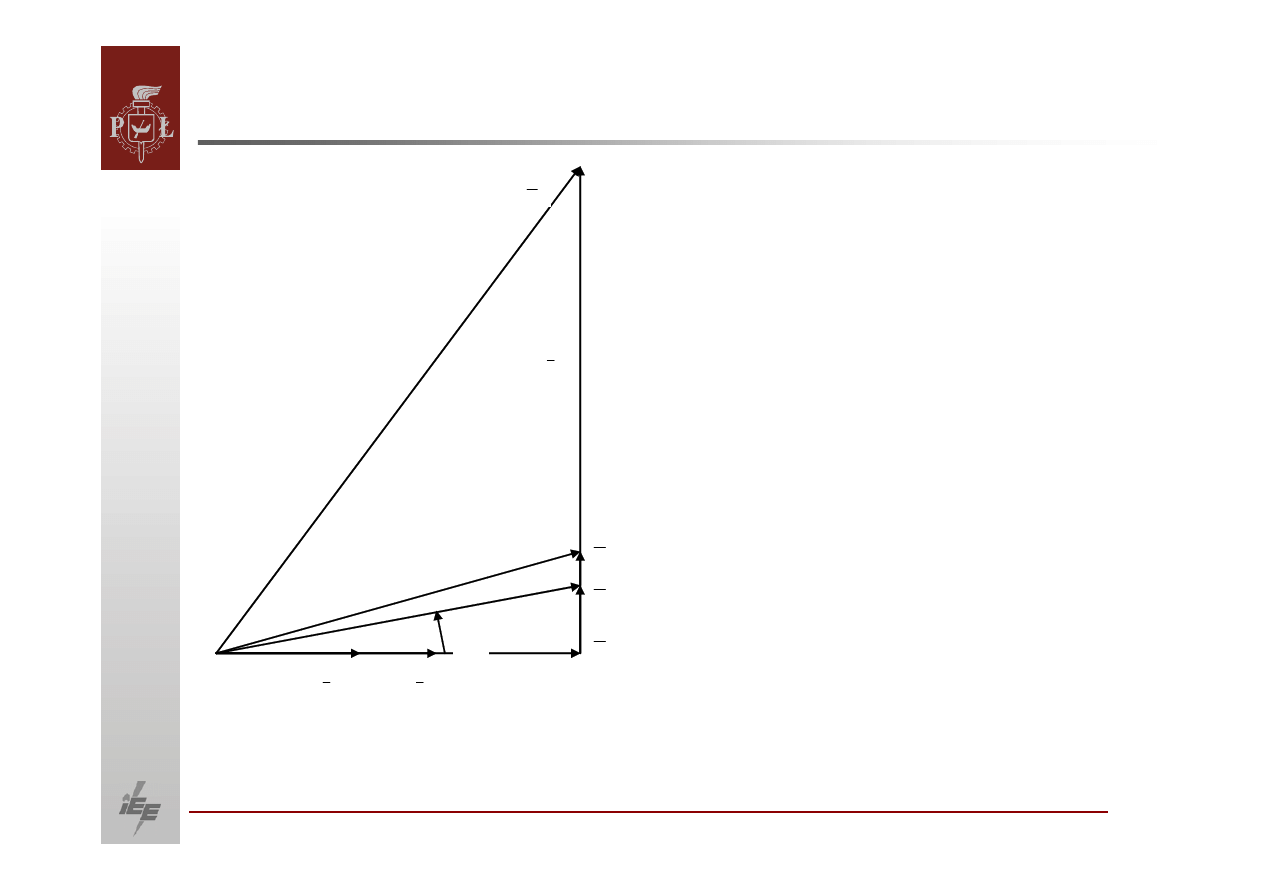
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
B
U
d
E
A
U
G
U
B
I
A
I
A
d
I
jX
⋅
UA
ϕ

13
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
Zadanie 2
km
Ω
06
,
0
=
kL
R
km
μS
76
,
2
=
kL
B
MVA
150
=
G
S
kV
75
,
15
=
=
rG
G
U
U
ind.
85
,
0
cos
=
G
ϕ
MW
10
=
=
E
D
P
P
ind.
80
,
0
cos
=
D
ϕ
(
)
MVA
100
200 j
S
A
+
=
nA
A
U
U
=
5
,
1
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
=
nA
A
AU
A
U
U
P
P
n
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
=
nA
A
AU
A
U
U
Q
Q
n
(
)
MVA
100
400 j
S
B
+
=
Obliczyć
rozpływ mocy, napięcia w węzłach i narysować
wykres wskazowy.

14
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
Ω
400
,
2
40
06
,
0
=
⋅
=
⋅
=
L
kL
L
l
R
R
μS
4
,
110
40
76
,
2
=
⋅
=
⋅
=
L
kL
L
l
B
B
MW
5
,
127
85
,
0
150
cos
=
⋅
=
⋅
=
G
G
G
S
P
ϕ
(
)
Mvar
0
,
79
85
,
0
1
150
cos
1
sin
2
2
=
−
⋅
=
−
⋅
=
⋅
=
G
G
G
G
G
S
S
Q
ϕ
ϕ
kV
121
75
,
15
121
75
,
15
1
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
′
T
G
G
U
U
υ
=
⋅
+
⋅
+
=
'
'
'
G
d
G
G
d
G
G
d
U
X
P
j
U
X
Q
U
E
=
+
+
=
⋅
+
⋅
+
=
185
115
121
121
176
5
,
127
121
176
0
,
79
121
j
j
(
)
kV
300
kV
185
236
1
.
38
o
j
e
j
=
+
=

15
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
kV
0
,
39
121
75
,
15
300
1
,
38
1
,
38
o
o
j
j
d
e
e
E
=
⋅
=
jw
48
,
2
75
,
15
0
,
39
1
,
38
1
,
38
o
o
j
j
d
e
e
E
=
=
Mvar
5
,
7
8
,
0
1
8
,
0
10
sin
cos
2
=
−
=
⋅
=
D
D
D
D
P
Q
ϕ
ϕ
MW
5
,
117
10
5
,
127
1
=
−
=
−
=
D
G
T
P
P
P
Mvar
5
,
71
5
,
7
79
1
=
−
=
−
=
D
G
T
Q
Q
Q
=
⋅
−
⋅
−
⋅
+
⋅
−
=
G
T
T
T
T
G
T
T
T
T
G
A
U
R
Q
X
P
j
U
X
Q
R
P
U
U
1
1
1
1
1
1
1
1
=
⋅
−
⋅
−
⋅
+
⋅
−
=
121
0
5
,
71
7
,
10
5
,
117
121
7
,
10
5
,
71
0
5
,
117
121
j
(
)
kV
2
,
115
kV
4
,
10
7
,
114
4
,
10
32
,
6
121
18
,
5
o
j
e
j
j
−
=
−
=
−
−
=
Mvar
8
,
13
7
,
10
121
5
,
71
5
,
117
2
2
2
1
2
1
2
1
2
1
1
=
+
=
⋅
+
=
T
T
T
T
T
X
U
Q
P
Q
Δ

16
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
(
)
(
)
MVA
7
,
57
5
,
117
8
,
13
5
,
71
5
,
117
1
1
1
j
j
j
S
S
S
T
T
A
T
+
=
−
+
=
−
=
Δ
MW
214
110
2
,
115
200
5
,
1
5
,
1
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
=
nA
A
AU
A
U
U
P
P
n
Mvar
110
110
2
,
115
100
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
=
nA
A
AU
A
U
U
Q
Q
n
MW
21
214
5
,
117
2
2
1
=
−
⋅
=
−
⋅
=
A
A
T
LA
P
P
P
Mvar
4
,
5
110
7
,
57
2
2
1
=
−
⋅
=
−
⋅
=
A
A
T
LA
Q
Q
Q
Mvar
733
,
0
4
,
110
2
1
2
,
115
2
1
2
2
−
=
⋅
⋅
−
=
⋅
⋅
−
=
L
A
YA
B
U
Q
Δ
MW
21
=
=
LA
L
P
P
(
)
Mvar
13
,
6
733
,
0
4
,
5
=
−
−
=
−
=
YA
LA
L
Q
Q
Q
Δ

17
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
=
⋅
−
⋅
−
⋅
+
⋅
−
=
′
A
L
L
L
L
A
L
L
L
L
A
B
U
R
Q
X
P
j
U
X
Q
R
P
U
U
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
+
⋅
+
⋅
−
=
2
,
115
4
,
2
13
,
6
16
21
2
,
115
16
13
,
6
4
,
2
21
2
,
115
j
(
)
kV
114
kV
05
,
3
9
,
113
13
,
0
92
,
2
85
,
0
44
,
0
2
,
115
53
,
1
o
j
e
j
j
j
−
=
−
=
−
−
−
−
=
kV
114
114
71
,
6
18
,
5
53
,
1
o
o
o
j
j
j
B
e
e
e
U
−
−
−
=
⋅
=
MW
0865
,
0
4
.
2
2
,
115
13
,
6
21
2
2
2
2
2
2
=
⋅
+
=
⋅
+
=
L
A
L
L
L
R
U
Q
P
P
Δ
Mvar
577
,
0
16
2
,
115
13
,
6
21
2
2
2
2
2
2
=
⋅
+
=
⋅
+
=
L
A
L
L
L
X
U
Q
P
Q
Δ
Mvar
717
,
0
4
,
110
2
1
114
2
1
2
2
−
=
⋅
⋅
−
=
⋅
⋅
−
=
L
B
YB
B
U
Q
Δ

18
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływ mocy w układzie promieniowym
MW
9
,
20
0865
,
0
21
=
−
=
−
=
L
L
LB
P
P
P
Δ
(
)
Mvar
27
,
6
717
,
0
577
,
0
13
,
6
=
−
−
−
=
−
−
=
YB
L
L
LB
Q
Q
Q
Q
Δ
Δ
MW
381
9
,
20
400
2
=
−
=
−
=
LB
B
B
T
P
P
P
Mvar
7
,
93
27
,
6
100
2
=
−
=
−
=
LB
B
B
T
Q
Q
Q
=
⋅
+
⋅
+
=
′
B
B
T
B
T
B
B
T
B
T
B
C
U
X
P
j
U
X
Q
U
U
2
2
2
2
=
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⋅
+
=
29
,
7
79
,
1
114
114
18
,
2
381
114
18
,
2
7
,
93
114
j
j
kV
116
29
,
7
116
60
,
3
o
j
e
j
=
+
=
19
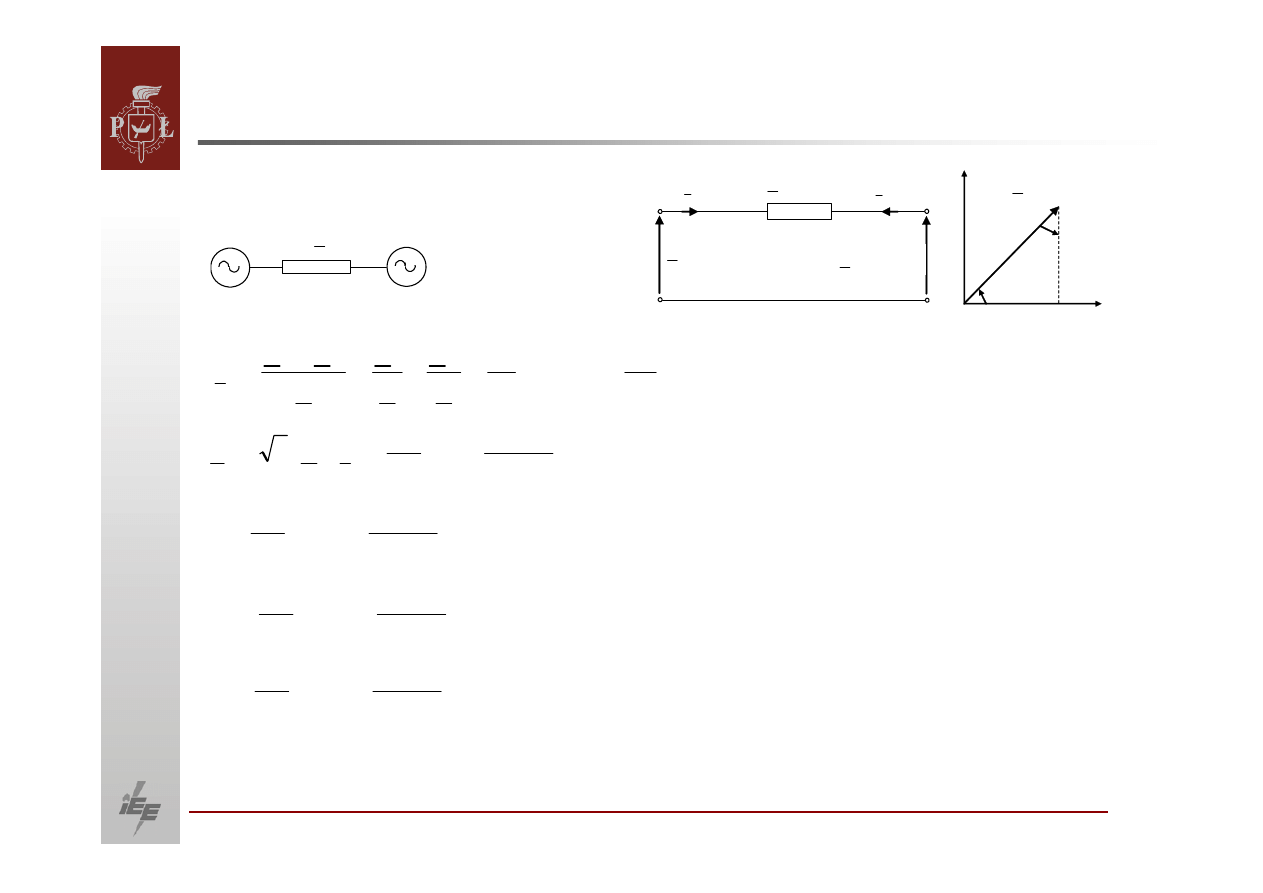
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
G1
G2
Z
2
I
θ
j
e
Z
Z
=
2
2
2
δ
j
e
E
E
=
1
I
1
1
1
δ
j
e
E
E
=
θ
α
Im
Re
θ
j
e
Z
Z
=
(
)
(
)
θ
δ
θ
δ
−
−
−
=
−
=
−
=
2
1
2
1
2
1
2
1
1
j
j
e
Z
E
e
Z
E
Z
E
Z
E
Z
E
E
I
(
)
θ
δ
δ
θ
+
−
⋅
−
=
⋅
⋅
=
2
1
2
1
2
1
*
1
1
1
3
j
j
e
Z
E
E
e
Z
E
I
E
S
(
)
=
+
−
⋅
⋅
−
⋅
=
θ
δ
δ
θ
2
1
2
1
2
1
1
cos
cos
Z
E
E
Z
E
P
(
)
=
+
⋅
⋅
−
⋅
=
θ
δ
θ
12
2
1
2
1
cos
cos
Z
E
E
Z
E
(
)
α
δ
α
−
⋅
⋅
+
⋅
=
12
2
1
2
1
sin
sin
Z
E
E
Z
E

20
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
(
)
=
+
−
⋅
⋅
−
⋅
=
θ
δ
δ
θ
2
1
2
1
2
1
1
sin
sin
Z
E
E
Z
E
Q
(
)
=
+
⋅
⋅
−
⋅
=
θ
δ
θ
12
2
1
2
1
sin
sin
Z
E
E
Z
E
(
)
α
δ
α
−
⋅
⋅
−
⋅
=
12
2
1
2
1
cos
cos
Z
E
E
Z
E
(
)
θ
δ
δ
θ
+
−
⋅
−
=
⋅
⋅
=
1
2
2
1
2
2
*
2
2
2
3
j
j
e
Z
E
E
e
Z
E
I
E
S
(
)
=
θ
+
δ
−
δ
−
θ
=
1
2
2
1
2
2
2
cos
Z
E
E
cos
Z
E
P
(
)
=
θ
+
δ
−
θ
=
21
2
1
2
2
cos
Z
E
E
cos
Z
E
(
)
(
)
α
+
δ
−
α
=
α
−
δ
+
α
=
12
2
1
2
2
21
2
1
2
2
sin
Z
E
E
sin
Z
E
sin
Z
E
E
sin
Z
E

21
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
(
)
=
+
−
⋅
⋅
−
⋅
=
θ
δ
δ
θ
1
2
2
1
2
2
2
sin
sin
Z
E
E
Z
E
Q
(
)
=
+
⋅
⋅
−
⋅
=
θ
δ
θ
21
2
1
2
2
sin
sin
Z
E
E
Z
E
(
)
α
δ
α
+
⋅
⋅
−
⋅
=
12
2
1
2
2
cos
cos
Z
E
E
Z
E
R
I
P
P
P
⋅
⋅
=
+
=
2
2
1
3
Δ
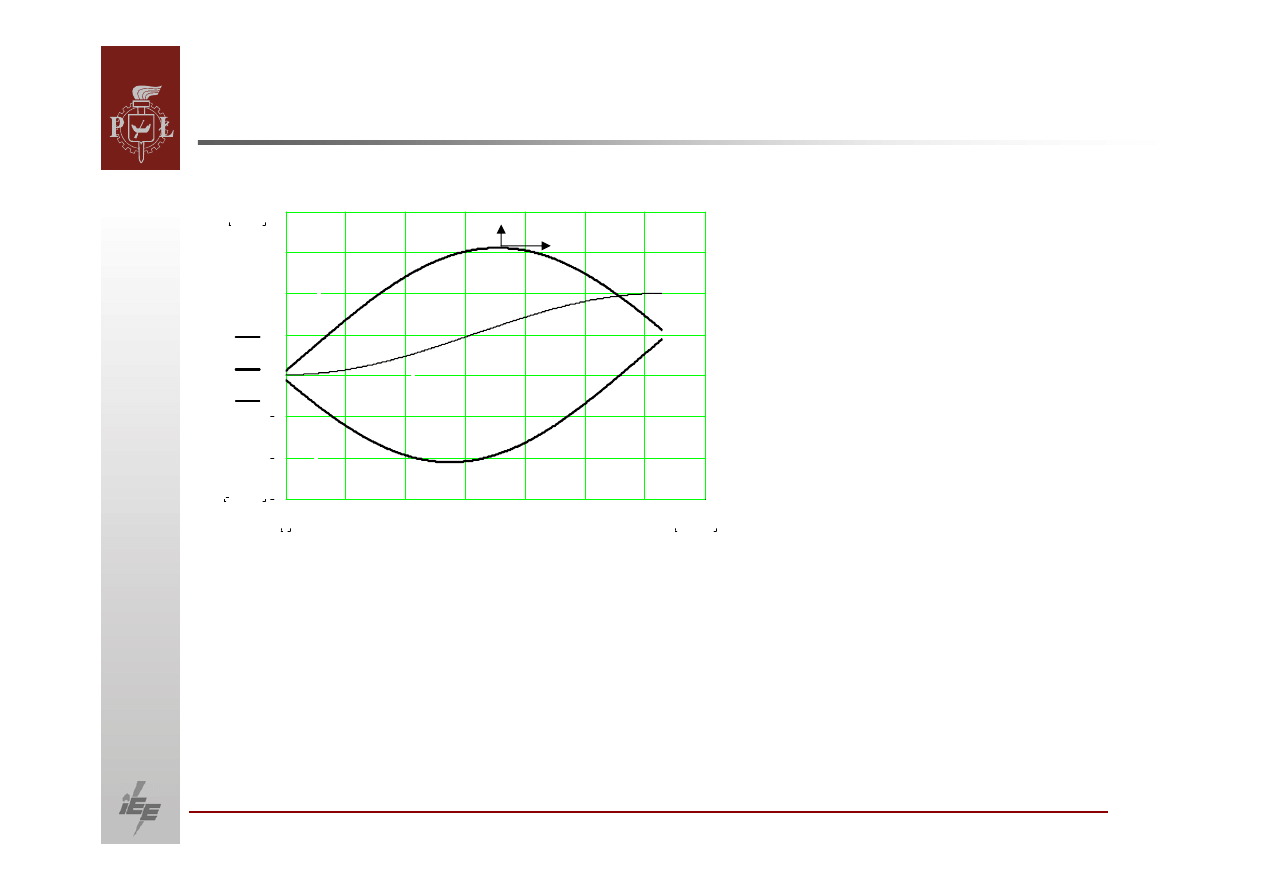
22
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
6.24168
4.20532
P1
i
P2
i
ΔP
i
3.141593
0
δ i.
0
0.5
1
1.5
2
2.5
3
3.5
6
4
2
0
2
4
6
8
1
P
.
rad
2
,
0
=
α
2
P
P
Δ
12
δ
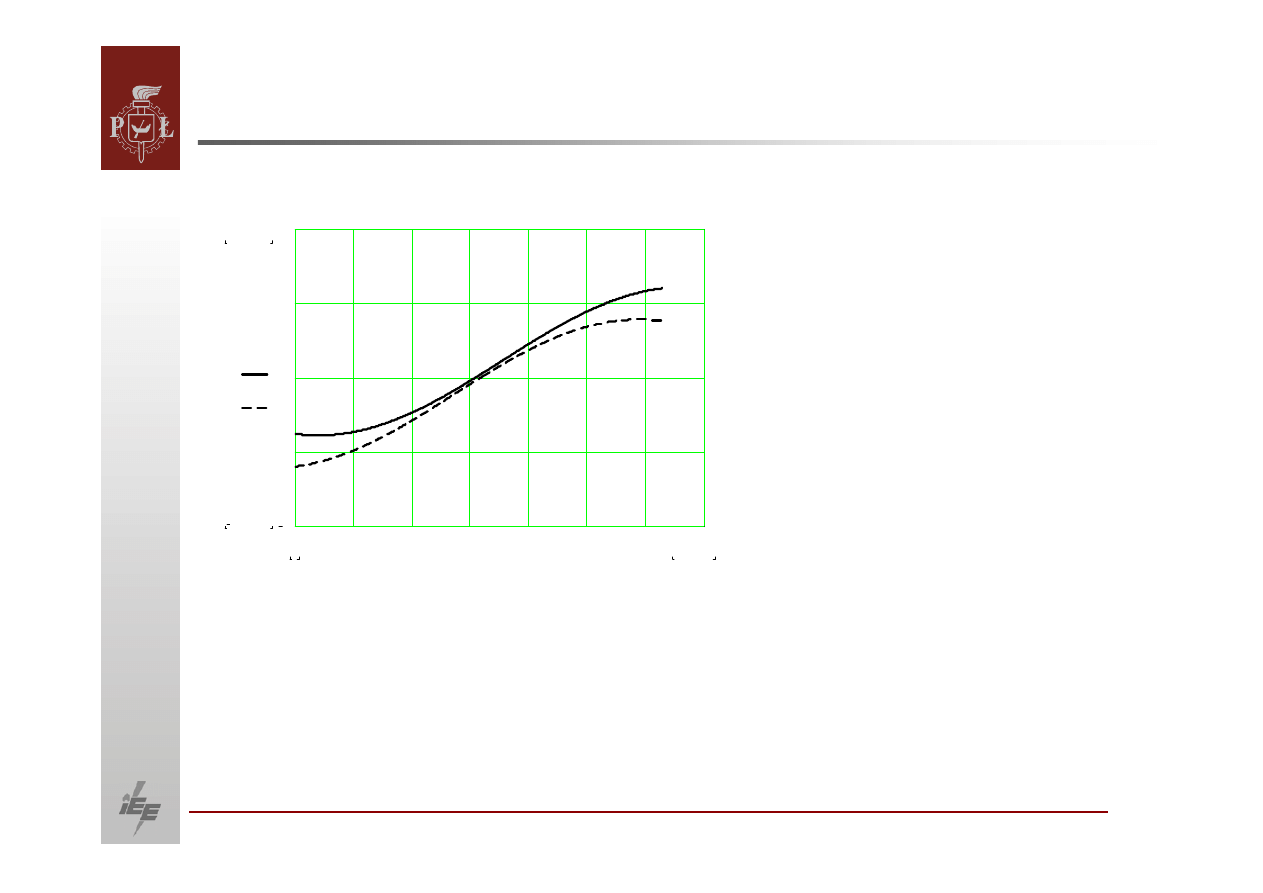
23
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
11.025749
0.980067
Q1
i
Q2
i
3.141593
0
δ i.
0
0.5
1
1.5
2
2.5
3
3.5
5
0
5
10
15
.
rad
2
,
0
=
α
12
δ
1
Q
2
Q

24
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
0
=
α
12
2
1
1
sin
δ
⋅
⋅
=
X
E
E
P
12
2
1
2
sin
δ
⋅
⋅
−
=
X
E
E
P
12
2
1
2
1
1
cos
δ
⋅
−
=
X
E
E
X
E
Q
12
2
1
2
2
2
cos
δ
⋅
⋅
−
=
X
E
E
X
E
Q
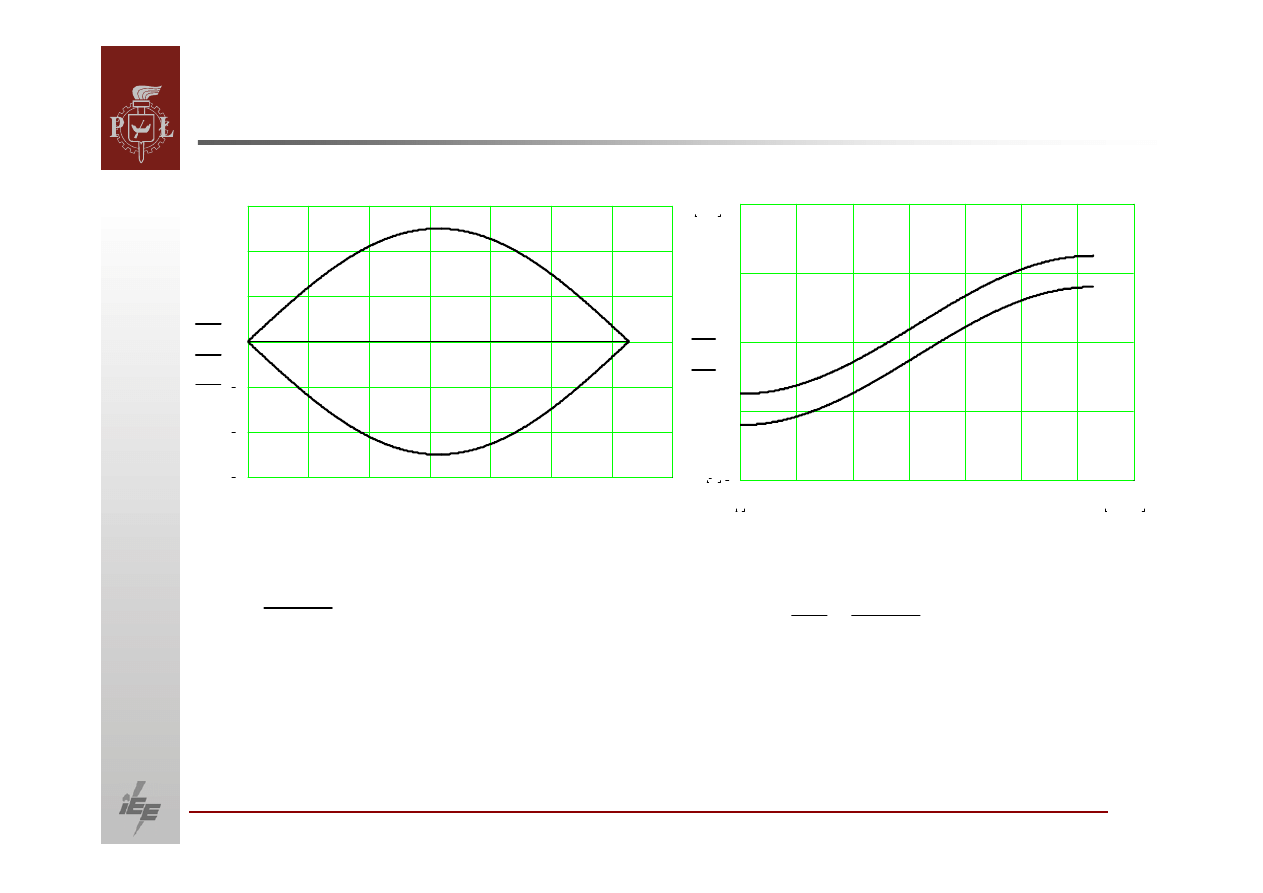
25
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
P1
i
P2
i
ΔP
i
0
0.5
1
1.5
2
2.5
3
3.5
6
4
2
0
2
4
6
0
=
α
11.25
1
Q1
i
Q2
i
3.141593
0
δ i.
0
0.5
1
1.5
2
2.5
3
3.5
5
0
5
10
15
12
δ
12
δ
1
P
2
P
1
Q
2
Q
Przy małych wartościach kąta
12
δ
12
2
1
1
δ
⋅
⋅
=
X
E
E
P
X
E
E
X
E
Q
2
1
2
1
1
−
=
Z powyższych wzorów wynika, że przy małych wartościach kąta
(mniej niż
30
stopni) moc czynna zależy przede wszystkim od tego kąta
a moc bierna od napięć.

26
OBLICZANIE PRZEPŁYWÓW MOCY.
Układ dwumaszynowy
Krzywa dla mocy czynnej posiada swoje maksimum. Moc tą
nazywamy
mocą
graniczną
przesyłu i wyraża się
ona zależnościami:
0
=
α
X
E
E
P
gr
2
1
1
⋅
=
X
E
E
P
gr
2
1
2
⋅
−
=
0
≠
α
Z
E
E
Z
E
P
gr
2
1
2
1
1
sin
⋅
+
⋅
=
α
Z
E
E
Z
E
P
gr
2
1
2
2
2
sin
⋅
−
⋅
=
α
Moce graniczne to największe moce jakie można przesłać
pomiędzy dwoma
punktami sieci elektroenergetycznej zdefiniowanych napięciami
oraz impedancją
pomiędzy nimi.
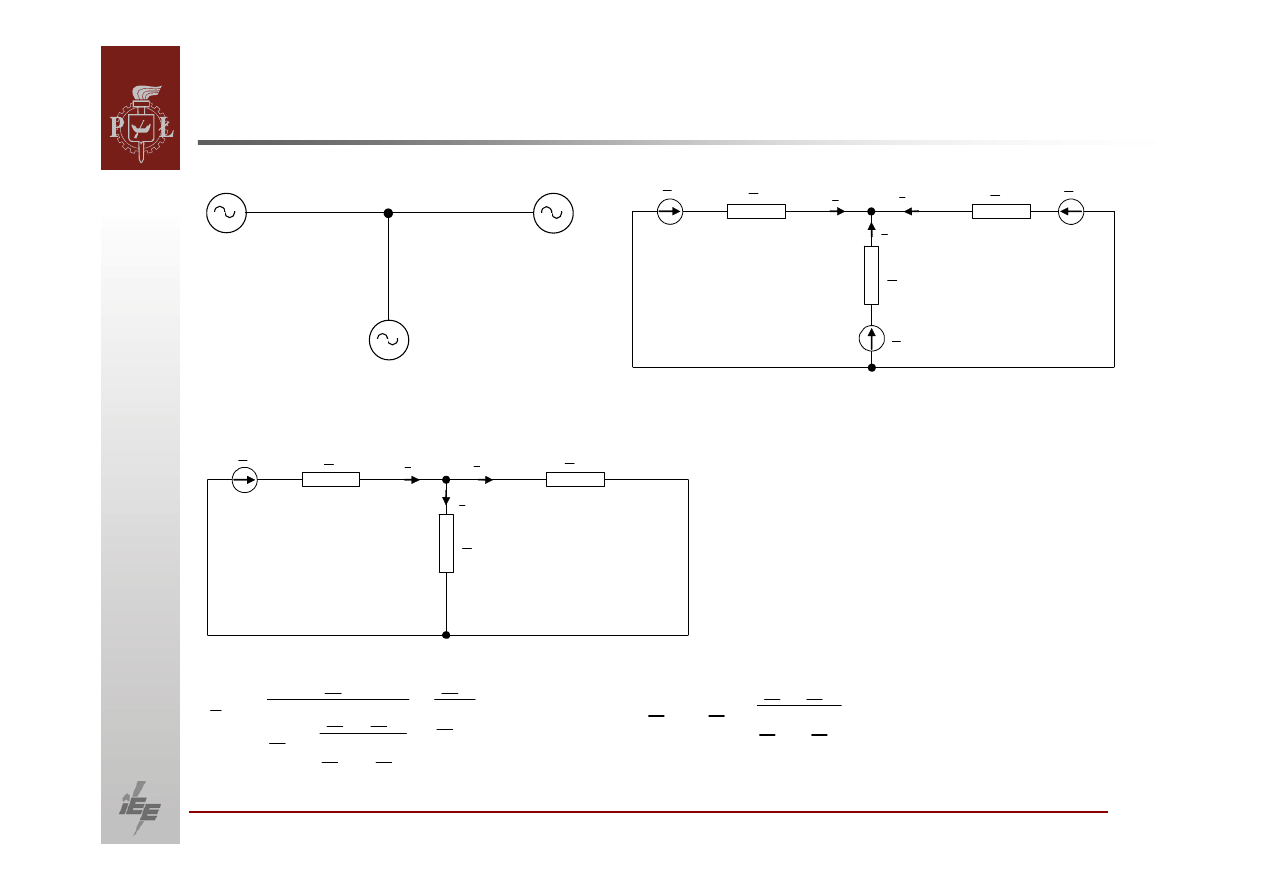
27
OBLICZANIE PRZEPŁYWÓW MOCY.
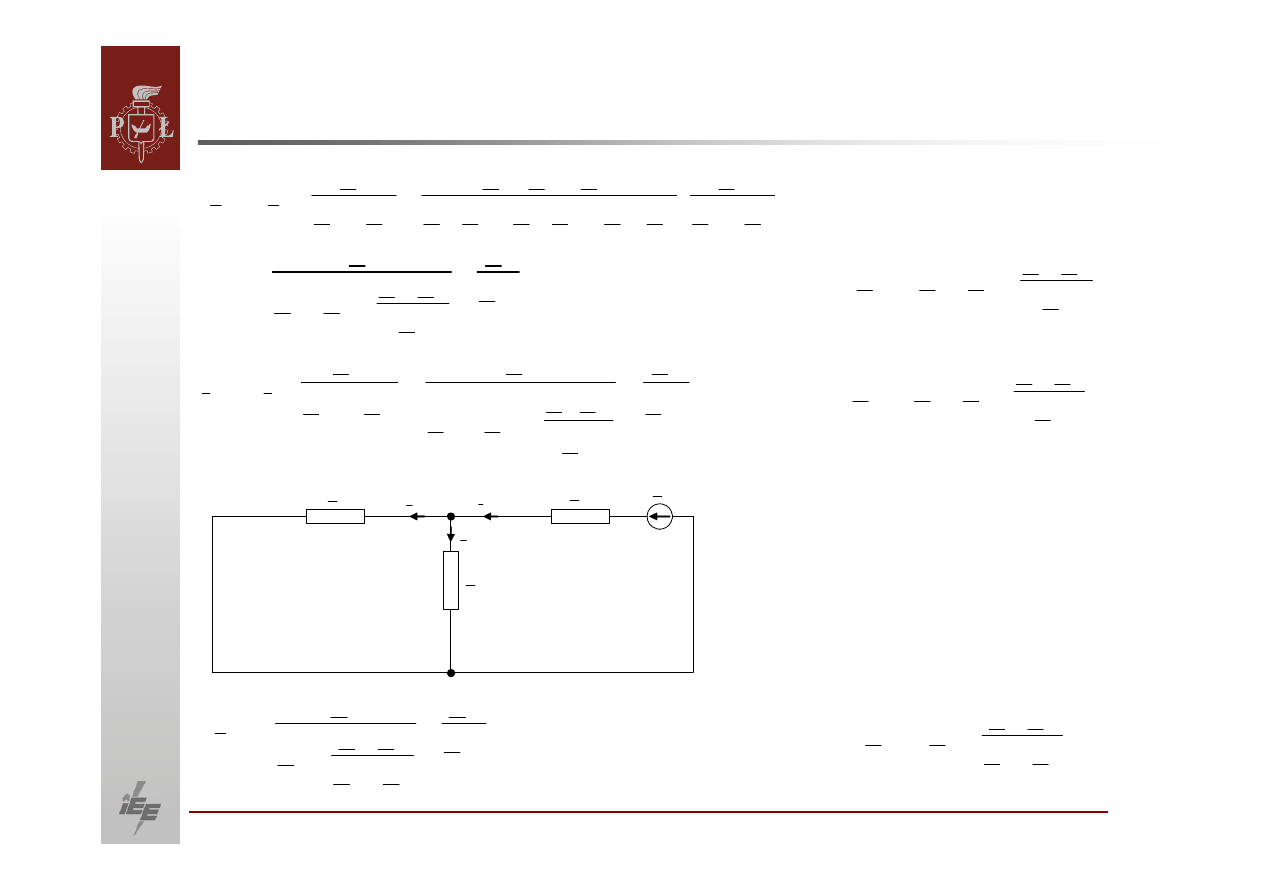
Przepływy mocy w układzie wielomaszynowym
G1
G2
G3
1
I
1
E
1
Z
2
I
2
Z
3
I
3
Z
3
E
2
E
Metoda superpozycji
11
I
1
E
1
Z
21
I
2
Z
31
I
3
Z
11
1
3
2
3
2
1
1
11
Z
E
Z
Z
Z
Z
Z
E
I
=
+
⋅
+
=
3
2
3
2
1
11
Z
Z
Z
Z
Z
Z
+
⋅
+
=
28
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływy mocy w układzie wielomaszynowym
(
)
=
+
⋅
⋅
+
⋅
+
⋅
+
⋅
=
+
⋅
=
3
2
3
3
2
2
1
3
1
3
2
1
3
2
3
11
21
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
E
Z
Z
Z
I
I
21
1
3
2
1
2
1
1
Z
E
Z
Z
Z
Z
Z
E
=
⋅
+
+
=
3
2
1
2
1
21
Z
Z
Z
Z
Z
Z
⋅
+
+
=
31
1
2
3
1
3
1
1
3
2
2
11
31
Z
E
Z
Z
Z
Z
Z
E
Z
Z
Z
I
I
=
+
+
=
+
=
2
3
1
3
1
31
Z
Z
Z
Z
Z
Z
⋅
+
+
=
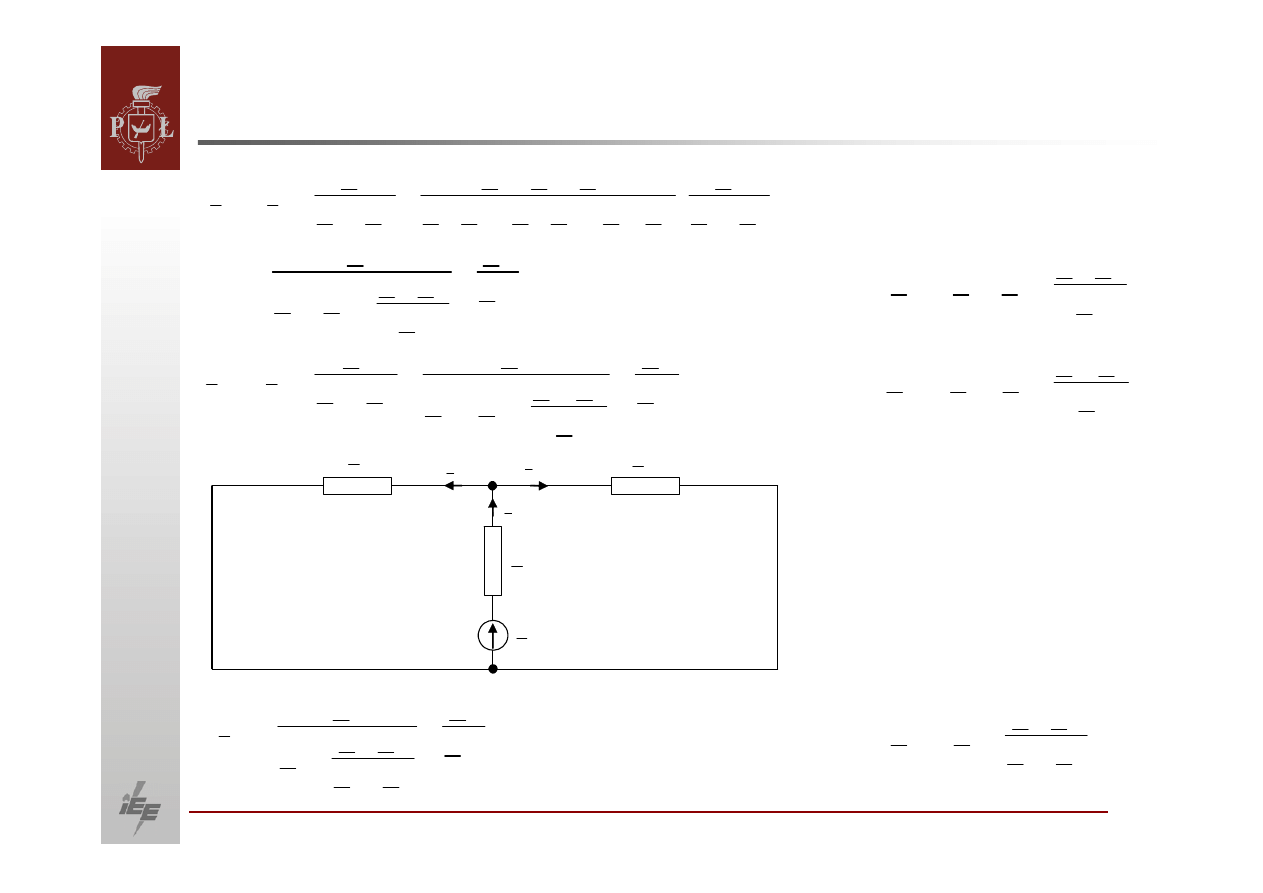
12
I
1
Z
22
I
2
E
2
Z
32
I
3
Z
22
2
3
1
3
1
2
2
22
Z
E
Z
Z
Z
Z
Z
E
I
=
+
⋅
+
=
3
1
3
1
2
22
Z
Z
Z
Z
Z
Z
+
⋅
+
=
29
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływy mocy w układzie wielomaszynowym
(
)
=
+
⋅
⋅
+
⋅
+
⋅
+
⋅
=
+
⋅
=
3
1
3
3
2
2
1
3
1
3
1
2
3
1
3
22
12
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
E
Z
Z
Z
I
I
12
2
3
2
1
2
1
2
Z
E
Z
Z
Z
Z
Z
E
=
⋅
+
+
=
3
2
1
2
1
12
Z
Z
Z
Z
Z
Z
⋅
+
+
=
32
2
1
3
2
3
2
2
3
1
1
22
32
Z
E
Z
Z
Z
Z
Z
E
Z
Z
Z
I
I
=
⋅
+
+
=
+
⋅
=
1
3
2
3
2
32
Z
Z
Z
Z
Z
Z
⋅
+
+
=
13
I
1
Z
23
I
2
Z
33
I
3
Z
3
E
33
3
2
1
2
1
3
3
33
Z
E
Z
Z
Z
Z
Z
E
I
=
+
⋅
+
=
2
1
2
1
3
33
Z
Z
Z
Z
Z
Z
+
⋅
+
=

30
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływy mocy w układzie wielomaszynowym
(
)
=
+
⋅
⋅
+
⋅
+
⋅
+
⋅
=
+
⋅
=
2
1
2
3
2
2
1
3
1
2
1
3
2
1
2
33
13
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
E
Z
Z
Z
I
I
13
3
2
3
1
3
1
3
Z
E
Z
Z
Z
Z
Z
E
=
⋅
+
+
=
2
3
1
3
1
13
Z
Z
Z
Z
Z
Z
⋅
+
+
=
23
3
1
3
2
3
2
3
2
1
1
33
23
Z
E
Z
Z
Z
Z
Z
E
Z
Z
Z
I
I
=
⋅
+
+
=
+
⋅
=
1
3
2
3
2
23
Z
Z
Z
Z
Z
Z
⋅
+
+
=
13
3
12
2
11
1
13
12
11
1
Z
E
Z
E
Z
E
I
I
I
I
−
−
=
−
−
=
23
3
21
1
22
2
23
21
22
2
Z
E
Z
E
Z
E
I
I
I
I
−
−
=
−
−
=
32
2
31
1
33
3
32
31
33
3
Z
E
Z
E
Z
E
I
I
I
I
−
−
=
−
−
=

31
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływy mocy w układzie wielomaszynowym
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
3
2
1
33
32
31
23
22
21
13
12
11
3
2
1
1
1
1
1
1
1
1
1
1
E
E
E
Z
Z
Z
Z
Z
Z
Z
Z
Z
I
I
I
E
Y
I
⋅
=
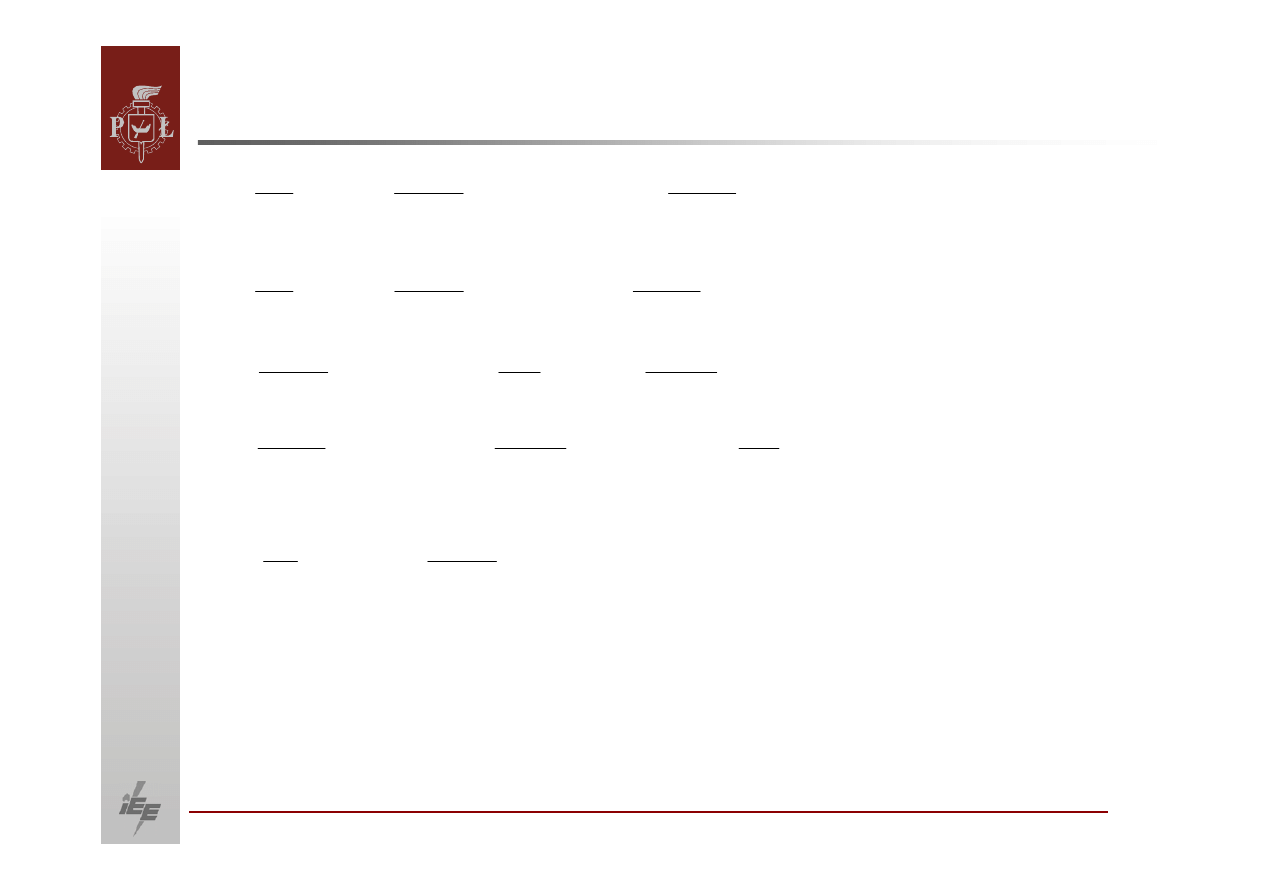
R
R
Y
nazywana jest macierzą
transferową
sieci elektroenergetycznej.
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⋅
=
⋅
=
*
13
*
3
*
12
*
2
*
11
*
1
1
*
1
1
1
Z
E
Z
E
Z
E
E
I
E
S
(
)
(
)
13
3
1
12
2
1
11
13
3
1
12
2
1
11
2
1
θ
δ
δ
θ
δ
δ
θ
+
−
+
−
⋅
−
⋅
−
=
j
j
j
e
Z
E
E
e
Z
E
E
e
Z
E
32
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływy mocy w układzie wielomaszynowym
(
)
(
)
13
3
1
13
3
1
12
2
1
12
2
1
11
11
2
1
1
cos
cos
cos
θ
δ
δ
θ
δ
δ
θ
+
−
⋅
⋅
−
+
−
⋅
⋅
−
⋅
=
Z
E
E
Z
E
E
Z
E
P
(
)
(
)
13
13
13
3
1
12
12
12
2
1
11
11
2
1
1
sin
sin
sin
α
δ
α
δ
α
−
⋅
⋅
+
−
⋅
⋅
+
⋅
=
Z
E
E
Z
E
E
Z
E
P
(
)
(
)
23
23
23
3
2
22
22
2
2
21
21
21
1
2
2
sin
sin
sin
α
δ
α
α
δ
−
⋅
⋅
+
⋅
+
−
⋅
⋅
=
Z
E
E
Z
E
Z
E
E
P
(
)
(
)
33
33
2
3
32
32
32
2
3
31
31
31
1
3
3
sin
sin
sin
α
α
δ
α
δ
⋅
+
−
⋅
⋅
+
−
⋅
⋅
=
Z
E
Z
E
E
Z
E
E
P
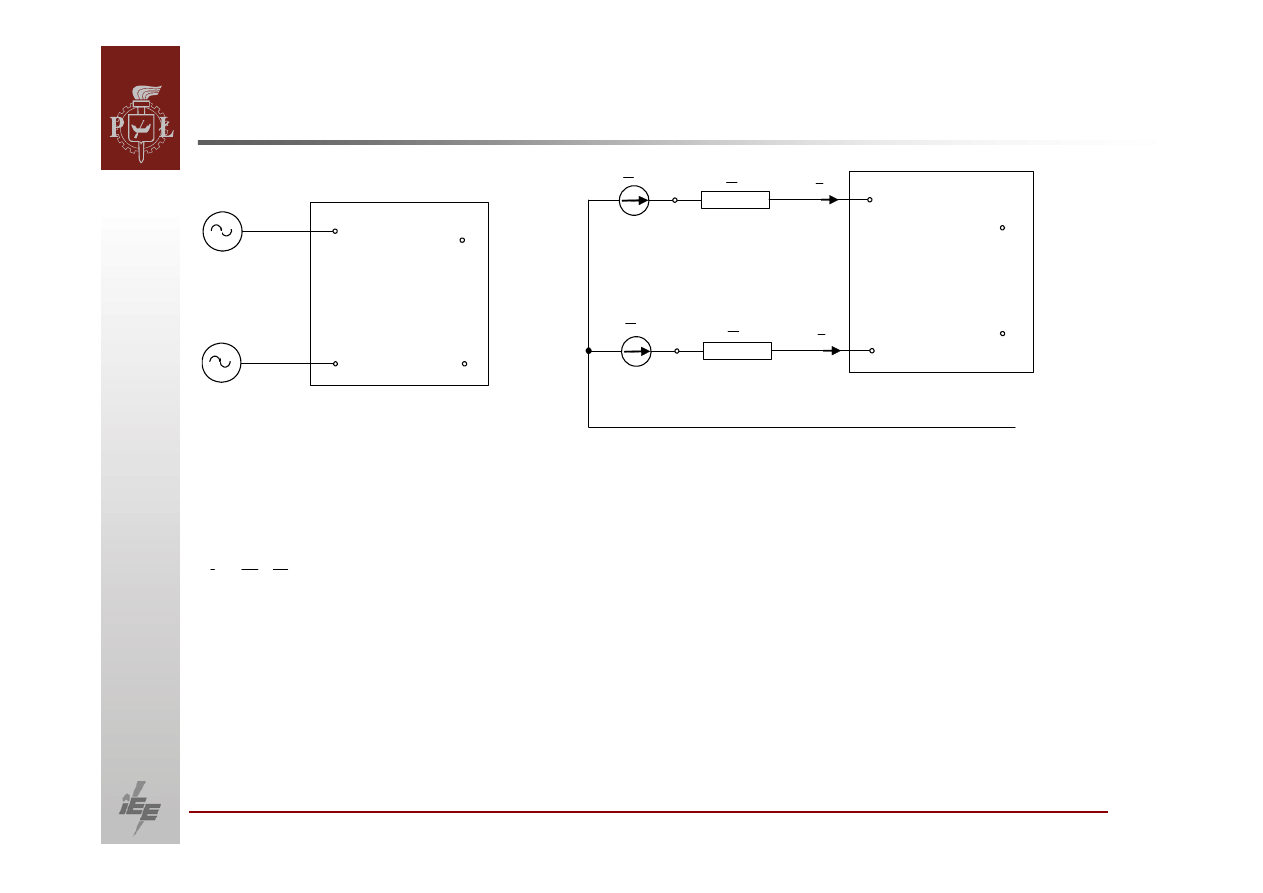
(
)
∑
≠
=
−
−
⋅
⋅
+
⋅
=
n
i
j
j
ij
j
i
ij
j
i
ii
ii
i
i
Z
E
E
Z
E
P
1
2
sin
sin
α
δ
δ
α

33
OBLICZANIE PRZEPŁYWÓW MOCY.
Przepływy mocy w układzie wielomaszynowym
(
)
(
)
13
13
13
3
1
12
12
12
2
1
11
11
2
1
1
cos
cos
cos
α
δ
α
δ
α
−
⋅
⋅
−
−
⋅
⋅
−
⋅
=
Z
E
E
Z
E
E
Z
E
Q
(
)
(
)
23
23
23
3
2
22
22
2
2
21
21
21
1
2
2
cos
cos
cos
α
δ
α
α
δ
−
⋅
⋅
−
⋅
+
−
⋅
⋅
−
=
Z
E
E
Z
E
Z
E
E
Q
(
)
(
)
33
33
2
3
32
32
32
2
3
31
31
31
1
3
3
sin
cos
cos
α
α
δ
α
δ
⋅
+
−
⋅
⋅
−
−
⋅
⋅
−
=
Z
E
Z
E
E
Z
E
E
Q
(
)
∑
≠
=
−
−
⋅
⋅
−
⋅
=
n
i
j
j
ij
j
i
ij
j
i
ii
ii
i
i
Z
E
E
Z
E
Q
1
2
cos
cos
α
δ
δ
α
34
OBLICZANIE PRZEPŁYWÓW MOCY.
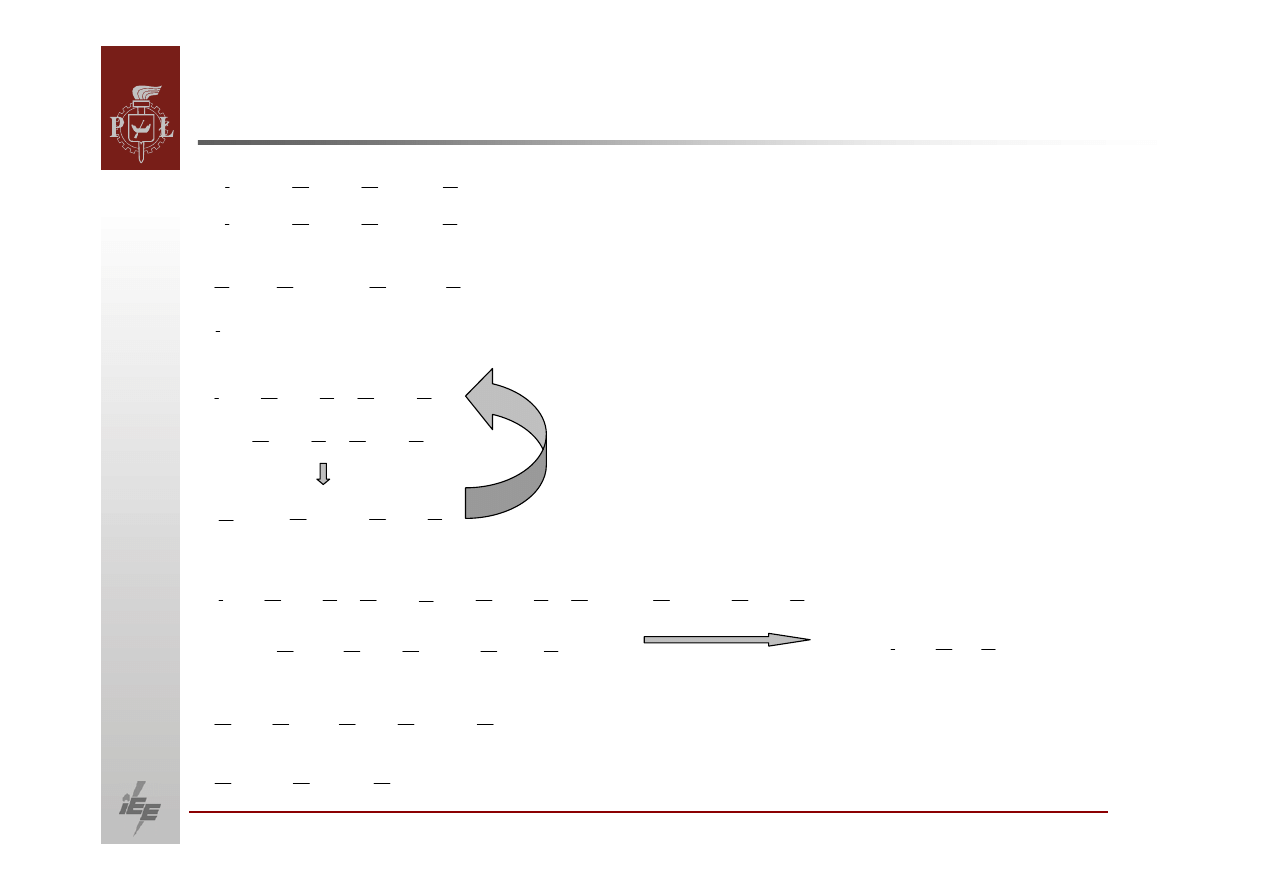
Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
G
1
G
k
M
M
M
M
1
k
k+1
n
M
M
1
I
1
E
1
Z
k
I
k
E
k
Z
M
M
M
M
M
M
k+1
k+k
k+k+1
k+n
Umyślony przewód powrotny
1
k
Dla węzła odniesienia umieszczonego w umyślonym przewodzie powrotnym
równania potencjałów węzłowych są
postaci:
U
Y
I
⋅
=
i
w
Wszystkie węzły rozpatrywanego systemu oznaczone jako
gdzie
, podzielimy na dwie grupy: R
i E.
Do zbioru R
zaliczymy węzły od 1 do k‐tego
czyli
R
w
j
∈
gdzie
k
j
÷
=1
Do zbioru E
zaliczymy pozostałe węzły czyli
E
w
m
∈
gdzie
.
.
(
)
n
k
i
+
÷
=1
(
) (
)
n
k
k
m
+
÷
+
=
1
35
OBLICZANIE PRZEPŁYWÓW MOCY.
Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
E
R
EE
ER
RE
RR
E
R
U
U
Y
Y
Y
Y
I
I
[
]
E
U
=
=
T
k
R
E
E
K
1
0
=
E
I
E
RE
RR
R
U
Y
E
Y
I
⋅
+
⋅
=
E
EE
ER
U
Y
E
Y
0
⋅
+
⋅
=
E
Y
Y
U
⋅
⋅
−
=
−
ER
EE
E
1
(
)
=
⋅
⋅
−
⋅
+
⋅
=
⋅
+
⋅
=
−
E
Y
Y
Y
E
Y
U
Y
E
Y
I
ER
EE
RE
RR
E
RE
RR
R
1
(
)
E
Y
Y
Y
Y
⋅
⋅
⋅
−
=
−
ER
EE
RE
RR
1
E
Y
I
⋅
=
R
R
ER
EE
RE
RR
R
Y
Y
Y
Y
Y
⋅
⋅
−
=
−1
ER
EE
D
Y
Y
Y
⋅
−
=
−1
to macierz dystrybucji napięć
w
sieci
elektroenergetycznej.

36
OBLICZANIE PRZEPŁYWÓW MOCY.
Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
k
Z
Z
Z
k
k
RR
1
1
0
0
1
0
0
0
1
1
2
1
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
K
K
M
O
M
K
M
M
M
Y
k
n
k
k
k
k
Z
Z
Z
k
k
RE
+
+
+
+
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
1
2
1
0
0
1
0
0
1
0
0
0
0
0
1
1
2
1
K
K
K
O
M
M
O
M
M
O
M
M
K
K
Y
[
]
0
Y
Y
RR
RE
−
=
⎥
⎦
⎤
⎢
⎣
⎡−
=
0
Y
Y
RR
ER
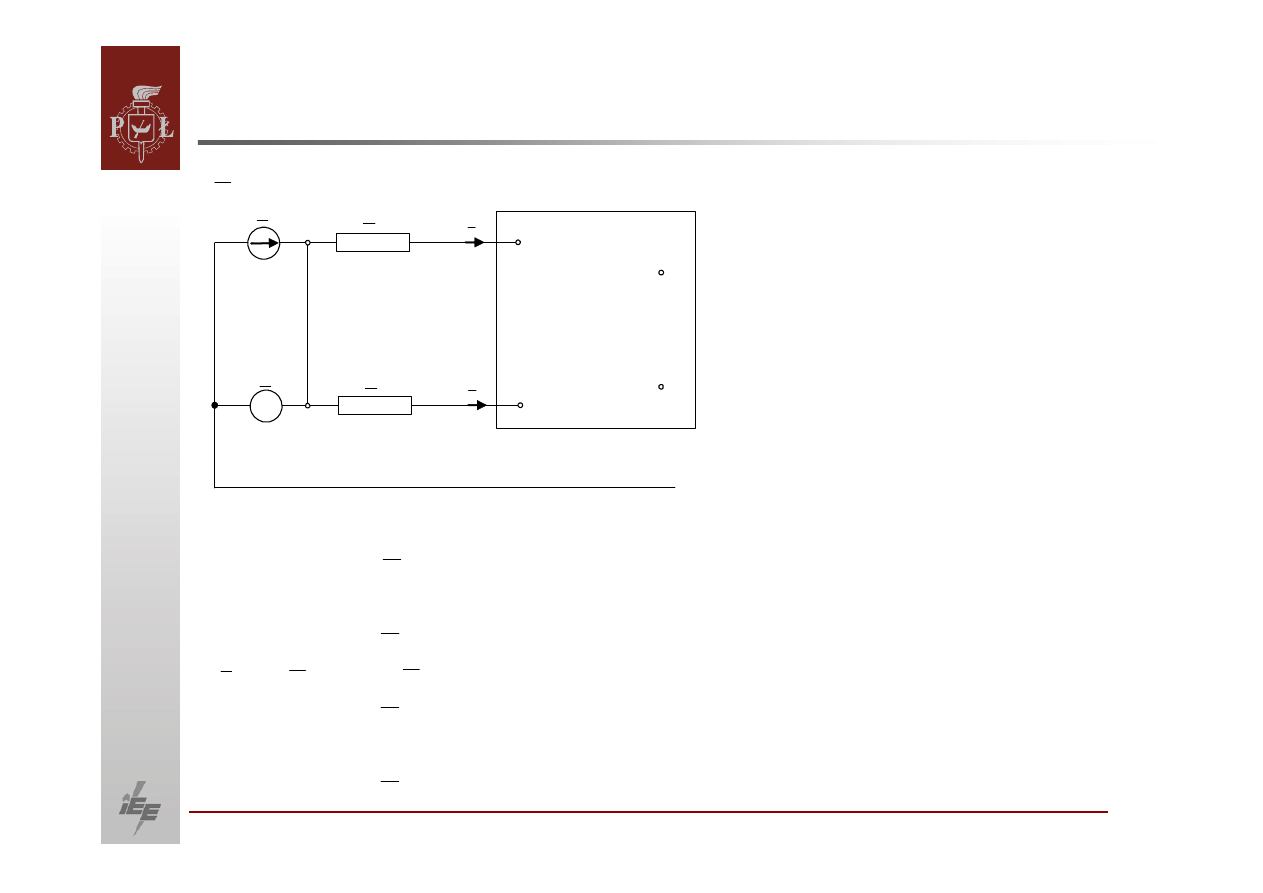
37
OBLICZANIE PRZEPŁYWÓW MOCY.
Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
1
I
E
1
Z
k
I
E
k
Z
M
M
M
M
M
M
k+1
k+k
k+k+1
k+n
Umyślony przewód powrotny
0
EE
Y
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
+
−
+
n
k
m
m
k
EE
m
U
U
E
U
U
I
Δ
Δ
Δ
Δ
M
M
M
M
1
1
1
0
0
0
0
Y

38
OBLICZANIE PRZEPŁYWÓW MOCY.
Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
n
k
k
k
k
n
k
k
k
k
k
nn
ng
gn
gg
EE
EE
+
+
+
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
+
+
+
=
=
−
K
K
M
M
1
2
2
1
1
2
1
1
Z
Z
Z
Z
Z
Y
[
]
=
⎥
⎦
⎤
⎢
⎣
⎡−
⋅
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅
−
−
=
0
Y
Z
Z
Z
Z
0
Y
Y
Y
RR
nn
ng
gn
gg
RR
RR
R
RR
gg
RR
RR
Y
Z
Y
Y
⋅
⋅
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
+
+
+
+
+
+
+
+
k
k
k
k
k
k
k
k
k
k
k
k
gg
Z
Z
Z
Z
,
1
,
,
1
1
,
1
K
M
O
M
K
Z

39
OBLICZANIE PRZEPŁYWÓW MOCY.
Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
2
1
1
1
i
ii
i
i
ii
i
i
Rii
Z
Z
Z
Z
Z
Z
Z
Y
−
=
⋅
⋅
−
=
j
i
ij
ij
ij
i
Rij
Z
Z
Z
Z
Z
Z
Y
⋅
−
=
⋅
⋅
−
=
1
1
(
) (
)
k
k
k
j
i
+
÷
+
=
1
,

40
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki odbiorów
p
N
n
U
U
P
P
α
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
=
q
N
n
U
U
Q
Q
α
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
=
2
,
1
4
,
0
÷
=
p
α
0
,
4
2
,
1
÷
=
q
α
6
,
0
=
p
α
0
,
2
=
q
α
2
=
=
q
p
α
α
const
P
U
P
U
R
N
N
o
=
=
=
2
2
const
Q
U
Q
U
X
N
N
o
=
=
=
2
2
1
=
=
q
p
α
α
const
U
P
U
P
I
N
N
=
⋅
=
⋅
=
3
3
'
const
U
Q
U
Q
I
N
N
=
⋅
=
⋅
=
−
3
3
''
0
=
=
q
p
α
α
41
OBLICZANIE PRZEPŁYWÓW MOCY.
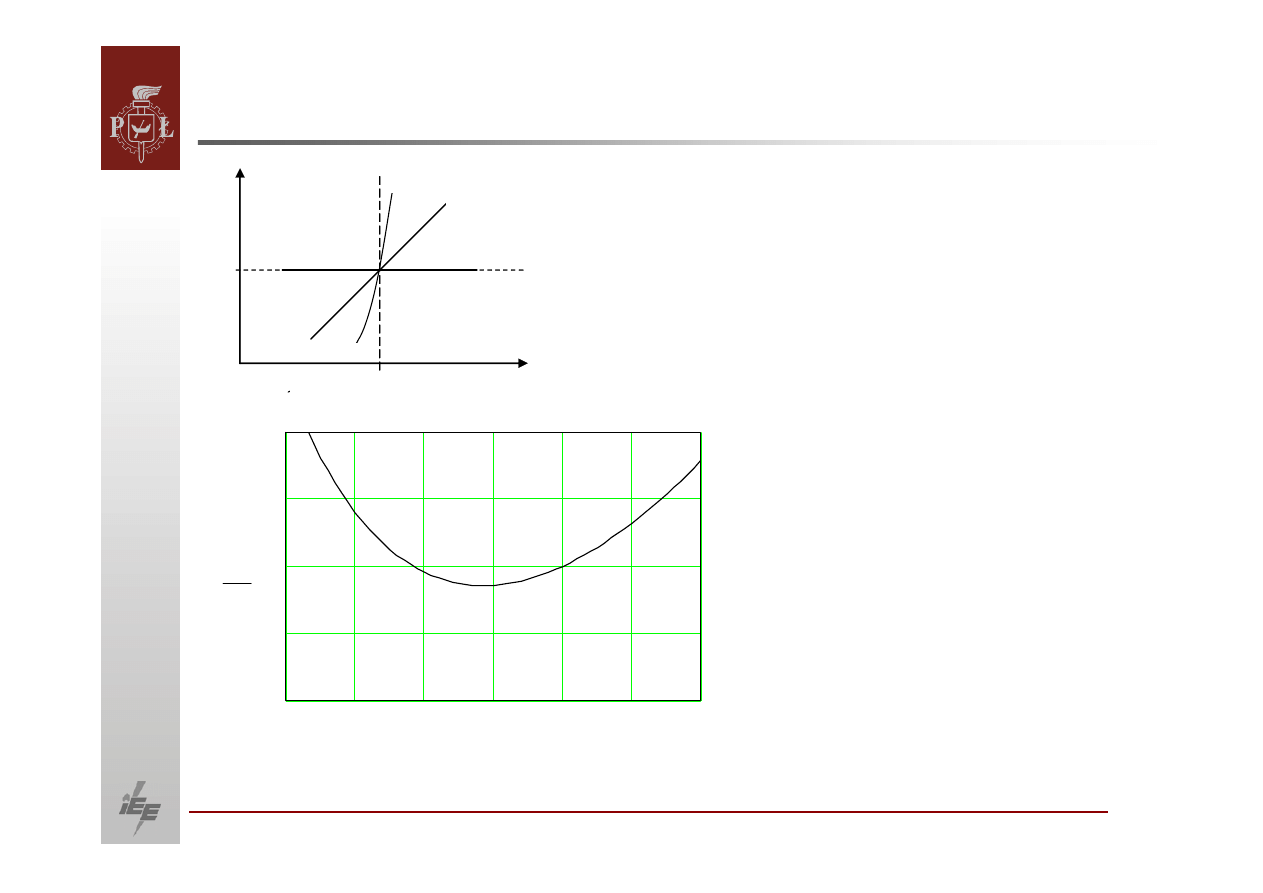
Charakterystyki odbiorów
P
n
P
U
n
U
0
=
p
α
1
=
p
α
1
>
p
α
0.6
0.7
0.8
0.9
1
1.1
1.2
0.8
0.9
1
1.1
Q
i
0 6 i 0 01
U

42
OBLICZANIE PRZEPŁYWÓW MOCY.
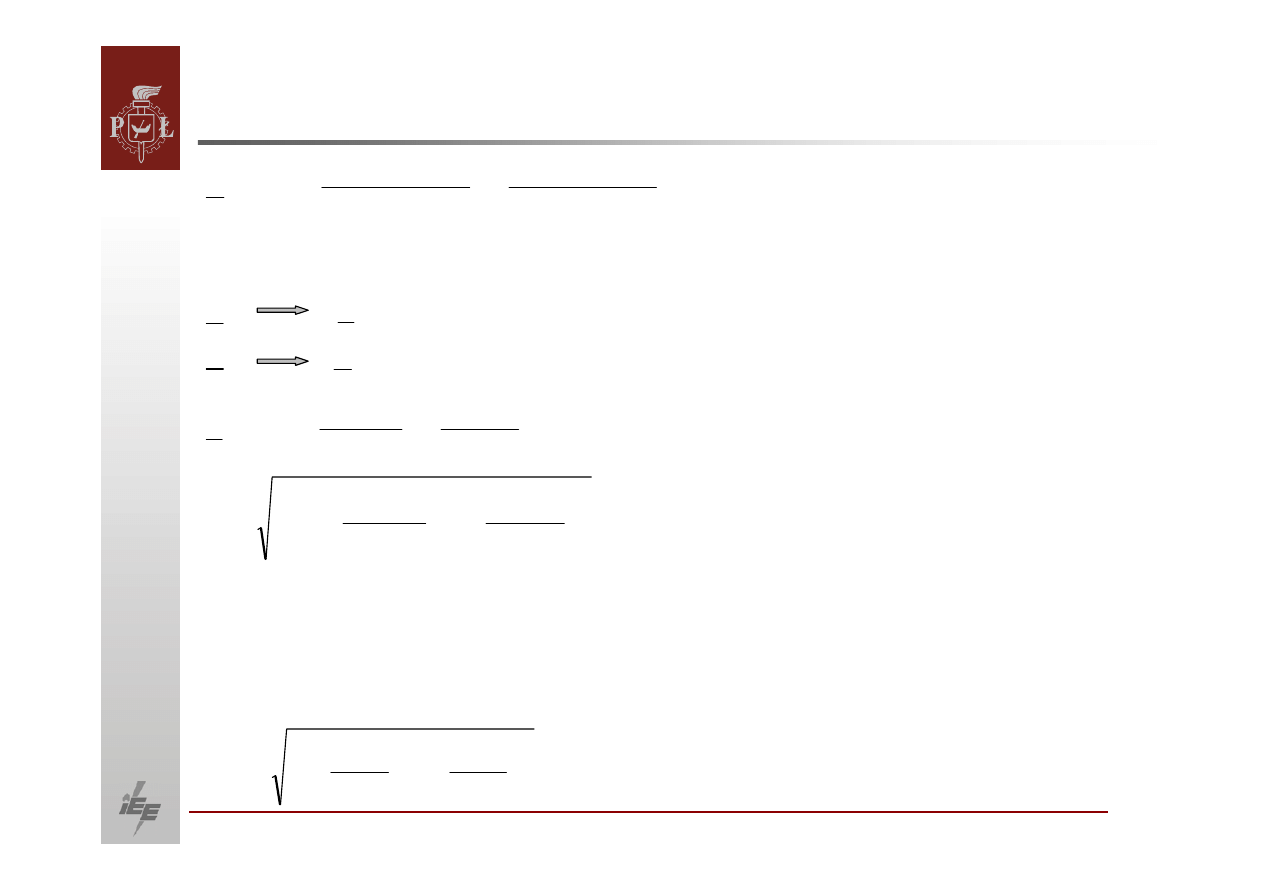
Charakterystyka węzła
0
=
S
R
0
=
L
R
0
≠
S
X
0
≠
L
X
L
S
X
X
<<
2
U
X
Q
U
L
o
⋅
≅
δ
2
n
L
o
n
U
X
Q
U
U
⋅
≅
δ
L
n
L
S
n
Z
X
U
X
X
U
S
2
2
1
,
1
1
,
1
⋅
≈
+
⋅
=
Z
o
n
S
Q
U
U
⋅
≅ 1
,
1
δ
Czym większa moc zwarciowa w węźle tym mniejsze spadki napięcia
wywołuje przepływ
mocy.
Gdyby moc zwarciowa wynosiła nieskończoność
to jest to tzw. sieć
sztywna.
Napięcie w węźle sieci sztywnej jest stałe niezależne od obciążenia.
Rozpatrzmy linię
elektroenergetyczną
zasilaną
z systemu
elektroenergetycznego przy następujących założeniach:
Spadek napięcia wyniesie:
Moc zwarciowa przy powyższych założeniach wynosi:
43
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
B
B
B
B
B
B
B
A
U
R
Q
X
P
j
U
X
Q
R
P
U
U
⋅
−
⋅
+
⋅
+
⋅
+
=
0
=
G
R
A
U
d
E
B
U
G
G
U
U
=
G
d
B
G
d
B
G
d
U
X
P
j
U
X
Q
U
E
⋅
+
⋅
+
=
2
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
+
=
G
d
B
G
d
B
G
d
U
X
P
U
X
Q
U
E
1
=
G
U
2
=
d
X
8
,
0
=
B
P
6
,
0
=
B
Q
72
2
1
2
8
0
1
2
6
0
1
2
2
,
,
,
E
d
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
=
to moduł
siły elektromotorycznej generatora wynosi:
Zakładając poniższe parametry generatora w jednostkach względnych:

44
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
Moduł
siły elektromotorycznej podnosimy do kwadratu i mnożymy przez :
Otrzymujemy równanie kołowe mocy postaci:
Równanie kołowe mocy przekształcamy względem mocy biernej:
Zależność
mocy biernej generatora od napięcia , siły elektromotorycznej
oraz mocy czynnej generatora zostanie zaprezentowana
na wykresach.
Zależność
powyższa i wykresy nie uwzględniają
regulatora napięcia generatora
i ograniczeń.
2
2
d
G
X
U
2
2
2
2
2
d
G
G
d
B
G
d
B
G
d
X
U
U
X
P
U
X
Q
U
E
∗
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
+
=
( )
2
2
2
2
B
B
d
G
d
G
d
P
Q
X
U
X
U
E
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
( )
d
G
B
d
G
d
B
X
U
P
X
U
E
Q
2
2
2
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
±
=
B
Q
G
U
d
E
B
P
45
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
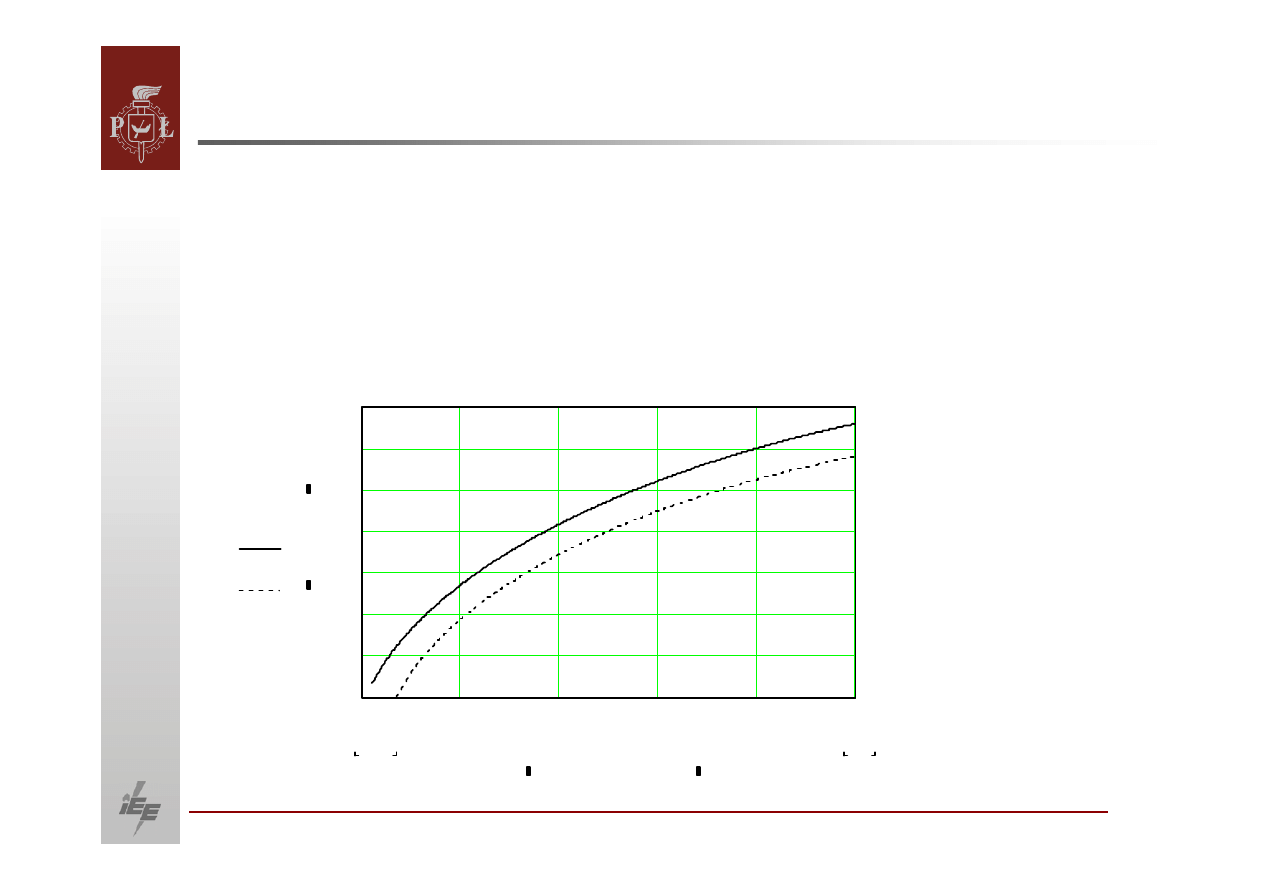
Zależność
mocy biernej produkowanej przez generator synchroniczny
od napięcia dla 2 różnych wartości siły elektromotorycznej generatora, gdzie
linia:
9ciągła ,
9kropkowana .
72
2,
E
=
6
2,
E
=
0.6
0.7
0.8
0.9
1
1.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.7
0
Q U
( )
Q1 U
( )
1.1
0.61
U
46
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
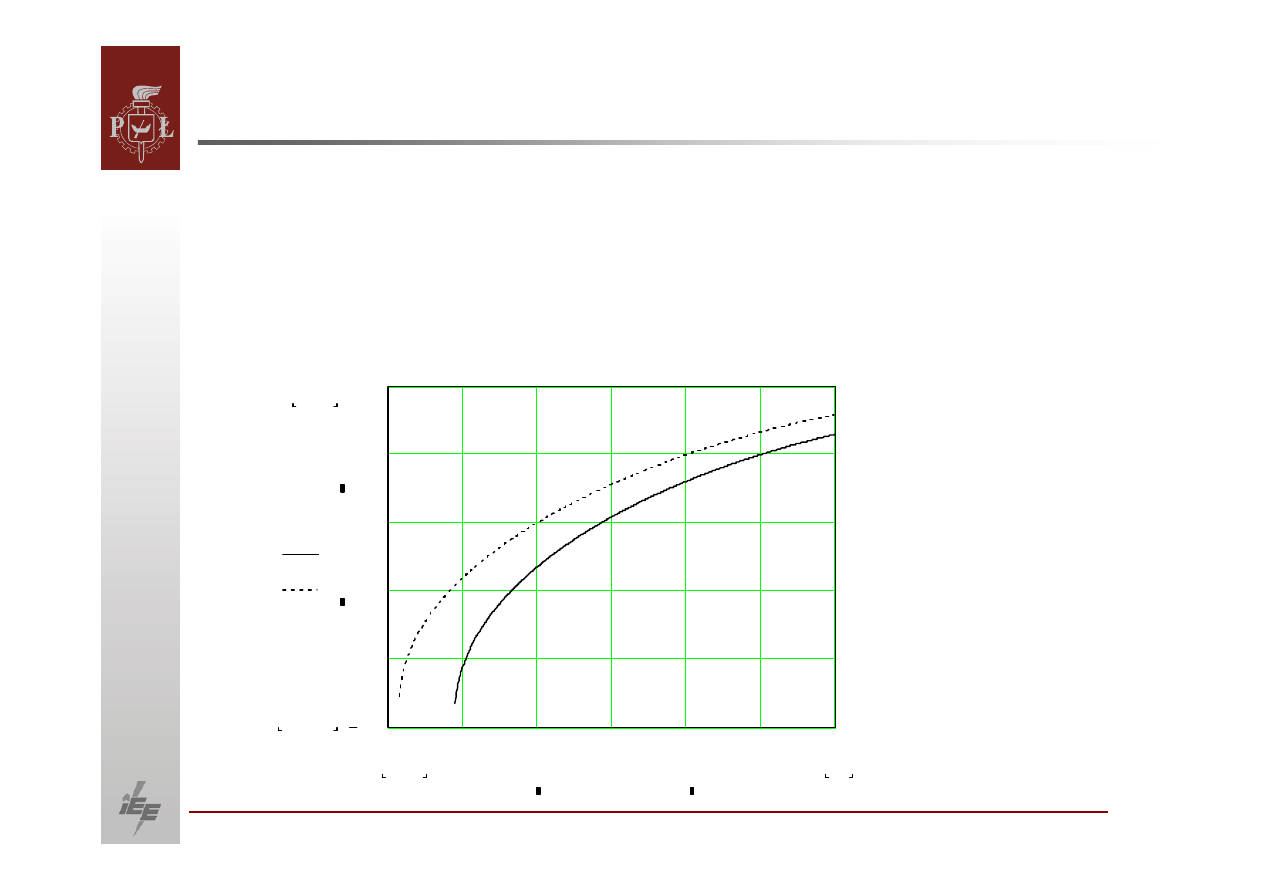
Zależność
mocy biernej produkowanej przez generator synchroniczny
od napięcia dla 2 różnych wartości mocy czynnej generatora, gdzie linia:
9 ciągła ,
9 kropkowana .
8
0,
P
=
7
0,
P
=
0.5
0.6
0.7
0.8
0.9
1
1.1
0.2
0
0.2
0.4
0.6
0.8
0.717
0.133
−
Q1 U
( )
Q2 U
( )
1.1
0.515
U
47
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
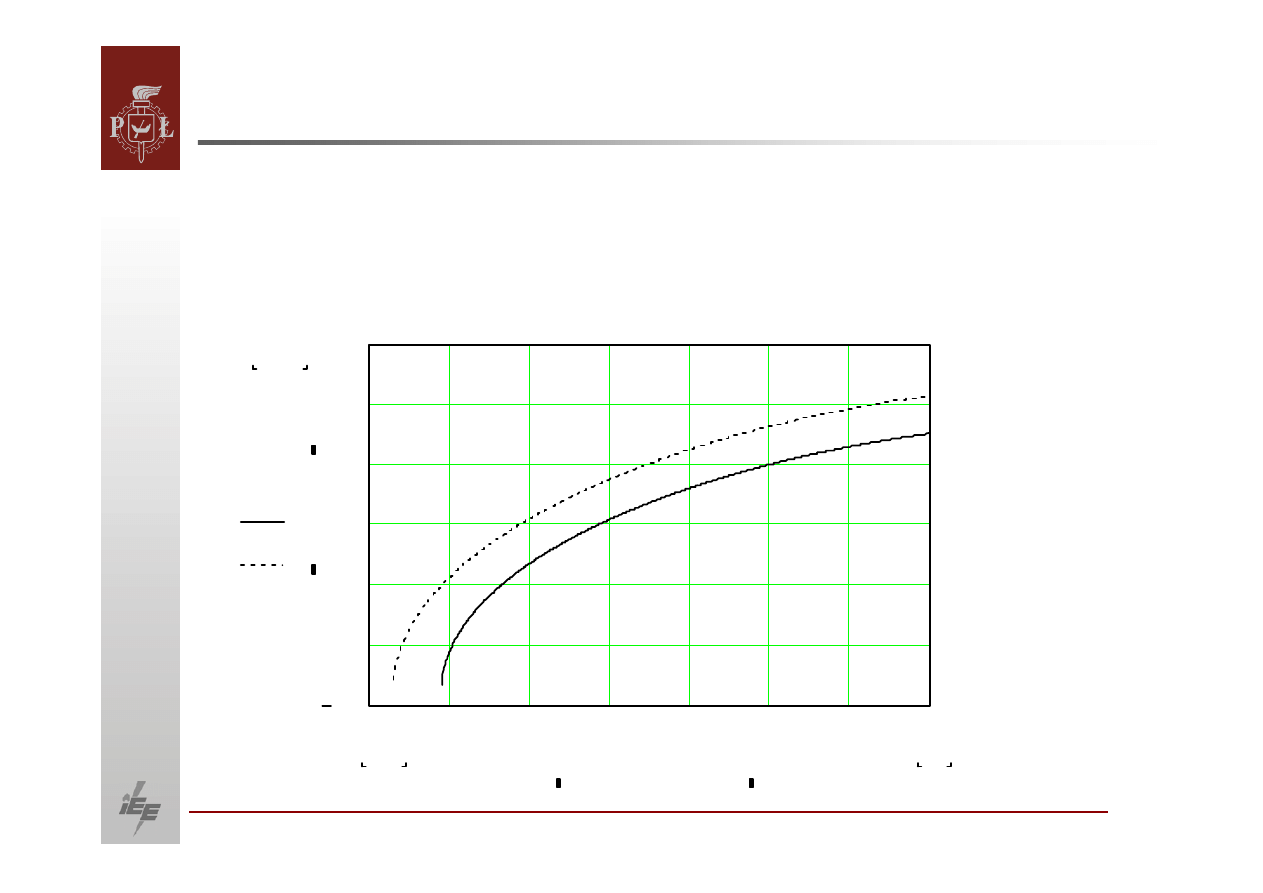
Zależność
mocy biernej produkowanej przez generator synchroniczny
od napięcia dla 2 różnych wartości reaktancji, gdzie linia:
9 ciągła reaktancja równa 2,0,
9 kropkowana reaktancja równa 1,8.
0.5
0.6
0.7
0.8
0.9
1
1.1
0.2
0
0.2
0.4
0.6
0.8
0.827
0.2
−
Q1 U
( )
Q2 U
( )
1.2
0.53
U
48
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
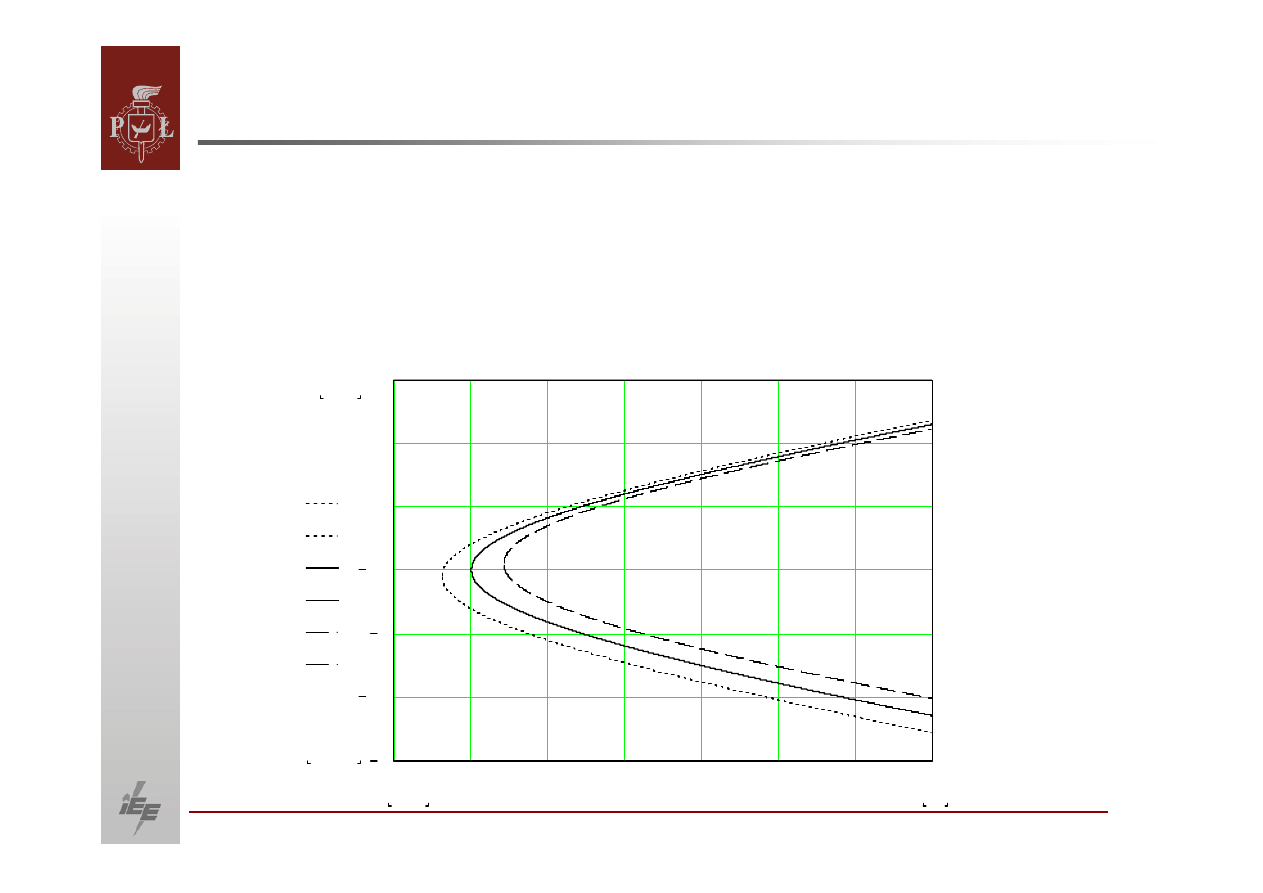
Zależność
mocy biernej produkowanej przez generator synchroniczny w funkcji
siły elektromotorycznej dla różnych napięć
na zaciskach generatora, gdzie linia:
‐
ciągła dla ,
‐
kropkowana dla ,
‐
kreskowana dla .
1
=
G
U
1
>
G
U
1
<
G
U
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
2
1.5
1
0.5
0
0.5
1
0.682
1.784
−
Q11 E
( )
Q01 E
( )
Q E
( )
Q1 E
( )
Q12 E
( )
Q02 E
( )
2.8
1.524
E
49
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
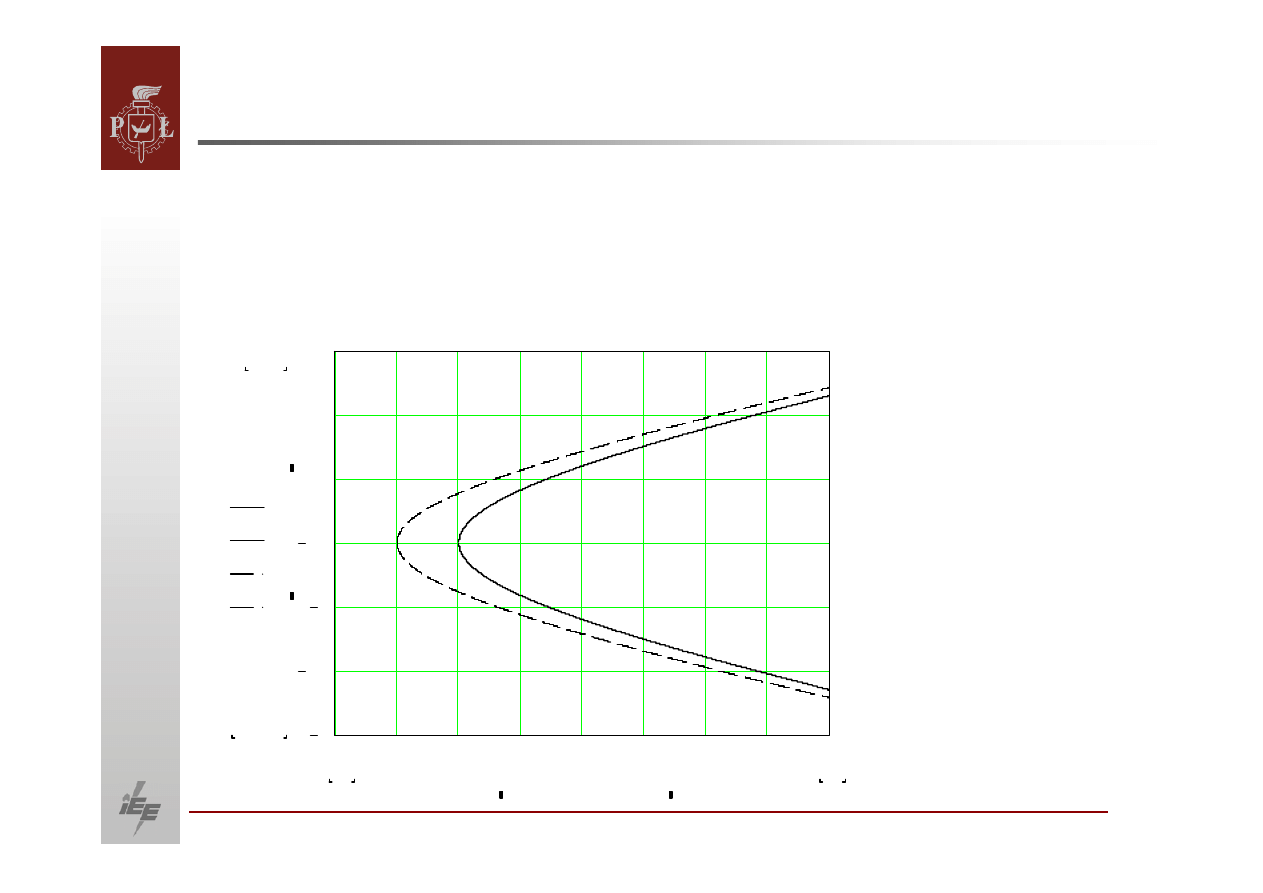
Zależność
mocy biernej produkowanej przez generator synchroniczny w funkcji
siły elektromotorycznej dla różnych mocy czynnej generatora, gdzie linia:
9ciągła dla ,
9kreskowana dla .
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
2
1.5
1
0.5
0
0.5
1
0.712
1.712
−
Q E
( )
Q1 E
( )
Q11 E
( )
Q01 E
( )
2.8
1.4
E
8
0,
P
=
7
0,
P
=
50
OBLICZANIE PRZEPŁYWÓW MOCY.
Charakterystyki napięciowe generatora
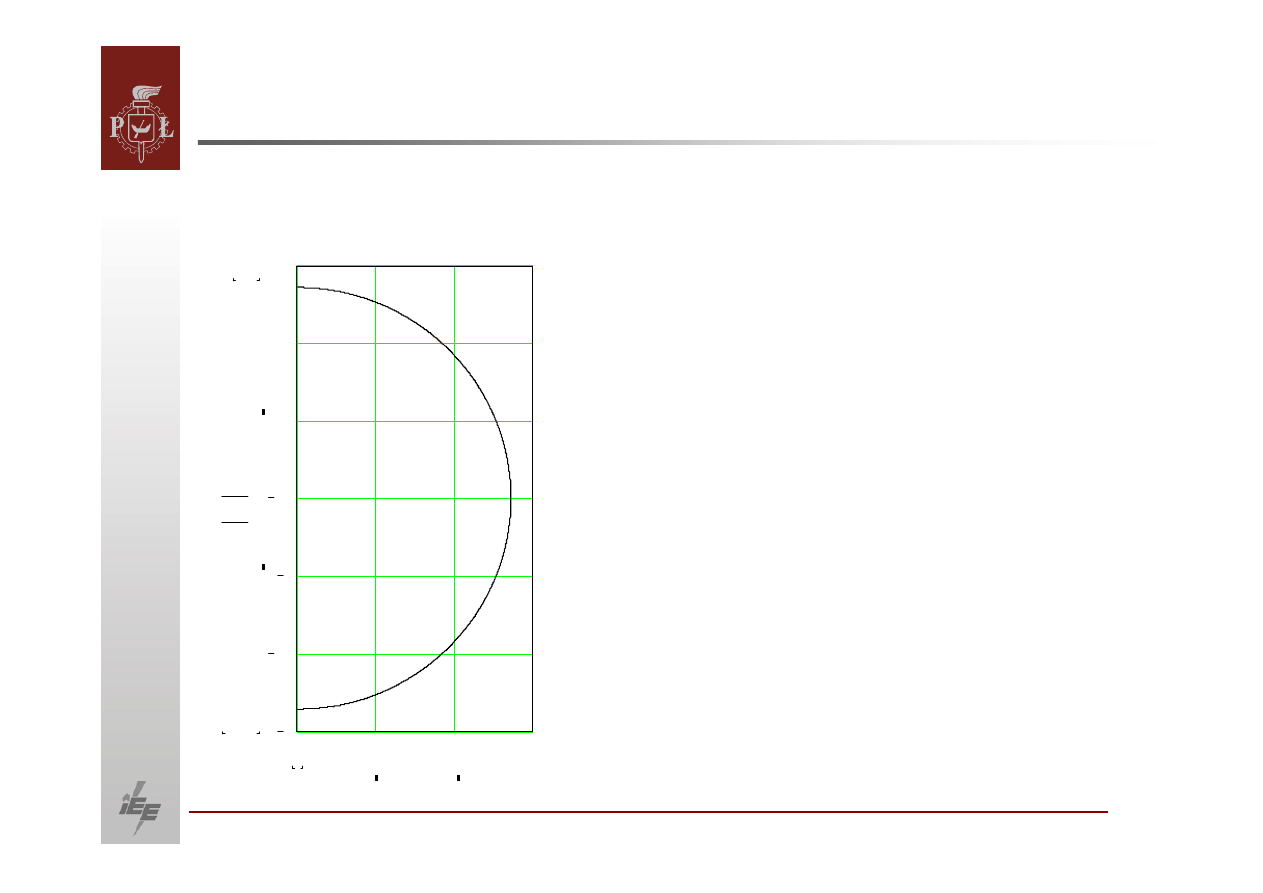
Zależność
mocy biernej produkowanej przez generator synchroniczny w funkcji
mocy czynnej.
0
0.5
1
1.5
2
1.5
1
0.5
0
0.5
1
0.86
1.86
−
Q P
( )
Q1 P
( )
1.5
0
P

51
OBLICZANIE PRZEPŁYWÓW MOCY.
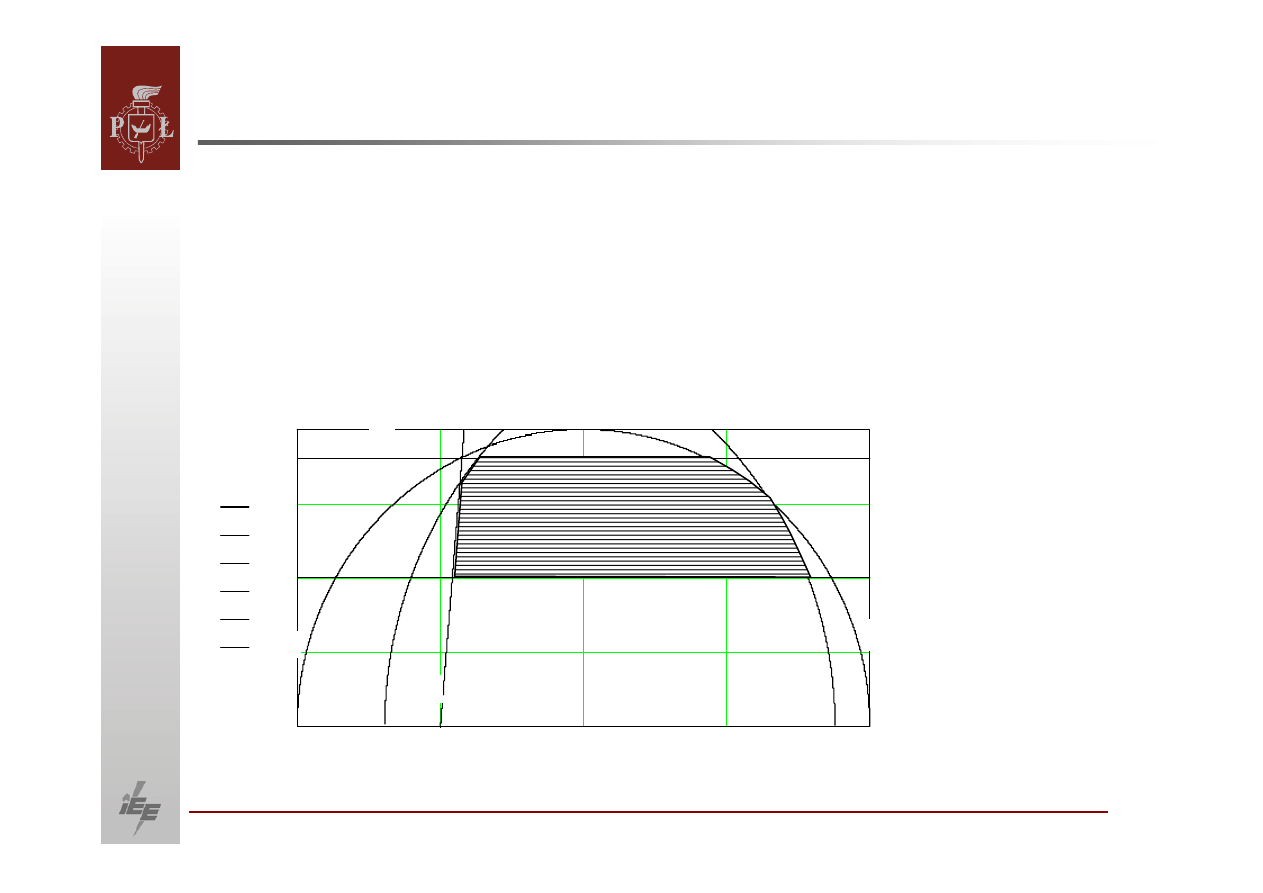
Dopuszczalny obszar pracy generatora
Dopuszczalny obszar pracy generatora synchronicznego jest ograniczony przez
następujące czynniki:
1)
Prąd generatora musi być
mniejszy równy od prądu znamionowego tego
generatora
Równanie powyższe tworzy okrąg na płaszczyźnie o środku w początku
układu współrzędnych i promieniu równym mocy znamionowej pozornej
generatora.
Krzywa 1.
2) Moc generatora musi być
większa równa od mocy minimalnej bloku
Krzywa 2.
3) Moc generatora musi być
mniejsza lub równa od mocy maksymalnej bloku
Krzywa 3.
rG
G
I
I
≤
(
)
2
2
2
3
rG
rG
G
G
I
U
Q
P
⋅
⋅
≤
+
min
G
G
P
P
≥
max
G
G
P
P
≤
Q
P,

52
OBLICZANIE PRZEPŁYWÓW MOCY.
Dopuszczalny obszar pracy generatora
4) Siła elektromotoryczna generatora musi być
mniejsza lub równa od
maksymalnej siły elektromotorycznej
Równanie powyższe tworzy okrąg na płaszczyźnie o środku w
punkcie
i promieniu równym .
Krzywa 4.
5) Kąt pomiędzy siłą
elektromotoryczną
generatora a napięciem sieci sztywnej
musi być
mniejszy lub równy od maksymalnej wielkości
Równanie powyższe tworzy prostą
o początku w
punkcie
i nachyleniu
równym kątowi .
Krzywa 5.
( )
2
max
2
2
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
≤
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
d
G
d
G
G
d
G
X
U
E
P
Q
X
U
Q
P,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
d
G
X
U
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
d
G
d
X
U
E
max
max
δ
δ
≤
S
d
U
E
(
)
(
)
max
2
δ
δ
tg
X
U
Q
P
tg
d
G
G
G
U
E
S
d
≤
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
d
G
X
U
2
max
δ
53
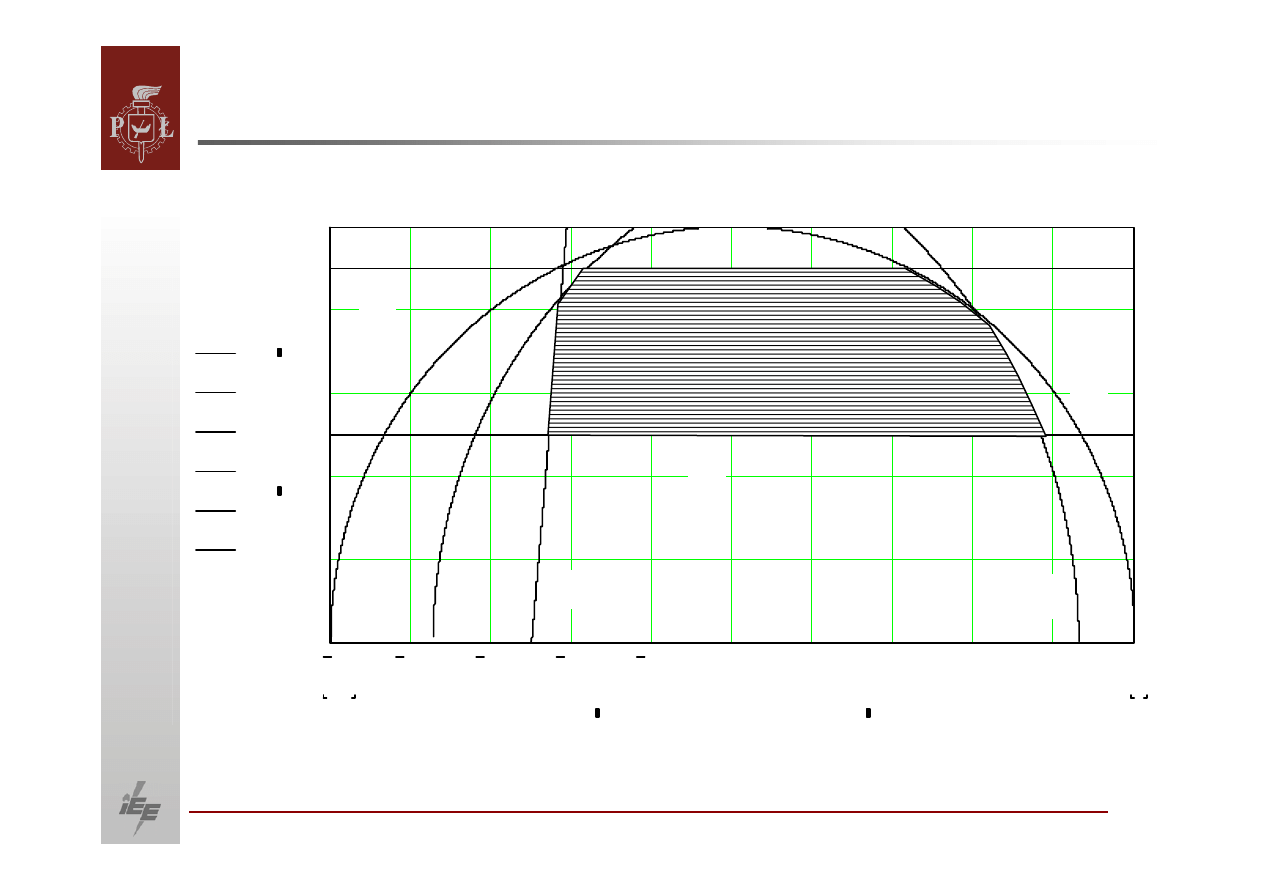
OBLICZANIE PRZEPŁYWÓW MOCY.
Dopuszczalny obszar pracy generatora
6) Temperatura skrajnych części stali statora musi być
mniejszy lub równy od
temperatury dopuszczalnej
Równanie powyższe nie daje się
opisać
prostą
analityczną
funkcją.
Charakterystyka taka jest określana na drodze pomiarowej.
Krzywa 6.
max
ϑ
ϑ
≤
stojana
1
−
0.5
−
0
0.5
0
0.25
0.5
0.75
1
P Q
( )
Pmin Q
( )
Pmax Q
( )
PE Q
( )
Pd Q
( )
PE1 Q
( )
Q
1
2
3
5
4
6
1
54
OBLICZANIE PRZEPŁYWÓW MOCY.
Dopuszczalny obszar pracy generatora
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
0
0.2
0.4
0.6
0.8
1
1
0
P Q
( )
Pmin Q
( )
Pmax Q
( )
PE Q
( )
Pd Q
( )
PE1 Q
( )
1
1
−
Q
1
2
3
5
4
6
1
Document Outline
- SYSTEMY ELEKTROENERGETYCZNE Rozdział 2 OBLICZANIE PRZEPŁYWÓW MOCY
- OBLICZANIE PRZEPŁYWÓW MOCY Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływ mocy w układzie promieniowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Układ dwumaszynowy
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływy mocy w układzie wielomaszynowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływy mocy w układzie wielomaszynowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływy mocy w układzie wielomaszynowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływy mocy w układzie wielomaszynowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływy mocy w układzie wielomaszynowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływy mocy w układzie wielomaszynowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Przepływy mocy w układzie wielomaszynowym
- OBLICZANIE PRZEPŁYWÓW MOCY. Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
- OBLICZANIE PRZEPŁYWÓW MOCY. Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
- OBLICZANIE PRZEPŁYWÓW MOCY. Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
- OBLICZANIE PRZEPŁYWÓW MOCY. Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
- OBLICZANIE PRZEPŁYWÓW MOCY. Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
- OBLICZANIE PRZEPŁYWÓW MOCY. Obliczanie macierzy transferowej. Metoda redukcji modelu sieci
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki odbiorów
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki odbiorów
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyka węzła
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Charakterystyki napięciowe generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Dopuszczalny obszar pracy generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Dopuszczalny obszar pracy generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Dopuszczalny obszar pracy generatora
- OBLICZANIE PRZEPŁYWÓW MOCY. Dopuszczalny obszar pracy generatora
Wyszukiwarka
Podobne podstrony:
Kanicki Systemy Rozdział 6
Kanicki Systemy Rozdzial 10 id Nieznany
Kanicki Systemy Rozdzial 5 id 2 Nieznany
Kanicki Systemy Rozdzial 3 id 2 Nieznany
Kanicki Systemy Rozdział 7
Kanicki Systemy Rozdział 4
Kanicki Systemy Rozdział 6
Kanicki Systemy Rozdzial 10 id Nieznany
Kanicki Systemy Rozdział 4
Kanicki Systemy Rozdział 3
Kanicki Systemy Rozdział 5
Obowiązki i uprawnienia operatora systemu rozdzielczego w świetle obowiązujących postanowień Prawa e
rozdzial 1 system?nkowy i?nki ok
rozdział v funkcja systemu szkolnego w procesach reprodukcji społecznej wg szcepańskiego OTRVY22YB
więcej podobnych podstron