MATLAB

PODSTAWY PROGRAMOWANIA

Ćwiczenia 2

DZIAŁANIA

NA WEKTORACH I MACIERZACH

Materiały opracowano na podstawie wiadomości zawartych w skrypcie:

MATLAB - podstawy programowania
Jankowski. R, Lubowiecka I., Witkowski W.
Politechnika Gdańska, 2001

Wydział Inżynierii Lądowej i Środowiska
Katedra Mechaniki Budowli i Mostów

copyleft by Marcin Kujawa & Łukasz Smakosz

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

2/26

Tworzenie skryptów

 Skrypt jest plikiem tekstowym zawierającym zestaw poleceń Matlaba.

 Pliki skryptowe mają rozszerzenie .m.

 W ich nazwach nie należy używać polskich znaków oraz spacji, nie mogą

rozpoczynać się liczbą, nie mogą pokrywać się z nazwami funkcji Matlaba

 Dostęp do edytora Matlaba jest możliwy przez File > New > Script, przez

odpowiednią ikonę lub skrót CTRL+N.

Opisywanie skryptów

 Każdy skrypt powinien mieć krótki opis zawartości i działania. Opis umieszcza się

za znakiem

%

. Taki opis pliku nazywamy komentarzem.

 Opis pliku można wywołać w Matlabie przy pomocy polecenia help

nazwa_skryptu

. Za opis pliku traktowane są pierwsze linie komentarza

nieprzerwane liniami innego typu.

Przykład:

% To jest opis skryptu test.m

clear, clc

% czyszczenie zmiennych i ekranu

a=2;

% opis wybranej komendy

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

3/26

Dostęp do elementów macierzy

Polecenie:

A(:,j)

wybiera j-tą kolumnę z macierzy A.

Polecenie:

A(i,:)

wybiera i-ty wiersz z macierzy A.

Polecenie:

A(i,a:b)

wybiera elementy od a do b z macierzy A z wiersza i.

Polecenie:

A(:)

wybiera całą macierz w postaci wektora kolumnowego.

Polecenie:

A(i:j)

wybiera elementy macierzy A od elementu i do j.

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

4/26

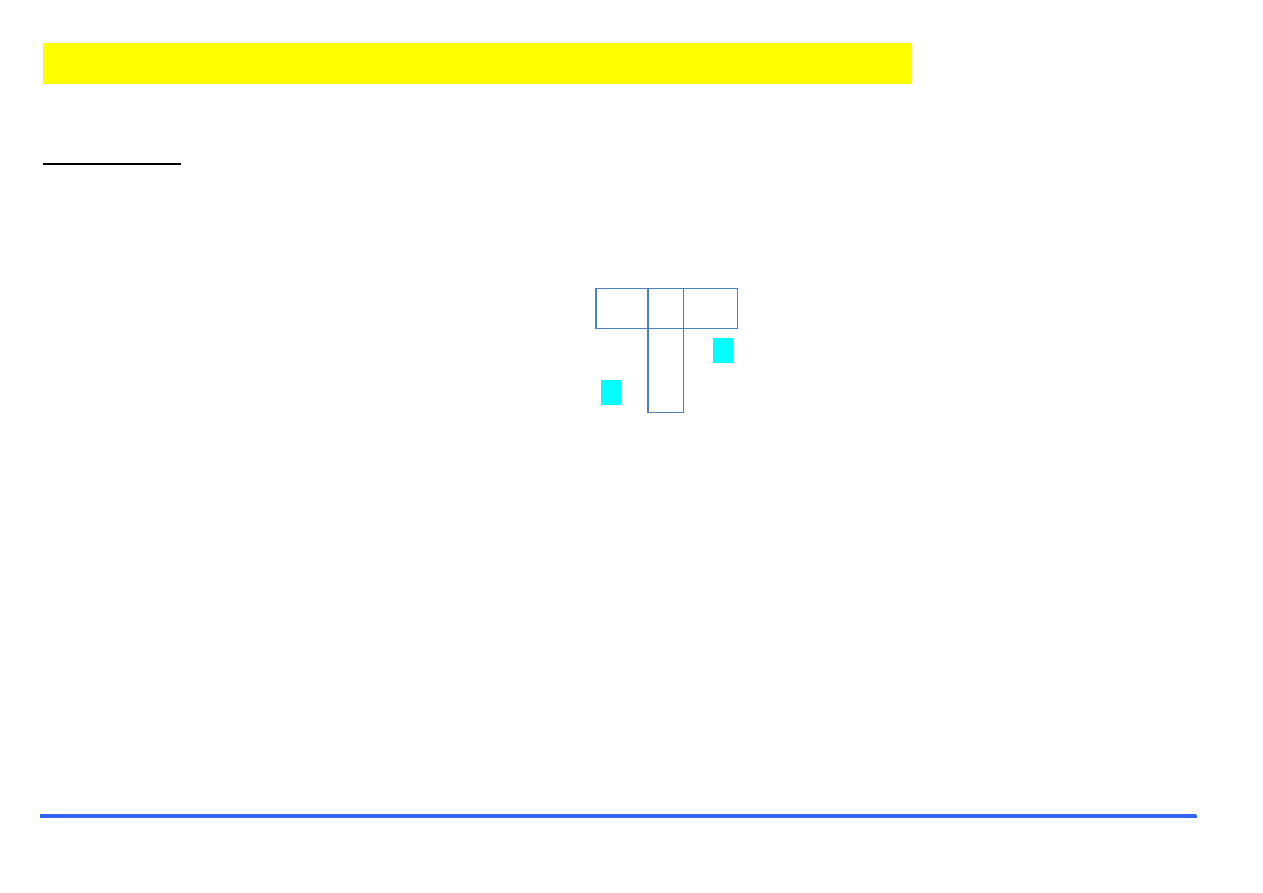
Odwołania do podmacierzy

Przykład:
Stwórz macierz A i zapisz zaznaczone podmacierze jako B i C.
Odczytaj wyróżnione elementy i zapisz je jako b i c.

9

5

1

1

2

3

3 7 11

4 5

6

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

5/26

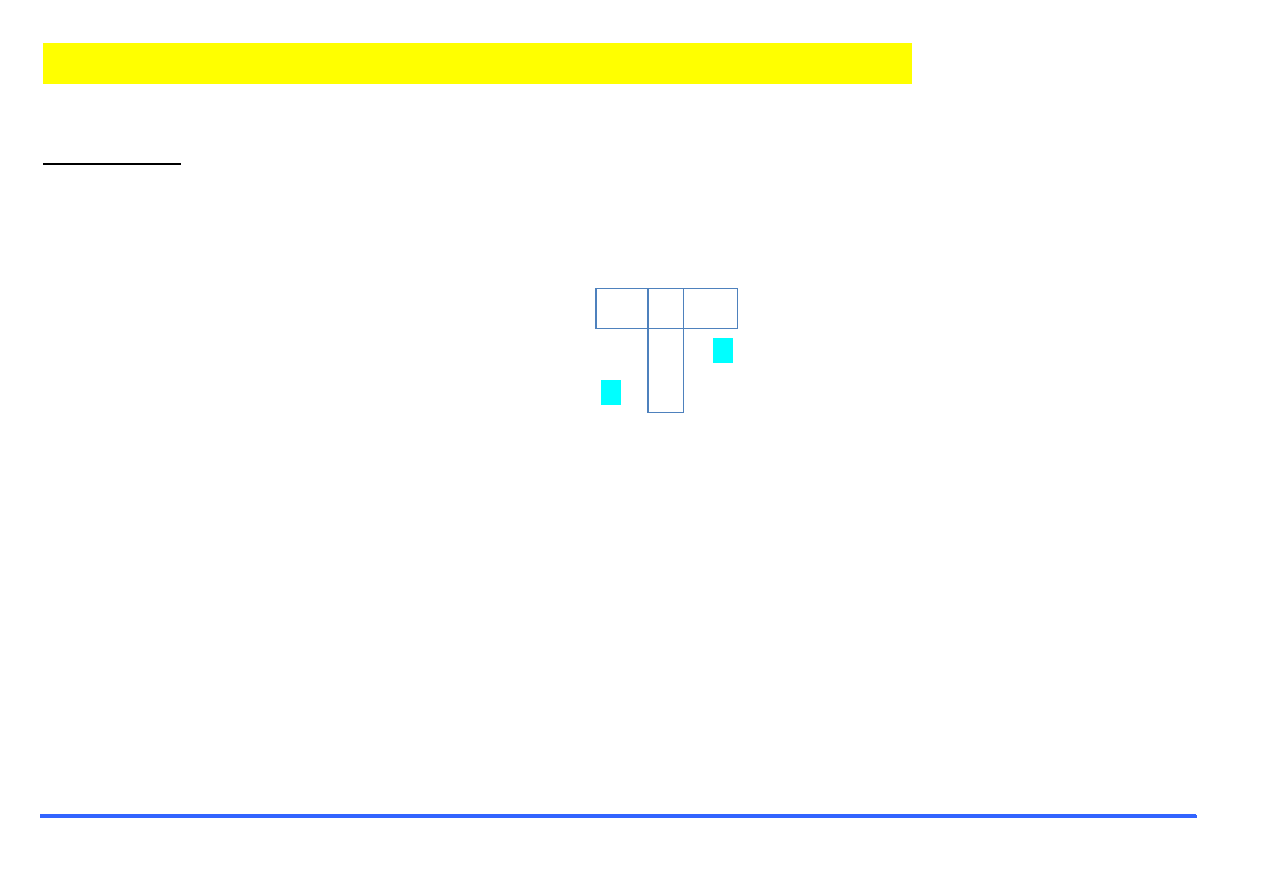
Odwołania do podmacierzy

Przykład:
Stwórz macierz A i zapisz zaznaczone podmacierze jako B i C.
Odczytaj wyróżnione elementy i zapisz je jako b i c.

9

5

1

1

2

3

3 7 11

4 5

6

clear, clc

A=[-9:4:11; 1:6]

% definicja macierzy A

B=A(1:2,[2 3])

% podmacierz z wierszy od 1 do 2 oraz kolumn 2 i 3

C=A(1,4:6)

% podmacierz z wiersza 1 oraz kolumn od 4 do 6

b=B(2,1)

% element znajdujący się w 2 wierszu i 1 kolumnie

c=C(1,2)

% element znajdujący się w 1 wierszu i 2 kolumnie

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

6/26

Usuwanie wektora z macierzy i nadpisywanie elementów

Przykład:
Stwórz macierz A, wyróżnione elementy zastąp liczbą a = sin(15°), następnie
usuń z niej zaznaczone wektory.

1 0 0
0 1 0
0 0 1

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

7/26

Usuwanie wektora z macierzy i nadpisywanie elementów

Przykład:
Stwórz macierz A, wyróżnione elementy zastąp liczbą a = sin(15°), następnie
usuń z niej zaznaczone wektory.

1 0 0
0 1 0
0 0 1

clear, clc

A=eye(3)

% generacja macierzy jednostkowej A

a=sin(pi/12)

% definicja zmiennej a; kat w radianach

A(3,1)=a

% nadpisanie elementu w 3 wierszu i 1 kolumnie

A(2,3)=a

% nadpisanie elementu w 2 wierszu i 3 kolumnie

A(1,:)=[]

% usuniecie 1 wiersza

A(:,2)=[]

% usuniecie 2 kolumny

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

8/26

Generacja wektorów i alokacja pamięci

Ze względu na czas wykonywania operacji dobrze jest przed przystąpieniem do
obliczeń stworzyć odpowiednie macierze do przechowywania danych.

Polecenie:

>> x(5)=0

wygeneruje wektor poziomy 5 elementowy wypełniony zerami.


Polecenie:

>> x(5,7)=0

lub

>> x=zeros(5,7)

wygeneruje macierz 5x7 wypełniona zerami.

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

9/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Wygeneruj zerową macierz A o wymiarach 3

×

5, następnie kolejne jej wiersze

zastąp wektorami x, y i z:

1 3 5 7 9

4

2 0 2 4

1 1 1 1 1

Usuń skrajne kolumny i zapisz wyraz znajdujący się na środku macierzy jako c.

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

10/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

clear, clc

% generacja macierzy zerowej i wektorow x, y, z

A=zeros(3,5);
x=[1:2:9];
y=[-4:2:4];
z=ones(1,5);

A(1,:)=x

% zastąpienie wiersza 1 wektorem x

A(2,:)=y

% zastąpienie wiersza 2 wektorem y

A(3,:)=z

% zastąpienie wiersza 3 wektorem z

A(:,[1 5])=[]

% usuniecie 1 i 5 kolumny

c=A(2,2)

% odczytanie wyrazu z 2 wiersza i 2 kolumny

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

11/26

Operacje na elementach wektora

Jeżeli x jest macierzą to operacje odnoszą się do poszczególnych kolumn
macierzy.

Inne przydatne funkcje

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

12/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Stwórz macierz B taką, że:

 skok we wszystkich wierszach wynosi 3,

 pierwszy wiersz zaczyna się od 1 i kończy na 7,

 pierwsza kolumna zaczyna się od 1 i kończy na 9 ze skokiem co 2.

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

13/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Stwórz macierz B taką, że:

 skok we wszystkich wierszach wynosi 3,

 pierwszy wiersz zaczyna się od 1 i kończy na 7,

 pierwsza kolumna zaczyna się od 1 i kończy na 9 ze skokiem co 2.

B=[1:3:7; 3:3:9; 5:3:11; 7:3:13; 9:3:15]

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

14/26

Przykład:

 Wyznacz średnią arytmetyczną ze wszystkich elementów macierzy B.
 Odczytaj wymiary macierzy B za pomocą funkcji size i przypisz je kolejno

zmiennym m i n.

 Wyznacz maksymalną wartość m-tego wiersza i minimalną wartość n-tej

kolumny macierzy B.

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

15/26

Przykład:

 Wyznacz średnią arytmetyczną ze wszystkich elementów macierzy B.
 Odczytaj wymiary macierzy B za pomocą funkcji size i przypisz je kolejno

zmiennym m i n.

 Wyznacz maksymalną wartość m-tego wiersza i minimalną wartość n-tej

kolumny macierzy B.

b1=mean(B)

% wektor srednich z kolumn mac. B

B_sr=mean(b1)

% srednia arytmetyczna z mac. B

[m,n]=size(B);

% odczytanie wymiarow B i przypisanie

ich wartosci zmiennym m (l.wierszy) oraz n(l.kolumn)

m1=B(m,:)

% zapisanie ostatniego wiersza jako m1

max_m=max (m1)

% max m-tego wiersza

n1=B(:,n)

% zapisanie ostatniej kolumny jako n1

min_n=min(n1)

% min n-tej kolumny

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

16/26

Działania macierzowe i tablicowe

Przykład:
Zdefiniuj macierz A i wektor x następnie podnieś je do drugiej potęgi
wykorzystując operacje tablicowe i macierzowe. Porównaj wyniki.

2

1

3

5

0

6

0

2

2

1 0 1 2

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

17/26

Działania macierzowe i tablicowe

Przykład:
Zdefiniuj macierz A i wektor x następnie podnieś je do drugiej potęgi
wykorzystując operacje tablicowe i macierzowe. Porównaj wyniki.

A=[2 -1 3;exp(2) 5 0;6 0 2*pi]
x=[-2:2]

at=A.^2, xt=x.^2

% op. tablicowe

am=A^2, xm=x^2

% op. macierzowe

2

1

3

5

0

6

0

2

2

1 0 1 2

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

18/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

 Zdefiniuj macierze A i B, następnie oblicz ich sumę i różnicę.

 Dodaj do elementów 1. wiersza macierzy B liczbę 2.

 Wykonaj mnożenie macierzy A i B (wybierz typ mnożenia).

2 3 4
4 3 2

,

5 5 5
5 5 5

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

19/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

 Zdefiniuj macierze A i B, następnie oblicz ich sumę i różnicę.

 Dodaj do elementów 1. wiersza macierzy B liczbę 2.

 Wykonaj mnożenie macierzy A i B (wybierz typ mnożenia).

clear, clc

A=[2:4;4:-1:2]

% generacja automatyczna

B=ones(2,3)*5

% mnozenie mac. przez skalar

sum_ab=A+B, roz_ab=A-B

% suma i roznica mac. A i B

B(1,:)=B(1,:)+2

% dodanie 2 do 1 wiersza mac. B

mn_ab=A.*B

% mozliwe tylko mn. tabl.

2 3 4
4 3 2

,

5 5 5
5 5 5

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

20/26

Odwracanie i transpozycja macierzy

Przykład:
Zdefiniuj macierze A i B, a następnie wyznacz macierze do nich odwrotne oraz
transponowane.

11 12 13
21

0

23

31 32 33

,

11 12 13
21 22 23
31 32 33

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

21/26

Odwracanie i transpozycja macierzy

Przykład:
Zdefiniuj macierze A i B, a następnie wyznacz macierze do nich odwrotne oraz
transponowane.

11 12 13
21

0

23

31 32 33

,

11 12 13
21 22 23
31 32 33

A=[11:13;21 0 23;31:33]
trans_a=A’

% transpozycja macierzy

odw_a=inv(A), odw_a= A^(-1)

% odwracanie macierzy

B=[11:13;21:23;31:33]
trans_b=B’

% transpozycja macierzy

odw_b=inv(B)

% odwracanie macierzy

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

22/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Zdefiniuj wektory x i y, a następnie oblicz ich iloczyn tablicowy oraz wektorowy.
Oblicz sumę kwadratów elementów wektora y.

1 3 5 7 9

4

2 0 2 4

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

23/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Zdefiniuj wektory x i y, a następnie oblicz ich iloczyn tablicowy oraz wektorowy.
Oblicz sumę kwadratów elementów wektora y.

1 3 5 7 9

4

2 0 2 4

clear, clc

x=[1:2:9]
y=[-6:3:6]

xy_tab=x.*y

% mnozenie tablicowe

xy_mac=x*y’

% mnozenie mac 1x5 * 5x1

xy_mac2=x’*y

% mnozenie mac 5x1 * 1x5

y_kwd=y*y’

% suma kwadratow

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

24/26

Algebra liniowa

det(A)

obliczanie wyznacznika macierzy A

eig(A)

obliczanie wartości własnych macierzy A

poly(A)

obliczanie współczynników wielomianu charakterystycznego
macierzy A

rank(A)

obliczanie rzędu macierzy A

diag(A)

wyznaczanie elementów leżących na głównej przekątnej
macierzy A

Przykład:
Wykorzystaj powyższe funkcje na macierzy A postaci:

2

1

3

5

0

6

0

2

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

25/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Rozwiąż układ równań liniowych:

3

1

1
2

1

3

3

2

2

Uwaga: układ można zapisać w postaci macierzowej A*x = B, którego
rozwiązaniem jest x = A

-1

*B

MATLAB

 2. Działania na wektorach i macierzach



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

26/26

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Rozwiąż układ równań liniowych:

3

1

1
2

1

3

3

2

2

Uwaga: układ można zapisać w postaci macierzowej A*x = B, którego
rozwiązaniem jest x = A

-1

*B

clear, clc
A=[1 3 0; 1/2 1 -3; 0 2 1]

% macierz wspolczynnikow 3x3

B=[1 3 2]'

% wektor kolumnowy wyrazow wolnych 3x1

x=inv(A)*B

% wektor kolumnowy niewiadomych 3x3 * 3x1