
1. LICZBY ZESPOLONE
1.1 PODSTAWOWE DEFINICJE I WŁASNOŚCI
Def. 1.1.1 (liczba zespolona, płaszczyzna zespolona)
Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych np. (x,y), (u,v), (a,b). Liczby zespolone oznaczamy
krótko przez z, w itp. Zbiór wszystkich liczb zespolonych oznaczmy przez C. Mamy zatem
{
}
R
y
x
y
x
z
C
def
∈
=
=
,
:
)
,
(
.
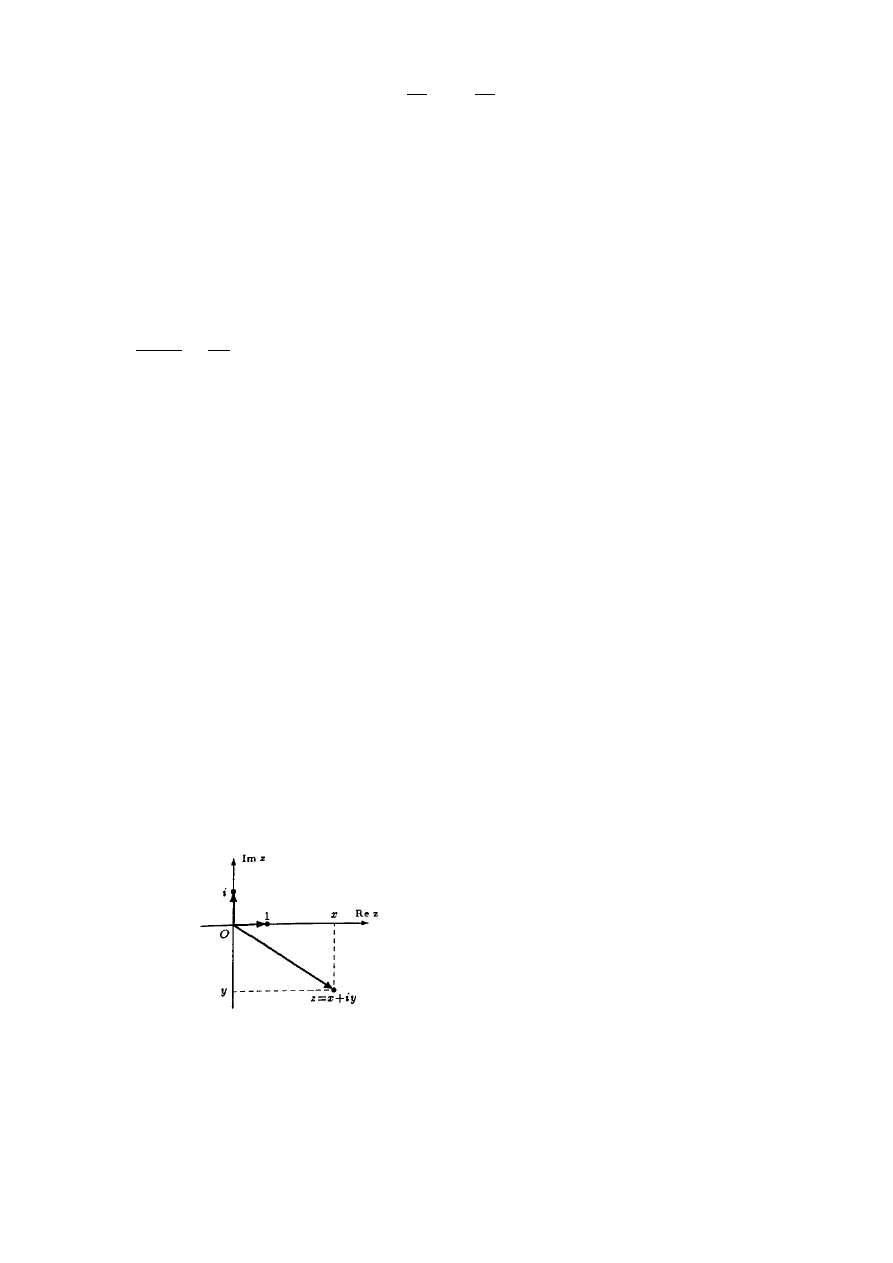
Uwaga. Liczbę zespoloną z = (x,y) przedstawiamy na płaszczyźnie w postaci punktu o współrzędnych (x,y) lub w postaci
wektora o początku w punkcie (0,0) i końcu w punkcie (x,y). W tej interpretacji zbiór wszystkich liczb zespolonych nazywamy
płaszczyzną zespoloną.
Def. 1.1.2 (równość, suma i iloczyn liczb zespolonych)
Niech
)
,
(
1
1
1
y
x
z
=
,
)
,
(
2
2
2
y
x
z
=
będą liczbami zespolonymi.
1. Równość liczb zespolonych określamy przez warunek:
2
1
2
1
2
1
oraz
y
y
x
x
z
z
def
=
=
⇔
=
.
2. Sumę liczb zespolonych określamy wzorem:
(
)
2
1
2
1
2
1
,
y
y
x
x
z
z
def
+
+
=
+
.
3. Iloczyn liczb zespolonych określamy wzorem:
(
)
1
2
2
1
2
1
2
1
2
1
,
y
x
y
x
y
y
x
x
z
z
def
+
−
=
⋅
.
Fakt 1.1.3 (własności działań w zbiorze liczb zespolonych)
Niech z
1
, z
2
, z
3
będą dowolnymi liczbami zespolonymi. Wtedy
1. dodawanie liczb zespolonych jest przemienne, tzn.
1
2
2
1
z
z
z
z
+
=
+
2. dodawanie liczb zespolonych jest łączne, tzn.
(
)
(
)
2
2
1
3
2
1
z
z
z
z
z
z
+
+
=
+
+
3. dla każdej liczby zespolonej z liczba zespolona
)
0
,
0
(
0
def
=
spełnia równość
z
z
=
+
0
4. dla każdej liczby zespolonej
)
,
( y
x
z
=
liczba
)
,
(
y
x
z
def
−
−
=
−
spełnia równość
0
)
(
=
−
+
z
z
5. mnożenie liczb zespolonych jest przemienne, tzn.
1
2
2
1
z
z
z
z
⋅
=
⋅
6. mnożenie liczb zespolonych jest łączne, tzn.
(
)
(
)
3
2
1
3
2
1
z
z
z
z
z
z
⋅
⋅
=
⋅
⋅
7. dla każdej liczby zespolonej z liczba zespolona
)
0
,
1
(
1
def
=
spełnia równość
z
z
=
⋅
1
8. dla każdej liczby zespolonej
0
)
,
(
≠
=
y
x
z
liczba zespolona
+
−
+
=
2
2
2
2
,
1
y
x
y
y
x
x
z
def
spełnia równość
1
1
=
⋅
z
z
9. mnożenie liczb zespolonych jest rozdzielne względem dodawania, tzn.
(
)
3
1
2
1
3
2
1
z
z
z
z
z
z
z
⋅
+
⋅
=
+
⋅
.
Uwaga. Liczby zespolone 0, –z, 1 oraz
z
1
wprowadzone odpowiednio w punktach 3, 4, 7 oraz 8 powyższego faktu są jedynymi
liczbami o żądanych w tych punktach własnościach. Liczby te nazywamy odpowiednio: elementem neutralnym dodawania,
elementem przeciwnym liczby z, elementem neutralnym mnożenia oraz elementem odwrotnym do liczby z.
Def. 1.1.4 (odejmowanie i dzielenie liczb zespolonych)
Niech z
1
, z
2
∈
C będą dowolnymi liczbami zespolonymi.
1. odejmowanie liczb zespolonych określamy wzorem:
)
(
2
1
2
1
z
z
z
z
def
−
+
=
−
2. dzielenie liczb zespolonych określamy wzorem:
2
1
2
1
1
z
z
z
z
def
⋅
=
, o ile z
2
≠
0.
Uwaga. Wszystkie reguły czterech podstawowych działań algebraicznych (dodawanie, odejmowanie, mnożenie, dzielenie)
znane z liczb rzeczywistych obowiązują także w zbiorze liczb zespolonych. W szczególności prawdziwe są wzory skróconego
mnożenia, wzory na sumę wyrazów ciągu arytmetycznego i geometrycznego itd.
Fakt 1.1.5 (zbiór liczb rzeczywistych jest podzbiorem zbioru liczb zespolonych)
Podzbiór R zbioru liczb zespolonych C złożony z liczb postaci (x,0), gdzie x
∈
R, ma następujące własności:
1.
)
0
,
(
)
0
,
(
)
0
,
(
2
1
2
1
x
x
x
x
+
=
+
,
2.
)
0
,
(
)
0
,
(
)
0
,
(
2
1
2
1
x
x
x
x
−
=
−
,
3.
)
0
,
(
)
0
,
(
)
0
,
(
2
1
2
1
x
x
x
x
⋅
=
⋅
,
4.
=
0
,
)
0
,
(
)
0
,
(
2
1
2
1
x
x
x
x
, gdzie x
2
≠
0.
Uwaga. Z własności tych wynika, zbiór R można utożsamiać ze zbiorem liczb rzeczywistych R. Będziemy pisali x zamiast
(x,0); w szczególności 0 = (0,0) oraz 1 = (1,0).
1.2 POSTAĆ ALGEBRAICZNA LICZBY ZESPOLONEJ
Def. 1.2.1 (jednostka urojona)
Liczbę zespoloną (0,1) nazywamy jednostką urojoną i oznaczamy ją przez i;
)
1
,
0
(
def
i
=
.
Fakt 1.2.2 (postać algebraiczna liczby zespolonej)
Każdą liczbę zespoloną można jednoznacznie zapisać w postaci:
iy
x
z
+
=
,
gdzie
R
y
x
∈
,
.
Uwaga. Ten sposób przedstawienia liczb zespolonych nazywamy ich postacią algebraiczną. Nie każde przedstawienie liczby
zespolonej w postaci x + iy jest jej postacią algebraiczną. Niezbędne jest dodanie warunku x, y
∈
R.
Def. 1.2.3 (część rzeczywista i urojona liczby zespolonej)
Niech x + iy będzie postacią algebraiczną liczby zespolonej z. Wówczas
1. liczbę x nazywamy częścią rzeczywistą liczby zespolonej z, co zapisujemy
x
z
def
=
Re
,
2. liczbę y nazywamy częścią urojoną liczby zespolonej z, co zapisujemy
y
z
def
=
Im
.
Liczbę zespoloną postaci
iy
, gdzie y
∈
R \ {0}, nazywamy liczbą czysto urojoną.
Rys. 1.2.1 Interpretacja geometryczna jednostek rzeczywistej i urojonej oraz liczby zespolonej
w postaci algebraicznej.
Uwaga. Dodawanie, odejmowanie i mnożenie liczb zespolonych w postaci algebraicznej wykonujemy tak, jak dodawanie,
odejmowanie i mnożenie wielomianów zmiennej i, przy warunku
1
2
−
=
i
. Przy dzieleniu przez liczbę zespoloną x + iy, gdzie
x, y
∈
R, należy dzielną i dzielnik pomnożyć przez liczbę x – iy, aby w mianowniku uzyskać liczbę rzeczywistą.
Fakt 1.2.4 (o równości liczb zespolonych w postaci algebraicznej)
Dwie liczby zespolone są równe wtedy i tylko wtedy, gdy ich części rzeczywiste i urojone są równe, tzn.

=
=
⇔
=
2
1
2
1
2
1
Im
Im
Re
Re
z
z
z
z
z
z
.
1.3 SPRZĘŻENIE I MODUŁ LICZBY ZESPOLONEJ
Def. 1.3.1 (sprzężenie liczby zespolonej)
Sprzężeniem liczby zespolonej z = x + iy, gdzie x, y
∈
R, nazywamy liczbę zespoloną z określoną wzorem:
iy
x
z
def
−
=
.
Liczba sprzężona do liczby zespolonej jest jej obrazem w symetrii osiowej względem osi Rez.
Fakt 1.3.2 (własności sprzężenia liczb zespolonych)
Niech z, z
1
, z
2
∈
C. Wtedy
1.
2
1
2
1
z
z
z
z
+
=
+
5.
z
z
z
Re
2
=
+
2.
2
1
2
1
z
z
z
z
−
=
−
6.
z
i
z
z
Im
2
=
−
3.
2
1
2
1
z
z
z
z
⋅
=
⋅
7.
( )
z
z
=
4.
2
1
2
1
z
z
z
z
=
, o ile z
2
≠
0
8.
( )
( )
z
z
Im
Im
−
=
Uwaga. Równości podane w punktach 1 i 3 prawdziwe są odpowiednio dla dowolnej liczby składników i czynników.
Def. 1.3.3 (moduł liczby zespolonej)
Modułem liczby zespolonej z = x + iy, gdzie x, y
∈
R, nazywamy liczbę rzeczywistą |z| określoną wzorem:
2
2
y
x
z
def
+
=
.
Moduł liczby zespolonej jest uogólnieniem wartości bezwzględnej liczby rzeczywistej. Geometrycznie moduł liczby zespolonej
z jest odległością punktu z od początku układu współrzędnych.
Uwaga. Moduł różnicy liczb zespolonych z
1
, z
2
jest długością odcinka łączącego punkty z
1
, z
2
płaszczyzny zespolonej.
Fakt 1.3.4 (własności modułu liczby zespolonej)
Niech z, z
1
, z
2
∈
C. Wtedy
1.
z
z
z
−
=
=
5.
2
1
2
1
z
z
z
z
−
≤
−
2.
2
1
2
1
z
z
z
z
⋅
=
⋅
6.
2
z
z
z
=
⋅
3.
2
1
2
1
z
z
z
z
=
, o ile z
2
≠
0
7.
z
z
≤
Re
4.
2
1
2
1
z
z
z
z
+
≤
+
8.
z
z
≤
Im
Uwaga. Warunki podane w punktach 2 i 4 powyższego faktu prawdziwe są także dla dowolnej liczby odpowiednio czynników
i składników. Przy obliczaniu ilorazu liczb zespolonych w i z
≠
0 wygodnie jest stosować tożsamość:
2
z
z
w
z
w
=
.
1.4 POSTAĆ TRYGONOMETRYCZNA LICZBY ZESPOLONEJ
Def. 1.4.1 (argument i argument główny liczby zespolonej)
Argumentem liczby zespolonej z = x + iy
≠
0, gdzie x, y
∈
R, nazywamy każdą liczbę
ϕ
∈
R spełniającą układ równań:
=
=
z
y
z
x
ϕ
ϕ
sin
cos
.
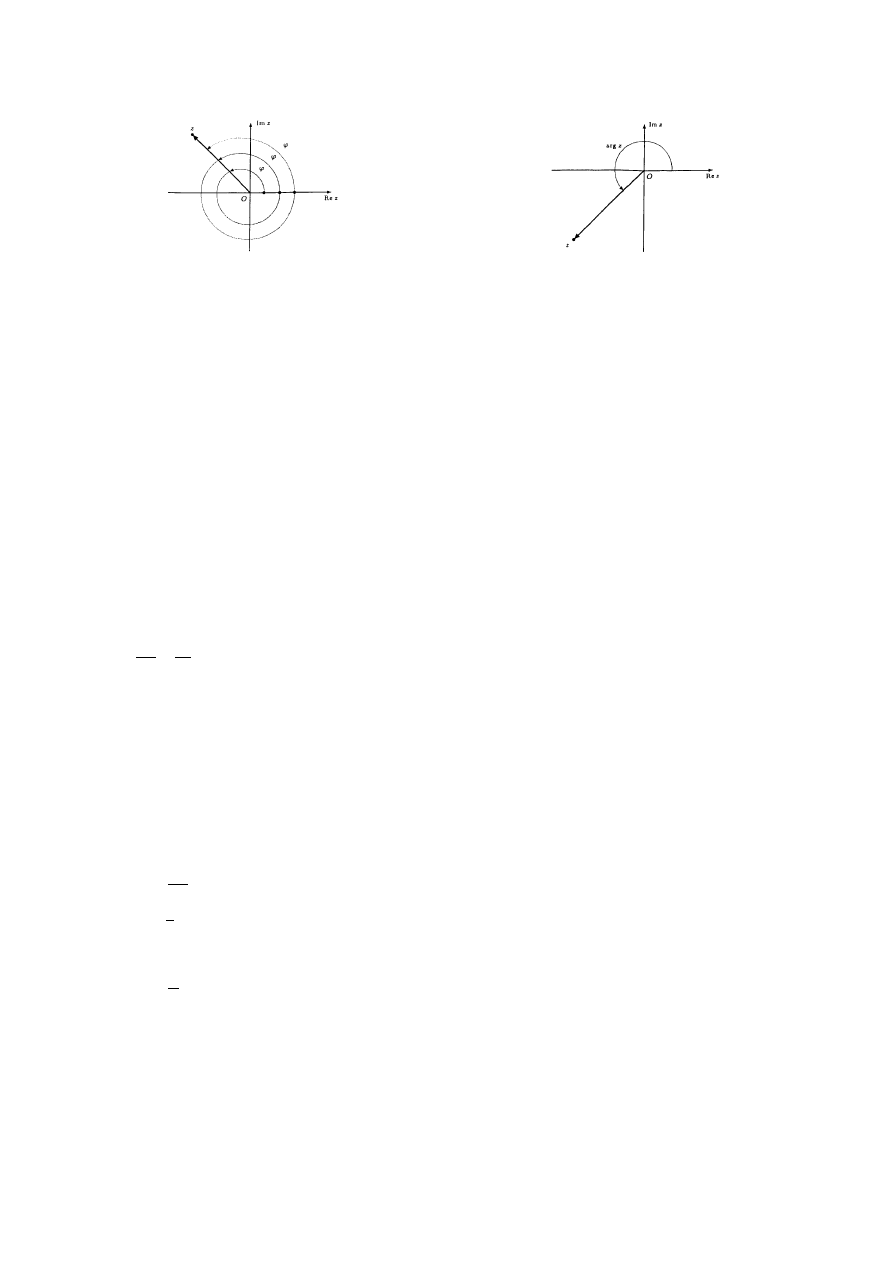
Przyjmujemy, że argumentem liczby z = 0 jest każda liczba
ϕ
∈
R. Argumentem głównym liczby zespolonej z
≠
0 nazywamy
argument
ϕ
tej liczby spełniający nierówność 0
≤
ϕ
< 2
π
. Przyjmujemy, że argumentem głównym liczby z = 0 jest 0. Argument
główny liczby zespolonej z oznaczamy przez
z
arg
. Każdy argument
ϕ
liczby zespolonej z
≠
0 ma postać
π
ϕ
k
z 2
arg
+
=
, gdzie k
∈
Z.
Rys. 1.4.1 Argument liczby zespolonej
Rys. 1.4.2 Argument główny liczby zespolonej
Uwaga. Argumenty liczby zespolonej są miarami z są miarami kąta zorientowanego utworzonego przez dodatnią część osi
rzeczywistej i wektor wodzący tej liczby (rys. 1.4.1). Argument główny liczby zespolonej jest najmniejszą nieujemną miarą
kąta zorientowanego utworzonego przez dodatnią część osi rzeczywistej i wektor wodzący tej liczby (rys. 1.4.2). Czasem
przyjmuje się, że argument główny liczby zespolonej jest liczbą z przedziału (-
π
,
π
].
Fakt 1.4.2 (postać trygonometryczna liczby zespolonej)
Każdą liczbę zespoloną z można przedstawić w postaci:
(
)
ϕ
ϕ
sin
cos
i
r
z
+
=
,
gdzie r
≥
0 oraz
ϕ
∈
R. Liczba r jest wówczas modułem liczby z, a
ϕ
jednym z jej argumentów.
Fakt 1.4.3 (równość liczb zespolonych postaci trygonometrycznej)
Liczby zespolone
(
)
1
1
1
1
sin
cos
ϕ
ϕ
i
r
z
+
=
,
(
)
2
2
2
2
sin
cos
ϕ
ϕ
i
r
z
+
=
, gdzie r
1
, r
2
≥
0 oraz
ϕ
1
,
ϕ
2
∈
R, są równe wtedy i tylko
wtedy, gdy:
0
2
1
=
=
r
r
albo
0
2
1
>
=
r
r
oraz
π
ϕ
ϕ
k
2
2
1
+
=
dla pewnego k
∈
Z.
Fakt 1.4.4 (mnożenie i dzielenie liczb zespolonych w postaci trygonometryczne)
Niech
(
)
1
1
1
1
sin
cos
ϕ
ϕ
i
r
z
+
=
,
(
)
2
2
2
2
sin
cos
ϕ
ϕ
i
r
z
+
=
, gdzie r
1
, r
2
≥
0 oraz
ϕ
1
,
ϕ
2
∈
R będą liczbami zespolonymi. Wtedy
1.
[
]
)
sin(
)
cos(
2
1
2
1
2
1
2
1
ϕ
ϕ
ϕ
ϕ
+
+
+
=
⋅
i
r
r
z
z
2.
[
]
)
sin(
)
cos(
2
1
2
1
2
1
2
1
ϕ
ϕ
ϕ
ϕ
−
+
−
=
i
r
r
z
z
, o ile z
2
≠
0.
Inaczej mówiąc, przy mnożeniu liczb zespolonych ich moduły mnożymy, a argumenty dodajemy. Podobnie, przy dzieleniu
liczb zespolonych ich moduły dzielimy, a argumenty odejmujemy.
Uwaga. Pierwszy ze wzorów w ostatnim fakcie jest prawdziwy także dla dowolnej liczby czynników.
Fakt 1.4.5 (o argumentach iloczynu, ilorazu, sprzężenia oraz liczby przeciwnej)
Niech z, z
1
, z
2
∈
C oraz niech n
∈
N. Wtedy
1.
π
k
z
z
z
z
2
arg
arg
)
arg(
2
1
2
1
+
+
=
dla pewnego k
∈
Z;
2.
( )
π
k
z
n
z
n
2
arg
arg
+
=
dla pewnego k
∈
Z;
3.
π
k
z
z
z
z
2
arg
arg
arg
2
1
2
1
+
−
=
dla pewnego k
∈
Z, o ile z
2
≠
0;
4.
( )
π
k
z
z
2
arg
arg
+
−
=
dla pewnego k
∈
Z;
5.
π
π
k
z
z
2
arg
)
arg(
+
+
=
−
dla pewnego k
∈
Z;
6.
π
k
z
z
2
arg
1
arg
+
−
=
dla pewnego k
∈
Z, o ile z
≠
0;
Uwaga. W rzeczywistości k może przyjmować wartości 1. 0 lub –1; 2. dowolne; 3. 0 lub 1; 4. 1; 5. 0, 1 lub –1; 6. 1.
Fakt 1.4.6 (wzór de Moivre’a)
Niech
(
)
ϕ
ϕ
sin
cos
i
r
z
+
=
, gdzie r
≥
0,
ϕ
∈
R oraz niech n
∈
N. Wtedy
(
)
ϕ
ϕ
n
i
n
r
z
n
n
sin
cos
+
=
.
Def. 1.4.7 (symbol
ϕ
i
e
)
Dla
ϕ
∈
R liczbę zespoloną cos
ϕ
+ isin
ϕ
oznaczamy krótko przez
ϕ
i
e
;

ϕ
ϕ
ϕ
sin
cos
i
e
def
i
+
=
.
Fakt 1.4.8 (własności symbolu
ϕ
i
e
)
Niech
ϕ
,
ϕ
1
,
ϕ
2
będą dowolnymi liczbami rzeczywistymi oraz niech k będzie dowolną liczbą całkowitą. Wtedy
1.
(
)
2
1
2
1
ϕ
ϕ
ϕ
ϕ
i
i
i
e
e
e
⋅
=
+
5.
0
≠
ϕ
i
e
2.
(
)
2
1
2
1
ϕ
ϕ
ϕ
ϕ
i
i
i
e
e
e
=
−
6.
π
ϕ
ϕ
ϕ
ϕ
l
e
e
i
i
2
2
1
2
1
+
=
⇔
=
, gdzie l
∈
Z
3.
( )
ϕ
ϕ
ik
k
i
e
e
=
7.
1
=
ϕ
i
e
4.
(
)
ϕ
π
ϕ
i
k
i
e
e
=
+
2
8.
( )
π
ϕ
ϕ
l
e
i
2
arg
+
=
dla pewnego l
∈
Z
Fakt 1.4.9 (postać wykładnicza liczby zespolonej)
Każdą liczbę zespoloną z można zapisać w postaci wykładniczej, tj. w postaci
ϕ
i
re
z
=
,
gdzie r
≥
0,
ϕ
∈
R. Liczba r jest wówczas modułem liczby z, a
ϕ
jej argumentem.
Fakt 1.4.10 (o równości liczb zespolonych w postaci wykładniczej)
Niech r
1
, r
2
≥
0 oraz
ϕ
1
,
ϕ
2
∈
R. Wówczas
0
2
1
2
1
2
1
=
=
⇔
=
r
r
e
r
e
r
i
i
ϕ
ϕ
albo
0
2
1
>
=
r
r
oraz
π
ϕ
ϕ
k
2
2
1
+
=
, gdzie k
∈
Z.
Fakt 1.4.11 (działania na liczbach zespolonych w postaci wykładniczej)
Niech
ϕ
i
e
z
=
,
1
1
ϕ
i
e
z
=
,
2
2
ϕ
i
e
z
=
, gdzie r, r
1
, r
2
≥
0 oraz
ϕ
,
ϕ
1
,
ϕ
2
∈
R, będą liczbami zespolonymi oraz niech k będzie liczbą
całkowitą. Wtedy
1.
ϕ
i
re
z
−
=
4.
ϕ
ik
k
k
e
r
z
=
2.
)
(
π
ϕ +
=
−
i
re
z
5.
)
(
2
1
2
1
2
1
ϕ
ϕ +
=
⋅
i
e
r
r
z
z
3.
ϕ
i
e
r
z
−
=
1
1
, o ile z
≠
0
6.
)
(
2
1
2
1
2
1
ϕ
ϕ −
=
i
e
r
r
z
z
, o ile z
2
≠
0
1.5 PIERWIASTKOWANIE LICZB ZESPOLONYCH
Def. 1.5.1 (pierwiastek z liczby zespolonej)
Pierwiastkiem stopnia n
∈
N z liczby zespolonej z nazywamy każdą liczbę zespoloną w spełniającą równość:
z
w
n
=
.
Zbiór pierwiastków stopnia n z liczby zespolonej z oznaczamy przez
n
z
.
Uwaga. Symbol
n
ma inne znaczenie w odniesieniu do liczb rzeczywistych, a inne do liczb zespolonych (w tym także
rzeczywistych traktowanych jak zespolone). Pierwiastek w dziedzinie rzeczywistej jest określony jednoznacznie i jest to
funkcja R
→
R dla n nieparzystych oraz [0,
∞
)
→
[0,
∞
) dla n parzystych. Pierwiastkowanie w dziedzinie zespolonej jest
natomiast rozwiązywaniem równania
z
w
n
=
, zatem
n
z
jest zbiorem rozwiązań tego równania. Symbolu pierwiastka w
dziedzinie zespolonej nie wolno używać do żadnych działań i obliczeń, gdyż podstawowe wzory dla pierwiastków, prawdziwe
w dziedzinie rzeczywistej tutaj nie mają sensu, np.
2
4
z
z
≠
.
Fakt 1.5.2 (wzór na pierwiastki z liczby zespolonej)
Każda liczba zespolona
(
)
ϕ
ϕ
sin
cos
i
r
z
+
=
, gdzie r
≥
0 oraz
ϕ
∈
R, ma dokładnie n pierwiastków stopnia n. Zbiór tych
pierwiastków ma postać:
{
}
1
1
0
,
,
,
−
=
n
n
w
w
w
z
,
gdzie
+
+
=
n
k
i
n
k
r
w
n
k
π
ϕ
π
ϕ
2
sin
,
2
cos
dla k = 0, 1, …, n – 1.
Uwaga. Dla k = 0, 1, …, n – 2 prawdziwa jest zależność:

k
k
k
n
i
n
w
n
i
n
w
w
=
=
+
π
π
π
π
2
sin
,
2
cos
2
sin
,
2
cos
0
1
.
Fakt 1.5.2 (interpretacja geometryczna zbioru pierwiastków z liczby zespolonej)
Zbiór pierwiastków stopnia n
≥
3 z liczby zespolonej
(
)
ϕ
ϕ
sin
cos
i
r
z
+
=
, gdzie r = |z| oraz
ϕ
= argz, pokrywa się ze zbiorem
wierzchołków n–kąta foremnego wpisanego w okrąg o promieniu
n
r
i środku w początku układu współrzędnych. Pierwszy
wierzchołek tego wielokąta jest w punkcie
+
=
n
i
n
r
w
n
ϕ
ϕ
sin
cos
0
, a kąt między promieniami wodzącymi kolejnych
wierzchołków jest równy
n
π
2
(rys. 1.5.1).
Rys. 1.5.1 Interpretacja geometryczna zbioru pierwiastków z liczby zespolonej
2. WIELOMIANY
2.1 PODSTAWOWE POJĘCIA I WŁASNOŚCI
Def. 2.1.1 (wielomian rzeczywisty)
Wielomianem rzeczywistym stopnia n
∈
N
∪
{0} nazywamy funkcję W: R
→
R określoną wzorem:
0
1
1
1
)
(
a
x
a
x
a
x
a
x
W
n
n
n
n
+
+
+
+
=
−
−
,
gdzie a
k
∈
R dla 0
≤
k
≤
n oraz a
n
≠
0. Ponadto przyjmujemy, że funkcja W(x)
≡
0 jest wielomianem stopnia –
∞
. Liczby a
k
, 0
≤
k
≤
n, nazywamy współczynnikami wielomianu W.
Def. 2.1.2 (wielomian zespolony)
Wielomianem zespolonym stopnia n
∈
N
∪
{0} nazywamy funkcję W: C
→
C określoną wzorem:
0
1
1
1
)
(
c
z
c
z
c
z
c
z
W
n
n
n
n
+
+
+
+
=
−
−
,
gdzie c
k
∈
C dla 0
≤
k
≤
n oraz c
n
≠
0. Ponadto przyjmujemy, że funkcja W(z)
≡
0 jest wielomianem stopnia –
∞
. Liczby c
k
, 0
≤
k
≤
n, nazywamy współczynnikami wielomianu W.
Uwaga. Każdy wielomian rzeczywisty można traktować jako wielomian zespolony rozszerzając jego dziedzinę z R na C. Tak
będziemy postępować przy omawianiu pierwiastków zespolonych wielomianów rzeczywistych. Wielomian zespolony lub
rzeczywisty będziemy nazywali krótko wielomianem.
Def. 2.1.3 (suma, różnica i iloczyn wielomianów)
Niech P i Q będą wielomianami. Sumę, różnicę i iloczyn wielomianów P i Q określamy w sposób naturalny, tj. przyjmujemy:
(
)
)
(
)
(
)
(
x
Q
x
P
x
Q
P
def
±
=
±
,
(
)
)
(
)
(
)
(
x
Q
x
P
x
Q
P
def
⋅
=
⋅
.
Def. 2.1.4 (podzielność wielomianów)
Mówimy, że wielomian S jest ilorazem, a wielomian R resztą z dzielenia wielomianu P przez wielomian Q, jeżeli dla każdego x
∈
R (x
∈
C) spełniony jest warunek
)
(
)
(
)
(
)
(
x
R
x
S
x
Q
x
P
+
⋅
=
oraz stopień reszty R jest mniejszy od stopnia dzielnika Q.
Jeżeli R(x)
≡
0, to mówimy, że wielomian P jest podzielny przez wielomian Q.
2.2 PIERWIASTKI WIELOMIANÓW
Def. 2.2.1 (pierwiastek wielomianu)
Liczbę rzeczywistą (zespoloną) x
0
nazywamy pierwiastkiem rzeczywistym (zespolonym) wielomianu W, jeżeli W(x
0
) = 0.
Tw. 2.2.2 (Bezout)
Liczba x
0
jest pierwiastkiem wielomianu W wtedy i tylko wtedy, gdy istnieje wielomian P taki, że
)
(
)
(
)
(
0
x
P
x
x
x
W
−
=
.
Uwaga. Reszta z dzielenia wielomianu W przez dwumian x – x
0
jest równa W(x
0
).
Def. 2.2.3 (pierwiastek wielokrotny wielomianu)

Liczba x
0
jest pierwiastkiem k–krotnym wielomianu W wtedy i tylko wtedy, gdy istnieje wielomian P taki, że
)
(
)
(
)
(
0
x
P
x
x
x
W
k
−
=
oraz
0
)
(
0
≠
x
P
.
Fakt 2.2.4 (o pierwiastkach wielokrotnych wielomianu)
Liczba x
0
jest pierwiastkiem k–krotnym wielomianu W wtedy i tylko wtedy, gdy
0
)
(
)
(
)
(
0
)
1
(
0
/
0
=
=
=
−
x
W
x
W
x
W
k
oraz
0
)
(
0
)
(
≠
x
W
k
.
Tw. 2.2.5 (o pierwiastkach całkowitych wielomianu)
Niech
0
1
1
1
)
(
a
x
a
x
a
x
a
x
W
n
n
n
n
+
+
+
+
=
−
−
będzie wielomianem o współczynnikach całkowitych oraz niech liczba całkowita p
≠
0 będzie pierwiastkiem wielomianu W.
Wtedy p jest dzielnikiem wyrazu wolnego a
0
.
Tw. 2.1.6 (o pierwiastkach wymiernych wielomianu)
Niech
0
1
1
1
)
(
a
x
a
x
a
x
a
x
W
n
n
n
n
+
+
+
+
=
−
−
będzie wielomianem stopnia n o współczynnikach całkowitych oraz niech liczba wymierna
q
p
, gdzie p i q są liczbami
całkowitymi względnie pierwszymi, będzie pierwiastkiem wielomianu W. Wtedy p jest dzielnikiem współczynnika a
0
, a q jest
dzielnikiem współczynnika a
n
tego wielomianu.
Uwaga. Jeżeli a
n
= 1, to wszystkie wymierne pierwiastki wielomianu są całkowite.
2.3 ZASADNICZE TWIERDZENIE ALGEBRY
Tw. 2.3.1 (zasadnicze twierdzenie algebry)
Każdy wielomian zespolony stopnia dodatniego ma co najmniej jeden pierwiastek zespolony.
Fakt 2.3.2 (o przedstawieniu wielomianu w postaci iloczynu dwumianów)
1. Każdy wielomian zespolony stopnia n
∈
N ma dokładnie n pierwiastków zespolonych (uwzględniając pierwiastki
wielokrotne).
2. Niech wielomian W stopnia n
∈
N ma pierwiastki zespolone z
j
o krotnościach odpowiednio k
j
, gdzie k
j
∈
N dla 1
≤
j
≤
m
oraz k
1
+ k
2
+ … + k
m
= n. Wtedy
m
k
m
k
k
n
z
z
z
z
z
z
c
z
W
)
(
)
(
)
(
)
(
2
1
2
1
−
⋅
⋅
−
⋅
−
=
,
gdzie c
n
jest współczynnikiem stojącym przy z
n
w wielomianie W.
Fakt 2.3.3 (wzory Viete’a)
Niech
0
1
1
1
)
(
c
z
c
z
c
z
c
z
W
n
n
n
n
+
+
+
+
=
−
−
będzie wielomianem zespolonym stopnia n
∈
N. Wówczas liczby z
1
, z
2
, ..., z
n
są
pierwiastkami wielomianu W (z uwzględnieniem krotności) wtedy i tylko wtedy, gdy
( )
−
=
−
=
+
+
+
=
+
+
+
−
=
+
+
+
−
−
−
−
−
−
−
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
c
c
z
z
z
z
z
c
c
z
z
z
z
z
z
z
z
z
c
c
z
z
z
z
z
z
c
c
z
z
z
0
1
3
2
1
3
1
2
4
2
1
3
2
1
2
1
3
1
2
1
1
2
1
1
...
...
...
...
.
Uwaga. Jeżeli znamy niektóre pierwiastki wielomianu, to wzory Viete’a pozwalają znaleźć pozostałe pierwiastki tego
wielomianu.
Fakt 2.3.4 (o pierwiastkach zespolonych wielomianu rzeczywistego)
Niech W będzie wielomianem o współczynnikach rzeczywistych. Wówczas liczba zespolona z
0
jest k–krotnym pierwiastkiem
wielomianu W wtedy i tylko wtedy, gdy liczba
0
z
jest pierwiastkiem k–krotnym tego wielomianu.
Tw. 2.3.5 (o rozkładzie wielomianu rzeczywistego na czynniki rzeczywiste)
Niech W będzie wielomianem stopnia n
∈
N o współczynnikach rzeczywistych. Ponadto niech x
j
będą pierwiastkami rzeczywi-
stymi tego wielomianu o krotności k
j
, gdzie k
j
∈
N dla 1
≤
j
≤
r oraz niech
j
j
z
z ,
, gdzie Imz
j
> 0, będą pierwiastkami
zespolonymi tego wielomianu o krotności l
j
, gdzie 1
≤
j
≤
s, przy czym
(
) (
)
n
l
l
k
k
s
r
=
+
+
+
+
+
...
2
...
1
1
. Wtedy
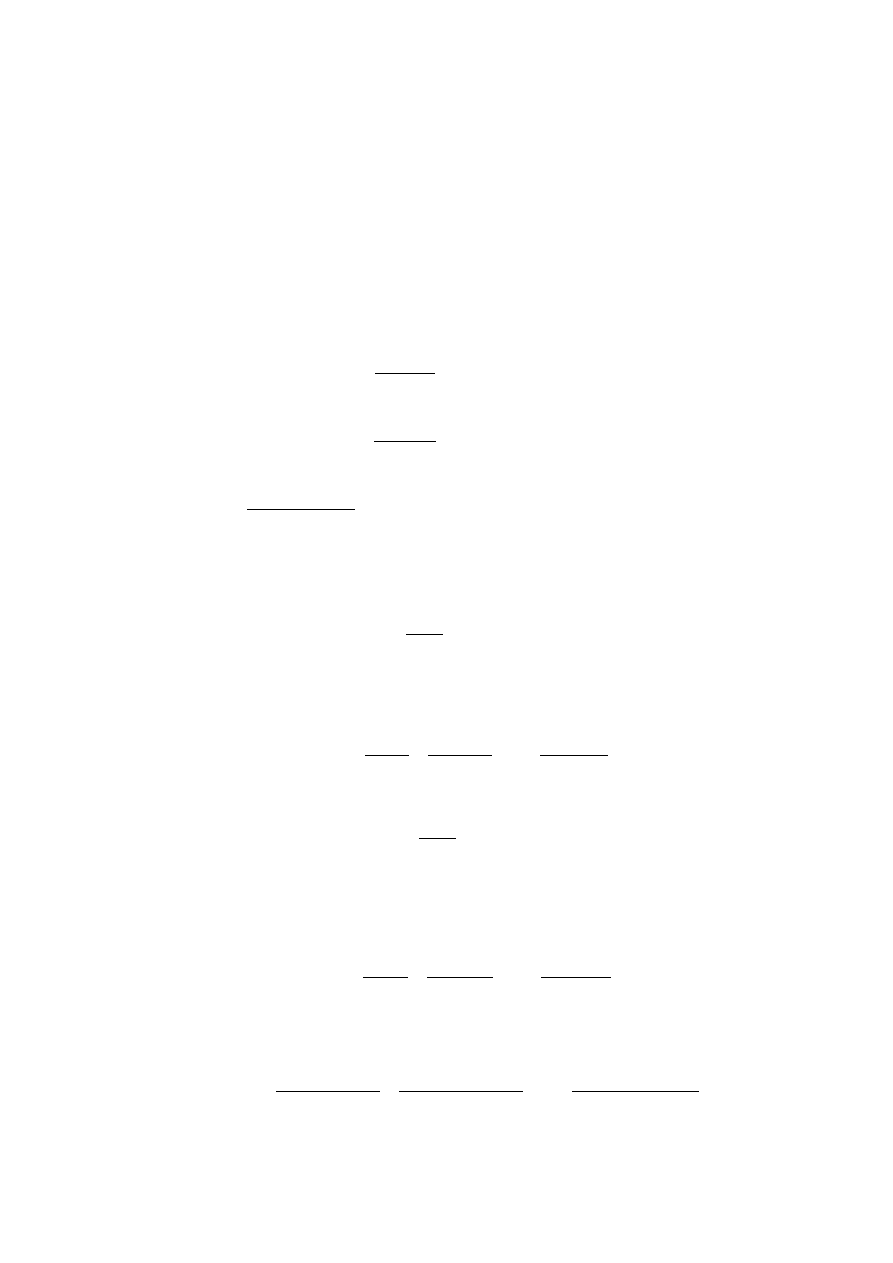
s
r
l
s
s
l
k
r
k
n
q
x
p
x
q
x
p
x
x
x
x
x
a
x
W
)
(
...
)
(
)
(
...
)
(
)
(
2
1
1
2
1
1
1
+
+
⋅
⋅
+
+
⋅
−
⋅
⋅
−
=
,
gdzie p
j
= –2Rez
j
oraz q
j
= |z
j
|
2
dla 1
≤
j
≤
s, a a
n
jest współczynnikiem wielomianu W stojącym przy x
n
.
Inaczej mówiąc, każdy wielomian rzeczywisty można przedstawić w postaci iloczynu wielomianów rzeczywistych stopnia co
najwyżej drugiego. Mówimy wówczas o rozkładzie wielomianu rzeczywistego na rzeczywiste czynniki nierozkładalne.
2.4 UŁAMKI PROSTE
Def. 2.4.1 (funkcja wymierna)
Funkcją wymierną rzeczywistą (zespoloną) nazywamy iloraz dwóch wielomianów rzeczywistych (zespolonych).
Def. 2.4.2 (funkcja wymierna właściwa)
Funkcję wymierną nazywamy właściwą, jeżeli stopień wielomianu w liczniku ułamka określającego tę funkcję jest mniejszy od
stopnia wielomianu w mianowniku.
Uwaga. Każda funkcja wymierna jest sumą wielomianu oraz funkcji wymiernej właściwej.
Def. 2.4.3 (ułamki proste)
1. Zespolonym ułamkiem prostym nazywamy zespoloną funkcję wymierną postaci:
n
a
z
A
)
(
+
, gdzie A, a
∈
C oraz n
∈
N.
2. Rzeczywistym ułamkiem prostym pierwszego rodzaju nazywamy rzeczywistą funkcję wymierną postaci:
n
a
x
A
)
(
+
, gdzie A, a
∈
R oraz n
∈
N.
3. Rzeczywistym ułamkiem prostym drugiego rodzaju nazywamy rzeczywistą funkcję wymierną postaci:
n
q
px
x
B
Ax
)
(
2
+
+
+
, gdzie p, q, A, B
∈
R oraz n
∈
N, przy czym
0
4
2
<
−
=
∆
q
p
Tw. 2.4.4 (o rozkładzie funkcji wymiernej na ułamki proste)
Każda funkcja wymierna właściwa rzeczywista (zespolona) jest sumą rzeczywistych (zespolonych) ułamków prostych.
Przedstawienie to jest jednoznaczne.
1. Zespolona funkcja wymierna właściwa postaci
)
(
)
(
z
Q
z
P
, gdzie
m
k
m
k
k
n
z
z
z
z
z
z
c
z
Q
)
(
...
)
(
)
(
)
(
2
1
2
1
−
⋅
⋅
−
−
=
,
jest sumą k
1
+ k
2
+ ... + k
m
zespolonych ułamków prostych, przy czym czynnikowi
i
k
i
z
z
)
(
−
odpowiada suma k
i
ułamków
prostych postaci:
(
)
(
)
i
i
k
i
ik
i
i
i
i
z
z
A
z
z
A
z
z
A
−
+
+
−
+
−
...
2
2
1
,
gdzie A
i1
, A
i2
, …,
i
k
Ai
∈
C dla 1
≤
i
≤
m.
2. Rzeczywista funkcja wymierna właściwa postaci
)
(
)
(
x
Q
x
P
, gdzie
s
r
l
s
s
l
l
k
r
k
k
n
q
x
p
x
q
x
p
x
q
x
p
x
x
x
x
x
x
x
a
x
Q
)
(
...
)
(
)
(
)
(
...
)
(
)
(
)
(
2
2
2
2
1
1
2
2
1
2
1
2
1
+
+
⋅
⋅
+
+
⋅
+
+
⋅
−
⋅
⋅
−
⋅
−
=
,
jest sumą k
1
+ k
2
+ ... + k
m
rzeczywistych ułamków prostych pierwszego rodzaju oraz l
1
+ l
2
+ ... + l
s
rzeczywistych ułamków
prostych drugiego rodzaju, przy czym
•
czynnikowi
i
k
i
x
x
)
(
−
odpowiada suma k
i
ułamków prostych pierwszego rodzaju postaci
(
)
(
)
i
i
k
i
ik
i
i
i
i
x
x
A
x
x
A
x
x
A
−
+
+
−
+
−
...
2
2
1
,
gdzie A
i1
, A
i2
, …,
i
k
Ai
∈
R dla 1
≤
i
≤
r.
•
czynnikowi
j
l
j
j
q
x
p
x
)
(
2
+
+
odpowiada suma l
j
ułamków prostych drugiego rodzaju postaci
(
)
(
)
j
j
j
l
j
j
jl
jl
j
j
j
j
j
j
j
j
q
x
p
x
C
x
B
q
x
p
x
C
x
B
q
x
p
x
C
x
B
+
+
+
+
+
+
+
+
+
+
+
+
2
2
2
2
2
2
1
1
...
,
gdzie
R
C
C
C
B
B
B
j
j
jl
j
j
jl
j
j
∈
,...
,
,
,...,
,
2
1
2
1
dla 1
≤
j
≤
s.
3. MACIERZE I WYZNACZNIKI
3.1 MACIERZE – PODSTAWOWE OKREŚLENIA
Def. 3.1.1 (macierz rzeczywista i zespolona)
Macierzą rzeczywistą (zespoloną) wymiaru m
×
n, gdzie m, n
∈
N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywi-
stych (zespolonych) ustawionych w m wierszach i n kolumnach.
Uwaga. Macierze będziemy oznaczali dużymi literami alfabetu np. A, B, X itp. Element macierzy A stojący w i–tym wierszu
oraz w j–tej kolumnie oznaczamy przez a
ij
. Macierz A można także zapisywać w postaci
n
m
ij
a
×
]
[
lub [a
ij
], gdy znany jest jej
wymiar. Macierze A lub B są równe, gdy mają te same wymiary m
×
n oraz a
ij
= b
ij
dla każdego 1
≤
i
≤
m oraz 1
≤
j
≤
n.
Def. 3.1.2 (rodzaje macierzy)
1. Macierz wymiaru m
×
n, której wszystkie elementy są równe 0 nazywamy macierzą zerową wymiaru m
×
n i oznaczmy
n
m
×
0
lub przez
0
, gdy znamy jej wymiar.
0
0
0
0
0
0
0
0
0
2. Macierz, której liczba wierszy równa się liczbie kolumn nazywamy macierzą kwadratową. Liczbę wierszy (kolumn)
nazywamy wtedy stopniem macierzy kwadratowej. Elementy macierzy, które mają ten sam numer wiersza co kolumny,
tworzą główną przekątną macierzy.
3. Macierz kwadratową stopnia n
≥
2, w której wszystkie elementy stojące nad główną przekątną są równe 0, nazywamy
macierzą trójkątną dolną stopnia n.
nn
n
n
n
a
a
a
a
a
a
a
a
a
a
3
2
1
33
32
31
22
21
11
0
0
0
0
0
0
Podobnie określa się macierz trójkątną górną.
nn
n
n
n
a
a
a
a
a
a
a
a
a
a
0
0
0
0
0
0
3
33
2
23
22
1
13
12
11
4. Macierz kwadratową stopnia n, w której wszystkie elementy nie stojące na głównej przekątnej są równe 0, nazywamy
macierzą diagonalną lub przekątniową stopnia n.
nn
a
a
a
a
0
0
0
0
0
0
0
0
0
0
0
0
33
22
11
Macierz diagonalną stopnia n, w której wszystkie elementy głównej przekątnej są równe 1, nazywamy macierzą
jednostkową stopnia n. Macierz jednostkową stopnia n oznaczamy przez I
n
lub przez I, gdy znany jest jej stopień.
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
3.2 DZIAŁANIA NA MACIERZACH
Def. 3.2.1 (suma i różnica macierzy)
Niech A = [a
ij
] i B = [b
ij
] będą macierzami wymiaru m
×
n. Sumą (różnicą) macierzy A i B nazywamy macierz C = [c
ij
], której
elementy określone są wzorem:
ij
ij
def
ij
b
a
c
+
=
−
=
ij
ij
def
ij
b
a
c
dla 1
≤
i
≤
m oraz 1
≤
j
≤
n. Piszemy wtedy C = A + B (C = A – B).
Def. 3.2.2 (mnożenie macierzy przez liczbę)
Niech A = [a
ij
] będzie macierzą wymiaru m
×
n oraz niech
α
będzie liczbą rzeczywistą lub zespoloną. Iloczynem macierzy A
przez liczbę
α
nazywamy macierz B = [b
ij
], której elementy są określone wzorem:
ij
def
ij
a
b
α
=
dla 1
≤
i
≤
m oraz 1
≤
j
≤
n. Piszemy wtedy B =
α
A.
Fakt 3.2.3 (własności działań na macierzach)
Niech A, B, C będą dowolnymi macierzami tego samego wymiaru rzeczywistymi lub zespolonymi oraz niech
α
,
β
będą
odpowiednio liczbami rzeczywistymi lub zespolonymi. Wtedy
1. A + B = B + A
5.
α
(A + B) =
α
A +
α
B
2. A + (B + C) = (A + B) + C
6. (
α
+
β
)A =
α
A +
β
A
3. A + 0 = 0 + A = A
7. 1
⋅
A = A
4. A + (–A) = 0
8. (
αβ
)A =
α
(
β
A)
Def. 3.2.4 (iloczyn macierzy)
Niech A = [a
ij
] ma wymiar m
×
n, a macierz B = [b
ij
] wymiar n
×
k. Iloczynem macierzy A i B nazywamy macierz C = [c
ij
],
wymiaru m
×
k, której elementy określone są wzorem:
nj
in
j
i
j
i
def
ij
b
a
b
a
b
a
c
+
+
+
=
...
2
2
1
1
dla 1
≤
i
≤
m oraz 1
≤
j
≤
n. Piszemy wtedy C = AB.
Uwaga. Element c
ij
iloczynu macierzy A i B otrzymujemy sumując iloczyny odpowiadających sobie elementów i–tego wiersza
macierzy A i j–tej kolumny macierzy B. Iloczyn macierzy A i B można obliczyć tylko wtedy, gdy liczba kolumn macierzy A
równa się liczbie wierszy macierzy B.
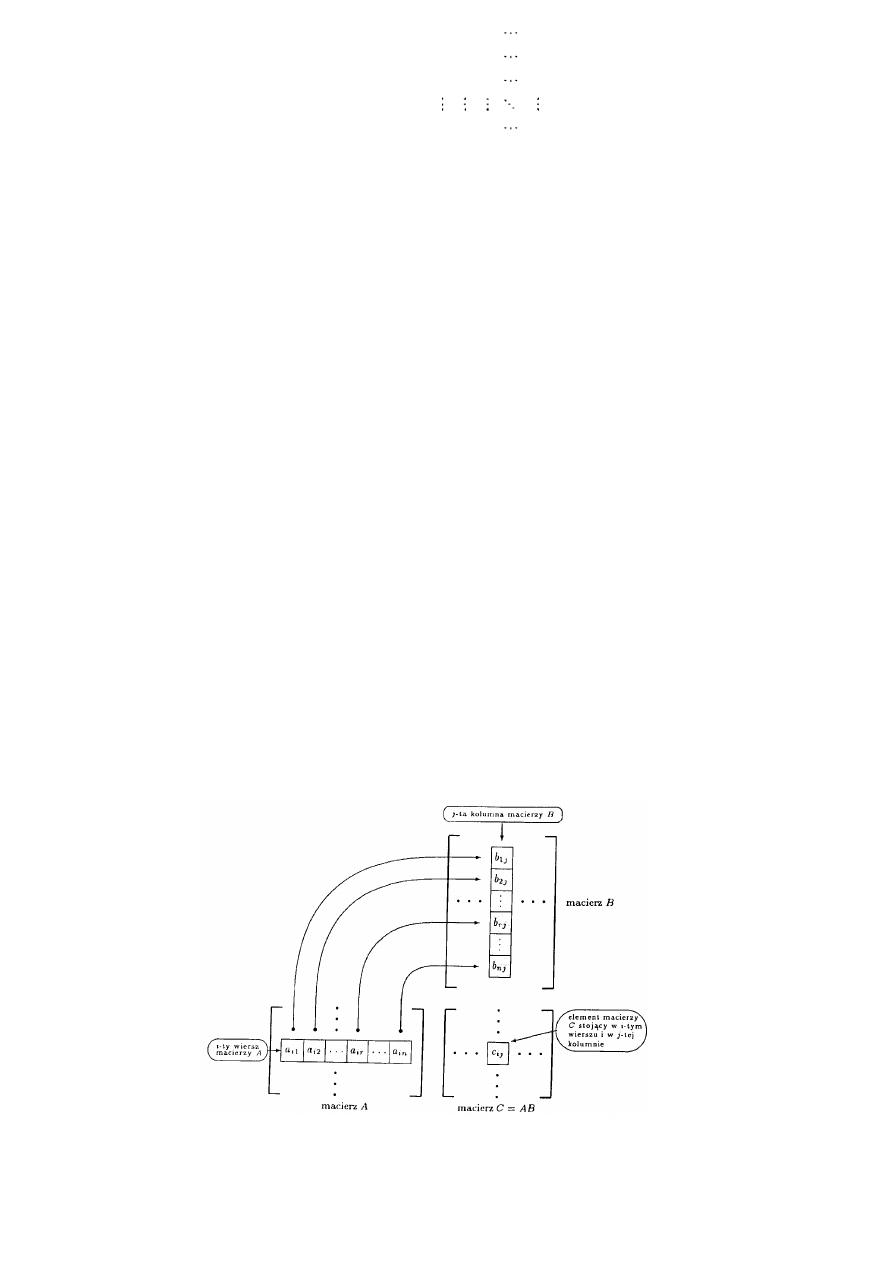
Rys. 3.2.1 Schemat obliczania elementów iloczynu macierzy A i B
Fakt 3.2.5 (własności iloczynu macierzy)
1. Niech macierz A ma wymiar m
×
n, a macierze B i C wymiar n
×
k. Wtedy

AC
AB
C
B
A
+
=
+
)
(
.
2. Niech macierze A, B mają wymiar m
×
n, a macierz C wymiar n
×
k. Wtedy
BC
AC
C
B
A
+
=
+
)
(
.
3. Niech macierz A ma wymiar m
×
n, a macierz B wymiar n
×
k oraz niech
α
będzie liczbą rzeczywistą lub zespoloną. Wtedy
)
(
)
(
)
(
AB
B
A
B
A
α
α
α
=
=
.
4. Niech macierz A ma wymiar m
×
n, macierz B ma wymiar n
×
k, a macierz C wymiar k
×
l. Wtedy
)
(
)
(
BC
A
C
AB
=
.
5. Niech macierz A ma wymiar m
×
n. Wtedy
A
A
I
AI
m
n
=
=
.
Uwaga. Własności podane w punktach 1 i 2 nazywamy rozdzielnością dodawania względem mnożenia, a własność podaną w
punkcie 4 łącznością mnożenia. Mnożenie macierzy kwadratowych nie jest przemienne, bowiem na ogół AB
≠
BA. Zamiast
czynników
n
A
AA...
będziemy pisali A
n
.
Def. 3.2.6 (macierz transponowana)
Niech A = [a
ij
] będzie macierzą wymiaru m
×
n. Macierzą transponowaną do macierzy A nazywamy macierz B = [b
ij
] wymiaru
n
×
m określoną wzorem:
ji
def
ij
a
b
=
dla 1
≤
i
≤
m oraz 1
≤
j
≤
n. Macierz transponowaną do macierzy A oznaczamy A
T
.
Uwaga. Przy transponowaniu, kolejne wiersze macierzy wyjściowej stają się kolejnymi kolumnami macierzy transponowanej.
Ilustrujemy to na przykładzie macierzy wymiaru 3
×
4.
=
=
34
24
14
33
23
13
32
22
12
31
21
11
34
33
32
31
24
23
22
21
14
13
12
11
,
a
a
a
a
a
a
a
a
a
a
a
a
A
a
a
a
a
a
a
a
a
a
a
a
a
A
T
.
Fakt 3.2.7 (własności transpozycji macierzy)
1. Niech A i B będą macierzami wymiaru m
×
n. Wtedy
T
T
T
B
A
B
A
+
=
+
)
(
.
2. Niech A będzie macierzą wymiaru m
×
n oraz niech
α
będzie liczbą rzeczywistą lub zespoloną. Wtedy
( )
A
A
T
T
=
oraz
( )
T
T
A
A
α
α
=
.
3. Niech A będzie macierzą wymiaru m
×
n, a B macierzą wymiaru n
×
k. Wtedy
T
T
T
A
B
AB
=
)
(
.
4. Niech A będzie macierzą kwadratową oraz niech r
∈
N. Wtedy
r
T
T
r
A
A
)
(
)
(
=
.
Def. 3.2.8 (macierz symetryczna i antysymetryczna)
Niech A będzie macierzą kwadratową.
1. Macierz A jest symetryczna wtedy i tylko wtedy, gdy
A
A
T
=
.
2. Macierz A jest antysymetryczna wtedy i tylko wtedy, gdy
A
A
T
−
=
.
Uwaga. Macierz jest symetryczna, gdy jej elementy położone symetrycznie względem głównej przekątnej są sobie równe.
Macierz jest antysymetryczna, gdy jej elementy położone symetrycznie względem głównej przekątnej różnią się tylko znakiem,
a elementy głównej przekątnej są równe 0.
Fakt 3.2.9 (własności macierzy symetrycznych i antysymetrycznych)
1. Niech A będzie dowolną macierzą kwadratową. Wtedy
a) macierz A + A
T
jest symetryczna,
b) macierz A – A
T
jest antysymetryczna.
2. Niech A będzie dowolną macierzą. Wtedy macierze AA
T
i A
T
A są symetryczne.
3. Każdą macierz kwadratową można jednoznacznie przedstawić w postaci sumy macierzy symetrycznej i antysymetrycznej:
(
) (
)
T
T
A
A
A
A
A
−
+
+
=
2
1
2
1
.
3.3 DEFINICJA INDUKCYJNA WYZNACZNIKA
Def. 3.3.1 (wyznacznik macierzy)
Wyznacznikiem macierzy kwadratowej nazywamy funkcję, która każdej macierzy rzeczywistej (zespolonej) A = [a
ij
] przypisuje
liczbę rzeczywistą (zespoloną) detA. Funkcja ta jest określona wzorem indukcyjnym:
1. jeżeli macierz A ma stopień n = 1, to
11
det
a
A
=
,
2. jeżeli macierz A ma stopień n
≥
2, to
n
n
n
A
a
A
a
A
a
A
1
1
1
12
12
2
1
11
11
1
1
det
)
1
(
...
det
)
1
(
det
)
1
(
det
+
+
+
−
+
+
−
+
−
=
gdzie A
ij
oznacza macierz otrzymaną z macierzy A przez skreślenie i–tego wiersza i j–tej kolumny.
Uwaga. Wyznacznik macierz A oznaczamy także przez det[a
ij
] lub |A|, a w formie rozwiniętej przez
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
2
1
2
22
12
1
12
11
det
lub
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
2
1
2
22
12
1
12
11
.
Będziemy mówili wymiennie stopień wyznacznika
↔
stopień macierzy, element wyznacznika
↔
element macierzy, wiersz
wyznacznika
↔
wiersz macierzy, kolumna wyznacznika
↔
kolumna macierzy.
Fakt 3.3.2 (reguły obliczania wyznaczników 2-go i 3-go stopnia)
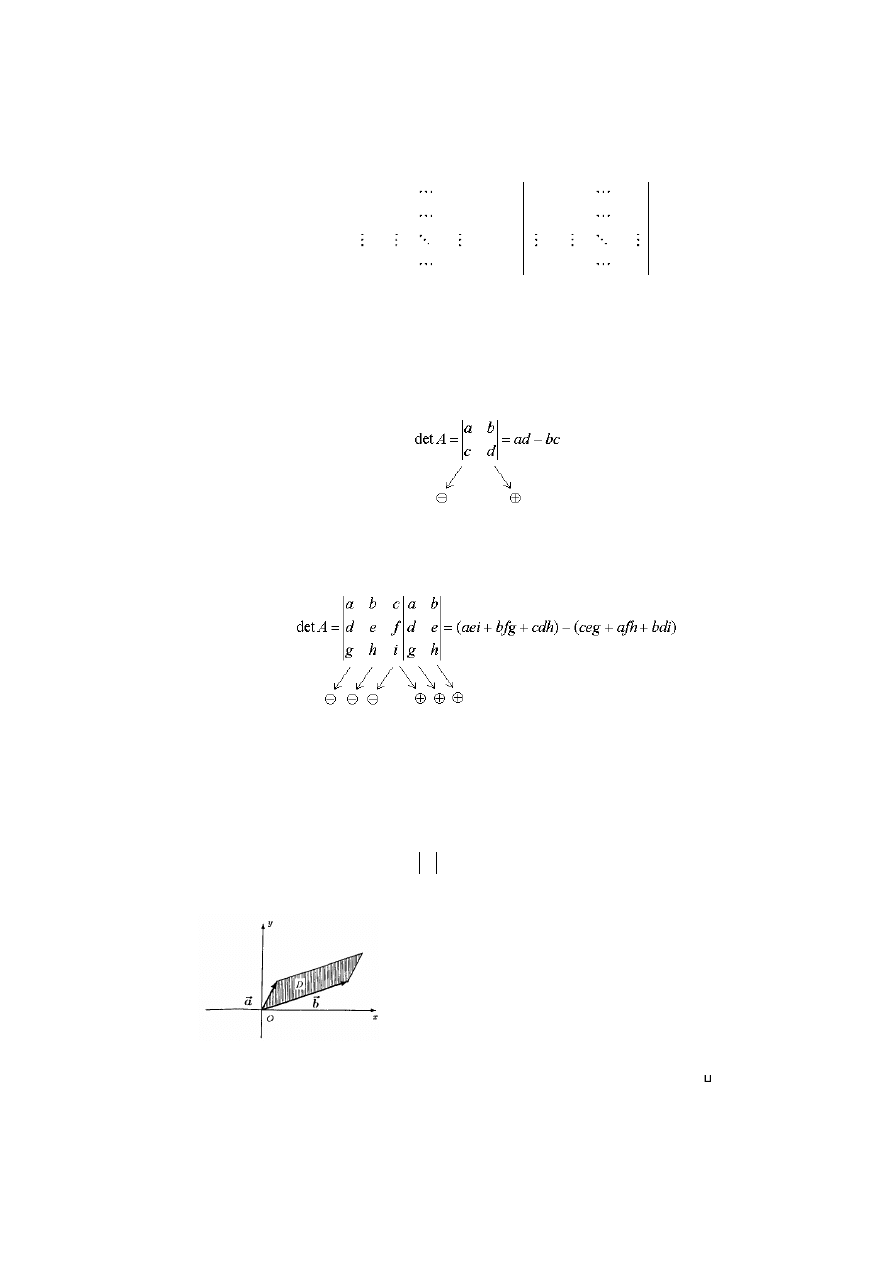
1. Niech
=
d
c
b
a
A
będzie macierzą stopnia 2. Wtedy
.
2. Niech
=
i
h
g
f
e
d
c
b
a
A
będzie nacierzą stopnia 3. Wtedy
.
Uwaga. Podany wyżej sposób obliczania wyznaczników stopnia 3 nazywamy regułą Sarrusa. Ten sposób obliczania
wyznaczników nie przenosi się na wyznaczniki wyższych stopni.
Fakt 3.3.3 (interpretacja geometryczna wyznaczników 2-go i 3-go stopnia)
1. Niech D oznacza równoległobok rozpięty na wektorach
)
,
(
1
1
y
x
a
=
,
)
,
(
2
2
y
x
b
=
(rys. 3.3.1). Pole |D| tego
równoległoboku wyraża się wzorem:
|
det
|
2
2
1
1
=
y
x
y
x
D
.
Rys. 3.3.1 Interpretacja geometryczna wyznacznika drugiego stopnia
2. Niech V oznacza równoległościan rozpięty na wektorach
)
,
,
(
1
1
1
z
y
x
a
=
,
)
,
,
(
2
2
2
z
y
x
b
=
,
)
,
,
(
3
3
3
z
y
x
c
=
(rys. 3.3.2).
Objętość |V| tego równoległościanu wyraża się wzorem:
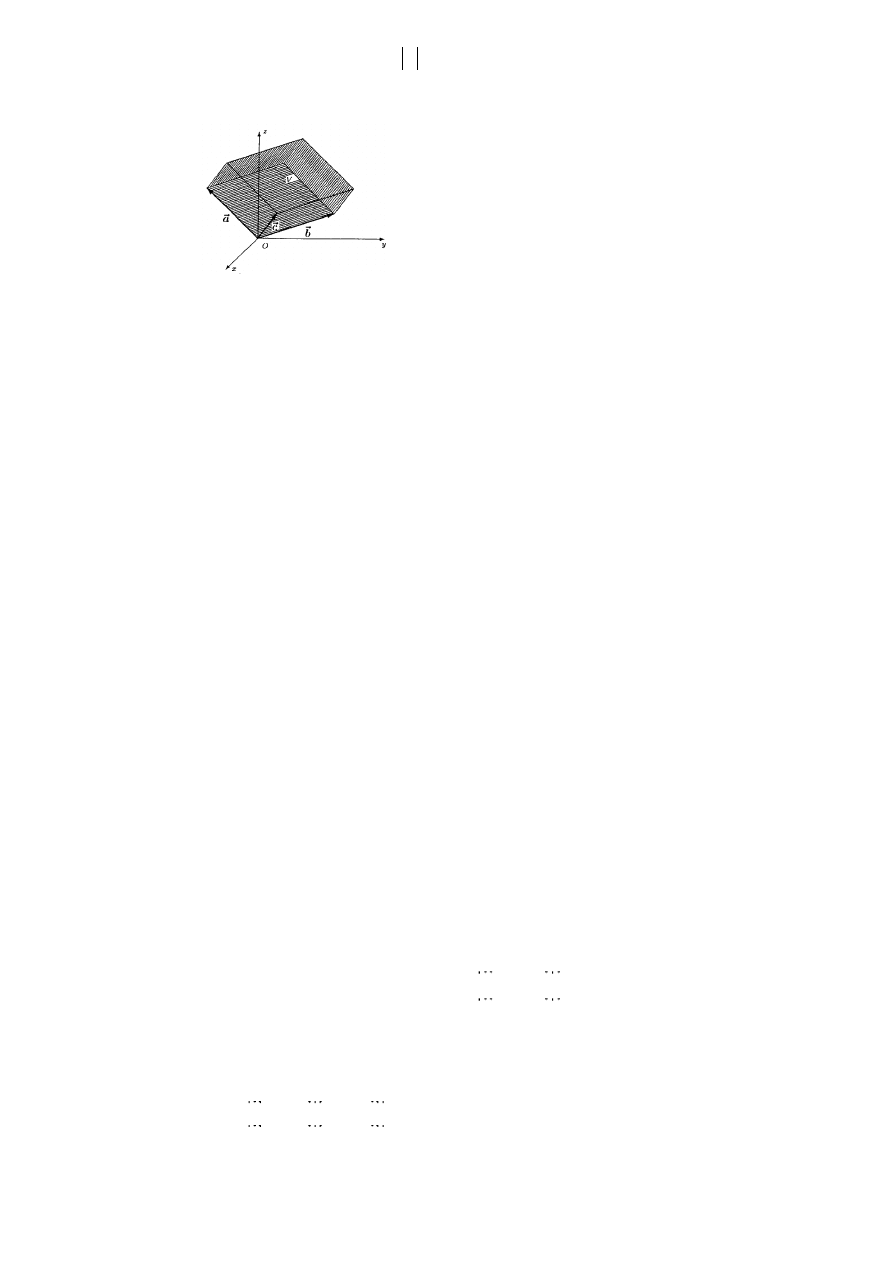
|
det
|
3
3
3
2
2
2
1
1
1
=
z
y
x
z
y
x
z
y
x
V
.
Rys. 3.3.2 Interpretacja geometryczna wyznacznika trzeciego stopnia
Def. 3.3.4 (dopełnienie algebraiczne)
Niech A = [a
ij
] będzie macierzą kwadratową stopnia n
≥
2. Dopełnieniem algebraicznym elementu a
ij
macierzy A nazywamy
liczbę:
ij
j
i
def
ij
A
D
det
)
1
(
+
−
=
,
gdzie A
ij
oznacza macierz stopnia n – 1 powstałą przez skreślenie i–tego wiersza i j–tej kolumny macierzy A.
Tw. 3.3.5 (rozwinięcia Laplace’a wyznacznika)
Niech A będzie macierzą kwadratową stopnia n
≥
2 oraz niech liczby 1
≤
i, j
≤
n będą ustalone. Wtedy wyznacznik macierzy A
można obliczyć ze wzorów:
1.
in
in
i
i
i
i
D
a
D
a
D
a
A
+
+
+
=
...
det
2
2
1
1
.
Inaczej mówiąc, wyznacznik macierzy jest równy sumie iloczynów elementów i–tego wiersza i ich dopełnień algebraicznych.
Wzór ten nazywamy rozwinięciem Laplace’a wyznacznika względem i–tego wiersza.
2.
nj
nj
j
j
j
j
D
a
D
a
D
a
A
+
+
+
=
...
det
2
2
1
1
.
Inaczej mówiąc, wyznacznik macierzy jest równy sumie iloczynów elementów j–tej kolumny i ich dopełnień algebraicznych.
Wzór ten nazywamy rozwinięciem Laplace’a wyznacznika względem j–tej kilumny.
Uwaga. Dla ustalonych liczb 1
≤
r, s
≤
n, gdzie r
≠
s, prawdziwe są wzory:
0
...
0
...
2
2
1
1
2
2
1
1
=
+
+
+
=
+
+
+
nr
ns
r
s
r
s
rn
sn
r
s
r
s
D
a
D
a
D
a
D
a
D
a
D
a
.
Inaczej mówiąc, suma iloczynów elementów dowolnego wiersza i dopełnień algebraicznych elementów innego wiersza jest
równa 0. Podobnie, suma iloczynów dowolnej kolumny i odpowiadających im dopełniń algebraicznych innej kolumny jest
równa 0.
Fakt 3.3.6 (wyznacznik macierzy trójkątnej)
Niech A = [a
ij
] będzie macierzą trójkątną dolną lub górną stopnia n
≥
2. Wtedy
nn
a
a
a
A
⋅
⋅
⋅
=
...
det
22
11
.
Inaczej mówiąc, wyznacznik macierzy trójkątnej jest równy iloczynowi elementów stojących na głównej przekątnej.
3.4 DEFINICJA PERMUTACYJNA WYZNACZNIKA
*
Def. 3.4.1 (permutacja)
Permutacją n–elementową, gdzie n
∈
N, nazywamy każde różnowartościowe odwzorowanie p zbioru {1, 2, …, n} na siebie.
Permutację taką zapisujemy w postaci
=
n
i
p
p
p
p
n
i
p
2
1
2
1
,
gdzie p
i
oznacza wartość permutacji p dla i, 1
≤
i
≤
n. Zbiór wszystkich permutacji n–elementowych oznaczamy przez P
n
.
Uwaga. Istnieje
n!
różnych permutacji n–elementowych.
Def. 3.4.2 (inwersja, znak permutacji)
Niech
=
n
j
i
p
p
p
p
p
n
j
i
p
2
1
2
1
będzie permutacją n–elementową. Para {p
i
, p
j
} elementów tej permutacji
tworzy inwersję, gdy
j
i
p
p
>
oraz
j
i
<
.
Znak permutacji p jest określony wzorem
k
def
p
)
1
(
)
sgn(
−
=
,
gdzie k oznacza liczbę par elementów tej permutacji, które tworzą inwersje.
Def. 3.4.3 (wyznacznik macierzy)
Niech A = [a
ij
] będzie macierzą kwadratową stopnia n. Wyznacznikiem macierzy A nazywamy liczbę detA określoną wzorem:
∑
∈
=
n
n
P
p
np
p
p
def
a
a
a
p
A
...
)
sgn(
det
2
1
2
1
,
gdzie
=
n
p
p
p
n
p
2
1
2
1
, a sumowanie obejmuje wszystkie (tj. n!) permutacje n–elementowe.
Uwaga. Obie definicje wyznacznika, indukcyjna i permutacyjna, są równoważne.
3.5 WŁASNOŚCI WYZNACZNIKÓW
Fakt 3.5.1 (własności wyznaczników)
1. Wyznacznik macierzy kwadratowej mającej kolumnę (wiersz) złożoną z samych zer jest równy 0.
0
0
0
0
0
2
1
2
22
21
1
12
11
=
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
2. Wyznacznik macierzy kwadratowej zmieni znak jeżeli między sobą przestawimy dwie kolumny (wiersze).
ni
nk
i
k
i
k
nk
ni
k
i
k
i
a
a
a
a
a
a
a
a
a
a
a
a
2
2
1
1
2
2
1
1
−
=
.
3. wyznacznik macierzy kwadratowej mającej dwie jednakowe kolumny (wiersze) jest równy 0.
0
=
ω
ω
β
β
α
α
.
4. Jeżeli wszystkie elementy pewnej kolumny (wiersza) macierzy kwadratowej zawierają wspólny czynnik, to czynnik ten
można wyłączyć przed wyznacznik tej macierzy.
nn
ni
n
n
n
i
n
i
nn
ni
n
n
n
i
n
i
a
a
a
a
a
a
a
a
a
a
a
a
c
a
ca
a
a
a
ca
a
a
a
ca
a
a
2
1
2
2
22
21
1
1
12
11
2
1
2
2
22
21
1
1
12
11
=
.
Ponadto
nn
ni
n
n
n
i
n
i
n
nn
ni
n
n
n
i
n
i
a
a
a
a
a
a
a
a
a
a
a
a
c
ca
ca
ca
ca
ca
ca
ca
ca
ca
ca
ca
ca
2
1
2
2
22
21
1
1
12
11
2
1
2
2
22
21
1
1
12
11
=
.
5. Wyznacznik macierzy kwadratowej, której elementy pewnej kolumny (wiersza) są sumami dwóch składników jest równy
sumie wyznaczników macierzy, w których elementy tej kolumny (wiersza) są zastąpione tymi składnikami.
nn
ni
n
n
n
i
n
i
nn
ni
n
n
n
i
n
i
nn
ni
ni
n
n
n
i
i
n
i
i
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
/
2
1
2
/
2
22
21
1
/
1
12
11
2
1
2
2
22
21
1
1
12
11
/
2
1
2
/
2
2
22
21
1
/
1
1
12
11
+
=
+
+
+
.
6. Wyznacznik macierzy nie zmieni się, jeżeli do elementów dowolnej kolumny (wiersza) dodamy odpowiadające im
elementy innej kolumny (innego wiersza) tej macierzy pomnożone przez dowolną liczbę.
nn
nk
nk
nj
n
n
n
k
k
j
n
k
k
j
nn
nk
nj
n
n
n
k
j
n
k
j
a
a
ca
a
a
a
a
a
ca
a
a
a
a
a
ca
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
+
+
+
=
2
1
2
2
2
2
22
21
1
1
1
1
12
11
2
1
2
2
2
22
21
1
1
1
12
11
.

Ogólnie: wyznacznik macierzy nie zmieni się, jeżeli do elementów dowolnego wiersza (kolumny) dodamy sumę odpowia-
dających im elementów innych wierszy (kolumn) tej macierzy pomnożonych przez dowolną liczbę.
7. Wyznaczniki macierzy kwadratowej i jej transpozycji są równe.
nn
n
n
n
n
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
2
1
2
22
12
1
21
11
2
1
2
22
21
1
12
11
=
Uwaga. Korzystając z powyższych własności wyznaczników można istotnie uprościć jego obliczanie. W tym celu w wybranym
wierszu lub kolumnie wyznacznika staramy się uzyskać możliwie najwięcej zer. Do oznaczenia podanych wyżej operacji na
macierzach będziemy stosowali następujące symbole:
1. w
i
↔
w
j
– oznacza zamianę między sobą i–tego oraz j–tego wiersza,
2. k
i
↔
k
j
– oznacza zamianę między sobą i–tej oraz j–tej kolumny,
3. cw
i
– oznacza pomnożenie i–tego wiersza przez liczbę c,
4. ck
i
– oznacza pomnożenie i–tej kolumny przez liczbę c,
5. w
i
+ cw
j
– oznacza dodanie do elemnetów i–tego wiersza odpowiadających im elementów j–tego wiersza pomnożonych
przez liczbę c,
6. k
i
+ ck
j
– oznacza dodanie do elemnetów i–tej kolumny odpowiadających im elementów j–tej kolumny pomnożonych przez
liczbę c,
Wymienione wyżej przekształcenia macierzy nazywamy operacjami elementarnymi.
Fakt 3.5.2 (algorytm Chió obliczania wyznaczników)
Niech A = [a
ij
] będzie macierzą kwadratową stopnia n
≥
3 oraz niech a
11
≠
0. Wówczas
⋅
=
−
/
/
3
/
2
/
3
/
33
/
32
/
2
/
23
/
22
2
11
det
)
(
1
det
nn
n
n
n
n
n
a
a
a
a
a
a
a
a
a
a
A
, gdzie
=
ij
i
j
ij
a
a
a
a
a
1
1
11
/
det
dla i, j = 2, 3, …, n.
Uwaga. Algorytm Chió stosujemy głównie do obliczania wyznaczników macierzy niwielkich stopni, których elementy są
liczbami całkowitymi. Algorytm ten w prosty sposób pozwala obniżać stopnie obliczanych wyznaczników.
/
/
/
3
/
2
/
/
/
3
/
2
/
3
/
3
/
33
/
32
/
2
/
2
/
23
/
22
2
11
3
2
3
2
3
3
33
32
2
2
23
22
1
1
13
12
1
1
31
21
11
)
(
1
nn
nj
n
n
in
ij
i
i
n
j
n
j
n
nn
nj
n
n
in
ij
i
i
n
j
n
j
n
j
n
i
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
↓
→
←
↑
=
↓
→
←
↑
→
←
↓
↑
−
, gdzie
=
ij
i
j
ij
a
a
a
a
a
1
1
11
/
.
Rys. 3.5.1 Schemat algorytmu Chió obliczania wyznaczników
Tw. 3.5.3 (Cauchy’ego o wyznaczniku iloczynu macierzy)
Niech A i B będą macierzami kwadratowymi tego samego stopnia. Wtedy
B
A
B
A
det
det
)
det(
⋅
=
⋅
.
Fakt 3.5.4 (wyznacznik Vandermonde’a)
Niech n
≥
2 oraz niech z
1
, z
2
, …, z
n
będą liczbami zespolonymi. Wtedy
∏
≤
<
≤
−
−
−
−
=
=
n
l
k
k
l
n
n
n
n
n
n
def
n
z
z
z
z
z
z
z
z
z
z
z
z
z
z
V
1
1
2
1
2
2
2
2
1
1
2
1
1
2
1
)
(
1
1
1
)
,...,
,
(
.
Jeżeli liczby z
1
, z
2
, …, z
n
są parami różne, to
0
)
,...,
,
(
2
1
≠
n
z
z
z
V
.
3.6 MACIERZ ODWROTNA
Def. 3.6.1 (macierz odwrotna)
Niech A będzie macierzą stopnia n. Macierzą odwrotną do macierzy A nazywamy macierz B spełniającą warunek:
AB = BA = I
n
,

gdzie I
n
oznacza macierz jednostkową stopnia n. macierz odwrotną do macierzy A oznaczamy przez A
–1
.
Uwaga. Jeżeli macierz A ma macierz odwrotną, to nazywamy ją odwracalną i wówczas detA
≠
0. Macierz odwrotna do danej
macierzy jest określona jednoznacznie.
Def. 3.6.2 (macierz osobliwa i nieosobliwa)
Macierz kwadratową A nazywamy macierzą osobliwą, gdy
0
det
=
A
.
W przeciwnym przypadku mówimy, że macierz A jest nieosobliwa.
Fakt 3.6.3 (warunek odwracalności macierzy)
Macierz kwadratowa jest odwracalna wtedy i tylko wtedy, gdy jest nieosobliwa.
Tw. 3.6.4 (o postaci macierzy odwrotnej)
Niech macierz A = [a
ij
] stopnia n będzie nieosobliwa. Wtedy
T
nn
n
n
n
n
D
D
D
D
D
D
D
D
D
A
A
=
−
2
1
2
22
21
1
12
11
1
det
1
,
gdzie D
ij
oznaczają dopełnienia algebraiczne elementów a
ij
macierzy A.
Uwaga. Dla macierzy nieosobliwej
=
d
c
b
a
A
wzór na macierz odwrotną ma postać:
−
−
−
=
−
a
c
b
d
bc
ad
A
1
1
.
Fakt 3.6.5 (własności macierzy odwrotnych)
Niech macierze A i B tego samego stopnia będą odwracalne oraz niech
α
∈
C\{0}. Wtedy macierze A
–1
, A
T
, AB,
α
A także są
odwracalne i prawdziwe są równości:
1.
( )
(
)
1
1
det
det
−
−
=
A
A
4.
( )
1
1
1
−
−
−
=
A
B
AB
2.
( )
A
A
=
−
−
1
1
5.
( )
( )
1
1
1
−
−
=
A
A
α
α
3.
( ) ( )
T
T
A
A
1
1
−
−
=
Fakt 3.6.6 (bezwyznacznikowy sposób znajdowania macierzy odwrotnej)
Niech A będzie macierzą nieosobliwą. Aby znaleźć macierz odwrotną do macierzy A postępujemy w następujący sposób. Z
prawej strony macierzy A dopisujemy macierz jednostkową I tego samego stopnia. Na wierszach otrzymanej w ten sposób
macierzy blokowej [A|I] będziemy wykonywać następujące operacje elementarne:
1. przestawiać między sobą dwa dowolne wiersze (w
i
↔
w
j
),
2. dowlny wiersz mnożyć przez stałą różną od zera (cw
i
),
3. do elementów dowolnego wiersza dodawać sumy odpowiadających im elementów innych wierszy pomnożonych przez
dowolne liczby (w
i
+ cw
j
).
Przy pomocy tych operacji sprowadzamy macierz blokową [A|I] do postaci [I|B]. Macierz B jest wtedy macierzą odwrotną do
macierzy A, tj. B = A
–1
.
[
]
[
]
1
wierszach
na
ania
dzia
|
|
−
→
A
I
I
A
l
Rys. 3.6.1 Schemat bezwyznacznikowego sposobu znajdowania macierzy odwrotnej.
3.7 ALGORYTM SPROWADZANIA MACIERZY DO POSTACI JEDNOSTKOWEJ
Fakt 3.7.1 (algorytm Gaussa)
Niech A będzie macierzą stopnia n
≥
2 o wyznaczniku różnym od zera. Macierz tę można przekształcić do macierzy
jednostkowej I
n
wykonując na jej wierszach następujące operacje elementarne:
1. zamiana między sobą dwóch dowolnych wierszy,
2. mnożenie dowolnego wiersza przez liczbę różną od zera,
3. dodawanie do elementów dowolnego wiersza odpowiadających im elementów innego wiersza pomnożonych przez
dowolną liczbę.
Macierz jednostkową uzyskamy w dwóch krokach:
I krok. Otrzymanie macierzy trójkątnej górnej z jedynkami na głównej przekątnej postaci:

1
0
0
0
1
0
0
1
0
1
3
2
23
1
13
12
n
n
n
b
b
b
b
b
b
Operacje elementarne wykonujemy tak, aby kolejne kolumny macierzy A uzyskały przedstawioną powyżej postać.
Przekształcenia zaczynamy od uzyskania odpowiedniej postaci pierwszej kolumny. Jeżeli a
11
≠
0, to wiersze w
1
, w
2
, …, w
n
macierzy A przekształacamy kolejno na wiersze
/
/
2
/
1
,...,
,
n
w
w
w
według wzorów:
−
=
−
=
=
/
1
1
/
/
1
21
2
/
2
11
1
/
1
w
a
w
w
w
a
w
w
a
w
w
n
n
n
.
Jeżeli natomiast a
11
= 0, to wiersze macierzy A przestawiamy tak, aby w jej lewym górnym rogu znalazł się element niezerowy i
dalej wykonujemy wymienione wcześniej operacje.
Kolejne kolumny z jedynkami na przekątnej i zerami poniżej przekątnej uzyskujemy stosując przedstawione wyżej postępowa-
nie do macierzy coraz niższych stopni, począwszy od stopnia n – 1 aż do stopnia 1 włącznie.
II krok. Otrzymanie macierzy jednostkowej postaci:
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
Wiersze
/
1
/
1
/
,...,
,
w
w
w
n
n
−
otrzymanej macierzy trójkątnej przekształcamy kolejno na wiersze
//
1
//
1
//
,...,
,
w
w
w
n
n
−
macierzy jednost-
kowej w następujący sposób:
−
−
−
−
=
−
−
=
−
=
=
−
−
−
−
−
−
−
−
−
//
1
//
3
13
//
2
12
/
1
//
1
//
2
//
1
1
2
/
22
//
2
//
1
/
1
//
1
/
//
...
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
w
b
w
b
w
b
w
w
w
b
w
b
w
w
w
b
w
w
w
w
.
Uwaga. Macierzy o wyznaczniku 0 nie można sprowadzić do macierzy jednostkowej. Algorytm Gaussa jest bardzo wygodnym
narzędziem przy obliczaniu wyznaczniow, odwracaniu macierzy, określaniu ich rzędów oraz przy rozwiązywaniu układów
równań liniowych.
4. UKŁADY RÓWNAŃ LINIOWYCH
4.1 PODSTAWOWE OKREŚLENIA
Def. 4.1.1 (układ równań liniowych, rozwiązanie układu równań)
Układem m równań liniowych z n niewiadomymi x
1
, x
2
, …, x
n
, gdzie m, n
∈
N, nazywamy układ równań postaci:
=
+
+
+
=
+
+
+
=
+
+
+
m
n
mn
m
m
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
...
...
...
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
,
gdzie a
ij
∈
R, b
i
∈
R dla 1
≤
i
≤
m, 1
≤
j
≤
n.
Rozwiązaniem układu równań liniowych nazywamy każdy ciąg (x
1
, x
2
, …, x
n
) n liczb rzeczywistych spełniających ten układ.
Układ równań, który nie ma rozwiązań nazywamy układem sprzecznym.
Uwaga. Powyższy układ równanń liniowych można zapisać w postaci macierzowej:
AX = B,
gdzie
=
mn
m
m
n
n
def
a
a
a
a
a
a
a
a
a
A
2
1
2
22
12
1
12
11
,
=
n
def
x
x
x
X
2
1
,
=
m
def
b
b
b
B
2
1
.

Macierz A nazywamy macierzą główną układu równań liniowych, macierz X macierzą (kolumną) niewiadomych, a B macierzą
(kolumną) wyrazów wolnych. Rozważa się także układy równań liniowych, w których macierze A, X oraz B są zespolone. W
przypadku „małej liczby” niewiadomych będziemy je oznaczać literami x, y, z, t, u, v, w.
Def. 4.1.2 (układ jednorodny i niejednorodny)
Układ równań liniowych postaci
AX = 0,
gdzie A jest macierzą wymiaru m
×
n, natomiast 0 jest macierzą zerową wymiaru m
×
1, nazywamy układem jednorodnym.
Układ równań liniowych postaci
AX = B,
w którym B jest macierzą niezerową nazywamy układem niejednorodnym.
Uwaga. Jednym z rozwiązań każdego układu jednorodnego AX = 0 jest macierz zerowa
=
0
0
0
X
wymiaru n
×
1, gdzie n oznacza liczbę kolumn macierzy A.
4.2 UKŁADY CRAMERA
Def. 4.2.1 (układ Cramera)
Układem Cramera nazywamy układ równań liniowych AX = B, w którym A jest macierzą nieosobliwą.
Tw. 4.2.2 (wzór Cramera)
Układ Cramera AX = B ma dokładnie jedno rozwiąznie. Rozwiązanie to jest określone wzorem
=
n
A
A
A
A
X
det
det
det
det
1
2
1
,
gdzie n oznacza stopień macierzy A, natomiast A
j
, dla 1
≤
j
≤
n, oznacza macierz A, w której j–tą kolumnę zastąpiono kolumną
wyrazów wolnych B, tzn.
=
nn
n
n
n
n
n
def
j
a
b
a
a
a
b
a
a
a
b
a
a
A
2
1
2
2
22
21
1
1
12
11
.
Uwaga. Równość określającą rozwiązanie układu równań liniowych nazywamy wzorem Cramera. Równość ta po rozpisaniu
przyjmuje postać:
A
A
x
det
det
1
1
=
,
A
A
x
det
det
2
2
=
, …,
A
A
x
n
n
det
det
=
,
zwaną wzorami Cramera.
Fakt 4.2.3 (metoda macierzy odwrotnej)
Rozwiązanie układu Cramera AX = B jest określone wzorem:
B
A
X
1
−
=
.
4.3 METODA ELIMINACJI GAUSSA DLA UKŁADÓW CRAMERA
Fakt 4.3.1 (metoda eliminacji Gaussa dla układów Cramera)
Niech AX = B będzie układem Cramera, w którym A jest macierzą stopnia n. Rozwiązanie tego układu znajdujemy w następu-
jący sposób:
1. budujemy macierz rozszerzoną układu postaci
[
]
=
n
nn
n
n
n
n
b
b
b
a
a
a
a
a
a
a
a
a
B
A
2
1
2
1
2
22
21
1
12
11
|
.
2. przekształcamy macierz rozszerzoną do postaci
[
]
X
I |
wykonując na jej wierszach następujące operacje elementarne:
a) zamianę między sobą dwóch dowolnych wierszy (w
i
↔
w
j
),
b) pomnożenie dowolnego wiersza przez liczbę różną od zera (cw
i
),
c) dodanie do elementów dowolnego wiersza odpowiadających im elementów innego wiersza pomnożonego przez dowolną
liczbę (w
i
+ cw
j
).
Operacje te mają na celu doprowadzenie macierzy rozszerzonej do postaci:
[
]
=
n
x
x
x
X
I
2
1
1
0
0
0
1
0
0
0
1
|
.
Ostatnia kolumna macierzy rozszerzonej (macierz X) jest wtedy rozwiązaniem wyjściowego układu równań.
[ ]
[ ]
X
I
B
A
|
|
wierszach
na
e
elementarn
operacje
→
Rys. 4.3.1 Schemat metody eliminacji Gaussa rozwiązywania układów równań liniowych.
Uwaga. Przy przekształcaniu macierzy rozszerzonej układu do postaci końcowej możemy wykorzystać algorytm Gaussa
sprowadzania macierzy nieosobliwej do postaci jednostkowej podany w fakcie 3.7.1.
Uwaga. Praktyczną wersją metody eliminacji Gaussa dla układów Cramera jest metoda kolumn jednostkowych. Polega ona
na przekształceniu macierzy rozszerzonej układu w celu doprowadzenia wszystkich kolumn macierzy tego układu do postaci
jednostkowej (tzn. z jedną jedynką i resztą zer). Jedynki z różnych kolumn muszą się przy tym znaleźć w różnych wierszach.
Końcowa postać [I
/
|X
/
] macierzy rozszerzonej będzie się różnić od postaci[I|X] jedynie kolejnością wierszy. Dla układu
Cramera z n niwiadomymi metoda ta wymaga n kroków, gdyż w każdym kroku przekształca się ostatecznie całą kolumnę.
Kolejność przekształcanych kolumn oraz położenie końcowych „jedynek” jest dowolna, przy czym wygodnie jest do
przekształcenia wybrać kolumnę składającą się z jedynki, „małych” liczb całkowitych i „dużej” liczby zer. W porównaniu z
klasycznym algorytmem Gaussa metoda ta nie wymaga przestawiania wierszy ani budowania macierzy trójkątnej. Wymaga
jednak wykonania większej liczby mnożeń.
Fakt 4.3.2 (algorytm przekształcania j–tej kolumny)
Chcąc w miejsce niezerowego elementu a
ij
otrzymać „jedynkę”, a na pozostałych miejscach j–tej kolumny same zera wystarczy
i–ty wiersz macierzy rozszerzonej podzielić przez a
ij
. Następnie należy od pozostałych kolejnych wierszy odejmować i–ty
wiersz mnożony odpowiednio przez a
1j
, a
2j
, …, a
i-1j
, a
i+1j
, …, a
nj
. Schematycznie przedstawimy to poniżej
→
→
−
−
−
−
+
−
+
−
+
+
−
−
.
.
.
.
.
0
0
1
0
0
.
.
.
.
.
1
.
.
.
.
.
1
1
1
1
1
1
1
1
1
:
1
1
1
i
nj
n
i
j
i
i
i
j
i
i
i
j
ij
i
w
a
w
w
a
w
w
a
w
w
a
w
nj
j
i
j
i
j
a
w
nj
j
i
ij
j
i
j
a
a
a
a
a
a
a
a
a
.
4.4 METODA ELIMINACJI GAUSSA DLA DOWOLNYCH UKŁADÓW RÓWNAŃ LINIOWYCH
Def. 4.4.1 (równoważność układów równań liniowych)
Niech A, A
/
, B, B
/
będą macierzami o wymiarach odpowiednio m
×
n, k
×
n, m
×
1, k
×
1. Ponadto niech
=
n
x
x
x
X
2
1
,
=
/
/
2
/
1
/
n
x
x
x
X
będą macierzami niewiadomych, przy czym ciąg
(
)
/
/
2
/
1
,...,
,
n
x
x
x
jest permutacją ciągu (x
1
, x
2
, …, x
n
). Mówimy, że układy
równań liniowych AX = B i A
/
X
/
= B
/
są równoważne, jeżeli zbiory ich rozwiązań są identyczne.
Fakt 4.4.2 (o równoważnym przekształcaniu układów równań)
Podane poniżej operacje na wierszach macierzy rozszerzonej [A|B] układu równań liniowych AX = B przekształcają go na
układ równoważny:
1. zamiana między sobą wierszy (w
i
↔
w
j
),
2. mnożenie wiersza przez stałą różną od zera (cw
i
),
3. dodawanie do ustalonego wiersza innego wiersza wyraz po wyrazie (w
i
+ w
j
),
4. skreślenie wiersza złożonego z samych zer (w
i
),
5. skreślenie jednego z wierszy równych lub proporcjonalnych (w
i
~ w
j
).
Dodatkowo otrzymuje się układ równoważny, jeżeli w macierzy A zamienimy miejscami dwie kolumny przy jednoczesnej
zamianie niewiadomych (k
i
↔
k
j
).

/
1
2
2
2
21
1
1
1
11
1
2
2
2
21
1
1
1
11
niewiadome
1
niewiadome
1
A
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
A
x
x
x
x
x
x
x
x
mn
mi
mj
m
n
i
j
n
i
j
k
k
mn
mj
mi
m
n
j
i
n
j
i
n
i
j
n
j
i
j
i
=
→
=
↓
↓
↓
↓
↓
↓
↓
↓
↔
Fakt 4.4.3. (metoda eliminacji Gaussa)
Niech AX = B będzie układem równań liniowych, gdzie A jest macierzą wymiaru m
×
n. Wówczas układ ten rozwiązujemy
następująco:
1. budujemy macierz rozszerzoną układu postaci:
[
]
=
↓
↓
↓
m
mn
m
m
n
n
n
b
b
b
a
a
a
a
a
a
a
a
a
B
A
x
x
x
2
1
2
1
2
22
21
1
12
11
niewiadome
2
1
|
2. na macierzy rozszerzonej dokonujemy równoważnych przekształceń układu sprowadzając ją do postaci:
[
]
=
↓
↓
↓
↓
↓
+
+
+
+
+
1
2
1
1
2
1
2
1
1
1
/
/
parametry
/
/
1
niewiadome
/
/
2
/
1
0
0
|
0
0
0
|
1
0
0
|
|
0
1
0
|
0
0
1
|
r
r
rn
rr
n
r
n
r
n
r
r
z
z
z
z
s
s
s
s
s
s
B
A
x
x
x
x
x
.
Wówczas,
a) jeżeli z
r+1
≠
0, to układ AX = B jest sprzeczny,
b) jeżeli z
r+1
= 0 i n = r, to układ AX = B jest równoważny układowi Cramera i jego jedyne rozwiązanie ma postać x
1
= z
1
, x
2
=
z
2
, …, x
n
= z
n
,
c) jeżeli z
r+1
= 0 i n > r, to układ AX = B ma nieskończenie wiele rozwiązań, przy czym r spośród zmiennych x
1
, x
2
, …, x
n
oznaczanych symbolami
/
/
2
/
1
,...,
,
r
x
x
x
zależy od pozostałych n – r zmiennych oznaczanych symbolami
/
/
2
/
1
,...,
,
n
r
r
x
x
x
+
+
w
następujący sposób:
−
=
+
+
+
+
+
+
+
+
/
/
2
/
1
2
1
2
2
2
1
2
1
2
1
1
1
3
2
1
/
/
2
/
1
n
r
r
rn
rr
rr
n
r
r
n
r
r
r
x
x
x
s
s
s
s
s
s
s
s
s
z
z
z
x
x
x
.
Uwaga. Liczba r jest wyznaczona jednoznacznie. Jest to tzw. rząd macierzy A. Zmienne
/
/
2
/
1
,...,
,
r
x
x
x
będziemy nazywać
zmiennymi zależnymi, a zmienne
/
/
2
/
1
,...,
,
n
r
r
x
x
x
+
+
zmiennymi niezależnymi lub parametrami. Podział zmiennych na zależne i
parametry nie jest jednoznaczny, ale nie jest też dowolny. Przy przekształcaniu macierzy rozszerzonej układu do postaci
końcowej możemy wykorzystać algorytm sprowadzania macierzy nieosobliwej do postaci jednozstkowej (patrz fakt 3.7.1). W
przeciwieństwie do układu Cramera, omówionego w poprzednim paragrafie, mogą pojawić się tu trzy nowe sytuacje:
1. wiersz złożony z samych zer – wtedy go skreślamy,
2. dwa wiersze równe lub proporcjonalne – wtedy skreślamy jeden z nich,
3. brak elementu niezerowego w kolejnej kolumnie powodujący niemożność ustawienia kolejnej jedynki na przekątnej –
wtedy całą kolumnę wraz z jej zmienną przestawiamy na miejsce przedostatnie przed kolumnę wyrazów wolnych (zmienna
ta staje się parametrem).
Uwaga. Praktyczną wersją metody eliminacji Gaussa dla dowolnych układów równań liniowych jest metoda kolumn
jednostkowych. Jest ona rozszerzeniem metody opisanej dla układów Cramera (patrz fakt 4.3.2) na przypadek ogólny. Polega
ona na równoważnym przekształceniu macierzy rozszerzonej układu, w celu doprowadzenia możliwie największej liczby
kolumn do postaci jednostkowej. Jedynki z różnych kolumn jednostkowych powinny się przy tym znależć w różnych
wierszach. Przekształcenie poszczególnych kolumn wykonujemy dokładnie tak samo, jak dla układów Cramera. Przy wyborze
tych kolumn oraz miejsc na jedynki mamy pełną dowolność. Jednoznacznie określona jest tylko liczba tych kolumn, ale
pojawia się ona w naturalny sposób na końcu postępowania. Najwygodniej jest brać do przekształceń kolumny zawierające
„małe” liczby całkowite i „dużo” zer. W przypadku dowolnych układów równań w trakcie postępowania mogą pojawić się
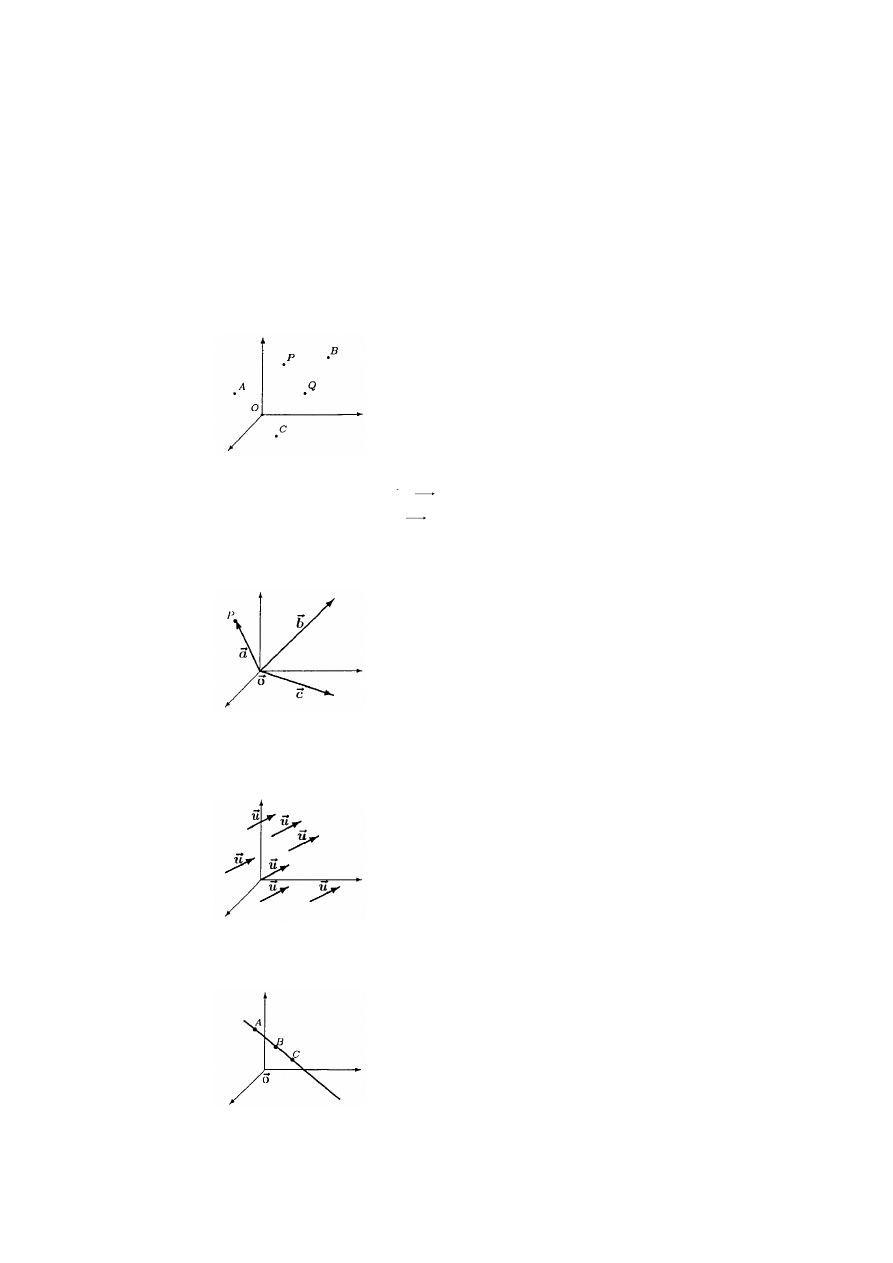
wiersze zerowe – wtedy je skreślamy, wiersze równe lub proporcjonalne – wtedy skreślamy jeden z nich. Może się także
zdarzyć, że w macierzy rozszerzonej układu pojawi się wiersz zerowy z elementem niezerowym w kolumnie wyrazów wolnych.
Taki układ równań jest oczywiście sprzeczny. Jeśli tak się nie zdarzy, to postępowanie kończy się wtedy, gdy liczba
wyróżnionych kolumn jest równa liczbie wierszy, które pozostały w macierzy. Rozwiązanie układu odczytujemy teraz z
końcowej postaci macierzy, wyróżnione „jedynki” wskazują zmienne zależne.
5. GEOMETRIA ANALITYCZNA W PRZESTRZENI
5.1 WEKTORY
Def. 5.1.1 (przestrzeń R
3
)
Przestrzenią R
3
nazywamy zbiór wszystkich uporządkowanych trójek (x,y,z) liczb rzeczywistych;
{
}
R
z
y
x
z
y
x
R
def
∈
=
,
,
:
)
,
,
(
3
.
Uwaga. Przestrzeń R
3
będziemy interpretować geometrycznie na trzy sposoby, tzn. jako:
1. zbiór wszystkich punktów P = (x,y,z) w przestrzeni (rys. 5.1.1). W tej interpretacji elementy przestrzeni R
3
nazywamy
punktami i oznaczamy przez A, B, C, P, Q itd. Liczby x, y, z nazywamy wtedy współrzędnymi punktu P = (x,y,z).
Rys. 5.1.1 Punkty w przestrzeni
2. zbiór wszystkich wektorów zaczepionych
OP
a
=
w przestrzeni. Wektory te mają wspólny początek O = (0,0,0), a końce
w punktach P = (x,y,z) (rys. 5.1.2). Wektor
OP
nazywamy wektorem wodzącym punktu P. W tej interpretacji elementy
przestrzeni R
3
nazywamy wektorami i oznaczamy przez
w
v
u
c
b
a
,
,
,
,
,
itd. Wektory wodzące punktów będziemy
oznaczali przez
1
0
,
,
r
r
r
itd. Liczby x, y, z nazywamy współrzędnymi wektora
)
,
,
(
z
y
x
a
=
.
Rys. 5.1.2 Wektory zaczepione
3. zbiór wszystkich wektorów swobodnych w przestrzeni. Przez wektor swobody
u (rys. 5.1.3) rozumiemy tutaj zbiór
wszystkich wektorów zaczepionych w różnych punktach, które mają ten sam kierunek, a zwrot oraz długość co wektor
u.
W tej interpretacji elementy przestrzeni R
3
także nazywamy wektorami.
Rys. 5.1.3 Wektory swobodne
Def. 5.1.2 (punkty współliniowe i współpłaszczyznowe)
1. Mówimy, że punkty A, B, C przestrzeni R
3
są współliniowe, gdy istnieje prosta, do której należą te punkty (rys. 5.1.4).
Rys. 5.1.4 Punkty A, B, C są współliniowe
2. Mówimy, że punkty K, L, M, N przestrzeni R
3
są współpłaszczyznowe, gdy istnieje płaszczyzna, do której należą te punkty.

Rys. 5.1.5 Punkty K, L, M, N są współpłaszczyznowe
Def. 5.1.3 (wektory współliniowe i współpłaszczyznowe)
1. Mówimy, że wektory
b
a,
są współliniowe, gdy istnieje prosta, w której zawarte są te wektory (rys. 5.1.6). Wektory
współliniowe będziemy nazywać także wektorami równoległymi; piszemy wtedy
b
a||
. Przyjmujemy, że wektor
o jest
równoległy do dowolnego wektora.
Rys. 5.1.6 Wektory
b
a,
są współliniowe
2. Mówimy, że wektory
w
v
u ,
,
są współpłaszczyznowe, gdy istnieje płaszczyzna, w której zawarte są te wektory.
Przyjmujemy, że wektor
o i dwa dowolne wektory są współpłaszczyznowe.
Rys. 5.1.7 Wektory
w
v
u ,
,
są współpłaszczyznowe
Def. 5.1.4 (działania na wektorach)
Niech
)
,
,
(
z
y
x
u
=
,
)
,
,
(
1
1
1
z
y
x
w
=
,
)
,
,
(
2
2
2
z
y
x
v
=
oraz niech
α
∈
R. Sumę wektorów w i v określamy wzorem:
)
,
,
(
2
1
2
1
2
1
z
z
y
y
x
x
v
w
def
+
+
+
=
+
.
Różnicę wektorów
w i v określamy wzorem:
)
,
,
(
2
1
2
1
2
1
z
z
y
y
x
x
v
w
def
−
−
−
=
−
.
Iloczyn wektora u przez liczbę rzeczywistą
α
określamy wzorem:
)
,
,
(
z
y
x
u
def
α
α
α
α =
.
Dodatkowo przyjmujemy oznaczenia
)
0
,
0
,
0
(
def
o
=
oraz
)
,
,
(
z
y
x
u
def
−
−
−
=
−
. Wektor
o nazywamy wektorem zerowym, a
wektor
u
−
wektorem przeciwmym do wektora
u
.
Fakt 5.1.5 (warunki równoległości i współpłaszczyznowości wektorów)
1. Mówimy, że wektory
a
i
b
są równoległe wtedy i tylko wtedy, gdy istnieje liczba rzeczywista
α
taka, że
a
b
α
=
.
2. Mówimy, że wektory
a
,
b
, c są współpłaszczyznowe wtedy i tylko wtedy, gdy istnieją liczby rzeczywiste
α
i
β
takie, że
b
a
c
β
α +
=
.
Fakt 5.1.6 (własności dziłań na wektorach)
Niech
w
v
u ,
,
będą wektorami w R
3
oraz niech
α
,
β
∈
R. Wtedy
1. dodawanie wektorów jest działaniem przemiennym,tj.
u
v
v
u
+
=
+
,
2. dodawanie wektorów jest działaniem łącznym, tj.
w
v
u
w
v
u
+
+
=
+
+
)
(
)
(
,
3. wektor
o jest elementem neutralnym dodawania, tj.
u
o
u
=
+
,
4. wektor
u
−
jest elementem przeciwnym do wektora
u
, tj.
o
u
u
=
−
+
)
(
,
5.
u
u
=
⋅
1
,
6.
)
(
)
(
u
u
β
α
αβ =
,
7.
)
)
(
u
u
u
β
α
β
α
+
=
+
,
8.
v
u
v
u
α
α
α
+
=
+
)
(
.
Fakt 5.1.7 (o własnościach rzutów wektorów)
Niech
w
v
u ,
,
będą dowolnymi wektorami w R
3
oraz niech
α
∈
R. Ponadto niech l będzie dowolną prostą w przestrzeni. Wtedy
1. rzut prostokątny sumy wektorów
v
u,
na prostą l jest równy sumie rzutów tych wektorów na tę prostą,
2. rzut prostokątny iloczynu wektora
w
przez liczbę
α
na prostą l jest równy iloczynowi rzutu tego wektora na tę prostą
przez liczbę
α
.
Def. 5.1.8 (układ współrzędnych w przestrzeni)
Układem współrzędnych w przestrzeni nazywamy trzy ustalone proste x, y, z przecinające się w jednym punkcie 0, które są
wzajemnie prostopadłe. Taki układ współrzędnych oznaczamy przez Oxyz. Proste Ox, Oy, Oz nazywamy osiami, a płaszczyzny
xOy, yOz, xOz płaszczyznami układu współrzędnych.
Def. 5.1.9 (orientacja układu współrzędnych w przestrzeni)
W zależności od wzajemnego położenia osi Ox, Oy, Oz układu współrzędnych wyróżniamy dwie jego orientacje: układ
prawoskrętny (rys. 5.1.8) i układ lewoskrętny (rys. 5.1.9).
Rys. 5.1.8 Układ współrzędnych o orientacji
prawoskrętnej
Rys. 5.1.9 Układ współrzędnych o orientacji
lewoskrętnej
Uwaga. Nazwa układ prawoskrętny pochodzi z następującej interpretacji: jeżeli prawą rękę umieścimy tak, aby kciuk
wskazywał dodatnią część osi Oz, to zgięte palce wskażą kierunek obrotu od osi Ox do osi Oy. Podobną interpretację ma układ
lewoskrętny.
Def. 5.1.10 (wersory na osiach układu współrzędnych)
Wektory
)
1
,
0
,
0
(
),
0
,
1
,
0
(
),
0
,
0
,
1
(
=
=
=
k
j
i
nazywamy wersorami odpowiednio na osiach Ox, Oy, Oz (rys. 5.1.8 i 5.1.9).
Def. 5.1.11 (długość wektora)
Długość wektora
)
,
,
(
z
y
x
v
=
jest określona wzorem:
2
2
2
z
y
x
v
def
+
+
=
.
Uwaga. Długość wektora
)
,
,
(
z
y
x
v
=
jest równa odległości punktu P = (x,y,z) od początku układu współrzędnych (rys.
5.1.10).
Rys. 5.1.10 Interpretacja geometryczna długości wektora
Fakt 5.1.12 (własności długości wektora)
Niech
v
u,
będą wektorami w R
3
oraz niech
α
∈
R. Wtedy
1.
0
≥
u
, przy czym
o
u
u
=
⇔
=
0
3.
v
u
v
u
+
≤
+
2.
u
u
⋅
= α
α
4.
v
u
v
u
−
≤
−
Uwaga. Nierówność 3 jest prawdziwa także dla dowolnej liczby składników. Nierówność tę ze względu na jej interpretację
geometryczną nazywamy nierównością trójkąta (rys. 5.1.11). równość w tej nierówności jest możliwa tylko wtedy, gdy
o
u
=
lub
o
v
=
albo, gdy
u
v
β
=
dla pewnego
β
> 0.

Rys. 5.1.11 Ilustracja nierówności trójkąta
Fakt 5.1.13 (położenie punktu podziału odcinka)
Niech
1
r oraz
2
r
będą wektorami wodzącymi odpowiednio punktów A i B. Punkt P podziału odcinka AB w stosunku 1 :
λ
,
gdzie
λ
> 0, ma wektor wodzący
λ
λ
+
+
=
1
2
1
r
r
r
.
Uwaga. Jeżeli
)
,
,
(
),
,
,
(
2
2
2
2
1
1
1
1
z
y
x
r
z
y
x
r
=
=
, to współrzędne wektora
)
,
,
(
z
y
x
r
=
wyrażają się wzorami:
+
+
=
+
+
=
+
+
=
λ
λ
λ
λ
λ
λ
1
1
1
2
1
2
1
2
1
z
z
z
y
y
y
x
x
x
.
Rys. 5.1.12 Podział odcinka AB w stosunku 1 :
λ
Fakt 5.1.14 (współrzędne środka masy układu punktów materialnych)
Niech
i
r
, gdzie 1
≤
i
≤
k, będą wektorami wodzącymi punktów materialnych P
i
o masach m
i
. Wektor wodzący środka masy C
tego układu punktów materialnych ma postać:
k
k
k
m
m
m
r
m
r
m
r
m
r
+
+
+
+
+
+
=
...
...
2
1
2
2
1
1
.
Uwaga. Jeżeli
)
,
,
(
i
i
i
i
z
y
x
r
=
, gdzie 1
≤
i
≤
k, to współrzędne wektora
)
,
,
(
z
y
x
r
=
wyrażają się wzorami:
+
+
+
+
+
+
=
+
+
+
+
+
+
=
+
+
+
+
+
+
=
k
k
k
k
k
k
k
k
k
m
m
m
z
m
z
m
z
m
z
m
m
m
y
m
y
m
y
m
y
m
m
m
x
m
x
m
x
m
x
...
...
...
...
...
...
2
1
2
2
1
1
2
1
2
2
1
1
2
1
2
2
1
1
.
5.2 ILOCZYN SKALARNY
Def. 5.2.1 (iloczyn skalarny)
Niech
v
u,
będą dowolnymi wektorami w R
3
. Iloczyn skalarny wektorów
u
i
v
określamy wzorem:
ϕ
cos
⋅
⋅
=
v
u
v
u
def
,
gdzie
ϕ
jest miarą kąta między wektorami
u
i
v
(rys. 5.2.1).

Rys. 5.2.1 Ilustracja do definicji iloczynu skalarnego
Uwaga. Miara kąta między wektorami niezerowymi
u
i
v
wyraża się wzorem:
v
u
v
u
⋅
=
cos
arc
ϕ
.
Rzut prostopadły wektora
u
na wektor
v
wyraża się wzorem:
v
v
v
u
w
⋅
=
2
.
Fakt 5.2.2 (wzór do obliczania iloczynu skalarnego)
Niech
)
,
,
(
1
1
1
z
y
x
u
=
oraz
)
,
,
(
2
2
2
z
y
x
v
=
będą wektorami w R
3
. Wtedy
2
1
2
1
2
1
z
z
y
y
x
x
v
u
+
+
=
.
Fakt 5.2.3 (własności iloczynu skalarnego)
Niech
w
v
u ,
,
będą dowolnymi wektorami w R
3
oraz niech
α
∈
R. Wtedy
1.
u
v
v
u
=
,
2.
( )
(
)
u
v
v
u
α
α
=
,
3.
(
)
w
v
w
u
w
v
u
+
=
+
,
4.
2
u
u
u
=
,
5.
v
u
v
u
⋅
≤
,
6. wektory
u
i
v
są prostopadłe
⇔
0
=
v
u
.
Uwaga. Równość podana w punkcie 3 jest prawdziwa także dla dowolnej liczby wektorów składników. Równość w nierówno-
ści 5 jest możliwa tylko wtedy, gdy wektory
u
i
v
są równoległe.
5.3 ILOCZYN WEKTOROWY
Def. 5.3.1 (iloczyn wektorowy)
Niech
u
i
v
będą niewspółliniowymi wektorami w R
3
. Iloczynem wektorowym uporządkowanej pary wektorów
u
i
v
nazywamy wektor
w, który spełnia warunki:
1. jest prostopadły do płaszczyzny rozpiętej na wektorach
u
i
v
(rys. 5.3.1),
2. jego długość jest równa polu równoległoboku rozpiętego na wektorach
u
i
v
, tj. równa
ϕ
sin
⋅
⋅
v
u
, gdzie
ϕ
jest miarą
kąta między wektorami
u
i
v
,
3. orientacja trójki wektorów
w
v
u ,
,
jest zgodna z orientacją układu współrzędnych Oxyz.
Iloczyn wektorowy pary wektorów
u
i
v
oznaczamy przez
v
u
×
. Jeżeli jeden z wektorów
u
,
v
jest wektorem zerowym lub
wektory te są współliniowe, to przyjmujemy, że
o
v
u
=
×
.
Rys.5.3.1 Wektor
w jest iloczynem wektorowym wektorów
u
i
v
.
Fakt 5.3.2 (wzór do obliczania iloczynu wektorowego)
Niech
)
,
,
(
1
1
1
z
y
x
u
=
oraz
)
,
,
(
2
2
2
z
y
x
v
=
będą wektorami w R
3
. Wtedy
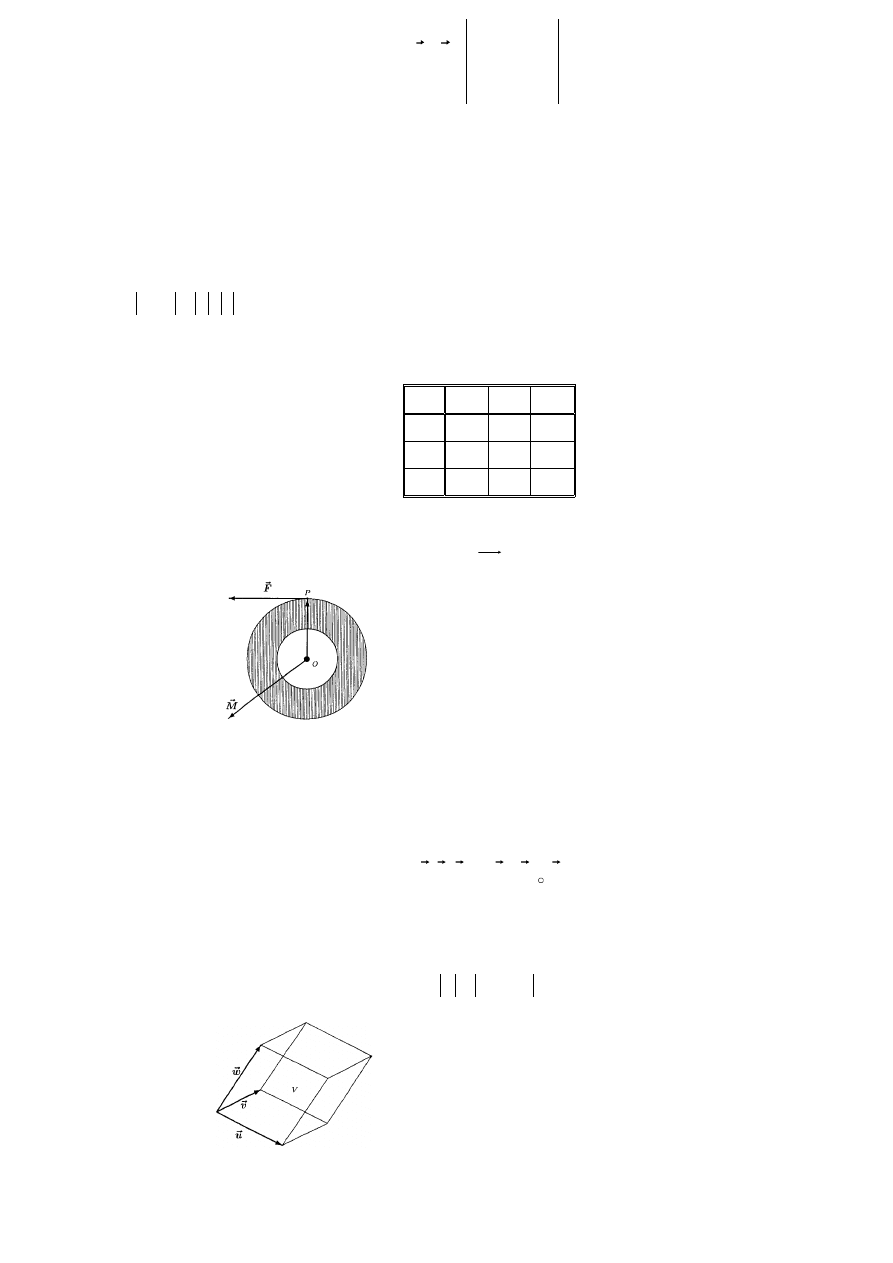
2
2
2
1
1
1
z
y
x
z
y
x
k
j
i
v
u
=
×
,
gdzie
k
j
i ,
,
oznaczają wersory odpowiednio na osiach Ox, Oy, Oz.
Fakt 5.3.3 (własności iloczynu wektorowego)
Niech
w
v
u ,
,
będą dowolnymi wektorami w R
3
oraz niech
α
∈
R. Wtedy
1.
u
v
v
u
×
−
=
×
,
2.
( )
(
)
v
u
v
u
×
=
×
α
α
,
3.
(
)
w
v
w
u
w
v
u
×
+
×
=
×
+
,
4.
w
u
v
u
w
v
u
×
+
×
=
+
×
)
(
,
5.
v
u
v
u
⋅
≤
×
,
6. wektory
u
i
v
są równoległe
⇔
0
=
×
v
u
.
Uwaga. Równość w nierówności 5 jest możliwa tylko wtedy, gdy wektory
u
i
v
są prostopadłe. Iloczyn wektorów zapisanych
jako kombinacje liniowe wersorów
k
j
i ,
,
można obliczyć stosując powyższe własności oraz wykorzystując tabelkę:
×
i
j
k
i
o
k
j
−
j
k
−
o
i
k
j
i
−
o
Def. 5.3.4 (moment siły)
Momentem siły
F
przyłożonej w punkcie P, względem punktu O nazywamy wektor
M
określony wzorem:
F
OP
M
×
=
.
Rys. 5.3.2 Moment siły
5.4 ILOCZYN MIESZANY
Def. 5.4.1 (iloczyn mieszany)
Niech
w
v
u ,
,
będą wektorami w R
3
. Iloczyn mieszany uporządowanej trójki wektorów
w
v
u ,
,
określamy wzorem:
(
) (
)
w
v
u
w
v
u
def
×
=
,
,
.
Fakt 5.4.2 (interpretacja geometryczna iloczynu mieszanego wektorów)
Iloczyn mieszany wektorów
w
v
u ,
,
jest równy (z dokładnością do znaku) objętości równoległościanu V rozpiętego na
wektorach
w
v
u ,
,
(rys. 5.4.1).
(
)
w
v
u
V
,
,
=
.
Rys. 5.4.1 Równoległościan rozpięty ma wektorach
w
v
u ,
,
Fakt 5.4.3 (wzór do obliczania iloczynu mieszanego)
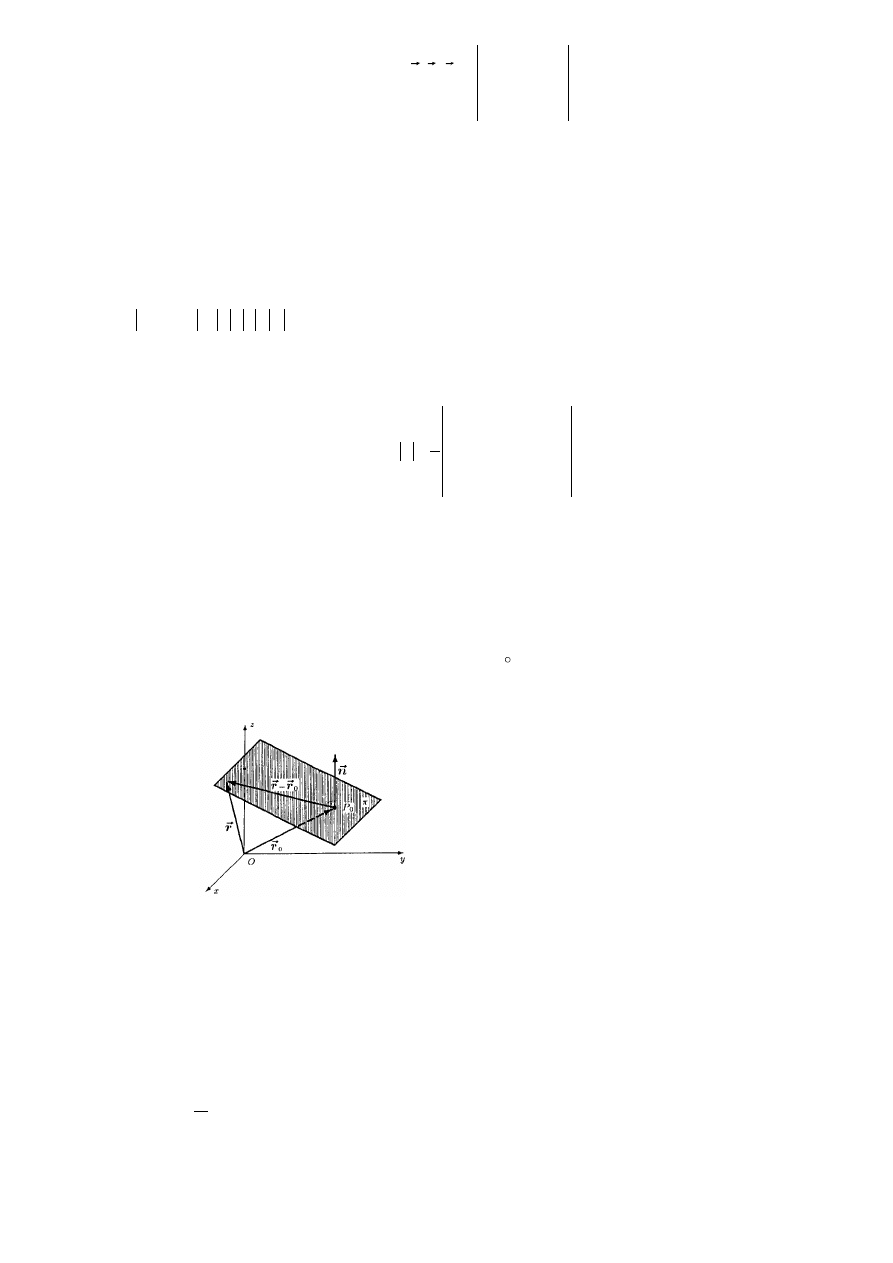
Niech
)
,
,
(
1
1
1
z
y
x
u
=
,
)
,
,
(
2
2
2
z
y
x
v
=
,
)
,
,
(
3
3
3
z
y
x
w
=
będą wektorami w R
3
. Wtedy
(
)
3
3
3
2
3
2
1
1
1
,
,
z
y
x
z
y
x
z
y
x
w
v
u
=
.
Fakt 5.4.4 (własności iloczynu mieszanego)
Niech
r
w
v
u
,
,
,
będą wektorami w R
3
oraz niech
α
∈
R. Wtedy
1.
)
,
,
(
)
,
,
(
u
w
v
w
v
u
=
,
2.
)
,
,
(
)
,
,
(
w
u
v
w
v
u
−
=
,
3.
)
,
,
(
)
,
,
(
)
,
,
(
w
v
r
w
v
u
w
v
r
u
+
=
+
,
4.
)
,
,
(
)
,
,
(
w
v
u
w
v
u
α
α
=
,
5. wektory
w
v
u ,
,
leżą w jednej płaszczyźnie
⇔
0
)
,
,
(
=
w
v
u
,
6.
w
v
u
w
v
u
⋅
⋅
≤
)
,
,
(
.
Uwaga. Równość w ostatniej nierówności jest możliwa tylko wtedy, gdy przynajmniej jeden z wektorów
w
v
u ,
,
jest zerowy
albo, gdy te wektory są wzajemnie prostopadłe.
Objętość czworościanu V o wierzchołkach A
1
= (x
1
,y
1
,z
1
), A
2
= (x
2
,y
2
,z
2
), A
3
= (x
3
,y
3
,z
3
), A
4
= (x
4
,y
4
,z
4
) wyraża się wzorem:
=
1
1
1
1
det
6
1
4
4
4
3
3
3
2
2
2
1
1
1
z
y
x
z
y
x
z
y
x
z
y
x
V
.
5.5 RÓWNANIA PŁASZCZYZNY
Fakt 5.5.1 (równanie normalne płaszczyzny)
Równanie płaszczyzny
π
przechodzącej przez punkt P
0
= (x
0
,y
0
,z
0
) o wektorze wodzącym
0
r
i prostopadłej do wektora
o
C
B
A
n
≠
=
)
,
,
(
(rys. 5.5.1) ma postać:
0
)
(
:
0
=
−
n
r
r
π
,
gdzie
)
,
,
(
0
0
0
z
y
x
r
=
jest wektorem wodzącym punktów przestrzeni. Wektor
n nazywamy wektorem normalnym tej
płaszczyzny.
Rys. 5.5.1 Płaszczyzna
π
przechodzi przez punkt P
0
i jest prostopadła do wektora
n
W formie rozwiniętej równanie płaszczyzny
π
przyjmuje postać:
0
)
(
)
(
)
(
:
0
0
0
=
−
+
−
+
−
z
z
C
y
y
B
x
x
A
π
.
Powyższe zależności nazywamy równaniami normalnymi płaszczyzny.
Fakt 5.5.2 (równanie ogólne płaszczyzny)
Każde równanie postaci:
0
:
=
+
+
+
D
Cz
By
Ax
π
,
gdzie |A| + |B| + |C| > 0, przedstawia płaszczyznę. Płaszczyzna ta ma wektor normalny
)
,
,
(
C
B
A
n
=
i przecina oś Oz w
punkcie
C
D
z
−
=
, o ile C
≠
0 (rys. 5.5.2).

Rys. 5.5.2 Płaszczyzna
π
jest opisana przez równanie Ax + By + Cz + D = 0, C
≠
0
Fakt 5.5.3 (równanie parametryczne płaszczyzny)
Równanie płaszczyzny
π
przechodzącej przez punkt P
0
= (x
0
,y
0
,z
0
) o wektorze wodzącym
0
r
i rozpiętej na niewspółliniowych
wektorach
)
,
,
(
1
1
1
c
b
a
u
=
i
)
,
,
(
2
2
2
c
b
a
v
=
(rys. 5.5.3) ma postać:
v
t
u
s
r
r
+
+
=
0
:
π
, gdzie s, t
∈
R
lub inaczej:
)
,
,
(
)
,
,
(
)
(
)
,
,
(
:
2
2
2
1
1
1
0
0
0
c
b
a
t
c
b
a
s
z
y
x
z
y
x
+
+
+
+
=
π
, gdzie s, t
∈
R.
W formie rozwiniętej równanie tej płaszczyzny przyjmuje postać:
+
+
=
+
+
=
+
+
=
2
1
0
2
1
0
2
1
0
:
tc
sc
z
z
tb
sb
y
y
ta
sa
x
x
π
, gdzie s, t
∈
R.
Powyższe zależności nazywamy równaniami parametrycznymi płaszczyzny.
Rys. 5.5.3 Płaszczyzna
π
przechodzi przez punkt P
0
i jest równoległa do wektorów u i v
Fakt 5.5.4 (równanie płaszczyzny przechodzącej przez 3 punkty)
Równanie płaszczyzny
π
przechodzącej przez 3 niewspółliniowe punkty P
i
= (x
i
,y
i
,z
i
), gdzie 1
≤
i
≤
3, (rys. 5.5.4) ma postać:
0
1
1
1
1
:
3
3
3
2
2
2
1
1
1
=
z
y
x
z
y
x
z
y
x
z
y
x
π
.
Rys. 5.5.4 Płaszczyzna wyznaczona przez trzy punkty
Fakt 5.5.5 (równanie odcinkowe płaszczyzny)
Równanie płaszczyzny
π
odcinającej na osiach Ox, Oy, Oz układu współrzędnych odpowiednio odcinki (zorientowane) a,
b, c
≠
0 (rys. 5.5.5) ma postać:
1
:
=
+
+
c
z
b
y
a
x
π
.
Powyższą zależność nazywamy równaniem odcinkowym płaszczyzny.
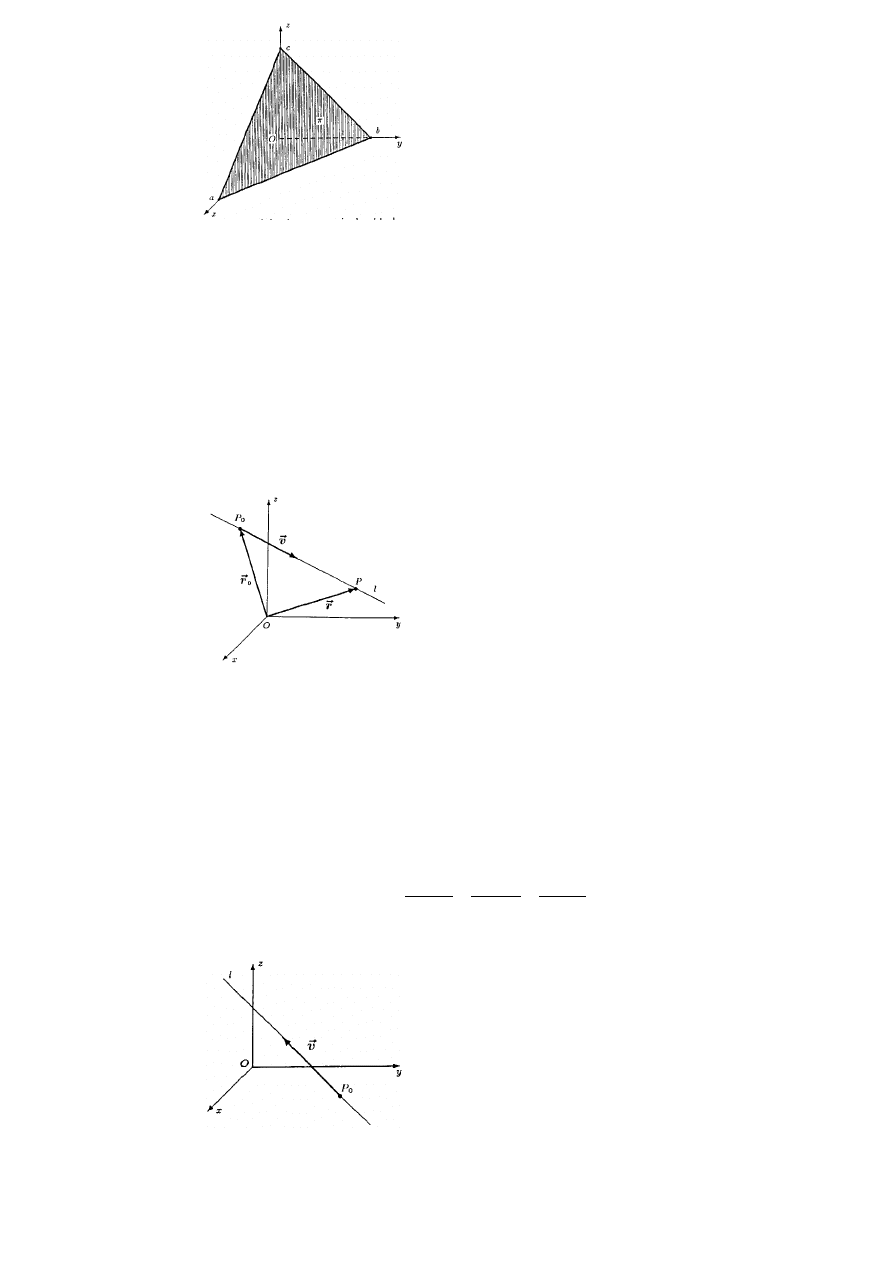
Rys. 5.5.5 Płaszczyzna odcinająca na osiach układu odcinki a, b, c
5.6 RÓWNANIA PROSTEJ
Fakt 5.6.1 (równanie parametryczne prostej)
Równanie prostej l przechodzącej przez punkt P
0
= (x
0
,y
0
,z
0
) o wektorze wodzącym
0
r
i wyznaczonej przez niezerowy wektor
kierunku
)
,
,
(
c
b
a
v
=
(rys. 5.6.1) ma postać:
v
t
r
r
l
+
=
0
:
, gdzie t
∈
R
lub inaczej:
)
,
,
(
)
,
,
(
)
,
,
(
:
0
0
0
c
b
a
t
z
y
x
z
y
x
l
+
=
, gdzie t
∈
R.
Powyższą zależność nazywamy równaniem parametrycznym prostej w postaci wektorowej.
Rys. 5.6.1 Prosta l przechodzi przez punkt P
0
i jest równoległa do wektora v
Po rozpisaniu na współrzędne parametryczne prosta przyjmuje postać:
+
=
+
=
+
=
ct
z
z
bt
y
y
at
x
x
l
0
0
0
:
, gdzie t
∈
R.
Fakt 5.6.2 (równanie kierunkowe prostej)
Równanie prostej l przechodzącej przez punkt P
0
= (x
0
,y
0
,z
0
) i wyznaczonej przez niezerowy wektor kierunku
)
,
,
(
c
b
a
v
=
(rys.
5.6.2) ma postać:
c
z
z
b
y
y
a
x
x
l
0
0
0
:
−
=
−
=
−
.
Ten sposób zapisu równania parametrycznego prostej nazywamy jej równaniem kierunkowym.
Rys. 5.6.2 Prosta l przechodzi przez punkt P
0
i jest równoległa do wektora v
Uwaga. Ponieważ jest to zapis umowny równania prostej, w mianownikach powyższych ułamków mogą wystąpić zera.
Fakt 5.6.3 (równanie krawędziowe prostej)
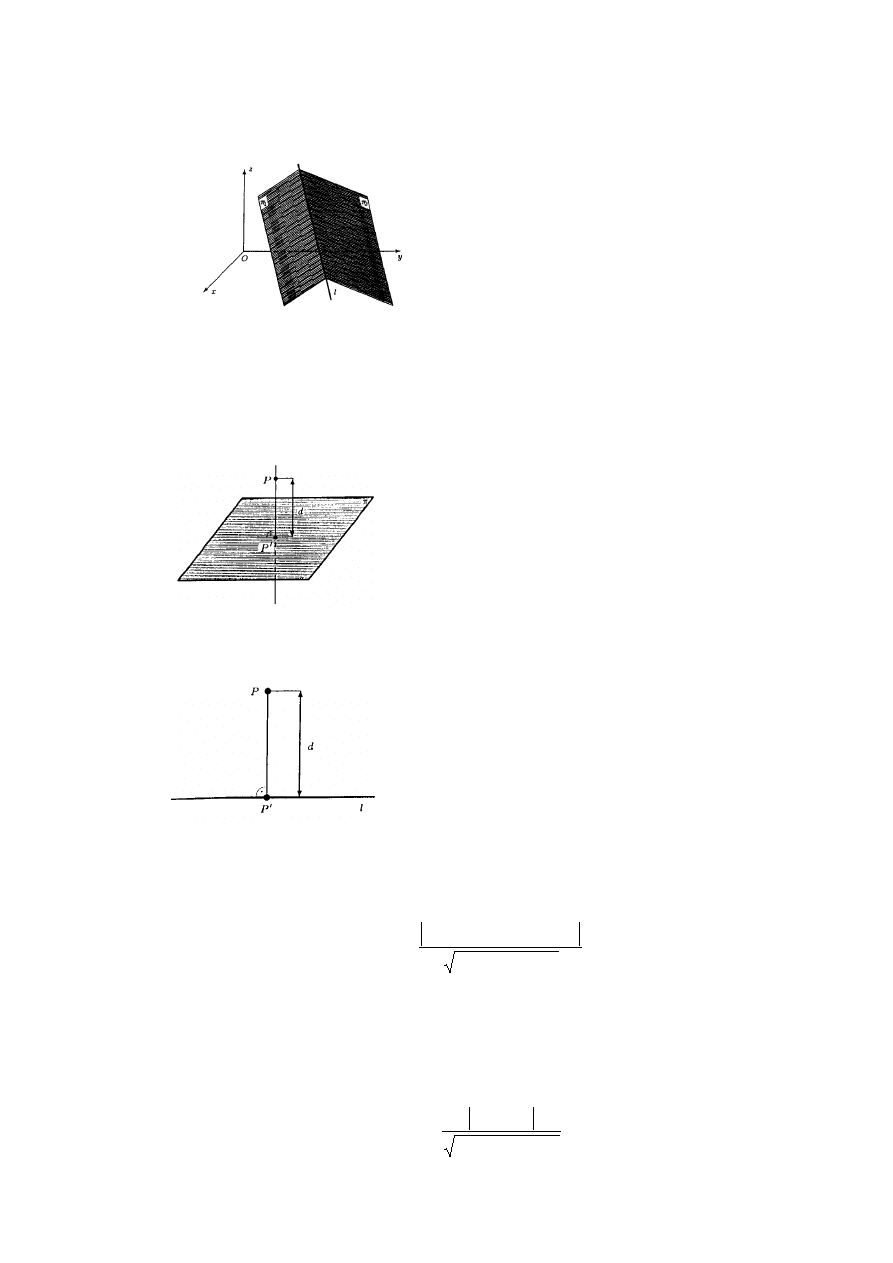
Równanie prostej l, która jest częścią wspólną dwóch nierównoległych płaszczyzn
0
:
1
1
1
1
1
=
+
+
+
D
z
C
y
B
x
A
π
,
0
:
2
2
2
2
2
=
+
+
+
D
z
C
y
B
x
A
π
(rys. 5.6.3), ma postać:
=
+
+
+
=
+
+
+
0
0
:
2
2
2
2
1
1
1
1
D
z
C
y
B
x
A
D
z
C
y
B
x
A
l
.
Ten sposób zapisu prostej nazywamy jej równaniem krawędziowym.
Uwaga. Wektor kierunkowy v prostej l ma postać
2
1
n
n
v
×
=
, gdzie
)
,
,
(
1
1
1
1
C
B
A
n
=
,
)
,
,
(
2
2
2
2
C
B
A
n
=
.
Rys. 5.6.3 Prosta l jest częścią wspólną płaszczyzn
π
1
i
π
2
5.7 WZAJEMNE POŁOŻENIA PUNKTÓW, PROSTYCH I PŁASZCZYZN
Def. 5.7.1 (rzut punktu na płaszczyznę i na prostą)
Rzutem prostopadłym punktu P na płaszczyznę
π
nazywamy punkt P
/
tej płaszczyzny (rys. 5.7.1) spełniający warunek:
π
⊥
/
PP
.
Rys. 5.7.1 Rzut prostopadły P
/
punktu P na płaszczyznę
π
oraz odległość d punktu P od tej płaszczyzny
Podobnie rzutem prostopadłym punktu P na prostą l nazywamy punkt P
/
tej prostej (rys. 5.7.2) spełniający warunek:
l
PP
⊥
/
.
Rys. 5.7.2 Rzut prostopadły P
/
punktu P na prostą l oraz odległość d punktu P od tej prostej
Uwaga. W podobny sposób definiuje się rzut ukośny punktu na płaszczyznę lub prostą w kierunku ustalonego wktora.
Fakt 5.7.2 (odległość punktu od płaszczyzny)
Odległość d punktu P
0
= (x
0
,y
0
,z
0
) od płaszczyzny
0
:
=
+
+
+
D
Cz
By
Ax
π
wyraża się wzorem:
2
2
2
0
0
0
C
B
A
D
Cz
By
Ax
d
+
+
+
+
+
=
.
Uwaga. Odległość punktu P od płaszczyzny
π
jest równa długości odcinka PP
/
, gdzie P
/
jest rzutem prostopadłym punktu P na
płaszczyznę
π
(rys. 5.7.1). Podobnie, odległość punktu P od prostej l jest równa długości odcinka PP
/
, gdzie P
/
jest rzutem
prostopadłym punktu P na prostą l (rys. 5.7.2).
Fakt 5.7.3 (odległość płaszczyzn równoległych)
Odległość d między płaszczyznami równoległymi
0
:
1
1
1
1
1
=
+
+
+
D
z
C
y
B
x
A
π
,
0
:
2
2
2
2
2
=
+
+
+
D
z
C
y
B
x
A
π
(rys. 5.7.3)
wyraża się wzorem:
2
2
2
2
1
C
B
A
D
D
d
+
+
−
=
.
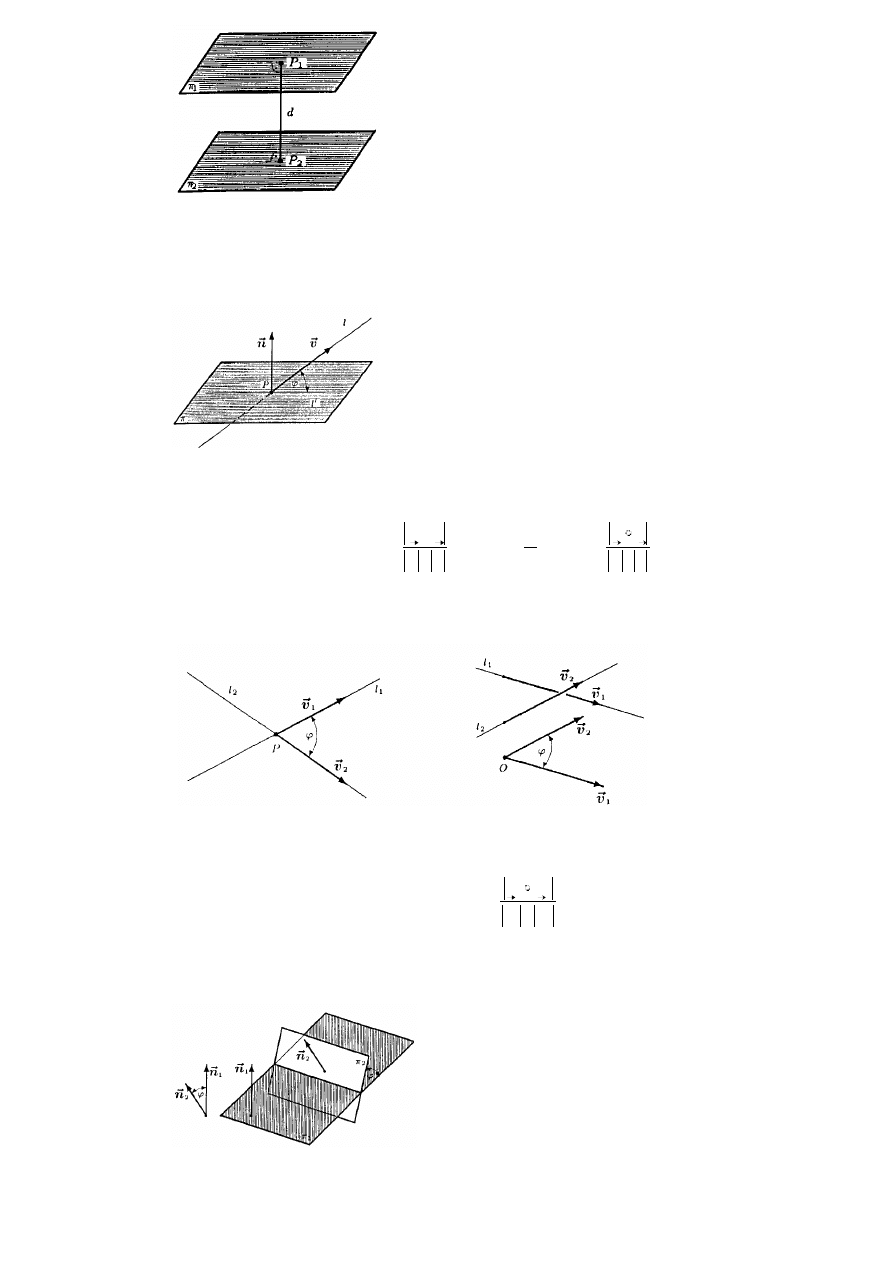
Rys. 5.7.3 Odległość między płaszczyznami
π
1
i
π
2
Def. 5.7.4 (kąt nachylenia prostej do płaszczyzny)
Kątem nachylenia prostej l do płaszczyzny
π
nazywamy kąt ostry
α
między prostą l, a jej rzutem prostopadłym l
/
na
płaszczyznę
π
(rys. 5.7.4). Jeżeli prosta l jest równoległa do płaszczyzny
π
, to przyjmujemy, że kąt jej nachylenia do tej
płaszczyzny jest równy 0.
Rys. 5.7.4 Kąt nachylenia prostej l do płaszczyzny
π
Fakt 5.7.5 (miara kąta nachylenia prostej do płaszczyzny)
Kąt nachylenia
ϕ
prostej o wektorze kierunkowym v do płaszczyzny o wektorze normalnym n wyraża się wzorem:
v
n
v
n
⋅
×
=
cos
arc
ϕ
lub
v
n
v
n
⋅
−
=
cos
arc
2
π
ϕ
.
Def. 5.7.6 (kąt między prostymi)
Kątem między prostymi nazywamy kąt ostry utworzony przez wektory kierunkowe tych prostych (rys. 5.7.5). Przyjmujemy, że
kąt między prostymi równoległymi jest równy 0.
Rys. 5.7.5 Kąt między prostymi przecinającymi się oraz między prostymi skośnymi
Fakt 5.7.7 (miara kąta między prostymi)
Miarą kąta
ϕ
między prostymi o wektorach kierunkowych
1
v i
2
v wyraża się wzorem:
2
1
2
1
cos
v
v
v
v
arc
⋅
=
ϕ
.
Def. 5.7.8 (kąt między płaszczyznami)
Kątem między płaszczyznami nazywamy kąt ostry między wektorami normalnymi tych płaszczyzn (rys. 5.7.6). Przyjmujemy,
że kąt między płaszczyznami równoległymi jest równy 0.
Rys. 5.7.6 Kąt między płaszczyznami
Fakt 5.7.9 (miara kąta między płaszczyznami)
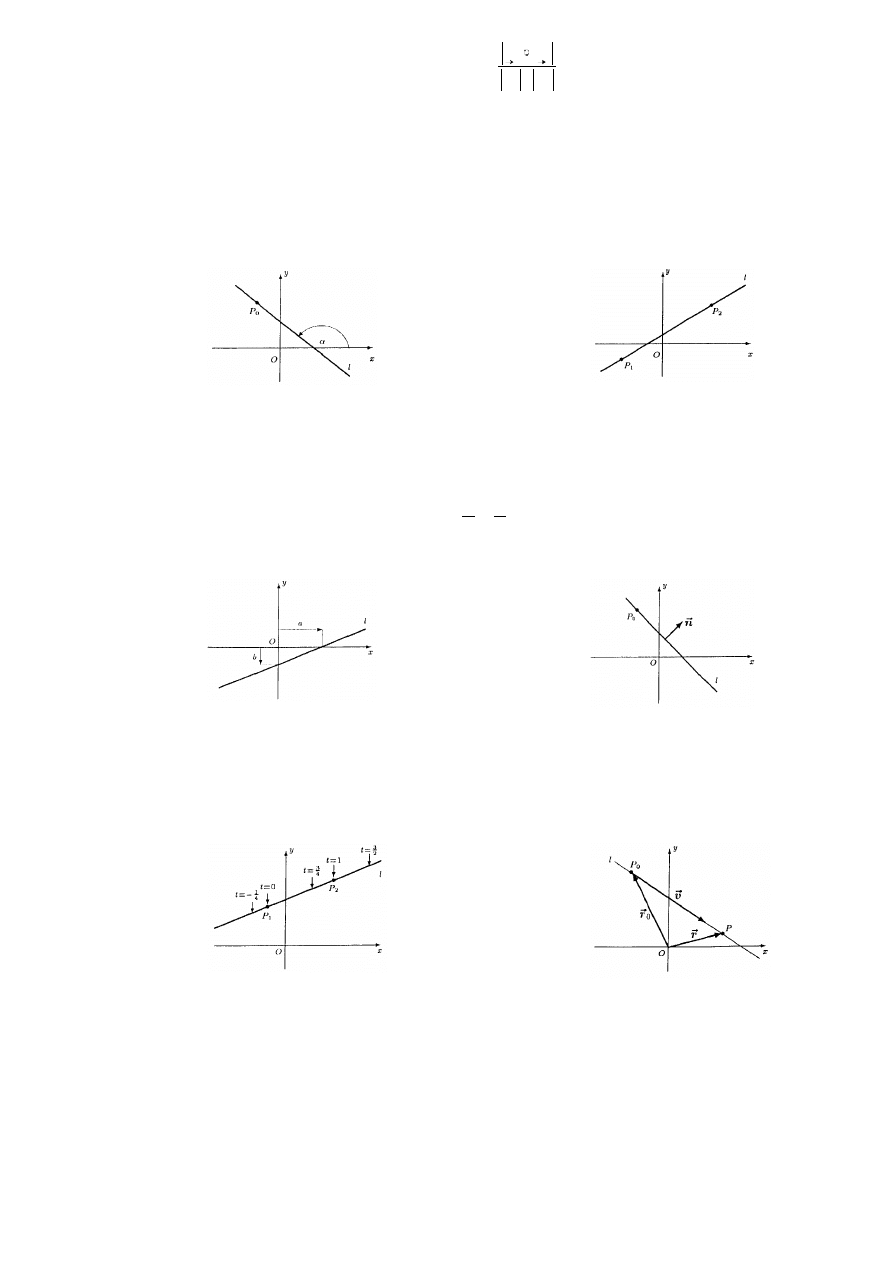
Miarą kąta
ϕ
między płaszczyznami
π
1
i
π
2
o wektorach normalnych odpowiednio
1
n i
2
n wyraża się wzorem:
2
1
2
1
cos
n
n
n
n
arc
⋅
=
ϕ
.
6. GEOMETRIA ANALITYCZNA NA PŁASZCZYŹNIE
6.1 PROSTA NA PŁASZCZYŹNIE
Fakt 6.1.1 (równanie prostej)
1. Równanie prostej l przechodzącej przez punkt P
0
= (x
0
,y
0
) i nachylonej od dodatniej części osi Ox pod kątem
α
(rys. 6.1.1)
ma postać:
)
(
tg
:
0
0
x
x
y
y
l
−
=
−
α
.
Rys. 6.1.1
Rys. 6.1.2
2. Równanie prostej l przechodzącej przez punkty P
1
= (x
1
,y
1
), P
2
= (x
2
,y
2
) (rys. 6.1.2) ma postać:
)
)(
(
)
)(
(
:
1
1
2
1
1
2
x
x
y
y
y
y
x
x
l
−
−
=
−
−
.
3. Równanie prostej l odcinającej na osiach Ox i Oy odcinki (skierowane) o długościach odpowiednio a i b, gdzie ab
≠
0,
(rys. 6.1.3) ma postać:
1
:
=
+
b
y
a
x
l
.
Jest to tzw. równanie odcinkowe prostej.
Rys. 6.1.3
Rys. 6.1.4
4. Równanie prostej l przechodzącej przez punkt P
0
= (x
0
,y
0
) i mającej wektor normalny
0
)
,
(
≠
=
B
A
n
(rys. 6.1.4) ma
postać:
0
)
(
)
(
:
0
0
=
−
+
−
y
y
B
x
x
A
l
.
Jest to tzw. równanie normalne prostej.
Rys. 6.1.5
Rys. 6.1.6
5. Równanie parametryczne prostej l przechodzącej przez punkty P
1
= (x
1
,y
1
), P
2
= (x
2
,y
2
) (rys. 6.1.5) ma postać:
−
+
=
−
+
=
t
y
y
y
y
t
x
x
x
x
l
)
(
)
(
:
1
2
1
1
2
1
, t
∈
R.
6. Równanie parametryczne (postać wektorowa) prostej l przechodzącej przez punkt P
0
o wektorze wodzącym
0
r
i mającej
kierunek zadany przez wektor v (rys. 6.1.6) ma postać:
v
t
r
r
l
+
=
0
:
, t
∈
R,
gdzie r jest promieniem wodzącym punktu P płaszczyzny.
Fakt 6.1.2 (warunki równoległości prostych)

1. Proste l
1
: A
1
x + B
1
y + C
1
= 0, l
2
: A
2
x + B
2
y + C
2
= 0 są równoległe wtedy i tylko, gdy
0
1
2
2
1
=
−
B
A
B
A
.
2. Proste l
1
: y = m
1
x + b
1
, l
2
: y = m
2
x + b
2
są równoległe wtedy i tylko wtedy, gdy
2
1
m
m
=
.
3. Proste
1
1
1
:
v
t
r
r
l
+
=
, t
∈
R,
2
2
2
:
v
t
r
r
l
+
=
, t
∈
R, są równoległe wtedy i tylko wtedy, gdy
2
1
v
k
v
=
dla pewnego k
≠
0.
Rys. 6.1.7 Proste równoległe
Fakt 6.1.3 (warunki prostopadłości prostych)
1. Proste l
1
: A
1
x + B
1
y + C
1
= 0, l
2
: A
2
x + B
2
y + C
2
= 0 są prostopadłe wtedy i tylko, gdy
0
2
1
2
1
=
+
B
B
A
A
.
2. Proste l
1
: y = m
1
x + b
1
, l
2
: y = m
2
x + b
2
są prostopadłe wtedy i tylko wtedy, gdy
1
2
1
−
=
m
m
.
3. Proste
1
1
1
:
v
t
r
r
l
+
=
, t
∈
R,
2
2
2
:
v
t
r
r
l
+
=
, t
∈
R, są prostopadłe wtedy i tylko wtedy, gdy
0
2
1
=
v
v
.
Rys. 6.1.8 Proste prostopadłe
Fakt 6.1.4 (kąt między prostymi)
1. Miara kąta ostrego
ϕ
utworzonego przez proste l
1
: A
1
x + B
1
y + C
1
= 0, l
2
: A
2
x + B
2
y + C
2
= 0 wyraża się wzorem:
2
2
2
2
2
1
2
1
2
1
2
1
)
(
)
(
)
(
)
(
cos
arc
B
A
B
A
B
B
A
A
+
+
+
=
ϕ
.
2. Miara kąta ostrego
ϕ
utworzonego przez proste l
1
: y = m
1
x + b
1
, l
2
: y = m
2
x + b
2
wyraża się wzorem:
2
1
2
1
1
g
arc
m
m
m
m
t
+
−
=
ϕ
.
Jeżeli m
1
m
2
= – 1, to przyjmujemy, że
2
π
ϕ =
.
Rys. 6.1.9 Kąt ostry między prostymi l
1
i l
2
Fakt 6.1.5 (odległości punktów i prostych)
1. Odległość d punktów P
1
= (x
1
,y
1
), P
2
= (x
2
,y
2
) wyraża się wzorem:
2
1
2
2
1
2
2
1
)
(
)
(
y
y
x
x
P
P
d
−
+
−
=
=
.
Rys. 6.1.10 Odległość punktów P
1
i P
2
Rys. 6.1.11 Odległość punktu P
0
od prostej l
2. Odległość d punktu P
0
= (x
0
,y
0
) od prostej l: Ax + By + C = 0 wyraża się wzorem:
2
2
0
0
0
)
,
(
B
A
C
By
Ax
l
P
d
d
+
+
+
=
=
.
3. Odległość d prostych l
1
: A
1
x + B
1
y + C
1
= 0, l
2
: A
2
x + B
2
y + C
2
= 0 wyraża się wzorem:
2
2
2
1
2
1
)
,
(
B
A
C
C
l
l
d
d
+
−
=
=
.
Rys. 6.1.12 Odległość dwóch prostych równoległych
6.2 PRZEKSZTAŁCENIA PŁASZCZYZNY
Fakt 6.2.1 (przekształcenia płaszczyzny)
1. Współrzędne punktu P
/
otrzymanego w wyniku przesunięcia punktu P = (x,y) o wektor
)
,
( b
a
v
=
wyrażają się wzorami:
+
=
+
=
b
y
y
a
x
x
P
/
/
/
:
.
Rys. 6.2.1 Przesunięcie punktu P o wektor v
Rys. 6.2.2 Symetrie względem osi układu współrzędnych
2. Współrzędne punktów P
/
i P
//
otrzymanych w wyniku symetrii punktu P = (x,y) odpowiednio względem osi Ox i Oy
wyrażają się wzorami:
−
=
=
y
y
x
x
P
/
/
/
:
,
=
−
=
y
y
x
x
P
//
//
//
:
.
3. Współrzędne punktu P
/
otrzymanego w wyniku symetrii punktu P = (x,y) względem początku układu współrzędnych
wyrażają się wzorami:
−
=
−
=
y
y
x
x
P
/
/
/
:
.
Rys. 6.2.3 Symetria względem początku układu
współrzędnych
Rys. 6.2.4 Obrót wokół początku układu współrzędnych o
kąt
α
4. Współrzędne punktu P
/
otrzymanego w wyniku obrotu punktu P = (x,y) wokół początku układu współrzędnych o kąt
α
(w
kierunku przeciwnym do ruchu wskazówek zegara) wyrażają się wzorami:
+
=
−
=
α
α
α
α
cos
sin
sin
cos
:
/
/
/
y
x
y
y
x
x
P
.
5. Współrzędne punktów P
/
i P
//
otrzymanych w wyniku podobieństw (powinowactw) punktu P = (x,y) w skali k względem
odpowiednio osi Ox i Oy wyrażają się wzorami:

=
=
ky
y
x
x
P
/
/
/
:
,
=
=
y
y
kx
x
P
//
//
//
:
.
Rys. 6.2.5 Podobieństwo w skali k=-
1
/
2
względem osi
Ox oraz podobieństwo w skali k=
1
/
3
względem osi Oy
Rys. 6.2.6 Jednokładność w skali k=2 względem
początku układu współrzędnych
6. Współrzędne punktu P
/
otrzymanego w wyniku jednokładności (podobieństwa) punktu P = (x,y) w skali k względem
początku układu współrzędnych wyrażają się wzorami:
=
=
ky
y
kx
x
P
/
/
/
:
.
Fakt 6.2.2 (równania krzywych przesuniętych i obróconych)
1. Niech
Γ
oznacza zbiór punktów (x,y)
∈
R
2
spełniających równanie F(x,y) = 0. Wtedy zbiór
Γ
/
otrzymany w wyniku
przesunięcia zbioru
Γ
o wektor
)
,
( b
a
v
=
jest opisany przez równanie:
0
)
,
(
:
/
=
−
−
Γ
b
y
a
x
F
.
Rys. 6.2.7 Zbiór
Γ
/
powstał w wyniku przesunięcia zbior
Γ
o wektor v
2. Niech
Γ
oznacza zbiór punktów (x,y)
∈
R
2
spełniających równanie F(x,y) = 0. Wtedy zbiór
Γ
/
otrzymany w wyniku obrotu
zbioru
Γ
wokół początku układu współrzędnych o kąt
α
jest opisany przez równanie:
0
)
cos
sin
,
sin
cos
(
:
/
=
+
−
+
Γ
α
α
α
α
y
x
y
x
F
.
Rys. 6.2.8 Zbiór
Γ
/
powstał ze zbioru
Γ
w wyniku jego obrotu wokół początku układu współrzędnych o kąt
α
Uwaga. Podobną postać mają równania zbiorów
Γ
/
otrzymanych w wyniku zastosowania do zbioru
Γ
= {(x,y)
∈
R
2
: F(x,y) = 0}
pozostałych przekształceń płaszczyzny, tj. symetrii osiowej lub punktowej, podobieństwa względem prostej lub punktu.
6.3 KRZYWE STOŻKOWE
Def. 6.3.1 (okrąg)
Okręgiem o środku w punkcie O i promieniu r > 0 nazywamy zbiór punktów płaszczyzny położonych w odległości r od punktu
O (rys. 6.3.1).
Rys. 6.3.1 Okrąg o środku w punkcie O i promieniu r
Fakt 6.3.2 (równanie okręgu)

Równanie okręgu o środku w początku układu współrzędnych i promieniu r > 0 ma postać:
2
2
2
r
y
x
=
+
.
Def 6.3.3 (elipsa)
Elipsą o ogniskach w punktach F
1
, F
2
oraz o dużej osi 2a, gdzie 2a > 2c = |F
1
F
2
|, nazywamy zbiór punktów płaszczyzny,
których suma odległości od ognisk F
1
i F
2
jest stała i równa 2a (rys. 6.3.2)
a
PF
PF
2
2
1
=
+
.
Rys. 6.3.2 Elipsa o ogniskach F
1
i F
2
Fakt 6.3.4 (równanie elipsy)
Równanie elipsy o środku w początku układu współrzędnych i półosiach a > 0 i b > 0 ma postać:
1
2
2
2
2
=
+
b
y
a
x
.
Zależność między półosiami a, b oraz ogniskową c elipsy ma postać:
2
2
2
c
b
a
=
−
.
Def. 6.3.5 (hiperbola)
Hiperbolą o ogniskach w punktach F
1
, F
2
oraz o dużej osi 2a, gdzie 2a < 2c = |F
1
F
2
|, nazywamy zbiór punktów płaszczyzny,
których wartość bezwzględna różnicy odległości od ognisk F
1
i F
2
jest stała i równa 2a (rys. 6.3.3)
a
PF
PF
2
2
1
=
−
.
Rys. 6.3.3 Hiperbola o ogniskach F
1
i F
2
Fakt 6.3.6 (równanie hiperboli)
Równanie hiperboli o środku w początku układu współrzędnych i półosiach rzeczywistej a > 0 i urojonej b > 0 ma postać:
1
2
2
2
2
=
−
b
y
a
x
.
Zależność między półosiami a, b oraz ogniskową c hiperboli ma postać:
2
2
2
c
b
a
=
+
.
Asymptoty hiperboli mają równania:
x
a
b
y
l
=
:
,
x
a
b
y
l
−
=
:
/
.
Def. 6.3.7 (parabola)
Parabolą o ognisku w punkcie F i kierownicy k, nazywamy zbiór punktów płaszczyzny, których odległość od ogniska jest
równa ich odległości od kierownicy (rys. 6.3.4).
)
,
( k
P
d
PK
PF
=
=
.

Rys. 6.3.4 Parabola o ognisku F i kierownicy k
Fakt 6.3.8 (równania paraboli)
1. Równanie paraboli, której ognisko F ma współrzędne
0
,
2
p
, gdzie p
≠
0, a kierownica k ma równanie
2
p
x
−
=
ma
postać:
px
y
2
2
=
.
2. Równanie
c
bx
ax
y
+
+
=
2
, gdzie a
≠
0, przedstawia parabolę. Osią tej paraboli jest prosta
a
b
x
2
−
=
, a wierzchołek
)
,
(
w
w
y
x
W
=
ma współrzędne określone wzorami:
a
b
x
w
2
−
=
,
a
y
w
4
∆
−
=
, gdzie
ac
b
4
2
−
=
∆
.
Jeżeli a > 0, to parabola ma ramiona skierowane do góry, a dla a < 0 na dół.
Rys. 6.3.5 Parabola o równaniu y = ax
2
+ bx + c, gdzie a
≠
0
Uwaga. Okrąg, elipsę, parabolę i hiperbolę nazywamy krzywymi stożkowymi, gdyż każda z nich jest przekrojem powierzchni
bocznej stożka pewną płaszczyzną.
Fakt 6.3.9 (równania parametryczne krzywych stożkowych)
1. Równanie parametryczne elipsy E o środku w początku układu współrzędnych i półosiach a > 0, b > 0 ma postać
=
=
t
b
y
t
a
x
E
sin
cos
:
, t
∈
[0,2
π
).
Gdy przyjmiemy a = b = r, to otrzymany równanie parametryczne okręgu.
2. Równanie paramrtryczne hiperboli H o środku w początku układu współrzędnych i półosi rzeczywistej a > 0 oraz półosi
urojonej b > 0 ma postać:
=
±
=
t
b
y
t
a
x
H
sh
ch
:
, t
∈
R.
Uwaga. Przyjmując we wzorze znak „+” otrzymamy prawą gałąź hiperboli, a przyjmując znak „–” otrzymamy lewą gałąź.
Fakt 6.3.10 (równania stycznych do krzywych stożkowych)
1. Równanie stycznej s do okręgu O: x
2
+ y
2
= r
2
wystawionej w punkcie P
1
= (x
1
,y
1
) należącym do tego okręgu ma postać:
2
1
1
:
r
y
y
x
x
s
=
+
.
Rys. 6.3.6 Styczna do okręgu O w punkcie P
1
2. Równanie stycznej s do elipsy
1
:
2
2
2
2
=
+
b
y
a
x
E
wystawionej w punkcie P
1
= (x
1
,y
1
) należącym do tej elipsy ma postać:
1
:
2
1
2
1
=
+
b
y
y
a
x
x
s
.
Rys. 6.3.7 Styczna do elipsy E w punkcie P
1
3. Równanie stycznej s do hiperboli
1
:
2
2
2
2
=
−
b
y
a
x
H
wystawionej w punkcie P
1
= (x
1
,y
1
) należącym do tej hiperboli ma
postać:
1
:
2
1
2
1
=
−
b
y
y
a
x
x
s
.
Rys. 6.3.8 Styczna do hiperboli h w punkcie P
1
4. Równanie stycznej s do paraboli P: y
2
= 2px wystawionej w punkcie P
1
= (x
1
,y
1
) należącym do tej paraboli ma postać:
)
(
:
1
1
x
x
p
y
y
s
+
=
.
Rys. 6.3.9 Styczna do paraboli P w punkcie P
1
Wyszukiwarka
Podobne podstrony:
Algebra liniowa 1 3 id 57241 Nieznany
algebra 0016 id 57154 Nieznany (2)
ALGEBRA zad 2 id 57346 Nieznany (2)
algebra 0026 id 57164 Nieznany (2)
algebra 0025 id 57163 Nieznany (2)
algebra part2 id 57041 Nieznany
algebra wyk2 id 57337 Nieznany (2)
algebra 0003 1 id 57140 Nieznany (2)
algebra 0013 id 57151 Nieznany (2)
algebra 0001 id 57138 Nieznany (2)
algebra 0007 id 57145 Nieznany (2)
badop gry liniowe id 78528 Nieznany (2)
algebra 0018 id 57156 Nieznany (2)
ALGEBRA zaj 6 id 57354 Nieznany (2)
algebra 0033 id 57171 Nieznany (2)
algebra 0014 id 57152 Nieznany (2)
algebra 0023 id 57161 Nieznany (2)
algebra 0019 id 57157 Nieznany (2)
więcej podobnych podstron