1
ALGEBRA – ZAJĘCIA VI
Forma kwadratowa
n
i
T
n
j
j
i
ij
x
A
x
x
x
a
x
x
f
1
1
)
,
(
Macierz A nazywana jest macierzą formy kwadratowej, a jej wyznacznik wyznacznikiem formy.
Warunkiem koniecznym i wystarczającym na to aby forma kwadratowa
Ax
x
T
, gdzie A jest macierzą
symetryczną stopnia n-tego, była dodatnio określona jest spełnienie następujących warunków:
,
0
11
a
0
det
22
21
12
11
a
a
a
a
,
0
det
33
31
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
, .....,
0
det A
Warunkiem koniecznym i wystarczającym na to aby forma kwadratowa
Ax
x
T
, gdzie A jest macierzą
symetryczną stopnia n-tego, była ujemnie określona jest spełnienie następujących warunków:
,
0
11
a
0
det
22
21
12
11
a
a
a
a
,
0
det
33
31
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
, .....,
0
det A
dla n parzystego,
a
0
det A
dla n nieparzystego
Warunkiem koniecznym i wystarczającym na to aby forma kwadratowa
Ax
x
T
, gdzie A jest macierzą
symetryczną stopnia n-tego, była dodatnio półokreślona jest spełnienie następujących warunków:
,
0
11
a
0
det
22
21
12
11
a
a
a
a
,
0
det
33
31
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
, .....,
0
det A
Warunkiem koniecznym i wystarczającym na to aby forma kwadratowa
Ax
x
T
, gdzie A jest macierzą
symetryczną stopnia n-tego, była ujemnie półokreślona jest spełnienie następujących warunków:
,
0
11
a
0
det
22
21
12
11
a
a
a
a
,
0
det
33
31
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
, .....,
0
det A
Zadanie 1. Zapisz formę kwadratową w postaci macierzowej o macierzy symetrycznej.
1)
2)
3)
4)
5)
Zadanie 2. Zbadaj określonośd formy kwadratowej
6)
7)
8)
2
9)
METODY ROZWIĄZYWANIA UKŁADÓW RÓWNAO:
1) Za pomocą macierzy odwrotnej : Ax=b
b
A
x
1
2) Układ Cramera
Układ równao liniowych Ax=b nazywamy układem Cramera wtedy i tylko wtedy gdy:
1. ilośd równao w układzie jest równa ilości niewiadomych
2. macierz A tego układu jest macierzą nieosobliwą
Wzory Cramera
Twierdzenie: jeżeli układ równao liniowych jest układem Cramera to posiada rozwiązanie
wyrażone wzorami nazywanymi wzorami Cramera
A
A
x
det
det
1
1
,
A
A
x
det
det
2
2
, ...,
A
A
x
n
n
det
det
j
A
det
(j=1,2,...,n) – jest wyznacznikiem macierzy powstałej z macierzy A w wyniku
zastąpienia jej j-tej kolumny kolumną wyrazów wolnych
3) Twierdzenie Kroneckera Capellego
Macierz uzupełniona powstaje przez dołączenie do macierzy A kolumny wyrazów wolnych b
b
A
U
Twierdzenie Kroneckera – Capellego
Układ równao liniowych Ax=b nie jest układem sprzecznym wtedy i tylko wtedy gdy rzA=rzU; przy
czym jeżeli rzA=rzU=n to układ jest układem oznaczonym, a jeżeli rzA=rzU<n to układ jest układem
nieoznaczonym.
Wniosek: jeżeli
rzU
rzA
to układ jest układem sprzecznym.
1
rzA
rzA
rzU
ROZWIĄZANIA BAZOWE
W układzie nieoznaczonym, w którym rzA=rzU=r<n, zmienne
nazywamy zmiennymi
bazowymi, a zmienne
zmiennymi swobodnymi. Rozwiązanie, w którym zmienne
swobodne przyjmują wartości równe zero, nazywamy rozwiązaniem bazowym. Wszystkich rozwiązao
bazowych może byd co najwyżej
.
n- ilośd zmiennych, które mogą byd zmiennymi niebazowymi (wszystkie oprócz stałych),
r- ilośd zmiennych niebazowych (ilośd parametrów).
Zadanie 3. Rozwiąż układ równao za pomocą macierzy odwrotnej:
2
2
2
1
2
3
z
x
z
y
x
z
y
x
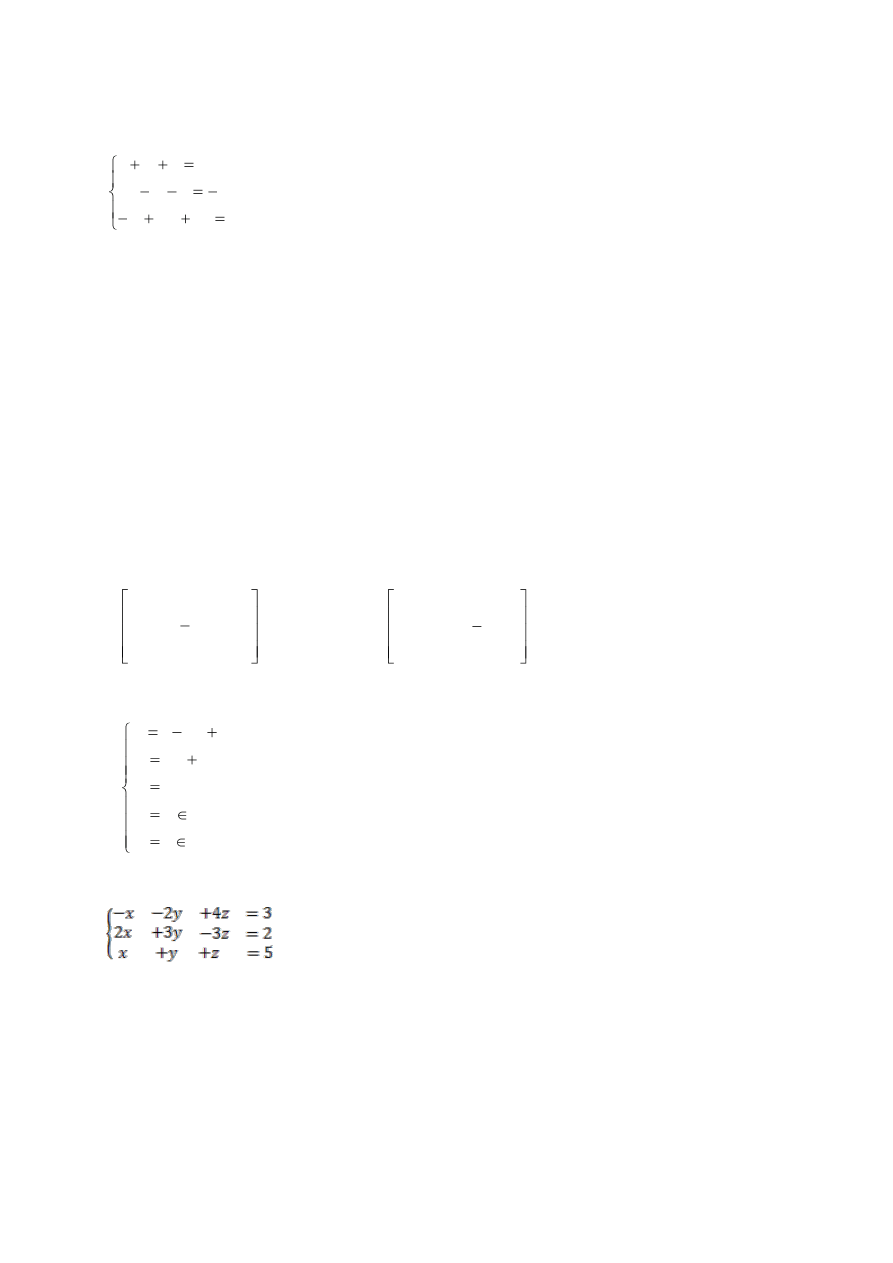
3
Zadanie 4. Za pomocą wzorów Cramera rozwiąż układ równao:
12
3
2
3
2
6
z
y
x
z
y
x
z
y
x
Zadanie 5. Napisz macierz uzupełnioną układu 5 równao z 4 niewiadomymi, wiedząc, że rzU = 5. Co
możesz powiedzied o tym układzie?
Zadanie 6. Napisz macierz układu równao tak, aby miała wymiar 3x7 i rząd równy 3. Co możesz
powiedzied o tym układzie równao?
Zadanie 7. Napisz przykład macierzy uzupełnionej układu 4 równao z 3 niewiadomymi tak, aby rząd
macierzy układu był równy 2 i układ ten był:
a) sprzeczny,
b) niesprzeczny.
Zadanie 8. Co możesz powiedzied o układzie 5 równao z 5 niewiadomymi, którego rząd macierzy:
a) uzupełnionej układu równao jest równy 5,
b) układu równao jest równy 5,
c) macierzy układu równao jest równy 4?
Zadanie 9. Czy rząd macierzy uzupełnionej układu równao może byd równy 5, jeżeli macierz układu
ma postad A
5x7
i rzA = 3?
Zadanie 10. Wyznacz wszystkie rozwiązania bazowe oraz dwa różne rozwiązania ogólne układu
równao, którego postad bazowa macierzy uzupełnionej wygląda następująco:
a)
0
0
0
0
0
0
1
1
1
0
0
2
3
0
1
b)
2
1
1
0
0
1
3
0
1
0
0
0
0
0
1
Zadanie 11. Ile może posiadad rozwiązao bazowych układ równao, którego rozwiązanie ogólne jest
postaci:
a)
R
b
x
R
a
x
x
b
a
x
b
a
x
5
4
3
2
1
3
2
2
7
1
Odpowiedź uzasadnij. Wyznacz wszystkie rozwiązania bazowe, jakie istnieją.
Zadanie 12. Podaj wszystkie rozwiązania bazowe układu równao: