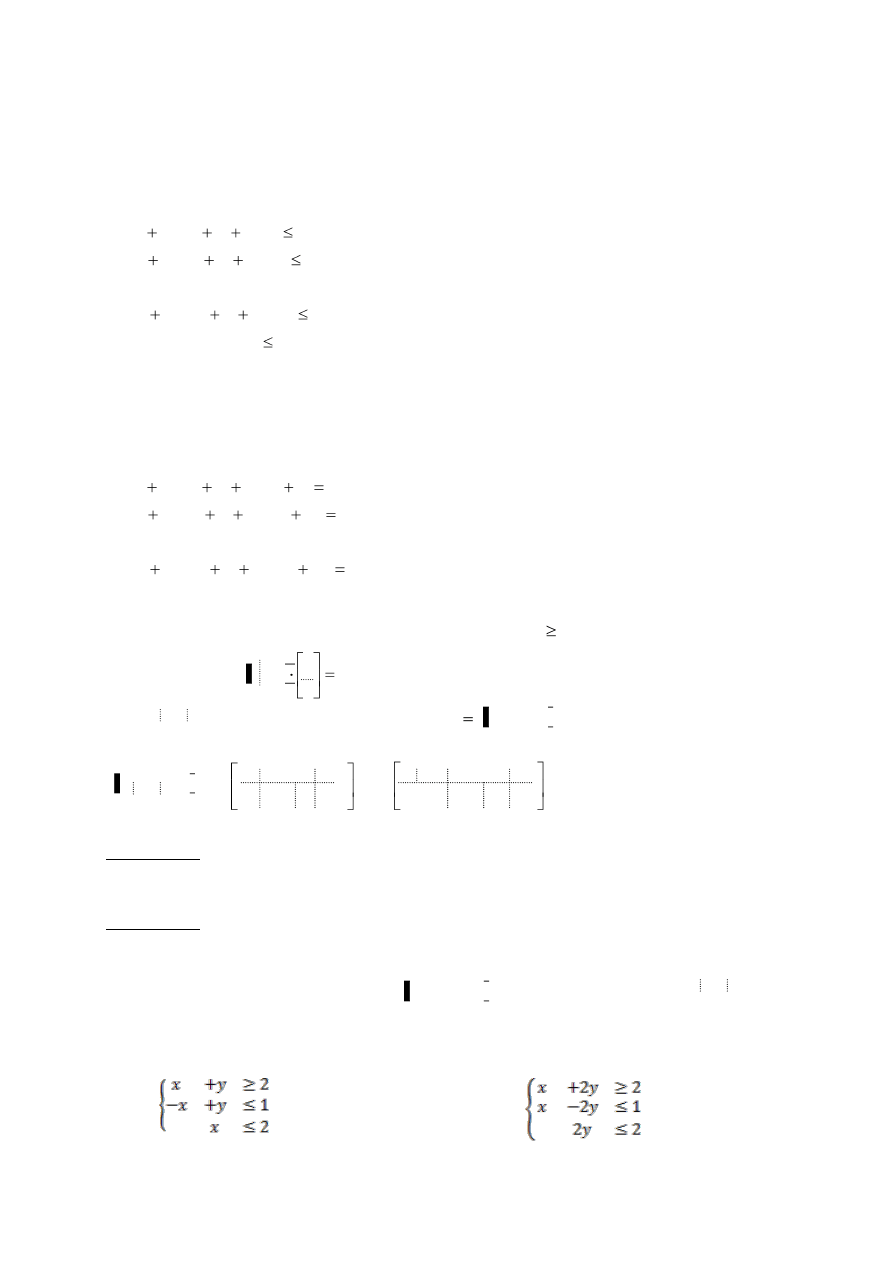
1

ALGEBRA – ZAJĘCIA VII

UKŁADY NIERÓWNOŚCI LINIOWYCH

Układ m nierówności liniowych o n niewiadomych ma postad:

m

n

mn

m

m

n

n

n

n

b

x

a

x

a

x

a

b

x

a

x

a

x

a

b

x

a

x

a

x

a

...

.....

..........

..........

..........

..........

...

...

2

2

1

1

2

2

2

22

1

21

1

1

2

12

1

11

Możemy zapisad :

b

Ax

Rozwiązaniem układu nierówności jest każdy punkt przestrzeni

n

R

(wektor i n współrzędnych),

którego współrzędne spełniają jednocześnie wszystkie nierówności tego układu. Zbiór takich
punktów (wektorów) nazywamy zbiorem rozwiązao układu nierówności liniowych.
Układ nierówności liniowych nazywamy sprzecznym, jeżeli zbiór rozwiązao tego układu jest zbiorem
pustym, w przeciwnym wypadku układ nazywamy układem nieoznaczonym.

m

m

n

mn

m

m

n

n

n

n

b

z

x

a

x

a

x

a

b

z

x

a

x

a

x

a

b

z

x

a

x

a

x

a

...

.....

..........

..........

..........

..........

...

...

2

2

1

1

2

2

2

2

22

1

21

1

1

1

2

12

1

11

Każdemu rozwiązaniu

0

0

2

0

1

,...,

,

n

x

x

x

układu nierówności odpowiada określone rozwiązanie

0

0

2

0

1

0

0

2

0

1

,...,

,

,

,...,

,

m

n

z

z

z

x

x

x

układu równao, przy czym wszystkie z 0.

Układ równao :

b

z

x

I

A

postad macierzy uzupełnionej powyższego układu

b

I

A

U

Postacie bazowe:

1

1

c

R

I

,

2

2

1

1

c

I

R

O

c

R

I

,

2

2

1

1

3

c

I

R

O

c

R

R

I

Twierdzenie 1:
Jeżeli macierz uzupełnioną układu równao, która odpowiada układowi nierówności sprowadzimy do
postaci bazowej 1 to układ nierówności nie będzie sprzeczny(ma rozwiązanie).
Twierdzenie 2:
Jeżeli macierz uzupełniona układu równao, który odpowiada układowi nierówności sprowadzimy do
postaci bazowej 2 lub 3 to układ nierówności nie będzie układem sprzecznym wtedy i tylko wtedy,

gdy układ równao o macierzy uzupełnionej

2

2

c

I

R

będzie posiadał przynajmniej jedno

nieujemne rozwiązanie bazowe.

Zadanie 1. Rozwiąż graficznie i algebraicznie układ nierówności:

1)

2)

2

3)

4)

5)

6)

7)

8)

9)

10)