14
Modele z czasem dyskretnym
Przykłady i zadania z tego rozdziału ilustruj ˛
a materiał zawarty w rozdziałach 12 i 15
ksi ˛
a˙zki.
14.1.
Metoda pajęczynowa
P
RZYKŁAD
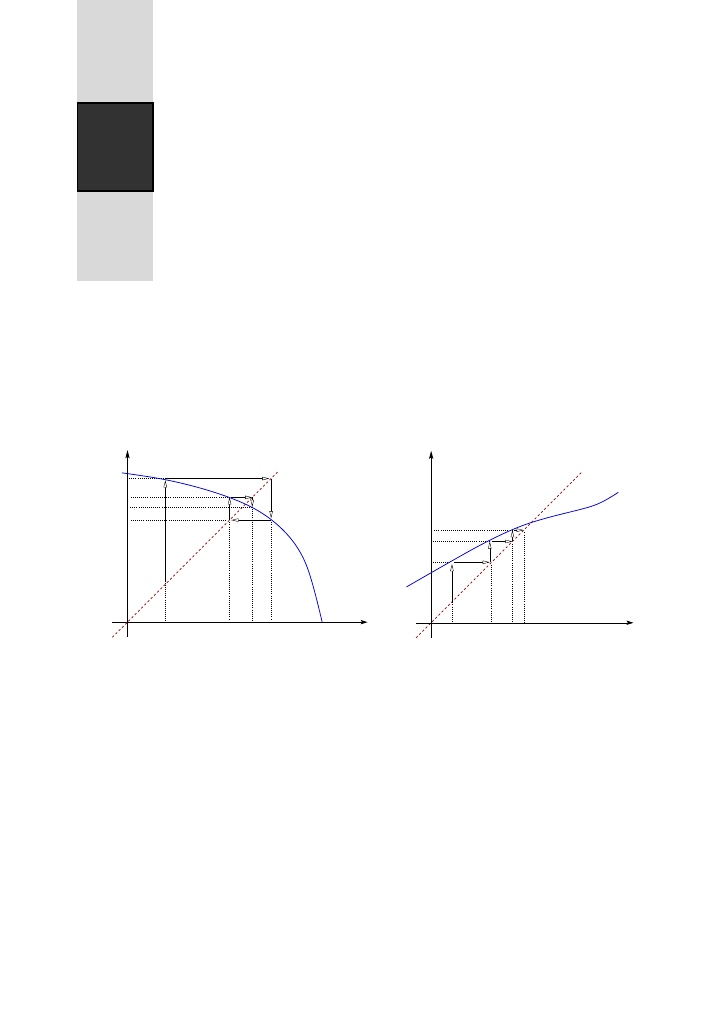
14.1. Na poni˙zszych rysunkach zilustrowano metod˛e paj˛eczynow ˛
a:
x
x
2
= f (x
1
)
x
4
= f (x
3
)
x
5
= f (x
4
)
x
3
= f (x
2
)
x
1
x
3
x
4
x
2
y
= f (x)
y
=
x
x
x
4
= f (x
3
)
x
3
= f (x
2
)
x
2
= f (x
1
)
x
1
x
2
x
3
x
4
y
= f (x)
y
=
x
Na rysunkach przedstawiono wykresy dwóch funkcji y
= f (x) (lini ˛a ci ˛agł ˛a) oraz
prostej y
= x lini ˛a przerywan ˛a. Przeci˛ecia si˛e tych krzywych to punkty stacjonarne
równania ró˙znicowego x
n
+1
= f (x
n
). Aby zobaczy´c, w jaki sposób zachowuje si˛e
rozwi ˛
azanie, post˛epujemy zgodnie z przedstawionym opisem.
Startujemy z dowolnego punktu x
1
poło˙zonego na osi 0X. Przesuwamy si˛e pio-
nowo w gór˛e (lub w dół), a˙z napotkamy wykres funkcji f . Osi ˛
agn˛eli´smy wysoko´s´c
f (x
1
)
= x
2
, aby x
2
odznaczy´c na osi 0X przesuwamy si˛e poziomo (w prawo lub
w lewo), a˙z napotkamy wykres prostej y
= x. Teraz znajdujemy si˛e nad punktem
x
2
na osi 0X. Dalej powtarzamy t˛e procedur˛e i obserwujemy, jak rozwi ˛
azanie si˛e za-
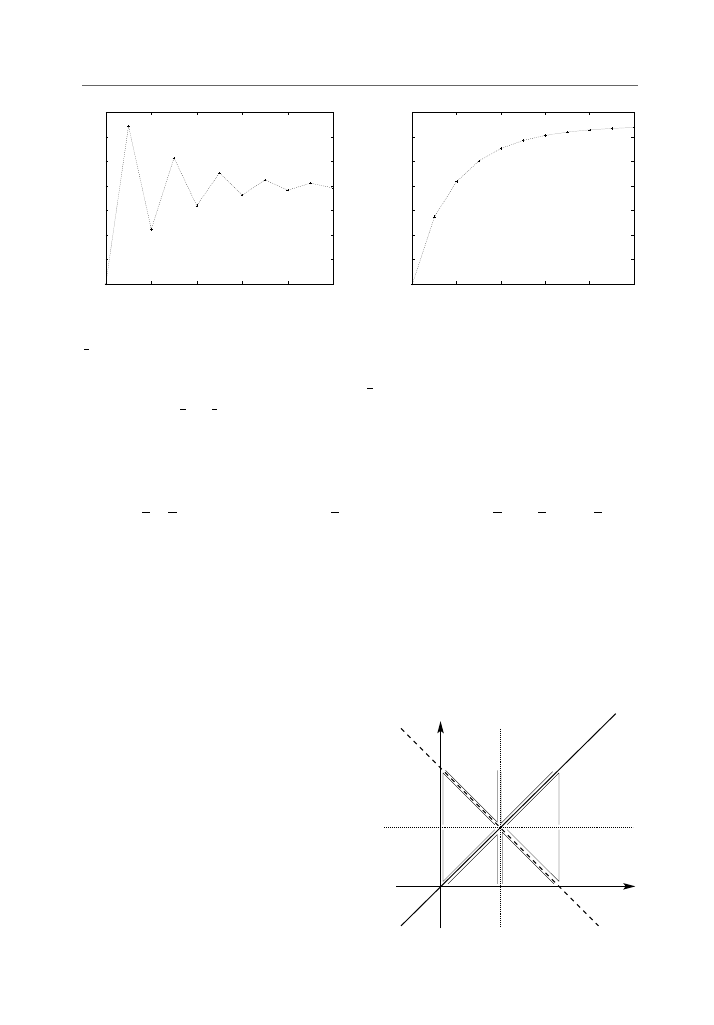
chowuje. Na powy˙zszych rysunkach rozwi ˛
azanie zbli˙za si˛e do punktu stacjonarnego;
w pierwszym przypadku oscyluj ˛
ac dookoła (na kolejnym rysunku po lewej stronie
przedstawiono przykład zachowania si˛e w czasie x
t
w tym przypadku), za´s w drugim
pozostaj ˛
ac zawsze po tej samej stronie punktu stacjonarnego (na rysunku po prawej
stronie przedstawiono przykład zachowania si˛e w czasie x
t
w tym przypadku).
90
Zbiór zadań z matematyki dla biologów
0.8
0.85
0.9
0.95
1
1.05
1.1
1.15
0
2
4
6
8
10
0.8
0.805
0.81
0.815
0.82
0.825
0.83
0.835
0
2
4
6
8
10
P
RZYKŁAD
14.2.
Zbada´c stabilno´s´c punktów stacjonarnych równania x
n
+1
=
3
2
x
n
(1
− x
n
)
= f (x
n
).
R
OZWI ˛
AZANIE
. Znajd´zmy najpierw punkty stacjonarne. S ˛
a to te punkty, w któ-
rych x
n
+1
= x
n
, czyli te, dla których x
=
3
2
x(1
− x). St ˛ad wynika, ˙ze albo ¯x
1
= 0,
albo
¯x
2
= 1 −
2
3
=
1
3
.
Zgodnie z twierdzeniem 15.1 z ksi ˛
a˙zki, punkty s ˛
a stabilne, je´sli
|f
′
(
¯x)| < 1. Za-
tem, aby zbada´c stabilno´s´c tych punktów, obliczmy warto´s´c pochodnej prawej strony
równania w tych punktach. Mamy:
f
′
(x)
=
3
2
−
3
x
,
⇒ f ( ¯x
1
)
= f (0) =
3
2
> 1,
f (
¯x
2
)
= f
1
3
=
3
2
−1 =
1
2
< 1.
Widzimy, ˙ze f (
¯x
1
) > 1, zatem punkt stacjonarny
¯x
1
jest niestabilny, natomiast
punkt
¯x
2
jest lokalnie asymptotycznie stabilny, gdy˙z
−1 < f
′
(
¯x
2
) < 1, a poniewa˙z
0 < f
′
(
¯x
2
), to rozwi ˛
azania zbli˙zaj ˛
a si˛e do tego punktu, pozostaj ˛
ac po jednej jego
stronie (nie oscyluj ˛
ac).
To samo mo˙zna zrobi´c, korzystaj ˛
ac z metody paj˛eczynowej, rysuj ˛
ac wykres funk-
cji prawej strony. Co wi˛ecej, metoda paj˛eczynowa, czy raczej rysunek, mo˙ze rozstrzyg-
n ˛
a´c stabilno´s´c punktu w przypadku gdy
|f
′
(
¯x)| = 1 i kryterium analityczne nie daje
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
000000000000000
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
111111111111111
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
00000000
00000000
00000000
00000000
00000000
00000000
00000000
11111111
11111111
11111111
11111111
11111111
11111111
11111111
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
00000000
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
11111111
0000000
0000000
0000000
0000000
0000000
0000000
0000000
0000000
0000000
0000000
0000000
0000000
0000000
0000000
1111111
1111111
1111111
1111111
1111111
1111111
1111111
1111111
1111111
1111111
1111111
1111111
1111111
1111111
a
y
a
x
odpowiedzi. Spójrzmy na rysunek zamiesz-
czony obok. Lini ˛
a ci ˛
agł ˛
a zaznaczono pro-
st ˛
a y
= x, natomiast lini ˛a przerywan ˛a
y
= −x + 2a. Linie kropkowane, to odpo-
wiednio proste x
= a i y = a. Rozwa˙zmy
takie równanie ró˙znicowe x
n
+1
= f (x
n
), ˙ze
f (a)
= a (czyli punkt ¯x = a jest punktem
stacjonarnym). Zauwa˙zmy, ˙ze w zale˙zno-
´sci od poło˙zenia punktu (x
n
, f (x
n
)), mo˙ze-
my wydedukowa´c, gdzie b˛edzie znajdował
si˛e punkt (x
n
+1
, f (x
n
+1
)). Mianowicie, je-
´sli punkt (x
n
, f (x
n
)) b˛edzie znajdował si˛e
w obszarze zaznaczonym pionowymi kres-
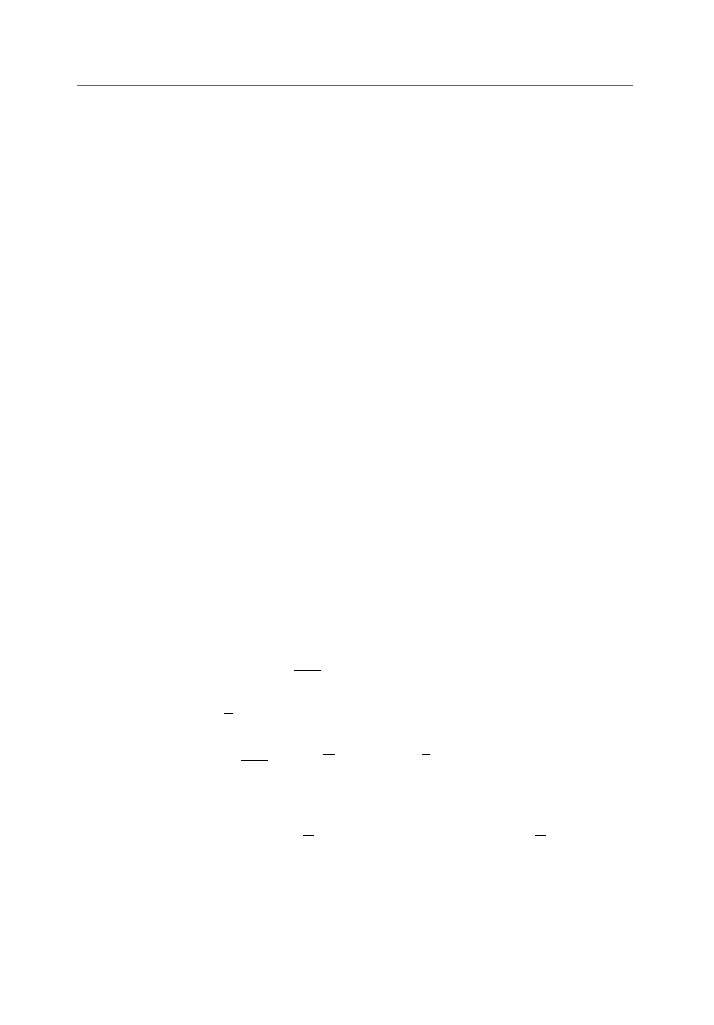
14. Modele z czasem dyskretnym
91
kami, to punkt x
n
+1
b˛edzie bli˙zej a, ale po tej samej stronie a co x
n
. Je´sli punkt
(x
n
, f (x
n
)) b˛edzie znajdował si˛e w obszarze zaznaczonym poziomymi kreskami, to
punkt x
n
+1
b˛edzie si˛e znajdował po drugiej stronie punktu stacjonarnego, ale tak˙ze bli-
˙zej punktu a ni˙z x
n
. Ponadto zauwa˙zmy, ˙ze je´sli punkt (x
n
, f (x
n
) b˛edzie znajdował si˛e
w obszarze zakreskowanym w kratk˛e lub lini ˛
a łaman ˛
a, to x
n
+1
b˛edzie dalej od punktu
a ni˙z x
n
, odpowiednio po drugiej stronie lub po tej samej stronie punktu stacjonarnego.
St ˛
ad mo˙zna wywnioskowa´c, co nast˛epuje: je´sli wykres funkcji f znajduje si˛e
(w otoczeniu punktu stacjonarnego) w obszarze zakreskowanym pionowo, to punkt
stacjonarny jest lokalnie stabilny i rozwi ˛
azania zbli˙zaj ˛
a si˛e do a, pozostaj ˛
ac po tej
samej stronie (nie ma oscylacji). Gdy wykres funkcji f znajduje si˛e w obszarze
zakreskowanym poziomo, to punkt jest lokalnie stabilny, ale rozwi ˛
azania zbli˙zaj ˛
a
si˛e do niego, oscyluj ˛
ac wokół a. W przypadku gdy wykres znajduje si˛e w obszarze
zaznaczonym lini ˛
a z ˛
abkowan ˛
a, punkt jest niestabilny i rozwi ˛
azania oddalaj ˛
a si˛e od
a, pozostaj ˛
ac po tej samej stronie punktu stacjonarnego. Gdy wykres jest w ob-
szarze zakratkowanym, rozwi ˛
azanie oddala si˛e od punktu stacjonarnego (który jest
niestabilny), oscyluj ˛
ac wokół a.
Czytelnikowi pozostawiamy zastanowienie si˛e i sprawdzenie (za pomoc ˛
a metody
paj˛eczynowej), co si˛e dzieje, gdy wykres funkcji znajduje si˛e po obu stronach punktu
stacjonarnego w obszarach ró˙znie zakreskowanych.
P
RZYKŁAD
14.3.
Rozwa˙zmy model opisuj ˛
acy ograniczony wzrost populacji.
W modelu logistycznym szybko´s´c wzrostu per capita malała wraz ze wzrostem za-
g˛eszczenia populacji. Rozs ˛
adnie jest przyj ˛
a´c, ˙ze wzrost per capita nie mo˙ze by´c
mniejszy ni˙z
−1 („co najwy˙zej jedna ´smier´c na jednego osobnika”). We´zmy zatem
funkcj˛e, która b˛edzie funkcj ˛
a malej ˛
ac ˛
a i b˛edzie d ˛
a˙zyła do
−1 w niesko´nczono´sci.
Wybieramy funkcj˛e f (N )
= ae
−bN
− 1 (oczywi´scie nie jest to jedyny mo˙zliwy czy
słuszny wybór – mo˙zna wybiera´c tak˙ze inne funkcje o własno´sciach wymienionych
powy˙zej). Wtedy otrzymujemy:
1N
N
= ae
−bN
− 1.
Przyjmuj ˛
ac teraz b
=
r
K
i a
= e
r
, otrzymujemy:
1N
N
= e
r
e
−
rN
K
− 1 = e
r
(
1
−
N
K
) − 1.
A zatem:
N
t
+1
− N
t
= N
t
e
r
1
−
Nt
K
− 1
H⇒
N
t
+1
= N
t
e
r
1
−
Nt
K
.
Zauwa˙zmy, ˙ze w tym modelu K mo˙zna traktowa´c jako pojemno´s´c ´srodowiska.
Gdy N
t
> K przyrost per capita jest ujemny (czyli liczebno´s´c populacji si˛e zmniej-
sza), podczas gdy dla N
t
< K jest dodatni (czyli liczebno´s´c populacji si˛e zwi˛eksza).

92
Zbiór zadań z matematyki dla biologów
Znale´z´c punkty stacjonarne i zbada´c ich stabilno´s´c.
R
OZWI ˛
AZANIE
. Szukamy punktów stacjonarnych, czyli takich ¯
N , ˙ze ¯
N
=
¯
N e
r
1
−
¯
N
K
. St ˛
ad od razu wida´c, ˙ze albo ¯
N
= 0, albo:
e
r
1
−
¯
N
K
= 1 H⇒
1
−
¯
N
K
= 0 H⇒ ¯
N
= K.
Zach˛ecamy Pa´nstwa do zbadania stabilno´sci tych punktów metod ˛
a paj˛eczynow ˛
a
po narysowaniu w jakim´s programie wykresu funkcji y
= xe
r(1
−x/K)
. My tutaj prze-
prowadzimy rozumowanie analityczne. Policzymy pochodn ˛
a prawej strony:
F (N )
= Ne
r
(
1
−
N
K
) H⇒ F
′
(N )
= e
r
(
1
−
N
K
) −
rN
K
e
r
(
1
−
N
K
).
W punkcie ¯
N
= 0 mamy F
′
(0)
= e
r
> 1, zatem ten punkt jest niestabilny.
W punkcie ¯
N
= K mamy F
′
(K)
= 1 − r, zatem ten punkt jest asymptotycznie
stabilny dla r
∈ (0, 2) (bo wtedy |F
′
(K)
| < 1), niestabilny dla r > 2 (bo wte-
dy F
′
(K) <
−1). Dla r = 2 z wykresu funkcji (i metody paj˛eczynowej) mo˙zna
wywnioskowa´c, ˙ze punkt jest asymptotycznie stabilny. Mianowicie, wykres funkcji
mie´sci si˛e (w otoczeniu punktu (K, F (K)) w obszarze zakreskowanym poziomo na
rysunku w przykładzie 14.2.
P
RZYKŁAD
14.4. Przypu´s´cmy, ˙ze w lesie wyst˛epuj ˛
a dwa gatunki drzew. Nazwijmy
je A i B. W ka˙zdym roku pewna liczba drzew ka˙zdego z gatunków umiera. Przypu-
´s´cmy, ˙ze ´srednio co roku umiera jedno na 50 drzew gatunku A i jedno na 10 drzew
gatunku B. Czwarta cz˛e´s´c zwolnionych miejsc jest zajmowana przez drzewa gatun-
ku A, za´s trzy czwarte przez drzewa gatunku B (mo˙zemy o tym my´sle´c jak o prawdo-
podobie´nstwie: drzewa gatunku A zajmuj ˛
a wolne miejsca z prawdopodobie´nstwem
25%, a drzewa gatunku B z prawdopodobie´nstwem 75%). Oznaczaj ˛
ac przez A
t
i B
t
liczebno´s´c populacji drzew gatunku A i B w roku t, konstruujemy model.
Liczebno´s´c drzew gatunku A roku t
+ 1 mo˙zemy policzy´c nast˛epuj ˛aco: ta cz˛e´s´c
drzew tego gatunku, które prze˙zyły wynosi 0,98A
t
; 0,02 drzew umarło i zwolniło
miejsca, z których to 25% zaj˛eły młode drzewa gatunku A (b˛edzie ich 0,02
· 0,25A
t
);
dodatkowo młode drzewa gatunku A zaj˛eły 25% miejsc zwolnionych przez umarłe
drzewa gatunku B (tych jest 0,10B
t
), czyli tych młodych drzew b˛edzie 0,10
· 0,25B
t
).
St ˛
ad otrzymujemy równanie:
A
t
+1
= (0,98 + 0,02 · 0,25)A
t
+ 0,10 · 0,25B
t
.
Analogicznie konstruujemy równanie opisuj ˛
ace liczebno´s´c drzew gatunku B w ro-
ku t
+ 1. Mamy:
B
t
+1
= 0,02 · 0,75A
t
+ (0,90 + 0,10 · 0,75)B
t
.

14. Modele z czasem dyskretnym
93
St ˛
ad otrzymujemy nasz model – układ równa´n:
A
t
+1
= 0,985A
t
+ 0,025B
t
,
B
t
+1
= 0,015A
t
+ 0,975B
t
.
Otrzymany liniowy układ równa´n mo˙zemy zapisa´c w postaci macierzowej jako:
A
t
+1
B
t
+1
=
0,985
0,025
0,015
0,975
|
{z
}
=M
A
t
B
t
.
T˛e macierz oznaczmy literk ˛
a M. Co mo˙zna powiedzie´c o strukturze tego lasu po dłu-
gim czasie?
R
OZWI ˛
AZANIE
. Zauwa˙zmy najpierw, ˙ze – je´sli we´zmiemy wektory
v
1
=
1
−1
i
v
2
=
5
3
oraz policzymy iloczyn macierzy M i wektora v
1
, a tak˙ze macierzy M i wektora v
2
,
to otrzymamy:
0,985
0,025
0,015
0,975
1
−1
=
0,96
−0,96
= 0,96v
1
oraz
0,985
0,025
0,015
0,975
5
3
=
5
3
= 1 · v
2
.
Przypu´s´cmy teraz, ˙ze pocz ˛
atkowym stanem układu (w chwili t
= 0) jest wektor
A
0
B
0
= w
0
= αv
1
+ βv
2
. Stan układu w chwili t opisuje wektor w
t
=
A
t
B
t
.
Zauwa˙zmy, ˙ze wtedy w
t
+1
= Mw
t
. Zatem:
w
1
= Mw
0
= M(αv
1
+ βv
2
)
= αMv
1
+ βMv
2
= 0,96αv
1
+ βv
2
.
Jak łatwo zauwa˙zy´c, powtarzaj ˛
ac powy˙zsze rachunki, otrzymamy:
w
t
= (0,96)
t
αv
1
+ βv
2
t
→∞
−−−→ βv
2
.
A wi˛ec, dla du˙zych t struktura gatunkowa lasu b˛edzie zbli˙zała si˛e do takiej, gdy
stosunek liczebno´sci drzew gatunku A do drzew gatunku B wynosi 5 do 3.
W zadaniu 14.4 proszeni s ˛
a Pa´nstwo o wyliczenie zachowania si˛e tego układu dla
konkretnych danych pocz ˛
atkowych.
P
RZYKŁAD
14.5. Rozwa˙zmy ro´slin˛e, która ˙zyje maksymalnie dwa lata. W pierw-
szym roku ˙zycia młode ro´sliny wydaj ˛
a nasiona, z których w roku nast˛epnym rozwijaj ˛
a
si˛e nowe ro´sliny. Z nasion wysianych przez dwie młode ro´sliny rozwija si˛e w roku na-
94
Zbiór zadań z matematyki dla biologów
st˛epnym ´srednio jedna młoda ro´slina. Czwarta cz˛e´s´c młodych ro´slin prze˙zywa zim˛e
i w nast˛epnym roku wydaje nasiona. Z nasion jednej starej ro´sliny (czyli w drugim
roku ˙zycia) w nast˛epnym roku kiełkuj ˛
a ´srednio dwie nowe młode ro´sliny.
Zaproponowa´c model opisuj ˛
acy rozwój tej populacji i przedyskutowa´c jej zacho-
wanie, gdy n
→ ∞, zakładaj ˛ac, ˙ze pocz ˛atkowo zag˛eszczenie młodych ro´slin wynosi
6, a starych ro´slin 3.
R
OZWI ˛
AZANIE
. Przez x
n
oznaczmy zag˛eszczenie młodych ro´slin (ro´slin
w pierwszym roku ˙zycia) w n-tym roku. Niech y
n
oznacza zag˛eszczenie starych ro´slin
(ro´slin w drugim roku ˙zycia) w n-tym roku. Z danych zadania wynika, ˙ze zag˛eszcze-
nie młodych ro´slin w roku n
+ 1 wynosi x
n
+1
=
1
2
x
n
+ 2y
n
, natomiast starych ro´slin
jest tyle, ile młodych przetrwało zim˛e, czyli y
n
+1
=
1
4
x
n
. St ˛
ad otrzymujemy:
x
n
+1
=
1
2
x
n
+ 2y
n
,
y
n
+1
=
1
4
x
n
.
Wstawiaj ˛
ac drugie równanie do pierwszego, dostajemy x
n
+1
=
1
2
x
n
+ 2 ·
1
4
x
n
−1
.
Szukamy rozwi ˛
aza´n postaci x
n
= λ
n
(por. ksi ˛
a˙zka, podrozdz. 12.5 i 15.5). Wstawiamy
x
n
= λ
n
do ostatniego równania i otrzymujemy:
λ
n
+1
=
1
2
λ
n
+
1
2
λ
n
−1
H⇒ λ
2
−
1
2
λ
−
1
2
= 0.
Równanie to ma dwa rozwi ˛
azania: λ
1
= 1 i λ
2
= −
1
2
. Zatem rozwi ˛
azania s ˛
a
postaci:
x
n
= A · 1
n
+ B ·
−
1
2
n
,
y
n
=
1
4
· A +
1
4
· B ·
−
1
2
n
−1
.
(⋆)
Stałe A i B wyznaczamy z danych pocz ˛
atkowych. Mamy:
x
0
= 6,
x
1
=
1
2
· x
0
+ 2 · y
0
=
1
2
· 6 + 2 · 3 = 9.
St ˛
ad otrzymujemy układ równa´n:
dla n
= 0 :
A
+ B = 6,
dla n
= 1 :
A
−
1
2
B
= 9.
Rozwi ˛
azujemy układ, znajduj ˛
ac A
= 8 i B = −2. Wstawiamy wyliczone A i B do
układu (⋆) i otrzymujemy ostateczn ˛
a posta´c rozwi ˛
azania naszego modelu:
x
n
= 8 +
−
1
2
n
−1
,
y
n
= 2 +
−
1
2
n
.
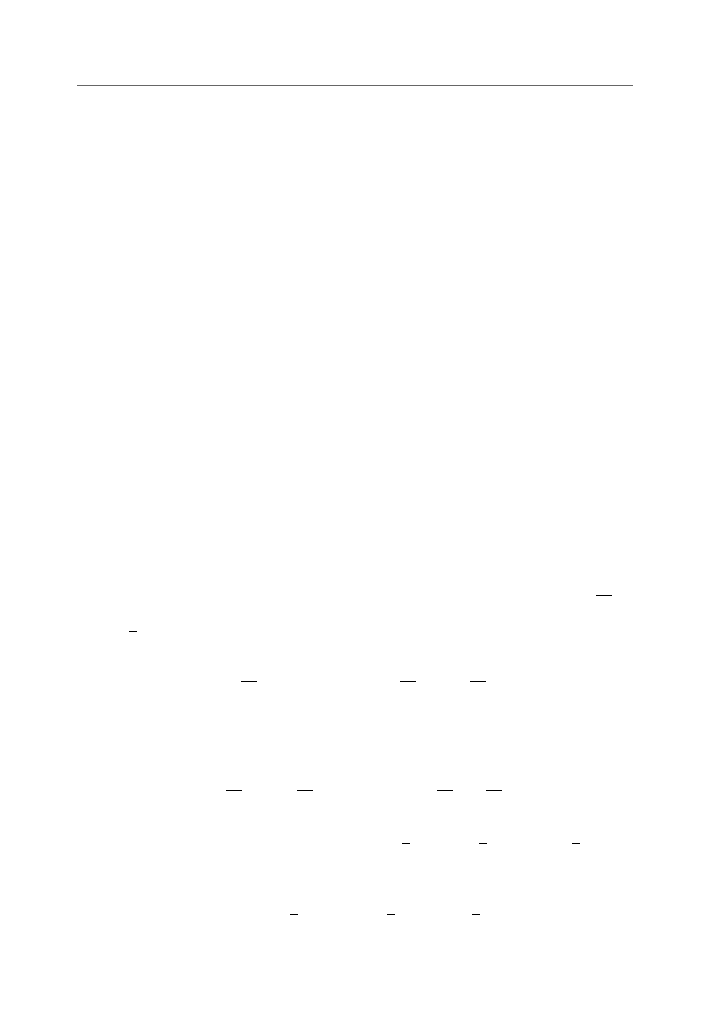
14. Modele z czasem dyskretnym
95
Teraz łatwo ju˙z zobaczy´c, ˙ze gdy n ro´snie, to zag˛eszczenie młodych ro´slin x
n
zbli˙za si˛e do 8, za´s zag˛eszczenie starych ro´slin zbli˙za si˛e do 2.
P
RZYKŁAD
14.6. Rozwa˙zmy populacj˛e, któr ˛
a mo˙zna podzieli´c na trzy równe klasy
wiekowe. Pierwsz ˛
a klas˛e stanowi ˛
a osobniki niedojrzałe, niezdolne do rozmna˙zania,
w´sród których panuje tak du˙za ´smiertelno´s´c, ˙ze tylko co szesnasty osobnik przechodzi
do klasy nast˛epnej – osobników w pełni dojrzałych. Ka˙zdy z dojrzałych osobników,
przed osi ˛
agni˛eciem wieku starczego, daje ´srednio 31 nowych osobników gatunku.
´Smiertelno´s´c w tej klasie wiekowej jest ni˙zsza, tak ˙ze wiek starczy osi ˛aga co drugi
osobnik. W wieku starczym osobniki mog ˛
a si˛e jeszcze rozmna˙za´c, ale ich zdolno-
´sci reprodukcyjne zostały zmniejszone, tak ˙ze do ko´nca ˙zycia ka˙zdy z nich ´srednio
wyda 15 nowych osobników tego gatunku. Skonstruowa´c model opisuj ˛
acy rozwój
opisanej wy˙zej populacji. Wyznaczy´c zag˛eszczenie osobników w ka˙zdej grupie wie-
kowej osobników niedojrzałych po 10 okresach, wiedz ˛
ac, ˙ze na pocz ˛
atku zag˛eszcze-
nie osobników niedojrzałych wynosi 10, zag˛eszczenie osobników dojrzałych 4, za´s
zag˛eszczenie osobników starych wynosi 2.
R
OZWI ˛
AZANIE
. Niech x
n
oznacza zag˛eszczenie osobników niedojrzałych w
n-tym okresie (zwró´cmy uwag˛e, ˙ze w zadaniu nie jest powiedziane, ile lat wynosi taki
okres – mo˙ze to by´c zarówno jeden rok, jak i mo˙zemy rozwa˙za´c wielko´s´c populacji
w okresach, na przykład, pi˛etnastoletnich), niech y
n
oznacza zag˛eszczenie osobników
dojrzałych w n-tym okresie, z
n
oznacza za´s zag˛eszczenie osobników w wieku star-
czym w n-tym okresie. Osobniki niedojrzałe w okresie n
+ 1 pojawiły si˛e za spraw ˛a
osobników dojrzałych (31x
n
) i starych (15z
n
): x
n
+1
= 31y
n
+ 15z
n
.
W kolejnym okresie zag˛eszczenie osobników dojrzałych jest zwi ˛
azane z osobni-
kami niedojrzałymi w poprzednim okresie, które prze˙zyły i dzi˛eki takiemu samemu
rozumowaniu wyliczymy zag˛eszczenie osobników w wieku starczym: y
n
+1
=
1
16
x
n
,
z
n
+1
=
1
2
y
n
. St ˛
ad mo˙zemy wyliczy´c, ˙ze:
z
n
+1
=
1
32
x
n
−1
,
H⇒ x
n
+1
=
31
16
x
n
−1
+
15
32
x
n
−2
.
Stosuj ˛
ac technik˛e pokazan ˛
a w ksi ˛
a˙zce (por. podrozdz. 12.5 i 15.5 w ksi ˛
a˙zce),
szukamy rozwi ˛
aza´n postaci x
n
= λ
n
. Wstawiamy x
n
= λ
n
do ostatniego równania:
λ
n
+1
=
31
16
λ
n
−1
+
15
32
λ
n
−2
H⇒ λ
3
−
31
16
λ
−
15
32
= 0.
Pierwiastkami tego równania s ˛
a liczby: λ
1
= −
5
4
, λ
2
= −
1
4
oraz λ
3
=
3
2
. Zatem
rozwi ˛
azanie jest postaci:
x
n
= A ·
−
5
4
n
+ B ·
−
1
4
n
+ C ·
3
2
n
.
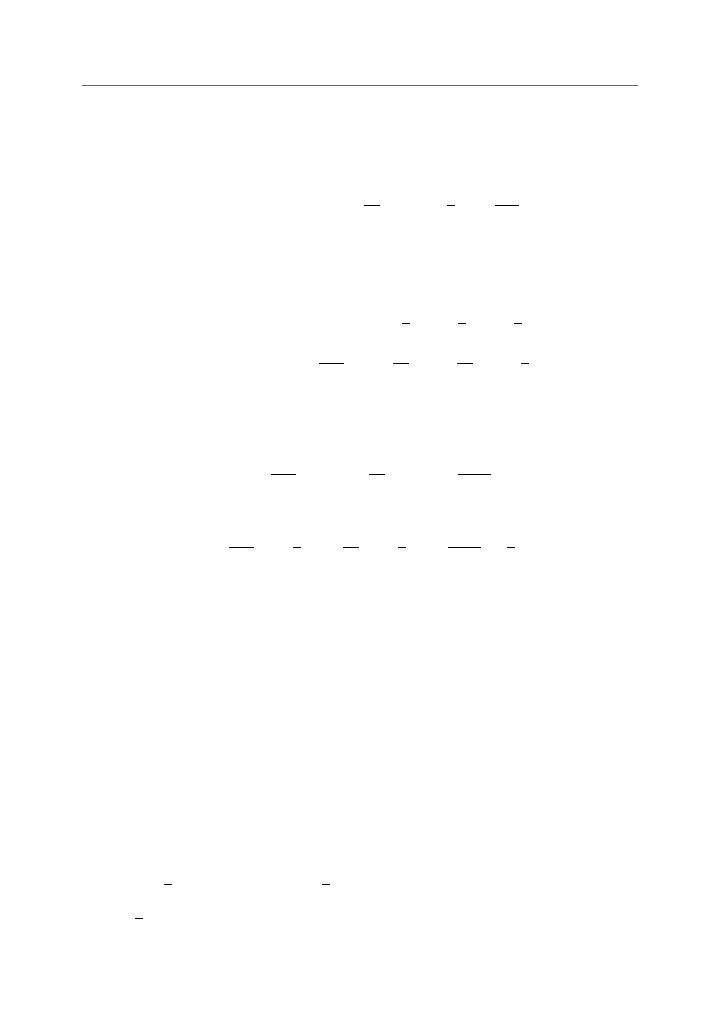
96
Zbiór zadań z matematyki dla biologów
Teraz, korzystaj ˛
ac z wiedzy o pocz ˛
atkowym zag˛eszczeniu ka˙zdej grupy wiekowej,
mo˙zemy wyznaczy´c stałe A, B i C. Zauwa˙zmy, ˙ze:
x
1
= 31y
0
+ 15z
0
= 154,
x
2
= 31y
1
+ 15z
1
= 31 ·
1
16
x
0
+ 15 ·
1
2
y
0
=
395
8
.
Korzystaj ˛
ac z wyprowadzonego wzoru na x
n
, otrzymujemy:
dla n
= 0 :
x
0
= 10 = A + B + C,
dla n
= 1 :
x
1
= 154 = −A ·
5
4
− B ·
1
4
+ C ·
3
2
,
dla n
= 2 :
x
2
=
395
8
= A ·
25
16
+ B ·
1
16
+ C ·
9
4
.
Mamy układ trzech równa´n liniowych z trzema niewiadomymi. Rozwi ˛
azuj ˛
ac go (co,
w tym przypadku, jest zaj˛eciem ˙zmudnym), otrzymujemy rozwi ˛
azanie:
A
= −
525
11
,
B
=
29
7
,
C
=
4896
77
.
A zatem:
x
n
= −
525
11
·
−
5
4
n
+
29
7
·
−
1
4
n
+
4896
77
·
3
2
n
.
St ˛
ad mamy, ˙ze zag˛eszczenie populacji osobników niedojrzałych po 10 okresach wy-
nosi x
10
≈ 3222.
14.2.
Pytania i zadania
Z
ADANIE
14.1. Korzystaj ˛
ac z metody paj˛eczynowej, zbada´c zachowanie si˛e rozwi ˛
a-
za´n równania ró˙znicowego x
n
+1
= f (x
n
) w zale˙zno´sci od warunku pocz ˛
atkowego
x
0
∈ R.
a) f (x)
= x
3
+ x,
b) f (x)
= x
3
− x,
c) f (x)
= ln x + 1,
d) f (x)
= e
x
−1
,
e) f (x)
= 1 − 2x(x − 1),
f) f (x)
= 2x(1 − x).
Z
ADANIE
14.2. Znajd´z punkty stacjonarne równania ró˙znicowego x
n
+1
= f (x
n
)
i zbadaj ich stabilno´s´c, gdy funkcja f jest dana wzorem:
a) 1
−
3
2
x(1
− x),
b) 1
−
5
2
x(1
− x),
c) x(2x
− 1),
d)
3
4
x
+ 5,
e) log
2
x
+ 1,
f) 5
x
−1
.

14. Modele z czasem dyskretnym
97
Z
ADANIE
14.3. Rozwa˙zmy pewn ˛
a populacj˛e wykazuj ˛
ac ˛
a cechy społeczne. Je´sli za-
g˛eszczenie populacji jest mniejsze od pewnej liczby L, to przyrost per capita jest
ujemny. Załó˙zmy tak˙ze, ˙ze dla zbyt licznej populacji, gdy jej liczebno´s´c przekracza
K, to przyrost per capita tak˙ze jest ujemny. Natomiast je´sli liczebno´s´c populacji mie-
´sci si˛e mi˛edzy L i K, to przyrost jest dodatni. Przy zało˙zeniu, ˙ze L < K, i przyjmuj ˛
ac
najprostsz ˛
a funkcj˛e spełniaj ˛
ac ˛
a powy˙zsze zało˙zenia, mianowicie N (N
− L)(K − N),
zbudowa´c dyskretny model opisuj ˛
acy rozwój tej populacji, znale´z´c punkty stacjonar-
ne i zbada´c ich stabilno´s´c.
Z
ADANIE
14.4. Dla modelu opisanego w przykładzie 14.4 znale´z´c graniczn ˛
a liczeb-
no´s´c drzew gatunku A i B oraz liczebno´sci tych populacji w kilku pierwszych latach,
gdy pocz ˛
atkowa liczebno´s´c drzew jest nast˛epuj ˛
aca:
a) A
0
= 700, B
0
= 100,
b) A
0
= 100, B
0
= 700.
Wskazówka. Znale´z´c warto´sci współczynników α i β, które pojawiły si˛e w przy-
kładzie 14.4 przy rozwi ˛
azywaniu układu równa´n αv
1
+ βv
2
=
A
0
B
0
, czyli α
+ 5β =
A
0
oraz
−α + 3β = B
0
.
Z
ADANIE
14.5. Pewna ro´slina ˙zyje maksymalnie dwa lata. Z ro´slin młodych, które
wykiełkowały, trzy czwarte do˙zywa drugiego roku. Ro´sliny młode mog ˛
a wyda´c na-
siona, tak ˙ze w roku nast˛epnym wykiełkuje ´srednio półtora nowej ro´sliny na ka˙zd ˛
a
młod ˛
a ro´slin˛e. Ro´sliny stare (w wieku dwóch lat) wydaj ˛
a nasiona, z których kiełkuje
w nast˛epnym roku ´srednio cztery trzecie młodej ro´sliny na ka˙zd ˛
a star ˛
a ro´slin˛e. Skon-
struowa´c model opisuj ˛
acy dynamik˛e tej populacji i przedyskutowa´c zachowanie si˛e
rozwi ˛
aza´n po wielu latach, przyjmuj ˛
ac, ˙ze pocz ˛
atkowe zag˛eszczenie ro´slin w wieku
jednego roku wynosi 5, natomiast zag˛eszczenie ro´slin w wieku dwóch lat jest rów-
ne 15.
Z
ADANIE
14.6. Rozwa˙zamy populacj˛e, któr ˛
a dzielimy na trzy równe grupy wie-
kowe. Pierwsza grupa to osobniki niedojrzałe, które nie mog ˛
a si˛e rozmna˙za´c i w´sród
nich panuje do´s´c wysoka ´smiertelno´s´c, tak ˙ze jedynie jedna dziewi ˛
ata cz˛e´s´c z nich do-
˙zywa wieku dojrzałego. Grupa druga – osobniki dojrzałe, które mog ˛
a si˛e rozmna˙za´c,
i w czasie zanim si˛e zestarzej ˛
a, wydaj ˛
a ´srednio 7 potomków na osobnika. ´Smiertel-
no´s´c w tej grupie jest zaniedbywalnie mała, tak ˙ze mo˙zemy przyj ˛
a´c, ˙ze wszystkie
osobniki dojrzałe do˙zywaj ˛
a wieku starczego. Grupa trzecia, to osobniki w wieku star-
czym. Niektóre z tych osobników mog ˛
a si˛e jeszcze rozmna˙za´c, wydaj ˛
ac do ko´nca
swojego ˙zycia ´srednio dwóch potomków na głow˛e.
Skonstruowa´c model opisuj ˛
acy rozwój tej populacji i przedyskutowa´c, jaka b˛e-
dzie struktura wiekowa populacji po długim czasie, je´sli pocz ˛
atkowo zag˛eszczenie
osobników niedojrzałych wynosi 100, dojrzałych 20, za´s starych 20.
Wskazówka. Pierwiastkami wielomianu, który skonstruuj ˛
a Pa´nstwo w trakcie
rozwi ˛
azywania zadania s ˛
a liczby: λ
1
= 1, λ
2
= −2/3, λ
3
= −1/3.
Wyszukiwarka
Podobne podstrony:
Zbior zadan z matematyki dla studentow chemii Wyd 5 e 0mkt
Zbiór zadań chemicznych dla geologów 12
Zbiór zadań matematycznych Z życia bocianów, Liczba par bociana białego w poszczególnych krajach Eur
Zbiór zadań chemicznych dla geologów 12
Zbiór zadań chemicznych dla geologów 12
Zbior zadan testowych Olimpiada biologiczna Praca zbiorowa
więcej podobnych podstron