
Analiza matematyczna 1/Wykład 6: Szeregi liczbowe
<
Szeregi liczbowe
Wyk ład ten poświęcony jest szeregom liczbowym. Definiujemy pojęcia szeregu, szeregu
zbieżnego. Podajemy warunek konieczny i warunek Cauchy'ego zbieżności szeregów.
Dowodzimy kryterium porównawczego zbieżności szeregów oraz twierdzenie o grupowaniu
wyrazów szeregu. Dowodzimy rozbieżności szeregu harmonicznego.
D
EFINICJA
6.1.
Niech
będzie ciągiem liczbowym.
(1) Szeregiem o wyrazach
(
) nazywamy ciąg
zwany ciągiem sum
częściowych, gdzie
dla
Szereg oznaczamy przez
(2) Szereg nazywamy zbieżnym, jeśli ciąg sum częściowych jest zbieżny.
Sumą szeregu nazywamy granicę ciągu sum częściowych i oznaczamy tym samym
symbolem co szereg, to znaczy
(3) Jeśli ciąg sum częściowych jest rozbieżny do
to mówimy, że szereg jest rozbieżny do
(lub, że ma sumę
niewłaściwą
) i piszemy
(4) Mówimy, że szereg jest bezwzględnie zbieżny, jeśli szereg
jest zbieżny.
(5) Mówimy, że szereg jest warunkowo zbieżny, jeśli jest on zbieżny, ale nie bezwzględnie zbieżny.
(6) Mówimy, że szereg jest rozbieżny, jeśli nie jest zbieżny.
P
RZYKŁAD
6.2.
Szeregiem o wyrazach
jest
Ciąg sum częściowych tego szeregu, to
Szereg ten jest rozbieżny.
Zachodzi następujący warunek konieczny zbieżności szeregów. Pozwala on w stosunkowo prosty sposób stwierdzić brak
zbieżności dla pewnych szeregów (nie spełniających tego warunku).
T
WIERDZENIE
6.3. [W
ARUNEK
KONIECZNY
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli szereg
jest zbieżny, to
D
OWÓD
6.3.
Niech
będzie ciągiem sum częściowych szeregu. Z założenia wiemy, że
Zauważmy, że
zatem
P
RZYKŁAD
6.4.
Zbadać zbieżność szeregu
Licząc granicę wyrazów tego szeregu dostajemy
zatem nie jest spełniony warunek konieczny zbieżności szeregów (porównaj
twierdzenie 6.3.
). Szereg jest rozbieżny.
P
RZYKŁAD
6.5.
Z szeregiem geometrycznym
spotkaliśmy się już na wykładzie 1 (patrz Przykład
przykład 1.12.
). Przypomnijmy, że
jeśli
to jest on zbieżny wtedy i tylko wtedy, gdy
i wówczas
Najprostszymi działaniami jakie możemy wykonać na szeregach są dodawanie/odejmowanie szeregów i mnożenie szeregu
przez liczbę. Kolejne twierdzenie mówi, iż operacje te "zachowują" zbieżność. Dowód (oparty na twierdzeniu o arytmetyce
granic ciągów) pozostawiamy jako proste ćwiczenie.
T
WIERDZENIE
6.6. [D
ZIAŁANIA
NA
SZEREGACH
]
Jeśli
i
są dwoma szeregami zbieżnymi oraz
to
(1) szeregi
są zbieżne oraz
(2) szereg
jest zbieżny oraz
Ponieważ szereg jest ciągiem (zwanym ciągiem sum częściowych) więc wszystkie twierdzenia dotyczące ciągów można
przenieść na pojęcie szeregu. W szczególności dla ciągu sum częściowych
szeregu
prawdziwe jest twierdzenie,
że ciąg ten jest zbieżny wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego. Mówi o tym poniższe twierdzenie.
T
WIERDZENIE
6.7. [W
ARUNEK
C
AUCHY
'
EGO
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
jest szeregiem, to szereg
jest zbieżny wtedy i tylko wtedy, gdy
Powyższy warunek nazywamy warunkiem Cauchy'ego dla szeregów.
Zauważmy, że
czyli warunek w powyższej definicji jest dokładnie warunkiem Cauchy'ego dla ciągów.
Kolejne twierdzenie będziemy często wykorzystywać przy sprawdzaniu czy dany szereg jest zbieżny.
T
WIERDZENIE
6.8. [Z
BIEŻNOŚĆ
A
BEZWZGLĘDNA
ZBIEŻNOŚĆ
]
Jeśli szereg
jest bezwzględnie zbieżny, to jest on zbieżny.
D
OWÓD
6.8.
Mamy pokazać zbieżność szeregu
Ustalmy dowolne
Ponieważ szereg
jest zbieżny, więc spełnia
warunek Cauchy'ego dla szeregów (patrz
twierdzenie 6.7.
), zatem
Zatem dla dowolnych
mamy
czyli szereg
spełnia warunek Cauchy'ego dla szeregów. Korzystając ponownie z
twierdzenie 6.7.
otrzymujemy, że
szereg
jest zbieżny.
Oprócz warunku koniecznego zbieżności szeregów (pomocnego przy rozstrzyganiu zbieżności szeregów) można podać wiele
warunków wystarczających zbieżności szeregów. Warunki te nazywamy kryteriami. Podstawowym kryterium w teorii szeregów
jest poniższe kryterium porównawcze. Mówi ono, że jeśli wyrazy szeregu szacują się przez wyrazy innego szeregu zbieżnego
(przynajmniej "od pewnego miejsca"), to wyjściowy szereg też jest zbieżny.
T
WIERDZENIE
6.9. [K
RYTERIUM
PORÓWNAWCZE
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
są szeregami takimi, że
dla
oraz
to
(1) jeśli szereg
jest zbieżny, to szereg
jest zbieżny;
(2) jeśli szereg
jest rozbieżny, to szereg
jest rozbieżny.
D
OWÓD
6.9.
(Ad (1)) Oznaczmy sumy cz ęściowe obu szeregów odpowiednio przez:
Ciągi
i
są rosnące (gdyż szeregi mają wyrazy nieujemne). Ciąg
jako zbieżny jest ograniczony, to znaczy
Dla
mamy zatem
zatem ciąg
jest ograniczony. Z
twierdzenia 4.15.
(1) wnioskujemy, że jest on zbieżny. Zatem szereg
jest
zbieżny.
(Ad (2)) Jest to równoważne (1).
Kolejne twierdzenie mówi o szeregu, w którym pogrupowano pewne wyrazy, to znaczy policzono sumy kolejnych wyrazów
pogrupowanych w skończone grupy, to znaczy
T
WIERDZENIE
6.10. [O
GRUPOWANIU
WYRAZÓW
SZEREGU
]
Jeśli
jest szeregiem zbieżnym,
jest ciągiem silnie rosnącym takim, że
, to szereg
jest zbieżny oraz
D
OWÓD
6.10.
Zauważmy, że ciąg sum częściowych szeregu pogrupowanego jest podciągiem ciągu sum częściowych wyjściowego szeregu.
Wystarczy zatem zastosowa ć
twierdzenie 3.25.
Szczegóły pozostawiamy jako proste ćwiczenie.
W
NIOSEK
6.11.
Jako konsekwencję powyższego twierdzenia dostajemy stwierdzenie, że "jeśli po pogrupowaniu wyrazów szeregu
otrzymamy szereg rozbieżny, to wyjściowy szereg też był rozbieżny".
Uwaga 6.12.
Twierdzenie odwrotne do twierdzenia 6.10. nie jest prawdziwe.
Aby to sprawdzić rozważmy następujący szereg naprzemienny
Oczywiście jest to szereg rozbieżny, gdyż nie spełnia warunku koniecznego zbieżności szeregów. Pogrupujmy wyrazy tego
szeregu "po dwa", to znaczy
W ten sposób szereg pogrupowany jest szeregiem zerowym
Jest on oczywiście zbieżny (do zera). Zatem ze zbieżności
szeregu pogrupowanego nie można nic wnioskować o zbieżności wyjściowego szeregu.
Uwaga 6.13.
W pewnych jednak sytuacjach ze zbieżności szeregu pogrupowanego można wnioskować o zbieżności szeregu
wyjściowego. Jest tak na przykład w przypadku szeregów o wyrazach nieujemnych. Jeśli
jest szeregiem o wyrazach
nieujemnych, to zbieżność tego szeregu jest równoważna zbieżności szeregu pogrupowanego. Załóżmy bowiem, że szereg
pogrupowany jest zbieżny. Wówczas jego ciąg sum częściowych jest ograniczony, powiedzmy przez
Ale wtedy
ciąg sum częściowych całego szeregu jest też ograniczony przez
(dlaczego?). Ponieważ ponadto ciąg sum częściowych
szeregu
jest rosnący (bo wyrazy
są nieujemne), zatem jest on zbieżny. Szczegółowe rozpisanie tego
rozumowania pozostawiamy jako ćwiczenie.
Na zakończenie podamy ważny przykład szeregu liczbowego, zwanego szeregiem harmonicznym oraz pewne jego uogólnienie.
Szereg ten będzie miał istotne zastosowanie w badaniu zbieżności innych szeregów dzięki kryterium porównawczemu.
P
RZYKŁAD
6.14.
Szereg
jest rozbieżny. Nazywamy go szeregiem harmonicznym.
D
OWÓD
PRZYKŁADU
6.14.
Aby stwierdzić rozbieżność szeregu harmonicznego, pogrupujmy jego wyrazy w następujący sposób:
Każda kolejna grup począwszy od drugiej ma dwa razy więcej składników od poprzedniej oraz wyrazy w każdej grupie szacują
się od dołu przez ostatni składnik postaci
gdzie jest numerem "grupy". Jeśli szereg który otrzymamy po pogrupowaniu
wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego wyrazy:
(patrz powyższy opis). Zatem szereg
nie spełnia warunku koniecznego zbieżności szeregów, a więc jest rozbieżny. Z
kryterium porównawczego zbieżności szeregów (patrz
twierdzenie 6.9.
) wynika, że szereg pogrupowany jest także rozbieżny. Z
wniosku 6.11.
wynika, że wyjściowy szereg harmoniczny jest rozbieżny.
P
RZYKŁAD
6.15.
Szereg
jest zbieżny wtedy i tylko wtedy, gdy
Nazywamy go uogólnionym szeregiem harmonicznym z
wykładnikiem
Jeśli
to zauważmy, że
zatem korzystając z kryterium porównawczego (patrz
twierdzenie 6.9.
) oraz udowodnionej już rozbieżności szeregu
harmonicznego dostajemy, że szereg
jest rozbieżny.
Załóżmy teraz, że
Zapiszmy
z pewnym
Zauważmy, że
Pogrupujmy wyrazy szeregu podobnie jak w części pierwszej dowodu oraz skorzystajmy z oszacowania powyżej:
Jeśli szereg, który otrzymamy po pogrupowaniu wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego
wyrazy:
Ale szereg o wyrazach
jest szeregiem geometrycznym zbieżnym (jego suma wynosi
). Zatem z kryterium
porównawczego (patrz
twierdzenie 6.9.
) wynika, że także szereg pogrupowany
jest zbieżny. Ponieważ w naszej
sytuacji mamy do czynienia z szeregiem o wyrazach dodatnich, więc ze zbieżności szeregu pogrupowanego możemy
wnioskować o zbieżności szeregu wyjściowego (patrz
uwaga 6.13.
).
Tę stronę ostatnio zmodyfikowano o 22:45, 6 wrz 2006;
Augustin Louis Cauchy (
17891857)
Nawigacja
Szukaj
Napisz do nas
OK
Szukaj

Analiza matematyczna 1/Wykład 6: Szeregi liczbowe
<
Analiza matematyczna 1
Szeregi liczbowe
Wyk ład ten poświęcony jest szeregom liczbowym. Definiujemy pojęcia szeregu, szeregu
zbieżnego. Podajemy warunek konieczny i warunek Cauchy'ego zbieżności szeregów.
Dowodzimy kryterium porównawczego zbieżności szeregów oraz twierdzenie o grupowaniu
wyrazów szeregu. Dowodzimy rozbieżności szeregu harmonicznego.
D
EFINICJA
6.1.
Niech
będzie ciągiem liczbowym.
(1) Szeregiem o wyrazach
(
) nazywamy ciąg
zwany ciągiem sum
częściowych, gdzie
dla
Szereg oznaczamy przez
(2) Szereg nazywamy zbieżnym, jeśli ciąg sum częściowych jest zbieżny.
Sumą szeregu nazywamy granicę ciągu sum częściowych i oznaczamy tym samym
symbolem co szereg, to znaczy
(3) Jeśli ciąg sum częściowych jest rozbieżny do
to mówimy, że szereg jest rozbieżny do
(lub, że ma sumę
niewłaściwą
) i piszemy
(4) Mówimy, że szereg jest bezwzględnie zbieżny, jeśli szereg
jest zbieżny.
(5) Mówimy, że szereg jest warunkowo zbieżny, jeśli jest on zbieżny, ale nie bezwzględnie zbieżny.
(6) Mówimy, że szereg jest rozbieżny, jeśli nie jest zbieżny.
P
RZYKŁAD
6.2.
Szeregiem o wyrazach
jest
Ciąg sum częściowych tego szeregu, to
Szereg ten jest rozbieżny.
Zachodzi następujący warunek konieczny zbieżności szeregów. Pozwala on w stosunkowo prosty sposób stwierdzić brak
zbieżności dla pewnych szeregów (nie spełniających tego warunku).
T
WIERDZENIE
6.3. [W
ARUNEK
KONIECZNY
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli szereg
jest zbieżny, to
D
OWÓD
6.3.
Niech
będzie ciągiem sum częściowych szeregu. Z założenia wiemy, że
Zauważmy, że
zatem
P
RZYKŁAD
6.4.
Zbadać zbieżność szeregu
Licząc granicę wyrazów tego szeregu dostajemy
zatem nie jest spełniony warunek konieczny zbieżności szeregów (porównaj
). Szereg jest rozbieżny.
P
RZYKŁAD
6.5.
Z szeregiem geometrycznym
spotkaliśmy się już na wykładzie 1 (patrz Przykład
). Przypomnijmy, że
jeśli
to jest on zbieżny wtedy i tylko wtedy, gdy
i wówczas
Najprostszymi działaniami jakie możemy wykonać na szeregach są dodawanie/odejmowanie szeregów i mnożenie szeregu
przez liczbę. Kolejne twierdzenie mówi, iż operacje te "zachowują" zbieżność. Dowód (oparty na twierdzeniu o arytmetyce
granic ciągów) pozostawiamy jako proste ćwiczenie.
T
WIERDZENIE
6.6. [D
ZIAŁANIA
NA
SZEREGACH
]
Jeśli
i
są dwoma szeregami zbieżnymi oraz
to
(1) szeregi
są zbieżne oraz
(2) szereg
jest zbieżny oraz
Ponieważ szereg jest ciągiem (zwanym ciągiem sum częściowych) więc wszystkie twierdzenia dotyczące ciągów można
przenieść na pojęcie szeregu. W szczególności dla ciągu sum częściowych
szeregu
prawdziwe jest twierdzenie,
że ciąg ten jest zbieżny wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego. Mówi o tym poniższe twierdzenie.
T
WIERDZENIE
6.7. [W
ARUNEK
C
AUCHY
'
EGO
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
jest szeregiem, to szereg
jest zbieżny wtedy i tylko wtedy, gdy
Powyższy warunek nazywamy warunkiem Cauchy'ego dla szeregów.
Zauważmy, że
czyli warunek w powyższej definicji jest dokładnie warunkiem Cauchy'ego dla ciągów.
Kolejne twierdzenie będziemy często wykorzystywać przy sprawdzaniu czy dany szereg jest zbieżny.
T
WIERDZENIE
6.8. [Z
BIEŻNOŚĆ
A
BEZWZGLĘDNA
ZBIEŻNOŚĆ
]
Jeśli szereg
jest bezwzględnie zbieżny, to jest on zbieżny.
D
OWÓD
6.8.
Mamy pokazać zbieżność szeregu
Ustalmy dowolne
Ponieważ szereg
jest zbieżny, więc spełnia
warunek Cauchy'ego dla szeregów (patrz
twierdzenie 6.7.
), zatem
Zatem dla dowolnych
mamy
czyli szereg
spełnia warunek Cauchy'ego dla szeregów. Korzystając ponownie z
twierdzenie 6.7.
otrzymujemy, że
szereg
jest zbieżny.
Oprócz warunku koniecznego zbieżności szeregów (pomocnego przy rozstrzyganiu zbieżności szeregów) można podać wiele
warunków wystarczających zbieżności szeregów. Warunki te nazywamy kryteriami. Podstawowym kryterium w teorii szeregów
jest poniższe kryterium porównawcze. Mówi ono, że jeśli wyrazy szeregu szacują się przez wyrazy innego szeregu zbieżnego
(przynajmniej "od pewnego miejsca"), to wyjściowy szereg też jest zbieżny.
T
WIERDZENIE
6.9. [K
RYTERIUM
PORÓWNAWCZE
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
są szeregami takimi, że
dla
oraz
to
(1) jeśli szereg
jest zbieżny, to szereg
jest zbieżny;
(2) jeśli szereg
jest rozbieżny, to szereg
jest rozbieżny.
D
OWÓD
6.9.
(Ad (1)) Oznaczmy sumy cz ęściowe obu szeregów odpowiednio przez:
Ciągi
i
są rosnące (gdyż szeregi mają wyrazy nieujemne). Ciąg
jako zbieżny jest ograniczony, to znaczy
Dla
mamy zatem
zatem ciąg
jest ograniczony. Z
twierdzenia 4.15.
(1) wnioskujemy, że jest on zbieżny. Zatem szereg
jest
zbieżny.
(Ad (2)) Jest to równoważne (1).
Kolejne twierdzenie mówi o szeregu, w którym pogrupowano pewne wyrazy, to znaczy policzono sumy kolejnych wyrazów
pogrupowanych w skończone grupy, to znaczy
T
WIERDZENIE
6.10. [O
GRUPOWANIU
WYRAZÓW
SZEREGU
]
Jeśli
jest szeregiem zbieżnym,
jest ciągiem silnie rosnącym takim, że
, to szereg
jest zbieżny oraz
D
OWÓD
6.10.
Zauważmy, że ciąg sum częściowych szeregu pogrupowanego jest podciągiem ciągu sum częściowych wyjściowego szeregu.
Wystarczy zatem zastosowa ć
twierdzenie 3.25.
Szczegóły pozostawiamy jako proste ćwiczenie.
W
NIOSEK
6.11.
Jako konsekwencję powyższego twierdzenia dostajemy stwierdzenie, że "jeśli po pogrupowaniu wyrazów szeregu
otrzymamy szereg rozbieżny, to wyjściowy szereg też był rozbieżny".
Uwaga 6.12.
Twierdzenie odwrotne do twierdzenia 6.10. nie jest prawdziwe.
Aby to sprawdzić rozważmy następujący szereg naprzemienny
Oczywiście jest to szereg rozbieżny, gdyż nie spełnia warunku koniecznego zbieżności szeregów. Pogrupujmy wyrazy tego
szeregu "po dwa", to znaczy
W ten sposób szereg pogrupowany jest szeregiem zerowym
Jest on oczywiście zbieżny (do zera). Zatem ze zbieżności
szeregu pogrupowanego nie można nic wnioskować o zbieżności wyjściowego szeregu.
Uwaga 6.13.
W pewnych jednak sytuacjach ze zbieżności szeregu pogrupowanego można wnioskować o zbieżności szeregu
wyjściowego. Jest tak na przykład w przypadku szeregów o wyrazach nieujemnych. Jeśli
jest szeregiem o wyrazach
nieujemnych, to zbieżność tego szeregu jest równoważna zbieżności szeregu pogrupowanego. Załóżmy bowiem, że szereg
pogrupowany jest zbieżny. Wówczas jego ciąg sum częściowych jest ograniczony, powiedzmy przez
Ale wtedy
ciąg sum częściowych całego szeregu jest też ograniczony przez
(dlaczego?). Ponieważ ponadto ciąg sum częściowych
szeregu
jest rosnący (bo wyrazy
są nieujemne), zatem jest on zbieżny. Szczegółowe rozpisanie tego
rozumowania pozostawiamy jako ćwiczenie.
Na zakończenie podamy ważny przykład szeregu liczbowego, zwanego szeregiem harmonicznym oraz pewne jego uogólnienie.
Szereg ten będzie miał istotne zastosowanie w badaniu zbieżności innych szeregów dzięki kryterium porównawczemu.
P
RZYKŁAD
6.14.
Szereg
jest rozbieżny. Nazywamy go szeregiem harmonicznym.
D
OWÓD
PRZYKŁADU
6.14.
Aby stwierdzić rozbieżność szeregu harmonicznego, pogrupujmy jego wyrazy w następujący sposób:
Każda kolejna grup począwszy od drugiej ma dwa razy więcej składników od poprzedniej oraz wyrazy w każdej grupie szacują
się od dołu przez ostatni składnik postaci
gdzie jest numerem "grupy". Jeśli szereg który otrzymamy po pogrupowaniu
wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego wyrazy:
(patrz powyższy opis). Zatem szereg
nie spełnia warunku koniecznego zbieżności szeregów, a więc jest rozbieżny. Z
kryterium porównawczego zbieżności szeregów (patrz
twierdzenie 6.9.
) wynika, że szereg pogrupowany jest także rozbieżny. Z
wniosku 6.11.
wynika, że wyjściowy szereg harmoniczny jest rozbieżny.
P
RZYKŁAD
6.15.
Szereg
jest zbieżny wtedy i tylko wtedy, gdy
Nazywamy go uogólnionym szeregiem harmonicznym z
wykładnikiem
Jeśli
to zauważmy, że
zatem korzystając z kryterium porównawczego (patrz
twierdzenie 6.9.
) oraz udowodnionej już rozbieżności szeregu
harmonicznego dostajemy, że szereg
jest rozbieżny.
Załóżmy teraz, że
Zapiszmy
z pewnym
Zauważmy, że
Pogrupujmy wyrazy szeregu podobnie jak w części pierwszej dowodu oraz skorzystajmy z oszacowania powyżej:
Jeśli szereg, który otrzymamy po pogrupowaniu wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego
wyrazy:
Ale szereg o wyrazach
jest szeregiem geometrycznym zbieżnym (jego suma wynosi
). Zatem z kryterium
porównawczego (patrz
twierdzenie 6.9.
) wynika, że także szereg pogrupowany
jest zbieżny. Ponieważ w naszej
sytuacji mamy do czynienia z szeregiem o wyrazach dodatnich, więc ze zbieżności szeregu pogrupowanego możemy
wnioskować o zbieżności szeregu wyjściowego (patrz
uwaga 6.13.
).
Tę stronę ostatnio zmodyfikowano o 22:45, 6 wrz 2006;
Augustin Louis Cauchy (
17891857)
Zobacz biografię
Nawigacja
Strona główna
Przedmioty
Uczelnie
O nas
MIMINF
MIMMAT
Szukaj
Napisz do nas
maruda@mimuw.edu.pl
OK
Szukaj
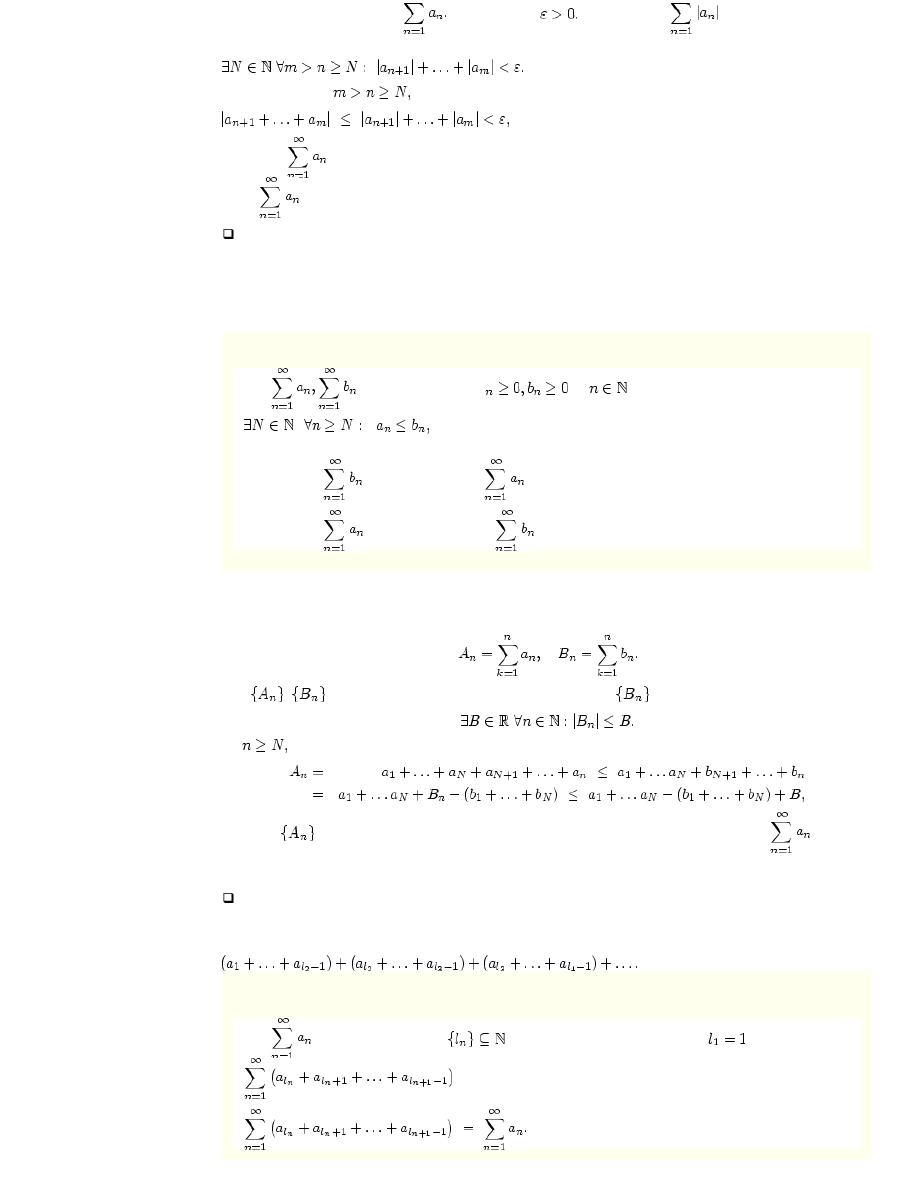
Analiza matematyczna 1/Wykład 6: Szeregi liczbowe
<
Analiza matematyczna 1
Szeregi liczbowe
Wyk ład ten poświęcony jest szeregom liczbowym. Definiujemy pojęcia szeregu, szeregu
zbieżnego. Podajemy warunek konieczny i warunek Cauchy'ego zbieżności szeregów.
Dowodzimy kryterium porównawczego zbieżności szeregów oraz twierdzenie o grupowaniu
wyrazów szeregu. Dowodzimy rozbieżności szeregu harmonicznego.
D
EFINICJA
6.1.
Niech
będzie ciągiem liczbowym.
(1) Szeregiem o wyrazach
(
) nazywamy ciąg
zwany ciągiem sum
częściowych, gdzie
dla
Szereg oznaczamy przez
(2) Szereg nazywamy zbieżnym, jeśli ciąg sum częściowych jest zbieżny.
Sumą szeregu nazywamy granicę ciągu sum częściowych i oznaczamy tym samym
symbolem co szereg, to znaczy
(3) Jeśli ciąg sum częściowych jest rozbieżny do
to mówimy, że szereg jest rozbieżny do
(lub, że ma sumę
niewłaściwą
) i piszemy
(4) Mówimy, że szereg jest bezwzględnie zbieżny, jeśli szereg
jest zbieżny.
(5) Mówimy, że szereg jest warunkowo zbieżny, jeśli jest on zbieżny, ale nie bezwzględnie zbieżny.
(6) Mówimy, że szereg jest rozbieżny, jeśli nie jest zbieżny.
P
RZYKŁAD
6.2.
Szeregiem o wyrazach
jest
Ciąg sum częściowych tego szeregu, to
Szereg ten jest rozbieżny.
Zachodzi następujący warunek konieczny zbieżności szeregów. Pozwala on w stosunkowo prosty sposób stwierdzić brak
zbieżności dla pewnych szeregów (nie spełniających tego warunku).
T
WIERDZENIE
6.3. [W
ARUNEK
KONIECZNY
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli szereg
jest zbieżny, to
D
OWÓD
6.3.
Niech
będzie ciągiem sum częściowych szeregu. Z założenia wiemy, że
Zauważmy, że
zatem
P
RZYKŁAD
6.4.
Zbadać zbieżność szeregu
Licząc granicę wyrazów tego szeregu dostajemy
zatem nie jest spełniony warunek konieczny zbieżności szeregów (porównaj
twierdzenie 6.3.
). Szereg jest rozbieżny.
P
RZYKŁAD
6.5.
Z szeregiem geometrycznym
spotkaliśmy się już na wykładzie 1 (patrz Przykład
przykład 1.12.
). Przypomnijmy, że
jeśli
to jest on zbieżny wtedy i tylko wtedy, gdy
i wówczas
Najprostszymi działaniami jakie możemy wykonać na szeregach są dodawanie/odejmowanie szeregów i mnożenie szeregu
przez liczbę. Kolejne twierdzenie mówi, iż operacje te "zachowują" zbieżność. Dowód (oparty na twierdzeniu o arytmetyce
granic ciągów) pozostawiamy jako proste ćwiczenie.
T
WIERDZENIE
6.6. [D
ZIAŁANIA
NA
SZEREGACH
]
Jeśli
i
są dwoma szeregami zbieżnymi oraz
to
(1) szeregi
są zbieżne oraz
(2) szereg
jest zbieżny oraz
Ponieważ szereg jest ciągiem (zwanym ciągiem sum częściowych) więc wszystkie twierdzenia dotyczące ciągów można
przenieść na pojęcie szeregu. W szczególności dla ciągu sum częściowych
szeregu
prawdziwe jest twierdzenie,
że ciąg ten jest zbieżny wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego. Mówi o tym poniższe twierdzenie.
T
WIERDZENIE
6.7. [W
ARUNEK
C
AUCHY
'
EGO
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
jest szeregiem, to szereg
jest zbieżny wtedy i tylko wtedy, gdy
Powyższy warunek nazywamy warunkiem Cauchy'ego dla szeregów.
Zauważmy, że
czyli warunek w powyższej definicji jest dokładnie warunkiem Cauchy'ego dla ciągów.
Kolejne twierdzenie będziemy często wykorzystywać przy sprawdzaniu czy dany szereg jest zbieżny.
T
WIERDZENIE
6.8. [Z
BIEŻNOŚĆ
A
BEZWZGLĘDNA
ZBIEŻNOŚĆ
]
Jeśli szereg
jest bezwzględnie zbieżny, to jest on zbieżny.
D
OWÓD
6.8.
Mamy pokazać zbieżność szeregu
Ustalmy dowolne
Ponieważ szereg
jest zbieżny, więc spełnia
warunek Cauchy'ego dla szeregów (patrz
Zatem dla dowolnych
mamy
czyli szereg
spełnia warunek Cauchy'ego dla szeregów. Korzystając ponownie z
otrzymujemy, że
szereg
jest zbieżny.
Oprócz warunku koniecznego zbieżności szeregów (pomocnego przy rozstrzyganiu zbieżności szeregów) można podać wiele
warunków wystarczających zbieżności szeregów. Warunki te nazywamy kryteriami. Podstawowym kryterium w teorii szeregów
jest poniższe kryterium porównawcze. Mówi ono, że jeśli wyrazy szeregu szacują się przez wyrazy innego szeregu zbieżnego
(przynajmniej "od pewnego miejsca"), to wyjściowy szereg też jest zbieżny.
T
WIERDZENIE
6.9. [K
RYTERIUM
PORÓWNAWCZE
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
są szeregami takimi, że
dla
oraz
to
(1) jeśli szereg
jest zbieżny, to szereg
jest zbieżny;
(2) jeśli szereg
jest rozbieżny, to szereg
jest rozbieżny.
D
OWÓD
6.9.
(Ad (1)) Oznaczmy sumy cz ęściowe obu szeregów odpowiednio przez:
Ciągi
i
są rosnące (gdyż szeregi mają wyrazy nieujemne). Ciąg
jako zbieżny jest ograniczony, to znaczy
Dla
mamy zatem
zatem ciąg
jest ograniczony. Z
(1) wnioskujemy, że jest on zbieżny. Zatem szereg
jest
zbieżny.
(Ad (2)) Jest to równoważne (1).
Kolejne twierdzenie mówi o szeregu, w którym pogrupowano pewne wyrazy, to znaczy policzono sumy kolejnych wyrazów
pogrupowanych w skończone grupy, to znaczy
T
WIERDZENIE
6.10. [O
GRUPOWANIU
WYRAZÓW
SZEREGU
]
Jeśli
jest szeregiem zbieżnym,
jest ciągiem silnie rosnącym takim, że
, to szereg
jest zbieżny oraz
D
OWÓD
6.10.
Zauważmy, że ciąg sum częściowych szeregu pogrupowanego jest podciągiem ciągu sum częściowych wyjściowego szeregu.
Wystarczy zatem zastosowa ć
twierdzenie 3.25.
Szczegóły pozostawiamy jako proste ćwiczenie.
W
NIOSEK
6.11.
Jako konsekwencję powyższego twierdzenia dostajemy stwierdzenie, że "jeśli po pogrupowaniu wyrazów szeregu
otrzymamy szereg rozbieżny, to wyjściowy szereg też był rozbieżny".
Uwaga 6.12.
Twierdzenie odwrotne do twierdzenia 6.10. nie jest prawdziwe.
Aby to sprawdzić rozważmy następujący szereg naprzemienny
Oczywiście jest to szereg rozbieżny, gdyż nie spełnia warunku koniecznego zbieżności szeregów. Pogrupujmy wyrazy tego
szeregu "po dwa", to znaczy
W ten sposób szereg pogrupowany jest szeregiem zerowym
Jest on oczywiście zbieżny (do zera). Zatem ze zbieżności
szeregu pogrupowanego nie można nic wnioskować o zbieżności wyjściowego szeregu.
Uwaga 6.13.
W pewnych jednak sytuacjach ze zbieżności szeregu pogrupowanego można wnioskować o zbieżności szeregu
wyjściowego. Jest tak na przykład w przypadku szeregów o wyrazach nieujemnych. Jeśli
jest szeregiem o wyrazach
nieujemnych, to zbieżność tego szeregu jest równoważna zbieżności szeregu pogrupowanego. Załóżmy bowiem, że szereg
pogrupowany jest zbieżny. Wówczas jego ciąg sum częściowych jest ograniczony, powiedzmy przez
Ale wtedy
ciąg sum częściowych całego szeregu jest też ograniczony przez
(dlaczego?). Ponieważ ponadto ciąg sum częściowych
szeregu
jest rosnący (bo wyrazy
są nieujemne), zatem jest on zbieżny. Szczegółowe rozpisanie tego
rozumowania pozostawiamy jako ćwiczenie.
Na zakończenie podamy ważny przykład szeregu liczbowego, zwanego szeregiem harmonicznym oraz pewne jego uogólnienie.
Szereg ten będzie miał istotne zastosowanie w badaniu zbieżności innych szeregów dzięki kryterium porównawczemu.
P
RZYKŁAD
6.14.
Szereg
jest rozbieżny. Nazywamy go szeregiem harmonicznym.
D
OWÓD
PRZYKŁADU
6.14.
Aby stwierdzić rozbieżność szeregu harmonicznego, pogrupujmy jego wyrazy w następujący sposób:
Każda kolejna grup począwszy od drugiej ma dwa razy więcej składników od poprzedniej oraz wyrazy w każdej grupie szacują
się od dołu przez ostatni składnik postaci
gdzie jest numerem "grupy". Jeśli szereg który otrzymamy po pogrupowaniu
wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego wyrazy:
(patrz powyższy opis). Zatem szereg
nie spełnia warunku koniecznego zbieżności szeregów, a więc jest rozbieżny. Z
kryterium porównawczego zbieżności szeregów (patrz
twierdzenie 6.9.
) wynika, że szereg pogrupowany jest także rozbieżny. Z
wniosku 6.11.
wynika, że wyjściowy szereg harmoniczny jest rozbieżny.
P
RZYKŁAD
6.15.
Szereg
jest zbieżny wtedy i tylko wtedy, gdy
Nazywamy go uogólnionym szeregiem harmonicznym z
wykładnikiem
Jeśli
to zauważmy, że
zatem korzystając z kryterium porównawczego (patrz
twierdzenie 6.9.
) oraz udowodnionej już rozbieżności szeregu
harmonicznego dostajemy, że szereg
jest rozbieżny.
Załóżmy teraz, że
Zapiszmy
z pewnym
Zauważmy, że
Pogrupujmy wyrazy szeregu podobnie jak w części pierwszej dowodu oraz skorzystajmy z oszacowania powyżej:
Jeśli szereg, który otrzymamy po pogrupowaniu wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego
wyrazy:
Ale szereg o wyrazach
jest szeregiem geometrycznym zbieżnym (jego suma wynosi
). Zatem z kryterium
porównawczego (patrz
twierdzenie 6.9.
) wynika, że także szereg pogrupowany
jest zbieżny. Ponieważ w naszej
sytuacji mamy do czynienia z szeregiem o wyrazach dodatnich, więc ze zbieżności szeregu pogrupowanego możemy
wnioskować o zbieżności szeregu wyjściowego (patrz
uwaga 6.13.
).
Tę stronę ostatnio zmodyfikowano o 22:45, 6 wrz 2006;
Augustin Louis Cauchy (
17891857)
Zobacz biografię
Nawigacja
Strona główna
Przedmioty
Uczelnie
O nas
MIMINF
MIMMAT
Szukaj
Napisz do nas
maruda@mimuw.edu.pl
OK
Szukaj
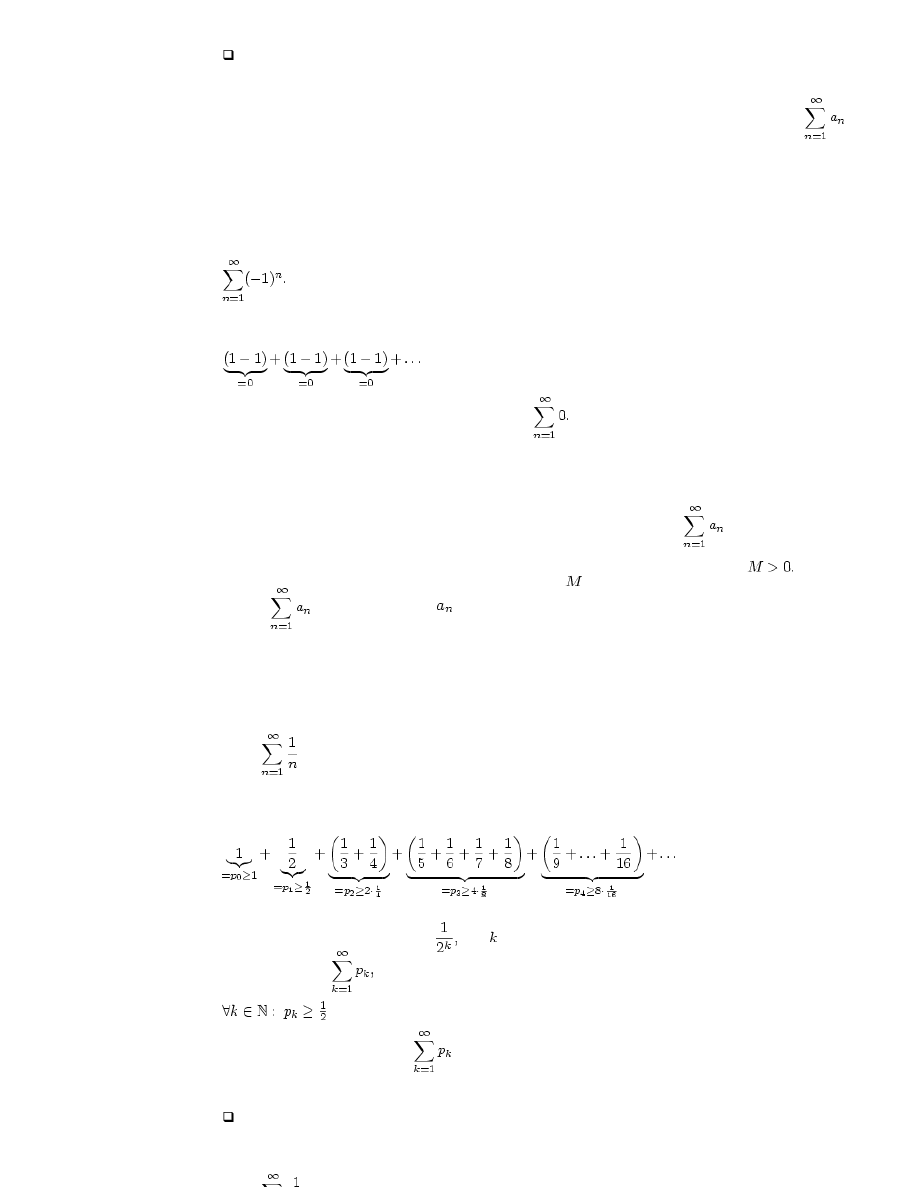
Analiza matematyczna 1/Wykład 6: Szeregi liczbowe
<
Analiza matematyczna 1
Szeregi liczbowe
Wyk ład ten poświęcony jest szeregom liczbowym. Definiujemy pojęcia szeregu, szeregu
zbieżnego. Podajemy warunek konieczny i warunek Cauchy'ego zbieżności szeregów.
Dowodzimy kryterium porównawczego zbieżności szeregów oraz twierdzenie o grupowaniu
wyrazów szeregu. Dowodzimy rozbieżności szeregu harmonicznego.
D
EFINICJA
6.1.
Niech
będzie ciągiem liczbowym.
(1) Szeregiem o wyrazach
(
) nazywamy ciąg
zwany ciągiem sum
częściowych, gdzie
dla
Szereg oznaczamy przez
(2) Szereg nazywamy zbieżnym, jeśli ciąg sum częściowych jest zbieżny.
Sumą szeregu nazywamy granicę ciągu sum częściowych i oznaczamy tym samym
symbolem co szereg, to znaczy
(3) Jeśli ciąg sum częściowych jest rozbieżny do
to mówimy, że szereg jest rozbieżny do
(lub, że ma sumę
niewłaściwą
) i piszemy
(4) Mówimy, że szereg jest bezwzględnie zbieżny, jeśli szereg
jest zbieżny.
(5) Mówimy, że szereg jest warunkowo zbieżny, jeśli jest on zbieżny, ale nie bezwzględnie zbieżny.
(6) Mówimy, że szereg jest rozbieżny, jeśli nie jest zbieżny.
P
RZYKŁAD
6.2.
Szeregiem o wyrazach
jest
Ciąg sum częściowych tego szeregu, to
Szereg ten jest rozbieżny.
Zachodzi następujący warunek konieczny zbieżności szeregów. Pozwala on w stosunkowo prosty sposób stwierdzić brak
zbieżności dla pewnych szeregów (nie spełniających tego warunku).
T
WIERDZENIE
6.3. [W
ARUNEK
KONIECZNY
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli szereg
jest zbieżny, to
D
OWÓD
6.3.
Niech
będzie ciągiem sum częściowych szeregu. Z założenia wiemy, że
Zauważmy, że
zatem
P
RZYKŁAD
6.4.
Zbadać zbieżność szeregu
Licząc granicę wyrazów tego szeregu dostajemy
zatem nie jest spełniony warunek konieczny zbieżności szeregów (porównaj
twierdzenie 6.3.
). Szereg jest rozbieżny.
P
RZYKŁAD
6.5.
Z szeregiem geometrycznym
spotkaliśmy się już na wykładzie 1 (patrz Przykład
przykład 1.12.
). Przypomnijmy, że
jeśli
to jest on zbieżny wtedy i tylko wtedy, gdy
i wówczas
Najprostszymi działaniami jakie możemy wykonać na szeregach są dodawanie/odejmowanie szeregów i mnożenie szeregu
przez liczbę. Kolejne twierdzenie mówi, iż operacje te "zachowują" zbieżność. Dowód (oparty na twierdzeniu o arytmetyce
granic ciągów) pozostawiamy jako proste ćwiczenie.
T
WIERDZENIE
6.6. [D
ZIAŁANIA
NA
SZEREGACH
]
Jeśli
i
są dwoma szeregami zbieżnymi oraz
to
(1) szeregi
są zbieżne oraz
(2) szereg
jest zbieżny oraz
Ponieważ szereg jest ciągiem (zwanym ciągiem sum częściowych) więc wszystkie twierdzenia dotyczące ciągów można
przenieść na pojęcie szeregu. W szczególności dla ciągu sum częściowych
szeregu
prawdziwe jest twierdzenie,
że ciąg ten jest zbieżny wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego. Mówi o tym poniższe twierdzenie.
T
WIERDZENIE
6.7. [W
ARUNEK
C
AUCHY
'
EGO
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
jest szeregiem, to szereg
jest zbieżny wtedy i tylko wtedy, gdy
Powyższy warunek nazywamy warunkiem Cauchy'ego dla szeregów.
Zauważmy, że
czyli warunek w powyższej definicji jest dokładnie warunkiem Cauchy'ego dla ciągów.
Kolejne twierdzenie będziemy często wykorzystywać przy sprawdzaniu czy dany szereg jest zbieżny.
T
WIERDZENIE
6.8. [Z
BIEŻNOŚĆ
A
BEZWZGLĘDNA
ZBIEŻNOŚĆ
]
Jeśli szereg
jest bezwzględnie zbieżny, to jest on zbieżny.
D
OWÓD
6.8.
Mamy pokazać zbieżność szeregu
Ustalmy dowolne
Ponieważ szereg
jest zbieżny, więc spełnia
warunek Cauchy'ego dla szeregów (patrz
twierdzenie 6.7.
), zatem
Zatem dla dowolnych
mamy
czyli szereg
spełnia warunek Cauchy'ego dla szeregów. Korzystając ponownie z
twierdzenie 6.7.
otrzymujemy, że
szereg
jest zbieżny.
Oprócz warunku koniecznego zbieżności szeregów (pomocnego przy rozstrzyganiu zbieżności szeregów) można podać wiele
warunków wystarczających zbieżności szeregów. Warunki te nazywamy kryteriami. Podstawowym kryterium w teorii szeregów
jest poniższe kryterium porównawcze. Mówi ono, że jeśli wyrazy szeregu szacują się przez wyrazy innego szeregu zbieżnego
(przynajmniej "od pewnego miejsca"), to wyjściowy szereg też jest zbieżny.
T
WIERDZENIE
6.9. [K
RYTERIUM
PORÓWNAWCZE
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
są szeregami takimi, że
dla
oraz
to
(1) jeśli szereg
jest zbieżny, to szereg
jest zbieżny;
(2) jeśli szereg
jest rozbieżny, to szereg
jest rozbieżny.
D
OWÓD
6.9.
(Ad (1)) Oznaczmy sumy cz ęściowe obu szeregów odpowiednio przez:
Ciągi
i
są rosnące (gdyż szeregi mają wyrazy nieujemne). Ciąg
jako zbieżny jest ograniczony, to znaczy
Dla
mamy zatem
zatem ciąg
jest ograniczony. Z
twierdzenia 4.15.
(1) wnioskujemy, że jest on zbieżny. Zatem szereg
jest
zbieżny.
(Ad (2)) Jest to równoważne (1).
Kolejne twierdzenie mówi o szeregu, w którym pogrupowano pewne wyrazy, to znaczy policzono sumy kolejnych wyrazów
pogrupowanych w skończone grupy, to znaczy
T
WIERDZENIE
6.10. [O
GRUPOWANIU
WYRAZÓW
SZEREGU
]
Jeśli
jest szeregiem zbieżnym,
jest ciągiem silnie rosnącym takim, że
, to szereg
jest zbieżny oraz
D
OWÓD
6.10.
Zauważmy, że ciąg sum częściowych szeregu pogrupowanego jest podciągiem ciągu sum częściowych wyjściowego szeregu.
Wystarczy zatem zastosowa ć
Szczegóły pozostawiamy jako proste ćwiczenie.
W
NIOSEK
6.11.
Jako konsekwencję powyższego twierdzenia dostajemy stwierdzenie, że "jeśli po pogrupowaniu wyrazów szeregu
otrzymamy szereg rozbieżny, to wyjściowy szereg też był rozbieżny".
Uwaga 6.12.
Twierdzenie odwrotne do twierdzenia 6.10. nie jest prawdziwe.
Aby to sprawdzić rozważmy następujący szereg naprzemienny
Oczywiście jest to szereg rozbieżny, gdyż nie spełnia warunku koniecznego zbieżności szeregów. Pogrupujmy wyrazy tego
szeregu "po dwa", to znaczy
W ten sposób szereg pogrupowany jest szeregiem zerowym
Jest on oczywiście zbieżny (do zera). Zatem ze zbieżności
szeregu pogrupowanego nie można nic wnioskować o zbieżności wyjściowego szeregu.
Uwaga 6.13.
W pewnych jednak sytuacjach ze zbieżności szeregu pogrupowanego można wnioskować o zbieżności szeregu
wyjściowego. Jest tak na przykład w przypadku szeregów o wyrazach nieujemnych. Jeśli
jest szeregiem o wyrazach
nieujemnych, to zbieżność tego szeregu jest równoważna zbieżności szeregu pogrupowanego. Załóżmy bowiem, że szereg
pogrupowany jest zbieżny. Wówczas jego ciąg sum częściowych jest ograniczony, powiedzmy przez
Ale wtedy
ciąg sum częściowych całego szeregu jest też ograniczony przez
(dlaczego?). Ponieważ ponadto ciąg sum częściowych
szeregu
jest rosnący (bo wyrazy
są nieujemne), zatem jest on zbieżny. Szczegółowe rozpisanie tego
rozumowania pozostawiamy jako ćwiczenie.
Na zakończenie podamy ważny przykład szeregu liczbowego, zwanego szeregiem harmonicznym oraz pewne jego uogólnienie.
Szereg ten będzie miał istotne zastosowanie w badaniu zbieżności innych szeregów dzięki kryterium porównawczemu.
P
RZYKŁAD
6.14.
Szereg
jest rozbieżny. Nazywamy go szeregiem harmonicznym.
D
OWÓD
PRZYKŁADU
6.14.
Aby stwierdzić rozbieżność szeregu harmonicznego, pogrupujmy jego wyrazy w następujący sposób:
Każda kolejna grup począwszy od drugiej ma dwa razy więcej składników od poprzedniej oraz wyrazy w każdej grupie szacują
się od dołu przez ostatni składnik postaci
gdzie jest numerem "grupy". Jeśli szereg który otrzymamy po pogrupowaniu
wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego wyrazy:
(patrz powyższy opis). Zatem szereg
nie spełnia warunku koniecznego zbieżności szeregów, a więc jest rozbieżny. Z
kryterium porównawczego zbieżności szeregów (patrz
) wynika, że szereg pogrupowany jest także rozbieżny. Z
wynika, że wyjściowy szereg harmoniczny jest rozbieżny.
P
RZYKŁAD
6.15.
Szereg
jest zbieżny wtedy i tylko wtedy, gdy
Nazywamy go uogólnionym szeregiem harmonicznym z
wykładnikiem
Jeśli
to zauważmy, że
zatem korzystając z kryterium porównawczego (patrz
twierdzenie 6.9.
) oraz udowodnionej już rozbieżności szeregu
harmonicznego dostajemy, że szereg
jest rozbieżny.
Załóżmy teraz, że
Zapiszmy
z pewnym
Zauważmy, że
Pogrupujmy wyrazy szeregu podobnie jak w części pierwszej dowodu oraz skorzystajmy z oszacowania powyżej:
Jeśli szereg, który otrzymamy po pogrupowaniu wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego
wyrazy:
Ale szereg o wyrazach
jest szeregiem geometrycznym zbieżnym (jego suma wynosi
). Zatem z kryterium
porównawczego (patrz
twierdzenie 6.9.
) wynika, że także szereg pogrupowany
jest zbieżny. Ponieważ w naszej
sytuacji mamy do czynienia z szeregiem o wyrazach dodatnich, więc ze zbieżności szeregu pogrupowanego możemy
wnioskować o zbieżności szeregu wyjściowego (patrz
uwaga 6.13.
).
Tę stronę ostatnio zmodyfikowano o 22:45, 6 wrz 2006;
Augustin Louis Cauchy (
17891857)
Zobacz biografię
Nawigacja
Strona główna
Przedmioty
Uczelnie
O nas
MIMINF
MIMMAT
Szukaj
Napisz do nas
maruda@mimuw.edu.pl
OK
Szukaj

Analiza matematyczna 1/Wykład 6: Szeregi liczbowe
<
Analiza matematyczna 1
Szeregi liczbowe
Wyk ład ten poświęcony jest szeregom liczbowym. Definiujemy pojęcia szeregu, szeregu
zbieżnego. Podajemy warunek konieczny i warunek Cauchy'ego zbieżności szeregów.
Dowodzimy kryterium porównawczego zbieżności szeregów oraz twierdzenie o grupowaniu
wyrazów szeregu. Dowodzimy rozbieżności szeregu harmonicznego.
D
EFINICJA
6.1.
Niech
będzie ciągiem liczbowym.
(1) Szeregiem o wyrazach
(
) nazywamy ciąg
zwany ciągiem sum
częściowych, gdzie
dla
Szereg oznaczamy przez
(2) Szereg nazywamy zbieżnym, jeśli ciąg sum częściowych jest zbieżny.
Sumą szeregu nazywamy granicę ciągu sum częściowych i oznaczamy tym samym
symbolem co szereg, to znaczy
(3) Jeśli ciąg sum częściowych jest rozbieżny do
to mówimy, że szereg jest rozbieżny do
(lub, że ma sumę
niewłaściwą
) i piszemy
(4) Mówimy, że szereg jest bezwzględnie zbieżny, jeśli szereg
jest zbieżny.
(5) Mówimy, że szereg jest warunkowo zbieżny, jeśli jest on zbieżny, ale nie bezwzględnie zbieżny.
(6) Mówimy, że szereg jest rozbieżny, jeśli nie jest zbieżny.
P
RZYKŁAD
6.2.
Szeregiem o wyrazach
jest
Ciąg sum częściowych tego szeregu, to
Szereg ten jest rozbieżny.
Zachodzi następujący warunek konieczny zbieżności szeregów. Pozwala on w stosunkowo prosty sposób stwierdzić brak
zbieżności dla pewnych szeregów (nie spełniających tego warunku).
T
WIERDZENIE
6.3. [W
ARUNEK
KONIECZNY
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli szereg
jest zbieżny, to
D
OWÓD
6.3.
Niech
będzie ciągiem sum częściowych szeregu. Z założenia wiemy, że
Zauważmy, że
zatem
P
RZYKŁAD
6.4.
Zbadać zbieżność szeregu
Licząc granicę wyrazów tego szeregu dostajemy
zatem nie jest spełniony warunek konieczny zbieżności szeregów (porównaj
twierdzenie 6.3.
). Szereg jest rozbieżny.
P
RZYKŁAD
6.5.
Z szeregiem geometrycznym
spotkaliśmy się już na wykładzie 1 (patrz Przykład
przykład 1.12.
). Przypomnijmy, że
jeśli
to jest on zbieżny wtedy i tylko wtedy, gdy
i wówczas
Najprostszymi działaniami jakie możemy wykonać na szeregach są dodawanie/odejmowanie szeregów i mnożenie szeregu
przez liczbę. Kolejne twierdzenie mówi, iż operacje te "zachowują" zbieżność. Dowód (oparty na twierdzeniu o arytmetyce
granic ciągów) pozostawiamy jako proste ćwiczenie.
T
WIERDZENIE
6.6. [D
ZIAŁANIA
NA
SZEREGACH
]
Jeśli
i
są dwoma szeregami zbieżnymi oraz
to
(1) szeregi
są zbieżne oraz
(2) szereg
jest zbieżny oraz
Ponieważ szereg jest ciągiem (zwanym ciągiem sum częściowych) więc wszystkie twierdzenia dotyczące ciągów można
przenieść na pojęcie szeregu. W szczególności dla ciągu sum częściowych
szeregu
prawdziwe jest twierdzenie,
że ciąg ten jest zbieżny wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego. Mówi o tym poniższe twierdzenie.
T
WIERDZENIE
6.7. [W
ARUNEK
C
AUCHY
'
EGO
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
jest szeregiem, to szereg
jest zbieżny wtedy i tylko wtedy, gdy
Powyższy warunek nazywamy warunkiem Cauchy'ego dla szeregów.
Zauważmy, że
czyli warunek w powyższej definicji jest dokładnie warunkiem Cauchy'ego dla ciągów.
Kolejne twierdzenie będziemy często wykorzystywać przy sprawdzaniu czy dany szereg jest zbieżny.
T
WIERDZENIE
6.8. [Z
BIEŻNOŚĆ
A
BEZWZGLĘDNA
ZBIEŻNOŚĆ
]
Jeśli szereg
jest bezwzględnie zbieżny, to jest on zbieżny.
D
OWÓD
6.8.
Mamy pokazać zbieżność szeregu
Ustalmy dowolne
Ponieważ szereg
jest zbieżny, więc spełnia
warunek Cauchy'ego dla szeregów (patrz
twierdzenie 6.7.
), zatem
Zatem dla dowolnych
mamy
czyli szereg
spełnia warunek Cauchy'ego dla szeregów. Korzystając ponownie z
twierdzenie 6.7.
otrzymujemy, że
szereg
jest zbieżny.
Oprócz warunku koniecznego zbieżności szeregów (pomocnego przy rozstrzyganiu zbieżności szeregów) można podać wiele
warunków wystarczających zbieżności szeregów. Warunki te nazywamy kryteriami. Podstawowym kryterium w teorii szeregów
jest poniższe kryterium porównawcze. Mówi ono, że jeśli wyrazy szeregu szacują się przez wyrazy innego szeregu zbieżnego
(przynajmniej "od pewnego miejsca"), to wyjściowy szereg też jest zbieżny.
T
WIERDZENIE
6.9. [K
RYTERIUM
PORÓWNAWCZE
ZBIEŻNOŚCI
SZEREGÓW
]
Jeśli
są szeregami takimi, że
dla
oraz
to
(1) jeśli szereg
jest zbieżny, to szereg
jest zbieżny;
(2) jeśli szereg
jest rozbieżny, to szereg
jest rozbieżny.
D
OWÓD
6.9.
(Ad (1)) Oznaczmy sumy cz ęściowe obu szeregów odpowiednio przez:
Ciągi
i
są rosnące (gdyż szeregi mają wyrazy nieujemne). Ciąg
jako zbieżny jest ograniczony, to znaczy
Dla
mamy zatem
zatem ciąg
jest ograniczony. Z
twierdzenia 4.15.
(1) wnioskujemy, że jest on zbieżny. Zatem szereg
jest
zbieżny.
(Ad (2)) Jest to równoważne (1).
Kolejne twierdzenie mówi o szeregu, w którym pogrupowano pewne wyrazy, to znaczy policzono sumy kolejnych wyrazów
pogrupowanych w skończone grupy, to znaczy
T
WIERDZENIE
6.10. [O
GRUPOWANIU
WYRAZÓW
SZEREGU
]
Jeśli
jest szeregiem zbieżnym,
jest ciągiem silnie rosnącym takim, że
, to szereg
jest zbieżny oraz
D
OWÓD
6.10.
Zauważmy, że ciąg sum częściowych szeregu pogrupowanego jest podciągiem ciągu sum częściowych wyjściowego szeregu.
Wystarczy zatem zastosowa ć
twierdzenie 3.25.
Szczegóły pozostawiamy jako proste ćwiczenie.
W
NIOSEK
6.11.
Jako konsekwencję powyższego twierdzenia dostajemy stwierdzenie, że "jeśli po pogrupowaniu wyrazów szeregu
otrzymamy szereg rozbieżny, to wyjściowy szereg też był rozbieżny".
Uwaga 6.12.
Twierdzenie odwrotne do twierdzenia 6.10. nie jest prawdziwe.
Aby to sprawdzić rozważmy następujący szereg naprzemienny
Oczywiście jest to szereg rozbieżny, gdyż nie spełnia warunku koniecznego zbieżności szeregów. Pogrupujmy wyrazy tego
szeregu "po dwa", to znaczy
W ten sposób szereg pogrupowany jest szeregiem zerowym
Jest on oczywiście zbieżny (do zera). Zatem ze zbieżności
szeregu pogrupowanego nie można nic wnioskować o zbieżności wyjściowego szeregu.
Uwaga 6.13.
W pewnych jednak sytuacjach ze zbieżności szeregu pogrupowanego można wnioskować o zbieżności szeregu
wyjściowego. Jest tak na przykład w przypadku szeregów o wyrazach nieujemnych. Jeśli
jest szeregiem o wyrazach
nieujemnych, to zbieżność tego szeregu jest równoważna zbieżności szeregu pogrupowanego. Załóżmy bowiem, że szereg
pogrupowany jest zbieżny. Wówczas jego ciąg sum częściowych jest ograniczony, powiedzmy przez
Ale wtedy
ciąg sum częściowych całego szeregu jest też ograniczony przez
(dlaczego?). Ponieważ ponadto ciąg sum częściowych
szeregu
jest rosnący (bo wyrazy
są nieujemne), zatem jest on zbieżny. Szczegółowe rozpisanie tego
rozumowania pozostawiamy jako ćwiczenie.
Na zakończenie podamy ważny przykład szeregu liczbowego, zwanego szeregiem harmonicznym oraz pewne jego uogólnienie.
Szereg ten będzie miał istotne zastosowanie w badaniu zbieżności innych szeregów dzięki kryterium porównawczemu.
P
RZYKŁAD
6.14.
Szereg
jest rozbieżny. Nazywamy go szeregiem harmonicznym.
D
OWÓD
PRZYKŁADU
6.14.
Aby stwierdzić rozbieżność szeregu harmonicznego, pogrupujmy jego wyrazy w następujący sposób:
Każda kolejna grup począwszy od drugiej ma dwa razy więcej składników od poprzedniej oraz wyrazy w każdej grupie szacują
się od dołu przez ostatni składnik postaci
gdzie jest numerem "grupy". Jeśli szereg który otrzymamy po pogrupowaniu
wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego wyrazy:
(patrz powyższy opis). Zatem szereg
nie spełnia warunku koniecznego zbieżności szeregów, a więc jest rozbieżny. Z
kryterium porównawczego zbieżności szeregów (patrz
twierdzenie 6.9.
) wynika, że szereg pogrupowany jest także rozbieżny. Z
wniosku 6.11.
wynika, że wyjściowy szereg harmoniczny jest rozbieżny.
P
RZYKŁAD
6.15.
Szereg
jest zbieżny wtedy i tylko wtedy, gdy
Nazywamy go uogólnionym szeregiem harmonicznym z
wykładnikiem
Jeśli
to zauważmy, że
zatem korzystając z kryterium porównawczego (patrz
) oraz udowodnionej już rozbieżności szeregu
harmonicznego dostajemy, że szereg
jest rozbieżny.
Załóżmy teraz, że
Zapiszmy
z pewnym
Zauważmy, że
Pogrupujmy wyrazy szeregu podobnie jak w części pierwszej dowodu oraz skorzystajmy z oszacowania powyżej:
Jeśli szereg, który otrzymamy po pogrupowaniu wyrazów oznaczymy
to zachodzi następujące oszacowanie na jego
wyrazy:
Ale szereg o wyrazach
jest szeregiem geometrycznym zbieżnym (jego suma wynosi
). Zatem z kryterium
porównawczego (patrz
) wynika, że także szereg pogrupowany
jest zbieżny. Ponieważ w naszej
sytuacji mamy do czynienia z szeregiem o wyrazach dodatnich, więc ze zbieżności szeregu pogrupowanego możemy
wnioskować o zbieżności szeregu wyjściowego (patrz
).
Tę stronę ostatnio zmodyfikowano o 22:45, 6 wrz 2006;
Augustin Louis Cauchy (
17891857)
Zobacz biografię
Nawigacja
Strona główna
Przedmioty
Uczelnie
O nas
MIMINF
MIMMAT
Szukaj
Napisz do nas
maruda@mimuw.edu.pl
OK
Szukaj
Wyszukiwarka
Podobne podstrony:
wazniak mimuw edu pl index php hihxyind
http, www strefawiedzy edu pl file php file= 28 Wyklady BD prezentacja2
http, www strefawiedzy edu pl file php file= 28 Wyklady BD prezentacja6
http, www strefawiedzy edu pl file php file= 28 Wyklady Bazy danych3
http, www strefawiedzy edu pl file php file= 28 Wyklady BD prezentacja4
http, moodle come uw edu pl file php file= 529 LAZARUS
http, www strefawiedzy edu pl file php file= 28 Wyklady BD prezentacja10
www ksiegarnia szostka pl index php cont=eshop&grmID=1&g
http, www strefawiedzy edu pl file php file= 28 Wyklady BD prezentacja9a
http, www strefawiedzy edu pl file php file= 28 Wyklady BD prezentacja5
http, www strefawiedzy edu pl file php file= 28 Wyklady BD prezentacja11a
więcej podobnych podstron