
Danuta Seroka, KKBiTB
1
Zadanie:
projektowanie strefy przypodporowej w stropie płytowo-belkowym
wg PN-B-03264:2002
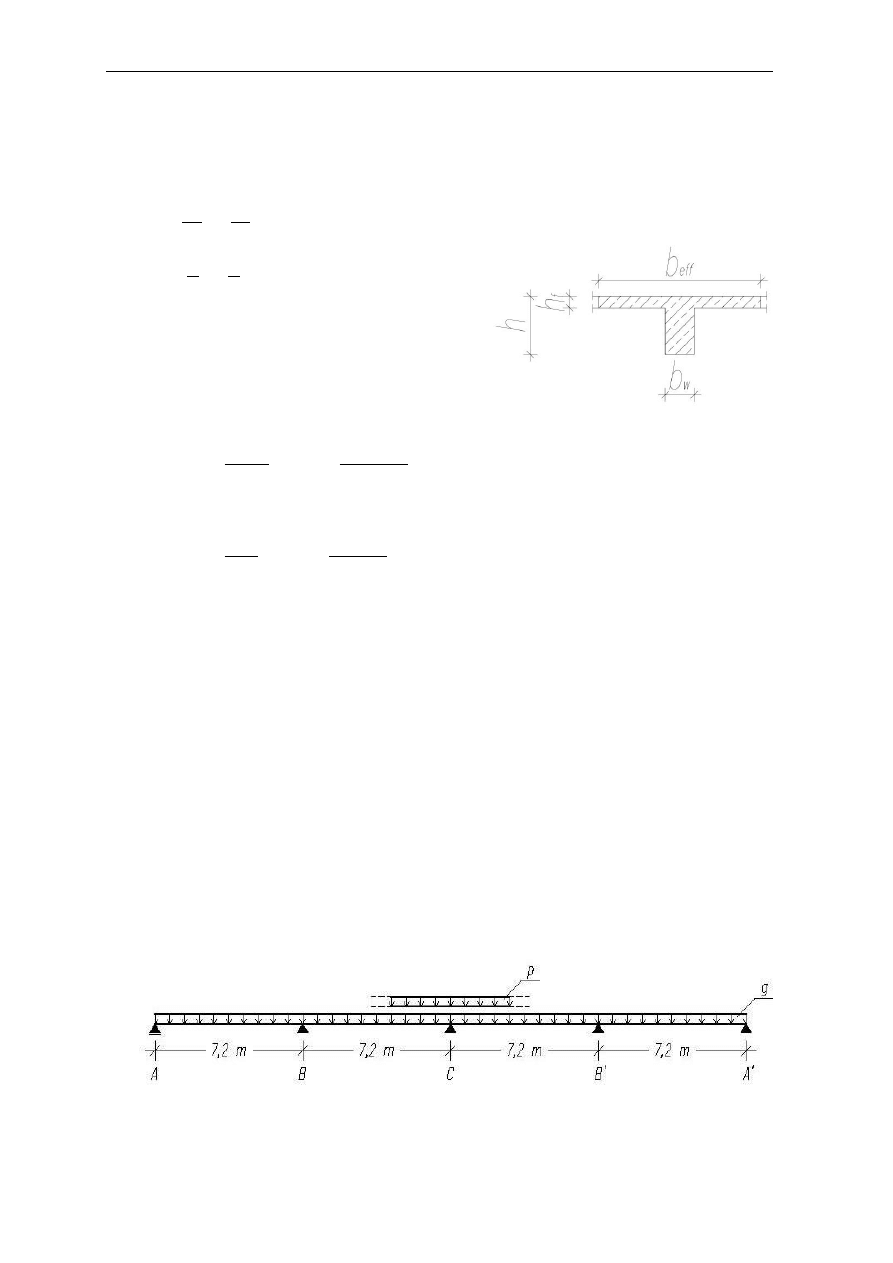
Dany jest strop płytowo-belkowy wg schematu jak na rysunku. Z uwagi na
ścinanie należy zaprojektować strefę przypodporową żebra stropu wg stanu
granicznego nośności, oraz sprawdzić rozwarcie rys ukośnych. Obciążenie
użytkowe p
k
=5kN/m
2
.
Dane:
L = 7,2 m
B = 3 m
Beton: C 30/37
MPa
f
MPa
f
MPa
f
ctd
cd
ck
33
,
1
20
30
Stal zbrojenia głównego: AIII N (RB 500 W)
5
,
0
420
500
lim
,
eff
yd
yk
MPa
f
MPa
f
2
2
20
142
,
3
4
0
,
2
cm
A
s
Stal zbrojenia na ścinanie: AIII N (RB 500 W)
MPa
f
MPa
f
yd
yk
420
500
2
2
6
283
,
0
4
6
,
0
cm
A
s
Danuta Seroka, KKBiTB
2
1 Przyjęcie wymiarów wstępnych i obliczenia statyczne
1.1 Geometria
m
do
L
do
h
z
5
,
0
6
,
0
4
,
0
12
1
18
1
- dla belek średnio i silnie obciążonych
m
do
h
do
b
z
w
25
,
0
25
,
0
167
,
0
2
1
3
1
cm
h
f
10
przyjęto szerokość podpory żebra b
z
= 0,4m.
współpracująca szerokość płyty b
eff
:
dla przęsła skrajnego AB:
m
h
b
m
L
b
b
f
w
w
eff
45
,
1
1
,
0
6
2
25
,
0
6
2
474
,
1
5
2
,
7
85
,
0
25
,
0
5
85
,
0
przyjęto b
eff
= 1,45m
dla przęsła wewnętrznego BC:
m
h
b
m
L
b
b
f
w
w
eff
45
,
1
1
,
0
6
2
25
,
0
6
2
258
,
1
5
2
,
7
7
,
0
25
,
0
5
7
,
0
przyjęto b
eff
= 1,258m
ciężar własny żebra i płyty:
m
kN
g
z
/
0
,
11
25
,
0
4
,
0
1
,
0
3
25
1
,
1
ciężar warstw wykończeniowych:
przyjęto orientacyjny ciężar wszystkich warstw wykończeniowych na stropie
m
kN
g
w
/
1
,
4
3
05
,
0
21
3
,
1
sumaryczne obciążenie stałe:
m
kN
g
g
g
w
z
/
1
,
15
obciążenie użytkowe:
m
kN
p
/
18
3
5
2
,
1
1.2 Schemat statyczny i obciążeń
Danuta Seroka, KKBiTB
3
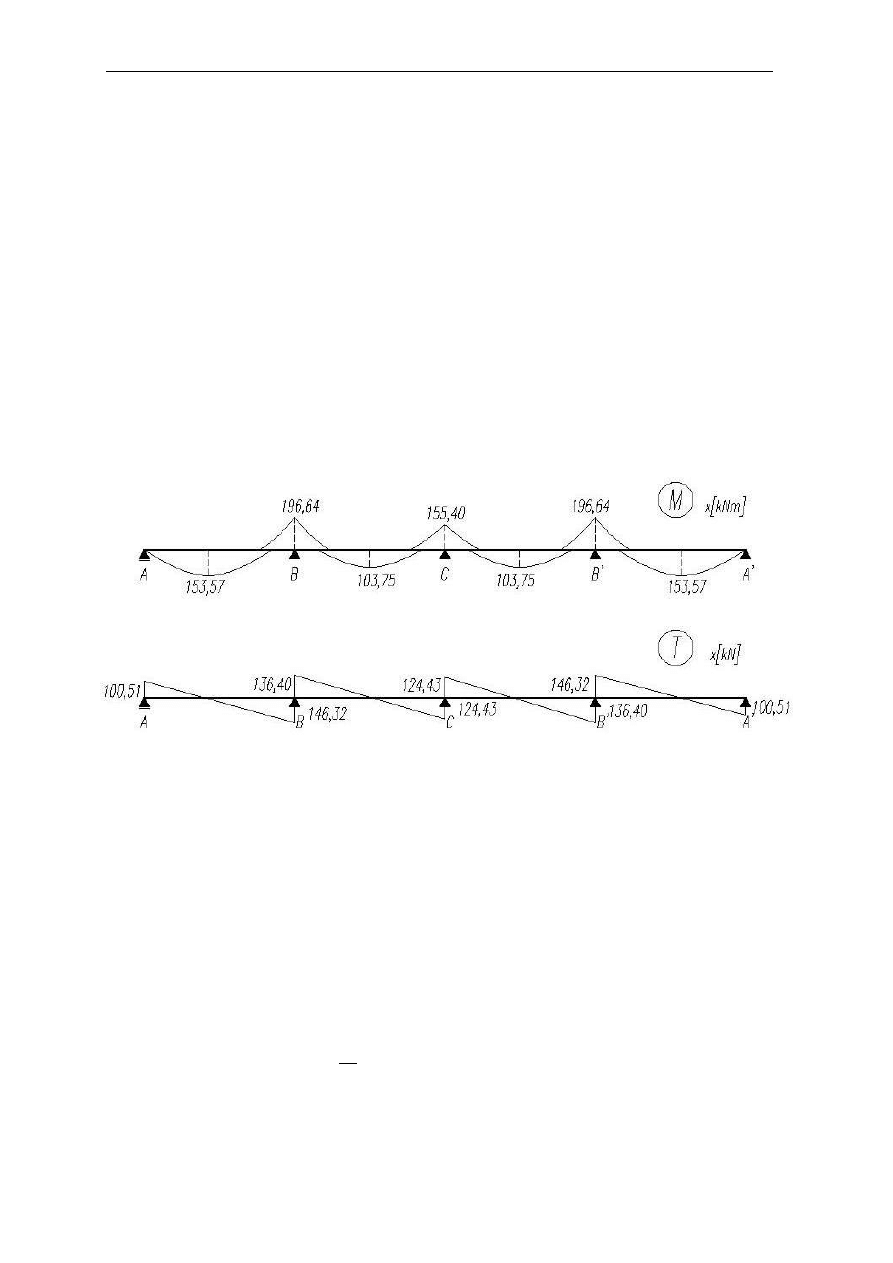
1.3 Siły wewnętrzne
momenty zginające
Współczynniki dla sił wewnętrznych wyznaczono na podstawie tablic Winklera:
kNm
M
AB
57
,
153
2
,
7
18
1
,
0
1
,
15
077
,
0
2
kNm
M
BC
75
,
103
2
,
7
18
081
,
0
1
,
15
036
,
0
2
kNm
M
B
6
,
196
2
,
7
18
121
,
0
1
,
15
107
,
0
2
kNm
M
C
4
,
155
2
,
7
18
107
,
0
1
,
15
071
,
0
2
siły tnące:
kN
V
P
A
51
,
100
2
,
7
18
446
,
0
1
,
15
393
,
0
kN
V
L
B
3
,
146
2
,
7
18
620
,
0
1
,
15
607
,
0
kN
V
P
B
4
,
136
2
,
7
18
603
,
0
1
,
15
536
,
0
kN
V
L
C
4
,
124
2
,
7
18
571
,
0
1
,
15
464
,
0
2 Wymiarowanie zbrojenia z uwagi na zginanie
2.1 Przęsło AB
m
a
h
d
m
a
a
m
h
cm
h
m
b
m
b
f
w
eff
45
,
0
05
,
0
1
,
0
5
,
0
25
,
0
45
,
1
1
2
1
2
f
cd
f
eff
f
h
d
f
d
h
b
M
kNm
522
1
,
0
5
,
0
45
,
0
10
20
45
,
0
1
,
0
45
,
1
3
kNm
M
M
Sd
f
57
,
153
- przekrój pozornie teowy

Danuta Seroka, KKBiTB
4
026
,
0
10
20
45
,
0
45
,
1
57
,
153
3
2
2
cd
eff
Sd
eff
f
d
b
M
5
,
0
027
,
0
2
1
1
lim
,
eff
eff
eff
- przekrój pojedynczo zbrojony
yd
cd
eff
eff
s
f
f
d
b
A
1
2
4
23
,
8
10
420
20
45
,
0
45
,
1
027
,
0
cm
zastosowano zbrojenie o średnicy 20mm
2
20
1
425
,
9
3
cm
A
A
s
prov
s
2.2
Przęsło BC
m
a
h
d
m
a
a
m
h
cm
h
m
b
m
b
f
w
eff
45
,
0
05
,
0
1
,
0
5
,
0
25
,
0
258
,
1
1
2
1
2
f
cd
f
eff
f
h
d
f
d
h
b
M
kNm
453
1
,
0
5
,
0
45
,
0
10
20
45
,
0
1
,
0
258
,
1
3
kNm
M
M
Sd
f
75
,
103
- przekrój pozornie teowy
0204
,
0
10
20
45
,
0
258
,
1
75
,
103
3
2
2
cd
eff
Sd
eff
f
d
b
M
5
,
0
021
,
0
2
1
1
lim
,
eff
eff
eff
- przekrój pojedynczo zbrojony
yd
cd
eff
eff
s
f
f
d
b
A
1
2
4
55
,
5
10
420
20
45
,
0
258
,
1
021
,
0
cm
zastosowano zbrojenie o średnicy 20mm
2
20
1
283
,
6
2
cm
A
A
s
prov
s
2.3 Podpora B
m
b
d
d
m
a
h
d
m
a
a
m
h
cm
h
m
b
z
f
w
517
,
0
6
4
,
0
45
,
0
6
45
,
0
05
,
0
1
,
0
5
,
0
25
,
0
1
2
1
zbrojenie dla momentu osiowego M
(B)
= 196,64kNm:
147
,
0
10
20
517
,
0
25
,
0
64
,
196
3
2
2
cd
w
Sd
eff
f
d
b
M
Danuta Seroka, KKBiTB
5
5
,
0
160
,
0
2
1
1
lim
,
eff
eff
eff
- przekrój pojedynczo zbrojony
yd
cd
w
eff
B
s
f
f
d
b
A
1
2
4
85
,
9
10
420
20
517
,
0
25
,
0
160
,
0
cm
zbrojenie dla momentu krawędziowego [M
(B)
] = 169,36kNm:
167
,
0
10
20
45
,
0
25
,
0
36
,
169
3
2
2
cd
w
Sd
eff
f
d
b
M
5
,
0
184
,
0
2
1
1
lim
,
eff
eff
eff
- przekrój pojedynczo zbrojony
yd
cd
w
eff
B
s
f
f
d
b
A
]
[
1
2
4
87
,
9
10
420
20
45
,
0
25
,
0
184
,
0
cm
2
]
[
1
1
1
87
,
9
)
,
max(
cm
A
A
A
B
s
B
s
s
zastosowano zbrojenie o średnicy 20mm
2
20
1
566
,
12
4
cm
A
A
s
prov
s
2.4 Podpora C
m
b
d
d
m
a
h
d
m
a
a
m
h
cm
h
m
b
z
f
w
517
,
0
6
4
,
0
45
,
0
6
45
,
0
05
,
0
1
,
0
5
,
0
25
,
0
1
2
1
zbrojenie dla momentu osiowego M
(C)
= 155,40kNm:
116
,
0
10
20
517
,
0
25
,
0
4
,
155
3
2
2
cd
w
Sd
eff
f
d
b
M
5
,
0
124
,
0
2
1
1
lim
,
eff
eff
eff
- przekrój pojedynczo zbrojony
yd
cd
w
eff
B
s
f
f
d
b
A
1
2
4
64
,
7
10
420
20
517
,
0
25
,
0
124
,
0
cm
zbrojenie dla momentu krawędziowego [M
(C)
] = 130,52kNm:
129
,
0
10
20
45
,
0
25
,
0
52
,
130
3
2
2
cd
w
Sd
eff
f
d
b
M
5
,
0
138
,
0
2
1
1
lim
,
eff
eff
eff
- przekrój pojedynczo zbrojony
yd
cd
w
eff
B
s
f
f
d
b
A
]
[
1
2
4
42
,
7
10
420
20
45
,
0
25
,
0
138
,
0
cm
2
]
[
1
1
1
64
,
7
)
,
max(
cm
A
A
A
B
s
B
s
s
zastosowano zbrojenie o średnicy 20mm
2
20
1
425
,
9
3
cm
A
A
s
prov
s
Danuta Seroka, KKBiTB
6
3
W
ymiarowanie zbrojenia z uwagi na ścinanie
Założenie 1: w każdym ścinanym przekroju należy uwzględnić 3
20 ,
tj. zbrojenie zginane zakotwione poza podporami na długość d+ l
bd
poza
sprawdzany na ścinanie
2
425
,
9
cm
A
sL
01
,
0
008
,
0
45
,
0
25
,
0
10
425
,
9
4
d
b
A
w
sL
L
Założenie 2: Wymiarowania zbrojenia na ścinanie przeprowadzone
zostanie w przekroju w odległości d od lica podpory, co należy uwzględnić
korygując wartości sił tnących.
3.1 Podpora A
m
d
m
b
w
45
,
0
25
,
0
g
p
d
b
V
V
z
Sd
d
Sd
2
kN
0
,
79
1
,
15
18
45
,
0
2
,
0
51
,
100
V
Rd1:
nośność na ścinanie elementu bez zbrojenia poprzecznego
d
k
6
,
1
15
,
1
45
,
0
6
,
1
MPa
f
MPa
f
cd
ctd
20
33
,
1
MPa
f
MPa
f
ywk
ywd
500
420
d
b
f
k
V
w
L
ctd
Rd
40
2
,
1
35
,
0
1
kN
45
,
92
45
,
0
25
,
0
008
,
0
40
2
,
1
10
33
,
1
15
,
1
35
,
0
3
kN
V
V
d
Sd
Rd
0
,
79
1
- występuje odcinek I rodzaju,
zbrojenie na ścinanie stosuje się jedynie konstrukcyjnie
V
Rd2:
nośność na ścinanie ze względu na ściskanie betonu
528
,
0
250
30
1
6
,
0
250
1
6
,
0
ck
f
z
b
f
V
w
cd
Rd
5
,
0
2
kN
V
kN
d
Sd
0
,
79
6
,
534
528
,
0
45
,
0
9
,
0
25
,
0
10
20
5
,
0
3
konstrukcyjny rozstaw strzemion:
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
Przyjęto strzemiona
6 dwucięte.

Danuta Seroka, KKBiTB
7
3.2 Podpora B (str. lewa)
m
d
m
b
w
45
,
0
25
,
0
g
p
d
b
V
V
z
Sd
d
Sd
2
kN
81
,
124
1
,
15
18
45
,
0
2
,
0
3
,
146
V
Rd1:
nośność na ścinanie elementu bez zbrojenia poprzecznego
d
k
6
,
1
15
,
1
45
,
0
6
,
1
MPa
f
MPa
f
cd
ctd
20
33
,
1
MPa
f
MPa
f
ywk
ywd
500
420
d
b
f
k
V
w
L
ctd
Rd
40
2
,
1
35
,
0
1
kN
45
,
92
45
,
0
25
,
0
008
,
0
40
2
,
1
33
,
1
15
,
1
35
,
0
kN
V
V
d
Sd
Rd
81
,
124
1
- występuje odcinek II rodzaju, zbrojenie na ścinanie
w postaci strzemion prostopadłych i prętów odgiętych
45
- założony teoretyczny kąt nachylenia krzyżulca betonowego
V
Rd3:
nośność ze względu na rozciąganie zbrojenia poprzecznego przyjętego
na ścinanie
Długość odcinka II rodzaju na którym potrzebne jest zbrojenie strzemionami:
kN
g
p
b
V
V
z
Sd
Sd
7
,
139
1
,
15
18
2
,
0
3
,
146
2
]
[
p
g
V
V
c
Rd
Sd
sw
1
]
[
m
d
m
35
,
1
3
43
,
1
18
1
,
15
45
,
92
7
,
139
Uwaga: gdyby projektowane było zbrojenie z uwagi na ścinanie
jedynie w postaci strzemion, dla odcinek c
sw
> 3d należałoby podzielić
na pododcinki.
32
31
3
Rd
Rd
Rd
V
V
V
- nośność odpowiednio dla strzemion i prętów
odgiętych
Założenie 1: minimum 50% siły ścinającej przenoszą strzemiona
Założenie 2: za odcinku II rodzaju przyjęto zbrojenie strzemionami
6
dwuciętymii ze stali A III N o przekroju
2
1
565
,
0
cm
A
sw
kN
V
V
d
Sd
Rd
63
5
,
0
31
cot
1
1
1
1
,
31
z
s
f
A
V
ywd
sw
Rd
m
z
V
f
A
s
Rd
ywd
sw
153
,
0
1
45
,
0
9
,
0
63
10
420
10
565
,
0
cot
3
4
1
,
31
1
1
1
Przyjęto rozstaw strzemion s
1
= 15 cm na długości 1,50 m
0015
,
0
25
,
0
15
,
0
10
565
,
0
4
1
1
1
w
sw
w
b
s
A
0009
,
0
500
30
08
,
0
08
,
0
min
,
1
yk
ck
w
f
f
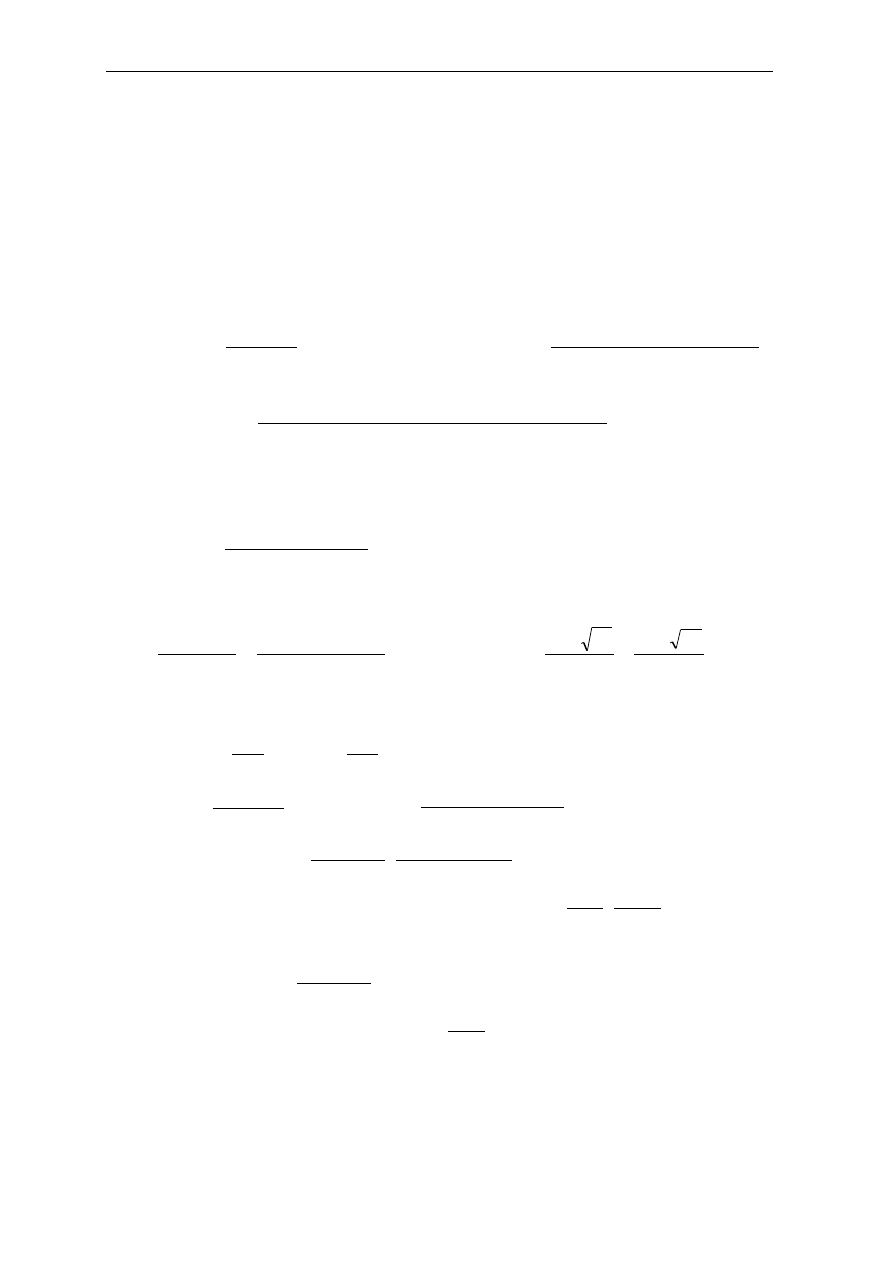
Danuta Seroka, KKBiTB
8
Siła na jaką należy zaprojektować zbrojenie prętami odgiętymi.
kN
V
V
V
Rd
d
Sd
Rd
81
,
61
31
Założenie 3: przyjęto odgięcie prętów pod kątem 45˚.
Maksymalny rozstaw prętów odgiętych:
d
a
d
s
2
,
0
cot
2
max
2
m
5
,
0
45
,
0
2
,
0
45
cot
05
,
0
45
,
0
przyjęto rozstaw:
m
a
d
s
4
,
0
05
,
0
45
,
0
2
2
zatem potrzebne są 4 pręty odgięte na odcinku II rodzaju (c
sw
= 143 cm)
sin
cot
cot
sin
cot
cot
2
2
2
2
2
32
z
f
s
V
A
z
s
f
A
V
V
ywd
Sd
sw
ywd
sw
Rd
Rd
Potrzebne pole zbrojenia przy rozstawie s
2
= 0,4m:
2
3
2
03
,
1
45
sin
45
cot
45
cot
45
,
0
9
,
0
10
420
4
,
0
81
,
61
cm
A
sw
Przyjęto zbrojenie w postaci jednego pręta odgiętego
12 w płaszczyźnie
o przekroju
2
2
131
,
1
cm
A
sw
Obliczeniowa nośność na ścinanie dla prętów odgiętych:
kN
V
Rd
02
,
68
45
sin
45
cot
45
cot
45
,
0
9
,
0
4
,
0
10
420
10
131
,
1
3
4
32
kN
V
V
Rd
Rd
81
,
61
32
- założone zbrojenie i rozstaw zapewnia minimalną
nośność z uwagi na różnicę ΔV
Rd
0016
,
0
45
sin
25
,
0
4
,
0
10
131
,
1
sin
4
2
2
2
w
sw
w
b
s
A
>
0009
,
0
500
30
08
,
0
08
,
0
min
,
2
yk
ck
w
f
f
V
Rd2:
nośność na ścinanie ze względu na ściskanie betonu
528
,
0
250
30
1
6
,
0
250
1
6
,
0
ck
f
cos
2
2
2
s
f
A
z
V
ywd
sw
kN
01
,
34
45
cos
4
,
0
10
420
10
131
,
1
45
,
0
9
,
0
3
4
cot
cot
2
cot
cot
1
cot
2
max
w
cd
b
f
z
V
kN
2
,
178
1
1
2
1
1
1
1
25
,
0
10
20
528
,
0
45
,
0
9
,
0
2
3
max
V
V
- należy przyjąc ΔV do obliczenia V
Rd2
V
z
b
f
V
w
cd
Rd
2
2
cot
1
cot
kN
V
kN
d
Sd
81
,
124
61
,
568
01
,
34
1
1
1
528
,
0
45
,
0
9
,
0
25
,
0
10
20
2
3
rozstaw strzemion na odcinku I rodzaju:
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
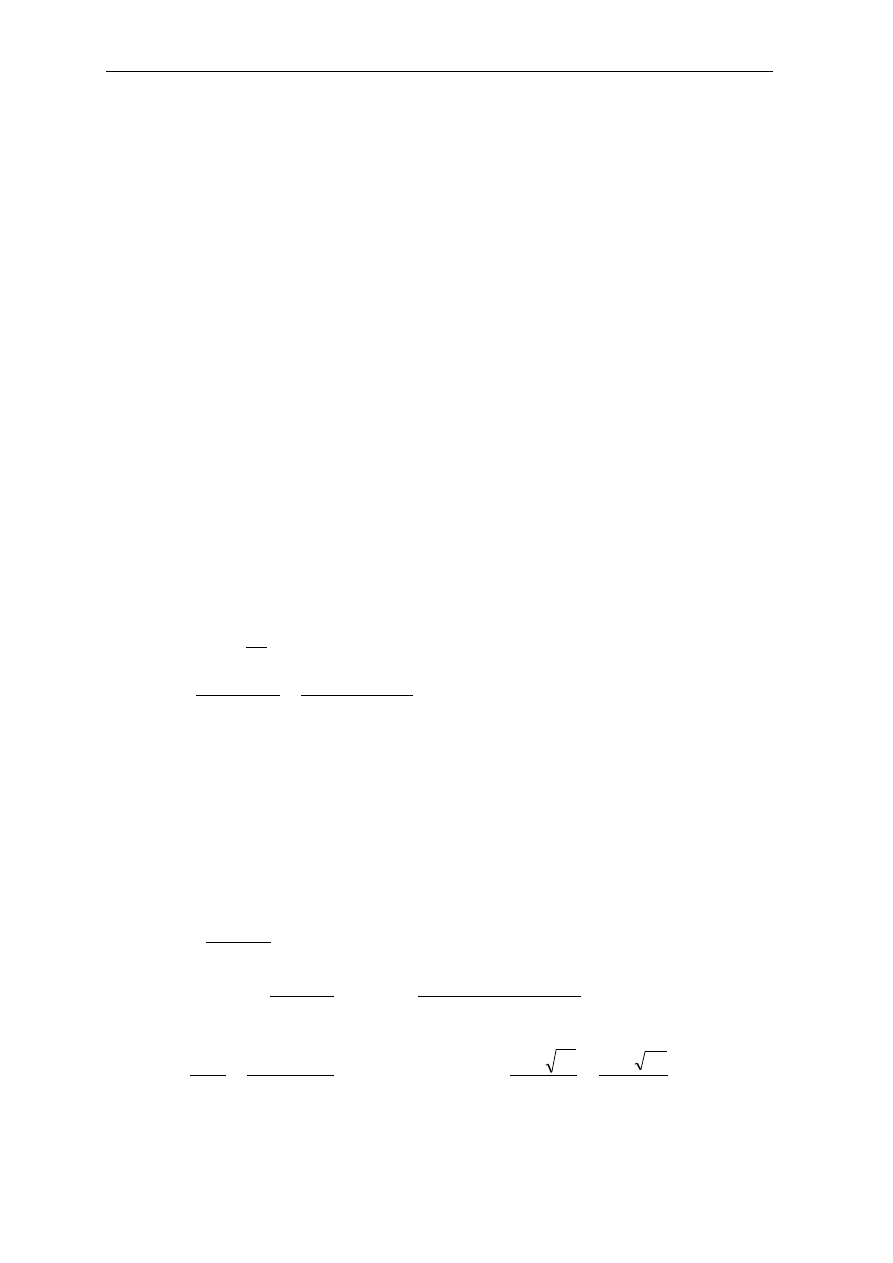
Danuta Seroka, KKBiTB
9
3.3 Podpora B (str. prawa)
m
d
m
b
w
45
,
0
25
,
0
g
p
d
V
V
Sd
d
Sd
2
,
0
kN
89
,
114
1
,
15
18
45
,
0
2
,
0
4
,
136
V
Rd1:
nośność na ścinanie elementu bez zbrojenia poprzecznego
d
k
6
,
1
15
,
1
45
,
0
6
,
1
MPa
f
MPa
f
cd
ctd
20
33
,
1
MPa
f
MPa
f
ywk
ywd
500
420
d
b
f
k
V
w
L
ctd
Rd
40
2
,
1
35
,
0
1
kN
45
,
92
45
,
0
25
,
0
008
,
0
40
2
,
1
33
,
1
15
,
1
35
,
0
kN
V
V
d
Sd
Rd
89
,
114
1
- występuje odcinek II rodzaju, zbrojenie na ścinanie
w postaci strzemion prostopadłych i prętów odgiętych
45
- założony teoretyczny kąt nachylenia krzyżulca betonowego
V
Rd3:
nośność ze względu na rozciąganie zbrojenia poprzecznego przyjętego
na ścinanie
Długość odcinka II rodzaju:
kN
g
p
b
V
V
z
Sd
Sd
78
,
129
1
,
15
18
2
,
0
4
,
136
2
]
[
p
g
V
V
c
Rd
Sd
sw
1
]
[
m
d
m
35
,
1
3
13
,
1
18
1
,
15
45
,
92
78
,
129
32
31
3
Rd
Rd
Rd
V
V
V
- nośność odpowiednio dla strzemion i prętów
odgiętych
Założenie 1: minimum 50% siły ścinającej przenoszą strzemiona
Założenie 2: za odcinku II rodzaju przyjęto zbrojenie strzemionami
6
dwuciętymi ze stali A III N o przekroju
2
1
565
,
0
cm
A
sw
kN
V
V
d
Sd
Rd
63
5
,
0
31
cot
1
1
1
31
z
s
f
A
V
ywd
sw
Rd
m
z
V
f
A
s
Rd
ywd
sw
153
,
0
1
45
,
0
9
,
0
63
10
420
10
565
,
0
cot
3
4
31
1
1
1
Przyjęto rozstaw strzemion s
1
= 15 cm na długości 1,2 m
0015
,
0
25
,
0
15
,
0
10
565
,
0
4
1
1
1
w
sw
w
b
s
A
0009
,
0
500
30
08
,
0
08
,
0
min
,
1
yk
ck
w
f
f
kN
V
V
V
Rd
d
Sd
Rd
89
,
51
31
Założenie 3: przyjęto odgięcie prętów pod kątem 45˚.
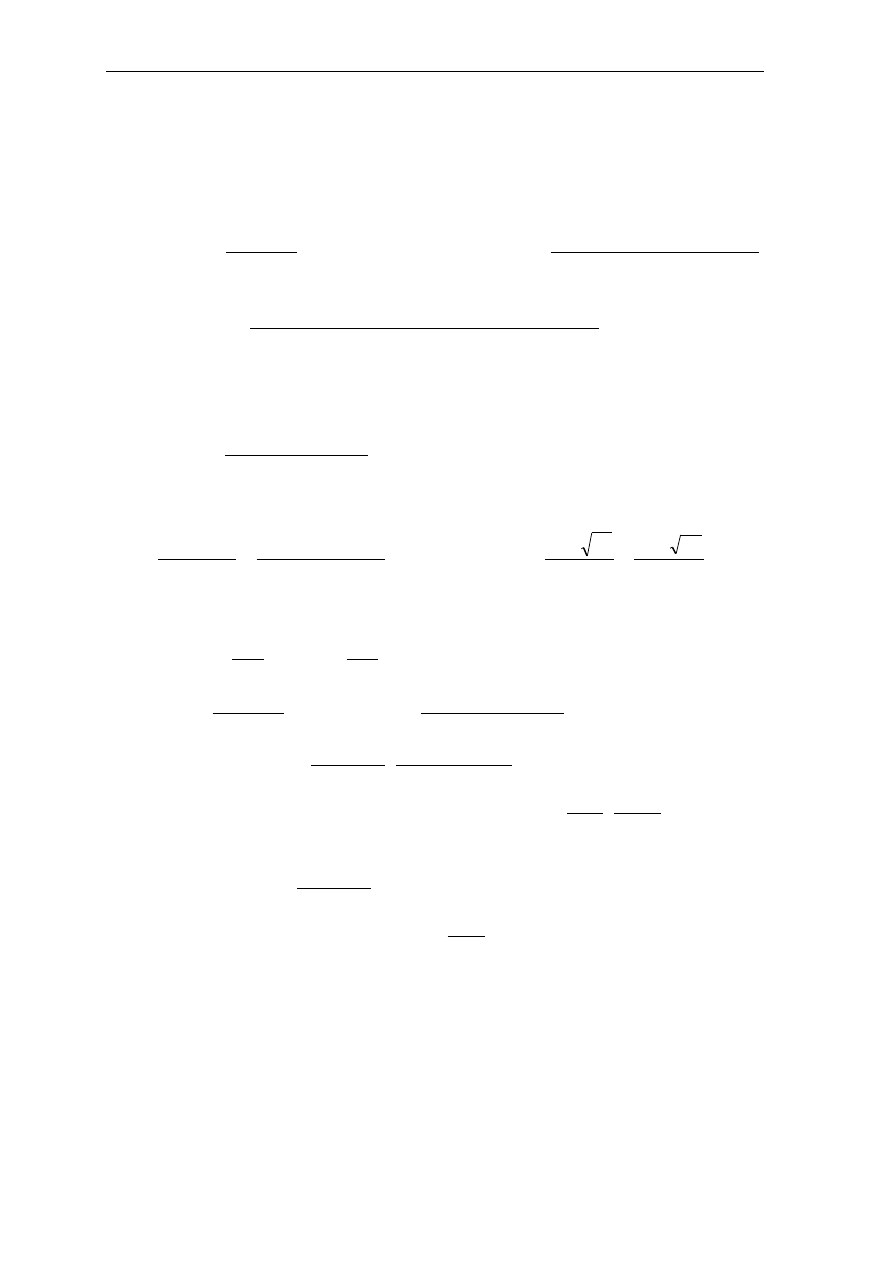
Danuta Seroka, KKBiTB
10
Maksymalny rozstaw prętów odgiętych:
d
a
d
s
2
,
0
cot
2
max
2
m
5
,
0
45
,
0
2
,
0
45
cot
05
,
0
45
,
0
przyjęto rozstaw:
m
a
d
s
4
,
0
05
,
0
45
,
0
2
2
zatem potrzebne są 3 pręty odgięte na odcinku II rodzaju (c
sw
= 113 cm)
sin
cot
cot
sin
cot
cot
2
2
2
2
2
32
z
f
s
V
A
z
s
f
A
V
V
ywd
Sd
sw
ywd
sw
Rd
Rd
Potrzebne pole zbrojenia przy rozstawie s
2
= 0,4m:
2
3
2
863
,
0
45
sin
45
cot
45
cot
45
,
0
9
,
0
10
420
4
,
0
89
,
51
cm
A
sw
Przyjęto zbrojenie w postaci jednego pręta odgiętego
12 w płaszczyźnie
o przekroju
2
2
131
,
1
cm
A
sw
Obliczeniowa nośność na ścinanie dla prętów odgiętych:
kN
V
Rd
02
,
68
45
sin
45
cot
45
cot
45
,
0
9
,
0
4
,
0
10
420
10
131
,
1
3
4
32
kN
V
V
Rd
Rd
89
,
51
32
- założone zbrojenie i rozstaw zapewnia minimalną
nośność z uwagi na różnicę ΔV
Rd
0016
,
0
45
sin
25
,
0
4
,
0
10
131
,
1
sin
4
2
2
2
w
sw
w
b
s
A
>
0009
,
0
500
30
08
,
0
08
,
0
min
,
2
yk
ck
w
f
f
V
Rd2:
nośność na ścinanie ze względu na ściskanie betonu
528
,
0
250
30
1
6
,
0
250
1
6
,
0
ck
f
cos
2
2
2
s
f
A
z
V
ywd
sw
kN
01
,
34
45
cos
4
,
0
10
420
10
131
,
1
45
,
0
9
,
0
3
4
cot
cot
2
cot
cot
1
cot
2
max
w
cd
b
f
z
V
kN
2
,
178
1
1
2
1
1
1
1
25
,
0
10
20
528
,
0
45
,
0
9
,
0
2
3
max
V
V
- należy przyjąc ΔV do obliczenia V
Rd2
V
z
b
f
V
w
cd
Rd
2
2
cot
1
cot
kN
V
kN
d
Sd
81
,
124
61
,
568
01
,
34
1
1
1
528
,
0
45
,
0
9
,
0
25
,
0
10
20
2
3
rozstaw strzemion na odcinku I rodzaju:
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
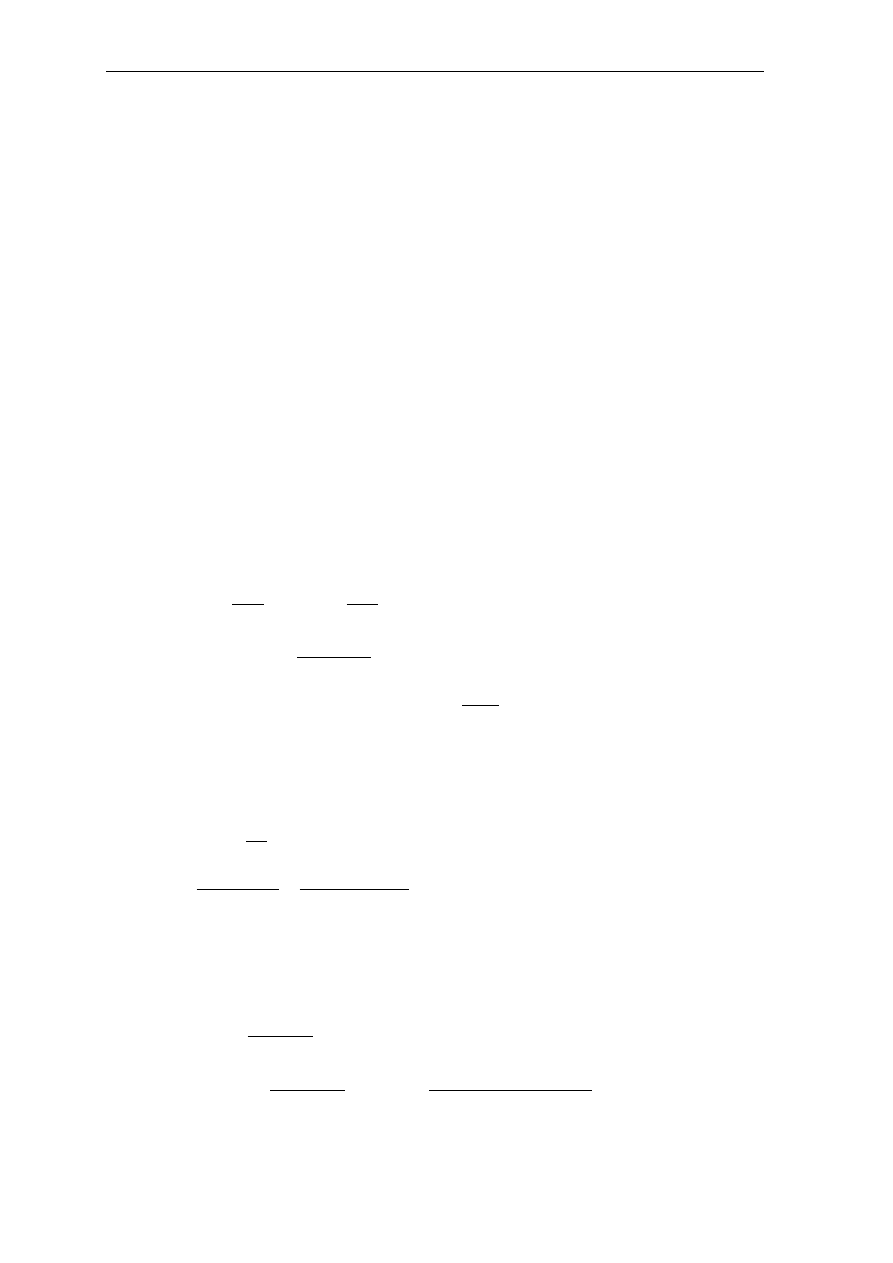
Danuta Seroka, KKBiTB
11
3.4 Podpora C (str. lewa)
m
d
m
b
w
45
,
0
25
,
0
g
p
d
V
V
Sd
d
Sd
2
,
0
kN
92
,
102
1
,
15
18
45
,
0
2
,
0
4
,
124
V
Rd1:
nośność na ścinanie elementu bez zbrojenia poprzecznego
d
k
6
,
1
15
,
1
45
,
0
6
,
1
MPa
f
MPa
f
cd
ctd
20
33
,
1
MPa
f
MPa
f
ywk
ywd
500
420
d
b
f
k
V
w
L
ctd
Rd
40
2
,
1
35
,
0
1
kN
45
,
92
45
,
0
25
,
0
008
,
0
40
2
,
1
33
,
1
15
,
1
35
,
0
kN
V
V
d
Sd
Rd
92
,
102
1
- występuje odcinek II rodzaju, zbrojenie na ścinanie
w postaci strzemion prostopadłych
45
- założony teoretyczny kąt nachylenia krzyżulca betonowego
V
Rd2:
nośność na ścinanie ze względu na ściskanie betonu
528
,
0
250
30
1
6
,
0
250
1
6
,
0
ck
f
2
2
cot
1
cot
z
b
f
V
w
cd
Rd
kN
V
kN
d
Sd
92
,
102
6
,
534
1
1
1
528
,
0
45
,
0
9
,
0
25
,
0
10
20
2
3
V
Rd3:
nośność na ścinanie ze względu na rozciąganie zbrojenia poprzecznego
przyjętego na ścinanie
Długość odcinka II rodzaju:
kN
g
p
b
V
V
z
Sd
Sd
81
,
117
1
,
15
18
2
,
0
4
,
124
2
]
[
p
g
V
V
c
Rd
Sd
sw
1
]
[
m
d
m
35
,
1
3
77
,
0
18
1
,
15
45
,
92
81
,
117
nie ma potrzeby dzielenia odcinka c
sw
na pododcinki.
Założenie 1: za odcinku II rodzaju przyjęto zbrojenie strzemionami
6
dwuciętymi ze stali A III N o przekroju
2
1
565
,
0
cm
A
sw
cot
1
1
1
3
z
s
f
A
V
V
ywd
sw
Rd
d
Sd
m
z
V
f
A
s
d
Sd
ywd
sw
093
,
0
45
cot
45
,
0
9
,
0
92
,
102
10
420
10
565
,
0
cot
3
4
1
1
1
Danuta Seroka, KKBiTB
12
Przyjęto rozstaw strzemion s
1
= 9 cm na długości 0,81 m
0025
,
0
25
,
0
09
,
0
10
565
,
0
4
1
1
1
w
sw
w
b
s
A
0009
,
0
500
30
08
,
0
08
,
0
min
,
1
yk
ck
w
f
f
rozstaw strzemion na odcinku I rodzaju:
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
4
Sprawdzenie nośności zbrojenia podłużnego przy ścinaniu
yd
sL
td
d
Sd
td
f
A
F
z
M
F
sprawdzenia należy dokonać na odcinkach II rodzaju w przekroju
wymiarowanym na ścinanie (w odległości d od lica podpory)
cot
cot
5
,
0
3
32
Rd
Rd
d
Sd
td
V
V
V
F
4.1 Podpora B (str. lewa)
kNm
d
a
V
M
M
n
Sd
Sd
d
Sd
53
,
101
45
,
0
2
,
0
3
,
146
6
,
196
- moment
zginający w przekroju sprawdzanym na ścinanie
m
d
45
,
0
m
b
a
z
n
2
,
0
2
kN
V
d
Sd
81
,
124
2
1
42
,
9
cm
A
s
MPa
f
yd
420
kN
F
td
01
,
30
45
cot
63
02
,
68
02
,
68
45
cot
81
,
124
5
,
0
kN
kN
F
td
84
,
395
10
420
10
42
,
9
69
,
280
01
,
30
45
,
0
9
,
0
53
,
101
3
4
kN
z
M
kN
F
td
43
,
485
45
,
0
9
,
0
6
,
196
69
,
280
max
warunki spełnione.
4.2 Podpora B (str. prawa)
`
98
,
107
45
,
0
2
,
0
4
,
136
6
,
196
kNm
d
a
V
M
M
n
Sd
Sd
d
Sd
- moment
zginający w przekroju sprawdzanym na ścinanie
m
d
45
,
0
m
b
a
z
n
2
,
0
2
kN
V
d
Sd
89
,
114
2
1
42
,
9
cm
A
s
MPa
f
yd
420

Danuta Seroka, KKBiTB
13
kN
F
td
62
,
27
45
cot
63
02
,
68
02
,
68
45
cot
89
,
114
5
,
0
kN
kN
F
td
84
,
395
10
420
10
42
,
9
23
,
294
62
,
27
45
,
0
9
,
0
98
,
107
3
4
kN
z
M
kN
F
td
43
,
485
45
,
0
9
,
0
6
,
196
23
,
294
max
warunki spełnione.
4.3 Podpora C (str. lewa)
`
52
,
74
45
,
0
2
,
0
4
,
124
4
,
155
kNm
d
a
V
M
M
n
Sd
Sd
d
Sd
- moment
zginający w przekroju
sprawdzanym na ścinanie
m
d
45
,
0
m
b
a
z
n
2
,
0
2
kN
V
d
Sd
92
,
102
2
1
42
,
9
cm
A
s
MPa
f
yd
420
kN
F
td
46
,
51
45
cot
92
,
102
5
,
0
kN
kN
F
td
84
,
395
10
420
10
42
,
9
47
,
235
46
,
51
45
,
0
9
,
0
52
,
74
3
4
kN
z
M
kN
F
td
704
,
383
45
,
0
9
,
0
4
,
155
47
,
235
max
warunki spełnione.
5
Rozwarcie rys ukośnych – SGU
Sprawdzenia należy dokonać w przekroju, który zwymiarowany został na
ścinanie, czyli w odległości d od lica podpory:
m m
w
f
E
w
ck
s
w
k
3
,
0
4
lim
2
d
b
V
w
d
Sd
2
2
2
1
1
1
3
1
w
w
2
1
w
w
w
Do sprawdzenia SGU wykorzystano siły tnące wyznaczone dla wielkości
charakterystycznych.

Danuta Seroka, KKBiTB
14
5.1 Podpora B (str. lewa)
kN
V
d
k
Sd
13
,
106
,
m
d
m
b
w
45
,
0
25
,
0
d
b
V
w
d
Sd
MPa
934
,
0
45
,
0
25
,
0
31
,
106
0031
,
0
0016
,
0
0015
,
0
2
1
w
w
w
7
,
0
- dla stali żebrowanej (A III N)
GPa
E
s
200
2
2
2
1
1
1
3
1
w
w
67
,
606
12
7
,
0
0016
,
0
6
7
,
0
0015
,
0
3
1
m m
w
f
E
w
ck
s
w
k
3
,
0
116
,
0
30
10
200
0031
,
0
67
,
606
934
,
0
4
4
lim
3
2
rysy mają rozwarcie mniejsze od granicznego.
5.2 Podpora B (str. prawa)
kN
V
d
k
Sd
57
,
97
,
m
d
m
b
w
45
,
0
25
,
0
d
b
V
w
d
Sd
MPa
867
,
0
45
,
0
25
,
0
57
,
97
0031
,
0
0016
,
0
0015
,
0
2
1
w
w
w
7
,
0
- dla stali żebrowanej (A III N)
GPa
E
s
200
2
2
2
1
1
1
3
1
w
w
67
,
606
12
7
,
0
0016
,
0
6
7
,
0
0015
,
0
3
1
m m
w
f
E
w
ck
s
w
k
3
,
0
098
,
0
30
10
200
0031
,
0
67
,
606
867
,
0
4
4
lim
3
2
rysy mają rozwarcie mniejsze od granicznego.
5.3 Podpora C (str. lewa)
kN
V
d
Sd
3
,
87
m
d
m
b
w
45
,
0
25
,
0
d
b
V
w
d
Sd
MPa
776
,
0
45
,
0
25
,
0
3
,
87

Danuta Seroka, KKBiTB
15
0025
,
0
1
w
w
7
,
0
- dla stali żebrowanej (A III N)
GPa
E
s
200
1
1
1
3
1
w
04
,
557
6
7
,
0
0025
,
0
3
1
m m
w
f
E
w
ck
s
w
k
3
,
0
089
,
0
30
10
200
0025
,
0
04
,
557
776
,
0
4
4
lim
3
2
rysy mają rozwarcie mniejsze od granicznego.
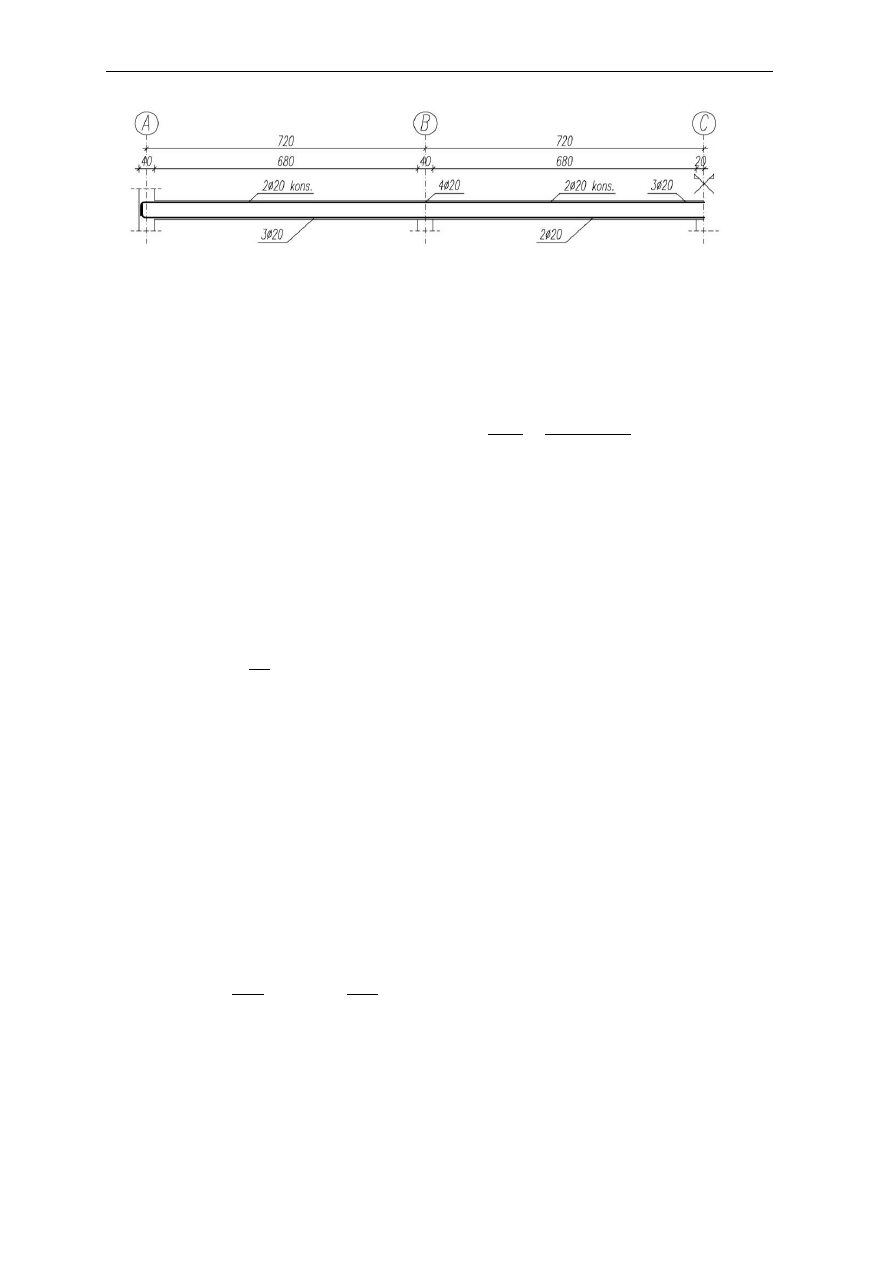
6
Szkic zbrojenia
6.1 Podpora A (str. prawa)
Rodzaj odcinka:
I rodzaju
Zbrojenie na ścinanie:
zbrojenie jedynie konstrukcyjne o maksymalnym rozstawie
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
; przyjęto rozstaw co 30 cm
6.2 Podpora B (str. lewa)
Rodzaj odcinka:
II rodzaju o długości 143 cm
Zbrojenie na ścinanie:
na odcinku II rodzaju:
c
sw1
= 150 cm ze strzemionami w rozstawie 15 cm
c
sw2
= 160 cm z prętem odgiętym w płaszczyźnie
12 w rozstawie 40 cm
na odcinku I rodzaju:
zbrojenie konstrukcyjne o maksymalnym rozstawie
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
;
przyjęto rozstaw co 30 cm
6.3 Podpora B (str. prawa)
Rodzaj odcinka:
II rodzaju o długości 113 cm
Zbrojenie na ścinanie:
na odcinku II rodzaju:
c
sw1
= 120 cm ze strzemionami w rozstawie 15 cm
c
sw2
= 120 cm z prętem odgiętym w płaszczyźnie
12 w rozstawie 40 cm
na odcinku I rodzaju:
zbrojenie konstrukcyjne o maksymalnym rozstawie
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
;
przyjęto rozstaw co 30 cm
Uwaga: w miejscu zmiany rodzaju odcinka można zastosować rozstaw przejściowy.
6.4 Podpora C (str. lewa)
Rodzaj odcinka:
II rodzaju o długości 77 cm
Zbrojenie na ścinanie:
na odcinku II rodzaju:
c
sw1
= 81 cm ze strzemionami w rozstawie 9 cm
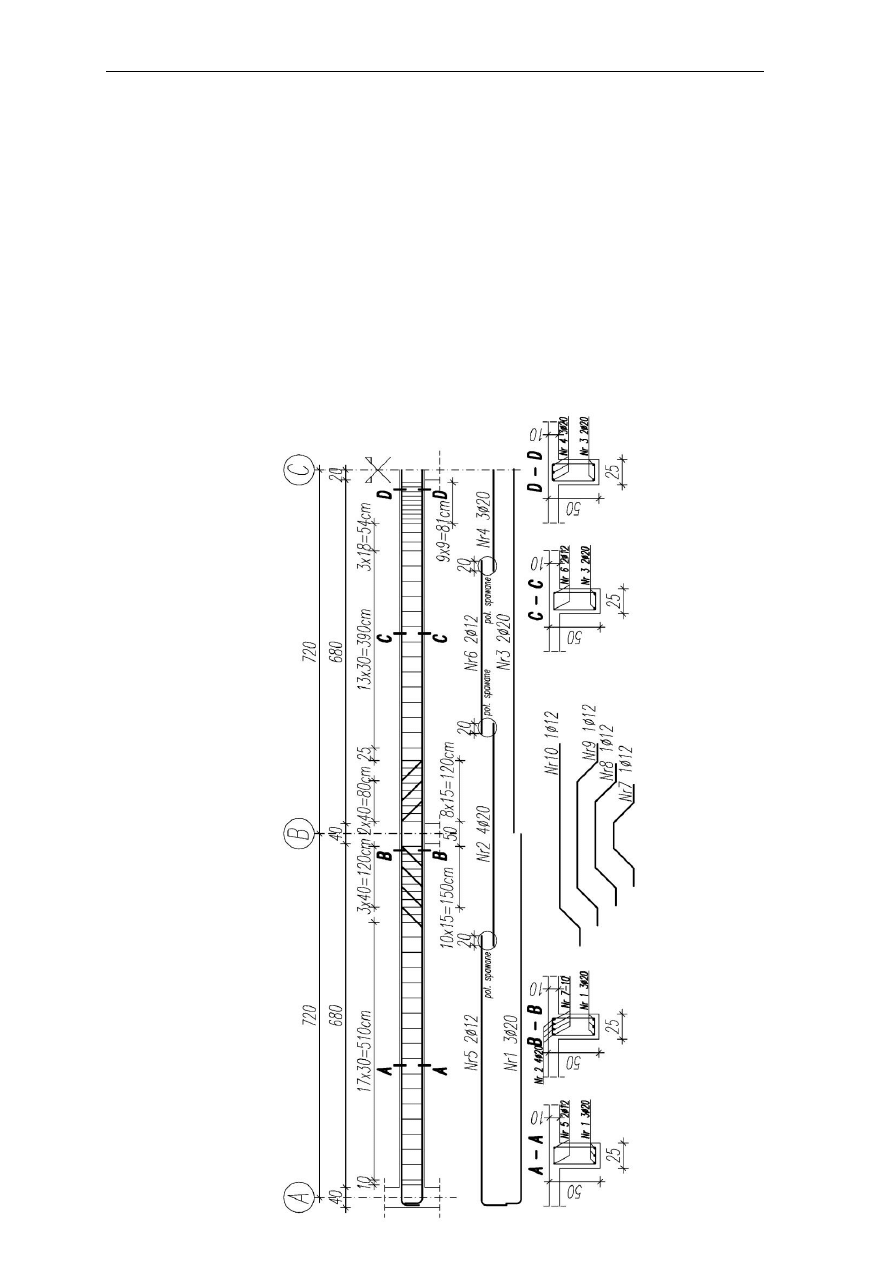
Danuta Seroka, KKBiTB
16
na odcinku I rodzaju:
zbrojenie konstrukcyjne o maksymalnym rozstawie
m
d
s
4
,
0
34
,
0
75
,
0
max
,
1
;
przyjęto rozstaw co 30 cm
Uwaga: w miejscu zmiany rodzaju odcinka zastosować rozstaw przejściowy np. 3x18cm.
6.5
Uwagi do zbrojenia głównego
1. pręty nr 7 do 10 są prętami dodatkowymi, nie pracują na zginanie i nie są wliczone w
stopień zbrojenia przy nośności V
Rd1
; pracują tylko na ścinanie
2. 2 pręty narożne nr 2 zespawane są na długości 10
= 20 cm z prętem
nr 5 po stronie lewej i z prętem nr 6 po stronie prawej; poza tym zakotwione są na
długość 2d+l
bd
od lica podpory
3. 2 pręty narożne nr 4 zespawane są na długości 10
= 20 cm z prętem nr 6 po stronie
lewej.
Wyszukiwarka
Podobne podstrony:
Zadanie na zaliczenie ćwiczeń 2010 - poprawka , 1
pomocy społecznej stan na 26 03 2010
Zadania na egzamin INiG 2010, studia calosc, studia całość, 3 semestr, inig, Matematyka stosowana, M
Zadanie na zaliczenie ćwiczeń 2010 , 1
PRZYKLADOWE ZADANIA TRB st 1 na kolokwium 2009 2010
Zadania z bankowości15 03 2010, Giełda i finanse, BANKOWOŚĆ
I 04.03.2010, STUDIA, na studia, psychologia wykłady, psychologia wyklady
30.03.2010, STUDIA, na studia, socjologia wychowania, Socjologia wychowania
23.03.2010, STUDIA, na studia, so
więcej podobnych podstron