Oosten Basic Category Theory (1995) [sharethefiles com]

BRICS

LS-95-1

J.
van

Oosten:

Basic

Category

Theory

BRICS

Basic Research in Computer Science

Basic Category Theory

Jaap van Oosten

BRICS Lecture Series

LS-95-1

ISSN 1395-2048

January 1995

Copyright c

1995, BRICS, Department of Computer Science

Reproduction of all or part of this work
is permitted for educational or research use
on condition that this copyright notice is
included in any copy.

See back inner page for a list of recent publications in the BRICS
Lecture Series. Copies may be obtained by contacting:

BRICS
Department of Computer Science
University of Aarhus
Ny Munkegade, building 540
DK - 8000 Aarhus C
Denmark

Telephone: +45 8942 3360
Telefax:

+45 8942 3255

Internet:

BRICS@daimi.aau.dk

BRICS publications are in general accessible through WWW and
anonymous FTP:

http://www. bri cs .aa u. dk/ BRI CS /

ftp

ftp.brics. aa u.d k

(cd

pub/BRICS )

Basic Category Theory

Jaap van Oosten

Jaap van Oosten

BRICS

Department of Computer Science

University of Aarhus

Ny Munkegade

DK-8000 Aarhus C, Denmark

asic

esearch

omputer

cience,

Centre of the Danish National Research Foundation.

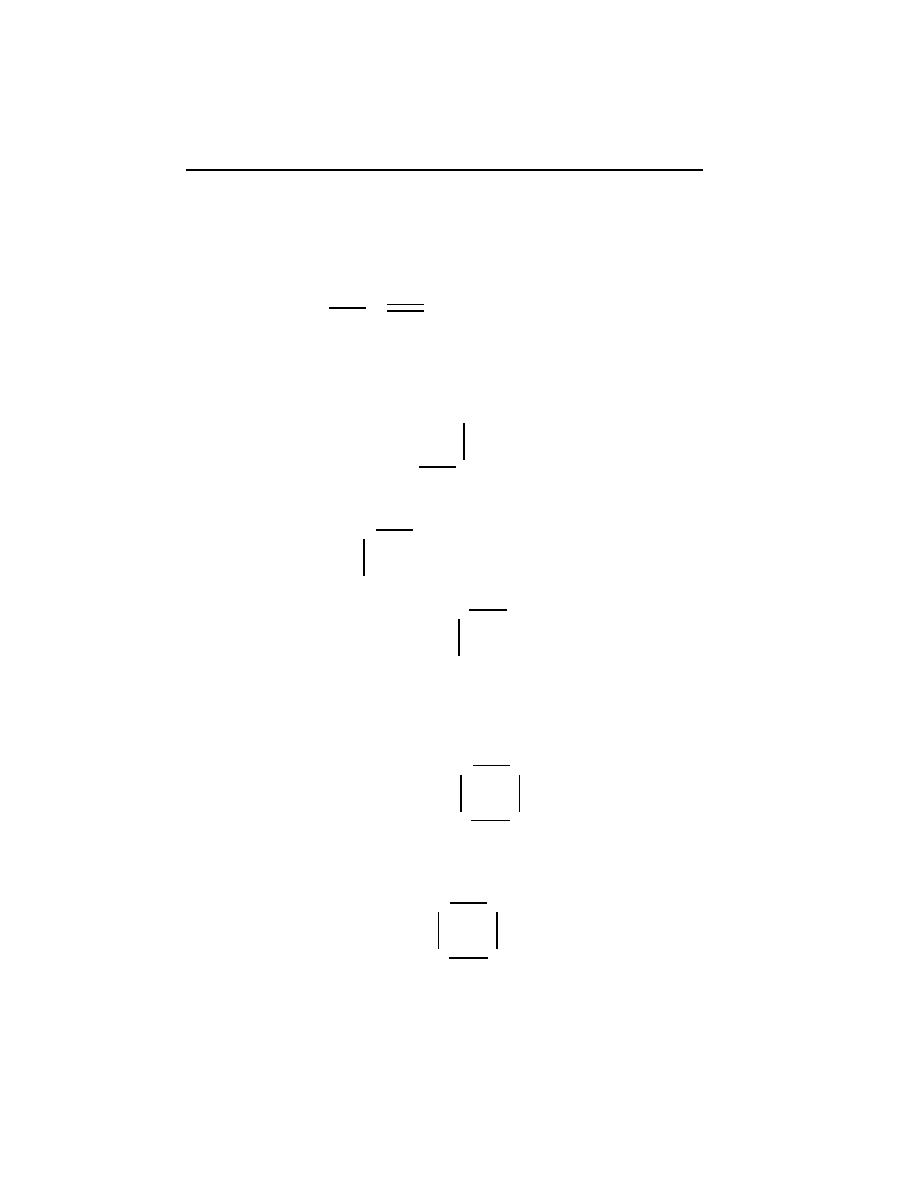
Preface

These notes contain the material of a short course on categories I gave in Arhus

in the autumn of 1994, as part of Glynn Winskel's semantics course. Later on,

while writing, I added some material, but not much.

The style in which they are written reects my view on category theory: it

is, especially at this low level, practice rather than theory which counts. I have

therefore given many proofs as exercises. If you really want to get a grip on the

subject, I strongly suggest you do as many of them as you can.

The same goes for the examples. They are the esh and bones of the theory,

and many of them have been chosen so they are a recurring theme functors

may be given as examples in chapter 1, be shown to constitute an

adjunction in chapter 5, while this may turn out to be a monadic situation in

chapter 6.

For the same reason, references are omitted. Even a sketchy proof, or a hint

of the crucial argument, is better than an intimidating reference to R].

Of course, the examples will be best understood by students who are familiar

with the mathematicalnotions involved, but in general these notes do not require

a lot of mathematical background, except for some basic knowledge of groups,

rings and topological spaces (although examples on the latter may be skipped,

since I have not pursued them through the whole text).

What I

did

presuppose is some familiarity with logic and the -calculus.

Although denitions are given, standard facts about substitution and the like

are suppressed (a teacher can easily supply them when he gives the course).

This familiarity does not include a good understanding of set theory or even

an inkling of the size problems one can run into. I've used the terms \set" and

\small" wherever necessary, although I don't suppose they mean much to many

students. For that reason I've also omitted a proof of Freyd's Adjoint Functor

Theorem and an explanation of the role of the solution set condition.

Apart from chapters 4 and 7, where in spite of the fact that the results are

well-known I haven't been able to nd references where they are treated in a

concise enough form, and so had to develop the material myself, everything is

pretty standard. I have consulted the following sources:

S. MacLane, Categories for the Working Mathematician, Springer (Berlin)

1971.

Still the best text. For non-mathematicians it may be a little tough going,

but it is worth the trouble.

F. Borceux, Handbook of Categorical Algebra, (Encyclopaedia of Math-

ematics and its Applications) Cambridge University Press (Cambridge)

1994.

Next best. Gives a lot of material in a very readable style also on spe-

cialized topics. Three volumes.

A strange error in the denition of Grothendieck universes in the rst

chapter, making the denition inconsistent, supports the point about set

theory, I made before.

Many concrete examples. The reader will nd many answers to my exer-

cises in this book.

M. Barr & C. Wells, Category Theory for Computing Science, Prentice

Hall (New York) 1990.

At this moment out of print. The emphasis on sketches is debatable, for

a rst course in the theory. Otherwise a very valuable source.

P.T. Johnstone, Stone Spaces, Cambridge University Press (Cambridge)

1982. Not a book on category theory proper, but a systematic study on

various dualities of the Stone type. A lot of material on posetal structures

like frames, Boolean algebras etc.

A. Asperti, Categorical Topics in Computer Science, Ph.D. Thesis, Pisa

1990. Later reworked into:

A. Asperti & G. Longo, Categories, Types, and Structures: An Introduc-

tion to Category Theory for the Working Computer Scientist (Foundations

of Computing), MIT Press (Cambridge Massachusetts) 1991.

M. Makkai & G. Reyes, First Order Categorical Logic (Lecture Notes in

Mathematics 611), Springer (Berlin) 1977.

\The" book on categorical logic. It is my feeling that a sequel is badly

needed. The main ideas are developed here.

S. MacLane & I. Moerdijk, Sheaves in Geometry and Logic (Universitext),

Springer 1992.

Treats topos theory, with important applications to logic. Can almost be

read from scratch.

J. Lambek & P. Scott, Introduction to higher order categorical logic, Cam-

bridge University Press (Cambridge) 1986.

This may very well be a book of the future, but for a rst acquaintance

with category theory the approach is too formal for my taste. Gives a

very elaborate account of the correspondences between type theories and

certain types of categories.

Of course this list doesn't make any pretense whatsoever at being complete or

even a guide into the literature. It mainly reects my personal attitude.

Acknowledgements

. I am grateful to the group of students who patiently

and critically sat through my lectures, and in particular to Thomas Hildebrandt

and Sren Bgh Lassen who pointed out mistakes in my original hand-written

notes.

The help of my oce mate Vladi Sassone, has been invaluable. A critical

reading by him of the whole rst version revealed a couple of embarassing mis-

takes (\the functor (

;

)

X also has a left adjoint", ha ha|there is no limit to

what a confused brain can come up with) then he put a lot of eort in the visual

layout of the text, teaching me

emacs

and L

TEX in the process, and designed

the rococo painting which is the title page.

It goes without saying that the remaining errors are mine, and that the poor

visual quality of the text is a testimony of my ignorance of L

TEX, which I am

not proud of.

References

R] J. Razdajev, Some facts about functors, Novosibirsk Journal of Diving

Research XLVII (1947), pp. 634-98 (Russian)

iii

Contents

1 Categories and Functors

1.1 Denitions and examples : : : : : : : : : : : : : : : : : : : : : : : 1

1.2 Some special objects and arrows : : : : : : : : : : : : : : : : : : 6

2 Natural transformations

2.1 The Yoneda lemma : : : : : : : : : : : : : : : : : : : : : : : : : : 9

2.2 Examples of natural transformations : : : : : : : : : : : : : : : : 12

2.3 Equivalence of categories an example : : : : : : : : : : : : : : : 14

3 (Co)cones and (co)limits

3.1 Limits : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 17

3.2 Limits by products and equalizers : : : : : : : : : : : : : : : : : 24

3.3 Colimits : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 25

4 A little piece of categorical logic

4.1 Regular categories and subobjects : : : : : : : : : : : : : : : : : 29

4.2 Coherent logic in regular categories : : : : : : : : : : : : : : : : : 33

4.3 The language

(

) and theory T(

) associated to a regular cat-

egory

: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 38

4.4 Example of a regular category : : : : : : : : : : : : : : : : : : : : 39

5 Adjunctions

5.1 Adjoint functors : : : : : : : : : : : : : : : : : : : : : : : : : : : 43

5.2 Expressing (co)completeness by existence of adjoints preserva-

tion of (co)limits by adjoint functors : : : : : : : : : : : : : : : : 48

6 Monads and Algebras

6.1 Algebras for a monad : : : : : : : : : : : : : : : : : : : : : : : : 54

6.2 T-Algebras at least as complete as

: : : : : : : : : : : : : : : : 59

6.3 The Kleisli category of a monad : : : : : : : : : : : : : : : : : : : 59

7 Cartesian closed categories and the

-calculus

7.1 Cartesian closed categories (ccc's) examples and basic facts : : : 63

7.2 Typed -calculus and cartesian closed categories : : : : : : : : : 67

7.3 Representation of primitive recursive functions in ccc's with nat-

ural numbers object : : : : : : : : : : : : : : : : : : : : : : : : : 70

Index

Categories

1 Categories and Functors

1.1 Denitions and examples

category

is given by a class

objects

and a class

arrows

which

have the following structure.

Each arrow has a

domain

and a

codomain

which are objects one writes

f : X

Y or X

Y if X is the domain of the arrow f, and Y its

codomain. One also writes X = dom(f) and Y = cod(f)

Given two arrows f and g such that cod(f) = dom(g), the

composition

of f and g, written gf, is dened and has domain dom(f) and codomain

cod(g):

Composition is

associative

, that is: given f : X

Y , g : Y

Z and

h : Z

W, h(gf) = (hg)f

For every object X there is an

identity

arrow id

, satisfying id

g = g for

every g : Y

X and fid

= f for every f : X

Y .

Exercise 1

. Show that id

is the

unique

arrow with domain X and codomain

X with this property.
Instead of \arrow" we also use the terms \morphism" or \map".

Examples

is the category with one object

and one arrow, id

is the empty category

c) A

preorder

is a set X together with a binary relation

which is reexive

(i.e. x

x for all x

X) and transitive (i.e. x

y and y

z imply x

for all xyz

X). This can be viewed as a category, with set of objects

X and exactly one arrow: x

y i x

Exercise 2

. Prove this. Prove also the converse: if

is a category such that

is a set, and such that for any two objects XY of

there is at most one

arrow: X

Y , then

is a preordered set.

d) A

monoid

is a set X together with a binary operation, written like mul-

tiplication: xy for xy

X, which is associative and has a unit element

X, satisfying ex = xe = x for all x

X. Such a monoid is a category

with one object, and an arrow x for every x

Categories

e) Set is the category which has the class of all sets as objects, and functions

between sets as arrows.

Most basic categories have as objects certain mathematical structures, and the

structure-preserving functions as morphisms. Examples:

f) Top is the category of topological spaces and continuous functions.

g) Grp is the category of groups and group homomorphisms.
h) Rng is the category of rings and ring homomorphisms.

i) Grph is the category of graphs and graph homomorphisms.
j) Pos is the category of partially ordered sets and monotone functions.

Given two categories

and

, a

functor

F :

consists of operations

and F

, such that for each f : X

Y , F

(f) :

(X)

(Y ) and:

for X

Z, F

(gf) = F

(g)F

(f)

(id

) = id

(X)

for each X

But usually we write just F instead of F

Examples

a) There is a functor U : Top

Set which assigns to any topological space

X its underlying set. We call this functor \forgetful": it \forgets" the

mathematicalstructure. Similarly,there are forgetful functors Grp

Set,

Grph

Set, Rng

Set, Pos

Set etcetera

b) For every category

there is a unique functor

and a unique one

c) Given two categories

and

we can dene the

product category

which has as objects pairs (CD)

, and as arrows:(CD)

) pairs (fg) with f : C

, and g : D

. There

are functors

and

d) Given two functors F :

and G :

one can dene the

composition GF :

. This composition is of course associative and

since we have, for any category

, the

identity functor

, we have a

category Cat which has categories as objects and functors as morphisms.

1. Categories and Functors

e) Given a set A, consider the set ~A of strings a

:::a

on the alphabet

;

consists of elements a

;

for each element a of A the sets

A and A

;

are disjoint and in 1-1 correspondence with each other), such

that for no x

A, xx

;

or x

;

x is a substring of a

:::a

. Given two

such strings ~a = a

:::a

~b = b

:::b

, let ~a ?~b the string formed by rst

taking a

:::a

:::b

and then removing from this string, successively,

substrings of form xx

;

or x

;

x, until one has an element of ~A.

This denes a group structure on ~A. ~A is called the

free group

on the set

Exercise 3

. Prove this, and prove that the assignment A

~A is part of a

functor: Set

Grp. This functor is called the

free functor

f) Every directed graph can be made into a category as follows: the objects

are the vertices of the graph and the arrows are paths in the graph. This

denes a functor from the category Dgrph of directed graphs to Cat. The

image of a directed graph D under this functor is called the category

generated

by the graph D.

Quotient categories

. Given a category

, a

congruence relation

species, for each pair of objects XY , an equivalence relation

the class of arrows

(XY ) which have domain X and codomain Y , such

that

for fg : X

Y and h : Y

Z, if f

g then hf

for f : X

Y and gh : Y

Z, if g

h then gf

hf.

Given such a congruence relation

, one can form the quotient cat-

egory

which has the same objects as

, and arrows X

Y are

-equivalence classes of arrows X

Y in

Exercise 4

. Show this and show that there is a functor

, which takes

each arrow of

to its equivalence class.

h) An example of this is the following (\homotopy"). Given a topological

space X and points xy

X, a

path

from x to y is a continuous mapping

f from some closed interval 0a] to X with f(0) = x and f(a) = y. If

f : 0a]

X is a path from x to y and g : 0b]

X is a path from y to z

there is a path gf : 0a+b]

X (dened by gf(t) =

f(t)

g(t

;

a) else )

from x to z. This makes X into a category, the

path category

of X,

and of course this also denes a functor Top

Cat. Now given paths

f : 0a]

X, g : 0b]

X, both from x to y, one can dene f

g if

Categories

there is a continuous map F : A

X where A is the area:

(01)

(b1)

(00)

(a0)

in IR

, such that

F(t0) = f(t)

F(t1) = g(t)

F(0s) = x

01]

F(st) = y

(st) on the segment (b1)

;

(a0)

One can easily show that this is a congruence relation. The quotient of the

path category by this congruence relation is a category called the category

homotopy classes

of paths in X.

i) let

be a category such that for every pair (XY ) of objects the class

(XY ) of arrows from X to Y is a set (such

is called

locally small

For any object C of

then, there is a functor h

Set which assigns

to any object C

the set

(CC

). Any arrow f : C

gives by

composition a function

(CC

)

(CC

), so we have a functor. A

functor of this form is called a

representable functor

j) Let

be a category and C an object of

. The

slice category

=C has as

objects all arrows g which have codomain C. An arrow from g : D

to h : E

C in

=C is an arrow k : D

E in

such that hk = g. Draw

like:

We say that

this diagram commutes

if we mean that hk = g.

Exercise 5

. Convince yourself that the assignment C

=C gives rise to a

functor

Cat.

k) Remember that for every group (G

) we can form a group (G?) by

putting f ? g = g

For categories the same construction is available: given

we can form

a category

which has the same objects and arrows as

, but with

reversed direction so if f : X

Y in

then f : Y

X in

. To

1. Categories and Functors

make it notationally clear, write "f for the arrow Y

X corresponding to

f : X

Y in

. Composition in

is dened by:

"f"g = gf

Often one reads the term \contravariant functor" in the literature. What I

call functor, is then called \covariant functor". A contravariant functor F

from

inverts the direction of the arrows, so F

(f) : F

(cod(f))

(dom(f)) for arrows f in

. In other words, a contravariant functor

from

is a functor from

(equivalently, from

Exercise 6

. Let

be locally small. Show that there is a functor (the \Hom

functor")

(

;

) :

Set, assigning to the pair (AB) of objects of

the set

(AB).

l) Given a partially ordered set (X

) we make a topological space by den-

ing U

X to be open i for all xy

X, x

y and x

U imply y

(U is \upwards closed", or an \upper set"). This is a topology, called the

Alexandro topology

w.r.t. the order

If (X

) and (Y

) are two partially ordered sets, a function f : X

Y is monotone for the orderings if and only if f is continuous for the

Alexandro topologies. This gives an important functor: Pos

Top.

Exercise 7

. Show that the construction of the quotient category in example

g) generalizes that of a quotient group by a normal subgroup. That is, re-

gard a group G as a category with one object show that there is a bijection

between congruence relations on G and normal subgroups of G, and that for

a normal subgroup N of G, the quotient category by the congruence relation

corresponding to N, is to the quotient group G=N.

m) \Abelianization". Let Abgp be the category of abelian groups and ho-

momorphisms. For every group G the subgroup GG] generated by all

elements of form aba

;

is a normal subgroup. G=GG] is abelian, and

for every group homomorphism : G

H with H abelian, there is a

unique homomorphism " : G=GG]

H such that the diagram

{{

G=GG]

commutes. Show that this gives a functor: Grp

Abgp.

Categories

n) \Specialization ordering". Given a topological space X, you can dene an

ordering

on X as follows: say x

y if for all open sets U, if x

then y

For many spaces,

is trivial (in particular when X is T

) but in case X

is for example the Alexandro topology on a poset (X

) as in l), then

y i x

Exercise 8

. If f : X

Y is a continuous map of topological spaces then

f is monotone w.r.t. the specialization orderings

. This denes a functor

Top

Pos.

1.2 Some special objects and arrows

We call an arrow f : A

mono

(or a monomorphism, or monomorphic) in a

category

, if for any other object C and for any pair of arrows gh : C

fg = fh implies g = h.

In Set, f is mono i f is an injective function. The same is true for Grp,

Grph, Rng, Preord, Pos,:::

We call an arrow f : A

epi

(epimorphism, epimorphic) if for any pair

gh : B

C, gf = hf implies g = h.

The denition of epi is \dual" to the denition of mono. That is, f is epi in

the category

if and only if f is mono in

, and vice versa. In general, given

a property P of an object, arrow, diagram,:::we can associate with P the dual

property P

: the object or arrow has property P

i it has P in

The

duality principle

, a very important, albeit trivial, principle in category

theory, says that any valid statement about categories, involving the proper-

ties P

:::P

implies the \dualized" statement (where direction of arrows is

reversed) with the P

replaced by P

Example

. If gf is mono, then f is mono. From this, \by duality", if fg is epi,

then f is epi.

Exercise 9

. Prove these statements.

In Set, f is epi i f is a surjective function. This holds (less trivially!) also

for Grp, but not for Mon, the category of monoids and monoid homomorphisms:
In Mon, the embedding

is an epimorphism.

For suppose

(Me?) two monoid homomorphisms which agree on the

nonnegative integers. Then

;

1) = f(

;

1) ? g(1) ? g(

;

1) = f(

;

1) ? f(1) ? g(

;

1) = g(

;

1. Categories and Functors

so f and g agree on the whole of

We say a functor F

preserves

a property P if whenever an object or arrow

(or:::) has P, its F-image does so.

Now a functor does not in general preserve monos or epis: the example of

Mon shows that the forgetful functor Mon

Set does not preserve epis.

An epi f : A

B is called

split

if there is g : B

A such that fg = id

(other names: in this case g is called a

section

of f, and f a

retraction

of g).

Exercise 10

. By duality, dene what a split mono is. Prove that every functor

preserves split epis and monos.
f : A

B is an

isomorphism

if there is g : B

A such that fg = id

and gf = id

We call g the

inverse

of f (and vice versa, of course) it is unique

if it exists. We also write g = f

;

Every functor preserves isomorphisms.

Exercise 11

. In Set, every arrow which is both epi and mono is an isomor-

phism. Not so in Mon, as we have seen. Here's another one: let CRng1 be the

category of commutative rings with 1, and ring homomorphisms (preserving 1)

as arrows. Show that the embedding

is epi in CRng1.

Exercise 12

i) If two of f, g and fg are iso, then so is the third

ii) if f is epi and split mono, it is iso

iii) if f is split epi and mono, f is iso.

A functor F

reects

a property P if whenever the F-image of something (object,

arrow,:::) has P, then that something has.

A functor F :

is called

full

if for every two objects AB of

F :

(AB)

(FAFB) is a surjection. F is

faithful

if this map is always

injective.

Exercise 13

. A faithful functor reects epis and monos.

An object X is called

terminal

if for any other object Y there is exactly one

morphism Y

X in the category. Dually, X is

initial

if for all Y there is

exactly one X

Y .

Exercise 14

. A full and faithful functor reects the property of being a termi-

nal (or initial) object.

Categories

Exercise 15

. If X and X

are two terminal objects, they are

isomorphic

that is there exists an isomorphism between them. Same for initial objects.

2. Natural transformations

2 Natural transformations

2.1 The Yoneda lemma

natural transformation

between two functors FG :

consists of a family

of morphisms (

: FC

GC)

indexed by the collection of objects of

satisfying the following requirement: for every morphism f : C

, the

diagram

commutes in

(the diagram above is called the naturality square). We say

= (

)

: F

)

G and we call

the

component at

C of the natural

transformation .

Given natural transformations : F

)

G and : G

)

H we have a natural

transformation = (

)

: F

)

H, and with this composition there is a

category

with functors F :

as objects, and natural transformations

as arrows.

One of the points of the naturality square condition in the denition of a

natural transformation is given by the following proposition. Compare with the

situation in Set: denoting the set of all functions from X to Y by Y

, for any

set Z there is a bijection between functions Z

and functions Z

(Set is

cartesian closed

: see chapter 7).

Proposition 2.1

For categories

and

there is a bijection:

Cat(

)

Cat(

)

Proof

. Given F :

dene for every object E of

the functor

by F

let F

(f) = F(id

f) :

F(EC

) = F

)

Given g : E

, the family (F(gid

) : F

(C)

(C))

is a

natural transformation: F

)

. So we have a functor F

(

;

)

Conversely, given a functor G :

we dene a functor ~G :

objects by ~G(EC) = G(E)(C), and on arrows by ~G(gf) = G(g)

G(E)(f) =

Categories

G(E

)(f)G(g)

G(E)(C) = ~G(EC)

(

)(

)

(

)

~G(E

C) = G(E

)(C)

(

)(

)

~G(EC

)

(

)

~G(E

) = G(E

)(C

)

Exercise 16

. Write out the details. Check that ~G as just dened, is a functor,

and that the two operations

Cat(

)

Cat(

)

are inverse to each other.
An important example of natural transformations arises from the functors h

Set (see example i) in the preceding chapter) dened on objects by

) =

C) and on arrows f : C

so that h

(f) is composition

with f:

C).

Given g : C

there is a natural transformation

: h

)

whose components are composition with g.

Exercise 17

. Spell this out.

We have, in other words, a functor

(

;

)

Set

This functor is also often denoted by Y and listens to the name

Yoneda embed-

ding

An embedding is a functor which is full and faithful and injective on objects.

That Y is injective on objects is easy to see, because id

C, and id

is in no other set h

(E) that Y is full and faithful follows from the

famous

Proposition 2.2 (Yoneda lemma)

For every object

of Set

and every

object

, there is a bijection

: Set

F(C)

. Moreover, this

bijection is

natural

and

in the following sense: given

g : C

2. Natural transformations

and

: F

)

Set

, the diagram

Set

(

)

F(C)

(

)

Set

)

commutes in

Set

Proof

. For every object C

, every element f of h

) =

C) is equal

to id

f which is h

(f)(id

If = (

) is a natural transformation: h

)

F then,

(f)

must be equal to F(f)(

(id

)). So is completely determined by

(id

)

F(C) and conversely, any element of F(C) determines a natural transformation

)

Given g : C

C in

and : F

)

in Set

, the map Set

(g) sends

the natural transformation = (

) : h

)

F to = (

)

where

: h

)

) is dened by

(h : C

) =

(

(gh))

Now

() =

(id

)

(

(g))

(F(g)(

(id

)))

= (

F(g))(f

())

which proves the naturality statement.

Corollary 2.3

The functor

Y :

Set

is full and faithful.

Proof

. Immediate by the Yoneda lemma, since

(CC

)

= h

(C)

= Set

)

and this bijection is induced by Y .
The use of the Yoneda lemma is often the following. One wants to prove that

objects A and B of

are isomorphic. Suppose one can show that for every

object X of

there is a bijection f

(XA)

(XB) which is natural in

Categories

X i.e. given g : X

X in

one has that

(XA)

(

)

(XB)

(

)

commutes.

Then one can conclude that A and B are isomorphic in

for, from what

one has just shown it follows that h

and h

are isomorphic objects in Set

that is, Y (A) and Y (B) are isomorphic. Since Y is full and faithful, A and B

are isomorphic by the following exercise:

Exercise 18

. Check: if F :

is full and faithful, and F(A) is iso-

morphic to F(B) in

, then A is isomorphic to B in

Exercise 19

. Suppose objects A and B are such that for every object X

there is a bijection f

(AX)

(BX), naturally in a sense you dene

yourself. Conclude that A and B are isomorphic (hint: duality + the previous).
This argument can be carried further. Suppose one wants to show that two

functors FG :

are isomorphic as objects of

. Let's rst spell out

what this means:

Exercise 20

. Show that F and G are isomorphic in

if and only if there is

a natural transformation : F

)

G such that all components

are isomor-

phisms (in particular, if is such, the family ((

)

;

) is also a natural

transformation G

)

F).

Now suppose one has for each C

and D

a bijection

(DFC)

(DGC)

natural in D and C. This means that the objects h

and h

of Set

are

isomorphic, by isomorphisms which are natural in C. By full and faithfulness

of Y , FC and GC are isomorphic in

by isomorphisms natural in C which

says exactly that F and G are isomorphic as objects of

2.2 Examples of natural transformations

a) Let M and N be two monoids, regarded as categories with one object as in

chapter 1. A functor F : M

N is then just the same as a homomorphism

2. Natural transformations

of monoids. Given two such, say FG : M

N, a natural transformation

)

G is (given by) an element n of N such that nF(x) = G(x)n for all

b) Let P and Q two preorders, regarded as categories. A functor P

is a monotone function, and there exists a unique natural transformation

between two such, F

)

G, exactly if F(x)

G(x) for all x

Exercise 21

. In fact, show that if

is a preorder and the category

small

i.e. the classes

and

are sets, then the functor category

is a preorder.

c) Let U : Grp

Set denote the forgetful functor, and F : Set

Grp the

free functor (see chapter 1). There are natural transformations " : FU

)

Grp

and : id

Set

)

UF.

Given a group G, "

takes the string = g

:::g

to the product g

(here, the \formal inverses" g

;

are interpreted as the real inverses in G!).

Given a set A,

(a) is the singleton string a.

d) Let i : Abgp

Grp be the inclusion functor and r : Grp

Abgp the

abelianization functor dened in example m) in chapter 1. There is " :

)

Abgp

and : id

Grp

)

ir.

The components

of are the quotient maps G

G=GG] the com-

ponents of " are isomorphisms.

e) There are at least two ways to associate a category to a set X: let F(X)

be the category with as objects the elements of X, and as only arrows

identities (a category of the form F(X) is called

discrete

and G(X) the

category with the same objects but with exactly one arrow f

: x

for each pair (xy) of elements of X (We might call G(X) an

indiscrete

category

Exercise 22

. Check that F and G can be extended to functors: Set

Cat and

describe the natural transformation : F

)

G which has, at each component,

the identity function on objects.

f) Every class of arrows of a category

can be viewed as a natural transfor-

mation. Suppose S

. Let F(S) be the discrete category on S as in

the preceding example. There are the two functors domcod : F(S)

giving the domain and the codomain, respectively. For every f

S we

have f : dom(f)

cod(f), and the family (f

S) denes a natural

transformation: dom

)

cod.

g) Let A and B be sets. There are functors (

;

)

A : Set

Set and (

;

)

B :

Set

Set. Any function f : A

B gives a natural transformation

(

;

)

(

;

)

Categories

h) A category

is called a

groupoid

if every arrow of

is an isomorphism.

Let

be a groupoid, and suppose we are given, for each object X of

, an

arrow

with domain X.

Exercise 23

. Show that there is a functor F :

in this case, which

acts on objects by F(X) = cod(

), and that = (

) is a natural

transformation: id

)

i) Given categories

and an object D of

, there is the constant functor

which assigns D to every object of

and id

to every arrow

Every arrow f : D

gives a natural transformation $

: $

)

dened by ($

)

= f for each C

j) Let

(X) denote the power set of a set X: the set of subsets of X. The

powerset operation can be extended to a functor

: Set

Set. Given a

function f : X

Y dene

(f) by

(f)(A) = fA], the image of A

under f.

There is a natural transformation : id

Set

)

such that

(x) =

(X) for each set X.

There is also a natural transformation :

)

. Given A

(X),

so A is a set of subsets of X, we take its union

(A) which is a subset of

X. Put

(A) =

(A).

2.3 Equivalence of categories an example

As will become clear in the following chapters, equality between objects plays

only a minor role in category theory. The most important categorical notions

are only dened \up to isomorphism". This is in accordance with mathematical

practice and with common sense: just renaming all elements of a group does

not give you really another group.

We have already seen one example of this: the property of being a terminal

object denes an object up to isomorphism. That is, any two terminal objects

are isomorphic. There is, in the language of categories, no way of distinguishing

between two isomorphic objects, so this is as far as we can get.

However, once we also consider functor categories, it turns out that there is

another relation of \sameness" between categories, weaker than isomorphism of

categories, and yet preserving all \good" categorical properties. Isomorphism of

Categories

atom

in a Boolean algebra is an element x such that 0 < x but for no

y we have 0 < y < x. A Boolean algebra is atomic if every x is the join of the

atoms below it:

x =

x and a is an atom

The category CABool is dened as follows: the objects are complete atomic

Boolean algebras, and the arrows are complete homomorphisms, that is: f :

C is a complete homomorphism if for every A

A) =

f(a)

and f(

A) =

f(a)

Exercise 25

. Show that 1 =

and 0 =

. Conclude that a complete

homomorphism preserves 1, 0 and complements.

Exercise 26

. Show that

A =

and conclude that if a function

preserves all

's, 1 and complements, it is a complete homomorphism.

Theorem 2.4

The category

CABool

is equivalent to

Set

Proof

. For every set X,

(X) is a complete atomic Boolean algebra and if

f : Y

X is a function, then f

;

(X)

(Y ) which takes, for each subset

of X, its inverse image under f, is a complete homomorphism. So this denes

a functor F : Set

CABool.

Conversely, given a complete atomic Boolean algebra B, let G(B) be the set

of atoms of B. Given a complete homomorphism g : B

C we have a function

G(g) : G(C)

G(B) dened by: G(g)(c) is the unique b

G(B) such that

g(b). This is well-dened: rst, there is an atom b with c

g(b) because

G(B) (B is atomic), so 1

= g(1

) =

g(b)

b is an atom

and:

Exercise 27

. Prove: if c is an atom and c

A, then there is a

A with

a (hint: prove for all ab that a

b = 0

b, and prove for ac with c

atom: c

c).

Secondly, the atom b is unique since c

g(b) and c

g(b

) means c

g(b)

g(b

) = g(b

) = g(0) = 0.

So we have a functor G : CABool

Set

Now the atoms of the Boolean algebra

(X) are exactly the singleton sub-

sets of X, so GF(X) =

which is clearly isomorphic to X. On the

other hand, FG(B) =

(

b is an atom

). There is a map from FG(B)

to B which sends each set of atoms to its least upper bound in B, and this map

is an isomorphism in CABool.

Exercise 28

. Prove the last statement: that the map from FG(B) to B,

dened in the last paragraph of the proof, is an isomorphism.

3. (Co)cones and (co)limits

3 (Co)cones and (co)limits

3.1 Limits

Given a functor F :

, a

cone

for F consists of an object D of

together

with a natural transformation : $

)

F ($

is the constant functor with

value D). In other words, we have a family (

: D

F(C)

), and the

naturality requirement in this case means that for every arrow f : C

F(C)

(

)

F(C

)

commutes in

(this diagram explains, I hope, the name \cone"). Let us denote

the cone by (D). D is called the

vertex

of the cone.

map of cones

(D)

) is a map g : D

such that

g =

for all C

Clearly, there is a category Cone(F) which has as objects the cones for F

and as morphisms maps of cones.

limiting cone

for F is a terminal object in Cone(F). Since terminal objects

are unique up to isomorphism, as we have seen, any two limiting cones are

isomorphic in Cone(F) and in particular, their vertices are isomorphic in

A functor F :

is also called a

diagram

of type

, and

is the

index category

of the diagram.

Let us see what it means to be a limiting cone, in some simple, important

cases.

i) A limiting cone for the unique functor ! :

(

is the empty category)

\is" a terminal object in

. For every object D of

determines, together

with the empty family, a cone for !, and a map of cones is just an arrow

. So Cone(!) is isomorphic to

ii) Let

be the discrete category with two objects xy. A functor

just a pair

of objects of

, and a cone for this functor consists of

an object C of

and two maps

since there are no nontrivial

arrows in

(C(

)) is a limiting cone for

i the following holds: for any

object D and arrows f : D

A, g : D

B, there is a unique arrow

Categories

h : D

C such that

commutes. In other words, there is, for any D, a 1-1 correspondence

between maps D

C and pairs of maps

This is

the property of a

product

a limiting cone for

is therefore called a

product cone, and usually denoted:

The arrows

and

are called

projections

iii) Let

denote the category x

y . A functor

is the same thing

as a parallel pair of arrows A

B in

I write

for this functor.

A cone for

is:

But

= f

= g

is already dened from

, so giving a cone is the

same as giving a map

: D

A such that f

= g

. Such a cone is

limiting i for any other map h : C

A with fh = gh, there is a unique

k : C

D such that h =

We call

, if it is limiting, an

equalizer

of the pair fg, and the diagram

B an equalizer diagram.

In Sets, an equalizer of fg is isomorphic (as a cone) to the inclusion

f(a) = g(a)

into A. In categorical interpretations of logical

3. (Co)cones and (co)limits

systems (see chapters 4 and 7), equalizers are used to interpret

equality

between terms

Exercise 29

. Show that every equalizer is a monomorphism.

Exercise 30

. If E

Y is an equalizer diagram, show that e

is an isomorphism if and only if f = g.

Exercise 31

. Show that in Set, every monomorphism ts into an equalizer

diagram.

iv) Let J denote the category

A functor F : J

is specied

by giving two arrows in

with the same codomain, say f : X

g : Y

Z. A limit for such a functor is given by an object W together

with projections

satisfying fp

= gp

, and such that,

given any other pair of arrows:

with gr = fs, there is a

unique arrow V

W such that

((

commutes.

The diagram

Categories

is called a

pullback diagram

. In Set, the pullback cone for fg is isomorphic

(xy)

f(x) = g(y)

with the obvious projections.

We say that a category

has binary products

(equalizers, pullbacks) i every

functor

(

, J

, respectively) has a limiting cone. Some

dependencies hold in this context:

Proposition 3.1

If a category

has a terminal object and pullbacks, it has

binary products and equalizers.

has binary products and equalizers, it has pullbacks.

Proof

. Let 1 be the terminalobject in

given objects X and Y , if

is a pullback diagram, then

is a product cone.

Given a product cone

and maps

we write

B for the unique factorization through the product. Write also

: Y

Y for

Now given fg : X

Y , if

is a pullback diagram, then E

Y is an equalizer diagram. This

proves the rst statement.

As for the second: given

let E

Z be an

3. (Co)cones and (co)limits

equalizer then

is a pullback diagram.

Exercise 32

. Let

a pullback diagram with f mono. Show that a is also mono. Also, if f is iso

(an isomorphism), so is a.

Exercise 33

. Given:

a) if both squares are pullback squares, then so is the composite square

b) If the right hand square and the composite square are pullbacks, then so

is the left hand square.

Exercise 34

. f : A

B is a monomorphism if and only if

is a pullback diagram.

Categories

A monomorphism f : A

B which ts into an equalizer diagram

is called a

regular mono

Exercise 35

. If

is a pullback and g is regular mono, so is b.

Exercise 36

. If f is regular mono and epi, f is iso. Every split mono is regular.

Exercise 37

. Give an example of a category in which not every mono is regular.

Exercise 38

. In Grp, every mono is regular This is not so easy].

Exercise 39

. In Pos, every mono is regular.

Exercise 40

. If a category

has binary products and a terminal object,

it has

all nite products

, i.e. limiting cones for every functor into

from a nite

discrete category.

Exercise 41

. Suppose

has binary products and suppose for every ordered

pair (AB) of objects of

a product cone

has been chosen.

a) Show that there is a functor:

;;

(the product functor) which

sends each pair (AB) of objects to A

B and each pair of arrows (f :

g : B

) to f

g =

b) From a), there are functors:

(

;;

)

;

(

;;

)

3. (Co)cones and (co)limits

sending (ABC) to (A

C) Show that there is a natural trans-

formation a = (a

ABC

) from (

;

)

;

(

;

)

such that for any four objects ABCD of

((A

AB C

AB CD

AB C D

C))

))

AB CD

D))

((B

BCD

commutes (This diagram is called \MacLane's pentagon").

A functor F :

is said to

preserve limits of type

if for all functors M :

, if (D) is a limiting cone for M in

, then (FDF = (F(

)

))

is a limiting cone for FM in

So, a functor F :

preserves binary products if for every product dia-

gram

its F-image

F(A

(

)

(

)

F(B)

F(A)

is again a product

diagram. Similarly for equalizers and pullbacks.

Some more terminology: F is said to

preserve all nite limits

if it preserves

limits of type

for every nite

. A category which has all nite limits is called

lex

(

left exact

cartesian

nitely complete

A category is called

complete

if it has limits of type

for all small

In general, limits over large (i.e. not small) diagrams do not exist. For ex-

ample in Set, there is a limiting cone for the identity functor Set

Set (its

vertex is the empty set), but not for the inclusion functor of the subcategory of

all nonempty sets into Set.

Exercise 42

. If a category

has equalizers, it has

all nite equalizers

: for

every category

of the form

...

every functor

has a limiting cone.

Categories

Exercise 43

. Suppose F :

preserves equalizers (and

has equaliz-

ers) and reects isomorphisms. Then F is faithful.

Exercise 44

. Let

be a category with nite limits. Show that for every

object C of

, the slice category

=C (example j) of 1.1) has binary products:

the vertex of a product diagram for two objects D

C, D

C is D

where

is a pullback square in

3.2 Limits by products and equalizers

In Set, every small diagram has a limit given a functor F :

Set with

small, there is a limiting cone for F in Set with vertex

)

F(E)

(F(f)(x

) = x

)

So in Set, limits are equationally dened subsets of suitable products. This

holds in any category:

Proposition 3.2

Suppose

has all small products (including the empty prod-

uct, i.e. a terminal object 1) and equalizers then

has all small limits.

Proof

. Given a set I and an I-indexed family of objects (A

I) of

, we

denote the product by

and projections by

an arrow

f : X

which is determined by the compositions f

f : X

is also denoted (f

I).

Now given

with

and

sets, we construct

F(i)

(

cod

(u)

)

(

)

dom

(u)

)

F(cod(u))

as an equalizer diagram. The family (

e : E

F(i)

) is a

natural transformation $

)

F because, given an arrow u

, say u : i

we have that

}}

{

F(i)

(

)

F(j)

3. (Co)cones and (co)limits

commutes since F(u)

e = F(u)

dom(

)

e =

cod(

)

e =

So (E) is a cone for F, but every other cone (D) for F gives a map

d : D

F(i) equalizing the two horizontal arrows so factors uniquely

through E.

Exercise 45

. Check that \small" in the statement of the proposition, can

be replaced by \nite": if

has all nite products and equalizers,

is nitely

complete.

3.3 Colimits

The dual notion of limit is colimit. Given a functor F :

there is clearly a

functor F

which does \the same" as F. We say that a

colimiting

cocone

for F is a limiting cone for F

So: a cocone for F :

is a pair (D) where : F

)

and a

colimiting cocone is an initial object in the category Cocone(F).

Examples

i) a colimiting cocone for ! :

\is" an initial object of

ii) a colimiting cocone for

is a

coproduct

of A and B in

usually denoted A + B or A

B there are

coprojections

coproduct

inclusions

with the property that, given any pair of arrows A

C, B

C there is a

unique map

: A

C such that f =

and g =

iii) a colimiting cocone for A

B (as functor

) is given by a map

C satisfying cf = cg, and such that for any B

D with hf = hg

there is a unique C

D with h = h

c. c is called a

coequalizer

for f and

g the diagram A

C a coequalizer diagram.

Exercise 46

. Is the terminology \coproduct inclusions" correct? That is, it

suggests they are monos. Is this always the case?
In Set, the coproduct of X and Y is the disjoint union (

(

Y )

Categories

of X and Y . The coequalizer of X

Y is the quotient map Y

where

is the equivalence relation generated by

i there is x

X with f(x) = y and g(x) = y

The dual notion of pullback is

pushout

. A pushout diagram is a colimiting

cocone for a functor ;

where ; is the category

. Such a diagram

is a square

which commutes and such that, given

with f = g, there is a

unique P

Q with = pa and = pb. In Set, the pushout of X

Y and

Z is the coproduct Y

Z where the two images of X are identied:

Exercise 47

. Give yourself, in terms of X

Y and X

Z, a formal denition

of a relation R on Y

Z such that the pushout of f and g is Y

being

the equivalence relation generated by R.
One can now dualize every result and exercise from the section on limits:

3. (Co)cones and (co)limits

Exercise 48

. f is epi if and only if

is a pushout diagram.

Exercise 49

. Every coequalizer is an epimorphism if e is a coequalizer of

f and g, then e is iso i f = g

Exercise 50

. If

has an initial object and pushouts,

has binary coproducts

and coequalizers if

has binary coproducts and coequalizers,

has pushouts.

Exercise 51

. If

is a pushout diagram, then a epi implies f epi,

and a regular epi (i.e. a coequalizer) implies f regular epi.

Exercise 52

. The composition of two puhout squares is a pushout if both

the rst square and the composition are pushouts, the second square is.

Exercise 53

. If

has all small (nite) coproducts and coequalizers,

has

all small (nite) colimits.

Exercise 54

. In Pos, X

Y is a regular epi if and only if for all yy

Y :

;

(y)

;

):x

Show by an example that not every epi is regular in Pos.

Exercise 55

. In Grp, every epi is regular.

Categories

4. A little piece of categorical logic

4 A little piece of categorical logic

One of the major achievements of category theory in mathematical logic and

in computer science, has been a unied treatment of semantics for all kinds of

logical systems and term calculi which are the basis for programming languages.

One can say that mathematical logic, seen as the study of classical rst

order logic, rst started to be a real subject with the discovery, by G'odel,

of the

completeness theorem

for set-theoretic interpretations: a sentence ' is

provable if and only if ' is true in all possible interpretations. This unites the

two approaches to logic: proof theory and model theory, makes logic accessible

for mathematical methods and enables one to give nice and elegant proofs of

proof theoretical properties by model theory (for example, the Beth and Craig

denability and interpolation theorems).

However the completeness theorem needs generalization once one considers

logics, such as intuitionistic logic (which does not admit the principle of excluded

middle), minimal logic (which has no negation) or modal logic (where the logic

has an extra operator, expressing \necessarily true"), for which the set-theoretic

interpretation is not complete. One therefore comes with a general denition of

\interpretation" in a category

of a logical system, which generalizes Tarski's

truth denition: this will then be the special case of classical logic and the

category Set.

In this chapter I treat, for reasons of space, only a fragment of rst order

logic: coherent logic. On this fragment the valid statements of classical and

intuitionistic logic coincide.

For an interpretation of a term calculus like the -calculus, which is of

paramount importance in theoretical computer science, the reader is referred

to chapter 7.

4.1 Regular categories and subobjects

Denition 4.1

A category

is called

regular

if the following conditions hold:

has all nite limits

b) For every arrow

, if

is a pullback (then

is called the

kernel pair

), the coequal-

izer of

exists

Categories

c) Regular epimorphisms (coequalizers) are

stable under pullback

, that is: in

a pullback square

is regular epi, so is

Exercise 56

. Set is regular. Prove that Pos is regular. Show that Top is not

regular the case of Top may cause you some trouble don't worry].

Proposition 4.2

In a regular category, every arrow

f : X

can be factored

f = me : X

where

is regular epi and

is mono and this

factorization is unique in the sense that if

is also

: X

with

mono and

regular epi, there is an isomorphism

: E

such that

e = e

and

= m

Proof

. Given f : X

Y we let X

E be the coequalizer of the kernel pair

X of f. Since fp

= fp

there is a unique m : E

Y such that

f = me. By construction e is regular epi we must show that m is mono, and

the uniqueness of the factorization.

Suppose mg = mh for gh : W

E we prove that g = h. Let

be a pullback square. Then

= meq

= mga = mha = meq

= fq

so there is a unique arrow V

Z such that

b : V

(because of the kernel pair property). It follows that

ga = eq

= ep

b = ep

b = eq

= ha

I claim that a is epi, so it follows that g = h. It is here that we use the

requirement that regular epis are stable under pullback. Now e

e : X

E is the composite

4. A little piece of categorical logic

and both maps are regular epis since both squares

and

are pullbacks. The map a, being the pullback of a composite of regular epis, is

then itself the composite of regular epis (check this!), so in particular epi.

This proves that m is mono, and we have our factorization.

As to uniqueness, suppose we had another factorization f = m

with m

mono and e

regular epi. Then m

= fp

= m

so since m

mono,

= e

. Because e is the coequalizer of p

and p

, there is a unique :

Then m

e = m

= f = me so since e epi, m = m

Now e

: X

is a coequalizer say U

is a coequalizer

diagram. Then it follows that ek = el (since mek = m

k = m

l = mel and

m mono) so there is a unique :

Then me = me

= me since m

mono and e epi, = id

. Similarly, = id

. So is the required isomor-

phism.

Exercise 57

. Check this detail: in a regular category

, if

is a

pullback diagram and b = c

with c

and c

regular epis, then a = a

for

some regular epis a

Subobjects

. In any category

we dene a

subobject

of an object X to be

an equivalence class of monomorphisms Y

X, where Y

X is equivalent to

X if there is an isomorphism : Y

with m

= m (then m

;

= m

follws). We say that Y

X represents a

smaller

subobject than Y

X if

there is : Y

with m

= m ( not necessarily iso but check that is

always mono).

The notion of subobject is the categorical version of the notion of subset in

set theory. In Set, two injective functions represent the same subobject i their

images are the same one can therefore identify subobjects with subsets. Note

Categories

however, that in Set we have a \canonical"

choice

of representative for each

subobject: the inclusion of the subset to which the subobject corresponds. This

choice is not always available in general categories.

We have a partial order Sub(X) of subobjects of X, ordered by the smaller-

than relation.

Proposition 4.3

In a category

with nite limits, each pair of elements of

Sub

(X)

has a greatest lower bound. Moreover, Sub

(X)

has a largest element.

Proof

. If Y

X and Y

X represent two subobjects of X and

is a pullback, then Z

X is mono, and represents the greatest lower bound

(check!).

Of course, the identity X

X represents the top element of Sub(X).

Because the factorization of X

Y as X

Y with e regular epi and

m mono, in a regular category

, is only dened up to isomorphism, it denes

rather a subobject of Y than a mono into Y this dened subobject is called the

image

of f and denoted Im(f) (compare with the situation in Set).

Exercise 58

. Im(f) is the smallest subobject of Y through which f factors:

for a subobject represented by n : A

Y we have that there is X

A with

f = na, if and only if Im(f) is smaller than the subobject represented by n.
Since monos and isos are stable under pullback, in any category

with pull-

backs, any arrow f : X

Y determines an order preserving map f

: Sub(Y )

Sub(X)

by pullback along

f: if E

Y represents the subobject M of Y and

is a pullback, F

X represents f

(M).

Exercise 59

. Check that f

is well dened and order preserving.

Proposition 4.4

In a regular category, each

preserves greatest lower bounds

and images, that is: for

f : X

i) for subobjects

N) = f

(M)

(N)

ii) if

is a pullback, then

(Im(g)) = Im(g

)

4. A little piece of categorical logic

Exercise 60

. Prove proposition 4.4.

4.2 Coherent logic in regular categories

The fragment of rst order logic we are going to interpret in regular categories

is the so-called coherent fragment.

The logical symbols are = (equality),

(conjunction) and

(existential

quantication). A

language

consists of a set of

sorts

ST::: a denumerable

collection of

variables

::: of sort S, for each sort and a collection of

function symbols

(f : S

:::S

S). The case n = 0 is not excluded (one

thinks of

constants

of a sort), but not separately treated. We now dene,

inductively, terms of sort S and formulas.

Denition 4.5

Terms of sort

are dened by:

is a term of sort

is a variable of sort

ii) if

:::t

are terms of sorts

:::S

respectively, and

(f : S

:::S

is a function symbol of the language, then

f(t

:::t

)

is a term of sort

Formulas are dened by:

is a formula (the formula \true")

ii) if

and

are terms of the same sort, then

t = s

is a formula

iii) if

and

are formulas then

)

is a formula

iv) if

is a formula and

a variable of some sort, then

is a formula.

interpretation

of such a language in a regular category

starts by choos-

ing for each sort S an object S ]] of

, and for each function symbol (f :

:::S

S) of the language, an arrow f ]] : S

]]

S ]] in

Given this, we dene interpretations t]] for terms t and ']] for formulas

', as follows.

Write FV (t) for the set of variables which occur in t, and FV (') for the set

free

variables in '.

We put FV (t)]] = S

]]

]] if FV (t) =

:::x

the same

for FV (')]]. Note: in the products FV (t)]] and FV (')]] we take a copy

of S ]] for every variable of sort S! Let me further emphasize that the empty

product is 1, so if FV (t) (or FV (')) is

, FV (t)]] (or FV (')]]) is the terminal

object of the category.

Categories

Denition 4.6

The interpretation of a term

of sort

is a morphism

t]] :

FV (t)]]

S ]]

and is dened by the clauses:

]]

is the identity on

S ]]

, if

is a variable of sort

ii) Given

]] : FV (t

)]]

]]

for

i = 1:::n

and a function symbol

(f : S

:::S

of the language,

f(t

:::t

)]]

is the map

FV (f(t

:::t

))]]

:::n

)

]]

S ]]

where

is the composite

FV (f(t

:::t

))]]

FV (t

)]]

]]

in which

is the appropriate projection, corresponding to the inclusion

FV (t

)

FV (f(t

:::t

))

Finally, we interpret formulas ' as

subobjects

']] of FV (')]]. You should try

to keep in mind the intuition that '(x

:::x

)]] is the \subset"

:::a

)

:::a

]

Denition 4.7

The interpretation

']]

as subobject of

FV (')]]

is dened as

follows:

]]

is the maximal subobject of

FV (

)]] = 1

ii)

t = s]]

FV (t = s)]]

is the equalizer of

FV(t = s)]]

FV (t)]]

FV (s)]]

]]

T ]]

and

are of sort

again, the left hand side maps are projections,

corresponding to the inclusions of

FV (t)

and

FV (s)

into

FV (t = s)

iii) if

']]

FV (')]]

and

]]

FV ()]]

are given and

FV ('

)]]

FV (')]]

FV ()]]

are again the suitable projections, then

)]]

FV ('

)]]

is the

greatest lower bound in

Sub(FV ('

)]])

(']])

and

( ]])

4. A little piece of categorical logic

iv) if

']]

FV (')]]

is given and

: FV (')]]

FV (

x')]]

the projec-

tion, let

(')]]

be the product of the interpretations of the sorts of the

variables in

FV (')

(so

(')]] = FV (')]]

occurs freely in

and

(')]] = FV (')]]

S ]]

x = x

does not occur free in

Write

: FV

(')]]

FV (')]]

Now take

x']]

FV (

x')]]

to be the image of the composition:

(

)

(']])

(')]]

FV (

x')]]

We have now given an interpretation of formulas. Basically, a formula ' is

true

under this interpretation if ']]

FV (')]] is the maximal subobject

but since we formulate the logic in terms of sequents we rather dene when a

sequent is true under the interpretation.

Denition 4.8

labelled sequent

is an expression of the form

where

and

are the formulas of the sequent (but

may be absent), and

is a nite set of variables which includes all the variables which occur free in a

formula of the sequent.

Let

]] = S

]]

:::x

there are projections

]]

FV (')]]

and (in case

is there)

]]

FV ()]]

we say that the

sequent

is true for the interpretation if

(

)

( ]])

(

)

(']])

subobjects of

]]

, and

is true if

(

)

(']])

is the maximal subobject of

]]

Exercise 61

. Show that the sequent

= x

) is true if and only if the

unique map S ]]

1 is a regular epimorphism.

We now turn to the logic. Instead of giving deduction rules and axioms, I

formulate a list of closure conditions which determine what sets of labelled se-

quents will be called a

theory

. I write

for

and

for

Denition 4.9

Given a language, a set

of labelled sequents of that language

is called a

theory

i the following conditions hold (the use of brackets around

caters in a, I hope, self-explanatory way for the case distiction as to whether

is or is not present):

is in

x = x

is in

for every variable

x = y

y = z

xyz

x = z

is in

for variables

xyz

of the same sort

ii) if

()

is in

then

()

is in

whenever

iii) if

()

is in

and

FV ()

then

(

)

and

(

)

are

Categories

iv) if

()

and

()

are in

then

()

and

()

are in

v) if

is in

and

is a variable not occurring in

then

is in

vi) if

occurs in

and

()

't=x]

is in

then

()

is in

does not occur in

and

()

and

()

x(x = x)

are in

then

()

is in

vii) if

()

is in

then

(t=x])

(

)

't=x]

is in

viii) if

()

't=x]

and

()

t = s

are in

then

()

's=x]

is in

ix) if

()

and

are in

then

()

is in

Exercise 62

. Show that the sequent '

(

)

' is in every theory, for every

formula ' of the language.
As said, the denition of a theory is a list of closure conditions: every item

can be seen as a rule, and a theory is a set of sequents closed under every rule.

Therefore, the intersection of any collection of theories is again a theory, and it

makes sense to speak, given a set of sequents S, of the theory Cn(S)

generated

Cn(S) =

T is a theory and S

We have the following theorem:

Theorem 4.10 (Soundness theorem)

Suppose

T = Cn(S)

and all sequents

are true under the interpretation in the category

. Then all sequents of

are true under that interpretation.

Before embarking on the proof, rst a lemma:

Lemma 4.11

Suppose

is substitutable for

. There is an obvious map

t] : FV (')

FV (t)]] = FV ('t=x])]]

FV (')]]

induced by

t]]

the components of

are projections except for the factor of

']]

corresponding to

, where it is

FV ('t=x])]]

FV (t)]]

]]

There is a pullback diagram:

't=x]]]

FV ('t=x])]]

]

']]

FV (')]]

4. A little piece of categorical logic

Exercise 63

. Prove this lemma not trivial. Use induction on ' and proposi-

tion 4.4].

Proof

. (of theorem 4.10) The proof checks that for every rule in the list of

denition 4.9, if the premiss is true then the conclusion is true in other words,

that the set of true sequents is a theory.

is true by the denition

]] = 1

= x

]] is the equalizer of two maps which are both the identity on S ]],

so isomorphic to S ]]. For x = y

y = z

xyz

x = z, just observe

that E

if E

is the equalizer of the two projections

S ]]

S ]].

ii) This is because if

and : ]]

]] is the projection,

is monotone.

iii)-iv) By the interpretation of

as the greatest lower bound of two subobjects,

and proposition 4.4.

v) Let

]]

FV (')]]

FV()]]

FV (

x)]]

the projections. Since by assumption

( ]])

()

(']]) there is a commu-

tative diagram

( ]])

]]

(']])

]]

By proposition 4.4,

(

x]]) is the image of the map

( ]])

]],

( ]])

(']]) in Sub(

]]).

vi) Suppose x occurs free in '. Consider the commutative diagram

]]

FV ()]]

FV ('t=x])]]

]

FV (')]]

FV (')

]]

with t] as in lemma4.11 and the other maps projections. Now ']]

(

x']])

because ']]

FV (')]]

FV (')

]] factors through

x']] by deni-

tion so if

( ]])

('t=x]]]) then with lemma 4.11,

( ]])

('t=x]]]) =

(']])

(

x']]) =

(

x']])

in Sub(]]) and we are done.

Categories

The case of x not occurring in ' is left to you.

vii) Direct application of lemma 4.11

viii-ix) Left to you.

Exercise 64

. Fill in the \left to you" gaps in the proof.

4.3 The language

L(C

)

and theory

)

associated to a

regular category

Given a regular category

(which, to be precise, must be assumed to be small),

we associate to

the language which has a sort C for every object of

, and a

function symbol (f : C

D) for every arrow f : C

D of

This language is called

(

) and it has trivially an interpretation in

The theory T(

) is the set of sequents of

(

) which are true for this inter-

pretation.

One of the points of categorical logic is now, that categorical statements

about objects and arrows in

can be reformulated as statements about the

truth of certain sequents in

(

). You should read the relevant sequents as

expressing that we can \do as if the category were Set".

Examples

a) C is a terminal object of

if and only if the sequents

x = y and

x(x = x) are valid, where xy variables of sort C

b) the arrow f : A

B is mono in

if and only if the sequent f(x) =

f(y)

x = y is true

c) The square

is a pullback square in

if and only if the sequents

h(x

) = d(y

)

(f(z) = x

g(z) = y)

and

f(z

) = f(z

)

g(z

) = g(z

)

z = z

are true

4. A little piece of categorical logic

d) the fact that f : A

B is epi can not similarly be expressed! But: f is

regular epi if and only if

(f(y) = x)

is true

e) A

C is an equalizer diagram i f is mono (see b) and the

sequent

g(x

) = h(x

)

(f(y) = x)

is true.

Exercise 65

. Check (a number of) these statements. Give the sequent(s) cor-

responding to the statement that

is a product diagram.

Exercise 66

. Check that the formulas

x' and

x(x = x

') are

equiva-

lent

, that is, every theory contains the sequents

x(x = x

and

x(x = x

for any containing the free variables of

x'.

Exercise 67

. Can you express: A

B is regular mono?

4.4 Example of a regular category

In this section, I treat an example of a type of regular categories which are

important in categorical logic. They are categories of (-valued sets for some

frame (. Let's dene some things.

Denition 4.12

frame (

is a partially ordered set which has suprema (least

upper bounds)

of all subsets

, and inma (meets)

for

nite

subsets

(so, there is a top element

and every pair of elements

has a meet

and moreover,

distributes over

, that is,

B =

for

(

Categories

Given a frame ( we dene the category

as follows:

Objects are functions X

(, X a set

Maps from (XE

) to (YE

) are functions X

Y satisfying the requirement

that E

(x)

(f(x)) for all x

It is easily seen that the identity function satises this requirement, and if two

composable functions satisfy it, their composition does so we have a category.

Proposition 4.13

is a regular category.

Proof

. Let

be any one-element set, together with the function which sends

to the top element of (. Then

( is a terminal object of

Given (XE

) and (YE

), a product of the two is the object (X

)

where E

(xy) is dened as E

(x)

(y).

Given two arrows fg : (XE

)

(YE

) their equalizer is (X

) where

X is

f(x) = g(x)

and E

is the restriction of E

to X

This is easily checked, and

is a nitely complete category.

An arrow f : (XE

)

(YE

) is regular epi if and only if the function f

is surjective and for all y

Y , E

(y) =

;

(y).

For suppose f is such, and g : (XE

)

(ZE

) coequalizes the kernel

pair of f. Then g(x) = g(x

) whenever f(x) = f(x

), and so for all y

Y , since

f(x) = y implies E

(x)

(g(x)), we have

(y) =

(x)

f(x) = y

(g(x))

so there is a unique map h : (YE

)

(ZE

) such that g = hf that is f is

the coequalizer of its kernel pair.

The proof of the converse is left to you.

Finally we must show that regular epis are stable under pullback. This is

an exercise.

Exercise 68

. Show that the pullback of

(I suppress reference

to the E

etc.) is (up to isomorphism) the set

(xy)

f(x) = g(y)

, with

E(xy) = E

(x)

(y) and then, use the distributivity of ( to show that

regular epis are stable under pullback.

Exercise 69

. Fill in the other gap in the proof: if f : (XE

)

(YE

)

is a regular epi, then f satises the condition given in the proof.

Exercise 70

. Given (XE

)

(YE

), give the interpretation of the for-

mula

x(f(x) = y), as subobject of (YE

4. A little piece of categorical logic

Exercise 71

. Characterize those objects (XE

) for which the unique map

to the terminal object is a regular epimorphism.

Exercise 72

. Give a categorical proof of the statement: if f is the coequalizer

of something, it is the coequalizer of its kernel pair.

Exercise 73

. Characterize the regular monos in

Categories

5. Adjunctions

5 Adjunctions

The following kind of problem occurs quite regularly: suppose we have a functor

and for a given object D of

, we look for an object G(C) which \best

approximates" D, in the sense that there is a map D

G(C) with the property

that any other map D

G(C

) factors uniquely as G(f) for f : C

We have seen, that if G is the inclusion of Abgp into Grp, the abelianization

of a group is an example. Another example is the )Cech-Stone compactication

in topology: for an arbitrary topological space X one constructs a compact

space X out of it, and a map X

X, such that any continuous map from

X to a compact space factors uniquely through this map.

Of course, what we described here is a sort of \right-sided" approximation

the reader can dene for himself what the notion for a left-sided approxiamtion

would be.

The categorical description of this kind of phenomena goes via the concept

adjunction

, which this chapter is about.

5.1 Adjoint functors

Let

be a pair of functors between categories

and

We say that F is

left adjoint

to G, or G is

right adjoint

to F, notation:

G, if there is a natural bijection:

(FDC)

D C

(DGC)

for each pair of objects C

. Two maps f : FD

C in

and

g : D

GC in

which correspond to each other under this correspondence

are called

transposes

of each other.

The naturality means that, given f : D

, g : C

C in

and

respectively, the diagram

(FDC)

D C

(DGC)

(FD

)

(

Ffg

)

(

fGg

)

commutes in Set. Remind yourself that given : FD

(Ffg)() :

C is the composite

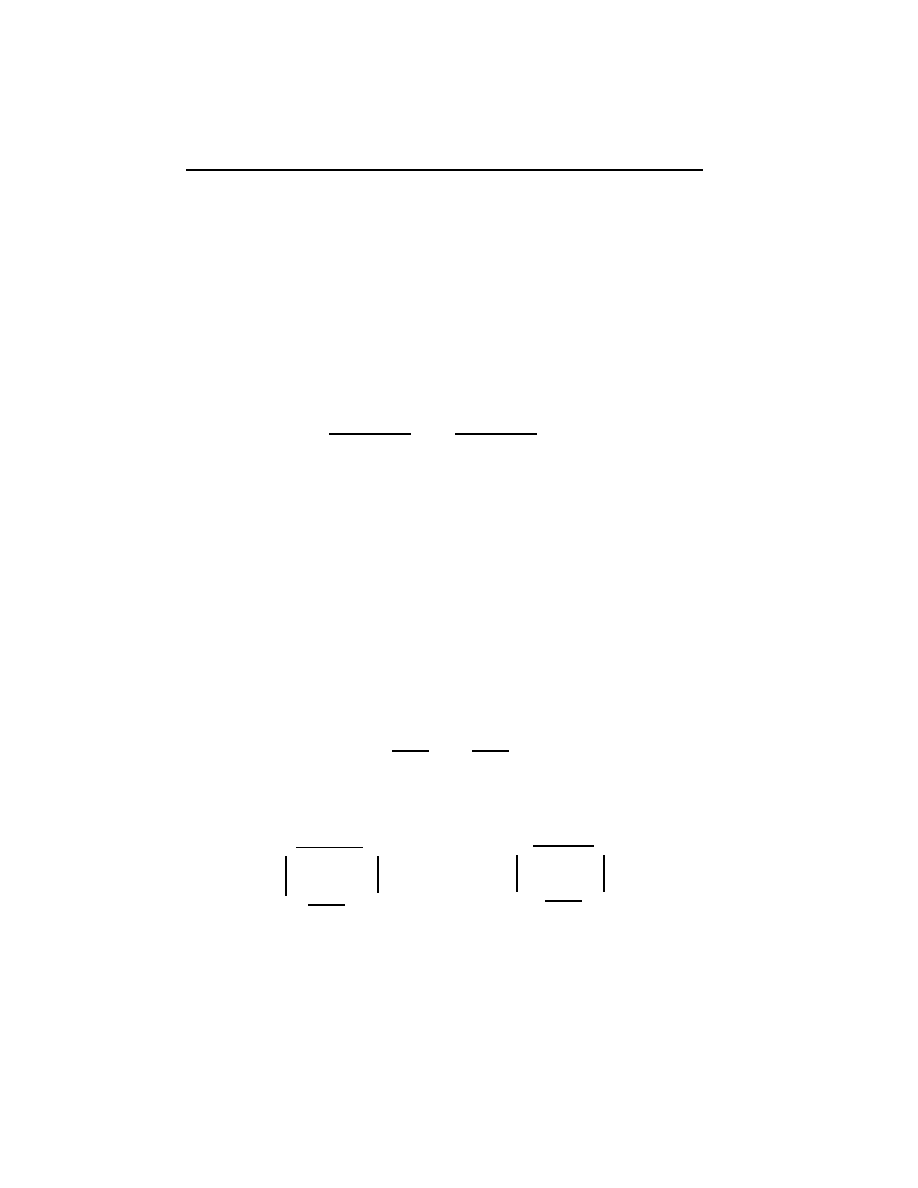
Categories

Such a family m = (m

) is then completely determined by

the values it takes on identities i.e. the values

DFD

(id

) : D

GFD

For, given : FD

C, since =

(id

)(id

() = m

(

(id

)(id

))

(id

G())(m

(id

))

which is the composite

D F

(id

)

GFD

(

)

G(C)

The standard notation for m

DFD

(id

) is

: D

GF(D).

Exercise 74

. Show that (

: D

) is a natural transformation:

)

By the same reasoning, the natural family(m

;

) is completely

determined by its actions on identities

;

GCC

(id

) : FGC

Again, the family (m

;

GCC

(id

)

) is a natural transformation: FG

)

. We denote its components by "

and this is also standard notation.

We have that m

;

( : D

GC) is the composite

FGC

Now making use of the fact that m

and m

;

are each others inverse we get

that for all : FD

C and : D

GC the diagrams

GFD

(

)

GFG(C)

(

)

and

(

)

FGFD

(

)

FGC

commute applying this to the identities on FD and GC we nd that we have

commuting diagrams of natural transformations:

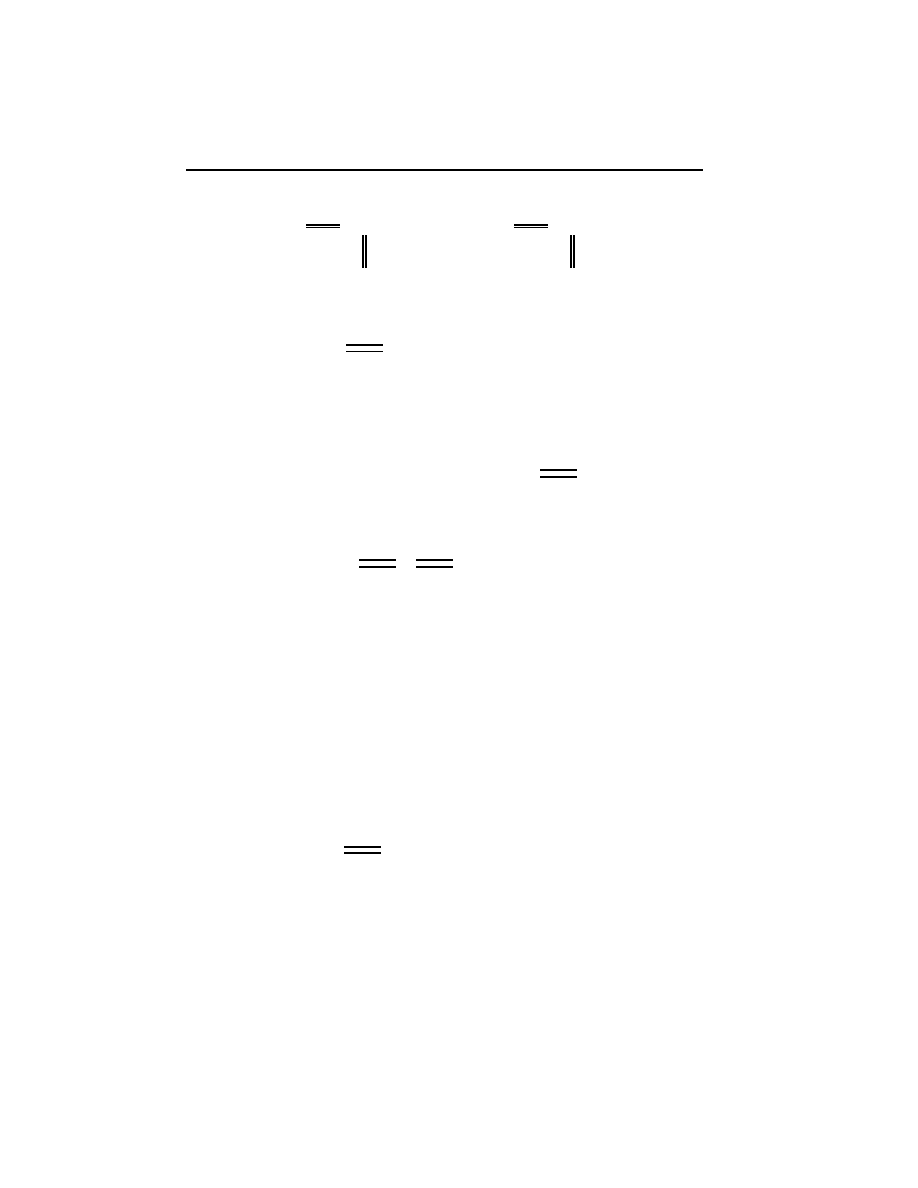
5. Adjunctions

GFG

FGF

"?F

Here ? G denotes (

) and G

" denotes (G("

)

Conversely, given

with natural transformations : id

)

and " : FG

)

which satisfy the above

triangle equalities

, we have that

The tuple (FG") is called an

adjunction

. is the

unit

of the adjunction,

" the

counit

Exercise 75

. Prove the last statement, i.e. given

, : id

)

and " : FG

)

satisfying (G

( ? G) = id

and (" ? F)

) = id

we have F

Exercise 76

. Given

, if F

and F

then

Examples

. The world is full of examples of adjoint functors. We have met

several:

a) Consider the forgetful functor U : Grp

Set and the free functor F :

Set

Grp. Given a function from a set A to a group G (which is an arrow

U(G) in Set) we can uniquely extend it to a group homomorphism

from ( ~A?) to G (see example e) of 1.1), i.e. an arrow F(A)

G in Grp,

and conversely. This is natural in A and G, so F

b) The functor Dgrph

Cat given in example f) of 1.1 is left adjoint to the

forgetful functor Cat

Dgrph

c) Given functors P

between two preorders P and Q, F

G if and

only if we have the equivalence

G(x)

F(y)

for x

Q if and only if we have FG(x)

x and y

GF(y) for all

Categories

d) In example m) of 1.1 we did \abelianization" of a group G. We made

use of the fact that any homomorphism G

H with H abelian, factors

uniquely through G=GG], giving a natural 1-1 correspondence

Grp(GI(H))

Abgp(G=GG]H)

where I : Abgp

Grp is the inclusion. So abelianization is left adjoint

to the inclusion functor of abelian groups into groups

e) The

free monoid

F(A) on a set A is just the set of strings on the alphabet

A. F : Set

Mon is a functor left adjoint to the forgetful functor from

Mon to Set

f) Given a set X we have seen (example g) of 2.2) the product functor (

;

)

X : Set

Set, assigning the product Y

X to a set Y .

Since there is a natural bijection between functions Y

Z and

functions Y

, the functor (

;

)

: Set

Set is right adjoint to

(

;

)

g) Example e) of 2.2 gives two functors FG : Set

Cat. F and G are

respectively left and right adjoint to the functor Cat

Set which assigns

to a (small) category its set of objects (to be precise, for this example to

work we have to take for Cat the category of

small

categories), and to a

functor its action on objects.

h) Given a regular category

we saw in 4.1 that every arrow f : X

can be factored as a regular epi followed by a monomorphism. This gives

rise to a monotone function: Sub(X)

Sub(Y ) dened as follows: if

Sub(X) is represented by m, Im

(M) is the image of fm (see 4.1).

We have seen that Im

(M)

(N) for any subobject N of

Y , so Im

is left adjoint to f

We can also express this logically: in the logic developed in chapter 4, for

any formulas M(x) and N(y), the sequents

x(f(x) = y

M(x))

N(y)

and

M(x)

N(f(x))

are equivalent.

One of the slogans of categorical logic is therefore, that \existential quan-

tication is left adjoint to substitution".

5. Adjunctions

i) Let

be a category with nite products for C

consider the slice

category

=C. There is a functor C

=C which assigns to D the

object C

C of

=C, and to maps D

the map id

has a left adjoint *

which takes the domain: *

C) = D.

j) Let P : Set

Set be the functor which takes the powerset on objects,

and for X

Y , P(f) : P(Y )

P(X) gives for each subset B of Y its

inverse image under f.

Now P might as well be regarded as a functor Set

Set

let's write "P

for that functor. Since there is a natural bijection:

Set(XP(Y ))

Set(YP(X)) = Set

( "P(X)Y )

we have an adjunction "P

Exercise 77

. Suppose that

is a functor and that for each object C of

there is an object GC of

and an arrow "

: FGC

C with the property that

for every object D of

and any map FD

C, there is a unique ~f: D

such that

FGC

commutes.

Prove that G :

extends to a functor G :

which is right

adjoint to F, and that ("

: FGC

) is the counit of the adjunction.

Construct also the unit of the adjunction.

Exercise 78

. Given

, for each object D of

we let (D

G) denote

the category which has as objects pairs (Cg) where C is an object in

and

g : D

GC is an arrow in

. An arrow (Cg)

) in (D

G) is an arrow

f : C

which makes

}}

{

commute.

Show that G has a left adjoint if and only if for each D, the category (D

has an initial object.

Categories

5.2 Expressing (co)completeness by existence of adjoints

preservation of (co)limits by adjoint functors

Given categories

and

, we dened for every functor F :

its

limit

(or limiting cone), if it existed, as a pair (D) with : $

)

F, and (D)

terminal in the category of cones for F.

Any other natural transformation

: $

)

F factors uniquely through

(D) via an arrow D

D in

and conversely, every arrow D

D gives

rise to a natural transformation

: $

)

So there is a 1-1 correspondence between

D) and

which is natural in D

Since every arrow D

gives a natural transformation $

)

(example i) of 2.2), there is a functor $

(

;

)

The above equation now means that:

Proposition 5.1

has all limits of type

(i.e. every functor

has a

limiting cone in

) if and only if

(

;

)

has a right adjoint.

Exercise 79

. Give an exact proof of this proposition.

Exercise 80

. Use duality to deduce the dual of the proposition:

has all

colimits of type

if and only if $

(

;

)

has a left adjoint.

Exercise 81

. (Uniqueness of adjoints) Any two left (or right) adjoints of a

given functor are isomorphic as objects of the appropriate functor category.

Exercise 82

has a right adjoint i

has a terminal object, and a

left adjoint i

has an initial object.

Exercise 83

. Suppose

has both an initial and a terminal object denote

by L the functor

which sends everything to the initial, and by R the

one which sends everything to the terminal object. L

Exercise 84

. Let F

G with counit " : FG

)

id. Show that " is a nat-

ural isomorphism if and only if G is faithful.
A very important aspect of adjoint functors is their behaviour with respect

to limits and colimits.

Theorem 5.2

Let

such that

. Then:

5. Adjunctions

preserves all limits which exist in

preserves all colimits which exist in

Proof

. Suppose M :

has a limiting cone (C) in

. Now a cone (D)

for GM is a natural family D

GM(E), i.e. such that

GM(E)

(

)

GM(E

)

commutes for every E

This transposes under the adjunction to a family (FD

) and

the naturality requirement implies that

(

)

commutes in

, in other words, that (FD) is a cone for M in

. There is,

therefore, a unique map of cones from (FD ~) to (C).

Transposing back again, we get a unique map of cones (D)

(GCG

That is to say that (GCG

) is terminal in Cone(GM), so a limiting cone for

GM, which was to be proved.

The argument for the other statement is dual.

Exercise 85

. Given

, F

G and M :

. Show that the

functor Cone(M)

Cone(GM) induced by G has a left adjoint.

From the theorem on preservation of (co)limits by adjoint functors one can

often conclude that certain functors cannot have a right or a left adjoint.

Examples

a) The forgetful functor Mon

Set does not preserve epis, as we have seen

in 1.2. In chapter 3 we've seen that f is epi i

is a pushout

since left adjoints preserve identities and pushouts, they preserve epis

therefore the forgetful functor Mon

Set does not have a right adjoint

Categories

b) The functor (

;

)

X : Set

Set does not preserve the terminal object

unless X is itself terminal in Set therefore, it does not have a left adjoint

for non-terminal X.

c) The forgetful functor Pos

Set has a left adjoint, but it cannot have a

right adjoint: it preserves all coproducts, including the initial object, but

not all coequalizers.

Exercise 86

. Prove the last example. Hint: think of the coequalizer of the fol-

lowing two maps

: one is the inclusion, the other is the constant zero map.

Another use of the theorem has to do with the computation of limits. Many

categories, as we have seen, have a forgetful functor to Set which has a left

adjoint. So the forgetful functor preserves limits, and since these can easily be

computed in Set, one already knows the \underlying set" of the vertex of the

limiting cone one wants to compute.
Does a converse to the theorem hold? I.e. given G :

which preserves

all limits does G have a left adjoint? In general

, unless

is suciently

complete, and a rather technical condition, the \solution set condition" holds.

The

adjoint functor theorem

(Freyd) tells that in that case there is a converse:

Denition 5.3 (Solution set condition)

G :

satises the solution

set condition (ssc) for an object

, if there is a

set X

of objects of

such that every arrow

factors as

(

)

for some

and

f : C

Theorem 5.4 (Adjoint Functor Theorem)

Let

be a complete category

and

G :

a functor.

has a left adjoint if and only if

preserves

all small limits and satises the ssc for every object

I won't prove the theorem, but you may like to try yourself. It is a, not too

trivial, exercise.

For small categories

, the ssc is of course irrelevant. But categories which

are small

and

complete are rather special:::they are complete preorders.

For preorders

we have: if

is complete, then G :

has a left

adjoint if and only if G preserves all limits, that is: greatest lower bounds

for all B

. For, put

F(d) =

G(c)

5. Adjunctions

Then F(d)

implies (since G preserves

)

G(c)

G(c

) which

implies d

G(c

) since d

G(c)

conversely, d

G(c

) implies

G(c)

so F(d) =

G(c)

Categories

6. Monads and Algebras

6 Monads and Algebras

Given an adjunction (FG") :

let us look at the functor T =

GF :

We have a natural transformation : id

)

T and a natural transformation

: T

)

T. The components

are

(D) = GFGFD

(

)

GFD = T(D)

Furthermore the equalities

and

}

hold. Here (T)

= T(

) : T

TD and (T)

: T

(Similar for T and T).

Exercise 87

. Prove these equalities.

A triple (T) satisfying these identities is called a

monad

. Try to see the

formal analogy between the dening equalities for a monad and the axioms for

a monoid: writing m(ef) for ef in a monoid, and for the unit element, we

have

m(em(gh)) = m(m(eg)h) (associativity)

m(e) = m(e) = e

(unit)

Following this one calls the

multiplication

of the monad, and its

unit

Example

. The powerset functor

: Set

Set (example j) of 2.2, with

and indicated there) is a monad (check).
Dually, there is the notion of a

comonad

(L") on a category

, with equalities

Given an adjunction (FG"), (FG = FG") is a comonad on

. We call

the

comultiplication

and " the

counit

(this is in harmony with the unit-counit

terminology for adjunctions).

Categories

Although, in many contexts, comonads and the notions derived from them

are at least as important as monads, the treatment is dual so I concentrate on

monads.

Every adjunction gives rise to a monad conversely, every monad arises from

an adjunction, but in more than one way. Essentially, there are a maximal and

a minimal solution to the problem of nding an adjunction from which a given

monad arises.

Example

. A monad on a poset P is a monotone function T : P

P with

the properties x

T(x) and T

(x)

T(x) for all x

P such an operation

is also often called a

closure operation

on P. Note that T

= T because T is

monotone.

In this situation, let Q

P be the image of T, with the ordering inherited

from P. We have maps r : P

Q and i : Q

P such that ri is the identity

on Q and ir = T : P

For x

P, y

Q we have x

i(y)

r(x)

y (check) so r

i and the

operation T arises from this adjunction.

6.1 Algebras for a monad

Given a monad (T) on a category

, we dene the category T-Alg of T

algebras

as follows:

Objects

are pairs (Xh) where X is an object of

and h : T(X)

X is

an arrow in

such that

(X)

(

)

T(X)

and

T(X)

commute

Morphisms

: (Xh)

(Yk) are morphisms X

Y in

for which

T(X)

(

)

T(Y )

commutes.

6. Monads and Algebras

Theorem 6.1

There is an adjunction between

-Alg and

which brings about

the given monad

Proof

. There is an obvious forgetful functor U

: T-Alg

which takes (Xh)

to X. I claim that U

has a left adjoint F

assigns to an object X the T-algebra T

(X)

T(X) to X

the map T(f) this is an algebra map because of the naturality of . That

(X)

T(X) is an algebra follows from the dening axioms for a monad T.

Now given any arrow g : X

(Yh) we let ~g : (T(X)

)

(Yh) be

the arrow T(X)

(

)

T(Y )

Y . This is a map of algebras since

(X)

(

)

(Y )

(

)

T(X)

(

)

T(Y )

commutes the left hand square is the naturality of the right hand square is

because (Yh) is a T-algebra.

Conversely, given f : (TX

)

(Yh) we have an arrow "f : X

Y by

taking the composite X

Y .

Now ~"f: TX

Y is the composite

(

)

(

)

By naturality of this is

which is f since (Yh) is a T-algebra.

Conversely, "~g : X

Y is the composite

(

)

Again by naturality of and the fact that (Yh) is a T-algebra, we conclude

that "~g = g. So we have a natural 1-1 correspondence

(XU

(Yh))

T-Alg(F

(X)(Yh))

and our adjunction.

Note that the composite U

is the functor T, and that the unit of the

adjunction is the unit of T the proof that for the counit " of F

we have

that

= U

T U

= T

Categories

is the original multiplication , is left to you.

Exercise 88

. Complete the proof.

Example

. The

group monad

. Combining the forgetful functor U : Grp

Set

with the left adjoint, the free functor Set

Grp, we get the following monad

on Set:

T(A) is the set of sequences on the alphabet A

;

is the set

;

of formal inverses of elements of A, as in example e) of 1.1) in which no

;

or a

;

a occur. The unit A

TA sends a

A to the string

. The

multiplication : T

(A)

T(A) works as follows. Dene (

;

)

;

: A

;

by a

;

= a

;

and (a

;

)

;

= a. Dene also (

;

)

;

on strings by (a

:::a

)

;

:::a

;

. Now for an element of TT(A), which is a string on the alphabet

T(A)

;

, say

:::

, we let

(

:::

) be the concatenation of the

strings ~

::: ~

on the alphabet A

;

, where ~

T(A), and

= (

)

;

T(A)

;

. Of course we still have to remove possible substrings

of the form aa

;

etc.

Now let us look at algebras for the group monad: maps T(A)

A such that

for a string of strings

:::

:::s

:::

:::s

we have that

:::h

) = h(

:::s

)

and

) = a for a

I claim that this is the same thing as a group structure on A, with multiplication

b = h(

The unit element is given by h(

) the inverse of a

A is h(

;

) since

ah(

;

)

) = h(

)h(

;

)

) =

;

) = h(

), the unit element

Try to see for yourself how the associativity of the monad and its algebras trans-

forms into associativity of the group law.

Exercise 89

. Finish the proof of the theorem: for the group monad T, there

is an equivalence of categories between T-Alg and Grp.
This situation is very important and has its own name:

6. Monads and Algebras

Denition 6.2

Given an adjunction

there is always a

com-

parison functor K :

-Alg for

T = GF

, the monad induced by the adjunc-

tion.

sends an object

to the

-algebra

GFG(C)

(

)

G(C)

We say that

monadic

over

is an equivalence.

Exercise 90

. Check that K(C) is a T-algebra. Complete the denition of

K as a functor. Check that in the example of the group monad, the functor

T-Alg

Grp dened there is a pseudo inverse to the comparison functor K.

In many cases however, the situation is not monadic. Take the forgetful functor

U : Pos

Set. It has a left adjoint F which sends a set X to the discrete

ordering on X (x

y i x = y). Of course, UF is the identity on Set and the

UF-algebras are just sets. The comparison functor K is the functor U, and this

is not an equivalence.

Exercise 91

. Why not? Hint: think of coproducts in both categories. Every

equivalence reects coproducts]
Another example of a monadic situation is of importance in domain theory.

Let Pos

be the category of partially ordered sets with a least element, and

order preserving maps which also preserve the least element.

There is an obvious inclusion functor U : Pos

Pos, and U has a left

adjoint F. Given a poset X, F(X) is X \with a bottom element added":

Given f : X

Y in Pos, F(f) sends the new bottom element of X to the new

bottom element of Y , and is just f on the rest. If f : X

Y in Pos is a map

and Y has a least element, we have F(X)

Y in Pos

by sending

to the

least element of Y . So the adjunction is clear.

The monad UF : Pos

Pos, just adding a least element, is called the

lifting

monad

. Unit and multiplication are:

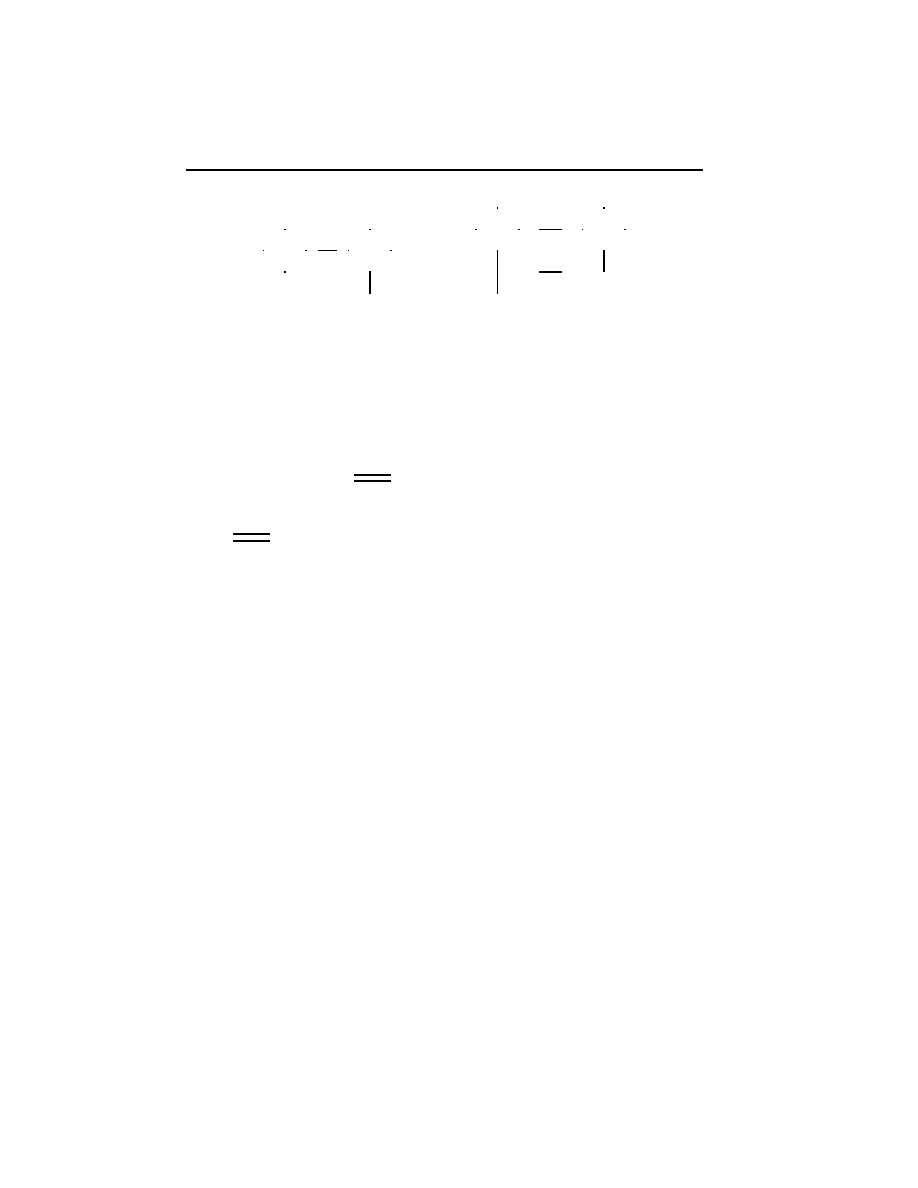
Categories

: X

T(X)

: T

(X)

T(X)

A T-algebra h : TX

X is rst of all a monotone map, but since h

= id

h is epi in Pos so surjective. It follows that X must have a least element h(

From the axioms for an algebra one deduces that h must be the identity when

restricted to X, and h(

) the least element of X.

Exercise 92

. Given

, F

G, T = GF. Prove that the com-

parison functor K :

T-Alg satises U

K = G and KF = F

where

T-Alg

as in theorem 6.1.

Another poset example: algebras for the power set monad

on Set (exam-

ple j)2.2). Such an algebra h :

(X)

X must satisfy h(

) = x and for

(X):

h(A)

) = h(

)

Now we can, given an algebra structure on X, dene a partial order on X by

putting x

y i h(

) = y.

Indeed, this is clearly reexive and antisymmetric. As to transitivity, if x

and y

z then

)=h(

xh(

)

)h(

)

)=h(

)

)=h(

)h(

)

)=z

so x

Furthermore this partial order is

complete

: least upper bounds for arbitrary

subsets exist. For

B = h(B) for B

X: for x

B we have h(

xh(B)

) =

B) = h(B) so x

B and if x

y for all x

B then

h(B)y

)=h(B

)

)=h(

)

)=y

6. Monads and Algebras

We can also check that a map of algebras is a

-preserving monotone

function. Conversely, every

-preserving monotone function between complete

posets determines a

-algebra homomorphism.

We have an equivalence between the category of complete posets and

preserving functions, and

-algebras.

Exercise 93

. Let P : Set

Set be the contravariant powerset functor,

and "P its left adjoint, as in j) of 5.1. Let T : Set

Set the induced monad.

a) Describe unit and multiplication of this monad explicitly.
b) Show that Set

is equivalent to T-Alg Hint: if this proves hard, have a

look at VI.4.3 of Johnstone's \Stone Spaces"].

c) Conclude that there is an adjunction

CABool

Set

which presents CABool as monadic over Set.

6.2

-Algebras at least as complete as

Let T be a monad on

. The following exercise is meant to show that if

has

all limits of a certain type, so does T-Alg. In particular, if

is complete, so is

T-Alg this is often an important application of a monadic situation.

Exercise 94

. Let

be a category such that every functor M :

has

a limiting cone. Now suppose M :

T-Alg. For objects E of

, let M(E) be

the T-algebra T(m

)

a) Let (D(

)) be a limiting cone for U

M :

. Using the

T-algebra structure on M(E) and the fact that U

M(E) = m

, show

that there is also a cone (TD(

)) for U

b) Show that the unique map of cones: (TD)

(D) induces a T-algebra

structure TD

D on D

c) Show that TD

D is the vertex of a limiting cone for M in T-Alg.

6.3 The Kleisli category of a monad

I said before that for a monad T on a category

, there are a \maximal and

a minimal solution" to the problem of nding an adjunction which induces the

given monad.

Categories

We've seen the category T-Alg, which we now write as

we also write

: T-Alg

for the forgetful functor. In case T arises from an adjunction

, there was a comparison functor

. In the diagram

}

we have that KF = F

and G

K = G.

Moreover, the functor K is unique with this property.

This leads us to dene a category T-Adj of adjunctions

such

that GF = T. A

map

of such T-adjunctions from

a functor K :

satisfying KF = F

and G

K = G.

What we have proved about T-Alg can be summarized by saying that the

adjunction

is a

terminal object

in T-Adj. This was the \maximal"

solution.

T-Adj has also an initial object: the

Kleisli category

of T, called

has the same objects as

, but a map in

from X to Y is an arrow X

T(Y )

. Composition is dened as follows: given X

T(Y ) and Y

T(Z) in

, considered as a composable pair of morphisms in

, the composition gf in

is the composite

T(Y )

(

)

(Z)

T(Z)

Exercise 95

. Prove that composition is associative. What are the identi-

ties of

The adjunction

is dened as follows: the functor G

sends the

object X to T(X) and f : X

Y (f : X

T(Y ) in

) to

T(X)

(

)

(Y )

T(Y )

The functor F

is the identity on objects and sends X

Y to X

T(Y ),

considered as X

Y in

6. Monads and Algebras

Exercise 96

. Dene unit and counit check F

Now for every adjunction

with GF = T, there is a unique com-

parison functor L :

such that GL = G

and LF

= F.

L sends the object X to F(X) and f : X

Y (so f : X

T(Y ) = GF(Y )

) to its transpose ~f: F(X)

F(Y ).

Exercise 97

. Check the commutations. Prove the uniqueness of L w.r.t. these

properties.

Categories

7. Cartesian closed categories and the

-calculus

7 Cartesian closed categories and the

-calculus

Many set-theoretical constructions are completely determined (up to isomor-

phism, as always) by their categorical properties in Set. We are therefore

tempted to generalize them to arbitrary categories, by taking the character-

istic categorical property as a denition. Of course, this procedure is not really

well-dened and it requires sometimes a real insight to pick the `right' categori-

cal generalization. For example, the category of sets has very special properties:

f : X

Y is mono if and only if fg = fh implies g = h for any two maps

gh : 1

X, where 1 is a terminal object (we say 1 is

a generator

)

objects X and Y are isomorphic if there exist monos f : X

Y and

g : Y

X (the Cantor-Bernstein theorem)

every mono X

Y is part of a coproduct diagram

And if you believe the axiom of choice, there is its categorical version:

Every epi is split

None of these properties is generally valid, and categorical generalizations based

on them are usually of limited value

In this chapter we focus on a categorical generalization of a set-theoretical

concept which has proved to have numerous applications: Cartesian closed cat-

egories as the generalization of \function space".

In example f) of 5.1 we saw that the set of functions Z

appears as the value

at Z of the right adjoint to the product functor (

;

)

X. A category is called

cartesian closed

if such right adjoints always exist. In such categories we may

really think of this right adjoint as giving the \object of functions (or arrows)",

as the treatment of the -calculus will make clear.

7.1 Cartesian closed categories (ccc's) examples and ba-

sic facts

Denition 7.1

A category

is called

cartesian closed

a ccc

if it has nite

products, and for every object

the product functor

(

;

)

has a right

adjoint.

Asperti, for example, restricts his interpretation of the

-calculus to ccc's where 1 is a

generator. You might as well immediately restrict to Set, then.

Categories

Of course, \the" product functor only exists once we have chosen a product

diagram for every pair of objects of

. In this chapter we assume that we

have such a choice, as well as a distinguished terminal object 1 and we assume

also that for each object X we have a

specied

right adjoint to the functor

(

;

)

X, which we write as (

;

)

(Many authors write X

)

(

;

), but I think

that overloads the arrows notation too much). Objects of the form Z

are

called

exponents

We have the

unit

Y X

and

counit

Y X

of the adjunction (

;

)

(

;

)

. Anticipating the view of Y

as the object

of arrows X

Y , we call "

evaluation

Examples

a) A preorder (or partial order) is cartesian closed if it has a top element 1,

binary meets x

y and for any two elements xy an element x

y satisfying

for each z:

y i z

b) Set is cartesian closed Cat is cartesian closed (2.1)

c) Top is not cartesian closed, however the category of locally compact spaces

and continuous maps is

d) Pos is cartesian closed. The exponent Y

is the set of all monotone maps

Y , ordered pointwise (f

g i for all x

X, fx

gx in Y )

e) Grp and Abgp are not cartesian closed. In both categories, the initial

object is the one-element group. Since for non-initial groups G, (

;

)

does not preserve the initial object, it cannot have a right adjoint

is cartesian closed

isn't (why?)

g) Set

is cartesian closed. Products and 1 are given \pointwise" (in fact

all limits are), that is F

G(C) = F(C)

G(C) and 1(C) is the terminal

1 in Set, for all C

The construction of the exponent G

is a nice application of the Yoneda

lemma. Indeed, for G

to be the right adjoint (at G) of (

;

)

F, we need

for every object C of

Set

FG)

Set

)

(C)

7. Cartesian closed categories and the

-calculus

where the last isomorphism is by the Yoneda lemma.
Now the assignment C

Set

FG) denes a functor

Set,

which we denote by G

. At the same time, this construction denes a

functor (

;

)

: Set

Set

, which is right adjoint to (

;

)

F. It is

a nice exercise to prove this.

h) A monoid is never cartesian closed unless it's trivial.

Exercise 98

. Show that every Boolean algebra is cartesian closed.

Exercise 99

. Show that CABool is not cartesian closed use 2.3].

Exercise 100

. Show that a complete partial order is cartesian closed if and

only if it's a frame see 4.4].

Exercise 101

. Let ( be a frame. By the preceding exercise, it is cartesian

closed denote by x

y the exponent in (. This exercise is meant to let you

show that

is cartesian closed.

a) Show that ( also has greatest lower bounds

B for all subsets B.

b) Given objects (XE

) and (YE

), dene their exponent (YE

)

(

)

as (Y

E) where Y

is the set of all functions X

Y in Set, and

E(f) =

(x)

(f(x))

Show that this denes a right adjoint (at (YE

)) of (

;

)

(XE

Some useful facts:

is cartesian closed if and only if it has nite products, and for each pair

of objects XY there is an object Y

and an arrow " : Y

Y such

that for every Z and map Z

Y there is a unique Z

such

that

commutes.

In a ccc, there are natural isomorphisms 1

1 (Y

)

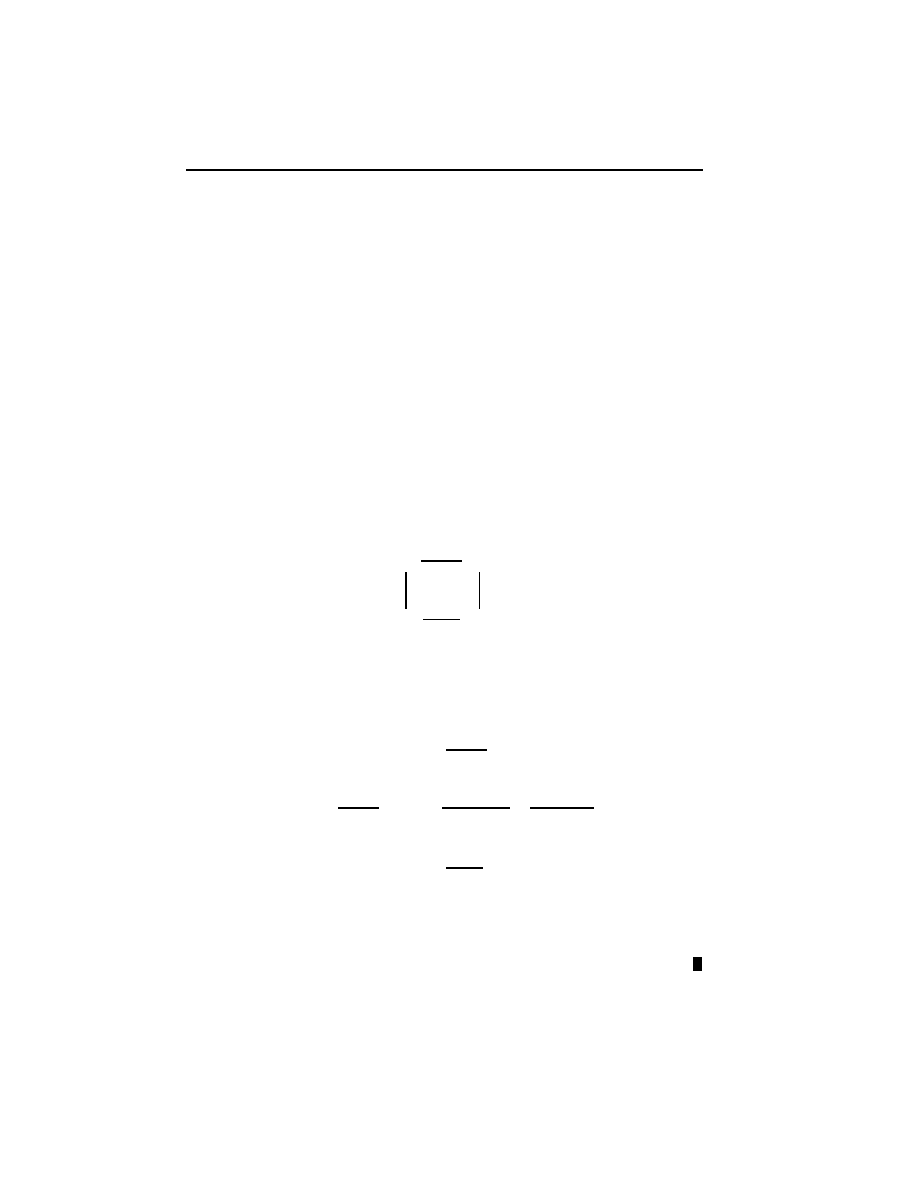
Categories

If a ccc has coproducts, we have X

(Y + Z)

Y ) + (X

Z) and

Exercise 102

. Prove these facts.

Recall that two maps Z

Y and Z

which correspond to each

other under the adjunction are calles each other's

transposes

Exercise 103

. In a ccc, prove that the transpose of a composite Z

;

if ~f is the transpose of f.

Lemma 7.2

In a ccc, given

f : X

let

: Y

be the transpose

Then for each

f : X

and

g : Y

the diagram

commutes.

Proof

. By the exercise, the transposes of both composites are the top and

bottom composites of the following diagram:

This diagram commutes because the right hand \squares" are naturality squares

for ", the lower left hand square commutes because both composites are the

transpose of Y

, and the upper left hand square commutes because both com-

posites are g

7. Cartesian closed categories and the

-calculus

Proposition 7.3

For every ccc

there is a functor

, assigning

(XY )

, and given

g : Y

and

f : X

: Y

is either of

the composites in the lemma.

Exercise 104

. Prove the proposition.

7.2 Typed

-calculus and cartesian closed categories

The -calculus is an extremely primitive formalism about functions. Basically,

we can form functions (by -abstraction) and apply them to arguments that's

all. Here I treat briey the

typed

-calculus.

We start with a set

type symbols

:::

Out of

we make the set of types as follows: every type symbol is a type,

and if T

and T

are types then so is (T

)

We have also

terms

of each type (we label the terms like t:T to indicate that

t is a term of type T):

we may have constants c:T of type T

for every type T we have a denumerable set of variables x

:Tx

:T:::

given a term t:(T

)

) and a term s:T

, there is a term (ts):T

given t:T

and a variable x:T

there is a term x:t:T

)

Terms x:t are said to be formed by -

abstraction

. This procedure binds the

variable x in t. Furthermore we have the usual notion of substitution for free

variables in a term t (types have to match, of course). Terms of form (ts) are

said to be formed by

application

In the -calculus, the only statements we can make are equality statements

about terms. Again, I formulate the rules in terms of theories. First, let us say

that a

language

consists of a set of type symbols and a set of constants, each of

a type generated by the set of type symbols.

equality judgement

is an expression of the form ;

t = s:T (to be read:

\; thinks that s and t are equal terms of type T "), where ; is a nite set of

variables which includes all the variables free in either t or s, and t and s are

terms of type T.

theory

is then a set

of equality judgements which is closed under the

following rules:

i) ;

t = s:T in

implies $

t = s:T in

for every superset $ of ;

ii) FV (t)

t = t:T is in

for every term t:T of the language (again, FV (t) is

the set of free variables of t)

if ;

t = s:T and ;

s = u:T are in

then so is ;

t = u:T

Categories

iii) if t(x

:::x

):T is a term of the language, with free variables x

,:::,x

and ;

= t

:::;

= t

are in

then

;

:::s

] = tt

:::t

]:T

is in

iv) if t and s are terms of type (T

)

), x a variable of type T

which does

not occur in t or s, and ;

(tx) = (sx):T

is in

, then ;

t =

s:(T

)

) is in

v) if s:T

and t:T

are terms and x a variable of type T

, then

FV (s)

FV (t)

((x:s)t) = st=x]:T

is in

Given a language, an interpretation of it into a ccc

starts by choosing objects

S ]] of

for every type symbol S. This then generates objects T ]] for every

type T by the clause

)

]] = T

]]

The interpretation is completed by choosing interpretations

]]

T ]]

for every constant c:T of the language.

Such an interpretation then generates, in much the same way as in chapter 4,

interpretations of all terms. For a nite set ; =

:::x

let's again

write ;]] for the product T

]]

]] (this is only dened modulo a

permutation of the factors of the product, but that will cause us no trouble).

The interpretation of t:T will now be an arrow

FV (t)]]

]]

T ]]

dened as follows:

x]] is the identity on T ]] for every variable x:T

given t]] : FV (t)]]

]]

and s]] : FV (s)]]

]] we let

(ts)]] : FV ((ts))]]

]] be the composite

FV ((ts))]]

]]

;

]]

where

and

are the projections from FV ((ts))]] to FV (t)]] and

FV (s)]], respectively

7. Cartesian closed categories and the

-calculus

given t]] : FV (t)]]

]] and the variable x:T

we let x:t]] : FV (t)

]]

be the transpose of

FV (t)

]]

where, if x occurs free in t so FV (t)

]]

FV (t)]], ~t is

just t]] and if x doesn't occur in t, ~t is t]] composed with the obvious

projection.

We now say that an equality judgement ;

t = s:T is

true

in this interpretation,

if the diagram

FV (t)]]

]]

;]]

T ]]

FV (s)]]

]]

commutes (again,

and

projections).

Lemma 7.4

Let

t(x

:::x

):T

have free variables

and let

be terms.

Let

: FV (tt

:::t

])]]

]]

be the obvious composite of projection and

]]

Then the composition

FV (tt

:::t

])]]

:::n

;

]] = FV (t)]]

]]

T ]]

is the interpretation

:::t

]]]

Exercise 105

. Prove the lemma take your time. This is not immediate].

Theorem 7.5

Let

be a set of equality judgements and

= Cn(S)

be the

least theory containing

. If every judgement of

is true in the interpretation,

so is every judgement in

Proof

. Again, we show that the set of true judgements is a theory, i.e. closed

under the rules in the denition of a theory.

i) and ii) are trivial

iii) follows at once by lemma 7.4

Categories

iv) Since ;

(;

)

and because of the inductive hypothesis, we have

that

FV (s)]]

]]

)

]]

;

]]

((

]]

FV (t)]]

]]

)

]]

commutes. Taking the transposes of both maps, we get the equality we want.

v) According to lemma 7.4, FV (st=x])]]

t=x

]]]

;

]] is

FV (st=x])]]

FV (s)]]

]]

This is the same as
FV (st=x])]]

]]

FV (s)

]]

x:s

]]

;

)

]]

which is

FV ((x:s)t)]]

((

x:s

)

)]]

;

]]

There is also a

completeness theorem

: if a judgement ;

t = s:T is true in all

possible interpretations, then every theory (in a language this judgement is in)

contains it.

The relevant construction is that of a syntactic cartesian closed category

out of a theory, and an interpretation into it which makes exactly true the

judgements in the theory. The curious reader can nd the, somewhat laborious,

treatment in Lambek & Scott's \Higher Order Categorical Logic".

7.3 Representation of primitiverecursive functions in ccc's

with natural numbers object

Dedekind observed, that in Set, the set ! is characterized by the following

property: given any set X, any element x

X and any function X

X, there

is a unique function F : !

X such that F(0) = x and F(x + 1) = f(F(x)).

Lawvere took this up, and proposed this

categorical

property as a denition

(in a more general context) of a \natural numbers object" in a category.

7. Cartesian closed categories and the

-calculus

Denition 7.6

In a category

with terminal object 1, a

natural numbers ob-

ject

is a triple

(0NS)

where

is an object of

and

arrows

, such that for any other such diagram

there is a

unique

map

: N

making

commute.

Of course we think of 0 as the zero element, and of S as the successor map. The

dening property of a natural numbers object enables one to \do recursion",

a weak version of which we show here: we show that every primitive recursive

function can be represented in a ccc with natural numbers object.

Denition 7.7

Let

be a ccc with natural numbers object

(0NS)

. We say

that a number-theoretic function

F :

represented

by an arrow

f :

if for any

-tuple of natural numbers

:::n

, the diagram

:::S

:::

)

commutes.

Recall that the class of

primitive recursive

functions is given by the following

clauses:

The constant zero function ~x:0 :

, the function x:x+ 1 :

and the projections ~x:x

are primitive recursive

The primitive recursive functions are closed under composition: if F

:::F

and G :

are primitiverecursive, then so is G(

:::F

) :

The primitive recursive functions are closed under

denition by primitive

recursion

: if G :

and H :

are primitive recursive,

and F :

is dened by F(0~x) = G(~x) and F(n + 1~x) =

H(nF(n~x)~x) then F is primitive recursive.

Categories

Proposition 7.8

In a ccc

with natural numbers object, every primitive re-

cursive function is representable.

Proof

. I do only the case for denition by primitive recursion. So by inductive

hypothesis we have arrows G and H representing the homonymous functions.

By interpretation of the -calculus, I use -terms: so there is an arrow

~x:G(~x) : 1

(

)

and an arrow

~x:H(n(~x)~x) : N

(

)

(

)

which is the interpretation of a term with free variables :N

(

)

and n:N this

map is the exponential transpose of the map which intuitively sends (n~x) to

(n(~x)~x). Now look at

~x:G

(

)

(

)

(

~x:H

(

)

))

(

)

By the natural numbers object property, there is now a unique map

"F =

: N

(

)

which makes the following diagram commute:

))

~x:G

(

)

(

)

(

~x:H

(

)

))

(

)

One veries that is the identity, and that the composite

(

)

represents F.

Exercise 106

. Make these verications.

That's it!!

Index

abelianization, 5

adjoint functor theorem, 50

adjunction, 45

Alexandro topology, 5

algebras for monad, 54

arrows, 1

associative, 1

atom in Boolean algebra, 16
Boolean algebra, 15

atomic, 16

complete, 15

category, 1

cartesian, 23

cartesian closed, 63

complete, 23

discrete, 13

nitely complete, 23

has binary products, 20

has equalizers, 20

has pullbacks, 20

indiscrete, 13

left exact, 23

lex, 23

locally small, 4

path, 3

quotient, 3

regular, 29

slice, 4

small, 13

ccc, 63

closure operation on poset, 54

cocone for a functor, 25

codomain, 1

coequalizer, 25

coequalizer diagram, 25

coherent logic, 33

colimiting cocone, 25

comonad, 53

comparison functor, 57

complement in a lattice, 15

composition, 1

comultiplication of comonad, 53

cone for a functor, 17

congruence relation, 3

coproduct, 25

coproduct inclusions, 25

coprojections, 25

counit of adjunction, 45

counit of comonad, 53
diagram commutes, 4

diagram of type

, 17

domain, 1

duality principle, 6
embedding, 10

epi, 6

epimorphism, 6

equality judgement in -calculus, 67

equalizer, 18

equalizer diagram, 18

equivalence of categories, 15

equivalent categories, 15

equivalent formulas, 39

evaluation in ccc, 64

exponents in ccc, 64
frame, 39

free group, 3

free monoid, 46

functor, 2

contravariant, 5

covariant, 5

faithful, 7

forgetful, 2

free, 3

full, 7

Hom, 5

INDEX

preserving a property, 7

preserving limits, 23

reecting a property, 7

representable, 4

generator, 63

group monad, 56

groupoid, 14

Grp, 2

Grph, 2
homotopy, 3
identity arrow, 1

image of a map, 32

index category of diagram, 17

initial object, 7

inverse of an arrow, 7

isomorphic objects, 8

isomorphism, 7
kernel pair of a map, 29

Kleisli category of monad, 60
labelled sequent, 35

-abstraction, 67

-calculus, 67

lattice, 15

distributive, 15

left adjoint functor, 43

lifting monad, 57

limiting cone, 17
MacLane's pentagon, 23

map, 1

monad, 53

monadic, 57

mono, 6

monoid, 1

monomorphism, 6

morphism, 1

multiplication of monad, 53
natural

bijection, 10

natural numbers object, 71

natural transformation, 9
objects, 1
Pos, 2

preorder, 1

primitive recursive function, 71

product category, 2

product cone, 18

product in category, 18

projections, 18

pseudo inverse of a functor, 15

pullback along a map, 32

pullback diagram, 20

pushout, 26
regular epi, 27

regular mono, 22

retraction, 7

right adjoint functor, 43

Rng, 2
section, 7

solution set condition (ssc), 50

specialization ordering, 6

split epi, 7

split mono, 7

stable under pullback, 30

subobject, 31
terminal object, 7

theory in -calculus, 67

theory in coherent logic, 35

Top, 2

transpose of map, 43

triangle equalities, 45
unit of adjunction, 45

unit of monad, 53
vertex of a cone, 17

INDEX

Yoneda embedding, 10

Yoneda lemma, 10