Microphone Techniques for Spatial Sound

Jussi Pekonen

TKK Helsinki University of Technology

Department of Signal Processing and Acoustics

[e-mail]

Abstract

With only one microphone neither the spatial impression of a room nor the position
of the sound source in the room can be captured for precise reproduction. Therefore,
techniques utilizing multiple microphones for producing the spatial attributes of a
sound in a room have been suggested. The techniques can be categorized with respect
to the number of required microphones or the operation principle of the microphone
set. In addition, different reproduction techniques may require different microphone
technique, thus forming a third classification rule for the microphone techniques. In
this paper, an overview of existing microphone techniques applicable for the spatial
sound purposes is given concentrating on the second classification approach with
the other classification rules in mind.

1. INTRODUCTION

Capturing the sound generated by a sound source, being either a single source or a set of
sources placed arbitrarily in a space, using only one microphone would not provide suffi-
cient information about the location of the source. By increasing the distance between the
source and the microphone, coloration of the room could provide some information about
the space where the source is located. However, since the signal captured by a single
microphone is monophonic, this information is useless for reproduction of the source lo-
cations. Therefore, alternative techniques for capturing the locations of the sound sources
must be used. In this paper, various microphone techniques are reviewed.

The next question is how to classify the existing techniques. An obvious choice would

be to categorize the techniques based on the number of required microphones. Alter-
natively, some microphone techniques have certain common attributes of the operation
principle, and thus they can be classified according to these operation principles. Thirdly,
different applications may require a specific microphone technique for the sound captur-
ing, and this can be understood as a third classification rule. In this paper, the second
classification approach is used with the other classification rules applied when required.

Before any techniques can be presented, the reader must be familiar with the concept

of microphone polar pattern. The polar pattern of a microphone informs how sensitive
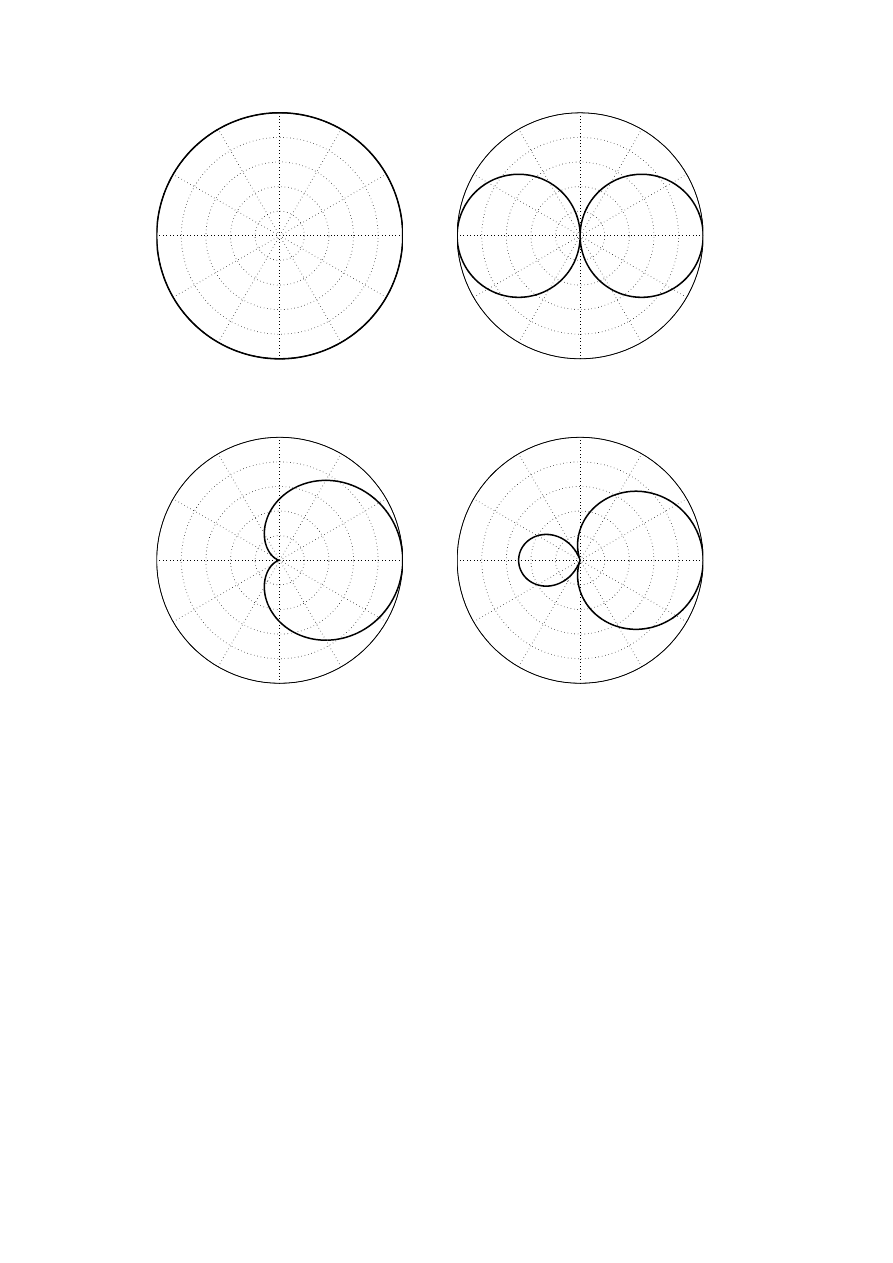
the microphone is to different directions. In Figure 1, the four most commonly used polar
patterns are illustrated, and the direction-dependent sensitivity can be expressed with

f (θ) = p

0

+ p

1

cos(θ),

(1)

1

0.2

0.4

0.6

0.8

1

0

30

60

90

120

150

180

210

240

270

300

330

(a)

0.2

0.4

0.6

0.8

1

0

30

60

90

120

150

180

210

240

270

300

330

(b)

0.2

0.4

0.6

0.8

1

0

30

60

90

120

150

180

210

240

270

300

330

(c)

0.2

0.4

0.6

0.8

1

0

30

60

90

120

150

180

210

240

270

300

330

(d)

Figure 1: The most common polar patterns of a microphone: (a) Omnidirectional, (b)
Dipole, (c) Cardioid, and (d) Hypercardioid, adapted from [1]. The polar patterns are
given with linear amplitude scale.

where p

0

and p

1

are pattern-dependent constants and θ is the angle of the direction. An

omnidirectional microphone, obtained with p

0

= 1 and p

1

= 0, captures sound from all

directions with equal sensitivity. A dipole microphone, also called as a figure-of-eight
or bidirectional microphone, expressed by p

0

= 0 and p

1

= 1, captures sound from

front and back of the microphone with opposite phases, and it does not capture sound
from the sides of the microphone. A cardioid microphone, obtained with p

0

= 0.5 and

p

1

= 0.5, captures sound mainly from the frontal semisphere, and no sound from the back

of the microphone. A hypercardioid microphone, expressed by p

0

= 0.25 and p

1

= 0.75,

captures sound from a beam in the frontal semisphere, and with a lower sensitivity from
a very narrow beam from the back of the microphone. The reader should note, that these
polar patterns are idealized, and practical microphones do not have exactly these polar
patterns, and especially at high frequencies the polar patterns tend to get narrower [1].

The remainder of this paper concentrates on explaining existing microphone tech-

niques applicable for spatial sound capturing. In Section 2, traditional stereophonic

2

microphone techniques are first presented, and binaural microphone techniques are dis-
cussed in Section 3. Section 4 presents techniques utilizing several microphones used
mainly in recording industry. In Section 5, the use of microphone arrays is discussed, and
other multimicrophone techniques used mainly in spatial sound research are presented in
Section 6. Finally, Section 7 concludes the paper.

2. TRADITIONAL STEREO MICROPHONE TECHNIQUES

In order to understand the philosophy behind the microphone techniques utilizing sev-
eral microphones, the reader should be familiar with the techniques traditionally used
for stereophonic recordings. Some of the techniques utilizing multiple microphones
can be understood as direct extensions to these stereophonic techniques, and since the
stereophony was the first step towards multichannel sound reproduction, the techniques
described here should also be considered as microphone techniques applicable for spa-
tial sound capturing. The traditional stereo microphone techniques can be classified into
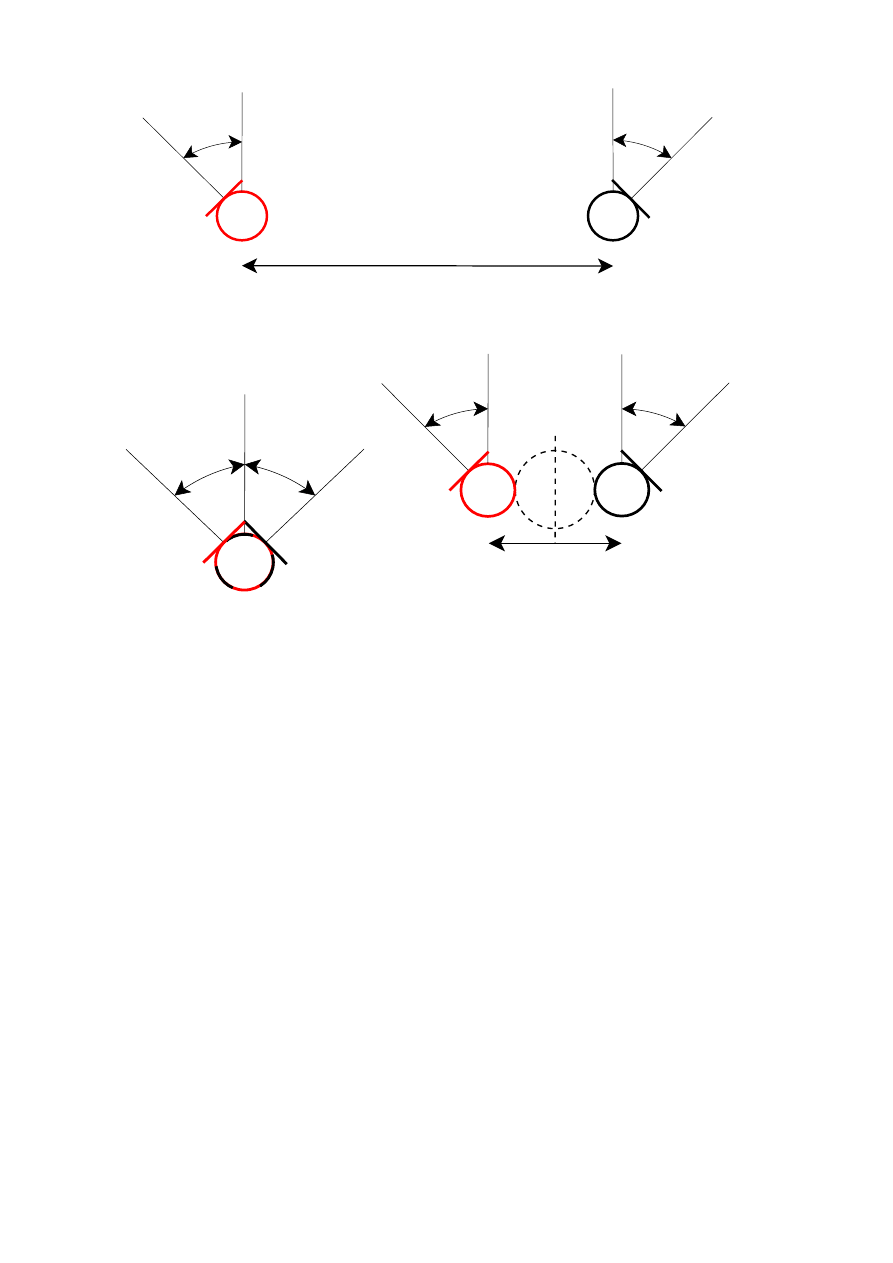
three categories based on the microphone setup [2, 3, 4, 5], and generic setups for these
three categories are given in Figure 2. In Section 2.1, the setup parameters of existing
techniques of spaced microphone pairs are presented. The setup parameters of some pop-
ular coincident microphone pair techniques are discussed in Section 2.2. In Section 2.3,
the setup parameters of some popular techniques of near coincident microphone pairs are
presented.

2.1. Spaced Microphone Pairs

In a spaced microphone pair the microphones are placed apart from each other to point
to the direction of the sound source. This technique is usually used in the recording of a
large instrument or a musical ensemble. Now, the directional information of the sound is
encoded in differences in both time of arrival and level of the sound signal. However, one
should note that the spacing causes phase differences between the microphones, which
then may cause amplification and attenuation of some frequencies [2, 3].

The most common spaced microphone pair approach is to use omnidirectional micro-

phones which are placed so that the distance d between them is from 20 centimeters to
couple of meters. The microphones are physically pointing towards the sound source,
θ

1

= θ

2

= 0

◦

, and the distance to the sound source range from one third to the half of the

distance between microphones. This setup is commonly called an AB pair. Obviously,
one could use any combination of polar patterns, position the microphones to have a de-
sired angle between them, as well as utilize baffles to modify the directional patterns of
the microphones. Some discussion about the effects of the microphone polar patterns and
use of baffles can be found in [3].

2.2. Coincident Microphone Pairs

Name coincident microphone pair is used for a setup where two microphones are placed
in an angle with respect to each other so that their capsules are almost located at the same
point. Due to the finite size of a microphone, the capsules can not be positioned exactly
at the same point. In practice, the microphones are usually placed on top of or next to
each other [3]. With this positioning, the direction of arrival is encoded only by the level
difference and the issue of phase difference between the microphones is not present [2, 3].

3

d

θ

1

θ

2

(a)

θ

1

θ

2

(b)

d

θ

1

θ

2

(c)

Figure 2: Microphone setup in (a) a spaced microphone pair, (b) a coincident microphone
pair, and (c) a near coincident microphone pair.

Various coincident microphone techniques exist, and the most commonly used are

XY, Blumlein and MS pairs. In an XY pair, two cardioid or hypercardioid microphones
are positioned symmetrically to face the sound source in an angle of 60° to 120°, i.e.,
θ

1

= θ

2

= 30

◦

− 60

◦

, between the microphones [3, 5]. Typically the angle is 90°. In a

Blumlein pair, the microphone positioning is similar to XY pair but the polar patterns
of the microphones are dipoles [6]. In an MS pair, an omnidirectional or a cardioid
microphone is positioned towards the sound source, i.e., θ

2

= 0

◦

, and a dipole microphone

is positioned in angle of θ

1

= 90

◦

with respect to the forward directing microphone so

that the positive beam of the dipole microphone points to the left [7].

2.3. Near Coincident Microphone Pairs

A near coincident microphone pair can be understood as compromise between a spaced
pair and a coincident pair as the microphones are positioned close enough to be practically
coincident at low frequencies yet far enough to encode the direction of arrival with a time
lag between the microphones [2, 3]. Yet again, the microphones usually have an angle be-
tween them. In some near coincident microphone pairs there is an absorbing baffle or ball
placed in between the microphones [8]. In addition, since the distance between the mi-
crophones is usually approximately the distance between human ears, the near coincident
approach can be understood as a rough approximation of the human hearing [3].

4

Since the near coincident microphone pairs try to simulate the human head and ears,

several techniques have been proposed. One popular technique is so called ORTF, devel-
oped by the French National Broadcasting Organization (Office de Radiodiffusion Tèlèvi-
sion Française), where two cardioid microphones are placed d = 17 centimeters apart in
an angle of 110°, i.e., θ

1

= θ

2

= 55

◦

. Another popular near coincident technique is NOS,

a technique developed by the Dutch Broadcasting Organization (Nederlandse Omroep
Stichting), where the angle between two cardioid microphones is 90°, i.e., θ

1

= θ

2

= 45

◦

and they are positioned d = 20 centimeters apart [3, 5].

An example of a near coincident pair utilizing an absorbing material between the mi-

crophones is a technique called Jecklin disk, where two omnidirectional microphones are
positioned d = 16.5 centimeters apart physically pointing towards the center of a circu-
lar baffle of diameter of 30 centimeters, i.e., θ

1

= θ

2

= −90

◦

. The baffle is positioned

perpendicular to the sound source [9]. Alternatively, one popular near coincident micro-
phone technique called a Blumlein shuffler utilizes a special postprocessing circuitry to
process the captured sound. In this approach, two usually omnidirectional microphones
are positioned d = 20 centimeters apart, and the signals captured by the microphones are
processed with a shuffler that creates the desired stereo image [10].

3. BINAURAL MICROPHONE TECHNIQUES

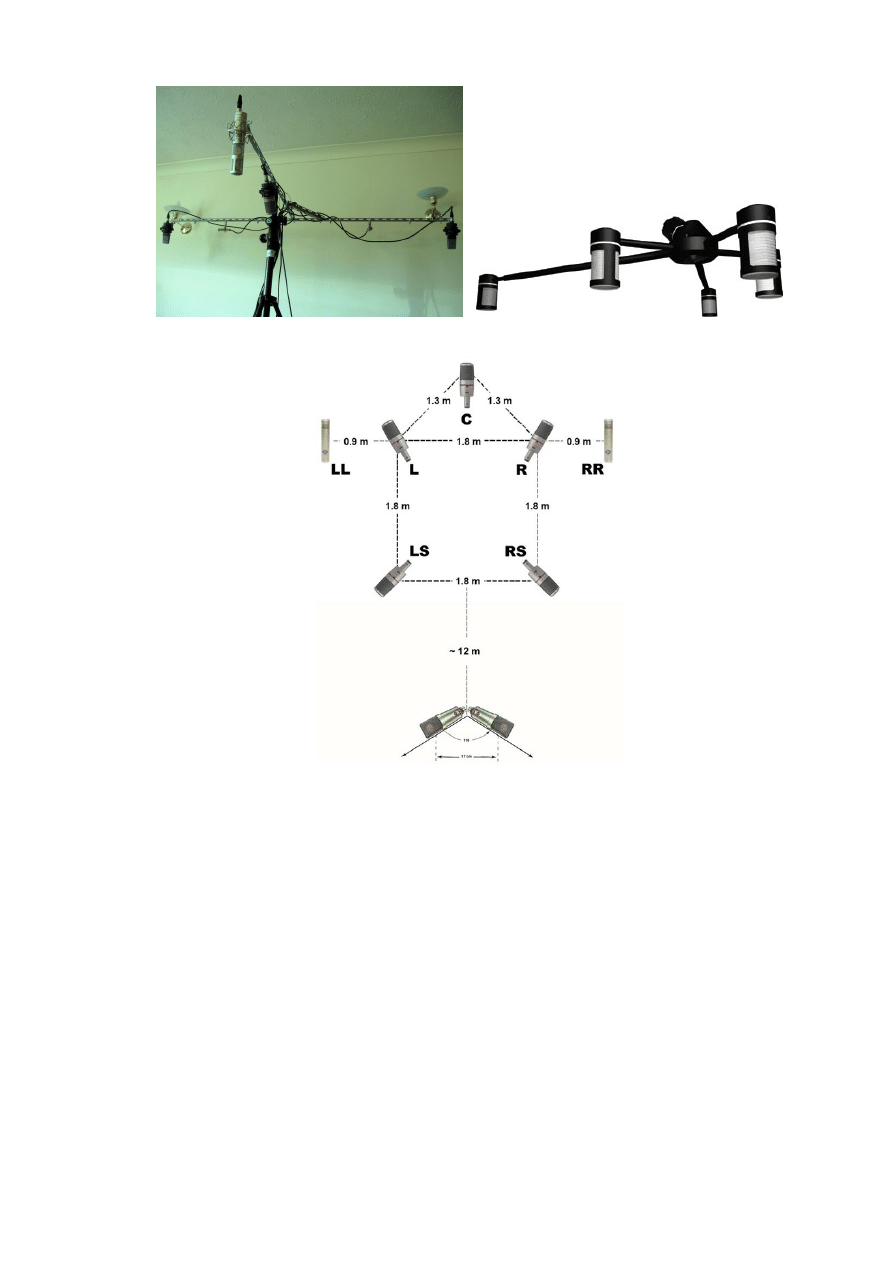
In binaural microphone techniques two microphones are positioned either at the ear canal
entrance of a human being or inside the ear canals of an artificial head, also called as a
dummy head, which simulates the effects applied to the sound by the human head. In
Figure 3, photographs of a dummy head and a miniature microphone positioned at the ear
canal entrance are given.

The binaural microphone techniques produce signals that correspond to the sound en-

tering the ears. Therefore, these signals can be used mainly for headphone listening as
they convey practically the same spatial information as if the listener ears would be posi-
tioned exactly at the same positions as the microphones [11, 12, 13]. If the signals were
listened to with loudspeakers, the produced sound is then colored by the listening envi-
ronment, thus ruining the attributes informing human beings of the spatial impressions,
as noted already in the earliest experiments of binaural sound transmission [11, 12, 13].

In addition, when performing binaural recordings one should note that the subject

whose head is used in the recording affects the produced microphone signals. The shape
and the size of the subject head and pinnae and the clothing of the subject color the in-
coming sound so that the recorded signals vary slightly from a listener to another. This
property of the effects of the head applied to the binaural sound, head related transfer
function (HRTF), is in special interest in the research of the spatial hearing [16].

As mentioned above, the binaural microphone techniques are in great interest in spa-

tial hearing research, as it concentrates on understanding the signal analysis performed
by the human brain in order to achieve the localization of the sound source. In recording
industry the binaural recordings have not gained popularity due to the problem of indi-
vidual HRTFs, but some manufacturers provide microphones sets for the purpose, see for
example [15].

5

(a)

(b)

Figure 3: Binaural microphone setups: (a) A dummy head, adopted from [14], and (b)
Ear canal microphones, adopted from [15].

4. TECHNIQUES UTILIZING MULTIPLE MICROPHONES

An obvious step towards multichannel microphone techniques is to extend the techniques
utilizing two microphones with additional microphones positioned in a desired setup. For
instance, one could place an additional microphone in between an AB pair, or to use
two AB pairs with different setups. Alternatively, one could combine different stereo
microphone setups, like an ORTF pair and an AB pair, or to use two MS pairs with one
pair facing towards and the other from the sound source [17, 3, 1, 18].

However, specific surround microphone techniques have been suggested and many of

them are available as a preconstructed setup. One of such techniques is so called Decca
tree, where three omnidirectional microphones are positioned in a tree-like shape so that
one microphone is physically pointing towards the sound source and the other two are
physically pointing to the sides positioned 1.5 meters behind the front facing microphone.
The distance between the side facing microphones is typically 2 meters [19]. Another
technique is so called Spider Microphone Array, where five microphones are positioned
at the ends of star shaped arms facing outwards from the center. The polar patterns of the
microphones can vary, and some manufacturers provide systems with electrically control-
lable microphone polar patterns [20]. A Fukada tree setup is quite similar to the Decca
tree, but it contains seven cardioid microphones positioned so that three microphones
form a triangle in a similar manner as in the Decca Tree. Two microphones are positioned
the left and right side of the triangle, and the two remaining microphones are positioned
to physically point to the back of the setup [21]. The setups of a Decca tree, Spider Mi-
crophone Array, and an extended Fukada tree utilizing an additional ORTF pair behind
the original tree are illustrated in Figure 4.

6

(a)

(b)

(c)

Figure 4: The setups of (a) Decca tree, adopted from [22], (b) Spider Microphone Array,
adopted from [20], and (c) an extended Fukada tree, adopted from [23].

The multimicrophone techniques described above are mainly used in the recording in-

dustry as they produce a desired coloration to the captured sound. However, in spatial
audio research the coloration of the sound is often not desirable, and therefore these tech-
niques are rarely used. Techniques applicable for research purposes are discussed in the
remainder of this paper.

5. MICROPHONE ARRAYS

In the microphone array techniques the microphones are positioned in a rather dense grid
in order to capture the sound field in the space very precisely [24]. Now, the direction of
arrival is encoded mainly in the time lag between the microphones. Yet, some directional
information is conveyed with the level differences. The microphone grids can be in theory

7

of any geometry, but in practice two grid geometries are used. In Section 5.1, the use of
linear microphone arrays are discussed. Section 5.2 presents another approach where the
microphones are positioned on the surface of a sphere.

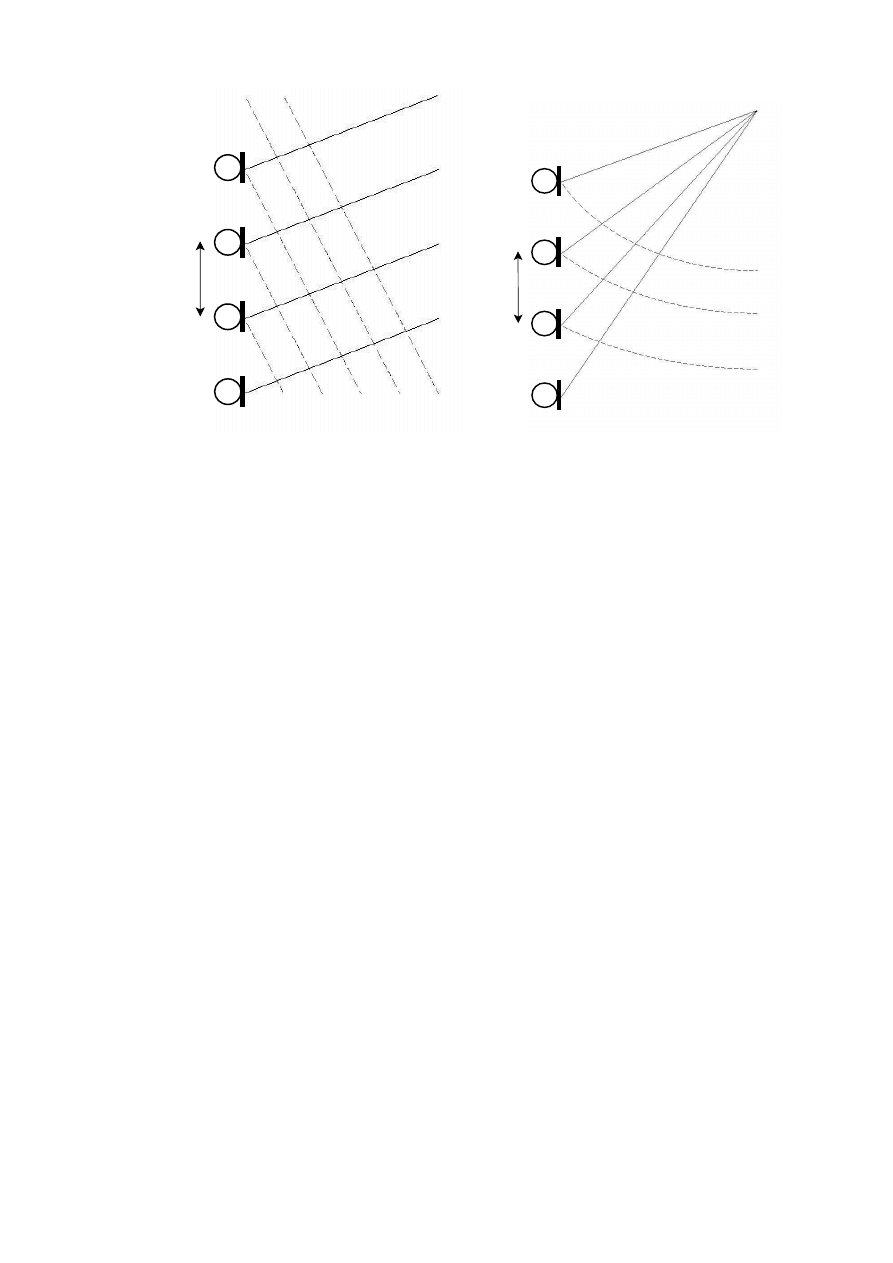
5.1. Linear Arrays

In a linear microphone array usually omnidirectional microphones are positioned in a lin-
ear grid, either in a line or a plane, and they are physically pointing towards the sound
source. This approach can be interpreted as a linear extension to an AB pair, see Sec-
tion 2.1. Usually, the distance between two adjacent microphones in the grid is con-
stant, thus making the analysis of the direction of arrival much easier. However, since in
practical applications a large array can not be utilized, smaller arrays with a nonuniform
microphone spacing are also used [25].

Now, mainly the difference in the time of arrival between two microphones conveys

the direction of sound source. The sound pressure of a plane wave at point r ∈ R

3

at time

instant t, expressed by [26]

p(r, t) = p

0

e

i(k·(r−r

0

)−ωt)

,

(2)

where k is the three dimensional wave number and ω is the frequency of the wave, states
that the amplitude of the sound pressure has no dependency on the distance to the source,
i.e., ||r − r

0

||, so the spatial information is conveyed only by the time difference between

the signals captured by the microphones. But when the sound source is close to the
array, the captured wavefront is spherical, pressure of which at point r at time instant t is
expressed by [26]

p(r, t) =

p

0

||r − r

0

||

e

i(k·(r−r

0

)−ωt)

,

(3)

indicating a dependency between the pressure amplitude and the distance to the source.
Therefore the microphone signals have some slight level differences too [27, 28]. These
aspects are illustrated in Figure 5 for both plane and spherical wave cases. The illustra-
tions show the cases only for a line array, but since they can be interpreted to be taken
from any line on an array plane containing microphones they are general illustrations of
the sound wave capturing of any linear array.

With plane waves, the direction of arrival can be obtained by analyzing the differences

in time of arrival between adjacent microphones. The time lags depend on the distance be-
tween the microphones, d

i,i+1

, as for larger distances the lag being larger than for smaller

distances. For spherical waves, the distance between the array and the sound source and
the incident angle can be obtained by analyzing the level and the time lag differences
between the microphones. The distance and the incident angle are encoded in both level
and time lag differences, so the analysis must take both aspects into account [27, 28].

One should note, that in a linear microphone array the time differences captured by

the microphones apply for the sides of the normal of the array if the microphones are om-
nidirectional [27, 28]. Therefore, if the direction of arrival analysis is performed blindly
without knowledge about the setup, the results can be from any side of the normal of
the array. For instance, if the recording is performed in a reverberant environment, the
reflections are then analyzed to be arrived from the space in front of a plane array. This
produces issues in reproduction if a loudspeaker array matching the microphone array
setup is used, since the reproduced sound includes unnatural reverberation.

Since the direction of the arrival is conveyed by the difference of time of arrival to the

microphones, one can construct a highly directive microphone by applying appropriate

8

.

.

.

.

.

.

i

− 1

i

i + 1

i + 2

d

i,i+1

(a)

.

.

.

.

.

.

i

− 1

i

i + 1

i + 2

d

i,i+1

(b)

Figure 5: (a) A plane wave and (b) a spherical wave arriving to a linear microphone array.

delays to the microphone signal. By varying the delays, the direction to which the con-
struction is most sensitive can be steered. Alternatively, a highly directive microphone can
be obtained by applying different gains for the microphone signals of the array [27, 28].
The research interested in this sensitivity steering topic, beamforming, can be utilized in
many applications, ranging from teleconferencing to sound source localization. Yet, the
same topic is found also in other fields of engineering, as for instance antenna arrays can
be interpreted to be equivalent to microphone arrays.

5.2. Spherical Arrays

The problem of bidirectional localization in linear microphone arrays can be solved by
positioning the microphones on a surface of a sphere so that they physically point out-
wards from the circle center. This approach is based on Helmholtz-Kirchhoff theorem
which states that a sound field both inside and outside of a closed surface is uniquely de-
termined when the sound pressure and the particle velocity are known on the surface and
the sphere contains no sources nor obstacles [26]. In order to simplify this note, the mi-
crophones are usually placed on a surface of a rigid sphere, thus relieving the requirement
to capture the particle velocity [29]. Therefore, omnidirectional microphones are usually
used. However, due to the finite size of microphones, the pressure on the sphere surface
is only approximated with a finite number of microphones, which are usually distributed
uniformly on the surface, again to make the analysis more easier.

Now, the microphones capture the sound field entering the sphere, and the direction

of arrival is then determined by the microphones capturing the sound first. In practice,
since the microphones can not be positioned infinitely close to each other, the direction of
arrival must be interpolated from the neighboring microphone signals of the microphone
capturing the sound first. Yet again, capturing of spherical waves produce also slight level

9

(a)

(b)

Figure 6: (a) A plane wave and (b) a spherical wave arriving to a spherical microphone
array.

differences between the microphones [29]. In Figure 6, the cases of capturing a plane and
a spherical wave with a spherical microphone array is illustrated. Again, the illustrations
are in two dimensions, presenting any cross-section of the sphere.

The differences of time of arrival between microphones depend on the density of the

microphones on the surface. When the microphone density is large, the time lags are
smaller, and vice versa. The same applies for the level differences in case of spherical
sound wavefront, as the spherical wave attenuates less when the distance between micro-
phones is smaller than when the distance is large [29].

Yet again, the spherical microphone arrays can be utilized in beamforming, and there

are applications where spherical arrays are preferred over plane arrays [29]. In those
applications, a small size of the sensor array is desirable, and a spherical array is then
more practical than a plane array.

However, whereas an almost ideal plane array is quite easy to construct, a spherical

array has some issues on the construction accuracy. If the microphones can not be in-
stalled on a perfect sphere or the microphone mountings can be positioned exactly on the
sphere surface, the array has some defects from sound diffraction. However, by applying
appropriate signal processing, the diffraction can be reduced and an ideal spherical array
can be approximated at low frequencies [30].

6. OTHER MICROPHONE TECHNIQUES FOR SPATIAL SOUND

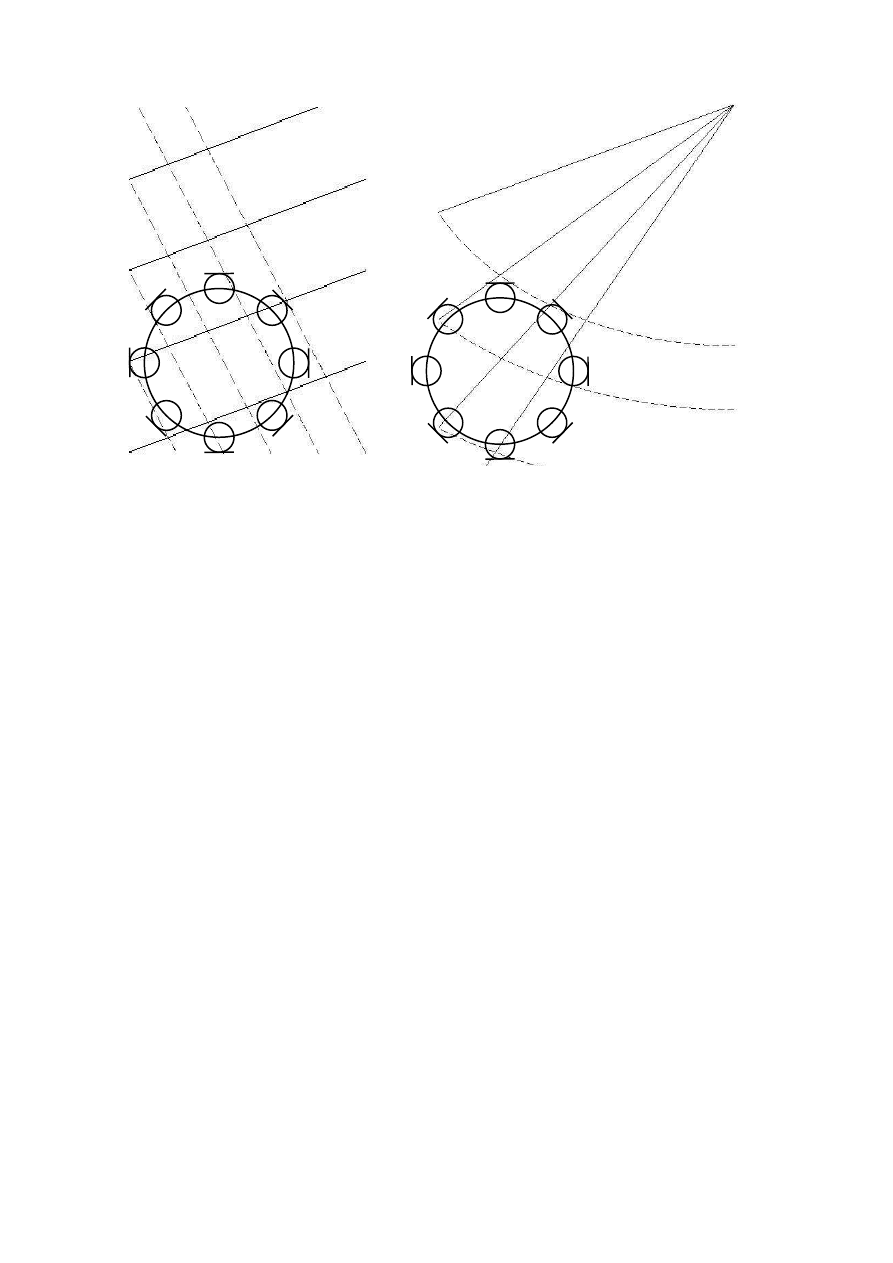
A popular microphone technique for spatial sound capturing is a so called B-format tech-
nique, which is used for instance in Ambisonics reproduction technique. A B-format
signal consists of four microphone signals, a pressure signal, a front-to-back signal, a
side-to-side signal, and a up-to-down signal [31, 32].

10

The B-format signals are obtained by utilizing an omnidirectional microphone for the

pressure signal (W), and bidirectional microphones pointing forward for the front-to-back
directional information signal (X), leftward for the side-to-side directional information
signal (Y), and upward for the up-to-down directional information signal (Z). Alterna-
tively, the B-format signal can be obtained with a so called SoundField microphone which
consists of four subcardioid, i.e., unidirectional microphones, with p

0

= 0.7 and p

1

= 0.7

in (1), positioned in the sides of a tetrahedron [31, 32, 33, 34]. By mixing the signals
obtained by the SoundField microphone using

W =

1

2

(A + B + C + D),

(4)

X =

1

2

(−A + B + C − D),

(5)

Y =

1

2

A + B − C − D,

(6)

Z =

1

2

(−A + B − C + D),

(7)

where A, B, C and D are the so called A-format signals obtained by the SoundField
microphone capsules pointing left back down, left front up, right front down and right
back up, respectively, the B-format signal can be obtained [32]. Both microphone setups
are illustrated in Figure 7.

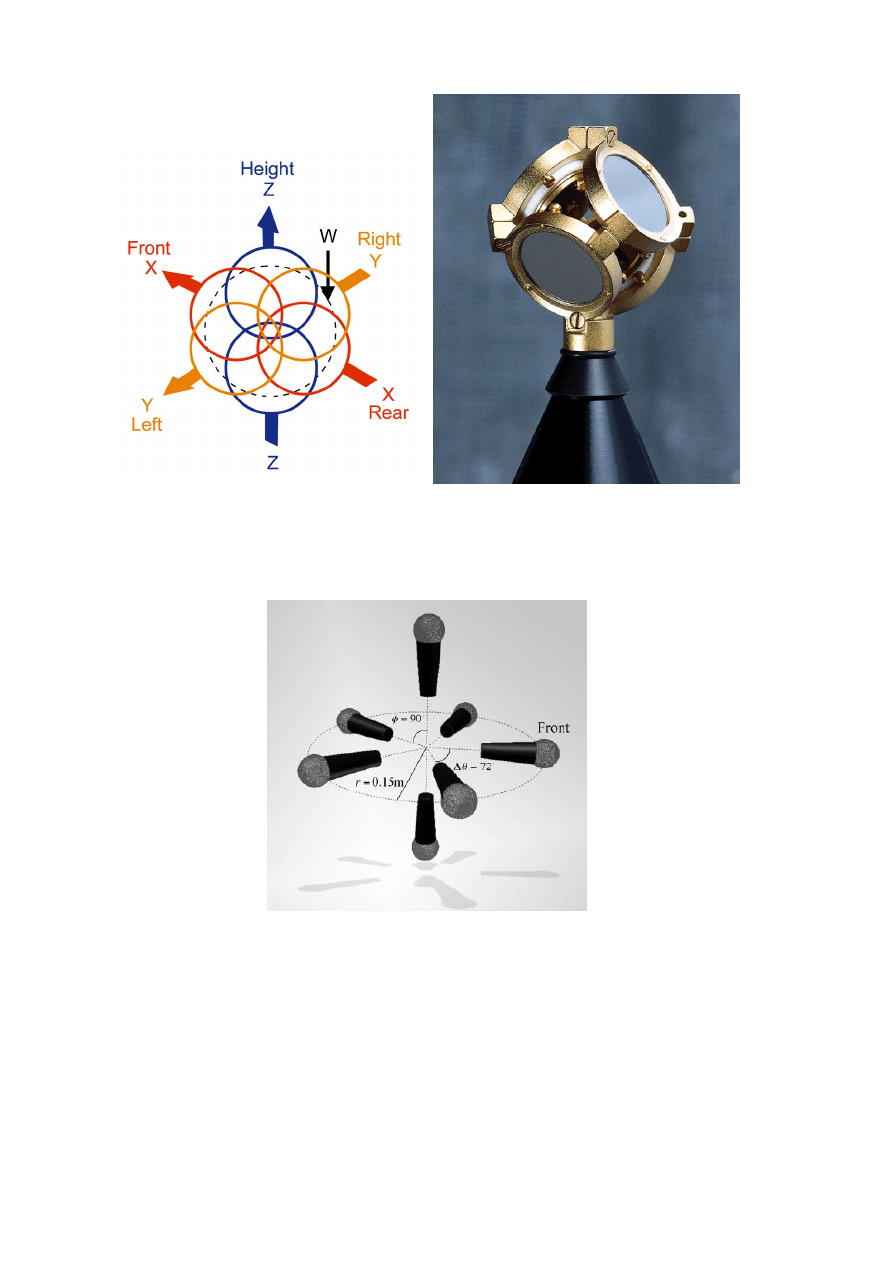
An alternative multimicrophone technique applicable for spatial sound capturing was

introduced by Johnston and Lam [35]. This technique consists of seven microphone, of
which five cardioid microphones are positioned equally spaced on the horizontal plane in
a circle pointing outwards from the center. The two remaining microphones are highly
directive, e.g., shotgun microphones, and they are positioned in the vertical axis passing
through the center of the circle formed by the cardioid microphones. The diameter of the
circle is 31 centimeters [36]. The Johnston setup is illustrated in Figure 8.

7. CONCLUSIONS

Depending on the spatial audio application, the microphone technique used to capture
the sound may play a quite important role. In commercial multichannel audio recordings,
techniques which produce a desired sound coloration may be more useful than a technique
that tries to capture the sound field as naturally as possible. In spatial audio research, the
desire is the opposite.

In recording industry, traditional stereo microphone techniques are widely used. How-

ever, since today more and more multichannel recordings are made, techniques special-
ized to capture multichannel audio have also been developed. In many cases these tech-
niques are just extensions to the traditional stereo techniques, but in some cases the tech-
nique is somewhat unique.

In spatial audio research, the techniques successfully used in recording industry have

usually not been found interesting. Instead, different techniques for capturing the cues of
the direction of arrival and the location of the sound source have been developed. The
approaches may include several microphones, as in microphone arrays, or just a couple
of special microphone positioned at the entrances of the ear canals of a human being.
Nevertheless, these approaches differ greatly from the techniques used in commercial
audio recordings.

11

(a)

(b)

Figure 7: B-format microphone technique as (a) a direct microphone setup and (b) a
soundfield microphone, adopted from [37].

Figure 8: Johnston microphone setup, adopted from [38].

In this paper, both of these aspects on spatial audio capturing were discussed on

presenting different microphone techniques for different purposes. First, the traditional
stereo microphone techniques were presented, as they founded the basis for further devel-
opment of multimicrophone techniques. Next, binaural techniques and multimicrophone
techniques used in recording industry were both briefly discussed. Both plane and spheri-
cal microphone arrays were also presented, and finally some other microphone techniques
applicable for spatial sound were discussed.

12

8. REFERENCES

[1] J. Eargle, The Microphone Book. St. Louis, Missouri, USA: Focal Press, 2001.

[2] R. T. Shafer, “A listening comparison of far-field microphone techniques,” in Pro-

ceedings of the 69th AES Convention

, (Los Angeles, California, USA), May 1981.

[3] R. Streicher and W. Dooley, “Basic stereo microphone perspective — a review,” in

Proceedings of the 2nd AES International Conference

, (Anaheim, California, USA),

April 1984.

[4] S. Pizzi, “Stereo microphone techniques for broadcast,” in Proceedings of the 76th

AES Convention

, (New York, New York, USA), October 1984.

[5] S. P. Lipshitz, “Stereo microphone techniques: Are the purists wrong?,” in Proceed-

ings of the 78th AES Convention

, (Anaheim, California, USA), May 1985.

[6] A. D. Blumlein, “British patent specification 394,325,” Journal of the Audio Engi-

neering Society

, vol. 6, pp. 91–98, 130, April 1958.

[7] W. L. Dooley and R. D. Streicher, “M-S stereo: A powerful technique for working

in stereo,” in Proceedings of the 69th AES Convention, (Los Angeles, California,
USA), May 1981.

[8] E. R. Madsen, “The application of velocity microphone to stereophonic recording,”

Journal of the Audio Engineering Society

, vol. 5, pp. 79–85, April 1957.

[9] J. Jecklin, “A different way to record classical music,” Journal of the Audio Engi-

neering Society

, vol. 29, pp. 329–332, May 1981.

[10] M. A. Gerzon, “Applications of blumlein shuffling to stereo microphone tech-

niques,” in Proceedings of the 93rd AES Convention, (New York, New York, USA),
October 1992.

[11] H. T. Sherman, “Binaural sound reproduction at home,” Journal of the Audio Engi-

neering Society

, vol. 1, no. 1, pp. 142–145, 1953.

[12] B. B. Bauer, “Some techniques toward better stereophonic perspective,” IEEE Trans-

actions on Audio

, vol. 11, pp. 88–92, May 1961.

[13] R. Kürer, G. Plenge, and H. Wilkens, “Correct spatial sound perception rendered by

a special 2-channel recording method,” in Proceedings of the 37th AES Convention,
(New York, New York, USA), October 1969.

[14] Georg

Neumann

GmbH,

“KU-100

dummy

head.”

http://www.

neumann.com/?lang=en&id=current_microphones&cid=ku100_

description

. Checked April 30, 2008.

[15] The

Sound

Professionals,

“SP-TFB-2

ear

canal

microphones.”

http:

//www.soundprofessionals.com/cgi-bin/gold/item/SP-TFB-2

.

Checked April 30, 2008.

[16] J. Blauert, Spatial Hearing — The Psychophysics of Human Sound Localization.

Cambridge, Massachusetts, USA: The MIT Press, 1999.

13

[17] J. M. Woram, “Experiments in four channel recording techniques,” in Proceedings

of the 39th AES Convention

, (New York, New York, USA), October 1970.

[18] M.-J. Meindl, U. Vette, and T. Görne, “Investigations of the effect of surround mi-

crophone setup on room perception,” in Proceedings of the 28th AES International
Conference

, (Piteå, Sweden), pp. 295–304, July 2006.

[19] T. Hiekkanen, T. Lempiäinen, M. Mattila, V. Veijanen, and V. Pulkki, “Reproduction

of virtual reality with multichannel microphone techniques,” in Proceedings of the
122nd AES Convention

, (Vienna, Austria), May 2007.

[20] Sound Performance Lab, “Atmos 5.1 surround miking system.”

http://www.

spl-usa.com./Atmos/in_detail.html

. Checked April 30, 2008.

[21] A. Fukada, “A challenge in multichannel music recording,” in Proceedings of the

19th AES International Conference on Surround Sound

, (Schloss Elmau, Germany),

June 2001.

[22] Dr

Jekyl

Mobile

Recordings,

“Recording

equipment.”

http://www.

dr-jekyl-mobile-recording.co.uk/equipment.html

.

Checked

April 30, 2008.

[23] AES Polish Student Section, “Nagranie 5.1 chóru politechniki gda´nskiej.”

http:

//sound.eti.pg.gda.pl/AES/content/view/50/54/lang,en/

.

Checked April 30, 2008.

[24] A. J. Berkhout, D. de Vries, and J. J. Sonke, “Array technology for acoustic wave

field analysis in enclosures,” Journal of the Acoustical Society of America, vol. 102,
pp. 2757–2770, November 1997.

[25] H. Teutsch, S. Spors, W. Herbordt, W. Kellermann, and R. Rabenstein, “An inte-

grated real-time system for immersive audio applications,” in Proceedings of IEEE
Workshop on Applications of Signal Processing to Audio and Acoustics

, (New Paltz,

New York, USA), pp. 67–70, October 2003.

[26] W. C. Elmore and M. A. Heald, Physics of Waves. Mineola, New York, USA: Dover

Publications Inc., 1961.

[27] G. W. Elko, “Superdirectional microphone arrays,” in Acoustic Signal Processing for

Telecommunication

(S. L. Gay and J. Benesty, eds.), ch. 10, pp. 181–237, Norwell,

Massachusetts, USA: Kluwer Academic Publishers, 2000.

[28] G. W. Elko, “Differential microphone arrays,” in Audio Signal Processing for Next-

Generation Multimedia Communication Systems

(Y. Huang and J. Benesty, eds.),

ch. 2, pp. 11–65, Norwell, Massachusetts, USA: Kluwer Academic Publishers,
2004.

[29] J. Meyer and G. W. Elko, “Spherical microphone arrays for 3D sound recording,” in

Audio Signal Processing for Next-Generation Multimedia Communication Systems
(Y. Huang and J. Benesty, eds.), ch. 3, pp. 67–89, Norwell, Massachusetts, USA:
Kluwer Academic Publishers, 2004.

14

[30] P. Gillett, M. Johnson, and J. Carneal, “Performance benefits of spherical diffracting

arrays versus free field arrays,” in Proceedings of IEEE International Conference on
Acoustics, Speech, and Signal Processing

, (Las Vegas, Nevada, USA), pp. 5264–

6267, April 2008.

[31] M. A. Gerzon, “The design of precisely coincident microphone arrays for stereo and

surround sound,” in Proceedings of the 50th AES Convention, (London, UK), March
1975.

[32] P. G. Craven and M. A. Gerzon, “Coincident microphone simulation covering three

dimensional space and yielding various directional outputs.” U.S. Patent 4,042,779,
August 1977.

[33] M. A. Gerzon, “Periphony: With-height sound reproduction,” Journal of the Audio

Engineering Society

, vol. 21, pp. 2–10, January/February 1973.

[34] M. A. Gerzon, “Ambisonics in multichannel broadcasting and video,” in Proceed-

ings of the 74th AES Convention

, (New York, New York, USA), October 1983.

[35] J. D. Johnston and Y. H. Lam, “Perceptual soundfield reconstruction,” in Proceed-

ings of the 109th AES Convention

, (New York, New York, USA), October 2000.

[36] J. D. Johnston and E. R. Wagner, “Microphone array for preserving soundfield per-

ceptual cues.” U.S. Patent 6,845,163, January 2005.

[37] H. Robjohns, “Is it possible to record in surround on only two tracks?,” Sound on

Sound

, December 2005. Available online

http://www.soundonsound.com/

sos/dec05/articles/qa1205_4.htm

, checked April 30, 2008.

[38] J. Hall and Z. Cvetkovi´c, “Coherent multichannel emulation of acoustic spaces,” in

Proceedings of the 28th AES International Conference

, (Piteå, Sweden), pp. 167–

176, July 2006.

15