Stochastic Analysis of the Power Output for a Wind Turbine

Edgar Anahua

∗

and Frank Boettcher

†

, Stephan Barth

†

, Joachim Peinke

†

ForWind - Center for Wind Energy Research,

University of Oldenburg

D-26111 Oldenburg, Germany Phone: [phone],

Fax: [phone]

email: [e-mail]

Matthias Lange

‡

energy

& meteo systems GmbH

26129 Oldenburg, Germany

We present a stochastic analysis of the power output for a wind turbine based on a Langevin

equation to see how fluctuations in the wind speed will affect the power performance charateristics.
In particular we show by means of a simple model, that the averaged power characteristics
determined by the IEC 61400-12 standard, varies with different turbulent wind fields. Furthermore,
we show that the mean power output is affected by the dynamical reaction of a wind turbine
on wind fluctuations. We propose a method to extract proper power characteristic of the wind
turbine from measured power output data and simultaneously measured wind data. This power
characteristic is independent of the averaging procedure.

I.

INTRODUCTION

For the determination of the power curve of a wind

turbine generator system (WTGS) one uses the IEC
standard [1, 2]. The power curve is obtained by means
of 10 min averages of longitudinal wind speed at the hub
hight and power output measurements:

hui → hL(u)i .

This standard procedure is limited to the local

conditions because wind fluctuations produced by

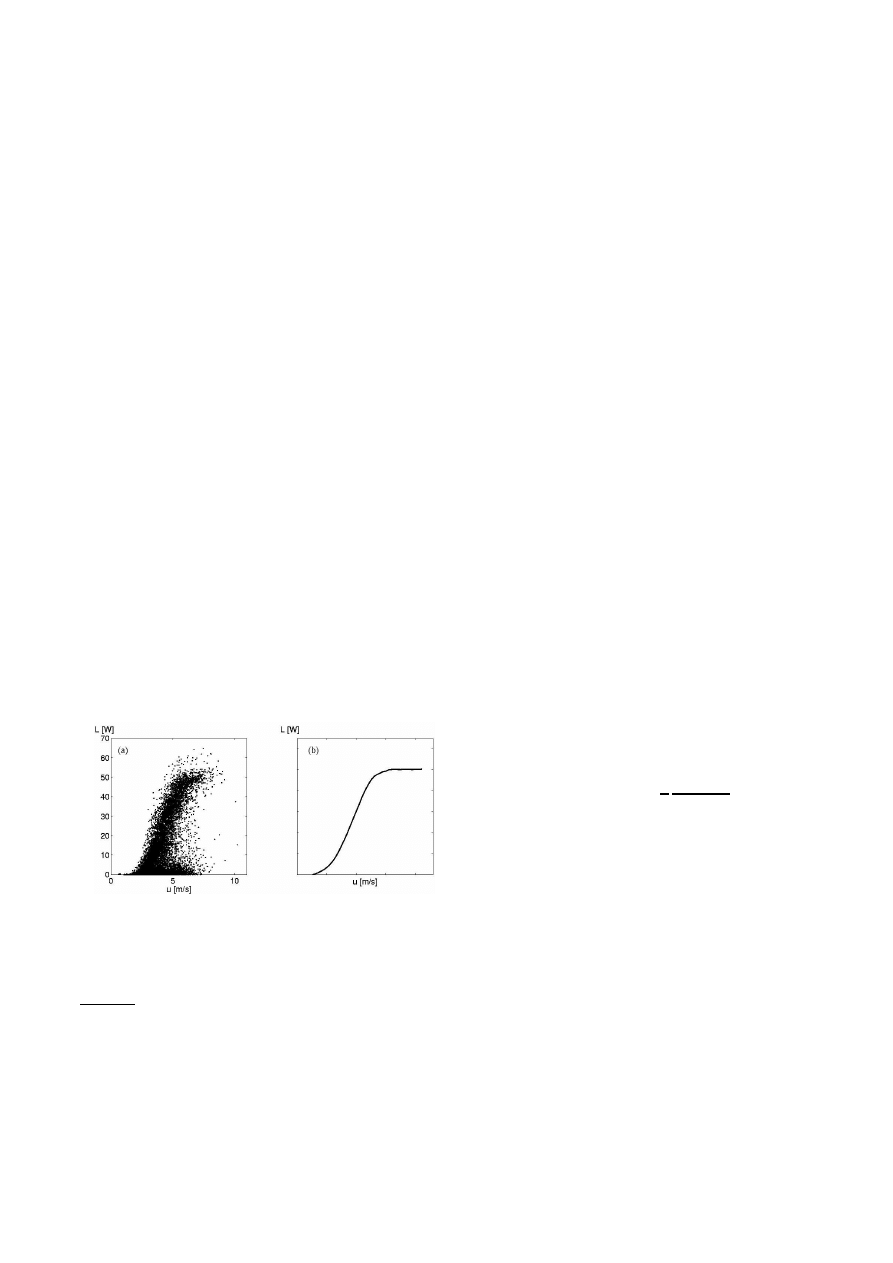
FIG. 1: a) Typical fluctuations of the wind power output
measurements of a small WTGS of 50Watt, 1sec mean val-
ues. b) Wind power curve of a large WTGS according to the
standard method.

∗

Also at the Energy and Semiconductor Research Laboratory, De-

partment of Physics, University of Oldenburg.

†

Electronic address: [e-mail]

‡

URL: http://www.energymeteo.de

flow distortion (e.g., roughness, buildings, orography)
and specific meteorological conditions (e.g., thermal
stabilities, wind shear) are not considered [3–5].

See

Fig.1. All these aspects affect the power output and also
relaxation (dynamical response) of the WTGS would
lead to a different power output [6].

The power curve, which is denoted by L(u) ∝ u

3

, is a

nonlinear function of the wind velocity which leads to
the following inequality:

L

(hui) 6= hL(u)i .

Currently a Taylor expansion of second order is com-
monly developed in order to include wind fluctuations
[4, 7].:

hL(u)i = L(hui) +

1
2

∂

2

L

(hui)

∂

hui

2

σ

2

.

(1)

Where σ = hu

0

2

i is the variance of wind velocity

fluctuations. But the distribution of wind fluctuations
presents an anomalous statistic around 10min mean
velocity, see Fig.2. Therefore higher order moments of
the wind fluctuations hu

0

n

i with u = hui + u

0

are needed

in order to predict them more accurately [8, 9].

hL(u)i ∝ h(hui + u

0

)

3

i

(2)

= hu

3

i + 3huiσ + hu

0

3

i .

(3)

In the following we present a stochastic analysis of

the power output for a WTGS based on a Langevin
equation to see how fluctuations in the wind speed will
affect the power performance charateristic. A derivation

2

-4

0

4

10

0

10

1

10

2

10

3

(u-

µ

) [m/s]

rel. frequency

FIG. 2: The figure shows an example of an anomalous distri-
bution of the wind velocity around a 10min mean value.

of dynamical equations for the power output of a WTGS
from measured data will be presented. We start with
the presentation of the dynamical relaxation description
of a WTGS. Next, we evaluate the deterministic and
the stochastic content of the power output dynamics
by means of a Langevin equation. Finally, an advanced
(dynamical) power curve is derived by fix-points of the
deterministic dynamics.

II.

DYNAMICS OF THE POWER CURVE

We focus on the instantaneous power output of a

WTGS defined by [6].:

L

(t) = L

f ix

(u) + `

0

(t) .

(4)

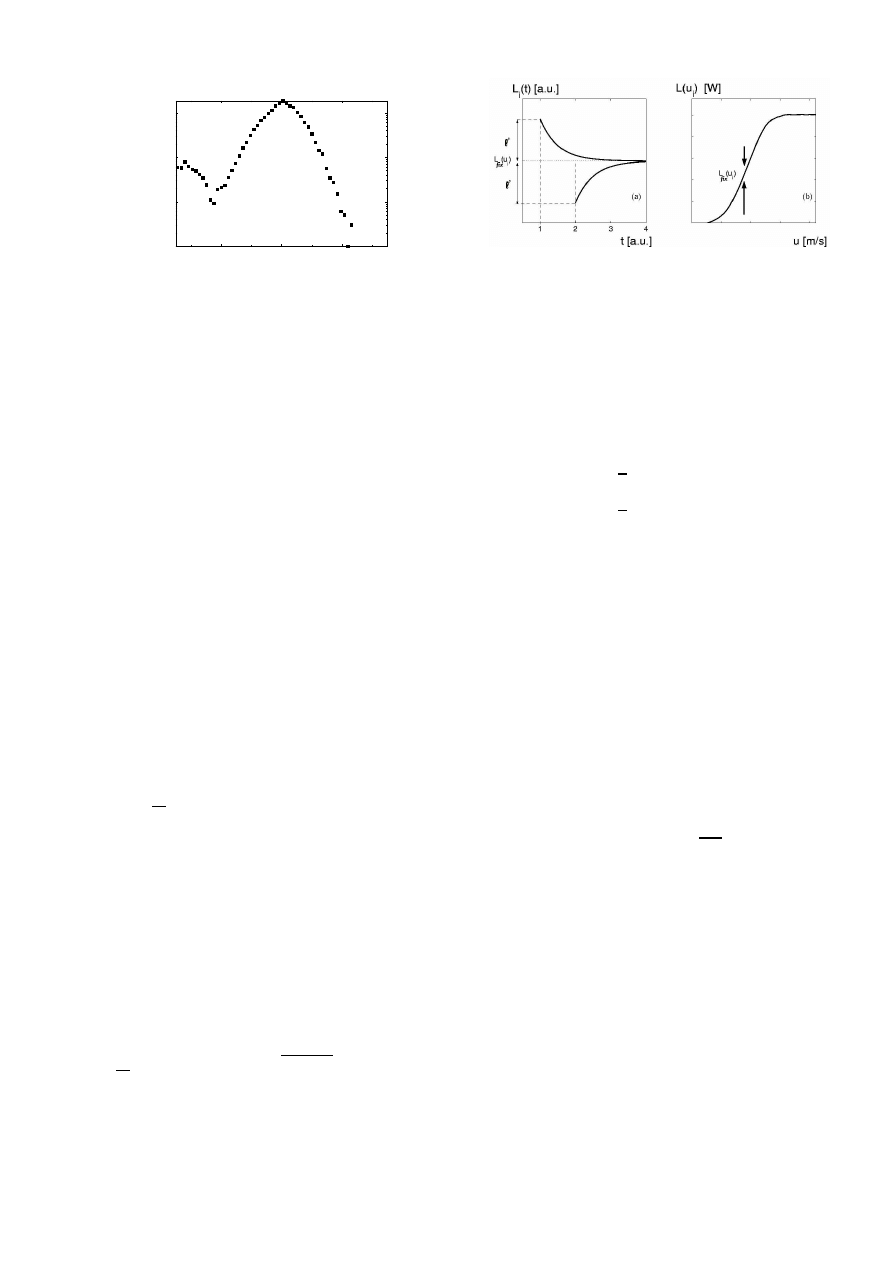
We describe the relaxation of L(t) on the stationary
power L

f ix

(u) as a simple exponential function of growth

and decay.

`

0

(t) ∝ ±e

−αt

(5)

d

dt

L

(t) = −α`

0

(t) + g(L

i

, t

)η(t) .

(6)

where −α`

0

(t) describes its relaxation of the fluctuations

which is proportional to an exponential function at time
t

and g(L, t)η(t) represents the influence of dynamical

noise from the system: e.g. switch-off, pitch and yaw
angle controls, etc. For ilustration see Fig.3.

In order to obtain a ’real’ power curve by means of fix-

points, we assume L(t) to be stationary and a stochastic
variable for wind speeds between: u

a

≤ u

i

< u

b

with

an evolution in time which can be described by a
Langevin-equation

[10–12].:

d

dt

L

(t) = D

(1)

(L) +

q

D

(2)

(L)

· Γ(t) .

(7)

FIG. 3: a) Schematic illustration of relaxation effects on the
instantaneous power output of a WTGS. b) Relaxations on
the power curve.

D

(1)

describes the deterministic evolution of L(t) and

D

(2)

reflects the influence of noise. D

(1)

is called drift-

and D

(2)

diffusion coefficient.

Γ(t) is the fluctuating

Langevin force. D

(1)

and D

(2)

can be evaluated by the

conditional moments.

D

(1)

(L) = lim

τ →

0

1
τ

hL(t + τ ) − L(t)i |

L

(t)=L

(8)

D

(2)

(L) = lim

τ →

0

1
τ

(L(t + τ) − L(t))

2

|

L

(t)=L

(9)

where the angles represent an ensemble average of the
included functions under the condition of L = L(u

i

).

Thus, D

(1)

and D

(2)

can be calculated directly from

measured data and the deterministic relation as well as
the noisy fluctuations can be evaluated [10].

We consider the simplified case of one-dimentional

dynamics of the power output only. Using measured
data of 1sec mean values of a small WTGS of 50Watt
[13] we calculate the drift and diffusion coefficients, see
Fig.4a and b.

The average of the Langevin-equation

with D

(1)

(L

f ix

) := 0 was applied in order to obtain

the stable fix-points (dynamical means). The slope of
these fix-points define the stability, thus L

f ix

(u

i

) of the

power output is found, see Fig.4a. The second term
of the Langevin-equation vanishes. The deterministic
dynamics of the power output can also be expressed by
the potential φ

D

(L), defined as

δφ

D

δL

= −D

(1)

(L). A

stable fix-point corresponds to the minimum of the drift
potential φ

D

(L), see Fig.5.

In order to get an understanding of the real power

curve dynamics grasped by the drift coefficients, the
additional noise has to be taken into account. In the
Fig.4b the corresponding magnitude of the noise are
expressed by the evaluated diffusion coefficients D

(2)

(L).

The noise will cause transitions between differents power
output states.

For the power curve, the noise will

produce fluctuations around the stable fix-points, see
Fig.5. D

(2)

has a minimum at L

f ix

which indicates a

pronounced stability of the power output.

3

FIG. 4: Deterministic and stochastic dynamics of the power
output given by D

(1)

and D

(2)

for wind speeds between:

5.16m/s ≤ u

i

< 5.67m/s.

FIG. 5: The corresponding potential

δφ

D

δL

= −D

(1)

(L) for the

deterministic dynamics of the power output. For ilustration,
the fix-point has been represented as a blue ball and the 10min
mean as a red square.

III.

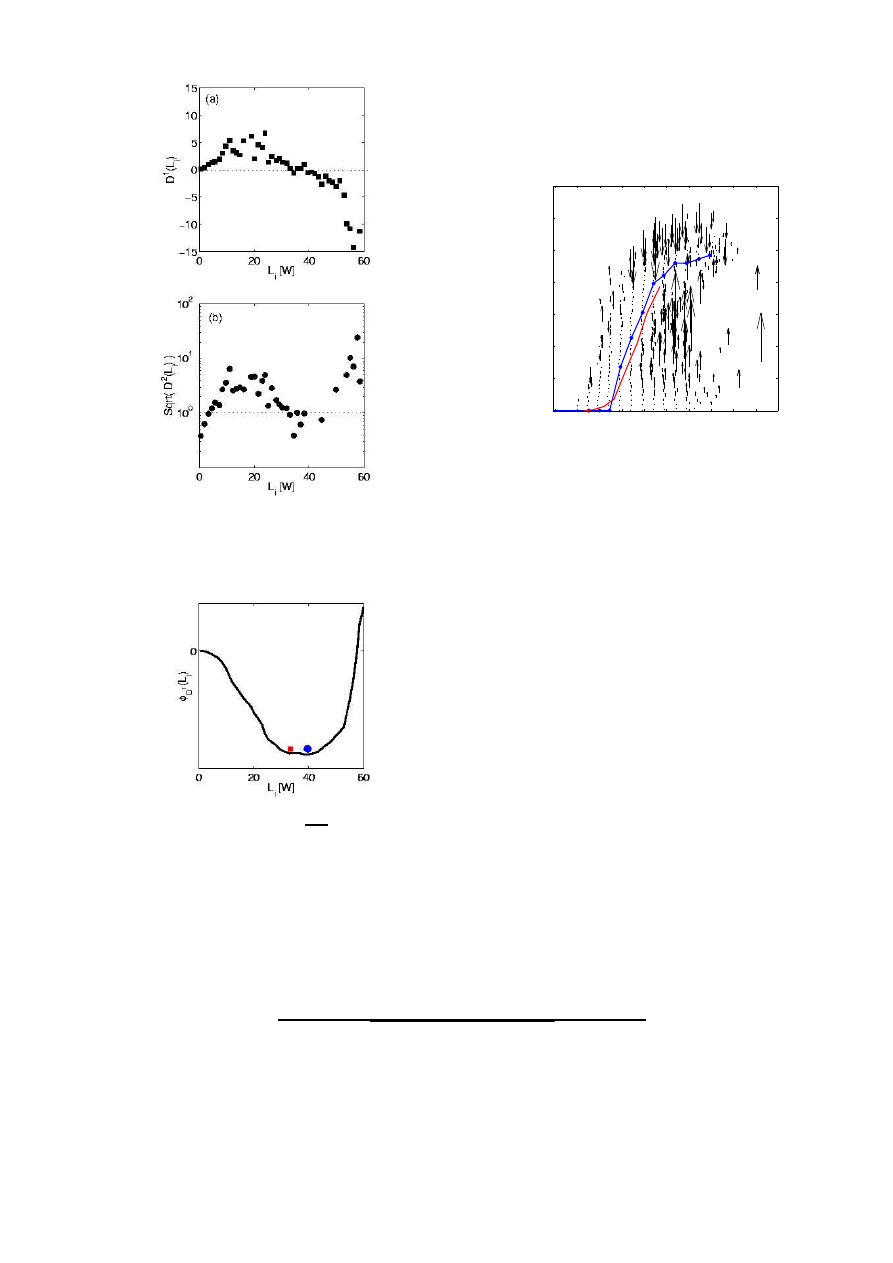
AN ADVANCED POWER CURVE

We estimate a new power curve which does not

consist of the averaged power values anymore but is

given by the fix-points of each wind velocity interval,
see Fig. 6. The results of the numerical calculation
for the deterministic dynamics of the power output are
plotted as one-dimentional vector field.

The arrows

represent values determined by the data analysis. Thus,

0

2

3

4

5

6

7

8

9 10 11

0

10

20

30

40

50

60

70

u [m/s]

L [W]

FIG. 6: Deterministic dynamics of the power output states
given by D

(1)

(L) per intervals of wind speeds. The arrows

represent the relaxations tendencies of the power output. The
blue bold dots indicate the stable fix-points and the red line
is the typical 10min mean values of the power curve.

we observe a clear difference between the fix-points and
the usually 10min mean values. Different relaxation ten-
dencies around the fix-points of the power for different
intervals of wind velocities are observed because of the
dynamical noise from the WTGS.

IV.

CONCLUSION

The averaged power output of the WTGS has been

described as function of relaxation and noise. Based on
a Langevin-equation the dynamical mean power output
of each wind velocity interval has been derived.
We propose an new procedure for power curve calibra-
tions because it describes the power curve more properly
and does not depend on the average procedure.
The advanced power curve could be used for different
situations of large WTG on turbulent winds and other
atmospheric parameters.

[1] IEC, Wind Turbine Generator Systems, Part 12: Wind

Turbine Power Performance Testing, IEC 61400-12,

Ed.1998.

[2] T. Burton, D. Sharpe, N. Jenkins, E. Bossanyi, Wind

4

Energy Handbook, Wiley, Cichester, 2001.

[3] R. Hunter, T.F. Pedersen, P. Dunbabin, I. Antoniou, S.

Frandsen, H. Klug, A. Albers, W.K. Lee, Task 1: Mea-
surement Method to Verify Wind Turbine Performance
Characteristics, European Wind Turbine Testing Proce-
dure Developments, Risoe Laboratory, Roskilde, 2001.

[4] A. Albers, C. Hinsch, Influence of Different Meteoro-

logical Conditions on the Power Performance of Large
WECS, DEWI Magazin, Nr. 9, Wilhelmshaven, 1996.

[5] M. Lange, D. Heinemann. Accuracy of Short Term Wind

Power Prediction Depending on Meteorological Condi-
tions, Proc. Global Wind Power Conference, European
Wind Energy Asociation, Paris, 2002.

[6] A. Rauh, J. Peinke, A phenomenological model for the

dynamic response of wind turbines to turbulent wind.
Journal of wind eng. Ind. and aerody. 92, 159-183, 2004.

[7] K. Keiser, H. Hohlen, W. Langreder, Turbulence correc-

tions for Power Curves, European Wind Energy Confer-
ence, Madrid, 2003.

[8] F. Boettcher, Ch. Renner, H.-P. Wald, J. Peinke. On the

statistic of wind gusts. Boundary Layer Meteorology, 108,
pp. 163-173. 2003.

[9] J. Peinke, S. Barth, F. Boettcher, D. Heinemann, B.

Lange. Turbulence, challenging problem for wind energy.
Phys. A 338,pp. 187-193. 2004.

[10] R. Friederich, S. Siegert, J. Peinke, St. Lueck, M. Siefert,

M. Lindemann, J. Raethjen, G. Deuschl, G. Pfister,
Extracting Model Equations from Experimental Data,
Phys. Lett. A 271, 217, 2000.

[11] F. Boettcher, E. Anahua, J. Peinke, The Dynamical Be-

haviour of Wind Gusts, Proc. of Global Wind Power Con-
ference, European Wind Energy Asociation, Paris, 2002.

[12] F. Boettcher, J. Peinke, Wind gust and their impact on

the power curve calibration and on extrem loads, Proc. of
Global Wind Power Conference, European Wind Energy
Asociation, Madrid, 2003.

[13] E. Anahua, ’Analisis of data, Turbulence and Windpower

Output’, MSc. Thesis, PPRE Universty of Oldenburg,
2001.