Replicated triangle and duo–trio tests: Discrimination capacity of assessors
evaluated by Bayes’ rule

S. Bayarri, I. Carbonell, L. Izquierdo

*

, A. Tárrega

Instituto de Agroquímica y Tecnología de Alimentos, CSIC, P.O. Box 73, 46100 Burjassot (Valencia), Spain

a r t i c l e

i n f o

Article history:
Received 5 September 2007
Received in revised form 21 February 2008
Accepted 23 February 2008
Available online 4 March 2008

Keywords:
Replicated difference tests
Bayesian inference

a b s t r a c t

Discrimination rates of panellists performing replicated difference tests are estimated in the present
paper according to Bayes’ rule by considering the successive replications as different steps and using
the posterior distribution obtained in each step as prior distribution of the following step. Data are also
successively obtained in real situations and, thus, this approach imitates what happens in practice and
differs from other published approaches which consider all replications as if they were simultaneously
observed. Before performing the first step, a non informative prior distribution is used as density function
of the discrimination rate but after the first step has been completed each prior distribution (posterior
distribution obtained in the previous step) is informative. The density functions of the discrimination
rates are not proper beta distributions but the sections of beta distributions corresponding to the interval
of the independent variable from 1/3 to 1 in triangle tests and from 1/2 to 1 in duo–trio tests.

Ó 2008 Published by Elsevier Ltd.

1. Introduction

Difference tests are widely used in food analysis and the statis-

tical approaches used to interpret their results have been object of
many papers. We recommend the book from

Bi (2006)

as an excel-

lent review in this area. The purpose of this paper is to study a very
specific aspect related with discrimination rates of panellists and
with independency among trials performed by a panellist. Thus,
only literature related with these points will be commented. We
refer to the above mentioned book for details that do not directly
affect our objectives.

Under the null hypothesis of no differences between the two

tested products each particular answer to a difference test follows
a Bernoulli distribution with parameter p (probability of success
p

= 1/3 for triangle tests, p = 1/2 for duo–trio tests). Thus, the

results from n trials follow a binomial distribution with parameter
p

. This holds whatever the number of trials a panellist can perform.

But if differences between the tested products exist the interpreta-
tion is not so simple. A way (see comments from

Bi, 2003

) is to

consider that the probability of success in each answer is a value
higher than p but constant for all answers. This implies the
assumption that all panellists and all replications from a panellist
are interchangeable. Nevertheless, when differences exist between
the products it is not logical to accept that the capability of notic-
ing them is exactly the same for all panellists. It seems more rea-
sonable to accept discrimination rates, h, different among

panellists, ranging in the interval from 0 to 1. Thus, the probability
conditioned to h of success in a single response of a panellist is
h

+ (1 h)p.

A simple approach (see

Meilgaard, Civille, & Carr, 1999

) is to as-

sume that panellists are divided in two groups, one formed by indi-
viduals who distinguish and always succeed in their answers and
another one by non-discriminators that only succeed by chance.
In terms of discrimination rates, h = 1 for all panellists of the first
group and h = 0 for all panellists of the second group. This assump-
tion may be reasonable when the panellists perform a unique test
and the only available result from each panellist is either a single
success or a single failure.

Carbonell, Carbonell, and Izquierdo

(2007)

applied this criterion to estimate the number of true dis-

criminators according to Bayes’ rule. But when replications from
a panellist are available and successes and failures are observed,
a panellist cannot be classified either as a complete discriminator
or a non-discriminator. It is more rational to accept that the dis-
crimination rate is an unknown value between 0 and 1 to be esti-
mated according with the observed number of successes and
failures.

Kunert (2001)

considered h a constant parameter for each

panellist whereas

Brockhoff (2003)

considered h a random variable

with a beta distribution.

Bi (2007)

also assumed a beta distribution

for h and used a Bayesian approach to estimate the probability of
success.

Duineveld and Meyners (2008)

applied a hierarchical

Bayesian approach for the same purpose.

When analysing replicated data from a panellist it is common to

treat the observed results, s successes out of n trials, as if they were
simultaneously obtained, but it is obvious that the results were
obtained step by step and in a given order, for instance a success

0950-3293/$ - see front matter Ó 2008 Published by Elsevier Ltd.
doi:10.1016/j.foodqual.2008.02.008

*

Corresponding author. Tel.: [phone]; fax: [phone].
E-mail address:

[e-mail]

(L. Izquierdo).

Food Quality and Preference 19 (2008) 519–523

Contents lists available at

ScienceDirect

Food Quality and Preference

j o u r n a l h o m e p a g e : w w w . e l s e v i e r . c o m / l o c a t e / f o o d q u a l

after a failure after a success. Bayesian inference performs in a sim-
ilar way, since a prior probability is combined with data obtained
in each step to infer the posterior probability, which, in its turn,
will be used as prior probability for the next step.

The purpose of this paper is to apply this criterion to estimate

the discrimination rate of individual panellists according to the
successive observed successes and failures in a series of difference
tests. The overall discrimination power of the whole panel is then
determined as a function of the individual discrimination rates.

2. Assumptions

2.1. Conditional probabilities of success and of failure

Conditioned to a given discrimination capacity (h) of the panel-

list the probability of success in a trial is, as mentioned above

pðs=hÞ ¼ h þ ð1 hÞp ¼ p þ ð1 pÞh

ð1Þ

where h is the discrimination capacity, considered continuously dis-
tributed in the range from 0 to 1, and p is the probability of success
just by chance, 1/3 for triangle tests and 1/2 for duo–trio tests.

The probability of failure, also conditioned to a given discrimi-

nation capacity of the panellist, is

pðf =hÞ ¼ 1 pðs=hÞ ¼ ð1 pÞð1 hÞ

ð2Þ

The probability of success conditioned to h is always given by

Expression

(1)

and, thus,

pðs

1

=

h

Þ ¼ pððs

2

=

s

1

Þ=hÞ ¼ pððs

2

=

f

1

Þ=hÞ ¼ ¼ pðs=hÞ ¼ p þ ð1 pÞh

ð3Þ

where s

1

means success in the first trial, s

2

/s

1

success in the second

trial given success in the first one and so on. In the same way

pðf

1

=

h

Þ ¼ pððf

2

=

s

1

Þ=hÞ ¼ pððf

2

=

f

1

Þ=hÞ ¼ ¼ pðf =hÞ

¼ 1 pðs=hÞ ¼ ð1 pÞð1 hÞ

ð4Þ

2.2. Marginal probabilities of success and of failure

The total probability of success of a panellist in a trial is ob-

tained by integration over all possible values of h from 0 to 1

pðsÞ ¼

Z

1

0

pðs; hÞdh ¼

Z

1

0

pðs=hÞpðhÞdh

ð5Þ

The probability of failure can also be obtained by integration

pðf Þ ¼

Z

1

0

pðf ; hÞdh ¼

Z

1

0

pðf =hÞpðhÞdh ¼

Z

1

0

ð1 pðs=hÞÞpðhÞdh

ð6Þ

or just as

pðf Þ ¼ 1 pðsÞ

ð7Þ

2.3. Tested samples

The discrimination rate of a panellist depends on her/his capa-

bility but also on the real differences between the samples tested.
If both are identical h is obviously 0 and if they are completely dif-
ferent h is 1 or very close to 1. In the theory discussed in this paper
the real differences between the two tested samples is not taken
into account but it is assumed that all panellists test the same sam-
ples in all repeated trials.

3. First trial

3.1. Marginal probabilities of success and of failure

Before the panellist performs the first trial, and if no previous

knowledge about the discrimination rate exists, it is reasonable
to accept a uniform prior distribution of h from 0 to 1 or, in other
words, a constant value for the density function p(h) of the distri-
bution of h.

In these conditions Expression

(5)

applied to the first trial

becomes

pðs

1

Þ ¼

Z

1

0

pðs

1

=

h

ÞpðhÞdh ¼ ct

Z

1

0

pðs=hÞdh ¼ ct

Z

1

0

ðp þ ð1 pÞhÞdh

¼ ct

1 þ p

2

since p(h) is a constant value and p(s

1

/h)=p(s/h)=p + (1-p)h (Expres-

sion

(3)

).

In the same way, Expression

(6)

becomes

pðf

1

Þ ¼ ct

Z

1

0

ð1 pÞð1 hÞdh ¼ ct

1 p

2

Table 1
Probabilities of success and failure in three successive triangle tests performed by a panellist

First test

a

Second test

Third test

Success

2/3

Given success in the first test

Success

39/54

Given two previous successes

Success

0.769

Failure

0.231

Failure

15/54

Given a previous success and a previous failure

Success

0.600

Failure

1/3

Given failure in the first test

Success

30/54

Failure

0.400

Failure

24/54

Given two previous failures

Success

0.500

Failure

0.500

a

Assuming a uniform prior distribution of the discrimination capacity of the panellist.

Table 2
Probabilities of success and failure in three successive duo–trio tests performed by a panellist

First test

a

Second test

Third test

Success

3/4

Given success in the first test

Success

7/9

Given two previous successes

Success

0.804

Failure

0.196

Failure

2/9

Given a previous success and a previous failure

Success

0.687

Failure

1/4

Given failure in the first test

Success

6/9

Failure

0.313

Failure

3/9

Given two previous failures

Success

0.625

Failure

0.375

a

Assuming a uniform prior distribution of the discrimination capacity of the panellist.

520

S. Bayarri et al. / Food Quality and Preference 19 (2008) 519–523

The value of the constant must be 1 to satisfy p(s

1

) + p(f

1

)=1. Thus,

p(s

1

)=(1 + p)/2 and p(f

1

)=(1 p)/2.

Table 1

lists these probabilities of success and failure for trian-

gle tests and

Table 2

for duo–trio tests.

3.2. Posterior distributions of the discrimination rate

According to Bayes’ rule the posterior density function of h gi-

ven a success in the first trial is

pðh=s

1

Þ ¼

pðs

1

=

h

ÞpðhÞ

pðs

1

Þ

¼

pðs=hÞ

pðs

1

Þ

¼

p

þ ð1 pÞh

1þp

2

ð8Þ

This is a linear function of h that in triangle tests (p = 1/3) sim-

plifies to 1/2 + h and in duo–trio tests to 2/3(1 + h).

In the same way, given a failure in the first test the posterior

density function of h is

pðh=f

1

Þ ¼

pðf

1

=

h

ÞpðhÞ

pðf

1

Þ

¼

pðf =hÞ

pðf

1

Þ

¼

ð1 pÞð1 hÞ

1p

2

¼ 2ð1 hÞ

ð9Þ

4. Second trial

4.1. Marginal probabilities of success and of failure

In the second test the posterior distribution of h obtained from

the first test, p(h/s

1

) in case of success, p(h/f

1

) in case of failure, is

used as prior distribution. In both cases, success and failure can
be observed. The possibilities are, thus, success after success (s

2

/

s

1

), success after failure (s

2

/f

1

), failure after success(f

2

/s

1

) and fail-

ure after failure (f

2

/f

1

). Adapting Expression

(5)

to these cases

pðs

2

=

s

1

Þ ¼

Z

1

0

pððs

2

=

s

1

Þ=hÞpðh=s

1

Þdh

pðs

2

=

f

1

Þ ¼

Z

1

0

pððs

2

=

f

1

Þ=hÞpðh=f

1

Þdh

pðf

2

=

s

1

Þ ¼

Z

1

0

pððf

2

=

s

1

Þ=hÞpðh=s

1

Þdh

pðf

2

=

f

1

Þ ¼

Z

1

0

pððf

2

=

f

1

Þ=hÞpðh=f

1

Þdh

Taking into account that all probabilities of success or failure condi-
tioned to h are, respectively, p(s/h) and 1 p(s/h) and substituting
the posterior density functions of h according to Expressions

(8)

and (9)

pðs

2

=

s

1

Þ ¼

Z

1

0

pðs=hÞ

pðs=hÞ

pðs

1

Þ

dh ¼

1

pðs

1

Þ

Z

1

0

ðpðs=hÞÞ

2

dh

ð10Þ

pðs

2

=

f

1

Þ ¼

Z

1

0

pðs=hÞ

pðf =hÞ

pðf

1

Þ

dh ¼

1

1 pðs

1

Þ

Z

1

0

pðs=hÞð1 pðs=hÞÞdh

pðf

2

=

s

1

Þ ¼

Z

1

0

pðf =hÞ

pðs=hÞ

pðs

1

Þ

dh ¼

1

pðs

1

Þ

Z

1

0

ð1 pðs=hÞÞpðs=hÞdh

pðf

2

=

f

1

Þ ¼

Z

1

0

pðf =hÞ

pðf =hÞ

pðf

1

Þ

dh ¼

1

1 pðs

1

Þ

Z

1

0

ð1 pðs=hÞÞ

2

dh

Substituting p(s

1

) by (1 + p)/2, p(f

1

) by (1 p)/2 and p(s/h) or p(f/h)

according to Expressions

(1) and (2)

the probabilities obtained are

those shown in

Tables 1 and 2

for triangle and duo–trio tests

respectively.

For instance, the probability of success after success is obtained

by

pðs

2

=

s

1

Þ ¼

2

1 þ p

Z

1

0

ðp þ ð1 pÞhÞ

2

dh ¼

2

1 þ p

1 þ p þ p

2

3

As shown in

Tables 1 and 2

a success is more probable after a suc-

cess than after a failure (39/54 and 30/54 for triangle,

Table 1

; 7/9

and 6/9 for duo–trio,

Table 2

). In the same way a failure is more

probable after a failure than after a success.

4.2. Posterior distributions of the discrimination rate

Applying Expression

(8)

, the posterior density function of h gi-

ven a success preceded by a success is

pðh=ðs

2

=

s

1

ÞÞ ¼

pððs

2

=

s

1

Þ=hÞpðh=s

1

Þ

pðs

2

=

s

1

Þ

¼

pðs=hÞpðh=s

1

Þ

pðs

2

=

s

1

Þ

and substituting p(h/s

1

) according to Expression

(8)

and p(s

2

/s

1

)

according to

(10)

pðh=ðs

2

=

s

1

ÞÞ ¼

pðs=hÞ

1

pðs

1

Þ

pðs=hÞ

1

pðs

1

Þ

R

1

0

ðpðs=hÞÞ

2

dh

¼

ðpðs=hÞÞ

2

R

1

0

ðpðs=hÞÞ

2

dh

In the same way

pðh=ðf

2

=

f

1

ÞÞ ¼

ð1 pðs=hÞÞ

2

R

1

0

ð1 pðs=hÞÞ

2

dh

‘

and

pðh=ðs

2

=

f

1

ÞÞ ¼ pðh=ðf

2

=

s

1

Þ ¼

ð1 pðs=hÞÞpðh=sÞ

R

1

0

ð1 pðs=hÞÞpðh=sÞdh

5. Further trials

For each combination of successes and failures in previous trials

performed by a panellist, success or failure can be observed in the
next trial. In general, 2

n

different series of events (i.e., success, fail-

ure, failure, success. . .) are possible being n the total number of tri-
als and considering different series those that, even when
constituted by the same number of successes (y) and failures
(n y), are present in different orders. Nevertheless, different ser-
ies can have the same probability if the same prior distribution of h
is used to compute them.

5.1. Posterior distribution of the discrimination rate

Generalising what was exposed above for the second test, the

posterior distributions of h after n trials are used as prior distribu-
tions to compute probabilities for the (n + 1)th trial. The number of
different posterior distributions of h after n trials is n + 1. Each one
of these distributions corresponds to one of the n + 1 possible val-
ues of y from 0 to n and will be used to compute the probability of

success in

n
y

series, all of them having the same probability but

differing due to the order in which previous successes and failures
were observed. The same distribution of h is also used to compute

the probabilities of other

n
y

series, all of them failures corre-

sponding one-to-one to successes. Alternatively, the probabilities
of failures can be obtained by p(f) = 1 p(s). In general, the density
functions of the posterior distribution of h after n tests given that y
successes and n y failures have been observed is

ðpðs=hÞÞ

y

ð1 pðs=hÞÞ

ny

R

1

0

ðpðs=hÞÞ

y

ð1 pðs=hÞÞ

ny

dh

ð11Þ

with y ranging from 0 to n.

Fig. 1

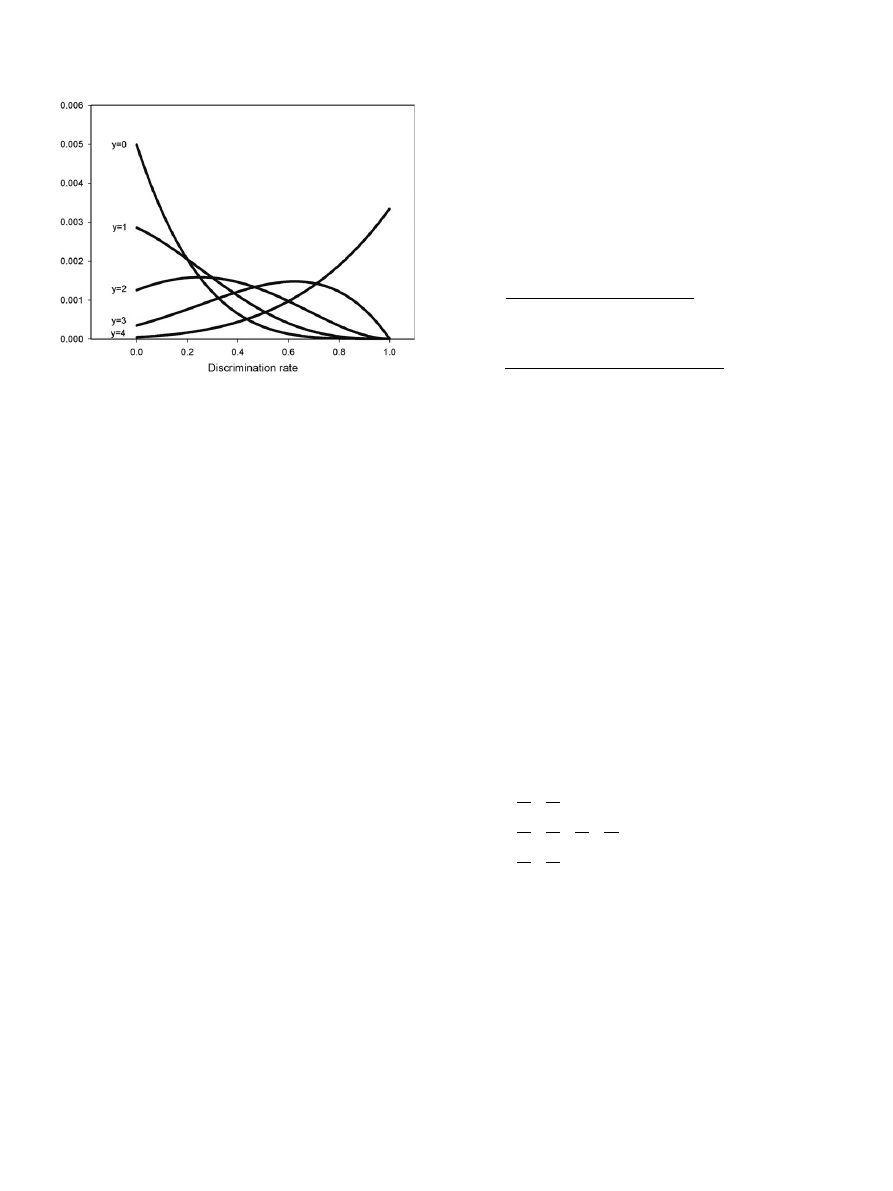
shows the posterior density functions of h for panellists

who performed 4 (n) triangle trials and succeeded in 0, 1, 2, 3, or
4 (y) of

them. Considering beta

a

,b

distributions (a = y + 1,

b

= n y + 1) the density functions in

Fig. 1

are the sections of

these beta distributions corresponding to the interval of the inde-
pendent variable, p(s/h), from 1/3 (h = 0) to 1 (h = 1). The proportion

S. Bayarri et al. / Food Quality and Preference 19 (2008) 519–523

521

of the area under the curve inside this interval (in relation to the
total area of the complete beta distribution) increases as y, the
number of successes, does. It is respectively 13%, 47%, 79%, 96%
and 99.6% for the values of y from 0 to 4 in the density functions
represented in

Fig. 1

. The area outside the interval is not negligible

even for relatively large values of n if the proportion of successes is
not too high. For instance, if the number of tests is 30 and the
number of successes is 10, 13, or 15, the area outside the interval
is 45%, 11% and 3%, respectively. These hypothetical results
can easily arise in practical applications of replicated triangle
tests such as in the estimation of the detection threshold of a
substance.

5.2. Comparison with other approaches

As mentioned above, published studies usually consider all rep-

lications as simultaneously obtained. In these conditions, and
when a Bayesian approach is applied, a prior (informative or non
informative) distribution for all replications must be selected.

Bi

(2007)

showed that different prior distributions produced clearly

different results and

Duineveld and Meyners (2008)

indicated that

the hyper prior distribution (these authors applied a hierarchical
Bayesian approach) affected the individual discrimination rates.
With our approach it is out of question to consider this aspect.
The posterior distributions are obtained step (replication) by step,
considering the posterior distribution from each step as prior dis-
tribution for the next one. According to this, only the prior distribu-
tion of the first step is not also a posterior distribution, since no
previous steps exist. We selected as prior distribution for this first
step a non informative distribution (beta

1,1

, the uniform distribu-

tion, since it is assumed that previous information does not exist
and, consequently, y = n = 0). Observe that the prior distribution
for the first step of our approach must necessarily be non informa-
tive, since, if previous information exists, this information would
imply knowledge about successes or failures of the panellist in pre-
vious tests, what simply means that this panellist is not in the first
step but in a posterior one.

In the aspect of considering a sequence of steps, the procedure

proposed in this paper remembers Walds’s and Rao’s sequential
analyses used for panel selection (

Bradley, 1953

). Panellists succes-

sive perform difference tests and in each step the ratio between to-
tal (from the first test to the last one) correct answers and total
number of tests is compared with critical values previously estab-
lished. The decision concerning a panellist may be, according to the
result of the comparison, selection, rejection or performance of a

new test. As the number of selected and rejected panellists in-
creases, the number of necessary further tests decreases. In these
methods only the number of correct answers is considered, but
not the discrimination rate (h) of the panellist, object of most re-
cent papers referred above.

5.3. Marginal probabilities of success and of failure

Expression

(11)

gives the posterior density function of the dis-

crimination rate of a panellist after n trials. Applying this expression,
the probability of success of this panellist in the (n + 1)th trial is

pðs

nþ1

Þ ¼

R

1

0

ðpðs=hÞÞ

y

ð1 pðs=hÞÞ

ny

pðs=hÞdh

R

1

0

ðpðs=hÞÞ

y

ð1 pðs=hÞÞ

ny

dh

ð12Þ

and the probability of failure

pðf

nþ1

Þ ¼

R

1

0

ðpðs=hÞÞ

y

ð1 pðs=hÞÞ

ny

ð1 pðs=hÞÞdh

R

1

0

ðpðs=hÞÞ

y

ð1 pðs=hÞÞ

ny

dh

Tables 1 and 2

show these probabilities for the third test in triangle

and duo–trio tests.

6. Performance of the whole panel

From a panellist, i, the basic aspect of interest is to estimate her/

his marginal probability of success in the next test (n

i

+ 1) that is

estimated according to the number of successes, y

i

, observed in

n

i

previous tests. Obviously, a unique observation is possible, a sin-

gle success or a single failure. From a panel formed by h panellists,
what interests is to estimate the probabilities of the possible num-
ber of successes, x, ranging from 0 to h. If the null hypothesis of no
differences between samples is true these probabilities obey the
binomial law with parameter p. But in case of real differences be-
tween the two samples the discrimination rates, h

i

, vary among

panellists and the probability of each possible value of x cannot
be computed according to the binomial formula. For instance, let
us suppose that two panellists perform a triangle test and that in
a previous test one panellist succeeded and the other one failed.
The probabilities of success and failure in the second test of each
one of these panellists are given in

Table 1

. Three possible number

of successes (x) exist, 0 (when both panellists failed), 1 (when only
one panellists succeeded), and 2 (when both succeeded). The cor-
responding probabilities are

Pðx ¼ 0Þ ¼

39
54

30
54

¼ 0:401

Pðx ¼ 1Þ ¼

39
54

24
54

þ

15
54

30
54

¼ 0:476

Pðx ¼ 2Þ ¼

15
54

24
54

¼ 0:123

The number of addends in each case is, as in the binomial for-

mula,

h

x

but with different probabilities in each addend which

does not allow to combine them. Nevertheless, these probabilities
(such as all discussed in this paper) can be easily calculated using
standard computer facilities. As a slightly more complicated exam-
ple let us suppose that four panellists are going to perform a trian-
gle test and that their backgrounds are 1, 4, 7, and 8 successes in 2,
5, 10, and 14 previous trials. Applying Expression

(12)

with the cor-

responding values of y and n, the respective probabilities of suc-
ceeding in the new trial are 0.60, 0.72, 0.67, and 0.57
respectively for each one of these four panellists. Thus, applying
the same procedure discussed for two panellists the probabilities
of 0, 1, 2, 3, and 4 successes in the hypothetical test that will be
performed by these four panellists are 0.02, 0.12, 0.32, 0.38, and
0.16, respectively.

Fig. 1. Posterior density functions of discriminations rates of panellists performing
four triangle trials according to the number of observed successes.

522

S. Bayarri et al. / Food Quality and Preference 19 (2008) 519–523

7. The order of successes and failures. Experience, fatigue or
lack of motivation

As exposed above, the discrimination rate of a panellist depend

on the total number of previous successes but not on the order
they occurred. Nevertheless, it seems that this order must be re-
lated in some extent with the behaviour of a panellist. Let us sup-
pose that in n successive tests failures accumulate in the first trials
and successes in the last ones. Intuitively, this suggests that the
panellist is getting experience. Although not the same, this situa-
tion resembles what in sensory profile occurs when panellists are
trained to reduce the residual variance. The opposite situation, suc-
cesses cumulated in the first trials and failures in the last ones, can
suggest fatigue or lack of motivation. It would be interesting to de-
velop an index to evaluate ‘‘experience” or ‘‘fatigue” according to
the ‘‘history” of the series of successive successes and failures ob-
served from a panellist. In this section some aspects related with
this idea are discussed with exploratory purposes.

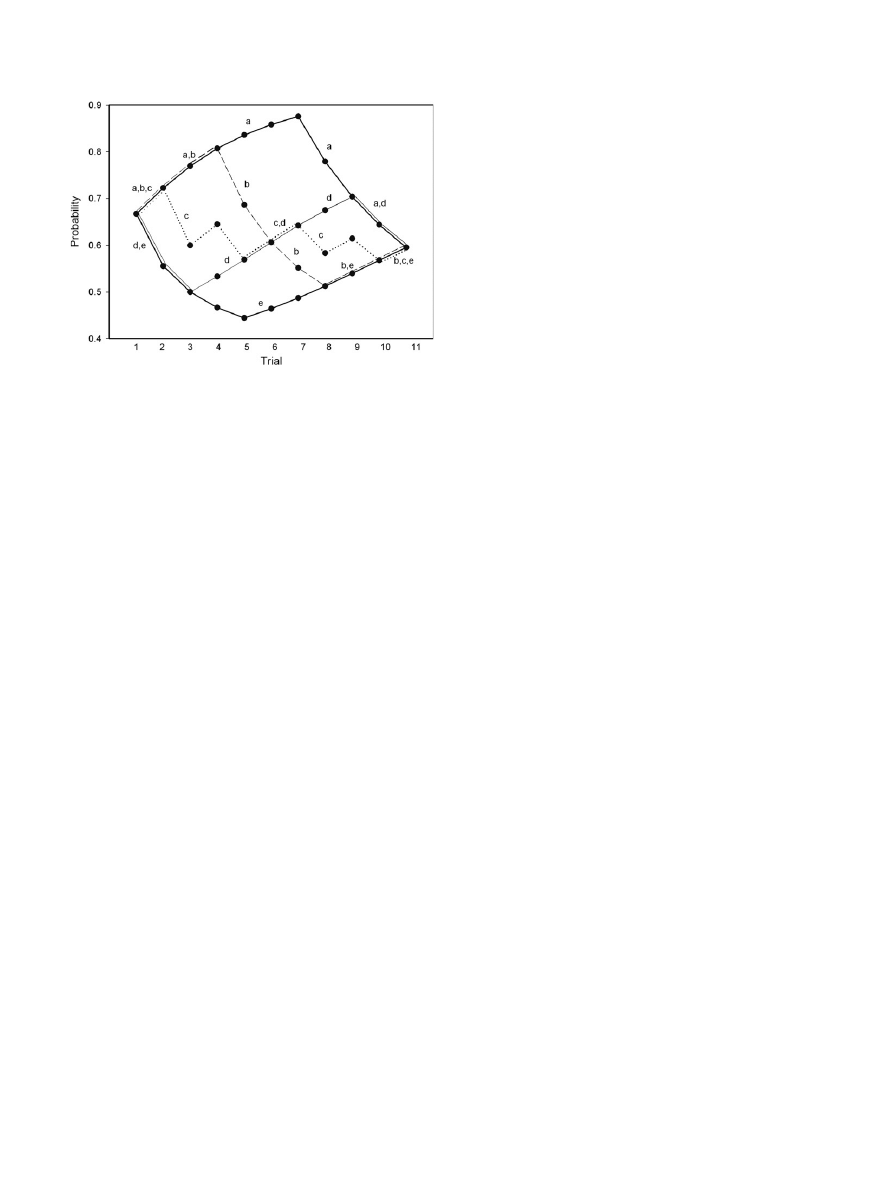
Let us suppose that 10 triangle trials have been performed by

some panellists, all of them succeeding in six and failing in four tri-
als. The probability of success in the 11th trial should be 0.595
according to Expression

(12)

for all panellists independently of

the order in which successes and failures happened. The number

of possible different orders is

10

6

= 210, from which 5, corre-

sponding to five hypothetical panellists, a to e, have been selected
and shown in

Fig. 2

. This figure represents the successive probabil-

ities of success of these five panellists in the 1st, 2nd, . . ., 11th trial
according to the order in which successes and failures were ob-
served (for the first three trials these probabilities of success have
been already shown in

Table 1

). Although the final probability of

success in the 11th trial is the same for all panellists, the paths
are completely different. Panellist a had six successes in the first
six trials what suggests a good discrimination capacity but failed
in the last trials what can be interpreted as lack of motivation or
as fatigue. Panellist e behaved in the opposite way what could sug-
gest low initial capacity of discrimination but improved as experi-

ence increased. When the objective of discrimination tests is to
detect subtle differences between samples, the ideal panellist is
somebody with total experience and completely motivated. Since
either experience or lack of motivation can increase as the number
of trials do, it is logical to give more positive importance to suc-
cesses and more negative importance to failures at the end of the
series of trials than at the beginning. Thus, a rough index to mea-
sure how a panellist is affected by the combination of experience
and fatigue could be obtained by assigning rank order numbers
to the performed trials, changing the signs of these numbers corre-
sponding to failures and adding up the obtained results. This index
is 13 (1 + 2 + 3 + 4 + 5 + 6 7 8 9 10) for panellist a and 35
for panellist e. Panellists b, c, and d, with successes and failures in
the beginning and at the end, have a common index of 11.

The indices so obtained can be of some usefulness to compare

the behaviours of panellists who performed the same number of
trials and had the same number of successes. It would be also use-
ful to develop indices to compare, according to the order in which
successes and failures were observed, panellists who performed
different number of tests.

8. Conclusion

By considering replicated difference tests as a succession of

steps (one per replication) the discrimination rate of a panellist
can be estimated by Bayes’ rule using as prior distribution in each
step the posterior distribution obtained in the previous step. The
overall rate of a test panel is evaluated as a function of the individ-
ual discrimination rates of each panellist. Standard computer facil-
ities are suitable to perform all these calculations.

Acknowledgements

This research was supported by the Spanish Government (Min-

isterio de Educación y Ciencia, project AGL2006-05809ALI) and
FEDER founds and by AGROALIMED (Conselleria d’Agricultura, Pes-
ca i Alimentació, Generalitat Valenciana, Spain). Authors also thank
Fondo Social Europeo for author Bayarri’s contract in the program
I3P from CSIC.

References

Bi, J. (2003). Difficulties and a way out: a Bayesian approach for sensory difference

and preference tests. Journal of Sensory Studies, 18, 1–18.

Bi, J. (2006). Sensory discrimination tests and measurements: Statistical principles,

procedures and tables. Oxford: Blackwell Publishing.

Bi, J. (2007). Bayesian analysis for proportions with an independent background

effect. British Journal of Mathematical and Statistical Psychology, 60, 71–83.

Bradley, R. (1953). Some statistical methods in taste testing and quality evaluation.

Biometrics, 9, 22–38.

Brockhoff, P. B. (2003). The statistical power of replications in difference tests. Food

Quality and Preference, 14, 405–417.

Carbonell, L., Carbonell, I., & Izquierdo, L. (2007). Triangle tests. Number of

discriminators estimated by Bayes’ rule. Food Quality and Preference, 18,
117–120.

Duineveld, K., & Meyners, M. (2008). Hierarchical Bayesian analysis of true

discrimination rates in replicated triangle tests. Food Quality and Preference,
19, 292–305.

Kunert, J. (2001). On repeated difference testing. Food Quality and Preference, 12,

385–391.

Meilgaard, M., Civille, G. V., & Carr, B. T. (1999). Sensory evaluation techniques (3rd

ed.). Boca Raton: CRC Press.

Fig. 2. Probability of success in 10 successive triangle trials as affected by success or
failure in previous trials.

S. Bayarri et al. / Food Quality and Preference 19 (2008) 519–523

523