J.Rusin@ib.uz.zgora.pl
MECHANIKA OGÓLNA
Zadanie nr 3
Wyznaczyć geometryczne charakterystyki układu figur płaskich
przedstawionego na schemacie
1
1
1
1 Ceownik normalny [
[[[180
h
1
= 18 cm = 0.180 m
b
1
= 7.0 cm = 0.070 m
e
z1
= 9.0 cm = 0.090 m
e
y1
= 1.92 cm = 0.0192 m
A
1
= 28.0 cm
2
= 2.800
·10
-3
m
2
J
y1
= 1350 cm
4
= 1.350
·10
-5
m
4
J
z1
= 114 cm
4
= 1.140
·10
-6
m
4
J
y1 z1
= 0
2
2
2
2 Kątownik równoramienny L 90
××××
90
××××
8
h
2
= b
2
= 9,0 cm = 0.090 m
e
y2
= e
z2
= 2.5 cm = 0.025 m
A
2
= 13.9 cm
2
= 1.390
·10
-3
m
2
ϕ
o2
= 45
°
=
π
/4
J
y2
= 104 cm
4
= 1.040
·10
-6
m
4
J
z2
= 104 cm
4
= 1.040
·10
-6
m
4
J
yg2
= 166 cm
4
= 1.660
·10
-6
m
4
J
zg2
= 43.1 cm
4
= 4.310
·10
-7
m
4
J
y2z2
=
J
yg2
−
J
zg2
2
sin
@
−
2
ϕ
o2
D
=
166 cm
4
−
43.1 cm
4
2
H
−
1
L
=
= −
61.450 cm
4
= −
6.145 10
−
7
m
4
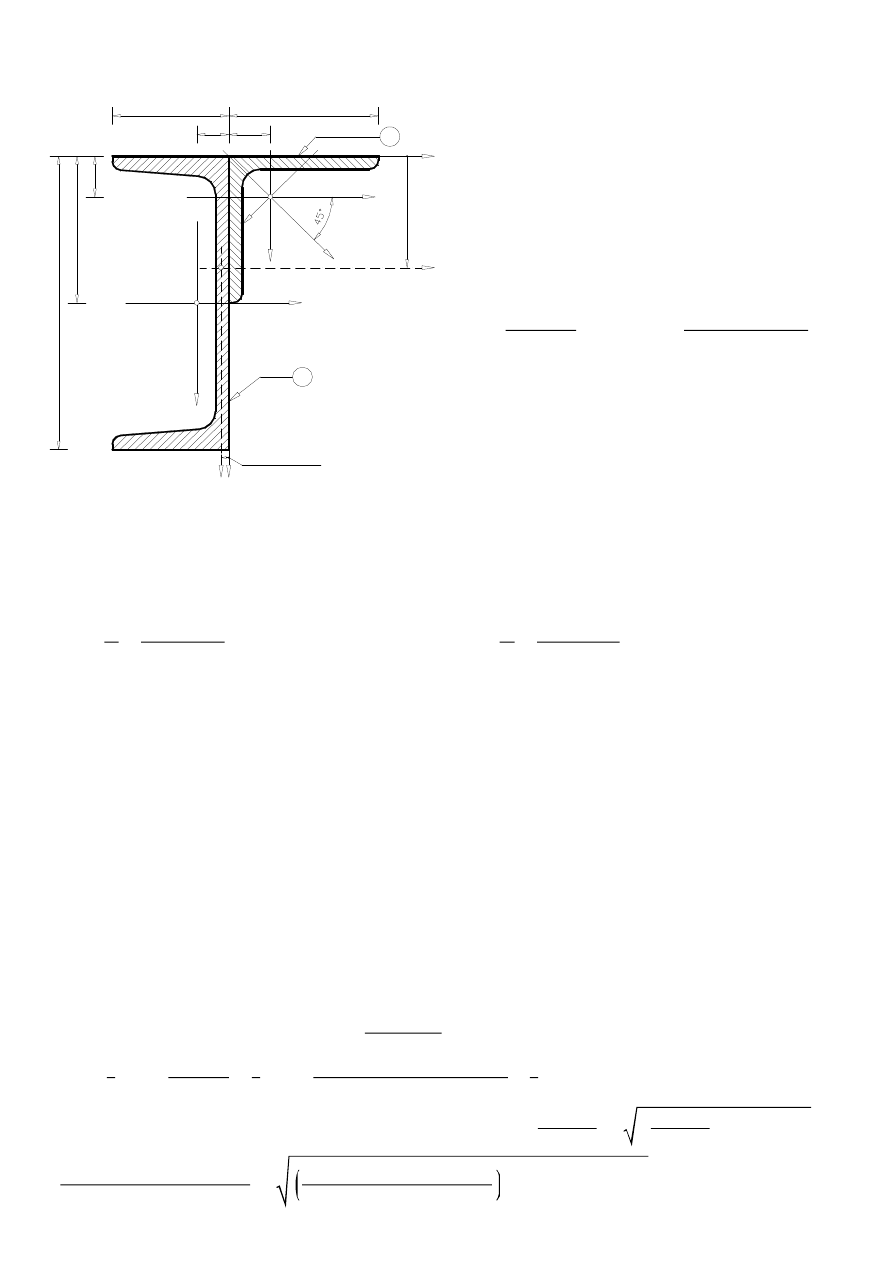
SCHEMAT ZADANIA
z
2
y
2
y
2g
z
2g
z
1
y
1
C
180
1
z
y
e
y1
e
y2
e
z2
e
z1
h
1
h
2
A
B
C
D
b
1
b
2
e
z
=
6
.8
4
4
c
m
e
y
= -0.454 cm
y
c
z
c
2
L 90
×
90
×
8
1.
Współrzędne środka układu centralnego.
1.1.
Pole przekroju.
A
=
‚
i
=
1
2
A
i
=
A
1
+
A
2
=
28.0 cm
2
+
13.9 cm
2
=
=
41.900 cm
2
=
4.190 10
−
3
m
2
1.2.
Moment statyczny przekroju względem osi y i z.
S
y
=
‚
i
=
1
2
z
i
A
i
=
e
z1
A
1
+
e
z2
A
2
=
9.0 cm 28.0 cm
2
+
2.5 cm 13.9 cm
2
=
286.750 cm
3
=
2.868 10
−
4
m
3
S
z
=
‚
i
=
1
2
y
i
A
i
= −
e
y1
A
1
+
e
y2
A
2
= −
1.92 cm 28.0 cm
2
+
2.5 cm 13.9 cm
2
= −
19.010 cm
3
= −
1.901 10
−
5
m
3
1.3.
Współrzędne środka ciężkości.
e
y
=
S
z
A
=
−
19.010 cm
3
41.9 cm
2
= −
0.454 cm
= −
0.0045 m
e
z
=
S
y
A
=
286.750 cm
3
41.9 cm
2
=
6.844 cm
=
0.0684 m
2.
Momenty bezwładności przekroju względem centralnego układu współrzędnych.
2.1.
Momenty bezwładności przekroju względem osi y
c
i z
c
.
J
yc
=
‚
i
=
1
2
I
J
yi
+
A
i
e
zi
2
M =
J
y1
+
A
1
H
e
z1
−
e
z
L
2
+
J
y2
+
A
2
H
e
z
−
e
z2
L
2
=
=
1350 cm
4
+
28.0 cm
2
H
9.0 cm
−
6.844 cm
L
2
+
104 cm
4
+
13.9 cm
2
H
6.844 cm
−
2.5 cm
L
2
=
=
1846.451 cm
4
=
1.846 10
−
5
m
4
J
zc
=
‚
i
=
1
2
I
J
zi
+
A
i
e
yi
2
M =
J
z1
+
A
1
H
e
y1
−
e
y
L
2
+
J
z2
+
A
2
H
e
y2
+
e
y
L
2
=
=
114 cm
4
+
28.0 cm
2
H
1.92 cm
−
0.454 cm
L
2
+
104 cm
4
+
13.9 cm
2
H
2.5 cm
+
0.454 cm
L
2
=
=
399.469 cm
4
=
3.995 10
−
6
m
4
2.2.
Moment dewiacji przekroju względem osi y
c
i z
c
.
J
yczc
=
‚
i
=
1
2
H
J
yizi
+
A
i
e
yi
e
zi
L
=
J
y1z1
+
A
1
H
−
e
y1
+
e
y
L H
e
z1
−
e
z
L
+
J
y2z2
+
A
2
H
e
y2
+
e
y
L H
e
z2
−
e
z
L
=
=
0
+
28.0 cm
2
H
−
1.92 cm
+
0.454 cm
L H
9.0 cm
−
6.844 cm
L
−
61.450 cm
4
+
+
13.9 cm
2
H
2.5 cm
+
0.454 cm
L H
2.5 cm
−
6.844 cm
L
= −
328.317 cm
4
= −
3.283 10
−
6
m
4
3.
Główne charakterystyki przekroju.
3.1.
Położenie osi głównych y
g
i z
g
.
ϕ
o
=
1
2
arctg
2 J
yczc
J
zc
−
J
yc
=
1
2
arctg
2
H
−
328.317 cm
4
L
399.469 cm
4
−
1846.451 cm
4
=
1
2
arctg
H
0.453796
L
=
0.213003 rad
=
12.204 °
3.2.
Momenty bezwładności przekroju względem osi y
g
i z
g
.
=
1846.451 cm
4
+
399.469 cm
4
2
+
−
1846.451 cm
4
−
399.469 cm
4
2
2
+
I
−
328.317 cm
4
M
2
=
1122.960 cm
4
+
−
794.501 cm
4
tg 2
ϕ
o
=
2 J
yczc
J
zc
−
J
yc
J
max
=
J
yg
J
min
=
J
zg
=
J
yc
+
J
zc
2
+
−
K
J
yc
−
J
zc
2
O
2
+
H
J
yczc
L
2
=
J.Rusin@ib.uz.zgora.pl
J
max
=
J
yg
=
1122.960 cm
4
+
794.501 cm
4
=
1917.461 cm
4
=
1.917
10
−
5
m
4
J
min
=
J
zg
=
1122.960 cm
4
−
794.501 cm
4
=
328.459 cm
4
=
3.285
10
−
5
m
4
4.
Kontrola rozwiązania.
4.1.
Biegunowy moment bezwładności przekroju (moment bezwładności względem początku układu współrzędnych).
J
o
=
J
yc
+
J
zc
=
1846.451 cm
4
+
399.469 cm
4
=
2245.920 cm
4
J
yg
+
J
zg
=
1917.461 cm
4
+
328.459 cm
4
=
2245.920 cm
4
=
2.246 10
−
5
m
4
Û
J
o
=
2245.920 cm
4
−
2245.920 cm
4
=
0.000 cm
4
H
0.0
% ≤
0.1
%
L
4.2.
Tensor bezwładności przekroju.
=
J
yc
J
zc
−
J
yczc
2
=
1846.451 cm
4
399.469 cm
4
−
H
−
328.317 cm
4
L
2
=
629 807.9 cm
8
J
yg
J
zg
=
1917.461 cm
4
328.459 cm
4
=
629 807.3 cm
8
=
6.298 10
−
11
m
8
Û
J
=
629807.9 cm
8
−
629 807.3 cm
8
=
0.6 cm
8
H
0.0001
% ≤
0.1
%
L
4.3.
Moment dewiacji względem osi głównych (
J
ygzg
=
0
).
J
ygzg
=
J
yc
−
J
zc
2
sin 2
ϕ
o
−
J
yczc
cos 2
ϕ
o
=
1846.451 cm
4
−
399.469 cm
4
2
sin
@
2
H
12.204 °
LD +
+
I−
328.317 cm
4
M
cos
@
2
H
12.204 °
LD =
723.491 cm
4
0.413232
−
328.317 cm
4
0.910626
=
=
298.970 cm
4
−
298.974 cm
4
= −
0.004 cm
4
≅
0
!
H
0.0013
% ≤
0.1
%
L
5.
Promienie bezwładności i elipsa bezwładności.
i
max
=
J max
A
=
i
zg
=
J yg
A
=
1917.461 cm4
41.900 cm2
=
6.765 cm
=
0.068 m
i
min
=
J min
A
=
i
yg
=
Jzg
A
=
328.459 cm4
41.900 cm2
=
2.800 cm
=
0.028 m
y
g
2
i
yg
2
+
Z
g
2
i
zg
2
=
1
⇒
y
g
2
H
28 mm
L
2
+
Z
g
2
H
68 mm
L
2
=
1
6.
Współrzędne punktów charakterystycznych w układzie współrzędnych centralnych i głównych.
Wzory transformacyjne:
y
g
=
y
c
cos
ϕ
o
+
z
c
sin
ϕ
o
z
g
=
z
c
cos
ϕ
o
−
y
c
sin
ϕ
o
Punkt A
y
Ac
= −
H
b
1
+
e
y
L
= −
H
7.0 cm
−
0.45 cm
L
=
= −
6.55 cm
z
Ac
= −
e
z
= −
6.84 cm
y
Ag
= −
6.55 cm cos 12.204 °
+
−
6.84 cm sin 12.204 °
= −
7.85 cm
z
Ag
= −
6.84 cm cos 12.204 °
+
+
6.55 cm sin 12.204 °
= −
5.30 cm
Punkt B
y
Bc
=
b
2
−
e
y
=
9.0 cm
+
0.45 cm
=
9.45 cm
z
Bc
= −
e
z
= −
6.84 cm
y
Bg
=
9.45 cm cos 12.204 °
+
−
6.84 cm sin 12.204 °
=
7.79 cm
z
Bg
= −
6.84 cm cos 12.204 °
+
−
9.45 cm sin 12.204 °
= −
8.68 cm
Punkt C
y
Cc
= −
e
y
=
0.45 cm
z
Cc
=
h
1
−
e
z
=
18 cm
−
6.84 cm
=
11.16 cm
y
Cg
=
0.45 cm cos 12.204 °
+
+
11.16 cm sin 12.204 °
=
2.80 cm
z
Cg
=
11.16 cm cos 12.204 °
+
−
0.45 cm sin 12.204 °
=
10.81 cm
Punkt D
y
Dc
= −
H
b
1
+
e
y
L
= −
H
7.0 cm
−
0.45 cm
L
=
= −
6.55 cm
z
Dc
=
h
1
−
e
z
=
18 cm
−
6.84 cm
=
11.16 cm
y
Dg
= −
6.55 cm cos 12.204 °
+
+
11.16 cm sin 12.204 °
= −
4.04 cm
z
Dg
=
11.16 cm cos 12.204 °
+
+
6.55 cm sin 12.204 °
=
12.29 cm
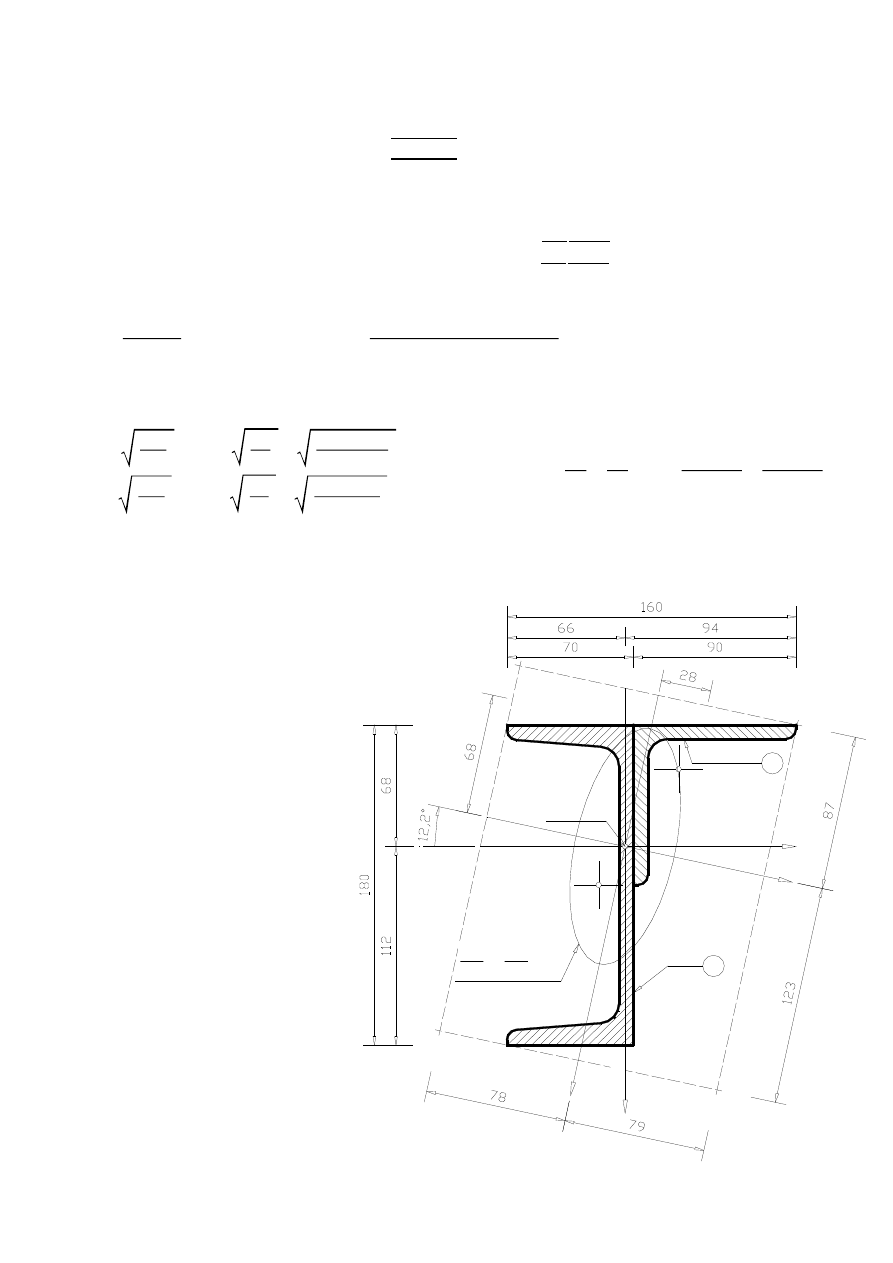
RYSUNEK ZESTAWCZY (wymiary długości w mm)
z
m
a
x
y
min
z
m
in
y
max
z
c
y
g
z
g
y
c
L
90
×
90
×
8
2
C
180
1
1918
cm
2246
cm
1846
cm
3
2
8
cm
4
0
0
cm
4
4
4
4
y
g
2
28
2
+
Z
g
2
68
2
=
1
4
A
B
C
D
Współrzędne ekstremalne w układzie głównym
y
max
=
y
Bg
=
7.79 cm
y
min
=
y
Ag
= −
7.85 cm
z
max
=
z
Dg
=
12.29 cm
z
min
=
z
Bg
= −
8.68 cm
Obliczenia wykonał/a: ………………….
Data: ……………..…...
J
=
£
J
yg
0
0
J
zg
ß = £
J
yc
J
yczc
J
yczc
J
zc
ß =
Wyszukiwarka
Podobne podstrony:
Zadanie nr 3 GP1 obliczenie błędów
Egzamin praktyczny Zadanie Nr 4
Zadanie nr 1 z treścią
Zadanie nr 3 screeny gotowe
zadanie nr 1 na zajęcia
Opis sposobów usunięcia usterki systemu zadanie nr 3
DANE DO ZADANIA NR 1
zadanie nr 7
zadanie nr 1
zadanie nr 2
zadanie nr 4
Zadanie nr 7
Zadanie nr I (wielokrotnego wyboru) + transkrypt + klucz, ROZUMIENIE ZE SLUCHU - przykladowe zadania
zadanie nr 17 tresc
zadanie nr 34 tresc
zadanie nr 83 tresc
zadanie nr 48 tresc
zadanie nr 69 tresc
zadanie nr 66 rozwiazanie
więcej podobnych podstron