6.6 Entropy Rate Balance for Control Volumes

237

Combining the mass and entropy rate balances

Solving for

and using Eq. 6.23 to evaluate changes in specific entropy

Thus, the second law of thermodynamics is also satisfied.

On the basis of this evaluation, the inventor’s claim does not violate principles of thermodynamics.

Since the specific heat c

p

of air varies little over the temperature interval from 0 to 79

C, c

p

can be taken as constant.

From Table A-20, c

p

Since temperature differences are involved in this calculation, the temperatures can be either in

C or K.

In this calculation involving temperature ratios, the temperatures must be in

K.

If the value of the rate of entropy production had been negative or zero, the claim would be rejected. A negative value is
impossible by the second law and a zero value would indicate operation without irreversibilities.

Such devices do exist. They are known as vortex tubes and are used in industry for spot cooling.

1.0 kJ /kg

# K.

0.454 kJ/kg # °K

0.6

c a1.0

kJ

kg

# °K

b

ln

255

294

a

8.314

28.97

kJ

kg

# °K

b

ln

1

5.0

d

0.4

c a1.0

kJ

kg

# K

b

ln

352

294

a

8.314

28.97

kJ

kg

# °K

b

ln

1

5.0

d

s

#

cv

m

#

1

0.4

c c

p

ln

T

2

T

1

R ln

p

2

p

1

d 0.6 c c

p

ln

T

3

T

1

R ln

p

3

p

1

d

s

#

cv

m

#

1

0.4m

#

1

1s

1

s

2

2 0.6m

#

1

1s

1

s

3

2 s

#

cv

m

#

2

1s

1

s

2

2 m

#

3

1s

1

s

3

2 s

#

cv

0

1m

#

2

m

#

3

2s

1

m

#

2

s

2

m

#

3

s

3

s

#

cv

❶

❷

❸

❹

❺

❸

❹

❺

In Example 6.8, we evaluate and compare the rates of entropy production for three com-

ponents of a heat pump system. Heat pumps are considered in detail in Chap. 10.

E X A M P L E 6 . 8

Entropy Production in Heat Pump Components

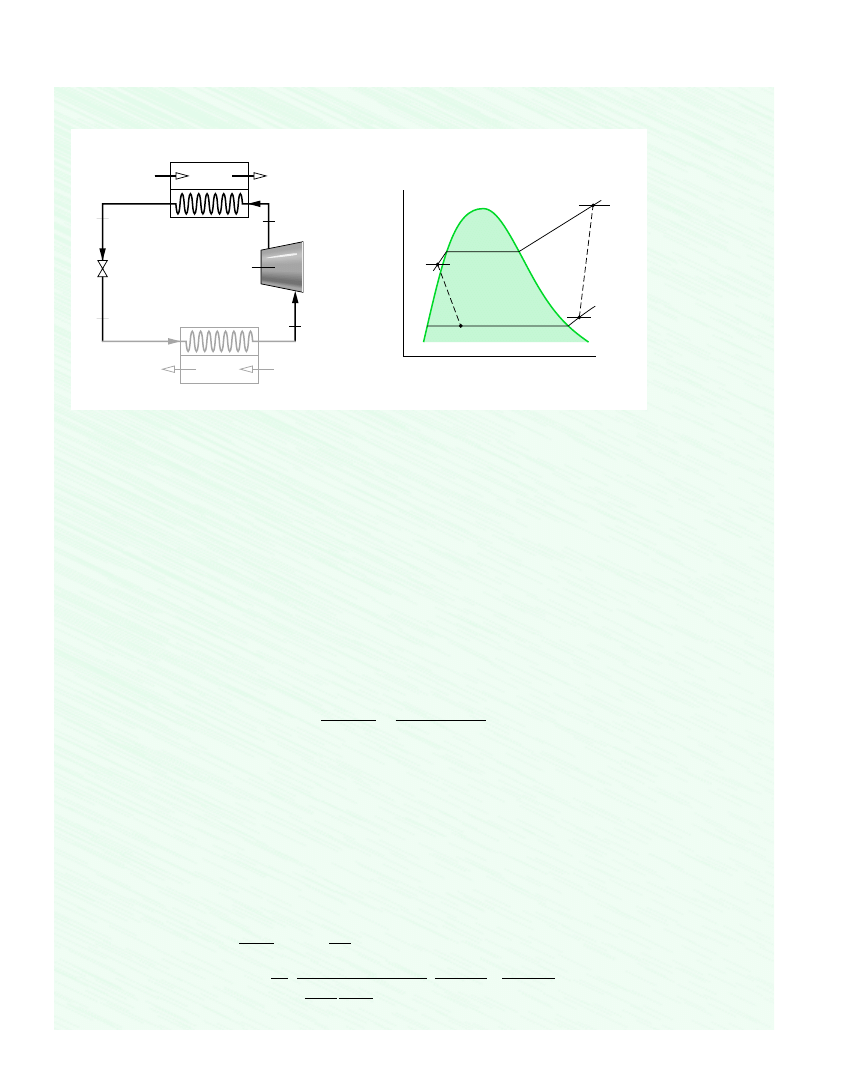
Components of a heat pump for supplying heated air to a dwelling are shown in the schematic below. At steady state,
Refrigerant 22 enters the compressor at

5C, 3.5 bar and is compressed adiabatically to 75C, 14 bar. From the com-

pressor, the refrigerant passes through the condenser, where it condenses to liquid at 28

C, 14 bar. The refrigerant then

expands through a throttling valve to 3.5 bar. The states of the refrigerant are shown on the accompanying T–s diagram.
Return air from the dwelling enters the condenser at 20

C, 1 bar with a volumetric flow rate of 0.42 m

3

/s and exits at

50

C with a negligible change in pressure. Using the ideal gas model for the air and neglecting kinetic and potential en-

ergy effects,

(a)

determine the rates of entropy production, in kW/K, for control volumes enclosing the condenser,

compressor, and expansion valve, respectively.

(b)

Discuss the sources of irreversibility in the components considered in

part (a).

S O L U T I O N

Known:

Refrigerant 22 is compressed adiabatically, condensed by heat transfer to air passing through a heat exchanger, and

then expanded through a throttling valve. Steady-state operating data are known.

Find:

Determine the entropy production rates for control volumes enclosing the condenser, compressor, and expansion valve,

respectively, and discuss the sources of irreversibility in these components.

238

Chapter 6 Using Entropy

Schematic and Given Data:

T

s

3

4

1

2

75

°C

–5

°C

28

°C

14 bar

3.5 bar

5

6

Expansion
valve

3

4

p

4

= 3.5 bar

p

3

= 14 bar

T

3

= 28

°C

Condenser

Indoor return air
T

5

= 20

°C

p

5

= 1 bar

(AV)

5

= 0.42 m

3

/s

1

2

T

1

= –5

°C

p

1

= 3.5 bar

p

2

= 14 bar

T

2

= 75

°C

Supply air
T

6

= 50

°C

p

6

= 1 bar

Evaporator

Outdoor air

Compressor

Assumptions:

1.

Each component is analyzed as a control volume at steady state.

2.

The compressor operates adiabatically, and the expansion across the valve is a throttling process.

3.

For the control volume enclosing the condenser,

and

.

4.

Kinetic and potential energy effects can be neglected.

5.

The air is modeled as an ideal gas with constant c

p

Analysis:

(a)

Let us begin by obtaining property data at each of the principal refrigerant states located on the accompanying schematic and

T–s diagram. At the inlet to the compressor, the refrigerant is a superheated vapor at

5C, 3.5 bar, so from Table A-9,

s

1

Similarly, at state 2, the refrigerant is a superheated vapor at 75

C, 14 bar, so interpolating in Table A-9

gives s

2

and h

2

294.17 kJ/kg.

State 3 is compressed liquid at 28

C, 14 bar. From Table A-7, s

3

s

f

(28

C)

and h

3

h

f

(28

C) 79.05 kJ/kg.

The expansion through the valve is a throttling process, so h

3

h

4

. Using data from Table A-8, the quality at state 4 is

and the specific entropy is

Condenser.

Consider the control volume enclosing the condenser. With assumptions 1 and 3, the entropy rate balance reduces to

To evaluate

requires the two mass flow rates,

and

, and the change in specific entropy for the air. These are ob-

tained next.

Evaluating the mass flow rate of air using the ideal gas model (assumption 5)

a0.42

m

3

s

b

11 bar2

a

8.314

28.97

kJ

kg

# K

b 1293 K2

`

10

5

N/m

2

1 bar

`

`

1 kJ

10

3

N

# m

` 0.5 kg/s

m

#

air

1AV2

5

v

5

1AV2

5

p

5

RT

5

m

#

ref

m

#

air

s

#

cond

0

m

#

ref

1s

2

s

3

2 m

#

air

1s

5

s

6

2 s

#

cond

s

4

s

f4

x

4

1s

g4

s

f4

2 0.1328 0.21610.9431 0.13282 0.3078 kJ/kg # K

x

4

1h

4

h

f4

2

1h

fg

2

4

179.05 33.092

1212.912

0.216

0.2936 kJ/kg

# K

0.98225 kJ/kg

# K

0.9572 kJ/kg

# K.

1.005 kJ/kg

# K.

Q

#

cv

0

W

#

cv

0

Figure E6.8

❶

6.6 Entropy Rate Balance for Control Volumes

239

The refrigerant mass flow rate is determined using an energy balance for the control volume enclosing the condenser together
with assumptions 1, 3, and 4 to obtain

With assumption 5, h

6

h

5

c

p

(T

6

T

5

). Inserting values

Using Eq. 6.23, the change in specific entropy of the air is

Finally, solving the entropy balance for

and inserting values

Compressor.

For the control volume enclosing the compressor, the entropy rate balance reduces with assumptions 1 and 3 to

or

Valve.

Finally, for the control volume enclosing the throttling valve, the entropy rate balance reduces to

Solving for

and inserting values

(b)

The following table summarizes, in rank order, the calculated entropy production rates:

Component

.

cv

(kW/ K)

compressor

17.5

10

4

valve

9.94

10

4

condenser

7.95

10

4

9.94 10

4

kW/K

s

#

valve

m

#

ref

1s

4

s

3

2 a0.07

kg

s

b 10.3078 0.29362

a

kJ

kg

# K

b

`

1 kW

1

kJ/s

`

s

#

valve

0

m

#

ref

1s

3

s

4

2 s

#

valve

17.5 10

4

kW/K

a0.07

kg

s

b 10.98225 0.95722 a

kJ

kg

# K

b

`

1

kW

1

kJ/s

`

s

#

comp

m

#

ref

1s

2

s

1

2

0

m

#

ref

1s

1

s

2

2 s

#

comp

7.95 10

4

kW

K

c a0.07

kg

s

b 10.2936 0.982252

kJ

kg

# K

10.52

10.0982 d

`

1 kW

1

kJ/s

`

s

#

cond

m

#

ref

1s

3

s

2

2 m

#

air

1s

6

s

5

2

s

#

cond

a1.005

kJ

kg

# K

b

ln

a

323

293

b R ln

a

1.0

1.0

b

0

0.098 kJ/kg # K

s

6

s

5

c

p

ln

T

6

T

5

R

ln

p

6

p

5

m

#

ref

a0.5

kg

s

b a1.005

kJ

kg

# K

b 1323 2932K

1294 .17 79 .052 kJ/kg

0.07 kg/s

m

#

ref

m

#

air

1h

6

h

5

2

1h

2

h

3

2

❷

❸

240

Chapter 6 Using Entropy

Entropy production in the compressor is due to fluid friction, mechanical friction of the moving parts, and internal heat trans-
fer. For the valve, the irreversibility is primarily due to fluid friction accompanying the expansion across the valve. The prin-
cipal source of irreversibility in the condenser is the temperature difference between the air and refrigerant streams. In this
example, there are no pressure drops for either stream passing through the condenser, but slight pressure drops due to fluid
friction would normally contribute to the irreversibility of condensers. The evaporator lightly shown in Fig. E6.8 has not been
analyzed.

Due to the relatively small temperature change of the air, the specific heat c

p

can be taken as constant at the average of

the inlet and exit air temperatures.

Temperatures in K are used to evaluate

but since a temperature difference is involved the same result would be ob-

tained if temperatures in

C were used. Temperatures in K must be used when a temperature ratio is involved, as in Eq. 6.23

used to evaluate s

6

s

5

.

By focusing attention on reducing irreversibilities at the sites with the highest entropy production rates, thermodynamic
improvements may be possible. However, costs and other constraints must be considered, and can be overriding.

m

#

ref

,

❶

❷

❸

6.7

Isentropic Processes

The term isentropic means constant entropy. Isentropic processes are encountered in many
subsequent discussions. The object of the present section is to explain how properties are re-
lated at any two states of a process in which there is no change in specific entropy.

6.7.1

General Considerations

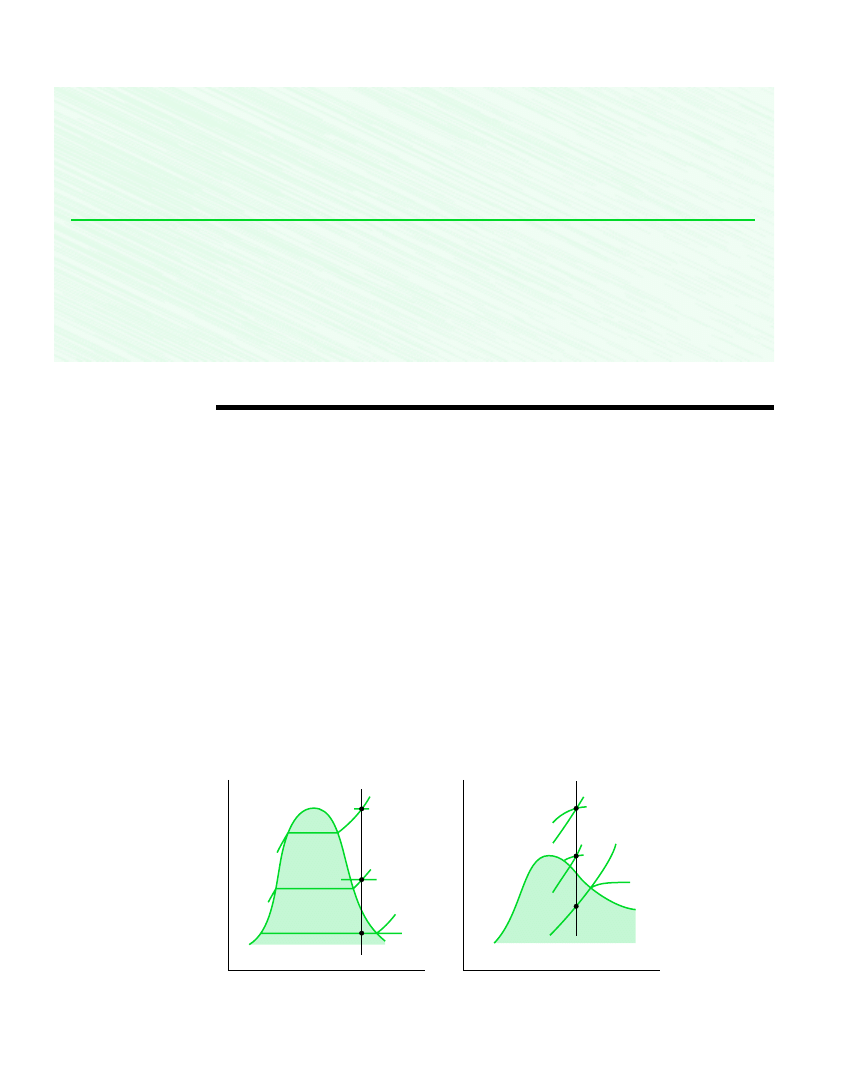
The properties at states having the same specific entropy can be related using the graphical
and tabular property data discussed in Sec. 6.3.1. For example, as illustrated by Fig. 6.9, tem-
perature–entropy and enthalpy–entropy diagrams are particularly convenient for determining
properties at states having the same value of specific entropy. All states on a vertical line
passing through a given state have the same entropy. If state 1 on Fig. 6.9 is fixed by pres-
sure p

1

and temperature T

1

, states 2 and 3 are readily located once one additional property,

such as pressure or temperature, is specified. The values of several other properties at states
2 and 3 can then be read directly from the figures.

Tabular data also can be used to relate two states having the same specific entropy. For

the case shown in Fig. 6.9, the specific entropy at state 1 could be determined from the
superheated vapor table. Then, with s

2

s

1

and one other property value, such as p

2

or T

2

,

Figure 6.9

T–s and h–s diagrams showing states having the same value of

specific entropy.

T

1

2

3

p

1

T

1

p

2

p

3

T

2

T

3

h

s

s

1

2

3

p

1

T

1

p

2

p

3

T

2

T

3