
24
Grain Property Values and Their
Measurement
Digvir S. Jayas and Stefan Cenkowski
CONTENTS
24.1 Introduction.......................................................................................................................................... 575
24.2 Physical Properties................................................................................................................................ 576
24.6 Optical Properties ................................................................................................................................. 596
24.7 Aerodynamic Properties ....................................................................................................................... 598
List of Symbols .............................................................................................................................................. 599
References ...................................................................................................................................................... 600
24.1 INTRODUCTION
The world produces annually about 2 billion tonnes (Gt)
of grains and oilseeds [1] that are handled and stored
on- and off-farm for periods of up to 3 y. Often the
storage period may be longer than 3 y, for example,
when the grain is stored for potential famine relief. To
design handling, inspection, and storage systems for
grains and oilseeds, data on many properties of indivi-
dual seeds and seeds in bulk are needed. The properties of
interest are: bulk and particle densities, porosity, round-
ness, sphericity, friction coefficients of grains against
commonly used bin wall materials, emptying and fill-
ing angles of repose, equilibrium moisture content
(EMC), specific heat, thermal conductivity, dielectric
constant, electrical conductivity, reflectance, terminal
ß
2006 by Taylor & Francis Group, LLC.

velocity, and drag coefficient. There are many
methods of measuring these properties. In this chap-
ter, only the methods that are currently in use or
widely accepted methods are described. Representa-
tive property values for common grains and oilseeds
are summarized from the published literature.
The properties of grains and oilseeds are measured
on representative samples and are affected by many
factors such as moisture content, growing location,
amount and type of foreign material in the sample,
and conditions of the surroundings. Many properties
also depend on other properties. For example, ther-
mal conductivity of bulk grain depends on its bulk
density. Care must be taken in obtaining a represen-
tative sample because the great care taken in measur-
ing a property will only give a good property value for
the sample used. Ideally, representative samples from
many different growing locations, growing years, and
cultivars should be used to arrive at a grain property
value that can be used in engineering design. Unfor-
tunately, such studies become cost prohibitive and
coordinated efforts among world scientists are needed
to improve on the database for grain properties. At
times, results of a well planned and executed project
on measurement of grain properties become less use-
ful when incomplete information about the sample is
given in the published literature. Therefore, when
reporting, a complete description of the sample
should be given. For example, usefulness of data on
bulk density of wheat without knowing at least its
moisture content and class of wheat may be dimin-
ished considerably for an engineering design.
24.2 PHYSICAL PROPERTIES
24.2.1 B
ULK
D
ENSITY
(T
EST
W
EIGHT
)
Bulk density is defined as the ratio of the mass of the
sample to the volume occupied by the bulk sample and
is expressed in the units of kg/m
3
. The bulk volume
includes the volume of intergranular air and grain. In
the grain trade, the term test weight is used, which is
defined as the mass of a measured volume of grain
expressed in kg/hL (lb/bu). Standard methods for de-
termining test weights are used by regulatory agencies
around the world (e.g., Canadian Grain Commission
[2]). The bulk density values reported in the literature
are usually determined for clean grain at a specified
moisture content by using the equipment and proced-
ure for determination of test weight. The values thus
determined are lower than the values that are expected
in storage. The bulk density of grain in storage can be
affected by the method used for filling the structure
and by the amount and type of foreign material in the
grain. For example, a bin filled using a spreader gives a
higher bulk density than a bin filled using a spout, or
increasing the drop height during spout filling in-
creases the bulk density. Also, the presence of foreign
materials that are finer and heavier than grain kernels
increases storage bulk density.
Bulk density of a clean grain sample (for corn, the
sample is not cleaned) is determined by filling a 500-
mL metallic container (90 mm diameter and 78 mm
high) from a funnel with a 38.1 mm opening and
having a flat slide gate. The opening of the funnel is
maintained at 44.1 mm above the top of the con-
tainer. Grain required to fill the container plus a
small additional amount are loaded into the funnel
whereas its gate is closed. When the gate is opened,
the sample flows freely from the funnel into the center
of the container and fills the container to overflowing.
The grain in the container is leveled by striking off the
excess grain with a round rod (19-mm diameter hard-
wood) using three equal zigzag movements at an
angle to the direction of movement of approximately
458. The mass of the grain in the container is meas-
ured and the bulk density (kg/m
3
) or the test weight
(kg/hL) is calculated (Canadian Grain Commission
[2]). The bulk density for common grains and oilseeds
are summarized in Table 24.1 (ASAE [3]).
TABLE 24.1
Approximate Bulk Density of Grains and Other Seeds
Seed
Bulk Density (kg/m
3
)
Alfalfa
772
Barley
618
Beans Lima dry
721
Buckwheat
618
Canola (rapeseed)
669
Corn shelled
721
Lentils
772
Oats
412
Peanuts, unshelled
Virginia type
219
Spanish
322
Rice, rough
579
Rye
721
Sorghum grain
721
Sunflower seed (nonoil)
309
Sunflower seed (oil)
412
Soybeans
772
Timothy seed
579
Wheat
772
Source: From ASAE, D241.4 Feb. 93, Density, specific gravity,
and mass–moisture relationships of grain for storage, 40th ed.,
Standards, Engineering Practices, and Data (Am. Soc. Ag. Eng.),
St. Joseph, MI, 1993, pp. 408–410. With permission.
ß
2006 by Taylor & Francis Group, LLC.

24.2.2 P
ARTICLE
D
ENSITY
Two other terms true density and kernel density are
used as synonyms to the particle density. Particle dens-
ity is defined as the ratio of the mass of a sample to the
volume occupied by the kernels (excluding the inter-
granular air) of the sample. The kernel volume can be
determined using either of these two methods: liquid
displacement method (LDM) and air comparison
pycnometer (ACP) (e.g., Model 930, Beckman Instru-
ments Inc., Fullerton, CA). In the LDM, a known
mass of grain is poured into a graduated cylinder
filled with a liquid to a known level. The change in
the volume of the liquid is determined by subtracting
the initial liquid volume reading from the final liquid
volume reading. The liquid should not be sorbed
(adsorbed or absorbed) by the solid particles; there-
fore, toluene is commonly used for grains and oil-
seeds. The main problem with the LDM is that tiny
air bubbles on the surface of the solid particles may
be present and included in the volume of the particles.
Also, liquid may not displace all the intergranular air.
The ACP measures the true volume of the solid par-
ticles. The particle densities of some grains are given
in Table 24.2 (ASAE [3]).
24.2.3 P
OROSITY
The terms percent voids, percent airspace, percent
pore volume, and porosity are used interchangeably
in the literature. Porosity is defined as the ratio of the
volume occupied by the intergranular air to the total
volume of the bulk sample and is expressed in per-
cent. Usually, the porosity is calculated from the bulk
and particle densities of a sample and thus can be
considered as a derived quantity*:
¼ 1
r
b
r
t
100:
(24:1)
TABLE 24.2
Porosity and Particle Density of Selected Seeds
Seed
Cultivar
Moisture Content (% wet basis)
Porosity (%)
Particle Density (kg/m
3
)
Barley
Coast (6 rows)
10.3
57.6
1130
Barley
Hannchen
9.7
44.5
1260
Barley
Synasota
9.8
45.4
1210
Barley
Trebi (6 rows)
10.7
47.9
1240
Barley
White hullness
10.4
39.5
1330
Buckwheat
Japanese
10.1
41.0
1100
Canola
Tobin
6.5
38.4
1150
Canola
Westar
6.7
38.9
1100
Corn, mixed
Yellow and white
9.0
40.0
1190
Corn, shelled
Yellow, dent
25.0
44.0
1270
Corn, shelled
Yellow, dent
15.0
40.0
1300
Flaxseed
5.8
34.6
1100
Grain sorghum
Blackhull kafir
9.9
36.8
1260
Grain sorghum
Yellow milo
9.5
37.0
1220
Millet
Siberian
9.4
36.8
1110
Oats
Iowar
9.7
51.4
950
Oats
Kanota
9.4
50.9
1060
Oats
Red Texas
10.3
55.5
0990
Oats
Victory
9.8
47.6
1050
Rice
Honduras
11.9
50.4
1110
Rice
Wataribune
12.4
46.5
1120
Rye
Common
9.7
41.2
1230
Soybeans
Wilson
7.0
33.8
1130
Wheat, hard
Turkey, winter
9.8
42.6
1300
Wheat, hard
Turkey, winter (yellow)
9.8
40.1
1290
Wheat, soft
Harvest Queen
9.8
39.6
1320
Source: From ASAE, D241, 4 Feb. 93, Density, specific gravity, and mass–moisture relationships of grain for storage, 40th ed.,
Standards, Engineering Practices, and Data (Am. Soc. Ag. Eng.), St. Joseph, MI, 1993, pp. 408–410. With permission.
*Symbols are defined in the List of Symbols.
ß
2006 by Taylor & Francis Group, LLC.
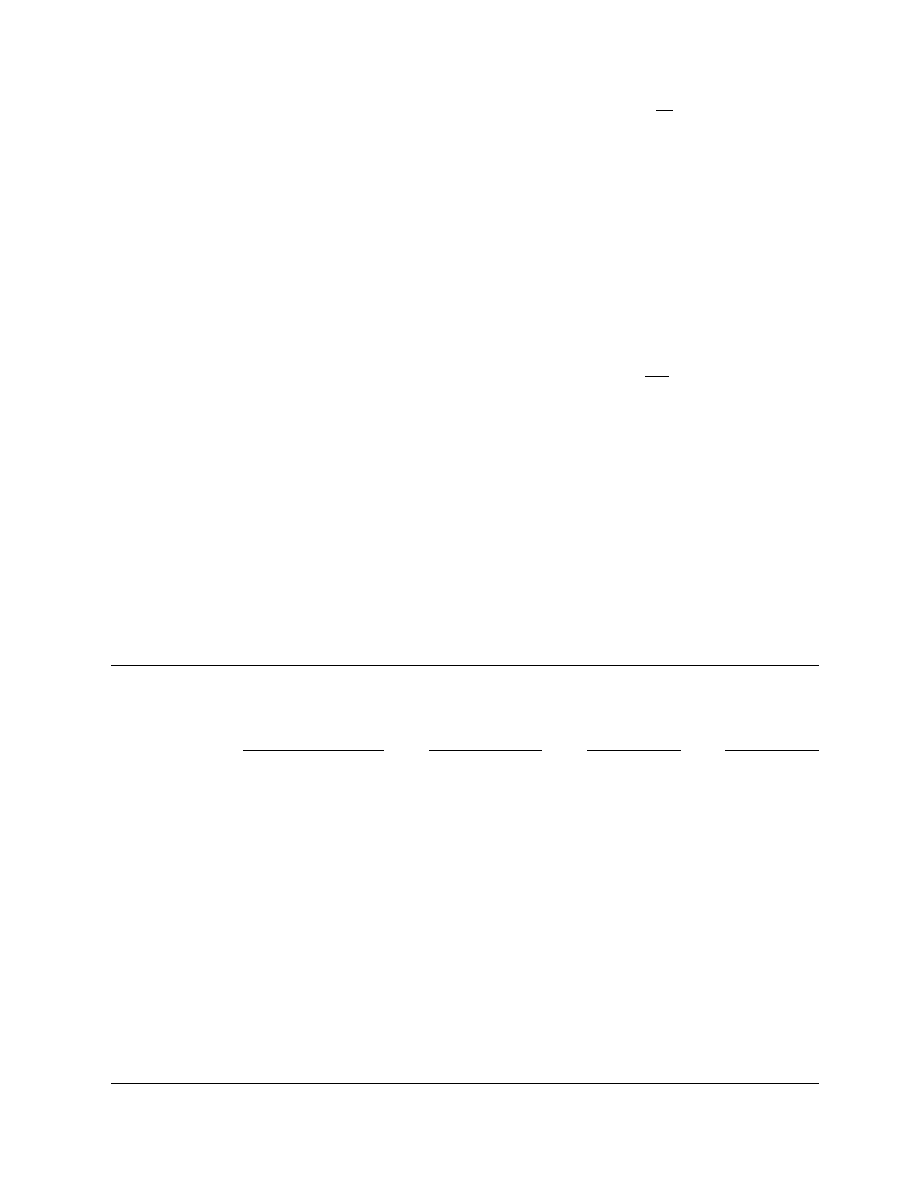
Porosit y can be measur ed directly using a method
describ ed by Day [4]. The por osities for common
seeds a re given in
24.2.4 P
ROJECTED
A
REA
Kernels of all grains and oilseeds, when dropp ed on a
flat horizont al surfa ce, rest in their most stable pos -
ition. The area covered (viewed from the direction
perpend icular to the surfa ce) by a kernel in its most
stable posit ion is defined as the project ed area (mm
2
)
and can be determ ined by tracin g the kernel on a
graph paper and by esti mating the numb er of squ ares
in the enclosed tracin g. A planimeter can also be used
for quantific ation of the area. The lengt h an d width of
the minimum rectangle that encloses the pro jected
area are de fined as princip al major and minor ax es
or lengt h and wi dth of grain kernels, respectivel y. The
length obta ined by traci ng along the circum ferenc e of
the project ed area is defi ned as the perimeter of a
kernel. The projecte d area, lengt h, width, an d perim -
eter of kernels can be measu red easily using a digit al
image process ing system [5] and the values for many
seed types are given in Table 24.3.
24.2.5 R
OUNDNESS
Roundn ess of a grain kernel is de fined as the ratio of
the kernel’ s projected area in its most stabl e position
to the area of the smallest circum scri bing circl e:
R
¼
A
p
A
c
(24 : 2)
24.2.6 E
QUIVALENT
V
OLUME
(E
QUIVALENT
D
IAMETER
)
A sphere whose volume is equal to the volume of a grain
kernel is defined as the equivalent sphere of the kernel.
The diameter of the sphere of equivalent volume is
defined as the equivalent diameter of the kernel. The
average equivalent volume of kernels can be determined
by using a particle density method (
and counting the kernels. The equivalent diameter is
calculated from the measured volume as
d
e
¼
6V
e
p
1 = 3
(24 : 3)
Common ly, the volume occupied by 10 00 ke rnels
(random ly selec ted) is measur ed and the average
equival ent volume and the diame ter are calculated
and report ed (
The geomet ric mean diame ter, D
g
, is another term
that is used to describ e the shape of ke rnels. It is
calculated as
D
g
¼ ( a b c )
1 =3
(24 : 4)
Physical ly, the terms a, b, and c are the lengt h, wi dth,
and height, respectivel y of the smallest parallelepi ped
that will full y en close the kernel.
TABLE 24.3
Physic al Dimens ions of Var ious Seeds
Seed Projected Area (mm
2
) Perimeter (mm)
a
Length (mm) Width (mm)
Mean SD
b
Mean SD
b
Mean SD
b
Mean SD
b
Wheat (HRS)
c
15.0 2.2 14.6 1.1 5.3 0.4 3.2 0.4
Barley 23.0 2.9 20.5 1.7 8.3 0.8 3.4 0.3
Canola 2.4 0.5 5.1 0.6 1.6 0.2 1.5 0.2
Brown mustard 1.9 0.3 4.5 0.5 1.5 0.2 1.3 0.2
Yellow mustard 3.9 0.6 6.8 0.6 2.2 0.2 1.9 0.2
Oriental mustard 2.4 0.3 5.1 0.4 1.7 0.2 1.5 0.2
Laird lentils 36.0 3.6 21.8 1.2 6.7 0.4 6.4 0.4
Eston lentils 16.0 2.0 14.5 1.0 4.5 0.3 4.3 0.3
Pea beans 40.0 4.6 23.4 1.4 7.8 0.5 6.1 0.5
Green peas
35.0
3.3
21.6
1.0
6.6
0.3
6.4
0.4
Black beans
45.0
5.7
25.3
1.7
8.4
0.6
6.6
0.6
Buckwheat
19.0
2.9
16.5
1.5
5.6
0.7
4.2
0.4
Flaxseed
6.4
0.5
10.1
0.4
3.9
0.2
1.8
0.1
a
b
SD
¼ Standard deviation based on n ¼ 1000.
c
HRS, Hard red spring.
Source: From Shatadal, P., Jayas, D.S., Hehn, J.L., and Bulley, N.R., Can. Agric. Eng., 37(3), 163, 1995. With permission.
ß
2006 by Taylor & Francis Group, LLC.

24.2.7 S
PHERICITY
Spherici ty of a ke rnel is define d as: the ratio of the
volume of a kernel to the vo lume of the smallest
circum scribing sph ere; or the rati o of the equival ent
diame ter of the kern el to the diame ter of the smallest
circum scribing sphere; or the rati o of the geomet ric
mean diameter of a kernel to the diame ter of the
smallest circum scrib ing sph ere.
24.2.8 S
URFACE
A
REA
Surface area is the area of the outer surfa ce of a kernel.
An approxim ate su rface area can be de termined by
assum ing grain ke rnels are ellip soids wi th major or
minor axes a and b, an d by calcul ating the surface
area of the ellipsoid using known mathe matical rela-
tionsh ips [6]. An approxim ate surfa ce area can also be
estimat ed by assum ing the kerne l as a sph ere of equiva-
lent diameter. A method of measur ing su rface area of
grains is by c oating grains with a single layer of meta l
particles [7–9] . A known mass of kernels is dipped in
varnish . The excess varnis h is remove d by roll ing ker-
nels on pa per tow el and by air drying. The kernels are
swirled with nickel particles and the mass of coa ted
kernels is determ ined. For convert ing the chan ge in
mass of the kernels to the surfa ce area, parti cles of
known geo metry (surf ace area) having specific gravi ty
simila r to the specific gravi ty of grain ke rnels are
coated in a sim ilar mann er and change in their mass
is determined . By applyin g the pr oportio nality rule the
surface area of particles is calculated. The surfa ce a rea
of some grains is given in Tabl e 24.4.
24.2.9 E
MPTYING AND
F
ILLING
A
NGLES OF
R
EPOSE
Emptying angles of repose of samples are measured by
emptying grain from a box (e.g., a wooden box 430 mm
long, 200 mm wide, and 430 mm high). The dimensions
of the box are arbitrary except that the accuracy of
measurement improves with increased length of slope.
The box is filled with samples to a depth of 350 mm.
Samples are allowed to flow out through a 50-mm high
and 200-mm wide rectangular opening provided along
the width of the box at the bottom of one end wall.
Emptying angles are calculated from measurements of
horizontal and vertical scale readings.
Fill ing angles of repose can be measur ed using a
box wi th one side made of Pl exiglass (e.g., a wooden
box 12 00 mm long, 100 mm wi de, and 76 0 mm high).
Sample s are allow ed to flow freel y through a 50-m m
square opening in a wooden hopper, whose center is
maintained 1000 mm above the bottom of the receiv-
ing box. Filling angles are calculated from measure-
ments of sample profile depth at two horizontally
spaced points 300 mm apart. The first point is chosen
approximately 100 mm away from the impact flat-
tened apex of the cone. Filling angles are measured
on both sides of the apex and averaged for individual
replicates. Typical values of emptying and filling
angles of repose of grains and oilseeds are given in
TABLE 24.4
Equivalent
a
Diameter (d
e
), Surface Area (A), and Volume (V
e
) of Kernels of Selected Seeds
Seed
d
e
(mm)
A (mm
2
)
V
e
(mm
3
)
Ref.
Beans
b
6.64
138
153
103
Corn
7.37
170
209
104
Corn
7.88
195
256
105
Corn, Inra 258
7.28
166
199
106
Corn, Velox
7.14
160
190
106
Corn, Dekalb XL72A
c
7.61
182
231
107
Corn, Pioneer 3388
c
7.16
161
192
107
Corn, N7A X N28
c
8.18
210
286
107
Flax
1.90
11.34
3.59
104
Fababeans
b
8.63
234
336
103
Lupin
b
5.73
103
98
103
Peas
b
6.28
124
130
103
Poppy seed
0.99
3.11
0.52
104
Wheat
3.48
38.04
22.07
104
a
Equivalent diameter was calculated from measured V
e
and A was calculated from d
e
.
b
Moisture content
¼ 0% wb.
c
Moisture content
¼ 10.5% wb.
ß
2006 by Taylor & Francis Group, LLC.

24.2.10 F
RICTION
C
OEFFICIENTS AGAINST
S
TRUCTURAL
M
ATERIALS
Coeffic ients of sli ding fri ction agains t v arious struc -
tural surfa ces are determ ined by using a tilting table .
The surface of inter est is atta ched to the tilting
table. A wooden fram e (305 mm long and 255 mm
wide), made of 18-mm square wood, is placed lengt h-
wise on the surfa ce to prev ent kernels from roll ing
down the surfa ce. It is filled wi th the sample and
leveled. The frame is lifted slowly to an approxim ate
height of 2–3 mm, so that the fram e does not rest on
the surfa ce. Usin g a man ually driven screw, the table
is tilted slowly until the sampl e starts to slide. The
angle of the tilting table is measur ed using a pro -
tractor and a plu mb bob. The co efficien t of fri ction
is calcul ated as the tangent of the angle measur ed [10] .
The fri ction coeffici ent agains t verti cal surfa ces is
needed in bin design. To measur e the fri ction coeffi-
cients agains t vertical walls, a system de scribed by
Irvine e t al. [11] can be used. The values of sliding
frictio n agains t fou r struc tural mate rials for common
grains and oils eeds are given in
24.3 HYGROSCOPIC PROPERTIES
24.3.1 M
OISTURE
M
EASUREMENT
A common method for de termining mois ture co ntent
of grains an d oilseeds is to dry samples in triplic ate in
a co nvection air oven at a specified tempe ratur e for a
specified durati on (
; ASAE [12]). Abou t
10–15 g samples a re weighed in covered aluminum
dishes . The dishes are unc overed and placed with
their covers in the oven at the set tempe rature. At
the end of the drying period, dishes are covered and
placed in a de siccator for coo ling to the room tem-
peratur e. The dishes wi th dried sample are weighed
again. Moisture co ntent of sampl es is calculated a s
the ratio of the mass loss divide d by the mass of the
original sample and is exp ressed in percent age on a
wet mass basis (wb ). In theo ries of grain dr ying, the
moisture co ntents of sampl es are usua lly express ed
on a dry mass ba sis (db), whi ch is calcul ated as the
ratio of the mass of water divide d by the mass of dry
matter an d is express ed as a percent age or decim al
fraction. To avoid confusi on as to which basis the
moisture con tent is report ed in a pa rticular chapter ,
it is suggested that the scientific commun ity adop t a
conventi on to report moisture co ntents on wet basis
in percent age and moisture content s on dry ba sis in
decim al fraction.
24.3.2 M
EASUREMENT OF
E
QUILIBRIUM
M
OISTURE
C
ONTENT
There are two common methods (static and dynami c)
for measuring the EMC–equilibrium relative humidity
(ERH) relationships of grains and oilseeds. The static
method is also known as the EMC method and the
dynamic method is also known as the ERH method.
In the static method, a sample of known mass is
allowed to reach equilibrium with air maintained at a
constant relative humidity and temperature. The
moisture content of the sample at equilibrium is
measured and is defined as the EMC. The constant
relative humidity environments are usually created
using saturated salt solutions in containers [13].
TABLE 24.5
Emptying and Filling Angles of Repose of Selected Seeds
Seed
Moisture Content (% wb)
Emptying Angle (8)
Filling Angle (8)
Ref.
Barley (cv. ‘Bedford’)
12.7
26
24
108
Durum wheat (cv. ‘Wakoma’)
12.7
24
24
108
Oats (cv. ‘Harmon’)
12.7
27
28
108
Rye (cv. ‘Gazelle’)
12.7
21
25
108
Rapeseed (cv. ‘Candle’)
8.1
26
24
108
Sunflower (cv. ‘Sundak’)
8.1
22
21
108
Soybean (cv. ‘McCall’)
8.1
29
—
108
Triticale (cv. ‘Carman’)
12.7
21
23
108
Wheat (cv. ‘Neepawa’)
12.7
27
26
108
Fababeans (cv. ‘Ackerperle’)
12.6
28
29
10
Flaxseed (‘McGregor’)
7.0
30
26
10
Lentils (cv. ‘Laird’)
13.8
24
24
10
50%-Hulless barley (cv. ‘Condor’)
14.5
24
23
109
95%-Hulless barley (cv. ‘Condor’)
14.0
24
23
109
ß
2006 by Taylor & Francis Group, LLC.

A container with a 10- to 15-g sample suspended in
the environment above the saturated salt solution is
kept at a constant temperature. The experiment must
be repeated at several temperatures and relative
humidities. The sample is weighed at a regular inter-
val of 3–12 h until the change in sample mass between
two successive readings is less than 0.01 g (at this
stage it is assumed that the sample has reached
TABLE 24.6
Coefficients of Sliding Friction against Four Different Structural Materials for Selected Seeds
Seed
Moisture
Content (% wb)
Galvanized
Steel
Steel Troweled
Concrete
Wood Floated
Concrete
Plywood
Ref.
Barley (cv. ‘Bedford’)
12.7
0.29
0.38
0.45
—
108
Durum wheat (cv. ‘Wakoma’)
12.7
0.29
0.39
0.45
—
108
Oats (cv. ‘Harmon’)
12.7
0.27
0.40
0.44
—
108
Rye (cv. ‘Gazelle’)
12.7
0.30
0.38
0.41
—
108
Rapeseed (cv. ‘Candle’)
8.1
0.24
0.30
0.39
—
108
Sunflower (cv. ‘Sundak’)
8.1
0.35
0.40
0.40
—
108
Soybean (cv. ‘McCall’)
8.1
0.27
0.33
0.34
—
108
Triticale (cv. ‘Carman’)
12.7
0.39
0.38
0.39
—
108
Wheat (cv. ‘Neepawa’)
12.7
0.32
0.42
0.47
—
108
Fababeans (cv. ‘Ackerperle’)
12.6
0.29
0.31
0.29
0.28
10
Flaxseed (‘McGregor’)
7.0
0.27
0.42
0.44
0.33
10
Lentils (cv. ‘Laird’)
13.8
0.25
0.34
0.31
0.24
10
50%-Hulless barley (cv. ‘Condor’)
14.5
0.29
0.39
0.40
0.31
109
95%-Hulless barley (cv. ‘Condor’)
14.0
0.32
0.40
0.41
0.32
109
TABLE 24.7
Oven Temperature and Heating Period for Moisture Content Determinations
Seed
Oven Temperature +18C
Heating Temperature
Sample Size (g)
h
min
Alfalfa
130
2
30
10
Barley
130
20
0
10
Beans, edible
103
72
0
15
Bluestem, yellow
100
1
0
1
Corn
103
72
0
15 or 100
a
Fescue
130
3
0
5
Flax
103
4
0
5–7
Mustard
130
4
0
10
Oats
130
22
0
10
Orchard grass
130
1
0
5
Parsnip
100
1
0
10
Rape (Canola)
130
4
0
10
Rye
130
16
0
10
Ryegrass
130
3
0
5
Safflower
130
1
0
10
Sorghum
130
18
0
10
Soybeans
103
72
0
15
Sunflower
130
3
0
10
Timothy
130
1
40
10
Wheat
130
19
0
10
a
Use 100 g if moisture exceeds 25%.
Source: From ASAE, S352, 2 Dec. 92, Moisture measurement—unground grain and seeds, 40th ed., Standards, Engineering Practices, and
Data (Am. Soc. Ag. Eng.), St. Joseph, MI, 1993, p. 449. With permission.
ß
2006 by Taylor & Francis Group, LLC.

equilibrium). Depending on the vapor pressure of the
moisture in the seeds and the vapor pressure of the air
above the saturated salt solution the sample may reach
equilibrium by picking up or giving off moisture, thus
resulting in either a sorption or desorption EMC
value. For grains and oilseeds, the sorption EMC is
lower than the desorption EMC at the same relative
humidity because of the hysteresis phenomenon that is
exhibited by biological materials. The moisture uptake
can be by chemisorption, adsorption, absorption, or a
combination as moisture content increases. The term
sorption includes all mechanisms of moisture uptake.
The time for the samples to reach equilibrium may
vary from 1 to 5 weeks depending on the relative
humidity and temperature. Therefore, mold usually
develops on samples in high humidity environments
and treatment of the sample with a mold inhibitor such
as propionic acid is required.
To reduce the time to reach equilibrium and to
reduce the problem with mold development, another
version of the static method is to force conditioned air
of known temperature and relative humidity over the
sample until the change in mass of the sample is small
(<0.01 g). A variation to this method can be used when
determining thin-layer drying or wetting characteristics
of a sample. The variation is that it is not necessary to
bring the sample to equilibrium, and the EMC is deter-
mined as M
e
by nonlinear regression of the equation:
M
M
e
M
i
M
e
¼ exp (Kt
N
)
(24:5)
In the dynamic method, a small amount of air is
brought into equilibrium with a 0.5–1.0 kg sample of
known moisture content by recirculating the air in a
sealed unit [14] that is housed in a room at a constant
temperature within +0.18C. The relative humidity of
the recirculating air is monitored until it becomes
constant at which stage it is assumed that equilibrium
has been attained and the measured relative humidity
is the ERH. The moisture content of the sample is
measured again. The average of the initial and final
moisture contents is taken as the EMC. Because the
amount of recirculating air is small, the change in
moisture content of the sample usually is within the
error limits of the method of moisture measurement
and some researchers take the initial moisture content
of the sample as the EMC. The time to reach equilib-
rium is reduced to 6–12 h depending on the conditions
of the sample. When determining a desorption iso-
therm by the dynamic method, the initial relative
humidity of the air must be well below the expected
ERH so the grain loses moisture to the air; and the
reverse must be guaranteed when determining the
sorption isotherm.
24.3.3 A
NALYSIS OF
EMC–ERH D
ATA
The EMC–ERH data of grains and oilseeds are ana-
lyzed by fitting various equations to the data using
nonlinear regression. The commonly used equations
are: the modified Henderson, Chung–Pfost, Halsey,
Oswin, and Guggenheim–Anderdon–de Boer (G.A.B)
(Table 24.8). The modified Henderson [15,16] and
modified Chung–Pfost [17,18] equations have been
adopted as standard equations by the American So-
ciety of Agricultural Engineers for describing EMC–
ERH data for cereals and oilseeds. The modified
Halsey [19,20] and modified Oswin [21,22] equations
have been shown to describe the EMC–ERH data of
many seeds satisfactorily [22,23]. The G.A.B. equa-
tion has recently been recognized as the most satis-
factory theoretical isotherm equation, but it does not
TABLE 24.8
Equilibrium Moisture Content–Equilibrium Relative
Humidity Relationships Used to Analyze Sorption
and Desorption Isotherms of Grains and Oilseeds
Modified Henderson Equation
RH
¼ 1 2 exp(2A(T þ C)M
B
)
Modified Chung–Pfost equation
RH
¼ exp
A
T
þ C
exp
BM
100
Modified Halsey equation
RH
¼ exp
exp (A
þ BT)
M
C
Modified Oswin equation
RH
¼
1
A
þ BT
M
C
þ1
Guggenheim–Anderson–de Boer (G.A.B.) equation
M
¼
ACB
RH
(1
B RH)(1 B RH þ CB RH)
Modified Guggenheim–Anderson–de Boer (G.A.B.) equation
M
¼
A(C=T )B
RH
(1
B RH)(1 B RH þ (C=T)B RH)
A, B, C are constants, M is percent water content dry basis, RH is
equilibrium relative humidity, decimal, and T is temperature, 8C.
Source: From Henderson, S.M., Agric. Eng., 33(1), 29, 1952;
Thompson, T.L., Peart, R.M., and Foster, G.H., Trans. ASAE, 11(4),
582, 1968; Chung, D.S. and Pfost, H.B., Trans. ASAE, 10(4), 552,
1967; Pfost, H.B., Maurer, S.G., Chung, D.S., and Milliken, G.A.,
Summarizing and reporting equilibrium moisture data for grains,
Paper No. 76–3520, ASAE, St. Joseph, MI, 1976; Halsey, G.,
J. Chem. Phys., 16, 931, 1948; Iglesias, H.A. and Chirife, J., J. Food
Technol., 11, 109, 1976; Oswin, C.R., J. Soc. Chem. Ind. London, 65,
419, 1946; Chen, C. and Morey, R.V., Trans. ASAE, 32(3), 983, 1989;
Jayas, D.S. and Mazza, G., Trans. ASAE, 34(5), 2099, 1991; Jayas,
D.S. and Mazza, G., Trans. ASAE, 36(1), 119, 1993.
ß
2006 by Taylor & Francis Group, LLC.

incorpora te the e ffect of tempe ratur e on the EMC–
ERH relat ionship . Jayas and Mazza [24] modified the
G.A.B. eq uation by dividing the con stant C by tem-
peratur e to give a three-p arameter equatio n. The co n-
stants of the most appropri ate equati ons for common
seeds are given in Tabl e 24.9 (ASAE [25] ).
24.4. THERMAL PROPERTIES
24.4.1 S
PECIFIC
H
EAT
Specific heat, c , is the amo unt of he at in kilojo ules
requir ed to ch ange the tempe ratur e of 1 kg of material
by 18:
c
¼
1
m
dq
du
(24 : 6)
Specific heat of a moist agricultural product can be
related to its dry, c
db
, or wet, c
wb
, mass. From the
relationships between dry and wet masses it follows that
c
db
¼ c
wb
(1
þ M ) (24 : 7)
It has been empir ically shown that the specific hea t of
moist agricu ltural products can be presen ted as a sum
of the specific heat of its dry mass, c
d
, and the sp ecific
heat of wat er he ld in the produ ct, c
w
[26–29]. The
followin g relat ionship holds for 1 kg of dry mass of
the pro duct:
c
db
¼ c
d
þ c
w
M (24 : 8)
Com prehen sive revie ws of the method s of mea-
surem ent of therm al pro perties of grains have been
publis hed [28,30,31 ]. Pre cision and accuracy of meas-
urement are impor tant fact ors to consider when a
method is con sidered for possible use. How ever, the
variation in comp osition, size, and shape of agric ul-
tural products pre cludes the ne ed for accuracies
greater than +2–5%.
The common proced ures for measur ement of the
specific he at of grains at constant pr essure are ice calo-
rimetry [32], mixtu re methods [33], indir ect methods ,
where the specific heat is calcul ated from other therm al
propert ies such as therm al con ductiv ity and diffusiv ity
[34–37 ], method of different ial scann ing calori metry
(DSC) [38] , guarded plate method, an d the adiabat ic
method [28]. Only the most common method—
the method of mixt ures an d the mo st modern method
that utilizes sophisticat ed instrumen tation—t he DSC
method, are discus sed in this section.
The method of mixtures [33,39] consists of adding
a known mass of mate rial at one elevat ed tempe ra-
ture to a know n mass of water at another tempe ratur e,
and measur ing the eq uilibrium tempe ratur e. The test
TABLE 24.9
Constant s of Selected Equati ons
a
for the Isoth erm of Various Seeds
Seed Equation
b
Isotherm Equation Constants
A
B
C
Barley PF 475.12 0.14843 71.996
Corn (shelled corn) HE 6.6612E-05 1.9677 42.143
Oats (cv. ‘Dumont’) PF 433.157 21.581 41.439
Rough rice, long grain (Australia) HE 4.1276E-05 2.1191 49.828
Medium grain (California) HE 3.5502E-05 2.31 27.396
Short grain (Japan)
HE
4.8524E-05
2.0794
45.646
Wheat durum (‘Wakooma’)
OS
13.101
2
0.052626
2.9987
Wheat hard red (‘Waldron’)
OS
15.868
2
0.10378
3.0842
Wheat hard red (‘Napayo’)
OS
14.736
2
0.05459
3.3357
Rapeseed (‘Candle’)
HL
3.0026
2
0.0048967
1.7607
Canola (‘Tobin’)
HL
3.489
2
0.010553
1.86
Flaxseed (‘Linnot’)
HE
0.000176
1.9054
56.228
Peanut kernel
HL
3.9916
2
0.017856
2.2375
Safflower seed
HE
0.000203
1.8883
57.4013
Sunflower seed
HE
0.00031
1.7459
66.603
a
b
HE, mdified Henderson; PF, modified Chung–Pfost; HL, modified Halsey; OS, modified Oswin.
Source: From ASAE, D245.5. Moisture relationships of plant-based agricultural products, 43rd ed., Standards, Engineering Practices, and
Data (Am. Soc. Ag. Eng.), St. Joseph, MI, 1996. With permission.
ß
2006 by Taylor & Francis Group, LLC.
apparat us usually consis ts of an isot hermal Dewar
flask wi th a capacit y of 1000 mL from which the
metal jacket is remove d to allow the use of a magnet ic
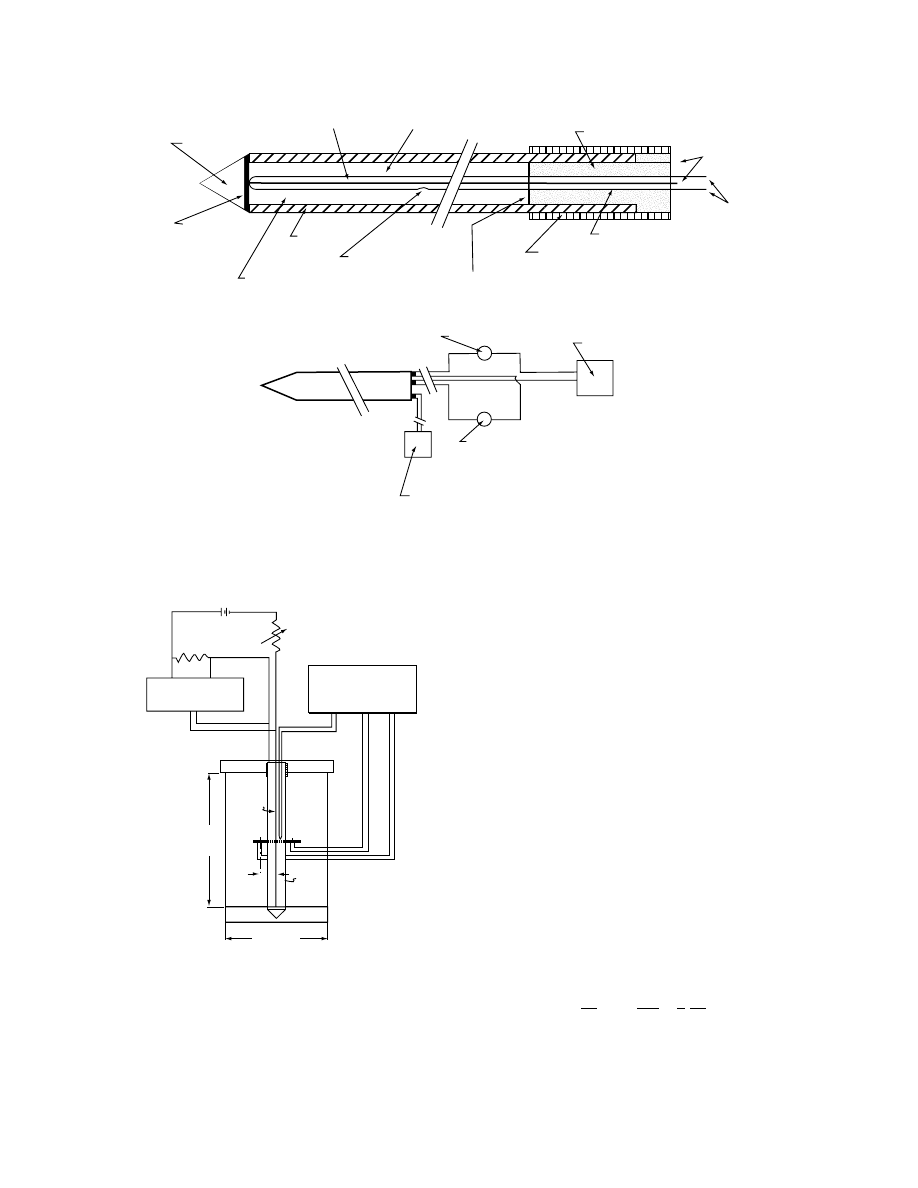
stirrer (Figur e 24.1). The flask is insul ated with a p-
proxim ately 4 cm of fibe rglass insul ation to mini mize
heat exchange with the surroundi ngs. An insul ating
cover is divide d into two parts to facilitate measur e-
ment of the calorimet er wat er tempe ratur e an d to
reduce heat losse s whi le trans ferring a grain sample
into the calori mete r. A glass rod, 13 cm long, is at-
tached to the smal ler part of the cover an d pro trudes
into the calori meter flask. A c opper–con stantan
thermo couple (36-gauge) is attach ed to the en d of
the rod to measur e the tempe ratur e of the ca lorimete r
water. A magnet ic stirrer is used to maint ain a co n-
stant tempe rature through out the flask. Calibra tion
of the calori meter can be accompl ished using granula r
alumin um of known specific heat. The reliab ility of
the equ ipment can be checked with granula r copp er
as a reference sampl e. The typic al testing procedu re
is as follows [33] : abo ut a 20-g wheat sample
(+ 0.0001 g) a t various initial tempe ratures ( 236 to
21 8 C) is placed into the calori meter fla sk filled wi th
200 + 0.1 g of distilled wat er at room tempe ratur e,
and the tempe rature of the water is recorded until
therma l eq uilibrium of the mixtu re is establ ished. A
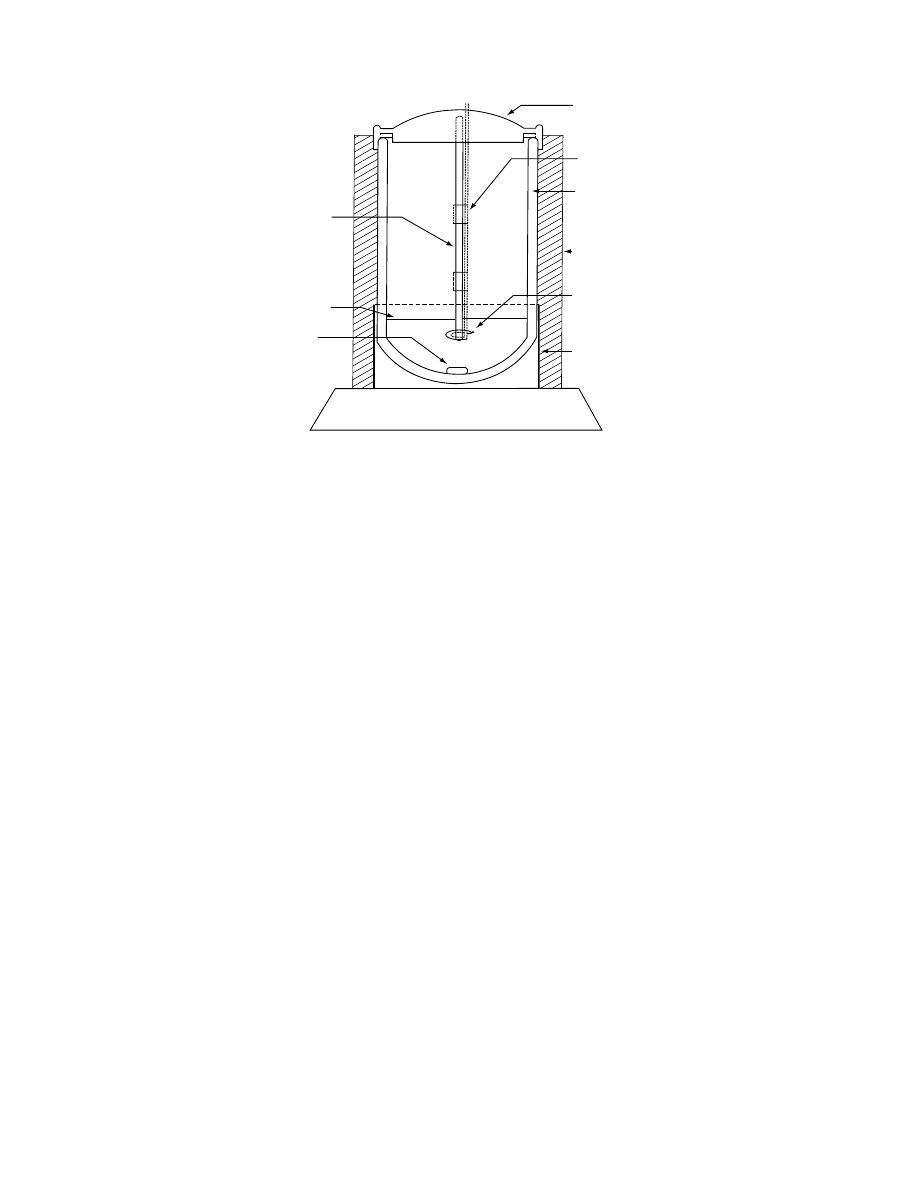
typical tempe ratur e–time cu rve of the water in the
calorimet er is shown in
. The tempe rature
of the mixt ure ( T
m
) is determ ined by extra polating
the straight -line portion of the tempe ratur e–time
curve ba ck to the transient tim e, which is the time at
which the sampl e is dropped into the calori meter
water. By equ ating the ch anges in the therm al energy
content s of the water and the sample, the foll owing
equati on can be written:
cm
s
( T
m
u
s
)
¼ ( m
w
þ E ) c
w
( T
c
T
m
) (24 : 9)
The water equivalent value, E, is obtained by rearran-
ging Equation 24.9 and conducting experiments with a
material such as water of known specific heat. The error
associated with specific heat values obtained with the
above-described apparatus is within 4.0% [40].
W hen using the method of mixtures water can be
replac ed with toluene . Tol uene has the added advan -
tages of a lower specific gravity (0.86) and specific
heat (0.39 kJ/(kg K)) than water; thus enab ling seed s
to sink more readily than in wat er, and resul ting in a
substa ntially great er temperatur e rise than is obtaine d
with wat er. With water, con densation on the calori m-
eter’s surface usu ally occurs, causing a loss of meas-
urement precision . Ther efore, a calorimet er of low
mass can be used [41]. The apparatus consists of two
closely fitting, thin-walled aluminum tubes of about
2.5 cm diame ter placed in a calori meter (
) .
The inner tube is used to house chilled toluene and a
sample. The outer tube is mounted by its top edge to a
sealing disk, which is attached to the cap of a screw-
top aluminum can. Air inside the can is dehydrated by
desiccant. The can is packed in melting ice, inside a
Glass rod
Water
Magnetic
stirring bar
Magnetic stirrer
Support
Thermocouple
Fiberglass
insulation
Isotherm Dewar
flask
Paper tape
Insulated cover
FIGURE 24.1 Schematic diagram of calorimeter. (From Viranichai, S., Effect of moisture content and temperature on
specific heat of wheat. M.Sc. dissertation (unpublished), Department of Agricultural Engineering, University of Manitoba,
MB, 1971. With permission.)
ß
2006 by Taylor & Francis Group, LLC.
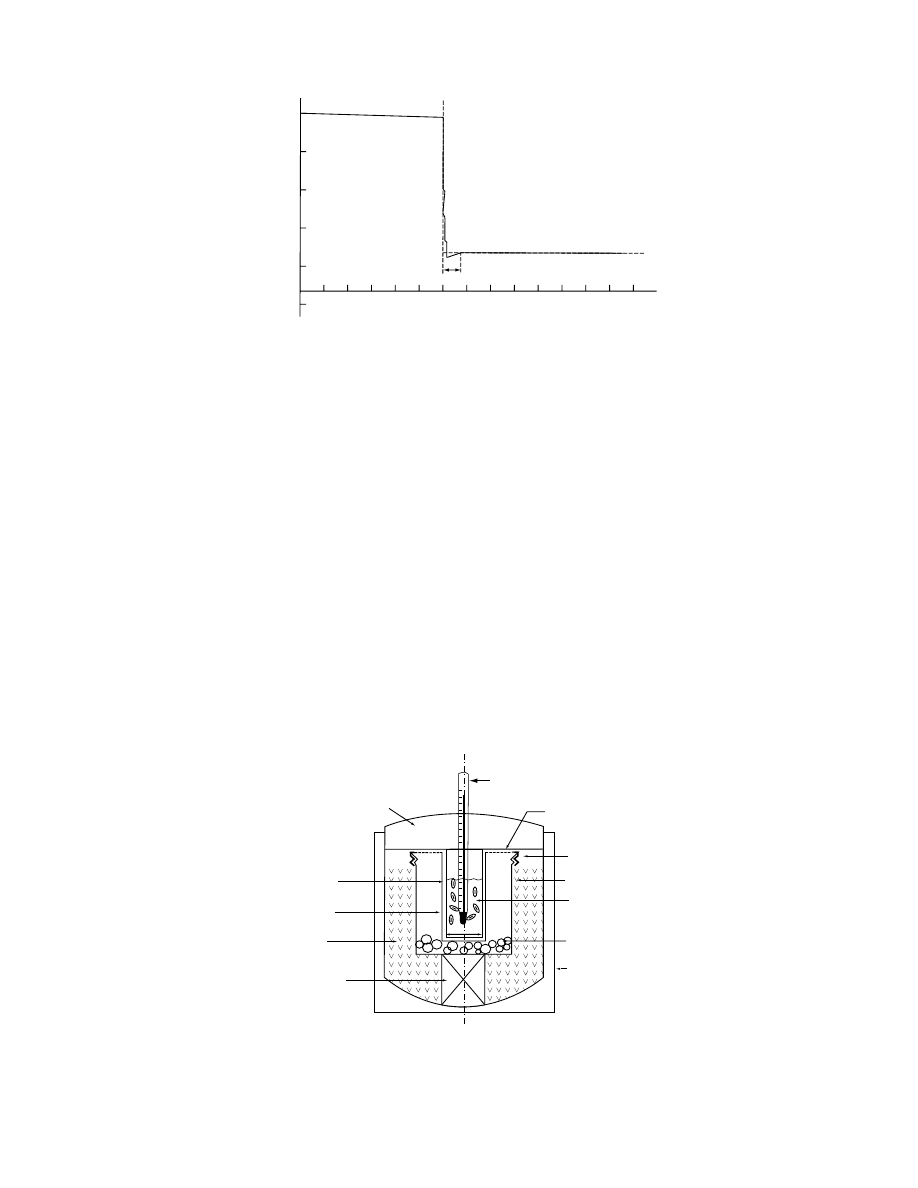
vacuum flask , to provide a con stant and uniform
surface temperatur e aroun d the calorimet er. Tem per-
ature record ing accuracy shou ld be 0.01 8 C.
W hen low mois ture content g rain is used in the
method of mixtu res, absorpt ion of water by the grain
generat es heat of hydratio n. Thi s heat results in in-
crease d tempe ratur e rises in the wat er, whi ch can lead
to erroneou s results. Therefor e, to mini mize the error,
it may be ne cessary to incorpo rate a correct ion facto r
in the resul ts [27].
The method of DSC is based on measur ing the
very small therm al effects pro duced during therm al
process es and is recomm end ed as well suit ed for de-
termining the effect of tempe ratur e on specific he at
[38,42]. In the DSC method, any gain or loss of ther-
mal energy is recorded a s the equipment war ms the
test material at a control led rate of tempe ratur e rise
over a selec ted tempe ratur e interva l. The disadva n-
tages of this method are that it requ ires a small sam-
ple size (5–15 mg), whi ch makes it difficult to obtain a
homogen eous, repres entat ive sampl e, and it is a com-
parative device that must be calibrated. The measur e-
ment of specific he at with DSC is based on the
assum ption that the temperatur e is unifor m in the
sample a nd the sample pan during a test. How ever,
due to the low therm al diffusiv ity of biologi cal ma-
terials, thermal lag within a sample may introduce
error in the measured specific heat.
The measured specific heats of dry mass of some
agricu ltural produ cts are given in
Because of differences in the chemical composition
between crops and among cultivars of the same
2
Stabilization period
0
20.5
21.0
21.5
22.0
22.5
23.0
4
30–40 s
T
m
T
c
6
Time, min
Temperature,
⬚C
8
10
12
14
Straight line portion
Extrapolated back
FIGURE 24.2 Temperature–time characteristic from calorimetric test. (From Viranichai, S., Effect of moisture content and
temperature on specific heat of wheat. M.Sc. dissertation (unpublished), Department of Agricultural Engineering, University
of Manitoba, MB, 1971. With permission.)
Thermometer
Expanded polystyrene
Inner thin-wall
aluminum tube
Outer thin-wall
aluminum tube
Melting ice
Rubber stopper
Aluminum cap
Thermos
Aluminum can
Chilled toluene
and grain
Layer of
desiccant
Sealing disk
(perspex sheet)
25 mm
FIGURE 24.3 The calorimeter assembly. Modified from Sharp, R.B. and Nash, J.E., J. Agric. Eng. Res., 10, 355, 1965. With
permission.)
ß
2006 by Taylor & Francis Group, LLC.

crop, empirical equations have been developed. Usu-
ally, these equations describe the relationship between
the specific heat and moisture contents of various
crops [27,28,33,34,43–47] (Table 24.11):
c
¼ a þ bM þ c
1
u
(24:10)
Much of the published data on specific heat and
other thermal properties of grains are of limited value
because not enough supporting data are included, such
as a detailed product description, and the estimated
error in measurement. The description of grain should
include the cultivar, the size of the individual kernels,
the maturity, and the pretreatment. Details of an ex-
periment should include the sample size, the surface
conditions of the kernel, the porosity, the temperature,
the relative humidity, the pressure, and the sam-
pling procedure. The equipment description should
provide sufficient detail so that one can duplicate
the experiment.
24.4.2 T
HERMAL
C
ONDUCTIVITY AND
D
IFFUSIVITY
Thermal conductivity, k, is described by the formula:
q
¼ kA
du
dx
(24:11)
For solid bodies the heat flux, q, is directly propor-
tional to the temperature gradient, Hu, and the thermal
conductivity, k, of the body. The minus sign refers
to the direction of the flux, which is opposite to the
direction of the temperature gradient. Therefore, if the
temperature gradient (for a certain time period) is
constant, the thermal conductivity defines the amount
of thermal energy that is transmitted within a unit time
and through a unit cross-sectional area. The area is
perpendicular to the direction of flow.
Factors influencing the choice of method for the
determination of the thermal conductivity have been
discussed in the literature [28,31,48]. Basically, methods
of measurement of the thermal conductivity are div-
ided into three categories: (1) steady-state techni-
ques, (2) quasistatic techniques, and (3) transient-state
techniques [28,31].
The advantages of the steady-state techniques are
simplicity of the mathematical equations and high
control of experimental variables. The disadvantages
are: long equilibration time associated with possible
moisture migration, restriction to the simple geom-
etry of the sample (sphere, cylinder, or slab), and the
presence of convection in granular materials. Thermal
TABLE 24.10
Specific Heat of the Dry Mass of Agricultural Seeds
Seed
Specific Heat c
d
, J/(kg K)
Ref.
Alfalfa
1172
110
Barley
1245
111
Beans
1293
111
Corn
1534
44
Corn
2035
105
Oats
1277
46
Oats
1282
111
Oats
993–1278
112
Rapeseed
1553–1569
111
Rice (rough)
1109
46
Rice
1637
47
Rice (white)
1197
46
Rye
1272
111
Sorghum
1397
27
Wheat
1097
33
Wheat
1185–1260
28
Wheat
1287–1299
112
Wheat
1276
111
Wheat
1454
44
TABLE 24.11
Formulas for Specific Heat Determination
of Selected Agricultural Products
Seed
Equation
a,b
and its
Working Range
c
Ref.
Alfalfa seed
c
¼ 1172 þ 33M’, 0 < M’ < 28%
110
Chick-peas
c
¼ 24.19 10
2
3
þ 1.19 10
1
u
þ 2.15 10
2
2
u
2
2
3.73
10
4
M
2
1.65
10
3
M
2
þ 1.38 10
2
Mu
39
292
T 308 K, 0.12 M 0.32
Corn
(shelled)
c
¼ 1470 þ 36M’, 1 M’ 30%
44
c
¼ 1370 þ 27M’, 0 M’ 60%
45
Lentils
c
¼ [0.577 þ 0.0071u þ
(0.0622 2 0.0914M)
10
2
M]1000
113
10 < T < 808C, 0.02 < M < 0.35
Oats
c
¼ 1277 þ 32M’, 10 M’ 17%
46
c
¼ 992 þ 50M’, 12 M’ 18%
Rapeseed
c
¼ 1356 þ 32M’, at 19.48C
34
c
¼ 1288 þ 28.4M’, at 1.78C 1
M’ 20%
c
¼ 1328 þ 28.0M’, at 24.48C
Rice (rough)
c
¼ 1109 þ 45M’, 10 < M’ < 17%
46
Rice (white)
c
¼ 1197 þ 38M’, 10 < M’ < 17%
Sorghum
c
¼ 1397 þ 32M’, 0 < M’ < 30%
27
Soybeans
c
¼ 1637 þ 19M’, 0 M’ 24%
47
Wheat
c
¼ 1260 þ 36M’, 5 < M’ < 35%
28
c
¼ 1098 þ 4010
2
M, 0
M < 0.25
33
c
¼ 1184 þ 30M’, 0 M’ 13.6%
43
c
¼ 1452 þ 30M’, 1 M’ 32%
44
a
c, specific heat (J/(kg K)).
b
u
Measured as temperature of air in equilibrium with seeds.
c
M, moisture content (kg H
2
O/kg db) and M’, moisture content % wb.
ß
2006 by Taylor & Francis Group, LLC.
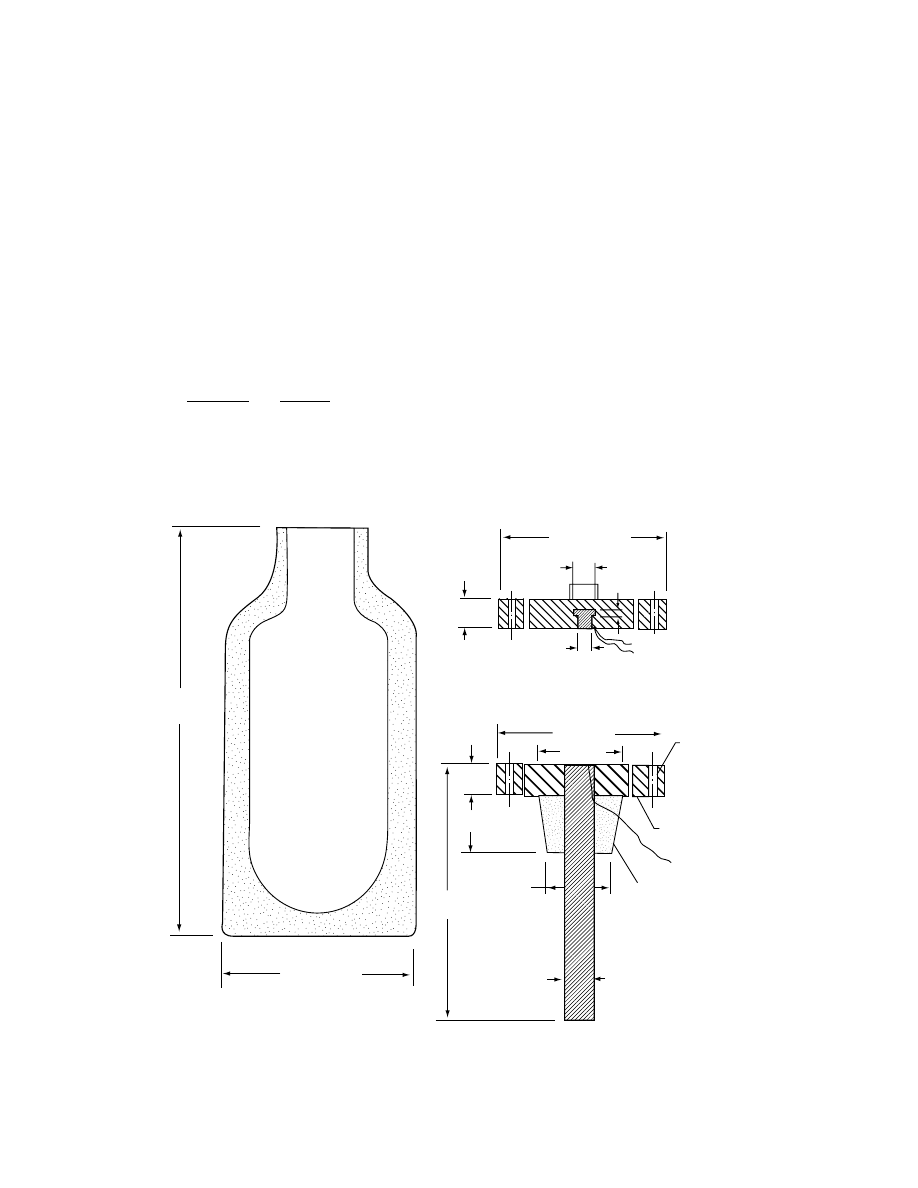
condu ctivities of grains have been measured by the
guarded hot-pl ate method [30] an d the con centric
spheres method [49].
The Fitch method [50] and its various modifications
[31] are the most common quasistatic techniques used to
measure the thermal conductivity. The main advantage
of this method is that the test is simple and can be
c arr ie d out in 10 mi n. For a bs olu te m ea su re me nt s, how -
ever, the accuracy is rather low. Figure 24.4 shows a
modified Fitch apparatus [51]. The sliced sample is
placed between two copper plates. One plate acts as a
heat source and the other plate as a heat sink. The
the rm al c onduc tiv ity is c al cula te d by E qua ti on 2 4. 12 ,
which is the solution of the governing differential equa-
tion for the temperature field within the sample [51].
ln
u
0
T
1
u
( t)
T
1
¼
Akt
Lm
cp
c
cp
(24 : 12)
The plot of the tempe rature ratio (u
0
–T
1
)/(u (t ) – T
1
)
versus tim e on a semilog paper is a stra ight line. The
thermal condu ctivity is calcul ated from the slope ( Ak /
Lm
cp
c
cp
) of the tempe rature histo ry.
The essent ial difference between a steady state
and a trans ient state is that the tempe rature at a
particular locat ion c hanges with time under trans ient
conditio ns. A line he at source prob e has been re-
commende d by many resear chers [28,29,52 ,53]. The
method is simp le, fast, an d requires a relative ly smal l
sample. A schema tic repres entat ion of the therm al
condu ctivity probe, the direct current (dc) su pply,
and the tempe ratur e measur ing system is sh own in
[54]. The prob e is inser ted into a sample
of a unifor m tempe ratur e and is heated at a constant
rate. The tempe ratur e adjacent to the line heat sou rce
is record ed. Var ious modificat ions of the line he at
source probe can be foun d in the lit erature. The
probe attached to a 20-cm diameter aluminum cylin-
der as a sampl e holder is one of them (
[35]. Other modifications are related to placement of
thermocouples directly on the heating element [55,56]
or at a fixed distance from it [43].
10 mm
20 mm
35 mm
3 mm hole
b. Copper plug assembly
6 mm
Thermocouple
wires
6
3 mm
150 mm
150 mm
45 mm
20 mm
40 mm
37 mm
140 mm
110 mm
260 mm
Polystyrene disc
Thermo couple wire
Cork
19 mm copper rod
c. Copper rod assembly
a. Vacuum flask (1 liter Cap.)
FIGURE 24.4 Modified Fitch apparatus. (From Zuritz, C.A., Sastry, S.K., McCoy, S.C., Murakami, E.G., and Blaisdell,
J.L., Trans. ASAE, 32, 711, 1989. With permission.)
ß
2006 by Taylor & Francis Group, LLC.
The determination of the thermal conductivity of
grain is based on the comparison of the temperature
history data obtained by using the line heat source
probe with the approximate analytical and numerical
methods [35,54]. The analytical method has the ad-
vantage of being quick in calculating thermal con-
ductivity. This method, however, requires a perfect
line source and a small diameter tube holding the line
heat source. In reality, this requirement is difficult to
meet. Therefore, a time-correction procedure has
been introduced [52,54,56]. Another objection to the
analytical method is that it cannot easily be used to
calculate the temperature distribution in the heated
grain and to compare it with the measured one. Such
a comparison can be easily accomplished by a numer-
ical method, where the estimated accuracy for ther-
mal conductivity is determined and the thermal
conductivity of the device is taken into account [54].
The analytical method for determination of the
thermal conductivity is presented below. The heat
flow from the line heat source (a heating wire) of
infinite length and infinitely small diameter imbedded
in an infinite homogeneous medium can be expressed
by the Fourier equation:
@u
@t
¼ a
@
2
u
@r
2
þ
1
r
@u
@r
(24:13)
Equation 24.13 is solved for a particular case of the
temperature at the line heat source for the heat input
Protective tip
Thermocouple wires
Silicon rubber
Copper leads
Copper leads
Styrofoam
handle
Insulating
disks
Digital ammeter
DC current supply
Digital voltmeter
Digital temp. meter
Thermocouple
junction
Space filled with
heat-conductive paste
Insulating
disc
Brass
tube
Thermocouple
wires
Constantan
heating wire
FIGURE 24.5 Thermal conductivity device. (From Papadakis, G., Giaglaras, P., and Kyritsis, S., J. Agric. Eng. Res., 45, 281,
1990. With permission.)
Oscilloscope
voltage, current
467 mm
Y
1
Y
2
Heater
6.4 mm
4.8 mm D. alum. tube
12 V
1
Ω
Potentiometer
recorder
time, temperature
203 mm
FIGURE 24.6 Schematic of thermal property apparatus.
(From Suter, D.A., Agrawal, K.K., and Clary, B.L.,
Trans. ASAE, 18, 370, 1975. With permission.)
ß
2006 by Taylor & Francis Group, LLC.

of q
l
. The tempe rature rise Du in the time inter val
between t
1
and t
2
is de termined as [52,57]
Du
¼
q
l
4p k
ln
t
2
t
1
(24 : 14)
To acc ommodat e the time-cor rection fact or, t
0
, Equa-
tion 24.14 is mo dified to the foll owing form [35,52,56 ]:
Du
¼
q
l
4pk
ln
t
2
t
0
t
1
t
0
(24 : 15)
The time-cor rection factor, t
0
, takes into accoun t
various effects (i.e., contact resistance s, position s of
thermo couples, specific he at of the pro be and sampl e)
and ha s to be de termined from experi menta l data.
Thus, dt/d u is plotted in relation to time. By diff eren-
tiation Equation 24.14 gives
dt
du
¼
4pk
q
l
t
c
(24 : 16)
Equation 24.16 can be repres ented as a plot of dt /du
in relat ion to correct ed tim e t
c
. Thus , the expres-
sion 4p k/ q
l
repres ents a slope an d at dt /du
¼ 0,
t
c
¼ t
0
whi ch is the time-cor recti on facto r util ized in
Equation 24.15.
The thermal conductivity of solid engineering
materials varies with chemical composition, physical
structure, state of the substance, temperature, and
moisture content. Because grains are stored, ventilated,
and dried in bulk, the bulk density of such products also
influences their thermal conductivity. At constant mois-
ture content the thermal conductivity can be expressed
as a linear function of the bulk density, r
b
:
k
¼ a þ br
b
(24 : 17)
Coeffic ients a and b for wheat , corn, and grain sor-
ghum at various mois ture co ntents an d at 22 8 C have
been given by Chang [58]. Also , the therm al con duct-
ivity of many grains can be expressed as a linear
functio n of mois ture con tent:
k
¼ k
d
þ a
1
M
þ b
1
u
(24 : 18)
gives common relationshi ps for de -
terminat ion of the therm al condu ctivity of selected
major seed types. To impr ove the fit of data to math-
ematical exp ressions, polyn omial equati ons are also
used or tempe rature is introd uced into the expression
[39,56].
Un steady-st ate or trans ient heat conduction com-
monly occurs during heating or coo ling of grains. It
involv es the accumu lation or deplet ion of heat wi thin
a body, which resul ts in tempe ratur e c hanges in the
kernel with tim e. The rate at whic h heat is diffused
out of or into a kernel or layer of ke rnels is depend ent
on the thermal diffusiv ity coeffici ent, a, of the grain:
a
¼
k
c r
t
(24 : 19)
The recomm ended method [29] for the determ in-
ation of the thermal diff usivity of individua l kernels is
to calcul ate it from experi menta lly measur ed values of
the thermal con ductivity of kernel material , specific
heat, and kernel (particle ) density —the so-cal led indir -
ect method. The method may lead to a pproxim ate
results with a relative error, which is difficul t to esti -
mate in respect to a true (real ) value, whi ch can onl y be
determined by direct measur ement s. The resul ts of
thermal prope rties for wheat an d corn [44] and for
single soyb eans [59] confi rm the abo ve.
The therm al diffusiv ity can also be measure d dir-
ectly by employ ing trans ient heat cond uction. The
basic diff erential equati on (Fou rier heat condu ction
equati on) governi ng heat condu ction in isotrop ic
bodies is used in this method. A recta ngular copp er
box filled with grain is placed in an ice bath (08C), and
the temperature at its center is recorded [44]. The
solution of the Fourier equation for the temperature
at the center of a slab is used:
u
c
u
0
¼
4
p
exp (
p
2
z)
1
3
exp (
9p
2
z)
þ
1
5
exp (
25p
2
z)
Þ
ð24:20Þ
and
z
¼
at
x
2
, dimensionless
(24:21)
For selected values of u
c
/u
0
obtained from the experi-
ments, the values of z can be obtained, and with the
measured values of time, t, and x the diffusivity is
calculated from Equation 24.21. The values of the
thermal diffusivities can also be determined for seeds
by solving the Fourier equation for either an infinite
cylind er [60], or a sphere [59] .
of thermal diffusivities for selected seed types
obtained with the direct or indirect method.
24.4.3 C
ONVECTIVE
H
EAT
T
RANSFER
C
OEFFICIENT
The main mechanism of air-to-particle heat transfer
during heating, cooling, and drying processes of
grains is forced convection. The forced convection
heat transfer coefficient (surface conductance), h, is
determined from the Nusselt number, Nu:
ß
2006 by Taylor & Francis Group, LLC.

TABLE 24.12
Equations for Calculating Thermal Conductivity, k (W/(m K)), for Grains and Oilseeds
Seed
Equations
a,b
(W/(m K))
Range
c
Ref.
Barley
k
¼ 0.173 þ 7.5110
2
4
T
þ1.5110
2
3
M’
9
M’ 23%
56
28
T 298C
Beans
k
¼ 0.0671 þ 32.84M
0.115
M 0.414
51
Corn
k
¼ 0.1409 þ 0.0011M’
0.9
M’ 30.2%
44
Corn
k
¼ 0.1326 þ 0.1547M 2 0.1454M
2
0
M 0.6
106
Chick-peas
k
¼ 2 5.0710
2
1
þ 2.5510
2
3
u
2
2.13
10
2
6
u
2
þ 4.2410
2
1
M
2
6.56
10
2
2
M
2
þ 6.4810
2
4
Mu
283
T 312 K
39
0.115
M 0.272
Lentils (cv. Laird)
k
¼ 0.193 þ 1.010
2
3
T
þ 1.5110
2
3
M’
9
M’ 23%
56
2
28
T 298C
Oats
k
¼ 0.0988 þ 0.307M
0
M 0.19
114
Peas
k
¼ 0.168 þ 8.410
2
4
T
þ 3.0510
2
3
M’
9
M’ 23%
56
2
28
T 298C
Rapeseed
k
¼ 0.1600 þ 0.043M
0
M 0.30
115
Rice, rough
k
¼ 0.0865 þ 0.0013M’
9.9
M’ 19.3%
116
Rice bran
k
¼ 20.0943 þ 3.8710
2
3
M’
þ 6.1910
2
4
T
þ 3. 1410
2
4
r
b
7
M’ 15%
117
410
r
b
490 kg/m
3
42
T 688C
Sorghum
k
¼ 0.0976 þ 0.0015M’
0
M’ 25%
27
Wheat (HRS)
k
¼ 0.1398 þ 0.0014M’, for T ¼ 208C
4.4
M’ 22.5%
118
k
¼ 0.1440 þ 0.0009M’, for T ¼ 58C
k
¼ 0.1365 þ 0.0014M’, for T ¼ 18C
k
¼ 0.1327 þ 0.0015M’, for T ¼ 268C
k
¼ 0.1407 þ 0.0009M’, for T ¼ 2178C
k
¼ 0.1436 þ 0.0009M’, for T ¼ 2278C
Wheat
k
¼ 0.1170 þ 0.0011M’
0.7
M’ 20.3%
44
a
k, Thermal conductivity W/(m K).
b
u
, Measured as temperature of air in equilibrium with seeds.
c
M, Moisture content kg H
2
O/kg db and M’, moisture content % wb.
TABLE 24.13
Thermal Diffusivities of Selected Seeds
Seed
Moisture Content % wb
Thermal Diffusivity (a, m
2
/s)
Method
Ref.
Chick-peas
12.0
11.6
10
2
8
Indirect
39
Corn, yellow dent
9.8
9.4
10
2
8
Direct
44
20.1
8.6
10
2
8
Rapeseed
10.5
9.2
10
2
8
Indirect
34
Rice, bran
7.0
9.7
10
2
8
Indirect
117
Rice, rough
12.0
16.4
10
2
8
Indirect
116
Soybeans
11.2
11.7
10
2
8
Direct
59
Wheat, soft
10.3
8.3
10
2
8
Direct
44
20.3
8.1
10
2
8
Wheat
9.2
11.4
10
2
8
Direct
43
Wheat
10.0
8.3
10
2
8
Direct
119
ß
2006 by Taylor & Francis Group, LLC.
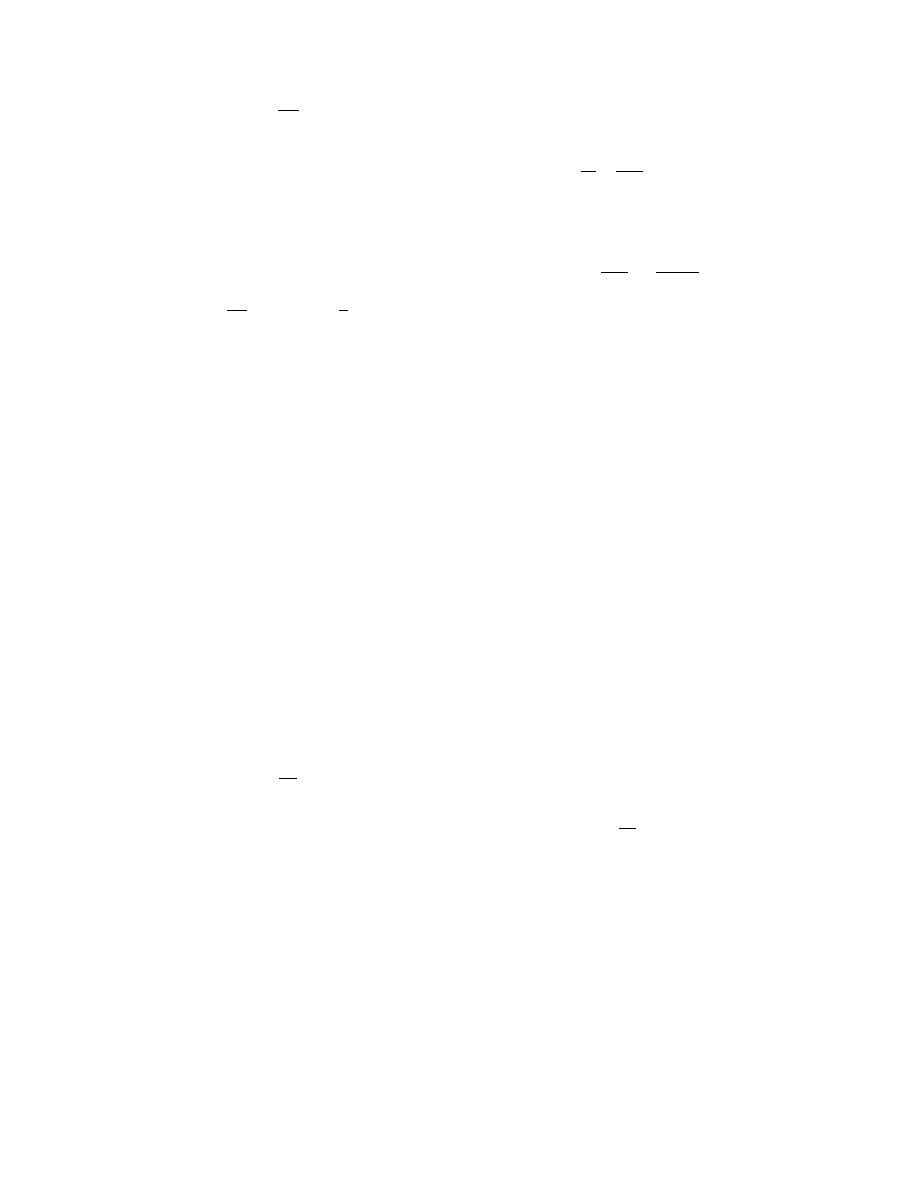
Nu
¼
hd
e
k
a
(24:22)
The Nu number is determined from empirical correl-
ations between the Reynolds number, Re, and the
Prandtl number, Pr :
Nu
¼ CRe
m
Pr
n
(24:23)
The Reynolds and the Prandtl numbers are expressed as
Re
¼
vd
e
n
and
Pr
¼
n
a
(24:24)
For the temperature range used in drying grains,
the Prandtl number is assumed to be constant and
its value is usually incorporated into a constant, C,
which simplifies Equation 24.23 to one variable—the
air velocity (dependent on the Re number).
One of the first experiments to determine heat trans-
fer coefficients commonly cited in agricultural engi-
neering publications is that of Lo¨f and Havley [61]
who investigated heat transfer coefficients from air to
a 0.9-m deep bed of granitic gravel ranging in size from
4.8 to 38.1. The temperature of the hot air passing
through the gravel was monitored at selected loca-
tions through the bed. The experiments were conducted
for air velocities from 0.08 to 0.44 m/s and the entrance
air temperatures were maintained over the range
38 to 1218C.
To determine the mean volumetric heat transfer
coefficient, h
cv
, in a deep bed of gravel it was assumed
that: (i) any particle is at a uniform temperature at any
given time, (ii) resistance to heat transfer by conduc-
tion in the fluid or solid is negligible, and (iii) the rate of
heat transfer is described by Newton’s equation [61]:
h
cv
¼ A
m
a
d
e
0:7
(24:25)
The constant A depends on the nature of the material,
the porosity, and the average temperature of the deep
bed.
Using the same theoretical approach, the heat
transfer coefficient in a 240-mm deep bed of bone-
dry barley malt was determined [62]. The experiments
were performed for airflow rates in the range 0.35 to
0.65 kg/(m
2
s) and inlet temperatures from 50 to 708C.
The results were expressed as
h
cv
¼ 49,320m
0:6906
a
(24:26)
The heat transfer coefficient can also be determined
based on a heat and mass balance for a thin layer of
grain in which no moisture transfer takes place [63].
Thus, the following differential equation is used:
du
dt
¼
h
cv
c
g
r
b
(T
u)
(24:27)
with the solution
h
cv
¼
c
g
r
b
t
ln
T
u
T
u
0
(24:28)
The slope of the logarithm of the temperature ratio
versus time is used to evaluate h
cv
for specific values
of t and u determined experimentally. For barley
dried in a thin layer in the airflow range 0.0056–
0.023 kg/s (assuming no shreokage) the following re-
lationship is valid [63]:
h
cv
¼ 21:0m
0:6
(24:29)
The results from Equation 24.25, Equation 24.26, or
Equation 24.28 can be used for the calculation of
Nusselt numbers and presented in the form of Equa-
tion 24.23.
24.4.4 L
ATENT
H
EAT OF
V
APORIZATION
To overcome the attractive forces between the
adsorbed water molecules and the internal surfaces of
grain kernels extra energy is needed in addition to the
heat required to change the water from liquid to vapor.
As the moisture content is lowered, there is an increase
in the amount of energy required to evaporate the
water molecules in seeds. The change of state from
liquid to vapor at constant temperature and pressure
is expressed by Clapeyron’s equation, which after re-
arranging and integrating has the following form:
ln P
v
¼
h
fg
h
fg
ln P
vs
þ C
(24:30)
The vapor pressure, P
v
, can be calculated as
P
v
¼ RHP
vs
(24:31)
where RH is the relative humidity in decimal form.
The values of the saturation vapor pressure, P
vs
, at
different temperatures can be obtained from the steam
tables [64]. The values of the RH in Equation 24.31 can
be replaced by the ERH obtained from the EMC versus
ERH relationship. The values of P
v
and P
vs
at the same
EMCs can be plotted on a log–log scale. The slope of
the resulting straight line gives the ratio h
fg
*/h
fg
.
ß
2006 by Taylor & Francis Group, LLC.

The foll owing form ula has been e stablished to
determ ine the de pendence of the late nt heat of vap or-
ization of water in grain as a functi on of the mois ture
content , M [65] :
h
fg
¼ h
fg
[1
þ a exp ( bM )] (24 : 32)
The coeffici ents a an d b for selected seeds have been
determ ined and are given in Table 24.14 [66]. The
variation in the late nt he ats of barley an d three c ulti-
vars of wheat are shown in
. The symbol s
repres ent the values of h
fg
* / h
fg
calcul ated from the
EMC data [25] for selec ted moisture con tents. The
curves repres ent the be st-fit line based on Equation
24.32. Als o, predicted results based on the coeffici ents
given for wheat by Gall aher [65] are incorpora ted in
Figure 24.7.
The differences in h
fg
* for wheat can be attribu ted
to a difference in the chemi cal comp osition between
wheat types, whi ch affect the EMC charact eristic s on
which the calcula tion of h
fg
* is based.
24.4.5 H
EAT OF
R
ESPIRATION
Under stora ge con ditions grains generat e heat as a
result of respirati on an d mold activity . From the
engineer ing poin t of view, de terminat ion of the
amount of he at generat ed allows for the pr oper de-
sign of grain ae ration systems to maint ain crop qual-
ity. In extre me cases rain, snow, humid air from a
roof leak or ven tilation opening cau se wet poc kets in
a grain bin. Heat generat ed within the pock et of wet
grain provides a favorab le en vironmen t for grow th of
microo rganisms and excess ive he at generat ion.
No theory adeq uately e xplains the heat of respi r-
ation in store d grain, althoug h the respi ration equ a-
tion has often be en used to estimat e he at produ ction
[67,68]:
C
6
H
12
O
6
þ 6O
2
! 6CO
2
þ 6H
2
O
þ en ergy (24 : 33)
For each gram of dry matter (C
6
H
12
O
6
), which is oxi-
dized, 15.7 kJ of heat is produced. Equation 24.33 pro-
vides a simple way of calculating the heat production
from the CO
2
production. According to Equation 24.33
the respiratory quotient (ratio of oxygen consumption
to carbon dioxide production) is equal to 1.0. However,
measured quotients frequently deviate from 1.0 [69].
Heat production under the adiabatic conditions
similar to those in naturally occurring pockets of
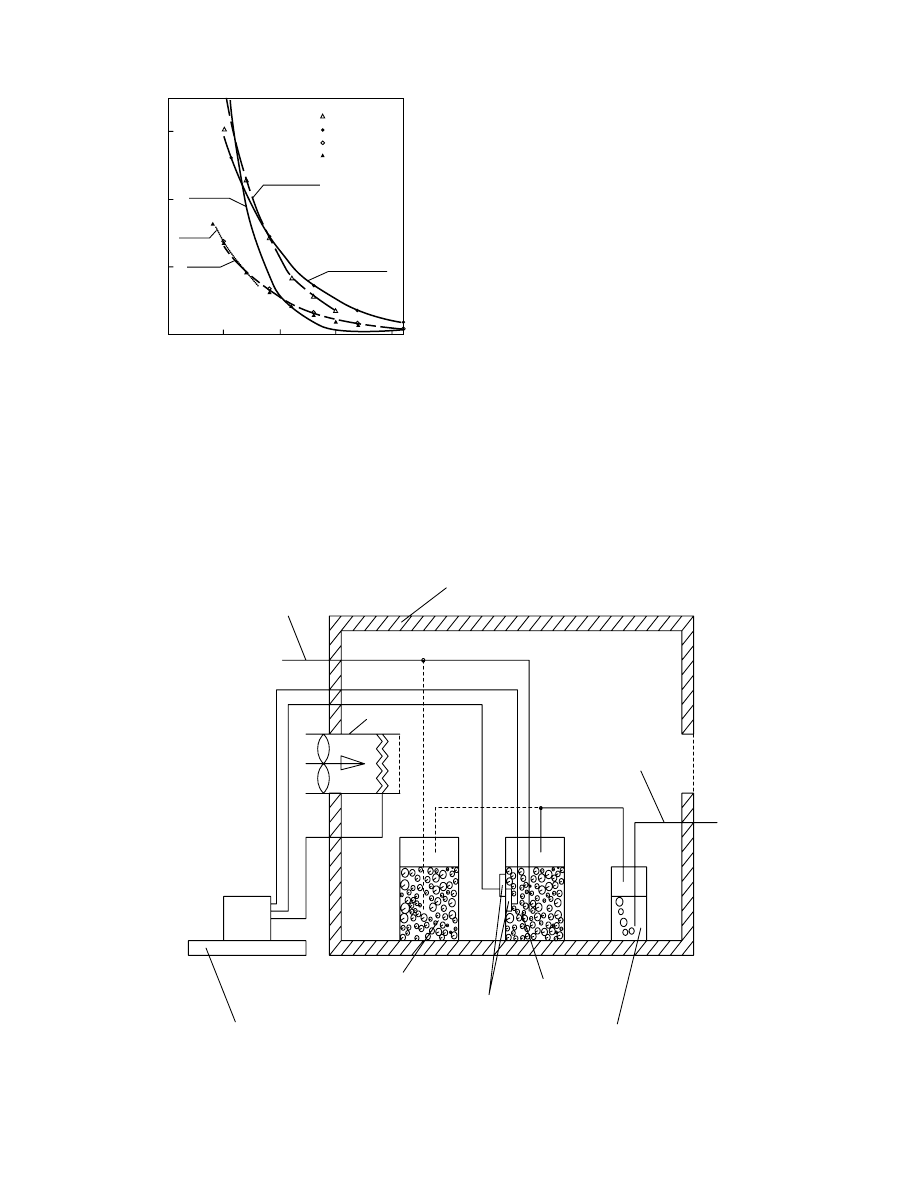
wet grain is measured in a specially designed calorim-
eter [70] (
). A grain sampl e is split and
placed in two identical 1-L Dewar flasks, which are
housed in an insulated chamber. One of the flasks,
from which grain is sampled regularly for determin-
ation of the moisture content and microfloral infec-
tion, is used as a reference flask. To avoid disturbing
the test flask during grain sampling, the temperatures
inside and outside the test flask are continuously
monitored by six thermocouples, three inside and
three outside. When grain in the test flask starts to
heat, due to metabolic activity, the inside temperature
rises, causing a difference between the inside and
outside temperatures. If the difference exceeds the
preset value of 0.5–0.78C, the electric heater is turned
on to heat the air in the chamber, and thus equalizing
the outside and the inside temperatures. The tempera-
ture gradient across the flask wall is minimized
TABLE 24.14
Derived Coefficients a and b in Equation 24.32 for Some Major Crops
Seed
Coefficients
Moisture Content Range (db)
a
b
Barley
1.0
2
19.9
0.09
M 0.22
Beans
0.5
2
16.0
0.09
M 0.28
Corn
2.1
2
17.0
0.10
M 0.24
Peanut kernel
1.5
2
29.2
0.06
M 0.13
Rice
3.2
2
21.7
0.10
M 0.14
Sorghum
1.2
2
19.6
0.10
M 0.24
Soybeans
0.4
2
13.9
0.06
M 0.26
Wheat, durum
0.8
2
18.1
0.10
M 0.26
Wheat, hard
1.7
2
17.6
0.10
M 0.26
Wheat, soft
3.9
2
23.6
0.10
M 0.20
Wheat (Gallaher [65])
23.0
2
40.0
0.10
M 0.18
Source: From Cenkowski, S., Jayas, D.S., and Hao, D., Can. Agric. Eng., 34, 281, 1992.
ß
2006 by Taylor & Francis Group, LLC.
throughou t the course of heati ng; co nsequentl y, no
heat is trans ferred from or to the grain in the fla sk.
Under the adiabat ic co ndition , the meta bolic he at
produc ed insi de the flask by the seed and micr oflora
is measur ed directly.
Duri ng the initial 11 d, the he at prod uction rate in
wheat, calcul ated from measur ed CO
2
prod uction,
followed the directly measured rate of heat produc-
tion (
) . On the average , the directly meas-
ured rates were 27 and 14% higher than those
calculated from CO
2
production for 23.0 and 27.2%
moisture contents, respectively.
The respiratory quotient is not constant during adia-
batic heating (
). For wheat at 27.2% mois-
ture, it increased from 1 to 4.2 in 4 d, and then decreased
gradually. The peak respiratory quotient was lower for
23.0% moisture content wheat. At both moisture con-
tents, the respiratory quotient stayed at about 0.8 after
the temperature of the grain reached 528C.
24.5 ELECTRICAL PROPERTIES
24.5.1 D
IELECTRIC
P
ROPERTIES
A biological material (a dielectric) can be exposed
to electric or magnetic fields in frequencies from dir-
ect current (0 Hz) to x-rays (
10
18
Hz). From direct
current to ac frequencies up to about 8 Hz, lumped
circuits (composed of serial and parallel resistances
and capacitance elements) are used to measure
Soft wheat
Soft wheat
Hard wheat
Hard wheat
Gallaher
1.3
1.2
1.1
1.0
0.05
0.10
0.15
Moisture content, decimal db
Ratio of latent heats,
h
fg
/h
fg
0.20
0.25
Barley
Barley
Durum
Durum wheat
*
FIGURE 24.7 Effect of moisture content on the latent heat
of vaporization of selected grains compared to Gallaher’s
model. (From Gallaher, G.L., Agric. Eng., 32, 34, 1951;
Cenkowski, S., Jayas, D.S., and Hao, D., Can. Agric.
Eng., 34, 281, 1992. With permission.)
Reference flask
Computer and control unit
Thermocouples
Water or salt solution
Test flask
Heater
Insulated box
Vacuum
Air
FIGURE 24.8 Computer controlled calorimeter. (From Zhang, Q., Muir, W.E., Sinha, R.N., and Cenkowski, S., Can. Agric.
Eng., 34, 233, 1992. With permission.)
ß
2006 by Taylor & Francis Group, LLC.
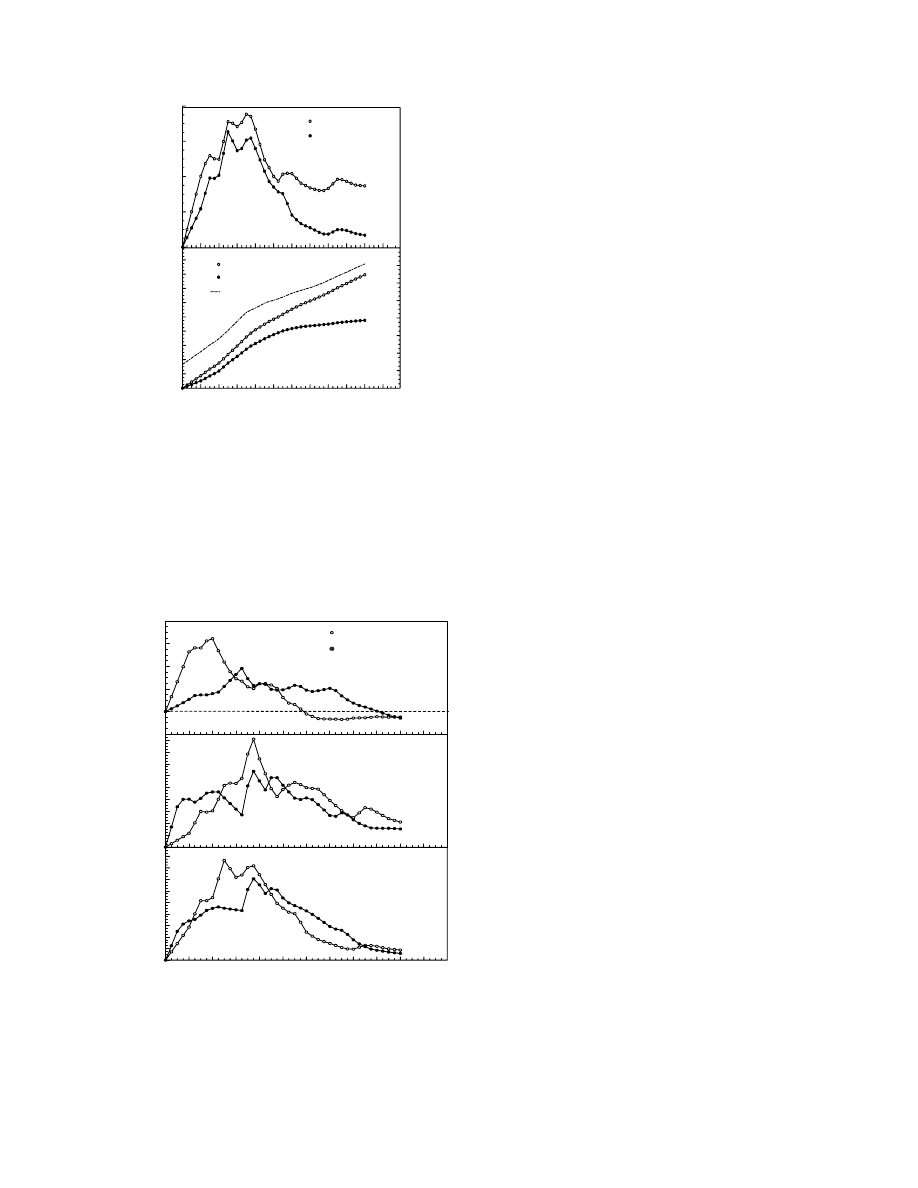
dielectri c propert ies (
). The propert ies of
the circui t elem ent may be measured in the range up
to 10
7
Hz by bridge arrange men ts and at the highe r
frequenci es (betw een 10
4
an d 10
8
Hz) in resonan t
circuits [71].
For wavelengt hs between mete rs an d millimete rs,
the dimens ions of the diele ctric (crop) become com-
parable to tho se of the wave s, and the phy sical dist inc-
tion between coil and cond enser begins to disappea r.
The tested mate rial is inserted into a wavegu ide and its
charact eristics can be determined by standin g wave
patterns. The wavelengt h range is know n as the inter -
ferenc e optics . As the wave lengt h shrinks , the diele c-
tric prop erties of a mate rial can be determ ined from
infrared to ultraviol et by refle ction and trans mission
measur ements (range of geomet rical optics ).
Bio logical mate rials have the ability to store and
dissipate elect rical energy from an applie d elect ro-
magnet ic fie ld. The prope rties resulting from elec-
trical chargin g a nd loss current s general ly related to
the material ’s elect rical cap acitance an d resistance
are the fund amenta l diele ctric propert ies. Thes e pro -
perties ha ve been of inter est because of their influence
on energy ab sorption in diele ctric heating . The di-
electric pro perties that are of inter est include the
dielectri c co nstant, «’, the diele ctric loss factor, «’’ ,
which are respect ively the real and imag inary parts
of the complex relative permi ttivity, «*
¼ «’ 2j «’’ , the
loss tangen t or dissip ation fact or, tan(d)
¼ «’’ / «’, and
the ac con ductivity , s
¼ v«
0
«
’’
[72].
The dielectri c constant may be measur ed by a Q -
Meter within the frequency range in whi ch it ope rates
and wi th a suitab le sample holder [73]. The Q -Mete r
is one of the common inst rument s in radio frequency
measur ement for determ ining the inducta nce, the ca p-
acitance, the Q of electronic comp onents, and the
resonant frequenci es of circuits. The Q -Met er in-
cludes a variab le frequency oscil lator wi th the outp ut
coupled to a series resonant circui t (
) [73] .
Electr ical propert ies of grain have bee n utilized
for quick mois ture tests based on the measur ement
of resistance , capacit ance, or elect rical cond uctivity .
Many studi es have be en devoted to the develop ment
of density-i ndepen dent function s of the diele ctric
propert ies that woul d permi t on-li ne measuremen t
of mois ture content [74–76 ]. Also, measuremen ts of
electrica l prop erties of grain and seed have been
employ ed for purp oses other than de termining mois -
ture con tent. For e xample, viable seeds of corn were
sorted from dead seeds by measur ing the cu rrent
conducted by individual soaked kernels between elec-
trodes connected to a 6-V dc source [77]. Another
application of electrical properties is electrostatic
separation where the ability of a seed to hold a sur-
face charge is determined mainly by its conductivity.
Directly measured
Based on CO2
Temperature
Directly measured
Based on CO2
Time, d
0
2
4
6
8
10 12 14 16 18 20 22 24
65
60
55
50
45
40
35
30
25
Temperature,
°C
160
120
80
40
0
180
160
140
120
100
80
60
40
20
0
Heat production rate,
mW/kg
Cumulative
heat production, kJ/kg
FIGURE 24.9 Means of cumulative heat production, heat
production rate, and temperature of wheat at 27.2% wet
basis moisture content. (From Zhang, Q., Muir, W.E.,
Sinha, R.N., and Cenkowski, S., Can. Agric. Eng., 34, 233,
1992. With permission.)
5
4
3
2
1
0
18
16
14
12
10
8
6
4
2
0
45
40
35
30
25
20
15
10
5
0
0
4
2
6
8
10 12 14 16 18 20 22 24
MC = 27.2% wb
MC = 23.0% wb
Time, d
CO
2
production rate
mg/(kg h)
O
2
consumption rate
mg/(kg h)
Respiratory rate
FIGURE 24.10 Comparison of CO
2
production and O
2
con-
sumption between wheat of different moisture content.
(From Zhang, Q., Muir, W.E., Sinha, R.N., and Cenkowski,
S., Can. Agric. Eng., 34, 233, 1992. With permission.)
ß
2006 by Taylor & Francis Group, LLC.
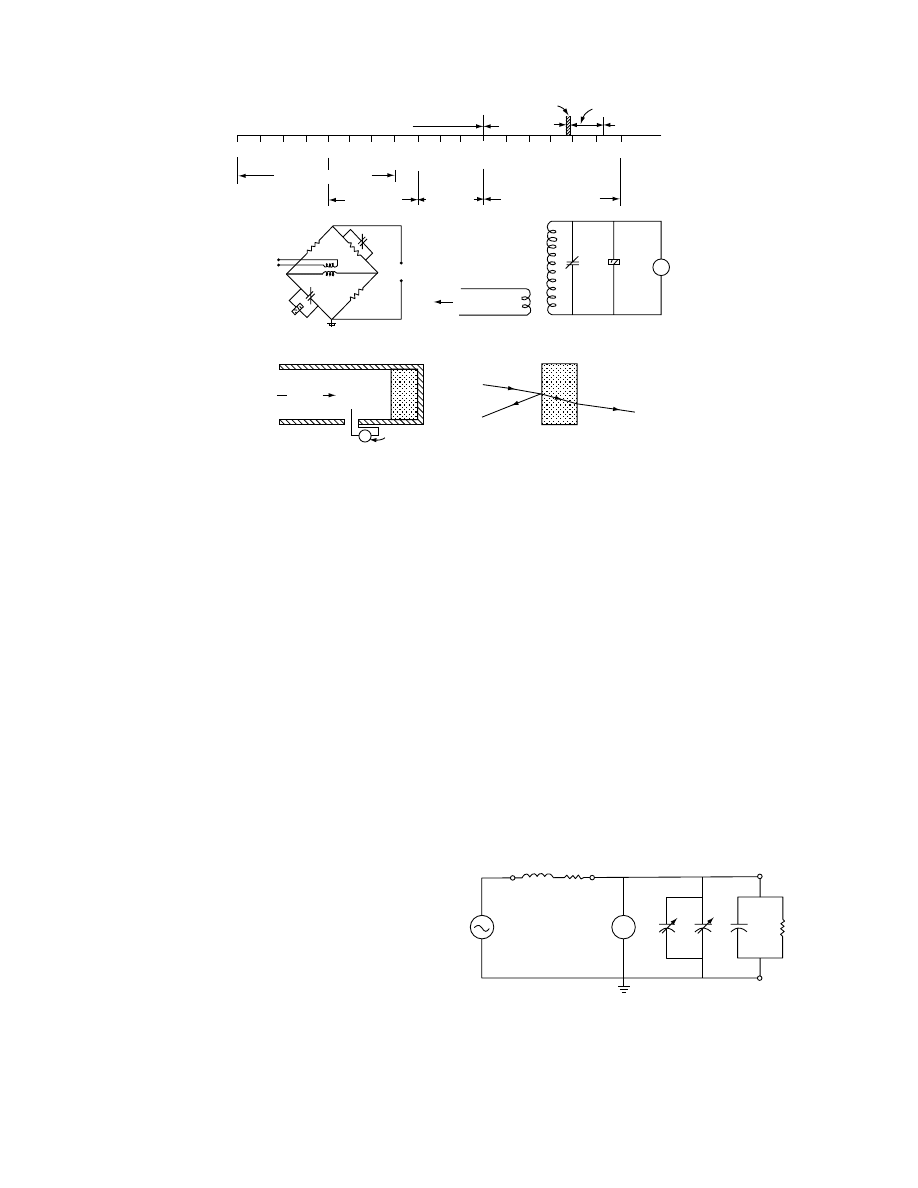
24.5.2 C
APACITANCE
-
AND
R
ESISTANCE
-B
ASED
M
EASUREMENTS
For sensing moisture content, a parallel-plate capaci-
tor may be used [78–80]. Capacitance measurements
are taken at frequencies of 1.0–4.5 MHz with a
Hewlett-Packard 4192 LF Impedance
Analyzer
equipped with the 16096A test fixture and a specially
constructed electrode assembly. Variations in kernel
shape and thickness cause capacitance variations. For
these reasons, the thickness, mass, and projected area
of individual kernels must also be measured [80].
Using a combination of a dc resistance measur-
ing meter (highly sensitive ohmmeter with a specially
designed electrode) and a capacitance-type meter, a
measure of moisture distribution in corn kernels can
be obtained. This information has been used to detect
heat damage in artificially dried corn [81,82].
24.5.3 M
EASUREMENTS BASED ON
E
LECTRICAL
C
ONDUCTIVITY
A moisture meter measuring the dc conductance in a
circuit was developed from the Wheatstone bridge
[83]. Because the electrical properties of whole grain
are preferentially affected by the moisture content
of the surface layers, the kernel is ground before
the test. In a test cell, the meal is compressed against
two coplanar electrodes to a standardized pressure
of 6.9 MPa. The electric current penetrates the sample
only to a depth of the order of the electrode se-
paration, so that the quantity of meal in the cell is
unimportant above a certain minimum.
The rate of water penetration in sorghum
kernels during tempering has been studied using a
Tag-Heppenstall (C.T. Taniabue, Brooklyn, NY)
electrical conductance moisture meter [84]. The tester
consists of a pair of corrugated rolls. When grain
passes between the rolls, it is slightly crushed and
thus acts as a path for the electric current. From the
current, I, that has passed through the grain, the
resistance, R, is determined by Ohm’s law (I
¼ E/R)
Radio frequencies
Visible
Infrared
Ultra-violet
Soft x-rays
Traveling wave
Standing
wave
Resonant
circuits
Schering bridge
Frequency in Hz
Detector
To signal
generator
Resonant circuit
Sample
Traveling wave
D
Traveling
detector
Standing wave
Input
Sample
Schering bridge
Sample
Input
Sample
10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
10
9
10
10
10
11
10
12
10
13
10
14
10
15
10
16
10
17
FIGURE 24.11 Frequency ranges and measuring techniques. (From Hippel, A.R., Dielectrics and Waves, John Wiley &
Sons, New York, 1954. With permission.)
L
R
v
C
R
x
FIGURE 24.12 Simplified diagram for Q-Meter series res-
onant measuring circuit with sample holder connected.
(From Nelson, S.O., Trans. ASAE, 22, 950, 1979. With
permission.)
ß
2006 by Taylor & Francis Group, LLC.
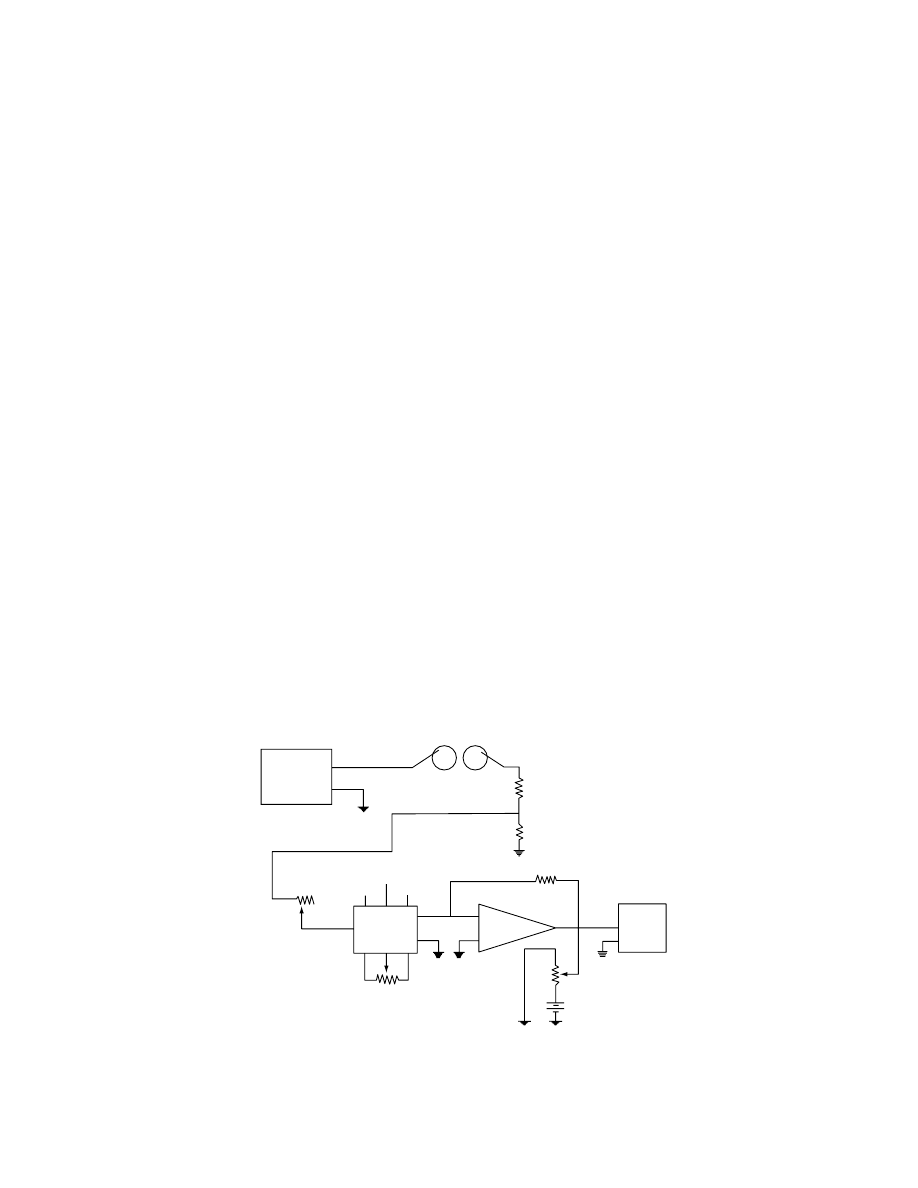
where E is the voltage used. The resistance is inversely
proportional to the moisture content. By measuring
the decrease in the apparent moisture in the outer
layers of grain at regular time intervals, the rate of
the water penetration into the kernel is determined.
A conductance-type meter similar to the Tag-
Heppenstall device has been designed to test single
corn kernels [85]. The rolls are about one third the
size of those of the Tag-Heppenstall; i.e., approxi-
mately 50 mm in diameter and 30 mm long, and the
idler roll is attached by a spring that gives the rolls
freedom to adjust to different size kernels. The rolls are
connected to a logarithmic amplifier that converts the
natural logarithmic response into a more useful line
response. The schematic of the instrument is shown in
Figure 24.13. The 100 V passing through the rolls is
reduced by a series of resistors so that the signal
reaching the recorder is 100 mV, and when the rolls
are shorted, the peak ammeter response is 100 units.
Tests showed that the response reached 100 units for
kernels with about 25% moisture.
The problems associated with blending grain ship-
ments that vary widely in moisture content are well
recognized. They include hazards of mold infection
and increased breakage susceptibility. A simple and
rapid method for detecting blends of corn varying
widely in moisture content has been reported in the
literature [86]. The detection is based on dual deter-
mination of moisture, i.e., by an oven drying method
and electrical conductance meter (Tag-Heppenstall,
model 8004, type 14, Weston Electrical Instruments
Corp. Newark, New Jersey) or by two electrical
methods
(conductance—Tag-Heppenstall
method
versus capacitance—Motomco moisture meter model
914, Motomco Inc., Patterson, New Jersey). In both
methods, the detection of blends of corn is based on
the difference in moisture content resulting from the
two methods.
24.6 OPTICAL PROPERTIES
Information on optical properties can be used for
automatic sorting, quantifying foreign materials [87],
and for objective classification of grain class and
variety [88]. The use of light transmittance or reflect-
ance offers a means for determining internal quality
of grains, moisture content [89], color, appearance
[90], the extent of smut spores on wheat [91]. Infrared
and far-red light has been used to change lettuce-seed
germination characteristics [92].
Energy can be transmitted from a body by electro-
magnetic waves. These vary from very short to very
long waves over a wide spectrum from cosmic to long
radio and electric waves. The spectrum of visible light
is usually divided into eight intervals, corresponding to
the following characteristic colors and wavelength
bands: violet (380–450 nm), light blue (450–480 nm),
blue (480–510 nm), green (510–550) nm), yellow-green
(550–575 nm), yellow (575–585 nm), orange (585–
620 nm), and red (620–760 nm). The infrared spectrum
is broader and falls between 0.7 and 100 mm. When
electromagnetic waves strike a body, they may be
absorbed, transmitted, or reflected. Absorption, reflec-
tion, and transmission may vary with wavelength [93]
and with the type of grain. Only 4% of the incident
radiation from a beam of light striking a typical grain
kernel is reflected [94]. The remaining radiation is
transmitted into the object. Of this portion, part is
absorbed by the object, part is reflected back to the
Variable
dc power
supply
+
−
−
R Slope
50 K
−15V +15V
COM
PPL4-N
Log module
2
1
3
25 K
I
ref
+
Output
QFT-2
E Balance
Recorder
E
o
10 M
1 M (megohm)
100 K (kilohm)
FIGURE 24.13 Electrical schematic of the instrument for determining moisture content of single kernels of corn. The
PPL4-N log module and the QFT-2 are manufactured by Teledyne Philbrick. (From Watson, C.A., Greenway, W.T.,
Davis, G., and McGinty, R.J., Cereal Chem., 56: 137–140, 1979. With permission.)
ß
2006 by Taylor & Francis Group, LLC.
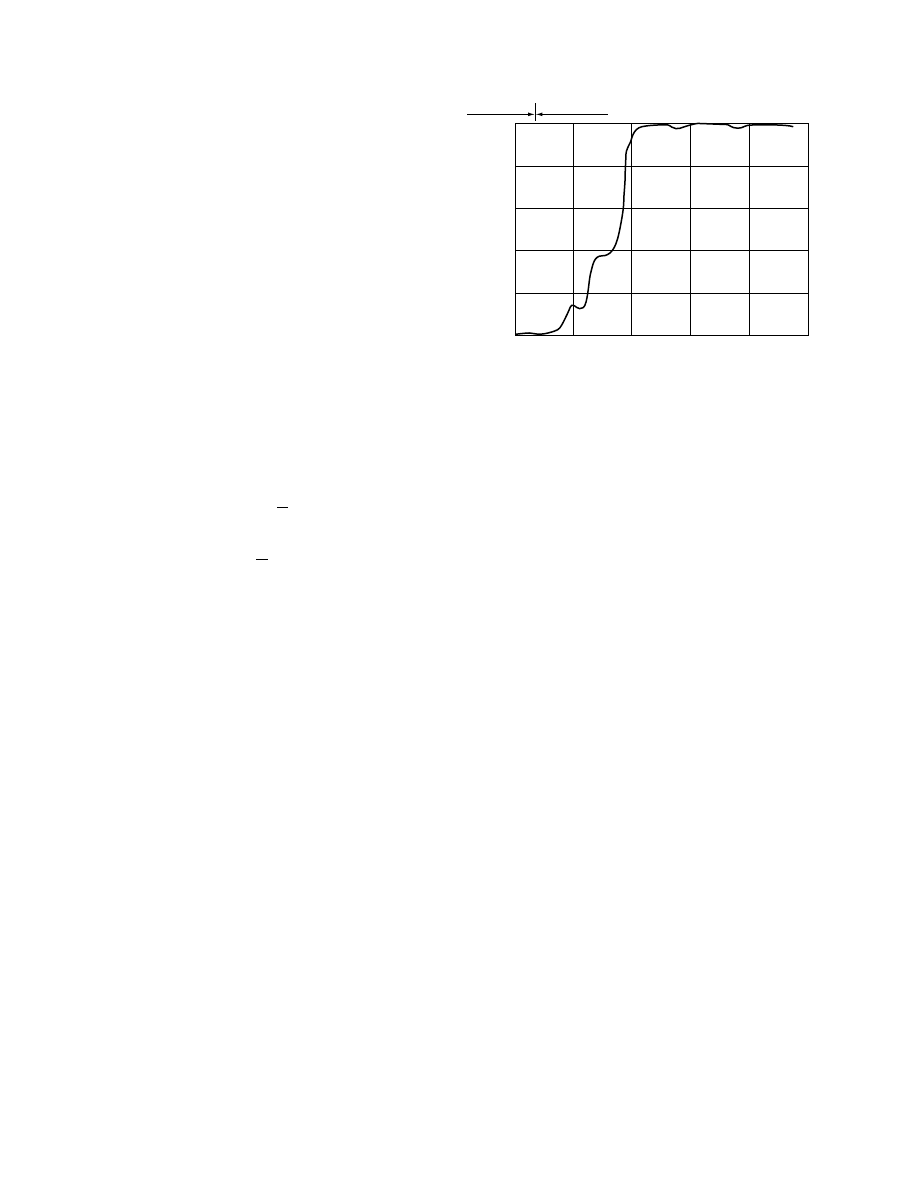
surface (body reflect ion), and part is transmit ted
through the object . The absorbed portion is trans -
formed to other forms of energy. For infrared radi-
ation (0.7–100 mm) the en ergy is transform ed into
heat. The amoun t of trans mitted rays absorbed by
the mate rial dep ends on the wave length and the phy s-
ical ch aracteris tics of the mate rial. Energy pa ssing
through a bulk sampl e of grain is a combinat ion of
transmit ted and reflect ed light. In the near-i nfrared
part of the spectr um (700–1 400 nm), a kernel of
wheat transmits about 2% an d reflect s 50% of the
radiation on the kernel [91]. A layer of steel ba lls of a
size similar to the kernels of wheat and of the same
layer thickne ss reflect a simila r amount of energy as
kernels of wheat but the amoun t of trans mitted light is
30 time s less. This indicates that some energy is trans -
mitted through indivi dual grain kernels.
Absor ption spectra are often charact erized by the
transmit tance, t , at a given wavelengt h:
Ano ther way of describ ing spectr a is in terms of
the ab sorbance, a:
t
¼
I
I
0
(24 : 34)
a
¼ log
I
0
I
¼ log t (24 : 35)
The absorbanc e is related to the thickne ss, L, of the
sample and the co ncentra tion, C , of absorbi ng mol-
ecules by the Beer–L ambert law [95] :
a
¼ «CL (24 : 36)
Accor ding to the law of conserva tion of en ergy, the
radiation incident on an object , I
o
, must be eq ual to
the sum of reflect ed, I
R
, absorbed , I
a
, and transmit -
ted, I
t
, rad iation:
I
o
¼ I
R
þ I
a
þ I
t
(24 : 37)
Spe cular reflection oc curs when the angle of re-
flectio n equals the an gle of incide nc e, wher eas diffu se
reflect ion is spread out evenly ov er a full hemisp here.
The main difficulty in measur ing the spectr al trans -
mittance prop erties of a kernel is the pro blem of
collecting suffici ent energy from the trans mitted sig-
nal. To co llect the maxi mum amo unt of light unde r
such co nditions the phot otube sho uld surround the
entire sample. The ne arest ap proach to this co ndition
can be atta ined by en closing the sampl e in a light -
integrati ng sphere with a phototube view ing a smal l
port in the sph ere to measur e the br ightness of the
sphere surface. Nearl y, all trans mitted light can be
collected by this arrange ment regardl ess of where it
emerg es from the grain [96].
Kno wledge of the spectral refl ectance of grain is
essential to design an infr ared grain dryer. The cho ice
of the so urce of infr ared radiat ion an d the thickne ss
of the grain sampl e both requir e this knowl edge. Fig-
ure 2 4.14 shows the variation in the absorpt ion of
infrared radiat ion for a 3 mm de pth of water. W ave-
length s longer than 1400 nm are complet ely absorbe d.
The intera ction betwee n the absorpt ion charact er-
istics of a mate rial and the intensit y of the light sou rce
can be illustrated in the followi ng example. Consid er
the drying of a material , whi ch has ab sorption char-
acterist ics as de scribed by the curve in Figure 24.14. It
is necessa ry to selec t a light source. The relat ive in-
tensity of the light shou ld be high enough under the
highest absorpt ion level (above 1400 nm) for the ma-
terial. From the three available sources of infrared
radiation (
) , the desired radiation source
charact eristic is the one with a filame nt tempe rature
of 2200 K. In this case 65% of the total energy of the
lamp (this is measur ed by the a rea under the relat ive
intensity curve and above 1400 nm wavelength) will
be completely absorbed when passing through the
sample. The light sources with filament temperatures
of 3500 or 1100 K are not desirable. In the first case
(3500 K) the maximum light intensity falls in the
range where absorption of the material is small. In
the second case (1100 K) the higher intensity charac-
teristic of the light source is beyond the range of the
absorption characteristics of the dried material.
Spectrophotometers are instruments that mea-
sure absorption or reflectance, and are not, as the
name implies, restricted to the visible light range.
0.6
1.0
1.4
1.8
2.2
2.6
0
20
40
60
80
100
Wavelength,
μm
Absorption, %
Visible
Infrared
FIGURE 24.14 Absorption of infrared radiation by a 3 mm
layer of water. (From Shuman, A.C. and Staley, C.H., Food
Technol., 4, 481, 1950. With permission.)
ß
2006 by Taylor & Francis Group, LLC.
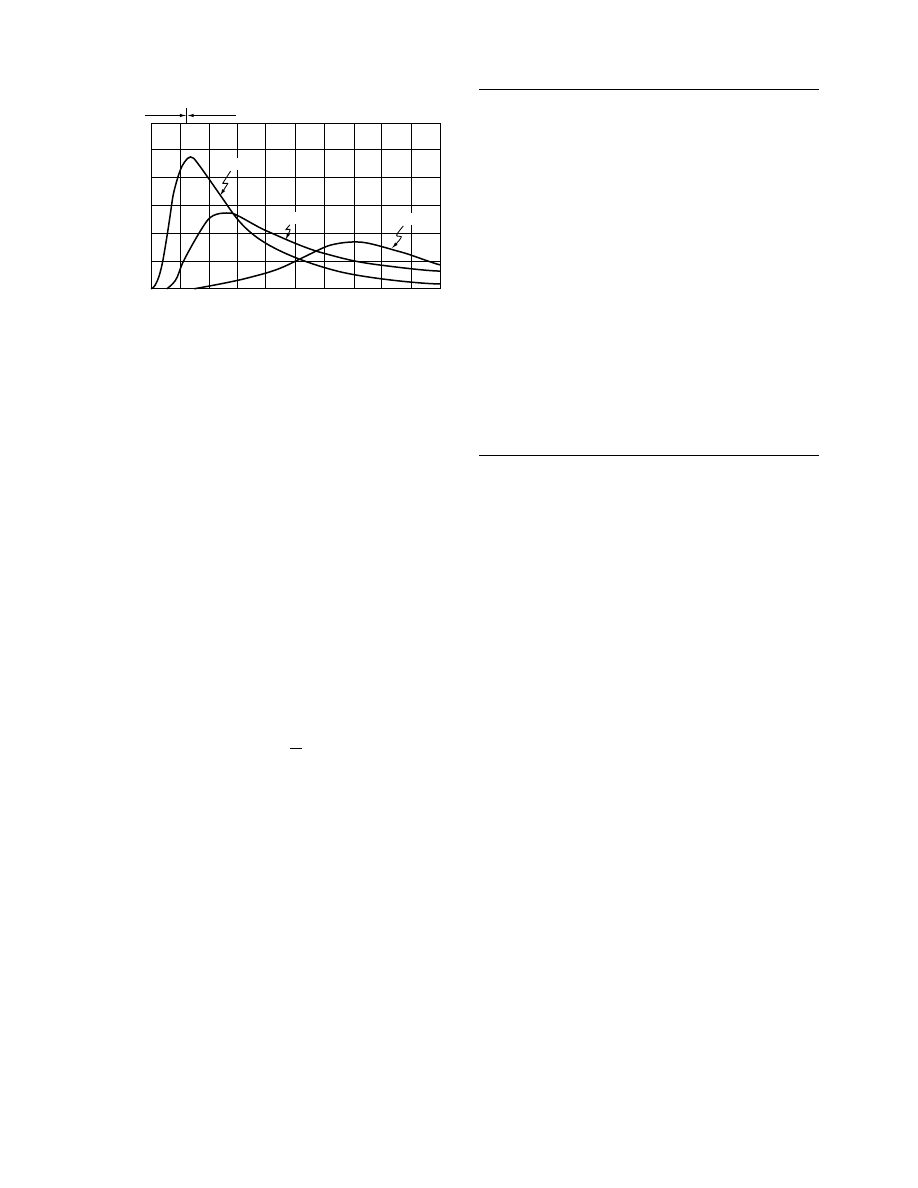
They include a light sou rce, wavelengt h selector, and
detecto r. There are many commerc ial spectr ophot o-
meters that are suitable for experi ments in the visi ble
and nonvisib le ranges. A greater fle xibility can be
obtaine d by assem bling an instrument from mod ular
compon ents availa ble from suc h sou rces as Oriel,
Bomem, PTR, Opti cs, and Spe x.
24.7 AERODYNAMIC PROPERTIES
In the de velopm ent of equipment for harvesting, han d-
ling, and cleani ng operation s, a knowled ge of the aero-
dynami c prop erties of various grains is necessa ry. The
aerodynam ic drag co efficient an d the terminal veloci ty
are the two most impor tant aerodynam ic prope rties.
The geometry of a solid body held in a free stream is
the major factor determining the drag force, F
D
, exerted
on a body. The drag force can be calculated from
F
D
¼ C
D
v
2
2
r
t
A
p
(24 : 38)
Values for the drag coeffici ent have been determined
for bodies of regula r shape such as spheres , cyli nders,
and fla t disks [97, 98]. The drag coeffici ents a re
usually sho wn on a log–l og plot, as a functio n of the
Reynol ds num ber.
M ost seed kernels are irre gular in shape. Thei r
drag coeffici ents de pend not only on the shape but
also on the orient ation of the kerne ls in the airstrea m.
Thus, an equivale nt diameter is used in the determ in-
ation of the Reynol ds number. Drag coeffici ents for
various crop s are given in Tabl e 24.15.
A free- falling body ce ases to acc elerate after some
time and the body attains a con stant term inal veloci ty.
The resistin g force be comes equal to the mass of the
body. The term inal veloci ty c an be calculated theoret -
ically for a spheri cal body by replac ing the drag force,
F
D
, in Equat ion 24.38 by its mass. For irre gularly
shaped kernels , the terminal veloci ty is de termined
experi mentally. There are two types of experi ments :
(i) free-fall tube and (ii) vertic al win d tunnel.
In the free-fal l tube, a kernel is held by partial
vacuum by a vacuu m dr op head (
) ;
the kernel free-fal ls after breaking the vacuum [99] .
The passage of the ke rnel through a light be am pro -
duces a vo ltage drop from the photocell whi ch starts a
counter. The ke rnel’s impac t on the receiver dia-
phragm, at the bottom of the tube, causes the second
voltage drop from the microp hone stopp ing the cou n-
ter. The height of fall is control led by chang ing the
length of the drop tube. Since the terminal velocity of
seeds ranges from approxim ately 5 to 15 m/s, the tube
always must be of a suffici ent lengt h. For exampl e,
testing soybeans requir es a tube at least 15 m long.
Other disadva ntages are that: (i) the seeds have a
tendency to fall off the cen ter line an d (ii) the move-
ment of the free-falli ng seeds is difficult to obs erve.
The ve rtical wind tunnel has app roximatel y a
1.8-m worki ng section wi th a taper of 38 on each
side (
). This diverg ence causes a redu c-
tion of the air veloci ty by ab out 25% pe r 1 m in length
and is essential for particle flotation and stability.
The taper enables a particle to float to a height corre-
sponding to its terminal velocity. The floating height
can be observed and measured. This technique has
been used to measure the terminal velocity of three
cultivars of wheat kernels [100], corn, soybeans,
wheat, oats, and barley [101], and milkweed pods
[102]. The advantage of the vertical wind tunnel over
the free-falling tube is that the first one does not
require as much headspace. The vertical wind tunnel
2200 K
1100 K
3500 K
Visible
Infrared
Relative intensity
Wavelength,
μm
0.2
0.6
1.0
1.4
1.8
2.2
2.6
3.0
3.4
3.8
4.2
0
20
40
60
80
100
120
FIGURE 24.15 Relative intensities of various sources of
infrared radiation. (From Shuman, A.C. and Staley, C.H.,
Food Technol., 4, 481, 1950. With permission.)
TABLE 24.15
Terminal Velocity of Seed Grains
Seed
Terminal
Velocities m/s
Drag
Coefficient
Reynolds
Number
Ref.
Alfalfa
5.5
0.50
601
120
Barley
7.3–9.0
—
—
101
Barley
7.0
0.50
2280
120
Corn
9.7–11.3
—
—
101
Corn
10.6
0.56
5770
120
Corn
11.4
0.56–0.70
5700
121
Flax
4.7
0.52
836
120
Oats
7.0–8.3
—
—
101
Oats
5.9–6.3
0.47–0.51
1900–2480
120
Oats
6.6
0.47–0.51
2000
121
Soybeans
14.5
0.45
6300
121
Soybeans
11.2–11.9
—
—
101
Soybeans
13.5
0.45
6280
120
Wheat
7.7–9.6
—
—
101
Wheat
9.0
0.50
2720
120
ß
2006 by Taylor & Francis Group, LLC.
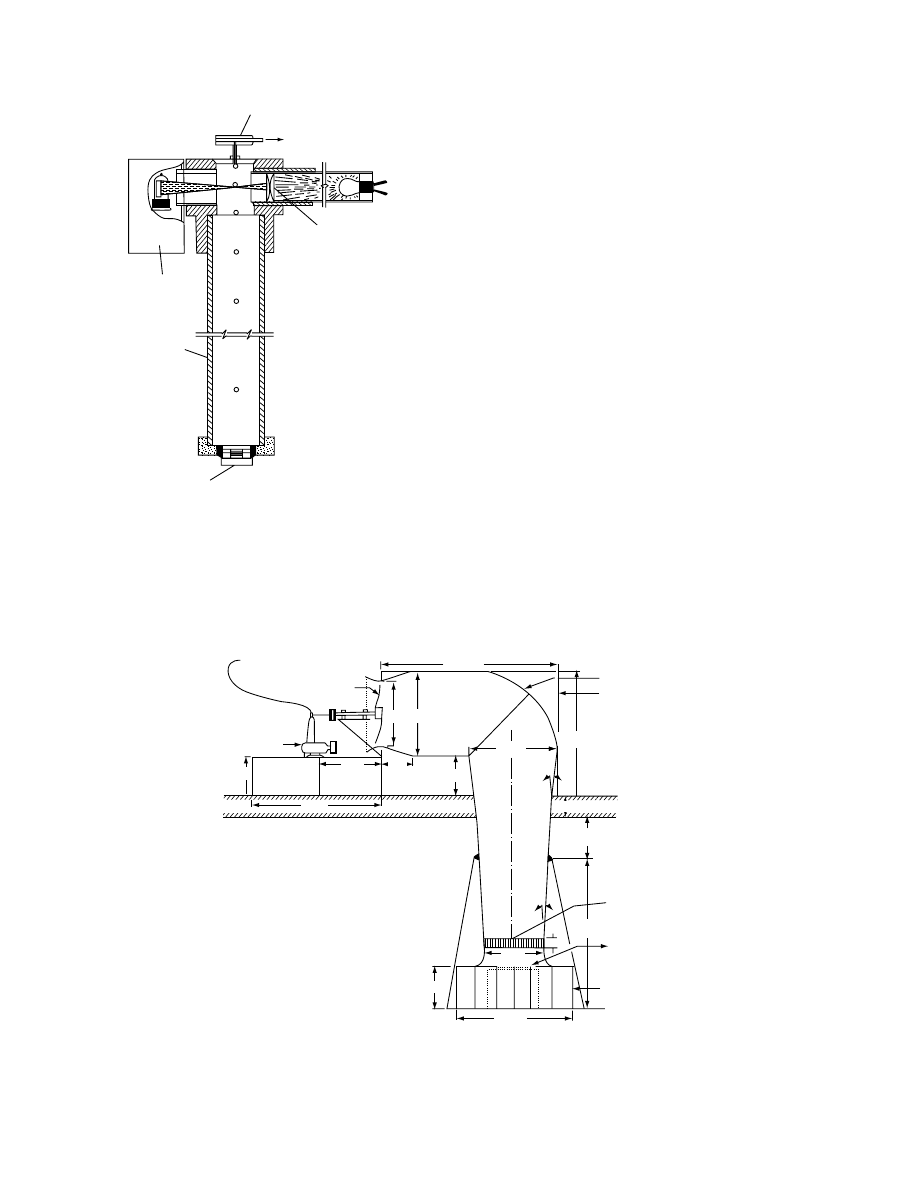
is of a compact struc ture and spinni ng of seeds can
be quite clearly observed and monit ored, howeve r,
the slightes t nonuni formity in the air velocity cau ses
undesir ed rotation and side movem ents of the seeds.
After determini ng the term inal velocity, the drag
coeffici ent c an be calcul ated using
The terminal velocity of selec ted seed grains is sum-
marized in
. The indica ted range reflect s
the influence of the geomet ric ch aracteris tics of dif-
ferent varietie s and the differen t-sized kernels wi thin
the same varie ty.
LIST OF SYMBOLS
A heat trans fer area, m
2
A constant
A
c
area of the smallest circum scribing circle, m
2
A
p
the projected area of a body normal to t he flow
or surface, m
2
a the long est dimension of a seed, mm
a
constant
a
1
coefficient which depends on a material
B
constant
b
constant
b
the longest dimension of a seed normal to a, mm
b
1
constant
C
constant
C
concentration of absorbing molecules, mole/L
Diaphragm
Microphone
Dropping tube
Photocell
Vacuum drop
Vacuum pump
FIGURE 24.16 Free-fall drop equipment. (From Keck, H.
and Goss, J.R., Trans. ASAE, 8:553–554, 557, 1965. With
permission.)
Honeycomb
16 Mesh screen
8 Vertical
guide vanes
1626
610
792
2175
152
568
305
1829
Plenum chamber
1220 inch wide
Deflector
1219
610
457
914
940 1194
2438
To an electronic
counter
Screen
Propeller fan
Tachometer
8 hp AC motor
610
1829
3
°
7
°
Note: All dimensions are in mm.
FIGURE 24.17 Diagram of a vertical wind tunnel. (From Bilanski, W.K. and Lal, R., Trans. ASAE, 8, 411, 416, 1965. With
permission.)
ß
2006 by Taylor & Francis Group, LLC.

C
D
the dra g coe fficient (dimensionl ess)
c the longest dimens ion of a seed normal to a and
b, mm
c specific heat of grain, J/(kg K)
c
1
constant
c
cp
specific heat of a copper plug, J/( kg K)
c
d
specific heat of dry matter of seeds, J/(kg K)
c
w
mean specific he at of water, J/(k g K)
D
g
geomet ric mean diame ter, m
d
e
equival ent diame ter, m
E mass of wat er having an equival ent therm al
capacit y to that of the calori meter flask, stirrer ,
therm ocouple, g
F
D
the total dra g force, N
h heat trans fer co efficien t (surface con ductance) ,
W/(m
2
K)
h
cv
volumetric heat transfer coefficient, kJ/(m
3
s K)
h
fg
* latent heat of vapo rization of wat er in seeds,
kJ/kg H
2
O
h
fg
latent heat of vaporization of free water, kJ/kg H
2
O
I intensit y of light trans mitted through the sampl e,
decim al
I
o
intensit y of light incident on the sampl e, decim al
j imaginary number
K drying constant, 1/s
k thermal cond uctivity , W/(m K)
k
a
thermal cond uctivity of the air, W/(m K)
k
d
thermal co nductiv ity of a layer of dry matter of
seeds, W/( m K)
L sample thickne ss, m
M moisture content db, kg H
2
O/ kg dr y matt er
M ’ moisture content , % wb
M
e
equilibrium moisture content , kg H
2
O/k g db
M
i
initial mois ture co ntent, kg H
2
O/kg db
m mass of the mate rial, kg
m airflow rate, kg/s.
m
a
airflow rate, kg/(m
2
s)
m
cp
mass of a c opper plug, kg
m
s
mass of the sampl e, kg
m
w
mass of water, kg
N drying coefficien t
n number of pa rticles
Nu Nusse lt number, dimensionle ss
Pr Prandtl number, dimens ionles s
P
v
actual pressur e of wat er vap or, Pa
P
vs
saturati on pressur e of water vapo r, Pa
q heat flow, or heat flux , W or W/m
2
q
amount of heat, kJ
q
l
heat input per unit length of line heater, W/m
R
roundness (decimal)
Re Reynolds number, dimensionless
RH relative humidity, decimal
r
distance of the grain layer from the zero axis
which represents the heat source, m
T
drying air temperature, 8C
T temperature of a copper plug (
), 8 C
T
c
initial temperature of water at transient time, 8C
T
m
temperature of the mixture extrapolated at tran-
sient time, 8C
T
1
temperature of a copper rod (Equation 24.12), 8C
t
time, s
t
c
corrected time, s
V
e
equivalent volume, m
3
V
n
net volume of particles, m
3
v
drying air velocity, m/s
v
free stream velocity, m/s
x
distance from the face of a slab, m
z
dimensionless number
G
REEK
S
YMBOLS
a
absorbance, decimal
a
thermal diffusivity of seeds, m
2
/s
H
gradient
d
loss angle of a dielectric, deg
«
molar absorptivity, L/(mole cm)
«
0
permittivity of free space, «
0
¼ 8.854 10
2
12
farad/m.
«
porosity, decimal
u
temperature of a grain layer, 8C
u
grain temperature, 8C
u
0
initial grain temperature, 8C
u
0
initial temperature of both sample and copper
plug, (Equation 24.12) 8C
u
0
initial temperature of a slab, 8C
u
c
temperature at center of a slab, 8C
u
s
initial temperature of the sample, 8C
n
kinematic viscosity of drying air, m
2
/s
r
density of fluid (air), kg/m
3
r
b
bulk density, kg/m
3
r
t
particle density, kg/m
3
s
ac conductivity, 1/(ohm m) or mhos/m
t
transmittance, decimal
v
angular frequency of the applied electric field
(v
¼ 2pf where f is the frequency of the
applied voltage), rad/s.
S
UBSCRIPTS
db
dry basis
R
reflected
wb wet basis
a
absorbed
t
transmitted
REFERENCES
1. Statistical Handbook 94, Canada Grains Council,
760–330 MainSt.,Winnipeg,MB, Canada(1994).
2. Grain Grading Handbook for Western Canada, Canadian
Grain Commission, Winnipeg, MB, Canada (1993).
ß
2006 by Taylor & Francis Group, LLC.

3. ASAE, D241, 4 Feb. 93, Density, specific gravity, and
mass–moisture relationships of grain for storage, 40th
ed., Standards, Engineering Practices, and Data (Am.
Soc. Ag. Eng.), St. Joseph, MI, 1993, pp. 408–410.
4. Day, C.L., Device for measuring voids in porous
materials, Agric. Eng., 45(1):36–37 (1964).
5. Shatadal, P., Jayas, D.S., Hehn, J.L., and Bulley,
N.R., Seed classification using machine vision, Can.
Agric. Eng., 37(3):163–167 (1995).
6. Wratten, F.T., Poole, W.D., Chesness, J.L., Ball, S.,
and Ramarao, V., Physical and thermal properties of
rough rice, Trans. ASAE, 12(6):801–803 (1969).
7. Hedlin, C.P. and Collins, S.H., A method of measur-
ing the surface area of granular material, Can. J. Chem.
Eng., 2:49 (1961).
8. Bakker-Arkema, F.W., Rosenau, J.R., and Clifford,
W.H., The effect of grain surface area on the heat and
mass transfer rates in fixed and moving beds of bio-
logical products, Trans. ASAE, 14(5):864–867 (1971).
9. Jindal, V.K., Mohsenin, N.N., and Husted, J.V., Sur-
face area of agricultural grains, Trans. ASAE,
17(4):721–725, 728 (1974).
10. Irvine, D.A., Jayas, D.S., White, N.D.G., and Britton,
M.G., Physical properties of flaxseed, lentils, and
fababeans, Can. Agric. Eng., 34:75–81 (1992).
11. Irvine, D.A., Jayas, D.S., Britton, M.G., and White,
N.D.G., Dynamic friction characteristics of bulk
seeds against flat vertical surfaces, Trans. ASAE,
35(2):665–669 (1992).
12. ASAE, S352, 2 Dec. 92, Moisture measurement—
unground grain and seeds, 40th ed., Standards, Engin-
eering Practices, and Data (Am. Soc. Ag. Eng.), St.
Joseph, MI, 1993, p. 449.
13. Rockland, L.B., Saturated salt solution for static con-
trol of relative humidity between 5 and 408C, Anal.
Chem., 32:1375–1376 (1960).
14. Flood, C.A. and White, G.M., Desorption equilibrium re-
lationship of popcorn, Trans. ASAE, 27(2):561–571 (1984).
15. Henderson, S.M., A basic concept of equilibrium
moisture, Agric. Eng., 33(1):29–32 (1952).
16. Thompson, T.L., Peart, R.M., and Foster, G.H.,
Mathematical simulation of corn drying—a new
model, Trans. ASAE, 11(4):582–586 (1968).
17. Chung, D.S. and Pfost, H.B., Adsorption and
desorption of water vapor by cereal grains and their
products. Part II: development of the general isotherm
equation, Trans. ASAE, 10(4):552–555 (1967).
18. Pfost, H.B., Maurer, S.G., Chung, D.S., and Milliken,
G.A., Summarizing and reporting equilibrium mois-
ture data for grains, Paper No. 76–3520, ASAE, St.
Joseph, MI, 1976.
19. Halsey, G., Physical adsorption on non-uniform
surfaces, J. Chem. Phys., 16:931–937 (1948).
20. Iglesias, H.A. and Chirife, J., Prediction of effect of
temperature on water sorption isotherms of food ma-
terials, J. Food Technol., 11:109–116 (1976).
21. Oswin, C.R., The kinetics of package life. III. Isotherm,
J. Soc. Chem. Ind. London, 65:419–421 (1946).
22. Chen, C. and Morey, R.V., Comparison of four EMC/
ERH equations, Trans. ASAE, 32(3):983–990 (1989).
23. Jayas, D.S. and Mazza, G., Equilibrium moisture
characteristics of safflower seeds, Trans. ASAE,
34(5):2099–2103 (1991).
24. Jayas, D.S. and Mazza, G., Comparison of five three-
parameter equations for the description of adsorption
data of oats, Trans. ASAE, 36(1):119–125 (1993).
25. ASAE, D245.5. Moisture relationships of plant-based
agricultural products, 43rd ed., Standards, Engineer-
ing Practices, and Data (Am. Soc. Ag. Eng.), St.
Joseph, MI, 1996.
26. Siebel, E., Specific heats of various products, Ice and
Refrigeration, 2:256–257 (1892).
27. Sharma, D.K. and Thompson, T.L., Specific heat and
thermal conductivity of sorghum, Trans. ASAE,
16:114–117 (1973).
28. Mohsenin, N.N., Thermal Properties of Foods and
Agricultural Materials, Gordon and Breach Science
Publishers, New York, 1980.
29. Sweat, V.E., Thermal properties of foods. In: Engin-
eering Properties of Foods (M.A. Roa and S.S. Rizvi,
Eds.), Marcel Dekker, New York, pp. 49–87 (1986).
30. Reidy, G.A. and Rippen, A.L., Methods for determin-
ing thermal conductivity in foods, Trans. ASAE, 14:
248–254 (1971).
31. Rahman, S., Food Properties Handbook, CRC Press,
New York, 1995.
32. Disney, R.W., The specific heat of some cereal grains,
Cereal Chem., 31:229–239 (1954).
33. Muir, W.E. and Viravanichai, S., Specific heat of
wheat, J. Agric. Eng. Res., 17:338–342 (1972).
34. Moysey, E.B., Shaw, J.T., and Lampman, W.P., The
effect of temperature and moisture on the thermal prop-
erties of rapeseed, Trans. ASAE, 20:768–771 (1977).
35. Suter, D.A., Agrawal, K.K., and Clary, B.L., Thermal
properties of peanut pods, hulls and kernels, Trans.
ASAE, 18:370–375 (1975).
36. Gordon, C. and Thorne, S., Determination of the ther-
mal diffusivity of food from temperature measurements
during cooling, J. Food Eng., 11:133–145 (1990a).
37. Gordon, C. and Thorne, S., A computerized method
for determining the thermal conductivity and specific
heat of foods from temperature measurements during
cooling, J. Food Eng., 11:175–185 (1990b).
38. Tang, J., Sokhansanj, S., Yannacopoulus, S., and
Kasap, S.O., Specific heat of lentil by differential scan-
ning calorimetry, Trans. ASAE, 34:517–522 (1991).
39. Dutta, S.K., Nema, V.K., and Bhardwaj, R.K., Ther-
mal properties of gram, J. Agric. Eng. Res., 39:269–
275 (1988).
40. Viranichai, S., Effect of moisture content and tem-
perature on specific heat of wheat. M.Sc. dissertation
(unpublished), Department of Agricultural Engineer-
ing, University of Manitoba, MB, 1971.
41. Sharp, R.B. and Nash, J.E., A method of determining
the specific heat of seeds, J. Agric. Eng. Res., 10:355–
358 (1965).
42. Tang, J., Thermal and hygroscopic characteristics of
lentil seed. Ph.D. dissertation (unpublished), Depart-
ment of Agricultural Engineering, University of Sas-
katchewan, SK, 1991.
ß
2006 by Taylor & Francis Group, LLC.

43. Babbitt, E.A., The thermal properties of grain in bulk,
Can. J. Res. Section F, 23:388–401 (1945).
44. Kazarian, E.A. and Hall, C.W., Thermal properties of
grains, Trans. ASAE, 8:33–38 (1965).
45. Koschatzky, R., Experimental determination of the
specific heat of corn, grasses, and legumes (in German),
Grundlagen der Landtechnik, 23:99–105 (1973).
46. Haswell, G.A., A note on the specific heat of rice, oats
and their products, Cereal Chem., 31:341–342 (1954).
47. Alam, A. and Shove, G.C., Hygroscopicity and ther-
mal properties of soybeans. ASAE Paper No. 72–320
ASAE, St. Joseph, MI, 1972.
48. Nesvadba, P., Methods for the measurement of ther-
mal conductivity and diffusivity of foodstuffs, J. Food
Eng., 1:93–113 (1982).
49. Oxley, T.A., The properties of grain in bulk, Soc.
Chem. Industries Trans., 63:53–57 (1944).
50. Fitch, A.L., A new thermal conductivity apparatus,
Am. Phys. Teacher, 3:135 (1935).
51. Zuritz, C.A., Sastry, S.K., McCoy, S.C., Murakami,
E.G., and Blaisdell, J.L., A modified Fitch device for
measuring the thermal conductivity of small food par-
ticles, Trans. ASAE, 32:711–718 (1989).
52. Hopper, F.C. and Lepper, F.R., Transient heat flow
apparatus for the determination of thermal conduct-
ivities, ASHVE Trans., 56:309–324 (1950).
53. Nix, G.H., Lowery, G.W., Vachon, R.I., and Tanger,
G.E., Direct determination of thermal diffusivity and
conductivity with a refined line-source technique. In:
Progress in Aeronautics and Astronautics: Thermophysics
of Spacecraft and Planetary Bodies, Vol. 20 (G. Heller,
Ed.), Academic Press, New York, 1967, pp. 865–878.
54. Papadakis, G., Giaglaras, P., and Kyritsis, S., A numer-
ical method for determining thermal conductivity of
porous media from in-situ measurements using a cylin-
drical heat source, J. Agric. Eng. Res., 45:281–293
(1990).
55. McGinnis, D.S., Automated line-heat source system
for the measurement of thermal conductivity and dif-
fusivity, Can. Agric. Eng., 29:201–207 (1987).
56. Alagusundaram, K., Jayas, D.S., and Muir, W.E.,
Thermal conductivity of bulk barley lentils and peas,
Trans. ASAE, 34:1784–1788 (1991).
57. Ingersoll, R.L., Zobel, O.L., and Ingersoll, A.C., Heat
Conduction with Engineering, Geological and other Ap-
plications, The University of Wisconsin Press, Madi-
son, 1954.
58. Chang, C.S., Thermal conductivity of wheat, corn,
and grain sorghum as affected by bulk densities and
moisture content, Trans. ASAE, 29:1447–1450 (1986).
59. Watts, K.C. and Bilanski, W.K., Methods for estimat-
ing the thermal diffusivity of whole soybeans, Trans.
ASAE, 16:1143–1145 (1973).
60. Poulsen, K.P., Thermal diffusivity of foods measured
by simple equipment, J. Food Eng., 1:115–122 (1982).
61. Lo¨f, G.O.G. and Havley, R.W., Unsteady-state heat
transfer between air and loose solids, Ind. Eng. Chem.,
40:1061–1070 (1948).
62. Bala, B.K. and Woods, J.L., Simulation of deep bed
malt drying, J. Agric. Eng. Res., 30:235–244 (1984).
63. Boyce, D.S., Grain moisture and temperature changes
with position and time during through drying, J. Agric.
Eng. Res., 10:333–341 (1965).
64. ASHRAE.
ASHRAE
Handbook:
Fundamentals,
American Society of Heating, Refrigerating and Air-
Conditioning Engineers, Inc., Atlanta, GA, 1989.
65. Gallaher, G.L., A method of determining the latent heat
of agricultural crops, Agric. Eng., 32:34–38 (1951).
66. Cenkowski, S., Jayas, D.S., and Hao, D., Latent heat
of vaporization for selected foods and crops, Can.
Agric. Eng., 34:281–286 (1992).
67. Lassik, E.A., A model for the removal of heat in
respiring grains. ASAE Paper No. 86–6509, ASAE,
St. Joseph, MI, 1986.
68. Multon, J.L., Preservation and Storage of Grains, Seed
and their By-products—Cereals, Oilseeds, Pulses and
Animal Feed, Lavoisier Publishing, New York, 1988.
69. Milner, M. and Geddes, W.F., Grain storage studies,
IV. Biological and chemical factors involved in the
spontaneous heating of soybeans, Cereal Chem.,
23:449–470 (1946).
70. Zhang, Q., Muir, W.E., Sinha, R.N., and Cenkowski,
S., Heat production in wet wheat under adiabatic
conditions, Can. Agric. Eng., 34:233–238 (1992).
71. Hippel, A.R., Dielectrics and Waves, John Wiley &
Sons, New York, 1954.
72. Nelson, S.O., Electrical properties of agricultural
products—a critical review, Trans. ASAE, 16:384–
400 (1973).
73. Nelson, S.O., Improved sample holder for Q-meter di-
electric measurements, Trans. ASAE, 22:950–954 (1979).
74. Kraszewski, A.W. and Nelson, S.O., Density-independent
moisture determination in wheat by microwave meas-
urement, Trans. ASAE, 34:1776–1783 (1991).
75. Lawrence, K.C. and Nelson, S.O., Radio-frequency
density-independent
moisture
determination
in
wheat, Trans. ASAE, 36:477–483 (1993).
76. Nelson, S.O., Lawrence, K.C., and Kraszewski, A.W.,
Sensing moisture content of pecans by RF impedance
and
microwave
resonator
measurements,
Trans.
ASAE, 35:617–623 (1992).
77. Dexter, S.T., Separation of living and dead corn (Zea
mays) kernels without germination, Agron. J., 57:95–
96 (1965).
78. Kandala, C.V.K., Nelson, S.O., and Lawrence, K.C.,
Moisture determination in single kernels of corn—a
nondestructive method, Trans. ASAE, 31:1890–1895
(1988).
79. Kandala, C.V.K., Nelson, S.O., and Lawrence, K.C.,
Non-destructive electrical measurement of moisture
content in single kernels of corn, J. Agric. Eng. Res.,
44:125–132 (1989).
80. Kandala, C.V.K., Nelson, S.O., and Lawrence, K.C.,
Nondestructive moisture determination in single ker-
nels of popcorn by radio-frequency impedance meas-
urement, Trans. ASAE, 35:1559–1562 (1992).
81. Kandala, C.K.V., Leffler, R.G., Nelson, S.O., and
Lawrence, K.C., Capacitive sensors for measuring
single-kernel moisture content in corn, Trans. ASAE,
30:793–797 (1987).
ß
2006 by Taylor & Francis Group, LLC.

82. Holaday, C.E., An electronic method for the measure-
ment of heat-damage in artificially dried corn, Cereal
Chem., 41:533–542 (1964).
83. Brockelsby, C.F., An instrument for estimating the
moisture content of grain and other materials by the
measurement of electrical conductance, Cereal Chem.,
28:83–94 (1951).
84. Abdelrahman, A.A. and Farrell, E.P., Use of an elec-
trical conductance moisture meter to study tempering
rates in grain sorghum, Cereal Chem., 58:307–308 (1981).
85. Watson, C.A., Greenway, W.T., Davis, G., and
McGinty, R.J., Rapid proximate method for deter-
mining moisture content of single kernels of corn,
Cereal Chem., 56:137–140 (1979).
86. Pomeranz, Y. and Czuchowska, Z., Rapid and simple
detection of a mixture of wet and dry corn, Cereal
Chem., 63:283–284 (1986).
87. Sapirstein, H.D., Neuman, M.R., Wright, E.H., Shwe-
dyk, E., and Bushuk, W., An instrumental system of
cereal grain classification using digital image analysis,
J. Cereal Sci., 6:3–14 (1987).
88. Neuman, M.R., Sapirstein, H.D., Shwedyk, E., and
Bushuk, W., Discrimination of wheat class and variety
by digital image analysis of whole grain samples,
J. Cereal Sci., 6:125–132 (1987).
89. Finney, E.E. and Norris, K.H., Determination of
moisture in corn kernel by near-infrared transmittance
measurements, Trans. ASAE, 21:581–584 (1978).
90. Neuman, M.R., Sapirstein, H.D., Shwedyk, E., and
Bushuk, W., Wheat grain colour analysis by digital
image processing. I. Methodology, J. Cereal Sci.,
10:175–182 (1989).
91. Birth, G.S., Measuring smut content of wheat, Trans.
ASAE, 3:19–21 (1960).
92. Borthwick, H.A., Hendriks, S.B., Toole, E.H., and
Toole,
V.K.,
Action
of
light
on
lettuce-seed
germination, The Botanical Gazette, 115:205–224
(1954).
93. Shuman, A.C. and Staley, C.H., Drying by infra-red
radiation, Food Technol., 4:481–484 (1950).
94. Mohsenin, N.N., Electromagnetic Radiation Proper-
ties of Foods and Agricultural Products, Gordon and
Breach Science Publishers, New York, 1984.
95. D.P. Shoemaker, C.W. Garland, and J.W. Nibler,
Experiments in Physical Chemistry, McGraw-Hill
Publishing Company, New York, NY (1989).
96. Norris, K.H., Measuring light transmittance proper-
ties of agricultural commodities, Agric. Eng., 10:640–
643 (1958).
97. Geankoplis, C.J., Transport Processes and Unit Oper-
ations, Allyn and Bacon, Newton, MA, 1983.
98. Azbel, D.S. and Cheremisinoff, N.P., Fluid Mechanics
and Unit Operations, Ann Arbor Science Publishers,
Ann Arbor, MI, 1983.
99. Keck, H. and Goss, J.R., Determining aerodynamic
drag and terminal velocities of agronomic seeds in free
fall, Trans. ASAE, 8:553–554, 557 (1965).
100. Bilanski, W.K. and Lal, R., Behavior of threshed
materials in a vertical wind tunnel, Trans. ASAE,
8:411–413, 416 (1965).
101. Song, H.J. and Litchfield, B., Predicting method of
terminal velocity for grains, Trans. ASAE, 34:225–
231 (1991).
102. Jones, D. and Von Bargen, K.L., Some physical proper-
ties of milkweed pods, Trans. ASAE, 35:243–246 (1992).
103. Bilowicka, E., Some physical properties of legume seeds
in relationship to their moisture content (in Polish), Zes-
zyty Problemowe Nauk Rolniczych, 147:47–59 (1974).
104. Bekasov, A.G. and Denisov, N.J., Crop Handling
after drying (in Russian) Zagotizdat, Moscow (1952).
105. Pabis, S. and Henderson, S.M., Grain drying theory.
III. The grain/air temperature relationship, J. Agric.
Eng. Res., 7:21–26 (1962).
106. Mu¨hlbauer, W., Analysis of the drying process of corn
kernels considering the direct current drying method
(in German), Proceedings of the Workshop for the Re-
search and Science of the MEG, Issue 1, Bumberg, 1974.
107. Nelson, S.O., Moisture dependent kernel and bulk
density relationship for wheat and corn, Trans.
ASAE, 23:139–143. (1980).
108. Muir, W.E. and Sinha, R.N., Physical properties of
cereal and oilseed cultivars grown in Western Canada,
Can. Agric. Eng., 30(1):51–55 (1988).
109. Rameshbabu, M., Jayas, D.S., Muir, W.E., White,
N.D.G., and Mills, J.T., Bulk and handling properties
of hulless barley, Can. Agric. Eng., 38(1):31–35 (1996).
110. Bern, C.J., The specific heat of alfalfa. M.Sc. thesis (un-
published), University of Nebraska, Lincoln, NE, 1964.
111. Mu¨hlbauer, W. and Scherer, R., The specific heat of
cereals (in German), Grundlagen der Landtechnik,
27:33–40 (1977).
112. Brooker, D.B., Bakker-Arkema, F.W., and Hall,
C.W., Drying Cereal Grains, The AVI Publishing,
Westport, CT, 1974.
113. Tang, J. and Sokhansanj, S., Postharvest technology
for lentils, ASAE Paper NC90–103, ASAE, St. Joseph,
MI, 1990.
114. Gadaj, S.P. and Cybulska, W., Thermal conductivity
of a layer of kernels (in Polish), Roczniki Nauk Rol-
niczych, 70-C-1:7–15 (1973).
115. Pabis, S., Bilowiecka, S.E., and Gadaj, S.P., Heat
transfer and thermal conductivity in a bed of grain
for selected agricultural products (in Russian), Eng.
Phys. J., 19:78–85 (1970).
116. Wratten, F.T., Poole, W.D., Chesness, J.L., Ball, S.,
and Ramarao, V., Physical and thermal properties of
rough rice, Trans. ASAE, 12:801–803 (1969).
117. Sreenarayann, V.V. and Chattopadhyay, P.K., Ther-
mal conductivity and diffusivity of rice bran, J. Agric.
Eng. Res., 34:115–121 (1986).
118. Chandra, S. and Muir, W.E., Thermal conductivity of
spring wheat at low temperature, Trans. ASAE,
14:644–646 (1971).
119. Gierzoi, A.P. and Samochetov, W.P., Grain Drying (in
Russian), Zagotizdat, Moscow, 1951.
120. Bilanski, W.K., Collinsand, S.H., and Chu, P., Aero-
dynamic properties of seed grains, Agric. Eng.,
43:216–134 (1962).
121. Sitkei, G., Mechanics of Agricultural Materials, Else-
vier Science Publishers, New York, 1986.
ß
2006 by Taylor & Francis Group, LLC.

Document Outline
- Table of Contents
- Chapter 024: Grain Property Values and Their Measurement
- 24.1 Introduction
- 24.2 Physical Properties
- 24.2.1 Bulk Density (Test Weight)
- 24.2.2 Particle Density
- 24.2.3 Porosity
- 24.2.4 Projected Area
- 24.2.5 Roundness
- 24.2.6 Equivalent Volume (Equivalent Diameter)
- 24.2.7 Sphericity
- 24.2.8 Surface Area
- 24.2.9 Emptying and Filling Angles of Repose
- 24.2.10 Friction Coefficients against Structural Materials
- 24.3 Hygroscopic Properties
- 24.4. Thermal Properties
- 24.5 Electrical Properties
- 24.6 Optical Properties
- 24.7 Aerodynamic Properties
- List of Symbols
- References
Wyszukiwarka
Podobne podstrony:
Herbs And Their Magickal Properties
Herbs and Their Magical Properties
Bradley Using ISO 3382 measures, and their extensions, to evaluate acoustical conditions in concert
MoS2 Preparation and their characterization
54 767 780 Numerical Models and Their Validity in the Prediction of Heat Checking in Die
Copyright Laws and their Downfalls Relating to?nada
Clothes and their Descriptions Worksheet
Medieval Writers and Their Work
German Converts to Islam and Their Ambivalent Relations with Immigrant Muslims
Choices, Values, and Frames D Kahneman, A Tversky
charged and rotating ADS black holes and their CFT duals
Cigarettes and Their?struction of the Brain
Analysis of?rm Subsidies and their?fects
MICROACTUATORS AND THEIR TECHNOLOGIES
grades of timber and their use
A comparison?tween English and German and their ancestors
HUMAN RIGHTS AND THEIR IMPORTANCE goood
więcej podobnych podstron