Ws zechnica Popołudniowa

Czy ws zys tko można policzyć na komputerze

prof. dr hab. Maciej M Sysło

prof. dr hab. Maciej M Sysło

Zes zyt dydaktyczny opracowa ny w ramach projektu edukacyjnego

— ponadregionalny program rozwija nia kompetencji

uczniów s zkół ponadgimna zjalnych w zakresie technologii
informacyjno-komunikacyjnych (ICT).

Wars zawska Wyższa Szkoła Informatyki

ul. Le wartows kiego 17, 00-169 Wars zawa

Projekt graficzny: FRYCZ I WICHA

Warsza wa 2010
Copyright © Wars zawska Wyższa Szkoła Informatyki 2010
Publikacja nie jes t przeznaczona do sprzedaży.

Uniwers ytet Wrocławski, UMK w Toruniu

s [e-mail], [e-mail]

< 4 >

Informatyka +

Przedmiotem wykładu jes t łagodne wprowadzenie do złożonoś ci problemów i algorytmów. Przewodnim pyta-
niem jes t, jak dobrze sprawują się algorytmy i komputery i czy komputery już mogą ws zys tko obliczyć. Z jed-
nej s trony, dla niektórych problemów (jak znajdowanie najmniejs zego elementu) znane s ą algorytmy, które
nie mają konkurencji, gdyż s ą bezwzglę dnie najleps ze , a z drugiej – is tnieją problemy, o których przypus zcza
się, że komputery nigdy nie będą w s ta nie ich rozwią zywać dostatecznie s zybko. Przedstawione zos taną pro-
blemy, dla których s ą znane algorytmy optymalne (tj. takie, których nie można już przyspieszyć), ora z takie
problemy, których nie potrafimy rozwiązywa ć szybko, nawet z użyciem najs zybs zych komputerów. Problemy
z tej drugiej grupy znajdują zas tos owanie na przykład w kryptografii. Rozwa żania bę dą ilus trowane praktycz-
nymi za s tosowaniami omawianych problemów i ich metod obliczeniowych.

Rozwa żania s ą prowadzone na elementarnym poziomie i do ich wysłuchania wys tarczy znajomoś ć informa-
tyki wynies iona z gimna zjum. Te zaję cia s ą adresowane do ws zys tkich uczniów w szkołach ponadgimnazjal-
nych, zgodnie bowiem z nową pods tawą programową , ks ztałceniem umiejętnoś ci algorytmicznego rozwią zy-
wania problemów mają być objęci wszyscy uczniowie.

1. Wprowadzenie ............................................................................................................................................. 5

2. Superkomputery i algorytmy ....................................................................................................................... 5

3. Przykłady trudnych problemów.................................................................................................................... 6

3.1. Najkrótsza tra s a zamknięta .................................................................................................................. 6

3.2. Rozkład liczby na czynniki pierws ze ...................................................................................................... 8

3.3. Podnos zenie do potęgi .......................................................................................................................... 9

3.4. Porzą dkowanie ...................................................................................................................................... 9

4. Pros te problemy i najleps ze algorytmy ich rozwią zywania .......................................................................... 9

4.1. Znajdowanie elementu w zbiorze – znajdowanie minimum .................................................................... 9

4.2. Kompletowanie podium zwycięzców turnieju .......................................................................................11

4.3. Jednoczesne znajdowa nie na jmniejszego i najwięks zego elementu .................................................... 13

4.4. Pos zukiwanie elementów w zbiorze .................................................................................................... 13

4.4.1. Pos zukiwanie elementu w zbiorze nieuporządkowanym ........................................................... 14

4.4.2. Pos zukiwanie elementu w zbiorze uporządkowanym ................................................................ 14

4.5. Algorytmy porządkowania .................................................................................................................. 16

4.5.1. Porządkowanie przez wybór....................................................................................................... 17

4.5.2. Porządkowanie przez s calanie ................................................................................................... 18

4.6. Obliczanie wartoś ci wielomianu – schemat Hornera ........................................................................... 19

5. Dwa trudne problemy, ponownie ................................................................................................................ 19

5.1. Badanie złożonoś ci liczb ..................................................................................................................... 20

5.2. Szybkie podnos zenie do potęgi ........................................................................................................... 20

Literatura

............................................................................................................................................... 21

> Czy ws zystko można policzyć na komputerze

< 5 >

Można odnieś ć wra żenie, że komputery są obecnie w stanie wykonać ws zelkie obliczenia i dos ta rczyć ocze -
kiwany wynik w krótkim czasie. Budowane s ą jednak cora z szybsze komputery, co może ś wiadczyć o tym, że
moc is tniejących komputerów nie jes t jednak wys tarczająca do wykonania ws zys tkich obliczeń, jakie nas in-
teresują , potrzebne s ą wię c jes zcze s zybs ze ma s zyny.

Zgodnie z nieformalnym prawem Moore’a , szybkoś ć dzia łania proces orów s tale rośnie i podwaja s ię co

24 mies iące. Jednak is tnieje wiele trudno rozwiązywalnych problemów, których obe cnie nie jes teś my w stanie
rozwią zać za pomocą żadnego komputera i zwię ks zanie s zybkości komputerów nie wiele zmienia tę s ytua cję.
Kluczowe s taje s ię wię c opracowywanie cora z s zybs zych algorytmów. Jak to ujął Ralf Gomory, s zef ośrodka
badawczego IBM:

Najlepszym sposobem przyspies za nia komputerów

jest obarcza nie ich mniejszą liczbą działań.

To „obarczanie komputerów” cora z mniejs zą liczbą działa ń należy odczytać, jako stos owanie w obliczeniach
komputerowych cora z s zybs zych algorytmów.

Zamieścimy tutaj pods tawowe informacje dotyczące na jszybs zych komputerów. Komputery, które w danej
chwili lub w jakimś okresie mają najwię ks zą moc obliczeniową przyjęło się na zywa ć s uperkomputerami. Pro-
wadzony jes t ranking najs zybs zych komputerów świata (patrz strona http:// www.top500.org/ ), a faktycznie
odbywa się wyś cig wś ród producentów superkomputerów i dwa ra zy w roku s ą publikowane lis ty rankingowe.
Szybkość dzia łania komputerów jes t oceniana na specjalnych zes tawa ch problemów, pochodzących z alge -
bry liniowej – s ą to na ogół układy równań liniowych, złożone z s etek tys ięcy a nawet milionów równań i nie-
wiadomych. Szybkoś ć komputerów podaje s ię w jednostkach zwanych FLOPS (lub flops lub flop/ s) – jes t to
akronim od FLoating point Operations Per Second, czyli zmiennopozycyjnych operacji na sekundę. Dla upros z-
czenia można przyjąć, że FLOPS to są dzia łania arytmetyczne (dodawanie, odejmowanie, mnożenie i dziele -
nie) wykonywane na liczbach dziesię tnych z kropką . W użyciu są jednos tki: YFlops (yotta flops) – 10

24

opera -

cji na s ekunde ę, ZFlops (zetta flops) – 10

21

, EFlops (e xa flops) – 10

18

, PFlops (peta flops) – 10

15

, TFlops (tera

flops) – 10

12

, GFlops (giga flops) –10

9

, MFlops (mega flops) – 10

6

, KFlops (kilo flops) – 10

3

.

W rankingu z lis topa da 2009 roku, najs zybs zym komputerem ś wiata był Cray XT Jaguar firmy Cra y, któ-

rego moc jes t 1.75 PFlops , czyli wykonuje on ponad 10

15

operacji na s ekundę. Komputer ten pracuje w Depart-

ment of Energy’s Oak Ridge Nationa l Laboratory w Stanach Zjednoczonych. Komputer Jaguar je st zbudowa -
ny z 224162 procesorów Opteron firmy AMD. Drugie miejs ce zajmuje komputer Roadrunner firmy IBM o mocy
1.04 PFlops. Dwa dalsze miejsca zajmują równie ż komputery Cray i IBM a w pierws zej dziesiątce są jes zcze
dwa inne komputery IBM.

Na początku 2010 roku najs zybs zym proce sorem PC był Intel Core i7 980 XE o mocy 107.6 GFlops .

Więks zą moc mają procesory graficzne , np. Te sla C1060 GPU (nVidia) ma moc 933 GFlops (w pojedynczej do-
kładnoś ci), a HemlockXT 5970 (AMD) osią ga moc 4640 GFlops (w podwójnej dokładności).

Bardzo dużą moc osią gają obliczenia wykonywane na rozpros zonych komputerach os obis tych połą-

czonych ze sobą za pomocą Interne tu. Na przykład, ma początku 2010 roku, Folding@Home os iągnął moc 3.8
PFlops , a komputery os obiste pracujące w projekcie sie ciowym GIMPS nad znalezieniem cora z większej licz-
by pierwszej osiągnę ły moc 44 TFlops.

Przy obecnym tempie wzros tu możliwoś ci superkomputerów przewiduje się, że moc 1 EFlops (10

18

ope -

racji na sekundę ) zos tanie os iągnięta w 2019 roku, natomia s t firma Cra y ogłosiła , że bę dzie w s tanie zbudo-
wać komputer o tej mocy w 2010 roku. Na ukowcy ocenia ją, że dla pe łne go modelowania zmian pogody na Zie -
mi w cią gu dwóch tygodni jes t potrzebny komputer o mocy 1 ZFlops (10

21

operacji na sekundę ). Przewiduje

się, że taki komputer pows tanie przed 2030 rokiem.

W dals zych rozwa żaniach będziemy przyjmować, że dysponujemy najs zybs zym komputerem, który ma

moc 1 PFlops, czyli wykonuje 10

15

= 1 000 000 000 000 000 operacji na sekundę.

< 6 >

Informatyka +

Ciekawi nas tera z, jak duże problemy możemy rozwią zywać za pomocą komputera o mocy 1 PFlops . W tabe -
li 1 zamieściliśmy cza s y obliczeń wykonanych na tym superkomputerze posługując się algorytmami o różnej
złożoności obliczeniowej (pracochłonności) i chcąc rozwią zywać problemy o różnych rozmiarach.

Tabela 1.
Czas y obliczeń za pomocą algorytmów o podanej złożoności, wykonywanych na superkomputerze o mocy
1 PFlps , czyli wykonującym 10

15

operacji na s ekundę (<< 1 s ek. oznacza w tabeli, że cza s obliczeń s tanowił nie -

wielki ułamek s ekundy); parame tr n okre śla rozmiar danych

Złożonoś ć algorytmu

n = 100

n = 500

n = 10 00

n = 10 000

log n

<< 1 s ek.

<< 1 sek.

<< 1 s ek.

<< 1 sek.

n

<< 1 s ek.

<< 1 sek.

<< 1 s ek.

<< 1 sek.

n log n

<< 1 s ek.

<< 1 sek.

<< 1 sek.

<< 1 sek.

n

2

<< 1 s ek.

<< 1 sek.

0,000 000 001 s ek.

0,000 0001 sek.

n

5

0,00 001 s ek.

0,03125 sek.

1 s ek.

1,15 dni

2

n

4*10

7

lat

1,038*10

128

la t

3,3977 *10

2 78

lat

n!

2,959*10

135

lat

Wyra źnie widać, że dwa os ta tnie w tabeli 1 a lgorytmy są całkowicie niepraktyczne nawet dla niewielkiej licz-
by danych (n = 100). Is tnieją jednak problemy, dla których ws zys tkich możliwych rozwiązań może być 2

n

lub

n!, za tem nawet s uperkomputery nie s ą w s tanie przejrze ć wszys tkich możliwych rozwią zań w poszukiwaniu
najleps ze go, a zdecydowanie szybszymi metodami dla tych problemów nie dys ponujemy.

Można ła two przeliczyć, że gdyby na s z s uperkomputer był s zybs zy, na przykład miał moc 1 ZFlops

(10

21

ope racji na s ekundę ), co ma nas tą pić dopiero ok. roku 2030, to dwa os ta tnie wie rs ze w tabeli 1 ule gły-

by tylko niewielkim zmianom, nie na tyle je dnak, by móc s tos ować dwa os ta tnie algorytmy w ce lach pra k-
tycznych.

W nas tępnym rozdziale prze ds tawimy kilka przykładowych problemów, dla których moc obliczeniowa

superkomputerów może nie być wys ta rczająca , by rozwią zywa ć je dla praktycznych rozmiarów danych. Ma to
złe i dobre s trony. Złe – bo nie jes teśmy w s ta nie rozwią zywać wielu wa żnych i is totnych dla człowieka pro-
blemów, takich np. jak prognozowanie pogody, prze widywanie trzęsień Ziemi i wybuchów wulkanów, czy te ż
planowanie optymalnych podróży lub komunikacji. Dobre za ś – bo możemy wykorzystywać trudne oblicze -
niowo problemy w metodach szyfrowania , dzięki czemu na s z przeciwnik nie jes t w stanie , nawet posługując
się najs zybs zymi komputerami, des zyfrować na s zych wiadomości, chocia ż my jes te śmy w s tanie s zybko je
kodować i wys yłać.

Podamy tutaj kilka doś ć prostych problemów, których rozwiązywanie może na s tręczać pewne trudności na -
we t z użyciem na jszybszych komputerów.

W tym rozdziale, ja k i w da ls zych, proble my de finiujemy w pos taci s pecyfikacji, która za wiera ś cis ły opis
Danych i oczekiwa nych Wyników. W spe cyfika cji s ą te ż za warte zależnoś ci mię dzy da nymi i wynikami. Spe -
cyfikacja problemu je s t równie ż spe cyfika cją a lgorytmu, który ten problem rozwią zuje , co ma na celu do-
kładne okreś lenie prze zna cze nia algorytmu, s ta nowi zatem powią zanie algorytmu z rozwią zywanym pro-
ble mem.

Je dnym z najbardziej znanych problemów dotyczących wyznaczania tras przeja zdu, jes t problem komiwoja-
żera , oznaczany zwykle jako TSP, od oryginalnej na zwy Travelling Sale sman Problem. W tym problemie mamy
dany zbiór miejscowoś ci ora z odle głoś ci mię dzy nimi. Należy znale źć drogę zamknię tą, przechodzącą przez
ka żdą miejscowoś ć dokładnie jeden ra z, która ma najkróts zą długoś ć.

> Czy ws zystko można policzyć na komputerze

< 7 >

Przykładem za stos owania problemu TSP może być zadanie wyznaczenia najkróts zej tra s y obja zdu pre -

zydenta kraju po ws zys tkich s tolicach województw (s tanów – w Stanach zje dnoczonych, landów – w Niem-
czech itp.). Na tej tra sie, prezydent wyje żdża ze stolicy kraju, ma odwiedzić s tolicę ka żde go województwa do-
kładnie jeden ra z i wrócić do s tolicy kraju. Zapis zmy specyfika cję tego problemu.

Problem komiwoja żera (TSP)
Dane:

n mia st (punktów) i odległoś ci między ka żdą parą mia s t.

Wyniki: Tra s a zamknięta , przechodząca prze z ka żde mia s to dokładnie jeden ra z, której długość jes t możli-

wie najmniejs za.

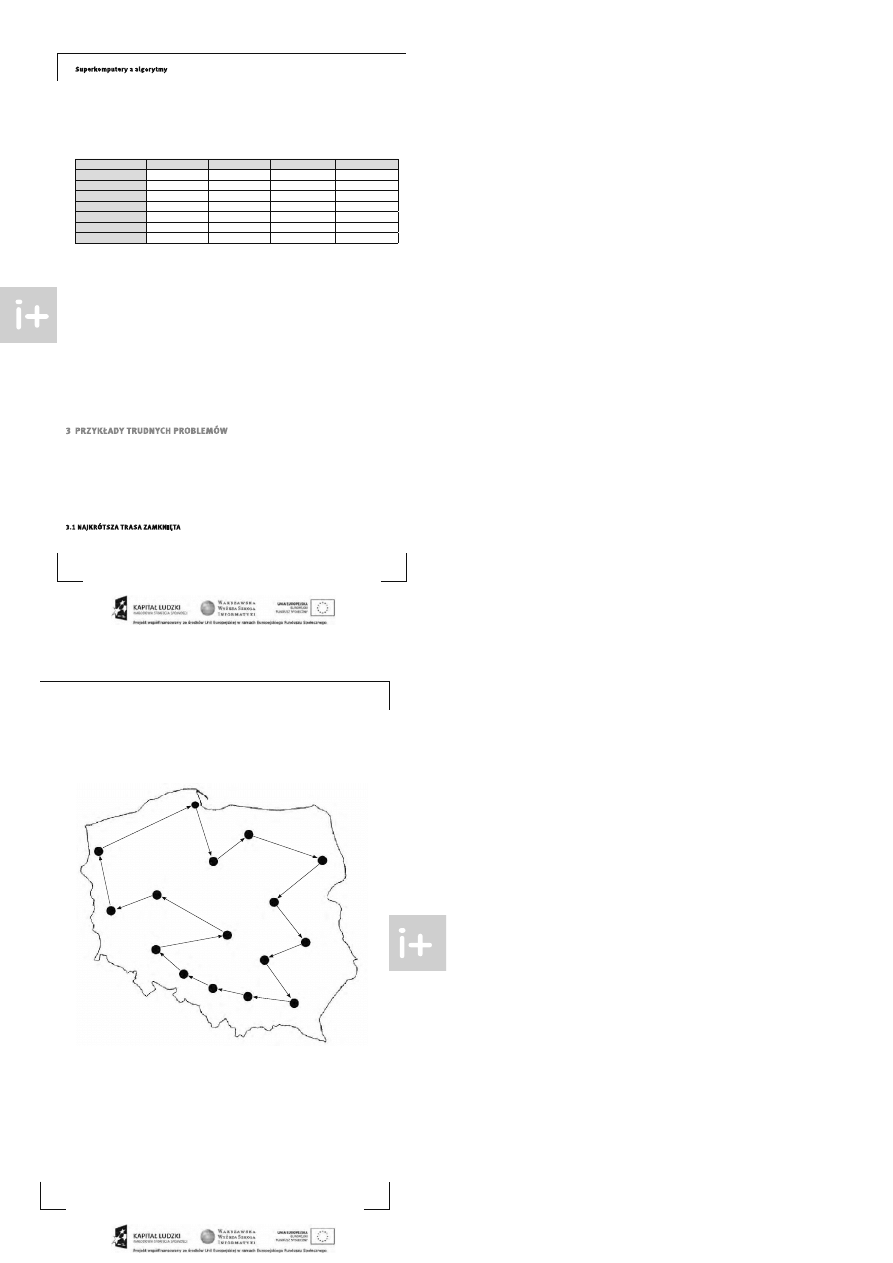
Rysunek 1.
Przykładowa tras a przejazdu prezydenta po s tolicach woje wództw

Na rys unku 1 przeds tawiliśmy jedną z możliwych tra s, ale nie jes teśmy pewni, czy jes t ona najkróts za . Ob-
sługa biura prezydenta może jednak chcieć znaleźć najkróts zą tra s ę. W tym celu pos tanowiono generować
ws zys tkie możliwe tras y – zas tanówmy się, ile ich jes t. To ła two policzyć. Z Wars zawy można się udać do jed-
nego z 15 mias t woje wódzkich. Bę dą c w pierws zym wybranym mie ście, do wyboru mamy jedno z 14 mias t.
Po wybraniu drugiego mias ta na tra sie, kolejne mia s to można wybrać spośród 13 mias t i tak dalej. Gdy osią -
gamy os tatnie mia s t, to czeka nas tylko powrót do Wars za wy. A zatem ws zys tkich możliwych wyborów jes t:
15*14*13*…*2*1. Oznaczmy tę liczbę nas tępująco:

15! = 15*14*13*…*2*1

a ogólnie

n! = n*(n – 1)*(n – 2)*…*2*1

Oznaczenie n! czytamy „n silnia”, a za tem n! jes t iloczynem kolejnych liczb ca łkowitych, od jeden do n. War-
tości tej funkcji dla kolejnych n ros ną bardzo s zybko, patrz tabela 2.

< 8 >

Informatyka +

Tabela 2.
Wartoś ci funkcji n!

n

n!

10

36288 00

15

1.30767*10

12

20

2.4329*10

18

25

1.55112*10

25

30

2.65253*10

32

40

8.15915*10

47

48

1.24139*10

61

10 0

9.3326*10

157

Z wa rtoś ci umie s zczonych w ta beli 2 wynika , że pos ługują c s ię s uperkompute re m w rea liza cji na s zki-
cowa nej me tody, s łużą ce j do znale zie nia na jkróts zej tra s y dla pre zydenta Pols ki, otrzyma nie takie j tra -
s y za bra łoby mnie j niż s e kundę . Je dna k w olbrzymim kłopocie zna jdzie s ię pre zydent Sta nów Zje dno-
czonych chcą c ta ką s amą me todą zna le źć na jkróts zą tra s ę obja zdu po s tolica ch ws zys tkich kontyne n-
ta lnych s ta nów (jes t ich 49, z wyją tkie m Ha wajów). Nie wie le zmie ni je go s ytuację przys pie s ze nie s uper-
komputerów.

Znane s ą metody rozwiązywania problemu komiwoja żera s zybs ze niż nas zkicowana powyżej, jednak

problem TSP pozos taje bardzo trudny. W takich przypadkach częs to s ą stos owane metody, które służą do
szybkiego znajdowania rozwią zań przybliżonych, nie koniecznie najkróts zych. Jedna z takich metod, zwa na
me todą najbliższego s ą siada , polega na przykład na przejeżdżaniu w ka żdym kroku do mia sta , które znajdu-
je się najbliżej mia s ta , w którym się znajdujemy. W rozwiązaniu na s zego problemu tą metodą , pierws zym od-
wiedzonym mia s tem powinna być Łódź, później Kielce, Lublin, Rzes zów, .., a nie jak na rys . 1 mamy Lubli, Rze -
szów, Kraków …, a Łódź gdzieś w trakcie podróży. Tra s a otrzymana me todą najbliżs zego s ąs iada jes t krótsza
niż tras a na szkicowana na rys . 1. W ogólnym przypadku ta metoda nie gwarantuje , że za wsze znajduje naj-
krótszą tras ę.

Liczby pierws ze s tanowią w pewnym s ensie „pierwia s tki” ws zys tkich liczb, ka żdą bowie m liczbę ca łkowi-
tą można jednoznacznie prze ds ta wić, z dokładnoś cią do kolejnoś ci, w pos taci iloczynu liczb pierws zych.
Na przykła d, 4 = 2*2; 10 = 2*5; 20 = 2*2*5; 23 = 23; dla liczb pierws zych te iloczyny s kła dają się z je dne j
liczby.

Ma te ma t ycy inte re s owali s ię liczba mi pie rws zymi od da wna . Pie rws ze s pis a ne rozwa ża nia i t wier-

dzenia dot yczą ce t ych liczb zna jduje my w dzia ła ch Euklide s a . Obe cnie liczby pie rws ze zna jdują wa ż-
ne za s tos owa nia w kryptogra fii, m.in. w a lgorytma ch s zyfrują cych. Do na jwa żnie js zych pyta ń, proble -
mów i wyzwa ń, zwią za nych z liczba mi pie rws zymi, na le żą na s tę pują ce za ga dnienia , które krótko ko-
me ntuje my:

1. Dana jes t doda tnia liczba całkowita n – czy n jes t liczbą pierws zą (złożoną )?

Ten problem ma bardzo duże znaczenie zarówno praktyczne (w kryptografii), jak i te oretyczne. Dopiero
w 2002 roku zos tał podany algorytm, który je dna k jes t interesują cy głównie z teore tycznego punktu widze -
nia. Jego złożonoś ć, czyli liczba wykonywanych operacji, zale ży wielomianowo od rozmiaru liczby n, czyli od
liczby bitów potrzebnych do zapis ania liczby n w komputerze (ta liczba jes t równa logarytmowi przy pods ta-
wie 2 z n). „Słabą” s troną więks zoś ci metod, które udzielają odpowiedzi na pytanie: „czy n je st liczba pierw-
szą czy złożoną” jes t udzielanie jedynie odpowiedzi „Tak” lub „Nie”. Na ogół najs zybs ze metody dające od-
powiedź na pytanie, czy n jes t liczbą złożoną , w przypadku odpowiedzi „Tak” nie podają dzielników liczby
n – dzielniki jes t znacznie trudniej znaleźć niż przekonać się, że liczba jes t złożona .

2. Dana jes t doda tnia liczba całkowita n – rozłóż n na czynniki pierwsze.

Ten problem ma olbrzymie znaczenie w kryptografii. Odpowiedź „Nie” udzielona na pytanie nr 1 nie pomaga
w rozwią zaniu tego problemu. Z drugiej s trony, możemy próbowa ć znaleźć dzielniki liczby n dzieląc ją przez
kolejne liczby, ale ta metoda je st mało pra ktyczna , gdyż w kryptografii wys tępują liczby n, które mają kilka se t
cyfr. Pis zemy o tym dokładniej w punkcie 5.1.

3. Dana jes t doda tnia liczba całkowita m – znajdź ws zys tkie liczby pierws ze mniejsze lub równe m.

> Czy ws zystko można policzyć na komputerze

< 9 >

To za danie zyska ło s woją popularnoś ć dzięki algorytmowi pochodzącemu ze Starożytnoś ci, który jes t znany
jako s ito Eratos thenes a. Generowanie kolejnych liczb pierws zych tą me todą ma jednak niewielkie znaczenie
praktyczne i jes t uzna wane raczej za ciekawos tkę.

4. Znajdź najwięks zą liczbę pierws zą, a faktycznie , znajdź liczbę pierws zą więks zą od najwię ks zej zna nej licz-

by pierwszej. (Zgodnie z twierdzeniem Euklides a , liczb pierwszych jes t nieskończenie wiele, a za tem nie is t-
nieje najwięks za liczba pierws za.)

To wyzwa nie cie s zy s ię olbrzymią popula rnoś cią . Uruchomiony je s t s pe cja lny s erwis interne towy

pod a dres e m ht tp:// www.me rs e nne .org/ , który je s t ws pólnym przeds ię wzię cie m s ie ciowym wie lu po-
s zukiwa czy. Obe cnie na jwię ks zą liczbą pierws zą je s t liczba 2

431126 09

– 1, bę dą ca liczbą Me rs e nne a . Licz-

ba ta ma 12 978 189 cyfr. Za pis a nie je j w e dytorze te ks u (75 cyfr w wie rs zu, 50 wie rs zy na s tronie) za ję -
łoby 3461 s tron.

W punkcie 5.1 wraca my do problemów nr 1 ora z 2 i przytaczamy znany algorytm badania, czy n jes t

liczbą pierws zą. Je śli n jes t liczbą złożoną, to możliwe je st w tym a lgorytmie generowanie kolejnych dzielni-
ków liczby n.

Podnos zenie do potęgi jes t bardzo pros tym, s zkolnym zadaniem. Na przykład, a by obliczyć 3

4

, wykonujemy

trzy mnożenia 4*4*4*4. A zatem w ogólności, aby obliczyć szkolną me todą wartoś ć x

n

, należy wykonać n – 1

mnożeń, o jedno mniej niż wynosi wykładnik potęgi. Czy ten algorytm jes t na tyle s zybki, by obliczyć na przy-
kład wartość:

x

123456789123 456789123 45678912345

która może pojawić przy s zyfrowaniu informacji przes yłanych w Interne cie? Odpowiemy na to pytanie w punk-
cie 5.2.

Problem porządkowania , częs to na zywany s ortowaniem, jes t jednym z najwa żniejs zych problemów w infor-
matyce i w wielu innych dziedzinach. Jego znaczenie jes t ściśle zwią zane z zarządzaniem danymi (informacja -
mi), w szczególności z wykonywaniem takich operacji na da nych, jak wyszukiwanie konkre tnych danych lub
umies zczanie danych w zbiorze.

Zauwa żmy, że mając n elementów, które chcemy uporządkować, is tnieje n! możliwych uporządko-

wań, wśród których chcemy znaleźć wła ś ciwe uporządkowanie. A za tem, prze strzeń możliwych rozwią za ń
w problemie porządkowania n liczb ma moc n!, czyli jes t taka sama jak w przypadku problemu komiwoja że -
ra . Jednak dzięki odpowiednim algorytmom, n elementów można uporzą dkować w cza sie proporcjonalnym
do n log n lub n

2

. Wię cej na temat porządkowania pis zemy w punkcie 4.5.

Dysponując uporządkowanym zbiorem danych, znale zienie w nim elementu lub umies zczenie nowego

z zachowaniem porządku jes t znacznie ła twiejsze i s zybsze , niż gdyby zbiór nie był uporządkowany – pisze -
my o tym w punkcie 4.4.2.

W tym rozdzia le przeds tawiamy kilka klas ycznych problemów algorytmicznych wraz z możliwie najleps zymi
algorytmami ich rozwią zywania. Problemy s ą rzeczywiś cie bardzo pros te, ale mają bardzo wa żne znaczenie
w informa tyce. Po pierws ze, s ą rozwią zywane bardzo czę sto w wielu bardziej złożonych s ytuacjach problemo-
wych, zarówno z użyciem komputera jak i bez jego pomocy. Po drugie, te problemy s tanowią elementy skła-
dowe wielu innych metod obliczeniowych i są wywoływane wielokrotnie, dlatego im s zybciej potrafimy je roz-
wią zywać, tym s zybciej działają metody rozwią zywania wielu innych problemów.

Zajmiemy się bardzo pros tym problemem, który ka żdy z Wa s rozwią zuje wielokrotnie w ciągu dnia. Chodzi
o znajdowanie w zbiorze elementu, który ma okre śloną wła snoś ć. Oto przykładowe s ytuacje problemowe:

■

zna jdź najwyżs zego ucznia w s wojej kla sie; a jak zmieni s ię Twój algorytm, jeś li chciałbyś znaleźć w kla sie
najniższe go ucznia?

< 10 >

Informatyka +

■

znajdź w s wojej klasie ucznia , któremu droga do szkoły zabiera najwię cej czasu;

■

znajdź najs tars zego ucznia w s wojej s zkole;

■

znajdź najwięks zą kartę w pota sowanej talii kart;

■

wyłonić najlepsze go tenisistę w s wojej klas ie.

Pos tawiony problem może wydać się zbyt pros ty, by zajmować s ię nim na informa tyce – ka żdy uczeń zapew-
ne potrafi wskazać me todę rozwiązywania, polegającą na s ys tematycznym przes zukaniu całego zbioru da-
nych. Tak pojawia się metoda prze s zukiwania ciągu, którą można na zwać przes zukiwaniem liniowym. Przy
tej okazji w dyskusji pojawi s ię zape wne również metoda pucharowa , która jes t czę sto s tos owana w rozgryw-
kach turniejowych.

Poczyńmy pewne założe nia , które wynikają za równo z prakt ycznych s ytuacji, ja k i odpowiada ją s to-

s owanym me todom rozwią zywa nia . Po pierws ze za kładamy, że prze s zukiwane zbiory elementów nie s ą
uporzą dkowane , np. kla s a – od na jwyżs ze go do najniżs ze go ucznia lub odwrotnie, gdyż, gdyby ta k było, to
rozwią zywa nie wymienionych wyżej proble mów i im podobnych byłoby dzie cinnie ła twe – wys ta rczyłoby
wziąć e lement z począ tku a lbo z końca takie go uporzą dkowania . Po drugie – przyjmujemy ta kże , że nie in-
tere s ują na s a lgorytmy rozwią zywania prze ds ta wionych s ytuacji problemowych, które w pierws zym kroku
porzą dkują zbiór prze s zukiwa ny, a na s tę pnie już pros to zna jdują pos zukiwa ne element y – to założe nie wy-
nika z faktu, że s ortowa nie cią gu jes t zna cznie bardziej pra cochłonne niż zna jdowa nie wyróżnionych ele -
mentów w cią gu.

Z powyższych za łożeń wynika doś ć naturalny wnios ek, że aby znaleźć w zbiorze pos zukiwany element

mus imy przejrze ć wszys tkie elementy zbioru, gdyż jakikolwiek pominięty element mógłby okazać się tym
szukanym elementem.

Przy projektowaniu algorytmów is totne jes t równie ż określenie , jakie działania (operacje) mogą być wykony-
wane w algorytmie. W przypadku problemu pos zukiwania s zczególnego elementu w zbiorze wys tarczy, je -
śli bę dziemy umieli porównać elementy mię dzy sobą . Przy porównywaniu kart nale ży uwzglę dnić ich kolory
i wartoś ci, natomia s t przy wyłanianiu najleps zego gracza w tenis a , porównania mię dzy graczami dokonuje się
na podstawie wyniku meczu między nimi.

Dla upros zczenia rozwa żań zakładamy, że danych jest n liczb w pos taci cią g: x

1

, x

2

, ..., x

n

. Oto specyfikacja roz-

wa żanego problemu:

Problem Min – Znajdowanie najmniejszego elementu w zbiorze
Da ne:

Liczba naturalna n i zbiór n liczb, dany w postaci ciągu x

1

, x

2

, ..., x

n

.

Wynik: Najmniejs za spośród liczb x

1

, x

2

, ..., x

n

– oznaczmy jej wartoś ć prze z min.

Na s zkicowany wyżej algorytm, polegający na przejrzeniu cią gu da nych od początku do końca , można zapis ać
w na s tępujący spos ób w pos tać lis ty kroków:

Algorytm Min – znajdowanie najmniejs zego elementu w zbiorze
Krok 1. Przyjmij za min pierws zy element w ciągu, czyli przypis z min := x

1

.

Krok 2. Dla kolejnych elementów x

i

, gdzie i = 2, 3, ..., n, je śli min jes t większe niż x

i

, to za min przyjmij x

i

,

czyli, je śli min > x

i

, to przypisz min := x

i

.

Metoda za s tos owana w algorytmie Min, polegająca na badaniu elementów cią gu da nych w kolejnoś ci, w ja-
kiej są us tawione, na zywa się prze szukiwaniem liniowym.

Algorytm Min może być łatwo zmodyfikowany tak, aby otrzymać algorytm Ma x, służący do znajdowania naj-
większe go elementu w cią gu – wys tarczy w tym celu zmienić tylko zwrot nierówności w kroku 2.

Częs to, poza znalezieniem elementu najmniejszego (lub najwięks zego) chci elibyśmy znać jego położ-

nie, czyli miejsce (numer) w cią gu danych. W tym celu wys tarczy wprowadź nową zmienną, np. imin, w której
będzie przechowywany numer a ktualnie najmniejs zego elementu.

> Czy ws zystko można policzyć na komputerze

< 11 >

W tych materiałach poprzestajemy na opisach algorytmów w postaci listy kroków. Inną reprezentacją algorytmu
jes t schemat blokowy. Najbardziej precyzyjną postać ma implementacja algorytmu w postaci programu w języ-
ku programowania. Działanie algorytmu można również zademons trować posługując się programem edukacyj-
nym. W materiałach do tego wykładu s ą udostępnione programy Ma szyna s ortująca i Sortowanie, które mogą
być wykorzys tane do eksperymentów z algorytmem Min i z algorytmami sortowania (patrz punkt 4.5).

W algorytmie Min pods tawową operacją jes t porówna nie dwóch elementów ze zbioru danych – policzmy
więc, ile porównań jes t wykonywanych w tym algorytmie. W ka żdej iteracji algorytmu jes t wykonywane jed-
no porównanie min > x

i

, a zatem w całym algorytmie jes t wykonywanych n – 1 porównań. Pozos tałe opera -

cje służą głównie do organizacji obliczeń i ich liczba jes t zwią zana z liczbą porównań. Na przykład, operacja
przypis ania min := x

i

może być wykonana tylko o jeden ra z wię cej – w kroku 1 i n – 1 ra zy w kroku 2. Możemy

więc podsumować nas ze rozumowanie bardzo wa żnym s twierdzeniem

najmniejs zy (lub największy) element w niepus tym zbiorze danych można zna leźć wyko-
nując o jedno porównanie mniej niż wynos i liczba wszys tkich elementów w tym zbiorze.

Za s tanówmy się tera z, czy w zbiorze złożonym z n liczb, można znale źć najmniejs zy element wykonując mniej
niż n – 1 porównań elementów tego zbioru? Udzielimy negatywnej odpowiedzi na to pytanie

1

, posługując

się interpretacją wziętą z kla s owego turnieju tenis a. Ile nale ży rozegrać me czów (to s ą właś nie porównania
w przypadku tego problemu), aby wyłonić najleps zego tenisis tę w kla sie? Lub inaczej – kiedy możemy powie -
dzieć, że Janek jes t w na s zej kla sie najleps zym tenisis tą? Mus imy mieć pewność, że ws zyscy pozos tali ucznio-
wie s ą od niego gorsi, czyli przegrali z nim, bezpośre dnio lub pośre dnio. A zatem ka żdy inny uczeń przegrał
przynajmniej je den mecz, czyli rozegranych zostało przynajmniej tyle meczów, ilu jest uczniów w klasie mniej
jeden. I to kończy na s ze uza s adnienie.

Z dotychcza sowych rozwa żań wynika, że algorytm Min jes t najleps zym algorytmem s łużącym do znaj-

dowania najmniejs zego elementu, gdyż wykonywanych jes t w nim tyle porównań, ile mus i wykonać jakikol-
wiek algorytm rozwiązywa nia tego problemu. O takim algorytmie mówimy, że jes t algorytmem optymalnym
pod względem złożonoś ci obliczeniowej.

Przedstawiony w poprzednim punkcie algorytm nie jes t jedyną me todą s łużącą do znajdowania najleps ze -
go elementu w zbiorze . Inną metodą je st tzw. s ys tem pucharowy, s tos owany czę sto przy wyłanianiu najlep-
s zego zawodnika bądź drużyny w turnieju. W metodzie tej „porównanie” dwóch zawodników (lub drużyn), by
s twierdzić, który jes t leps zy („więks zy”), pole ga na rozegraniu meczu, który kończy s ię zwycię stwem jedne -
go z zawodników.

Nurtować może pytanie, czy znajdowanie najleps zego za wodnika s ys temem pucharowym nie jes t czas em
metodą bardziej efektywną pod wzglę dem liczby wykonywanych porówna ń (czyli rozegranych meczy), niż
przes zukiwanie liniowe , opis ane w poprzednim rozdziale. Na rysumku 2(a) jes t przeds tawiony fragment tur-
nieju, rozegranego między ośmioma zawodnikami. Zwycięzcą okaza ł s ię Janek po roze graniu w całym turnie -
ju siedmiu meczów. A za tem podobnie jak w przypadku metody liniowej, aby wyłonić zwycię zcę, czyli najlep-
s zego zawodnika (elementu) wśród ośmiu zawodników, należa ło rozegrać o je den mecz mnie niż wys tą piło
w turnieju zawodników. Nie jes t to przypadek.

Powyższa prawidłowość wynika z nas tępującego faktu: s chemat turnieju jes t drzewem binarnym,

a w takim drzewie liczba wierzchołków poś rednich jes t o jeden mniejs za od liczby wierzchołków końcowych.
Wierzchołki końcowe to zawodnicy przys tępujący do turnieju, a wierzchołki pośrednie odpowiadają rozegra -
nym meczom.

1

Posługujemy się tutaj argumentacją za czerpniętą z ksią żki Hugona Steinhaus a , Kalejdoskop matematyczny (WSiP, War-

s za wa 1989, rozdz. III), [5].

< 12 >

Informatyka +

a)

Janek

Janek

Edek

Kuba

Janek

Bartek

Edek

Kuba

Ka zik

Jurek

Janek

Bartek

Wojtek

Edek

Bolek

Edek

Kuba

Bartek

Edek

Kuba

Ka zik

Jurek

X

Bartek

Wojtek

Edek

Bolek

b)

Rysunek 2.
Drzewo przykładowych rozgrywek w turnieju tenis owym (a) ora z drzewo znajdowania drugie go najleps zego
zawodnika turnieju (b)

Bardzo ciekawy problem postawił około 1930 roku Hugo Steinhaus: jaka jes t najmniejsza liczba meczów tenis o-
wych potrzebnych do wyłonienia najlepszego i drugiego najlepszego zawodnika turnieju. W turniejach drugą na-
grodę otrzymuje zwykle zawodnik pokonany w finale. I tutaj Steinhaus miał słus zne wątpliwości, czy jest to wła-
ściwa decyzja, tzn., czy pokonany w finale jes t drugim najleps zym zawodnikiem turnieju, czyli czy jes t leps zy od
wszys tkich pozos tałych zawodników z wyjątkiem zwycięzcy turnieju. Wątpliwoś ci H. Steinhausa były uzasadnio-
ne – spójrzmy na drzewo turnieju przeds tawione na rysunek 2(a). Zwycięzcą w tym turnieju jes t Janek, który w fina-
le pokonał Edka. Edkowi przyznano więc drugą nagrodę, chociaż wyka zał, że jes t leps zy jedynie od Bolka, Bartka
i Wojtka (gdyż przegrał z Bartkiem). Nic nie wiemy, jakby Edek grał przeciwko zawodnikom z poddrzewa, z którego
jako zwycięzca zos tał wyłoniony Janek. Jak można naprawić ten błąd organizatorów rozgrywek tenisowych? Istnie-
je prosty sposób znalezienia drugiego najlepszego zawodnika turnieju – rozegrać jeszcze jedną pe łną rundę z po-
minięciem zwycięzcy turnieju głównego. Wówcza s, najlepszy i drugi najlepszy zawodnik zawodów zos taliby wyło-
nieni w 2n–3 meczach. Steinhaus oczywiście znał to rozwią zanie, ale pytał o najmniejszą potrzebną liczbę meczów.

Jeś li chcemy, aby drugi najleps zy zawodnik nie musia ł być wyłaniany w nowym pe łnym turnieju, to mu-

simy umieć s korzys tać ze wszys tkich wyników głównego turnieju. Pos łużymy s ię drzewem turnieju z rysun-
ku 2(a). Zauwa żmy, że Edek jes t oczywiś cie najlepszy wśród zawodników, którzy w drze wie rozgrywek znaj-
dują się w wierzchołkach leżących poniżej najwyżs zego wierzchołka , który on zajmuje. Mus imy więc jedynie
porównać go z zawodnikami drugiego poddrzewa. Aby i w tym poddrzewie wykorzys tać wyniki dotychcza so-
wych meczów, eliminujemy z nie go Janka — zwycię zcę turnieju i ws tawiamy Edka na jego początkowe miejs ce
X. Spowoduje to, że Edek zos tanie porównany z najleps zymi za wodnikami w drugim poddrzewie . Na rysun-
ku 2(b) oznaczyliśmy przerywana linią me cze , które zos taną rozegrane w tej czę ści turnieju – Jurek z Edkiem
i zwycięzca tego meczu z Kubą , a wię c dwa doda tkowe mecze.

Algorytm ten można, po zmianie słownictwa , za stos ować do znajdowania największej i drugiej naj-

większej liczby w zbiorze danych.

Ile porównań jes t wykonywa nych w opis anym algorytmie znajdowania najlepszego i drugiego najleps zego za-
wodnika w turnieju? Najleps zy zawodnik jes t wyłania ny w n – 1 meczach, gdzie n jes t liczbą ws zys tkich za-
wodników. Z kolei, aby wyłonić drugiego najlepsze go zawodnika , trzeba roze grać tyle meczów, ile jes t pozio-
mów w drze wie turnieju głównego (z wyjątkiem pierws zego poziomu). Dla uproszczenia przyjmijmy, że drze -
wo je st pe łne, tzn. ka żdy zawodnik ma parę, czyli w ka żdej rundzie turnieju gra parzys ta liczba zawodników.
Stą d wynika , że na najwyżs zym poziomie jest jeden zawodnik, na poziomie niżs zym – dwóch, na kolejnym
– czterech itd. Czyli, liczba za wodników rozpoczynających turniej jes t potę gą liczby 2, zatem n = 2

k

, gdzie k

jes t liczbą poziomów drzewa – oznaczmy ją przez log

2

n. Algorytm wykonuje więc (n – 1) + (log

2

n – 1) = n +

log

2

n – 2 porównań. Jeś li n nie jes t potęgą liczby 2, to na ogół w turnieju niektórzy zawodnicy otrzymują wol-

ną kartę, a podana liczba jes t oszacowa niem z góry liczby rozegranych meczów.

> Czy ws zystko można policzyć na komputerze

< 13 >

Prze ds tawiony powyżej algorytm znajdowania najlepsze go i drugiego najleps zego zawodnika turnieju

jes t równie ż optymalny, tzn. jes t najs zybs zy w sens ie liczby rozegranych meczów (porównań).

Jedną z miar, okreś lającą , jak bardzo s ą porozrzucane wartoś ci obserwowanej w doś wiadczeniu wielkoś ci,
jes t rozpiętoś ć zbioru, czyli różnica między najwię ks zą (w s krócie, maksimum) a najmniejs zą wartoś cią ele -
mentu (w skrócie, minimum) w zbiorze. Interes ujące jes t więc jednoczesne znalezienie najmniejs zej i najwięk-
s zej wartości w zbiorze liczb. Na podstawie dotychczas owych rozwa żań, dotyczących wyznaczania najmniej-
s zej i najwięks zej wartości w zbiorze liczb, ła two można poda ć algorytm zna jdowania jednocześ nie obu tych
elementów w zbiorze. W tym celu s tosujemy najpierw algorytm Min do całego zbioru, a później algorytm Ma x
do zbioru z us uniętym minimum. W takim a lgorytmie „jednoczesnego wyznaczania” minimum i maksimum
w ciągu złożonym z n liczb jes t wykonywanych (n – 1) + (n – 2) = 2n – 3 porównań. Ale czy rzeczywiście te dwie
wielkoś ci są wyznaczane je dnocze śnie?

Pos ta ra my się zna cznie przyspies zyć to pos tępowanie , a bę dzie to pole gało na rze czywiś cie je dno-

czes nym s zuka niu na jmnie js zego i na jwięks ze go ele mentu w ca łym zbiorze. W t ym ce lu zauwa żmy, że je -
ś li dwie liczby x i y s pe łnia ją nierównoś ć x ≤ y, to x jes t ka ndydatem na najmniejs zą liczbę w zbiorze, a y je s t
ka ndyda tem na na jwięks zą liczbę w zbiorze . (Je ś li prawdziwa je s t nie równoś ć przeciwna , to wnios kujemy
odwrotnie.) A za te m, porównują c ele menty pa ra mi, można podzielić dany zbiór ele mentów na dwa pod-
zbiory, ka ndydatów na minimum i kandyda tów na maksimum, i w t ych zbiorach – które s ą nie ma l o poło-
wę mniejs ze niż orygina lny zbiór! – s zuka ć odpowiednio minimum i maksimum. Gdy zbiór ma niepa rzys tą
liczbę eleme ntów, to os tatni ele ment cią gu dodajemy do je dnego i do drugie go podzbioru ka ndydatów. Po-
s tępowanie to jes t zilus trowane przykładem na rys . 3, a opis algorytmu pozos ta wiamy do s amodzielnego
wykonania .

Kandyda ci na maksimum

3

2

5

8

5

6 ma x = 8

Podzia ł zbioru

3 ≤ 1

2 ≤ 2 5 ≤ 3 4 ≤ 8 2 ≤ 5

6

Kandyda ci na minimum

1 2 3 4 2

6 min = 1

Rysunek 3.
Przykład pos tępowania podcza s jednoczesnego znajdowania minimum i maksimum w cią gu liczb

Nas zkicowany algorytm jes t przykładem metody, leżącej u podstaw bardzo wielu efektywnych algorytmów.
Można w nim wyróżnić dwa etapy:

■

podziału danych na dwa podzbiory (kandydatów na minimum i kandydatów na maksimum);

■

za s tos owanie znanych a lgorytmów Min i Ma x do utworzonych podzbiorów danych.

Jes t to przykład za s ady (metody) dziel i zwycię żaj, jednej z naje fektywniejszych metod algorytmicznych w in-
forma tyce – patrz punkty 4.4.2 i 4.5.2. Dziel – odnosi się do podziału zbioru danych na podzbiory, zwykle
o jednakowej liczbie elementów, do których na s tępnie s ą s tos owane odpowiednie algorytmy. Zwycięs two –
to efekt końcowy, czyli efektywne rozwią zanie rozwa żanego problemu.

Obliczmy, ile porównań między elementami danych jes t wykonywanych w powyżs zym algorytmie. Gdy

n jes t liczbą parzys tą, to w kroku podziału jes t wykonywanych n/ 2 porównań, a znalezienie min oraz znalezie -
nie ma x wymaga ka żde n/ 2 – 1 porównań. Ra zem je st to 3n/ 2 – 2 porównania . Gdy n jes t liczbą nieparzys tą ,
to otrzymujemy liczbę porównań

3n/ 2

– 2, gdzie

x

oznacza tzw. powałę liczby, czyli najmniejs zą liczbę cał-

kowitą k spe łniającą nierównoś ć x ≤ k. A za tem, w tym algorytmie jes t wykonywanych

3n/ 2

– 2 porówna nia,

czyli ok. n/ 2 mniej porównań niż w algorytmie naiwnym, nas zkicowanym na począ tku tego punktu. Dodajmy,
że jes t to równie ż algorytm optymalny pod wzglę dem liczby wykonywa nych porównań.

Komputery ułatwiają szybkie pos zukiwanie informacji umies zczonych na płytach CD i na serwerach sie ci In-
ternet. Jes t to za sługą szybkoś ci działania procesorów, jak równie ż dobrej organizacji pracy, dzięki czemu po-
zos taje im ... niewiele do roboty.

< 14 >

Informatyka +

W punkcie 4.1. zajmowaliśmy się zna jdowaniem s zczególnych elementów w zbiorze nieuporządkowa -

nym, najmniejs zego i najwięks zego. Tera z będziemy rozwa żać problem pos zukiwania w ogólniejs zej postaci.

Problem pos zukiwania ele me ntu w zbiorze
Da ne:

Zbiór elementów w pos ta ci cią gu n liczb x

1

, x

2

, ..., x

n

. Wyróżniony element y.

Wynik: Jeś li y na leży do tego zbioru, to podaj jego miejs ce (indeks) w cią gu, a w przeciwnym ra zie – s ygna -

lizuj brak takiego elementu w zbiorze.

Problem pos zukiwania ma bardzo wiele zas tos owań i jes t rozwiązywa ny prze z komputer na przykład wtedy,
gdy w jakimś us talonym zbiorze informacji s taramy się znaleźć konkre tną informację. Rozwa żana prze z nas
wers ja tego problemu jes t bardzo prosta, na ogół bowiem zbiory i ich elementy mają bardzo złożoną pos tać,
nie s ą ograniczone tylko do pojedynczych liczb. Przeds tawione przez na s me tody mogą być jednak uogólnio-
ne na ba rdziej złożone s ytuacje problemowe.

W na s tępnych podpunktach, najpierw rozwią zujemy problem poszukiwania w dowolnym zbiorze ele -

mentów, a później – w zbiorze uporządkowanym.

Je śli nic nie wiemy o elementach w ciągu danych x

1

, x

2

, ..., x

n

, to aby s twierdzić, czy wśród nich jes t element

równy danemu y, musimy sprawdzić ka żdy z elementów tego cią gu, gdyż element y może się znajdować w do-
wolnym miejscu cią gu, a w s zczególnoś ci może go tam nie być. W takim przypadku s tos ujemy przes zukiwa-
nie (lub pos zukiwanie) liniowe , które s tos owaliś my w punkcie 4.1 do znajdowania w ciągu elementu najmniej-
szego lub najwięks zego. Na ogół takie przes zukiwanie odbywa się „od lewej do prawej”, czyli od początku do
końca cią gu. Można je opis ać na s tępująco.

Algorytm pos zukiwania liniowego (dla specyfikacji powyżej)
Krok 1. Dla i = 1, 2, ..., n, jeśli x

i

= y, to przejdź do kroku 3.

Krok 2. Komunikat: W cią gu danych nie ma elementu równego y. Zakończ algorytm.
Krok 3. Element równy y znajduje się na miejs cu i w ciągu danych. Zakończ algorytm.

Je śli element y znajduje się w prze szukiwanym cią gu, to algorytm kończy działanie po na tknię ciu się na nie -
go po raz pierws zy, a jeśli nie ma go w tym cią gu to kończy s ię po dojś ciu do końca ciągu. W obu przypadkach
liczba działa ń jes t proporcjonalna do liczby elementów w cią gu. W pierwszym przypadku najwię cej operacji
jes t wykonywanych wówcza s , gdy pos zukiwany element jes t na końcu ciągu.

Ciekawe własnoś ci ma niewielka modyfikacja powyżs ze go algorytmu, wykorzys tująca spe cja lny element,
umies zczony na końcu cią gu, zwany wartownikie m. Rolą wartownika jes t „pilnowanie”, by proces przes zuki-
wania nie wys zedł poza ciąg. Jak wiemy, gdy ciąg zawiera element o wartości y, to przes zukiwanie kończy się
na tym elemencie. Aby mieć pe wnoś ć, że przeszukiwanie za wsze zakończy się na elemencie o wartoś ci y, do-
łączamy na końcu ciągu element o wartoś ci y. W efekcie, prze szukiwanie zaws ze zakończy się znalezieniem
elementu o wartości y, nale ży jedynie spra wdzić, czy ten element znajduje się na dołączonej pozycji zbioru,
czy też wystąpił wcześ niej. W pierws zym przypadku, badany zbiór nie zawiera elementu równe go y, a w dru-
gim – y nale ży do zbioru. Wida ć s tąd, że dołączony do zbioru element odgrywa rolę jego wartownika – nie mu-
simy bowiem spra wdzać, czy przeglądanie objęło ca ły zbiór czy nie – zaws ze zatrzyma się ono na s zukanym
elemencie , którym może być dołączony wła śnie element.

W tym punkcie zakłada my, że poszukiwania elementów (informacji) s ą prowadzone w uporządkowanych cią -
gach elementów – chcemy albo znaleźć element, a lbo umieś cić go w takim cią gu z zachowaniem uporządko-
wania.

Zbiory mogą mieć różną s trukturę – mogą to być ksią żki w bibliote ce, ha sła w encyklopedii, liczba w us talo-
nym przedziale lub numery w ksią żce telefonicznej. Te przykłady są bliskie codziennym s ytuacjom, w których

> Czy ws zystko można policzyć na komputerze

< 15 >

nale ży ods zuka ć pewną informację i zapewne s tos owane prze z Was w tych przypadkach metody s ą podobne
do opis anych tutaj. Nas zymi rozwa żaniami chcemy utwierdzić Wa s w przekonaniu, że:

integralną częś cią informacji je st jej uporządkowanie,

gdyż w przeciwnym ra zie ... nie jes t to informacja . To s twierdzenie nie je st naukowym określeniem informa -
cji

2

, ale odnosi s ię do informacji w potocznym znaczeniu.

Wykonaj tera z ćwiczenie, które zape wne wykonywa łeś już niera z w s woim życiu, nie zdając s obie na -

wet z tego s pra wy. We ź do ręki jedną z ksią żek: słownik ortograficzny, słownik polsko-angielski lub ks iążkę
telefoniczną , wybierz trzy słowa zaczynające się na litery: c, k ora z w i zna jdź je w wybranej ksią żce. Zanotuj,
ile ra zy ją otwierałaś , zanim znala złeś stronę z pos zukiwanym słowem.

Jeśli ksią żka , którą wybra łeś , ma między 1000 a 2000 s tron, to dla znale zienia jednego s łowa nie po-

winieneś otwierać jej częś ciej niż 11 ra zy; jeśli ma między 500 a 1000 stron – to nie częś ciej niż 10 razy; jeś li
między 250 a 500 s tron – to nie czę ściej niż 9 ra zy itp.

Skąd to wiemy? Przypuszczamy, że w pos zukiwaniu hasła, po zajrzeniu na wybraną s tronę wies z, że znaj-

duje się ono przed nią, albo po niej, możes z więc jedną z części ksią żki pominąć w dals zych poszukiwaniach. Co
więcej, w nieodrzuconej częś ci kartek wybiera sz jako kolejną tę, która jes t bliska środka, lub leży w pobliżu lite -
ry, na którą zaczyna się pos zukiwany wyraz. Stosujes z więc – może nawet o tym nie wiedząc – metodę pos zuki-
wania, która polega na podziale (połowieniu) przes zukiwanego zbioru. Możesz ją za stosować, bo przeszukiwa-
ny zbiór jest uporządkowany. A ile prób musiałbyś wykonać, gdyby hasła w słowniku nie były uporządkowane?
Porównaj tera z:

■

W alfabetycznym s pisie telefonów na 1000 s tronach wys tarczy przejrzeć co najwyżej 10 s tron, by znaleźć
numer telefonu danej os oby.

■

A jeś li miałbyś znaleźć os obę, która ma telefon o numerze 1234567, to w najgors zym przypadku musia łbyś
przejrzeć ws zystkie 1000 s tron!

Czy to porównanie nie ś wiadczy o potędze uporzą dkowania i o s ile algorytmu za s tos owanego do uporządko-
wane go wyka zu?

Przedstawiony s posób pos zukiwania przez połowienie w zbiorze uporządkowanym ilus trują , że ta metoda
jes t kolejnym zas tos owaniem za s ady dziel i zwycię żaj.

Algorytm pos zukiwania prze z połowienie jes t zwany również binarnym pos zukiwaniem. Przyjmijmy, że prze -
s zukiwany cią g liczb jes t umie szczony w tablicy x[k..l] i za łóżmy dla upros zczenia, że wartoś ć pos zukiwane -
go elementu y mie ści się w prze dziale wartości elementów w tej tablicy, czyli x

k

≤ y ≤ x

l

. Algorytm, który poda -

jemy gwarantuje, że w trakcie jego działa nia prze szukiwany przedział za wiera pos zukiwany element y, czy-
li x

lewy

≤ y ≤ x

pra wy

. Ta wła sność ora z to, że długość tego przedzia łu zmniejs za się w ka żdej iteracji (zob. krok 3),

zapewniają, że poniżs zy algorytm jes t poprawny i skończony.

Algorytm pos zukiwania przez połowienie (algorytm binarnego przes zukiwania)
Dane:

Uporządkowany ciąg liczb w tablicy x[k..l], tzn. x

k

≤ x

k+1

≤ … ≤ x

l

; ora z element y spełniający nie -

równoś ci x

k

≤ y ≤ x

l

.

Wyniki: Takie s (k ≤ s ≤ l), że x

s

= y, lub przyjąć s = –1, jeśli y ≠ x

i

dla ka żde go i (k ≤ i ≤ l).

Krok 1. lewy := k; prawy := l;

{Początkowe końce przes zukiwanego przedziału.}

Krok 2. Jeśli lewy > pra wy, to przypis z s := –1 i zakończ algorytm.

{Ozna cza to, że poszukiwanego elementu y nie ma w przes zukiwa nej tablicy.}

Krok 3. s:=(lewy + pra wy) div 2;

{Operacja div oznacza dzielenie ca łkowite.}

Jeśli x

s

= y, to zakończ a lgorytm. {Zna leziono element y w przes zukiwanej tablicy.}

Jeśli x

s

< y, to lewy :=s + 1, a w przeciwnym ra zie pra wy := s – 1.

Wróć do kroku 2.

2

W te orii informacji, informacja jes t definiowana jako „miara niepe wności zajś cia pewnego zdarzenia s pośród s kończo-

nego zbioru zdarzeń możliwych” – na pods tawie Nowej encyklopedii pows zechnej PWN.

< 16 >

Informatyka +

Pytanie o liczbę porównań w powyżs zym algorytmie można s formułować na s tępująco: ile ra zy nale ży od-
rzucać połowę bie żące go ciągu, by pozos ta ł tylko je den element (zauwa żmy tutaj, że jeś li elementu y nie ma
w cią gu, to kontynuujemy algorytm a ż do wyczerpania ws zystkich elementów, czyli wykonujemy o jeden krok
więcej). Jeśli n = 32, to jeden element pozos taje po pięciu podziałach, a je śli n = 16 – to po cztere ch. Stąd
można wywnioskować, że je śli wartoś ć n zawiera s ię między 16 a 32, to wykonujemy nie więcej niż pięć po-
równań. Ta obserwacja ma zwią zek z potęgą liczby 2, a dokładniej – z na jmniejs zym wykładnikiem k potęgi 2

k

,

której wartoś ć nie jes t mniejsza od n, czyli n ≤ 2

k

. Pojawia się więc tutaj w naturalny s pos ób funkcja odwrotna

do potęgowania – logarytm. Można nawet przyjąć „informat yczną” definicję tej funkcji:

log

2

n jes t równy liczbie kroków prowadzących od n do 1, w których

bieżąca liczba jes t zas tępowana prze z zaokrą glenie w górę jej połowy.

Algorytm binarne go przes zukiwania ma dość is totne uogólnienie, gdy dla elementu y, bez względu na to, czy
należy do cią gu czy nie, chcemy znaleźć ta kie miejsce, by po ws tawieniu go tam, ciąg pozos tał uporządkowa-
ny. Odpowiedni algorytm można w tym przypadku na zwać binarnym umie szczaniem i je st on pros tym roz-
szerzeniem powyżs zego algorytmu.

Czy rzeczywiś cie przeszukiwanie binarne jest najszybszą metodą znajdowania elementu w ciągu uporządko-
wanym? Wyobra źmy sobie, że mamy znaleźć w ksią żce telefonicznej numer telefonu Pana Bogusza Alfreda.
Wtedy zapewne skorzys tamy z tego, że litera B jes t blisko początku alfabetu i, ows zem, zas tosujemy metodę
podziału, ale w pierws zej próbie nie będziemy jednak dzielić ksią żki na dwie połowy, ale raczej spróbujemy tra -
fić blisko tych s tron, na których znajdują się nazwiska zaczynające się na literę B. W dalszych krokach będzie -
my pos tępować podobnie. Tę obs erwację można wykorzys tać w algorytmie pos zukiwania . Zauwa żmy najpierw,
że w algorytmach binarnych jes t sprawdzana jedynie relacja , czy dana liczba y jest większa (lub mniejs za lub
równa) od wybranej z ciągu, natomias t nie sprawdzamy i nie wykorzystujemy tego, jak bardzo jes t więks za.
Podcza s odnajdywania wyrazów w encyklopediach korzystamy natomias t z informacji, w jakim miejscu alfabe -
tu znajduje się litera, którą rozpoczyna się pos zukiwany wyra z, i w zależności od tego wybieramy odpowied-
nią porcję kartek. Strategia ta nazywa się interpolacyjnym poszukiwaniem, gdyż uwzględnia nie tylko położe-
niu s zukanej liczby względem środka ciągu, ale uwzględnia jej wartoś ć względem rozpiętości krańcowych war-
tości w cią gu. Szczegółowe informacje na temat interpolacyjnego poszukiwania można znaleźć w ksią żce [6].

Porządkowanie, nazywane również częs to s ortowaniem, ma olbrzymie znaczenie niemal w każdej działalnoś ci czło-
wieka. Jeśli elementy w zbiorze są uporządkowane zgodnie z jakąś regułą (np. książki lub ich karty katalogowe we-
dług liter alfabetu, słowa w encyklopedii, daty, numery telefonów według nazwisk właś cicieli), to wykonywanie wielu
operacji na tym zbiorze staje się znacznie łatwiejsze i s zybsze. Między innymi dotyczy to operacji (patrz punkt 4.4):

■

sprawdzenia czy dany element, czyli element o us talonej wartoś ci cechy, według której zbiór zos tał
uporządkowany, znajduje się w zbiorze,

■

znale zienia elementu w zbiorze, jeśli w nim jes t,

■

dołączenia nowe go elementu w odpowie dnie miejs ce, aby zbiór pozos tał nadal uporządkowany.

Komputery w dużym s topniu za wdzię czają s woją s zybkoś ć temu, że działają na uporządkowanych informa-
cja ch. To s amo odnosi się do na s , gdy pos ługujemy się informacjami i komputerami. Je śli chcemy na przykład
sprawdzić, czy w ja kimś katalogu dyskowym znajduje się plik o podanej na zwie, rozszerzeniu, cza sie utwo-
rzenia lub rozmiarze, to najpierw odpowiednio porządkujemy listę plików i wtedy na ogół znajdujemy odpo-
wiedź na tychmia s t.

Dla upros zczenia , problem porządkowania s formułujemy dla liczb, chocia ż wiele praktycznych problemów
może dotyczyć porządkowa nia innych obiektów prze chowywanych w komputerze.

> Czy ws zystko można policzyć na komputerze

< 17 >

Proble m porządkowania (s ortowania)
Dane: Liczba naturalna n i ciąg n liczb x

1

, x

2

, ..., x

n

Wynik: Uporządkowanie te go cią gu liczb od najmniejs zej do najwięks zej.

Z założenia , że p orządkujemy tylko liczby względem ich wartości wynika , że intere sują na s a lgorytmy, w któ-
rych główną operacją jes t porówna nie, wykonywane między eleme nta mi danych. W ogólnym s formułowaniu
problemu porządkowa nia , porządkowane obiekty mogą być bardziej złożone , np. s łowa (przy tworzeniu słow-
nika), a dre s y (do ks iążki telefonicznej) czy bard zo złożone zes tawy danych, jak np. informacje o koncie banko-
wym i je go wła ścicielu.

Znanych je st bardzo wiele algorytmów porządkowania liczb i innych obiektów przechowywanych

w komputerze. Temu zagadnieniu poś wię cono wiele opa słych ksią żek, np. Donald Knuth napis ał na ten tema t
ponad 1000 s tron jeszcze w latach 60. XX wieku, patrz [4]. W dals zej częś ci tego punktu prezentujemy dwa
najbardziej znane a lgorytmy porządkowania – przez wybór oraz s ortowanie przez scalanie. Pierws zy z nich
jes t iteracją poznanego wcze śniej algorytmu i ma złożonoś ć proporcjonalną do n

2

, gdzie n jes t liczbą porząd-

kowanych elementów, a drugi – to przykład me tody dziel i zwycię żaj, bę dą cy jedną z najszybszych me tod s or-
towania. Złożonoś ć te go drugiego algorytmu wynosi nlog n.

Działa nie prezentowanych algorytmów porządkowania , jak i wielu innych algorytmów sortują cych moż-

na obejrzeć w programa ch edukacyjnych Ma szyna s ortująca i Sortowanie , które zna jdują s ię w folderze z ma -
teriałami do tych zajęć.

Jeden z najpros ts zych algorytmów porządkowania można wyprowadzić korzys tając z tego, co już poznaliśmy
w poprzednich punktach. Zauwa żmy, że jeś li mamy us tawić elementy w kolejnoś ci od najmniejs zego do naj-
więks zego, to najmniejs zy element w zbiorze powinien się znale źć na początku tworzone go ciągu, za nim po-
winien być umies zczony najmniejszy element w zbiorze pozos ta łym po usunięciu najmniejs zego elementu
itd. Taki algorytm jes t więc iteracją znane go algorytmu znajdowania Min w cią gu i nosi na zwę algorytmu po-
rządkowania przez wybór. Oto jego opis:

Algorytm porządkowani przez wybór – Sele ctionSort
Dane:

Liczba naturalna n i cią g n liczb x

1

, x

2

, ..., x

n

.

Wynik: Uporządkowanie dane go ciągu liczb od najmniejs zej do najwięks zej. (Uwa ga . Elementy cią gu da ne -

go i wynikowego oznaczamy tak s amo, gdyż porządkowanie odbywa się „w tym s amym miejscu”.)

Krok 1. Dla i = 1, 2, ..., n – 1 wykonaj kroki 2 i 3, a na stępnie zakończ algorytm.
Krok 2. Znajdź k takie, że x

k

jes t najmniejs zym elementem w cią gu x

i

, ..., x

n

.

Krok 3. Zamień miejscami elementy x

i

oraz x

k

.

Złożonoś ć algorytmu Sele ctionSort
Aby obliczyć, ile porównań i zamian elementów, w zależności od liczby elementów w ciągu n, jes t wykonywa -
nych w a lgorytmie SelectionSort wys tarczy zauwa żyć, że ten algorytm jes t iteracją algorytmu znajdowania
najmniejs ze go elementu w ciągu, a ciąg, w którym szukamy najmniejs zego elementu, je st w kolejnych itera -
cjach coraz króts zy. Liczba przes tawień elementów jes t równa liczbie iteracji, gdyż elementy s ą przes ta wia-
ne je dynie na końcu ka żdej iteracji, których jes t n – 1, a wię c wynosi n –1. Jeśli za ś chodzi o liczbę porównań,
to wiemy, że algorytm znajdowania minimum w ciągu wykonuje o jedno porównanie mniej niż jes t elementów
w ciągu, a zatem cały algorytm porządkowania przez wybór, dla cią gu da nych złożonego na początku z n ele -
mentów wykonuje liczbę porównań równą :

(n – 1) + (n – 2) + (n – 3) + … + 3 + 2 + 1

Wa rtoś ć tej s umy można obliczyć wieloma sposobami, np. ja ko sumę pos tępu arytmetycznego i otrzymujemy

Zauwa żmy, że otrzyma ny wzór na liczbę porównań w a lgorytmie porządkowania przez wybór jes t dokładną
liczbą działa ń wykonywanych w algorytmie, bez względu na to, jak daleko porządkowany ciąg jest już upo-
rządkowany.

< 18 >

Informatyka +

Metoda dziel i zwycię żaj realizowana rekurencyjnie jes t jedną z najsilniejs zych te chnik komputerowe go roz-
wią zywania problemów. W tej me todzie, czę ś ć organizacji obliczeń jes t „zrzucana na komputer”, faktycznie
więc wykorzys tywana je s t potęga komputerów. W tym punkcie zas tosujemy metodę dziel i zwycię żaj w algo-
rytmie porządkowania przez s calanie. W tym algorytmie jes t wykorzys tywana metoda s calania uporządko-
wanych ciągów, czyli ich łączenia w jeden cią g.

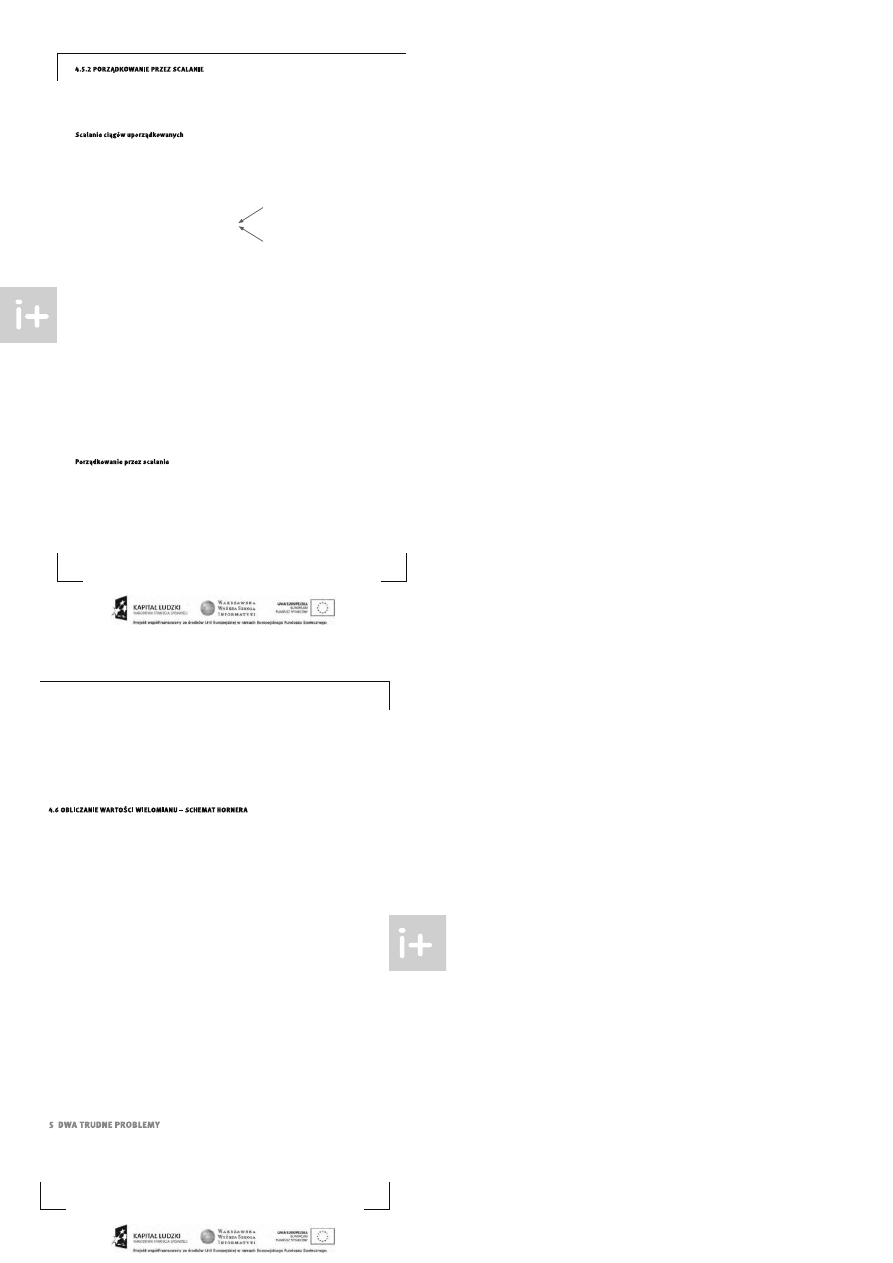
Przyjmijmy, że scalamy ciągi uporzą dkowane i wynik s calania ma być równie ż cią giem uporządkowa nym.
Można to wykonać w bardzo prosty sposób: patrzymy na począ tki danych cią gów i do tworzonego ciągu prze -
nosimy mniejszy z elementów czołowych lub którykolwiek z nich, je śli s ą równe, patrz rys . 4.

Scalony ciąg

Scalone cią gi

3 5 7 10 12

1 3 5 7 10 12

1 2 6 9 11 15 17 20

Scalanie

1 2 6 9 11 15 17 20

Rysunek 4.
Przykład scalania dwóch cią gów uporządkowanych

Aby określić, ile porównań wykonuje algorytm s calający dwa ciągi zauwa żmy, że z wyjątkiem elementu prze -
noszonego na końcu, przeniesienie ka żde go innego elementu może być zwią zane z wykonaniem porówna-
nia między elementami danych ciągów. Tak jes t wtedy, gdy w kroku prze d prze dos tatnim, oba scalane cią gi
zawierają jes zcze po jednym elemencie. Przypuś ćmy więc, że na początku jeden ciąg zawiera k elementów
a drugi ma l elementów. razem n, czyli n = k + l. Ta dys kusja prowadzi do konkluzji, że bez względu na liczno-
ści danych ciągów, ich s calenie może wymagać wykonania n – 1 porównań.

Z tej dyskusji wynika je szcze jeden wniosek – ponie wa ż nie potrafimy prze widzieć, który z ciągów i kie -

dy wyczerpie się w trakcie s calania, tworzony cią g nie może być umie szczany na miejs cu cią gów danych do
sca lenia , musi wię c być tworzony na nowym miejs cu. Zatem potrzebna je st dodatkowa pamięć – mówimy
w takim przypadku, że ta me toda nie działa „w miejscu” (in situ).

Algorytm s calania dwóch ciągów uporządkowanych – Scal
Da ne:

Dwa uporządkowane ciągi x i y.

Wynik: Uporzą dkowany ciąg z, będący s caleniem ciągów x i y.
Krok 1. Dopóki oba ciągi x i y nie są puste wykonuj na s tępującą operację:

przenieś mniejs zy z najmniejs zych elementów z cią gów x i y do ciągu z.

Krok 2. Do końca cią gu z dopis z elementy pozos tałe w jednym z cią gów x lub y.

Algorytm s calania dwóch uporządkowanych cią gów można s tosować do tworzenia uporządkowa nych cią gów
z podcią gów już uporządkowanych. Mógłby być pożytek z te go algorytmu przy porządkowaniu, gdybyś my
potrafili najpierw uporządkować te podcią gi. Załóżmy wię c, że te podciągi porządkujemy... tą samą meto-
dą – w tym celu przydaje s ię rekurencja. W algorytmie porządkowania przez s calanie porządkowany cią g jes t
dzielony w ka żdym kroku na dwa , niemal równej długoś ci podcią gi, które rekurencyjnie są porządkowane tą
samą me todą . Warunkiem zakończenia rekurencji w tym algorytmie jes t s ytuacja , gdy ciąg ma je den element,
wtedy nie można go już podzielić na podciągi, chocia ż nie ma nawet po co – jes t to bowiem cią g już uporząd-
kowany. Jak zwykle , w opisie algorytmu rekurencyjne go, po na zwie algorytmu wys tępuje układ parame trów
określających rozwiązywany problem, który jes t wykorzys tany w treś ci algorytmu, w odwołaniu do niego s a-
mego przy rozwią zywaniu mniejs zych podproblemów.

1

> Czy ws zystko można policzyć na komputerze

< 19 >

Algorytm porządkowania przez scalanie Merge Sort (l,p,x)
Dane:

Cią g liczb x

l

, x

l+1

, …, x

p

Wynik: Uporządkowanie tego cią gu liczb od najmniejs zej do najwięks zej.
Krok 1. Je śli l < p, to przyjmij s:=(l+p) div 2 i wykonaj trzy na stępne kroki.
Krok 2. Za s tos uj ten sam algorytm do cią gu (l,s ,x), czyli wykonaj MergeSort(l,s ,x).
Krok 3. Za s tos uj ten sam algorytm do ciagu (s+1,p,x), czyli wykonaj MergeSort(s+1,p,x)
Krok 4. Za s tosuj algorytm s calania Scal do cią gów (x

l

, …, x

s

), (x

s+1

, …, x

p

) i wynik umieś ć z powrotem w ciągu

(x

l

, …, x

p

).

Złożoność s ortowania cią gu n liczb przez scalanie wynosi około nlogn, jes t zatem znacznie mniejsza niż zło-
żonoś ć algorytmu s ortowania przez wybór .

Obliczanie wartości wielomianu o zadanych współczynnikach jes t jedną z najczęś ciej wykonywanych ope -
racji w komputerze. Wynika to z wa żnego faktu matematycznego, zgodnie z którym ka żdą funkcję (np. funk-
cje trygonometryczne) można za s tą pić wielomianem, którego pos tać zależy od funkcji i od tego, ja ką chcemy
uzyskać dokładność obliczeń. Najefektywniejs zym spos obem obliczania wartoś ci wielomianu jes t schemat
Hornera , wynikający z na s tępujące go przeks ztałcenia pos taci wielomianu:

w

n

(x) = a

0

x

n

+ a

1

x

n–1

+ ... + a

n–1

x + a

n

= (a

0

x

n–1

+ a

1

x

n–2

+ ... + a

n–1

)x + a

n

= ((a

0

x

n–2

+ a

1

x

n–3

+ ... + a

n–2

)x + a

n–1

)x + a

n

=

= (...((a

0

x + a

1

)x + a

2

)x + ... + a

n–2

)x + a

n–1

)x + a

n

Ten os tatni wzór można zapis ać w nas tępującej pos taci algorytmicznej:

y := a

0

y: = yz + a

i

dla i = 1, 2, ..., n.

Stąd otrzymujemy algorytm:

Algorytm: Schemat Hornera
Dane:

n – nieujemna liczba całkowita (s topień wielomianu);
a

0

, a

1

, ... , a

n

– n+1 współczynników wielomianu;

z – wartoś ć argumentu.

Wynik: y = w

n

(z) – wartoś ć wielomianu s topnia n dla wartoś ci argumentu x = z.

Krok 1. y := a

0

– począ tkową wartością jes t współczynnik przy najwyższej potę dze.

Krok 2. Dla i = 1, 2, …, n oblicz wartoś ć dwumianu y := yz + a

i

Z pos taci algorytmu wynika , że obliczenie wartości wielomianu s topnia n wymaga wykonania n mnożeń i n
dodawań. Udowodniono, że je st to najs zybs zy spos ób oblicza nia wartoś ci wielomianu.

Schemat Hornera ma wiele za s tosowań, m.in. do:

■

obliczania dziesiętnej wartoś ci liczby, danej w s ys temie o pods ta wie p – współczynniki wielomianu są
w tym przypadku cyframi {0, 1, …, p – 1} a a rgumentem p, pods ta wa s ystemu.

■

s zybkie go obliczania wartoś ci potęgi (patrz punkt 5.2).

Wracamy tutaj do dwóch problemów przeds tawionych w rozdziale 3. Jednym z nich jes t sprawdzanie, czy dana
liczba jes t liczbą pierws zą, a drugim – szybkie podnoszenie do potęgi. Dla pierwszego z tych problemów nie
mamy dobrej wiadomoś ci, nie jes t bowiem znana żadna metoda s zybkiego tes towania pierwszości liczb. Ko-
rzysta się z tego na przykład w s zyfrze RSA, częś cią kluczy w tej metodzie jes t liczba będąca iloczynem dwóch
dużych liczb pierwszych i brak znajomości tego rozkładu jes t gwarancją bezpieczeńs twa tego s zyfru.

Drugim problemem je st podnoszenie do dużych potęg i tutaj mamy bardzo dobrą wiadomoś ć – podno-

s zenie do nawet bardzo dużych potęg, za wierających se tki cyfr, trwa ułamek sekundy.

< 20 >

Informatyka +

Dla problemu badania , czy dana liczba n jest liczbą pierwszą, czy złożoną, dysponujemy pros tym algorytmem, któ-
ry polega na dzieleniu n przez kolejne liczby naturalne i wystarczy dzielić tylko przez liczby nie większe niż √n, gdyż
liczby n nie można rozłożyć na iloczyn dwóch liczb większych od √n. Algorytm ten ma bardzo pros tą pos tać:

var i,n:integer;

i:=2;

while i*i <= n do begin

if n mod i = 0 then return 1; {n jest podzielne przez i}

i=i+1

end;

return 0 {n jest liczba pierwsz

ą }

Ten fra gment programu zwraca 0, je śli n jes t liczbą pierws zą , i 1, gdy n jes t liczbą złożoną . W tym drugim przy-
pa dku znamy także podzielnik liczby n. Ten fragment programu można rozs zerzyć do programu generujące -
go ws zystkie dzielniki liczby n.

Liczba operacji wykonywanych przez powyższy program jest w najgors zym przypadku (gdy n jest liczbą pierw-

szą ) proporcjonalna do √n, a więc jeśli n = 10

m

, to wykonywanych jest 10

m/ 2

operacji. Zatem są niewielkie szanse, by

tym algorytmem rozłożyć na czynniki pierws ze liczbę, która ma kilkaset cyfr, lub stwierdzić, że się jej nie da rozłożyć.

Rozkła dem liczby złożonej na czynniki pierws ze mogą być zainteres owani ci, którzy starają się złamać szyfr
RSA. Wiadomo, że je dna z liczb tworzących kluch publiczny i prywatny jes t iloczynem dwóch liczb pierw-
szych. Znajomoś ć tych dwóch czynników umożliwia utworzenie klucza prywa tnego (tajne go). Je dnak ich wiel-
koś ć – s ą to liczby pierws ze o kilkus et cyfrach (200-300) s toi na przes zkodzie w rozkładzie n.

Is tnieje wiele algorytmów, które służą do tes towania pierwszości liczb ora z do rozkładania liczb na czynni-
ki pierwsze. Niektóre z tych algorytmów mają charakter probabilis tyczny – wynik ich działania jes t poprawny
z prawdopodobieńs twem bliskim 1. Żaden jednak algorytm, przy obe cnej mocy komputerów, nie umożliwia
rozkładania na czynniki pierws ze liczb, które maja kilkas et cyfr. Szyfr RSA pozos taje więc nadal be zpiecznym
sposobem utajniania wiadomoś ci, w tym również przes yłanych w s ieciach komputerowych.

Wracamy tutaj do obliczania wartoś ci potęgi x

m

, dla dużych wartoś ci wykładnika m. W punkcie 3.3 podaliś my

przykład dla m = 12345678912345678912345678912345. Stosując „s zkolny” algorytm, czyli kolejne mno-
żenia , i korzystając z na sze go superkomputera , obliczenie potęgi dla te go wykładnika zaję łoby 3*10

8

la t. Ten

wykładnik jes t faktycznie nie wielką liczbą , w porównaniu z wykładnikami, jakie pojawiają się przy s tos owa -
niu s zyfru RSA, potrzebny jes t więc znacznie efektywniejs zy algorytm.

Do wyprowadzenia algorytmu s zybkiego potęgowania posłużymy s ię rekurencyjnym za pis em opera-

cji potę gowania:

1

jeś li m = 0

x

m

=

{

(x

m/ 2

)

2

,

jeś li m jes t liczbą parzys tą

(x

(m–1)/ 2

)

2

x

jeś li m jes t liczbą nieparzys tą

Na przykład, jeś li chcemy obliczyć x

22

, to powyżs za zale żnoś ć rekurencyjna prowa dzi przez na stępujące od-

wołania rekurencyjne: x

22

= (x

11

)

2

= ((x

5

)

2

x)

2

= (((x

2

)

2

x)

2

x)

2

.

Warto zauwa żyć, jaki jes t zwią zek kolejności wykonywania mnożeń, wynikającej z powyżs zej zale żno-

ści rekurencyjnej, z pos tacią binarną wykładnika , zapisaną z użyciem schema tu Hornera . Dla na szego przy-
kładu mamy m = (22)

10

= (10110)

2

. Porównując kolejność mnożeń z pos tacią binarną widać, że podnos zenie

do kwadratu odpowiada kolejnym pozycjom w rozwinięciu binarnym, a mnożenie przez x odpowiada cyfrze 1
w rozwinięciu binarnym. A za tem, liczba mnożeń je st nie większa niż dwa ra zy długość binarnego rozwinięcia
wykładnika. Wiemy skądinąd, że długoś ć rozwinięcia binarnego liczby m wynosi ok. log

2

m. Mamy w przybli-

żeniu log

2

12345678912345678912345678912345 = 104, a za tem podniesienie do tej potęgi wymaga wyko-

nania nie więcej niż ok. 200 mnożeń.

W ta beli 3 zamieś ciliśmy wartoś ci logarytmu przy pods ta wie 2 z rosnących wartoś ci liczby m.

> Czy ws zystko można policzyć na komputerze

< 21 >

Tabela 3.
Przybliżona długość rozwinię cia binarne go liczby m

m

log

2

m

10

4

10

10

6

20

10

9

30

10

12

40

10

20

6 6,5

10

50

166

10

10 0

332,2

Z ta beli 3 wynika, że obliczenie wartoś ci potęgi dla wykładnika o s tu cyfrach wymaga wykonania nie wię cej
niż 670 mnożeń, a to trwa nawet na komputerze os obis tym ułamek sekundy.

Problem potęgowania jes t najlepszą ilus tracją powiedzenia Ralfa Gomory’ego, że prawdziwe przys pies zenie
obliczeń os iągamy dzięki efektywnym algorytmom, a nie szybszym komputerom.

1. Cormen T.H., Leis erson C.E., Rives t R.L., Wprowadzenie do a lgorytmów, WNT, Warszawa 1997
2. Gurbiel E., Hard-Olejniczak G., Kołczyk E., Krupicka H., Sysło M.M., Informatyka , Część 1 i 2, Podręcznik dla

LO, WSiP, Wars zawa 2002-2003

3. Ha rel D., Algorytmika . Rzecz o istocie informatyki, WNT, Wars za wa 1992
4. Knuth D.E., Sztuka programowania, Tomy 1 – 3, WNT, Warsza wa 2003
5. Steinhaus H., Kalejdoskop matematyczny, WSiP, Wars zawa 1989
6. Sysło M.M., Algorytmy, WSiP, Wars zawa 1997
7. Sysło M.M., Pira midy, s zys zki i inne konstrukcje algorytmiczne, WSiP, Wars zawa 1998. Kolejne rozdziały tej

ksią żki s ą zamies zczone na s tronie: http:// www.wsipnet.pl/ kluby/ informatyka _eks tra.php?k=69

8. Wirth N., Algorytmy + struktury danych = programy, WNT, Wars zawa 1980.

< 22 > Notatki

Informatyka +

Notatki

< 23 >

W projekcie

, poza wykładami i warsztatami,

przewidziano następujące działania:

■

24-godzinne kursy dla uczniów w ramach modułów tematycznych

■

24-godzinne kursy metodyczne dla nauczycieli, przygotowujące

do pracy z uczniem zdolnym

■

nagrania 60 wykładów informatycznych, prowadzonych

przez wybitnych specjalistów i nauczycieli akademickich

■

konkurs y dla uczniów, trzy w ciągu roku

■

udział uczniów w pracach kół naukowych

■

udział uczniów w konferencjach naukowych

■

obozy wypoczynkowo-naukowe.

Szczegółowe informacje znajdują się na stronie projektu