FUNDAMENTOWANIE - PROJEKT

Wykonał: Michał Mazur

indeks 187595

grupa środa 9:15

Prowadzący: dr inż. Olgierd Puła

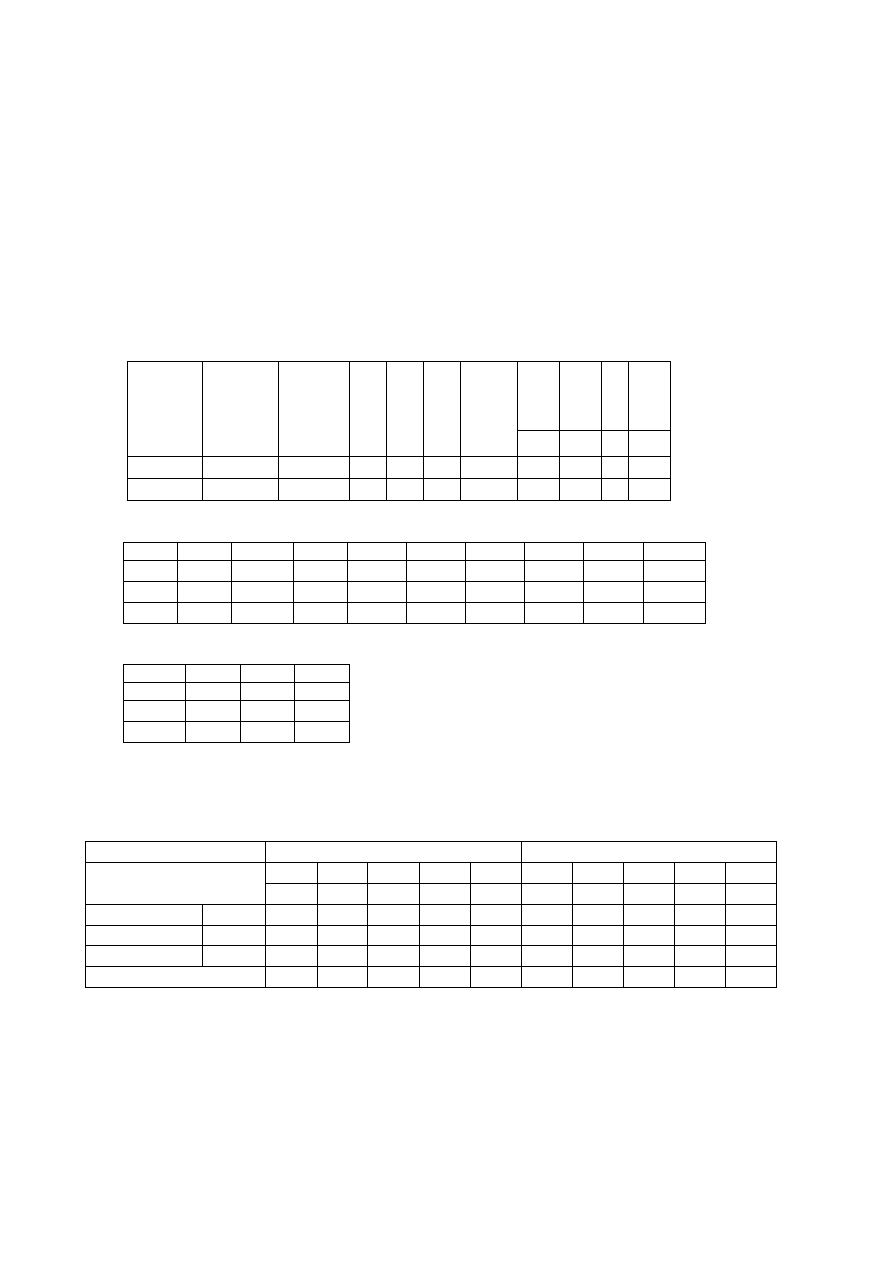
1. Dane wyjściowe i niezbędne założenia

a) Lokalizacja: Wrocław
b) Poziom przemarzania: 0,8 m
c) Długość stopy fundamentowej: L=3,0m
d) Szerokość stopy fundamentowej: B=1,8m
e) Wysokość stopy fundamentowej: d

f

=0,65m

f) Długość słupa na stopie: l

s

=0,45m

g) Szerokość słupa na stopie: b

s

=0,35m

h) Poziom wierzchu fundamentu: p.w.f=-0,55m
i) Poziom terenu: p.t = 120,5
j) Warunki gruntowo wodne

symbol

gruntu

wg PN-

81/B-

03020

Miąższość

Grupa

konsoli-
dacyjna

I

C

I

D

I

L

stan

wilgo-

tności

ρ

s

ρ

w

n

ρ

d

t*m

-3

t*m

-3

% t*m

-3

Pπ

5,1

0,55

2,65 1,65

6

1,56

Gπ

4,4

B

0,80

0,20

m

2,68 2,10 20 1,75

n

e

w

sat

Sr

γ

s

γ

d

γ

γ

sat

γ'

M

o

1

%

kN/m

3

kN/m

3

kN/m

3

kN/m

3

kN/m

3

Mpa

0,413 0,702 26,507 0,226 26,00

15,27

16,19

15,68

14,68

68,000

0,347 0,531 19,829 1,009 26,29

17,17

20,60

17,51

16,51

37,000

M

β

φ

c

MPa

1

°

kPa

85,000 0,80

32,00 0,00

49,333 0,75

18,20 31,00

k) Obciążenia

SCHAMAT 1

SCHEMAT 2

ODDZIAŁYWANIA

CHARAKTERYSTYCZNE

V

K

H

x;K

H

Y;K

M

X;K

M

Y;K

V

K

H

x;K

H

Y;K

M

X;K

M

Y;K

kN

kN

kN

kNm kNm

kN

kN

kN

kNm kNm

Stałe

G

1590

70

0

0

150

1590

70

0

0

150

Zmienne

Q

210

65

30

120

100

370

30

25

120

100

Wyjątkowe

A

190

15

20

40

50

190

25

20

60

30

RAZEM

1990

150

50

160

300

560

55

45

180

130

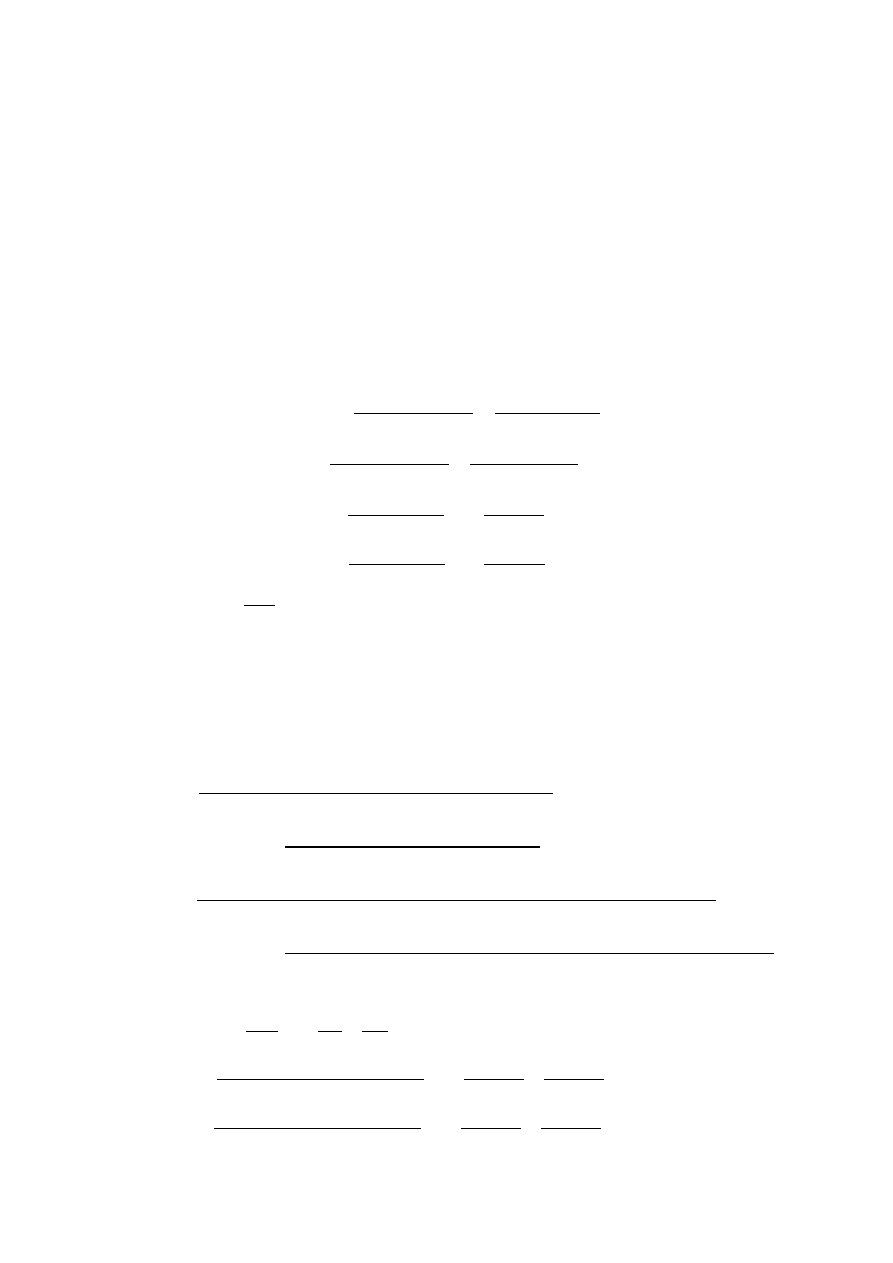
2. SPRAWDZENIE WARUNKU GEO WG PODEJŚCIA DA2

2.1 Wyznaczenie dodatkowych obciążeo stałych



Ciężar własny fundamentu

𝑉

𝐺1,𝑘

= 1,8 ∙ 3 ∙ 0,65 ∙ 25,0 = 87,75 𝑘𝑁



Ciężar gruntu nad fundamentem

𝑉

𝐺2,𝑘

= 1,8 ∙ 3 − 0,35 ∙ 0,45 /2 ∙ 0,2 ∙ 18,5 = 9,70𝑘𝑁



Ciężar posadzki nad fundamentem

𝑉

𝐺3,𝑘

= 1,8 ∙ 3 − 0,35 ∙ 0,45 /2 ∙ 0,25 ∙ 23 = 15,07 𝑘𝑁

𝑉

𝐺𝑘𝐹

= 112,52 𝑘𝑁

2.2 Wyznaczenie mimośrodów od obciążeo stałych

𝑒

𝐵

=

𝑀

𝐺𝑘𝑥

+ 𝑑

𝑓

∙ 𝐻

𝐺𝑘𝑦

𝑉

𝐺𝑘

+ 𝑉

𝐺𝑘𝐹

=

0 + 0,65 ∙ 0

1590 + 112,52

= 0

𝑒

𝐿

=

𝑀

𝐺𝑘𝑦

+ 𝑑

𝑓

∙ 𝐻

𝐺𝑘𝑥

𝑉

𝐺𝑘

+ 𝑉

𝐺𝑘𝐹

=

150 + 0,65 ∙ 70

1590 + 112,52

= 0,115𝑚

𝑞

𝑚𝑎𝑥

=

1590 + 89,87

1,8 ∙ 3

1 +

6 ∙ 0,115

3

= 387,69 𝑘𝑃𝑎

𝑞

𝑚𝑖𝑛

=

1590 + 89,87

1,8 ∙ 3

1 −

6 ∙ 0,115

3

= 242,87𝑘𝑃𝑎

𝑞

𝑚𝑎𝑥

𝑞

𝑚𝑖𝑛

= 1,6 < 2 - fundament nie wymaga przesunięcia o mimośród.

Przyjęto mimośród równy 0,15m

2.3 Wyznaczenie mimośrodu od obciążeo charakterystycznych stałych, zmiennych i

wyjątkowych

Przyjęto 𝑒

𝑥𝑠

= 0,15 𝑚

SCHEMAT I

𝑒

𝐵

=

𝑀

𝐺𝑘𝑥

+ 𝑀

𝑄𝑘𝑥

+ 𝑀

𝐴𝑘𝑥

+ 𝑑

𝑓

∙ 𝐻

𝐺𝑘𝑦

+ 𝐻

𝑄𝑘𝑦

+ 𝐻

𝐴𝑘𝑦

𝑉

𝐺𝑘

+ 𝑉

𝑄𝑘

+ 𝑉

𝐺𝑘𝐹

+ 𝑉

𝐴𝑘𝐹

=

0 + 120 + 40 + 0,65 ∙ 0 + 30 + 20

1590 + 210 + 190 + 112,52

= 0,092 𝑚

𝑒

𝐿

=

𝑀

𝐺𝑘𝑦

+ 𝑀

𝑄𝑘𝑦

+ 𝑀

𝐴𝑘𝑦

+ 𝑑

𝑓

∙ 𝐻

𝐺𝑘𝑥

+ 𝐻

𝑄𝑥

+ 𝐻

𝐴𝑥

− 𝑉

𝐺𝑘

+ 𝑉

𝑄𝑘

+ 𝑉

𝐴𝑘

∙ 𝑒

𝑥𝑠

𝑉

𝐺𝑘

+ 𝑉

𝑄𝑘

+ +𝑉

𝐴𝑘

+ 𝑉

𝐺𝑘𝐹

=

150 + 100 + 50 + 0,65 ∙ (70 + 65 + 15) − 1590 + 210 + 190 ∙ 0,15

1590 + 210 + 190 + 112,52

= 0,047𝑚

𝑞

𝑚𝑎𝑥 /𝑚𝑖𝑛

=

𝑉

𝑘

𝐵 ∙ 𝐿

1 ±

6𝑒

𝐿

𝐿

±

6𝑒

𝐵

𝐵

𝑞

𝑚𝑎𝑥

=

1590 + 210 + 190 + 112,52

1,8 ∙ 3

1 +

6 ∙ 0,092

1,8

+

6 ∙ 0,047

3

= 544,85𝑘𝑃𝑎

𝑞

𝑚𝑖𝑛

=

1590 + 210 + 190 + 112,52

1,8 ∙ 3

1 −

6 ∙ 0,092

1,8

−

6 ∙ 0,048

3

= 233,86 𝑘𝑃𝑎

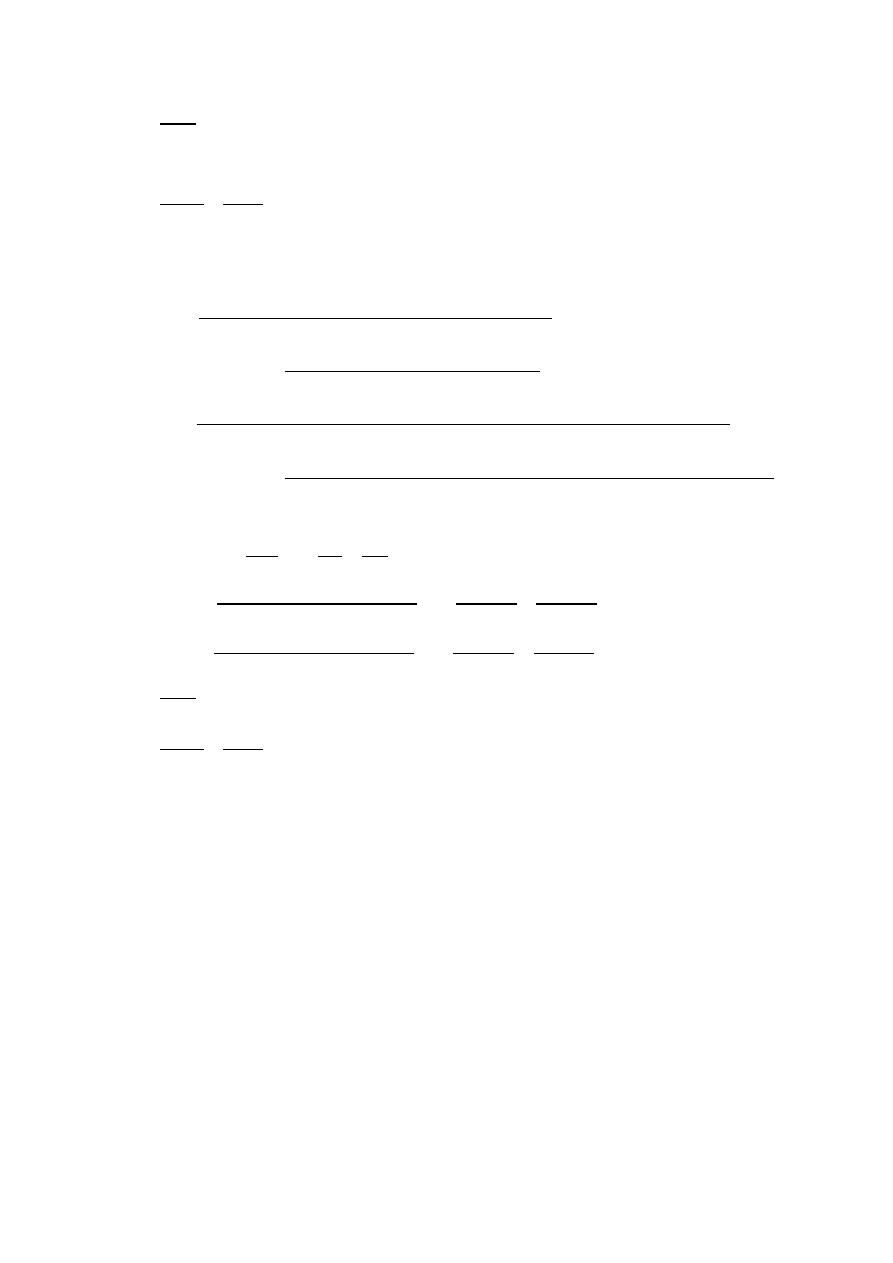
𝑞

𝑚𝑎𝑥

𝑞

𝑚𝑖𝑛

= 2,33

Sprawdzamy, czy siła wypadkowa położona jest w rdzeniu przekroju:

0,092

1,8

+

0,047

3

= 0,067 < 0,166

SCHEMAT II

𝑒

𝐵

=

𝑀

𝐺𝑘𝑥

+ 𝑀

𝑄𝑘𝑥

+ 𝑀

𝐴𝑘𝑥

+ 𝑑

𝑓

∙ 𝐻

𝐺𝑘𝑦

+ 𝐻

𝑄𝑘𝑦

+ 𝐻

𝐴𝑘𝑦

𝑉

𝐺𝑘

+ 𝑉

𝑄𝑘

+ 𝑉

𝐴𝑘

+ 𝑉

𝐺𝑘𝐹

=

0 + 120 + 60 + 0,65 ∙ 0 + 25 + 20

1590 + 370 + 190 + 112,52

= 0,093𝑚

𝑒

𝐿

=

𝑀

𝐺𝑘𝑦

+ 𝑀

𝑄𝑘𝑦

+ 𝑀

𝐴𝑘𝑦

+ 𝑑

𝑓

∙ 𝐻

𝐺𝑘𝑥

+ 𝐻

𝑄𝑘𝑥

+ 𝐻

𝐴𝑘𝑥

− 𝑉

𝐺𝑘

+ 𝑉

𝑄𝑘

+ 𝑉

𝐴𝑘

∙ 𝑒

𝑥𝑠

𝑉

𝐺𝑘

+ 𝑉

𝑄𝑘

+ 𝑉

𝐺𝑘𝐹

=

150 + 100 + 30 + 0,65 ∙ 70 + 30 + 25 − 1590 + 370 + 190 ∙ 0,15

1590 + 370 + 190 + 112,52

= 0,017𝑚

𝑞

𝑚𝑎𝑥 /𝑚𝑖𝑛

=

𝑉

𝑘

𝐵 ∙ 𝐿

1 ±

6𝑒

𝐿

𝐿

±

6𝑒

𝐵

𝐵

𝑞

𝑚𝑎𝑥

=

1590 + 370 + 190 + 112,52

1,8 ∙ 3

1 +

6 ∙ 0,093

1,8

+

6 ∙ 0,017

3

= 562,5𝑘𝑃𝑎

𝑞

𝑚𝑖𝑛

=

1590 + 370 + 190 + 112,52

1,8 ∙ 3

1 −

6 ∙ 0,093

1,8

−

6 ∙ 0,017

3

= 275,47𝑘𝑃𝑎

𝑞

𝑚𝑎𝑥

𝑞

𝑚𝑖𝑛

= 2,04

0,093

1,8

+

0,017

3

= 0,057 < 0,166

2.4 Obliczenie B’ i L’
SCHEMAT I

𝐵

′

= 1,8 − 2 ∙ 0,092 = 1,617 𝑚

𝐿

′

= 3 − 2 ∙ 0,047 = 2,906𝑚

𝐴

′

= 𝐵

′

∙ 𝐿

′

= 4,7𝑚

2

SCHEMAT II

𝐵

′

= 1,8 − 2 ∙ 0,093 = 1,615𝑚

𝐿

′

= 3 − 2 ∙ 0,017 = 2,966 𝑚

𝐴

′

= 𝐵

′

∙ 𝐿

′

= 4,79𝑚

2

Ponieważ fundament dla obciążeo ze schematu pierwszego ma mniejsze wymiary, dalsze

obliczenia będą dotyczyły tego schematu

𝐵′

𝐿′

=

1,617
2,906

= 0,556

𝐿′

𝐵′

=

2,906
1,617

= 1,797

2.5 Współczynniki częściowe dla parametrów geotechnicznych:



Obliczenie współczynników uwzględniających nachylenie siły wypadkowej

działającej w podstawie fundamentu:

𝑚

𝐵

=

2 +

𝐵

′

𝐿

′

1 +

𝐵

′

𝐿

′

= 1,643

𝑚

𝐿

=

2 +

𝐿′

𝐵

′

1 +

𝐿

′

𝐵

′

= 1,358

𝑚 = 𝑚

𝜃

= 𝑚

𝐿

𝑐𝑜𝑠

2

𝜃 + 𝑚

𝐵

𝑠𝑖𝑛

2

𝜃

𝜃 = 𝑎𝑟𝑐𝑡𝑔

𝐻

𝑌

𝐻

𝑋

= 𝑎𝑟𝑐𝑡𝑔

30 + 20

70 + 65 + 15

= 𝑎𝑟𝑐𝑡𝑔0,333 = 18,44°

𝑚 = 𝑚

𝜃

= 1,358𝑐𝑜𝑠

2

18,44° + 1,643𝑠𝑖𝑛

2

18,44° = 1,386



Obliczenie współczynników nośności dla piasku średniego

𝜙

′

= 𝜙 + 2 = 32° + 2° = 34°

𝑁

𝑞

= 𝑒

𝜋𝑡𝑔 𝜙

′

𝑡𝑔

2

45° +

𝜙

′

2

= 29,440

𝑁

𝑐

= 𝑁

𝑞

− 1 𝑐𝑡𝑔𝜙

′

=42,164

𝑁

𝛾

= 2 𝑁

𝑞

− 1 𝑡𝑔𝜙

′

=38,366



Obliczenie współczynników kształtu

𝑠

𝑞

= 1 +

𝐵′

𝐿′

𝑠𝑖𝑛𝜙′ = 1,311

𝑠

𝑐

=

𝑠

𝑞

𝑁

𝑞

− 1

𝑁

𝑞

− 1

= 1,322

𝑠

𝛾

= 1 − 0,3

𝐵′

𝐿′

= 0,833



Obliczenie współczynników nachylenia podstawy

α=0°
𝑏

𝑞

= 𝑏

𝛾

= (1 − 𝛼𝑡𝑔𝜙

′

)

2

= 1

𝑏

𝑐

= 𝑏

𝑞

−

1 − 𝑏

𝑞

𝑁

𝑐

∙ 𝑡𝑔𝜙′

= 1



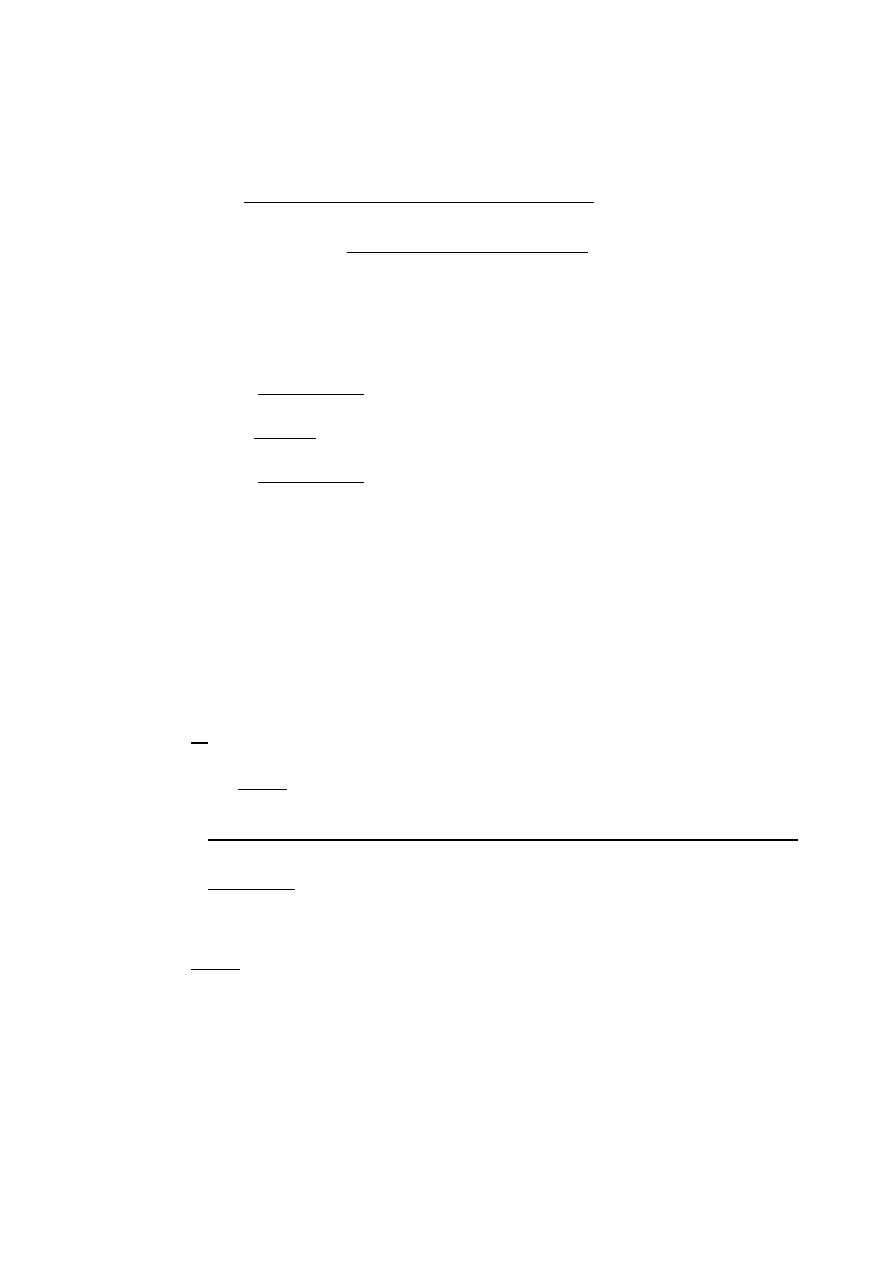
Obliczenie współczynników uwzględniających pochylenie siły wypadkowej
działającej w podstawie fundamentu

Siła wypadkowa H

k

:

𝐻

𝑘

= 𝐻

𝐺𝑘𝑥

+ 𝐻

𝑄𝑘𝑥

+ 𝐻

𝐴𝑘𝑥

2

+ 𝐻

𝐺𝑘𝑦

+ 𝐻

𝑄𝑘𝑦

+ 𝐻

𝐴𝑘𝑦

2

𝐻

𝑘

= 70 + 65 + 15

2

+ 0 + 30 + 20

2

= 158,11 𝑘𝑁

𝑉

𝑘

= 𝑉

𝐺𝑘

+ 𝑉

𝑄𝑘

+ +𝑉

𝐴𝑘

+ 𝑉

𝐺𝑘𝐹

𝑉

𝑘

= 1590 + 210 + 190 + 112,52 = 2102,5 𝑘𝑁

𝑖

𝑞

= (1 −

𝐻

𝑉

𝑘

+ 𝐴

′

𝑐

′

𝑐𝑡𝑔𝜙

′

)

𝑚

= 0,897

𝑖

𝑐

= 𝑖

𝑞

−

1 − 𝑖

𝑞

𝑁

𝑐

∙ 𝑡𝑔𝜙′

= 0894

𝑖

𝛾

= (1 −

𝐻

𝑉

𝑘

+ 𝐴

′

𝑐

′

𝑐𝑡𝑔𝜙

′

)

𝑚+1

= 0,830

Obciążenie obok fundamentu:

𝑞

′

= 0,25𝑚 ∗ 23 + 0,85 ∗ 18,5 = 21,475𝑘𝑃𝑎

2.6 Nośnośd obliczeniowa dla warunków gruntowych z odpływem.

𝑉

𝑑

= 𝑉

𝐺𝑘

∙ 𝛾

𝐺1

+ 𝑉

𝑄𝑘

∙ 𝛾

𝐺1

+ 𝑉

𝐴𝑘

∙ 𝛾

𝐺1

+ 𝑉

𝐺𝑘𝐹

= 1590 ∙ 1,35 + 210 ∙ 1,5 + 1,0 ∙ 190 + 112,52 ∙ 1,35 = 2803,4 𝑘𝑁

Nośnośd obliczeniowa:

𝑉

𝑑

𝐴

′

= 𝑞

′

𝑁

𝑞

𝑏

𝑞

𝑠

𝑞

𝑖

𝑞

+ 0,5𝛾

′

𝐵

′

𝑁

𝛾

𝑏

𝛾

𝑠

𝛾

𝑖

𝛾

𝑞

𝐸𝑑

=

2803,4

4,7

= 596,67 𝑘𝑃𝑎

<

21,475 ∙ 29,440 ∙ 1,0 ∙ 1,311 ∙ 0,897 + 0,5 ∙ 16,19 ∙ 1,617 ∙ 38,366 ∙ 1,0 ∙ 0,833 ∙ 0,83

1,4

=

1090,95𝑘𝑃𝑎

1,4

= 779,25

Wskaźnik wykorzystania nośności

596,67
779,25

∙ 100% = 76,57%

Warunek nośności został spełniony

3. Wymiarowanie stopy fundamentowej

3.1 Obciążenia

SCHAMAT 1

SCHEMAT 2

ODDZIAŁYWANIA

CHARAKTERYSTYCZNE

V

K

H

x;K

H

Y;K

M

X;K

M

Y;K

V

K

H

x;K

H

Y;K

M

X;K

M

Y;K

kN

kN

kN

kNm

kNm

kN

kN

kN

kNm

kNm

Stałe

G

1590

70

0

0

150

1590

70

0

0

150

Zmienne

Q

210

65

30

120

100

370

30

25

120

100

Wyjątkowe

A

190

15

20

40

50

190

25

20

60

30

RAZEM OBLICZENIOWE

2651,5

207

65

220

402,5

2891,5

164,5

57,5

240

382,5

𝑒

𝐵

=

𝑀

𝑑𝑥

+ 𝑑

𝑓

∙ 𝐻

𝑑𝑦

𝑉

𝑑

𝑒

𝐿

=

𝑀

𝑑𝑦

+ 𝑑

𝑓

∙ 𝐻

𝑑𝑥

− 𝑉

𝑑

∙ 𝑒

𝑥𝑠

𝑉

𝑑

Schemat I

𝑞

𝐸𝑑

=

2651,5

5,4

= 491,02 𝑘𝑃𝑎

Schemat II

𝑞

𝐸𝑑

=

2891,5

5,4

= 535,46 𝑘𝑃𝑎

Schemat I

𝑒

𝐵

=

220 + 0,65 ∙ 65

2651,5

= 0,10 𝑚

𝑒

𝐿

=

402,5 + 0,65 ∙ 207 − 2651,5 ∙ 0,15

2651,5

= 0,05 𝑚

𝑞

𝑑𝑚𝑎𝑥

= 𝑞

𝐸𝑑

1 +

6𝑒

𝐿

𝐿

+

6𝑒

𝐵

𝐵

= 491,02 1 +

6 ∙ 0,05

3

+

6 ∙ 0,1

1,8

= 704,5 𝑘𝑃𝑎

𝑞

𝑑𝑚𝑖𝑛

= 𝑞

𝐸𝑑

1 −

6𝑒

𝐿

𝐿

−

6𝑒

𝐵

𝐵

= 491,02 1 −

6 ∙ 0,05

3

−

6 ∙ 0,1

1,8

= 277,53 𝑘𝑃𝑎

𝑞

𝑑1

= 𝑞

𝐸𝑑

1 −

6𝑒

𝐿

𝐿

+

6𝑒

𝐵

𝐵

= 491,02 1 −

6 ∙ 0,05

3

+

6 ∙ 0,1

1,8

= 601,3 𝑘𝑃𝑎

𝑞

𝑑2

= 𝑞

𝐸𝑑

1 +

6𝑒

𝐿

𝐿

−

6𝑒

𝐵

𝐵

= 491,02 1 +

6 ∙ 0,05

3

+

6 ∙ 0,1

1,8

= 380,74 𝑘𝑃𝑎

𝑞

𝑑𝑚𝑎𝑥

𝑞

𝑑𝑚𝑖𝑛

=

704,5

277,53

= 2,54

Schemat II

𝑒

𝐵

=

240 + 0,65 ∙ 57,5

2891,5

= 0,1 𝑚

𝑒

𝐿

=

382,5 + 0,65 ∙ 164,5 − 2891,5 ∙ 0,15

2891,5

= 0,02 𝑚

𝑞

𝑑𝑚𝑎𝑥

= 𝑞

𝐸𝑑

1 +

6𝑒

𝐿

𝐿

+

6𝑒

𝐵

𝐵

= 535,46 1 +

6 ∙ 0,02

3

+

6 ∙ 0,1

1,8

= 727,31 𝑘𝑃𝑎

𝑞

𝑑𝑚𝑖𝑛

= 𝑞

𝐸𝑑

1 −

6𝑒

𝐿

𝐿

−

6𝑒

𝐵

𝐵

= 535,46 1 −

6 ∙ 0,02

3

−

6 ∙ 0,1

1,8

= 343,61 𝑘𝑃𝑎

𝑞

𝑑1

= 𝑞

𝐸𝑑

1 −

6𝑒

𝐿

𝐿

+

6𝑒

𝐵

𝐵

= 535,46 1 −

6 ∙ 0,02

3

+

6 ∙ 0,1

1,8

= 686,05 𝑘𝑃𝑎

𝑞

𝑑2

= 𝑞

𝐸𝑑

1 +

6𝑒

𝐿

𝐿

−

6𝑒

𝐵

𝐵

= 535,46 1 +

6 ∙ 0,02

3

−

6 ∙ 0,1

1,8

= 384,87 𝑘𝑃𝑎

𝑞

𝑑𝑚𝑎𝑥

𝑞

𝑑𝑚𝑖𝑛

=

727,31
343,61

= 2,12

Bardziej niekorzystny jest schemat II. Wykres naprężeo dla schematu II wygląda następująco:

3.2 Wyznaczenie momentów zginających dla maksymalnych naprężeo działających na

wspornik

Jako obciążenie wsporników przyjęto stałe naprężenie maksymalne 727,31 kPa

- wartośd momentu zginającego na kierunku L:

długośd wsporników stopy:

𝑠

𝐿𝐿

=

𝐿
2

+ 𝑒

𝑠

−

𝑙

𝑠

2

+ 0,15𝑙

𝑠

=

3
2

+ 0,15 −

0,45

2

+ 0,15 ∙ 0,45 = 1,493𝑚

𝑠

𝐿𝑃

=

𝐿
2

− 𝑒

𝑠

−

𝑙

𝑠

2

+ 0,15𝑙

𝑠

=

3
2

− 0,15 −

0,45

2

+ 0,15 ∙ 0,45 = 1,193 𝑚

𝑀

𝑑𝐿𝐿

= 𝐵 ∙ 0,5 ∙ 𝑞

𝑚𝑎𝑥

∙ 𝑠

𝐿𝐿

2

= 1,8 ∙ 0,5 ∙ 727,31 ∙ 1,493

2

= 1458,1 𝑘𝑁𝑚

- wartośd momentu zginającego na kierunku B:

𝑠

𝐵𝐿

= 𝑠

𝐵𝑃

=

𝐵

2

−

𝑏

𝑠

2

+ 0,15𝑏

𝑠

=

1,8

2

−

0,35

2

+ 0,15 ∙ 0,35 = 0,778𝑚

𝑀

𝑑𝐵𝐿

= 𝐿 ∙ 0,5 ∙ 𝑞

𝑚𝑎𝑥

∙ 𝑠

𝐵𝐿

2

= 3 ∙ 0,5 ∙ 727,31 ∙ 0,778

2

= 659,5 𝑘𝑁𝑚

3.3 Wyznaczenie momentów zginających dla średnich naprężeo działających na wspornik

- na kierunku L:

𝑞

𝑎

=

727,31 + 686,05

2

= 706,68𝑘𝑃𝑎

𝑞

𝑏

=

343,61 + 384,87

2

= 364,24𝑘𝑃𝑎

𝑞

𝐼

= 706,68 −

706,68 − 364,24

3

∙ 1,493 = 536,32 𝑘𝑃𝑎

𝑞′

𝐼

= 364,24 +

706,68 − 364,24

3

∙ 1,193 = 500,36 𝑘𝑃𝑎

𝑀

𝑑𝐿

= 𝐵 ∙ 0,5 ∙ 𝑞

𝐼

∙ 𝑠

𝐿𝐿

2

= 1,8 ∙ 0,5 ∙ 536,32 ∙ 1,493

2

= 1075,2𝑘𝑁𝑚

- na kierunku B:

𝑞

𝑎

=

343,61 + 686,05

2

= 514,83 𝑘𝑃𝑎

𝑞

𝑏

=

727,31 + 384,87

2

= 556,09 𝑘𝑃𝑎

𝑞

𝐼𝐼

= 556,09 −

556,09 − 514,83

1,8

∙ 0,778 = 538,27 𝑘𝑃𝑎

𝑀

𝑑𝐵

= 𝐿 ∙ 0,5 ∙ 𝑞

𝐼𝐼

∙ 𝑠

𝐵𝐿

2

= 3 ∙ 0,5 ∙ 538,27 ∙ 0,778

2

= 488,08 𝑘𝑁𝑚

3.4 Wyznaczenie powierzchni zbrojenia dla średnich naprężeo działających na wspornik

Beton C 30/37, f

ctd

=1,4 MPa , f

cd

=21,4 MPa

Stal gatunek B500SP f

yd

=435 MPa

Otulina c=5 cm

Wstępnie przyjęto pręty o średnicy 20 mm

Przyjęto otulinę prętów zbrojenia stopy 50 mm oraz zbrojenie

𝑑

𝐿

= 0,65 − 0,05 − 0,5 ∙ 0,02 = 0,59 𝑚

𝐴

𝑠

=

𝑀

𝑓

𝑦𝑑

∙ 0,9 ∙ 𝑑

𝐿

- powierzchnia zbrojenia na kierunku L:

𝐴

𝑠

=

1075 ,2

435000 ∙0,9∙0,59

= 46,55𝑐𝑚

2

𝐴

𝑠,𝑚𝑖𝑛

= 0,0013 ∙ 𝐵 ∙ 𝑑 = 0,0013 ∙ 180 ∙ 65 = 15,21𝑐𝑚

2

𝐴

𝜙20

=

𝜋2

2

4

= 3,14𝑐𝑚

2

𝐴

𝑠

𝐴

𝜙20

=

46,55

3,14

= 14,82

Przyjęto 15 pręty φ20 o łącznej powierzchni 47,12cm

2

- powierzchnia zbrojenia dla kierunku B:

𝑑

𝐵

= 0,65 − 0,05— 0,02 − 0,5 ∙ 0,012 = 0,574 𝑚

𝐴

𝑠

=

488,08

435000 ∙ 0,9 ∙ 0,574

= 21,72 𝑐𝑚

2

𝐴

𝑠,𝑚𝑖𝑛

= 0,0013 ∙ 𝐿 ∙ 𝑑 = 0,0013 ∙ 300 ∙ 65 = 25,35 𝑐𝑚

2

𝐴

𝜙12

=

𝜋1,2

2

4

= 1,13𝑐𝑚

2

𝐴

𝑠

𝐴

𝜙 12

=

25,35

1,13

= 22,414

Przyjęto 23 prętów φ12 o łącznej powierzchni 26,01cm

2

- rozmieszczenie zbrojenia

Zbrojenie na kierunku L

l

s

/L = 0,45/3= 0,15

Pasmo środkowe o szerokości 0,5B = 0,9 m

0,626𝐴

𝑠

= 0,626 ∙ 47,12 = 29,5 𝑐𝑚

2

9 Ф20 co 11 cm = 28,3 cm

2

Dwa pasma skrajne o szerokości 0,25B = 0,45 m

0,187𝐴

𝑠

= 0,187 ∙ 58,5 = 8,81 𝑐𝑚

2

3 Ф20 co 13 cm = 9,42 cm

2

Zbrojenie na kierunku B

b

s

/B = 0,35/1,8= 0,194

Pasmo środkowe o szerokości 0,5L = 1,5 m
0626𝐴

𝑠

= 0,626 ∙ 26,01 = 16,28 𝑐𝑚

2

15 Ф12 co 11cm = 16,97 cm

2

Dwa pasma skrajne o szerokości 0,25L = 0,75 m
0,187𝐴

𝑠

= 0,167 ∙ 33,06 = 4,86 𝑐𝑚

2

4Ф12 co 17 cm = 4,52cm

2

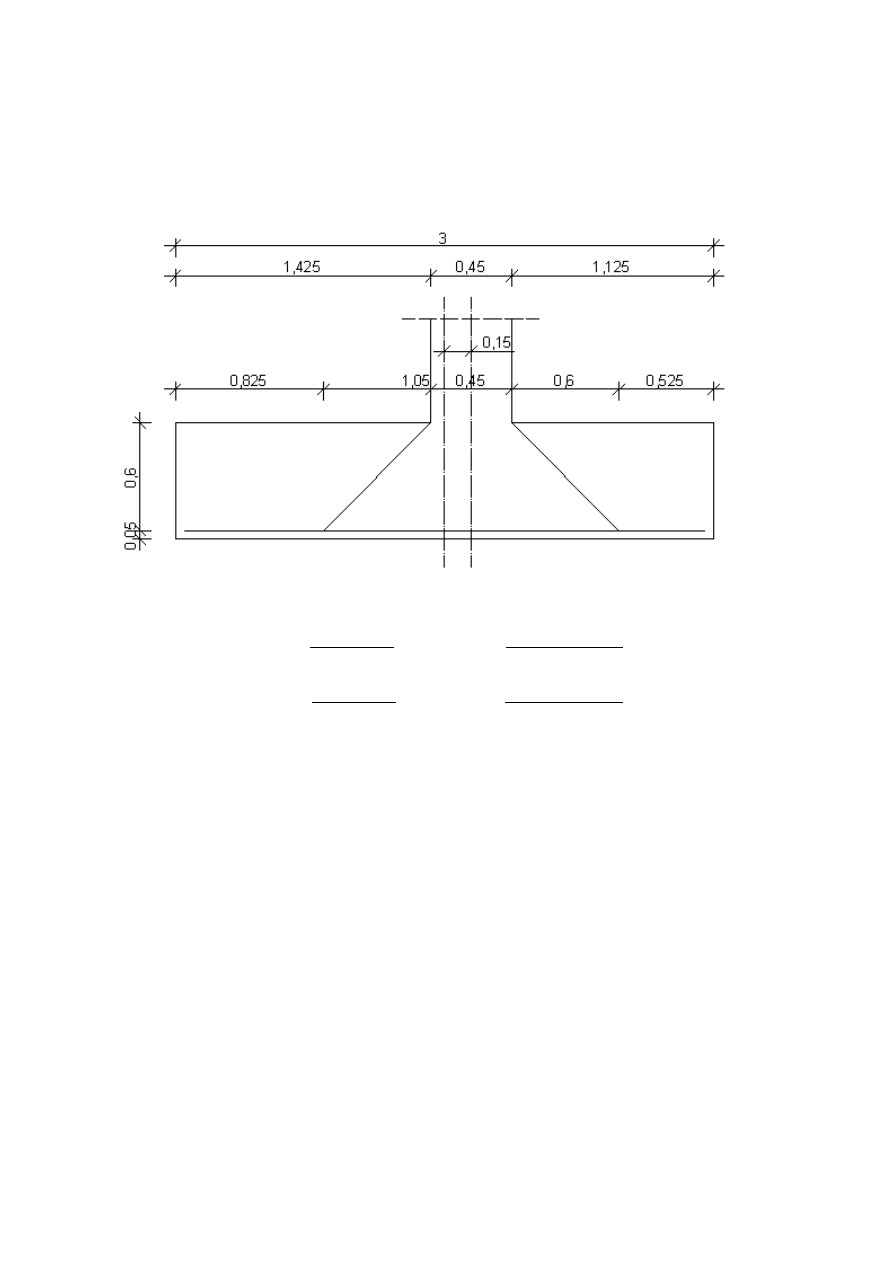
4. Sprawdzenie stopy fundamentowej na przebicie

Sprawdzenie przebicia na kierunku L

𝑞

𝐸𝑑𝐿

= 𝑞

𝐸𝑑𝑎

−

𝑞

𝐸𝑑𝑎

− 𝑞

𝐸𝑑𝑏

𝐿

𝑐

𝐿

= 706,68 −

706,68 − 364,24

3

0,825 = 612,51 𝑘𝑃𝑎

𝑞

𝐸𝑑𝑃

= 𝑞

𝐸𝑑𝑎

−

𝑞

𝐸𝑑𝑎

− 𝑞

𝐸𝑑𝑏

𝐿

𝑐

𝑃

= 706,68 −

706,68 − 364,24

3

0,525 = 646,76 𝑘𝑃𝑎

Siła przebijająca na odcinku prawej odsadzki

𝑃

𝑃

= 0,5 𝑞

𝐸𝑑𝑏

+ 𝑞

𝐸𝑑𝑃

𝑐

𝑝

∙ 𝐵 = 0,5 ∙ 364,24 + 646,76 ∙ 0,525 ∙ 1,8 = 477,7 𝑘𝑁

Siła przebijająca na odcinku lewej odsadzki

𝑃

𝐿

= 0,5 𝑞

𝐸𝑑𝑎

+ 𝑞

𝐸𝑑𝐿

𝑐

𝐿

∙ 𝐵 = 0,5 ∙ 706,68 + 612,51 ∙ 0,825 ∙ 1,8 = 979,5 𝑘𝑁

𝑃 = 𝑓

𝑐𝑡𝑑

∙ 𝐵 ∙ 𝑑 = 𝑓

𝑐𝑡𝑑

∙ 𝐵 ∙ tan 45° ∙ 𝑑

𝐵

= 1400 ∙ 1,8 ∙ tan 45° ∙ 0,574 = 1446,5 𝑘𝑁

𝑷

𝑷

≤ 𝑷 - przebicie nie wystąpi.

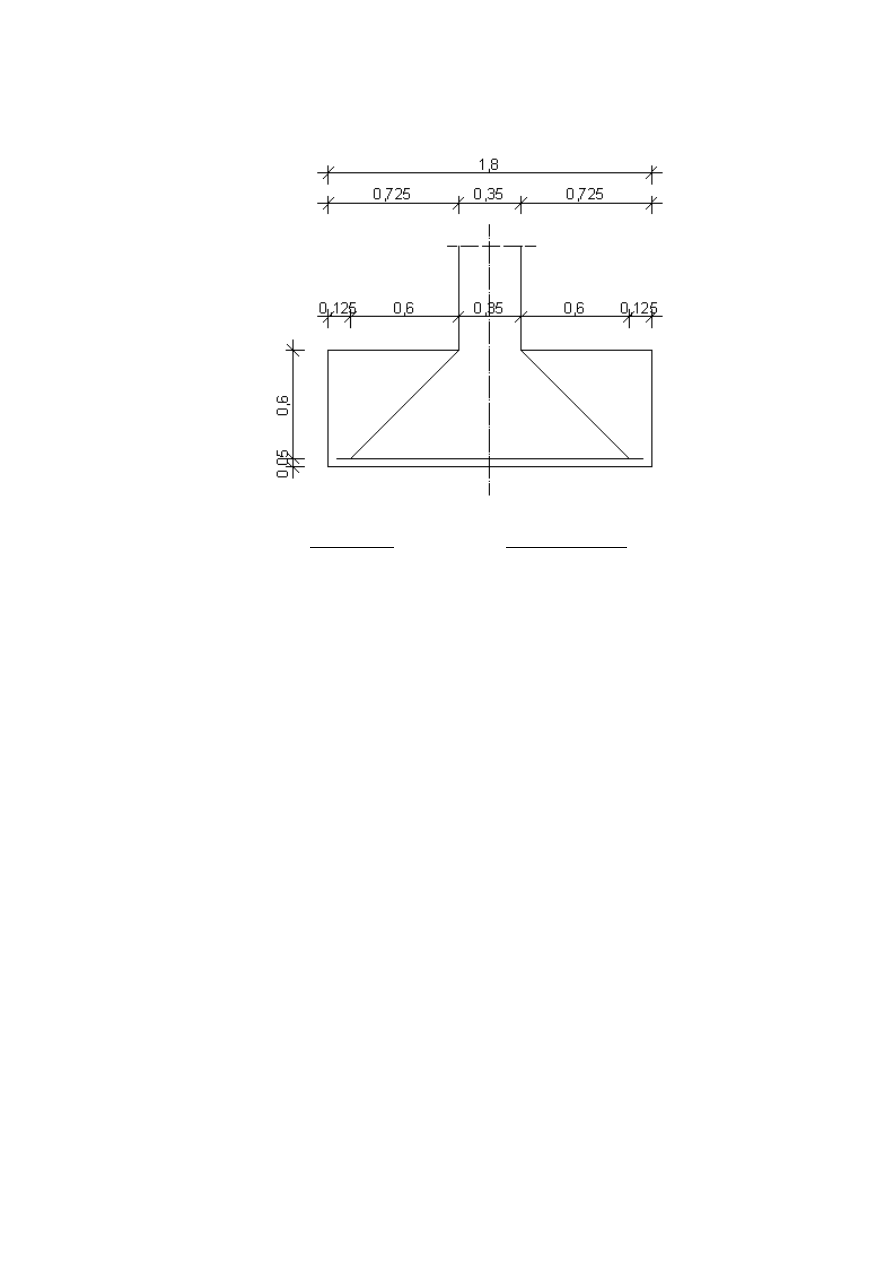
Sprawdzenie przebicia na kierunku B

𝑞

𝐸𝑑𝐿

= 𝑞

𝐸𝑑𝑎

−

𝑞

𝐸𝑑𝑎

− 𝑞

𝐸𝑑𝑏

𝐵

𝑐

𝐿

= 556,09 −

556,09 − 514,83

1,8

0,125 = 553,23 𝑘𝑃𝑎

Siła przebijająca na odcinku lewej odsadzki

𝑃

𝐿

= 0,5 𝑞

𝐸𝑑𝑎

+ 𝑞

𝐸𝑑𝐿

𝑐

𝐿

∙ 𝐿 = 0,5 ∙ 556,09 + 553,23 ∙ 0,125 ∙ 3 = 208 𝑘𝑁

Wytrzymałośd betonu na przebicie z jednej strony fundamentu

𝑃 = 𝑓

𝑐𝑡𝑑

∙ 𝐿 ∙ 𝑑 = 𝑓

𝑐𝑡𝑑

∙ 𝐿 ∙ tan 45° ∙ 𝑑

𝐵

= 1400 ∙ 3 ∙ tan 45° ∙ 0,574 = 2410,8𝑘𝑁

𝑷

𝑷

≤ 𝑷 - przebicie nie wystąpi.