
SPECIAL FUNCTIONS and POLYNOMIALS
Gerard ’t Hooft
Stefan Nobbenhuis
Institute for Theoretical Physics
Utrecht University, Leuvenlaan 4
3584 CC Utrecht, the Netherlands
and
Spinoza Institute
Postbox 80.195
3508 TD Utrecht, the Netherlands
Many of the special functions and polynomials are constructed along standard
procedures In this short survey we list the most essential ones.
October 4, 2005
1
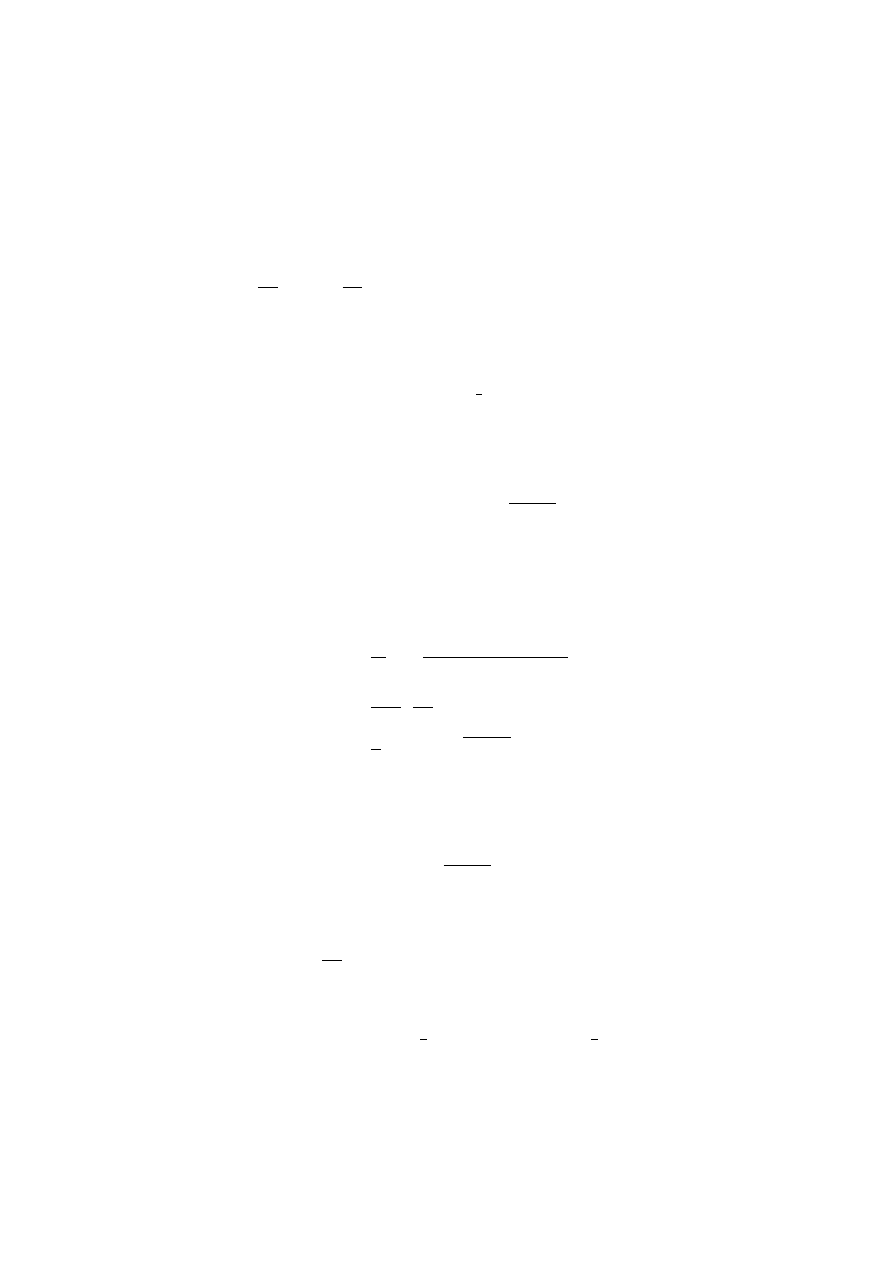
1
Legendre Polynomials P
`
(x) .
Differential Equation:
(1 − x
2
) P
`
00
(x) − 2x P
`
0
(x) + `(` + 1) P
`
(x)
=
0 ,
or
d
dx
(1 − x
2
)
d
dx
P
`
(x) + `(` + 1) P
`
(x)
=
0 .
(1.1)
Generating function:
∞
X
`=0
P
`
(x)t
`
= (1 − 2xt + t
2
)
−
1
2
for
|t| < 1, |x| ≤ 1.
(1.2)
Orthonormality:
Z
1
-1
P
`
(x) P
`
0
(x) dx =
2
2` + 1
δ
` `
0
,
(1.3)
∞
X
`=0
P
`
(x)P
`
(x
0
)(2` + 1) = 2δ(x − x
0
) .
(1.4)
Expressions forP
`
(x) :
P
`
(x) =
1
2
`
[`/2]
X
ν=0
(−1)
ν
(2` − 2ν)!
ν! (` − ν)! (` − 2ν)!
x
`−2ν
(1.5)
=
1
`! 2
`
d
dx
`
(x
2
− 1)
`
,
(1.6)
=
1
π
Z
π
0
(x +
√
x
2
− 1 cos ϕ)
`
dϕ .
(1.7)
Recurrence relations:
` P
`−1
− (2` + 1) x P
`
+ (` + 1) P
`+1
= 0 ;
P
`
= x P
`−1
+
x
2
− 1
`
P
0
`−1
;
xP
0
`
− ` P
`
= P
0
`−1
;
xP
0
`
+ (` + 1) P
`
= P
0
`+1
;
d
dx
[P
`+1
− P
`−1
] = (2` + 1) P
`
.
(1.8)
Examples:
P
0
= 1 ,
P
1
= x ,
P
2
=
1
2
(3x
2
− 1) ,
P
3
=
1
2
x(5x
2
− 3) .
(1.9)
1
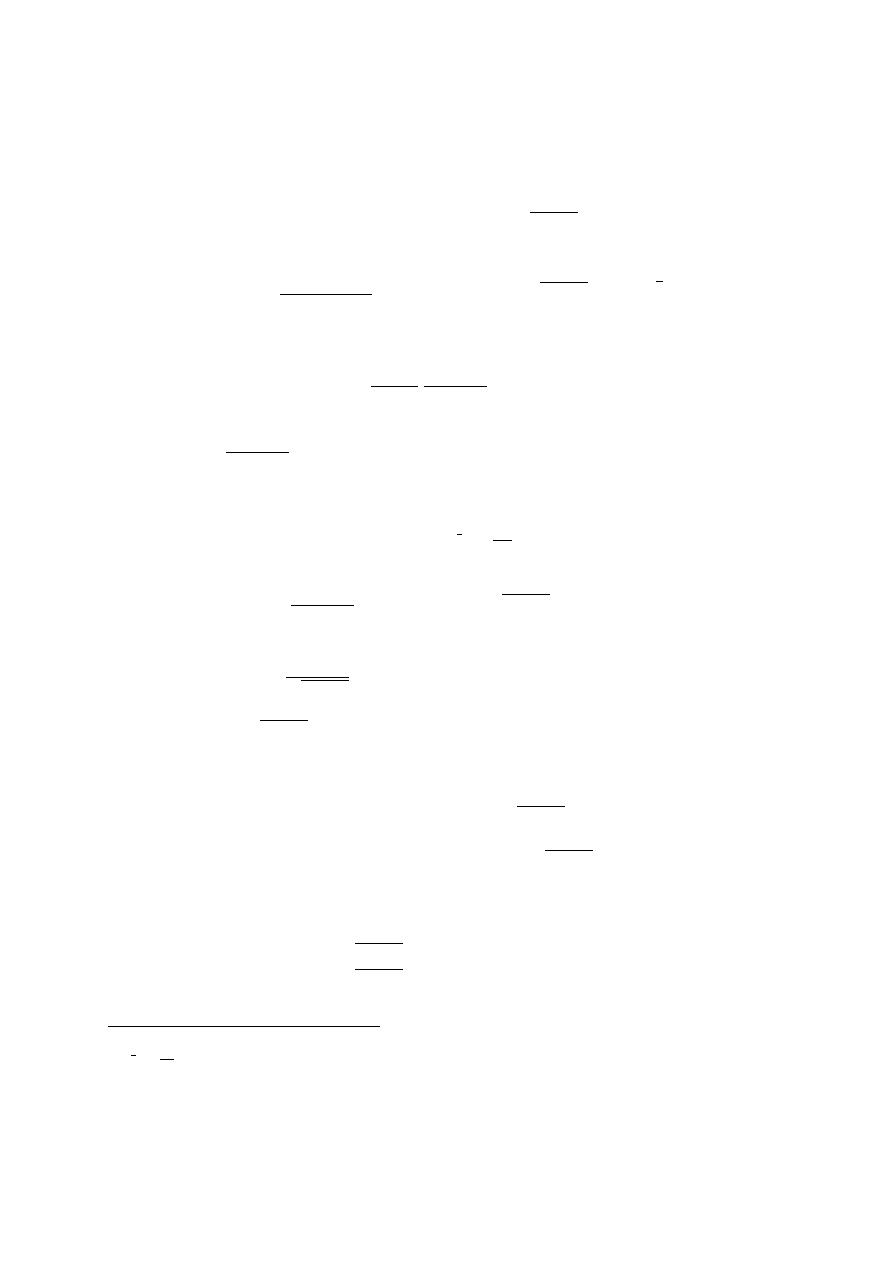
2
Associated Legendre Functions P
m
`
(x) .
Differential equation:
(1 − x
2
) P
m
`
(x)
00
− 2x P
m
`
(x)
0
+
`(` + 1) −
m
2
1 − x
2
P
m
`
(x) = 0 .
(2.1)
Generating function:
∞
X
`=0
`
X
m=0
P
m
`
(x) z
m
y
`
m!
=
h
1 − 2y
x + z
√
1 − x
2
+ y
2
i
−
1
2
.
(2.2)
Orthogonality:
Z
1
-1
P
m
`
(x) P
m
`
0
(x) dx =
2
2` + 1
(` + m)!
(` − m)!
δ
` `
0
,
( `, `
0
≥ m ) .
(2.3)
∞
X
`=m
(2` + 1)
(` − m)!
(` + m)!
P
m
`
(x) P
m
`
(x
0
) = 2δ(x − x
0
) ,
( |x| < 1 and |x
0
| < 1 ) .
(2.4)
Expressions for P
m
`
(x)
1
:
P
m
`
(x) = (1 − x
2
)
1
2
m
d
dx
!
m
P
`
(x) .
(2.5)
P
m
`
(x) =
(` + m)!
`! π
(−1)
m/2
Z
π
0
x +
√
x
2
− 1 cos ϕ
`
cos mϕ dϕ .
(2.6)
Recurrence relations:
P
m+1
`
−
2mx
√
1 − x
2
P
m
`
+ {`(` + 1) − m(m − 1)}P
m−1
`
= 0
(2.7)
√
1 − x
2
P
m+1
`
(x) = (1 − x
2
) P
m
`
(x)
0
+ mx P
m
`
(x) ,
(2` + 1)x P
m
`
= (` + m) P
m
`−1
+ (` + 1 − m) P
m
`+1
,
(2.8)
x P
m
`
= P
m
`−1
− (` + 1 − m)
√
1 − x
2
P
m−1
`
,
P
m
`+1
− P
m
`−1
= (2` + 1) P
m−1
`
√
1 − x
2
,
(2.9)
and various others.
Examples:
P
1
1
=
√
1 − x
2
,
P
2
2
= 3(1 − x
2
) ,
P
1
2
= 3x
√
1 − x
2
,
P
2
3
= 15 x(1 − x
2
) .
(2.10)
1
Note that some authors define P
m
`
(x) with a factor (−1)
m
, giving P
m
`
(x) = (−1)
m
(1 −
x
2
)
1
2
m
d
dx
m
P
`
(x) . Obviously this minus sign propagates to the generating function, the recurrence
relations and the explicit examples, when m is odd.
2

3
Bessel J
n
(x) and Hankel H
n
(x) functions.
Differential equation (for both J
n
and H
n
):
x
2
J
00
n
(x) + x J
0
n
(x) + (x
2
− n
2
) J
n
(x) = 0 .
(3.1)
Generating function (if n integer):
∞
X
n=−∞
J
n
(αx)
s
α
n
= e
x
2
(s −
α
2
s
)
,
(3.2)
J
−n
= (−1)
n
J
n
.
Orthogonality:
Z
∞
0
ξ J
n
(αξ) J
n
(βξ) dξ =
1
α
δ(|α| − |β|) .
(3.3)
Z
a
0
ξ J
n
(αξ) J
n
(βξ) dξ =
a
2
2
{J
n+1
(αa)}
2
δ
αβ
.
(3.4)
if in the 2
nd
relation α, β are roots of the equation J
n
(αξ) = 0.
Expressions for J
n
(x) (for n integer):
J
n
(x) =
∞
X
k=0
(−1)
k
k! (k + n)!
x
2
n+2k
=
1
2πi
x
2
n
I
t
−n−1
dt e
t−x
2
/4t
.
(3.5)
J
n
(x) =
1
π
Z
π
0
cos (nθ − x sin θ) dθ .
(3.6)
Recurrence relations (for both J
n
and H
n
):
d
dx
{x
n
J
n
(x)} = x
n
J
n−1
(x) ;
J
n−1
(x) + J
n+1
(x) =
2n
x
J
n
(x) ;
J
0
n
(x)
=
J
n−1
(x) −
n
x
J
n
(x) =
n
x
J
n
(x) − J
n+1
(x) =
1
2
(J
n−1
(x) − J
n+1
(x)) .(3.7)
Relations between Hankel and Bessel functions:
H
(1)
n
(x) =
i
sin nπ
e
−nπi
J
n
(x) − J
−n
(x)
;
H
(2)
n
(x) =
−i
sin nπ
e
nπi
J
n
(x) − J
−n
(x)
,
(3.8)
so that
J
n
(x) =
1
2
H
(1)
n
(x) + H
(2)
n
(x)
;
J
−n
(x) =
1
2
e
nπi
H
(1)
n
(x) + e
−nπi
H
(2)
n
(x)
.
(3.9)
3

4
Spherical Bessel Functions j
`
(x).
Differential equation:
(xj
`
)
00
+
x −
`(` + 1)
x
j
`
= 0 .
(4.1)
Generating Function:
∞
X
`=0
j
`
(x) t
`
`!
= j
0
√
x
2
− 2xt
.
(4.2)
Orthogonality:
Z
∞
0
x
2
j
`
(αx) j
`
(βx) dx =
π
2α
δ(α − β) .
(4.3)
Z
∞
−∞
j
`
(x) j
`
0
(x) dx =
π
2` + 1
δ
``
0
.
(4.4)
Expressions for j
`
:
j
`
(x) =
r
π
2x
J
`+
1
2
(x) = (−1)
`
x
`
d
xdx
!
`
sin x
x
,
(4.5)
j
`
(x) =
x
`
2
`+1
`!
Z
1
−1
e
ixs
(1 − s
2
)
`
ds
=
2
`
`!
(2` + 1)!
x
`
1 −
1
1! (` +
3
2
)
x
2
2
+
1
2!(` +
3
2
)(` +
5
2
)
x
2
4
− . . .
. (4.6)
Recurrence relations:
j
`+1
=
`
x
j
`
− j
0
`
=
2` + 1
x
j
`
− j
`−1
.
(4.7)
Examples:
j
0
(x) =
sin x
x
;
j
1
(x) =
sin x
x
2
−
cos x
x
;
j
2
(x) =
3 sin x
x
3
−
3 cos x
x
2
−
sin x
x
.
(4.8)
4

5
Hermite Polynomials H
n
(x).
Differential equation:
H
00
n
(x) − 2x H
0
n
(x) + 2n H
n
(x) = 0 ,
or
d
2
dx
2
H
n
(x) e
−
1
2
x
2
+ (2n − x
2
+ 1) H
n
(x) e
−
1
2
x
2
= 0 .
(5.1)
Generating function:
∞
X
n=0
H
n
(x) s
n
/n! = e
−s
2
+2sx
.
(5.2)
Orthogonality:
Z
∞
−∞
H
n
(x) H
m
(x) e
−x
2
dx = 2
n
n!
√
π δ
nm
(5.3)
∞
X
n=0
H
n
(x) H
n
(y)/(2
n
n!) =
√
π δ(x − y) e
x
2
.
(5.4)
More general:
∞
X
n=0
H
n
(x) H
n
(y) s
n
/(2
n
n!) =
1
√
1 − s
2
exp
−s
2
(x
2
+ y
2
) + 2sxy
1 − s
2
.
(5.5)
Expressions for H
n
:
H
n
(−x) = (−1)
n
H
n
(x);
(5.6)
H
n
(x) = (−1)
n
e
x
2
d
dx
n
e
−x
2
;
(5.7)
H
n
(x) = (−1)
n/2
n!
n/2
X
k=0
(−1)
k
(2x)
2k
(2k)! (
1
2
n − k)!
,
if n even,
H
n
(x) = ( − 1)
n−1
2
n!
n−1
2
X
k=0
(−1)
k
(2x)
2k+1
(2k + 1)!
n−1
2
− k
!
,
if n odd.
(5.8)
Recurrence relations:
d
m
H
n
(x)
dx
m
=
2
m
n!
(n − m)!
H
n−1
(x) ,
(5.9)
x H
n
(x) =
1
2
H
n+1
(x) + n H
n−1
(x) ,
(5.10)
H
n
(x) =
2x −
d
dx
H
n−1
(x) .
(5.11)
Examples:
H
0
(x) = 1 ,
H
1
(x) = 2x ,
H
2
(x) = 4x
2
− 2 .
(5.12)
5

6
Laguerre Polynomials L
n
(x).
Differential equation:
x L
00
n
(x) + (1 − x) L
0
n
(x) + n L
n
(x) = 0 .
(6.1)
Generating function:
2
∞
X
n=0
L
n
(x) z
n
=
1
1 − z
e
−xz
1−z
.
(6.2)
Orthogonality:
Z
∞
0
L
n
(x) L
m
(x) e
−x
dx = δ
nm
.
(6.3)
Expressions for L
n
:
L
n
(x) =
e
x
n!
d
dx
n
(x
n
e
−x
)
=
(−1)
n
n!
x
n
−
n
2
1!
x
n−1
+
n
2
(n − 1)
2
2!
x
n−2
− . . . + (−1)
n
n!
.
(6.4)
Recurrence relation:
(1 + 2n − x) L
n
− n L
n−1
− (n + 1)L
n+1
= 0 ;
x L
0
n
(x) = n L
n
(x) − n L
n−1
(x) .
(6.5)
Examples:
L
0
(x) = 1 ;
L
1
(x) = 1 − x ;
L
2
(x) =
1
2!
(x
2
− 4x + 2).
(6.6)
2
It’s important to note that sometimes different definitions are used for the Laguerre and Associated
Laguerre polynomials, where the Generating Function has the form:
P
∞
n=0
L
n
(x) z
n
/n! =
1
1−z
e
−xz
1−z
. In
this case the Expressions given for L
n
should be multiplied by n! .
6
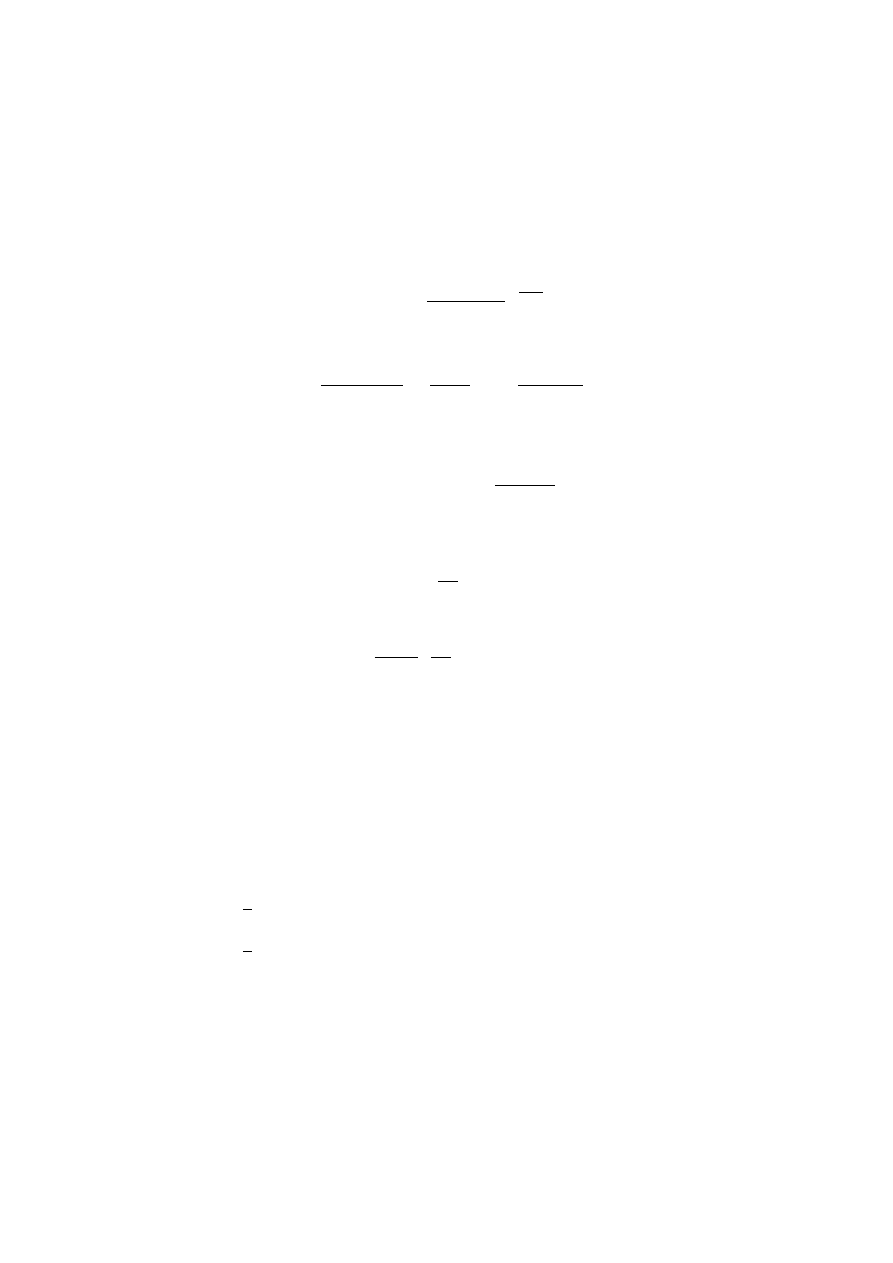
7
Associated Laguerre Polynomials L
k
n
(x) .
Differential equation:
x L
k
n
00
+ (k + 1 − x) L
k
n
0
+ n L
k
n
= 0 .
(7.1)
Generating function:
∞
X
n=0
L
k
n
(x) z
n
=
1
(1 − z)
k+1
e
−xz
1−z
.
(7.2)
∞
X
k=0
∞
X
n=k
L
k
n
(x) z
n
u
k
k!
=
1
1 − z
exp
−xz + u
1 − z
.
(7.3)
Orthogonality:
Z
∞
0
L
k
n
(x) L
k
m
(x) x
k
e
−x
dx =
(n + k)!
n!
δ
nm
.
(7.4)
Expressions for L
k
n
:
L
k
n
(x) = (−1)
k
d
dx
k
L
n+k
(x) .
(7.5)
L
k
n
(x) =
e
x
x
−k
n!
d
dx
n
(x
n+k
e
−x
) .
(7.6)
Recurrence relation:
L
k
n−1
(x) + L
k−1
n
(x) = L
k
n
(x) ;
x L
k
0
n
(x) = n L
k
n
(x) − (n + k)L
k
n−1
(x) .
(7.7)
Examples:
L
k
0
(x) = 1 ;
L
k
1
(x) = −x + k + 1 ;
L
k
2
(x) =
1
2
h
x
2
− 2(k + 2)x + (k + 1)(k + 2)
i
;
L
k
3
(x) =
1
6
h
−x
3
+ 3(k + 3)x
2
− 3(k + 2)(k + 3)x + (k + 1)(k + 2)(k + 3)
i
. (7.8)
7

8
Tschebyscheff
3
Polynomials T
n
(x).
Differential equation:
(1 − x
2
)
d
2
dx
2
T
n
(x) − x
d
dx
T
n
(x) + n
2
T
n
(x) = 0 .
(8.1)
Generating function:
∞
X
n=0
T
n
(x) y
n
=
1 − xy
1 − 2xy + y
2
.
(8.2)
Symmetry relation:
T
n
(x) = T
−n
(x).
(8.3)
Orthogonality:
Z
1
−1
T
m
(x)T
n
(x)
√
1 − x
2
dx =
(
1
2
πδ
nm
m, n 6= 0
π
m = n = 0
(8.4)
Expression for T
n
:
T
n
(x) = cos(n cos
−1
x)
(8.5)
T
n
(x) =
1
2
hn
x + i
√
1 − x
2
o
n
+
n
x − i
√
1 − x
2
o
n
i
.
(8.6)
Recurrence relation:
T
n+1
− 2x T
n
(x) + T
n−1
= 0
(8.7)
(1 − x
2
)T
0
n
(x) = −nx T
n
(x) + n T
n−1
(x).
(8.8)
Examples:
T
0
(x) = 1 ;
T
1
(x) = x ;
T
2
(x) = 2x
2
− 1 ;
T
3
(x) = 4x
3
− 3x.
(8.9)
3
Transliterations Chebyshev and Tchebicheff also occur.
8
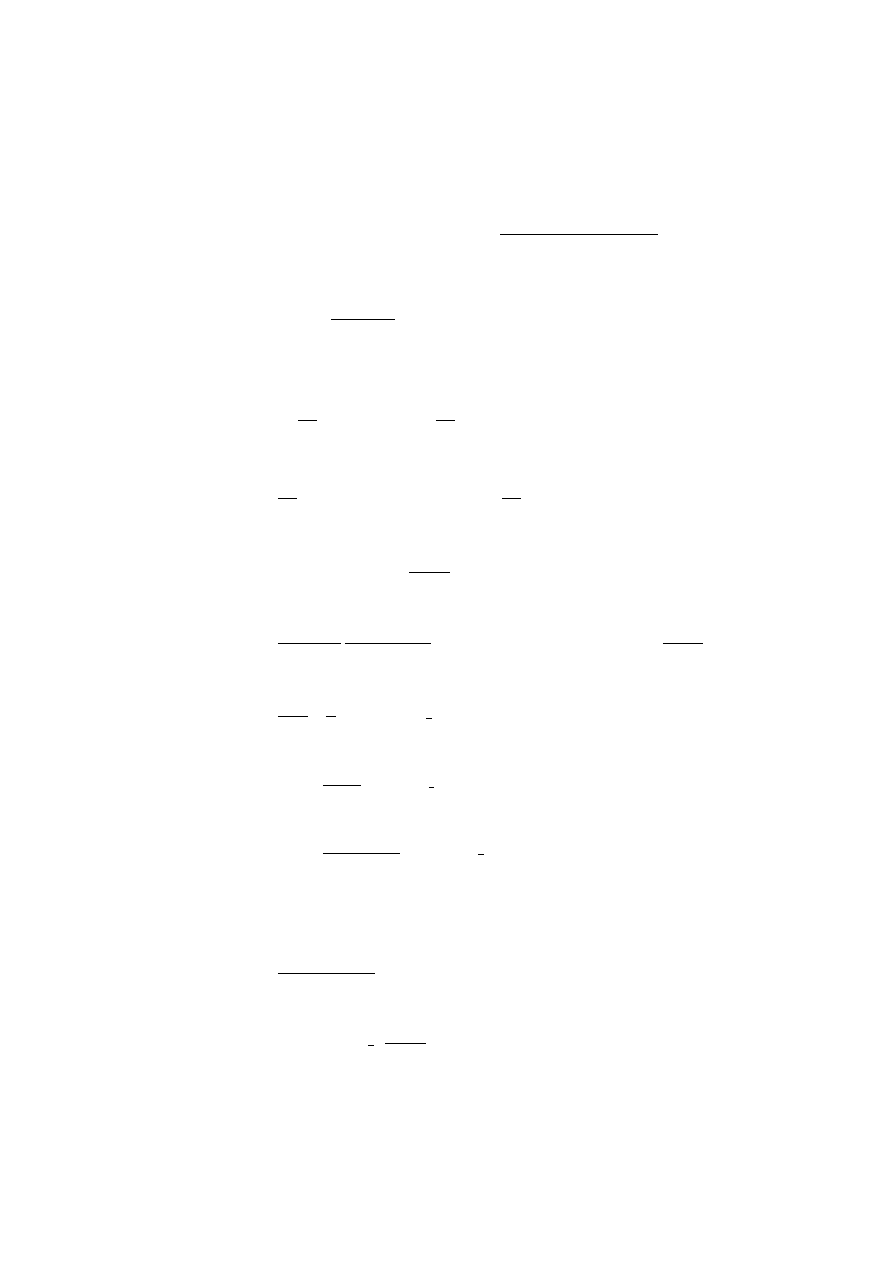
9
Remark.
All of the functions discussed here are special cases of “hypergeometric functions”
m
F
n
(a
1
, a
2
, . . . a
m
; b
1
, b
2
, . . . b
n
; z) defined by:
m
F
n
(a
1
, a
2
, . . . a
m
; b
1
, b
2
, . . . b
n
; z) =
∞
X
r=p
(a
1
)
r
(a
2
)
r
. . . (a
m
)
r
z
r
(b
1
)
r
(b
2
)
r
. . . (b
n
)
r
r!
,
(9.1)
where
(a)
r
≡
Γ(a + r)
Γ(a)
;
r a positive integer.
(9.2)
Differential equations:
m = n = 1:
z
d
dz
2
1
F
1
+ (b − z)
d
dz
1
F
1
− a
1
F
1
= 0 .
(9.3)
m = 2, n = 1:
z(1 − z)
d
dz
2
2
F
1
+
c − (a + b + 1)z
d
dz
2
F
1
− ab
2
F
1
= 0 .
(9.4)
We have:
P
`
(x) =
2
F
1
−`, ` + 1; 1;
1 − x
2
;
(9.5)
P
m
`
(x) =
(` + m)!
(` − m)!
(1 − x
2
)
m/2
2
m
m!
2
F
1
m − `, m + ` + 1; m + 1;
1 − x
2
;
(9.6)
J
n
(x) =
e
−ix
n!
x
2
n
1
F
1
(n +
1
2
; 2n + 1; 2ix) ;
(9.7)
H
2n
(x) = (−1)
n
(2n)!
n!
1
F
1
(−n;
1
2
; x
2
) ;
(9.8)
H
2n+1
(x) = (−1)
n
2(2n + 1)!
n!
x
1
F
1
(−n;
3
2
; x
2
) ;
(9.9)
L
n
(x) =
1
F
1
(−n; 1; x) ;
(9.10)
L
k
n
(x) =
Γ(n + k + 1)
n!Γ(k + 1)
1
F
1
(−n; k + 1; x) ;
(9.11)
T
n
(x) =
2
F
1
−n, n;
1
2
;
1 − x
2
.
(9.12)
9

References
[1] H. Margenau and G.M. Murphy, The Mathematics of Physics and Chemistry, D. van
Nostrand Comp. Inc., 1943, 1956.
[2] I.S. Gradshteyn and I.W. Ryzhik, Tables of Integrals, Series and Products, Acad.
Press, New York, San Francisco, London, 1965.
[3] W.W. Bell, Special Functions for Scientists and Engineers, D. van Nostrand Comp.
Ltd., 1968.
10
Wyszukiwarka
Podobne podstrony:
L 3 Complex functions and Polynomials
L 3 Complex functions and Polynomials
MEDC17 Special Function Manual
Euler’s function and Euler’s Theorem
Collagens structure, function, and biosynthesis
augocm h8 truck scanner function and model list
MEDC17 Special Function Manual
Euler’s function and Euler’s Theorem
Betcke T OPTIMAL SCALING OF GENERALIZED AND POLYNOMIAL EIGENVALUE PROBLEMS
NSA DIA Special Missile and Astronautics Center
Different Worlds Unacknowledged Special Operations and Covert Action
The Relationship Between Personality Organization, Reflective Functioning and Psychiatric Classifica
Fortenbaugh; Aristotle s Analysis of Friendship Function and Analogy, Resemblance and Focal Meaning
Functional and Computational Assessment of Missense Variants in the Ataxia Telangiectasia Mutated (A
Enteric infections, diarrhea and their impact on function and development
Functional Origins of Religious Concepts Ontological and Strategic Selection in Evolved Minds
więcej podobnych podstron