Combustion, Explosion, and Shock Waves, Vol. 37, No. 6, pp. 655–663, 2001

Numerical Analysis of Conditions for Ignition

of Compact Metal Specimens and Foil in Oxygen

UDC 620.22;546.21

V. I. Bolobov

1

and N. A. Podlevskikh

1

Translated from Fizika Goreniya i Vzryva, Vol. 37, No. 6, pp. 46–55, November–December, 2001.
Original article submitted November 10, 2000.

The conditions for ignition of compact specimens and a foil made of iron, nickel,
copper, and stainless steel in oxygen under pressures of 0.1–70 MPa are studied with
the use of modified equations and dimensionless parameters of the heat theory of
ignition of metal particles. Calculation results are compared with experimental data.

At present time, oxygen finds various applications

in science and engineering, where it is used at high tem-
peratures and pressures. To ensure safe operation of
structural materials under these conditions, it is neces-
sary to study ignition mechanisms of metals and alloys
shaped like compact articles and to infer how the oxy-
gen pressure affects their ignition temperature T

∗

exp

. It

has been shown experimentally (see, e.g., [1–7]) that
compact specimens made of widely used materials such
as stainless steel [4], copper and copper alloys [5], nickel
and nickel alloys [6], and iron and carbon steel [7] ignite
in oxygen under conditions of natural convection only
at the melting temperature of the metal (T

melt

) or basic

component of the oxide film. The pressure of the oxi-
dizing medium (up to 70 MPa) has little effect on the
values of T

∗

exp

[4–7].

2

In the present paper, the critical parameters of ig-

nition of the above-mentioned materials are studied by
a numerical method under experimental conditions of
[4–7]; the question of whether the dimensionless param-
eters of the heat theory of ignition of metal particles [8]
may be used in the calculations is considered.

CHOOSING THE KINETIC CONSTANTS

An analysis of the data available in the literature

shows that little is known about the kinetics of pre-
ignition oxidation of metal structural materials in oxy-

1

Russian Scientific Center “Applied Chemistry,”
St. Petersburg 197198.

2

According to [3], specimens of molybdenum-containing al-

loys ignite at T < T

melt

after the oxide film is destroyed by

MoO

2

and MoO

3

vapors for T

∗

exp

= f (p

O

2

).

gen under high pressure. Therefore, as the initial data
for calculations, we chose the kinetic constants of high-
temperature oxidation of iron, stainless steel, and nickel
in decomposition products of N

2

O (0.33/0.67 O

2

/N

2

composition; p = 1.5 MPa) determined in [9] under the
conditions close to the experimental conditions of [4–
7]. (In [9], an increase in the diameter of the middle
part of a cylindrical bar was measured after its oxi-
dation and Joule heating. It was found that, for all
materials, the time evolution of the oxide-film thickness
was described by the equation of a parabola; the activa-
tion energy E and the preexponent K

0

in the Arrhenius

equation were calculated for the constant of oxidation
rate K

T

determined at T = 1415–1570 K.) For cop-

per, we used the kinetic parameters of high-temperature
(T = 823–1173 K) oxidation of the material in air deter-
mined by the gravimetric method in [10]. To estimate
the effect of discrepancies in the values of the kinetic
constants determined by different authors on calcula-
tion results, we solved the problem of ignition of iron
repeatedly with the use of the data on the kinetics of
the oxide film of the material in air [10].

To estimate the discrepancy in the kinetics of ox-

idation of metals in oxygen at different pressures and
in an O

2

–N

2

mixture, we used the following considera-

tions. For metals and alloys with oxide films possessing
protective properties (as in our case), the rate of high-
temperature oxidation is limited by the diffusion rate of
anions and cations through a layer of solid oxides and
depend little [for nickel, v

∼ K

m

p

, where m

≈ 0.17] or

does not depend (for iron, steel, and copper) [10] on
the partial pressure of a gaseous oxidizer (for the values
of p exceeding the oxide-dissociation pressure, which is

0010-5082/01/3706-0655 $25.00 c

2001

Plenum Publishing Corporation

655

656

Bolobov and Podlevskikh

TABLE 1

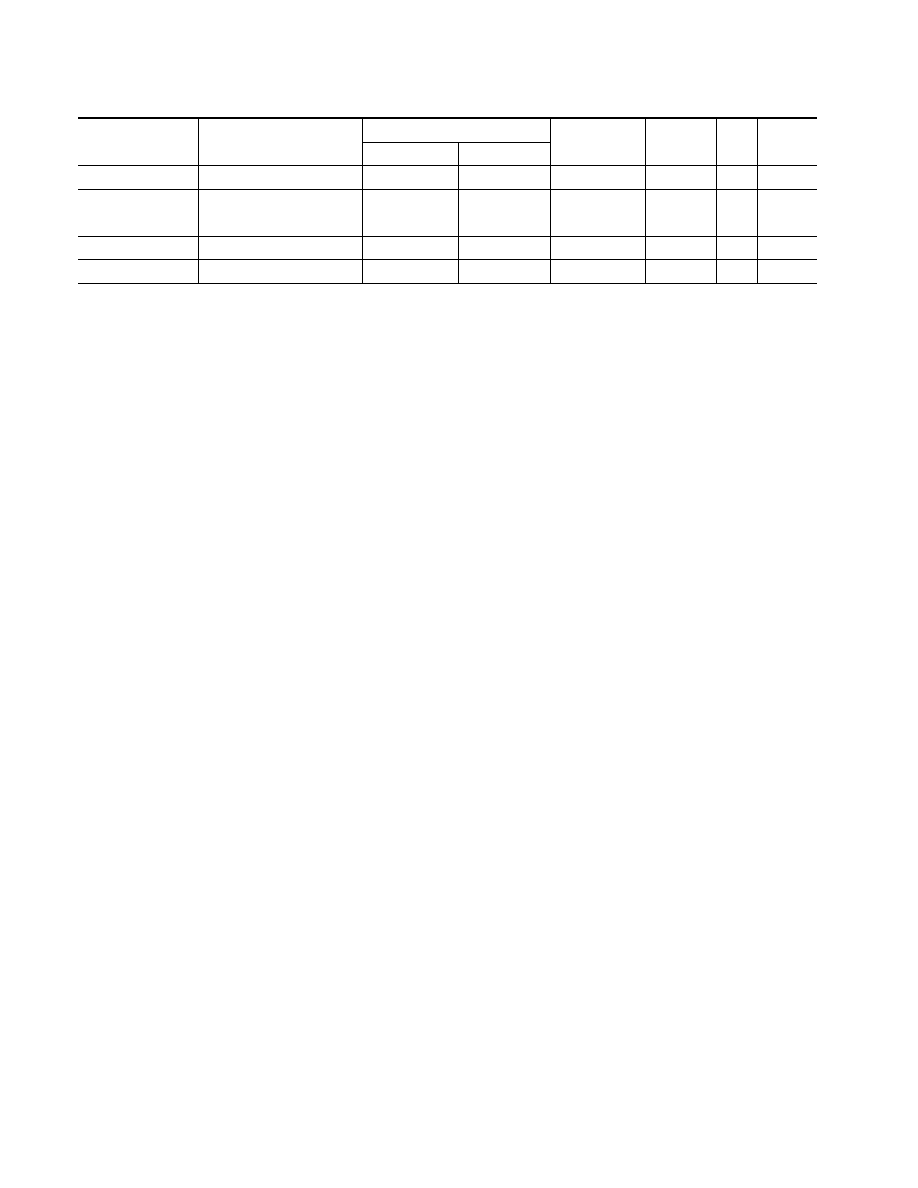
Results of X-Ray Phase and Gravimetric Tests of Specimens in Oxygen and Kinetic Constants Chosen

Material

Composition of scale

δ, µm

K

0

,

E,

m

Q,

for p

O

2

= 0.2 and 20 MPa

p

O

2

=0.2 MPa

p

O

2

=20 MPa

m

2

/sec

kJ/mole

MJ/kg

Copper

0.95Cu

2

–0.05Cu

360

370

5.9

· 10

−5

[10]

158 [10]

0

0.8

Iron

0.85FeO–0.15Fe

34

80

110

6.1

· 10

−4

[10]

170 [10]

0

3.0

9.5

· 10

−4

[9]

190 [9]

Nickel

NiO

—

—

7.8

· 10

−4

[9]

225 [9]

0.17

2.5

12Kh18N10T steel

(Cr,Fe)

2

O

3

0.86.2

0.85.0

0.8 0.14 [9]

0.8290 [9]

0.80

0.84.2

much lower than 0.1 MPa). For this reason, the oxi-
dation of these metals in air (nitrogen–oxygen mixture)
and oxygen at different pressures occurs in the same
manner, and they cannot be distinguished by kinetics
or scale structure [11].

The validity of this conclusion was supported in [9]

by comparing the thicknesses and phase compositions
of oxide films on metals oxidized in an O

2

–N

2

mixture

(p = 1.5 MPa) and air (p = 0.1 MPa). In this paper,
we verified this conclusion by the gravimetric method:
specimens of iron, stainless steel, and copper were kept
for t = 3600 sec under pressure 0.2 and 20 MPa [5] at
1273 K until their ignition.

It was found that an increase in pressure by two

orders of magnitude has little effect on the rate of pre-
ignition oxidation of the materials in question and the
phase composition of the scale in oxygen at different
pressures is close to the composition of films formed on
these materials in decomposition products of N

2

O [9]

and in air [10, 11].

The experimental values of the

increment in the specimen mass m calculated for the
thickness δ with allowance for the phase composition
are listed in Table 1. The kinetic parameters of oxida-
tion of metals borrowed from [9, 10] and thermal effects
Q [12] calculated with allowance for the phase compo-
sition of the scale are also given therein.

MATHEMATICAL MODEL
OF THE PROCESS

Using the basic assumptions of the theory of ig-

nition of particles [8], we calculated the conditions for
ignition of large-scale structures. To this end, we con-
sidered the possibility of the thermal mechanism [8] of
ignition of iron, nickel, stainless steel, and copper taken
in the form of:
— compact specimens subjected to the Joule heating in
“cold” oxygen under natural convection (experimental
conditions in [4–7]);

— foil heated in vacuum in contact with oxygen of the
same temperature [7].

In the first case, we considered the thermal bal-

ance of the middle part of a nonuniformly heated metal
bar of diameter d = 3 mm and working-part length
L = 40 mm in oxygen (p = 0.1–70 MPa). In contrast
to the heat-removal conditions for particles [8] or a uni-
formly heated plate [13], which ignite in an immovable
medium at relatively low pressure and temperature, this
problem is characterized by the necessity of taking into
account the heat losses in the “cold” ends of the speci-
men, heat losses due to radiation, and dependence of the
intensity of convective heat exchange on the pressure of
the medium. In view of these factors, the analytical
solution of the problem with the use of dimensionless
parameters [8] encounters serious difficulties. In the sec-
ond case, we calculated thermograms of self-heating of
a vertically installed foil of height H = 5 mm and thick-
ness h = 0.01–0.1 mm at different initial temperatures.
It was assumed that the foil was in contact with oxygen
(p = 0.14 MPa) at the same temperature (the dimen-
sions of specimens and the pressure correspond to the
experimental conditions of [7]).

The problem was solved under the following as-

sumptions used in [14] in calculating the critical ignition
parameters of compact metal specimens in fluorine:

• heat exchange with the medium is almost quasi-

stationary;

• the radial temperature distribution can be ig-

nored (the Biot criterion Bi

≤ 0.01); for the foil, the

temperature gradients are negligible in all directions;

• the temperature profile along the working part of

the specimen is close to a parabola;

• the temperatures of the gas and specimen ends

are equal and do not vary with time; for the foil, the
temperature of the gas is equal to the temperature of
the furnace and does not vary with time;

• the radiant flux toward the specimen can be ig-

nored in view of the low temperature of the walls of the
reaction chamber in the tests of [4–7];

Numerical Analysis of Conditions for Ignition of Compact Metal Specimens and Foil

657

• the kinetic equations governing oxidation of met-

als are valid within the entire temperature range con-
sidered.

With allowance for [8], the generalized equations

governing the self-heating of the specimen and foil have
the form

h

eff

2

c

p

ρ

dT

dt

= q + q

ch.r.

− q

α

− q

ε

− q

λ

;

(1)

q

ch.r.

= Qρ

dδ

dt

= Qρ

K

0

K

m

p

δ

n

exp

−

E

RT

,

(2)

where t is the time, T is the current temperature of the
central part of the specimen, R is the universal gas con-
stant, δ is the thickness of the oxide film, ρ is the density
of the metal, c

p

is the specific heat at constant pressure,

n is the exponent characterizing the dependence of the
oxidation rate on the oxide-film thickness, h

eff

is the

radius of the cylindrical specimen or the foil thickness,
K

0

is the preexponent in the Arrhenius equation, K

p

is

the ratio of the pressure used in the calculations to the
partial pressure of oxygen to which the kinetic param-
eters of oxidation correspond, m is the experimentally
determined coefficient that takes into account the prop-
erties of the oxide film, Q is the thermal effect of the
reaction per 1 kg of oxygen times the ratio of densities of
oxide and metal, q and q

ch.r.

are the heat fluxes applied

to the specimen owing to the Joule heat and chemical
reaction of metal oxidation, respectively, per unit area
of the central part of the specimen (for the foil, q = 0),
q

λ

, q

α

, and q

ε

are the thermal fluxes due to the heat

conduction to the cold ends of the specimen, convection,
and radiation, respectively, per unit area of the central
part of the bar, q

λ

= λ

w

d(T

− T

amb

)/2a

2

(for the foil,

q

λ

= 0), q

α

= λ

0

(T

− T

amb

)Nu/l (Nu = 0.54Ra

0.25

for

natural convection for Ra > 1) [15], q

ε

= εσ

0

T

4

[for the

foil, q

ε

= εσ

0

(T

4

− T

4

amb

)]. Here T

amb

is the ambient

temperature, l is the specimen diameter or foil thick-
ness, ε is the emissivity of metals with an oxide film
(ε

≈ 0.8 [16]), σ

0

is the Stefan–Boltzmann constant, λ

0

and λ

w

are the thermal conductivities of the gas and

metal, respectively [λ

0

= f (p, (T

amb

+ T )/2)], a is the

distance from the center of the bar to the “cold” clamps
of current taps in the tests in [4–7] (a = L/2), and Nu
and Ra are the Nusselt and Rayleigh criteria, respec-
tively.

The initial conditions: for t = 0, T = T

amb

[the

value of T

amb

is constant for the specimen (323 K) and

varied for the foil] and δ

0

= 10

−9

m [8].

To obtain a family of curves of the temperature of

the central part of the specimen as a function of time,
we integrated Eqs. (1) and (2) by a numerical method
for increasing values of q. For each thermogram, we de-
termined the maximum temperature of the central part

of the specimen T

max

and the final stationary tempera-

ture T

fin

at which the value of q

ch.r.

becomes negligible

because of the oxide-film growth. We note that, un-
der given heat-exchange conditions, the specimen would
have the temperature T

fin

if there were no chemical in-

teraction with the medium. It was assumed that the
temperature T

fin

corresponds to the initial temperature

T

0

of the specimen self-heated owing to the chemical

reaction at its surface. We constructed the curves T

max

and T

fin

= f (q) to determine the critical parameters of

ignition q

∗

and T

∗

0

. We assumed that the critical condi-

tions occur if a small variation in the heat flux around
q

∗

leads to a jump in the temperature T

max

, i.e., the

following condition holds:

dT

max

dq

q=q

∗

→ ∞.

(3)

For a value of q closest to q

∗

, we determined the

maximum temperature at the central part of the spec-
imen under subcritical conditions (T

∗

max

) and the max-

imum subcritical self-heating (∆T

max

= T

∗

max

− T

fin

).

The values of q = q

∗

corresponded to the ignition tem-

perature of the metal T

∗

0

= lim

q

→q

∗

T

fin

, which was taken

to be the initial temperature of self-heating that led to
ignition of the specimen.

For the foil, we integrated Eqs. (1) and (2) for in-

creasing values of T

0

(in this case, T

0

= T

amb

) to find

the minimum initial temperature of self-heating T

∗

0

that

corresponds to ignition of the metal. For T

0

≤ T

∗

0

, we

determined the maximum temperature T

∗

max

attained in

the foil without ignition and the maximum subcritical
heating of the material (∆T

max

= T

∗

max

− T

0

).

IGNITION CONDITIONS
FOR COMPACT SPECIMENS

Calculations show that theoretically,

3

among the

metals considered, compact specimens made of iron (for
both kinds of oxidation kinetics [9, 10]) and stainless
steel can ignite in oxygen according to the thermal
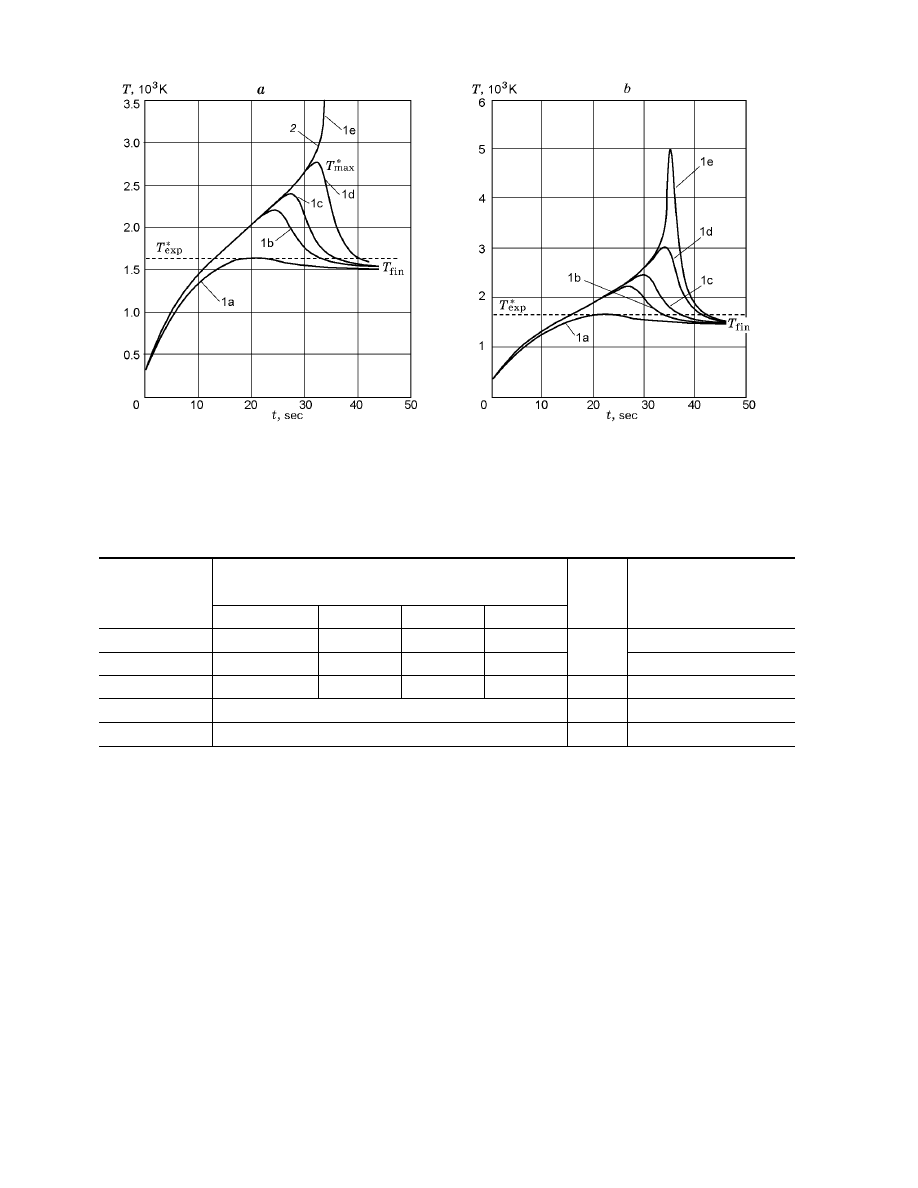
mechanism [8]. It is noteworthy that, for iron [10], the
ignition mechanism has some distinguishing features.

For stainless steel and iron [9] in oxygen at different

pressures, the calculated thermograms (Fig. 1a) are sim-
ilar to the curves of heating of metal particles [8]: in the
region of subcritical heating, the temperature reaches
the maximum T

max

and tends to the temperature T

fin

that the specimen would have if there were no chemical
interaction with the medium (curves 1a–e in Fig. 1a); in
the ignition region, the temperature curves have an in-
flection point (for a temperature close to T

∗

max

in the re-

3

Without allowance for phase transformations.

658

Bolobov and Podlevskikh

Fig. 1. Calculated thermograms of heating and ignition of cylindrical iron specimens (d = 3 mm) in oxygen
for p = 0.1 MPa, where curves 1a–1e refer to T

fin

and curve 2 refers to T

max

: (a) kinetics of [9] for q = 432

(1a), 478.1036 (1b), 478.1886 (1c), 478.1915 (1d), and 478.1916 kW/m

2

(1e); (b) kinetics of [10] for q = 385

(1a), 411.279 (1b), 411.3687 (1c), 411.3778 (1d), and 411.3780 kW/m

2

(1e).

TABLE 2

Ignition Conditions for Compact Metal Specimens in Oxygen

Calculated critical parameters

Material

for p = 0.1 and 70 MPa (in parentheses)

T

∗

exp

, K

∆T

exp

= T

∗

exp

− T

∗∗

0

, K

q

∗

, 10

3

kW/m

2

T

∗

max

, K

T

∗

0

, K

∆T

max

, K

Iron [10]

0.41 (1.29)

—

1445 (1540)

1450 (1828)

1644

234 (175)

Iron [9]

0.48 (1.4)

2672 (2894)

1525 (1606)

1147 (1288)

176 (129)

Stainless steel [9]

0.55 (1.54)

2295 (2357)

1708 (1756)

603 (631)

1683

63 (49)

Nickel [9]

Degenerated ignition conditions

≥1673

28 (22)

Copper [10]

No ignition or noticeable self-heating

1338

4 (3)

Note. T

∗∗

0

is the initial temperature of self-heating of compact specimens, for which the melting point is attained.

gion of subcritical heating) after which the temperature
increases progressively with time (curve 2 in Fig. 1a) to
infinity (if the total burnup of the specimen is ignored).
The regions of subcritical heating and ignition are sep-
arated by the critical value of the heat flux q

∗

for which

the dependence T

max

(q) (curve 1 in Fig. 2a) satisfies

condition (3). In this case, the maximum temperature
of iron [9] and stainless steel specimens under subcritical
conditions is a finite quantity (T

∗

max

in Figs. 1a and 2a).

If the kinetic parameters of oxidation of iron [10]

are used in Eq. (2), the maximum temperature jumps
from 2895 to 5000 K for a very small variation in q from
411.3778 to 411.3780 kW/m

2

(see Fig. 1b). Then, the

temperature tends to the stationary value T

fin

rather

than to infinity as in the case of iron [9]. For large val-
ues of q, the maximum is shifted toward higher tempera-
tures. Therefore, it is impossible to determine uniquely
the value of T

∗

max

for iron [10] (Fig. 2b).

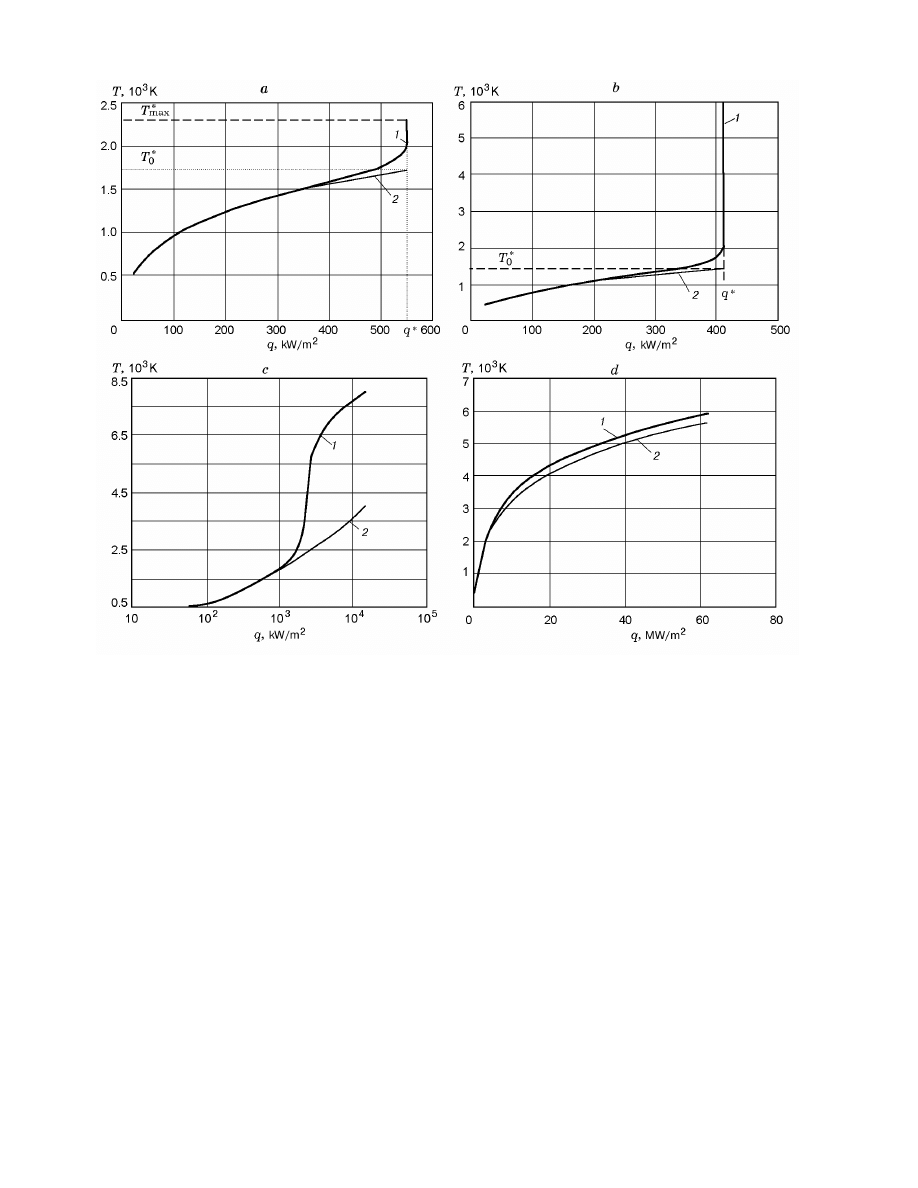
For nickel, the calculated thermograms are similar

to the thermograms of iron [10] (Fig. 1b), whereas the
dependence of the maximum temperature on heat flux
is described by an S-shaped curve (Fig. 2c) typical of
the degenerated ignition conditions. According to the
calculations, copper specimens do not ignite and do not
experience noticeable self-heating up to a temperature
of 6000 K, which is the maximum within the temper-

Numerical Analysis of Conditions for Ignition of Compact Metal Specimens and Foil

659

Fig. 2. Temperatures T

max

(curves 1) and T

fin

(curves 2) versus heat flux for steel (iron [9]) (a), iron [10] (b),

nickel (c), and copper (d).

ature range considered (Fig. 2d). The fact that nickel
and copper do not ignite by the thermal mechanism [8]
can be explained by intense conductive heat removal
from the specimens owing to the high conductivities λ

w

of these materials [at 1273 K, 80 and 336 W/(m

· K),

respectively] compared to iron and steel [30 and 29
W/(m

· K), respectively].

The parameters q

∗

, T

∗

max

, T

∗

0

, and ∆T

max

= T

∗

max

−T

fin

of materials that can ignite according to the ther-

mal mechanism [8] are listed in Table 2 for p

O

2

= 0.1

and 70 MPa.

A comparison of the data given in Table 2 with

the kinetic constants of oxidation used in calculations
(see Table 1) shows that the parameters of the metals
T

∗

max

, T

∗

0

, and ∆T

max

correlate with the corresponding

values of the activation energy of the oxidation reaction
E: as E increases, the maximum temperature T

∗

max

to

which a compact specimen from a given metal could
be heated without ignition and the maximum subcriti-
cal self-heating of the specimen ∆T

max

decrease rapidly,

whereas the ignition temperature T

∗

0

increases.

As for the effect of pressure, an analysis of the

components of heat removal in the period prior to ig-
nition q

out

shows that heat is removed from the cen-

tral part of iron and steel specimens mainly by ra-
diation and heat conduction (e.g., for iron, q

out

=

0.57q

ε

− 0.37q

λ

− 0.06q

α

) at low pressures (0.1 MPa)

and by convection (q

out

= 0.23q

ε

− 0.13q

λ

− 0.64q

α

) at

high pressures (70 MPa). Since, by assumption, the ox-
idation rate weakly depends on the oxygen pressure and
q

ch.r.

= const(p

O

2

), an increase in pressure and, hence,

in q

out

causes a monotonic increase in q

∗

, T

∗

max

, T

∗

0

, and

∆T

max

.

660

Bolobov and Podlevskikh

COMPARISON
WITH EXPERIMENTAL RESULTS

The experimental values of the ignition tempera-

tures of materials in oxygen are listed in Table 2 (T

∗

exp

and dashed curve in Fig. 1). For iron, T

∗

exp

is equal to

the temperature at which a liquid eutectic FeO–γFe is
formed at the metal–oxide interface [7]. For stainless
steel and nickel, the value of T

∗

exp

is close to the melt-

ing point of the metal [4, 6]. For copper, T

∗

exp

corre-

sponds to the melting point of the eutectic Cu

2

O–αCu

[5]. The last column in Table 2 gives the calculated val-
ues of subcritical self-heating of specimens (∆T

exp

) to

the temperature T

max

that corresponds to the ignition

temperature T

∗

exp

observed in experiments.

One can see from Table 2 that, for all the ma-

terials considered, the calculated maximum tempera-
tures of subcritical heating T

∗

max

are higher than the

temperature T

∗

exp

= T

melt

, at which the metal or ox-

ide film melts. As a result, the oxide film is broken
and the specimens ignite. Depending on the material,
the calculated values of self-heating of specimens to
their experimentally determined ignition temperature
(∆T

exp

= T

∗

exp

− T

∗∗

0

) are different: several hundreds of

degrees for iron and several tens of degrees for steel
and nickel, whereas self-heating for copper is practi-
cally absent. (For all the materials, the value of ∆T

exp

decreases as the pressure increases, which can be ex-
plained by the fact that the period of induction and,
hence, the thickness of the oxide film increase by the
beginning of self-heating.)

For this reason, iron is a

unique material (among the materials studied in [4–7])
for which the maxima of subcritical heating on exper-
imental thermograms are pronounced.

Judging from

small values of ∆T

exp

, compact specimens of copper,

nickel, and steel ignite by the Friedman–Macek mecha-
nism [17], whereas the ignition of iron specimens can be
considered as a transient mechanism between that de-
scribed in [17] and the Khaikin–Bloshenko–Merzhanov
thermal mechanism [8].

CONDITIONS FOR IGNITION OF FOIL

Calculations show that, owing to small heat re-

moval q

out

, all the considered metals in the form of foil

can ignite in oxygen at a temperature lower than the
temperature of any phase transformations in the metal
or oxide film which can lead to the failure of the latter
(T

∗

0

< T

melt

). The calculated values of T

∗

0

and ∆T

max

for foil ignited in oxygen (p = 0.14 MPa) and experi-
mental values of T

∗

exp

are listed in Table 3. (For iron, the

value of T

∗

exp

is taken from [7]; the data for steel, nickel,

and copper were obtained by the method proposed in [7]
and were not published previously.)

As in the case of compact specimens, the ignition

temperature of foil T

∗

0

increases with the activation en-

ergy of pre-ignition oxidation of the metal. It is minimal
for copper (E = 158 kJ/mole) and maximal for stainless
steel (E = 290 kJ/mole).

Good correlation between the calculated and ex-

perimental values of T

∗

0

supports the conclusion that

the foil specimens from these materials ignite in oxygen
according to the thermal mechanism [8]. The validity
of the assumptions used in the calculations is also con-
firmed.

ANALYSIS OF CRITICAL
PARAMETERS OF IGNITION

We consider the question whether the critical pa-

rameters of ignition of metal particles (χ and Ω

∗

) [8]

can be used to determine the temperature parameters
of ignition (T

∗

max

, T

∗

0

, and ∆T

max

) of large-scale metal

bodies and bodies under different conditions of heat ex-
change with the ambient medium.

We calculated the parameters introduced in [8],

which can be written as

γ

≡

c

p

RT

2

h

eff

2EQδ

∗

0

;

χ

≡

QρEk

0

K

m

p

T

2

αRδ

∗

0

exp

−

E

RT

;

θ

≡

∆T E

RT

2

;

β

≡

T R

E

;

Ω

≡

χ

γ

=

2Q

2

(E/R)

2

ρK

0

K

m

p

T

4

αc

p

h

eff

exp

−

E

RT

,

(4)

where α = ∂q

out

/∂T is the overall heat-transfer coeffi-

cient and δ

∗

0

is the thickness of the oxide film at the mo-

ment the critical self-heating begins [δ

∗

0

= δ

0

= 10

−9

m

for foil and

≈10

−5

m (according to calculations) for the

specimens].

Table 4 lists the dimensionless parameters calcu-

lated at T = T

∗

0

for compact specimens (metals ignited

by the thermal mechanism [8]) and foil (given in ascend-
ing order of the values of E of the materials studied).
The values of α at T = T

∗

0

used in the calculations of χ

and Ω

∗

are also given in Table 4.

In accordance with [8], the criterion that describes

the critical conditions for ignition of metal particles is
chosen depending on the parameter γ: χ

cr

= 1/e for

γ

1 and Ω

∞

cr

= 1.57 for γ

1 (for a parabolic law of

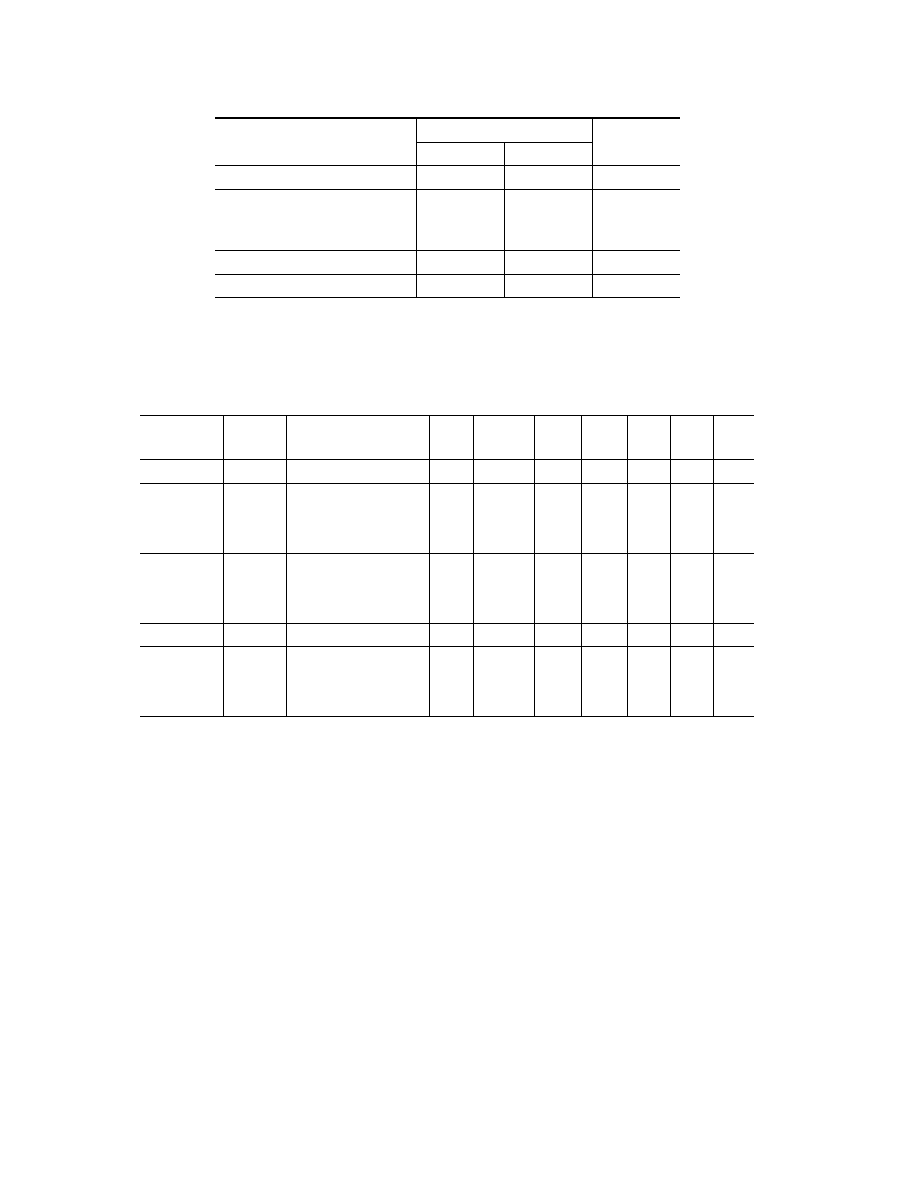
Numerical Analysis of Conditions for Ignition of Compact Metal Specimens and Foil

661

TABLE 3

Values of T

∗

0

and ∆T

max

for Foil Ignited in Oxygen

Material and thickness of the foil

T

∗

0

, K

∆T

max

, K,

calculations

experiment

calculations

Copper, h = 0.01 mm

1133

1153

543

1182 [10]

532 [10]

Iron, h = 0.5 mm

1233

∗

1273 [9]

547 [9]

Nickel, h = 0.05 mm

1393

1543

520

Stainless steel, h = 0.01 mm

1396

1483

218

Note. The asterisk indicates the value for iron containing 0.22% C (St. 3 steel).

TABLE 4

Dimensionless Parameters of Critical Conditions for Ignition of Foil

and Compact Metal Specimens in Oxygen

Material

E,

Shape of the specimen

p

O

2

,

α,

β

θ

melt

γ

χ

Ω

∗

kJ/mole

MPa

kW/m

2

Copper [19]

158

Foil

0.14

0.30

0.060

8.0

114

284

2.49

Foil

0.14

0.34

0.058

7.8

1018

2441

2.40

Iron [19]

170

Cylinder

0.1

0.79

0.071

14.1

0.59

2.2

3.67

Cylinder

70

1.56

0.075

15.7

0.61

2.1

3.39

Foil

0.14

0.42

0.056

7.7

1054

2445

2.32

Iron [18]

190

Cylinder

0.1

0.90

0.067

11.3

0.60

2.1

3.56

Cylinder

70

1.66

0.071

11.3

0.61

2.0

3.35

Nickel [18]

225

Foil

0.14

0.55

0.052

7.21

190

419

2.21

Stainless

Foil

0.14

0.60

0.040

3.9

130

250

1.93

steel [18]

290

Cylinder

0.1

1.11

0.049

7.0

0.60

1.9

3.10

Cylinder

70

1.82

0.050

7.1

0.62

1.8

2.94

oxidation). The calculated values of γ given in Table 4
lie within the interval 10

−1

–10

3

, and the critical condi-

tions for ignition in our case should be determined from
the condition Ω

∗

= const. At the same time, one can

see that this parameter does not remain constant: it in-
creases in the transition from foil to compact specimens
and decreases with an increase in the activation energy
of the oxidation reaction of the metal for specimens of
one type. An analysis of the data given in Table 4 shows
that, for all the metal foils, the parameter Ω

∗

is a func-

tion of the product βθ:

Ω

∗

= 1.68 + 1.60βθ.

(5)

The limiting value Ω

∗

= 1.68 (for βθ = 0) is close to the

value Ω

∞

cr

= 1.57, which determines the critical condi-

tions for ignition of metal particles [8].

The form of dependence (5) can be explained

by the fact that self-heating of foil is more intense
(θ

melt

= 3.9–8.0 in Table 4) than that of a particle

(θ

melt

= 3.3 [8]) and, hence, the product βθ is larger

(0.157–0.48); therefore, it cannot be ignored as was done
in [8] in determining Ω

∞

cr

for particles.

One can see

from Table 4 that, as the activation energy increases,
the quantities β and θ

melt

decrease for specimens of one

type; therefore, for metals with high activation energy,
for example, steel, we have βθ

→ 0, and Ω

∗

→ Ω

∞

cr

[8].

(It is noteworthy that, for compact specimens, the quan-
tity Ω

∗

is also a linear function of the product βθ, and

for different oxygen pressures, the corresponding lines
pass through approximately the same point with the
coordinates Ω

∗

= 2.75 and βθ = 0.)

662

Bolobov and Podlevskikh

We found that, for Ω/Ω

∗

< 0.7, the dependence

of the dimensionless temperature θ of foil and compact
specimens on Ω/Ω

∗

can be approximated by a linear

function with a slightly different proportionality coeffi-
cient compared to [8]:

θ = 2.2(Ω/Ω

∗

).

(6)

PRACTICAL USE OF THE
CALCULATION DATA IN ENGINEERING

To answer the question whether the averaged value

of Ω

∗

can be used in determining the critical tempera-

ture parameters by Eq. (4), we calculated the ignition
temperatures T

∗

0

of specimens and foil from the mate-

rials studied for the their arithmetical mean (see Ta-
ble 4) value of Ω

∗

(Ω

∗

= 2.85). Moreover, using Eq. (6)

with Ω

∗

= 2.85, we determined the temperature T

∗∗

0

corresponding to the onset of self-heating of compact
specimens for which the melting point T

melt

is attained.

The latter was recorded in [4–7] as the ignition temper-
ature T

∗

exp

. By analogy with [8], we solved the following

transcendental equation for T

∗∗

0

:

∆T

exp

= T

melt

− T

∗∗

0

= 1.54

Q

2

(E/R) ρ K

0

K

m

p

(T

∗∗

0

)

2

αc

p

h

eff

× exp

−

E

RT

∗∗

0

.

(7)

The calculations show that, for all the materials

ignited by the thermal mechanism and for all types of
specimens and oxygen pressures, the values of T

∗

0

cal-

culated by formula (4) for Ω

∗

= 2.85 differ from those

obtained by integrating Eqs. (1) and (2) by no more
than 40 K (or 3%). The difference between the values
of T

∗∗

0

calculated by formula (7) and those computed

numerically does not exceed this error either.

Since this error is acceptable, this method of deter-

mining the conditions for ignition of specimens can be
used in engineering practice to estimate the conditions
of safe exploitation of metal structures contacting cor-
rosive media. For this purpose, the following algorithm
is proposed:

1) Using the data available in the literature, de-

termine the kinetic parameters (K

0

, E, and n) of high-

temperature oxidation of a structural material in a given
medium and the thermal effect of the reaction;

2) For quasi-stationary conditions of heat ex-

change, calculate the dependence of the overall heat-
transfer coefficient of the most heated zone of the struc-
ture on temperature;

3) Using Eq. (4) with Ω

∗

= 2.85, determine the

ignition temperature T

∗

0

of the structure from the given

material by the substitution method for corresponding
values of α = f (T ) [in this case, T

∗

0

is the minimum

temperature of the surface (chemical interaction with
the medium is not taken into account) at which self-
heating owing to the metal-oxidation reaction leads to
ignition of the structure];

4) Using the existing data on the phase composition

of the products of interaction of the material with the
corrosive medium and their physicochemical properties,
determine the minimum temperature at which the pro-
tective film on the material can be destroyed (usually,
as a result of melting of the component or metal at the
temperature T

melt

);

5) For the chosen value of T

melt

, use Eq. (7) to

calculate the temperature T

∗∗

0

corresponding to the on-

set of critical self-heating of the metal structure, which
results in the destruction of the protective film and ig-
nition of the metal;

6) Compare the determined values of T

∗

0

and T

∗∗

0

with expected temperature regimes of operation of the
structure to infer whether the operation conditions are
safe.

CONCLUSIONS

1. With the use of the mathematical model pro-

posed, the critical conditions for ignition of compact
specimens and foil from iron (for two oxidation kinet-
ics), 12Kh18N10T stainless steel, and technical nickel
and copper in oxygen at p = 0.1–70 MPa under natural
convection have been calculated.

2. It has been found that compact copper spec-

imens do not ignite at temperatures up to 6000 K,
whereas the critical conditions for ignition of nickel are
degenerate.

Theoretically, specimens from iron and

stainless steel can ignite in oxygen according to the
mechanism proposed in [8] at the maximum tempera-
tures of subcritical self-heating (T

∗

max

= 2295–2894 K),

which are much higher than the melting points of the
metals or oxide films (T

melt

= 1644–1683 K) at which

specimens ignite in tests.

3. All the considered materials in the form of foils

have been shown to be able to ignite in oxygen accord-
ing to the thermal mechanism [8] at temperatures T

∗

0

lower than the temperature at which the oxide film is
destroyed. The calculated values of T

∗

0

increase with

the activation energy of pre-ignition oxidation and sat-
isfactorily correlate with experimental data.

Numerical Analysis of Conditions for Ignition of Compact Metal Specimens and Foil

663

4. It has been shown that the parameter Ω

∗

de-

termining the critical conditions for ignition of metal
particles [8] is not a constant in the case of ignition
of compact specimens and foil (Ω

∗

= 1.93–3.67) and

increase with the activation energy of the oxidation re-
action of the materials.

5. An algorithm of calculating the ignition temper-

atures of metal structures with the use of the averaged
value of Ω

∗

has been proposed.

REFERENCES

1. L. E. Dean and W. R. Thompson, “Ignition character-

istics of metals and alloys,” J. Amer. Rocket Soc., 31,

No. 7, 78–85 (1961).

2. B. A. Ivanov and A. P. Nikonov, “Ignition and com-

bustion of compact metals in oxygen,” in: Problems in

Engineering Workplace Hygiene (collected scientific pa-

pers) [in Russian], No. 63, Metallurgiya, Moscow (1970),

pp. 55–63.

3. Yu. V. Frolov, A. N. Pivkina, and V. V. Gusel’nikov,

“Ignition and combustion of high-temperature alloys in

oxygen,” Fiz. Goreniya Vzryva, 24, No. 4, 19–21 (1988).

4. V. I. Bolobov, A. Yu. Berezin, P. F. Drozhzhin,

and A. S. Shteinberg, “Ignition of compact stainless-

steel specimens in high-pressure oxygen,” Fiz. Goreniya

Vzryva, 27, No. 3, 3–7 (1991).

5. V. I. Bolobov and A. Yu. Berezin, “Conditions for ig-

nition of copper and copper alloys in oxygen,” Fiz.

Goreniya Vzryva, 34, No. 2, 47–50 (1998).

6. V. I. Bolobov, “Effect of pressure on the ignition tem-

perature of compact samples of nickel alloys in oxygen,”

Fiz. Goreniya Vzryva, 35, No. 2, 54–58 (1999).

7. V. I. Bolobov,“Conditions for ignition of iron and carbon

steel in oxygen,” Fiz. Goreniya Vzryva, 37, No. 3, 52–57

(2001).

8. B. I. Khaikin, V. N. Bloshenko, and A. G. Merzhanov,

“Ignition of metal particles,” Fiz. Goreniya Vzryva, 6,

No. 4, 474–488 (1970).

9. V. I. Bolobov and K. M. Makarov, “High-temperature

oxidation of some metals in the presence of atomic oxy-

gen,” Zashchita Metallov, 28, No. 6, 1007–1010 (1992).

10. O. Kubashewski and B. E. Hopkins, Oxidation of Metals

and Alloys, Butterworths, London (1965).

11. J. B´

enard (ed.),

Oxydation des Metaux,

Vol. 1,

Gauthier-Villars, Paris (1962).

12. A. P. Zefirov, Thermodynamic Properties of Inorganic

Substances: Handbook [in Russian], Atomizdat, Moscow

(1965).

13. S. S. Rybanin, N. I. Peregudov, T. V. Rybanina, and

S. L. Sobolev, “Critical conditions and period of induc-

tion for combustion of a metal plate in an immobile ox-

idizing atmosphere,” Fiz. Goreniya Vzryva, 22, No. 3,

3–10 (1986).

14. V. I. Bolobov, P. F. Drozhzhin, and V. G. Nechaeva,

“High-temperature oxidation and ignition of some

metallic materials in fluorine,” Fiz. Goreniya Vzryva,

34, No. 4, 34–42 (1998).

15. S. S. Kutateladze, Fundamentals of the Heat Transfer

Theory [in Russian], Nauka, Novosibirsk (1970).

16. K. P. Yakovlev (ed.), Physicochemical Handbook [in Rus-

sian], ´

Energiya, Moscow (1962).

17. R. Friedman and A. Macek, “Ignition and combustion

of aluminium particles in hot ambient gases,” Combust.

Flame, 6, 9 (1962).