Combustion, Explosion, and Shock Waves, Vol. 38, No. 4, pp. 435–445, 2002

Role of the Structure of Heterogeneous Condensed Mixtures

in the Formation of Agglomerates

UDC 536.46

S. A. Rashkovskii

1

Translated from Fizika Goreniya i Vzryva, Vol. 38, No. 4, pp. 65–76, July–August, 2002.
Original article submitted August 3, 2001.

Mathematical simulation of the structure of metallized heterogeneous condensed mix-
tures is performed. Evolution of a system of aluminum particles is studied in the
case a heat wave passes over the mixture. It is shown that rapid heating of a het-
erogeneous condensed mixture forms a system of “clusters” of contacting aluminum
particles, which may sinter to form a porous system that melts and disperses into
individual droplets with further heating under the action of surface-tension forces.
After coalescence, these droplets form agglomerates. The structure of “clusters” of
contacting particles is studied, and the mean-mass size of metal particles is deter-
mined as a function of dispersion of the components and their concentration in the
heterogeneous condensed mixture. It is shown that contacting aluminum particles in
the heterogeneous condensed mixture form fractal-like structures, which may play a
significant role in the course of combustion of the mixture.

Key words: agglomeration of aluminum, combustion of composite rocket propel-

lants, propellant structure, ammonium perchlorate, binder.

INTRODUCTION

Modern heterogeneous condensed mixtures (HCM)

may contain several types of disperse components with
different dispersion and properties.

In the course of

combustion, some of them act as oxidizers (ammonium
perchlorate, HMX, RDX, etc.), and some may work as
combustibles (for instance, metals: aluminum, magne-
sium, and boron). A typical feature of HCM is the ran-
dom character of distribution of disperse components in
them. HCM combustion involves interaction (mechani-
cal, thermal, chemical, etc.) of various components and
a change in their phase state and chemical composition.
The character of this interaction affects the structure
of the reaction region, the burning rate of HCM as a
macroscopic system, and also the chemical composition
and structure of combustion products. This is most pro-
foundly manifested in combustion of metallized HCM,
which is accompanied by coalescence of metal particles
into agglomerates. In this case, the metal fuel in the liq-
uid and gaseous phase may actively enter the chemical

1

Moscow Institute of Thermal Engineering,
Moscow 127276; [e-mail].

reaction with oxygen-containing products of decompo-
sition of other components.

The process of metal agglomeration in HCM com-

bustion has many stages [1–8] and starts in the depth
of the condensed phase (c-phase) from inert heating of
components in a heat wave. Heating of the contact-
ing metal particles in HCM leads to their sintering [9],
melting, and coalescence due to surface-tension forces
into larger structures — subagglomerates, which pass to
the surface and join other subagglomerates to form ag-
glomerates. Enlargement of agglomerates on the burn-
ing surface is associated with capturing of new subag-
glomerates or with joining other subagglomerates on the
burning surface. The final stages of the agglomeration
process are ignition, combustion, and separation of ag-
glomerates from the burning surface [1–8].

The “initial conditions” of agglomeration are deter-

mined by the HCM structure, in particular, by the pres-
ence of contacting metal particles in the initial HCM [6].
Naturally, the presence of contacting metal particles in
HCM is not a sufficient condition for agglomerate for-
mation. Some other conditions related to sintering of
the contacting particles, their melting, and coalescence

0010-5082/02/3804-0435 $27.00 c

2002

Plenum Publishing Corporation

435

436

Rashkovskii

into subagglomerates should be satisfied. These con-
ditions are fulfilled for a certain dispersion of the ini-
tial metal particles in HCM and certain parameters of
the heat wave, which are related to the HCM burning
rate [1]. Thus, the presence of contacting metal parti-
cles in HCM is a necessary but not a sufficient condition
for the formation of agglomerates.

There are no doubts now that the HCM structure

exerts a determining effect on HCM combustion and, in
particular, on the formation of condensed combustion
products (agglomerates).

Indirectly, the HCM structure has been always

taken into account in simulation of the agglomeration
process. Examples can be the model of “pockets” [1,
4–6], which are some structural cells formed by ammo-
nium perchlorate (AP) particles within which agglom-
erates are formed, or models that use the coordination
number of metal particles in HCM composition [6, 10],
which is a factor determining the capability of metal
particles to join in the course of heating in the heat
wave.

It should be noted that the pocket model is phe-

nomenological, since the notion of a pocket itself is
rather conventional. An analysis of the structure of real
HCM and structures obtained by mathematical simula-
tion [11], HCM has no isolated (in the rigorous meaning)
regions bounded by particles of oxidizers, where inde-
pendent formation of agglomerates can occur. Using
the terminology of Babuk et al. [4], we can state that
the formation of agglomerates always includes an “in-
terpocket” mechanism, which implies that metal parti-
cles grouped near different particles of the oxidizer can
join into a single agglomerate. In addition, the pocket
model does not allow one to describe the dynamics of
agglomerate formation.

Obviously, the closed theory of agglomeration

should be statistical and should be based on a dynamic
model that describes all stages of agglomerate develop-
ment. Such a model was proposed in [7, 8] and employed
the spectrum of agglomerates determined by the HCM
structure as the initial data.

The objective of the present work is to study the

structure of metallized HCM and its influence on the
initial process of agglomerate formation.

HCM STRUCTURE
AND ITS BASIC ELEMENTS

Some recent papers deal with modeling of the HCM

structure or its characteristic cell [11–13]. The final ob-
jective of these works is to relate the statistical HCM
structure with the laws of its combustion. These mod-

els allow one to hope for direct (non-phenomenological)
modeling of processes in the c-phase of HCM in the case
of transition of a heat wave, which lead to coarsening of
metal particles — agglomeration.

A general method for modeling the statistical struc-

ture of disperse systems, including HCM, was proposed
in [11]. This method offers an effective description of
both metal-free and metallized systems with an arbi-
trary size distribution of disperse components.

The

disperse components of HCM are considered as hard
spheres. Simulation of the HCM structure implies ran-
dom arrangement of a system of particles with a given
size distribution inside a certain region of space.

The algorithm of random arrangement of an arbi-

trary system of hard spheres in a given region of space
is based on solving the system of equations [11]

d x

i

d t

=

X

j

6=i

x

i

− x

j

| x

i

− x

j

|

∆

ij

,

(1)

∆

ij

=

1

if

|x

i

− x

j

| < r

i

+ r

j

,

0

if

|x

i

− x

j

| > r

i

+ r

j

,

(2)

where x

i

is the radius vector of the center of the ith

sphere, r

i

is the radius of the ith sphere, and t is the

“time.”

System (1), (2) is solved under random initial con-

ditions: the initial coordinates of the centers of particles
are set by a generator of random numbers. The calcula-
tion is continued until no pairs of intersecting particles
remain in the system. Justification of the method and
its detailed description can be found in [11].

Heating of the c-phase of HCM in the heat wave

leads to sintering of the contacting metal particles [9].
Groups of sintered metal particles, which are isolated
from each other, form “clusters.” The clusters may have
a complicated internal structure characterized by the
coordination number, which is the mean number of con-
tacts per one particle of the cluster [6]. Obviously, the
higher the coordination number of the cluster, other
conditions being equal, the higher its strength.

The size of the clusters of contacting metal parti-

cles in HCM and their connectivity are determined by
the mass content of metal in HCM, dispersion of its par-
ticles, and mass content of disperse oxidizers in HCM
and the spectrum of their particles. The clusters can
be rather strong spatial structures that perform certain
functions in the course of HCM combustion and metal
agglomeration. Thus, extended clusters can play the
role of thermal bridges intensifying the heat flux from
the burning surface inside the c-phase and, hence, in-
creasing the HCM burning rate. Rather large clusters
can serve as a basis of the frame layer near the HCM
burning surface and retain agglomerates on the burning

Role of the Structure of Condensed Mixtures in the Formation of Agglomerates

437

surface, favoring their growth. It is possible to imag-
ine a situation where an agglomerate is retained on the
burning surface by a cluster extended into the depth of
the c-phase, which is a “donor” of this agglomerate. As
the binder burns out, the burning surface moves; due to
melting of the upper part of the cluster, part of its mass
passes to the agglomerate, and the agglomerate itself,
moving along the cluster under the action of capillary
forces, follows the burning surface until the whole clus-
ter passes to the agglomerate or the repulsive force from
gaseous combustion products becomes greater than the
cluster strength.

Melting of metal particles in the heat wave may

lead to the coalescence of the initial metal particles
in the cluster and to the formation of a large drop-
subagglomerate.

In this case, a subagglomerate is a

cluster in a melted state. At the same time, rapid melt-
ing of rather large clusters can lead to the formation
of a liquid porous structure, which is unstable. In this
case, cluster melting can be accompanied by its split-
ting (dispersion) under the action of capillary forces and
gas-dynamic forces from the side of gaseous combustion
products with the formation of several smaller drops-
subagglomerates, the sum of their masses being equal
to the mass of the cluster. Note, the process in the
combustion wave is rather fast, and there may be not
enough time for the ultimate coalescence into a single
drop or splitting into several drops. In this case, the
sizes of subagglomerates arriving on the burning sur-
face are greater than their sizes in the form of a single
(monolithic) drop. This process is characterized by the
ratio of the time that passed from the moment of melt-
ing of the initial metal particles before their arrival on
the burning surface to the time of coalescence of the
cluster into a single drop due to capillary forces. We
give the quantitative criterion of this process.

The time t

melt

from the beginning of melting of the

drop to its arrival on the burning surface can be evalu-
ated using the model proposed in [1]. Simple transfor-
mations allow us to obtain the formula

t

melt

=

æ

u

2

ln

h

1

1 + c

Al

ρ

Al

u

2

D

2

Al

/12λæ

T

s

− T

0

T

melt

− T

0

i

, (3)

where λ and æ are the thermal conductivity and ther-
mal diffusivity of HCM, c

Al

and ρ

Al

are the specific heat

and density of aluminum particles, u is the HCM burn-
ing rate, D

Al

is the diameter of the initial aluminum

particles, T

0

and T

s

are the initial HCM temperature

and the temperature of the HCM burning surface, and
T

melt

is the melting point of aluminum. Formula (3) is

valid only for aluminum particles of diameter [1]

D

Al

<

12λæ

c

Al

ρ

Al

u

2

T

s

− T

melt

T

melt

− T

0

1/2

,

i.e., only for those particles that have enough time to
reach the melting point in the heat wave within the c-
phase.

The characteristic time of coalescence of melted

particles under the action of surface tension has the or-
der µD

cl

/σ, where µ and σ are the viscosity and surface

tension of the metal of the drop in the melted state and
D

cl

is the characteristic size of the cluster prior to melt-

ing.

For µD

cl

/σt

melt

1, the particles rapidly arrive

on the HCM burning surface, and the cluster has not
enough time for ultimate coalescence into a single drop
or for splitting into several small drops.

Vice versa,

for µD

cl

/σt

melt

1, evolution of the cluster under the

action of capillary forces is completed in the HCM sur-
face layer, and one or several melted drops arrive on the
burning surface, their total mass being equal to the mass
of the initial cluster. Thus, large clusters may arrive on
the burning surface in the form of a system of sintered
particles, and their melting and integration into a drop-
agglomerate occur already on the burning surface or in
the gas flame. At the same time, comparatively small
clusters, due to capillary forces, may transform into one
or several drops-subagglomerates prior to reaching the
burning surface.

Within the HCM c-phase and frame layer, subag-

glomerates are not mobile; therefore, coalescence of in-
dividual subagglomerates before reaching the burning
surface is little probable and is possible only on the
burning surface or in the gas flame of HCM.

Thus, the process of formation of agglomerates

from initial metal particles can be conventionally di-
vided into the following stages: (i) sintering of initial
metal particles into clusters; (ii) melting of clusters;
(iii) capillary compression of clusters and their splitting
into smaller ones with the formation of subagglomer-
ates; (iv) arrival of subagglomerates on the burning sur-
face and collision with agglomerates already located on
the burning surface; (v) their coalescence into larger ag-
glomerates; (vi) entrainment of agglomerates from the
surface under the action of gaseous products of HCM
decomposition.

The first three stages of the process are examined

in the present work.

In what follows, we consider HCM containing two

disperse components, which are collectively called AP
(coarse particles) and aluminum (fine particles). We as-
sume that all particles of one kind are identical. This is
true for real HCM containing narrow fractions of pow-
ders of disperse components.

The volume concentration of particles of pow-

dered aluminum in HCM is determined by the formula
ν

Al

= ςρ

p

/ρ

Al

, where ς is the mass fraction of aluminum

438

Rashkovskii

in HCM; the diameter of particles of disperse AP is D

AP

and their volume concentration in HCM is ν

AP

.

To

estimate the HCM density (ρ

p

), we used the formula

ρ

p

= (1

− ν

AP

− ν

Al

)ρ

b

+ ν

AP

ρ

AP

+ ν

Al

ρ

Al

, where ρ

b

,

ρ

AP

, and ρ

Al

are the densities of the binder, AP, and

aluminum, ρ

b

= 900 kg/m

3

, ρ

AP

= 1950 kg/m

3

, and

ρ

Al

= 2700 kg/m

3

.

From considerations of dimensionality, the mean-

mass diameter D

0

43

of subagglomerates formed after

melting of clusters of contacting aluminum particles can
be represented in the form

D

0

43

= D

Al

f (D

Al

/D

AP

, ν

Al

, ν

AP

),

(4)

where f is a dimensionless function, which depends on
whether the dispersion of the melted clusters occurred
or not. Depending on the ratio of diameters D

Al

/D

AP

,

we conventionally speak about finely disperse aluminum
(D

Al

/D

AP

→ 0) or about the relatively coarsely dis-

perse aluminum if D

Al

/D

AP

acquires a finite, though

small value.

Note that the notion of a “finely disperse particle”

in this work is purely geometric and is related to the
relative size of aluminum and AP particles only.

FINELY DISPERSE ALUMINUM

We consider HCM containing finely disperse parti-

cles of aluminum. Formally, from Eq. (4), we obtain

D

∞

43

= D

Al

f (0, ν

Al

, ν

AP

).

(5)

From the viewpoint of modeling of the HCM structure,
this limiting transition is equivalent to independent ar-
rangement of aluminum and AP particles: AP particles
are located in the HCM volume without allowance for
aluminum particles, and aluminum particles are located
in the space between AP particles as in the empty space.

Thus, to model the structures formed by finely dis-

perse particles in HCM, it is sufficient to place these
particles randomly, with an effective volume concen-
tration ν

eff

Al

= ν

Al

/(1

− ν

AP

), in the empty space. In

the dimensionless form, where all sizes are normalized
to the diameter of aluminum particles, the problem re-
duces to arrangement of spheres of unit diameter in a
cube [11] and is characterized by only one parameter
ν

eff

Al

. The calculation was performed for “specimens”

of sizes 10

× 10 × 10, 20 × 20 × 20, and 30 × 30 × 30.

The method of identification of clusters of contacting
particles is described in [11].

We consider the mean-mass sizes of subagglomer-

ates formed as a result of melting of clusters without
dispersion, i.e., we assume that the total mass of the
cluster transforms into one subagglomerate — spherical
drop.

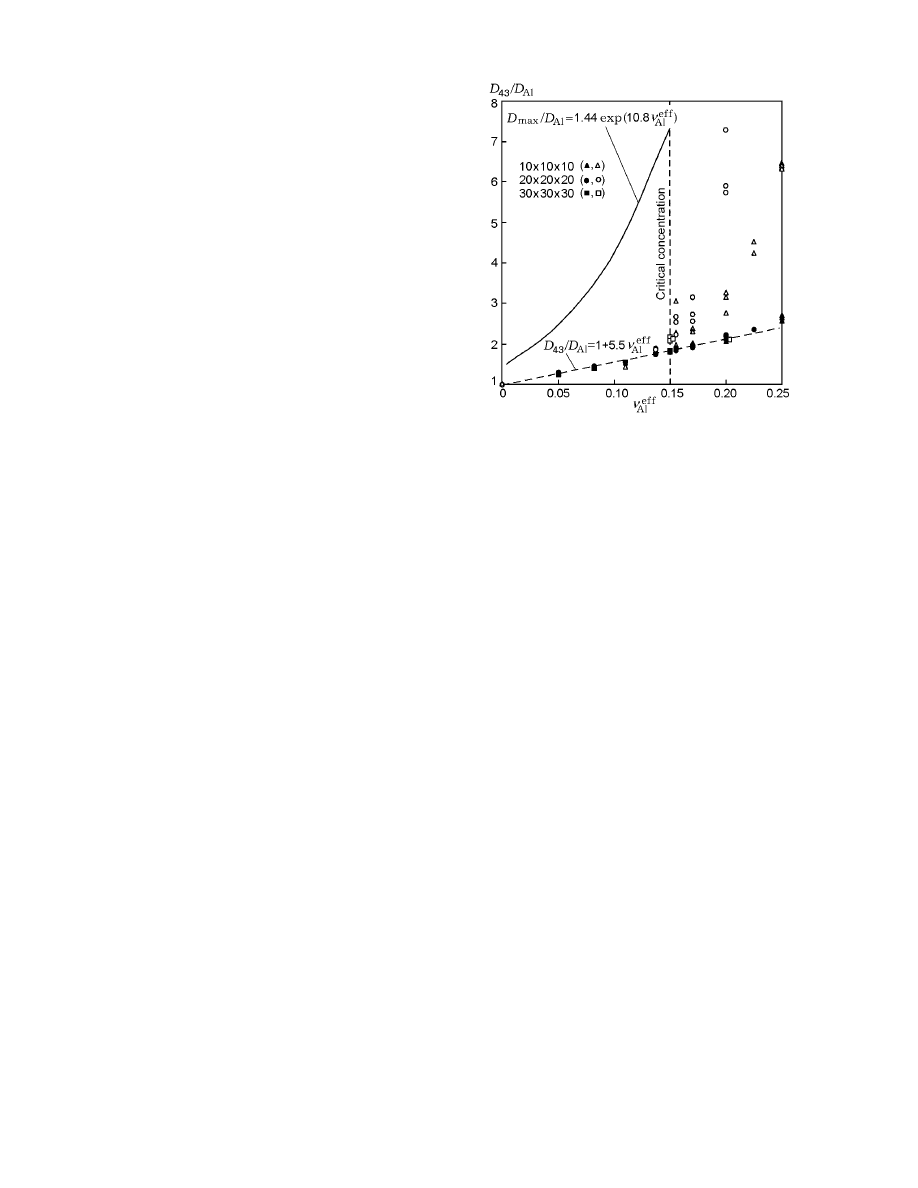
Fig. 1. Mean-mass diameter of subagglomerates ver-
sus the volume concentration of finely disperse alu-
minum in HCM: the open and filled points show the
data without and with allowance for dispersion of
clusters, respectively.

The dependence of D

43

/D

Al

on the effective con-

centration of aluminum in HCM ν

eff

Al

for the case consid-

ered is plotted in Fig. 1 by open points. For ν

eff

Al

< ν

cr

,

where ν

cr

≈ 0.15, all the calculation values (indepen-

dent of the “specimen” size) are grouped around one
linear dependence

D

43

= (1 + aν

eff

Al

)D

Al

,

(6)

where a = 5–6. For ν

eff

Al

> ν

cr

, the mean-mass size of the

clusters drastically increases: the calculation points de-
viate noticeably from the linear dependence (6), and a
significant scatter of the calculation values for an identi-
cal concentration of aluminum is observed. The smaller
the size of the calculation “specimen,” the greater the
scatter; the greater the “specimen” size, the slower the
numerical points deviate from dependence (6) with in-
creasing ν

eff

Al

. These features are explained by the fact

that, for ν

eff

Al

< ν

cr

(ν

cr

≈ 0.15), the system con-

tains only isolated clusters whose sizes are substantially
smaller than the size of the calculation “specimen.”
With increasing aluminum concentration, the size of
clusters (on the average) increases; the appearance of
a cluster extended through the entire “specimen” (per-
colation cluster) and including a significant mass of the
initial aluminum particles becomes more probable [11].
For ν

eff

Al

> ν

cr

, a percolation cluster whose mass varies

from one calculation to another emerges in the system
with a probability close to unity, which increases the

Role of the Structure of Condensed Mixtures in the Formation of Agglomerates

439

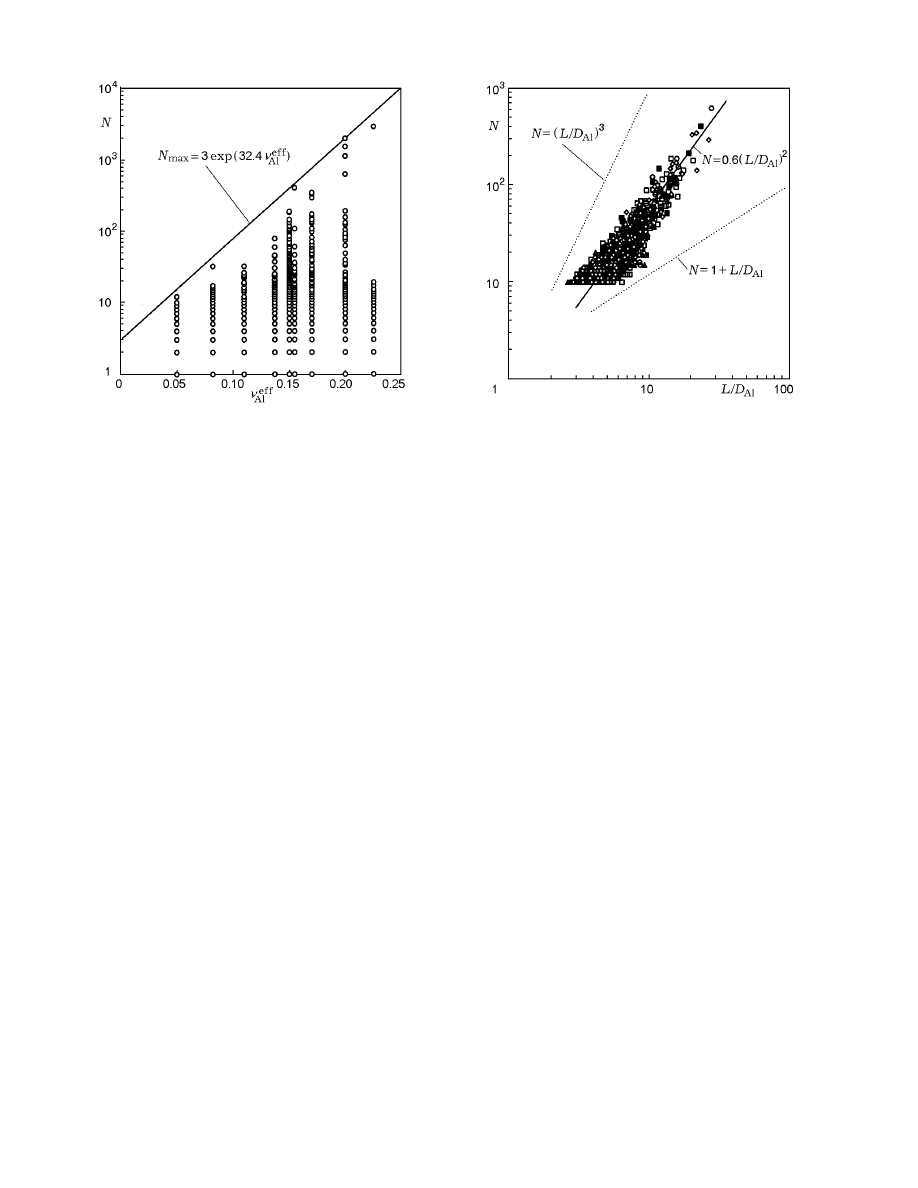
Fig. 2. Number of initial aluminum particles in clus-
ters for different initial concentrations of aluminum
in HCM (the curve indicates the upper boundary).

scatter in the values of D

43

. Thus, the concentration

ν

cr

≈ 0.15 is the percolation limit for a system of iden-

tical spherical particles.

The number of initial aluminum particles in dif-

ferent clusters for different effective concentrations of
aluminum is plotted in Fig. 2 for specimens 20

× 20 × 20

and 30

× 30 × 30.

For each value of ν

eff

Al

, there is a maximum number

of particles united into one cluster. The curve

N

max

= 3 exp (32.4 ν

eff
Al

)

(7)

limits all the calculation values from above and may be
considered as the dependence (in the statistical mean-
ing) of the maximum number of initial particles in the
cluster on the effective concentration of aluminum in
HCM. The estimate shows that dependence (7) limits
the mass of the maximum cluster with a probability of
higher than 0.96.

Thus, the mass of the greatest cluster and, hence,

the maximum possible diameter of subagglomerates

(without dispersion) equal to D

max

/D

Al

= N

1/3

max

≈

1.44 exp (10.8 ν

eff

Al

) increase exponentially with the con-

centration ν

eff

Al

.

Figure 1 shows the dependence of

D

max

/D

Al

on ν

eff

Al

. The dependence is plotted only for

the values ν

eff

Al

< ν

cr

, for which it makes sense. The-

oretically, for an infinite specimen, without allowance
for dispersion, we have D

max

/D

Al

→ ∞ as ν

eff

Al

→ ν

cr

.

The finite value of the diameter of the maximum sub-
agglomerate for ν

eff

Al

= ν

cr

, which was obtained in cal-

culations, is related to the finite size of the calculation

Fig. 3. Number of particles in the cluster versus its
maximum size.

HCM “specimens.” The exponential growth of the ag-
glomerate size with increasing aluminum concentration
in HCM was experimentally observed in [3]. In prac-
tice, this is manifested in the form of very large single
agglomerates found after burning of the HCM specimen.

In some recent works, the fractal character of en-

ergy release in HCM combustion is grounded [14]. Ob-
viously, this is possible only if the initial HCM structure
contains some fractal structures. An analysis of the re-
sults of mathematical simulation shows that there are
no fractal structures (in the rigorous meaning of this
notion) in the initial HCM structure, but it was found
that the clusters of the contacting metal particles in the
initial HCM form fractal-like structures.

An analysis shows that the clusters, on the average,

are extended in one of the directions. Figure 3 shows
the dependence of the number of particles in the clus-
ter on the maximum linear size of the cluster (L is the
greatest distance between the centers of its particles)
for various values of ν

eff

Al

. The calculation points are

grouped around the power dependence

N = A(L/D

Al

)

D

,

(8)

which is typical of fractal structures. Here D is a coeffi-
cient that may be considered as the “fractal dimension”
of the cluster and A is a constant factor. For identical
fine aluminum particles, D = 2 and A = 0.6.

A similar dependence was obtained for soot aggre-

gates formed in combustion of hydrocarbon fuels [15];
the fractal dimension of the aggregates is 1.74. This
is indicative of a single mechanism of formation of the

440

Rashkovskii

structure of aggregates (clusters) of particles regardless
of their nature.

The lower dotted curve in Fig. 3 corresponds to

the maximum possible length of the cluster for a given
number of particles, when the cluster is a straight-line
chain. The upper dotted curve in Fig. 3, vice versa,
refers to compact arrangement of particles in the clus-
ter, when they are concentrated inside a sphere of the
minimum possible diameter. Since the clusters are ex-
tended along a certain axis, they can be considered as
linear heat- and electroconducting elements connecting
the HCM burning surface with its deep layers.

A comparison of dependences (7) and (8) shows

that the maximum size of the greatest cluster increases
exponentially with increasing effective concentration of
aluminum in HCM: (L/D

Al

)

max

= 2.2 exp (16.2 ν

eff

Al

).

This dependence allows one to estimate the area of ap-
plicability of the above-considered method of indepen-
dent arrangement of AP and fine aluminum particles in
modeling the HCM structure. Obviously, this procedure
is admissible only if the characteristic distance between
AP particles ∆

AP

= k

D

D

AP

is significantly greater than

the size of the maximum cluster of aluminum particles
(∆

AP

L

max

). Here k

D

≈ (1/ν

AP

− 1)

1/3

is the pro-

portionality coefficient.

Thus, independent arrangement of AP and alu-

minum particles in the HCM volume during modeling
of the HCM structure is possible only for

D

Al

/D

AP

< (k

D

/2.2) exp (

−16.2 ν

Al

/(1

− ν

AP

)).

(9)

From this relation, for example, it follows that, for
ν

Al

= 0.1 and ν

AP

= 0.4, the structure of clusters is in-

dependent of the AP particle size if D

Al

/D

AP

< 0.035,

and for ν

AP

= 0.6 and the same value of ν

Al

, if

D

Al

/D

AP

< 0.007.

If inequality (9) is not satisfied, the mean-mass

size of subagglomerates or clusters depends on the AP
particle size even for finely disperse initial aluminum
particles. It follows from here that limit (5) of depen-
dence (4) is valid only if condition (9) is satisfied.

One important characteristic of the cluster is the

coordination number determining the strength of the
cluster and, hence, the strength of the frame layer on
the burning surface and also the tendency of the cluster
to integration into a single drop after its melting.

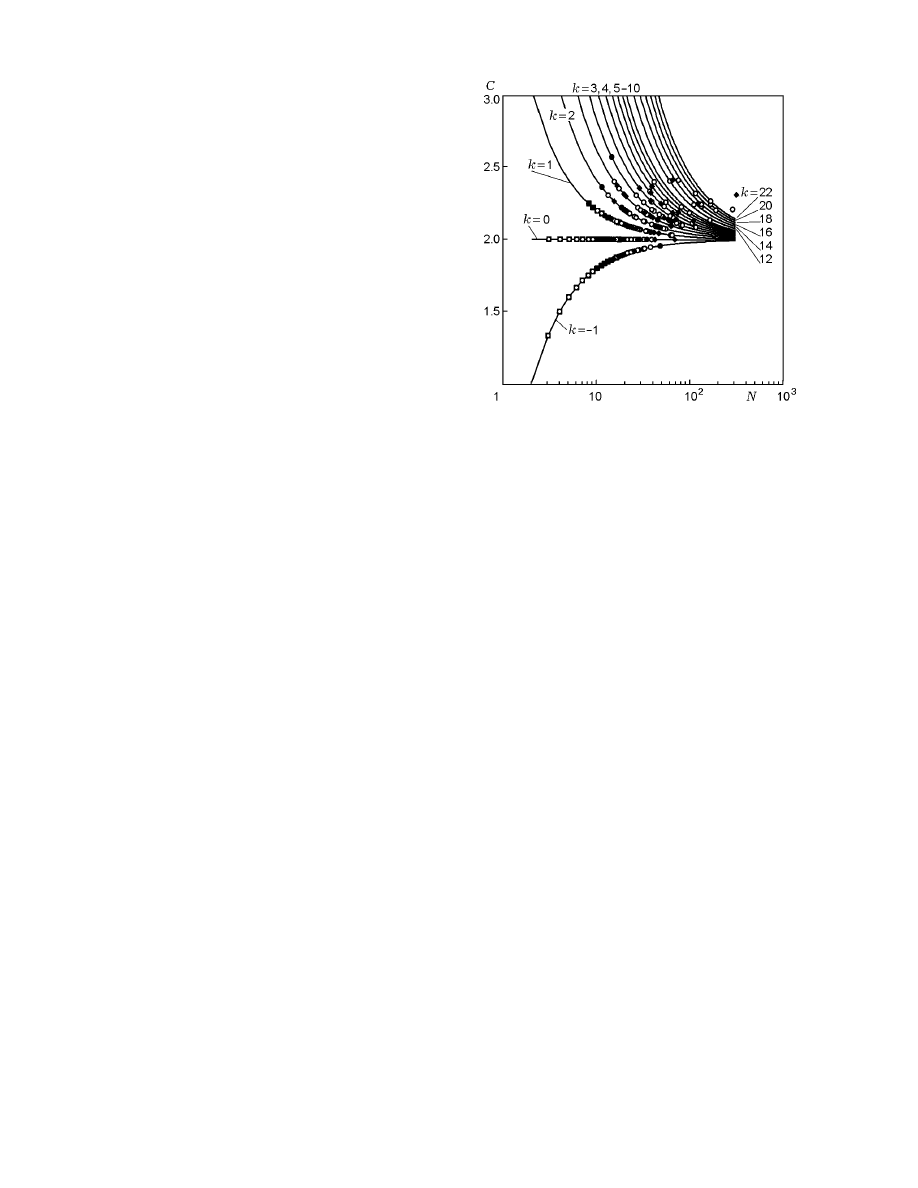
The points in Fig. 4 show the coordination numbers

C of the clusters, which were obtained by modeling the
HCM structure, as a function of the number of parti-
cles N in the cluster. The dependence C(N ) falls into a
discrete number of branches asymptotically approach-
ing the value C = 2, which is also one of the branches of
this dependence. Within each branch, the dependence
C(N ) is regular. The scatter of coordination numbers

Fig. 4. Coordination number of the cluster versus
the number of initial aluminum particles in the clus-
ter: the points are the coordination numbers of the
clusters obtained by modeling the HCM structure
and the curves show dependence (10).

of the clusters is manifested in the fact that they can
belong to different branches of the dependence C(N ).

The coordination number of the cluster is related

to the number of particles in the cluster as

C = 2 + 2 k/N,

(10)

where k =

−1, 0, 1, 2, . . . is the structural factor de-

termining the type of the cluster. Each branch of the
dependence C(N ) corresponds to its own value of k and
its own type of the cluster. Dependences (10) are plot-
ted by curves in Fig. 4.

An analysis of clusters that refer to different

branches of the dependence shows that clusters of differ-
ent types have a different number s of cyclic structures
(loops). The structural factor is related to the number
of loops in the cluster by the relation k = s

− 1. Fig-

ure 5 shows several simplest types of clusters for the
first three values of the parameter k, which illustrate
dependence (10). Note, dependence (10) can be readily
derived from the theory of graphs.

DISPERSION OF CLUSTERS
DURING MELTING

We consider the evolution of the cluster in the case

of rapid melting, which may occur in the course of HCM
combustion.

Role of the Structure of Condensed Mixtures in the Formation of Agglomerates

441

k = -1

k = 0

k = 1

Fig. 5. Simplest types of clusters for the first three
values of the structural factor k.

After rapid melting of clusters, an unstable sys-

tem of contacting liquid particles is formed.

Cap-

illary forces are responsible for mutual attraction of
particles connected by liquid bridges, and the system
shrinks into more compact structures. For compara-
tively small clusters, this process leads to the forma-
tion of one drop-subagglomerate from the cluster; for
comparatively large clusters, because of their hetero-
geneous structure, dispersion of the liquid porous sys-
tem is possible, which leads to the formation of several
drops-agglomerates from the cluster.

We consider the model of dispersion of a liquid

metal system under the action of capillary forces. We
represent the melted cluster in the form of a system of
point particles with paired attraction forces acting be-
tween them; these forces are responsible for capillary
interaction of the contacting melted particles of alu-
minum. Under the action of these forces, some par-
ticles come closer, and some particles go apart. Thus,
the evolution of the melted cluster can be approximately
described by a system of equations of motion of point
particles under the action of forces of mutual attrac-
tion. When two particles, in the course of evolution of
the system, go apart at a distance greater than some
critical value r

cr

, the liquid bridge connecting them is

broken, and mutual attraction of the particles vanishes.
In the course of time, all possible bridges between the
particles in the system will be broken, and the parti-
cles retaining the bridges will integrate into individual
drops-subagglomerates.

We assume that the processes of melting of initial

metal particles and breaking of bridges between them

are rather fast, i.e., the inequality µD

cl

/σt

melt

1 is

satisfied.

Because of the high viscosity of the melted metal,

the process of evolution of the melted cluster under the
action of capillary forces is low inertial.

This means that the inertial terms in the equations

of motion may be neglected. Assuming that the force
of viscosity, on the average, is proportional to particle
velocity, we can significantly simplify the equations of
evolution. By analogy with [11], we can easily show that
the motion of particles is described by Eq. (1), where the
quantity ∆

ij

is proportional to the capillary force acting

between the melted aluminum particles connected by a
liquid bridge. We introduce the parameters ϕ

ij

= 1

if the aluminum particles are connected by the liquid
bridge and ϕ

ij

= 0 if there is no capillary connection

between these particles.

In the course of evolution of the system of parti-

cles, owing to breakdown of bridges, the parameters ϕ

ij

change from 1 to 0; the reverse process of the formation
of contacts of previously non-contacting aluminum par-
ticles may be neglected. The reason is that the latter
process is more probable at large deformations of the
initial structure in the course of evolution, whereas the
breakdown of all possible bridges and, hence, dispersion
of the clusters finish already at rather small deforma-
tions of the system. We assume that the particles i and
j were in contact in the initial cluster, i.e., ϕ

ij

= 1,

and the distance between the centers of these particles
exceeded the value r

cr

at a certain time in the course of

evolution of the melted cluster. From this moment to
the end of calculations, we assumed that ϕ

ij

= 0. Since

there is only one linear scale in a system of identical
aluminum particles, we assumed that r

cr

= k

s

D

Al

. The

test calculations in the range k

s

= 1.2–2 showed that the

exact value of the parameter k

s

weakly (within several

percent) affects the mean-mass diameter of subagglom-
erates formed upon dispersion of clusters; therefore, in
subsequent calculations, we assumed that k

s

= 1.5.

The capillary force acting between two particles de-

pends on the distance between their centers and on the
size of these particles; the capillary force decreases with
increasing distance between the particles. Dispersion
was calculated for different dependences of the capillary
force on the distance between the particles. The calcu-
lations show that the particular form of this dependence
has a weak effect on the final results. The reason is that
the bridges are broken at comparatively small changes
in the distance between the particles, and the capillary
force changes little within these limits. This allows one
to consider the capillary force to be constant within the
entire time of evolution of the system. Then, redefining
the time scale, as it was done in [11], we obtain the fol-

442

Rashkovskii

lowing expression for the dimensionless capillary force
∆

ij

:

∆

ij

=

−ϕ

ij

.

(11)

The calculation was performed in two stages. At

the first stage, for given HCM parameters, the hard
spheres were located in a given volume (simulation of
the initial HCM structure), and clusters were identified.
At the second stage, system (1), (11) was solved, which
describes cluster evolution after melting under the ac-
tion of capillary forces; the technique used to solve this
system was described in [11].

To calculate the mass of subagglomerates, it is in-

sufficient to take into account the breakdown of all pos-
sible capillary bridges, which occurs already within sev-
eral first steps of calculations. If the calculation is ter-
minated immediately after all bridges are broken, it may
yield an underestimated mass of subagglomerates. In-
deed, if the aluminum concentration in the initial HCM
is rather high, there may exist small clusters located
(encapsulated) inside larger clusters but not contacting
with the latter. Subsequent compression of the large
melted subagglomerate results in absorption of all small
clusters encapsulated in it, which increases the mean
mass of subagglomerates. To take this effect into ac-
count, the calculations included a periodic analysis of
the mass distribution function of subagglomerates (clus-
ters), and new clusters of contacting and intersecting
particles were identified.

The calculation of the dis-

persion process was terminated when the distribution
function changed no longer, which indicated termina-
tion of dispersion processes and capturing of small clus-
ters by the large ones. An analysis of the calculation
results shows that this procedure allows one to model
not only the capturing of smaller clusters encapsulated
in the large cluster but also encapsulation of small AP
particles by agglomerates, which was observed experi-
mentally.

The convergence of the algorithm was proved by a

series of calculations with different values of the time
step. For the three-dimensional problem, the mass dis-
tribution functions of subagglomerates were compared;
for the two-dimensional problem (disks on the plane),
a visual comparison of arrangement of particles in the
computational domain was performed. Complete coin-
cidence was observed for the time step decreased from
0.01 to 0.001 (the time is dimensionless).

Note, the algorithm of dispersion is, in a cer-

tain sense, reciprocal to the method of viscous suspen-
sion [11]: in the latter case, repulsion forces act between
the particles, which are necessary to eliminate intersec-
tion of particles; in the former case, vice versa, there
are attraction forces modeling coalescence of particles
due to capillary effects.

The filled points in Fig. 1 show the calculation re-

sults for the mean-mass diameter of subagglomerates
after dispersion of clusters. Within the entire calcu-
lated range of aluminum concentrations, the mean-mass
diameter of subagglomerates is described by a single de-
pendence (6). For v

eff

Al

< 0.15 (i.e., below the percola-

tion level), the calculated particle size is identical with
and without allowance for dispersion. This indicates
that small stable clusters are formed in the system if
the aluminum concentration is comparatively low; upon
melting, these clusters do not split into smaller ones and
do not merge with others.

COARSELY DISPERSE ALUMINUM

As was shown above, for finely disperse aluminum,

the mean-mass size of subagglomerates in the limit
D

Al

/D

AP

→ 0 is proportional to the diameter of initial

aluminum particles. For a system of identical particles,
this follows from the reasons of dimensionality, since the
problem has only one linear scale: D

Al

. This situation is

retained only as long as condition (9) holds. Otherwise,
the spectrum of subagglomerates (clusters) depends on
the distribution of AP particles in the HCM volume.
The estimates show that relation (9) is valid for real
HCM only for very low concentrations of aluminum.

If relation (9) is not satisfied, the mean-mass di-

ameter of subagglomerates tends to a finite value in the
presence of AP particles in the system, even in the limit
D

Al

/D

AP

→ 0, especially at high concentrations of alu-

minum, when dispersion plays the main role.

When condition (9) is not satisfied, dependence (4)

acquires the form

D

43

= D

AP

D

1

43

(D

Al

/D

AP

, ν

Al

, ν

AP

),

(12)

where

D

1

43

(D

Al

/D

AP

, ν

Al

, ν

AP

)

is

the

dimen-

sionless

function,

which

has

the

finite

limit

lim

D

Al

/D

AP

→0

D

1

43

(D

Al

/D

AP

, ν

Al

, ν

AP

) = D

1

43

(0, ν

Al

, ν

AP

).

This means that the mean-mass diameters of subag-
glomerates for fine aluminum particles, when condition
(9) is not satisfied, are proportional to the AP particle
diameter:

D

0

43

= D

AP

D

1

43

(0, ν

Al

, ν

AP

).

(13)

Thus, for fine aluminum particles, criterion (9) sep-

arates the cases where the mean-mass diameter of sub-
agglomerates is proportional to the diameter of the ini-
tial aluminum particles and where it is proportional to
the diameter of the initial AP particles.

Aluminum particles that do not satisfy condition

(9) are conventionally called coarsely disperse particles.
In this case, AP particles directly affect the distribution

Role of the Structure of Condensed Mixtures in the Formation of Agglomerates

443

of aluminum particles in the HCM volume and, hence,
the spectrum of clusters and subagglomerates. In mod-
eling such HCM, independent arrangement of aluminum
and AP particles is no longer allowed.

In modeling the HCM structure with coarse alu-

minum particles by the method of viscous suspen-
sion [11], large (AP) and small (aluminum) particles
were jointly arranged in a given volume.

For simplicity, we assume that AP and aluminum

powders have narrow fractions. Thus, the problem re-
duces to arrangement of two types of solid spherical
particles in a given volume. All particles within one
type are identical.

We use dimensionless linear scales normalized to

the AP particle diameter. In the variables considered,
the AP particle diameter equals unity, and the alu-
minum particle diameter is d

Al

= D

Al

/D

AP

.

The calculations were performed both without dis-

persion of clusters and with allowance for their disper-
sion during melting in the combustion wave. In calcula-
tions, we used the algorithms of [11] and those described
above. It was found in calculations that the clusters
of contacting aluminum particles, which arise in the c-
phase when the heat wave passes, have also a fractal-like
structure and are described by relation (8). In partic-
ular, for ν

AP

= 0.38 and various values of ν

Al

and d

Al

,

we obtained A = 0.8 and D = 1.8. Thus, the presence
of large AP particles slightly decreases the fractal di-
mension of clusters. In the case considered, the clusters
have the same statistical structure as that in the ab-
sence of AP particles. In particular, the coordination
number of the clusters is described by dependence (10)
(see also Figs. 4 and 5).

The influence of AP particles is mainly manifested

in the dispersion of clusters in the combustion wave
and in the formation of subagglomerates. The gener-
alized calculation results for the process of dispersion
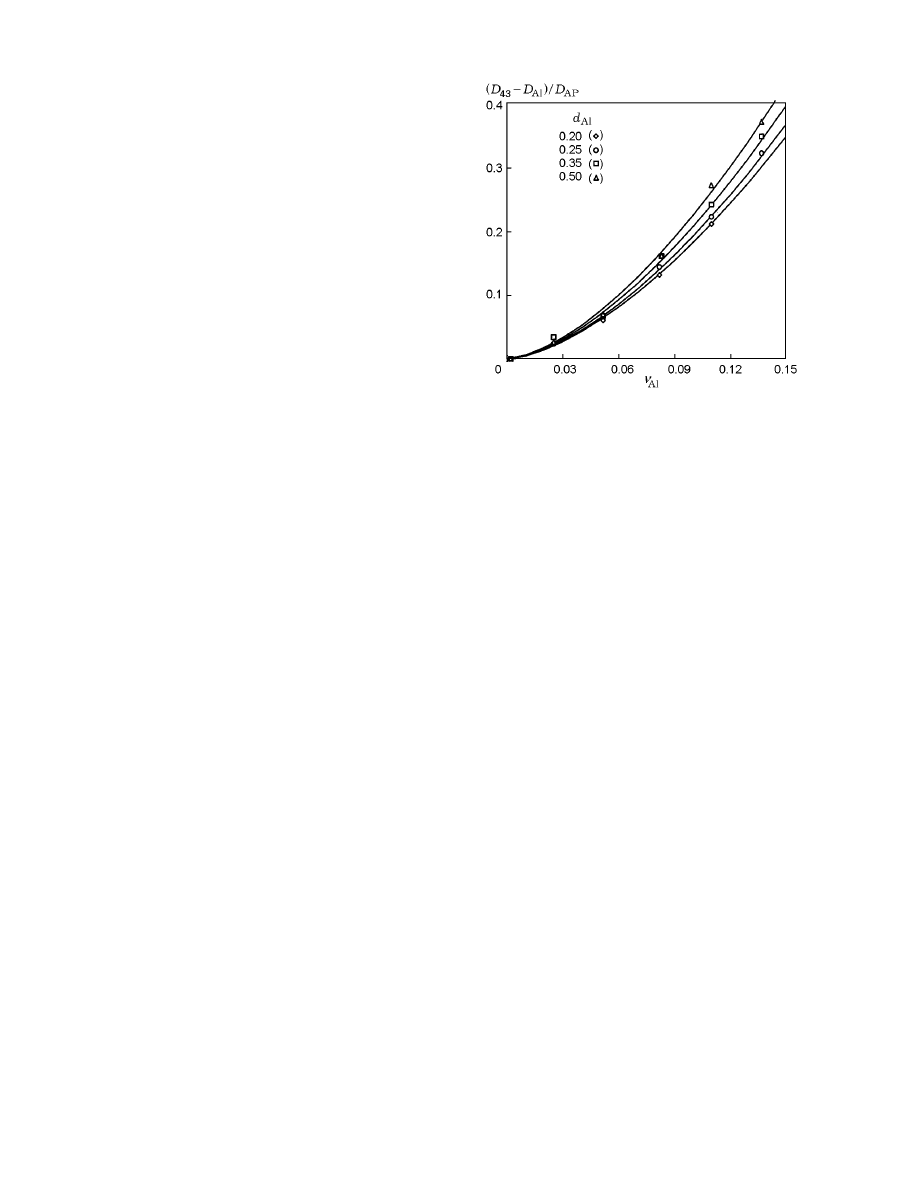
of clusters are plotted in Fig. 6 in the form of the rela-
tive mean-mass diameter of subagglomerates versus the
aluminum concentration ν

Al

for various values of d

Al

for ν

AP

= 0.38 (the calculation results are shown by

points). The results obtained are well approximated by
the analytical dependence

d

43

= d

Al

+ αd

m
Al

(ν

eff

Al

)

n

(14)

for

α = 4.79,

m = 0.22,

n = 1.6

(15)

(solid curves in Fig. 6).

Dependence (14) can be extended to arbitrary val-

ues of ν

AP

, if we assume that the coefficients α, m, and

n are functions of ν

AP

. The limiting case ν

AP

= 0 cor-

responds to the above-considered case of independent
arrangement of aluminum and AP particles when condi-
tion (9) is satisfied. Thus, for ν

AP

→ 0, dependence (14)

Fig. 6. Mean-mass diameter of subagglomerates af-
ter dispersion versus the volume concentration of alu-
minum in HCM for coarse aluminum particles for
ν

AP

= 0.38: the points are the calculation results,

and the curves show dependence (14).

should transform to dependence (6). In other words, as
ν

AP

→ 0, we have α → 5.5, m → 1, and n → 1. As-

suming that the dependence of α, m, and n on ν

AP

is

linear, we obtain

α = 5.5

− 2ν

AP

, m = 1

− 2ν

AP

, n = 1 + 1.5ν

AP

.

(16)

The calculation by formula (14) with parameters (16)
for ν

AP

= 0.38 yields an error of less than 10% as com-

pared to the data of Eq. (15), which is fairly acceptable
if we take into account the approximate character of the
model.

Dependences (14) and (16) show that the ef-

fect of dispersion of the initial aluminum particles on
the mean-mass diameter of subagglomerates becomes
weaker with increasing ν

AP

. The same conclusion fol-

lows from the above analysis.

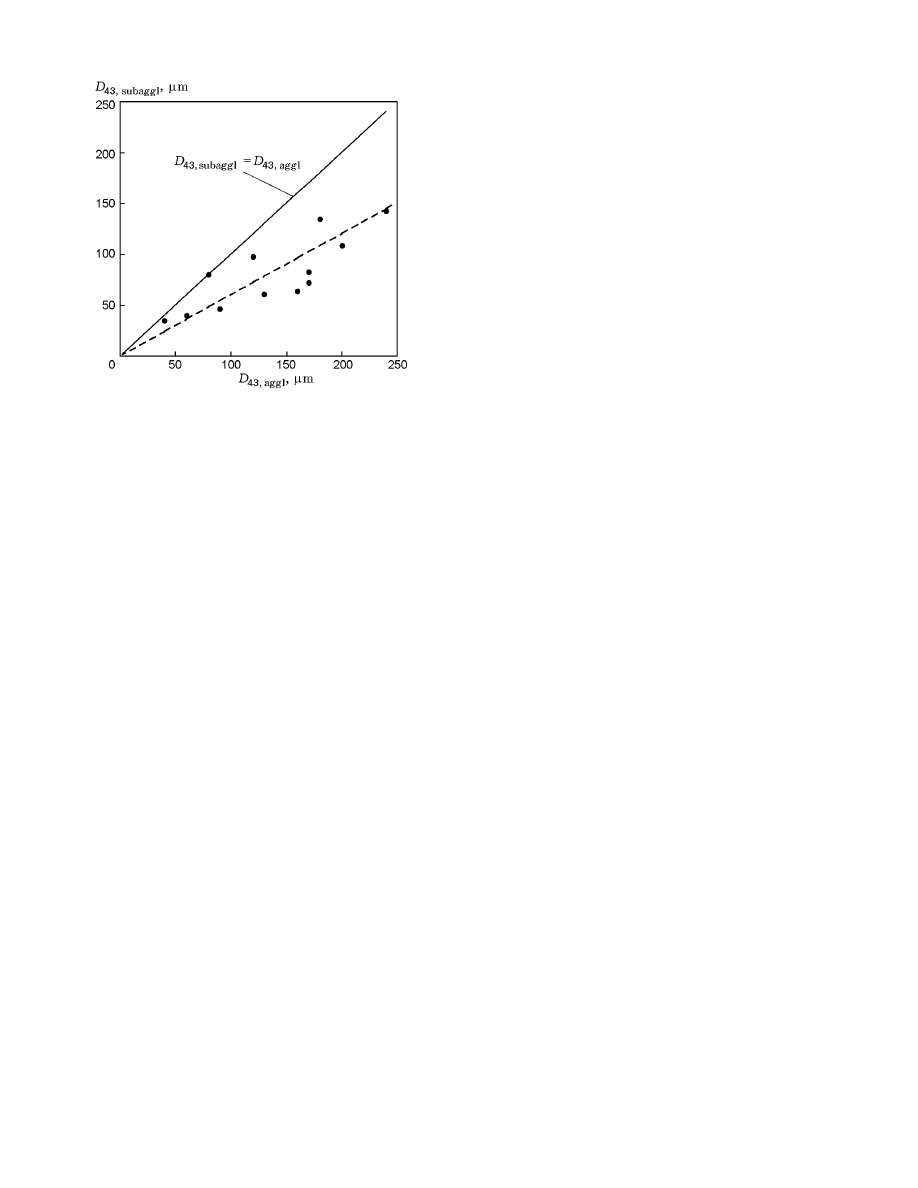
For comparison, Fig. 7 shows the mean-mass diam-

eters of agglomerates obtained experimentally [5] for a
certain class of HCM and the mean-mass sizes of sub-
agglomerates calculated by formulas (14) and (16) for
the same compositions. On the average, the calculated
mean-mass diameters of subagglomerates are 1.7 times
smaller than the size of agglomerates formed. This in-
dicates that the agglomeration process does not end by
the formation of subagglomerates from clusters of con-
tacting particles: intense integration of individual sub-
agglomerates into larger particles, agglomerates, pro-
ceeds at the burning surface. On the average, integra-
tion of five subagglomerates is required to form the final
agglomerates for all the compositions considered. The

444

Rashkovskii

Fig. 7. Comparison of experimental values of the
mean-mass size of agglomerates obtained in [5] and
the mean-mass size of subagglomerates calculated by
formulas (14) and (16): the dashed curve is the ap-
proximation of experimental data.

reason may be that dispersion of the cluster in the near-
surface layer does not have enough time to end prior to
reaching the burning surface, and subagglomerates are
connected by bridges from melted or sintered aluminum
particles.

CONCLUSIONS

Mathematical simulation of the structure of met-

allized heterogeneous condensed mixtures is performed.
The evolution of a system of aluminum particles in the
c-phase is studied in the case of a heat wave passing
over the HCM. It is shown that a system of clusters
of contacting aluminum particles is formed upon rapid
heating of the heterogeneous condensed mixture. The
particles may sinter to form a porous system which,
upon further heating, melts and disperses into indi-
vidual drops — subagglomerates under the action of
surface-tension forces.

The structure of clusters of contacting particles

and the mean-mass diameters of subagglomerates are
examined, depending on the dispersion of components
and their concentration in HCM. It is shown that the
contacting aluminum particles in a heterogeneous con-
densed mixture form fractal-like structures, which may
play a significant role in the HCM combustion process.

A correlation dependence of the mean-mass size of

subagglomerates on the parameters of the initial HCM
is obtained.

It is shown that, in the case of low concentrations

of aluminum in HCM, the mean-mass diameters of sub-
agglomerates are proportional to the diameter of the
initial aluminum particles and depend weakly on disper-
sion of AP particles; for comparatively high concentra-
tions, the mean-mass size of subagglomerates depends
on dispersion of AP particles. This property, appar-
ently, is also inherent in agglomerates.

REFERENCES

1. N. S. Cohen, “A pocket model for aluminum agglom-

eration in composite propellants,” AIAA J., 21, No. 5,

720–725 (1983).

2. T. K. Sambamurthi, E. W. Price, and R. K. Sigman,

“Aluminum agglomeration in solid-propellant combus-

tion,” AIAA J., 22, No. 8, 1132–1138 (1984).

3. L. Ya. Kashporov, Yu. V. Frolov, G. A. Ostretsov, and

V. N. Stepanov, “Investigation of the agglomeration

of the condensed phase with the combustion of model

compositions with a high content of powdered metals,”

Combust. Expl. Shock Waves, 11, No. 1, 27–35 (1975).

4. V. A. Babuk, V. P. Belov, V. V. Khodosov, and

G. G. Shelukhin, “Investigation of the agglomeration

of aluminum particles during the combustion of met-

allized composite condensed systems,” Combust. Expl.

Shock Waves, 21, No. 3, 287–291 (1985).

5. V. G. Grigor’ev, V. E. Zarko, and K. P. Kutsenogii,

“Experimental investigation of the agglomeration of alu-

minum particles in burning condensed systems,” Com-

bust. Expl. Shock Waves, 17, No. 3, 245–250 (1981).

6. V. G. Grigor’ev, K. P. Kutsenogii, and V. E. Zarko,

“Model of aluminum agglomeration during the combus-

tion of a composite propellant,” Combust. Expl. Shock

Waves, 17, No. 4, 356–362 (1981).

7. S. A. Rashkovsky, “Metal agglomeration in solid propel-

lants combustion: Part 1. Dynamical model of process,”

Combust. Sci. Technol., 136, 125–148 (1998).

8. S. A. Rashkovsky, “Metal agglomeration in solid pro-

pellants combustion: Part 2. Numerical experiment,”

Combust. Sci. Technol., 136, 149–169 (1998).

9. V. D. Gladun, Yu. V. Frolov, L. Ya. Kashporov, et al.,

“Coalescence of particles of powdered metals and their

compounds,” Preprint, Inst. Chemical Physics, Acad. of

Sci. of the USSR, Chernogolovka (1976).

10. V. A. Val’tsiferov and A. E. Stepanov, “Calculation of

metal particle coordination numbers in mixed condensed

systems,” Combust. Expl. Shock Waves, 25, No. 4, 440–

441 (1989).

Role of the Structure of Condensed Mixtures in the Formation of Agglomerates

445

11. S. A. Rashkovskii, “Structure of heterogeneous con-

densed mixtures,” Combust. Expl. Shock Waves, 35,

No. 5, 523–531 (1999).

12. V. M. Frolov, “Calculation of statistical cross-section

of composite solid propellant system with account for

anisotropic distribution of the binder,” Combust. Expl.

Shock Waves, 30, No. 4, 437–442 (1994).

13. V. A. Babuk, V. A. Vasil’ev, and V. V. Sviridov, “Mod-

eling the structure of composite solid rocket fuel,” Com-

bust. Expl. Shock Waves, 35, No. 2, 144–148 (1999).

14. Yu. V. Frolov and A. N. Pivkina, “Fractal structure and

features of energy-release (combustion) processes in het-

erogeneous condensed systems,” Combust. Expl. Shock

Waves, 33, No. 5, 513–527 (1997).

15. U. O. Koylu, C. S. McEnally, D. E. Rosner, and L. D. Pf-

efferle, “Simultaneous measurements of soot volume

fraction and particle size/microstructure in flames us-

ing a thermophoretic sampling technique,” Combust.

Flame, 110, 494–507 (1997).