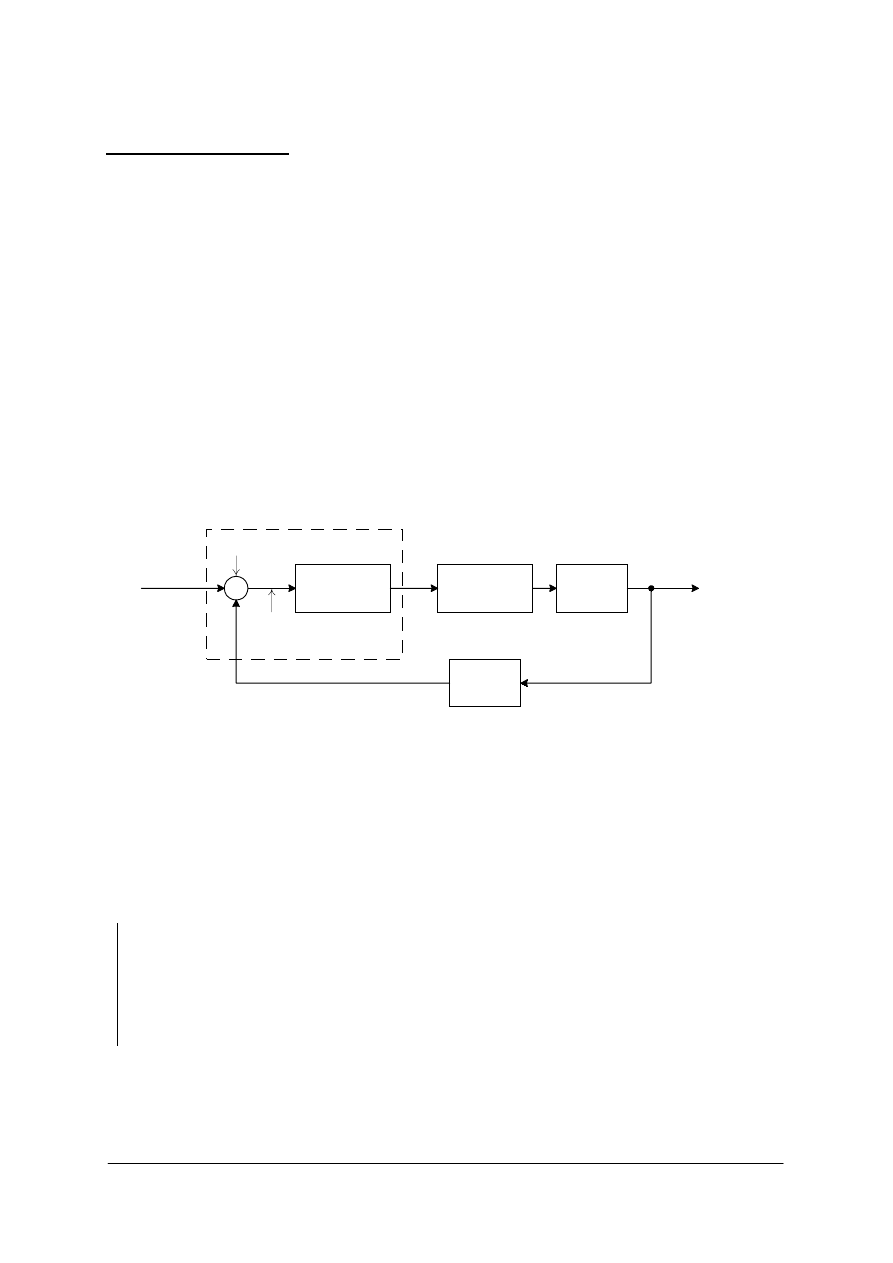
Ostatnia aktualizacja: 03-04-23



M. Tomera

R E G U L A T O R Y

1. WPROWADZENIE

Regulator automatyczny jest urz!dzeniem, którego zadaniem jest sterowanie procesem . W uk"adach
z ujemnym sprz#$eniem zwrotnym regulator wyznacza zadan! warto%& wielko%ci steruj!cej na
podstawie uchybu regulacji, czyli ró$nicy pomi#dzy warto%ci! pomierzon! a warto%ci! zadan! tej
wielko%ci . Na rysunku 1 przedstawiono schemat blokowy uk"adu sterowania przemys"owego, który
sk"ada si# z regulatora automatycznego, urz!dzenia wykonawczego, obiektu i czujnika (element
pomiarowy). Sygna" wyj%ciowy z regulatora podawany jest na urz!dzenie wykonawcze, takie jak
zawór, silnik elektryczny, si"ownik hydrauliczny lub pneumatyczny. Urz!dzenie wykonawcze
dokonuje przestawienia punktu pracy obiektu, stosownie do sygna"u steruj!cego po to aby sygna"
wyj%ciowy pokrywa" si# z sygna"em zadanym.

Czujnik lub element pomiarowy jest urz!dzeniem, które przetwarza zmienn! wyj%ciow! na inn!

odpowiedni! zmienn!, tak! jak przesuni#cie, ci%nienie lub napi#cie, które mo$e zosta& u$yte do
porównania wyj%cia z wej%ciowym sygna"em zadanym. Element ten znajduje si# w p#tli sprz#$enia
zwrotnego uk"adu regulacji. Sygna" zadany równie$ musi by& przetworzony do tych samych jednostek
w jakich jest sygna" sprz#$enia z czujnika lub elementu pomiarowego.

Sygna"

zadany

Wzmacniacz

Wykonawczy

sygna" uchybu

Wykrywacz uchybu

Urz!dzenie

wykonawcze

Obiekt

Czujnik

−

Wyj%cie

Regulator automatyczny

u(t)

e(t)

r(t)

y(t)

Rys. 1. Schemat blokowy uk"adu sterowania przemys"owego.

2. KLASYFIKACJA REGULATORÓW PRZEMYS!OWYCH

Najbardziej znanym regulatorem u$ywanym w praktyce jest regulator PID, w którym w nazwie
znajduj! si# litery pochodz!ce od rodzajów sterowania jakie on w sobie zawiera: proporcjonalne P
(ang. proporcjonal), ca"kuj!ce I (ang. Integral), ró$niczkuj!ce D (ang. Derivative). Stosowane s!
równie$ wersje uproszczone regulatora PID sk"adaj!ce si# z wybranych elementów sk"adowych tego
regulatora (P, I, PI, PD). Regulatory przemys"owe w zale$no%ci od rodzaju sterowania klasyfikowane
s! nast#puj!co:

1. Regulator dwupo"o$eniowy
2. Regulator proporcjonalny P
3. Regulator ca"kuj!cy I
4. Regulator proporcjonalno-ca"kuj!cy PI
5. Regulator proporcjonalno-ró$niczkuj!cy PD
6. Regulator proporcjonalno-ca"kuj!co-ró$niczkuj!cy PID

W wi#kszo%ci regulatorów przemys"owych jako 'ród"a mocy wykorzystywane s!: napi#cie, olej lub
gaz. W zale$no%ci od rodzaju 'ród"a mocy regulatory mog! by& klasyfikowane jako pneumatyczne,
hydrauliczne lub elektroniczne. Rodzaj u$ytego regulatora zale$y od natury obiektu, warunków

Regulatory automatyczne

2

operacyjnych uwzgl#dniaj!cych bezpiecze(stwo, koszt, dost#pno%&, niezawodno%&, dok"adno%&, wag#
i rozmiar.

3. RODZAJE REGULATORÓW

3.1. REGULATOR DWUPO!O"ENIOWY

W uk"adach sterowania dwupo"o$eniowego, element wykonawczy ma tylko dwa ustalone po"o$enia,
które w wielu przypadkach polegaj! na za"!czeniu lub wy"!czeniu urz!dzenia. Sterowanie
dwupo"o$eniowe jest stosunkowo proste i niedrogie i z tych powodów jest szeroko stosowane
zarówno w uk"adach sterowania przemys"owego jak i gospodarstwa domowego.

Sygna" wyj%ciowy z regulatora oznaczany jest zazwyczaj jako u(t), natomiast wej%ciem do

regulatora jest wykonawczy sygna" uchybu e(t). W sterowaniu dwupo"o$eniowym sygna" wyj%ciowy
u(t) przyjmuje jedn! z dwu warto%ci: maksymaln! lub minimaln!; w zale$no%ci od tego czy sygna"
wykonawczy uchybu jest dodatni lub ujemny.







>

<

=

0

)

(

0

)

(

)

(

2

1

t

e

U

t

e

U

t

u

dla

dla

(1)

gdzie

1

U oraz

2

U s! sta"ymi. Minimalna warto%&

1

U jest zazwyczaj równa zero lub

2

U

−

.

Dwupo"o$eniowe regulatory s! zazwyczaj urz!dzeniami elektrycznymi w których najcz#%ciej
elektryczny solenoid steruje zaworem. Pneumatyczne regulatory dwupo"o$eniowe z bardzo du$ym
wzmocnieniem zachowuj! si# jak regulatory dwupo"o$eniowe i czasami nazywane s!
dwupo"o$eniowymi regulatorami pneumatycznymi.

−

u(t)

e(t)

U

1

U

2

−

e(t)

U

1

U

2

strefa

nieczu"o%ci

u(t)

(a)

(b)

Rys. 2. Schemat blokowy regulatora dwupo"o$eniowego, (a) bez strefy nieczu"o%ci, (b) ze stref! nieczu"o%ci.

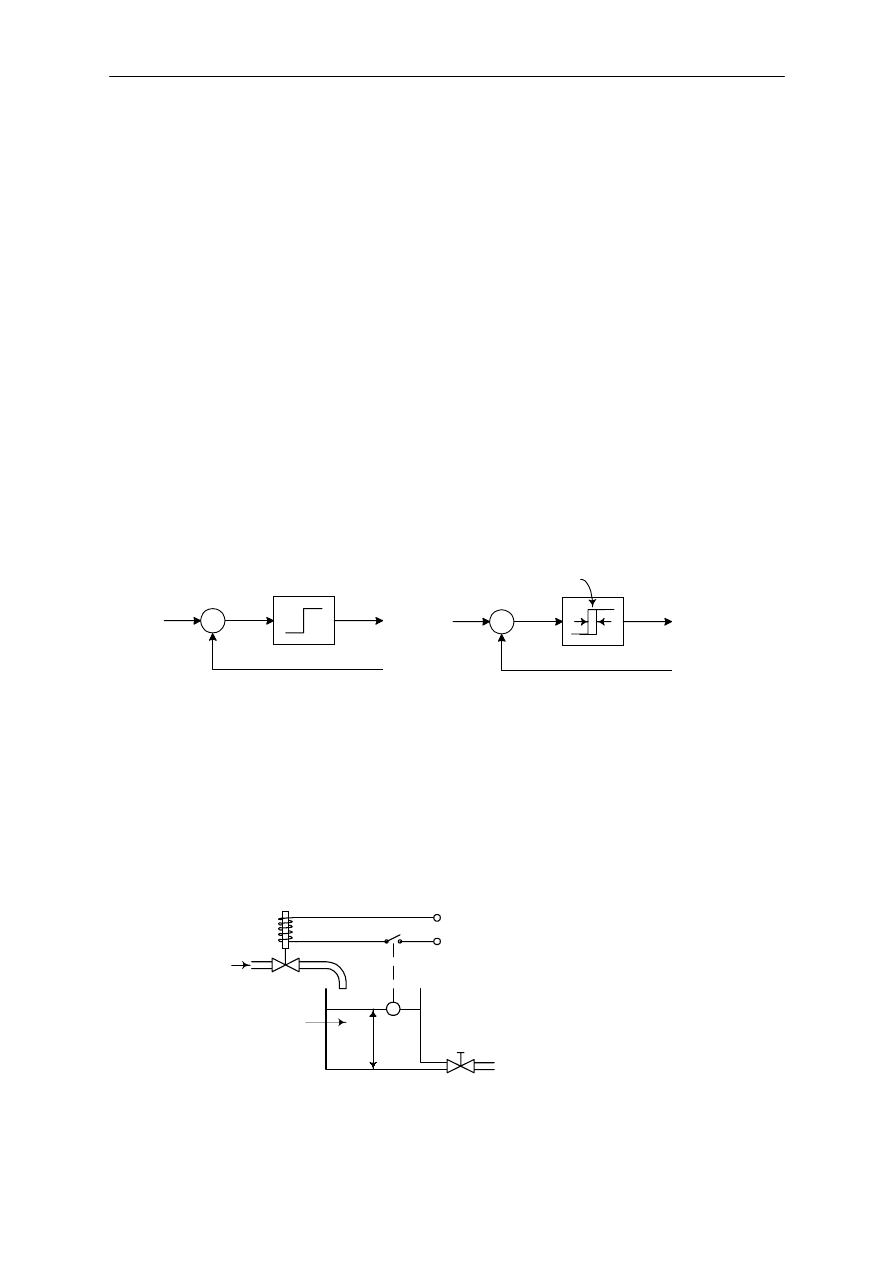
Na rysunku 2(a) i 2(b) pokazane zosta"y schematy blokowe regulatora dwupo"o$eniowego. Zakres,
który musi zosta& pokonany przez wykonawczy sygna" uchybu, aby pojawi"o si# prze"!czenie,
nazywany jest stref! nieczu"o%ci. Strefa nieczu"o%ci zaznaczona zosta"a na rysunku 2(b). Taka strefa
nieczu"o%ci powoduje, $e regulator utrzymuje sta"! warto%& wyj%ciow!, a$ wykonawczy sygna" uchybu
przekroczy nieznacznie warto%& zero. W pewnych przypadkach, strefa nieczu"o%ci jest wynikiem
tarcia lub luzów w uk"adzie. Bardzo cz#sto wprowadza si# tak! stref#, aby zabezpieczy& uk"ad przed
zbyt cz#stymi operacjami prze"!cze( mechanizmu.

Rozwa$, uk"ad sterowania poziomem cieczy w zbiorniku pokazany na rysunku 3, gdzie zawór

elektromagnetyczny zastosowany zosta" do sterowania przep"ywem wody.

h

V

q

i

Rys. 3. Uk"ad sterowania poziomem cieczy.

Regulatory automatyczne

3

Taki zawór mo$e by& otwarty lub zamkni#ty. Z takim dwupo"o$eniowym sterowaniem, pr#dko%&
przep"ywu wody jest sta"! dodatni! lub równ! zero. Jak zosta"o to pokazane na rysunku 4, wyj%ciowy
sygna" przemieszcza si# pomi#dzy dwoma ograniczeniami wymaganymi do tego aby element
wykonawczy przesuwa" si# z jednej ustalonej pozycji w drug!. Zauwa$, $e krzywa wyj%cia pod!$a
jedn! z dwóch krzywych ekspotencjalnych, jedna odpowiada krzywej nape"niania, a druga krzywej
opró$niania zbiornika. Takie oscylacje wyj%ciowe pomi#dzy dwoma ograniczeniami s! typowymi
charakterystykami odpowiedzi uk"adu sterowanego dwupo"o$eniowo.

t

h(t)

Strefa nieczu"o#ci

0

Rys. 4. Poziom h(t) w uk"adzie sterowania poziomem cieczy z rysunku 3.

Z rysunku 4 wida&, $e amplituda oscylacji wyj%ciowych mo$e zosta& zredukowana przez zmniejszenie
strefy nieczu"o%ci. Zmniejszenie strefy nieczu"o%ci powoduje zwi#kszenie liczby prze"!cze( na minut#
i w efekcie skrócenie czasu $ycia urz!dzenia.

3.2. REGULATOR PROPORCJONALNY P

Dla regulatora proporcjonalnego, zale$no%& pomi#dzy wyj%ciem regulatora u(t) i wykonawczym
sygna"em uchybu e(t)

)

(

)

(

t

e

K

t

u

p

=

(2)

Transmitancja regulatora proporcjonalnego

p

R

K

s

E

s

U

s

G

=

=

)

(

)

(

)

(

(3)

gdzie

p

K jest wzmocnieniem proporcjonalnym. Regulator proporcjonalny jest w istocie

wzmacniaczem z przestrajalnym wzmocnieniem.

3.3. REGULATOR CA!KUJ#CY I

W regulatorze ze sterowaniem ca"kuj!cym, warto%& wyj%ciowa regulatora u(t) jest przyrostem
proporcjonalnym do wykonawczego sygna"u uchybu e(t).

)

(

)

(

t

e

K

dt

t

du

i

=

(4)

lub

∫

=

t

i

dt

t

e

K

t

u

0

)

(

)

(

(5)

gdzie

i

K jest przestrajaln! sta"!. Transmitancja regulatora ca"kuj!cego

s

K

s

E

s

U

s

G

i

R

=

=

)

(

)

(

)

(

(6)

Regulatory automatyczne

4

3.4. REGULATOR PROPORCJONALNO-CA!KUJ#CY PI

Sterowanie regulatora proporcjonalno-ca"kuj!cego zdefiniowane jest jako

∫

+

=

t

i

p

dt

t

e

K

t

e

K

t

u

0

)

(

)

(

)

(

(7)

lub w postaci transmitancji









+

=

=

s

T

K

s

E

s

U

s

G

i

p

R

1

1

)

(

)

(

)

(

(8)

gdzie

i

T nazywa si# czasem ca"kowania.

3.5. REGULATOR PROPORCJONALNO-RÓ"NICZKUJ#CY PD

Sterowanie regulatora proporcjonalno-ró$niczkuj!cego zdefiniowane jest jako

dt

t

de

K

t

e

K

t

u

d

p

)

(

)

(

)

(

+

=

(9)

i w postaci transmitancji

(

)

s

T

K

s

E

s

U

s

G

d

p

R

+

=

=

1

)

(

)

(

)

(

(10)

gdzie

d

T nazywane jest czasem ró$niczkowania.

3.6. REGULATOR PROPORCJONALNO-CA!KUJ#CO-RÓ"NICZKUJ#CY PID

Po"!czenie sterowania proporcjonalnego, ca"kuj!cego i ró$niczkuj!cego nosi nazw# sterowania PID.
To po"!czenie ma zalety ka$dego z trzech sk"adników. Równanie regulatora w postaci czasowej

dt

t

de

T

K

dt

t

e

T

K

t

e

K

t

u

d

p

t

i

p

p

)

(

)

(

)

(

)

(

0

∫

+

+

=

(9)

lub w postaci transmitancji









+

+

=

=

s

T

s

T

K

s

E

s

U

s

G

d

i

p

R

1

1

)

(

)

(

)

(

(10)

gdzie

p

K jest wzmocnieniem proporcjonalnym,

i

T czasem ca"kowania oraz

d

T czasem

ró$niczkowania. Schemat blokowy regulatora PID pokazany jest na rysunku 5.

K

p

(1 + T

i

s +T

i

T

d

s

2

)

T

i

s

−

U(s)

E(s)

Rys. 5. Schemat blokowy regulatora PID.

ZAK!ÓCENIA W UK!ADZIE REGULACJI

Na rysunku 6 przedstawiony zosta" uk"ad zamkni#ty regulacji w którym uwzgl#dnione zosta"y
zak"ócenia. Kiedy w uk"adzie liniowym obecne s! dwa wej%cia (sygna" zadany i zak"ócenia), ka$de
z nich mo$e by& rozwa$ane oddzielnie. Wyj%cia odpowiadaj!ce ka$demu z sygna"ów z osobna mog!
by& dodawane w celu otrzymania kompletnego wyj%cia. Sygna"y wej%ciowe do uk"adu wprowadzane
s! na w#ze" sumacyjny ze znakiem plus lub minus.

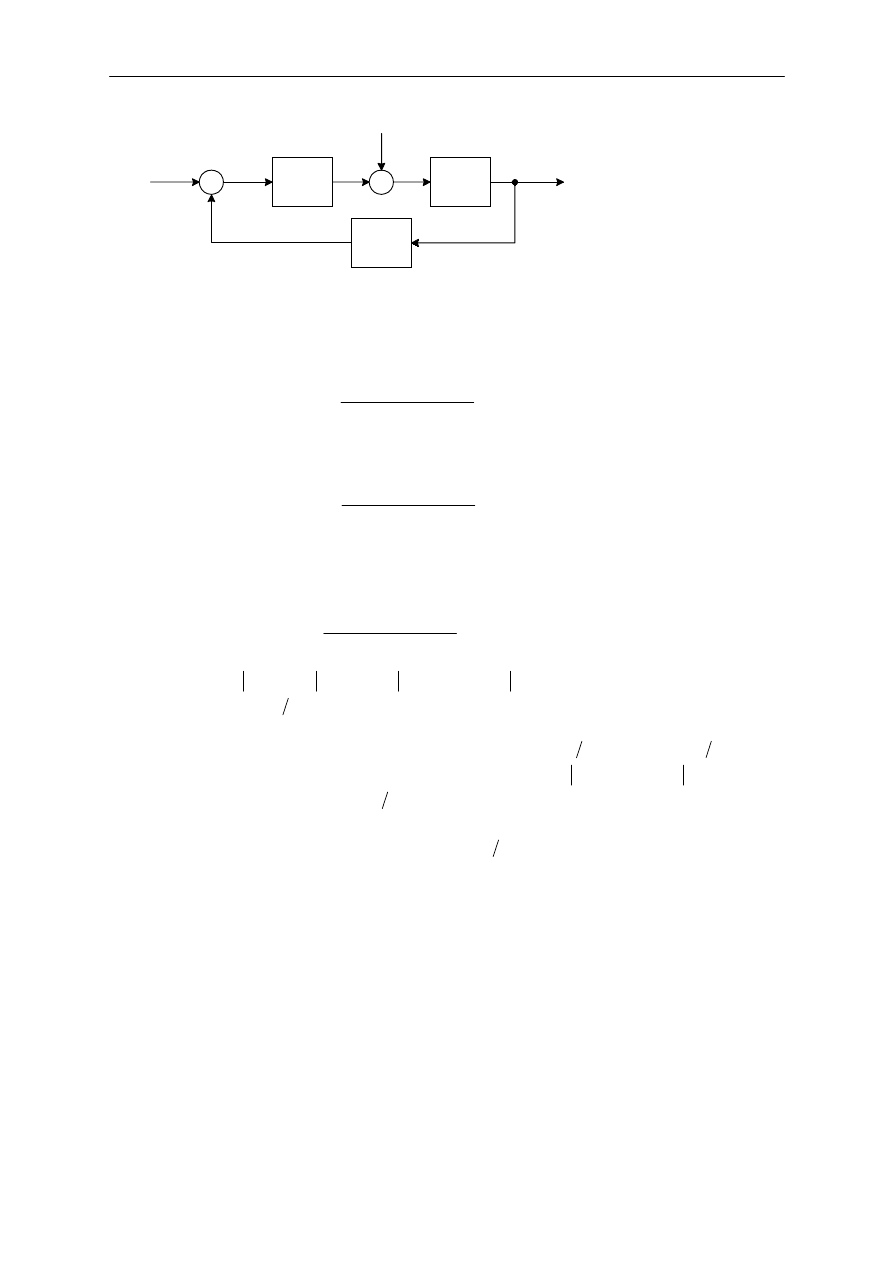
Regulatory automatyczne

5

G

1

(s)

−

Y(s)

E(s)

G

1

(s)

G

2

(s)

H(s)

Z(s)

Zak"ócenia

R(s)

Rys. 6. Schemat blokowy uk"adu zamkni#tego z uwzgl#dnieniem zak"óce(.

Rozwa$ony zostanie uk"ad pokazany na rysunku 6. Rozpatruj!c wp"yw oddzia"ywania zak"óce( Z(s)
mo$na za"o$y&, $e sygna" zadany jest równy zero, wówczas mo$na obliczy& sk"adow! odpowiedzi
powodowan! tylko przez zak"ócenie. Odpowied' ta mo$e zosta& wyznaczona z zale$no%ci

)

(

)

(

)

(

1

)

(

)

(

2

1

2

s

H

s

G

s

G

s

G

s

Y

z

+

=

(11)

Z drugiej strony mo$na rozwa$y& odpowied' powodowan! przez sygna" zadany R(s) przy za"o$eniu,
$e zak"ócenia s! równe zero, wówczas t! sk"adow! mo$na obliczy& ze wzoru

)

(

)

(

)

(

1

)

(

)

(

)

(

2

1

2

1

s

H

s

G

s

G

s

G

s

G

s

Y

R

+

=

(12)

Odpowied' Y(s) uwzgl#dniaj!ca zarówno oddzia"ywanie sygna"u zadanego R(s) jak i zak"óce( Z(s)
mo$e by& uzyskana przez dodanie dwóch powy$szych zale$no%ci (11) i (12)

)

(

)

(

)

(

s

Y

s

Y

s

Y

z

R

+

=

[

]

)

(

)

(

)

(

)

(

)

(

)

(

1

)

(

2

2

1

2

s

Z

s

R

s

G

s

H

s

G

s

G

s

G

+

+

=

(13)

W przypadku gdy

1

)

(

)

(

1

>>

s

H

s

G

oraz

1

)

(

)

(

)

(

2

1

>>

s

H

s

G

s

G

. W tym przypadku, transmitancja

uk"adu zamkni#tego

)

(

)

(

s

Z

s

Y

z

staje si# prawie równe zero i wp"yw zak"óce( zostanie usuni#ty. Jest

to zaleta uk"adu zamkni#tego.

Z drugiej strony, transmitancja uk"adu zamkni#tego

)

(

)

(

s

R

s

Y

R

staje si#

)

(

1

s

H

gdy

wzmocnienie

)

(

)

(

)

(

2

1

s

H

s

G

s

G

zwi#ksza si#. Oznacza to, $e je%li

1

)

(

)

(

)

(

2

1

>>

s

H

s

G

s

G

wówczas

transmitancja uk"adu zamkni#tego

)

(

)

(

s

R

s

Y

R

staje si# niezale$na od

)

(

1

s

G

oraz

)

(

2

s

G

i staje si#

odwrotnie proporcjonalna do H(s) co powoduje $e zmiany w transmitancjach

)

(

1

s

G

oraz

)

(

2

s

G

nie

wp"ywaj! na transmitancj# uk"adu zamkni#tego

)

(

)

(

s

R

s

Y

R

. Stanowi to kolejn! zalet# uk"adu

zamkni#tego. Mo$na "atwo si# zorientowa&, $e transmitancja uk"adu zamkni#tego z jednostkowym
sprz#$eniem zwrotnym, H(s) = 1 prowadzi do zrównania wej%cia z wyj%ciem.

5. WP!YW RODZAJU REGULATORA NA JAKO$% STEROWANIA

Regulatory automatyczne

6

5.1. UK!AD STEROWANIA Z REGULATOREM PROPORCJONALNYM P

5.&.&. Uchyb w stanie ustalonym w odpowiedzi na sygna" zadany R(s)

Rozwa$ony zostanie uk"ad pokazany na rysunku 7 i zostanie wyznaczony uchyb w stanie ustalonym
pojawiaj!cy si# po podaniu wymuszenia skokowego na wej%cie. Transmitancja obiektu

1

)

(

+

=

Ts

k

s

G

(14)

natomiast transmitancja uchybowa

K

p

k

Ts + 1

−

Y(s)

Regulator

proporcjonalny

R(s)

Obiekt

Rys. 7. Uk"ad sterowania proporcjonalnego.

)

(

1

1

)

(

)

(

)

(

s

G

s

R

s

E

s

G

e

+

=

=

(15)

czyli uchyb

)

(

1

1

1

)

(

)

(

1

1

)

(

s

R

Ts

k

K

s

R

s

G

s

E

p

+

+

=

+

=

(16)

Na wymuszenie skokowe R(s) = R/s otrzymuje si#

s

R

k

K

Ts

Ts

s

E

p

⋅

+

+

+

=

1

1

)

(

(17)

t

y(t)

0

uchyb ustalony

y(t)

r(t)

Rys. 8. Odpowied' skokowa uk"adu z rysunku 7.

Uchyb w stanie ustalonym

k

K

R

s

R

k

K

Ts

Ts

s

s

sE

t

e

e

p

p

s

s

t

u

+

=

⋅

+

+

+

=

=

=

→

→

∞

→

1

1

1

lim

)

(

lim

)

(

lim

0

0

(18)

Uk"ady bez integratora w torze bezpo%rednim maj! zawsze w odpowiedzi skokowej uchyb w stanie
ustalonym. Taki uchyb w stanie ustalonym czasami nazywany jest offsetem. Na rysunku 8 pokazana
jest odpowied' skokowa uk"adu z rysunku 7.

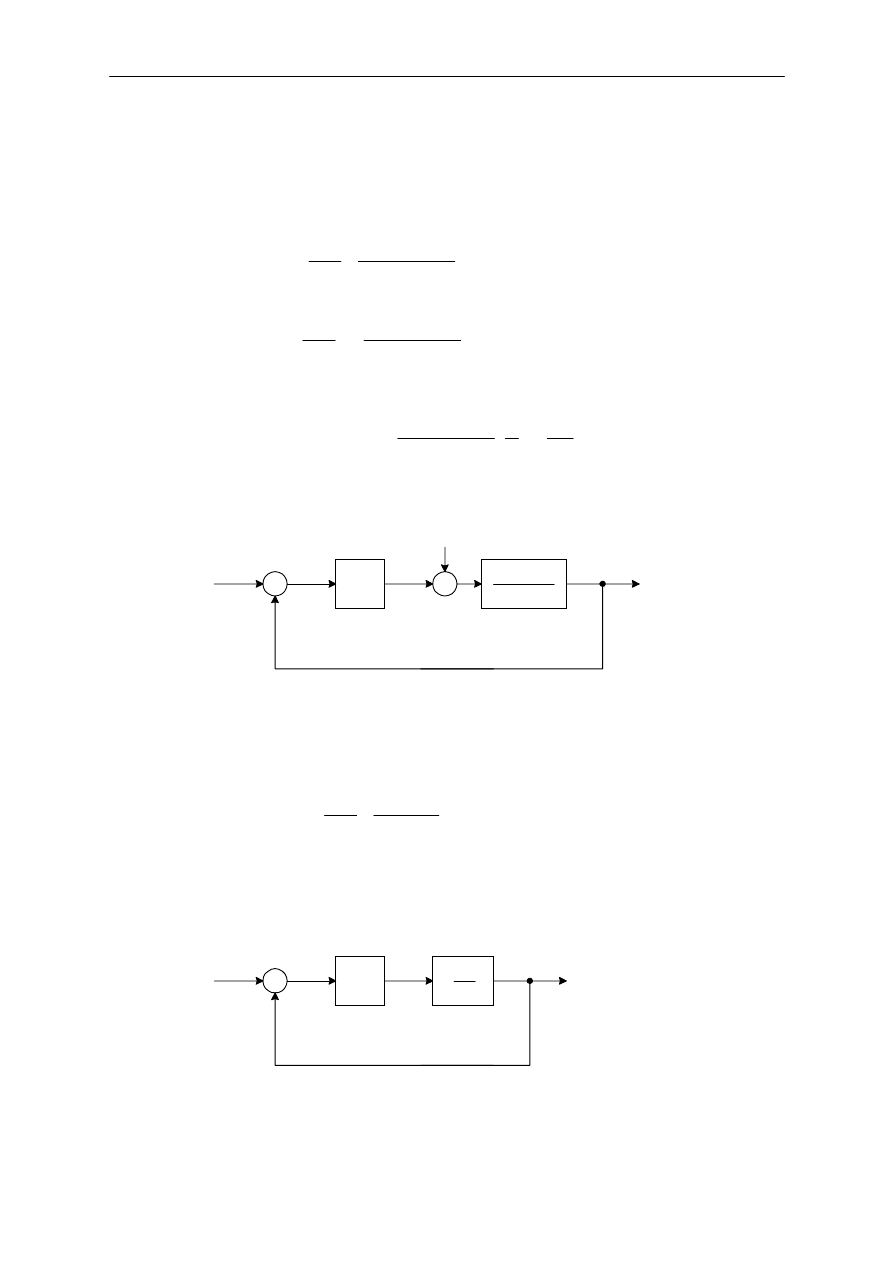
Regulatory automatyczne

7

5.&.2. Uchyb w stanie ustalonym w odpowiedzi na sygna" zak"ócenia Z(s)

Rozwa$ony zostanie wp"yw zak"ócenia wiatrowego pojawiaj!cy si# w sterowaniu statkiem na kursie.
Rozwa$any uk"ad pokazany zosta" na rysunku 9. Regulator proporcjonalny wypracowuje sygna"
zadany Z(s) (zadane wychylenie steru) dla statku opisanego tutaj modelem Nomoto I rz#du.
Oddzia"ywuj!ca si"a wiatru zosta"a oznaczona jako Z(s). Zak"adaj!c, $e sygna" zadany (kurs zadany)
jest równy zero R(s) = 0, transmitancja pomi#dzy Y(s) oraz Z(s) jest opisana zale$no%ci!

k

K

s

Ts

k

s

Z

s

Y

p

+

+

=

2

)

(

)

(

(19)

natomiast transmitancja uchybowa

k

K

s

Ts

k

s

Z

s

E

p

+

+

−

=

2

)

(

)

(

(20)

Uchyb w stanie ustalonym pojawiaj!cym si# w wyniku oddzia"ywania zak"óce( o amplitudzie Z
opisany jest wzorem

p

p

s

s

t

u

K

Z

s

Z

k

K

s

Ts

k

s

s

sE

t

e

e

−

−

=

⋅

+

+

−

=

=

=

→

→

∞

→

2

0

0

lim

)

(

lim

)

(

lim

(21)

Uchyb w stanie ustalonym mo$e by& zmniejszany przez zwi#kszanie warto%ci wzmocnienia

p

K , lecz

wzrost tej warto%ci mo$e powodowa& wzrost oscylacji w odpowiedzi uk"adu.

K

p

−

Y(s)

Regulator

proporcjonalny

R(s)

Obiekt

k

s(Ts + 1)

Z(s)

E(s)

U(s)

Rys. 9. Schemat blokowy uk"adu sterowania z uwzgl#dnieniem zak"óce(.

5.&.3. Regulator P w uk"adzie sterowania obiektem bezw"adno#ciowym

Rozwa$ony zostanie uk"ad pokazany na rysunku 10. W tym przypadku, transmitancja uk"adu
zamkni#tego

p

p

K

Js

K

s

Z

s

Y

+

=

2

)

(

)

(

(22)

St!d pierwiastki równania charakterystycznego

0

2

=

+

p

K

Js

(23)

znajduj! si# na osi urojonej i odpowied' skokowa b#dzie oscylacyjn! o sta"ej amplitudzie, jak
pokazano to na rysunku 11.

K

p

−

Y(s)

Regulator

proporcjonalny

R(s)

Obiekt

1

Js

2

Rys. 10. Uk"ad sterowania proporcjonalnego w uk"adzie z obiektem bezw"adno%ciowym.

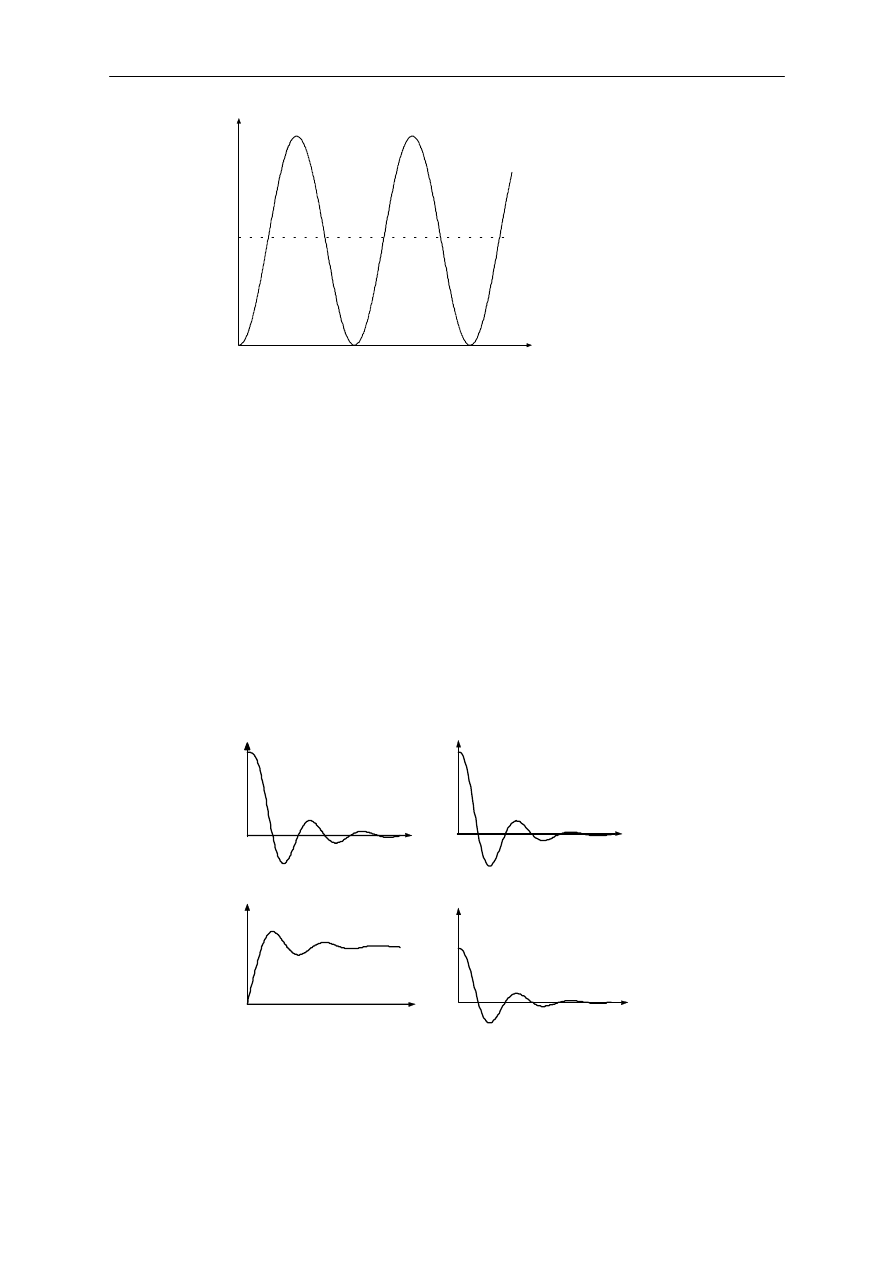
Regulatory automatyczne

8

y(t)

t

&

0

Rys. 11. Jednostkowa odpowied' skokowa uk"adu z rysunku 10.

5.2. REGULATOR CA!KUJ#CY I

W uk"adzie z regulatorem proporcjonalnym zastosowanym do sterowania obiektem, którego
transmitancja nie zawiera integratora 1/s, w odpowiedzi na wymuszenie skokowe pojawia si# uchyb
w stanie ustalonym (offset). Je%li regulator b#dzie zawiera" sterowanie ca"kuj!ce to ta sta"a warto%&
mo$e zosta& usuni#ta.

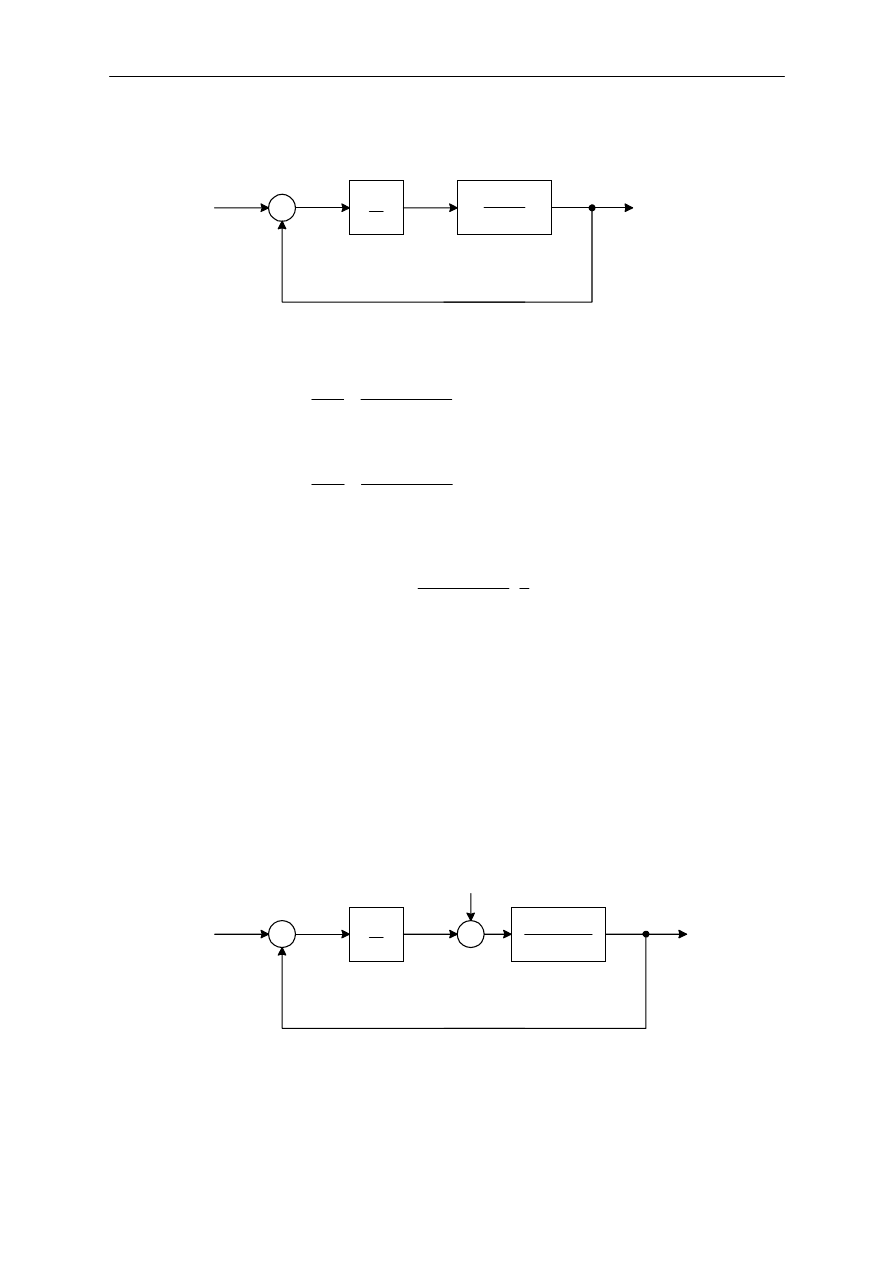
W sterowaniu obiektem przy u$yciu regulatora ca"kuj!cego, sygna" sterowania, sygna"

wyj%ciowy jest obszarem znajduj!cym si# pod krzyw! wykonawczego przebiegu czasowego sygna"u
uchybu. Sygna" sterowania u(t) w przypadku regulatora ca"kuj!cego mo$e mie& niezerow! warto%&,
kiedy sygna" wykonawczy uchybu e(t) jest zerem, jak pokazano to na rysunku 12(a). Taka sytuacja nie
jest mo$liwa w przypadku regulatora proporcjonalnego, gdzie niezerowy sygna" sterowania wymaga
niezerowego sygna"u wykonawczego uchybu. Na rysunku 12(b) przedstawiono krzyw! e(t) w funkcji t
i odpowiadaj!ca krzywa u(t) w funkcji czasu t kiedy regulator jest typu proporcjonalnego. Sterowanie
ca"kuj!ce zastosowane do usuwania uchybu w stanie ustalonym mo$e prowadzi& do oscylacyjnej
odpowiedzi, wolno zanikaj!cych drga( lub nawet do drga(, których amplituda narasta; obie te
sytuacje s! niepo$!dane.

e(t)

e(t)

u(t)

u(t)

t

t

t

t

(a)

(b)

Rys. 12. Przebiegi sygna"u uchybu e(t) i sygna"u steruj!cego u(t); (a) krzywe ilustruj!ce niezerowy sygna"

steruj!cy, gdy sygna" wykonawczy uchybu jest równy zero (sterowanie ca"kuj!ce), (b) krzywe
pokazuj!ce zerowe sterowanie, kiedy sygna" wykonawczy uchybu jest równy zero (sterowanie
proporcjonalne).

Regulatory automatyczne

9

5.2.&. Sterowanie obiektem typu inercja I rz'du

Rozwa$ony zostanie uk"ad pokazany na rysunku 13. Zastosowany tutaj zosta" regulator ca"kuj!cy.

K

i

s

1

Ts + 1

−

Y(s)

Regulator

ca"kuj!cy

R(s)

Obiekt

Rys. 13. Schemat blokowy uk"adu sterowania ca"kuj!cego.

Transmitancja uk"adu zamkni#tego

(

)

i

i

K

Ts

s

K

s

R

s

Y

+

+

=

1

)

(

)

(

(24)

natomiast transmitancja uchybowa

(

)

(

)

i

K

Ts

s

Ts

s

s

R

s

E

+

+

+

=

1

1

)

(

)

(

(25)

Je%li uk"ad jest stabilny, uchyb w stanie ustalonym w odpowiedzi na wymuszenie skokowe mo$e by&
wyznaczony przez zastosowanie twierdzenia o warto%ci granicznej

(

)

(

)

0

1

1

1

lim

)

(

lim

)

(

lim

0

0

=

⋅

+

+

+

=

=

=

→

→

∞

→

s

K

Ts

s

Ts

s

s

s

sE

t

e

e

i

s

s

t

u

(26)

W tym uk"adzie (rys. 13) sterowanie ca"kuj!ce eliminuje uchyb w stanie ustalonym pojawiaj!cy si#
w odpowiedzi na wymuszenie skokowe. Jest to wa$ne polepszenie jako%ci sterowania w stosunku do
sterowania proporcjonalnego (rys. 7).

5.2.&. Sterowanie obiektem typu ca"kuj(cego z inercj(

Je%li regulator ca"kuj!cy zostanie zastosowany do sterowania statkiem na kursie (lub do sterowania
innym obiektem zawieraj!cym biegun w zerze) jako pokazano to na rysunku 14, wówczas uk"ad staje
si# niestabilny poniewa$ równanie charakterystyczne

0

2

3

=

+

+

k

K

s

Ts

i

(27)

ma pierwiastki z dodatnimi cz#%ciami rzeczywistymi. Takie uk"ady niestabilne nie mog! by&
stosowane w praktyce.

K

i

s

−

Y(s)

Regulator

ca"kuj!cy

R(s)

Obiekt

k

s(Ts + 1)

Z(s)

E(s)

U(s)

Rys. 14. Schemat blokowy uk"adu sterowania ca"kuj!cego obiektem ca"kuj!cym z inercj!.

5.3. UK!AD STEROWANIA Z REGULATOREM PROPORCJONALNO-CA!KUJ#CYM PI

Aby wyeliminowa& sta"! warto%& uchybu w uk"adzie z rysunku 9 b#d!c! wynikiem dzia"aj!cych
zak"óce(, nale$y regulator proporcjonalny przez regulator proporcjonalno-ca"kuj!cy PI.

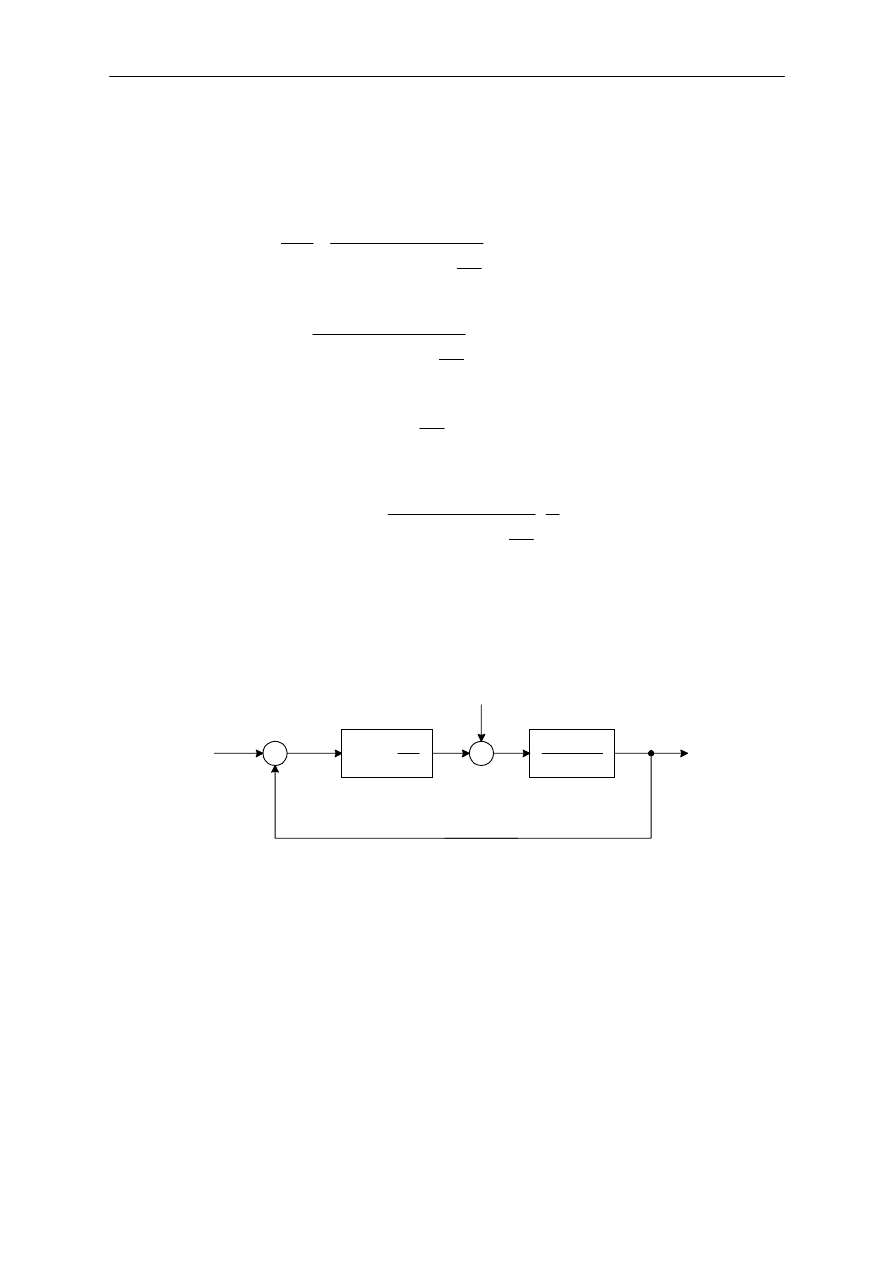
Regulatory automatyczne

10

Je%li sterowanie ca"kuj!ce dodawane jest do regulatora, wówczas tak d"ugo jak d"ugo wyst#puje

sygna" uchybu podawane jest sterowanie w celu wyeliminowania tego uchybu w takim przypadku gdy
rozwa$any uk"ad sterowania jest stabilny.

Na rysunku 15 przedstawiony jest regulator proporcjonalno-ca"kuj!cy steruj!cy obiektem

ca"kuj!cym z inercj!. Transmitancja pomi#dzy Y(s) oraz Z(s) (przy za"o$eniu R(s) = 0) jest opisana
zale$no%ci!

i

p

p

T

K

ks

K

s

Ts

sk

s

Z

s

Y

+

+

+

=

2

3

)

(

)

(

(28)

Przy braku sygna"u zadanego, sygna" uchybu wyznaczany jest ze wzoru

)

(

)

(

2

3

s

Z

T

K

ks

K

s

Ts

sk

s

E

i

p

p

+

+

+

−

=

(29)

Je%li uk"ad sterowania jest stabilny, wówczas pierwiastki równania charakterystycznego

0

2

3

=

+

+

+

i

p

p

T

K

ks

K

s

Ts

(30)

maj! ujemne cz#%ci rzeczywiste i wówczas uchyb w stanie ustalonym mo$e by& wyznaczony
z twierdzenia o warto%ci granicznej.

0

lim

)

(

lim

)

(

lim

2

3

0

0

=

⋅

+

+

+

−

=

=

=

→

→

∞

→

s

Z

T

K

k

K

s

Ts

sk

s

s

sE

t

e

e

i

p

p

s

s

t

u

(31)

Czyli uchyb w stanie ustalonym w wyniku oddzia"ywania skokowych zak"óce( w uk"adzie z rysunku
15 mo$e by& wyeliminowany w przypadku zastosowania regulatora proporcjonalno-ca"kuj!cego PI.
Dodanie sterowania ca"kuj!cego do regulatora proporcjonalnego powoduje podniesienie rz#du uk"adu
z drugiego na trzeci. St!d uk"ad sterowania mo$e sta& si# niestabilny dla du$ych warto%ci
wzmocnienia

p

K pierwiastki równania charakterystycznego mog! mie& dodatnie cz#%ci rzeczywiste.

(Uk"ad drugiego rz#du jest zawsze stabilny je%li wszystkie wspó"czynniki s! dodatnie).

−

Y(s)

Regulator

PI

R = 0

Obiekt

K

p

(1 +

)

1

T

i

s

k

s(Ts + 1)

Z(s)

E(s)

Rys. 15. Schemat blokowy uk"adu sterowania z uwzgl#dnieniem zak"óce(.

5.4. REGULATOR PROPORCJONALNO-RÓ"NICZKUJ#CY PD

5.4.&. Sterowanie ró)niczkuj(ce

Sterowanie ró$niczkuj!ce dodane do regulatora proporcjonalnego powoduje, $e regulator ma wi#ksz!
wra$liwo%&. Zalet! u$ycia sterowania ró$niczkuj!cego jest to, $e reaguje ono na przyrost zmian
uchybu wykonawczego i wyznacza odpowiedni! poprawk# na sterowanie, która zabezpiecza przed
powstaniem zbyt du$ej amplitudy oscylacji sygna"u wykonawczego uchybu. Czyli sterowanie
ró$niczkuj!ce uprzedza sygna" wykonawczy uchybu, inicjuje wcze%niejsz! akcj# korekcyjn! co
powoduje wzrost stabilno%ci uk"adu. Chocia$ sterowanie ró$niczkuj!ce nie wp"ywa bezpo%rednio na
uchyb w stanie ustalonym, to wprowadza t"umienie do uk"adu i pozwala na u$ycie wi#kszej warto%ci
wzmocnienia K, którego zwi#kszenie poprawia dok"adno%& w stanie ustalonym.

Poniewa$ sterowanie ró$niczkuj!ce reaguje na pr#dko%& zmian uchybu wykonawczego, a nie na

sam uchyb, wi#c sterowanie ró$niczkuj!ce nigdy nie wyst#puje samodzielnie w uk"adach sterowania.

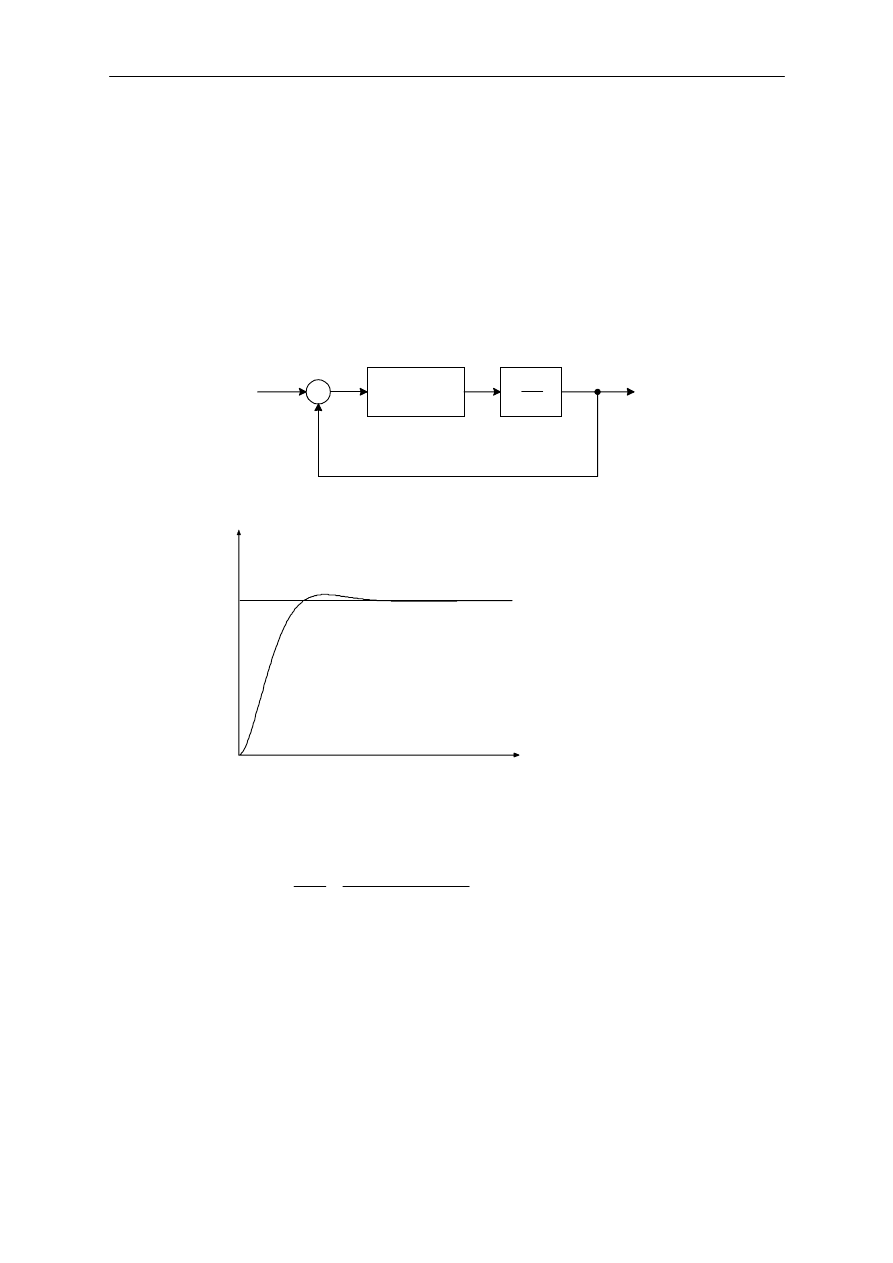
Regulatory automatyczne

11

Jest ono zawsze u$ywane w kombinacji ze sterowaniem proporcjonalnym lub proporcjonalno-
ca"kuj!cym.

5.4.2. Sterowanie obiektem inercyjnym

Zmodyfikowany zostanie uk"ad z rysunku 10, zamiast regulatora proporcjonalnego u$yty zostanie
regulator proporcjonalno-ró$niczkuj!cy PD o transmitancji

(

)

s

T

K

d

p

+

1

. Sygna" wyj%ciowy

(steruj!cy) z regulatora jest proporcjonalny do











 +

.

e

T

e

K

d

p

. Sterowanie ró$niczkuj!ce w istocie ma

dzia"anie uprzedzaj!ce, na podstawie pomiaru pr#dko%ci uchybu przewiduje du$e przeregulowania
w czasie i wytwarza stosown! kontrreakcj# zanim te du$e oscylacje si# pojawi!.

Rozwa$ony zostanie uk"ad sterowania z rysunku 16.

K

p

(1+T

d

s)

−

Y(s)

Regulator

PD

R(s)

Obiekt

1

Js

2

Rys. 16. Sterowanie proporcjonalno-ró$niczkuj!ce uk"adem z obiektem bezw"adno%ciowym.

y(t)

t

0

Rys. 17. Odpowied' skokowa uk"adu z rysunku 16.

Transmitancja uk"adu zamkni#tego opisana jest wzorem

(

)

p

d

p

d

p

K

s

T

K

Js

s

T

K

s

R

s

Y

+

+

+

=

2

1

)

(

)

(

(32)

Równanie charakterystyczne

0

2

=

+

+

p

d

p

K

s

T

K

Js

(33)

ma dwa pierwiastki w lewej pó"p"aszczy'nie dla dodatnich warto%ci J,

p

K oraz

d

T . Wi#c sterowanie

ró$niczkuj!ce wprowadza t"umienie do uk"adu. Typowa odpowied' y(t) na wymuszenie skokowe
pokazana zosta"a na rysunku 17. Jasno wida&, $e nast!pi"a poprawa krzywej odpowiedzi w stosunku
do tej pokazanej na rysunku 11.

5.4.3. Sterowanie w uk"adzie z obiektem II rz#du

Kompromis pomi#dzy akceptowaln! odpowiedzi! przej%ciow! i dopuszczalnym uchybem w stanie
ustalonym mo$e by& uzyskany przez zastosowanie sterowania proporcjonalno-ró$niczkuj!cego.

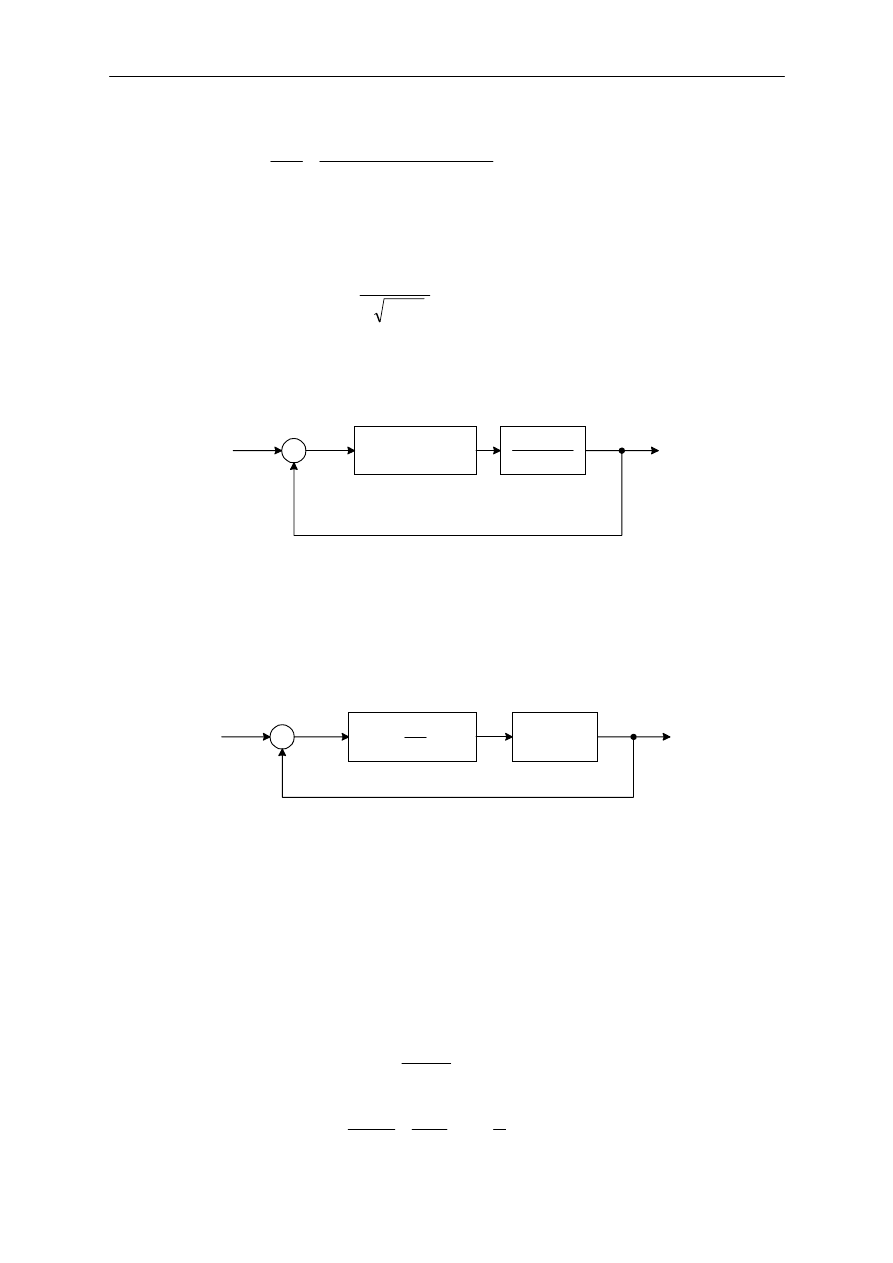
Regulatory automatyczne

12

Rozwa$ony zostanie uk"ad pokazany na rysunku 18. Transmitancja zamkni#ta tego uk"adu

(

)

(

)

k

K

s

k

T

K

Ts

k

s

T

K

s

R

s

Y

p

d

p

d

p

+

+

+

+

=

1

1

)

(

)

(

2

(34)

Równanie charakterystyczne

(

)

0

1

2

=

+

+

+

k

K

s

k

T

K

Ts

p

d

p

(35)

Wspó"czynnik t"umienia

ζ

dla tego uk"adu

kJ

K

k

T

K

p

d

p

2

1

+

=

ζ

(36)

Mo$liwe jest uczynienie zarówno uchybu w stanie ustalonym na wymuszenie liniowo narastaj!ce i
maksymalne przeregulowanie na wymuszenie skokowe odpowiednio ma"ymi przez takie dobranie
parametrów

p

K i

d

K , aby

ζ

zawiera"o si# w przedziale pomi#dzy 0.4 oraz 0.7.

K

p

(1 +T

d

s)

−

Y(s)

Regulator

PD

R(s)

Obiekt

k

s(Ts + 1)

E(s)

Rys. 16. Uk"ad sterowania proporcjonalno-ró$niczkuj!cego obiektem ca"kuj!cym z inercj!

5.5. REGULATOR PROPORCJONALNO-CA!KUJ$CO-RÓ%NICZKUJ$CY PID

Na rysunku 17 przedstawiony zosta" uk"ad sterowania obiektem przy u$yciu regulatora PID. Je%li da
si# wyznaczy& model matematyczny obiektu, wówczas mo$liwe jest zastosowanie ró$nych technik
projektowania do okre%lenia takich parametrów regulatora, które pozwol! na uzyskanie zadanych
wymaga( dotycz!cych odpowiedzi przej%ciowej uk"adu zamkni#tego i uchybu w stanie ustalonym.

−

Y(s)

R(s)

K

p

(1 +

1

T

i

s

Obiekt

E(s)

+T

d

s)

Rys. 17. Uk"ad sterowania proporcjonalno-ca"kuj!co-ró$niczkuj!cego obiektem

Je%li obiekt jest z"o$ony i jego model matematyczny nie mo$e by& "atwo okre%lony, wówczas
analityczne wyznaczenie parametrów regulatora nie jest mo$liwe. Wówczas stosowane s! metody
eksperymentalnego strojenia parametrów regulatora.

6. POMIARY W!ASNO$CI DYNAMICZNYCH OBIEKTÓW REGULACJI METOD*

SKOKU JEDNOSTKOWEGO

Optymalne nastawy regulatorów opracowywane s! zazwyczaj w postaci tabel, wykresów, wzorów
empirycznych zwykle dla obiektów podzielonych na dwie klasy: obiekty statyczne i obiekty
astatyczne, których charakterystyki aproksymuje si# nast#puj!cymi transmitancjami:

−

obiekty statyczne

1

)

(

+

=

−

Ts

Ke

s

G

sT

o

(37)

−

obiekty astatyczne

Ts

e

s

Ke

s

G

sT

sT

o

o

−

−

=

=

)

(

;

T

K

1

=

(38)

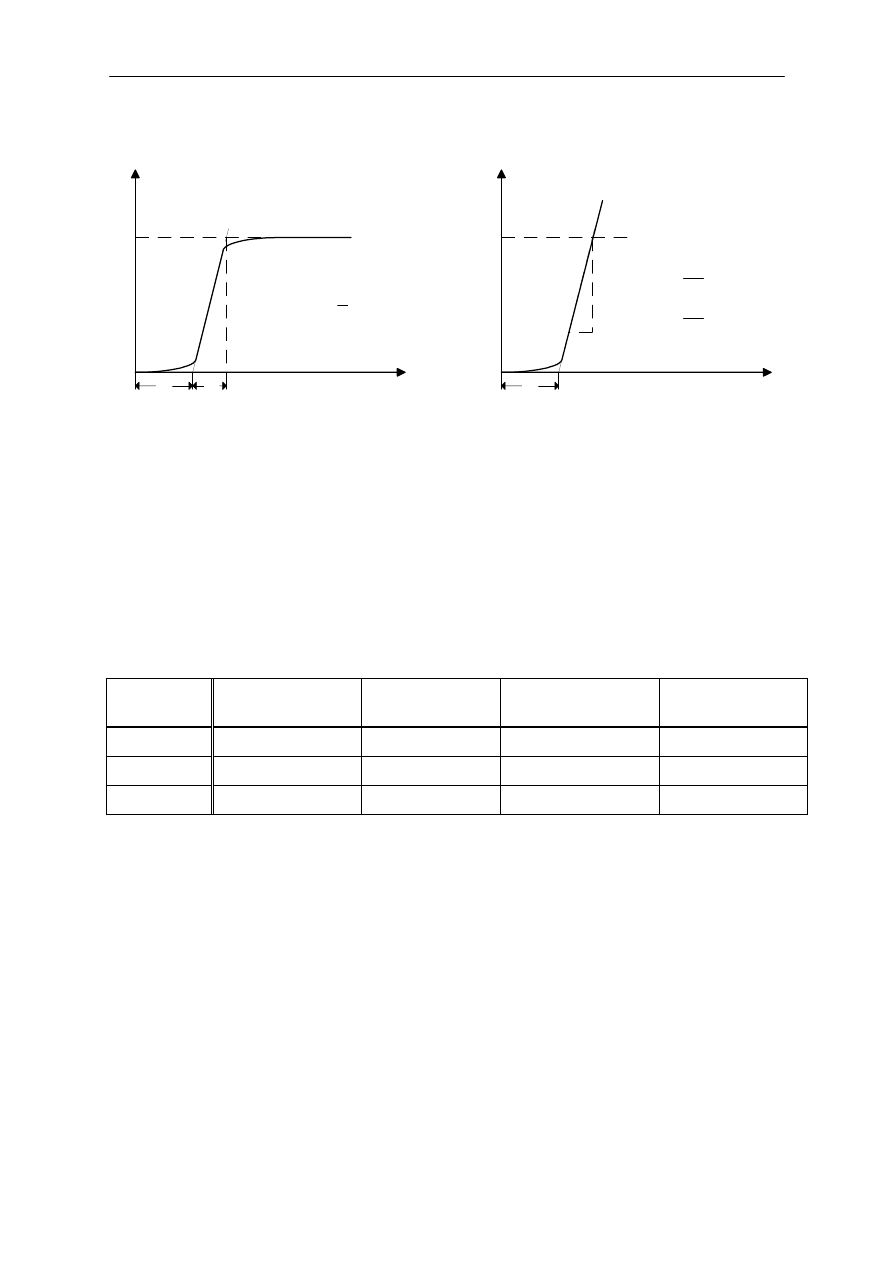
Regulatory automatyczne

13

Sposób wyznaczania parametrów modelu K, T,

o

T odwzorowuj!cego obiekt na podstawie odpowiedzi

na skok jednostkowy pokazano na rysunku 18.

K

y(t)

t

T

o

T

Nachylenie R=

K

T

u

y(t)

t

T

o

∆

t

∆

y

T =

∆

t

∆

y

u

R =

∆

y

∆

t

(a)

(b)

Rys. 18. Sposób okre%lenia parametrów K, T,

o

T

na podstawie odpowiedzi skokowej (jednostkowej) procesu.

(a) dla obiektu statycznego, (b) dla obiektu astatycznego.

7. STROJENIE REGULATORÓW PID

Sterowanie proporcjonalne z nastaw! K

p

ma wp"yw na zmniejszanie czasu narastania i b#dzie

zmniejsza"o uchyb w stanie ustalonym, lecz nigdy nie b#dzie go eliminowa"o. Sterowanie ca"kuj!ce
z nastaw! K

i

ma wp"yw na eliminowanie uchybu w stanie ustalonym, lecz pogarsza odpowied'

w stanie przej%ciowym. Sterowanie ró$niczkuj!ce z nastaw! K

d

ma wp"yw na zwi#kszenie stabilno%ci

uk"adu, zmniejszaj!c przeregulowanie i poprawiaj!c odpowied' przej%ciow!. Wp"yw nastawy ka$dego
sterowania K

p

, K

d

oraz K

i

na uk"ad zamkni#ty zebrany zosta" w tabeli 1.

Tabela 1. Nastawy parametrów wed"ug zasad Zieglera-Nicholsa,

Czas narastania

Przeregulowanie

Czas ustalania

Uchyb w stanie

ustalonym

K

p

Zmniejszenie

Zwi#kszenie

Ma"a zmiana

Zmniejszenie

K

i

Zmniejszenie

Zwi#kszenie

Zwi#kszenie

Eliminacja

K

d

Ma"a zmiana

Zmniejszenie

Zmniejszenie

Ma"a zmiana

Zwi!zki te nie zawsze s! dok"adnie takie jak podane w tabeli 1, faktycznie zmiana jednej z tych
zmiennych mo$e powodowa& zmian# pozosta"ych. Z tego powodu tabela ta powinna by& u$ywana
jako odniesienie przy okre%laniu warto%ci K

p

, K

i

oraz K

d

.

Na bazie obserwacji eksperymentalnych strategii strojenia regulatorów PID w procesach

przemys"owych, Ziegler i Nichols zaproponowali dwie metody doboru nastaw. Metody te wymagaj!
pomiaru odpowiedzi uk"adu i s! powszechnie stosowane dla uk"adów typu 0 najcz#%ciej spotykanych
w uk"adach sterowania (np. sterowanie poziomem, temperatur!, ci%nieniem, przep"ywem, itd.).
Metody doboru nastaw opracowane przez Zieglera i Nicholsa opieraj!ca si# odpowiedzi skokowej
i mo$liwe s! do zastosowania w tych uk"adach w których odpowied' skokowa uk"adu otwartego jest
bez przeregulowa( tak jak ta pokazana na rysunku 18a. Ziegler i Nichols opracowali dwie metody
strojenia regulatorów dla takich modeli.

7.1. PIERWSZA REGU!A. METODA BAZUJ#CA NA ODPOWIEDZI SKOKOWEJ.

Ziegler i Nichols zauwa$yli, $e odpowied' skokowa wi#kszo%ci uk"adów sterowania ma kszta"t
podobny do tego z rysunku 18a. Krzywa ta mo$e by& otrzymana z danych eksperymentalnych lub
symulacji dynamicznej obiektu.
Krzywa o kszta"cie S jest charakterystyczna dla uk"adów wy$szych rz#dów.

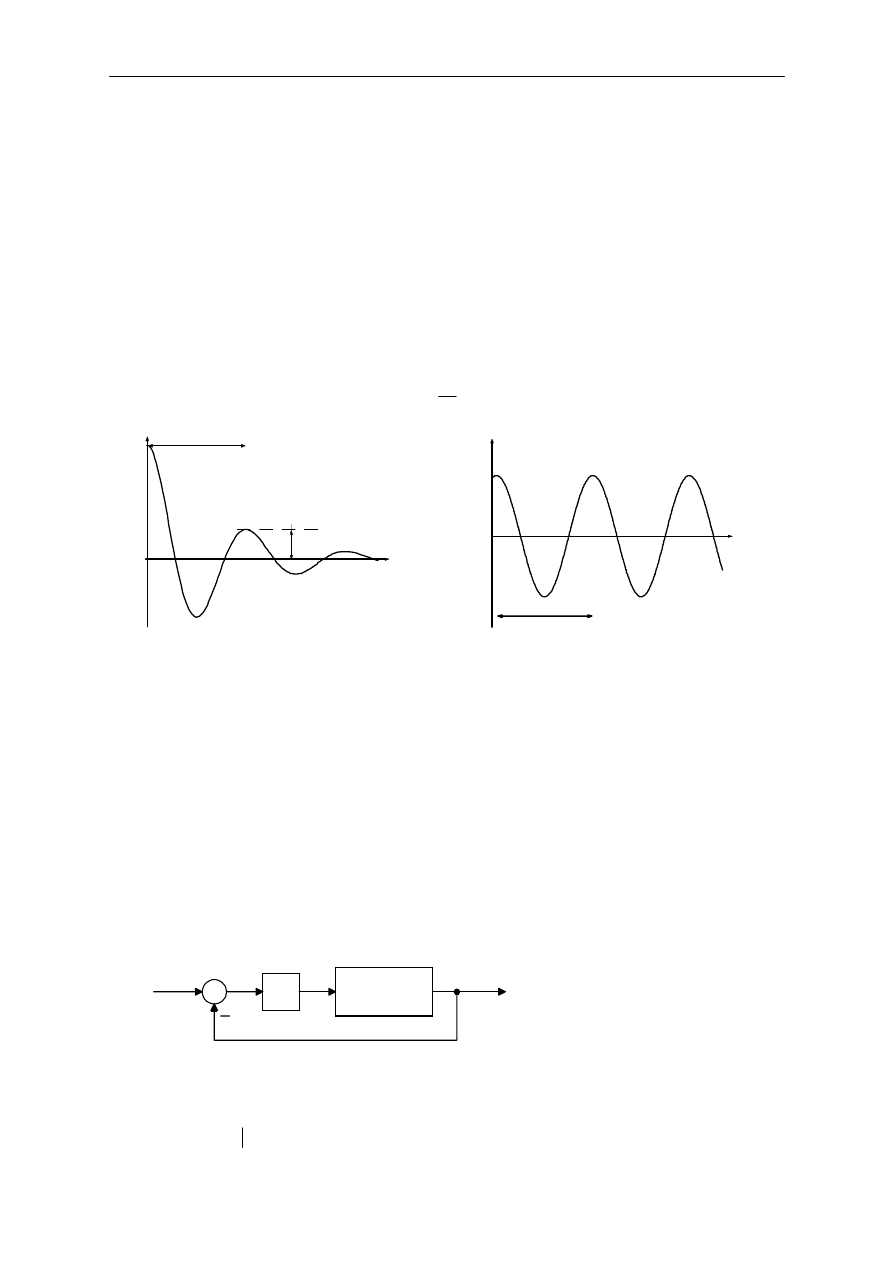
Regulatory automatyczne

14

Transmitancja (37) aproksymuje uk"ady wy$szych rz#dów prostym uk"adem I rz#du z

dodatkowym opó'nieniem T

o

wyra$onym w sekundach. Sta"e w równaniu (37) mog! by& okre%lone z

odpowiedzi skokowej procesu. Je%li styczna narysowana jest w punkcie przegi#cia krzywej
odpowiedzi, wówczas nachylenie linii jest wyznaczane ze wzoru R=K/T, a przeci#cie stycznej z osi!
czasu okre%la czas opó'nienia T

o

.

W pierwszej metodzie wybór parametrów regulatora opiera si# na wspó"czynniku zanikania

równym w przybli$eniu 0.25. Oznacza to, $e dominuj!ca sk"adowa przej%ciowa zanika do jednej
czwartej swojej warto%ci maksymalnej po jednym okresie oscylacji (rys. 19a). Takie zanikanie
odpowiada wspó"czynnikowi

ζ

= 0.21 w uk"adzie II rz#du i warto%& ta ustalona zosta"a na zasadzie

kompromisu pomi#dzy szybk! odpowiedzi! i wystarczaj!cym zapasem stabilno%ci.

Autorzy symulowali równania dla ró$nych uk"adów na komputerze analogowym i stroili

parametry regulatorów, a$ uzyskali odpowiedzi przej%ciowe zanikaj!ce do 25% poprzedniej warto%ci
w jednym okresie. Metoda Zieglera-Nicholsa bazuj!ca na odpowiedzi skokowej daje dobre rezultaty
gdy spe"niony jest nast#puj!cy warunek :

6

.

0

15

.

0

o

<

<

T

T

.

&

t

0

Okres

0.25

osc

y(t)

t

T

(a)

(b)

Rys. 19. Przebiegi czasowe (a) kwadratowy wspó"czynnik zanikania, (b) uk"ad na granicy stabilno%ci

7.2. DRUGA REGU!A. METODA Z WYZNACZANIEM WZMOCNIENIA KRYTYCZNEGO

W drugiej metodzie kryterium strojenia parametrów opiera si# na ocenie uk"adu znajduj!cego si# na
granicy stabilno%ci. Ten algorytm strojenia mo$e by& stosowany dla uk"adów typu 0 posiadaj!cych
rz!d > 2. Mo$e by& równie$ zastosowana do samostrojenia regulatorów PID. Metoda ta mo$liwa jest
do zastosowania je%li mo$liwe jest znalezienie wzmocnienia przy którym wykres Nyquista przecina
punkt krytyczny lub kiedy linia pierwiastkowa przecina o% liczb urojonych. Wzmocnienie to mo$e by&
znalezione eksperymentalnie, wymaga si# wówczas zwi#kszania wzmocnienia w uk"adzie
zamkni#tym a$ na wyj%ciu pojawi! si# oscylacje o sta"ej amplitudzie. Jest to w niektórych
zastosowaniach praktycznych bardzo niebezpieczna operacja. Zwi#ksza si# wzmocnienie
proporcjonalne a$ zauwa$y si# oscylacje o sta"ej amplitudzie, odpowiada to wzmocnieniu
krytycznemu K

kr

(rys. 20) i oscylacjom o okresie T

osc

(rys. 19b). Okres oscylacji powinien by&

mierzony kiedy amplituda oscylacji jest do%& ma"a.

Proces

K

kr

r(t)

e(t)

y(t)

u(t)

Rys. 20. Okre%lenie wzmocnienia krytycznego i okresu oscylacji

Wzmocnienie statyczne dla p#tli otwartej uk"adu

( )

0

o

=

=

s

s

GH

K

Regulatory automatyczne

15

Metoda strojenia bazuj!ca na wzmocnieniu krytycznym daje dobre rezultaty gdy spe"niony jest
warunek:

20

2

o

<

<

kr

K

K

lecz znów odpowied' uk"adu zamkni#tego zawiera oscylacje. Parametry regulatora zaproponowane
przez Zieglera i Nicholsa dla typowego regulatora pokazane s! w tabeli 2

Tabela 2. Nastawy parametrów wed"ug zasad Zieglera-Nicholsa,

Optymalne warto%ci parametrów

Próba skokowa (R, T

o

, a=R/T

o

)

Granica stabilno%ci (K

kr

,,T

osc

)

Typ

regulatora

K

p

T

i

T

d

K

p

T

i

T

d

P

1/a

−

−

0.5K

kr

−

−

PI

0.9/a

3T

o

−

0.45K

kr

T

osc

/1.2

−

PID

1.2/a

2T

o

0.5T

o

0.6K

kr

T

osc

/2

T

osc

/8

7.3. Inne optymalne regu"y nastaw regulatorów PID

W tabelach 3 i 4 zebrane zosta"y zasady doboru nastaw regulatorów dla obiektów statycznych i
astatycznych opisanych transmitancjami (37) oraz (38) wed"ug kryteriów: 0% i 20% przeregulowania
oraz minimum ca"ki kwadratu uchybu.

Tabela 3. Optymalne nastawy regulatorów w przypadku obiektów statycznych z opó'nieniem (37),

o

RT

a

=

Przeregulowanie

%

0

≈

Minimum czasu regulacji

R

t

Przeregulowanie

%

20

≈

Minimum czasu regulacji

R

t

dt

t

e

∫

∞

0

2

)

(

min

Typ

regulatora

K

p

T

i

T

d

K

p

T

i

T

d

K

p

T

i

T

d

P

0.3/a

−

−

0.7/a

−

−

−

−

−

PI

0.6/a

0.8T

o

+0.5T

−

0.7/a

T

o

+0.3T

−

1/a

T

o

+0.35T

−

PID

0.95/a

2.4 T

o

0.4 T

o

1.2/a

2.0 T

o

0.4 T

o

1.4/a

1.3 T

o

0.5 T

o

Tabela 4. Optymalne nastawy regulatorów w przypadku obiektów astatycznych z opó'nieniem (11)

Przeregulowanie

%

0

≈

Minimum czasu regulacji

R

t

Przeregulowanie

%

20

≈

Minimum czasu regulacji

R

t

dt

t

e

∫

∞

0

2

)

(

min

Typ

regulatora

K

p

T

i

T

d

K

p

T

i

T

d

K

p

T

i

T

d

P

o

37

.

0

T

T

⋅

−

−

o

7

.

0

T

T

⋅

−

−

−

−

−

PI

o

46

.

0

T

T

⋅

o

75

.

5

T

⋅

−

o

7

.

0

T

T

⋅

o

3 T

⋅

−

o

1

T

T

⋅

o

3

.

4

T

⋅

−

PID

o

65

.

0

T

T

⋅

o

5 T

⋅

o

23

.

0

T

⋅

o

1

.

1

T

T

⋅

o

2 T

⋅

o

37

.

0

T

⋅

o

36

.

1

T

T

⋅

o

6

.

1

T

⋅

o

5

.

0

T

⋅

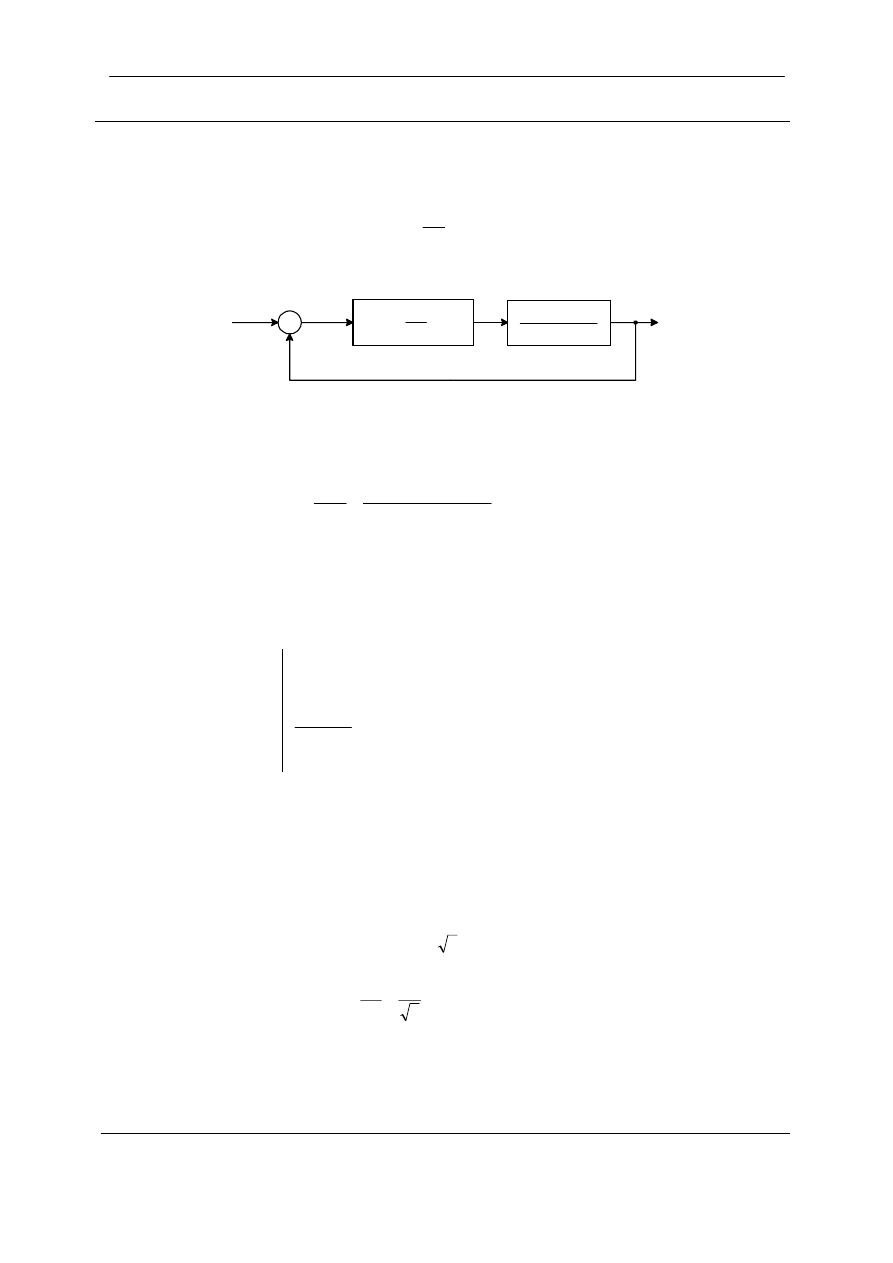
Regulatory automatyczne

16

Przyk"ad &

Rozwa$ uk"ad pokazany na rysunku 21 w którym regulator PID zastosowany zosta" do
sterowania uk"adem. Regulator PID ma transmitancj#









+

+

=

s

T

s

T

K

s

G

d

i

p

R

1

1

)

(

(1.1)

Zastosuj regu"y Zieglera-Nicholsa do strojenia parametrów

p

K ,

i

T oraz

d

T .

−

R(s)

K

p

(1 +

1

T

i

s

E(s)

+T

d

s)

Y(s)

1

s(s+1)(s+5)

PID

Rys. 21. Sterowanie obiektem przy u$yciu regulatora PID

Rozwi!zanie: Zastosowana zostanie druga metoda Zieglera-Nicholsa. Po ustawieniu

i

T =

∞

oraz

d

T = 0, transmitancja uk"adu zamkni#tego

( )(

)

p

p

K

s

s

s

K

s

R

s

Y

+

+

+

=

5

1

)

(

)

(

(1.2)

Poszukiwane wzmocnienie krytyczne

kr

K stanowi warto%& przy której uk"ad znajduje si# na

granicy stabilno%ci. Wyznaczenie tej warto%ci mo$e zosta& dokonane przy u$yciu kryterium
Routha. Dla równania charakterystycznego uk"adu zamkni#tego

0

5

6

2

3

=

+

+

+

p

K

s

s

s

(1.3)

tablica Routha jest nast#puj!ca

3

s

1

5

2

s

6

K

p

1

s

6

30

p

K

−

0

s

K

p

Na podstawie badania wspó"czynników pierwszej kolumny tablicy Rutha, wzmocnienie przy
którym pojawiaj! si# drgania niegasn!ce K

p

= 30, czyli wzmocnienie krytyczne

30

=

kr

K

(1.4)

Podstawiaj!c

kr

K do równania pomocniczego w wierszu przy s

2

mo$na wyznaczy& okres

oscylacji w uk"adzie

0

6

2

=

+

kr

K

s

(1.5)

czyli

5

j

j

s

±

=

±

=

ω

(1.6)

St!d okres oscylacji

81

.

2

5

2

2

=

=

=

π

ω

π

osc

T

[s]

(1.7)

Korzystaj!c z tabeli 2, wyznaczone warto%ci parametrów regulatora PID

18

6

.

0

=

⋅

=

kr

p

K

K

(1.8)

41

.

1

5

.

0

=

⋅

=

osc

T

T

i

[s]

(1.9)

35

.

0

125

.

0

=

⋅

=

osc

T

T

d

[s]

(1.10)

Regulatory automatyczne

17

ZAGADNIENIA KONTROLNE

&. Co to jest regulator P? Zapisz jego transmitancj#.
2. Jaki wp"yw ma regulator P na uchyb w stanie ustalonym w zale$no%ci od typu obiektu?
3. Co to jest regulator PI? Zapisz jego transmitancj#.
4. Regulator PI ma parametry K

p

i K

i

. Podaj wp"yw regulatora PI na uchyb w stanie ustalonym.

Czy regulator PI zmienia typ uk"adu?

5. Podaj wp"yw regulatora PI na czas narastania i czas ustalania w uk"adzie regulacji.
6. Co to jest regulator PD? Zapisz jego transmitancj#.
7. Regulator PD ma parametry K

p

i K

d

. Podaj wp"yw regulatora PD na uchyb w stanie ustalonym.

Czy regulator PD zmienia typ uk"adu?

8. Je%li regulator PD jest tak zaprojektowany, $e pierwiastki równania charakterystycznego maj!

lepsze t"umienie, ni$ w uk"adzie oryginalnym to czy wówczas równie$ zostanie zmniejszone
maksymalne przeregulowanie?

(Tak) (Nie)

9. Podaj wp"yw regulatora PD na czas narastania i czas ustalania w uk"adzie regulacji.

&0. Co to jest regulator PID? Zapisz jego transmitancj#.

ZADANIA

Na podstawie: Kuo B. C. Automatic Control of Dynamic Systems, 7th ed, Addison-Wesley & Sons
Inc. (1995)

P

ROBLEM

4-&8.

Rysunek 4P-18 przedstawia uk"ad sterowania temperatur! przep"ywu powietrza. Zbiornik z gor!c!
wod! dostarcza wody, która wp"ywa do wymiennika ciep"a w celu ogrzania powietrza. Czujnik
temperatury mierzy temperatur# powietrza na wylocie T

AO

i przesy"a j! do uk"adu porównuj!cego z

temperatur! odniesienia T

r

. Uchyb temperatury T

e

jest przesy"any do regulatora o transmitancji G

c

(s).

Wyj%cie regulatora, którym jest sygna" elektryczny jest przetwarzane na sygna" pneumatyczny przez
przetwornik. Wyj%cie urz!dzenia wykonawczego steruje pr#dko%ci! przep"ywu wody zaworem
trójdrogowym. Rysunek 4P-18(b) przedstawia schemat blokowy uk"adu.

Zdefiniowane zosta"y nast#puj!ce parametry i zmienne: dM

w

jest przyrostem przep"ywu

cieplnego p"ynu

u

K

dM

M

w

=

, K

M

= 0.054 kg/s/V, T

w

temperatura wody

w

R

w

dM

K

T

=

, K

R

=

65

°

C/kg/s, oraz T

AO

jest temperatur! wyj%ciow! powietrza.

Równanie wymiany ciep"a pomi#dzy wod! i powietrzem

AO

w

AO

c

T

T

dt

dT

−

=

τ

,

c

τ

= 10 s.

Równanie temperatury czujnika

s

AO

s

s

T

T

dt

dT

−

=

τ

,

s

τ

= 2 s.

(a) Narysuj funkcjonalny schemat blokowy, który zawiera wszystkie transmitancje uk"adu.
(b) Wyprowad' transmitancj# T

AO

(s)/T

r

(s) kiedy G

c

(s) = 1.

(c) Dobierz typ regulatora PID i jego parametry

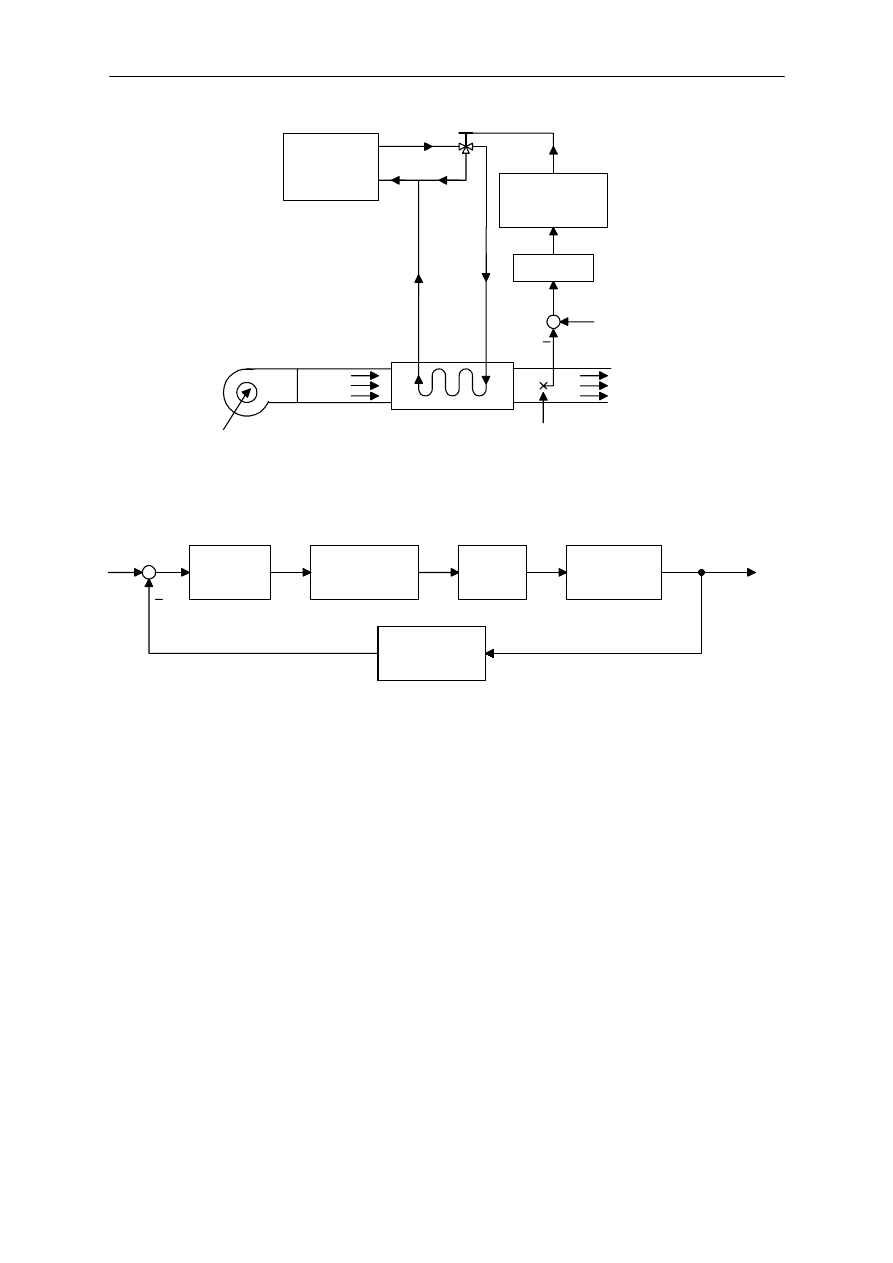
Regulatory automatyczne

18

.

M

A

Czujnik

temperatury T

s

Ogrzane

powietrze T

AO

T

r

T

e

Regulator

Przetwornik

pneumatyczno-

elektryczny

u(t)

Zbiornik z

ciep"! wod!

Zawór

.

M

w

p(t)

Wymiennik

ciep"a

Pobór

powietrza T

Ai

Dmuchawa

(a)

Regulator

G

c

(s)

T

e

Przetwornik
elektryczno-

pneumatyczny

u

p(t)

Zawór

Wymiennik

ciep"a

dM

w

T

r

Wyj%ciowa

temperatura

powietrza T

A0

Czujnik

temperatury

T

s

(b)

Rys. 4P-18.

LITERATURA

&. Dorf R.C., R.H. Bishop, Modern Control Systems, Addison

−

Wesley Longman, Inc., 1998.

2. Franklin, G F, Powell, J D & Emami-Naeini, A. Feedback Control of Dynamic Systems, 3rd ed,

Addison-Wesley, 1994.

3. Kuo B. C., Automatic Control of Dynamic Systems, 7

th

ed, Addison-Wesley & Sons Inc., 1995.

4. Ogata K., Modern Control Engineering, Prentice Hall,2002.
5. Poradnik in$yniera automatyka, Warszawa, 1973.