Daniel Papla

Krzysztof Piontek

Akademia Ekonomiczna we Wrocławiu

Próba zastosowania wielokryterialnego

wspomagania decyzji w badaniu efektywności

rynków kapitałowych

Wstęp

Na cenę akcji na giełdzie wpływa wiele rodzajów informacji. Wśród nich

ważną rolę odgrywają publikowane przez firmy dane finansowe oraz inne,
publicznie dostępne informacje o spółce. Jednakże brak jest zgodności co do
tego, w jaki sposób informacje te wpływają na ceny poszczególnych akcji.
Jedną z teorii próbujących wyjaśnić to zagadnienie jest teoria średniej
efektywności rynków kapitałowych. Chociaż od powstania tej teorii minęło
kilkadziesiąt lat (por. Cootner (1964), Fama (1970)), ciągle prowadzone są
badania mające na celu jej weryfikację. Pojawiają się też nowe metody badania
efektywności. W referacie tym zaprezentowano próbę zastosowania
wielokryterialnego wspomagania decyzji (WWD) jako metody badania średniej
efektywności Giełdy Papierów Wartościowych w Warszawie.

Inwestor wybierający pojedynczy papier wartościowy lub portfel, w sposób

naturalny spotyka się z problemem wielokryterialnego podejmowania decyzji.
Wybór akcji do portfela stawia przed inwestorem zadanie porównania akcji
wielu firm. Każda akcja opisana jest przez pewien zbiór ocen (charakterystyk).
Charakterystyki te, odzwierciedlające atrakcyjność inwestycyjną danego
papieru wartościowego, mogą być zarówno w postaci danych ilościowych, jak i
jakościowych. Na ich podstawie należy wybrać odpowiednie spółki ze zbioru
potencjalnych możliwości, posługując się np. metodami WWD.

W referacie tym podjęto próbę ukazania związku pomiędzy dynamiką

szeregu czasowego cen akcji (stóp zwrotu) a kształtowaniem się w czasie
poziomu wskaźników rynkowych i finansowych. Metoda opiera się na badaniu
średniej korelacji pomiędzy rankingami teoretycznymi generowanymi na
podstawie metod WWD i rankingami stóp zwrotu. Kluczowym zagadnieniem
jest poszukiwanie zestawu wag, określających ważności poszczególnych
kryteriów, który maksymalizuje badaną korelację rankingów.

1. Efektywność – definicja, rodzaje

Podstawy teorii efektywności rynków kapitałowych można znaleźć w pracy

Famy z 1970 (por. Fama (1970)). Rynek jest efektywny, gdy spełnionych jest
kilka założeń (por. Reilly (1989)):
a) na rynku działa niezależnie od siebie wielu uczestników, którzy podejmują

decyzje w sposób racjonalny,

b) nowe informacje dotyczące akcji napływają w sposób losowy

i w większości przypadków są od siebie niezależne,

c) inwestorzy reagują na nowo napływające informacje natychmiast, co

powoduje prawie natychmiastową zmianę ceny danego papieru.

Rynek efektywny charakteryzuje się tym, że wykorzystanie w inwestowaniu

wszelkich informacji dotyczących akcji nie daje stałych, ponadprzeciętnych
zysków. Dzieje się tak dlatego, że te informacje już są odzwierciedlone w cenie
danego papieru (por. Jajuga, Kuziak, Markowski, 1997).

Efektywność można podzielić ze względu na zakres tych informacji na

słabą, średnią (inaczej pół-silną – ang. semistrong) i silną:

- Słaba efektywność występuje wtedy, gdy w cenie akcji odzwierciedlone są

wszystkie informacje z przeszłych notowań takie jak ceny, obroty, liczba
transakcji itp.

- Rynek jest średnio efektywny, jeżeli oprócz informacji giełdowych

również odzwierciedlone są wszystkie publicznie dostępne informacje.

- Silna efektywność oznacza, że odzwierciedlone są wszelkie informacje,

w tym informacje poufne (por. Fama, 1970).

Jak już wcześniej wspomniano efektywność pociąga za sobą nieskuteczność

(tzn. niemożność osiągania stałych ponadprzeciętnych zysków) strategii
inwestycyjnych wywodzących się z analizy technicznej i metod prognozowania
kursów akcji w przypadku słabej efektywności oraz analizy fundamentalnej w
przypadku średniej efektywności. Badanie efektywności można więc
sprowadzić do badania skuteczności strategii inwestycyjnych. Podejście takie
zaprezentowano w niniejszej pracy.

Jedną z możliwych strategii inwestycyjnych jest tworzenie portfeli akcji.

Ponieważ wyboru akcji do portfela można dokonać na podstawie różnego
rodzaju informacji, może być to narzędziem umożliwiającym weryfikację
hipotezy o efektywności rynku, z uwzględnieniem różnych rodzajów
efektywności. Praca ta skupia się na średniej efektywności właśnie ze względu
na zastosowanie metody wykorzystującej zarówno informacje giełdowe, jak i
pozostałe publicznie dostępne. Uzyskanie wysokiej wartości współczynnika
średniej korelacji rankingów, stabilnych wag oraz założenie, że wyznaczone na
podstawie danych historycznych wagi będą odzwierciedlały również w
przyszłości preferencje inwestorów, umożliwiałoby stworzenie strategii
inwestycyjnej polegającej na wyborze do portfela kilku papierów
wartościowych o najwyższej pozycji w teoretycznym rankingu. Znalezienie

−

przy pomocy zastosowanej w tej pracy metody

−

portfela o ponadprzeciętnym

dochodzie pozwoliłoby na odrzucenie hipotezy o średniej efektywności giełdy.
Jednakże brak takiego portfela nie daje niestety podstaw do przyjęcia badanej
hipotezy, ponieważ nie można z całą pewnością stwierdzić, czy jakaś inna
metoda nie pozwoliłaby na znalezienie portfela o pożądanych
charakterystykach.

2. Inwestowanie jako wielokryterialny problem podejmowania decyzji

Wielokryterialne wspomaganie decyzji ma miejsce wtedy, gdy do określenia

optymalności danego rozwiązania stosuje się narzędzia uwzględniające więcej
niż jedno kryterium (por. Roy (1990), Krawczyk 1990)).

Wyróżnia się trzy typy decyzji, dla których stosuje się wspomaganie

wielokryterialne:

•

wybór najlepszego obiektu (akcji) (problematyka

α

),

•

klasyfikacja (problematyka

β

) ,

•

porządkowanie (ranking) (problematyka

γ

).

Z reguły, ze względu na dywersyfikację ryzyka, inwestor rzadko

zainteresowany jest rozwiązaniem problematyki

α

.

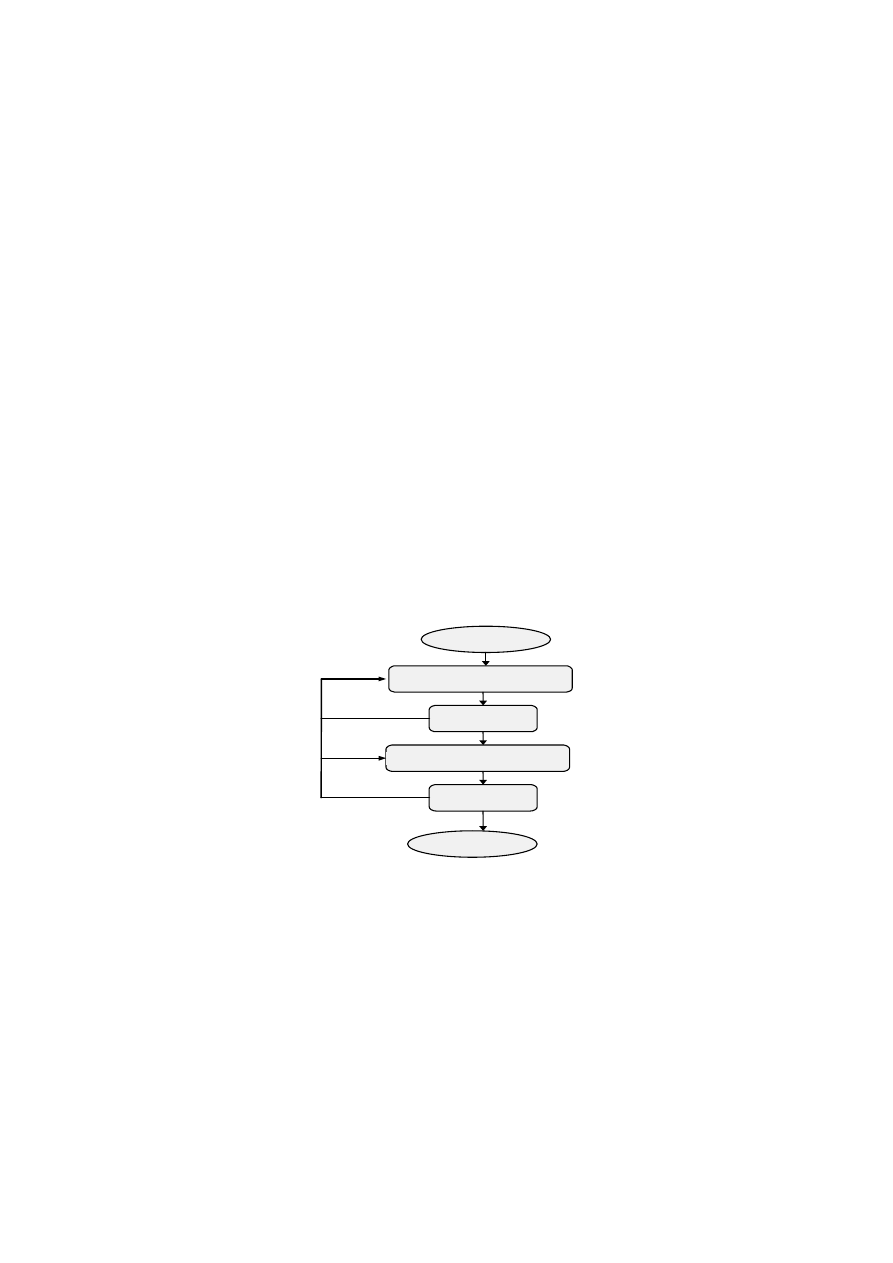
Wybór portfela papierów wartościowych obejmuje dwa podstawowe etapy

podejmowania decyzji, przedstawione na rys. 1:

•

selekcję aktywów (wybór akcji oraz ewentualnie instrumentów wolnych

od ryzyka),

•

ustalenie proporcji poszczególnych składników w wartości portfela

(czyli alokację aktywów do portfela).

W pracy tej ujęto jedynie pierwszy etap powyższej procedury.

Rys. 1. Etapy tworzenia portfela papierów wartościowych.

Na rys. 2 przedstawiony jest pierwszy etap procedury, czyli selekcja akcji do

portfela, który może być podzielony na dwa podetapy, przy czym każdy z nich
może stanowić samodzielny algorytm selekcji, bądź mogą być stosowane
łącznie w dowolnej kolejności:

•

podetap A - rozwiązanie problemu

β

(ograniczenie zbioru),

•

podetap B - rozwiązanie problemu

γ

(ranking).

s e l e k c j a a k c j i d o p o r t f e l a

s t a r t

a k c e p t a c j a

n i e

t a k

u s t a l e n i e s t r u k t u r y p o r t f e l a

n i e

t a k

a k c e p t a c j a

k o n i e c

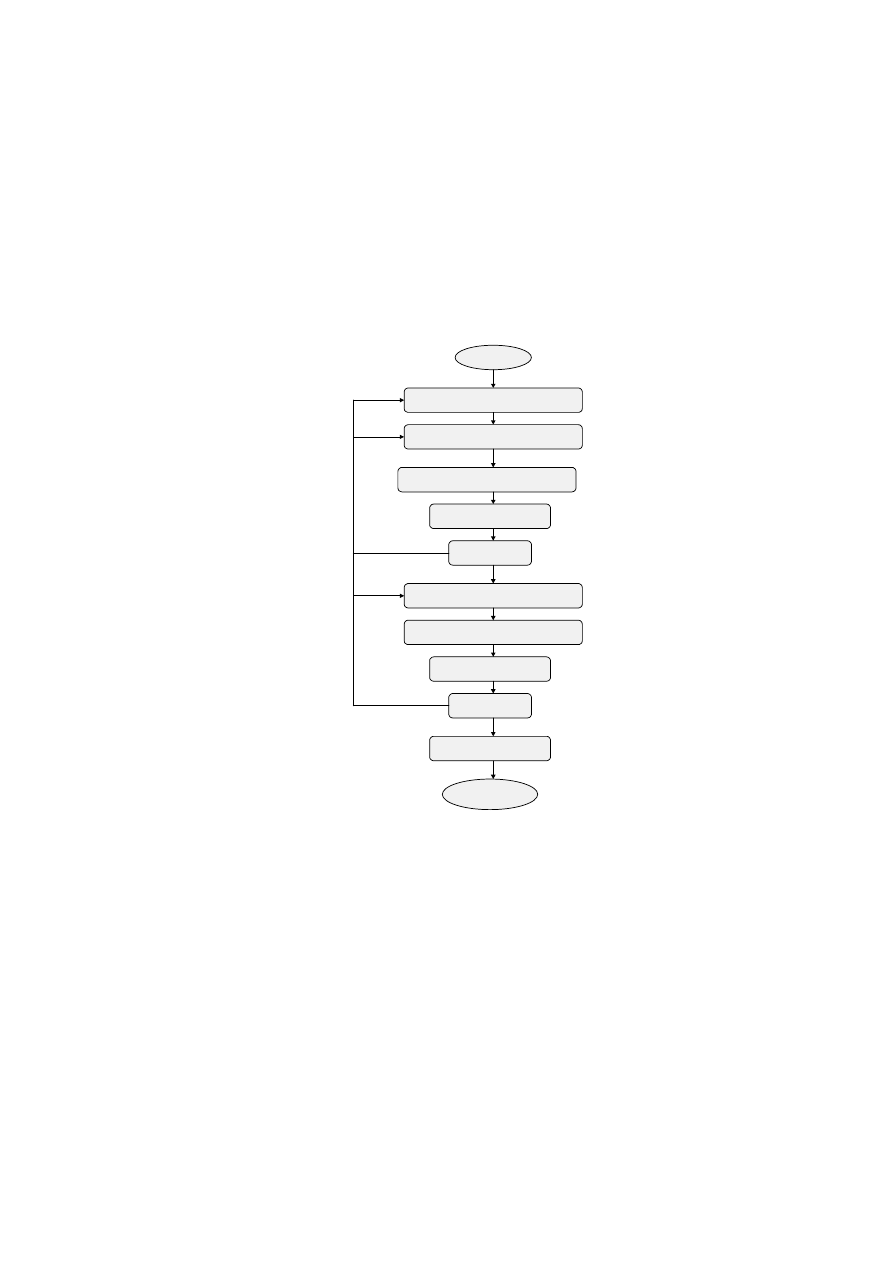
W dalszej części zajmiemy się jedynie podetapem B, podczas którego

decydent musi wprowadzić do systemu następujące dane:

•

zgodny z jego doświadczeniem zbiór kryteriów oceny (może to być zbiór

wszystkich dostępnych inwestorowi kryteriów lub jego zawężony podzbiór),

•

stopień ważności poszczególnych kryteriów (wagi),

•

rodzaj metody generującej ranking.

Rys. 2. Etapy selekcji akcji do portfela.

Do metod wielokryterialnego wspomagania wyboru portfela można

zaliczyć:

1)

Metody redukcji zbioru spółek:

•

metoda hierarchii grupowej kryteriów (por. (Dominiak (1995b)):

•

metoda wielokryterialnego dyskretnego interaktywnego programowania
celowego (por. Dominiak (1995a)),

•

analiza dyskryminacyjna (por. Tarczyński (1997), Czekała (1998)),

•

ELECTRE (por. Roy (1990)),

start

weryfikacja zbioru kryteriów

ustalenie progów weta

nie

tak

redukcja zbioru

akceptacja

prezentacja wyników

ustalenie ważności ocen kryteriów

porządkowanie akcji

prezentacja wyników

nie

tak

koniec

podjęcie decyzji

akceptacja

2)

Metody tworzące ranking spółek:

•

wskaźnik pozycji finansowej (WPFIN) (por. Baranowski (1994)),

•

taksonomiczna miara atrakcyjności inwestycji (TMAI) (por. Tarczyński

(1997)),

•

PROMETHEE (por. Jurek (1995)),

•

BIPOLAR (por. Konarzewska-Gubała(1991)).

W powyższych metodach najwięcej problemów sprawia dobranie

odpowiednich wag odpowiadających ważności poszczególnych kryteriów.
Możliwe są m.in. następujące sposoby ustalania wag:

•

na podstawie wartości charakterystyk opisujących wartości rozpatrywane i
referencyjne zbiory odniesienia (por. Konarzewska-Gubała (1991)),

•

tak, aby siła oddziaływań odpowiednich grup kryteriów była jednakowa (por.
Tarczyński (1997)),

•

korzystając z wiedzy i doświadczenia ekspertów (por. Gospodarowicz (1997),

•

korzystając z danych historycznych (por. Piontek (1998)).

Ostatnią metodę można wykorzystać, jeśli decydent opierając się na danych

historycznych ma możliwość porównania wyników otrzymanych metodą WWD z
wynikami rzeczywistymi. Z jednej strony metoda wielokryterialnego
wspomagania decyzji generuje ranking, który dla ustalonego punktu czasowego,
zbioru potencjalnych obiektów i kryteriów jest jedynie funkcją ocen ważności
kryteriów. Drugi ranking otrzymujemy analizując stopy zwrotu dla danych akcji
po upływie założonego horyzontu czasowego inwestycji. Inwestor powinien
wybrać taki zestaw wag, który zapewnia największą zgodność obu rankingów.
Jest to metoda najtrudniejsza i najbardziej pracochłonna, lecz pozwala ustalić
prawdopodobne średnie ważności ocen kryteriów, którymi kierują się inwestorzy.
Zakłada się, że wyznaczone na podstawie danych historycznych wagi będą
odzwierciedlały preferencje inwestorów także w przyszłości.

Do oceny zgodności obu rankingów można zastosować współczynnik

korelacji rang Spearmana (por. Steczkowski, Zeliaś (1997)).

Znalezienie odpowiedniego zestawu wag sprowadza się więc do znalezienia

maksimum funkcji korelacji pomiędzy dwoma rankingami. Jest to funkcja
k-zmiennych, gdzie k jest liczbą kryteriów.

Dla skwantyfikowanych, ograniczonych wartości wag znalezienie maksimum

korelacji jest typowym problemem optymalizacji kombinatorycznej. Trudności z
rozwiązaniem problemów kombinatorycznych rosną wraz z liczbą zmiennych,
czyli w naszym przypadku kryteriów. Przeszukiwanie całej przestrzeni rozwiązań
powoduje, że uzyskany punkt jest najlepszy, jednak czas obliczeń przy
stosowaniu takich metod, spowodowany dużą, często nawet wykładniczą
złożonością obliczeń, dyskwalifikuje takie rozwiązanie. Konieczne staje się
stosowanie metod przybliżonych: specjalizowanych i metaheurystyk (np.
algorytmów genetycznych lub - tak jak w tej pracy - symulowanego wyżarzania).

Koniec procedury doboru wag następuje wtedy, gdy współczynnik korelacji

posiada wartość satysfakcjonującą decydenta, lub gdy nie można znaleźć już
zestawu wag poprawiającego zgodność rankingów.

4. Symulowane wyżarzanie jako metoda optymalizacji

Do maksymalizacji współczynnika korelacji pomiędzy rankingami, który jest

w tym przypadku funkcją celu, użyto algorytmu symulowanego wyżarzania ze
względu na jego prostotę oprogramowania i skuteczność.

Pomysł tej metody powstał pod wpływem obserwacji schładzania i zastygania

roztopionych metali.

Podstawą jej jest zaproponowana w 1953 r. przez Metropolisa zależność (por.

Metropolis (1953)), która przedstawia prawdopodobieństwo przejścia układu ze
stanu o energii E

1

do stanu o energii E

2

(prawdopodobieństwo przejścia z punktu

o wartości funkcji celu E

1

do punktu o wartości funkcji celu E

2

):









<

≥

=













−

1

2

1

2

gdy

gdy

1

1

2

E

E

e

E

E

P

T

E

E

(1)

gdzie: T - parametr sterujący.

Bardzo ważnym parametrem metody symulowanego wyżarzania jest T -

nazywany z reguły „temperaturą”. Zmniejszanie tego parametru w czasie
obliczeń („schładzanie”), zmniejsza prawdopodobieństwo przejścia do punktu o
mniejszej wartości funkcji celu i gwarantuje „zbieżność” procedury. Istnieje
jednak niebezpieczeństwo, że znalezione zostanie jedynie maksimum lokalne. W
pracy tej zastosowano tzw. „schładzanie wykładnicze” (por. Kirkpatrick (1983),
Hanczar (1998)). Charakteryzują je cztery parametry: t

p

– „temperatura

początkowa”, n - liczba „temperatur”, przez które będzie przechodził układ, f -
współczynnik „schładzania”, N - liczba rozwiązań generowanych w jednej
„temperaturze”. Współczynnik „schładzania” f jest liczbą z przedziału (0, 1), zaś
kolejne „temperatury” można określić wzorem t

i

= f t

i-1

. Im f jest mniejsze, tym

„temperatura” maleje szybciej.

Etapy procesu symulowanego wyżarzania:

1. Wybór początkowego zestawu wag (np. losowy).
2. Obliczenie wartości funkcji celu E

1

dla wybranego zestawu wag.

3. Zakłócenie wybranej losowo wagi o losowo wybraną wartość.
4. Obliczenie wartości funkcji celu E

2

dla nowego zestaw wag.

5. Przyjęcie nowego zestawu wag jako wyjściowego z prawdopodobieństwem
opisanym wzorem (1).

Etapy 2-5 należy powtórzyć N razy dla aktualnej „temperatury”.

6. Zmniejszenie „temperatury”.
Etapy 2-6 należy powtórzyć n razy, aż do osiągnięcia maksimum lub wartości
satysfakcjonującej decydenta.

5. Wyniki badań empirycznych

Przedstawione dalej wyniki badań są kontynuacją obliczeń zamieszczonych w

pracy Piontka (por. Piontek (1998)).

Zbiór analizowanych spółek stanowiących zbiór wariantów decyzyjnych

został ograniczony do rynku podstawowego GPW w Warszawie z wyłączeniem
sektora bankowego i ubezpieczeń. Usunięcie ze zbioru banków i towarzystw
ubezpieczeniowych spowodowane jest odmiennym charakterem tych spółek
i nieporównywalnością wskaźników.

Zestaw kryteriów zaproponowany został w taki sposób, aby można było

sprawdzić możliwość selekcji akcji do portfela na podstawie ogłaszanych
miesięcznych wyników finansowych spółek. Aby uwzględnić wpływ ostatniego
raportu miesięcznego, lecz także aby zmniejszyć wpływ przypadkowych wahań,
zastosowano odmienne od ogólnie przyjętych formuły obliczania niektórych
wskaźników.

Do zbioru potencjalnych kryteriów wybrano następujące kryteria:

•

P/E - cena waloru w dniu analizy podzielona przez zysk na jedną akcję za
ostatnie trzy miesiące pomnożony razy cztery,

•

APREC - procentowa zmiana kursu waloru w stosunku do kursu sprzed
miesiąca,

•

MC/S - kapitalizacja spółki podzielona przez sprzedaż za ostatnie trzy
miesiące pomnożoną przez cztery,

•

KAPIT - liczba akcji w obrocie razy kurs akcji,

•

ROE - zysk netto za ostatnie trzy miesiące pomnożony razy cztery podzielony
przez wartość kapitału własnego odczytaną z ostatniego dostępnego raportu
kwartalnego,

•

NPM - zysk netto za trzy ostatnie miesiące podzielony przez przychody ze
sprzedaży za ostatnie trzy miesiące,

•

R - oczekiwana stopa zwrotu (arytmetyczna pięciosesyjna stopa zwrotu dla
ostatnich 50 sesji),

•

BETA - współczynnik modelu Sharpe’a wyznaczany dla modelu liniowego,
jednoindeksowego względem indeksu WIG (pozostałe parametry jak dla R).

Dla każdej z trzech wybranych metod ustalania rankingu (TMAI,

PROMETHEE, WPFIN) zastosowano trzy horyzonty czasowe (10, 20 i 30 dni).
Badane są wiec korelacje rankingu teoretycznego wygenerowanego dla
poszczególnych metod z rankingiem 10-cio, 20-to i 30-to dniowych stop zwrotu z
akcji. Dla każdej z kombinacji metoda - horyzont przeprowadzono serię 10
procesów maksymalizacji korelacji dla różnych, losowo wybranych, wartości
początkowych wag. W tab. 1 przedstawiono po 3 najlepsze zestawy wag dla
każdej kombinacji.

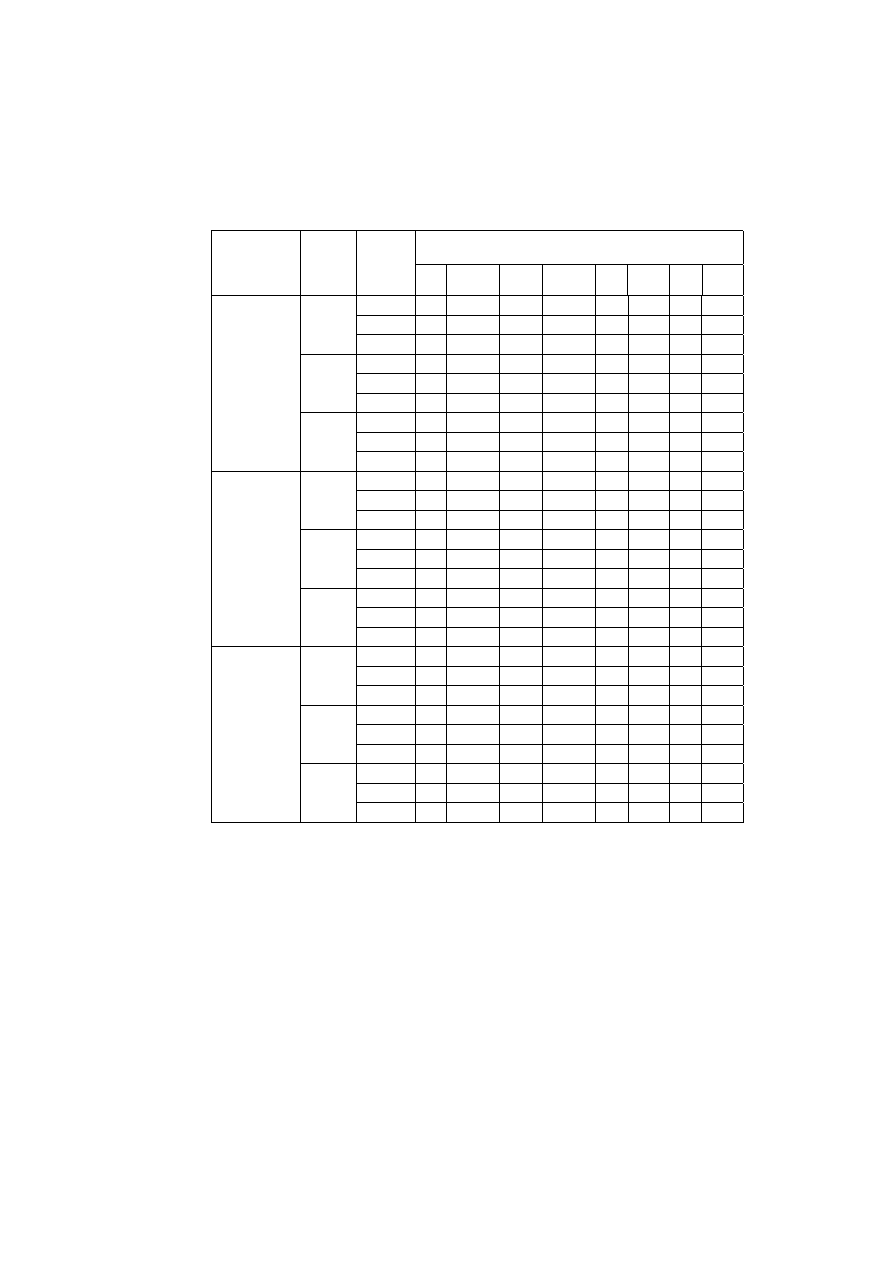
Tabela 1. Korelacje i wagi uzyskane dla wybranych kryteriów.

Unormowane wagi

Metoda

Horyzont
czasowy
(dni)

Korelacja

P/E APREC MC/S KAPIT ROE NPM R

BETA

0.1726

0.09 0.37

0.27

0.1

0

0

0

0.16

0.1711

0.11 0.39

0.27

0.06

0

0

0

0.17

10

0.1708

0.07 0.41

0.3

0.04

0

0

0

0.18

0.1074

0.08 0.37

0.33

0.06

0

0

0

0.17

0.1073

0.09 0.36

0.17

0.22

0

0

0

0.16

20

0.1067

0.1 0.37

0.33

0.05

0

0

0

0.15

0.0557

0.1 0.35

0.25

0.15

0

0

0

0.16

0.0549

0.08 0.38

0.38

0

0

0.01

0

0.16

TMAI

30

0.0521

0.09 0.39

0.37

0

0

0

0.01 0.14

0.2106

0.05 0.38

0.28

0.14

0

0

0

0.16

0.2097

0.08 0.37

0.34

0.02

0

0.04

0

0.15

10

0.2091

0.02 0.61

0.04

0.01

0

0

0

0.32

0.1235

0.05 0.58

0.03

0

0

0

0

0.34

0.1228

0

0.63

0.06

0

0

0

0

0.31

20

0.1224

0.02 0.65

0

0

0

0

0

0.33

0.0605

0

0.67

0.03

0

0

0

0.02 0.28

0.0593

0

0.39

0

0.27

0

0

0

0.34

PROMETHEE

30

0.0578

0

0.35

0.26

0

0

0.21

0

0.18

0.1936

0

0.52

0.03

0

0.08 0.08

0.01 0.28

0.1931

0

0.37

0.24

0

0

0.21

0

0.19

10

0.1921

0

0.37

0.31

0

0

0.16

0

0.17

0.0959

0.22 0.58

0

0

0

0

0.03 0.17

0.0951

0.04 0.36

0.23

0

0.02 0.14

0

0.2

20

0.0932

0.57 0.14

0

0

0

0.06

0.23 0

-0.004

0.52 0.13

0

0

0

0.08

0.27 0

-0.0061 0.51 0.1

0.13

0

0

0.06

0.21 0

WPFIN

30

-0.0074 0.52 0.11

0

0

0

0.08

0.29 0

Źródło: Obliczenia własne.

Jak widać, korelacje są dosyć niskie. Ponieważ jednak wagi dla większości

kombinacji metoda-horyzont są zbliżone (dla różnych punktów startowych
procedury), można przypuszczać, że zbliżono się znacznie do maksimum
globalnego. Potwierdza to skuteczność symulowanego wyżarzania w
rozwiązywaniu problemów optymalizacyjnych.

W tabeli 2 przedstawione są przykładowe wartości korelacji dla

poszczególnych miesięcy dla metody Promethee i rożnych horyzontów
czasowych. Przy pomocy tej metody osiągnięto największą korelację pomiędzy
rankingami.

Tabela 2. Korelacje dla metody Promethee
Horyzont

10 dni

20 dni

30 dni

marzec’98

0,2852

0,1620

0,2082

luty’98

0,2364

0,0360

-0,0038

styczeń’98

0,4214

0,4140

0,1572

grudzień’97

0,2910

0,0426

-0,1715

listopad’97

-0,0355

0,1488

0,1452

październik’97

0,0654

-0,0622

0,0279

średnia

0,2106

0,1235

0,0605

Źródło: Obliczenia własne.

O tym, czy wyznaczony współczynnik korelacji Spearmana może być uznany

za istotny decyduje wynik zastosowania właściwego testu niezależności ( por.
Steczkowski, Zeliaś (1997)). Dla testu jednostronnego (H

0

:

ρ

s

=0 i H

1

:

ρ

s

>0) dla

n=55 obiektów w rankingach wartości krytyczne wynoszą odpowiednio
r

s

(

α

,n)=0.22 dla poziomu istotności

α

=0.05 i r

s

=0.31 dla

α

=0.01.Znacząco

większe od zera (przy poziomie istotności

α

=0.05) są więc tylko cztery korelacje

dla 10-cio dniowego horyzontu czasowego. Potwierdza to przypuszczenia, że
informacja zawarta w wynikach miesięcznych powinna wpływać na kursy akcji
najsilniej na przestrzeni kilku sesji od chwili ogłoszenia. Później objawia się
wpływ innych informacji i czynników.

Warto zaznaczyć, że stosując metodę symulowanego wyżarzania udało się

znacznie poprawić wartość średniej korelacji dla poszczególnych horyzontów i
metod. Najwyższy, uzyskany bez użycia metod heurystycznych, współczynnik
średniej korelacji wynosił dla metody Promethee 0.1266.

Na podstawie analizy otrzymanych wag, można stwierdzić, że rozwiązany

został problem znajdowania maksimum funkcji wielu zmiennych i wyznaczania
optymalnego zestawu wag. Dalsze prace nad zwiększeniem współczynnika
korelacji, a tym samym znalezieniem lepszej strategii inwestycyjnej powinny
podążać w następujących kierunkach:

•

zwiększenie zestawu lub zmiana zbioru kryteriów,

•

wybór odmiennych formuł matematycznych do wyznaczania wartości
poszczególnych kryteriów (być może lepsze wyniki dają nawet te same
kryteria, lecz wyznaczane według innych formuł) ,

•

badanie stabilności w czasie wag maksymalizujących korelację między
rankingami.

Uzyskanie wysokiej wartości współczynnika średniej korelacji oraz

stabilnych w czasie wag oznaczałoby znalezienie strategii inwestycyjnej
przynoszącej niewątpliwie ponadprzeciętne dochody, co potwierdziłoby hipotezę
nieefektywności Giełdy Papierów Wartościowych w Warszawie.

Ponieważ współczynniki korelacji uzyskane w badaniach empirycznych

okazały się zbyt niskie, tworzenie portfeli byłoby niecelowe, nie mogłyby one

osiągnąć ponadprzeciętnych dochodów. Oznacza to, że w obecnej postaci metoda
ta nie pozwala na odrzucenie hipotezy o efektywności warszawskiej giełdy.
Celowe jednak wydaje się zbadanie możliwości modyfikacji tej metody, co
będzie przedmiotem przyszłych badań autorów.

Literatura:
Baranowski M.: Wskaźnik pozycji finansowej. Penetrator 9/94, Kraków.
Czekała M.: Analiza fundamentalna i techniczna. Wydawnictwo AE we
Wrocławiu, Wrocław 1997.
Dominiak C.: Interaktywna procedura wspomagająca selekcję akcji do portfela.
Penetrator 4/95, Kraków.
Dominiak C.: Selekcja akcji do portfela. Penetrator 3/95, Kraków.
Fama, E. F.: Efficient Capital Markets: A Review of Theory and Empirical Work,
Journal of Finance, 25, 1970.
Gospodarowicz A.: Metody analizy i oceny pakietów programowych.
Wydawnictwo AE we Wrocławiu, Wrocław 1997.
Hanczar P.: Symulowane wyżarzanie - optymalizacja procesów logistycznych. w:
Ekonometria czasu transformacji. Materiały z XXXIV Konferencji Statystyków,
Ekonometryków i Matematyków Polski Południowej. Wyd. AE Katowice 1998.
Jajuga K., Kuziak K., Markowski P.: Inwestycje finansowe, AE Wrocław 1997.
Jurek R.: Fundamentaliści i portfolio. Penetrator 3/95, Kraków.
Kirkpatrick S., Gelatt C. D., Vecchi M. P.: Optimization by simulated annealing.
Science 220, 1983.
Konarzewska-Gubała E.: Wspomaganie decyzji wielokryterialnych. System
“BIPOLAR”. Prace AE we Wrocławiu Nr 551, Wrocław 1991.
Krawczyk S.: Matematyczna analiza sytuacji decyzyjnych. PWE, Warszawa
1990.
Metropolis N., Rosenbluth A., Rosenbluth M., Teller A., Teller E.: Equation of
state by fast computing machinaes. Journal of Chemical Physics 21, 1953.
Piontek K.: Zastosowanie wielokryterialnego wspomagania decyzji w procesie
selekcji akcji do portfela. Materiały z konferencji Inwestycje Finansowe i
Ubezpieczenia w Okresie Transformacji Polskiej Gospodarki. Prace AE we
Wrocławiu Nr 813 (w druku).
Reilly Frank K.: Investment Analysis and Portfolio Management, The Dryden
Press, Chicago, Fort Worth, San Francisco, Philadelphia, Montreal, Toronto,
London, Sydney, Tokyo, 1989.
Roy B.: Wielokryterialne wspomaganie decyzji. WNT, Warszawa 1990.
Steczkowski J., Zeliaś A.: Metody statystyczne w badaniu zjawisk jakościowych.
AE Kraków 1997.
Tarczyński W.: Rynki kapitałowe - metody ilościowe. PLACET, Warszawa
1997.