1
Temat:
Algorytmy- rodzaje, sposoby przedstawiania, analiza
i ocena złożoności obliczeniowej algorytmów
Pojęcie algorytmu, rola i miejsce algorytmu
w rozwiązywaniu problemu
Struktury danych
Reprezentacja algorytmów:
• Zapis w języku naturalnym- lista kroków
• Schemat blokowy
• Zapis w pseudokodzie
Czas wykonania a złożoność obliczeniowa, notacja O
duże
Analiza złożoności obliczeniowej
algorytmu wyszukiwania sekwencyjnego
2
Rola i miejsce algorytmu w rozwiązywaniu problemu
Algorytm
to sposób (schemat) postępowania prowadzący do
rozwiązania danego, konkretnego problemu. Lub mówiąc inaczej algorytm
to skończony ciąg operacji na obiektach (mogą to być np. liczby, relacje
między liczbami typu a>b, teksty) ze ściśle ustalonym porządkiem
wykonywania, dający możliwość realizacji zadania z określonej klasy.
Algorytm w sensie informatycznym wykorzystuje określone dane o
zdefiniowanych strukturach (np. liczby całkowite, rzeczywiste, zespolone,
tablice jedno i wielowymiarowe) i daje określone wyniki.
Algorytm powinien posiadać cechy:
Poprawność – dla każdego zestawu poprawnych danych wyniki
powinny być poprawne;
Skończony- dla każdego zestawu poprawnych danych algorytm
powinien dawać poprawne wyniki po skończonej liczbie kroków,
Określoność – z algorytmu musi wynikać jednoznacznie jaka ma
być realizowana następna operacja,
Efektywność- algorytm powinien realizować zadanie przy możliwie
najmniejszej liczbie kroków,
Uniwersalność- powinien rozwiązywać nie tylko specyficzne
zadanie ale całą klasę zadań.
Algorytm można zapisać w postaci:
Listy kroków,
Schematu blokowego (flow diagram, flow chart),
Pseudokodu
Wśród algorytmów wyróżnia się:
sekwencyjne – instrukcje wykonywane kolejno, ale mogą
też wystąpić ewentualne rozgałęzienia,
iteracyjne- to algorytmy w których pewne grupy instrukcji są
wykonywane wielokrotnie (ściśle zadaną liczbę razy lub wynikającą z
przebiegu obliczeń),
rekurencyjne- to algorytmy które wywołują same siebie dla
zmieniających się danych
Algorytm powinien posiadać specyfikację gdzie określamy dane z jakich
algorytm korzysta oraz wyniki które powinien dawać, a także niezbędne w
realizacji zmienne pomocnicze.
W algorytmach mogą również występować wyrażenia które są
zbudowane ze zmiennych, stałych, operatorów (np. +, - , *, /) i funkcji
matematycznych. Wyrażenia mogą też przybierać postać wyrażeń
warunkowych. Wówczas do ich budowy wykorzystywane są operatory
relacyjne (np. =, >, <, <=, >=, <>). W algorytmach występują często tzw.
operacje przypisania (np. x:=x +5), określające, że obliczona wartość
wyrażenia z prawej strony zostanie podstawiana pod zmienną ze strony
lewej.
3
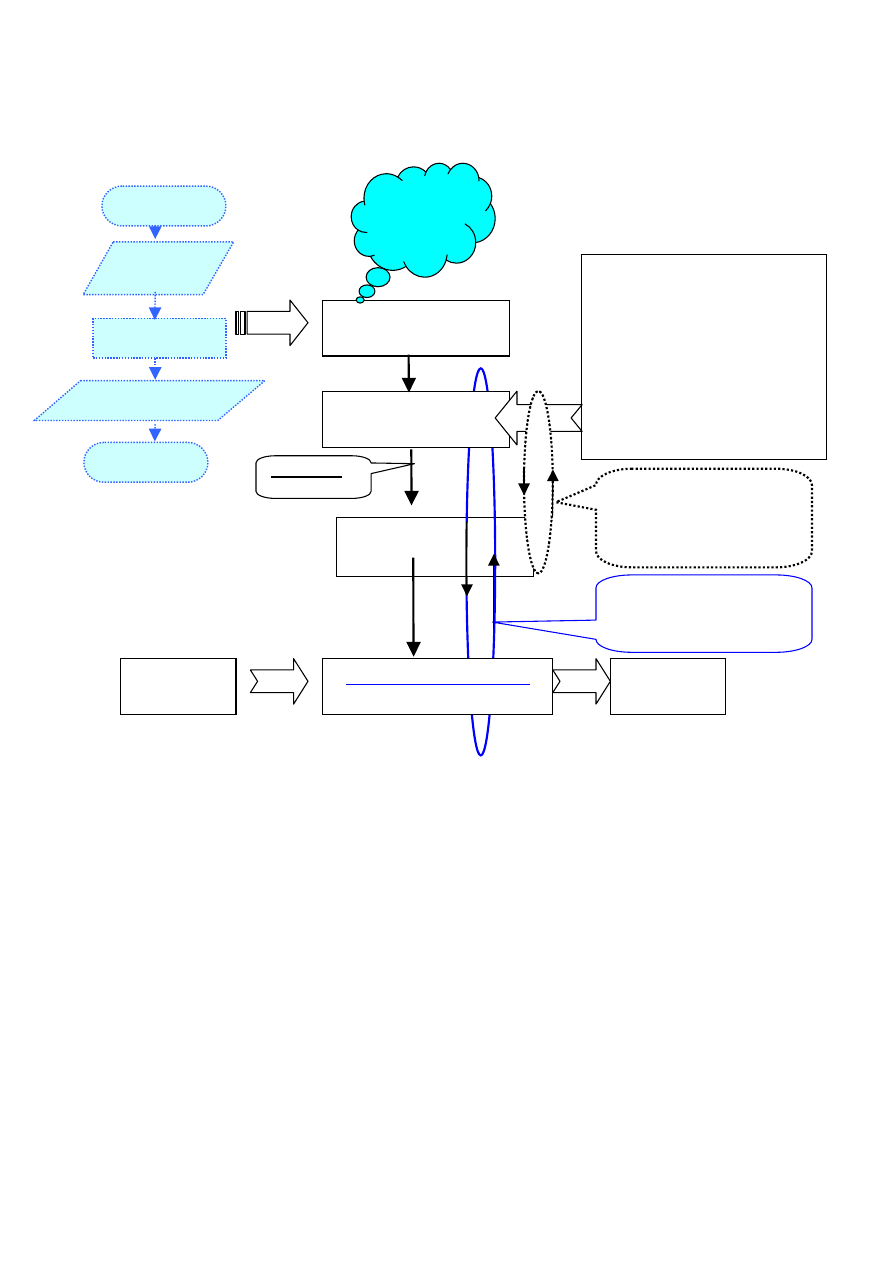
Rozwiązanie danego problemu przy zastosowaniu
komputera wymaga realizacji etapów:
Na rysunku pokazano drogę od problemu, który wymaga rozwiązania do
programu komputerowego rozwiązującego problem, przy założeniu, że
potrafimy poprawnie sformułować algorytm. Pętle sugerują, że niektóre
etapy będą powtarzane z powodu różnego rodzaju błędów, których
trudno uniknąć przy bardziej złożonych problemach. Pierwsza grupa
błędów wynika zwykle z błędnych zapisów algorytmu w języku
programowania.
Aby skompilować program (tzn. przetłumaczyć go na ciąg rozkazów w
zapisie zero-jedynkowym zrozumiałym dla komputera) to musi on być
całkowicie zgodny ze standardem danego języka. Ale uzyskanie
programu programu poprawnego językowo nie musi oznaczać, że
poprawnie rozwiązuje problem. Stąd może ponownie wynikać
konieczność zmiany jego wersji źródłowej – co pokazuje większa pętla.
Czasami również będzie konieczność jej rozszerzenia tzn. zmiany
algorytmu.
Program
wynikowy
2. Testowanie –
usuwanie błędów
logicznych
Algorytm
Algorytm
Algorytm
Algorytm
Problem !
Wykonanie programu
Program
źródłowy
Wyniki
Dane
Start
Wprowadź: a
Wprowadź
:
b
Oblicz: P:=a*b
Pisz:”Pole wynosi P=” P
Stop
program pole
var
a, b, p: real;
begin
readln(a);
readln(b);
p:=a*b;
write(’Pole P=
’,p:4:2,’ cm2’)
end.
Kompilacja
1
. Uruchamianie
(usuwanie błędów
jezykowych
4
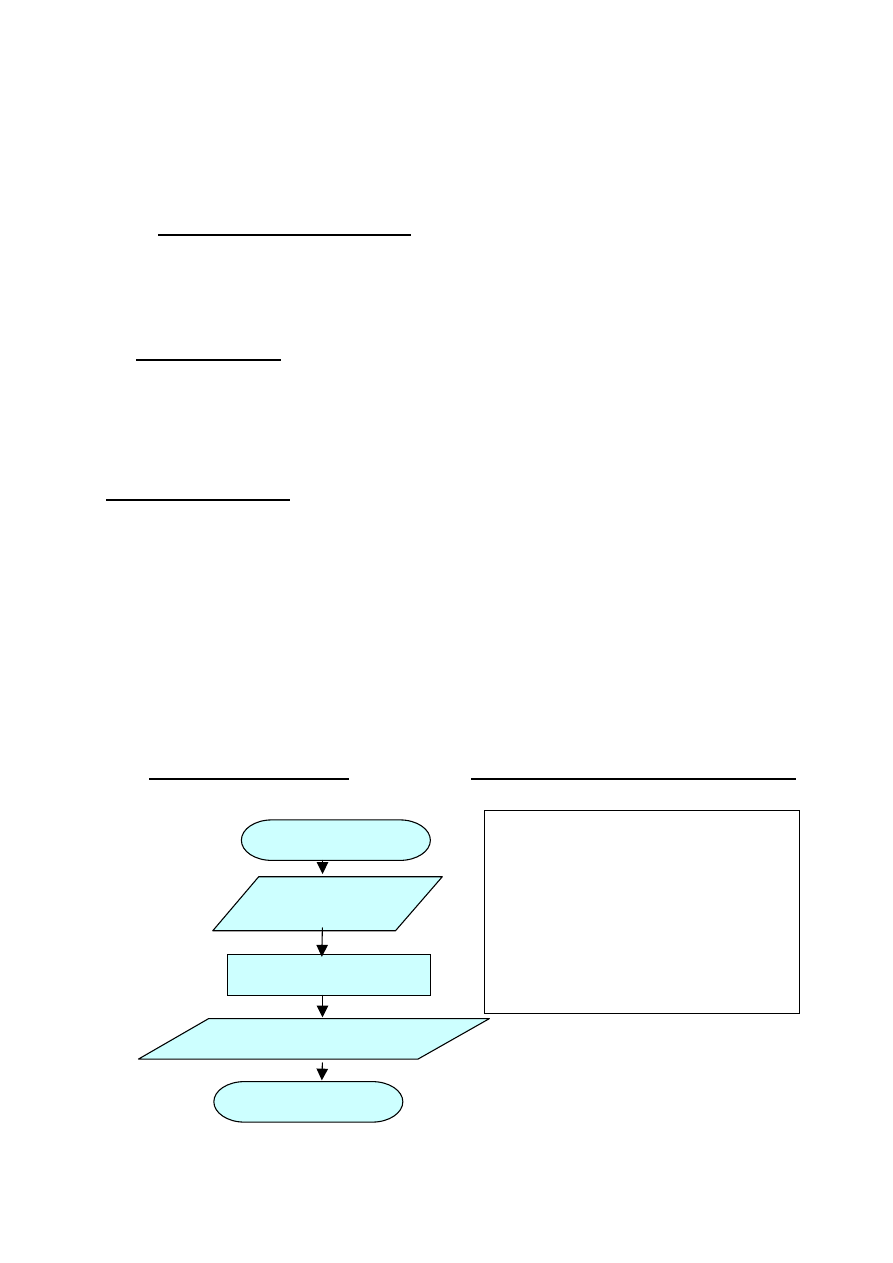
Przykład sformułowania algorytmu
Zadanie
Sformułuj algorytm obliczający pole prostokąta. Zapisz algorytm w postaci listy
kroków, schematu blokowego i pseudokodu.
a)
Specyfikacja algorytmu:
Dane wejściowe:
a-
pierwszy bok, liczba rzeczywista dodatnia- w cm,
b-
drugi bok, liczba rzeczywista dodatnia- w cm.
Wynik
: P –pole prostokąta (w cm
2
)
Lista kroków:
K1: Wczytaj wartość pierwszego boku do zmiennej a,
K2: Wczytaj wartość drugiego boku i podstaw pod zmienną b,
K3: Oblicz pole i podstaw pod zmienną p
K4: Wyświetl wynik p
b) Pseudokod:
Program pole
{nagłówek}
zmienne
a,b,p: real
{deklaracja zmiennych}
begin
{początek właściwego programu}
czytaj (a)
{wczytanie danych}
czytaj(b)
P:=a*b
{obliczenia}
wyświetl(„Pole wynosi P=”, p)
{wyświetl wynik}
end
{koniec właściwego programu}
c) Schemat blokowy:
d) Zapis w
języku programowania
( np. Pascal)
Start
Wprowadź: a
Wprowadź: b
Oblicz: P:=a*b
Pisz:”Pole wynosi P=” P
Stop
program pole
var
a, b, p: real;
begin
readln(a);
readln(b);
p:=a*b;
write(’Pole P= ’,p:4:2,’ cm2’)
end.
5
Reprezentacja algorytmów
Najbardziej ogólną formą i jednocześnie mało precyzyjną jest opis
słowny w języku naturalnym. Ta forma niesie ryzyko niejednoznaczności
przy złożonych algorytmach. Stosuje się ją dla zasugerowania
rozwiązania.
Popularnym sposobem jest lista kroków postępowania. Kroki
stanowią opis operacji i są zazwyczaj mieszaniną sformułowań
matematycznych i języka naturalnego. Kolejność kroków jest zgodna z
opisem. Wyjątkiem jest operacja przejścia do wskazanego kroku lub też
zakończenia algorytmu.
Przykład:
Problem znalezienia największego wspólnego dzielnika (NWD(n,m) )
dwu liczb całkowitych m i n:
Najbardziej znanym jest algorytm Euklidesa (ok. 300r p.n.e.).
Specyfikacja
Dane: m, n – liczby całkowite, Założenie: n
≥ m
Wynik: NWD(n,m)
Algorytm:
K1. Podziel n przez m. Niech r będzie resztą z dzielenia.
K2. jeśli r=0 to wynikiem jest m. KONIEC.
K3. Wykonaj:
n:=m
m:=r
Przejdz do K1
Przykład: 1 NWD(n=12, m=6)
K1. n/m=12/6= 2 r=0
K2 r=0 . Stąd m=6 jest poszukiwaną liczbą tzn.
NWD(12,6)=6
Przykład: 2 NWD(n=12, m=8)
K1. n/m=12/8= 1 r=4
K2 r≠0 .
K3 n:= 8 m:=4
K1 n/m=8/4=2 r=0
K2 r=0 . Stąd m=4 jest . czyli
NWD(12,8)=4
6
Algorytm NWD(n,m) (powtórzenie):
K1. Podziel n przez m. Niech r będzie resztą z dzielenia.
K2. jeśli r=0 to wynikiem jest liczba
„m”
. KONIEC.
K3. Wykonaj:
n:=m
m:=r i przejdz do K1
Przykład: 3
Określić NWD(n=44, m=16)
K1. n/m=44/16= 2 r=12
K2 r≠0 .
K3 n:= 16 m:=12
K1 n/m=16/12=1 r=4
K2 r≠0 .
K3 n=12 m=4
K1 n/m=3 r=0
K2 r=0 . Stąd m=4 jest .
NWD(44,16)=4
Dowód algorytmu:
Rozważmy zależność:
n
= q*m +r 0 ≤ r < m (*)
gdzie: q- iloraz liczb n i m (liczba całkowita m div n)
r- reszta z dzielenia (n modulo m)
Jeżeli r=0 to każdy dzielnik liczby m jest dzielnikiem n. Zatem największy
dzielnik m (czyli liczba m !) jest dzielnikiem n.
Jeśli r > 0 t z (*) wynika, że każdy wspólny dzielnik liczb „n”, „m” jest
dzielnikiem „r” a także każdy wspólny dzielnik liczb „r”, „m” jest
dzielnikiem „n”. Zatem liczby „n”, „m” oraz „m”, „r” mają te same
wspólne dzielniki – więc też największy z nich jest wspólny. Można więc
parę liczb „n”, „m” zastąpić parą „m”, „r” do jest równoważne: NWD(n,m
)= NWD(m,r ),i co ma miejsce w K3.Ponadto z nierówności 0 ≤ r < m
wynika, że ciąg reszt „r” otrzymywanych w K1 jest ograniczony i malejący,
a ponieważ jego wyrazy są całkowite to po skończonej liczbie kroków
wystąpią równości:
n
= q*m +r r =0
Oznacza to, że w kroku K2 zostanie osiągnięty koniec, a wtedy
NWD(n’,m’.) będzie równy aktualnej wartośći „m’ ”. c.b.d.o.
7
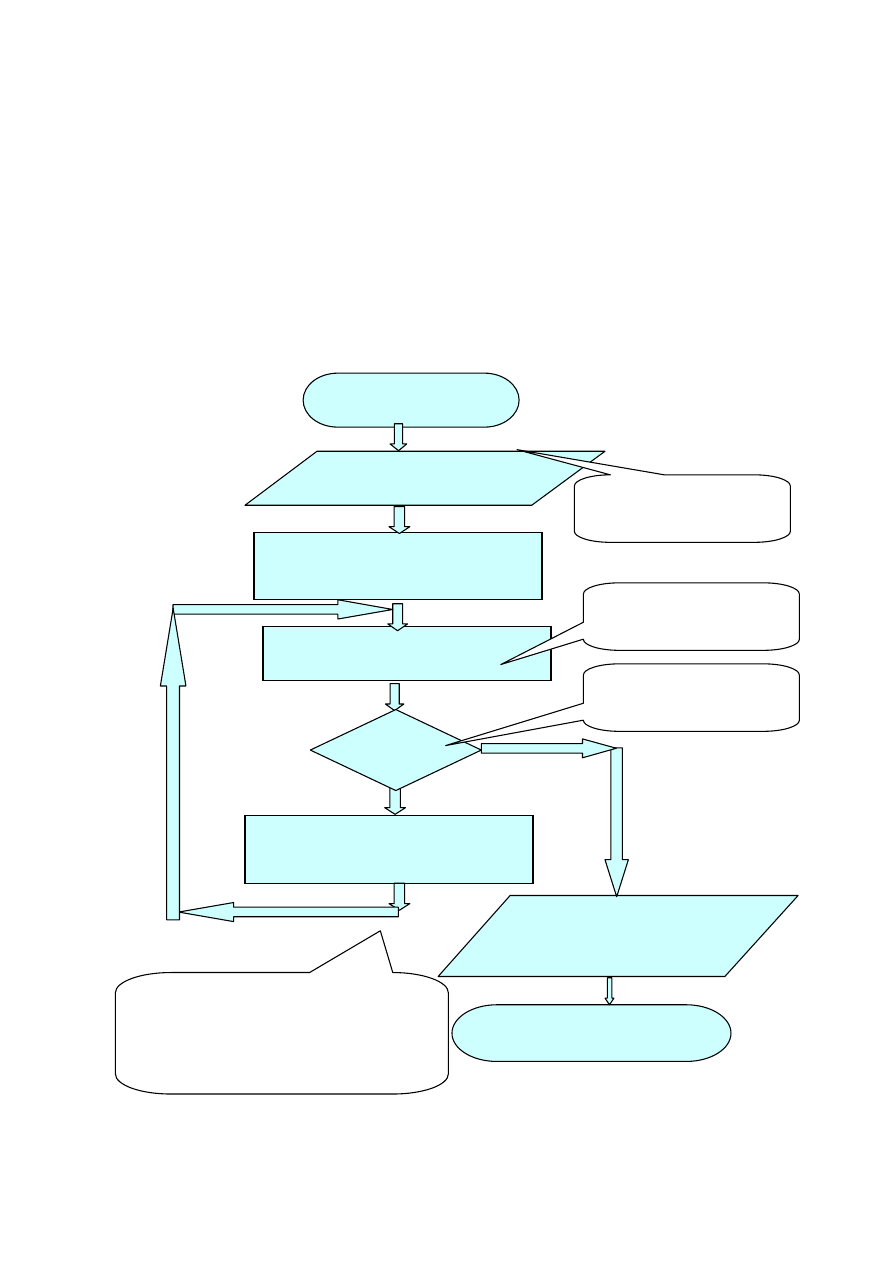
Reprezentacja blokowa algorytmu NWD
Schemat blokowy (sieć działań) składa się z symboli graficznych w
których opisywane są operacje algorytmu.
Stosuje się różne kształty symboli dla rozróżnienia operacji. Następstwo
operacji określają strzałki. Jest doskonałą komunikacją między
„zleceniodawcą” a programistą. Jednak złożone problemy trudno jest
przedstawić przy pomocy tego typu schematów. Dlatego stosuje się różne
poziomy szczegółowości (od ogółu do szczegółu- schemat zstępujący ).
NIE
TAK
START
KONIEC
Wprowadź: n,m
a := n
b:=m
r≠0
n := m
m := r
Wypisz:
NWD(
a,b
)= m
r:= n mod m
Kształty Wejścia/
Wyjścia
Instrukcje
przypisania
Podjęcia decyzji
(sterowanie)
W Wordzie elementy graficzne
występują w zakładce :
Rysuj
Autokształty
Schematy
blokowe
Strzałki blokowe
8
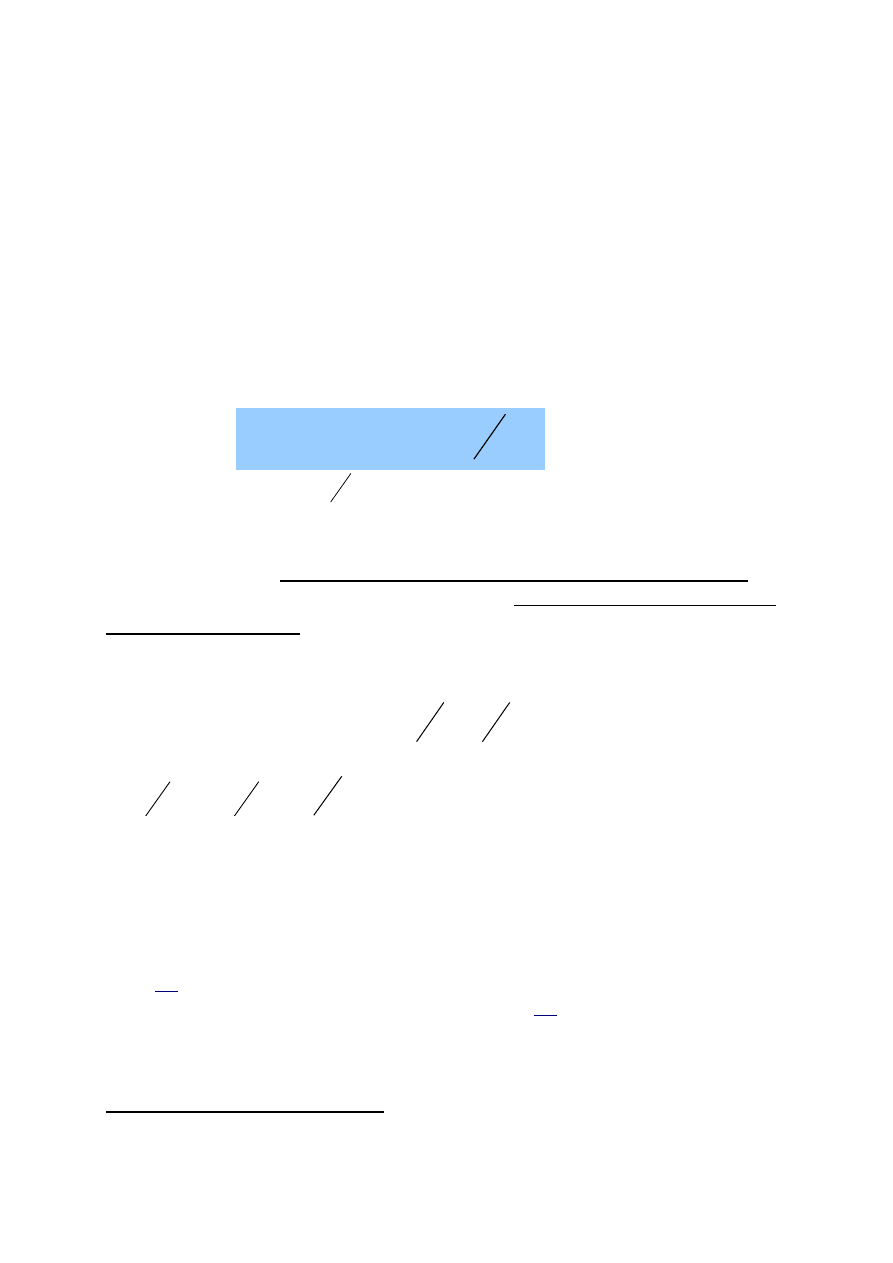
Operacja „MODULO”
Można zdefiniować dodawanie, odejmowanie i inne operacje, tzw.
"modulo". Są one istotne w w teorii algorytmów i metodach szyfrowania.
Niech n mod m oznacza standardową „operację modulo. Z definicji:
n mod m=n-((n div m)*m)
gdzie: div- dzielenie całkowite np. 365 div 7 =52
( a zwykłe dzielenie daje 365/7= 52.14285)
stąd: 365 mod 7 = 365 – 52*7 = 365 – 364= 1
Inny zapis:
m
m
n
n
m
n
−
=
mod
gdzie:
m
n
- podłoga z dzielenia liczb n i m.
Zapis
x
czytamy: Dla dowolnej liczby rzeczywistej x
x
(czytaj: „podłoga
x”- floor ) oznacza największą liczbę całkowitą mniejszą lub równą x.
Zapis
x
(czytamy „sufit x”-ceiling ) oznacza najmniejszą liczbę całkowitą
większą lub równą x. Dla wszystkich liczb rzeczywistych:
1
1
+
<
≤
≤
<
−
x
x
x
x
x
Dla każdej liczby całkowitej n:
n
n
n
=
+
2
2
Dla każdej liczby rzeczywistej n ≥0 i liczb całkowitych a,b ≥0:
ab
n
b
a
n
=
/
(
)
(
)
b
b
a
b
a
/
1
−
−
≥
Powyższe relacje zachodzą dla funkcji sufit (ale znak relacji odwrotny!!)
Dzielenie modulo
Dzielenie modulo zwraca resztę z dzielenia. Tzn jeżeli dzielimy 2 liczby
całkowite (tylko na takich liczbach operacja ta jest dozwolona) to często
wynikiem jest ułamek. np wynik dzielenia 3/2 będzie 1 (jeżeli wynik ma być
typu
int
) żeby określić jaka liczba jest po przecinku stosujemy dzielenie
modulo. Wynik dzielenia też jest zawsze typu
int
Jeżeli wynikiem dzielenia jest liczba całkowita np: 4/2=2, to wynikiem
dzielenia modulo jest 0 (4 %2=0). W ten sposób bada się parzystość
liczby.
Przykłady operacji modulo .
16 mod 16 = 0 10 mod 16 = 10 17 mod 16= 1 20 mod 16 = 4
9
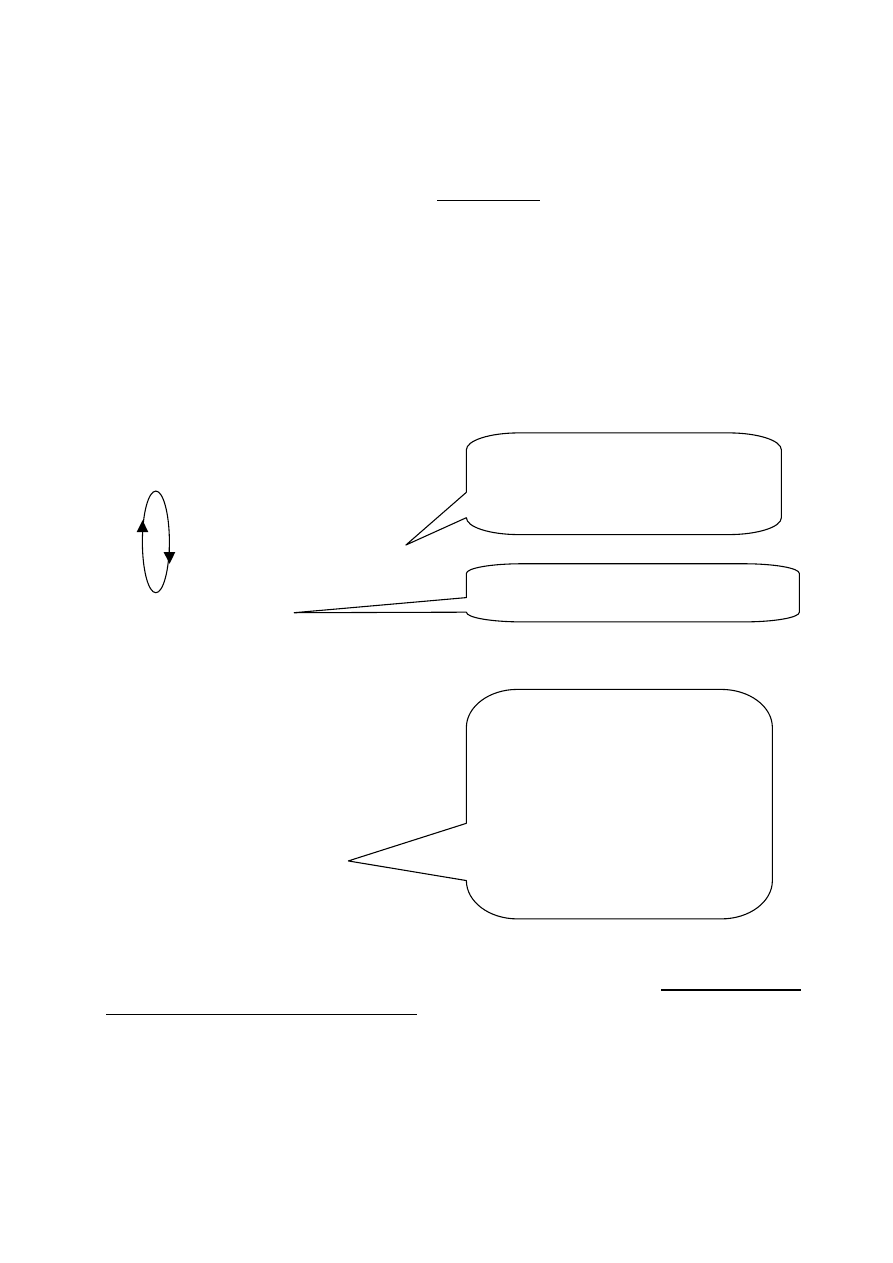
Reprezentacja algorytmu NWD w pseudokodzie
Formą opisu algorytmów jest tzw. pseudokod (pseudojęzyk), zbliżony do
języka wysokiego poziomu np. Pascala lub C. Pseudojęzyk nie uwzględnia
technik programowania np. stosuje abstrakcyjne typy danych zamiast
standardowych, pomija obsługę błędów i deklaracje zmiennych lokalnych.
Dopuszcza nieformalne opisy zmiennych i parametrów, korzysta też
z języka naturalnego i symboliki matematycznej. Ma to na celu
uproszczenie opisu algorytmu i zrozumienie logiki działania a
jednocześnie zachowanie specyfiki języka, co ułatwia implementację. Oto
opis algorytmu NWD(n,m):
function
EUCLID(n,m)
r:= n
mod
m
while
r≠0
do
n:= m
m:= r
r:= n
mod
m
return
m
Inna forma zapisu:
function
EUCLID(n,m)
r:= n
mod
m
while
r≠0
do
begin
n:= m
m:= r
r:= n
mod
m
end
return
m
Nagłówek określa nazwę algorytmu i jego parametry (n,m). Oba parametry
są przekazywane przez wartość . tzn, że otrzymują one wartości, których
zmiany wewnątrz programu będą poza nim niewidoczne. Instrukcja
„return” poza zakresem „while” kończy algorytm. Jako wynik zwracana
jest wartość m.
while
r≠0
do
- powtarzaj to co
poniżej dopóki r jest różne od
zera
Zwróć jako wynik aktualną
wartość m
Inne- zaznaczenie bloku
powtarzalnych instrukcji
obramowane jak w Pascalu
begin
....
end-
lub też jak w C++
{
.........
}
10
Metody konstruowania algorytmów
Prawie każdy problem można zakwalifikować do jakiejś klasy, dla
której znane są algorytmy rozwiązania. Gdy nie ma gotowego rozwiązania
to przydatne mogą być metody tworzenia algorytmów:
• metoda „dziel i zwyciężaj”
• programowanie dynamiczne,
• metoda zachłanna
• metoda prób i błędów
Każdy z algorytmów, niezależnie od metody którą stosuje, korzysta z kolei
z pewnych technik realizacyjnych. Z tego punktu widzenia możemy
wyróżnić rozwiązania :
• iteracyjne- obliczenia są wykonywane sekwencyjnie w pętlach
bazujących na instrukcjach np. „while” i „for”,
• rekurencyjne – program realizujący, wielokrotnie wywołuje sam
siebie siebie. Ta skomplikowana technika jest możliwa dzięki
mechanizmowi stosu.
Metoda „dziel i zwyciężaj” (
divide and conquer
)- jej najprostsze
zastosowanie i wyjaśnienie to tzw. wyszukiwanie binarne. Polega on na
stwierdzeniu czy liczba „x” występuje w pewnym ciągu liczb (tzw. kluczy)
rosnąco uporządkowanych. Naturalnym opisem problemów
rozwiązywanych metodą „dziel i zwyciężaj” jest stosowanie rekurencji.
Najbardziej znanym rozwiązaniem wykorzystującym „dziel i zwyciężaj” jest
najszybszy znany aktualnie algorytm sortowania QuickSort.
Programowania dynamiczne również stosuje podział na podproblemy
i metodą wstępującą dochodzi do rozwiązania. Przykładem jest tzw. ciąg
Fibonacciego stosowany w opisie zjawisk przyrodniczych i informatyce.
Metoda zachłanna
( greedy algorithms)
- może być przedstawiona w
postaci np. problemu wydawania reszty po dokonaniu zakupów. Wydaje
się resztę zaczynając od największych nominałów i ich krotności. Jest
stosowana również w problemie wyznaczenia najkrótszych dróg (połączeń)
w sieci.
Metoda „prób i błędów” jest stosowana gdy nie można wyrażenie określić
reguły obliczeniowej. W kolejnych krokach dokonuje się wyborów
poprawiając rozwiązanie. Niekiedy trzeba tu dokonywać „nawrotów”.
Przykładem jest tzw. problem plecakowy, który może być interpretowany
np. jako upakowanie kontenerów w ładowni statku.
Dla podanych metod są stosowane zarówno wersje iteracyjne
i rekurencyjne algorytmów.
11
Algorytmy iteracyjne- reprezentacja w języku programowania
Algorytmy iteracyjne cechuje wielokrotna powtarzalność pewnych
obliczeń, realizowana zwykle z wykorzystaniem pętli. Np. w przypadku
algorytmu obliczania silni ( n! ) sposób obliczania można zapisać
następująco:
O!=1
1!=1
2!=1*2
3!=1*2*3
…………….
n! = 1*2*3* … *j*…*(n-2)*(n-1)*n
Z definicji wynika, że obliczenie silni dla wartości n wymaga mnożenia
przez siebie wszystkich kolejnych liczb naturalnych. Operacją podstawową
jest mnożenie kolejnej liczby „j” przez wartość s, która jest
dotychczasowym iloczynem liczb 1,2,3,…,(j-1). Czyli
n! = s * j*…*(n-2)*(n-1)*n
Ta operacja jest tu powtarzalną a jej liczba powtórzeń jest z góry
określona. W implementacji programowej można zastosować tzw. pętlę
for. Jej najprostsza struktura w pseudokodzie jest następująca:
for j= Liczba_początkowa :krok: Liczba_koncowa do
begin instrukcje powtarzane w pętli end
W przypadku obliczania silni pętla przyjmie postać:
for j= 1 : 1 : n do
lub prościej
for j= 1: n do
begin
s := s *j
end
Ponieważ nowa wartość iloczynu s jest wartością poprzednią mnożoną
przez bieżącą wartość j -to na początku wartość s musi być ustawiona tak,
aby była niezmienniczą względem mnożenia tzn. s=1.
W języku Matlab skrypt (czyli ciąg instrukcji) obliczający wartość
silnia(n) można zapisać:
% SKRYPT OBLICZA WART.
n=input
(‘Podaj n=’
);
if
n>0
s=1;
for
j=1:n
s=s*j;
end
sprintf
(‘%d != d%’
,n,s)
elseif
n==0
disp
(‘0! = 1’
);
else
disp(
‘Silnia nie istnieje’
);
end
Okno edytora Matlaba i okno Command uruchamiania skryptu
Silnia_ITERACYJNIE.m
wraz z wynikiem obliczeń dla n=8
12
Algorytmy rekurencyjne- reprezentacja w języku programowania
Obliczanie silni dla liczby całkowitej n>0 jest też definiowane wzorem
nazywanym wzorem (algorytmem) rekurencyjnym:
n! = (n-1)*n
Zaletą takiego definiowania jest krótki zapis, ale sama realizacja jest
złożona.
Aby wykorzystać wzór rekurencyjny trzeba go zaprogramować w postaci
tzw. funkcji.
Funkcja rekurencyjna- to funkcja która wywołuje sama siebie.
W Matlabie funkcja zaczyna się słowem kluczowym function, oraz być
zapisana w pliku o nazwie zgodnej z nazwą funkcji (to wymaga by plik miał
nazwę silnia.m). Ostatnia z wykonywanych instrukcji funkcji musi zapewnić
podstawienie wartości - w tym przypadku musi to być nadanie wartości
zmiennej s. Parametr w nawiasie (tu n) jest przekazany z zewnątrz (z
miejsca wywołania) przez tzw. wartość.
function
s = silnia(n)
sprintf(
'Wchodzę z n=%d'
,n);
disp(ans);
if
n==0
s=1;
else
s=n * silnia(n-1);
end
Śledzenie rekurencji w obliczaniu silni przy pomocy powyższej funkcji:
>> silnia(6)
% przykładowe uruchamienie funkcji z konsoli
Wchodzę z n=6
Wchodzę z n=5
Wchodzę z n=4
Wchodzę z n=3
Wchodzę z n=2
Wchodzę z n=1
Wchodzę z n=0
720
>>
W przypadku wywołania w postaci s= silnia(6) wynik jest w zmiennej s.
To oznacza (5!)*6- czyli trzeba obliczyc 5! –
rekur.: Silnia(5)
To oznacza (4!)*5*6 itd
13
Czas wykonania programu a złożoność obliczeniowa.
Niech będzie dany pewien algorytm A o którym przyjmiemy założenia:
• czas wykonania operacji elementarnej wynosi 1µs,
• czas wykonania algorytmu (liczba operacji) jest proporcjonalny do
pewnej funkcji matematycznej
W tabeli przedstawiono czasy wykonania programów dla algorytmów
różnej klasy.
Rozmiar danych (wartość n w algorytmie)
Klasa
algorytmu
10
20
30
40
50
n
0,000 01s 0,000 02s 0,000 03s 0,000 04
0,000 05
n
2
0,000 1s
0,000 4s
0,000 09s 0,001 6s
0,002 5s
n
3
0,001s
0,008s
0,027s
0,064s
0,125s
2
n
0,001s
1,0s
17,9min
12,7dni
35,7
lat
3
n
0,59s
58min
6,5
lat
3855
wieków
2*10
6
wieków
n
!
3,6s
756
wieków
8,4*10
6
wieków
9,6*10
48
wieków
2,6*10
66
wieków
Algorytmy ocenia się na podstawie różnych kryteriów zależnych od
okoliczności ich stosowania. Zazwyczaj istotna jest prostota i „elegancja”,
czas działania, dokładność obliczeń (dla algorytmów numerycznych).
Często wybór algorytmu jest kompromisem między np. prostotą a
efektywnością. Algorytmy prostsze są łatwiejsze do zrozumienia,
implementacji programowej i testowania, ale zwykle ich czas realizacji jest
dłuższy. Bardziej efektywne algorytmy są zwykle bardziej skomplikowane.
Wymagają stosowania bardziej złożonych technik programowania np.
rekurencji.
Podstawowymi zasobami każdego algorytmu są :
czas wykonania,
wielkość zajmowanej pamięci
.
Analiza algorytmu polega na określeniu niezbędnych zasobów do jego
wykonania. Należy uwzględnić też jego poprawność, prostotę i
użyteczność praktyczną. Analiza kilku algorytmów dla danego problemu
pozwala zwykle na wybór najlepszego pod względem czasu jak i pamięci.
Wielkość zasobów komputerowych potrzebnych do wykonania
algorytmu określa się mianem
złożoności obliczeniowej.
Dla wielu
algorytmów czas ich wykonania i wielkość pamięci powiększa się gdy
14
wzrasta wielkość zestawu danych. Dlatego często złożoność obliczeniowa
traktowana jest jako funkcja zależna od rozmiaru danych wejściowych,
nazywanego rozmiarem problemu lub zadania, który jest liczbą całkowitą
wyrażającą wielkość zestawu danych. Na przykład w problemie
sortowania za rozmiar problemu przyjmuje się liczbę elementów ciągu
wejściowego, a przy wyznaczaniu wyznacznika macierzy- liczbę wierszy
i kolumn.
Pozostaje
jeszcze
kwestia
określania
jednostki
złożoności
obliczeniowej. W przypadku złożoności pamięciowej za jednostkę
przyjmuje się komórkę pamięci.
W zależności od kontekstu może to być bajt lub inna jednostka pamięci
zajmowanej przez wartość typu prostego. Np. dla algorytmów działających
na zmiennych typu real, jest to zwykle 8 bajtów.
W przypadku złożoności czasowej w algorytmie wyróżnia się
charakterystyczne operacje o tej własności, że całość wykonanej przez
algorytm pracy jest proporcjonalna do liczby tych operacji. Są to operacje
dominujące. Np. w algorytmie sortowania liczb taką operacją jest
porównanie dwu elementów ciągu wejściowego i ich ewentualne
przestawienie, a w algorytmach obliczania wyznacznika macierzy-
operacje arytmetyczne +,*,- /.
Jednostką miary złożoności czasowej jest wykonanie jednej operacji
dominującej.
Zaletą tak zdefiniowanej złożoności czasowej jest jej uniwersalność
i niezależność od:
szybkości procesora,
cech języka programowania i umiejętności programisty.
Złożoność czasowa staje się miarą jego efektywności czasowej, a
własności algorytmu zależą tylko od niego i rozmiaru danych.
W rzeczywistości nie jest zupełnie prawdą ponieważ czas wykonania
algorytmu np. sortowania może się różnić dla danych o tym samym
rozmiarze. Np. w posortowanym ciągu wejściowym nie wystąpią
przestawienia elementów, a gdy jest odwrotnie posortowany liczba
przestawień jest największa. Stąd czasami bierze się pod uwagę tylko
operacje porównania.
Do oceny złożoności czasowej algorytmów wykorzystuje się pewne
notacje, które mówią jak wygląda ta złożoność obliczeniowa jeśli liczba
danych „n” rośnie.
Najczęściej stosowaną jest notacja O duże
. Celem
stosowania tej notacji jest pokazanie charakteru wzrostu złożoności
obliczeniowej (np. liniowa, kwadratowa, logarytmiczna).
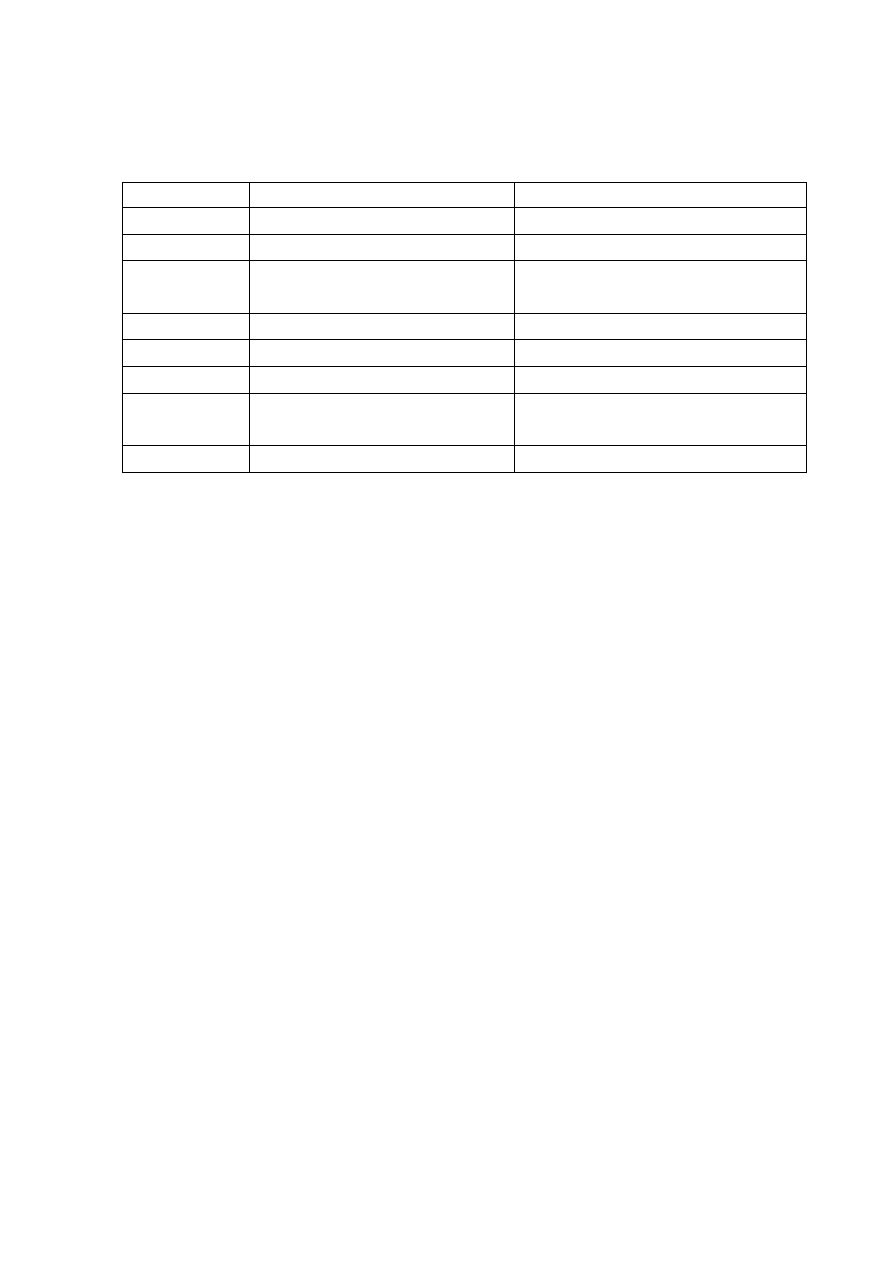
15
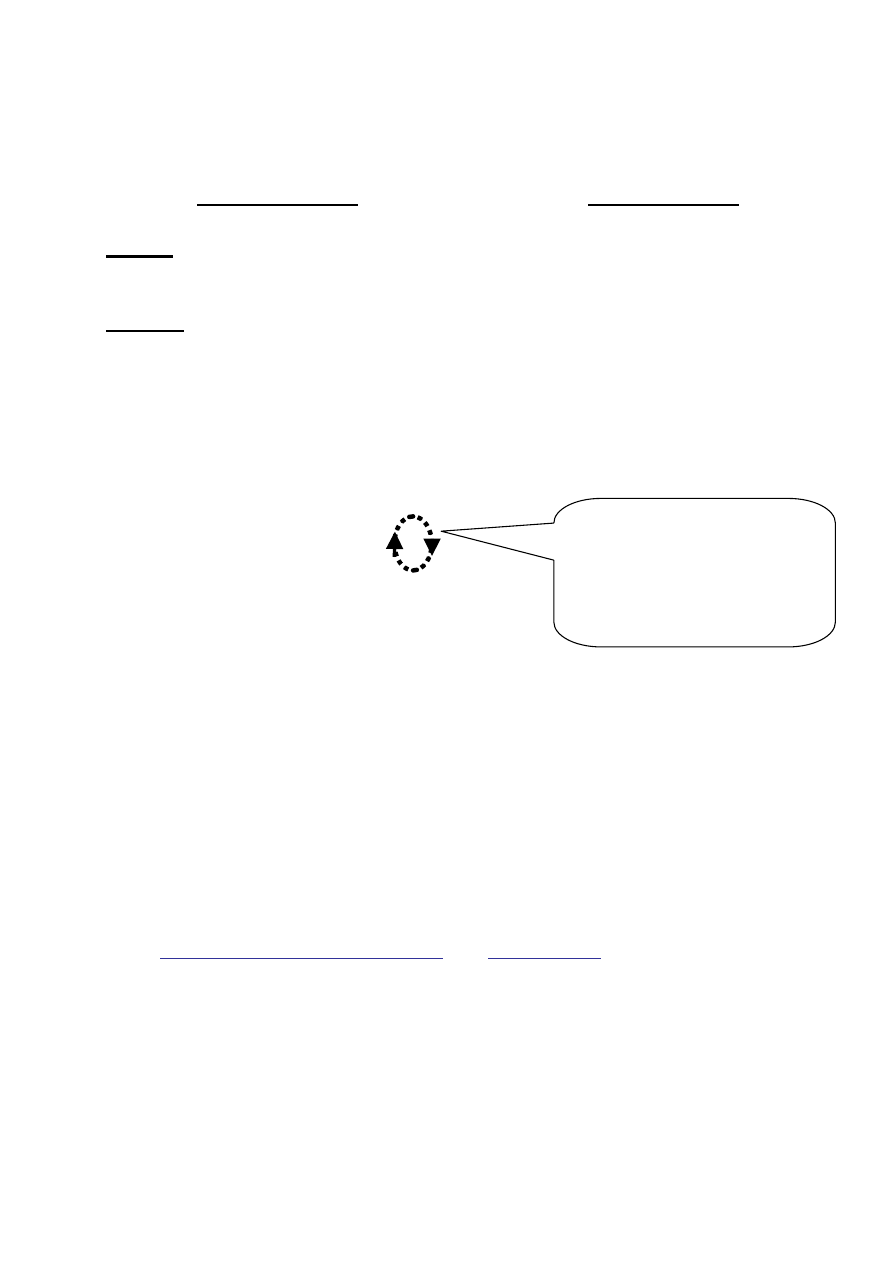
Oto przykłady najważniejszych rodzajów złożoności algorytmów
n
Rodzaj złożoności
Przykład
O(1)
Stała
Dostęp do elementu tablicy
O(logn)
logarytmiczna
Przeszukiwanie binarne
0(n)
liniowa
Przeszukiwanie
sekwencyjne
O(nlogn)
Liniowo-logarytmiczna
Sortowanie kopcowe
0(n
2
)
kwadratowa
Sortowanie bąbelkowe
O(n
3
)
sześcienna
Mnożenie macierzy
O(2
n
)
wykładnicza
Algorytm plecakowy
Wieże Hanoi
O(n
!
)
wykładnicza
Generowanie permutacji
Gdzie:
O(…) tzw notacja O duże określająca złożoność obliczeniową algorytmu
Jest oczywistym, że złożoność obliczeniowa przekłada się na czas
obliczeń na konkretnej platformie sprzętowej (komputerze).
16
Analiza złożoności algorytmu przeszukiwania sekwencyjnego
Problem przeszukiwania określony jest też jako wyszukiwania. Jego
specyfikacja jest następująca:
Dane:
x
element
i
a
tablicy
w
a
a
a
liczb
n
Ciąi
n
[]
,
,
,
2
1
K
Wynik:
Indeks „k” taki, że x=a
k
lub –1, gdy x nie ma w ciągu
Najprostszy algorytm zwany jest przeszukiwaniem sekwencyjnym
(sequential search), polega na przeglądaniu kolejnych elementów ciągu i
kończy się, gdy poszukiwany element zostanie znaleziony lub cały ciąg
zostanie przeszukany. Algorytm można zapisać następująco:
Function SEQUENTIAL-SEARCH(a[1..n],x)
1
for k:=1 to n do
2
if x=a[k] then
3
return k
4
return –1
Można powiedzieć złożoność algorytmu zależy gdzie w tablicy znajduje
się szukany element” – jeśli w ogóle jest!
Operacjami dominującymi w algorytmie są porównania. Ich liczba jest
równa liczbie wykonań pętli for. Najlepszy przypadek jest jeśli x jest
pierwszym elementem ciągu, a najgorszy gdy ostatnim lub nie występuje.
Zatem:
W(n)=T(n)=n -(przypadek Worst)
B(n) =T(1)=1 (przypadek Best)
Stosując notację O duże:
T(n)=W(n)=O(n)
W ocenie algorytmów bardziej istotne są oceny pesymistyczne,
czyli najdłuższe czasy działania dla dowolnych danych rozmiaru
n z powodu, że:
• Algorytm nie będzie działał dłużej,
• Przypadek pesymistyczny jest częsty np. brak inf. w bazie,
Przypadek „średni” - często zbliżony do pesymistycznego
W każdym obiegu pętli
for
sprawdza się czy element
tablicy jest równy
szukanemu elementowi
x
(wiersz2) . Jeśli tak jest
zwracana jest wartość
in
deksu
k
(wiersz 3)
17
Dalej przedstawiono analizę przypadku średniego. Założymy że
prawdopodobieństwo zdarzenia , że
x
występuje w ciągu wynosi
p
, oraz
że jeśli w nim występuje to prawdopodobieństwo zdarzenia, że występuje
na pozycji
k
wynosi
p/n
, a prawdopodo-bieństwo zdarzenia, że nie
występuje w ciągu wynosi
(1-p)
.
Zatem p-stwo
p
k
zdarzenia
ω
k,
że algorytm wykona
k
porównań przy
poszukiwaniu wartości
x
wynosi:
)
(
)
1
(
1
,
,
2
,
1
(
n
k
p
n
p
n
k
n
p
p
k
=
−
+
−
=
=
K
Przypadek
k=n
oznacza:
• Element x jest na pozycji n (ostatniej),
• Lub element x nie występuje, ale żeby to stwierdzić trzeba przejrzeć
wszystkie elementy od 1 do n.
Stąd pk dla k=n jest sumą zdarzeń.
Niech
X
n
oznacza zmienną losową, której wartościami są liczby porównań
wykonywanych przez algorytm dla danych rozmiaru
n:
( )
)
,
,
2
,
1
(
n
k
k
X
k
n
K
=
=
ω
Jej wartość oczekiwana wynosi:
( )
( )
(
)
(
)
(
) ( )
2
2
1
1
2
1
1
1
1
1
1
p
p
n
p
n
n
n
n
p
p
n
k
n
p
p
n
n
p
k
p
X
X
E
n
k
n
k
n
k
k
k
n
n
+
−
=
−
+
+
=
=
−
+
=
−
+
=
=
∑
∑
∑
=
=
=
ω
Ostatecznie średnia A(n) (Average) liczba porównań w algorytmie przy
założeniu, że p-stwo wystąpienia poszukiwanego elementu wynosi
p
, jest
określona zależnością:
( )
( )
2
2
1
p
p
n
X
E
n
A
n
+
−
=
=
Na podstawie tej zależności rozpatrzmy przypadki:
Jeśli
p=1,
tzn.
x
na pewno występuje - to
A(n)=(n+1)/2
. Czyli
średnio przeszukuje się połowę ciągu,
Jeśli
p=1/2
, to
A(n)=(3n+1)/4
Czyli średnio przeszukuje się 3/4
elementów ciągu,
Jeśli
p jest bliskie zera
to
A(n)
jest bliski
n.
Czyli średnio trzeba
przeszukać cały ciąg.
X –nie wystąpi w ciągu
Ale taka suma =n(n+1)/2
18
Przeszukiwanie binarne- Zastosowanie metody
„dziel i zwyciężaj”. Złożoność obliczeniowa algorytmu
Specyfika przeszukiwania binarnego jest następująca:
Dane:
x
element
szukany
i
a
a
a
liczb
n
Ciąi
n
,
,
,
2
1
K
O ciągu zakładamy, że jego elementy są uporządkowane niemalejąco.
Wynik:
Indeks „k” taki, że x=a
k
lub –1, gdy x nie ma w ciągu
Można zastosować algorytm przeszukania binarnego (binary search),
który jest znacznie efektywniejszy niż sekwencyjny.
Algorytm jest oparty na metodzie
„dziel i zwyciężaj”.
Załóżmy początkowo, że w rozpatrywanym ciągu
i=1, j=n.
j
i
i
i
a
a
a
a
,
,
,
2
1
K
+
+
Dla jego środkowego elementu o indeksie k=(i+j)/2 wystąpi jeden z
trzech przypadków:
x=a[k] –
element
x
został znaleziony na pozycji
k
, należy więc
zakończyć algorytm,
x<a[k] -
element
x
może wystąpić tylko w lewej połowie, więc należy
ją rozpatrzyć przyjmując
j=k-1
,
x>a[k] -
element x może wystąpić tylko w prawej połowie, , więc
należy ją rozpatrzyć przyjmując
i=k+1
,
Jeśli po wykonaniu kolejnego kroku zachodzi nierówność
i >j
, to
poszukiwanie kończy się niepomyślnie, a jego wynikiem jest
–1
.
Function
BINARY-SEARCH(a[1..n])
i:=1,
j:=1
while
i ≤ j
do
k:= (i +j)
div
2
if
x= a [k]
then
return
k
else
if
x < a [k]
then
j := k-1
else
i := k +1
return
–1
To jest wersja
iteracyjna
algorytmu
wyszukiwania
19
Złożoność czasową można wyrazić jako liczbę wykonań pętli
while
w
zależności od
n.
W każdym wykonaniu mają miejsce w zasadzie dwa
porównania. Można traktować jako operację i przyjąć że w każdej pętli
jest jedna operacja dominująca.
Czyli dla n=1 wykonywana jest jedna operacja dominująca, zaś dla n >1
problem jest redukowany do problemu 2-razy mniejszego, gdy wykonanie
operacji dominującej nie kończy się sukcesem- czyli gdy poszukiwany
element nie jest środkowym w ciągu. Złożoność czasową można tu
wyrazić w postaci zapisu z rekurencją (analiza opiera się na intuicji):
( )
)
1
(
1
2
)
1
(
1
>
+
=
=
n
n
T
n
n
T
(1)
Metodą indukcji można pokazać, że dla dowolnych n
zachodzi wzór:
( )
1
log
2
+
=
n
n
T
(7)
Zazwyczaj uważa się, że jeden algorytm jest lepszy od drugiego,
jeśli jego złożoność obliczeniowa jest funkcją niższego rzędu względem
rozmiaru danych. W przypadku przeszukiwania sekwencyjnego jest nią
funkcja liniowa a w przypadku binarnego funkcja logarytmiczna. Zatem
lepszym powinien być algorytm przeszukiwania binarnego
.
Tab. Porównanie złożoności czasowej algorytmów
przeszukiwania ciągów
n
Sekwencyjne
binarne
10
10
4
100
100
7
1000
1000
10
10 000
10 000
14
100 000
100 000
17
1 000 000
1 000 000
20
20
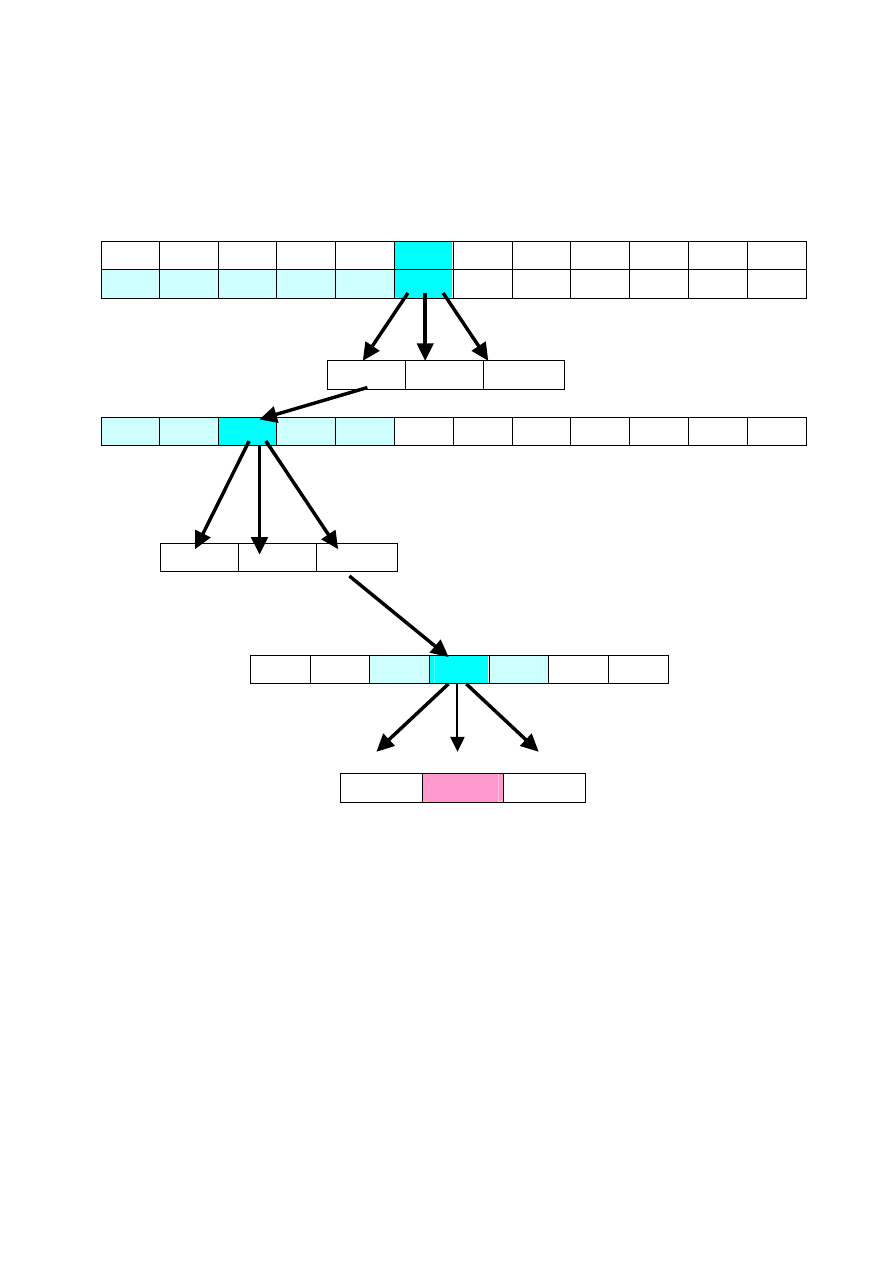
Przeszukiwanie binarne. Przykład.
Niech będzie dany ciąg 12 liczb przedstawiony w tabeli.
Poszukujemy liczby x=18.
0
1
2
3
4
5
6
7
8
9
10
11
1
2
6
18
20
23
29
32
34
39
40
41
Left=0 right=11 mid=( Left + right)/2=5
Tab[mid]=23
18<23 18=23 18>23
1
2
6
18
20
23
29
32
34
39
40
41
Left=0 right=mid=4 mid=( Left + right)/2=2
Tab[mid]=6
18<6 18=6 18>6
1
2
6
18
20
23
29
Left=mid=2 right=4 mid=( Left +
right)/2=3
Tab[mid]=18
18<18 18=18 18>18
gdzie:
left- lewy indeks przeszukiwanej części tablicy wejściowej,
right- prawy lewy indeks przeszukiwanej części tablicy,
mid- indeks elementu środkowego analizowanego aktualnie
fragmentu tablicy
Poszukiwanie kończy się pomyślnie po 3 etapach.
21
Poszukiwanie binarne. Metoda iteracyjna i rekurencyjna –
porównanie algorytmów.
Algorytm iteracyjny ma postać:
Function
BINARY-SEARCH(a[1..n], x)
i:=1
j:=n
while
i ≤ j
do
k:= (i +j)
div
2
if
x= a [k]
then
return
k
else
if
x < a [k]
then
j := k-1
else
i := k +1
return
–1
Algorytm rekurencyjny można przedstawić w postać:
function
BINARY-SEARCH2(a[1..n], x, i, j)
if i>j then
return –1
k:=(i + j) div 2
if x = a[k] then
return k
else if x < a[k] then
return
BINARY-SEARCH2
(a, x, i, k-1 )
else
return
BINARY-SEARCH2
(a, x, k+1, j )
Sprawdzenie czy element x znajduje się w tablicy a[1..n] polega na
wywołaniu:
BINARY-SEARCH2
(a, x, 1, n )
To jest wersja
iteracyjna
algorytmu
poszukiwania
22
Aby bardziej upodobnić nagłówek do wersji iteracyjnej można pozbyć się
dwu ostatnich parametrów (tzn i, j), ukrywając rekurencję przez
wyodrębnienie wewnętrznej funkcji poszukującej SEARCH.
function
BINARY-SEARCH3(a[1..n], x)
function SEARCH(i, j)
if i>j then
return –1
k:=(i + j) div 2
if x = a[k] then
return k
else if x < a[k] then
return SEARCH(i, k - 1)
else
return SEARCH(k+1, j)
return SEARCH(1, n)
Jedyną instrukcją BINARY-SEARCH3 jest return SEARCH(1,n),
która uaktywnia funkcję SEARCH(i,j)