
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
Z
ESTAW PRZYGOTOWANY PRZEZ SERWIS
WWW
.
ZADANIA
.
INFO
POZIOM PODSTAWOWY
17
KWIETNIA
2010
C
ZAS PRACY
: 170
MINUT
Zadania zamkni˛ete
Z
ADANIE
1
(1
PKT
.)
Je ˙zeli liczba 3b jest o 20% wi˛eksza od połowy liczby 2a
+
b, to liczba a jest wi˛eksza od b o
A) 100%
B) 80%
C) 50%
D) 200%
R
OZWI ˛
AZANIE
Zapisujemy podany warunek
3b
=
1, 2
·
2a
+
b
2
=
0, 6
(
2a
+
b
)
/ : 0, 6
5b
=
2a
+
b
4b
=
2a
⇒
a
=
2b.
Zatem a jest wi˛eksze od b o 100%.
Odpowied´z: A
Z
ADANIE
2
(1
PKT
.)
Stosunek miar k ˛
atów czworok ˛
ata jest równy 6:7:8:9. Najmniejszy k ˛
at tego czworok ˛
ata ma
miar˛e
A) 60
◦
B) 72
◦
C) 54
◦
D) 12
◦
R
OZWI ˛
AZANIE
Je ˙zeli k ˛
aty czworok ˛
ata oznaczymy przez 6x, 7x, 8x, 9x, to poniewa ˙z suma k ˛
atów w czworo-
k ˛
acie wynosi 360
◦
, mamy równanie
6x
+
7x
+
8x
+
9x
=
360
◦
30x
=
360
◦
⇒
x
=
12
◦
.
Zatem najmniejszy k ˛
at ma miar˛e 6x
=
72
◦
.
Odpowied´z: B
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
3
(1
PKT
.)
Połow ˛
a odwrotno´sci sze´scianu liczby 8
19
jest
A) 2
170
B) 4
−
86
C)
1
8
57
D)
1
2
170
R
OZWI ˛
AZANIE
Liczymy
1
2
·
1
(
8
19
)
3
=
1
2
·
1
8
57
=
1
2
·
1
2
3
·
57
=
=
1
2
·
1
2
171
=
1
2
172
=
1
4
86
=
4
−
86
.
Odpowied´z: B
Z
ADANIE
4
(1
PKT
.)
Warto´s´c wielomianu x
3
+
x
+
2 dla argumentu
3
√
2
−
3
√
4 jest równa
A) 5
3
√
4
−
5
3
√
16
B) 5
3
√
16
+
5
3
√
4
C) 5
3
√
16
−
5
3
√
16
D) 5
3
√
4
−
5
3
√
2
R
OZWI ˛
AZANIE
B˛edziemy korzysta´c ze wzoru skróconego mno ˙zenia
(
a
−
b
)
3
=
a
3
−
3a
2
b
+
3ab
2
−
b
3
Liczymy
(
3
√
2
−
3
√
4
)
3
+
3
√
2
−
3
√
4
+
2
=
=
2
−
3
·
3
√
4
·
3
√
4
+
3
·
3
√
2
·
3
√
16
−
4
+
3
√
2
−
3
√
4
+
2
=
=
2
−
3
3
√
2
·
8
+
3
·
3
√
4
·
8
−
4
+
3
√
2
−
3
√
4
+
2
=
=
2
−
6
3
√
2
+
6
3
√
4
−
4
+
3
√
2
−
3
√
4
+
2
= −
5
3
√
2
+
5
3
√
4.
Odpowied´z: D
Z
ADANIE
5
(1
PKT
.)
Który z narysowanych trójk ˛
atów jest podobny do trójk ˛
ata, w którym miary dwóch k ˛
atów
wynosz ˛
a 55
◦
i 65
◦
?
75
o
60
o
65
o
75
o
55
o
60
o
55
o
75
o
A)
B)
C)
D)
Materiał pobrany z serwisu
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Je ˙zeli dwa k ˛
aty trójk ˛
ata maj ˛
a miary 55
◦
i 65
◦
to trzeci k ˛
at ma miar˛e
180
◦
−
55
◦
−
65
◦
=
60
◦
.
Musimy wi˛ec wybra´c trójk ˛
at, którego dwa k ˛
aty s ˛
a po´sród liczb 55
◦
, 65
◦
, 60
◦
.
Odpowied´z: C
Z
ADANIE
6
(1
PKT
.)
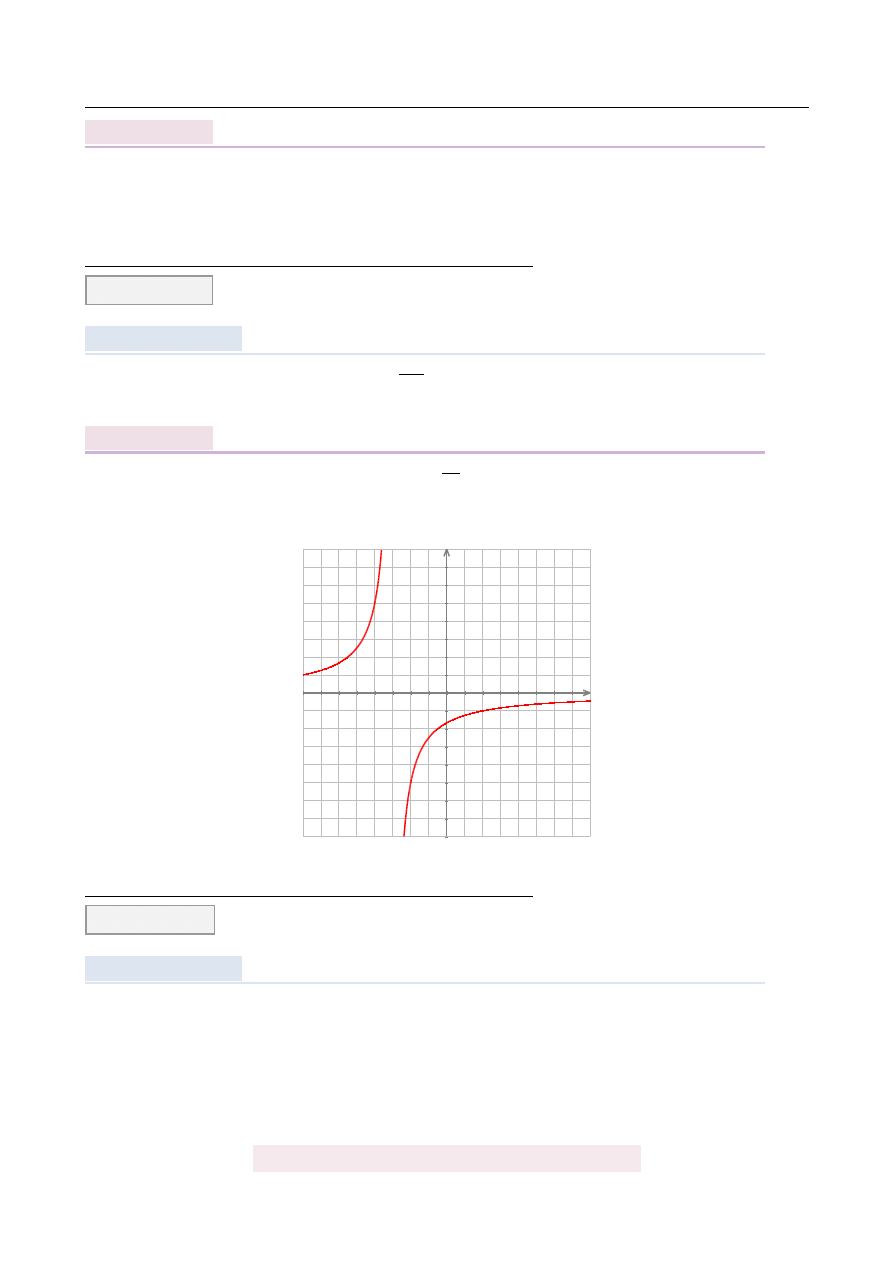
Wska ˙z zbiór, w którym funkcja f
(
x
) =
−
5
x
+
3
jest rosn ˛
aca.
A)
R
\ {−
3
}
B)
R
\ {
3
}
C)
(−
∞, 3
)
D)
(
3,
+
∞
)
R
OZWI ˛
AZANIE
Wykresem danej funkcji jest hiperbola y
=
−
5
x
przesuni˛eta o 3 jednostki w lewo. Je ˙zeli j ˛
a
sobie naszkicujemy to wida´c, ˙ze funkcja ta jest rosn ˛
aca na ka ˙zdym z przedziałów
(−
∞,
−
3
)
i
(−
3,
+
∞
)
(ale nie na sumie tych przedziałów!).
-5
-1
-3
+5
x
-5
-1
+1
+5
y
W takim razie jedyna poprawna odpowied´z to
(
3,
+
∞
)
.
Odpowied´z: D
Z
ADANIE
7
(1
PKT
.)
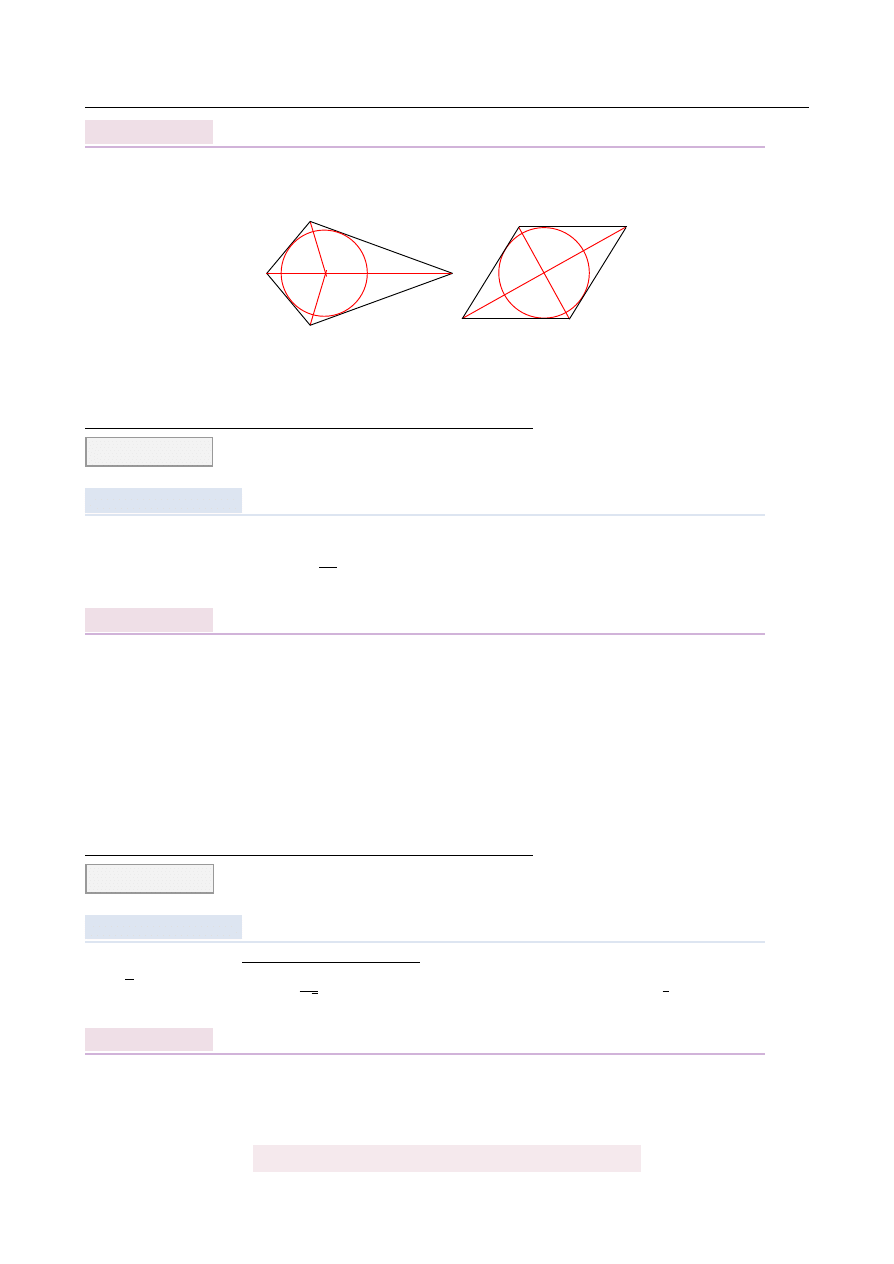
Które z poni ˙zszych zda ´n nie jest prawdziwe?
A) Na ka ˙zdym prostok ˛
acie mo ˙zna opisa´c okr ˛
ag.
B) W ka ˙zdy romb mo ˙zna wpisa´c okr ˛
ag.
C) Na ka ˙zdym równoległoboku mo ˙zna opisa´c okr ˛
ag.
D) W ka ˙zdy deltoid mo ˙zna wpisa´c okr ˛
ag.
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Zarówno w rombie jak i w deltoidzie dwusieczne wszystkich k ˛
atów wewn˛etrznych przeci-
naj ˛
a si˛e w jednym punkcie, wi˛ec w ka ˙zd ˛
a z tych figur mo ˙zna wpisa´c okr ˛
ag.
Powinno by´c te ˙z jasne, ˙ze na ka ˙zdym prostok ˛
acie mo ˙zna opisa´c okr ˛
ag (jego ´srodkiem jest
punkt przeci˛ecia si˛e przek ˛
atnych). Je ˙zeli równoległobok nie jest prostok ˛
atem, to nie mo ˙zna
na nim opisa´c okr˛egu, bo symetralne przeciwległych boków w ogóle si˛e nie przecinaj ˛
a.
Odpowied´z: C
Z
ADANIE
8
(1
PKT
.)
Zbiorem warto´sci funkcji kwadratowej f
(
x
) = −
x
2
+
2ax
−
a
2
−
2a jest przedział
(−
∞,
−
18
i
.
Zatem
A) a
=
9
B) a
=
√
18
C) a
= −
18
D) a
+
9
=
0
R
OZWI ˛
AZANIE
Zapiszmy wzór funkcji f w postaci kanonicznej
f
(
x
) = −
x
2
+
2ax
−
a
2
−
2a
= −(
x
−
a
)
2
−
2a.
Wykresem tej funkcji jest wi˛ec parabola o ramionach skierowanych w dół i wierzchołku w
punkcie
(
a,
−
2a
)
. Zatem zbiorem jej warto´sci jest przedział
(−
∞,
−
2a
i
. Mamy wi˛ec
−
2a
= −
18
⇒
a
=
9.
Odpowied´z: A
Z
ADANIE
9
(1
PKT
.)
Warto´s´c wyra ˙zenia
sin 15
◦
cos 75
◦
+
cos 15
◦
sin 75
◦
tg 22,5
◦
·
tg 67,5
◦
jest równa
A)
√
2
B)
1
√
2
C) 1
D)
1
2
R
OZWI ˛
AZANIE
Materiał pobrany z serwisu
4

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Korzystamy ze wzorków
sin
(
90
◦
−
α
) =
cos α
cos
(
90
◦
−
α
) =
sin α
tg
(
90
◦
−
α
) =
ctg α
=
1
tg α
.
Liczymy
sin 15
◦
cos 75
◦
+
cos 15
◦
sin 75
◦
tg 22, 5
◦
·
tg 67, 5
◦
=
=
sin 15
◦
cos
(
90
◦
−
15
◦
) +
cos 15
◦
sin
(
90
◦
−
15
◦
)
tg 22, 5
◦
·
tg
(
90
◦
−
22, 5
◦
)
=
=
sin 15
◦
sin 15
◦
+
cos 15
◦
cos 15
◦
tg 22, 5
◦
·
1
tg 22,5
◦
=
=
sin
2
15
◦
+
cos
2
15
◦
=
1.
Licznik mogli´smy te ˙z obliczy´c korzystaj ˛
ac ze wzoru
sin
(
α
+
β
) =
sin α cos β
+
sin β cos α.
Odpowied´z: C
Z
ADANIE
10
(1
PKT
.)
Która z liczb jest równa liczbie
3
√
10000?
A)
9
√
100000
B) 100
4
3
C) 1000
2
9
D)
1
100
− 2
3
R
OZWI ˛
AZANIE
Liczymy
3
√
10000
=
10
4
3
9
√
100000
=
10
5
9
100
4
3
=
10
8
3
1000
2
9
=
10
6
9
=
10
2
3
1
100
−
2
3
=
10
4
3
.
Odpowied´z: D
Z
ADANIE
11
(1
PKT
.)
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
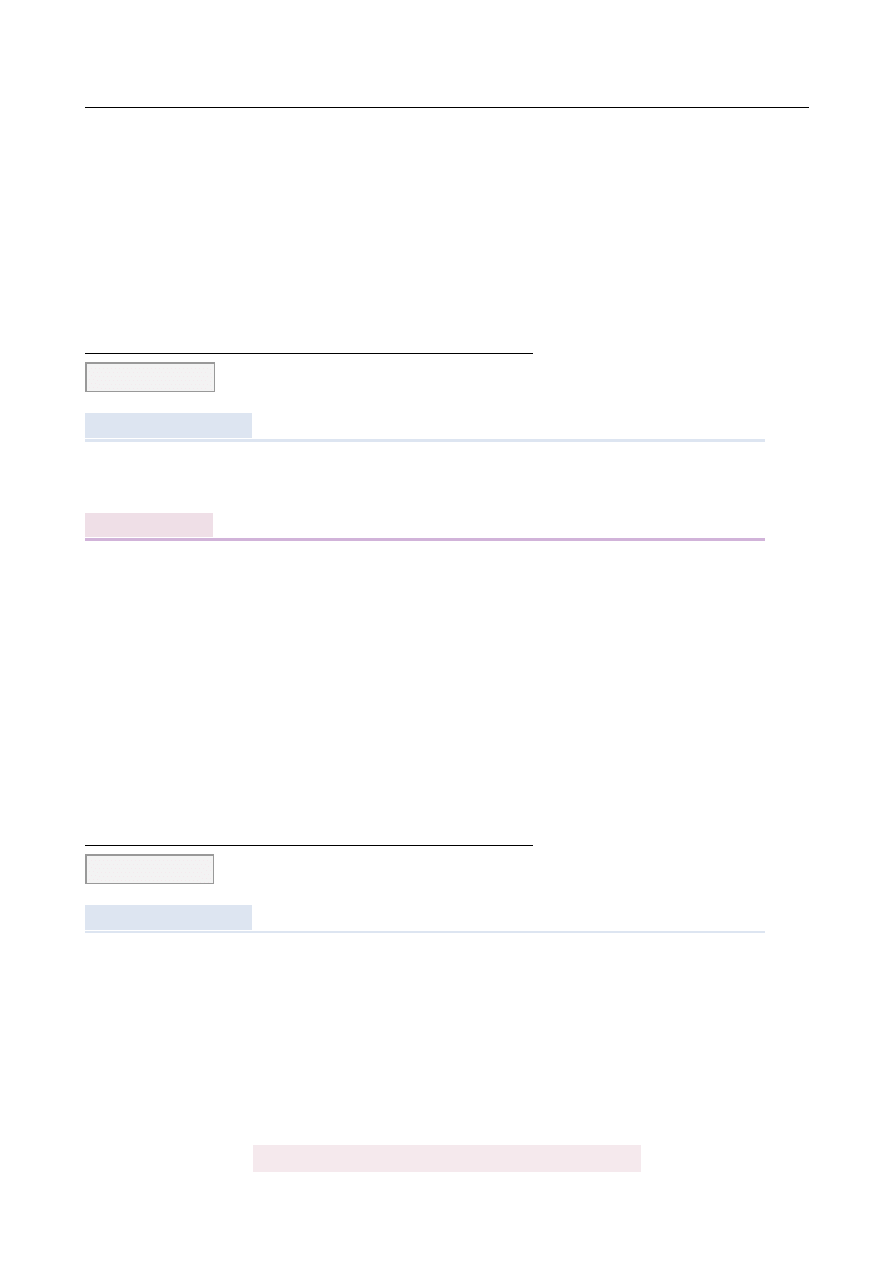
Bok AB czworok ˛
ata ABCD wpisanego w okr ˛
ag jest ´srednic ˛
a okr˛egu oraz
|]
C
| =
120
◦
.
A
B
C
α
120
o
D
Zatem k ˛
at α ma miar˛e
A) 30
◦
B) 45
◦
C) 50
◦
D) 60
◦
R
OZWI ˛
AZANIE
Dorysujmy przek ˛
atn ˛
a AC.
A
B
C
α
90
o
O
D
α
K ˛
at ACB jest oparty na ´srednicy, wi˛ec ma miar˛e 90
◦
. Ponadto k ˛
aty ACD i ABD s ˛
a oparte
na tym samym łuku, wi˛ec maj ˛
a równe miary. Mamy wi˛ec
α
+
90
◦
=
120
◦
⇒
α
=
30
◦
.
Odpowied´z: A
Z
ADANIE
12
(1
PKT
.)
Rozwi ˛
azaniem równania
3x
5
−
10x
3
−
16
3x
4
−
10x
2
−
16
=
0 jest liczba
A) x
= −
2
B) x
=
1
C) x
= −
1
D) x
=
2
R
OZWI ˛
AZANIE
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Sprawdzamy, dla której z podanych liczb licznik si˛e zeruje. Po kolei wstawiamy 1,-1,2,-2.
3
−
10
−
16
= −
23
−
3
+
10
−
16
= −
9
3
·
32
−
10
·
8
−
16
=
96
−
80
−
16
=
0
−
3
·
32
+
10
·
8
−
16
= −
96
+
80
−
16
= −
32.
Wida´c, ˙ze pierwiastkiem mo ˙ze by´c tylko x
=
2 (w zasadzie powinni´smy jeszcze sprawdzi´c,
˙ze nie jest to miejsce zerowe mianownika, ale poniewa ˙z wiemy, ˙ze jedna z odpowiedzi jest
poprawna, nie musimy tego robi´c).
Odpowied´z: D
Z
ADANIE
13
(1
PKT
.)
Liczba log
2
6
3
+
log
2
6
2
+
log
6
4 log
6
3 jest
A) dodatnia
B) mniejsza od 1
C) ujemna
D) niewymierna
R
OZWI ˛
AZANIE
Sposób I
Poniewa ˙z log
6
x
>
0 dla x
>
1 wi˛ec wida´c, ˙ze ka ˙zdy składnik danego wyra ˙zenia jest dodat-
ni. Zatem całe wyra ˙zenie jest dodatnie.
Sposób II
Liczymy
log
2
6
3
+
log
2
6
2
+
log
6
4 log
6
3
= (
log
6
3
)
2
+ (
log
6
2
)
2
+
log
6
2
2
log
6
3
=
= (
log
6
3
)
2
+
2 log
6
2 log
6
3
+ (
log
6
2
)
2
= (
log
6
3
+
log
6
2
)
2
= (
log
6
6
)
2
=
1.
Jest to oczywi´scie liczba dodatnia.
Odpowied´z: A
Z
ADANIE
14
(1
PKT
.)
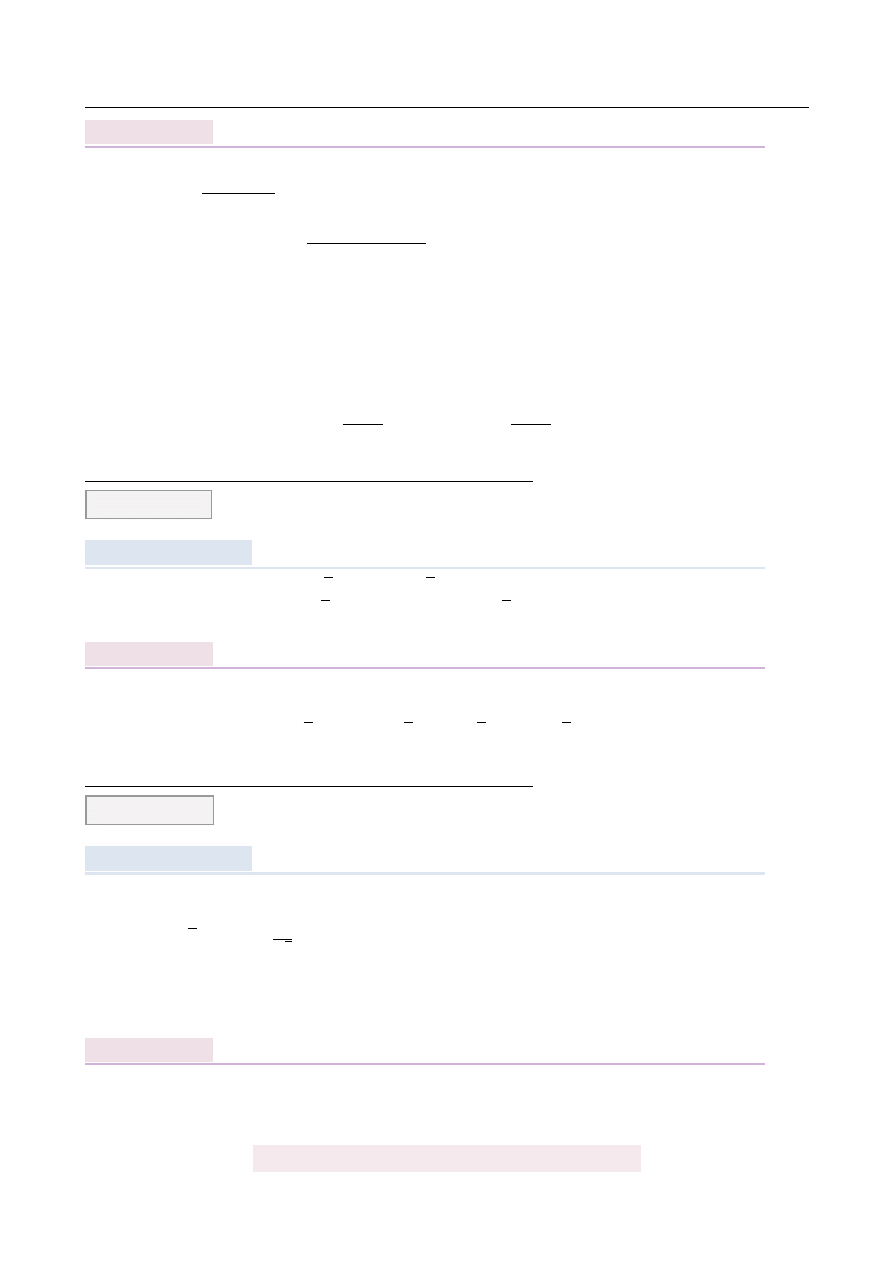
Suma n pocz ˛
atkowych wyrazów ci ˛
agu arytmetycznego a
n
=
10
−
2n, gdzie n
>
1 jest równa
14. Zatem
A) n
=
2
B) liczba n
+
3 dzieli si˛e przez 5
C) n
=
3
D) n
=
4
Materiał pobrany z serwisu
7
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Mamy do czynienia z ci ˛
agiem arytmetycznym o pierwszym wyrazie a
1
=
8 i ró ˙znicy r
=
−
2. Ze wzoru
2a
1
+(
n
−
1
)
r
2
·
n na sum˛e pocz ˛
atkowych wyrazów ci ˛
agu arytmetycznego mamy
równanie
2
·
8
−
2
(
n
−
1
)
2
·
n
=
14
(
8
−
n
+
1
) ·
n
=
14
(
9
−
n
) ·
n
=
14
9n
−
n
2
=
14
n
2
−
9n
+
14
=
0
∆
=
81
−
56
=
25
n
=
9
−
5
2
=
2
∨
n
=
9
+
5
2
=
7.
Zatem n
=
2 lub n
=
7. W obu przypadkach n
+
3 dzieli si˛e przez 5.
Odpowied´z: B
Z
ADANIE
15
(1
PKT
.)
Wykres funkcji f
(
x
) = (
x
+
√
5
)
8
− (
x
−
√
5
)
8
przecina o´s Oy w punkcie
A)
(
0, 0
)
B)
(
0, 2
√
5
)
C)
(
0,
√
5
)
D)
(
0, 2
·
5
4
)
R
OZWI ˛
AZANIE
Punkt przeci˛ecia wykresu funkcji z osi ˛
a Oy ma współrz˛edne
(
0, f
(
0
))
. W naszym przypadku
mamy
f
(
0
) = (
0
+
√
5
)
8
− (
0
−
√
5
)
8
= (
√
5
)
8
− (−
√
5
)
8
=
5
4
−
5
4
=
0.
Odpowied´z: A
Z
ADANIE
16
(1
PKT
.)
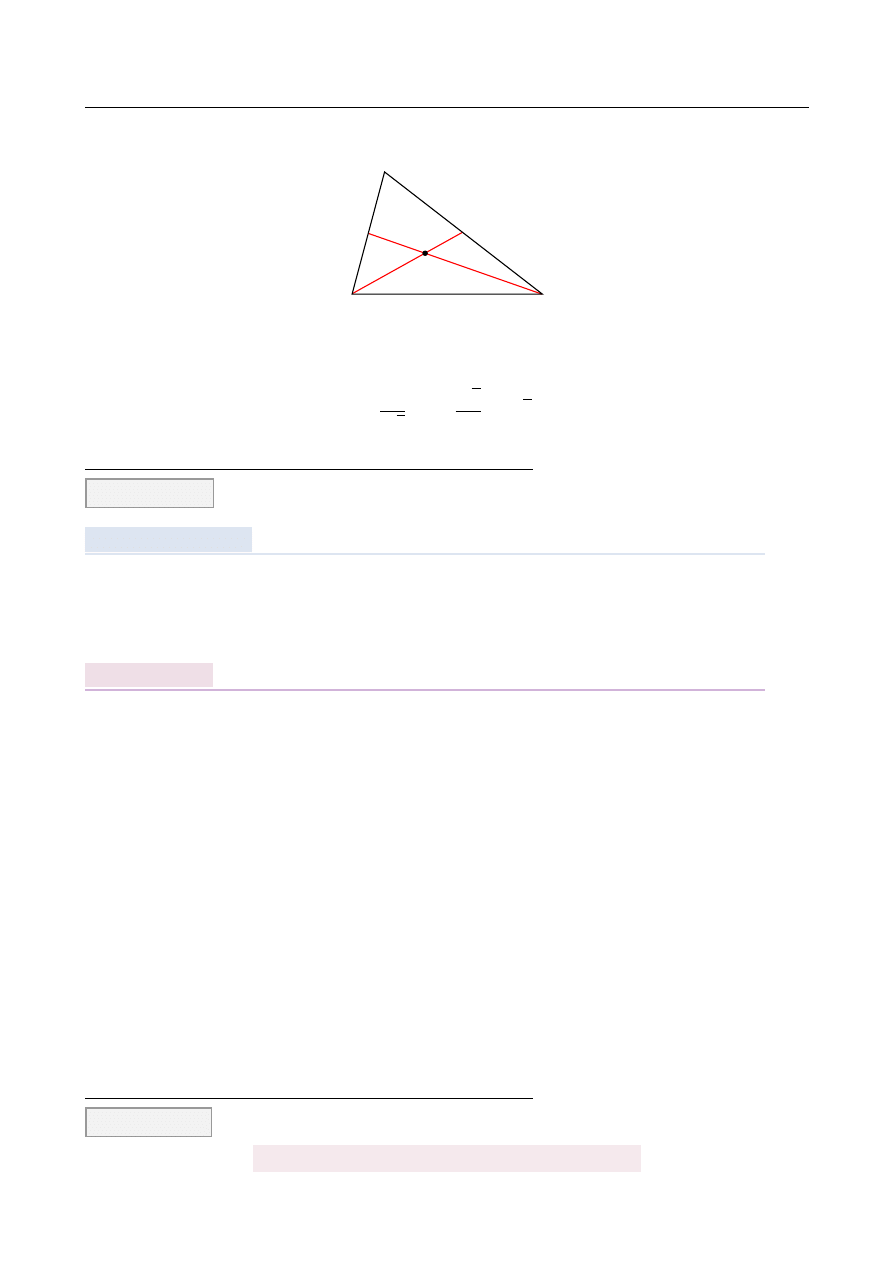
Punkt P jest punktem wspólnym ´srodkowych AD i BE w trójk ˛
acie ABC. Wówczas odcinki
AP i PD mog ˛
a mie´c długo´sci
A)
|
AP
| =
√
2,
|
PD
| =
1
√
2
B)
|
AP
| =
3,
|
PD
| =
6
C)
|
AP
| =
9,
|
PD
| =
3
D)
|
AP
| =
3,
|
PD
| =
9
R
OZWI ˛
AZANIE
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Rozpoczynamy od rysunku.
A
B
C
D
E
P
Poniewa ˙z ´srodkowe dziel ˛
a si˛e w stosunku 2:1 licz ˛
ac od wierzchołka, odcinek AP musi
by´c dwa razy dłu ˙zszy od PD. Sprawdzaj ˛
ac po kolei łatwo zauwa ˙zy´c, ˙ze
2
·
1
√
2
=
2
·
√
2
2
=
√
2.
Odpowied´z: A
Z
ADANIE
17
(1
PKT
.)
Pi˛e´c spo´sród sze´sciu ró ˙znokolorowych kul wkładamy do pi˛eciu ponumerowanych szuflad
tak, ˙ze w ka ˙zdej szufladzie znajduje si˛e jedna kula. Na ile ró ˙znych sposobów mo ˙zna to zro-
bi´c?
A) 120
B) 720
C) 24
D) 126
R
OZWI ˛
AZANIE
Sposób I
Najpierw musimy wybra´c pi˛e´c kul, które znajd ˛
a si˛e w szufladach – mo ˙zna to zrobi´c na 6 spo-
sobów (wystarczy ustali´c, która kula odpada). Potem 5 kul nale ˙zy umie´sci´c w 5 szufladach
– to mo ˙zna zrobi´c na
5!
=
5
·
4
·
3
·
2
·
1
=
120
sposobów (pierwsz ˛
a kul˛e mo ˙zemy wło ˙zy´c na 5 sposobów, drug ˛
a na 4, itd.). Ł ˛
acznie jest wi˛ec
6
·
120
=
720
sposobów.
Sposób II
Ustawiamy 6 kul w dowolnej kolejno´sci – mo ˙zemy to zrobi´c na
6
·
5
·
4
·
3
·
2
=
720
sposobów i pierwsze 5 wkładamy do szuflad. Jest wi˛ec 720 takich układów.
Odpowied´z: B
Materiał pobrany z serwisu
9

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
18
(1
PKT
.)
Równanie prostej przechodz ˛
acej przez punkty
(
5, 11
)
,
(
7, 15
)
,
(
9, 19
)
to
A) y
−
2x
−
1
=
0
B) y
−
3x
+
4
=
0
C) y
−
x
+
6
=
0
D) x
−
2y
=
1
R
OZWI ˛
AZANIE
Sposób I
Mo ˙zna zauwa ˙zy´c, ˙ze współrz˛edne podanych punktów spełniaj ˛
a warunek y
=
2x
+
1 i to
jest szukana prosta.
Sposób II
Szukamy prostej postaci y
=
ax
+
b. Aby wyznaczy´c a i b podstawiamy dwa pierwsze punk-
ty.
(
11
=
5a
+
b
15
=
7a
+
b.
Odejmujemy od drugiego równania pierwsze i mamy 4
=
2a, czyli a
=
2. Z drugiego rów-
nania b
=
15
−
7a
=
1. Zatem szukana prosta to y
=
2x
+
1.
Sposób III
Korzystamy ze wzoru
y
−
y
A
=
y
B
−
y
A
x
B
−
y
A
(
x
−
x
A
)
na równanie prostej przechodz ˛
acej przez punkty A
= (
x
A
, y
A
)
i B
= (
x
B
, y
B
)
. W naszej
sytuacji mamy
y
−
11
=
15
−
11
7
−
5
(
x
−
5
)
y
−
11
=
2
(
x
−
5
)
y
=
2x
+
1.
Odpowied´z: A
Z
ADANIE
19
(1
PKT
.)
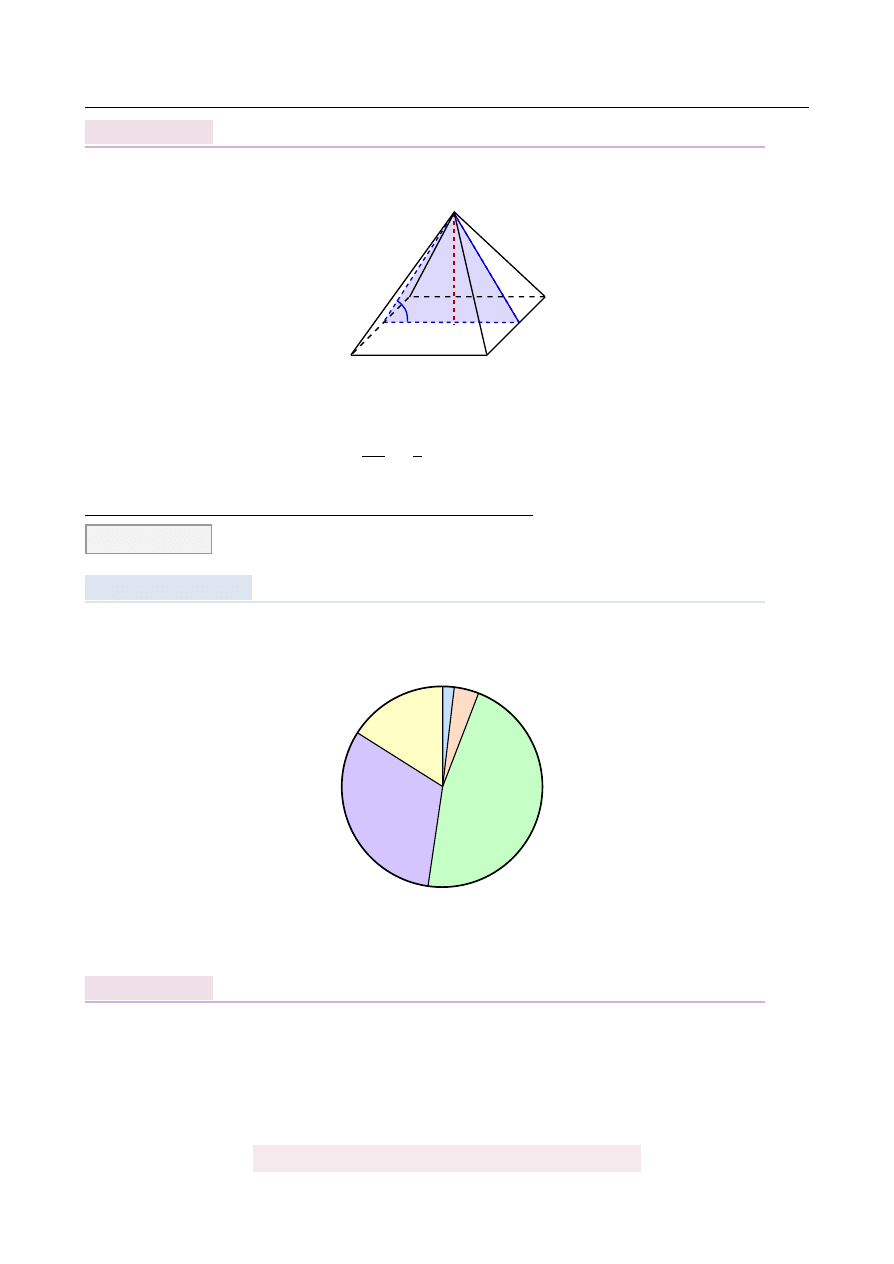
Kraw˛ed´z podstawy ostrosłupa prawidłowego czworok ˛
atnego jest dwa razy dłu ˙zsza od jego
wysoko´sci. K ˛
at nachylenia ´sciany bocznej do podstawy ma miar˛e
A) α
=
30
◦
B) α
=
45
◦
C) α
=
60
◦
D) α
=
75
◦
Materiał pobrany z serwisu
10
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Rozpoczynamy od szkicowego rysunku.
A
B
C
D
S
E
2a
a
a
α
F
Je ˙zeli kraw˛ed´z podstawy ma długo´s´c 2a, to wysoko´s´c ostrosłupa ma długo´s´c a oraz
tg α
=
SE
EF
=
a
a
=
1
⇒
α
=
45
◦
.
Odpowied´z: B
Z
ADANIE
20
(1
PKT
.)
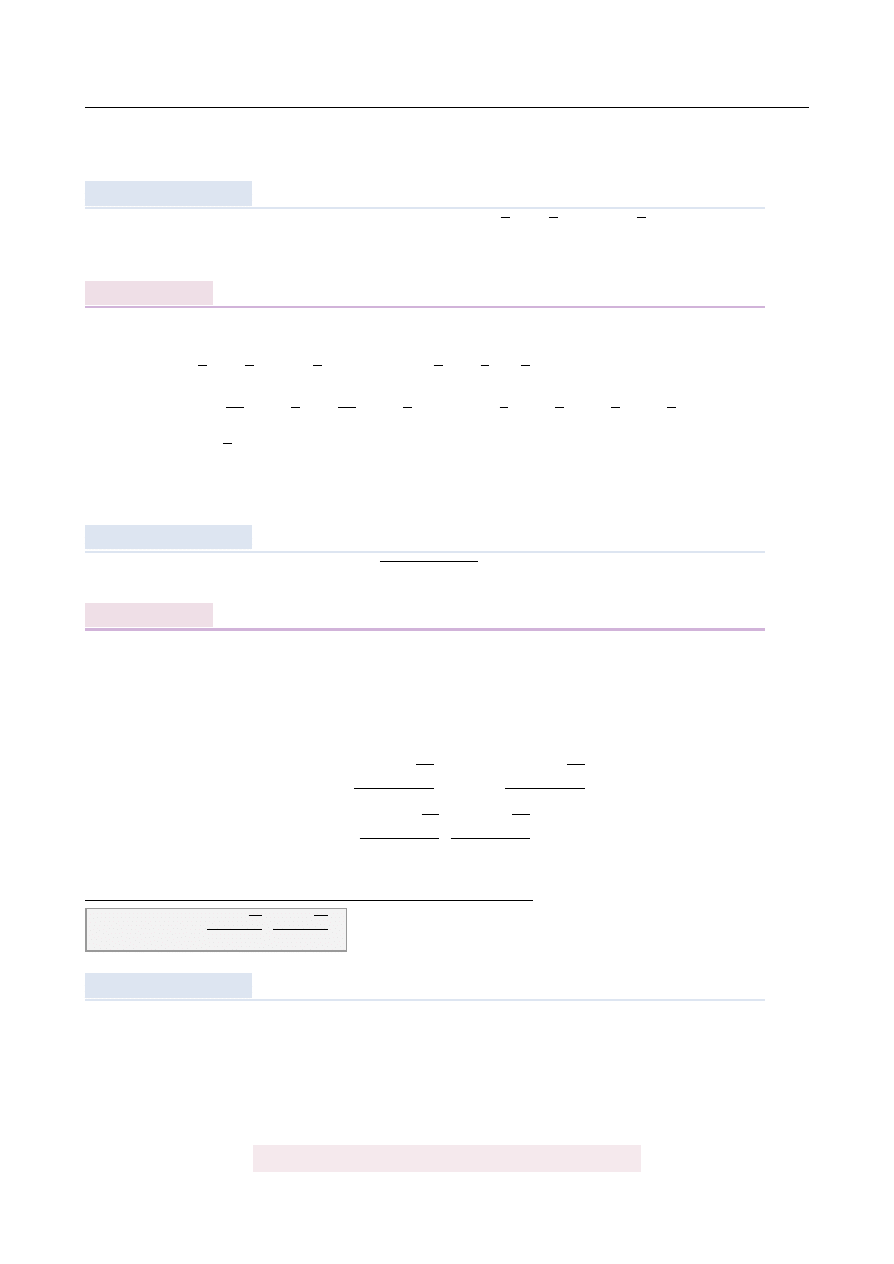
Diagram przedstawia ile procent rodzin mieszkaj ˛
acych w jednym z łódzkich bloków posia-
da 0,1,2,3 lub 4 dzieci.
0
1
3
4
2
16%
32%
46%
4%
2%
´Srednia liczba dzieci przypadaj ˛acych na jedn ˛a rodzin˛e jest równa
A) 1,22
B) 1,44
C) 2
D) 2,5
R
OZWI ˛
AZANIE
Sposób I
Liczymy ´sredni ˛
a wa ˙zon ˛
a
0, 16
·
0
+
0, 32
·
1
+
0, 46
·
2
+
0, 04
·
3
+
0, 02
·
4
=
1, 44.
Materiał pobrany z serwisu
11

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Sposób II
Powiedzmy, ˙ze w bloku mieszka 100 rodzin. Wtedy dzieci jest
16
·
0
+
32
·
1
+
46
·
2
+
4
·
3
+
2
·
4
=
144.
Zatem na jedn ˛
a rodzin˛e przypada ´srednio
144
100
=
1, 44
dziecka.
Odpowied´z: B
Z
ADANIE
21
(1
PKT
.)
Warunek „przynajmniej jedna z liczb x, y, z jest niezerowa” jest równowa ˙zny warunkowi
A) xyz
6=
0
B) xyz
6=
0 oraz x
+
y
+
z
6=
0
C) x
2
+
y
2
+
z
2
>
0
D) xyz
6=
0 oraz x
3
+
y
3
+
z
3
6=
0
R
OZWI ˛
AZANIE
Je ˙zeli np. x
=
0 i y
= −
z
6=
0 to tylko jedna z odpowiedzi jest spełniona:
x
2
+
y
2
+
z
2
>
0.
Musi to wi˛ec by´c poprawna odpowied´z. Rzeczywi´scie tak jest, warunek
x
2
+
y
2
+
z
2
>
0
nie jest spełniony dokładnie w jednym przypadku, gdy x
=
y
=
z
=
0.
Odpowied´z: C
Z
ADANIE
22
(1
PKT
.)
Układ równa ´n
(
3x
+
py
=
2
qx
+
5y
=
4
z niewiadomymi x i y ma niesko ´nczenie wiele rozwi ˛
aza ´n.
Zatem liczba p
+
q jest równa
A) 6
B)
17
2
C)
13
2
D) 15
R
OZWI ˛
AZANIE
Je ˙zeli układ ma mie´c niesko ´nczenie wiele rozwi ˛
aza ´n, to proste odpowiadaj ˛
ace równaniom
układu musz ˛
a si˛e pokrywa´c. To oznacza, ˙ze jedno równanie musi by´c wielokrotno´sci ˛
a dru-
giego. Patrz ˛
ac na prawe strony równa ´n widzimy, ˙ze drugie równanie musi powstawa´c z
pierwszego przez mno ˙zenie przez 2. W takim razie q
=
6 i p
=
5
2
. St ˛
ad
p
+
q
=
6
+
5
2
=
17
2
.
Odpowied´z: B
Materiał pobrany z serwisu
12
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zadania otwarte
Z
ADANIE
23
(2
PKT
.)
Wyka ˙z, ˙ze dla ka ˙zdej liczby naturalnej n, liczby
(
√
3
+
√
2
)
4n
, 2
n
,
(
√
6
−
2
)
4n
s ˛
a kolejnymi
wyrazami ci ˛
agu geometrycznego.
R
OZWI ˛
AZANIE
Musi uzasadni´c, ˙ze kwadrat ´srodkowej liczby jest iloczynem liczb s ˛
asiednich. Liczymy
(
√
3
+
√
2
)
4n
· (
√
6
−
2
)
4n
=
h
(
√
3
+
√
2
)(
√
6
−
2
)
i
4n
=
=
√
18
−
2
√
3
+
√
12
−
2
√
2
4n
=
3
√
2
−
2
√
3
+
2
√
3
−
2
√
2
4n
=
= (
√
2
)
4n
=
2
2n
= (
2
n
)
2
,
co ko ´nczy uzasadnienie.
Z
ADANIE
24
(2
PKT
.)
Wyznacz dziedzin˛e funkcji f
(
x
) =
4
√
2
−
4x
2
−
3x.
R
OZWI ˛
AZANIE
Wyra ˙zenie pod pierwiastkiem musi by´c nieujemne, wi˛ec
2
−
4x
2
−
3x
>
0
/
· (−
1
)
4x
2
+
3x
−
2
6
0
∆
=
9
+
32
=
41
x
1
=
−
3
−
√
41
8
,
x
2
=
−
3
+
√
41
8
x
∈
*
−
3
−
√
41
8
,
−
3
+
√
41
8
+
.
Odpowied´z:
D
−
3
−
√
41
8
,
−
3
+
√
41
8
E
Z
ADANIE
25
(2
PKT
.)
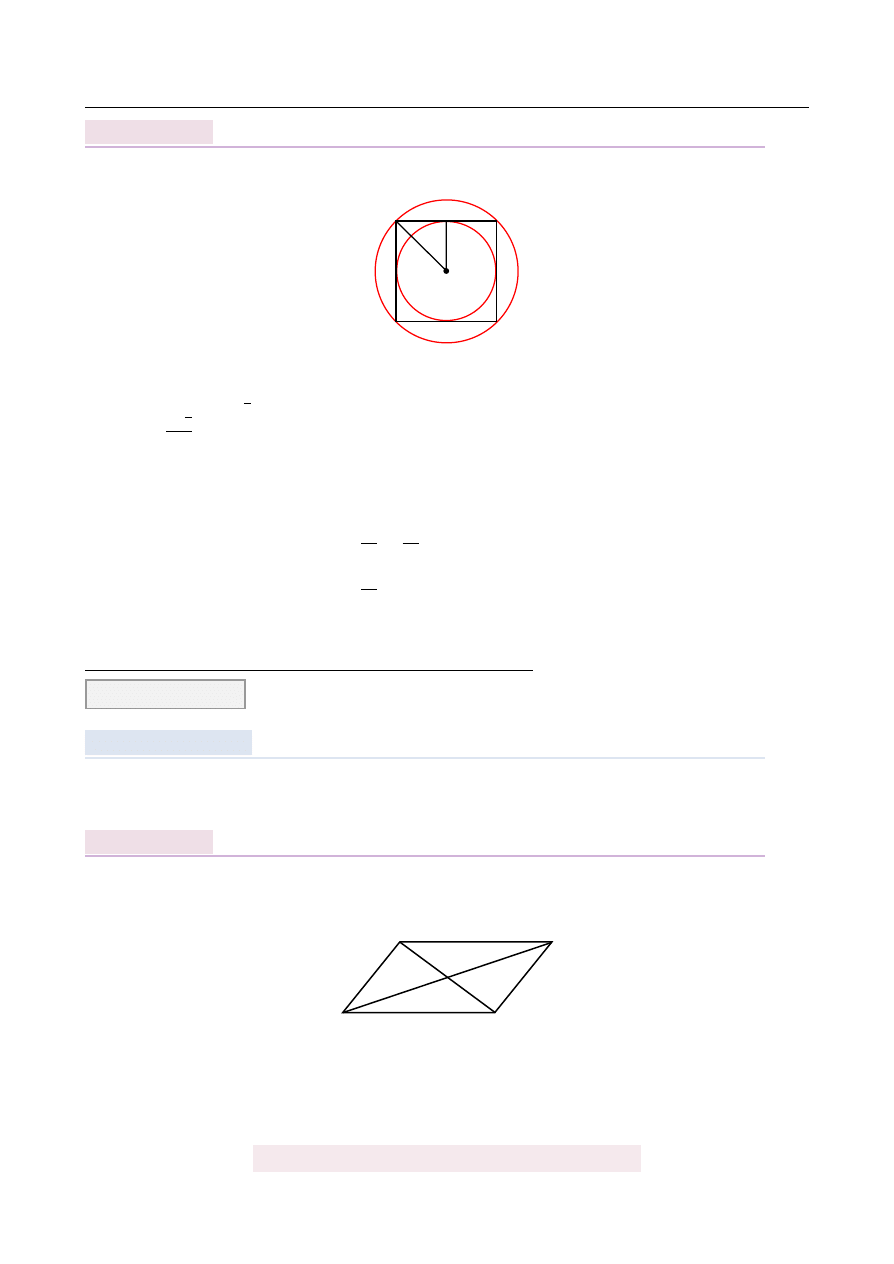
Oblicz pole kwadratu wiedz ˛
ac, ˙ze ró ˙znica pól kół opisanego i wpisanego w ten kwadrat jest
równa π.
Materiał pobrany z serwisu
13
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Rozpoczynamy od rysunku.
A
B
C
D
r
R
a
Je ˙zeli oznaczymy długo´s´c boku kwadratu przez a to promie ´n okr˛egu wpisanego w kwa-
drat jest równy r
=
a
2
, a promie ´n okr˛egu opisanego jest równy połowie długo´sci przek ˛
atnej,
czyli R
=
a
√
2
2
. Z podanej ró ˙znicy pól otrzymujemy równanie
πR
2
−
πr
2
=
π
/ : π
R
2
−
r
2
=
1
a
2
2
−
a
2
4
=
1
a
2
4
=
1
a
2
=
4.
Odpowied´z: P
=
4
Z
ADANIE
26
(2
PKT
.)
Wyznacz współrz˛edne wierzchołka B równoległoboku ABCD je ˙zeli A
= (−
37, 17
)
, C
=
(
39, 15
)
, D
= (
19,
−
27
)
.
R
OZWI ˛
AZANIE
Ze wzgl˛edu na du ˙ze współrz˛edne trudno wykona´c dokładny rysunek, ale naszkicujmy rów-
noległobok z przek ˛
atnymi.
A
B
C
D
S
Sposób I
Materiał pobrany z serwisu
14

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Kluczowe w tym zadaniu jest to, ˙ze przek ˛
atne równoległoboku dziel ˛
a si˛e na połowy. W
takim razie punkt S jest ´srodkiem odcinków AC i BD. Mamy wi˛ec
S
=
A
+
C
2
=
−
37
+
39
2
,
17
+
15
2
= (
1, 16
)
.
Teraz łatwo wyznaczy´c współrz˛edne punktu B
= (
x
B
, y
B
)
.
S
=
B
+
D
2
(
1, 16
) =
x
B
+
19
2
,
y
B
−
27
2
(
2
=
x
B
+
19
⇒
x
B
= −
17
32
=
y
B
−
27
⇒
y
B
=
59.
Zatem B
= (−
17, 59
)
.
Sposób II
Zadanie łatwo rozwi ˛
aza´c u ˙zywaj ˛
ac wektorów.
−→
AB
=
−→
DC
[
x
+
37, y
−
17
] = [
39
−
19, 15
+
27
] = [
20, 42
]
(
x
+
37
=
20
⇒
x
= −
17
y
−
17
=
42
⇒
y
=
59.
Zatem B
= (−
17, 59
)
.
Odpowied´z: B
= (−
17, 59
)
Z
ADANIE
27
(2
PKT
.)
Rozwi ˛
a ˙z nierówno´s´c 3x
+ (
3x
+
1
) + · · · + (
3x
+
99
) <
2010, gdzie lewa strona jest sum ˛
a
kolejnych wyrazów ci ˛
agu arytmetycznego.
R
OZWI ˛
AZANIE
Z lewej strony dodajemy do siebie 100 wyrazów, zatem ich suma jest równa
3x
+ (
3x
+
99
)
2
·
100
=
50
(
6x
+
99
)
.
Musimy wi˛ec rozwi ˛
aza´c nierówno´s´c
50
(
6x
+
99
) <
2010
/ : 30
5
(
2x
+
33
) <
67
10x
+
165
<
67
10x
< −
98
x
< −
9, 8.
Odpowied´z: x
< −
9, 8
Materiał pobrany z serwisu
15
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
28
(2
PKT
.)
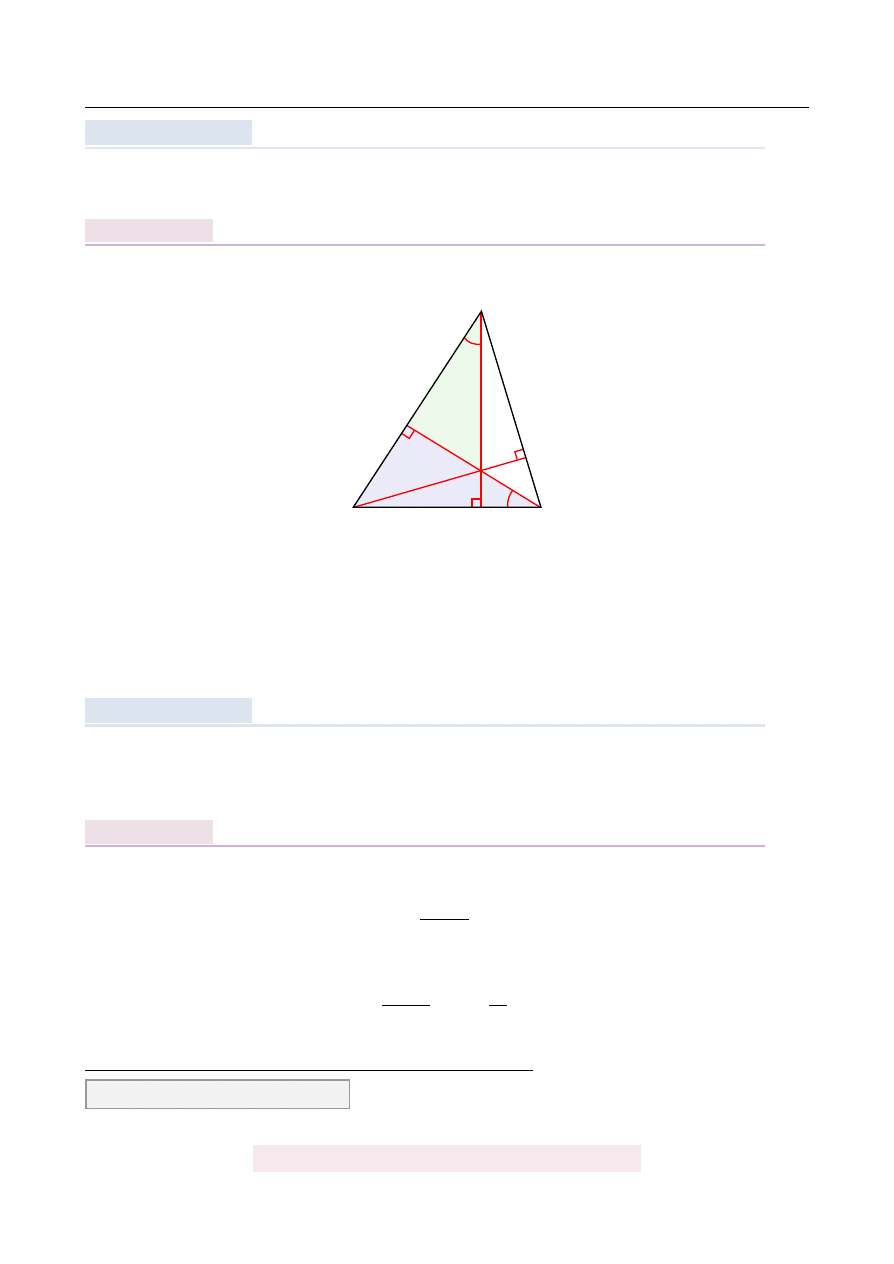
Punkt S jest punktem przeci˛ecia si˛e wysoko´sci trójk ˛
ata ostrok ˛
atnego ABC. Wyka ˙z, ˙ze je ˙zeli
|
CS
| = |
AB
|
to
|]
ACB
| =
45
◦
.
R
OZWI ˛
AZANIE
Rozpoczynamy od rysunku.
A
B
C
S
α
α
D
E
Zauwa ˙zmy, ˙ze
]
EBA
=
90
◦
− ]
A
= ]
ACS,
czyli trójk ˛
aty ABE i SCE s ˛
a prostok ˛
atne i maj ˛
a równe k ˛
aty. S ˛
a wi˛ec podobne. Ponadto z
zało ˙zenia maj ˛
a równe przeciwprostok ˛
atne AB
=
SC, wi˛ec s ˛
a przystaj ˛
ace. To oznacza, ˙ze
EB
=
CE, czyli trójk ˛
at prostok ˛
atny BEC jest równoramienny. Wówczas
]
EBC
= ]
ECB
=
45
◦
.
Z
ADANIE
29
(2
PKT
.)
Przy jednoczesnej pracy 40 identycznych pomp nadmuchowych, ˙z ˛
adany przepływ powie-
trza mo ˙zna zrealizowa´c w ci ˛
agu 24 godzin. W ci ˛
agu ilu godzin mo ˙zna zrealizowa´c ten sam
przepływ powietrza przy jednoczesnej pracy 60 pomp?
R
OZWI ˛
AZANIE
Je ˙zeli oznaczymy przez P prac˛e jak ˛
a maj ˛
a wykona´c pompy, to wiemy, ˙ze wydajno´s´c jednej
pompy to
P
24
·
40
.
W takim razie w ci ˛
agu jednej godziny 60 pomp wykona prac˛e
P
24
·
40
·
60
=
P
16
.
Na wykonanie całej pracy potrzeba wi˛ec 16 godzin.
Odpowied´z: W ci ˛
agu 16 godzin
Materiał pobrany z serwisu
16
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
30
(4
PKT
.)
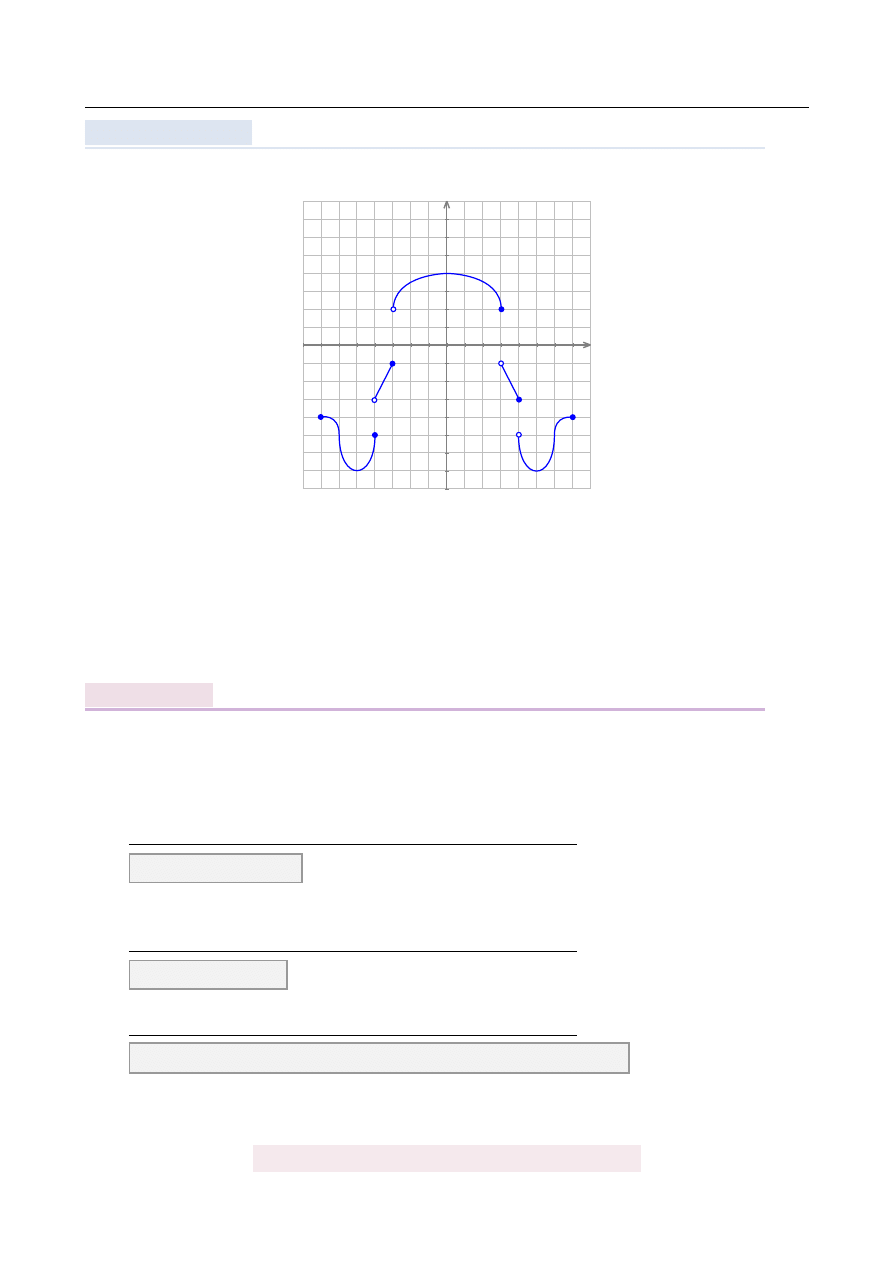
Dany jest wykres funkcji y
=
f
(
x
)
okre´slonej dla x
∈ h−
7, 7
i
.
-5
-1
+1
+5
x
-5
-1
+1
+5
y
Odczytaj z wykresu:
a) rozwi ˛
azania równania f
(
x
+
3
) = −
1;
b) miejsca zerowe funkcji y
=
f
(
x
) −
2;
c) maksymalne przedziały monotoniczno´sci funkcji f
(
x
)
.
R
OZWI ˛
AZANIE
a) Z wykresu widzimy, ˙ze funkcja f
(
x
)
przyjmuje warto´s´c -1 tylko dla argumentu x
=
−
3. Mamy st ˛
ad
x
+
3
= −
3
⇐⇒
x
= −
6.
Odpowied´z: x
= −
6
b) Miejsca zerowe funkcji y
=
f
(
x
) −
2 odpowiadaj ˛
a argumentom, w których warto´sci
funkcji f
(
x
)
s ˛
a równe 2. Jest tylko jeden taki punkt: x
=
3.
Odpowied´z: x
=
3
c) Odczytujemy z wykresu.
Odpowied´z: Malej ˛
aca:
h−
7,
−
5
i
,
h
0, 5
i
, rosn ˛
aca:
h−
5, 0
i
,
h
5, 7
i
Materiał pobrany z serwisu
17
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
31
(4
PKT
.)
Na prostej y
= −
3x
+
2 wyznacz punkt, którego suma kwadratów odległo´sci od osi układu
współrz˛ednych jest najmniejsza.
R
OZWI ˛
AZANIE
Szukamy punktu postaci P
= (
x, y
) = (
x,
−
3x
+
2
)
. Odległo´s´c tego punktu od osi Ox to
|
x
|
,
a odległo´s´c od osi Oy to
| −
3x
+
2
|
. Zatem suma kwadratów tych liczb to
|
x
|
2
+ | −
3x
+
2
|
2
=
x
2
+ (
2
−
3x
)
2
=
x
2
+
4
−
12x
+
9x
2
=
10x
2
−
12x
+
4.
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w gór˛e, wi˛ec jej naj-
mniejsz ˛
a warto´s´c otrzymamy w wierzchołku, czyli dla
x
=
−
b
2a
=
12
20
=
3
5
.
Wtedy
y
= −
3x
+
2
= −
3
·
3
5
+
2
=
−
9
5
+
2
=
−
9
+
10
5
=
1
5
.
Odpowied´z:
(
3
5
,
1
5
)
Z
ADANIE
32
(6
PKT
.)
Listonosz losowo rozmieszcza 4 listy w 6 skrzynkach na listy. Jakie jest prawdopodobie ´n-
stwo, ˙ze przynajmniej dwa listy znajd ˛
a si˛e w tej samej skrzynce?
R
OZWI ˛
AZANIE
O zdarzeniach elementarnych my´slimy jak o ci ˛
agach numerów skrzynek, do których trafiły
kolejne listy. Ka ˙zdy list mo ˙ze trafi´c do jednej z 6 skrzynek, wi˛ec
|
Ω
| =
6
·
6
·
6
·
6
=
6
4
.
Zamiast liczy´c prawdopodobie ´nstwo p zdarzenia opisanego w zadaniu, łatwiej jest policzy´c
prawdopodobie ´nstwo p
0
zdarzenia przeciwnego, czyli zdarzenia, w którym ka ˙zdy list trafi
do innej skrzynki. Takich zdarze ´n jest
6
·
5
·
4
·
3
(pierwszy list mo ˙ze trafi´c dowolnie, drugi do jednej z pozostałych 5 skrzynek itd.). Zatem
p
0
=
6
·
5
·
4
·
3
6
4
=
5
·
4
·
3
6
3
=
10
6
2
=
5
18
.
St ˛
ad
p
=
1
−
p
0
=
1
−
5
18
=
13
18
.
Odpowied´z:
13
18
Materiał pobrany z serwisu
18
Wyszukiwarka
Podobne podstrony:
Rok 2010 04 17 Prob Pod Arkusz
Rok 2010 04 24 Prob Pod Arkusz
Rok 2010 04 10 Prob Pod Arkusz
C3A4 Transaction in foreign trade Polish ver 2010 10 17
2006 04 17
arkusz Matematyka poziom r rok 2010 4393 MODEL
Prawo pytania Gr.1, UE ROND - UE KATOWICE, Rok 1 2010-2011, semestr 1, Prawo
rr RĂłznice Indywidualne Wszytskie pytania, Studia, Psychologia, SWPS, 2 rok, Semestr 04 (lato), Psy
arkusz Matematyka poziom p rok 2010 5979 MODEL
arkusz fizyka poziom r rok 2010 8710 MODEL
2011.04.10 - 438 1 test z odpow, Testy, testy sędziowskie
Plan pracy na rok 2010, świetlica, plan pracy
biofizyka wersja F2, Farmacja Poznań, I ROK (2010-2011), biofizyka
Pytania - Statystyka, Studia, Psychologia, SWPS, 2 rok, Semestr 04 (lato), Metodologia ze statystyką
więcej podobnych podstron