Chemical Engineering and Processing 41 (2002) 427 – 436

Microwave vacuum drying of porous media: experimental study

and qualitative considerations of internal transfers

C. Pe´re´, E. Rodier *

Laboratoire de Ge´nie des Proce´de´s des Solides di

6ise´s-UMR CNRS

2392

, Ecole des Mines d

’

Albı´, Albı´ CT,

81013

, Cedex

09

, France

Received 18 April 2001; received in revised form 17 July 2001; accepted 31 July 2001

Abstract

This paper deals with experimental results obtained on a laboratory scale dryer. Two porous media were dried, a packing of

initially water saturated glass beads and a packing of initially unsaturated pharmaceutical granules. For the first one, the main
parameter is permeability of the bed varying the beads diameter and for the second one it is the porosity of the bed varying the
amount of product. These experiments were carried out at fixed incident power and pressure level. In the first period of the drying,
it was observed that permeability was a limiting parameter to internal mass transfers when free liquid water is expulsed, revealing
high gas pressure gradients inside the product. They occur when we have a massive vaporisation with ebullition. As for the
porosity of the granules bed, it has no effect on mass transfers. In the second period, we have no influence of both parameters
on the drying kinetics. In the last period, so in the hygroscopic field or below the irreducible saturation, the internal mass transfers
are governed by the electromagnetic energy absorption. © 2002 Elsevier Science B.V. All rights reserved.

www.elsevier.com/locate/cep

1. Introduction

Combining microwaves and vacuum to perform a

drying operation presents three major interests. Mi-
crowaves speed up the drying because of their ability to
heat up the solvent in the product in an instantaneous
and homogeneous way. Vacuum enhances the mass
transfer because of an increased pressure gradient be-
tween the inside and the outside of the sample to dry
and maintains a low temperature level essential for
thermolabile products. Hence, this drying technic is of
an unquestionable importance for industries as phar-
maceutical ones. Yet it needs to be well controlled to
provide a high quality product. For instance too high
pressure gradients inside the product may deteriorate it
and this can be avoided sending an optimized incident
power.

A further research on the transfer phenomena in-

volved is then required. Up to date researchers studied
on one hand the effect of drying conditions on the
product quality, for instance Chatrah [1] or Killeen [2]

who compare mechanical properties of granules dried
by different processes or Poska [3] who investigates the
innocuousness of the microwaves on the product. On
another hand heat and mass transfers in the product
were modelled for example by Ni [4]. However, as it
difficult to obtain accurate experimental results in order
to validate a model, both parts are rarely linked which
puts a brake on the understanding of the phenomena
involved. To go further in this way we present an
experimental set up properly equipped to establish en-
ergetic and mass balance. A ‘model’ porous media,
glass beads, was chosen in this study in order to analyse
the influence of the bed permeability on the drying
kinetics. In addition, we give some qualitative consider-
ations about the liquid and gas internal transfers. In a
more practical part pharmaceutical granules were used
in order to analyse their behaviour when dried in this
way.

First, we remind some general points about internal

transfers and microwave and vacuum drying. Second,
an experimental part presents the set up and the results
obtained on the two different porous media, initially
saturated glass beads and unsaturated pharmaceuticals
granules. Five different glass beads diameters are tested
with a fixed total porosity and eight different total

* Corresponding author. Tel.: + 33-563-49-3153; fax: + 33-563-49-

3025.

E-mail address

:

[e-mail]

(E. Rodier).

0255-2701/02/$ - see front matter © 2002 Elsevier Science B.V. All rights reserved.
PII: S 0 2 5 5 - 2 7 0 1 ( 0 1 ) 0 0 1 6 1 - 1

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

428

porosities are used with the packing of pharmaceutical
granules. Several experimental conditions are used in
order to study the internal transport mechanism during
different drying conditions, evaporation and vaporisa-
tion. Lastly, we discuss the results essentially in terms
of internal mass transfers and their limiting parameters
such as permeability.

2. Preliminary: internal mass transfers and specificities
of microwave and vacuum drying

The motions of liquid and gas phases through a

porous media as it is dried are commonly described by
a liquid convection owing to capillary forces, a diffu-
sion of the water vapour in the gas phase owing to
vapour concentration gradients and a gas phase con-
vection due to the total pressure gradients [5,6].

One of the specificities of the microwave drying

process is the type of product heating. Electromagnetic
energy is mainly absorbed by liquid water owing to its
high loss factor compared with that of dry product [7].
Hence, the heating occurs in the whole product instan-
taneously when microwaves are applied. Hence, con-
ductive heat transfer resistance becomes unimportant.

Considering conventional drying, internal moisture

flow is commonly due to liquid flow driven by capillary
forces and vapour flow by diffusion. With dielectric
heating two other mechanisms resulting from internal
vaporisation of moisture may be important. These are
filtration flow of the liquid phase caused by high gas
pressure generated in regions where air pockets exist,
and convective flow of the gaseous phase due to the
excess pressure created when the moisture is held in the

pendular state [8 – 10]. Some authors [7,11] showed ex-
perimentally that over-pressures can take place inside
the media during microwave drying and induce a phe-
nomena of ‘water pumping’.

Vacuum reduces the boiling point of the solvent and

allows a low temperature drying. When the pressure
outside the product decreases the vapour diffusion
from the surface product increases. The vacuum allows
the pressure gradients inside the porous media as it was
already shown during vacuum conductive drying of
glass beads [12,13]. In this case over-pressures were
observed when the product temperature was closed to
the boiling point.

3. Experiments and materials

3

.

1

. Laboratory scale microwa

6e 6acuum dryer

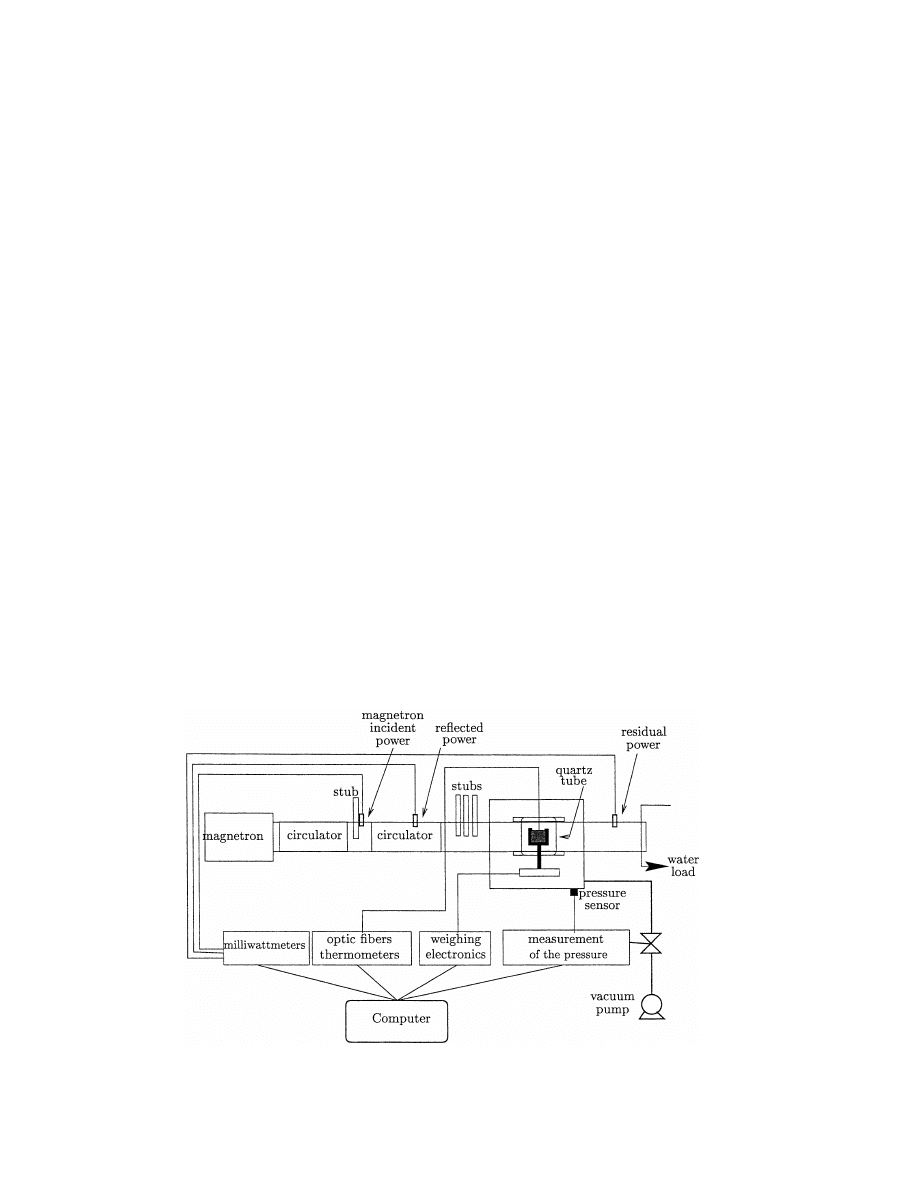
The laboratory scale apparatus (Fig. 1) is composed

of a cylindrical vacuum chamber (approx. 100:1)
crossed by an horizontal single mode microwave guide
[14].

Most of the wave guide is at atmospheric pressure,

except inside a vertical quartz tube. Quartz is chosen
since it does not absorb microwaves. These are gener-
ated by a magnetron at one end of the wave guide.
Two circulators and four stubs are located on this
guide in order to protect the magnetron against
reflected power and to control the incident power arriv-
ing on the product. Three milliwattmeters measure the
incident, the reflected and the residual power; the
power absorbed by the sample can thus be calculated
by:

Fig. 1. Laboratory scale dryer.

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

429

Fig. 2. Configuration of the sample holder.

Table 1
Glass beads packing characteristic

221

371

184

443

Mean diameter (

mm)

546

Initial water content

25%

Initial water saturation

100%

30

51

25

58

Pore radius (

mm)

73

0.53

1.51

2.15

Kozeny permeability (m

2

×10

10

)

3.27

0.37

P

abs

=

P

incident

−

P

reflected

−

P

residual

(1)

A PTFE sample holder is put in the middle of the

quartz tube (cf. Fig. 2). It stands on the plate of a
weighing instrument whose electronic part is placed
outside the vacuum chamber. Thus, the water content
of the sample can be measured continuously. The tem-
perature of the product can be measured by optical
fibre probes. The pressure in the vacuum chamber is
maintained between a high and a low threshold con-
trolled by a vacuum pump connected to an automatic
control valve.

During a drying operation, the values of mass (preci-

sion

90.001 g), sample temperature (precision:9

0.1 °C), microwave power (precision

90.1 W) and

pressure (precision

90.1 kPa) are recorded continu-

ously. However, it is not possible to measure at the
same time the weight and the temperature, as the
friction of the temperature probe in the product dis-
turbs the weight measurement. Thus, to obtain the
mass and the temperature evolutions two experiments
are necessary.

3

.

2

. Materials and preparation

3

.

2

.

1

. Glass beads

The glass beads are treated by sulfochromic acid in

order to clean their surface and make it hydrophilic.
Five granulometric classes are used, with respective
diameters of 184, 221, 371, 443 and 546

mm. These

mean volume diameters were determined with a laser
granulometer from Malvern. The density of the differ-
ent classes are measured by an helium pycnometer,
micromeretics, and found equal to 2.48 g cm

− 3

.

An experimental procedure was set up to obtain

constant and reproducible initial water content and
porosity for the beds of glass beads in a sample holder.
The sample holder is first filled with distilled water, and
a mixture of water and glass beads is then added. This
mixture is made of 50 cm

3

of glass beads for 100 cm

3

of

water, and was previously submitted to ultrasound for
10 min in order to eliminate the adsorbed air bubbles
on the glass beads. The sample holder is then vibrated
to obtain an homogeneous packing. The water content
is measured with an infrared dessicator. The values of
dry basis water content range from 0.249 to 0.251. The
porosity lies between 0.382 and 0.388, and the satura-
tion of the porous medium is around 99.5%.

It is well known that gas overpressure can take place

during microwave drying of a porous media [8,15,16].
In order to avoid any modification of the unconsoli-
dated bed due to the movement of the particles, it is
necessary to screw a perforated lid on the top of the
sample holder and the diameter of the holes was chosen
so that the lid does not induce any additional mass
transfer resistance.

The totality of the glass beads samples used for the

drying experiments are characterized by initial water
content, porosity, pore radius and permeability. The
pore radius and the permeability are calculated by [17]:

K =

d

2

m

3

36h

K

(1 −

m)

2

(2)

r

p

=

'

8K

m

(3)

with d the diameter of the glass beads, h

K

the Kozeny –

Carman constant equal to 4.5 and

m the porosity of

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

430

Table 2
Mixing and granulation conditions

6×10

−3

m

3

mixer volume
initial quantity of powder

0.5 kg
3.2 m s

−1

Agitation speed during mixing

5 min

Duration of mixing operation

0.1 kg

Quantity of water
flow for wetting

2×10

−2

l min

−1

3.2 m s

−1

Agitation speed during granulation

5 min

Duration of granulation operation

sample. The total porosity of each sample is calculated
by the following relation Eq. (4):

m

calculated

total

=

volume of sample holder-volume of dry product

volume of sample holder

(4)

To obtain the volume of the dry product we took

into account the initial water content and the density of
the granules. The total porosity, the pore radius and the
permeability calculated by the Eq. (3) (pore radius is
known by porosimetry, porosity is also known, so we
can calculate the permeability) are summarized in the
Table 3.

3

.

2

.

3

. Experimental runs

The experiments are carried out for two incident

powers (

^mw=20 or 40 W—this incident power is

the residual power obtained without sample in the
sample holder). Two vacuum pressure levels were cho-
sen, 1.1 and 7 kPa. At the beginning of the experimen-
tal procedure, the microwaves are applied on the
product when the pressure reaches roughly 10 kPa. The
recorded values of the pressure show that the low
pressure level is obtained within 30 s for 1.1 kPa and 20
s for 7 kPa. This short time corresponds to a negligible
decrease of the moisture content and show that the
initial ambient temperature is quickly above the boiling
point for 1.1 kPa (10 °C) and below the boiling point
for 7 kPa (40 °C).

4. Results

4

.

1

. E

6olutions of drying kinetics and temperature of

glass beads

In order to discuss whether we are in evaporation or

vaporisation conditions we have to remind what these
terms mean. Evaporation is commonly defined as a
phase change in presence of a mixed surrounding atmo-
sphere when vapour pressure is less than the total gas
pressure. Vaporisation is a phase change in the absence
of any other gas at the interface than the vaporised one,
either in a closed system containing only water or in an
ebullition regime where vapour replaces air at the inter-
face. Mass balance on the vacuum chamber allowed us
to evaluate vapour and air pressures according to the
following Eq. (5):

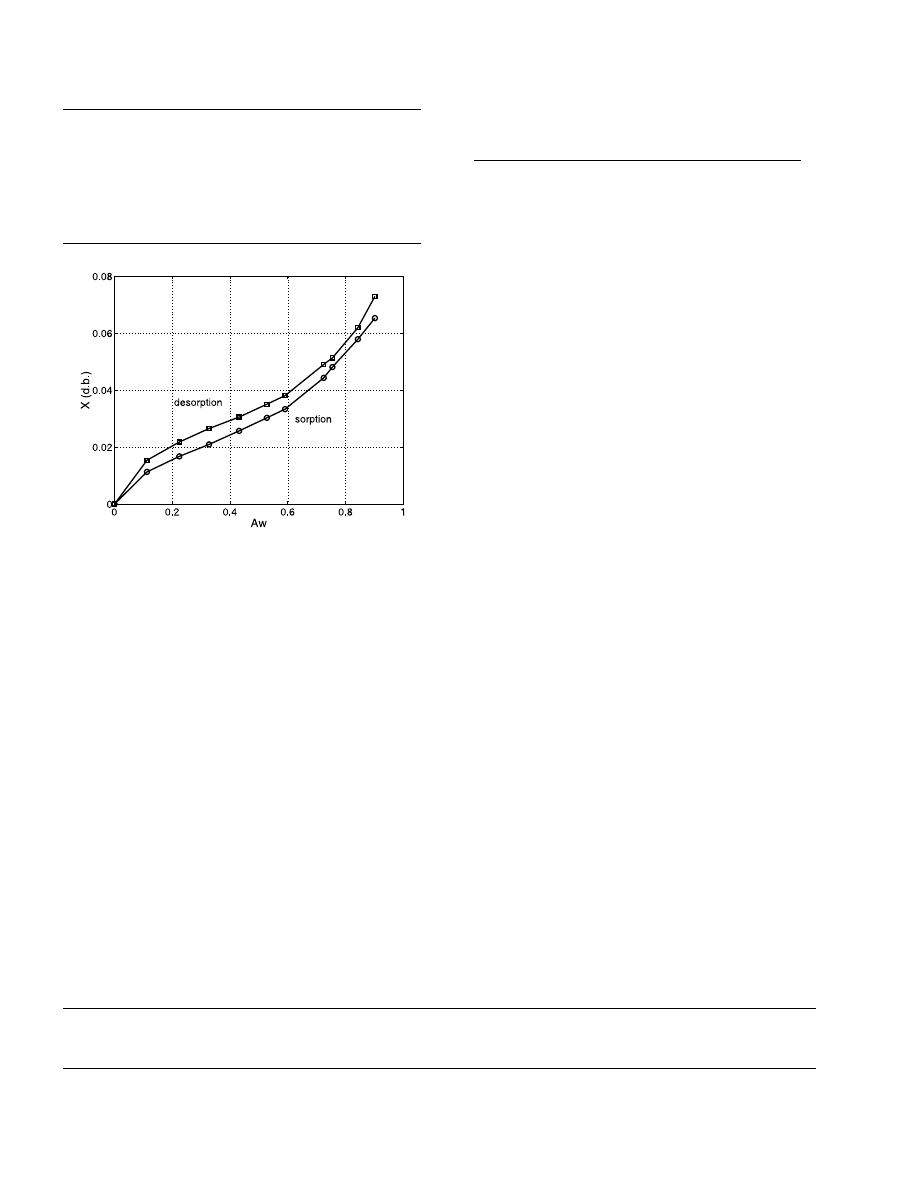
Fig. 3. Water content versus water activity for pharmaceutical gran-
ules at 20 °C.

packing. The packing of glass beads characteristics are
summarized in the Table 1.

3

.

2

.

2

. Pharmaceutical granules

The pharmaceutical granules are made of lactose

(66% in mass), starch (31% in mass) and polyvynilpy-
rolidone (3% in mass). To obtain granules with homo-
geneous characteristics a mixing and a granulation are
carried out in a pharmaceutical mixer-granulator
(Diosna). The mixing and granulation conditions are
presented in the Table 2.

The granulometric distribution is obtained by sieving

100 g of product. The diameter of the granules obtained
varies from 0.5 to 1 mm. The water activity was mea-
sured by the COST9O procedure [18]. The hygroscopic
field was so determined: it extends from a water content
in dry basis of 0 to 10% as it is shown on the Fig. 3.

In order to modify the permeability of the granules

bed we introduced in the sample holder an increasing
mass of granules by applying different pressures to the

Table 3
Pharmaceutical granules packing characteristic

0.590

0.622

0.655

0.422

0.695

m

total

calculated

0.480

0.525

0.560

35

28

20

16

12

Pore radius (

mm)

40

38

38

1.11

1.82

Permeability (m

2

×10

10

)

3.81

0.72

6.55

13.1

0.84

0.89

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

431

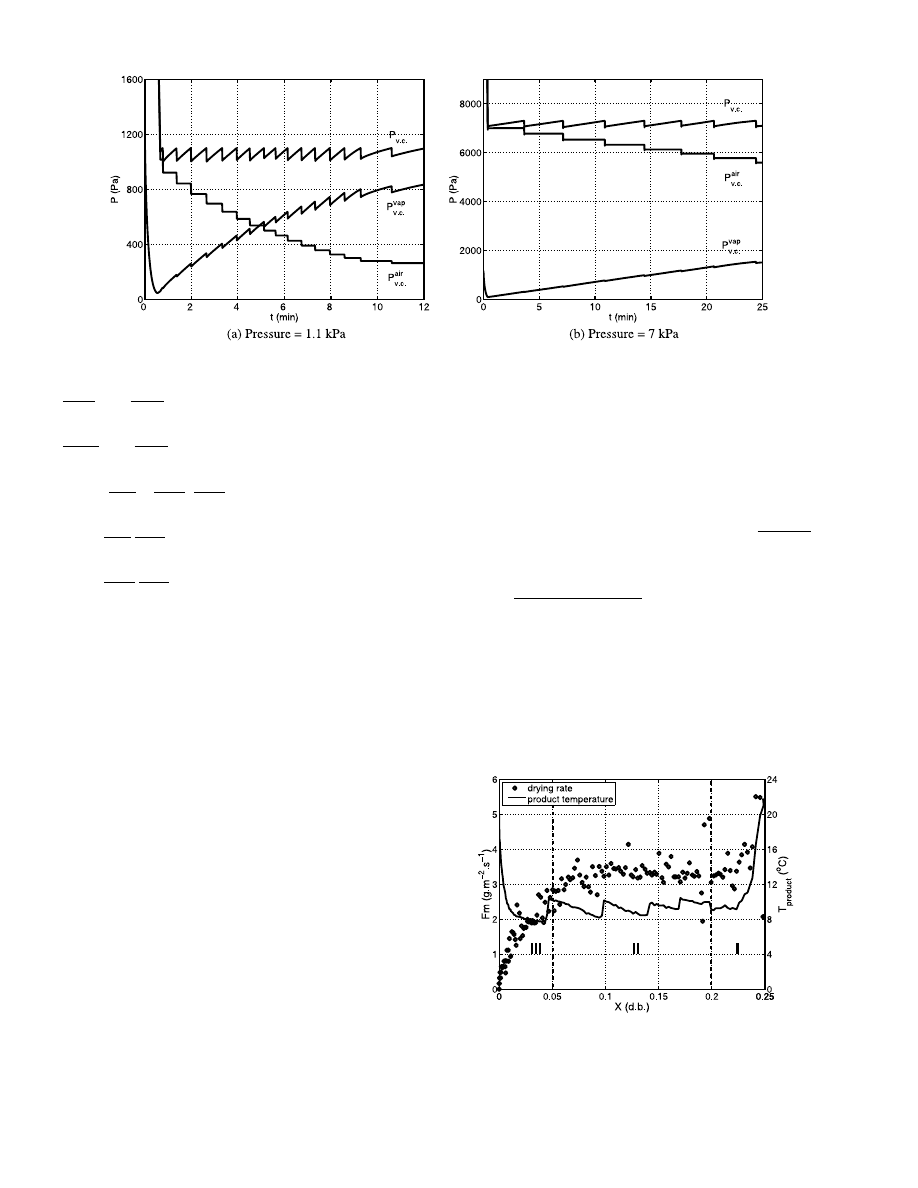
Fig. 4. Evolutions of total pressure and partial pressures of vapour and air in the vacuum chamber for the experiments on the glass beads.

dm

air

dt

= −

q

pump

V

vc

m

air

(5)

dm

vap

dt

= −

q

pump

V

vc

m

vap

+ F

m

A

(6)

P

vc

=

m

air

M

air

+

m

vap

M

vap

RT

vc

V

vc

(7)

P

vc

air

=

m

air

M

air

RT

vc

V

vc

(8)

P

vc

air

=

m

vap

M

vap

RT

6c

V

6c

(9)

These values are presented on Fig. 4a, b. The small

perturbations on each curve are due to the switching on
and off of the vacuum pump. At 1.1 kPa and on a time
interval from 3 to 10 min which corresponds roughly to
the constant drying rate period, the molar vapour
fraction goes from 0.35 to 0.73. As for 7 kPa, during
the constant drying rate period, so between 10 and 20
min, the molar vapour fraction varies from 0.1 to 0.18.
We can consider that these values are minimum ones
for what happens at the interface between the product
and the surrounding atmosphere.

The Fig. 5 shows the drying kinetic and the product

temperature for a 40 W incident power and for a 1.1
kPa vacuum level and for 315

mm diameter. We take as

definition of the drying rate, the mass of water drained
off per square meter and per second. The surface area
used in this calculation is the free surface of the sample
holder. Three periods are present: the first one (I), for
water content between 0.25 and 0.20 during which the
drying rate decreases to a pseudo-constant period; the
second one (II) between 0.20 and 0.05 with a pseudo-
constant drying rate period and the last one (III) be-
tween 0.05 and 0 which is the falling drying rate period.
The small perturbations on the temperature curves
correspond to the switching on and off of the vacuum
pump. We present in Fig. 6a comparison between the

measured absorbed power and a calculated energetic
balance including the heating up of the product or the
sensitive heat and the latent heat of vaporisation. These
values have been calculated using the experimental
temperature and mass flux by the following relation Eq.
(10):

P

calculated

= F

m

A

DH(T

product

) + m

product

(t)C

p

(X)

dT

product

dt

(10)

C

p

(X) =

XC

p

water

+ C

p

glass beads

1 + X

(11)

At the beginning of the drying the calculated heat is

much higher than the absorbed power. We conclude
here that we have expulsion of liquid water, phe-
nomenon due to a massive vaporisation with ebullition
inside the porous medium. We have already noticed
that the initial ambient temperature was higher than the
boiling point. The corresponding sensitive heat of the

Fig. 5. Drying rate and product temperature evolutions versus dry
basis water content for glass beads at 1.1 kPa and for a 40 W incident
power.

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

432

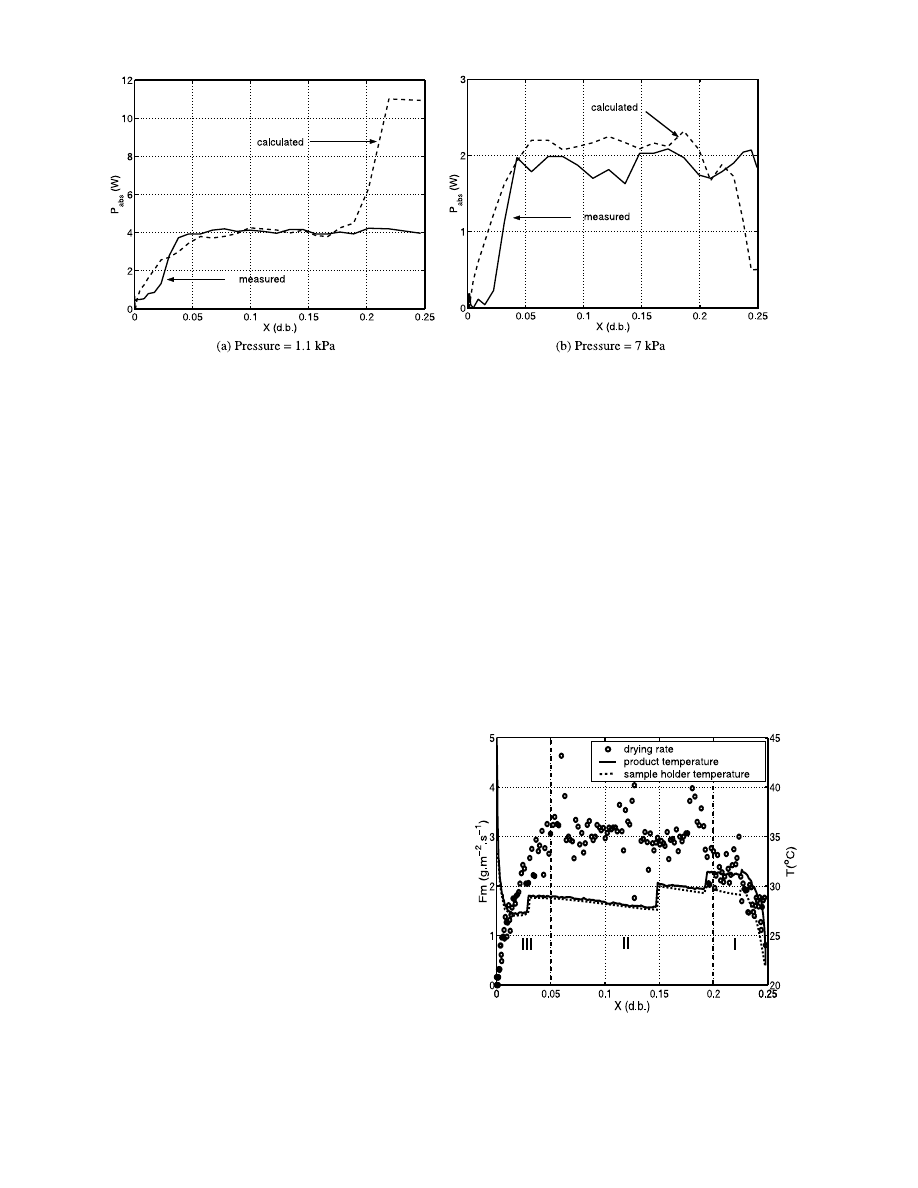
Fig. 6. Evolutions of the experimental and the calculated absorbed power for the experiment on glass beads at for a 40 W incident power.

material allows an important vaporization and so ap-
pearance of vapour bubbles. The vapour bubbles grow-
ing induce a total pressure gradient inside the porous
media. The depression between the chamber pressure
and the total pressure inside the media favors the liquid
expulsion. It is now admitted that microwaves can
induce high overpressures in a porous medium [8,19].
Some authors [20] have shown that for materials such
as brick, microwaves applied in the early stages of
drying induce a ‘free water pumping’ from the inside to
the outside of the pores. The second period of drying
corresponds to a stabilization at the boiling point, it is
a vaporisation period. Regarding the values of vapour
fraction in the chamber we can admit that the gas phase
in the product is pure vapour. Here the calculated heat
is of the same order of the absorbed power.

The Fig. 7 shows the drying kinetics and the product

temperature for a 40 W incident power and for a 7 kPa
vacuum level and for glass beads with a 315

mm diame-

ter. On Fig. 6b we have a comparison between the
calculated and the experimental heats involved.

As for the experiments at 1.1 kPa we have three

distinct periods. The first period corresponds to the
heating up of the product. Fig. 7 shows that at the
beginning of the drying the sample holder temperature
is lower than the product one and the initial ambient
temperature is lower than the boiling point. Hence, we
suppose that recondensation on the surface of the
sample holder may occur. In the second period we
notice that the product temperature during the pseudo-
constant period is lower than the boiling point. The
molar fraction of vapour in the chamber remains low
during this period. Hence at the interface of the
product we may not have a pure vapour phase but a
mixed one. It allows us to conclude to an evaporation
mechanism. On an energetic point of view, we see that
in this period the power absorbed by the product is of

the same order of the latent heat of the water
vapourised.

Conclusions for both pressure levels were verified for

a 20 W incident power.

4

.

2

. E

6olutions of drying kinetics and temperature of

pharmaceutical granules

The Fig. 8a and b shows the drying kinetics and the

product temperature for a 40 W incident power and for
a 1.1 and 7 kPa vacuum level obtained with the phar-
maceutical granules.

The drying kinetics of pharmaceutical granules, com-

pared with the ones obtained with glass beads do not
present any constant drying rate period. These evolu-
tions often occur for food or pharmaceutical products.

Fig. 7. Drying rate and product temperature evolutions versus dry
basis water content for glass beads at 7 kPa and for a 40 W incident
power.

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

433

Fig. 8. Drying rate and product temperature evolutions versus dry basis water content for pharmaceutical granules and for a 40 W incident power.

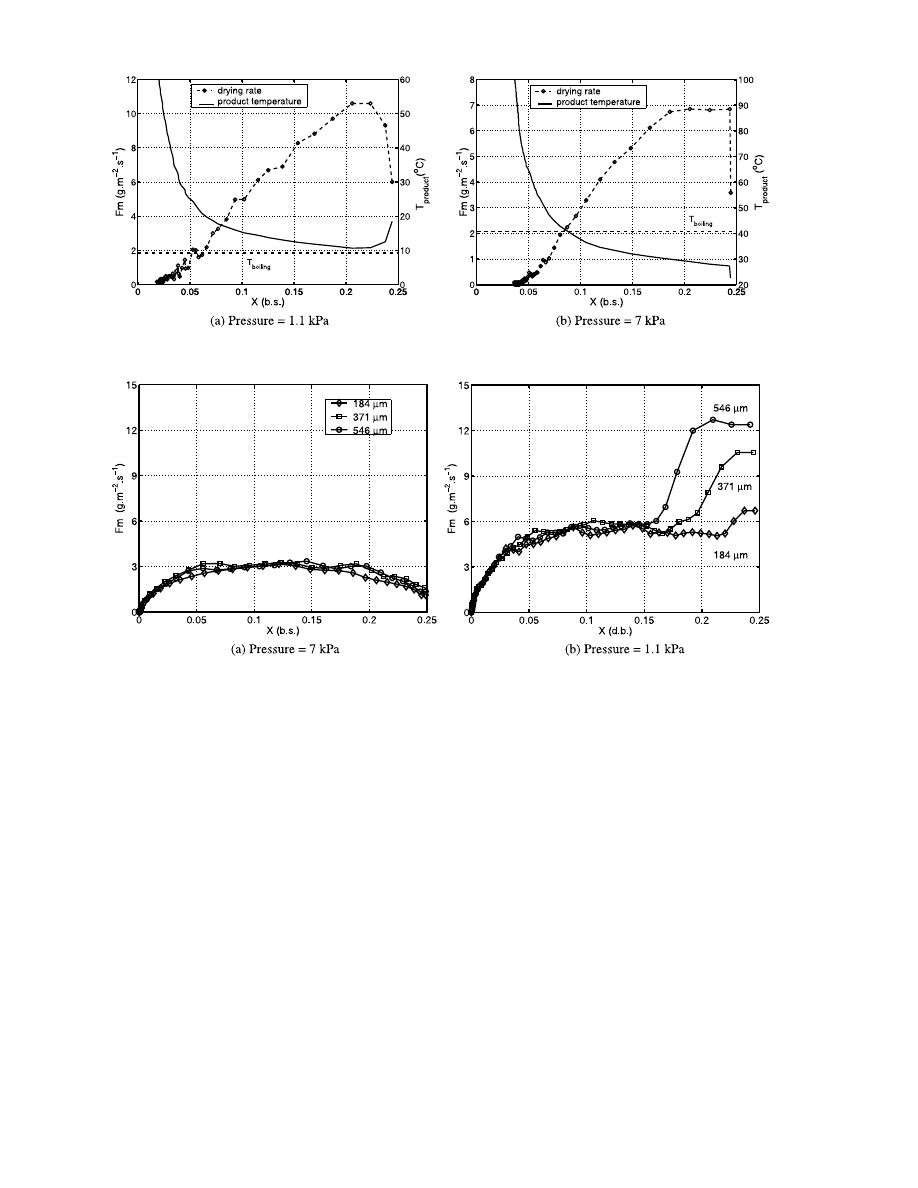
Fig. 9. Drying rate versus dry basis water content for several sizes of glass beads and for a 40 W incident power.

For the experiments at 1.1 kPa, the product tempera-

ture is always higher or at the same level as the boiling
point (10 °C) so the drying mechanism is a vaporiza-
tion one. As the pharmaceutical granules are composed
of starch absorbing microwaves and are hygroscopic
for water content lower than 0.10 the temperature
increases higher than the boiling point in the hygro-
scopic field.

On the other hand, at 7 kPa, except the hygroscopic

field, the product temperature is lower than the boiling
point (

:40 °C). The drying occurs with an evapora-

tion mechanism for the free water domain.

5. Study of internal transfers: influence of the bed
permeability on the drying kinetics

In this part we propose to study the influence of the

bed permeability on the drying kinetics using the pack-
ing of glass beads (with a fixed total porosity) and
pharmaceutical granules with a varying porosity.

5

.

1

. Glass beads

The Fig. 9a shows the evolution of drying rate versus

the dry basis water content for three different sizes of
glass bead at 7 kPa. We represent only three diameters
to keep the figure unoverloaded.

We have explained with the Fig. 7 that during all the

drying the main mechanism is an evaporation mecha-
nism. So for the range of the permeabilities we tested
and for evaporation drying, we can conclude that there
is no influence of the bed permeability on drying kinet-
ics. Moreover, for the five diameters, the time of end of
drying are the same enhancing that there is no influence
of bed permeability on drying kinetics.

For the experiments at 1.1 kPa (Fig. 9b) we observe

a strong influence of the permeability during the first
period. Here, vaporization drying takes place with liq-
uid expulsion [21]. During this step, higher the perme-
ability is, more important the liquid expulsion is. As for
the gravity we can suspect it is negligible in comparison
with liquid motions induced by over-pressures.

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

434

The heating up by microwaves being uniform, it

may allow an uniform liquid and gas water distribu-
tion inside the porous media. But this is only true if
the sample size is small enough compared with the
microwave wavelength in the product. In our case this
assumption is verified since the characteristic dimen-
sion of the sample is 1 cm and the microwave wave-
length in the product is always higher than 2 cm [22].
Moreover we do not observe temperature gradients on
the height of the product indicating a moving inter-
face where the phase change takes place. Obviously, it
does not mean that there are no local temperature
gradients but we do not measure them. We conclude
that water and gas phase are uniformly distributed
over the height of the sample in a macroscopic point
of view.

In such case some authors [12,13] conclude that the

internal mass transfer is mainly governed by the gradi-
ent of the total pressure of the gas phase. Sahota [23]
has showed experimentally that for a permeability
equal to 7 × 10

− 12

m

2

over-pressures were approxi-

mately equal to 100 kPa. We assume that over our
permeability range (from 3.7 × 10

− 11

to 3.27 × 10

− 10

m

2

)

we have enough over-pressures in our media to

govern mass transfers. Then the permeability to the
liquid phase will be a limiting parameter in the liquid
expulsion.

During the second and the third period there is no

significant influence of the bed permeability on the
drying kinetics. We assume again an uniform liquid
and gas phases distribution on the height of the sam-
ple until the irreducible saturation (X

:0.06) which is

the water left in the porous media in the funicular
state. In the second period we admit that total pres-
sure gradients still exist. In the third period or below
the irreducible saturation, pressure gradient may drop
as microwave absorption decreases significantly. Capil-
lary pressure may then become important. But the
major limitation here may be the total absorbed
power by the product. These conclusions are admitted
for the five different diameters of glass beads and for
the two incident powers.

5

.

2

. Pharmaceutical granules

We explained earlier that we obtained eight differ-

ent porosities in the sample holder varying from 0.42
to 0.69. In order to facilitate the reading of the curves
we present four experiments, those for porosity equal
to 0.48, 0.56, 0.62 and 0.69. We showed on Fig. 8a, b
that the vacuum level does not induce differences be-
tween the kinetics at 1.1 and 7 kPa. We only present
the experiments which were carried out at 1.1 kPa and
for 20 W incident power (Fig. 10).

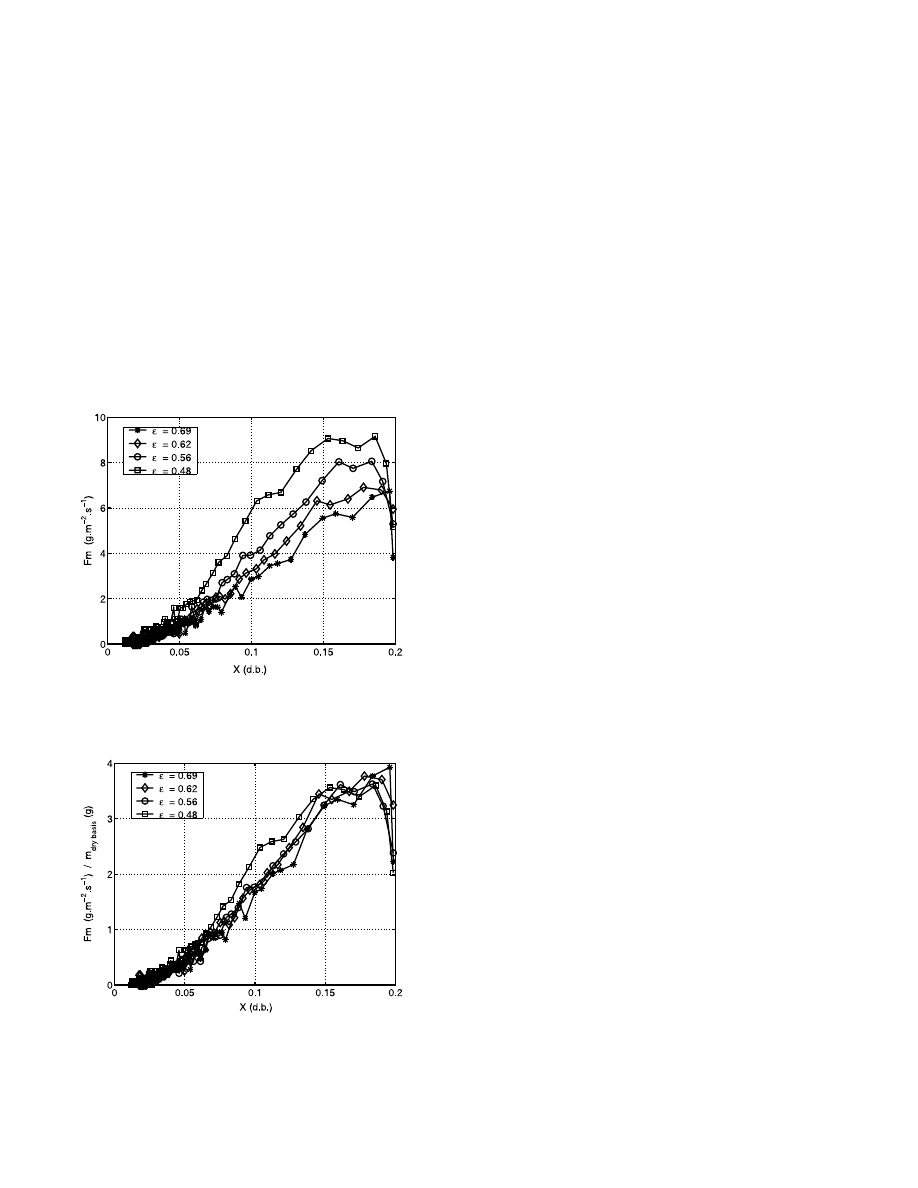
The Fig. 10 represents the evolutions of drying ki-

netics versus dry basis water content. We can observe
a strong influence of the total porosity on the drying
kinetic. More the porosity decreases and more the
drying rate increases. The parameter in our experi-
ments is the porosity in the sample holder and, there-
fore, the weight of dry material. So when the porosity
decreases in the sample holder the quantity of dry
product increases. So, as the initial water content is
the same for each experiment it is necessary to reduce
drying rate to dry basis weight. The Fig. 11 represents
the ratio of the drying rate by the dry basis weight
versus the dry basis water content. The influence of
the porosity on the drying kinetics does not appear
with this kind of representation. So permeability is
not a limiting parameter in this kind of experiments.
We can obtain the same conclusions if we represent
the evolution of the total absorbed power reduced by
the dry basis weight (Fig. 12a, b).

Fig. 10. Drying rate versus dry basis water content for several total
porosity of granules for a 20 W incident power and a pressure of 1.1
kPa.

Fig. 11. Drying rate versus dry basis water content for several total
porosity of granules for a 20 W incident power and a pressure of 1.1
kPa.

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

435

Fig. 12. Absorbed power versus dry basis water for a 40 W incident power.

As the packing of pharmaceutical granules is initially

unsaturated, pressure gradients generated are not high
enough to induce liquid water expulsion. We assume
again that the total pressure gradient governs the inter-
nal mass transport phenomena from the beginning of
the drying to the hygroscopic domain (X

:0.10). These

conclusions are valid in our configuration since the
water is uniformly heated in the sample inducing a
macroscopic uniform distribution of the liquid and of
the gas phase over the height of the sample.

In the hygroscopic domain the main limitation is the

absorption of electromagnetic energy by hygroscopic
water which is not as efficient as the one absorbed by
the free water. The drying kinetics are here closely
linked to the evolution of the absorbed power.

We can conclude that at an industrial scale, such

pharmaceutical granules will not be mechanically dete-
riorated by pressure gradients in the product in similar
conditions. Besides, the control of the process is condi-
tioned by a precise control of the source term through
the measure of the residual power for instance [22].

6. Conclusions

We presented here some experimental results ob-

tained by microwave and vacuum drying of initially
water saturated packing of glass beads and of unsatu-
rated packing of pharmaceutical granules.

The glass beads taught us that the main limitation to

mass internal transfer is the liquid convection when we
have vaporisation with an ebullition mechanism. In
that case we have high enough pressure gradients inside
the product to expulse some liquid water. The only
other limiting phenomenon is the absorption of mi-
crowaves which is reduced whenever the water is no
more free, that is here at the very end of the drying
when there is only capillary water.

Drying of pharmaceutical granules did not put in

evidence any other limitation than the absorption of
microwaves by hygroscopic water. Drying kinetics are
closely linked to the evolution of the absorbed power.
With this kind of unsaturated porous media pressure
gradients are not high enough to deteriorate the
product.

In the future it would be interesting to go further in

the permeability effect investigating lower pore diame-
ters. It would also be worth studying the transfers
mechanisms in the boundary layer at the interface
between the product and the surrounding atmosphere.

Acknowledgements

The authors wish to thank the research institute of

pharmaceutical company Pierre Fabre for the financial
support of this work, Institut de Recherche Pierre
Fabre, Centre de De´veloppement, Rue Jean Rostand,
BP 687, 31319 Labe´ge Innopole, France

Appendix A. Nomenclature

A

surface area of the sample holder (m

2

)

d

diameter of the glass beads (

mm)

pore radius (

mm)

r

p

F

m

drying rate (g m

−2

s

−1

)

total permeability (m

2

)

K

air weight in vacuum chamber (kg)

m

air

vapour weight in vacuum chamber (kg)

m

vap

product weight (kg)

m

product

molecular weight of air (kg mol

−1

)

M

air

molecular weight of vapour (kg mol

−1

)

M

vap

P

abs

absorbed power (W)

C. Pe´re´, E. Rodier

/

Chemical Engineering and Processing

41 (2002) 427 – 436

436

P

ca1culated

absorbed power (W)

partial vapour pressure in vacuum chamber

P

vc

vap

(kPa)

P

vc

air

partial air pressure in vacuum chamber

(kPa)

P

6c

total pressure in vacuum chamber (kPa)

q

pump

Volume flow of the vacuum pump (m

3

s

−1

)

t

time (min)
product temperature (°C or K)

T

product

T

vc

vacuum chamber temperature (°C or K)
volume of vacuum chamber (m

3

)

V

dry basis water content (kg

water

/kg

dry solid

)

X
^

inc

experimental incident power (W)
experimental incident power (W)

^

ref.

experimental incident power (W)

^

res.

m

bed porosity

References

[1] M. Chatrath, J. Staniforth, The relative influence of dielectric

and other drying techniques, Drying Technology 8 (5) (1990)
1089 – 1109.

[2] M. Killeen, Comparison of granular and tablet properties for

products produced by forced air and microwave/vacuum drying,
Pharmaceutical Engineering 19 (2) (1999) 48 – 63.

[3] R. Poska, Integrated mixing granulating and microwave drying:

a development experience, Pharmaceutical Engineering 11 (1)
(1991) 9 – 13.

[4] H. Ni, A. Datta, K. Torrance, Moisture transport in intensitive

microwave heating of biomaterials: a multiphase porous media
model, International Journal of Heat and Mass Transfer 42
(1999) 1501 – 1512.

[5] M. Quintard, J. Puiggali, Numerical modelling of transport

processes during the drying of a granular porous medium, Heat
and Technology 4 (2) (1986) 37 – 57.

[6] J. Puiggali, M. Quintard, Properties and simplify assumptions

for classical drying models, Advances in drying 5 (1992) 109 –
142.

[7] I. Turner, P. Jolly, Combined microwave convective drying

porous media, Drying Technology 9 (5) (1991) 1209 – 1269.

[8] R. Perkin, Drying porous materials electromagnetic energy gen-

erated at radio and microwave frequencies, Progress in Filtration
and Separation 3 (1983) 205 – 266.

[9] R. Perkin, Heat and mass transfer characteristics of dielectrics

treting, In: International Conference on High Frequency Mi-
crowave Processing and Heating, 1989.

[10] R. Perkin, Simplified modelling for drying non hygroscopic

capillary porous body using combination dielectric convective
heating, Drying Technology 8 (5) (1990) 931 – 951.

[11] C. Wei, H. Davis, E. Davis, J. G], Heat and mass transfer in

water-laden sandstone: microwave heating, AIChE Journal 31
(5) (1985) 842 – 848.

[12] A. Hocine, Etude expe´rimentale du sechage par contact sous

vide de matenaux poreux simples., These de Doctorat, Institut
National Polytechnique de Lorraine (1985).

[13] C. Moyne, Transferts couple´s chaleur-masse lors du se´chage:

prise en compte du mouvement de la phase gazeuse., These de
Docteur-e´ s-Sciences, Institut National Polytechnique de Lor-
raine (1987).

[14] C. Pe´re´, E

´ tude du se´chage sous vide et sous micro-ondes de billes

de verre et de granule´s pharmaceutiques, These de Doctorat,
E

´ cole des Mines de Paris (1999).

[15] P. Jones, A. Rowley, Dielectric drying, Drying Technology 14

(5) (1996) 1063 – 1098.

[16] I. Turner, V. Rudolph, Convective and microwave enhanced

drying of glass beads, Proceedings of the 8th International
Drying Symposium, Vol. A, 1992, pp.553-572.

[17] F. Dullien, Porous Media: Fluid Transport and Pore Structure,

Academic Press, New York, 1979.

[18] R. Jowitt, P. Wagstaff, The certification of the water content of

microcrystalline cellulose (mcc) at 10 water activities, Tech. rep.,
Commission of European Communities, BCR Information
(1989).

[19] P. Perre, Transferts couple´s en miheux poreux non-sature´s.

possibilite´s et limitations de la formulation macroscopique,v
Habihtation a´ diriger des recherches, Institut National Polytech-
nique de Lorraine (1992).

[20] P. Jolly, I. Turner, Non linear solutions one dimensionnal mi-

crowave heating, Journal of Microwave Power and Electromag-
netic Energy 25 (1990) 3 – 15.

[21] C. Pe´re´, E. Rodier, O. Louisnard, J. Schwartzentruber, Investi-

gations on microwave and vacuum drying experiments: drying of
a model porous medium at laboratory scale, in: Proceeding of
the 12th International Drying Symposium, 2000, CD-ROM pa-
per 116.

[22] C. Pe´re´, E. Rodier, O. Louisnard, Microwave vacuum drying of

porous media: Verification of a semi empirical formulation of
the total absorbed power, Drying Technology 19 (5), in press.

[23] M. Sahota, P. Pagni, Heat and mass transfer in porous media

subject to fires, International Journal of Heat and Mass Transfer
22 (1979) 1069 – 1081.