jfpp_420

611..621

MODELING WITH SHRINKAGE DURING THE VACUUM DRYING

OF CARROT (DAUCUS CAROTA)

AROLDO ARÉVALO-PINEDO

1,3

, FERNANDA E. XIDIEH MURR

2

,

ZILDA D. SALLES ARÉVALO

1

and ABRAHAM D. GIRALDO-ZUÑIGA

1

1

Faculty of Food Engineering

Federal University of Tocantins (UFT)

Av. NS–15, ALC NO-14, CEP: 77123-360 Palmas, TO, Brazil

2

Faculty of Food Engineering

Campinas State University

PO Box 6121, Campinas, SP, Brazil

Accepted for Publication March 3, 2009

ABSTRACT

The drying kinetics of carrot slices have been measured in a vacuum

chamber, the experiments were carried out at various temperatures (50, 60
and 70C) under conditions of low pressures (5, 15 and 25 kPa). It was
observed that the best values of diffusivity were obtained at the major tem-
perature and low pressure for the samples pretreated by freezing. The
experimental data were modeled using Fick’s diffusional model in terms of
moisture concentration with and without shrinkage. It is found that the cal-
culated values of effective diffusivity for the drying process considering
no shrinkage were greater than those for the drying process considering
shrinkage.

PRACTICAL APPLICATIONS

Vacuum drying is the effective method of removal of moisture from fruits

and vegetables. In this research, the experimental study and modeling on
drying kinetics during the vacuum drying of carrot was studied. Also, the effect
of the pretreatments, pressure and temperature on the vacuum drying kinetics
was determined. A diffusion model based on Fick’s second law of diffusion
with and without shrinkage was used to describe the transport mechanism in
the falling drying rate regions. The results from this research can be used as

3

Corresponding author. FAX: [phone]; EMAIL: [e-mail]

Journal of Food Processing and Preservation 34 (2010) 611–621.
DOI: 10.1111/j.1745-4549.2009.00420.x

611

© 2010 Wiley Periodicals, Inc.

reference for vacuum drying and modeling kinetics drying of carrot and
vegetables.

INTRODUCTION

Vacuum drying is a unit operation in chemical and engineering processes,

in which moist material is dried under subatmospheric pressures. The lower
pressure allows drying temperature to be reduced and higher quality to be
obtained than with classical air process at atmospheric pressure (Fernando and
Thangavel 1987; Kompany et al. 1993; Jaya and Das 2003). The material
usually employed for vacuum drying are temperature-sensitive, easily oxidiz-
able, biotechnological products, etc. (Nastaj 1994; Bialobrzewski and Misiak
1997; Markowski and Bialobrzewski 1998).

A number of authors have suggested the physical predrying treatments of

solid food materials as means to both improve product quality and to modify
the structure of food raw material so as to improve mass transfer coefficients
in drying (Arévalo-Pinedo 2003).

Significant changes in chemical composition and structure can be

observed as water and other volatiles are removed from moist material. One
of the most important physical changes that the food suffers during drying is
the reduction of its external volume. Loss of water and heating cause
stresses in the cellular structure of the food leading to change in shape and
decrease in dimension (Major et al. 2004). Fruits and vegetables have
high initial moisture contents suffer alterations of their original form during
the drying process because of significant shrinkage. Animal and vegetable
cells exhibit a property denominated “turgor,” where liquid contained in the
cell wall creates pressure on the cell, compressing the liquid inside the
cell.

During the drying process, water leaves the cell causing a decrease in

the tension that the liquid exerts against the cell wall. This decrease in
tension causes shrinkage of the material. The quantification of this phenom-
enon is important because it allows the analysis of the drying kinetics and
consequently of the whole drying phenomenon. Shrinkage considerations in
drying models are hindered because there is no pertinent information about
shrinkage coefficients or functional relationships between shrinkage and
available mass diffusivities in the literature (Prado 1998).

This paper aims the experimental study and modeling on drying kinetics

during the vacuum drying of carrot samples. Comparison of the diffusivity
calculated values without and with considering the shrinkage is also an objec-
tive of this work.

612

A. ARÉVALO-PINEDO ET AL.

MATERIALS AND METHODS

Raw Material

Carrots (Daucus carota) were purchased from the local market hand-

peeled and washed in running tap water. The carrots were cut into slabs with
5-mm thickness, 40-mm length and 20-mm width. Slabs samples subjected to
water blanching were immersed in hot water at 95C for 5 min and then cooled
at room temperature. Slabs samples destined to be frozen were placed in a
freezer at

-20C for a period of 3 h. The frozen samples were then allowed to

thaw at room temperature.

Shrinkage and Vacuum Drying

Using the analogy between thermal expansion and shrinkage caused by

moisture content variation, Charm (1971) suggested a linear equation in order
to express the change in length as a function of moisture content. A linear
correlation between linear dimensions (length, width and thickness) and mois-
ture content was applied.

The drying equipment has been described in detail in a previous work

(Arévalo-Pinedo 2003). The equipment was designed to allow for various
temperatures and pressures inside the drying chamber and various shapes and
sizes of samples. Vacuum conditions were maintained by a vacuum pump and
monitored from a manometer. Two steel plates, heated by an electric resistance
lodged between them, provided the thermal energy. An automatic regulator
controlled the temperature of the plates.

Experimental methodology consisted in putting food samples on the hot

plate, the door of the chamber was closed, and the chamber was put under
vacuum. Carrot samples were withdrawn from the dryer at regular periods of
time and their weights determined by an analytical balance with a precision of
10

-5

g. For different experiments the temperature of the plate was set at 50, 60

and 70C, respectively; and the pressure of the chamber at 5, 15 and 25 kPa,
respectively.

Modeling of Drying

The method consists of an analysis of the drying process considering a

diffusional model. The differential equation based on Fick’s second law for the
diffusion of water during drying is

∂

∂

= ∇⋅

∇

(

)

W

t

D

W

ef

(1)

613

VACUUM DRYING MODEL FOR CARROT (DAUCUS CAROTA)

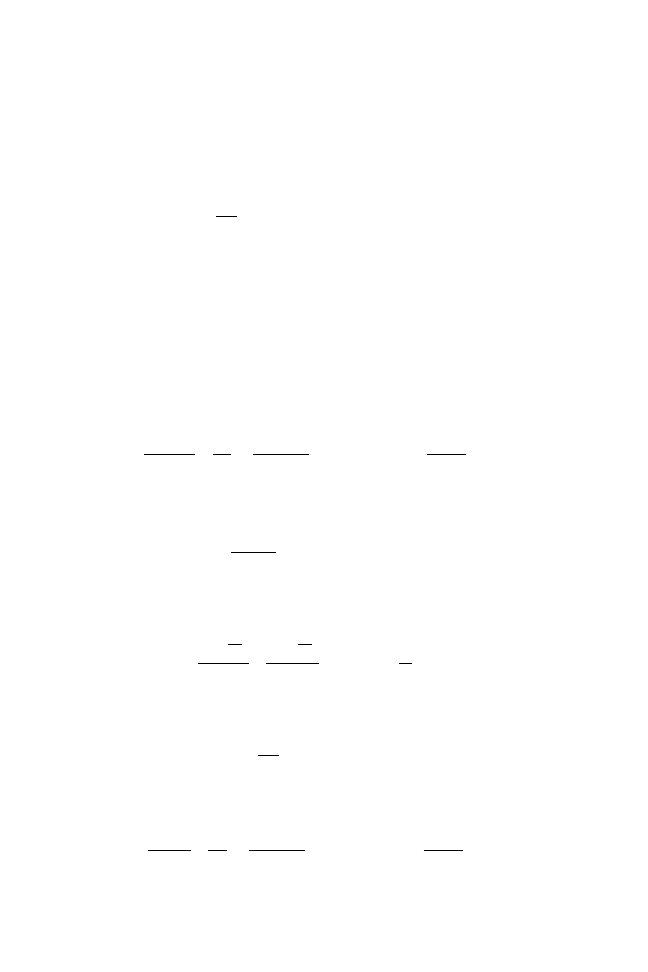
For the drying process, the concentration may be converted to moisture

content per unit of dry material. Considering shrinkage as negligible, Eq. (1)
could be expressed (Sherwood 1929) as

∂

∂

=

∇

(

)

=

∇

(

)

X

t

D

X

D

X

efx

efx

2

2

(2)

with t

= 0; X = X

o

; t

> 0; z = 0; ∂X/∂z = 0; t > 0; z = L; X = X

e

; and where D

efx

is

moisture diffusivity without shrinkage (m

2

/s), L is diffusional path (m), X is

moisture content (kg water/kg dry solid), X

e

is equilibrium moisture content at

the pressure condition prevailing, inside the vacuum dryer (kg water/kg dry
solid) and X

o

is initial moisture content of carrot (kg water/kg dry solid).

The evaporation through the side surfaces of the samples can be

neglected, because of the small superficial area of the side’s surfaces in
comparison with the two other surfaces. For the unidirectional diffusion in the
flat plate one may obtain (Crank 1975):

X

X

X

X

n

n

D

t

L

n

−

−

=

+

(

)

−

+

[

]

⋅

⎛

⎝⎜

⎞

⎠⎟

=

∞

∑

e

o

e

efx

8

1

2

1

2

1

2

2

2

2

2

0

π

π

exp

(3)

Adding the density of dry solid (

r

s

) in Eq. (1) we obtain

∂

∂

= ∇⋅

∇

[

]

(

)

(

)

ρ

ρ

s

ef

s

X

t

D

X

(4)

Or, for constant weight of dry solid (Park 1998; Uddin et al. 2004):

∂

( )

∂

=

∂

( )

∂

=

∇ ⎛⎝

⎞

⎠

X

X

V

t

X

X

V

t

X D

X

V

s

s

s

ef

2

(5)

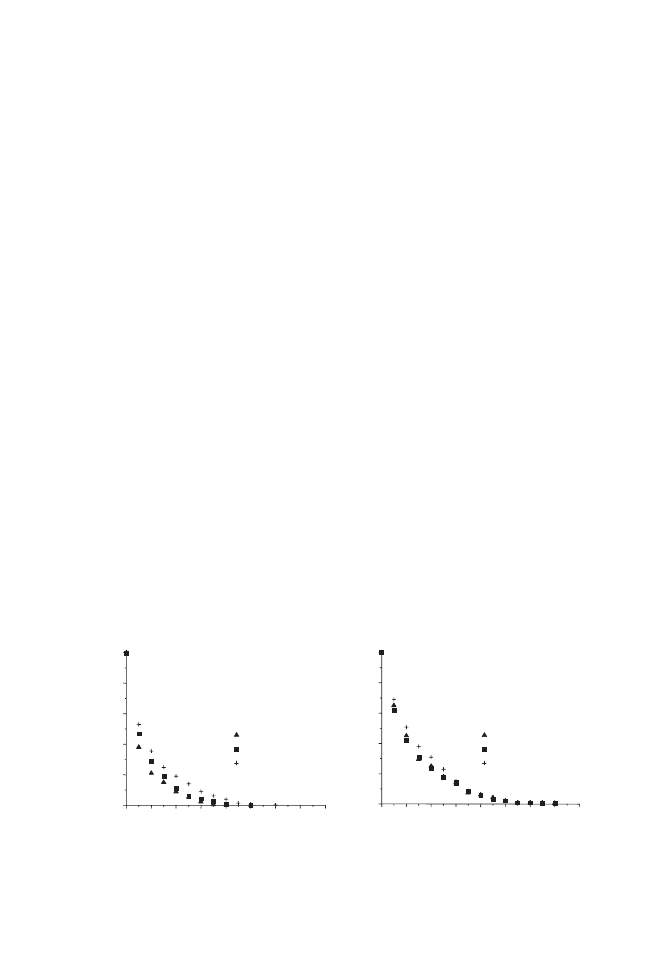
Substituting Y

= X/V (Park 1998), we have

∂

∂

=

∇

(

)

Y

t

D

Y

efy

2

(6)

with t

= 0; Y = X

o

/V

o

; t

> 0; z = 0; ∂Y/∂z = 0; t > 0; z = L; Y = X

e

/V

e

.

Y

Y

Y

Y

n

n

D

t

L

n

−

−

=

+

(

)

−

+

(

)

⋅

⎡
⎣⎢

⎤
⎦⎥

=

∞

∑

e

o

e

efy

8

1

2

1

2

1

2

2

2

2

2

0

π

π

exp

(7)

614

A. ARÉVALO-PINEDO ET AL.

where D

efy

is the effective diffusivity considering the shrinkage (m

2

/s) and V is

the sample volume (m

3

).

RESULTS AND DISCUSSION

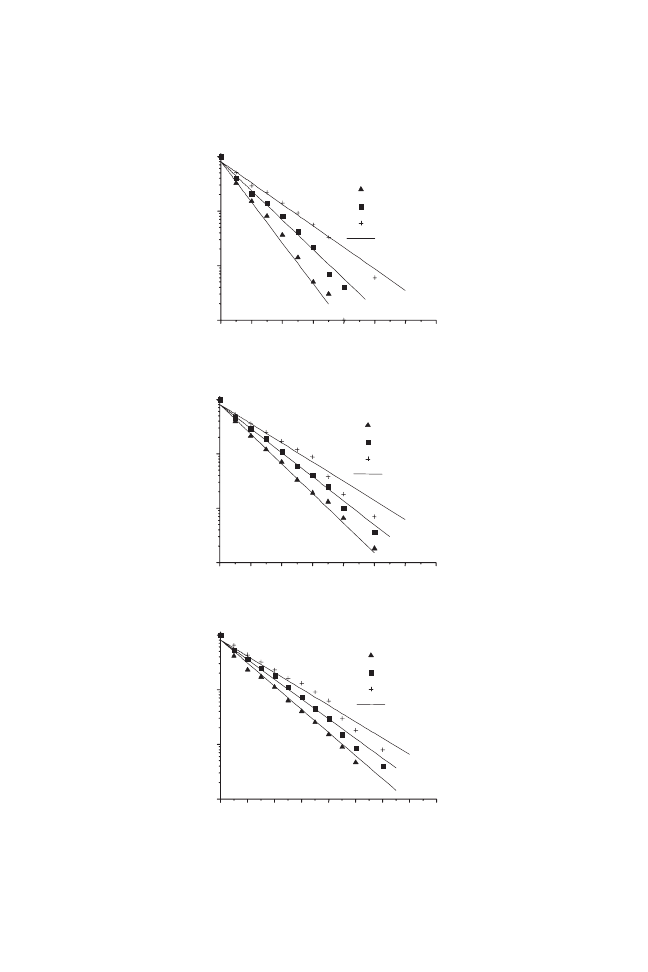
Effect of Pretreaments on Drying Rate

Figure 1 show the vacuum drying kinetic of carrot samples with pretreat-

ments and in nature at 60C and 5 and 25 kPa, respectively. These figures show
the effects of pretreatments and pressures on the drying rate, it can be observed
that both pretreatments increases the drying rate, and freezing had a more
significant influence than blanching on the rate of moisture transport in carrots.
The biggest loss of water occurred for samples with freezing pretreatment and
lowest pressure.

The overall drying velocity of carrots dried after the application of freez-

ing pretreatment was significantly faster than those of pretreatment where
freezing was not involved. This indicates that in order to increase the drying
kinetic, this vegetables need to be frozen as part of any pretreatment. The
higher drying kinetics and shorter drying time of samples freezing prior to
drying is because freezing causes cell disruption, which allows moisture to be
removed more easily (Mazza 1983; Eshtiaghi et al. 2003).

The effect of pressure on drying rate for carrot is also observed. In

general, there is increase in drying rate with the decrease of pressure and type
of pretreatment applied (Kompany et al. 1993). An increase in the drying rate
was observed with decrease of pressure, however, it is noted that the drying
rate does not depend on the pretreatments at high pressure for carrots.

8

0,0

0,2

0,4

0,6

0,8

1,0

P = 5 kPa
T = 60

o

C

C. prefrozen
C. blanched
C. in nature

(X -

Xe

) /

(

X

o

-

Xe

)

Time ( h )

Time ( h )

0,0

0,2

0,4

0,6

0,8

1,0

P = 25 kPa
T = 60

o

C

C. prefrozen
C. blanched
C. in nature

(X -

Xe

) /

(

X

o

-

Xe

)

0

1

2

3

4

5

6

7

8

0

1

2

3

4

5

6

7

FIG. 1. EFFECT OF PRETREATMENTS ON DRYING KINETICS OF CARROT AT

TEMPERATURE 60C AND PRESSURES 5 AND 25 kPa, RESPECTIVELY

615

VACUUM DRYING MODEL FOR CARROT (DAUCUS CAROTA)

The time required to dry the carrot samples is considerably reduced by

freezing and lowest pressure. It may be observed from Fig. 1 that for prefrozen
carrot, the time to reduce the moisture content ratio of 0.05 at 60C were 3 h at
5 kPa and 5.5 h at 25 kPa, respectively.

Moisture Diffusivities

Diffusivity parameters were evaluated based on diffusional models

without shrinkage (Eq. 3) and with shrinkage (Eq. 7), as shown in Tables 1 and
2, Figs. 2 and 3. In the tables it can be seen that effective moisture diffusivity
varies not only with pressures and temperature but also with pretreatment.
Prefrozen samples have shown higher diffusivity values in comparison with
blanching and in nature samples. It is evident what diffusivity has a tendency
to increase with decrease of pressure because of air expansion caused by the
vacuum and water vapor present in food, creating a puffed structure. This
expanded structure provides large area to volume ratio for good heat and mass
transfer facilitating the water transport, consequently increasing drying rate
and diffusivity (Drouzas et al. 1999; Jaya and Das 2003).

Observing the values on Tables 1 and 2 one can also see that the calcu-

lated values of diffusivity with shrinkage of the sample D

efy

are smaller than

the values of diffusivity without shrinkage D

efx

. This demonstrates that the

diffusivity calculated without consideration of the shrinkage phenomenon
overestimates the mass transfer by diffusion. This fact was also observed by
Araújo et al. (2004) for nectarine and by Park (1998) who studied the drying
of salted fish muscle.

TABLE 1.

VALUES OF EFFECTIVE DIFFUSIVITY DURING VACUUM DRYING OF CARROT SLABS

AT DIFFERENT PRESSURES AND TEMPERATURES BASED ON EQ. (3)

P (kPa)

T (C)

Freezing

Blanching

In nature

D

efx

·10

9

(m

2

/s)

R

2

E (%)

D

efx

·10

9

(m

2

/s)

R

2

E (%)

D

efx

·10

9

(m

2

/s)

R

2

E (%)

5

70

4.84

0.98

1.57

3.54

0.98

1.63

2.74

0.98

1.65

60

3.49

0.98

1.70

2.87

0.99

1.81

2.34

0.98

1.73

50

2.53

0.95

2.53

2.27

0.95

2.84

1.94

0.95

2.66

15

70

3.61

0.96

1.68

2.63

0.96

2.05

2.26

0.96

1.85

60

2.70

0.95

1.82

2.20

0.97

1.94

1.84

0.96

1.84

50

2.17

0.95

2.41

1.94

0.95

1.99

1.47

0.96

2.66

25

70

2.17

0.97

1.60

2.34

0.97

1.92

2.02

0.96

1.92

60

1.93

0.95

2.03

1.66

0.97

2.13

1.54

0.96

2.01

50

1.65

0.95

2.63

1.27

0.95

3.01

1.47

0.95

3.17

P, pressure (kPa); T, temperature (C).

616

A. ARÉVALO-PINEDO ET AL.

With regard to diffusivity, its value decreased from 3.40

¥ 10

-9

to

1.12

¥ 10

-9

m

2

/s for carrots prefrozen, 2.18

¥ 10

-9

to 1.13

¥ 10

-9

m

2

/s for

carrots blanched and 1.73

¥ 10

-9

to 1.11

¥ 10

-9

m

2

/s for carrots in nature when

pressure increased from 5 to 25 kPa; the obtained values are in the comparable
range for similar dried vegetables products reported in the literature (Kiranou-
dis et al. 1993; Kompany et al. 1993).

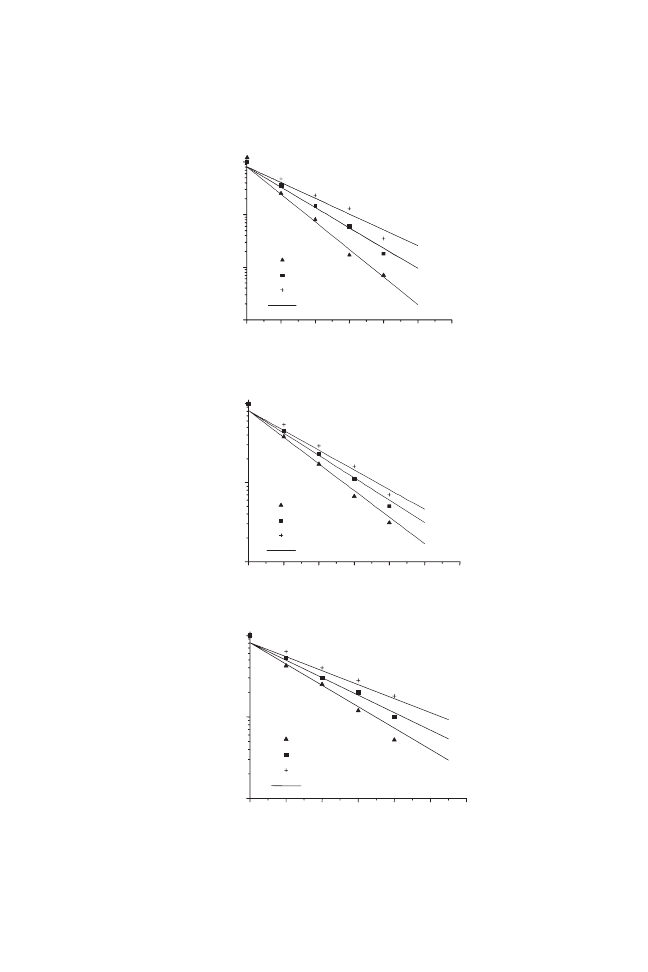
The good agreement of the diffusion model with the experimental data is

observed, which indicates that the equation based on Fick’s law may be used
to predict the moisture diffusion of carrot, which was evident in Figs. 2 and 3.

CONCLUSION

Major factors affecting the drying kinetics of carrot slabs were freezing

pretreatment and pressure of drying chamber. The diffusional model with and
without considering the shrinkage with three terms of the Fourier series proved
to be excellent fits for the drying curves of carrots. The calculated values of
diffusivity for the vacuum drying considering no shrinkage were greater than
those for the drying process considering the shrinkage.

ACKNOWLEDGMENTS

This work was supported by CAPES (Conselho Nacional de Pesquisa e

Aperfeiçoamento de Pessoal Superior) and the Faculty of Food Engineering –
UNICAMP, Campinas, SP, Brazil.

TABLE 2.

VALUES OF EFFECTIVE DIFFUSIVITY DURING VACUUM DRYING OF CARROT SLABS

AT DIFFERENT PRESSURES AND TEMPERATURES BASED ON EQ. (7)

P (kPa)

T (C)

Freezing

Blanching

In nature

D

efx

·10

9

(m

2

/s)

R

2

E (%)

D

efx

·10

9

(m

2

/s)

R

2

E (%)

D

efx

·10

9

(m

2

/s)

R

2

E (%)

5

70

3.40

0.98

1.88

2.18

0.98

1.96

1.73

0.98

1.99

60

2.66

0.97

1.94

1.83

0.97

1.92

1.41

0.97

1.80

50

1.94

0.97

2.86

1.64

0.96

2.04

1.13

0.97

1.75

15

70

2.13

0.97

1.94

1.22

0.97

1.83

1.26

0.97

1.88

60

1.20

0.97

1.88

1.47

0.97

1.70

1.14

0.96

1.97

50

1.42

0.96

1.77

1.42

0.97

1.80

1.12

0.97

1.83

25

70

1.47

0.97

1.97

1.40

0.97

1.67

1.19

0.98

1.75

60

1.18

0.97

2.04

1.28

0.96

2.41

1.36

0.97

2.01

50

1.12

0.96

2.91

1.13

0.96

2.33

1.11

0.96

2.18

P, pressure (kPa); T, temperature (C).

617

VACUUM DRYING MODEL FOR CARROT (DAUCUS CAROTA)

0

1

2

3

4

5

6

7

0,001

0,01

0,1

1

P = 5 kPa

a

b

c

70

o

C

60

o

C

50

o

C

eqn (3)

(X

- X

e

) /

(

X

o

-

X

e

)

Time ( h )

Time ( h )

Time ( h )

0

1

2

3

4

5

6

7

0,001

0,01

0,1

1

P = 5 kPa

70

o

C

60

o

C

50

o

C

eqn (3)

(X

-

X

e

)

/

(X

o

-

X

e

)

0

1

2

3

4

5

6

7

8

0,001

0,01

0,1

1

P = 5 kPa

70

o

C

60

o

C

50

o

C

eqn (3)

(X

- X

e

)

/ (X

o

- X

e

)

FIG. 2. MODELING OF VACUUM DRYING KINETICS AT DIFFERENT TEMPERATURES

AND CONSTANT PRESSURE FOR CARROT SAMPLES

(a) Prefrozen. (b) Blanched. (c) In nature.

618

A. ARÉVALO-PINEDO ET AL.

0

1

2

3

4

5

6

0,001

0,01

0,1

a

b

c

1

P = 5 kPa

70 C
60 C
50 C
Eqn (7)

(Y

- Y

e

) /

(Y

o

-

Y

e

)

Time ( h )

Time ( h )

Time ( h )

0

1

2

3

4

5

6

0,01

0,1

1

P = 5 kPa

70 C
60 C
50 C
Eqn (7)

(Y

-

Y

e

) /

(

Y

o

-

Y

e

)

0

1

2

3

4

5

6

0,01

0,1

1

P = 5 kPa

70 C
60 C
50 C
Eqn (7)

(Y -

Ye)

/

(Yo

-

Ye)

FIG. 3. MODELING VACUUM DRYING KINETICS BASED ON EQ. (7) AT DIFFERENT

TEMPERATURES AND PRESSURE OF 5 kPa FOR CARROT SAMPLES

(a) Prefrozen. (b) Blanched. (c) In nature.

619

VACUUM DRYING MODEL FOR CARROT (DAUCUS CAROTA)

REFERENCES

ARAÚJO, E.A.F., RIBEIRO, S.C.A., AZOUBEL, P.M. and MURR, F.E.X.

2004. Drying kinetics of nectarine (Prunus persica) with and without
shrinkage. Proceedings of the 14th International Drying- Symposium,
São Paulo, Brazil.

ARÉVALO-PINEDO, A. 2003. Vacuum drying of carrot (Daucus carota) and

pumpkin (Cucurbita maxima): Study of the characteristics of process.
PhD Thesis, Campinas, UNICAMP.

BIALOBRZEWSKI, I. and MISIAK, W. 1997. A stand for investigation of

vacuum-drying kinetics – Short report. Pol. J. Food Nutr. Sci. 6/47(3),
133–138.

CHARM, S.E. 1971. Dehydration of foods. In The Fundamentals of Food

Engineering, 2nd Ed., The AVI Publishing Company, Westport, CT.

CRANK, J. 1975. The Mathematics of Diffusion, 2nd Ed., p. 114, Claredon

Press, Oxford.

DROUZAS, A.E., TSAMI, E., SARAVACOS, G.D. 1999. Microwave/vacuum

drying of model fruit gel. J. Food Eng. 39, 117–122.

ESHTIAGHI, M.N., STUTE, R. and KNORR, D. 2003. High pressure and

freezing pretreatment effects on drying, rehydration, texture and color of
green beans, carrots and potatoes. J. Food Sci. 59, 1168–1170.

FERNANDO, W.J.N. and THANGAVEL, T. 1987. Vacuum drying character-

istics of coconut. Drying Technol. 5(3), 363–372.

JAYA, S. and DAS, H. 2003. A vacuum drying model for mango pulp. Drying

Technol. 21(7), 1215–1234.

KIRANOUDIS, C.T., MAUROLIS, Z.B. and MARINOS-KOURIS, D. 1993.

Mass transfer model building in drying. Drying Technol. 11(6), 1251–
1270.

KOMPANY, E., BENCHIMOL, J., ALLAF, K., AINSEBA, B. and

BOUVIER, J.M. 1993. Carrot dehydration for instant rehydration: Dehy-
dration kinetics and modeling. Drying Technol. 11(3), 451–470.

MAJOR, L., SILVA, M.A. and SERENO, A.M. 2004. Effect of drying on

cellular structure of apple tissue. Proceeding of the 14th International
Drying Symposium, pp. 1876–1883, São Paulo, Brazil.

MARKOWSKI, M. and BIALOBRZEWSKI, I. 1998. Kinetics of vacuum

drying of celery. Pol. J. Food Nutr. Sci. 7/48(4), 707–712.

MAZZA, G. 1983. Dehydration of carrots: Effects of pre-drying treatments on

moisture transport and product quality. J. Food Technol. 18, 113–123.

NASTAJ, J.F.A. 1994. A mathematical model for the continous vacuum drying

of highly viscous foodstuffs. Drying Technol. 7(1), 47–58.

PARK, K.J. 1998. Diffusional model with and without shrinkage during salted

fish muscle drying. Drying Technol. 16(3–5), 889–905.

620

A. ARÉVALO-PINEDO ET AL.

PRADO, M.E.T. 1998. Drying of dates (Phoenix dactyulifera L.) to obtain

dried date. Master’s Degree Thesis, Campinas, UNICAMP.

SHERWOOD, T.K. 1929. The drying of solids I. Ind. Eng. Chem. 21(1),

12–16.

UDDIN, M.S., HAWLADER, M.N.A. and HUI, X. 2004. A comparative study

on heat pump, microwave and freeze drying of fresh fruits. Proceeding of
the 14th International Drying Symposium, p. 2035–2042, São Paulo,
Brazil.

621

VACUUM DRYING MODEL FOR CARROT (DAUCUS CAROTA)

Copyright of Journal of Food Processing & Preservation is the property of Wiley-Blackwell and its content may

not be copied or emailed to multiple sites or posted to a listserv without the copyright holder's express written

permission. However, users may print, download, or email articles for individual use.