KOD
ZDAJĄCEGO
Miejsce na identyfikację szkoły
LISTOPAD
2010
Za rozwiązanie
wszystkich zadań
można otrzymać
łącznie 50 punktów.
PESEL ZDAJĄCEGO
Wpisuje zdajàcy przed rozpocz´ciem pracy
ARKUSZ PRÓBNEJ MATURY
Z OPERONEM
MATEMATYKA
POZIOM PODSTAWOWY
Czas pracy 170 minut
In struk cja dla zda ją ce go
1.
Sprawdź, czy ar kusz eg za mi na cyj ny za wie ra 16 stron
(za da nia 1–34). Ewen tu al ny brak zgłoś prze wod ni czą -
ce mu ze spo łu nad zo ru ją ce go eg za min.
2.
Roz wią za nia zadań i od po wie dzi za pisz w miej scu
na to prze zna czo nym.
3.
W roz wią za niach za dań ra chun ko wych przed staw tok
ro zu mo wa nia pro wa dzą cy do osta tecz ne go wy ni ku.
4.
Pisz czy tel nie; uży waj dłu go pi su/pió ra tyl ko z czar nym
tu szem/atra men tem.
5.
Nie uży waj ko rek to ra, a błęd ne za pi sy wy raź nie prze -
kreśl.
6.
Za pi sy w brud no pi sie nie będą oce niane.
7.
Obok numeru każdego zadania podana jest maksymalna
liczba punktów możliwych do uzyskania.
8. Możesz ko rzy stać z zestawu wzorów matematycznych,
cyrkla i li nij ki oraz kal ku la to ra.
Życzymy powodzenia
!
Arkusz opracowany przez Wydawnictwo Pedagogiczne OPERON.
Kopiowanie w całości lub we fragmentach bez zgody wydawcy zabronione. Wydawca zezwala na kopiowanie zadań
przez dyrektorów szkół biorących udział w programie Próbna Matura z OPERONEM.
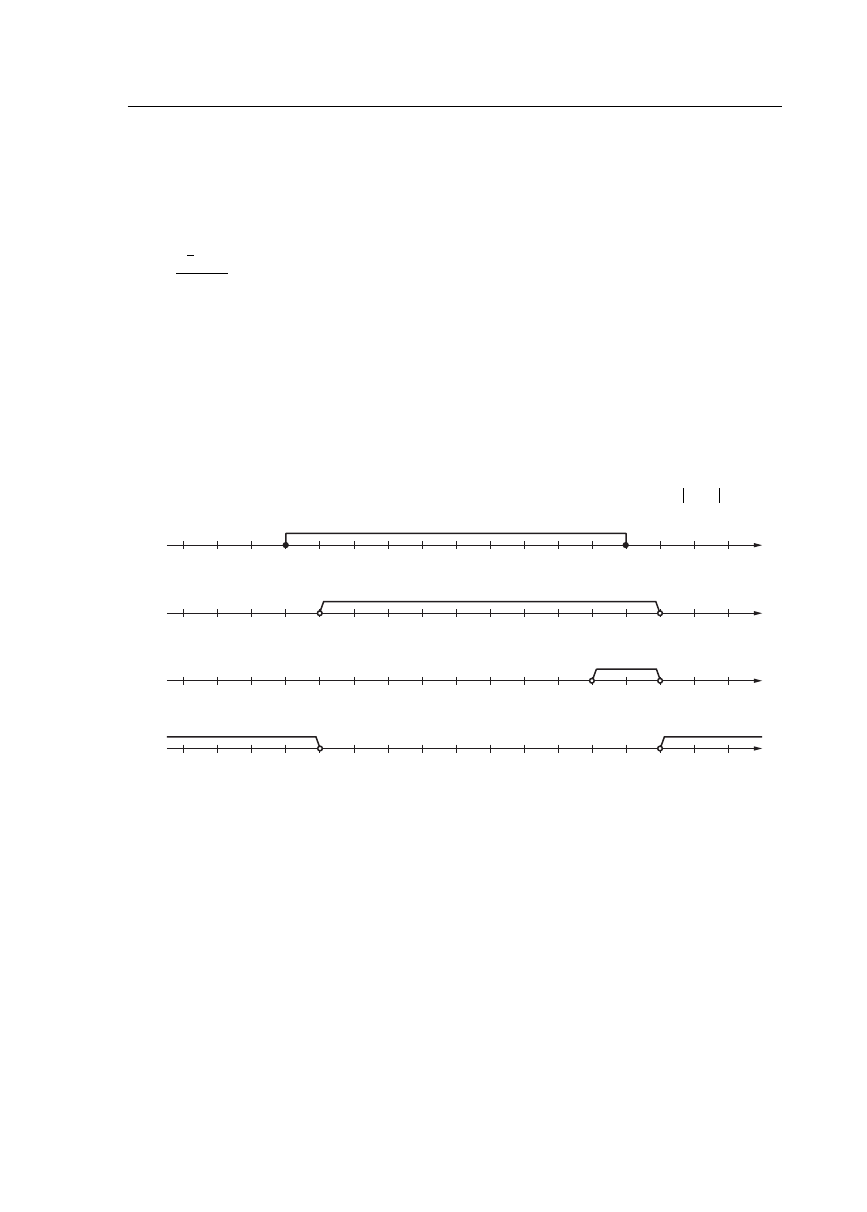
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
ZA DA NIA ZA MKNIĘ TE
W zadaniach od 1. do 25. wybierz i zaznacz poprawną odpowiedź.
Zadanie 1. (1 pkt)
Liczba jest
równa
A. 1
B. –1
C. 2
D. 4
Zadanie 2. (1 pkt)
Liczba jest
równa
A.
B.
C. 2
D. 9
Zadanie 3. (1 pkt)
Wybierz i zaznacz rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności
.
Zadanie 4. (1 pkt)
Stół kosztował 320 zł. Ile kosztuje stół po podwyżce ceny o
?
A. zł
B. zł
C. zł
D. zł
Zadanie 5. (1 pkt)
Dane są wielomiany
oraz
. Wielomian
jest
równy
A. B. C. D.
,
4
0 5
4
4
0
2
1
1
$
-
-
36
4
log
log
3
3
-
32
log
3
144
log
3
5
x
1 <
-
%
20
384
256
340
400
( )
( )
W x
M x
-
( )
M x
x
x
2
5
3
2
=
-
+
( )
W x
x
x
3
2
4
3
2
=
-
+
x
4
9
3
+
x
2
1
3
+
x
2
1
3
-
x
x
4
4
9
3
2
-
+
X
– 6
– 7
– 8
A.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8
X
– 6
– 7
– 8
B.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8
X
– 6
– 7
– 8
C.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8
X
– 6
– 7
– 8
D.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8
2

BRUD NO PIS
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
3
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Zadanie 6. (1 pkt)
Funkcja liniowa
ma miejsce zerowe równe . Zatem
A. B. C. D.
Zadanie 7. (1 pkt)
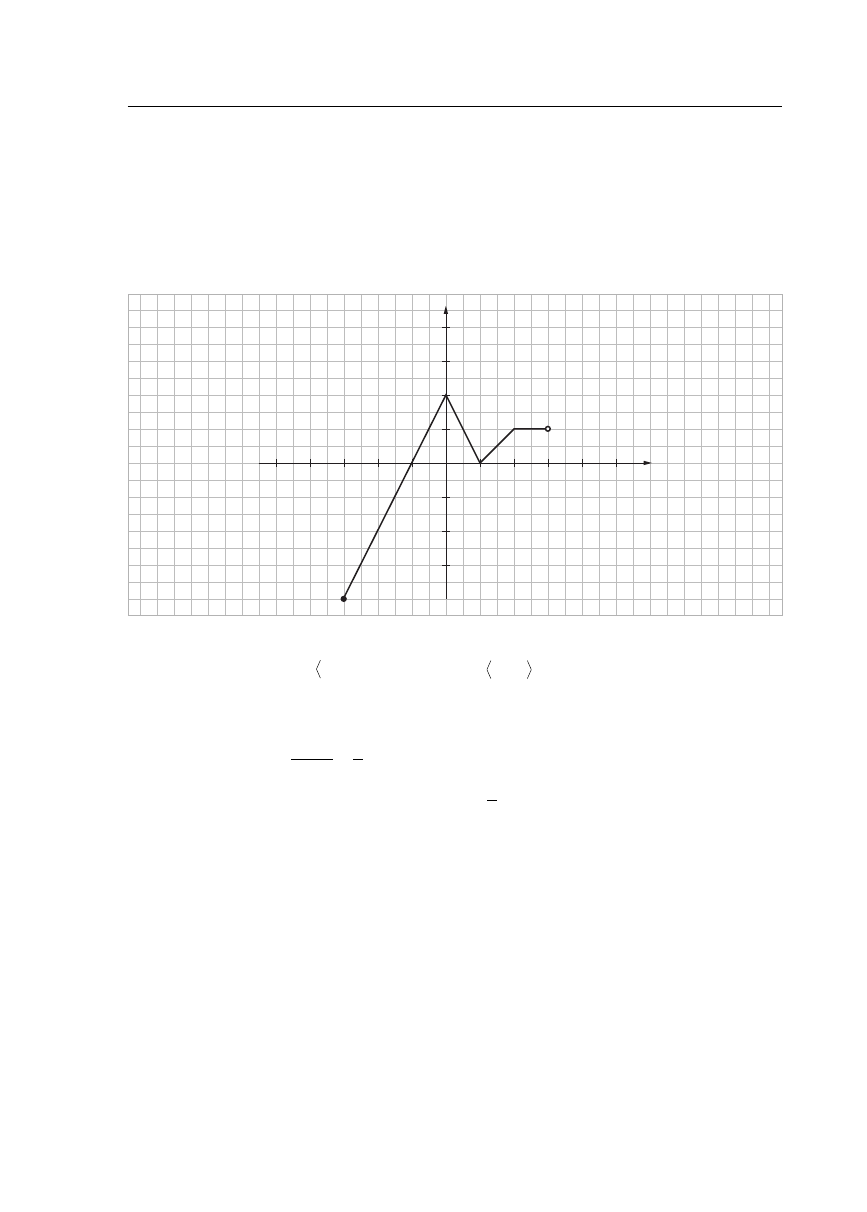
Na rysunku jest przedstawiony wykres funkcji
.
Zbiór wartości tej funkcji to
A. B. C. D.
Zadanie 8. (1 pkt)
Rozwiązaniem równania
jest liczba
A. 8
B.
C.
D.
Zadanie 9. (1 pkt)
Równanie
A. ma trzy pierwiastki
B. ma dwa pierwiastki
C. ma jeden pierwiastek
D. nie ma pierwiastków
Zadanie 10. (1 pkt)
Zbiorem rozwiązań nierówności
jest zbiór
A. B. C. D.
2
( )
(
1)
5
f x
m
x
=
-
+
6
m =
1,5
m = -
1
m =
5
m =
( )
y
f x
=
X
Y
1
– 3
– 2
– 1
0
2
3
4
– 5
– 4
– 3
– 2
– 1
2
1
3
4
5
(
, 3)
3
-
,
4 2
-
,
3 3
-
h
(
1, 3)
-
x
x
2
4
6
3
2
-
-
=
10
-
2
1
10
6
9
1
x
x
2
+
+
= -
x
x
1
2
0
>
-
+
^
^
h
h
,
1 2
-
^
h
,
,
1
2
,
3
3
-
-
]
]
g
g
,
2 1
-
^
h
,
,
2
1
,
3
3
-
-
]
]
g
g
4

BRUD NO PIS
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
5

Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Zadanie 11. (1 pkt)
Wykres funkcji kwadratowej
ma dwa punkty wspólne z prostą o równaniu
A. B. C. D.
Zadanie 12. (1 pkt)
Iloraz ciągu geometrycznego
jest równy
oraz
. Wtedy wyraz
jest równy
A. B. C. D.
Zadanie 13. (1 pkt)
W ciągu arytmetycznym
dane są:
i
. Wtedy wyraz
jest równy
A. B. C. D.
Zadanie 14. (1 pkt)
Suma miar kątów pewnego wielokąta wypukłego jest równa
. Tym wielokątem jest
A. czworokąt
B. siedmiokąt
C. pięciokąt
D. sześciokąt
Zadanie 15. (1 pkt)
Kąt
jest ostry i
. Wartość wyrażenia
jest
A. mniejsza od
B. równa 1
C. większa od
D. równa
Zadanie 16. (1 pkt)
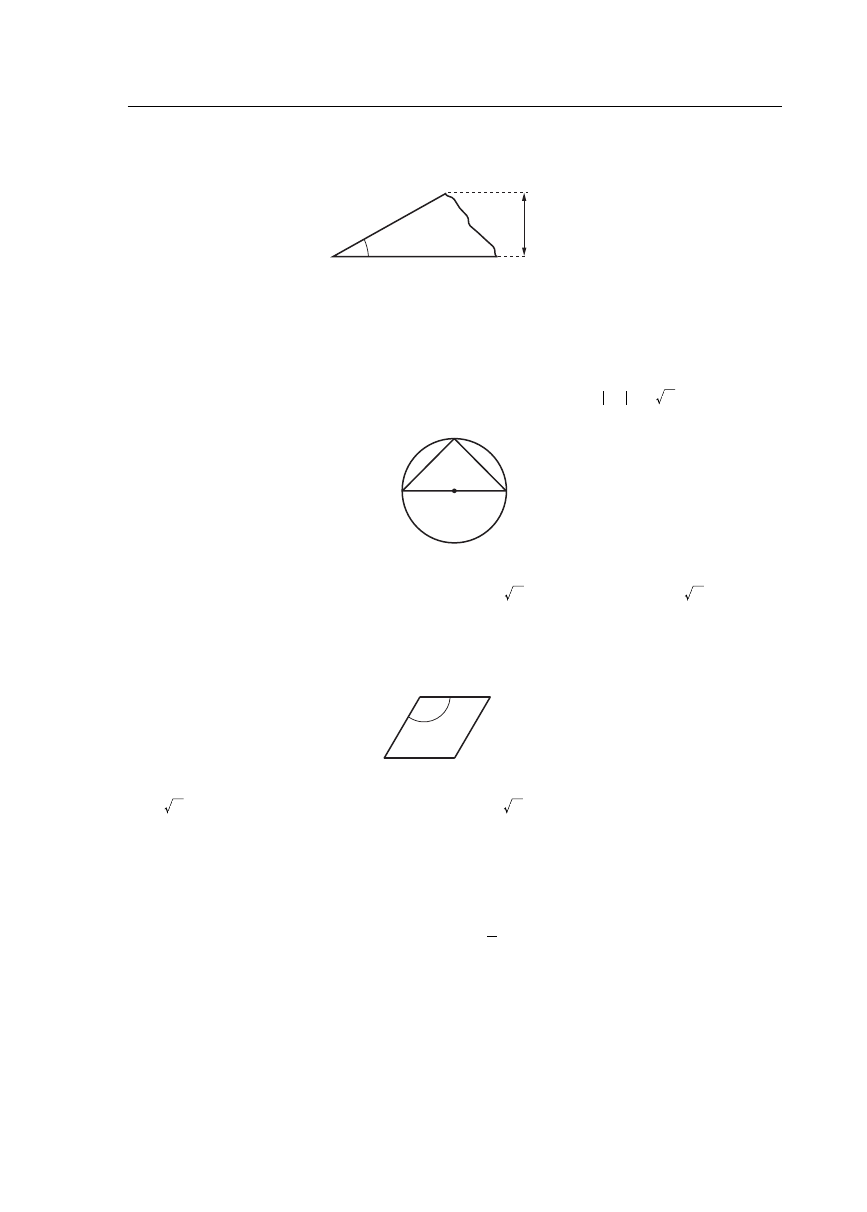
Trapez prostokątny ma wymiary podane na rysunku.
Wysokość tego trapezu jest równa
A. B. C. D.
Zadanie 17. (1 pkt)
Wysokość trójkąta równobocznego jest równa . Pole tego trójkąta jest równe
A. B. C. D.
( )
1
f x
x
2
= -
+
1
x = -
1
x =
y
1
= -
y
1
=
a
5
4
a
2
= -
2
1
a
n
^ h
2
1
2
-
2
1
-
2
a
3
3
a
4
=
1
a
2
= -
a
n
^ h
1
0
2
3
-
°
540
sin
cos
2
a
a
+
cos
3
1
a =
a
1
-
1
0
3
6
5
4
1
3
3
4
3
3
2
3
6
6
9
5

BRUD NO PIS
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
7
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Zadanie 18. (1 pkt)
Na szczyt góry o wysokości względnej
m prowadzi droga długości
km.
Miara kąta , jaki tworzy droga na szczyt z podstawą góry, jest równa
A. B. C. D.
Zadanie 19. (1 pkt)
W okrąg o średnicy
wpisano trójkąt równoramienny
, w którym
.
Długość tego okręgu jest równa
A. B. C. D.
Zadanie 20. (1 pkt)
Romb ma wymiary podane na rysunku.
Pole tego rombu jest równe
A. B. C. D.
Zadanie 21. (1 pkt)
Współczynnik kierunkowy prostej równoległej do prostej o równaniu
jest równy
A. B. C. D.
Zadanie 22. (1 pkt)
Środek okręgu o równaniu
leży w punkcie
A. B. C. D.
6
CB
2
=
ABC
AB
36r
12r
6
2
r
12
2
r
72 3 cm
2
64 cm
2
32 3 cm
2
128 cm
2
4
2
1
0
x
y
-
+
=
4
2
-
2
1
2
(
2)
1
x
y
2
2
+
+
=
(0,
2)
S =
-
(0, 2)
S =
(2, 0)
S =
,
S
1
2
=
-
]
g
°
45
°
60
°
30
°
15
0,5
250
a
0,5 km
a
250 m
A
C
B
8 cm
120°
8

BRUD NO PIS
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
9

Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Zadanie 23. (1 pkt)
Punkty
i
są wierzchołkami kwadratu
. Obwód tego kwadratu jest równy
A. B. C. D.
Zadanie 24. (1 pkt)
Stosunek długości krawędzi prostopadłościanu jest równy
. Pole powierzchni całkowitej tego
prostopadłościanu jest równe
. Suma długości tych trzech krawędzi prostopadłościanu jest zatem
równa
A. B. C. D.
Zadanie 25. (1 pkt)
Średnia arytmetyczna wzrostu czterech chłopców jest równa
cm. Chłopcy mają:
cm,
cm,
cm,
cm. Najwyższy chłopiec mierzy
A. cm
B. cm
C. cm
D. cm
BRUD NO PIS
180
190
195
185
170
150
170
x
185
5
12
6
8
1 : 2 : 3
88
KLAM
,
L
6
4
=
-
]
g
,
K
0 4
=
]
g
40
10
100
24
10

ZADANIA OTWARTE
Rozwiązania zadań o numerach od 26. do 34. należy zapisać w wyznaczonych miejscach pod treścią
zadania.
Zadanie 26. (2 pkt)
Rozwiąż równanie
.
Odpowiedź: .......................................................................................................................................................
Zadanie 27. (2 pkt)
Rozwiąż nierówność
.
Odpowiedź: .......................................................................................................................................................
x
3
0
>
2
x
5
+
-
^
^
h
h
2
6
12
0
x
x
x
3
2
+
-
-
=
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
11

Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Zadanie 28. (2 pkt)
Wykaż, że jeżeli
, to równanie
ma dwa pierwiastki.
Zadanie 29. (2 pkt)
Wykaż, że jeżeli
jest kątem ostrym i
, to
jest liczbą niewymierną.
(
1)
0
x
k x
2
+
-
=
0
k >
cos a
2
tg a =
a
12
Zadanie 30. (2 pkt)
W trójkącie prostokątnym
na boku
obrano punkt
oddalony od punktu
o
i od punktu
o . Przez punkt
poprowadzono prostą równoległą do boku
, przecinającą bok
w punkcie
. Oblicz długość odcinka
.
Odpowiedź: .......................................................................................................................................................
Zadanie 31. (2 pkt)
W trapezie równoramiennym miara kąta ostrego jest równa
, a podstawy mają długości:
cm i
cm.
Oblicz pole trapezu.
Odpowiedź: .......................................................................................................................................................
6
A
D
AB
ABC
BC
AC
D
4
B
DE
E
A
12
C
B
10
16
45°
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
13

Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Zadanie 32. (4 pkt)
W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe
, a pole ściany bocznej jest
równe
. Oblicz objętość ostrosłupa.
Odpowiedź: .......................................................................................................................................................
100
65
14
Zadanie 33. (4 pkt)
W pudełku znajduje się kul białych i czarne. Wyciągamy z niego jedną kulę, odkładamy ją i losujemy
drugą kulę. Oblicz prawdopodobieństwo, że wyciągniemy kule różnych kolorów.
Odpowiedź: .......................................................................................................................................................
Zadanie 34. (5 pkt)
Iloczyn pewnej liczby i liczby o 1 od niej większej jest równy . Oblicz sumę tych liczb.
Odpowiedź: .......................................................................................................................................................
2
6
6
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
15

Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
BRUD NO PIS (nie pod le ga oce nie)
16
Wyszukiwarka
Podobne podstrony:
j pol ark pods
WISL Pods I cyklu AT
2 1 I B 03 ark 02 zbiorczy plan kolizji
Inwentaryzacja Ark 14 plan sytułacyjny
j ang ark pdst
kol pods 0 pop 1
2 1 V 1 02 ark 12
2 1 V 1 02 ark 07id 20006 Nieznany
OPERON 2014 Teatr klucz
Krakow nowapr2 Nowa ark I proba Nieznany
więcej podobnych podstron