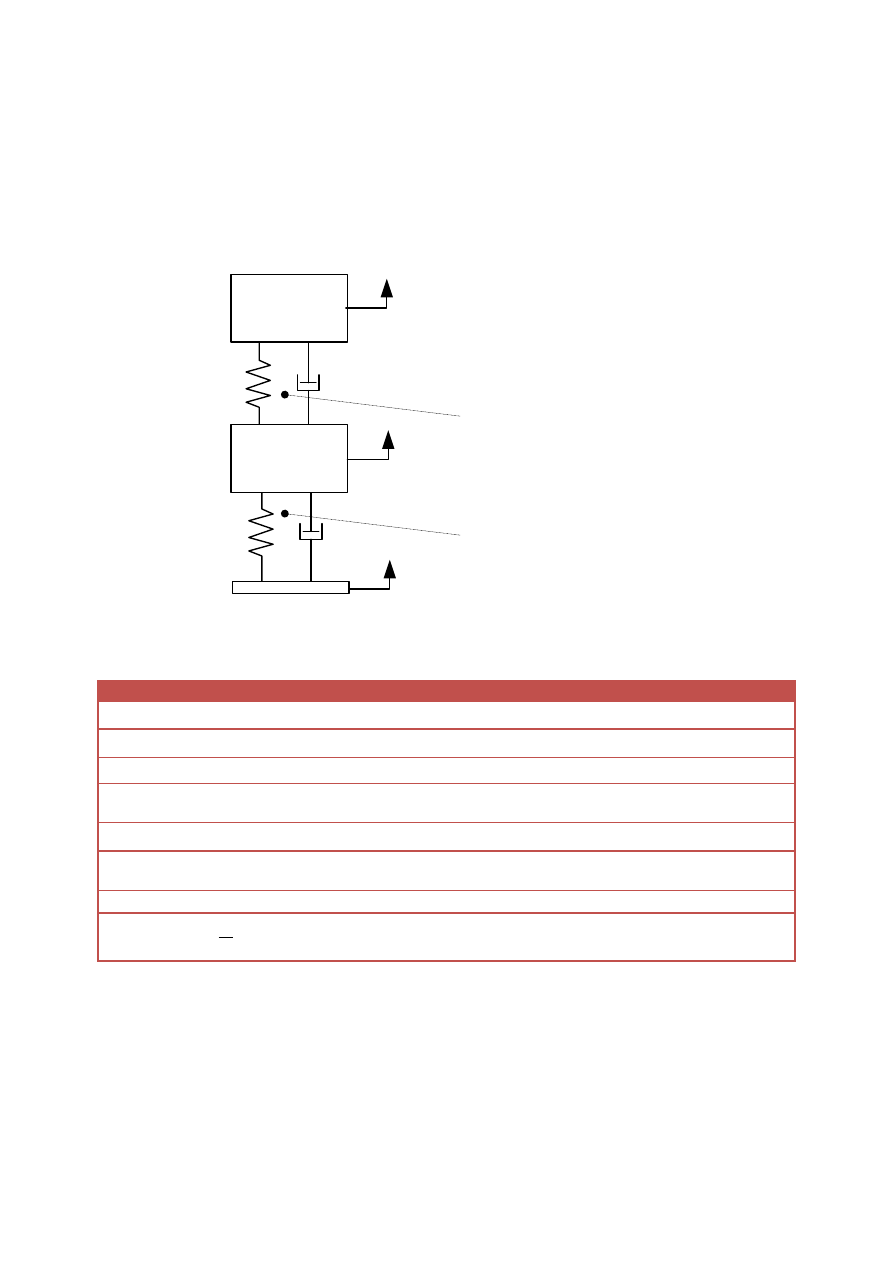
1. Model dynamiczny siedzenia kierowcy.
Poniżej przedstawiono schemat układu kierowca-fotel. W pierwszym stopniu
zawieszenia amortyzowany jest fotel kierowcy, natomiast drugi stopień zawieszenia
odwzorowuje oddziaływanie fotela na kierowcę.
w t
1
x
2
x
1
b
2
c
2
b
1
c
1
m
2
m
Pierwszy stopień
zawieszenia
Drugi stopień
zawieszenia
2. Dane
Symbol i wartość
Opis
1
80
m
kg
masa kierowcy
2
30
m
kg
masa siedzenia
0,15
f
m
całkowite ugięcie statyczne sprężyn
0,15
f
k
współczynnik udziału pierwszego stopnia zawieszenia w
całkowitym ugięciu
1
0, 05
bezwymiarowy współczynnik tłumienia drugiego stopnia
2
0,8
bezwymiarowy współczynnik tłumienia pierwszego
stopnia
4
L
m
długość fali
25
m
v
s
90
/
km h
prędkość pojazdu
3. Równania różniczkowe ruchu
Układ posiada dwa stopnie swobody. Równania ruchu wyprowadzam korzystając z
metody Lagrange'a II rodzaju. Jako współrzędne uogólnione wybieram
1
2
,
x x
. Postać
równań ruchu jest następująca:
k
p
k
p
i
i
i
i
E
E
E
E
d
D
Q
dt
q
q
q
gdzie:
k
E
energia kinetyczna układu
p
E
energia potencjalna układu
D
funkcja dyssypacji energii
Q
siły uogólnione
q
współrzędna uogólniona
q
prędkość uogólniona
a) Wyznaczanie energii kinetycznej układu
2
2
1 1
2 2
1
1
2
2
k
E
m x
m x
b) Wyznaczanie energii potencjalnej układu
2
2
1
1
2
2
2
1
1
2
2
p
E
c x
x
c
x
w
gdzie
1
2
,
c c
- współczynnik sztywności sprężyn obliczony w oparciu o ugięcie
statyczne układu i wpływ ugięcia na pierwszy stopień sprężynowania
1
1
6155
1
f
m
N
c
g
m
f
k
1
2
2
47960
f
m
m
N
c
g
f k
m
sin
u t
A
t
- wymuszenie kinematyczne
0,03
A
- amplituda wymuszenia kinematycznego
2
39, 27
v
rad
L
s
- częstość wymuszenia kinematycznego
c) Wyznaczanie funkcji dyssypacji energii
2
2
1
1
2
2
2
1
1
2
2
D
b x
x
b x
w
gdzie
1
2
,
b b
współczynniki tłumienia układu. Obliczamy je ze wzoru:
1
1
1 1
2
70
N s
b
m c
m
2
2
1
2
2
2
3675
N s
b
m
m c
m
cos
w t
A
t
- pochodna wymuszenia kinematycznego
d) Praca wirtualna sił oraz siły uogólnione
0
W
1,2
0
Q
Wyznaczam pochodne
1 1
1
k
p
E
E
m x
x
2 2
2
k
p
E
E
m x
x
1 1
1
k
p
E
E
d
m x
dt
x
1 2
2
k
p
E
E
d
m x
dt
x
1
1
2
1
k
p
E
E
c x
x
x
1
1
2
2
2
2
k
p
E
E
c x
x
c
x
w
x
1
1
2
1
D
b x
x
x
1
1
2
2
2
2
D
b x
x
b x
w
x
1
0
Q
2
0
Q
Układ równań różniczkowych ruchu
1 1
1
1
2
1
1
2
2 2
1
1
2
2
2
1
1
2
2
2
0
0
m x
c x
x
b x
x
m x
c x
x
c
x
w
b x
x
b x
w
lub w postaci macierzowej
Mx Bx Cx Q
1
1
1
1
1
1
1
1
2
2
1
1
2
2
1
1
2
2
2
2
0
0
0
m
x
b
b
x
c
c
x
m
x
b b
b
x
c c
c
x
c w b w
4. Drgania swobodne
Drgania swobodne analizujemy przyrównując prawą stronę układu równań
różniczkowych do zera
1
1
1
1
1
1
1
1
2
2
1
1
2
2
1
1
2
2
0
0
0
0
m
x
b
b
x
c
c
x
m
x
b b
b
x
c c
c
x
Rozwiązań szczególnych układu równań poszukujemy w następującej postaci
1
1
2
2
st
st
x
A e
x
A e
,
1
1
2
2
st
st
x
A se
x
A se
2
1
1
2
2
2
st
st
x
A s e
x
A s e
Podstawiając przewidywane rozwiązania do układu równań otrzymujemy
2
1
1
1
1
1
1
2
2
1
1
2
1
2
1
2
0
0
A
s m
sb
c
sb
c
A
sb
c
s m
s b
b
c
c
Układ równań posiada rozwiązanie niezerowe wówczas gdy wyznacznik główny macierzy
jest równy 0.
2
1
1
1
1
1
2
1
1
2
1
2
1
2
4
3
2
2400
301718,05
4771766,9
27713862,68
295207905,89
s m
sb
c
sb
c
W
sb
c
s m
s b
b
c
c
W
s
s
s
s
Równanie charakterystyczne:
4
3
2
2400
301718,05
4771766,9
27713862,68
295207905,89
0
s
s
s
s
Miejsca zerowe równania charakterystycznego:
1
2
3
4
15,92
108, 23
0,78
8, 41
0,78
8, 41
s
s
s
i
s
i
8, 41
b
rad
s
- częstość drgań tłumionych
1,34
2
b
b
f
Hz
- częstotliwość drgań tłumionych
2
0,75
b
b
T
s
- okres drgań tłumionych
Układowi nadano następujące warunki początkowe
1
2
0
0,05
0
0,01
x
m
x
m
Odpowiedź układu na tak przyjęte warunki początkowe pokazano na poniższym rysunku.
Przebiegi wykonano w oparciu o numeryczne rozwiązanie przedstawionych równań
różniczkowych. Wykorzystano do tego celu algorytm Rungego-Kutty IV rzędu. Symulacji
dokonano dla czasu 5s.
Rys. 1 Drgania swobodne tłumione
W przypadku gdy
1
2
0
b
b
, wówczas analizować będziemy drgania nietłumione. Równanie
charakterystyczne będzie równe
4
2
2400
4771766,9
295207905,89
0
s
s
a pierwiastki równania charakterystycznego będą równe:
1
2
3
4
8, 2
8, 2
42,6
42,6
s
i
s
i
s
i
s
i
częstość drgań
nietłumionych
częstotliwość drgań
nietłumionych
okres drgań nietłumionych
1
8, 2
rad
s
1
1,31
f
Hz
1
0,76
T
s
2
42,6
rad
s
2
6,8
f
Hz
2
0,14
T
s
Przebiegi czasowe układu bez tłumienia wytrąconego z położenia równowagi są pokazane
poniżej. Przyjęto następujące warunki początkowe
1
2
0
0,05
0
0,01
x
m
x
m
1
2
0
0
0
0
x
x
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
-0.05
-0.04
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
0.04
t[s]
x
1
,x
2
[
m
]
kierowca
fotel
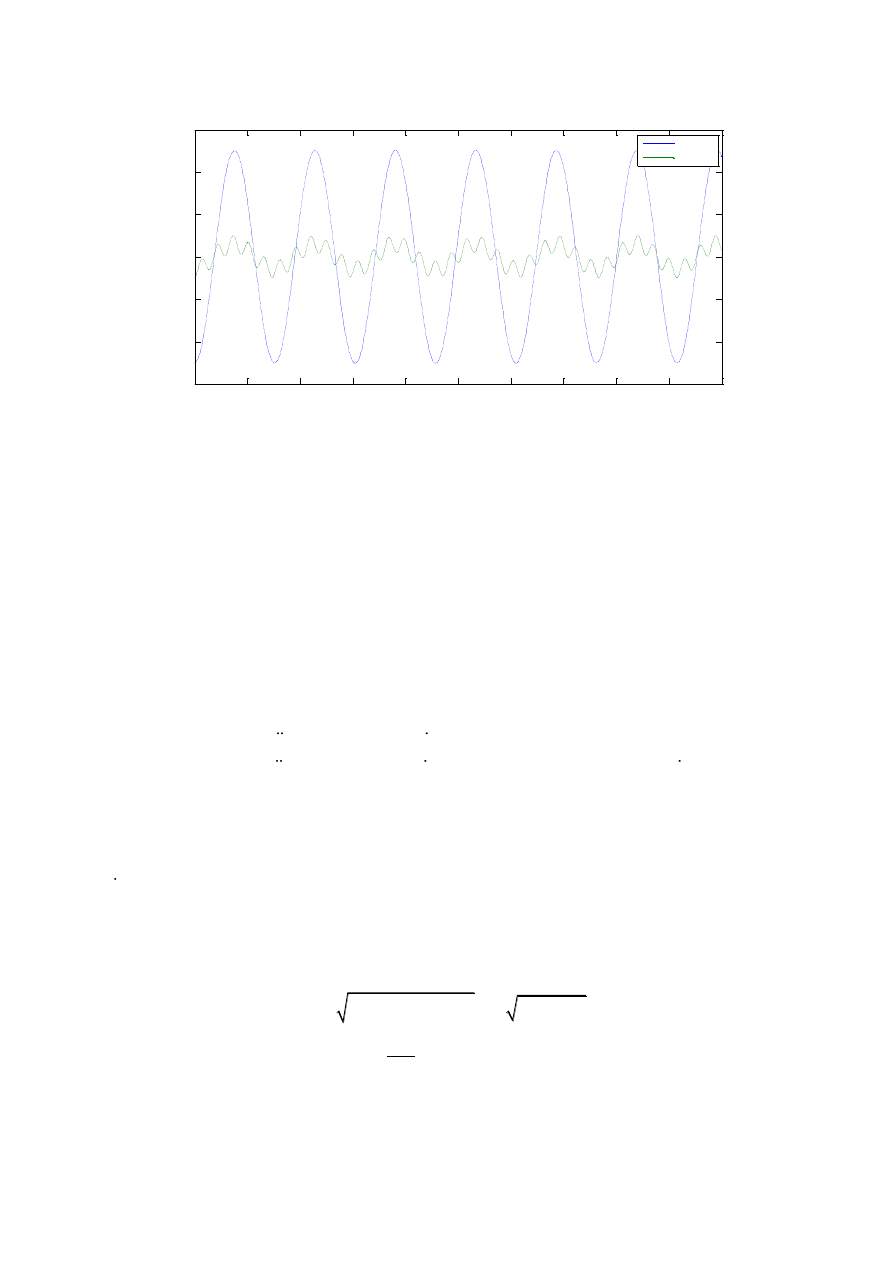
Rys. 2 Drgania swobodne nietłumione
Na rysunku są widoczne dwie formy drgań fotela kierowcy. Druga forma drgań nie ujawniała
się podczas drgań z tłumieniem.
5. Drgania wymuszone
Celem analizy drgań wymuszonych jest sporządzenie charakterystyk amplitudowo-
częstotliwościowych. Drgania pochodzące z podwozia samochodu przekazywane na fotel
kierowcy poprzez układ sprężysto-tłumiący będą stanowiły harmoniczne wymuszenie
kinematyczne. Układ równań w postaci macierzowej dla układu z wymuszeniem
przedstawiony jest poniżej.
1
1
1
1
1
1
1
1
2
2
1
1
2
2
1
1
2
2
2
2
0
0
0
m
x
b
b
x
c
c
x
m
x
b b
b
x
c c
c
x
c w b w
gdzie:
sin
cos
w
A
t
w
A
t
Zapis prawej strony równania macierzowego można przekształcić do postaci:
2
2
2
2
2
2
2
2
2
2
2
2
2
sin
cos
sin
arctan
c A
t
b A
t
C
t
C
Ac
Ab
A c
b
b
c
Dokonajmy następujące podstawienie
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
t[s]
x
1
,x
2
[
m
]
kierowca
fotel
sin
i
t
i t i
C
t
Ce
Ce e
Drgania swobodne tłumione jak widać na rys.1 po pewnym czasie wygasają. Po tym
czasie układ będzie drgał tylko na skutek występującego wymuszenia z taką samą częstością i
pewną ustaloną amplitudą. Celem naszym będzie wyznaczenie charakterystyk amplitudowo
częstotliwościowych, które w sposób jednoznaczny określą amplitudę drgań fotela kierowcy
oraz samego kierowcy w funkcji częstości wymuszenia. Podstawienie za sin(ωt+τ) funkcję
e
i(ωt+τ)
jest nietożsame, dlatego interesuje nas tylko część zespolona rozwiązania gdyż
cos
sin
i
t
e
t
i
t
Jeżeli nie interesuje nas przesunięcie fazowe to doskonałym odwzorowaniem będzie
przedstawienie modułu amplitudy w funkcji częstości wymuszenia. Przewidywane
rozwiązanie układu równań będziemy poszukiwać w postaci:
1
1
2
2
i t
i t
x t
A e
x t
A e
1
1
2
2
i t
i t
x t
i A e
x t
i A e
2
1
1
2
2
2
i t
i t
x t
A e
x t
A e
Podstawiając następnie do układu równań i upraszczając przez e
iωt
otrzymamy:
2
1
1
1
1
1
1
2
2
1
1
2
1
2
1
2
0
i
A
m
i b
c
i b
c
A
Ce
i b
c
m
i
b
b
c
c
Szukane amplitudy wyznaczamy metodą wyznacznikową.
4
3
2
2400
301718,05
4771766,9
27713862,68
295207905,89
W
i
i
1
1
1
2
2
1
2
1
2
1
0
303813,07
8856237,18
100964,76
26649303, 47
i
i b
c
W
Ce
m
i
b
b
c
c
W
i
cos
sin
i
e
i
2
1
1
1
2
1
1
2
2
2
0
115104
303813,07
8856237,18+i
346359,45
+100964,76
26649303,47
i
m
i b
c
W
i b
c
Ce
W
1
1
2
2
W
A
W
W
A
W
1
1
2
2
W
A
W
W
A
W
Charakterystyki amplitudowo-częstotliwościowe:
2
2
1
2
2
4
2
2
2
2
2
2
2
2
4
2
303813, 07
8856237,18
100964, 76
26649303, 47
2400
4771766, 9
295207905,89
27713862, 68 301718,05
115104
303813,07
8856237,18
+
346359,45
+100964,76
26649303,47
2400
4771766, 9
A
A
2
2
2
2
295207905,89
27713862, 68 301718,05
Za pomocą oprogramowania MATLAB narysowano wyżej przedstawione funkcje.
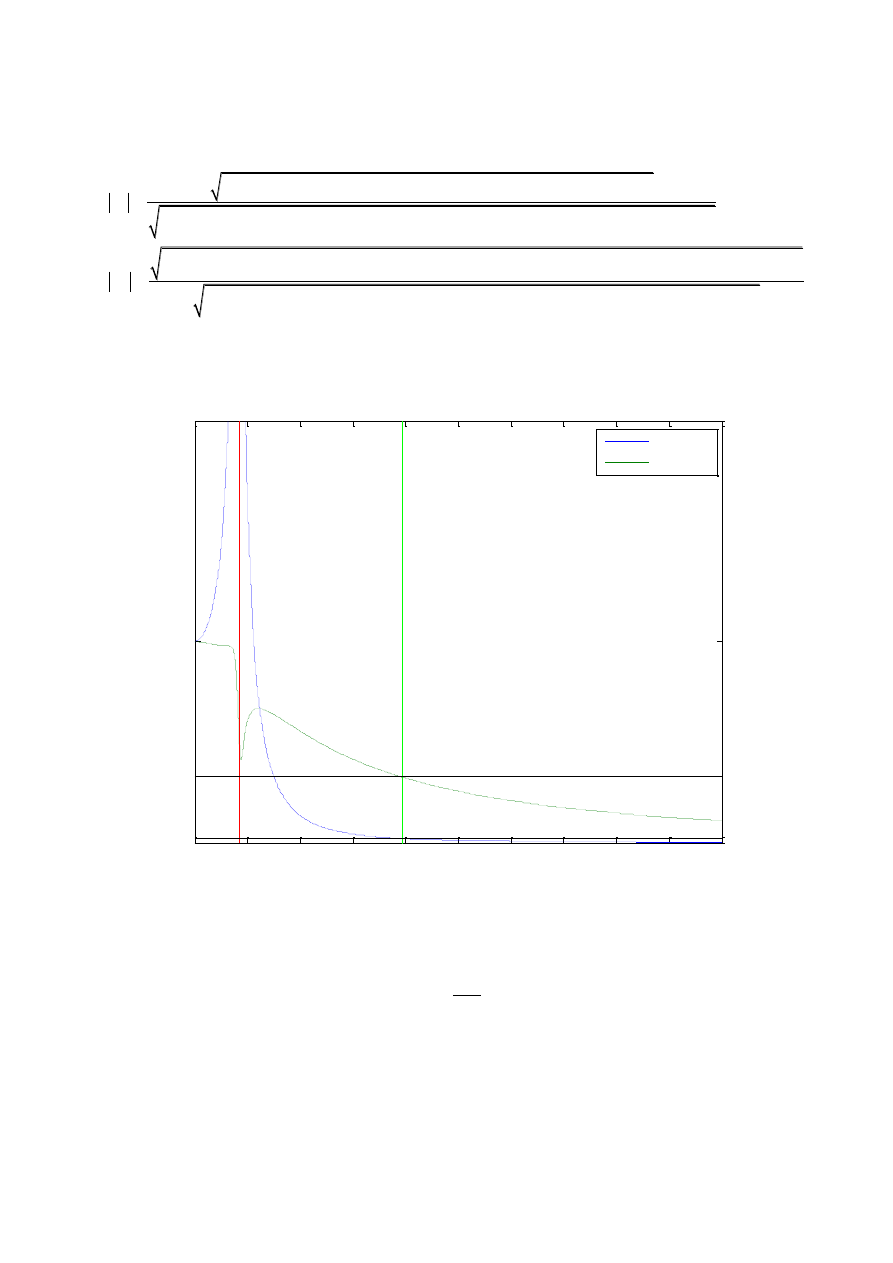
Rys. 3 Charakterystyka amplitudowo częstotliwościowa układu tłumionego
Na charakterystyce umieszczono przerywaną linią czerwoną znacznik częstości
drgań własnych tłumionych układu
8, 41
rad
s
. Amplituda drgań kierowcy dla takiej
częstości wymuszenia osiąga ekstremalne wartości. Zjawisko to nazywane jest rezonansem i
jest zazwyczaj niekorzystne. W takim stanie zdecydowanie pogarsza się komfort jazdy
kierowcy. Jest również przyczyną złego samopoczucia i może powodować utratę
koncentracji. Częstość wymuszenia w rozpatrywanym przypadku jest większa od częstości
drgań własnych układu. W związku z tym rejestrujemy znacznie mniejsze amplitudy drgań.
0
10
20
30
40
50
60
70
80
90
100
0.0018
0.031
0.0951
1
Częstość wymuszenia [rad/s]
A
m
pl
itu
da
d
rg
ań
[
m
]
częstość wymuszenia
kierowca
fotel
Zostały one zaznaczone na osi pionowej na rysunku 3. Za pomocą metod numerycznych
wyznaczono przebiegi czasowe układu kierowca-fotel dla rozpatrywanych warunków pracy.
Przebiegi te przedstawiono na rysunku poniżej. Do symulacji założono jednakowe warunki
początkowe jak w przypadku drgań swobodnych.
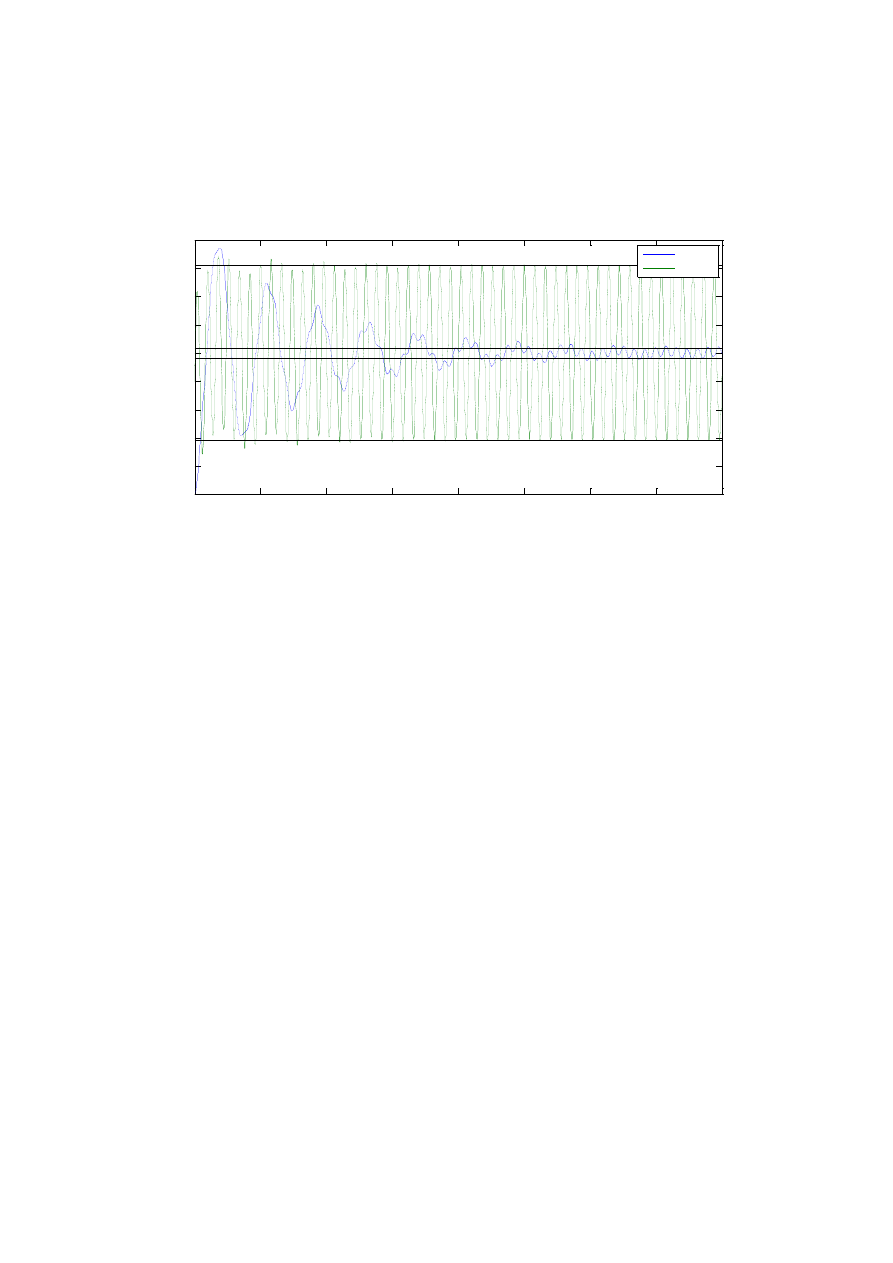
Rys. 4 Przebiegi czasowe drgań wymuszonych
Wykresy przedstawiają przemieszczenie kierowcy i fotela w czasie. W pierwszej fazie
rejestrujemy drgania własne układu. Po krótkiej chwili drgania własne ustają i układ drga
wyłącznie z częstością wymuszenia i ustaloną amplitudą. Można zaobserwować, że drgania
kierowcy znacznie wolniej osiągają stan ustalony. Widać, że w pierwszej fazie drgań
kierowca ulega drganiom wolnozmiennym, których częstość wraz z upływem czasu zmierza
do częstości drgań wymuszenia.
6. Literatura
"Teoria drgań" - Zbigniew Osiński
"Drgania Maszyn" - Ryszard Gryboś
0
1
2
3
4
5
6
7
8
-0.05
-0.04
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
0.04
t[s]
x
1
,x
2
[
m
]
kierowca
fotel