Wykład 1. 4 października 2010

Zbiory liczbowe

=

{0, 1, −1, 2, −2, . . . } − zbiór liczb całkowitych

∗

=

{1, −1, 2, −2, . . . } − zbiór liczb całkowitych różnych od zera

=

+

=

{1, 2, 3, 4, 5, . . . } − zbiór liczb naturalnych (całkowitych dodatnich)

−

=

{−1, −2, −3, −4, −5, . . . } − zbiór liczb całkowitych ujemnych

sign k = sign(k) =















0, k = 0,
1, k

∈

+

−1, −k ∈

+

− znak liczby k

=

−

=

{k − l : k, l ∈

}

Liczby naturalne wprowadzamy aksjomatycznie (aksjomatyka Peano) jako zbiór

w którym wyróżniony jest element 0 (najmniejsza liczba naturalna) i operacja na-

stępnika, która każdemu elementowi n z

przyporządkowuje liczbę n

0

w ten sposób,

że

◦ 0 nie jest następnikiem żadnej

◦◦ różne liczby nie mogą mieć tego samego następnika

◦ ◦ ◦ jedynym podzbiorem Z ⊂

takim, że 0

∈ Z oraz jeśli n ∈ Z to również n

0

∈ Z,

jest zbiór

Z =

.

Na trzecim aksjomacie oparta jest zasada indukcji matematycznej:

jeśli chcemy wykazać pewną własność T (n) dla wszystkich liczb naturalnych to

musimy sprawdzić, że

?

dla liczby 0 zachodzi własność T (0)

??

jeśli dla n zachodzi własność T (n) to dla n

0

zachodzi własność T (n

0

).

Przykład. Przy pomocy następnika definiujemy sumę liczb naturalnych

n

+ 0 = n, n + m

0

= (n + m)

0

.

Ponadto 0

0

= 1 i wtedy n

0

= (n + 0)

0

= n + 0

0

= n = 1.

Zatem następnikiem liczby n jest liczba n + 1.
Startując od 0 i wykonując kolejno operację następnika otrzymujemy kolejne liczby

naturalne, możemy w ten sposób otrzymać je wszystkie.

1

Dla zbioru X zdefiniujmy X

0

= X

∪ {X}. Możemy wziąć 0 = ∅ oraz jeśli n = X to

n

0

= X

0

. Mamy stąd

1 = 0

0

=

∅

0

=

{∅}, 2 = 1

0

=

{∅}

0

=

{∅, {∅}}, itd.

Przykład. Niech T (n): 36

|10

n

− 4, co oznacza, że 10

n

− 4 = 36k.

Jeśli założymy tę własność dla n to dla n + 1 będziemy mieli

10

n+1

− 4 = 10 · 10

n

− 4 = 10 · (10

n

− 4) + 36 = 10 · 36k + 36 = 36(10k + 1)

co oznacza, że dla n

0

własność T zachodzi. Ale nie zachodzi ona dla żadnej liczby

naturalnej bo liczba 10

n

− 4 nie jest podzielna przez 9 - przez 9 jest podzielna liczba

10

n

− 1.

Operatory sumy i iloczynu.

0

X

k=0

a

k

= a

0

,

n+1

X

k=0

a

k

=

n

X

k=0

a

k

+ a

n+1

n

P

k=n

0

a

k

=

n

P

k=0

a

k

−

n

0

−1

P

k=0

a

k

lub, jeśli a

k

nie są określone dla k < n

0

to kładziemy

n

X

k=n

0

a

k

=

n

X

k=0

f

a

k

,

f

a

k

=







a

k

, k

­ n

0

,

0, k < n

0

.

0

Y

k=0

a

k

= a

0

,

n+1

Y

k=0

a

k

=

n

Y

k=0

a

k

· a

n+1

.

Własności operacji sumowania:

•

n

P

k=0

(a

k

+ b

k

) =

n

P

k=0

a

k

+

n

P

k=0

b

k

•

n

P

k=0

αa

k

= α

n

P

k=0

a

k

•

n

P

k=0

a

k

=

n

P

k=0

a

n−k

,

n

P

k=0

1 = n + 1.

Przykład. Niech S

n

= 0 + 1 +

· · · + n =

n

P

k=0

k

. Mamy

2S

n

=

n

X

k=0

k

+

n

X

k=0

(n

− k) =

n

X

k=0

(k + n

− k)

=

n

X

k=0

n

= n

n

X

k=0

1 = n(n + 1),

2

skąd mamy S

n

=

n(n+1)

2

.

|k| = k · sign k − wartość bezwzględna liczby k

Własności wartości bezwzględnej:

• | − k| = |k| ­ 0,

• |k · l| = |k| · |l|,

• |k + l| ¬ |k| + |l|.

Twierdzenie o dzieleniu z resztą w

.

Jeżeli a i b są liczbami całkowitymi, b

6= 0, to istnieje dokładnie jedna para liczb

całkowitych d i r takich, że

a

= b

· d + r, 0 ¬ r < |b|.

d

= d(a, b) - wynik dzielenia a przez b, r = r(a, b) - reszta z dzielenia a przez b.

Np.

−37 = (−7) · 6 + 5, d(−37, −7) = 6, r(−37, −7) = 5,

37 = 7

· 5 + 2, d(37, 7) = 5, r(37, 7) = 2.

Sformułowanie twierdzenia o dzieleniu z resztą jest przykładem zdania logicznego

w postaci implikacji.

Zdaniem logicznym jest każde

∗

zdanie orzekające. Zdania logiczne oznaczamy

najczęściej p, q, r, s, t, . . . .

(

∗

Za zdanie logiczne nie uznajemy raczej ”zdania” typu

Zdanie w tej ramce jest fałszywe )

Zdaniu p przypisujemy jego wartość w(p), którą najczęściej

∗

jest 0 lub 1 (mówimy

wtedy o logice dwuwartościowej). Jeżeli w(p) = 1 to mówimy, że zdanie jest prawdziwe
a przy w(p) = 0 mówimy o fałszywości zdania.

Z pojedynczych zdań możemy tworzyć zdania używając spójników zdaniowych

∨, ∧, =⇒, ⇐⇒ oraz operacji negacji

:

p

∨ q (p lub q) - alternatywa zdań p i q

p

∧ q (p i q) - koniunkcja zdań p i q

p

⇒ q (jeżeli p to q, z p wynika q, p pociąga q ) - implikacja zdań p i q, p - poprzednik

implikacji, q - następnik implikacji

p

⇔ q (p wtedy i tylko wtedy, gdy q) - równoważność zdań p i q

p

(nie p) - negacja zdania p

3

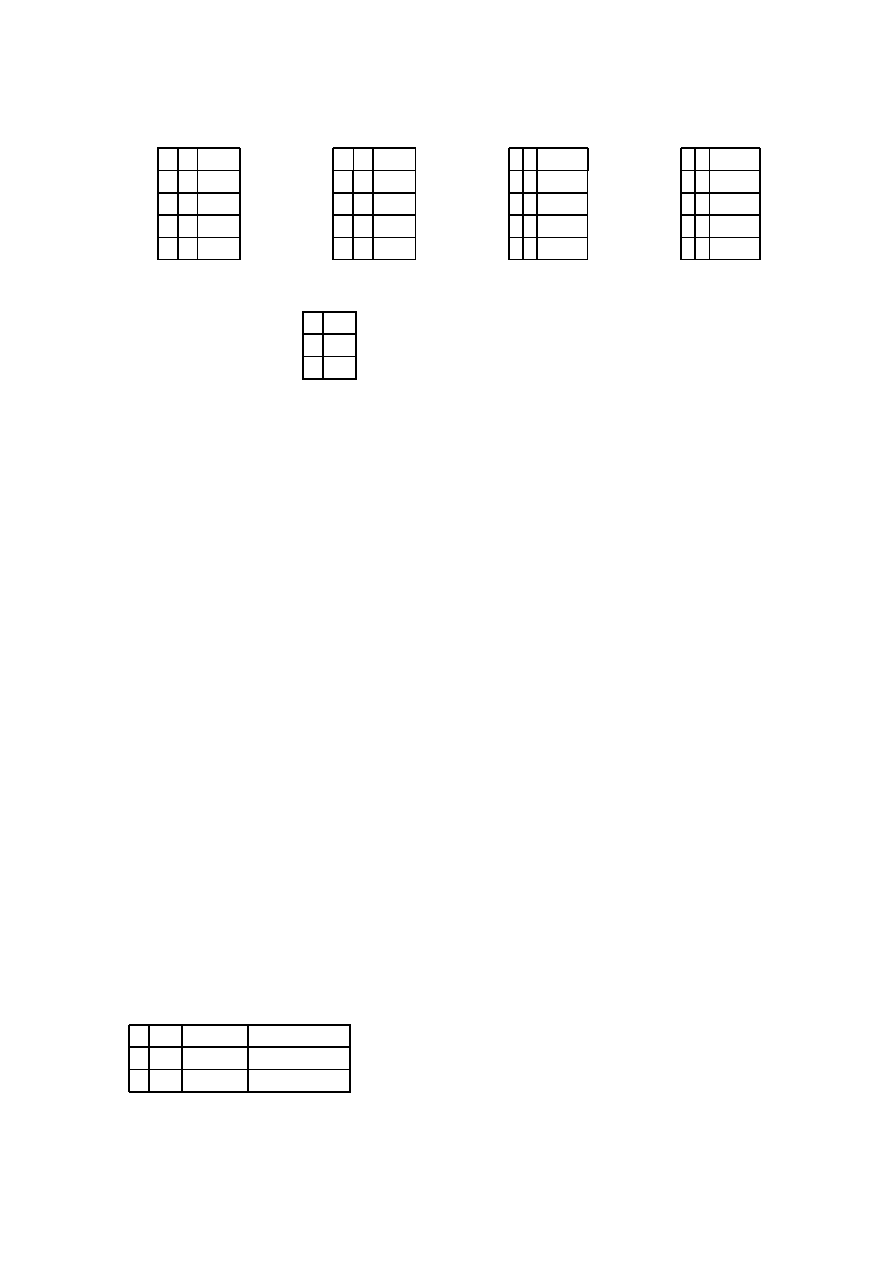
Wartości logiczne spójników i negacji są najczęściej określane przy pomocy tabelek,

np. dla koniunkcji, alternatywy, implikacji i równoważności mamy

p q p

∧ q

0 0

0

1 0

0

0 1

0

1 1

1

p q p

∨ q

0 0

0

1 0

1

0 1

1

1 1

1

p q p

⇒ q

0 0

1

1 0

0

0 1

1

1 1

1

p q p

⇔ q

0 0

1

1 0

0

0 1

0

1 1

1

Dla negacji mamy

p

p

0 1
1 0

w

(

p

) = r(w(p) + 1, 2)

Mamy wzory:

dla koniunkcji

w

(p

∧ q) = r(w(p) · w(q), 2) = w(p) · w(q)

dla alternatywy

w

(p

∨ q) = r(w(p) · w(q) + w(p) + w(q), 2)

dla implikacji

w

(p

⇒ q) = r(w(p) · w(q) + w(p) + 1, 2)

dla równoważności

w

(p

⇔ q) = r(w(p) + w(q) + 1, 2)

Zdanie utworzone ze zdań p, q, . . . i pewnej ilości spójników nazywamy tautologią

(lub prawem rachunku zdań) jeśli jego wartość wynosi 1 przy dowolnych wartościach
zdań składowych.

Np. prawa de Morgana są przykładem tautologii

(p

∨ q) ⇔ (

p

∧

q

)

(p

∧ q) ⇔ (

p

∨

q

)

prawo wyłączonego środka p

∨

p

prawo podwójnej negacji

(

p

)

⇔ p.

Tautologie można sprawdzać przy pomocy odpowiednich tabelek lub wykorzystując

powyższe wzory:

p

p

(

p

)

(

p

)

⇔ p

0 1

0

1

1 0

1

1

w

(

(

p

)) = r(w(

p

)+1, 2) = r(w(p)+2, 2) = w(p).

w

(p

∨

p

) = r(w(p)

· w(

p

) + w(p) + w(

p

), 2)

= r(w(p)

· w(p) + w(p) + w(p) + w(p) + 1, 2) = r(4w(p) + 1, 2) = 1.

4

Wykład 2. 11 października 2010

Kwantyfikatory.
Zdanie w którym występuje zmienna nazywamy formą zdaniową. Oznaczamy je

często ϕ(x), ψ(x), np.

ϕ

(x) : x

2

¬ 0, ψ(x) : x

2

=

−1.

Jeśli za zmienną podstawimy konkretną wartość to staje się ono zwykłym zdaniem,
prawdziwym lub fałszywym.

Zdania typu dla każdego x ze zbioru X zachodzi ϕ(x) oraz istnieje y ze zbioru Y

dla którego ψ

(y) jest prawdą zapisujemy odpowiednio

∀x ∈ Xϕ(x)

∃y ∈ Y ψ(y)

Wyrażenie dla każdego które oznaczamy

∀ nazywamy kwantyfikatorem ogólnym

lub dużym a wyrażenie istnieje nazywamy kwantyfikatorem szczegółowym lub
małym.

Kwantyfikatory tego samego rodzaju można pisać w dowolnej kolejności, łączyć ze

sobą, natomiast nie można zmieniać kolejności między dużym i małym, np. w zdaniu

∀ε > 0∃n

0

∀n ­ n

0

|a

n

− g| < ε

zawarta jest definicja równości lim

n→∞

a

n

= g podczas gdy zdanie

∃n

0

∀ε > 0 ∀n ­ n

0

|a

n

− g| < ε

jest równoważne zdaniu

∀n ­ n

0

a

n

= g.

Prawa de Morgana dla kwantyfikatorów

∀x ∈ X ϕ(x) ⇔ ∃x ∈ X

ϕ

(x)

∃x ∈ X ϕ(x) ⇔ ∀x ∈ X

ϕ

(x).

Zasadę indukcji przy pomocy kwantyfikatorów możemy zapisać następująco:

w

(T (0)) = 1

∧ w(∀n ­ 0 (T (n) ⇒ T (n + 1))) = 1 ⇔ ∀n ­ 0 w(T (n)) = 1.

Nieco ogólniejsza zasada indukcji:

w

(T (n

0

)) = 1

∧ w(∀n ­ n

0

(T (n)

⇒ T (n + 1))) = 1 ⇔ ∀n ­ n

0

w

(T (n)) = 1.

Regułę tę otrzymamy z podstawowej zasady indukcji rozpatrując własność T

0

(n) =

T

(n + n

0

).

Indukcja wsteczna.

5

∀n ­ n

0

w

(T (n)) = 1

⇔ w(∀n ­ n

0

+1(T (n)

⇒ T (n−1))) = 1 ∧∀n ∈ A w(T (n)) = 1,

gdzie

A jest nieskończonym zbiorem liczb naturalnych, domyślnie pewnej szczególnej

postaci np. kwadratów liczb naturalnych, czy też potęg dwójki.

Przykład. Nierówność Cauchy’ego między średnią arytmetyczną i geometryczną:

∀n ­ 2 ∀a

n

>

0

a

1

+

· · · + a

n

n

­

n

√

a

1

· · · · · a

n









∀n ­ 2 ∀a

n

>

0

n

P

k=1

a

k

n

­

n

v

u

u

t

n

Y

k=1

a

k













∀n ­ 2 ∀a

n

>

0

1

n

n

X

k=1

a

k

­

n

Y

k=1

a

k

!

1/n





Dla n = 2 nierówność jest równoważna nierówności

(a

1

+ a

2

)

2

− 4a

1

a

2

­ 0 ⇔ (a

1

− a

2

)

2

­ 0,

skąd łatwo uzasadnić nierówność Cauchy’ego dla n = 2

k

, np.

a

1

+ a

2

+ a

3

+ a

4

4

=

a

1

+a

2

2

+

a

3

+a

4

2

2

­

s

a

1

+ a

2

2

·

a

3

+ a

4

2

­

q

√

a

1

· a

2

·

√

a

3

· a

4

=

4

√

a

1

a

2

a

3

a

4

.

a

1

+

· · · + a

n−1

n

− 1

= (a

1

+

· · · + a

n−1

)(

1

n

− 1

−

1

n

) + (a

1

+

· · · + a

n−1

)

1

n

=

1

n

(a

1

+

· · · + a

n−1

+

1

n

− 1

(a

1

+

· · · + a

n−1

))

­

a

1

· · · · · a

n−1

·

1

n

− 1

(a

1

+

· · · + a

n−1

)

1/n

,

a

1

+

· · · + a

n−1

n

− 1

1−1/n

­ (a

1

· · · · · a

n−1

)

1/n

⇓

a

1

+

· · · + a

n−1

n

− 1

­ (a

1

· · · · · a

n−1

)

1/n−1

.

a, b

∈ , b > 0

r

(a, b) := a( mod b).

b

↔ m ­ 2 r(a, m) = a( mod m).

m

=

{0, 1, . . . , m − 1} - zbiór reszt przy dzieleniu przez m.

2

=

{0, 1}

s, t

∈

m

s

+

m

t

= s + t(

mod m) = r(s + t, m)

s

·

m

t

= s

· ( mod m) = r(s · t, m).

Reszty można dodawać, mnożyć odejmować a w pewnych przypadkach dzielić:

6

• dodawanie i mnożenie reszt są przemienne i łączne

• ∀s ∈

m

s

+

m

0 = s

• ∀s ∈

m

s

·

m

1 = s

• zachodzi rozdzielność mnożenia względem dodawania

(s +

m

t

)

·

m

= (s

·

m

u

) +

m

(t

·

m

u

)

• ∀s ∈

m

∃t ∈

m

s

+

m

t

= 0.

Mamy

t

=:

−s =







s, s

= 0

m

− s, 0 < s ¬ m − 1.

• ∀s ∈

m

\ {0}∃t ∈

m

s

·

m

t

= 1

⇔ m jest liczbą pierwszą

t

:= s

−1

= s

−1

( mod m), np. (m

− 1)

−1

= (m

− 1)

−1

( mod m) = m

− 1.

s

: t = s

·

m

t

−1

m

­ 2 jest liczbą pierwszą ⇔ (m = m

1

· m

2

⇒ (m

1

= 1

∨ m

1

= m)

P - zbiór liczb pierwszych, P = {2, 3, 5, . . . }
r

(a, b) = 0 to b

|a

m

∈ P ⇔ ∀a, b ∈

m

|a · b ⇒ (m|a lub m|b)

Zasadnicze twierdzenie arytmetyki

Dla dowolnej liczby naturalnejm > 1 istnieje dokładnie jeden układ licz pierwszych

p

1

¬ · · · ¬ p

k

takich, że

m

= p

1

· · · · · p

k

Największy wspólny dzielnik.

• NW D(0, 0) = 0

• a, b ∈

, a

6= 0 lub b 6= 0 to NW D(a, b) = d ⇔ (d|a ∧ d|b ∧ ∀c ∈

(c

|a∧c|b ⇒

c

¬ d) (musi być wtedy c|d)

Twierdzenie o największym wspólnym dzielniku

∃ x, y ∈

N W D

(a, b) = xa + yb

N W D

(a, b) = 1 to a, b - względnie pierwsze.

7

Zastosowanie.

s

∈

m

, s, m względnie pierwsze to

1 = xs + ym

⇒ xs = 1 − my ⇒ s

−1

= x(

mod m).

Chińskie twierdzenie o resztach.

m

1

, . . . , m

s

∈

, m

j

­ 2 liczby parami względnie pierwsze, r

j

∈

m

j

, j

= 1, . . . , s

to istnieje dokładnie jeden element x

∈

m

1

·····m

s

, taki, że r(x, m

j

) = r

j

, j

= 1, . . . , s.

Mamy wzór

x

=

s

X

j=1

r

j

r

(m

j

,

m

1

· · · · · m

s

m

j

)

−1

( mod m

1

· · · · · m

s

).

Np. Dla s = 2 m

1

= k, m

2

= k + 1 mamy

x

= r

1

+ r

2

k.

Algorytm Euklidesa.

a

­ b NW D(a, b) = NW D(b, r(a, b))

r

0

= r(a, b), r

1

= r(b, r

0

), r

2

= r(r

0

, r

1

)

r

k+1

= r(r

k−1

, r

k

)

r

0

> r

1

> . . .

∃n r

n+1

= 0, r

n

6= 0

r

n

= N W D(a, b)

8

Wykład 3. 18 października 2010

Algorytm Euklidesa.

a

­ b NW D(a, b) = NW D(b, r(a, b))

r

0

= r(a, b), r

1

= r(b, r

0

), r

2

= r(r

0

, r

1

)

r

k+1

= r(r

k−1

, r

k

)

r

0

> r

1

> . . .

∃n r

n+1

= 0, r

n

6= 0

r

n

= N W D(a, b)

- zbiór liczb wymiernych (ułamków)

x

=

k

l

- ułamek, k

∈

- licznik, l

∈

∗

- mianownik

x

=

m

n

, m, n

∈

, n

­ 0 lub x = −

m

n

.

3 x = {(m, n)} = {(k, l)} ⇔ ml = nk.

n

= n

1

N W D

(m, n), m = m

1

N W D

(m, n)

⇒

m

n

=

m

1

n

1

, N W D

(m

1

, n

1

) = 1.

9

1. Liczby zespolone.
Liczby zespolone

pojawiły si¸e po raz pierwszy w ksi¸ażce włoskiego matematyka

Rafaela Bombelliego ”Algebra”

napisanej ok. roku 1560 a opublikowanej w 1572.

Liczba zespolona z

to element postaci

z

= x + yi, gdzie x, y

∈

oraz i =

√

−1.

Przyjmujemy, że jeżeli z = x + yi, w = x

1

+ y

1

i

to

z

= w

⇔ x = x

1

, y

= y

1

.

Jeżeli z = x+yi to liczby rzeczywiste x i y nazywaj¸a si¸e odpowiednio cz¸eści¸a rzeczywist¸a
i cz¸eści¸a urojon¸a liczby z i oznaczamy je

x

=

<z, y = =z.

Zatem z =

<z + =zi oraz z = w ⇔ <z = <w i =z = =w.

Definiujemy 0 := 0 + 0i, 1 = 1 + 0i. Przez

oznaczamy zbiór liczb zespolonych.

Dodawanie i odejmowanie liczb zespolonych.

(x + yi) + (x

1

+ y

1

i

) := (x + x

1

) + (y + y

1

)i

czyli

<(z + w) = <z + <w, =(z + w) = =z + =w.

(x + yi)

− (x

1

+ y

1

i

) := (x

− x

1

) + (y

− y

1

)i

czyli

<(z − w) = <z − <w, =(z − w) = =z − =w.

−z = −(x + yi) = −x + (−y)i = −x − yi − liczba przeciwna :

<(−z) = −<z, =(−z) = −=z.

10

Własności dodawania.
(1)

∀z, w ∈

z

+ w = w + z (przemienność)

(2)

∀z ∈

z

+ 0 = 0 + z = z (0 jest elementem neutralnym dodawania)

(3)

∀z ∈

z

+ (

−z) = (−z) + z = 0 (liczba przeciwna jest elementem

odwrotnym dla dodawania

)

(4)

∀z, w, v ∈

(z + w) + v = z + (w + v) (ł¸aczność dodawania).

Własności (1)–(4) wynikaj¸a z odpowiednich własności liczb rzeczywistych.

Mnożenie i dzielenie liczb zespolonych.

Liczba sprz¸eżona

: z = x + yi, z := x

− yi.

Moduł liczby zespolonej: z

= x + yi,

|z| :=

√

x

2

+ y

2

.

Mnożenie liczb zespolonych

:

(x + yi)

· (x

1

+ y

1

i

) := (xx

1

− yy

1

) + (xy

1

+ yx

1

)i.

(x + 0i)

· (x

1

+ 0i) = xx

1

+ 0i

∀a ∈

a

· (x + yi) = ax + ayi

z

= 0

⇔ x = y = 0 ⇔ |z|

2

= 0; z

6= 0 ⇒ |z|

2

6= 0

z

· z = |z|

2

Własności mnożenia:
(1)

∀z, w ∈

z

· w = w · z (przemienność)

(2)

∀z ∈

z

· 1 = 1 · z (1 jest elementem neutralnym)

(3)

∀z, w, v ∈

(z

· w) · v = z · (w · v) (ł¸aczność)

(4)

∀z, w, v ∈

(z + w)

· v = z · v + w · v (rozdzielność mnożenia

wzgl¸edem dodawania

)

Dowody (3),(4): obliczamy lewe i prawe strony i porównujemy.

(5)

∀z ∈

\ {0} z ·

1

|z|

2

z

= 1 (liczba

1
z

=

1

|z|

2

z element odwrotny do z

)

z

w

= z : w = z

1

w

=

1

|w|

2

z

· w =

z

· w

|w|

2

w

z

=

1

z

w

Własności sprz¸

eżenia liczby zespolonej.

(S1)

∀x, y ∈

x

= x, yi =

−yi.

(S2)

∀z, w ∈

z

+ w = z + w, z

− w = z − w.

(S3)

∀z, w ∈

z

· w = z · w,

z

w

=

z

w

.

(S4)

∀z ∈

<z =

z+z

2

,

=z =

z−z

2i

.

(S5)

∀z ∈

z

· z = |z|

2

.

Ad S3) Wystarczy sprawdzić pierwsz¸a równość gdy w = x

1

∈

i w = y

1

i, y

1

∈

,

gdyż jeśli wzór b¸edzie prawdziwy w takich przypadkach to

z

· w = z · x

1

+ z

· y

1

i

(S2)

= z

· x

1

+ z

· y

1

i

= z

· x

1

+ z

· (−y

1

i

) = z

· w

11

z

· x

1

= xx

1

+ yx

1

i

⇒ z · x

1

= xx

1

− yx

1

i

= (x

− yi) · x

1

= z

· x

1

;

z

· (y

1

i

) = xy

1

i

− yy

1

=

−yy

1

+ xy

1

i

⇒

z

· (y

1

i

) =

−yy

1

− xy

1

i

= (

−y − xi) · y

1

=

−y − xi

−i

· (−y

1

i

) = (x +

y

i

)(y

1

i

) = (x

− yi)(y

1

i

) = z(y

1

i

);

z

w

· w = z ⇒

z

w

· w = z ⇒

z

w

=

z

w

.

Własności modułu liczby zespolonej.

(M1)

∀z ∈

|z| = |z| ­ 0; |<z| ¬ |z|, |=z| ¬ |z|;

(M2)

|z| = 0 ⇔ z = 0;

(M3)

∀z, w ∈

|z · w| = |z| · |w|;

z

w

=

|z|

|w|

;

(M4)

∀z, w ∈

|z + w|

2

=

|z|

2

+

|w|

2

+ 2

<(zw);

(M5)

∀z, w ∈

|z + w|

2

+

|z − w|

2

= 2

|z|

2

+ 2

|w|

2

;

(M6)

∀z, w ∈

|z + w| ¬ |z| + |w|.

Ad (M3): (M3)

⇔ |z · w|

2

=

|z|

2

· |w|

2

:

|z · w|

2

= z

· w · z · w = z · w · z · w = z · z · w · w = |z|

2

· |w|

2

;

z

w

· w = z ⇒

z

w

· |w| ⇒

z

w

=

|z|

|w|

.

Ad (M4)

|z + w|

2

= (z + w)

· z + w = (z + w)(z + w) = z · z + w · w + z · w + z · w

=

|z|

2

+

|z|

2

+ z

· w + z · w =

(S4)

=

|z|

2

+

|w|

2

+ 2

<(z · w).

Ad (M5)

|z + w|

2 (M 4)

=

|z|

2

+

|w|

2

+ 2

<(z · w),

|z − w|

2

=

|z|

2

+

|w|

2

+ 2

<(z · (−w)),

|z + w|

2

+

|z − w|

2

= 2

|z|

2

+ 2

|w|

2

+ 2

<(z · w − z · w) = 2|z|

2

+ 2

|w|

2

.

Ad (M6)

|z + w|

2

=

|z|

2

+

|w|

2

+ 2

<(z · w) ¬ |z|

2

+

|w|

2

+ 2

|<(z · w)| ¬ |z|

2

+

|w|

2

+ 2

|z · w|

=

|z|

2

+

|w|

2

+ 2

|z| · |w| = (|z| + |w|)

2

⇒ |z + w| ¬ |z| + |w|.

Zastosowanie:
Niech z = x + yi, w = u + vi, x, y, u, v

∈

|z|

2

= x

2

+ y

2

=: n

∈

,

|w|

2

= u

2

+ v

2

=: m

∈

;

12

n

· m = |z|

2

· |w|

2

=

|(xu − yv) + (xv + yu)i|

2

= (xu

− yv)

2

+ (xv + yu)

2

,

oraz xu

− yv, xv + yu ∈ .

Wniosek: jeśli liczby naturalne m i n s¸a sumami dwóch kwadratów liczb całkowitych

to ich iloczyn ma również t¸e własność

Postać trygonometryczna liczby zespolonej.

Niech z

∈

, z

6= 0. Wtedy możemy napisać

z

= x + yi =

q

x

2

+ y

2

·

x

√

x

2

+ y

2

+

y

√

x

2

+ y

2

i

!

.

Oznaczmy

q

x

2

+ y

2

= r,

x

√

x

2

+ y

2

= s,

y

√

x

2

+ y

2

= t.

Wtedy r =

|z| oraz punkt (s, t) leży na okr¸egu jednostkowym gdyż s

2

+ t

2

= 1. Dlatego

istnieje liczba ϕ

∈

taka, że s = cos ϕ, t = sin ϕ.

Liczb¸e ϕ nazywamy argumentem liczby z i definiujemy

arg z =

{ϕ ∈

: ϕ

− argument z}

Ponadto

∃! ϕ

0

∈ [0, 2π), ϕ

0

- argument z.

ϕ

0

=: Arg z - argument główny z:

{Arg z} = arg z ∩ [0, 2π).

Mamy

arg z =

{Arg z + 2kπ : k ∈ } = {ϕ + 2kπ : k ∈ },

gdzie ϕ jest dowolnym ustalonym argumentem liczby z. Zatem

z

= r(cos ϕ + sin ϕi), r =

|z|, ϕ ∈ arg z

i jest to tzw. postać trygonometryczna liczby zespolonej z. Mamy przy tym

z

= w

⇔ |z| = |w| i arg z = arg w ⇔ |z| = |w| i Arg z = Arg w.

Niech z = r

1

(cos ϕ

1

+ sin ϕ

1

i

), w = r

2

(cos ϕ

2

+ sin ϕ

2

i

). Wtedy

z

· w = r

1

r

2

(cos ϕ

1

+ sin ϕ

2

i

)(cos ϕ

12

+ sin ϕ

2

i

) = r

1

r

2

(cos(ϕ

1

+ ϕ

2

) + sin(ϕ

1

+ ϕ

2

)i),

z

w

=

r

1

(cos ϕ

1

+ sin ϕ

1

i

)

r

2

(cos ϕ

2

+ sin ϕ

2

i

)

=

r

1

r

2

(cos(ϕ

1

− ϕ

2

) + sin(ϕ

1

− ϕ

2

)i),

czyli

arg(z

· w) = {ϕ

1

+ ϕ

2

: ϕ

1

∈ arg z, ϕ

2

∈ arg w} = arg z + arg w,

arg

z

w

=

{ϕ

1

− ϕ

2

: ϕ

1

∈ arg z, ϕ

2

∈ arg w} = arg z − arg w.

Wzór de Moivre’a.

13

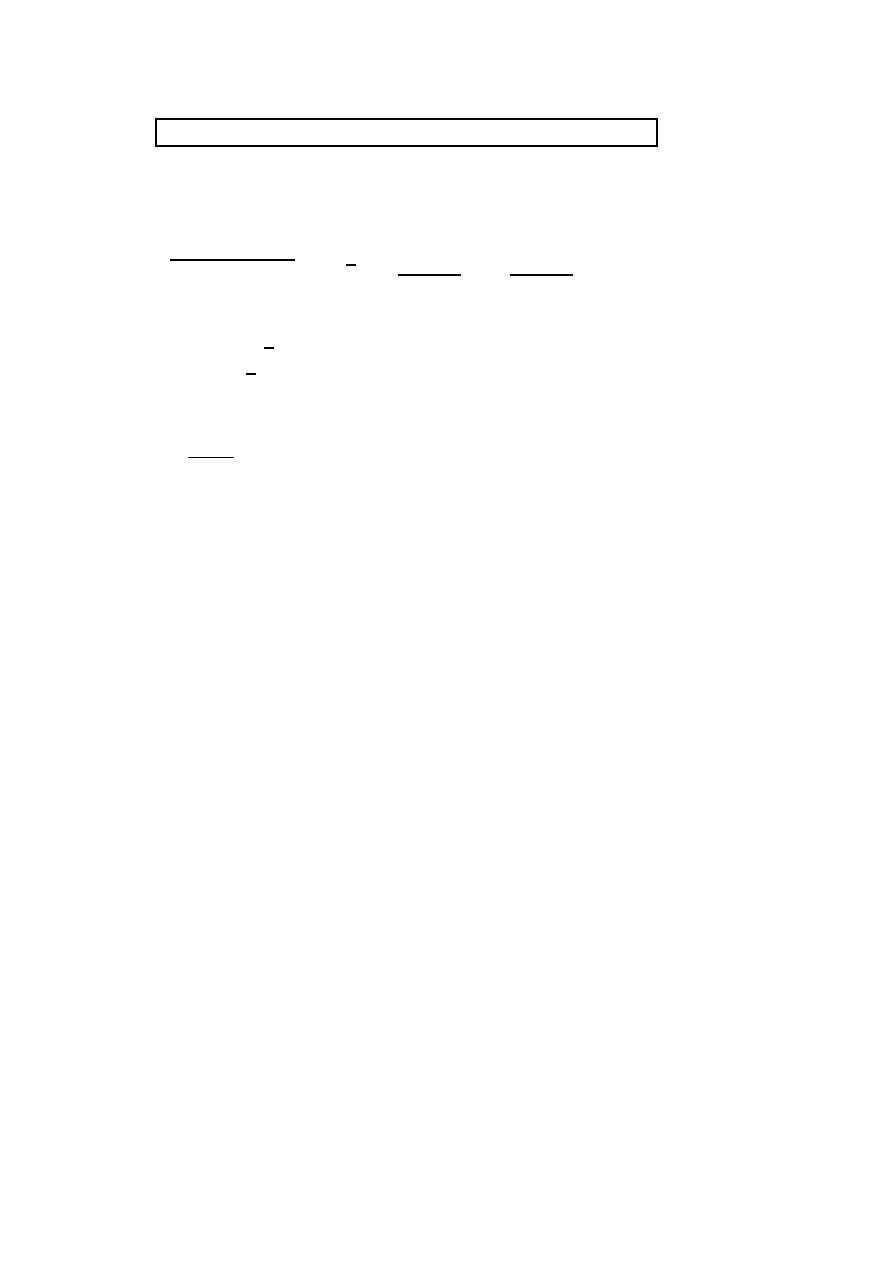
Jeżeli ϕ

∈ arg z to

z

n

= (r(cos ϕ + sin ϕi))

n

= r

n

(cos nϕ + sin nϕi), n

∈

(n

∈ ).

Dla n

∈

wzór dowodzimy przez indukcj¸e, a dla k

∈ , k < 0 wykorzystujemy

dzielenie liczb w postaci trygonometrycznej.

Pierwiastki stopnia n z liczby zespolonej.

n

q

r

(cos ϕ + sin ϕi) =

(

n

√

r

cos

ϕ

+ 2kπ

n

+ sin

ϕ

+ 2kπ

n

i

!

: k = 0, 1, . . . , n

− 1

)

=

{w

k

: k = 0, 1, . . . , n

− 1}.

Mamy bowiem

n

√

z

=

{w ∈

: w

n

= z

}.

Jeśli w

∈

n

√

z

to w = ρ(cos ψ + sin ψi) i z wzoru de Moivre’a ρ

n

= r, nψ

∈ arg z ⇒

nψ

= ϕ + 2kπ. Ale

k

= m

· n + k

0

, k

0

∈ {0, 1, . . . , n − 1}

to ψ =

ϕ+2k

0

π

n

+ 2mπ, co oznacza w = w

k

0

. Oczywiście dla wszystkich k w

n

k

= z.

14

(I)

=

2

- definicja liczb zespolonych jako punktów płaszczyzny. Liczby

zespolone jako wektory.

Y

ϕ

X

z

= x + yi

x

y

w

z

+ w

z

− w

1

i

(x, y) + (x

1

, y

1

) := (x + x

1

, y

+ y

1

)

(x, y)

· (x

1

, y

1

) := (xx

1

− yy

1

, xy

1

+ yx

1

)

(x, y) = (x, 0) + (0, y) = (x, 0)

· (1, 0) + (y, 0) · (0, 1)

1 = (1, 0), i = (0, 1), x = (x, 0), y = (y, 0)

z

= (x, y) = x + yi

O

z

= (x, y) - wektor zaczepiony w pocz¸atku układu współrz¸ednych O

x, y

współrz¸edne wektora z

x

- rzut wektora z na oś OX

15

y

- rzut wektora z na oś OY

ϕ

- k¸at (skierowany) osi OX z z

|z| - długość wektora z
|z − w| - odległość punktów z i w
z

◦ w = (w, y) ◦ (x

1

, y

1

) = xx

1

+ yy

1

- iloczyn skalarny wektorów z i w

z

◦ w = <(z · w).

{z ∈

:

|z − z

0

| = R} = O(z

0

, R

),

{z ∈

:

|z − z

0

| < R} = K(z

0

, R

),

{z ∈

:

|z − z

1

| + |z − z

2

| = R} = E(z

1

, z

2

, R

), (R >

|z

1

− z

2

| ).

O

(z

1

, R

) - okr¸ag, K(z

0

, R

) - koło,

E(z

1

, z

2

, R

) - elipsa o ogniskowych w punktach z

1

i

z

2

.

(II)

C = {f :

2

−→

2

: f jest złożeniem jednokładności o środku O

i skali r

­ 0 oraz obrotu o k¸at ϕ wzgl¸edem osi OX}

Y

ϕ

r

X

y

x

x

r

= cos ϕ

y
r

= sin ϕ

f

(x, y) =?

f

(x, y) = f (x(1, 0) + y(0, 1)) = xf (1, 0) + yf (0, 1)

(1, 0)

−→ (r, 0) −→ (r cos ϕ, r sin ϕ),

(0, 1)

−→ (0, r) −→ (r cos(ϕ +

π

2

), r sin(ϕ +

π

2

) = (

−r sin ϕ, r cos ϕ),

f

(x, y) = x(r cos ϕ, r sin ϕ) + y(

−r sin ϕ, r cos ϕ)

= (r cos ϕx

− r sin ϕy, r sin ϕx + r cos ϕy).

dodawanie odwzorowań

↔ dodawanie liczb zesplonych

składanie odwzorowań

↔ mnożenie liczb zespolonych

odwzorowanie odwrotne

↔ odwrotność liczby zespolonej

(III)

16

f

:

2

−→

2

- odwzorowanie liniowe:

f

(a(s, t)) = af (s, t), f ((s, t) + (s

1

, t

1

)) = f (s + s

1

, t

+ t

1

) = f (s, t) + f (s

1

, t

1

),

f

(s, t) = sf (1, 0) + tf (0, 1).

Ogólna postać odwzorowania liniowego

2

−→

2

:

f

(s, t) = (as + bt, a

1

s

+ b

1

t

) = sf (1, 0) = tf (0, 1),

f

(1, 0) = (a, a

1

), f (0, 1) = (b, b

1

).

C = {f :

2

−→

2

: f (s, t) = (zs

− yt, ys + xt), x, y ∈

(ustalone)

}

dodawanie odwzorowań

↔ dodawanie liczb zespolonych

składanie odwzorowań

↔ mnożenie liczb zespolonych

odwzorowanie odwrotne

↔ odwrotność liczby zespolonej

f

(s, t) = (xs

− yt, ys + xt), f(1, 0) = (x, y), f(0, 1) = (−y, x).

f

(s + ti) = (x + yi)

· (s + ti).

17

(IV)
f

:

2

−→

2

- odwzorowanie liniowe

Zamiast (s, t) b¸edziemy pisać

"

s

t

#

.

Możemy napisać

f

"

s

t

#

=

"

as

+ bt

a

1

s

+ b

1

t

#

=

"

a b

a

1

b

1

# "

s

t

#

.

Odwzorowaniu f odpowiada tablica (macierz)

f

↔

"

a b

a

1

b

1

#

Sum¸e macierzy definiujemy jako macierz odpowiadaj¸ac¸a sumie odwzorowań, iloczyn
macierzy definiujemy jako tablic¸e która odpowiada składaniu odwzorowań. Jeżeli

f

↔

"

a b

a

1

b

1

#

, g

↔

"

˜

a ˜

b

˜

a

1

˜b

1

#

to

f

+ g

↔

"

a b

a

1

b

1

#

+

"

˜

a ˜b

˜

a

1

˜b

1

#

,

f

◦ g ↔

"

a b

a

1

b

1

#

·

"

˜

a ˜b

˜

a

1

˜b

1

#

"

a b

a

1

b

1

#

+

"

˜

a ˜b

˜

a

1

˜b

1

#

:=

"

a

+ ˜

a

b

+ ˜b

a

1

+ ˜

a

1

b

1

+ ˜b

1

#

"

a b

a

1

b

1

#

·

"

˜

a ˜b

˜

a

1

˜b

1

#

:=

"

a

˜

a

+ b˜

a

1

a˜b

+ b˜b

1

a

1

˜

a

+ b

1

˜

a

1

a

1

˜b + b

1

˜b

1

#

.

Zbiór macierzy (tablic) o dwóch wierszach i dwóch kolumnach oznaczmy

M

(2,2)

. Defi-

niujemy

C :=

("

x

−y

y x

#

, x, y

∈

)

.

dodawanie macierzy

↔ dodawanie liczb zespolonych

mnożenie macierzy

↔ mnożenie liczb zespolonych

Sk¸ad bior¸a si¸e powyższe macierze?
Oznaczmy przez f

z

odwzorowanie

−→

dane wzorem

f

z

(w) = z

· w.

Jest to odwzorowanie

liniowe bo

f

z

(w

1

+ w

2

) = z(w

1

+ w

2

) = zw

1

+ zw

2

= f

z

(w

1

) + f

z

(w

2

), w

1

, w

2

∈

f

z

(tw) = z(tw) = t(zw) = tf

z

(w), w

∈

, t

∈

.

Oznaczmy zbiór tych odwzorowań

liniowych przez

C

18

Odwzorowanie

Φ :

3 z −→ f

z

∈ C

spełnia warunki:

- jest bijekcj¸a,
- Φ(z + w) = Φ(z) + Φ(w), Φ(z

· w) = Φ(z) ◦ Φ(w).

Mówimy, że Φ jest wtedy izomorfizmem.
Ponieważ przy ustalonej bazie

B mamy izomorfizm f

z

−→ M

f

z

to musimy tylko

znaleźć postać macierzy M

f

z

. W tym celu przyjmijmy

B = {1, i}. Jeżeli

M

f

z

=

"

a b
a

1

b

1

#

to

"

a
a

1

#

= f

z

(1),

"

b
b

1

#

= f

z

(i)

i otrzymamy

f

z

(1) = z

· 1 = z = x + yi =

"

x
y

#

,

f

z

(i) = zi = (x + iy)i =

−y + xi =

"

−y
x

#

.

Ostatecznie

M

f

z

=

"

x

−y

y

x

#

.

Dla liczby zespolonej w postaci macierzy mamy nast¸epuj¸ac¸a jej postać trygonome-

tryczn¸a

"

x

−y

y

x

#

=

"

r

0

0 r

#

·

"

cos φ

− sin φ

sin φ

cos φ

#

.

Macierz

A =

"

a b
c d

#

nazywamy symetryczn¸a jeśli A = A

T

czyli b = c.

Macierz symetryczn¸a A nazywamy dodatnio określon¸a , co zapisujemy A > 0 jeśli

∀(x, y) ∈

2

\ {(0, 0)} ax

2

+ 2bxy + cy

2

>

0.

A > 0

⇔ ad − b

2

>

0, a > 0, d > 0.

Macierz kwadratow¸a B nazywamy ortogonaln¸a jeśli macierz transponowana B

T

jest

macierz¸a odwrotn¸a do B

B

· B

T

= B

T

· B = I.

Jedynymi macierzami ortogonalnymi wymiaru 2 s¸a macierze postaci

B =

"

cos φ

− sin φ

sin φ x cos φ

#

lub

19

B =

"

cos φ sin φ
sin φ

− cos φ

#

=

"

cos φ

− sin φ

sin φ cos φ

#

·

"

1 0
0

−1

#

.

W pierwszym przypadku mamy det B = 1 a w drugim det B =

−1.

20

Twierdzenie spektralne
Jeżeli A jest macierz¸a symetryczn¸a dodatnio określon¸a to istnieje macierz ortogo-

nalna C taka, że

A = C

·

"

λ

1

0

0 λ

2

#

· C

T

,

gdzie liczby dodatnie λ

1

, λ

2

s¸a wartościami własnymi macierzy A czyli pierwiastkami

równania

det(A

− λI) = 0 ⇔ λ

2

− (a + d)λ + ad − b

2

= 0.

Jeśli λ

1

6= λ

2

to macierz C jest dokładnie jedna i jest równa unormowanym warto-

ściom własnym

odpowiadaj¸acym λ

1

i λ

2

. Oznacza to, że

C =

"

a b
c d

#

,

A

"

a
c

#

= λ

1

"

a
c

#

,

A

"

b
d

#

= λ

2

"

b
d

#

oraz a

2

+ c

2

= 1, b

2

+ d

2

= 1.

Dla dodatnio określonej macierzy symetrycznej A istnieje jej pierwiastek kwadra-

towy

√

A = A

1

2

czyli macierz symetryczna dodatnio określona taka, że

A

1

2

· A

1

2

= A.

Jest ona zdefiniowana nast¸epuj¸aco

A

1

2

= C

·

"

√

λ

1

0

0

√

λ

2

#

· C

T

.

Twierdzenie o rozkładzie biegunowym.
Je´li macierz C jest nieosobliwa (det C

6= 0) to istniej¸a: dodatnio określona macierz

symetryczna A i ortogonalna macierz B takie, że

C = A

· B.

Szkic dowodu.

Przypuśćmy, że mamy rozkład C = A

· B. Wtedy

C

· C

T

= A

· B · B

T

· A

T

=

·A · A

T

= A

2

.

Macierz C

· C

T

jest symetryczna i dodatnio określona, st¸ad

A =

CC

T

1/2

.

Wtedy

B =

CC

T

−1/2

C

jest macierz¸a ortogonaln¸a.

Jeśli macierz A ma dwie różne wartości własne a niekoniecznie jest symetryczna to

dla niej również zachodzi twierdzenie spektralne je´li jest przemienna ze swoj¸a macierz¸a
transponowan¸a A

· A

T

= A

T

· A = I (mówimy, że A jest normalna):

21

A = C

·

"

λ

1

0

0 λ

2

#

· C

T

.

Wtedy również

A

n

= C

·

"

λ

n

1

0

0 λ

n

2

#

· C

T

.

Jeśli macierz A ma dwie różne wartości własne λ

1

, λ

2

a nie jest normalna to można

znaleźć macierz nieosobliw¸a B tak¸a, że

A = B

·

"

λ

n

1

0

0 λ

n

2

#

· B

−1

i A

n

= B

·

"

λ

n

1

0

0 λ

n

2

#

· B

−1

.

Jeśli λ

1

, λ

2

∈

to macierz B ma elementy rzeczywiste, s¸a one liczbami zespolonymi

gdy wartości własne A s¸a liczbami zespolonymi.

Ci¸

ag Fibonacciego.

Ci¸ag Fibonacciego F

n

określony jest warunkami

F

0

= 0, F

1

= 1, F

n+2

= F

n

+ F

n+1

.

Łatwo sprawdzamy, że wtedy

"

F

n−1

F

n

F

n

F

n+1

#

=

"

0 1
1 1

#

n

.

Wartościami własnymi macierzy

"

0 1
1 1

#

s¸a pierwiastki równania

λ

2

− λ − 1 = 0.

Łatwo obliczamy, że

λ

1

=

1
2

+

1
2

√

5, λ

2

=

1
2

−

1
2

√

5.

Macierz C ma postać

C =







1

√

1+λ

2
1

1

√

1+λ

2
2

λ

1

√

1+λ

2
1

λ

2

√

1+λ

2
2







.

Zadanie.
Podać wzór na F

n

.

22