Prof. Edmund Wittbrodt

Równania różniczkowe ruchu postępowego, obrotowego i płaskiego bryły

Ruch postępowy bryły

Równania różniczkowe ruchu. Jeżeli ciało, do którego przyłożono siły

1

2

,

, ...,

n

P P

P

, porusza się ruchem postępowym, to

przyspieszenie

a

tego ciała obliczamy z twierdzenia o ruchu środka masy

1

=

=

=

∑

n

C

i

i

ma

W

P

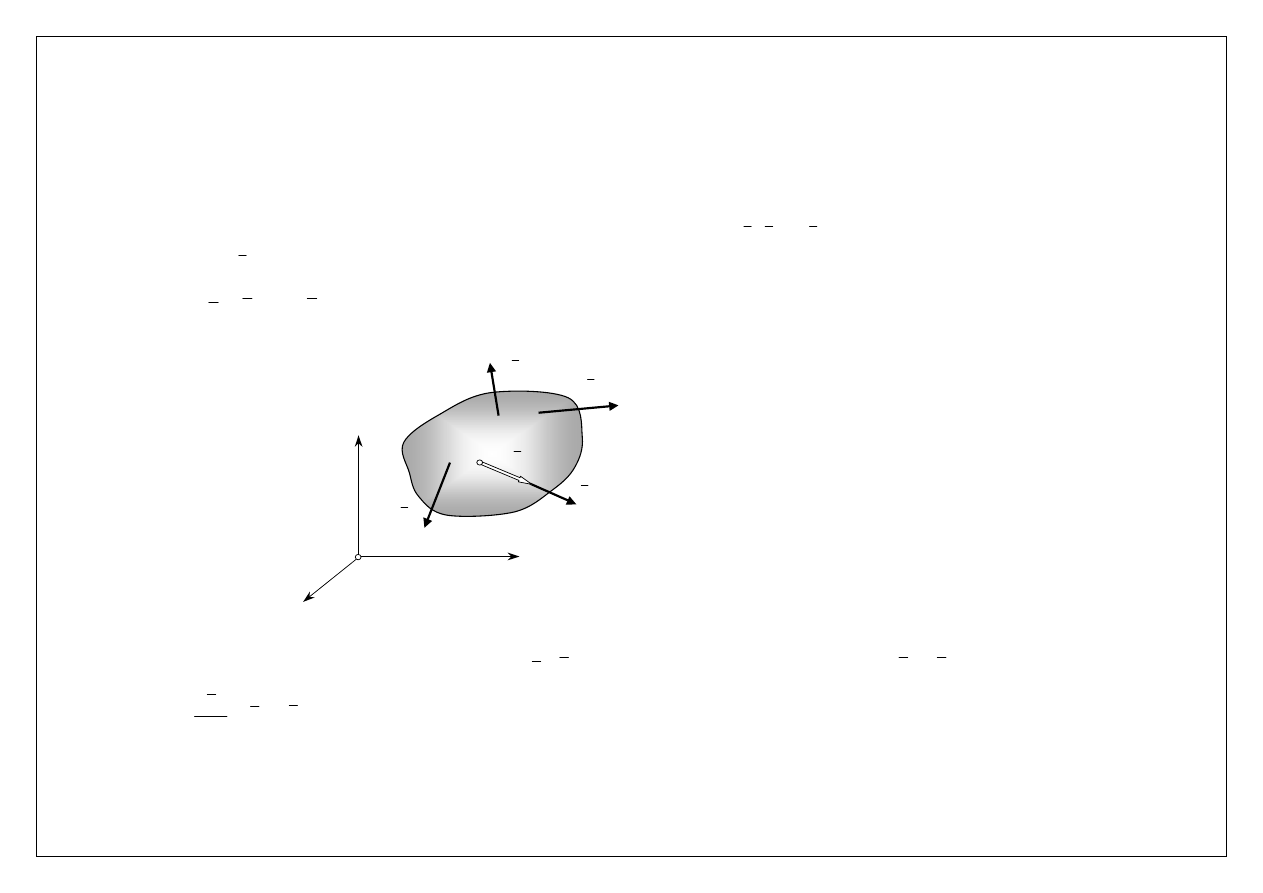
Bryła w ruchu postępowym

Ponieważ ciało porusza się ruchem postępowym (

0

ω

=

), to kręt ciała względem środka masy

0

C

K

=

, a zatem

0

C

C

dK

M

dt

=

=

.

Powyższy warunek musi być spełniony, jeżeli ciało ma poruszać się ruchem postępowym.

O

C

z

y

x

2

P

1

P

n

P

a

W

Prof. Edmund Wittbrodt

Przy opisie ruchu postępowego we współrzędnych prostokątnych

równania różniczkowe ruchu postępowego

zapisujemy w

postaci trzech równań skalarnych:

=

&&

C

Cx

mx

W

,

=

&&

C

Cy

my

W

,

(4.66)

=

&&

C

Cz

mz

W

,

gdzie

,

,









C

Cx

Cy

Cz

W

W

W

W

.

Prof. Edmund Wittbrodt

Ruch obrotowy bryły

Równania różniczkowe ruchu. Równanie różniczkowe ruchu obrotowego wokół nieruchomej osi, np. z, możemy otrzymać
korzystając z zasady d’Alemberta, która przyjmuje postać

2

1

( )

0

zi

t

z

i

m

M

dA

M

ρ

=

= −

+

=

∑

∫

.

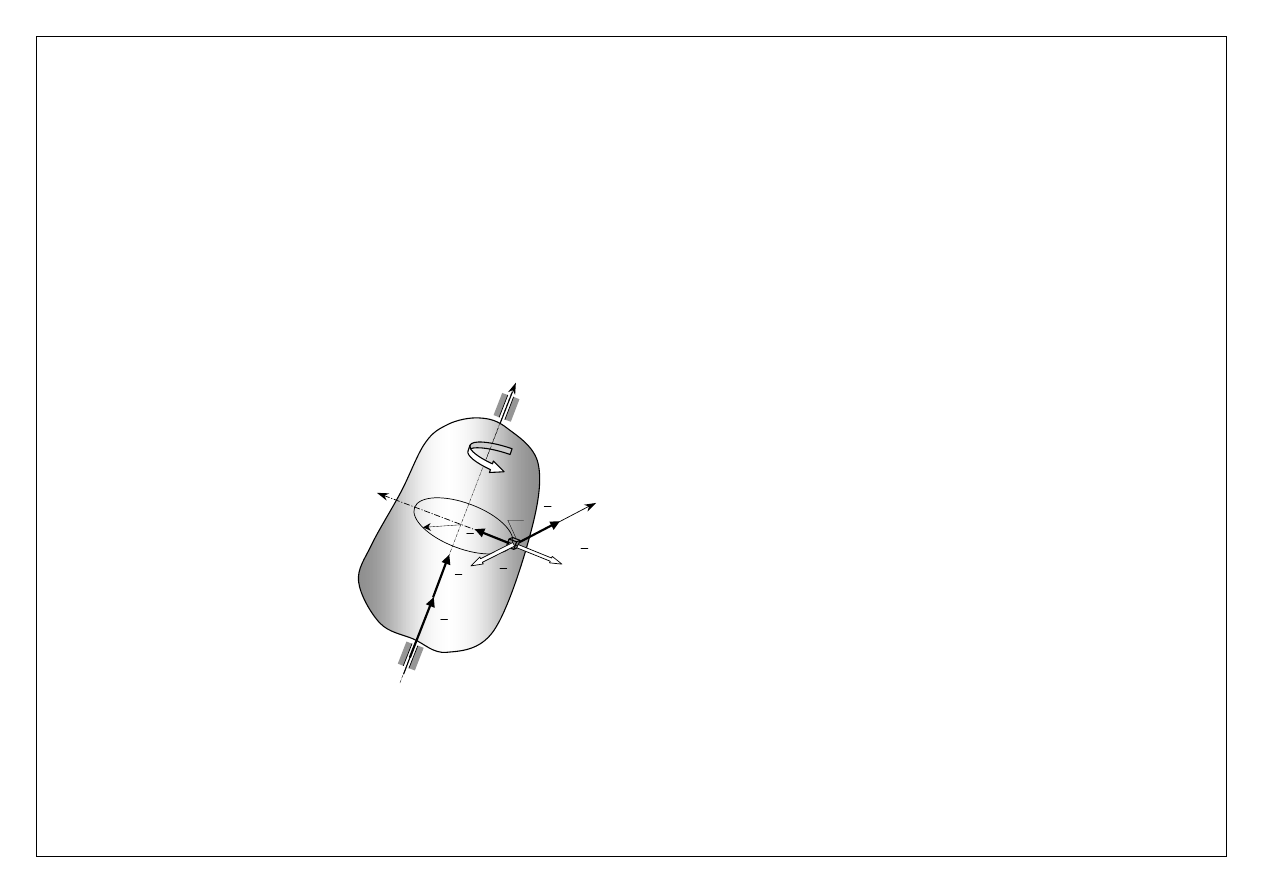
Dynamika ruchu obrotowego bryły

ω

ε

ρ

z

n

t

n

dA

t

dA

t

a

n

a

dm

z

M

Prof. Edmund Wittbrodt

Ponieważ

t

t

dA

a dm

=

,

natomiast zgodnie z (3.33) mamy

t

a

ρε

=

,

otrzymujemy

2

( )

z

m

dm

M

ρ ε

=

∫

.

Przyspieszenie kątowe

ε ϕ

=

&&

jest stałe, niezależnie od położenia rozważanego punktu, natomiast wyrażenie

2

( )

m

dm

ρ

∫

jest

masowym momentem bezwładności J

z

bryły względem osi obrotu. Zatem ostateczna postać równania (4.76) jest następująca

z

z

J

M

ϕ

=

&&

.

Równanie to nosi nazwę

równania różniczkowego ruchu obrotowego

.

W praktyce, w dynamice ruchu obrotowego często wygodniej jest korzystać z zasad dynamiki, podobnie jak to miało
miejsce w dynamice punktu materialnego.

Prof. Edmund Wittbrodt

Ruch płaski bryły

Równania różniczkowe ruchu. Dla otrzymania równań dynamiki ruchu płaskiego wykorzystamy twierdzenie o ruchu środka
masy oraz twierdzenie dotyczące krętu względem środka masy. Na podstawie pierwszego otrzymujemy

C

C

ma

W

=

,

gdzie:

C

a

– przyspieszenie środka masy, m – masa ciała,

C

W

– wektor siły wypadkowej zredukowanej do środka masy.

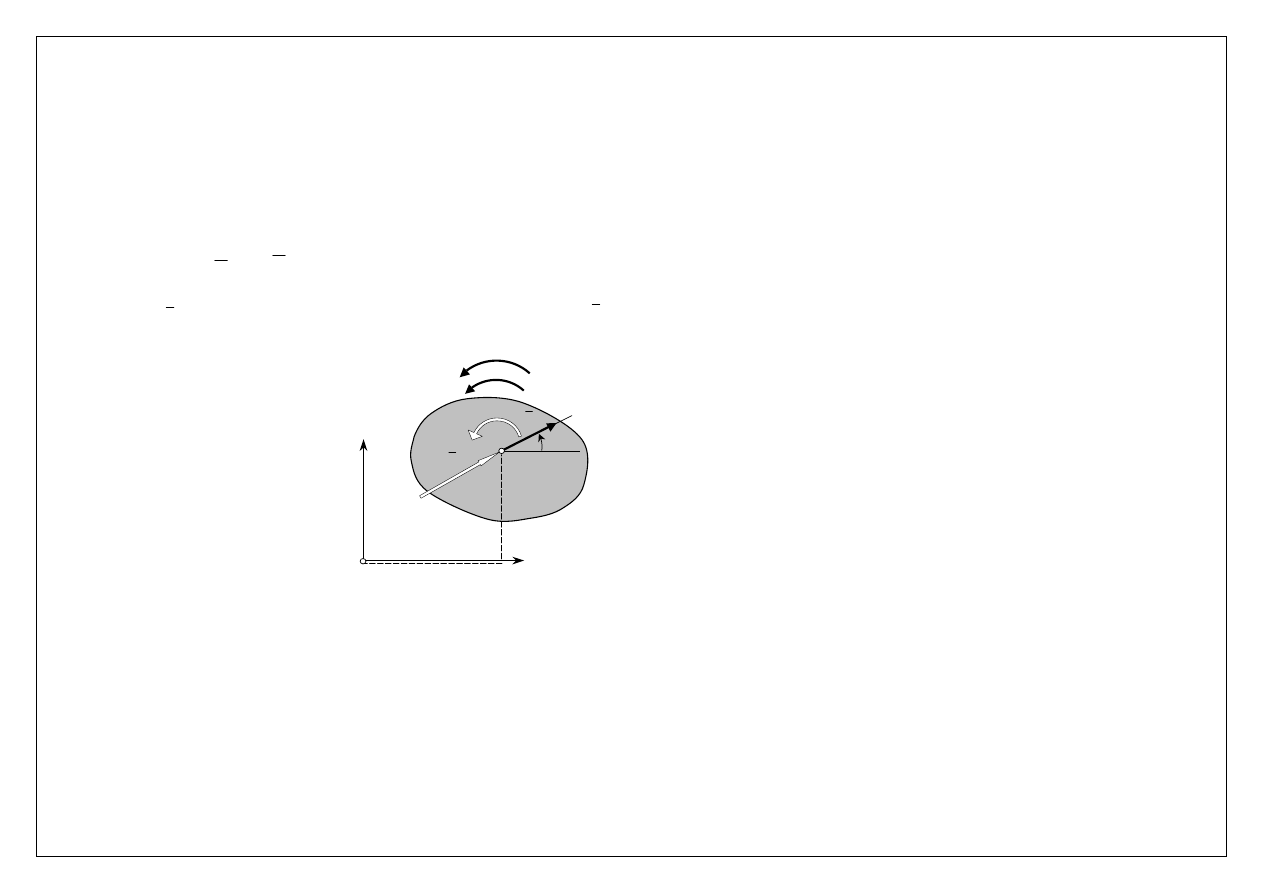
Dynamika ruchu płaskiego bryły

Z kolei na podstawie drugiego twierdzenia mamy

1

n

z

C

iC

C

K

J

M

M

ω

=

=

=

∑

&

&

,

gdzie: J

C

– masowy, osiowy moment bezwładności względem osi przechodzącej przez środek masy i prostopadłej do

płaszczyzny ruchu, M

C

– moment wypadkowy względem tej samej osi przechodzącej przez środek masy.

O

C

y

x

C

W

x

C

y

C

α

M

C

ω

ε

C

a

Prof. Edmund Wittbrodt

Powyższe równania możemy zapisać w postaci trzech równań skalarnych:

C

x

mx

W

=

&&

,

C

y

my

W

=

&&

,

C

C

J

M

ϕ

=

&&

.

Powyższe równania noszą nazwę

równań różniczkowych ruchu płaskiego

.