Destabilization of velocity feedback controllers

with stroke limited inertial actuators

Oliver Nicholas Baumann and Stephen John Elliott

Institute of Sound and Vibration Research, University of Southampton, University Road, Southampton,

Hampshire SO17 1BJ United Kingdom

[e-mail], [e-mail]

Abstract:

It has been observed when using inertial actuators for the active

reduction of structural vibration, that velocity feedback controllers are liable
to become unstable if the actuator is subject to stroke saturation. This article
presents a simple nonlinear, time domain model of an inertial actuator
mounted on a single degree of freedom system. At low amplitudes the actua-
tor, when used in a velocity feedback control loop, increases the effective
damping of the structure. At higher amplitudes the system is shown to be-
come unstable, however, and generates limit cycle oscillations having a pre-
dictable frequency.

© 2007 Acoustical Society of America
PACS numbers: 43.40.Vn, 43.25.Ts, 43.40.Ga [MRS]
Date Received: December 5, 2006

Date Accepted:

March 23, 2007

1. Introduction

Velocity feedback control, in which the velocity of a structure is fed back to a collocated force
actuator, is a well-known method of increasing damping and, hence, reducing the vibration of
the structure on which it acts.

1

The use of inertial, or proof mass, actuators as the forcing device

in such controllers has also been well documented.

2–5

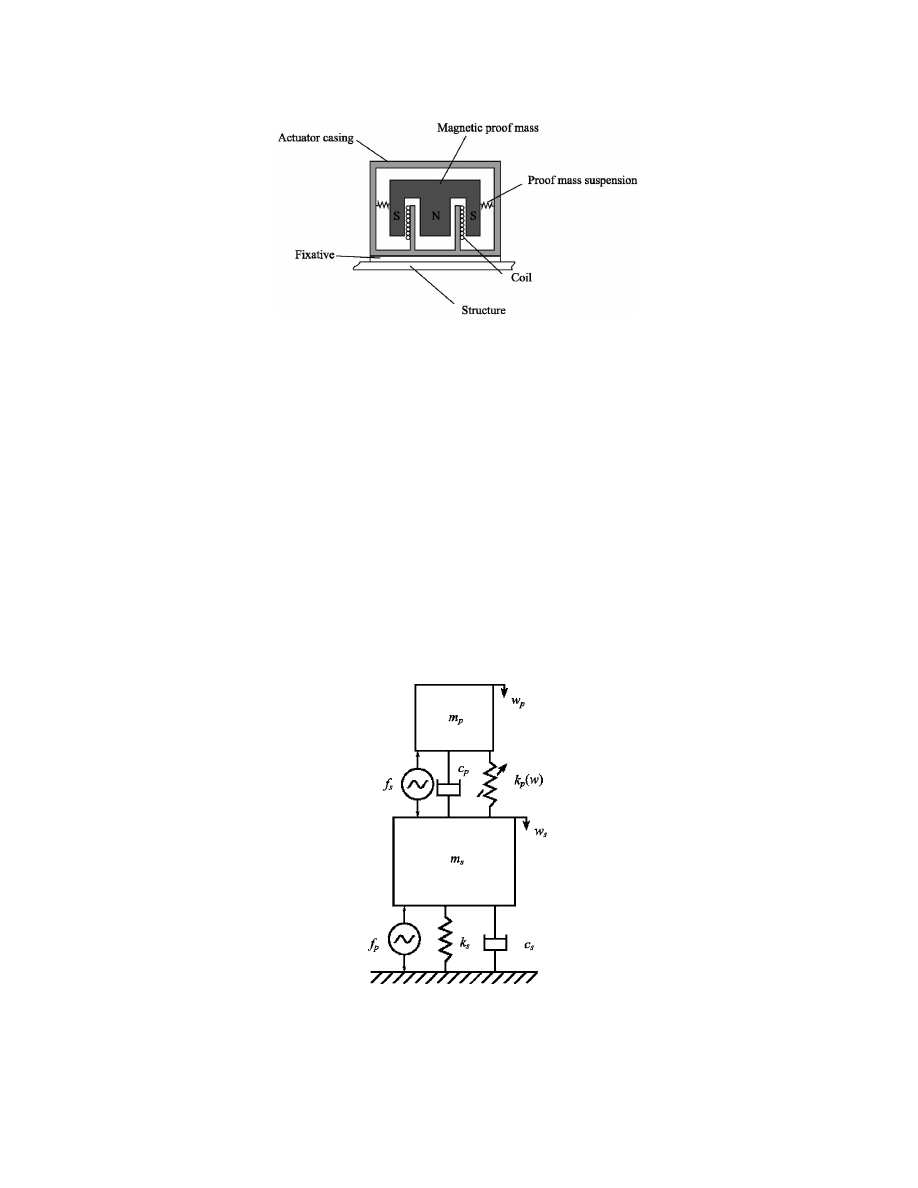
Figure 1 shows the cross section of such

a device comprising a proof mass, which in this case also acts as the magnet, a conducting coil,
and a casing. The device is attached to the structure to which one wishes to apply a force. The
current in the coil serves to produce a force which acts between the actuator proof mass and the
casing and, thus, the structure.

In any practical actuator design, the stroke of the proof mass is limited by the dimen-

sions of the casing or end-stops which are incorporated in the design. When the actuator is
subject to large or prolonged inputs, the proof mass will hit the end-stops and, hence, the dis-
placement will saturate, resulting in an impulse which is transmitted to the structure.

The issue of stroke saturation has been addressed by Chase et al.

6

in which the authors

observe that stroke saturation can lead to destabilizing forces in the control of a buckling beam
and performance degradation in vibration control. The authors propose a solution involving the
implementation of a secondary controller which feeds back the relative displacement and ve-
locity of the proof mass, a concept which has seen more attention recently.

5

It should be noted,

however, that the system under control in this case, namely, the buckling beam, was inherently
unstable and the purpose of control was to stabilize the system. Earlier work

7,8

investigated both

linear and nonlinear controllers, which are reported to reduce the tendency of the actuator proof
mass to collide with its end-stops, although the cited motivation for this work was to prevent
damage to the system and no mention was made of the system’s stability. It has been observed
by the authors, however, that, when velocity feedback loops are used in practice to control
structural vibration, the forces due to the displacement saturation of the proof mass can desta-
bilize the system. This problem is particularly severe in a system with multiple actuators and
local velocity controllers, since instability in one loop has been observed to induce instability in
all other loops.

9

This work concentrates on the modelling of a stroke limited inertial actuator

used in a velocity feedback control regime on a simple, but inherently stable, dynamic system.
It is observed that for large disturbances that result in control inputs which cause the actuator to
saturate, the modelled system becomes unstable, as has been observed experimentally.

O. N. Baumann and S. J. Elliott: JASA Express Letters

关DOI: 10.1121/1.2731018兴

Published Online 17 April 2007

J. Acoust. Soc. Am. 121

共5兲, May 2007

© 2007 Acoustical Society of America EL211

In this paper we present a lumped parameter model of an inertial actuator on a struc-

ture modelled as a single degree of freedom. The finite stroke of the actuator proof mass is
modelled as a nonlinear stiffness. The actuator is then driven using a current proportional to the
velocity of the structure. The response of the system to an impulsive force is presented in the
form of time series data and shown to become unstable for large impulse magnitudes.

2. The lumped parameter model

The actuator, attached to a single degree of freedom structure is modelled using a lumped pa-
rameter system as in Fig. 2. In practice the single degree of freedom structure would typically
model the lowest structural resonance. The actuator proof mass m

p

is, therefore, coupled to the

structural mass m

s

via the stiffness and damping parameters associated with its suspension,

k

p

共w兲 and c

p

, respectively, where k

p

共w兲 is dependant on the relative displacement of the inertial

mass and the structure w

共t兲. This allows the displacement saturation of the proof mass to be

modelled as the suspension system taking a very large stiffness. The mass associated with the
structure is connected to an inertial reference via the stiffness and damping parameters k

s

and

c

s

, respectively. The displacements of the proof mass and structure are defined as w

p

共t兲 and

w

s

共t兲, respectively, so that the relative displacement w共t兲=w

p

共t兲−w

s

共t兲. The primary force f

p

共t兲

Fig. 1. A schematic of an inertial actuator in cross section.

Fig. 2. A lumped parameter model of the actuator and structure.

O. N. Baumann and S. J. Elliott: JASA Express Letters

关DOI: 10.1121/1.2731018兴

Published Online 17 April 2007

EL212 J. Acoust. Soc. Am. 121

共5兲, May 2007

O. N. Baumann and S. J. Elliott: Velocity feedback controllers

acts between the structure and the inertial reference and the secondary force due to the current
in the actuator coil f

s

共t兲 acts between the proof mass and the structure. To avoid numerical

problems associated with parameter discontinuities, we define the stiffness to be a continuous
function of the form

k

p

共w兲 = k

lin

冉

1 +

共w共t兲兲

N−1

w

0

N

冊

,

共1兲

where k

lin

is the stiffness of the proof mass suspension when the proof mass is in its linear

range, being between −w

0

and w

0

, and N is an odd integer related to the rate at which the

stiffness of the suspension increases as the proof mass approaches saturation. In this way,
as the actuator proof mass approaches the limits of its linear range, it is prevented from
moving any further, relative to the structure, by the increase in stiffness. The secondary
force, acting between the structure and the proof mass, then becomes progressively less
effective. This relatively simple model of the proof mass saturation has been adopted to
ensure that both momentum and energy are conserved in the collision of the proof mass and
its end stops. The variable N may be altered to approximately model different types of
end-stop, a hard end-stop corresponding to a high value, N = 49 is used in the simulations
below, and a soft end-stop to a lower value. When the actuator proof mass is small com-
pared with w

0

, the stiffness is constant and the relative displacement varies linearly with

the applied force. As the relative displacement approaches ±w

0

, the proof mass makes

contact with the end-stops and the force required to appropriate further extension increases
significantly. The dynamics of system described above may be expressed in state space
form

x˙

共t兲 = Ax共t兲 + B

p

f

p

共t兲 + B

s

f

s

共t兲,

共2兲

where x is the state vector comprising the displacements and velocities of the proof and struc-
tural masses, A is the system matrix describing the coupled dynamics of the masses, B

p

and B

s

describe the relationship between the system states and the primary and secondary forces, re-
spectively.

We define the output of the system y to be the velocity of the structure mass which is

related to the state vector via the output equation

y

共t兲 = Cx共t兲.

共3兲

With fixed gain, direct velocity feedback the secondary force is defined to be

f

s

共t兲 = − hy共t兲 = − hCx共t兲,

共4兲

where h is the feedback gain, such that Eq.

共2兲 becomes

x˙

共t兲 = A

0

x

共t兲 + B

p

f

p

共t兲,

共5兲

where

A

0

=

关A − hB

s

C

兴.

共6兲

3. Stability

For linear systems, the stability of the system under fixed gain feedback control may be evalu-
ated by plotting the polar response of the open loop frequency response −hG

s

共j

␻

兲 in which

G

s

共j

␻

兲 is derived from the Fourier transform of the state equation without control

G

s

共j

␻

兲 = C关j

␻

I − A

兴

−1

B

s

.

共7兲

The Nyquist plot for the system described by the parameters given in Table 1 is shown

in Fig. 3 for h = 20. It should be noted that this Nyquist plot is only valid for the system acting
within its linear range. A complete discussion of the interpretation of such a plot as the proof

O. N. Baumann and S. J. Elliott: JASA Express Letters

关DOI: 10.1121/1.2731018兴

Published Online 17 April 2007

J. Acoust. Soc. Am. 121

共5兲, May 2007

O. N. Baumann and S. J. Elliott: Velocity feedback controllers EL213

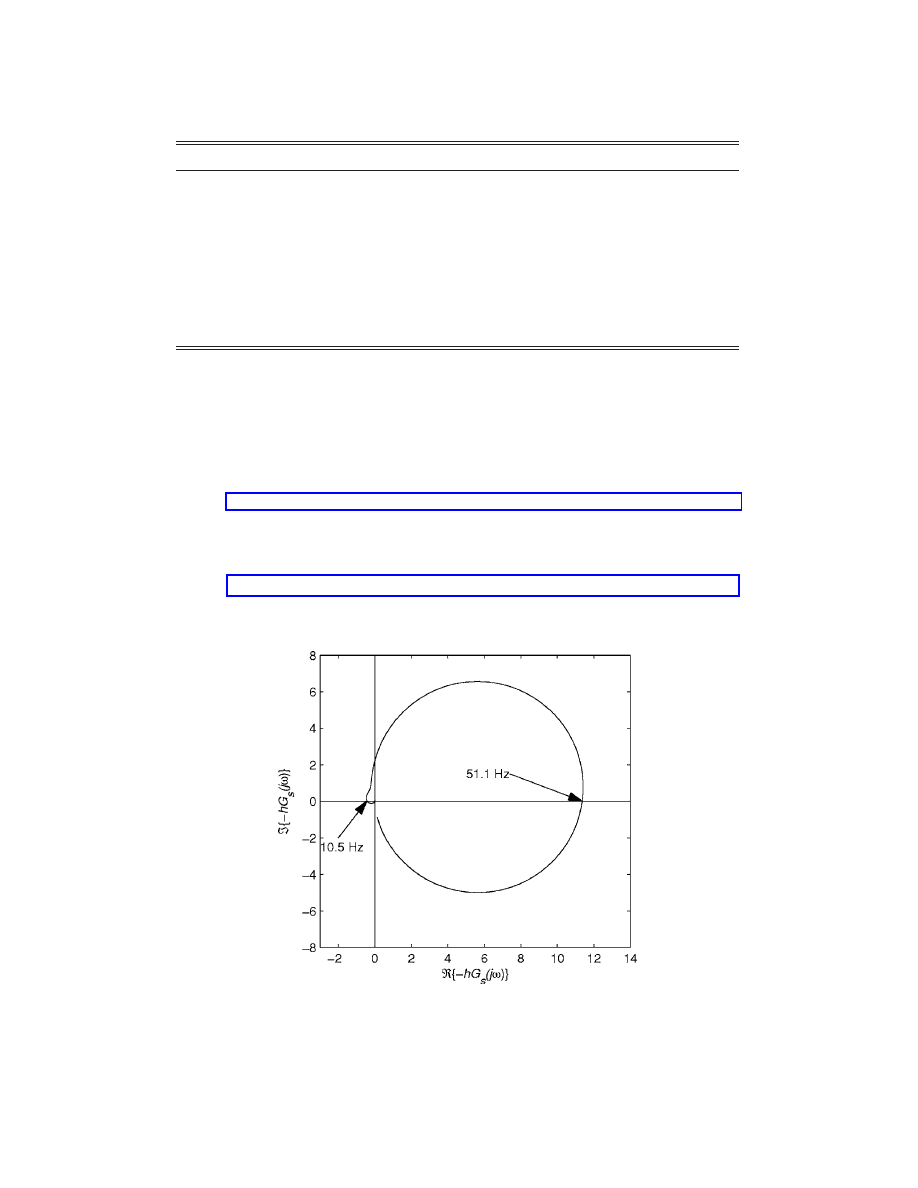
mass enters saturation is beyond the scope of this communication. The system is only condi-
tionally stable in that a finite increase in gain will result in the locus encircling the

共−1,0兲 point.

As the feedback gain is increased, the effective damping of the structural mass is increased, but
the effective damping in the proof mass is reduced. This effect may be clearly observed in the
impulse response of the system for increasing gains. Animation Mm. 1 shows the response of
system to an impulse without control, h = 0. The time series data is simulated using Matlab’s
ODE45 ordinary differential equation solver with variable time-steps.

Mm. 1 Animation of the system without control

共287 KB兲. This file is of type “.mpeg”.

Animation Mm. 2 shows the response of the system to the same impulse but with a

velocity feedback controller with a gain of 20 N / ms

−1

. It is clear from this animation that while

the vibration of the structural mass has been significantly reduced, the vibration of the proof
mass has been increased.

Mm. 2 Animation of the system with control

共508 KB兲. This file is of type “.mpeg”.

In both of the previous examples, the magnitude of the initial impulse subjected to the

structural mass was relatively small such that the proof mass did not hit its end-stops and the

Table 1. Table of model parameters.

Property

Value

m

p

0.032 kg

k

p

140 N / m

c

p

1.39 Ns/ m

m

s

0.05 kg

k

s

5000 N / m

c

s

0.32 Ns/ m

Force constant

1 N / A

f

0

共actuator兲

10.5 Hz

f

0

共structure兲

50.3 Hz

f

0

共connected system兲

39.3 Hz

Fig. 3. Nyquist plot of the open loop frequency response function for a control gain of 20.

O. N. Baumann and S. J. Elliott: JASA Express Letters

关DOI: 10.1121/1.2731018兴

Published Online 17 April 2007

EL214 J. Acoust. Soc. Am. 121

共5兲, May 2007

O. N. Baumann and S. J. Elliott: Velocity feedback controllers

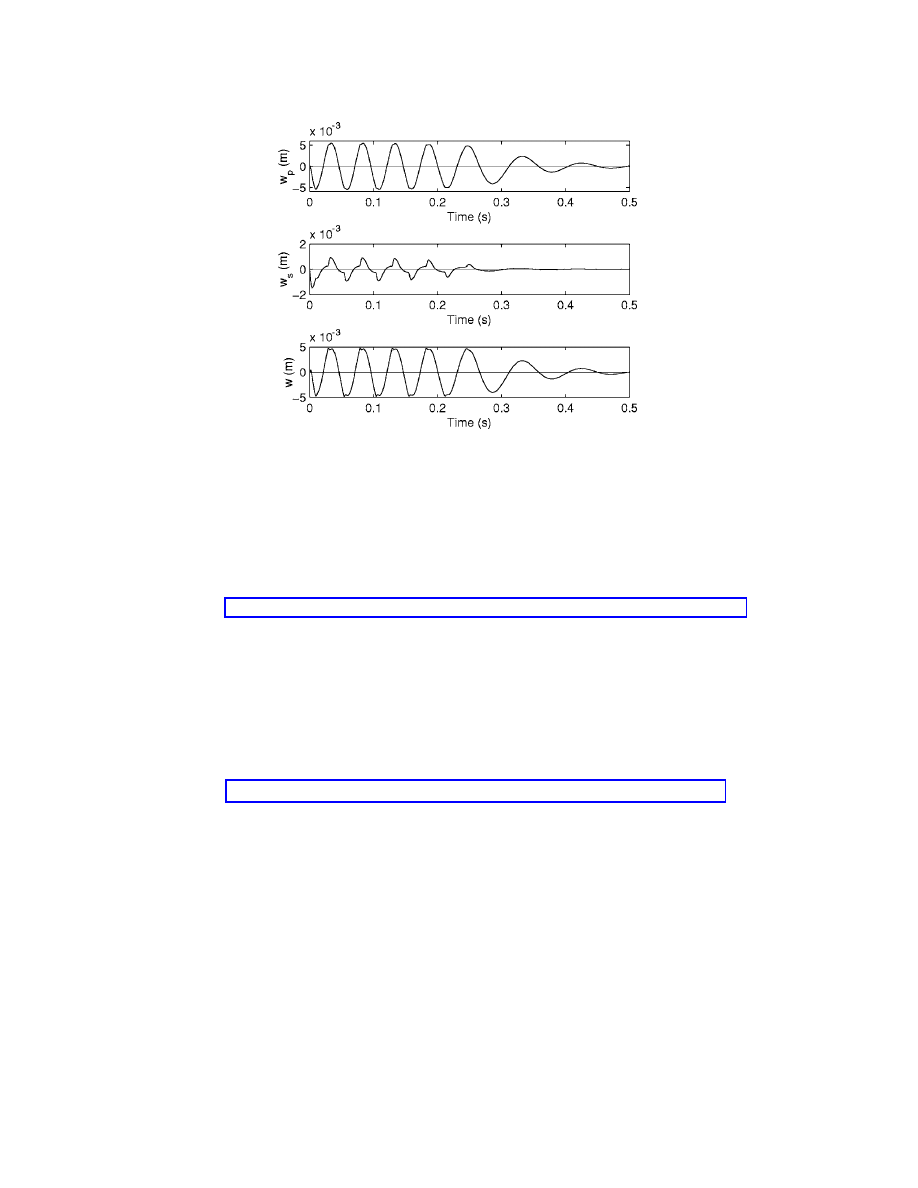
actuator operates within its linear range. For an actuator model with a ±5 mm stroke and a value
of N = 49, increasing the magnitude of the primary force impulse, while maintaining a feedback
gain of 20 N / ms

−1

, causes the proof mass to saturate. Figure 4 shows the response of the system

to the larger impulse. Along with the proof and structural mass displacements, the relative dis-
placement of the two, w

共t兲, is also shown which is bounded by the imposed stroke limit of

5 mm. Again, the corresponding animation is given in Mm. 3.

Mm. 3 Animation of the system with control under saturation

共768 KB兲. This file is of

type “.mpeg”.

It is clear from the figure and animation that, as the proof mass hits the end of its

stroke, it imparts an impulse-like force to the structural mass but that this behavior decays away.
Increasing the magnitude of the initial impulse only slightly above that used in Fig. 4 and Mm.
3 results in the responses given in Fig. 5. It is clear from this figure that the small increase in the
initial force magnitude results in an unstable system. It is also worth noting that the relative
displacement of the two masses at the moment of impact contains a significant amount of high
frequency content, the magnitude of which increases with the velocity of the impact. The cor-
responding animation, Mm. 4, depicts the system becoming unstable. Note that once the system
becomes unstable, after 0.7 s, control is turned off.

Mm. 4 Animation of the unstable system

共1466 KB兲. This file is of type “.mpeg”.

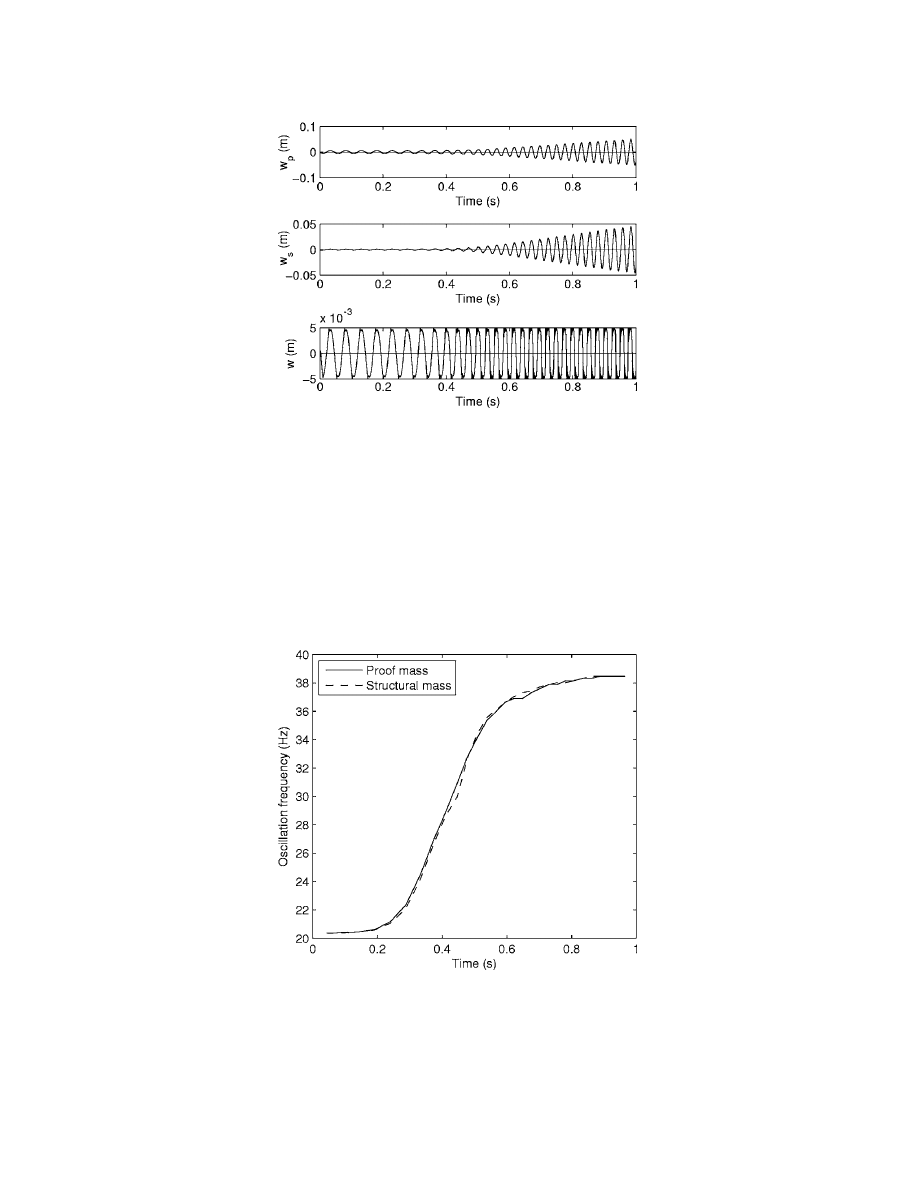
It can also be seen in Fig. 5 that as the system becomes unstable the oscillation fre-

quency of both of the masses become the same and increase over time. By detecting the zero
crossings of the signal we are able to plot this oscillation frequency as a function of time. This is
done for both the proof and structural masses in Fig. 6. This figure shows that the oscillation of
both masses starts off just above 20 Hz, close to the natural frequency of the proof mass on its
suspension, but quickly increases to a value approaching 39 Hz. This corresponds to the natural
frequency of the system in which the two masses are rigidly connected, oscillating on the struc-
tural support. Indeed this is the case for a significant proportion of the cycle as the proof mass is
pushed up against its end-stops. As the combined structure passes through the extremes of its
motion however the proof mass leaves its end-stops and, with the aid of the control force,
quickly moves through its stroke, hitting the opposite end-stop, and imparting an impulse of
considerable magnitude to the system, which is in phase with the velocity of the structural mass
and thus acts to increase its energy.

Fig. 4. Time series depicting the displacement responses of the proof and structure masses with control to a large
impulse.

O. N. Baumann and S. J. Elliott: JASA Express Letters

关DOI: 10.1121/1.2731018兴

Published Online 17 April 2007

J. Acoust. Soc. Am. 121

共5兲, May 2007

O. N. Baumann and S. J. Elliott: Velocity feedback controllers EL215

Attempts to overcome this by decreasing the value of N in Eq. (1), and thus softening

the end-stops and increasing the time over which the impact energy is imparted to the system,
has been found to make matters worse in that the initial force magnitude required to send the
system unstable is reduced. Also, making the actuator damping nonlinear, in a similar way the
stiffness, has been found to increase the impulse level before the instability occurs for low
feedback gains, but not suppress the instability. This behavior remains a topic of ongoing re-
search.

Fig. 5. Time series depicting the displacement responses of the proof and structure masses with control to a large
impulse.

Fig. 6. Plot of the oscillation frequencies of the proof and structural masses determined from the time series of Fig.
5 as a function of time.

O. N. Baumann and S. J. Elliott: JASA Express Letters

关DOI: 10.1121/1.2731018兴

Published Online 17 April 2007

EL216 J. Acoust. Soc. Am. 121

共5兲, May 2007

O. N. Baumann and S. J. Elliott: Velocity feedback controllers

4. Conclusions

A model is presented of a simple structure controlled by direct velocity feedback with a satu-
rating inertial actuator. The linear impulse response of the system shows that increasing the
feedback gain of a velocity feedback controller resulted in a reduction in vibration of the struc-
ture accompanied by an increase in vibration of the proof mass. Increasing the magnitude of the
initial impulse while maintaining a constant feedback gain, for which the closed loop system
acting within its linear range is stable, resulted in stroke saturation and eventually instability of
the feedback controller. The instability is due to the force imparted to the system as the proof
mass hits its end-stops being in phase with the velocity of the structure and so reduces the
damping of the system. If the initial magnitude is large enough, then the impulsive forces are
large enough to overcome the damping of the system, resulting in instability.

This work presents a model of an inherently stable system with a stroke limited inertial

actuator used in a velocity feedback regime. When the primary force, acting on the structure,
exceeds a particular value, such that the actuator saturates, the forces due to the saturation result
in the instability of the model. This agrees with the observation which has been made for prac-
tical systems in which inertial actuators are used for velocity feedback. The solution to this
problem probably lies in the use of a nonlinear controller and the investigation thereof remains
a topic of ongoing research.

Acknowledgments

The work of O. B. is supported by the Data and Information Fusion Defence Technology Centre.

References and links

1

M. J. Balas, “Feedback control of flexible systems,” IEEE Trans. Autom. Control AC-23, 673–674 (1978).

2

S. Griffin, S. A. Lane, C. Hansen, and B. Cazzolato, “Active structural-acoustic control of a rocket fairing using
proof mass actuators,” J. Spacecr. Rockets 38, 219–225 (2001).

3

L. Benassi and S. J. Elliott, “Active vibration isolation using an inertial actuator with local displacement
feedback control,” J. Sound Vib. 278, 705–724 (2004).

4

S. J. Elliott, M. Serrand, and P. Gardonio, “Feedback stability limits for active isolation systems with reactive
actuators,” J. Vibr. Acoust. 123, 250–261 (2001).

5

C. Paulitsch, P. Gardonio, and S. J. Elliott, “Active vibration control using an inertial actuator with internal
damping,” J. Acoust. Soc. Am. 119, 2131–2140 (2006).

6

J. G. Chase, M. Yim, and A. A. Berlin, “Integrated centering control of inertially actuated systems,” Control
Eng. Pract. 7, 1079–1084 (1999).

7

D. K. Lindner, G. A. Zvonar, and D. Borojevic, “Nonlinear control of proof-mass actuator,” J. Guid. Control
Dyn. 20, 464–470 (1997).

8

D. K. Lindner, G. A. Zvonar, and D. Borojevic, “Performance and control of proof-mass actuators accounting
for stroke saturation,” J. Guid. Control Dyn. 17, 1103–1108 (1994).

9

O. N. Baumann and S. J. Elliott, “The stability of decentralized multichannel velocity feedback controllers
using inertial actuators,” J. Acoust. Soc. Am. 121, 188–196 (2007).

O. N. Baumann and S. J. Elliott: JASA Express Letters

关DOI: 10.1121/1.2731018兴

Published Online 17 April 2007

J. Acoust. Soc. Am. 121

共5兲, May 2007

O. N. Baumann and S. J. Elliott: Velocity feedback controllers EL217