62

IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, VOL. 6, NO. 1, FEBRUARY 2010

H-Infinity State Feedback Control for a Class of

Networked Cascade Control Systems

With Uncertain Delay

Congzhi Huang, Yan Bai, and Xiangjie Liu

Abstract—Based on practical industrial process control, a typ-

ical configuration for networked cascade control systems (NCCSs)
is analyzed. This kind of NCCSs with state feedback controllers,
in which the network-induced delay is uncertain and less than a
sampling period, is studied. The sufficient condition for the stabi-
lizability of the NCCSs without disturbances is proposed, and the
state feedback stabilization control laws are derived via Lyapunov
stability theory and linear matrix inequality (LMI) approach. For
the NCCSs with disturbances, the criterion of its robust asymp-
totically stability is derived and the

-suboptimal state feedback

control laws are designed. The

-optimal state feedback

control laws are also put forward by optimizing a set of LMIs. A
simulation example of a NCCS for the main steam temperature in
a power plant is given to demonstrate the effectiveness of the pro-
posed approaches.

Index Terms—Linear matrix inequality, networked cascade con-

trol system (NCCS), state feedback control, uncertain delay.

I. I

NTRODUCTION

C

ASCADE control (CC), first proposed by Franks and
Worley in [1], is a very effective strategy to improve

control system performance, especially in the presence of dis-
turbances. As it has an inner loop, a CC system has the ability
to quickly attenuate the disturbances in the inner loop, and
the system performance is therefore improved. As a result, the
CC architecture has become one of the most important control
architectures and has found great applications in industrial
process control, such as power plants [2], chemical plants [3],
and so on.

Nowadays, real-time networks are more and more employed

to transmit various information in industrial process control.
Feedback control system wherein the control loops are closed
via real-time networks, is called a networked control system [4]
(NCS for short). One important feature of an NCS is that the
sensor data and control data are all transmitted through real-time
networks, which brings a lot of benefits, such as largely reduced
wiring and system cost, facility of system maintenance and di-
agnostics, and so on. As a result, NCS has found a great number

Manuscript received December 27, 2008; revised August 15, 2009 and Au-

gust 31, 2009. First published November 13, 2009; current version published
February 05, 2010. This work was supported in part by National Natural Sci-
ence Foundation of China under Grant 60974051, in part by the Program for
New Century Excellent Talents in University under Grant NCET-06-0207, and
in part by the Construction Project from Beijing Municipal Commission of Ed-
ucation, Beijing, China. Paper no. TII-09–06–0118.R1.

The authors are with the Department of Automation, North China Electric

Power University, Beijing, 102206, China (e-mail: [e-mail];
[e-mail]; [e-mail]).

Digital Object Identifier 10.1109/TII.2009.2033589

of applications in industrial process control, and has been the re-
search focus of the control theory academia in the past decades,
see surveys in [5]–[6] and special issues in [7]–[11].

CC system, wherein the control loops are closed via a real-

time network, is called a networked cascade control system [12],
[13] (NCCS for short thereafter). A NCCS is a special kind
of CC system as well as a particular type of NCS, and thus it
has the merits of both of them. Due to these prominent advan-
tages, NCCS has been widely implemented in practical indus-
trial process control for decades. However, the insertion of net-
works into the control loops makes the system analysis and de-
sign become extremely complicated. In a NCCS, there are three
intelligent field devices: a primary sensor, a secondary sensor,
and an actuator. The network may merely exist in either one of
the primary control loop and the secondary control loop, or in
both of them, which depends on the practical configuration since
the controllers can be placed arbitrarily in the three intelligent
field devices [13]. The network-induced delay is unavoidable
while the data packet is transmitted through the network, and the
data packet may be lost, for reasons of reliability. Both of them
are determined by the medium access control methods and the
hardwares adopted. The delay and packet dropout can degrade
the performance of the system, and even make the system un-
stable [14], [15]. Some ideal assumptions under the traditional
CC system theory, such as nondelayed accurate transmission of
the real-time data in the control loops, and the synchronization
among different control components, are no longer true. There-
fore the traditional CC theory must be reevaluated before appli-
cation of NCCSs.

Generally, in a NCCS, due to the uncertainty of the network

transmission and network load, the network-induced delay is
usually uncertain. To deal with the uncertainty, robust

con-

trol is an effective tool to describe and analyze these problems.
Besides, the controllers can be designed directly and conve-
niently in this way, and the complicated tuning procedures will
be omitted. As a result, the robust

control theory is found

in a lot of applications for the analysis and synthesis of NCSs.
The robust stability for an uncertain linear system was studied
in [16], but it only considered a constant delay. In [17], the
NCS with random packet dropout was modeled as a Markovian
jumping linear system, and an

optimal controller was

designed in terms of an

norm performance. Based on the

free weighting matrix method, an

state feedback controller

was developed for a class of NCSs with time-varying but
bounded delays in [18]. In [19], an

controller was derived

by solving a set of LMIs for the communication-constrained
NCSs with random packet dropout. The NCSs with both data

1551-3203/$26.00 © 2009 IEEE

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

HUANG et al.: H-INFINITY STATE FEEDBACK CONTROL FOR A CLASS OF NETWORKED CASCADE CONTROL SYSTEMS WITH UNCERTAIN DELAY

63

Fig. 1. Configuration diagram of a typical NCCS.

packet dropout and network-induced delay were considered in
[20], and an

controller was designed based on multiob-

jective optimization technology. A uniform model for an NCS
was established in [21], taking into account both network and
state quantization. A quantized state feedback

controller

was designed to make the system global and asymptotically
stable. In continuous time domain, the robust

state feed-

back controllers were designed in terms of LMIs for an NCS
with both delay and packet dropout, see [22]–[25]. Based
on delay-dependent approach, a robust

controller was

designed in [26] for a class of uncertain nonlinear NCSs, which
can be represented by a T-S fuzzy model with uncertainties.

However, due to the structural complexity of the CC system,

few papers have ever discussed the application of robust
control in a NCCS. In this paper, the robust

state feedback

control laws for a class of NCCSs, in which the network-induced
delay is uncertain and less than a sampling period, are analyzed
and designed. The rest of the paper is organized as follows: In
Section II, a closed-loop model of the NCCSs is established in
discrete time domain by state space method. Based on Lyapunov
stability theory and LMI approach, the sufficient condition for
the robust asymptotically stability of the NCCSs without dis-
turbances is derived in Section III, and the state feedback stabi-
lization control laws are also developed. Section IV is concerned
with the robust asymptotically stability of the NCCSs with dis-
turbances, and the -optimal state feedback

control laws

are designed. A simulation example considering power plant
cascade steam temperature is presented in Section V to verify
the effectiveness of the proposed methods. Conclusions are fi-
nally given in Section VI, and the future research directions are
also pointed out.

Notation:

is the identity matrix with appropriate dimen-

sions,

represents the induced matrix 2-norm. The notation

(respectively,

) for

means that

is a

real symmetric positive-definite (respectively, negative-definite)
matrix.

II. M

ODELING OF

NCCS

Based on practical industrial process control, four typical

configurations of NCCSs were put forward and analyzed in
[13]. The second type of NCCS, so called Type II NCCS is
studied here, and the configuration diagram is shown in Fig. 1.

In Fig. 1, the primary sensor

is connected with the pri-

mary plant

, while the secondary sensor

is combined

with the secondary plant

.

is the actuator installed in the

field connected with the secondary plant, and

is a real-time

network, which may be industrial Ethernet, or some fieldbus.
The primary controller

, and the secondary controller

,

are placed in the primary sensor

and the actuator

, respec-

tively. The primary controller sends out the control command
and the secondary sensor sends out the state variables of the sec-
ondary plant via the same network in most cases, and therefore

Fig. 2. Equivalent block diagram of typical NCCS in Fig. 1.

the two network-induced delays can be equivalently placed at
the input of the secondary controller. Since the secondary con-
troller considered here is linear, the network-induced delay
can be viewed as only existing between the secondary controller
and the actuator, as shown in Fig. 2.

The type of NCCS depicted in Fig. 2 is studied hereinafter,

and for the convenience of narration, the following assumptions
are made beforehand: 1) The state variables of the primary and
secondary plants are both available for the corresponding con-
trollers, respectively. 2) Both the sensors are time-driven, which
means that they periodically sample the states of the plants and
send them to the corresponding controllers. 3) Both the con-
trollers are event-driven. The primary controller computes the
control output and sends it to the secondary controller on ob-
taining the latest samples of the primary plant states. The sec-
ondary controller computes the control command and sends it
to the actuator as soon as it receives the latest samples of the
secondary plant and the command from the primary controller.
4) The actuator is also event-driven. It actuates the plants once
it receives the latest control command. 5) The delay

is un-

certain and less than a sampling period , i.e.,

. Data

packet is transmitted in single packet without any loss. 6) The
sampling times of the sensors, the transmission time from the
primary sensor to the primary controller as well as from the sec-
ondary controller to the actuator, and the computational time of
the controllers, are all negligible or lumped into

for they are

much less than

. 7) The gains of the primary and secondary

sensors are both 1, but if needed in the analysis, the dynamics
of the two measurement components could be included in the
primary and secondary plants, respectively. The gain of the ac-
tuator is also assumed to be 1.

With the reference to be zero, the primary controller is a static

state feedback controller. It is given by

(1)

where

is the state variable of the primary plant.

and

are the state feedback gain matrix and the control output

of the primary controller, respectively. The static state feedback
is also adopted in the secondary controller, which can be de-
scribed by

(2)

where

is the state variable of the secondary plant.

and

are the state feedback gain matrix and the control output

of the secondary controller, respectively.

Combining (1) and (2), results in

(3)

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

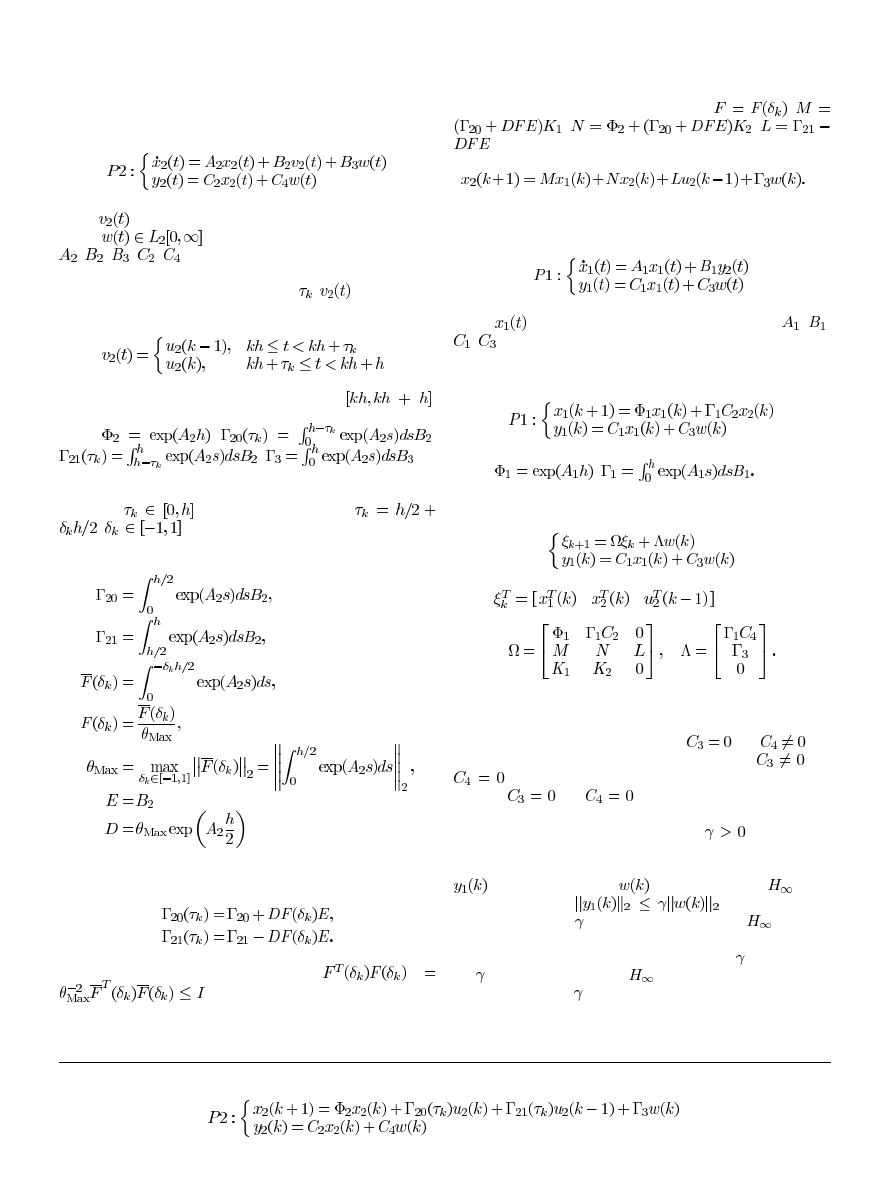
64

IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, VOL. 6, NO. 1, FEBRUARY 2010

The secondary plant is continuous-time linear time invariant,

and its state space equations are expressed as

(4)

where

is the control command actually received by the ac-

tuator.

is the disturbance with limited energy.

,

,

,

,

are constant matrices with appropriate di-

mensions.

In view of the network-induced delay

,

is a piecewise

function shown as

.

(5)

Discretizing (4) in the sampling period

,

yields equation (6) shown at the bottom of the page,
where

,

,

,

.

Next we transform the uncertainty of the delay into the uncer-

tainty of the coefficient matrices. The network-induced delay is
subject to

. It can be represented as

,

.

Let

then

In addition, it is easy to deduce that

.

For the convenience of analysis, denote

,

,

,

, then (6) can be rewritten as

(7)

The primary plant is also continuous-time linear time in-

variant, which is described by

(8)

where

is the state variable of the primary plant.

,

,

,

are constant matrices with appropriate dimensions.

After discretization of (8), we obtain its discrete time state

space representation

(9)

where

,

Combining (3), (6), (7) and (9), the closed-loop model of the

NCCS is presented as follows:

(10)

where

Remark 1:

In the closed-loop model of the NCCS established

as (10), both the inner loop disturbance and the outer loop dis-
turbance are considered. In addition, if

and

, the

disturbance only exists in the inner loop, while if

and

, the disturbance only appears in the outer loop. Spe-

cially, if

and

, there are no disturbances in the

NCCS.

Definition 1:

Given a certain constant

, if there exist

state feedback control laws (1) and (2), which make the NCCS
(10) robust asymptotically stable, and the primary plant output

and the disturbance

are subject to the

norm

bounded constraint

under zero initial

conditions, then the -suboptimal state feedback

stabiliza-

tion control laws exit for the closed-loop NCCS(10), and the
disturbance attenuation degree of the system is . Furthermore,
the -optimal state feedback

control laws can be obtained

by minimization of .

(6)

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

HUANG et al.: H-INFINITY STATE FEEDBACK CONTROL FOR A CLASS OF NETWORKED CASCADE CONTROL SYSTEMS WITH UNCERTAIN DELAY

65

III. R

OBUST

A

SYMPTOTICALLY

S

TABILITY OF

NCCS W

ITHOUT

D

ISTURBANCES

In order to derive the sufficient conditions for the robust

asymptotically stability of NCCS (10) without disturbances,
the following two lemmas are vital.

Lemma 1:

[27] Given constant matrices

,

, and

,

where

,

, then

holds

The following lemma is used to deal with the uncertainties of

the network-induced delays in a NCCS.

Lemma 2:

[28] Given constant matrices

,

, and

,

where

, for any

subject to

,

holds if there exists a constant

scalar

satisfying

Theorem 1:

For the NCCS (10) without disturbances

, if there exist symmetric positive-definite matrices

,

,

,

and a scalar

such that the following inequality holds

in (11) shown at the bottom of the page, then the closed-loop
NCCS (10) with the state feedback control laws (1) and (2) is
said to be robust asymptotically stable.

Proof:

Define a Lyapunov functional as

(12)

Taking the derivative of the Lyapunov functional along the

solution of (10), we obtain

where

shown in (13) at the

bottom of the page.

In order to ensure the asymptotically stability of the closed-

loop system, we must have

, which results in

.

By Lemma 1, the following is true shown in (14) at the bottom
of the page.

Applying Lemma 1 twice, (15) is equivalent to (14)

(15)

(11)

(13)

(14)

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

66

IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, VOL. 6, NO. 1, FEBRUARY 2010

Substituting

,

,

into (15), and assuming that the first

equation shown at the bottom of the page, (15) can be rewritten
as

(16)

By Lemma 2, (16) holds if there exists a constant

such

that shown in (17) at the bottom of the page.

Incorporating the first two terms of (17), and applying Lemma

1, we can obtain (11). That completes the proof.

Corollary 1:

If there exist symmetric positive-definite ma-

trices

,

,

, and

,

with appropriate dimensions, such

that shown in (18) at the bottom of the page, then the NCCS

closed-loop system (10) without disturbances is said to be ro-
bust asymptotically stable. In addition, the state feedback stabi-
lization control laws are given by

(19)

Proof:

By Theorem 1, if there exist symmetric posi-

tive-definite matrices

,

,

satisfying (11), the NCCS

closed-loop system(10) without disturbances is asymptoti-
cally stable. Pre-multiplying and post-multiplying (11) by

, and letting

,

,

,

,

yields (18).

As a result, the state feedback control gains are computed as

, and

.

IV. R

OBUST

A

SYMPTOTICALLY

S

TABILITY OF

NCCS W

ITH

D

ISTURBANCES

The robust asymptotically stability of the NCCS closed-loop

system (10) with disturbances is considered hereinafter.

Theorem 2:

For a given constant

, if there exist sym-

metric positive-definite matrices

,

,

, and a constant

such that the following inequality holds as shown in (20) at the
bottom of the next page, then the NCCS closed-loop system (10)

(17)

(18)

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

HUANG et al.: H-INFINITY STATE FEEDBACK CONTROL FOR A CLASS OF NETWORKED CASCADE CONTROL SYSTEMS WITH UNCERTAIN DELAY

67

with disturbances is said to be asymptotically stable with distur-
bance attenuation degree as . The state feedback control laws
(1) and (2) are the -suboptimal state feedback

control laws

for the system.

Proof:

By choosing a Lyapunov functional as (12),

under Theorem 1, the closed-loop system (10) is asymp-
totically stable if (20) holds. Define a performance index
functional as:

.

If the disturbance attenuation degree is

, the fol-

lowing condition must be satisfied:

,

i.e.,

. For the NCCS with any nonzero disturbance

satisfying

and zero initial conditions,

shown in the second equation

at bottom of the page, yields

and

therefore,

if

.

Applying Lemma 1 four times to

, yields (21) shown

at the bottom of the page. Substituting

,

,

into (21), and

denote the fourth equation shown at the bottom of the page, (21)
can be rewritten as (22) shown at the bottom of the next page.

(20)

(21)

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

68

IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, VOL. 6, NO. 1, FEBRUARY 2010

By Lemma 2, (22) holds if there exists a constant

such

that the following is true in (23) shown at the bottom of the page.

Combining the first two terms of (23), and applying Lemma 1,

results in (20).

Corollary 2:

For the NCCS (10) with disturbances, given a

constant

, if there exist symmetric positive-definite ma-

trices

,

,

, and matrices

,

with appropriate dimen-

sions, satisfying the following inequality shown in (24) at the
bottom of the page, then the -suboptimal state feedback
control laws exist, and the gain matrices are

, and

.

Proof:

Premultiplying and postmultiplying (20) by

and letting

,

,

,

,

, (24) is

available and the gain matrices are computed as in Corollary 2.

Corollary:

For the NCCS closed-loop system (10), if there

exist symmetric positive-definite matrices

,

,

, matrices

,

with appropriate dimensions, and a scalar

such that the following optimization problem is feasible:

shown in (25) at the bottom of the page.

Then the -optimal state feedback

control laws exist, and

(22)

(23)

(24)

(25)

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

HUANG et al.: H-INFINITY STATE FEEDBACK CONTROL FOR A CLASS OF NETWORKED CASCADE CONTROL SYSTEMS WITH UNCERTAIN DELAY

69

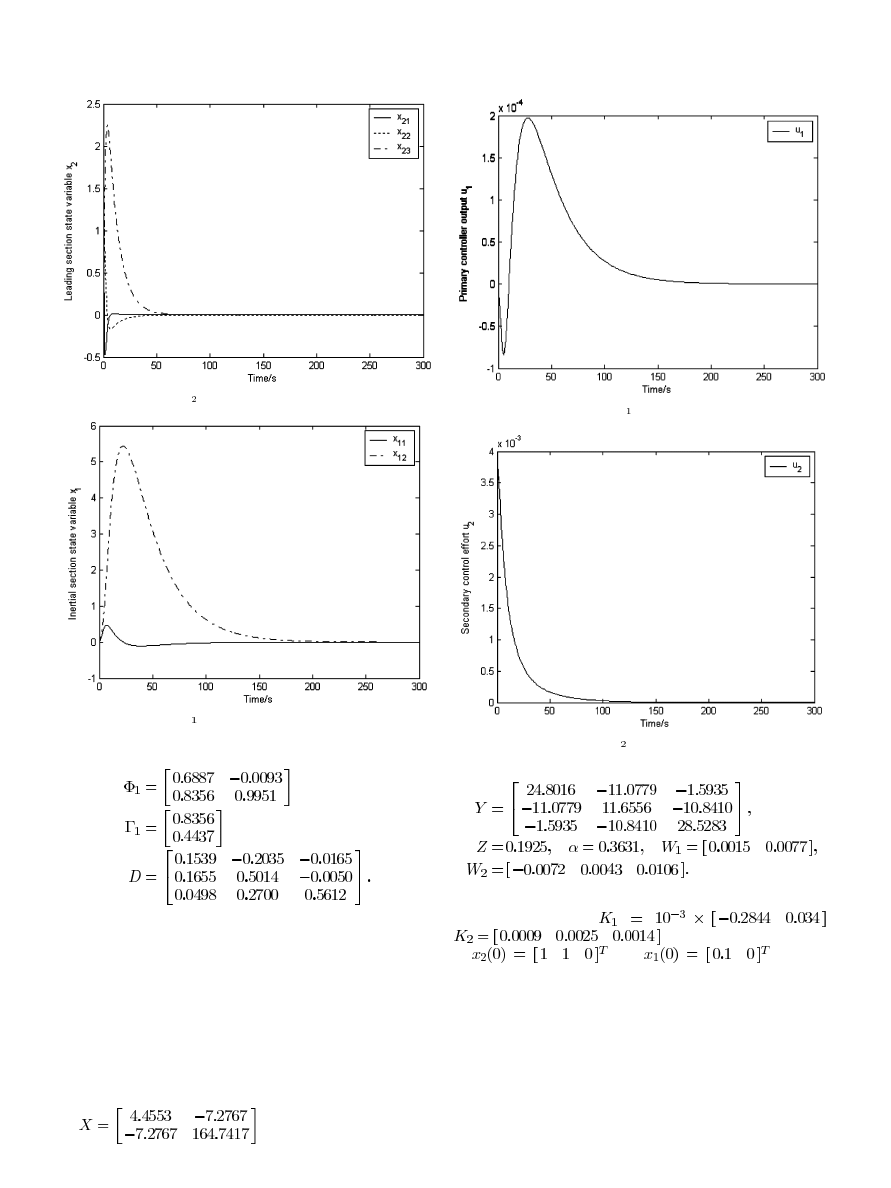
Fig. 3. Schematic diagram of NCCS for main steam temperature.

the gain matrices of the -optimal state feedback

control

laws are:

,

.

By solving optimization problem (25), the optimal solution

is available, and the minimum disturbance attenuation degree is

.

V. S

IMULATION

E

XAMPLES

In a power plant boiler-turbine system, the superheater is an

important part of the steam generation process, where steam is
superheated before entering the turbine that drives the gener-
ator. Proper control of the superheated steam temperature is ex-
tremely important to ensure the overall efficiency and safety of
the power plant. The attemperator is an effective means of low-
ering the temperature of the steam.

In the process, two time constants are associated with the

superheater. One represents the time taken for changes in the
firing rate to affect the steam temperature, the other is the time
taken for the steam and water mixture leaving the attemperator
to appear at the outlet of the final superheater. They are respec-
tively called the leading section and the inertial section. Because
of the long time constants associated with the superheater, the
single-loop control by measuring the temperature of the steam
leaving the final superheater, and modulating the flow of cooling
water to the spray attemperator, would produce excessive devi-
ations in temperature.

These difficulties are addressed by the application of a CC

system as shown in Fig. 3. The temperature of the steam leaving
the secondary superheater is measured and fed to a controller.
In this controller the measured-value signal is compared with a
fixed desired-value signal and the controller’s output forms the
desired-value input for a secondary controller. The secondary
controller compares this desired-value signal with a measure-
ment representing the temperature of the steam immediately
after the spray-water attemperator. The real-time information
in the both control loops are transmitted via the same commu-
nication network with a sampling period of 1 s. Assume the
two network-induced delays are both equivalent to

, which

is time-varying and not longer than a sampling period, i.e.,

And therefore, Fig. 3 can be equivalently transformed to

Fig. 4.

Fig. 4. Block diagram of NCCS for main steam temperature.

It is assumed that the transfer functions of the inertial

and leading sections are:

,

, respectively.

The state-space representation of the leading section is de-

scribed by

where the state variables of the leading section are defined as

is the output of the leading section, which is also the

leading section outlet steam temperature.

After discretization, the following coefficents are available:

The state-space representation of the inertial section is written

as

where the state variables of the inertial section are denoted as

is the output of the inertial section, which is also the

main steam temperature.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

70

IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, VOL. 6, NO. 1, FEBRUARY 2010

Fig. 5. State response of

x in NCCS without disturbances.

Fig. 6. State response of

x in NCCS without disturbances.

By discretization, the following coefficients are obtained:

The state feedback control laws for the NCCS without and

with disturbances, will be designed according to the corollaries
proposed above by using the LMI toolbox in MATLAB, respec-
tively, and the state responses of the inertial and leading sec-
tions will be presented for the system under the given initial
conditions.

A. State Feedback Stabilization Control Laws for NCCS
Without Disturbances

For the NCCS without disturbances, the feasible solution of

(18) can be computed as follows:

Fig. 7. Primary controller output

u in NCCS without disturbances.

Fig. 8. Secondary control effort

u in NCCS without disturbances.

Therefore, the gain matrices of the state feedback stabiliza-
tion control laws are:

,

. Given the initial conditions

as

, and

, the state

responses of the leading and inertial sections are presented as
Figs. 5 and 6, respectively.

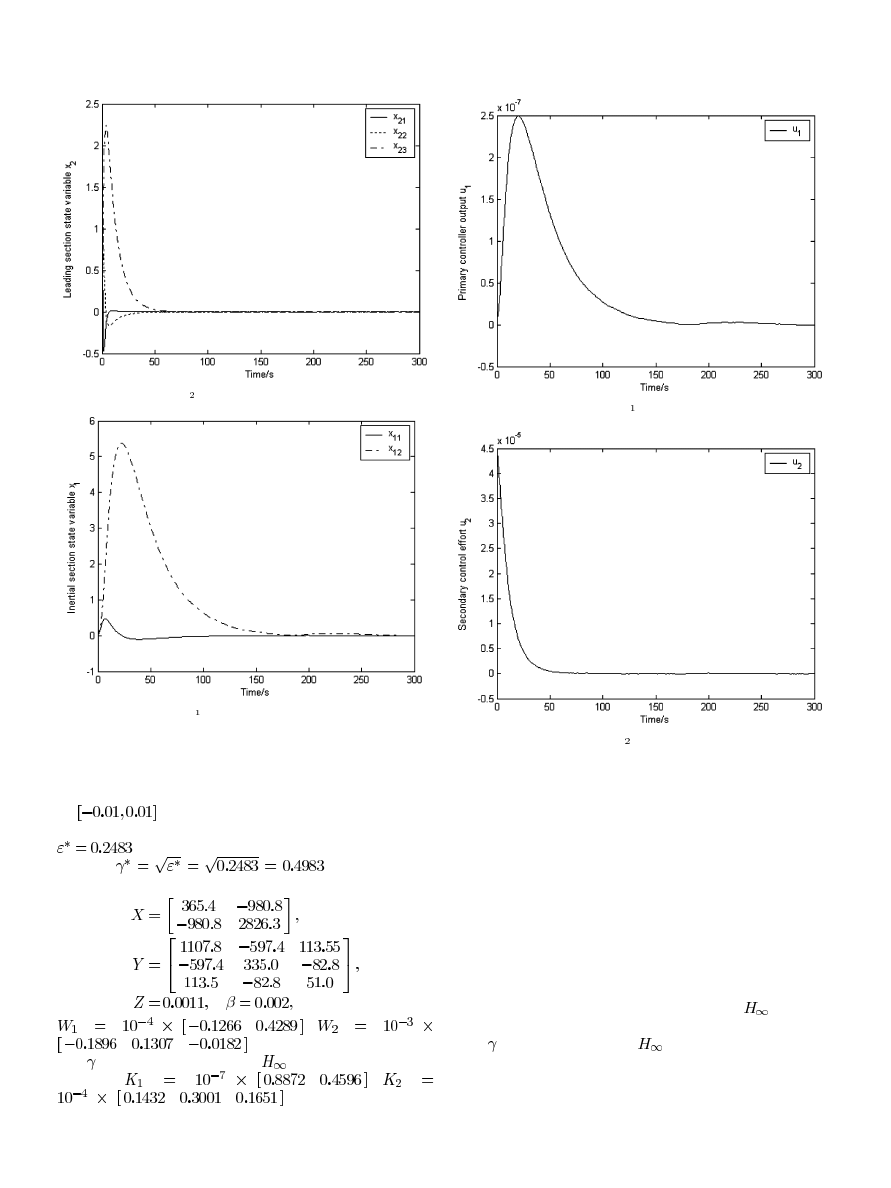
As can be seen clearly from the figures, the NCCS closed-

loop system without disturbances is asymptotically stable. The
inner loop is much faster than the outer loop. The states of the
leading section can reflect the response tendency in advance,
resulting in the convergence of the final inertial section output.
This effect can also be reflected by Figs. 7 and 8, where the
control effort in the attemperator offers a quick response, under
the set-point coming from the primary controller output.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

HUANG et al.: H-INFINITY STATE FEEDBACK CONTROL FOR A CLASS OF NETWORKED CASCADE CONTROL SYSTEMS WITH UNCERTAIN DELAY

71

Fig. 9. State response of

x in NCCS with disturbances.

Fig. 10. State response of

x in NCCS with disturbances.

B. State Feedback Stabilization Control Laws for NCCS With
Disturbances

It is assumed that the disturbance is randomly distributed

in

for the NCCS with disturbances, and by

solving the optimization problem(25), the optimal solution is

, and therefore the minimal disturbance attenuation

degree is

. The matrices are

computed as follows:

,

.

The

gain

matrices

of

the

-optimal state feedback

controllers are com-

puted as

,

. Under the same ini-

tial conditions as the previous case, the state responses of the
leading and inertial sections are given in Figs. 9 and 10.

Fig. 11. Primary controller output

u in NCCS with disturbances.

Fig. 12. Secondary control effort

u in NCCS with disturbances.

As can be seen clearly, the NCCS closed-loop system with

disturbances can still be asymptotically stable. The disturbance
imposed on the NCCS is effectively attenuated. The states of
the leading section converge to zeros within 50 s. Similar effect
with the former case can also be observed from Figs. 11 and 12,
showing the control effort in the attemperator and its set-point
under these disturbances.

VI. C

ONCLUSION

Based on Lyapunov stability theory and LMI approach, the

sufficient conditions for the asymptotically stability of a class of
NCCSs with and without disturbances are derived, taking into
account the uncertain delay. The state feedback

stabiliza-

tion control laws for the NCCSs without disturbances, as well
as the -optimal state feedback

control laws for the NCCSs

with disturbances are designed, respectively. By solving feasi-
bility and optimization problems of LMIs, the two controllers
can be obtained simultaneously at one time without any trou-
blesome tuning procedures. Simulation examples are given to
show the effectiveness of the proposed approaches. However,

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.

72

IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, VOL. 6, NO. 1, FEBRUARY 2010

the states of the plants are not always available, and the output
feedback control is often used in practical engineering. How
to design output feedback control laws such that the NCCS is
asymptotically stable and has a prescribed

performance, is

the future research direction.

A

CKNOWLEDGMENT

The authors are extremely grateful to the anonymous re-

viewers and the editors of this journal for their valuable
suggestions in improving the quality of the paper.

R

EFERENCES

[1] R. G. Franks and C. W. Worley, “Quantitive analysis of cascade con-

trol,” Ind. Eng. Chem., vol. 48, no. 6, pp. 1074–1079, 1956.

[2] M. Xu, S.-Y. Li, and W.-J. Cai, “Cascade generalized predictive control

strategy for boiler drum level,” ISA Transactions, vol. 44, no. 3, pp.
399–411, Jul. 2005.

[3] T. M. Teo, S. Lakshminarayanan, and G. P. Rangaiah, “Performance

assessment of cascade control systems,” J. Inst. Eng., vol. 45, no. 6, pp.
27–38, 2005.

[4] W. Zhang, M. S. Branicky, and S. M. Phillips, “Stability of networked

control system,” IEEE Control Syst. Mag., vol. 21, no. 1, pp. 84–99,
Feb. 2001.

[5] T. C. Yang, “Networked control system: A brief survey,” IEE Proc.

Control Theory Appl.

, vol. 153, no. 4, pp. 403–412, Jul. 2006.

[6] J. P. Hespanha, P. Naghshtabrizi, and Y.-G. Xu, “A survey of recent

results in networked control systems,” Proc. IEEE, vol. 95, no. 1, pp.
138–162, Jan. 2007.

[7] L. G. Bushnell, “Networks and control,” IEEE Control Syst. Mag., vol.

21, no. 1, pp. 21–22, Feb. 2001.

[8] P. Antsaklis and J. Baillieul, “Guest editorial special issue on net-

worked control systems,” IEEE Trans. Autom. Control, vol. 49, no. 9,
pp. 1421–1423, Sep. 2004.

[9] P. Antsaklis and J. Bailliful, “Special issue on technology of networked

control systems,” Proc. IEEE, vol. 95, no. 1, pp. 5–8, Jan. 2007.

[10] T. J. Koo and S. Sastry, “Special issue on networked embedded hybrid

control systems,” Asian J. Control, vol. 10, no. 1, pp. 1–2, Jan. 2008.

[11] N. H. El-Farra and P. Mhaskar, “Special issue on control of networked

and complex process systems,” Comput. Chem. Eng., vol. 32, no. 9, pp.
1963–1963, Sep. 2008.

[12] Y. Bai and C.-Z. Huang, “Analysis and modeling of a class of net-

worked cascade control systems,” (in Chinese) Inf. Control, vol. 36,
no. 3, pp. 273–277, Jun. 2007.

[13] C.-Z. Huang, Y. Bai, and X.-L. Li, “Fundamental issues in networked

cascade control systems,” in Proc. IEEE Int. Conf. Autom. Logistics,
Qingdao, China, Sep. 2008, pp. 3014–3018.

[14] T. J. Harris, C. T. Seppala, and L. D. Desborough, “A review of perfor-

mance monitoring and assessment techniques for univariate and mul-
tivariate control systems,” J. Process Control, vol. 9, no. 1, pp. 1–17,
Feb. 1999.

[15] J. Yu and S.-J. Qin, “Statistical MIMO controller performance moni-

toring. Part I: Data-driven covariance benchmark,” J. Process Control,
vol. 18, no. 3-4, pp. 277–296, Mar. 2008.

[16] X. Li and C. E. de Souza, “Delay-dependent robust stability and sta-

bilization of uncertain linear delay systems: A linear matrix inequality
approach,” IEEE Trans. Autom. Control, vol. 42, no. 8, pp. 1144–1148,
Aug. 1997.

[17] P. Seiler and R. Sengupta, “An

H approach to networked control,”

IEEE Trans. Autom. Control

, vol. 50, no. 3, pp. 356–364, Mar. 2005.

[18] H. Zhao, M. Wu, G.-P. Liu, and J.-H. She, “H-infinity control for net-

worked control systems (NCS) with time-varying delays,” J. Control
Theory Appl.

, vol. 3, no. 2, pp. 157–162, 2005.

[19] H. Ishii, “

H

control with limited communication and message

losses,” Syst. Control Lett., vol. 57, no. 4, pp. 322–331, Apr. 2008.

[20] Y.-L. Wang and G.-H. Yang, “

H controller design for networked

control systems via active-varying sampling period method,” Acta Au-
tomatica Sinica

, vol. 34, no. 7, pp. 814–818, Jul. 2008.

[21] C. Peng and Y.-C. Tian, “Networked

H control of linear systems

with state quantization,” Inf. Sci., vol. 177, no. 24, pp. 5763–5774, Dec.
2007.

[22] D. Yue, Q.-L. Han, and C. Peng, “State feedback controller design of

the networked control systems,” IEEE Trans. Circuits Syst.-II:Express
Briefs

, vol. 51, no. 11, pp. 640–644, Nov. 2004.

[23] D. Yue, Q.-L. Han, and J. Lam, “Network-based robust

H control of

systems with uncertainty,” Automatica, vol. 41, no. 6, pp. 999–1007,
Jun. 2005.

[24] X.-F. Jiang, Q.-L. Han, S.-R. Liu, and A.-K. Xue, “A new

H stabi-

lization criterion for networked control systems,” IEEE Trans. Autom.
Control

, vol. 53, no. 4, pp. 1025–1032, May 2008.

[25] B. Tang, G.-P. Liu, and W.-H. Gui, “Improvement of state feedback

controller design for networked control systems,” IEEE Trans. Circuits
Syst.-II: Express Briefs

, vol. 55, no. 5, pp. 464–468, May 2008.

[26] H.-G. Zhang, J. Yang, and C.-Y. Su, “T-S fuzzy-model-based robust

H design for networked control systems with uncertainties,” IEEE
Trans. Ind. Inf.

, vol. 3, no. 4, pp. 289–301, Nov. 2007.

[27] M. S. Mahmoud, “Robust

H control of discrete systems with uncer-

tain parameters and unknown delays,” Automatica, vol. 36, no. 4, pp.
627–635, Apr. 2000.

[28] G.-M. Xie and L. Wang, “Stabilization of networked control systems

with time-varying network-induced delay,” in Proc. 43rd IEEE Conf.
Decision Control

, Atlantis, Paradise Island, Bahamas, Dec. 2004, pp.

3551–3556.

Congzhi Huang

was born in 1982. He received the

B.E. degree in automation from the Department of
Automation, North China Electric Power University,
Beijing, China, in 2005, and the M.S. degree in pat-
tern recognition and intelligent systems. He is cur-
rently working towards the Ph.D. degree in control
theory and control engineering at the Department of
Automation, North China Electric Power University.

His main research interests include networked cas-

cade control system, control theory and applications.

Yan Bai

was born in 1954. He received the B.E. de-

gree in chemical automation and meters from Dalian
Institute of Technology (now Dalian University
of Technology), Dalian, Liaoning, China, in 1982
and the Ph.D. degree in control theory and control
engineering from Northeast University, Shenyang,
Liaoning, China, in 1998.

Currently, he is a Professor in the Department of

Automation, North China Electric Power University.
He had been a Visiting Scholar at Kyoto University,
Japan, from 1992 to 1993. His main research inter-

ests include distributed control systems, wireless sensor networks and intelli-
gent control of complex systems. He has been devoted in the research of dis-
tributed control systems and fieldbus control systems for over 20 years. He has
been an author or coauthor of more than 100 scientific papers as well as seven
monographs.

Prof. Bai is a Director of the Fieldbus Specialized Commission, China In-

strument Manufactures Association, a member of Editorial Board of Chinese
Chemical Automation and Instrument, and specially invited as a reviewer of the
Proceedings of the Chinese Society for Electric Engineering

.

Xiangjie Liu

was born in 1966. He received the

Ph.D. degree in electrical and electronic engineering
from the Research Center of Automation, North-
eastern University, Shenyang, Liaoning, China, in
1997.

He subsequently held a Postdoctoral position

with the China Electric Power Research Institute
(CEPRI), Beijing, China, until 1999. He has been an
Associate Professor at CEPRI since 1999. He was
a Research Associate with the University of Hong
Kong. He joined the National University of Mexico

in 2001, where he was a Professor with the Research Center of Applied Science
and Technology Development. He is now a Professor with the Department of
Automation, North China Electric Power University, Beijing, China. His current
research areas include fuzzy control, neural networks, adaptive and predictive
control, intelligent control theory and its application in industrial process.

Prof. Liu is a member of Technical Committee on Process Control of the

Chinese Association of Automation, a member of the Editorial Board of the
Chinese Journal of Control Engineering

and the Chinese Journal of Electric

Power Automation Equipment

.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:47:23 UTC from IEEE Xplore. Restrictions apply.