
c
O
J
The Boltzman Distribution (01:00 ............................................................................................................ 2
The Two Lagrangange Multiplier Conditions......................................................................................... 2
How many distinct configurations (10:00 ............................................................................................. 2
Approximation when N becomes large (24:00 ...................................................................................... 3
Maximize using Lagrange Multipliers (36:00......................................................................................... 3
Giving the Boltzmann distribution P(i)=e
-(1+ɲ)
e
-ɴEi
.................................................................................. 4
Set the Lagrange Multipliers (ɲ ɴ) to Satisfy Constraints ...................................................................... 4
Why is T = 1/ɴ ? Susskind note 2.3 ....................................................................................................... 4
(ɲ ) is The Partition Function
................................................................................... 5
(ɴ temperature) is a function of the average energy......................................................................... 5
Solving for the Lagrange Multipliers Susskind notes 2.1 ....................................................................... 5
The Two Basic Formulas (59:00 ................................................................................................................ 6
The Partition Function Z(ɴ)=ɇ e
-ɴEi
........................................................................................................ 6
Temperature ʹEnergy RelaƟonship E = эlog Z(ɴ)/эɴ .......................................................................... 6
Defintion of Helmholtz Free Energy ( A = -T log Z = -log Z / ɴ ) .................................................................. 6
Helmholtz Free Energy Susskind notes 2.2 ........................................................................................... 6
Relationship between Helmholtz Free Energy and Entropy .................................................................. 7
Entropy in terms of log Z (71:00 ........................................................................................................... 7
Brief Theory of Flucuations (72:00 ........................................................................................................... 8
Variance in Energy ............................................................................................................................... 8
The variance in energy is the 2
nd
derivative of logX wrt ɴ (84:00 ....................................................... 9
Fluctuations Susskind notes 3 .............................................................................................................. 9
Standard Definitions using Boltzman Constants (95:00 .......................................................................... 10

a
â
÷ ÷
a
a J
Ô
O
O
O
®
[
â
®
^
O
m
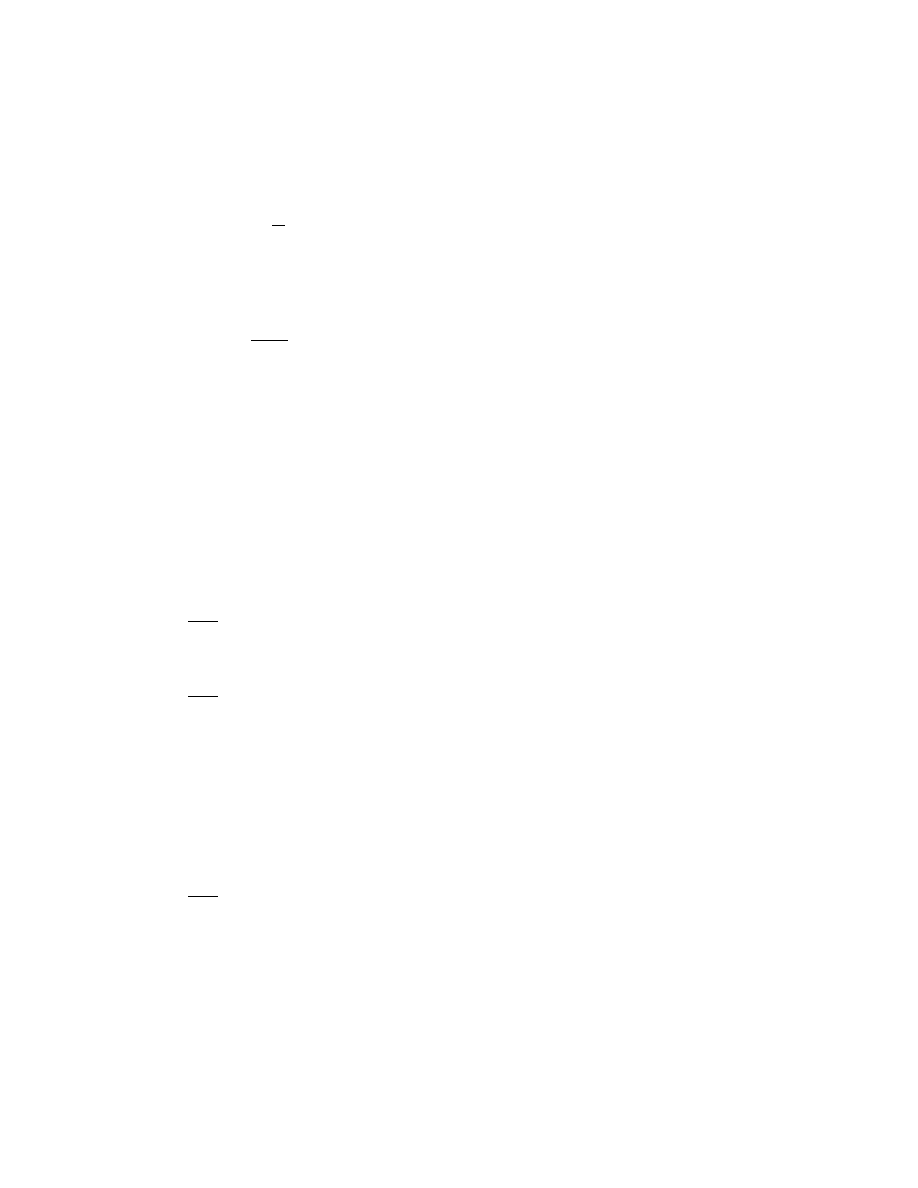
!
®
!
"
#
"
! O
O
O
O
"
#$#%&
O $
' ® m
O
' ®
0
%
(
)
%
*+, *+, -
%
*+,
./0 - - ® *+, -
./0 - - ® *+, 1 2
3
./0 - - ® *+, 1 4
#
&
*+,
./0 - ® *+,
#
#" " ÷"
./0 - ® *+,®®
%" "
./0 - ®® *+, ® - ®*+,
#
'
*+,
- ® *+, ®
^ ^
!
O
%^
^ #" "
#" O#
"

â
â ÷ Ô
(#" )(#
" )
*
- ®*+, ® - 5 ® - 6 ®
+
- ®® *+, ® - 5® - 6®
"
â $
, $
i
" "
Y
"
" " " "
" "
i O
i
-
"
"
" #$%
&'($
&)*
® (
)®
(
)7"
!
Ô
(
®
8
O&
®
9
:;<!
8
8
(
)7"
!
c
()$ cJ
$ *$
.
+ a%,)-c. /
O[
&
O
Ô
/

û
-û
7
*+, =>
O
û
?û 1 û? -
@® 8
7
- *+, = û?
0O 0
û
?û
O
&
%
($a # 0
!#"
® m
8
(
)7"
!
8
(
)7"
!
1
O
(
)7"
!
= A®
(
)®
"! &$
"!
%
)$ "
!#"
8
(
)7"
!
2
B
B7
(
)7"
!
- (
)7"
!
C (
)7"
!
-
"
!
B
B7
(
)7"
!
-
8
B
B7
(
)7"
!
-
8
B
B7
(
)7"
!
3
(
)7"
!
-
8®7
B8®7
B7
4 "
!
1
&
-
B 8®7
B7
c
" c. /
O% Ô

%
= (
)7"
!
O*
®
8
(
)7"
!
Ô
(
)7"
!
-
7
(
)7"
!
-
8
7
= -
B 8
B7
O+
Ô
OOO
!
%
a
a 0 12
a
# 0 3)$%4
&)*
O
A® (
)7"
!
"!
a
5*6 *A%7 3)$,7)
&
-
B 8®7
B7
2
O
0*0%&a 3%& 3,)$
'
õ
-
8
7
-? *+, =
O
O
0*c. /
OOO !
0
-D *+,
-
8
(
)7"
!
®
6 1 *+, = 6 1 *+, =
0 O $

-6® - õ
õ
- ?
O
O
ûõ
û - ?û - û?
0
ûõ
-û?
O
%
6 O
0**
'
õ
-
8
7
-? *+, =
O
&
-
B 8®7
B7
'
- ® *+, ®
'
"
®
9
:;<!
8
8
(
)7"
!
-
8
(
)7"
!
®-6 - *+, =
*
8
(
)7"
!
®6 1 *+, =
%* $
8
(
)7"
!
6 1 *+, =
8
(
)7"
!
4
8
(
)7"
!
6 6
O
" O
(
)7"
!
= A®
+
6 1 *+, =
'
6® - õ
O
? - õ
1
* 38
0 & '
'
õ
-
8
7
O
&
-
B 8®7
B7
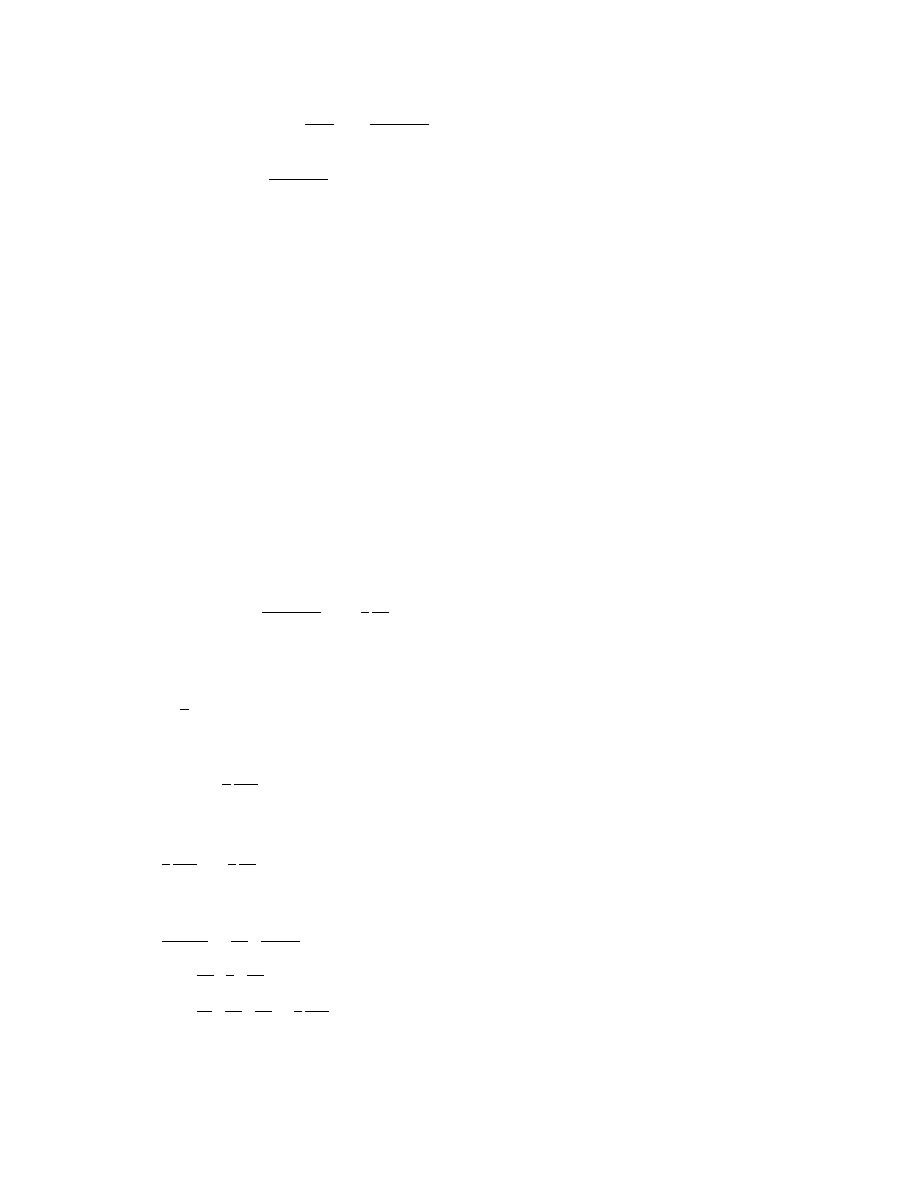
6® - õ 6
8
7
- 6
B 8®7
B7
O
*+, = - 6
B 8®7
B7
a 0 8
â 5 5
OO
#®®
-
E FGHI®
- ® 1
E
#®
- 1
E
#5 5
2
#
E #E #
O
#®®
-
E #®
-
E
O
#
E - #E
*
0& 5
O
#E -
B 8®7
B7
-
8
B8
B7
/
#5
O
E
®
8
(
)7"
!
"
O
O
O&
#
E
8
B
8
B7
/ O OO&
O'
8
B
8
B7
- J
8
B8
B7
K
B
8
B7
B
B7
J
B 8
B7
K
-
B
B7
J
8
B8
B7
K
-
8
B8
B7
B8
B7
1
8
B
8
B7

a
"
"" 9):
O'
#
E - #E
B
8
B7
" O
B 8
B7
-
O*
#
E - #E
®
-
B"
B7
06
O
®
-
B"
B7
-
"
@
@
7
?
"
@
[J ÷ J÷
O/
O*
®
-
B"
B7
-
"
@
@
7
?
"
@
L ?
O*
?ML
O$
, O*
0 c.
!
%
%
ââ
-
|
- ®NO
®
|
O - |O
O
|
O
!
|®
O
P
®
®â
Ô
$
|
O -
8
7
=
|
O -
8
7
=

®
|
O - |O
®
m
=
7
= - Q
m
=
7
=R
®
7
*+, = -
7
0
®
?
û
û
?
/J
®
?
LST(H(L
"
@
â
â r
®
U?
L
L
"
@
U m m
)
%â
7
O
%
c
J 21
0$
04
%
0%4
% .
Wyszukiwarka
Podobne podstrony:
38704322 SM04 Ideal Gas Point Particles Pressure Free Energy Calculations
Free Energy Projects 2
Free Energy & Technological Survival Homemade Wireless Antenna
Magnetic Energy Free Energy
Kto,blokuje tą wiedzę Antenna To Replace?tteries And Provide Unlimited Free Energy For Electric?rs
Free Energy Bedini Device And Method For Pulse Charging A Battery Patent Info 2004
Free energy circuits
free energy pl
Free Energy Projects 1
Final Secret of Free Energy Bearden
Bedini Radiant Battery Charger (Free Energy)
Nowoczesne technologie - energia za darmo, Free Energy Różne materiały
Zjawisko kawitacji, Free Energy, Dokumenty(1)
Jak napędzać samochód energią punktu zerowego, Free Energy
Darmowa energia- silniki, Free Energy
Free Energy Eolica (Muy Bueno)
Pasywne rezonatory pól torsyjnych, Free Energy
20 Years Bearden Bedini Free Energy Generation Solid State Battery Charger
Free Energy Projects 2
więcej podobnych podstron